Abstract
A two species stage-structured commensalism model is proposed and studied in this paper. Local and global stability property of the boundary equilibrium and the positive equilibrium are investigated, respectively. If the stage-structured species is extinct, then depending on the intensity of cooperation, the species may still be extinct or become persistent. If the stage-structured species is permanent, then the final system is always globally asymptotically stable, which means the species is always permanent. Our study shows that increasing the intensity of the cooperation between the species is one of very useful methods to avoid extinction of the endangered species. Such a finding may be useful in protecting the endangered species. An example together with its numeric simulations is presented to verify our main results.
Similar content being viewed by others
1 Introduction
The aim of this paper is to investigate the dynamic behaviors of the following stage-structured commensalism system:
with \(x_{1}(0)>0, x_{2}(0)>0\), and \(y(0)>0\), where α, β, \(\delta_{1}\), \(\delta_{2}\), d, \(b_{2}\), \(a_{2}\), and γ are all positive constants, \(x_{1}(t)\) and \(x_{2}(t)\) are the densities of the immature and mature first species at time t, y is the density of the second species at time t. For the simplicity of our model, we only consider the stage structure of immaturity and maturity of the first species and do not consider the stage structure of the second species. The following assumptions are made in formulating model (1.1):
-
1.
For the first species, the per capita birth rate of the immature population is \(\alpha > 0\); The per capita death rate of the immature population is \(\delta_{1}> 0\); The per capita death rate of the mature population is proportional to the current mature population with a proportionality constant \(\delta_{2} > 0\); \(\beta >0\) denotes the surviving rate of immaturity to reach maturity; The mature species is density-dependent with the parameter \(\gamma >0\).
-
2.
The second species is only beneficial to the mature first species, and their relationship is bilinear (\(dx_{2}y\)).
-
3.
The second species satisfies the logistic model, where \(b_{2}\) is the intrinsic growth rate of the second species, and \(\frac{a_{2}}{b_{2}}\) is the catching capacity of the second species.
During the last decade, many scholars investigated the dynamic behaviors of the mutualism model or commensalism model [1–25]. Han and Chen [15] proposed the following commensalism model with feedback controls:
They first showed that the subsystem, i.e., the two species commensalism model
admits a unique globally asymptotically stable positive equilibrium. After that, they further showed that system (1.2) admits a unique globally stable positive equilibrium, which means that feedback control variables have no influence on the stability property of system (1.2). Several scholars argued that discrete models are more suitable if the species have non-overlapping generations. Xie et al. [16] proposed the following discrete commensal symbiosis model:
They obtained a set of sufficient conditions which ensure the existence of the positive periodic solution of system (1.4). Xue et al. [17] further proposed a discrete commensalism model with delays, they investigated the almost periodic solution of the system. Li et al. [21] studied the positive periodic solution of a discrete commensalism model with Holling II functional response. Wu [13] argued that it may be more suitable to assume that the relationship between two species is of nonlinear type instead of linear one, and she established the following two species commensal symbiosis model:
where \(a_{i}, b_{i}, i=1,2\), p and \(c_{1}\) are all positive constants, \(p\geq 1\). The results of [13] were then generalized by Wu et al. [12] to the following commensalism model with Allee effect:
where \(a_{i}, b_{i}, i=1,2\), p, u, and \(c_{1}\) are all positive constants, \(p\geq 1\).
Recently, several scholars studied the influence of partial closure on the non-selective harvesting commensalism model. Deng and Huang [21] studied the dynamic behaviors of the following system:
where \(r_{1}\), \(r_{2}\), \(K_{1}\), \(K_{2}\), α are all positive constants. E is the combined fishing effort used to harvest, and m (\(0< m<1\)) is the fraction of the stock available for harvesting. They showed that depending on the fraction of the stock available for harvesting, the system may undergo extinction, partial survival, or two species may coexist in a stable state. The dynamic behaviors of the system become complicated compared with the non-harvesting system. Lin [10] further studied the dynamic behaviors of a commensal symbiosis model with non-monotonic functional response and non-selective harvesting in a partial closure.
On the other hand, many scholars investigated the dynamic behaviors of the stage-structured species, see [26–45], and the references cited therein. In constructing a stage-structured model, two different ideas were applied. Firstly, assume that the species needs time to grow up, and this leads to the delayed model. Aiello and Freedman [42] for the first time proposed the following stage-structured single species model:
They showed that system (1.8) admits a unique positive equilibrium which is globally asymptotically stable. Many scholars [26–39] used the idea of Aiello and Freedman to establish stage-structured ecological models. For example, Chen et al. [28] studied the persistence property of the following stage-structured predator–prey model:
They obtained a set of sufficient conditions which ensure the global asymptotic stability of the positive equilibrium. Chen et al. [34] proposed and studied the following May type stage-structured cooperation model:
They showed that with introduction of the stage structure, the May type cooperative system may admit partial survival property, that is, despite the cooperation between the species, the species may still be driven to extinction due to the stage structure. They finally drew the conclusion: the cooperation between the species has no influence on the persistence property of the system.
Another way to construct a stage-structured ecosystem is to assume that there is a proportional number of immature species that become mature species [40, 41, 43, 44]. Recently, Khajanchi and Banerjee [41] proposed the following stage-structured predator–prey model with ratio-dependent functional response:
The authors investigated the stability property of the positive equilibrium and boundary equilibrium. In system (1.11), without predator species, the system will reduce to the following single species stage-structured system:
Though system (1.12) seems very simple, in [43], we showed that if
holds, the equilibrium \(O(0,0)\) is globally asymptotically stable, which means extinction of the species. Therefore, the dynamic behaviors of system (1.12) are very different to the dynamic behaviors of system (1.8). It is in this sense that we need to do more work on a non-delay stage-structured ecosystem.
Recently, in [43], we proposed the following single species stage-structured system incorporating partial closure for the populations and non-selective harvesting:
where α, β, \(\delta_{1}\), \(\delta_{2}\), \(q_{1}\), \(q_{2}\), E, and γ are all positive constants, \(x_{1}(t)\) and \(x_{2}(t)\) are the densities of the immature and mature species at time t. Our study showed that the birth rate of the immature species and the fraction of the stocks for the harvesting play a crucial role in the dynamic behaviors of the system.
One could easily see that in system (1.1), without the cooperation of the second species, the first species is described by (1.12). Hence, one interesting issue is proposed:
Assume that without the cooperation of the second species, the first species in system ( 1.1 ) will be driven to extinction, i.e., assume inequality ( 1.13 ) holds. Is it possible for the species 1 to avoid the extinction due to the cooperation of the second species, or will the first species be driven to extinction despite the cooperation of the second species, just like the dynamic behaviors of system ( 1.10 )?
We will try to find the answer in the rest of the paper.
The paper is arranged as follows. We investigate the existence and local stability property of the equilibria of system (1.1) in Sect. 2. In Sect. 3, by constructing some suitable Lyapunov function, we are able to investigate the global stability property of the equilibria. Section 4 presents some numerical simulations to show the feasibility of the main results. We end this paper with a brief discussion.
2 Local stability of the equilibria
Before we study the local stability property of the equilibrium points of system (1.1), we would like to introduce the stability result of equilibrium of system (1.12). The following lemma is Theorems 4.1 and 4.2 of [43].
Lemma 2.1
Assume that
holds, then the boundary equilibrium \(O(0,0)\) of system (1.12) is globally stable. Assume that
holds, then the positive equilibrium \(B(x_{1}^{*},x_{2}^{*})\) of system (1.12) is globally stable, where
Lemma 2.2
\(R_{3}^{+}\) is the invariant set of system (1.1).
Proof
Note that from system (1.1), for all \(x_{1}\), \(x_{2}\), \(y>0\), one has
It immediately follows that \(R_{3}^{+}\) is the invariant set of system (1.1). □
Now we are in a position to investigate the local stability property of system (1.1).
The equilibria of system (1.1) are determined by the following system:
The system always admits two boundary equilibria: \(A_{1}(0,0,0)\), \(A_{2} (0,0, \frac{b_{2}}{a_{2}} )\). Also, if
then the system admits another boundary equilibrium \(A_{3} (x_{1} ^{*}, x_{2}^{*},0 )\), where
Assume that
then system (1.1) admits a unique positive equilibrium \(A_{4} (x _{1}^{**},x_{2}^{**}, y^{**} )\), where
Obviously, \(x_{1}^{**}\), \(x_{2}^{**}\), and \(y^{**}\) satisfy the equations
We shall now investigate the local stability property of the above equilibria.
The variational matrix of system (1.1) is
Theorem 2.1
\(A_{1}(0,0,0)\) is unstable.
Proof
From (2.9) we could see that the Jacobian matrix of the system about the equilibrium point \(A_{1}(0,0,0)\) is given by
The characteristic equation of the above matrix is
Hence, it has one positive characteristic root \(\lambda_{1}=b_{2}\); consequently, \(A_{1}(0,0,0)\) is unstable. This ends the proof of Theorem 2.1. □
Remark 2.1
Theorem 2.1 shows that it is impossible for the system to be driven to extinction, that is, the two species in system (1.1) could not be extinct at the same time.
Theorem 2.2
Assume that
then \(A_{2}(0,0,\frac{b_{2}}{a_{2}})\) is locally asymptotically stable. Assume that
then \(A_{2}(0,0,\frac{b_{2}}{a_{2}})\) is unstable.
Proof
From (2.9) we could see that the Jacobian matrix of the system about the equilibrium point \(A_{2}(0,0,\frac{b_{2}}{a_{2}})\) is given by
The characteristic equation of the above matrix is
Hence, it has one negative characteristic root \(\lambda_{1}=-b_{2}<0\), the other two characteristic roots are determined by the equation
Note that the two characteristic roots of Eq. (2.16) satisfy
Under assumption (2.13), \(\lambda_{2}\lambda_{3}<0\), hence at least one characteristic root is positive; consequently, \(A_{2}(0,0,\frac{b_{2}}{a _{2}})\) is unstable. Under assumption (2.12), it implies that \(\delta_{2}>\frac{db_{2}}{a_{2}}\), and so, from (2.17), one has \(\lambda_{2}+\lambda_{3}<0, \,\, \lambda_{2}\lambda_{3}>0\). Hence, \(\lambda_{2}<0, \lambda_{3}<0\). That is, under assumption (2.12), three characteristic roots of matrix (2.14) are all negative; consequently, \(A_{1}(0,0,\frac{b_{2}}{a_{2}})\) is locally asymptotically stable. This ends the proof of Theorem 2.2. □
Remark 2.2
Assume that (2.1) holds, then for the system without cooperation, it follows from Lemma 2.1 that the first species will be driven to extinction. If the cooperative coefficient d is small enough, then inequality (2.12) holds. It follows from the first part of Theorem 2.2 that in this case the first species will still be driven to extinction despite the cooperation of the second species.
Theorem 2.3
\(A_{3}(x_{1}^{*},x_{2}^{*}, 0)\) is unstable.
Proof
From (2.9) we could see that the Jacobian matrix of the system about the equilibrium point \(A_{3}(x_{1}^{*},x_{2}^{*}, 0)\) is given by
The characteristic equation of the above matrix is
Hence, it has one positive characteristic root \(\lambda_{1}=b_{2}\); consequently, \(A_{3}(x_{1}^{*},x_{2}^{*},0)\) is unstable. This ends the proof of Theorem 2.3. □
Remark 2.3
Theorem 2.3 shows that it is impossible for the second species to be driven to extinction while the first species is asymptotically stable.
Theorem 2.4
Assume that (2.6) holds, then \(A_{4}(x_{1}^{**},x _{2}^{**},y^{**})\) is locally asymptotically stable.
Proof
From (2.9) we could see that the Jacobian matrix of the system about the equilibrium point \(A_{4}(x_{1}^{**},x_{2}^{**}, y ^{**})\) is given by
Noting that
also, from the second equation of (2.6), we have
The characteristic equation of the above matrix is
where
Hence, it has one negative characteristic root \(\lambda_{1}=-b_{2}<0\), the other two characteristic roots are determined by the equation
Note that from the expression of \(x_{2}^{**}\) and condition (2.6), the two characteristic roots of Eq. (2.22) satisfy
Hence, \(\lambda_{2}<0, \lambda_{3}<0\), therefore, all of the three characteristic roots are negative. Consequently, \(A_{4}(x_{1}^{**},x _{2}^{**},y^{**})\) is locally asymptotically stable. This ends the proof of Theorem 2.4. □
Remark 2.4
Condition (2.6) is necessary to ensure the existence of the positive equilibrium. Theorem 2.4 shows that if the positive equilibrium exists, it is locally asymptotically stable.
3 Global stability
We showed in Sect. 2 that \(A_{1}(0,0,0)\) and \(A_{3}(x_{1}^{*}, x _{2}^{*}, 0)\) are unstable, while under assumption (2.12), \(A_{2}(0,0,\frac{b _{2}}{a_{2}})\) is locally asymptotically stable; and if the positive equilibrium exists, it is locally asymptotically stable. One interesting issue is to investigate the global stability property of the equilibria. In this section we will try to obtain some sufficient conditions which could ensure the global asymptotic stability of the equilibria \(A_{2}\) and \(A_{4}\) of system (1.1).
Theorem 3.1
Assume that
then \(A_{2}(0,0,\frac{b_{2}}{a_{2}})\) is globally asymptotically stable.
Proof
We will prove Theorem 3.1 by constructing some suitable Lyapunov function. Let us define a Lyapunov function
where
One could easily see that the function \(V_{1}\) is zero at the boundary equilibrium \(A_{2}(0,0,\frac{b_{2}}{a_{2}})\) and is positive for all other positive values of \(x_{1}\) and \(x_{2}\). The time derivative of \(V_{1}\) along the trajectories of (1.1) is
It then follows from (3.1) and (3.4) that \(D^{+}V_{1}(t)<0\) strictly for all \(x_{1}, x_{2}, y>0\) except the boundary equilibrium \(A_{2}(0,0,\frac{b _{2}}{a_{2}})\), where \(D^{+}V_{1}(t)=0\). Thus, \(V_{1}(x_{1},x_{2},y)\) satisfies Lyapunov’s asymptotic stability theorem, and the boundary equilibrium \(A_{2}(0,0,\frac{b_{2}}{a_{2}})\) of system (1.1) is globally asymptotically stable.
This completes the proof of Theorem 3.1. □
Remark 3.1
Under the assumption \(\alpha \beta <\delta_{2}( \beta +\delta_{1})\), it follows from Lemma 2.1 that the first species will be driven to extinction. Obviously, if \(\frac{db_{2}}{a_{2}}\) is small enough, then inequality (3.1) holds. Moreover, it follows from Theorem 3.1 that \(A_{2}(0,0,\frac{b_{2}}{a _{2}})\) is globally asymptotically stable, which means that the first species is still driven to extinction. That is, if the cooperation is limited, then, despite the cooperation between the two species, the species is still driven to extinction.
Theorem 3.2
Assume that
holds, then \(A_{4}(x_{1}^{**},x_{2}^{**},y^{**})\) is globally asymptotically stable.
Proof
We will prove Theorem 3.2 by constructing some suitable Lyapunov function. Let us define a Lyapunov function
where \(k_{1}\), \(k_{2}\), \(k_{3}\) are some positive constants to be determined later.
One could easily see that the function \(V_{2}\) is zero at the equilibrium \(A_{4}(x_{1}^{**},x_{2}^{**},y^{**})\) and is positive for all other positive values of \(x_{1}\), \(x_{2}\), and y. The time derivative of \(V_{2}\) along the trajectories of (1.1) is
Note that from the relationship of \(x_{1}^{**}\), \(x_{2}^{**}\), and \(y^{**}\) (see (2.8)) we have
Also, from (2.7) and (2.8), we have
from the third equation of (2.8), we have
Applying (3.8)–(3.10) to (3.7) leads to
Now let us choose \(k_{2}=1\), \(k_{1}=\frac{\beta x_{1*}}{x_{2*}\alpha }\), \(k_{3}=\frac{d^{2}}{4\gamma a_{2}}\), then
Hence, \(D^{+}V_{2}(t)<0\) strictly for all \(x_{1}, x_{2}, y>0\) except the positive equilibrium \(A_{4}(x_{1}^{**}, x_{2}^{**}, y^{**})\), where \(D^{+}V_{2}(t)=0\). Thus, \(V_{2}(x_{1},x_{2}, y)\) satisfies Lyapunov’s asymptotic stability theorem, and the positive equilibrium \(A_{4}(x _{1}^{**}, x_{2}^{**}, y^{**})\) of system (1.1) is globally asymptotically stable.
This completes the proof of Theorem 3.2. □
Remark 3.2
Condition (3.5) is necessary to ensure the existence of positive equilibrium. Theorem 3.2 shows that if the positive equilibrium exists, it is globally asymptotically stable. Hence, it is impossible for the system to have a bifurcation phenomenon.
Remark 3.3
Assume that \(\alpha \beta >\delta_{2}(\beta +\delta _{1}) \) holds, then inequality (3.5) always holds. From Lemma 2.1, we know that in this case system (1.12) admits a unique positive equilibrium. That is, if system (1.12) admits the unique positive equilibrium, then for the commensalism model, the system still admits the unique positive equilibrium which is globally asymptotically stable.
Remark 3.4
Assume that \(\alpha \beta <\delta_{2}(\beta +\delta _{1}) \) holds, then if \(\frac{db_{2}}{a_{2}}\) is large enough, inequality (3.5) still holds. From Lemma 2.1, we know that in this case the boundary equilibrium \(O(0,0)\) of system (1.12) is globally asymptotically stable, which means extinction of the species. Then, for the commensalism model, if the cooperative effect is large enough, then the system admits the unique positive equilibrium which is globally asymptotically stable, which means the species is permanent. Therefore, for the endangered species, the intensity of cooperation between the species plays the essential role in the persistence property of the species.
Remark 3.5
Theorems 3.1 and 3.2 depict a very intuitive biological phenomenon. From Zhang et al. [45], we can regard \(\frac{\alpha }{\delta _{2}}\) as a relative birth rate of the first mature species, \(\frac{\beta }{\beta +\delta _{1}}\) as a relative transformation rate of the first immature species. Then conditions (3.1) and (3.5) are equivalent to
and
respectively. Hence, with the help of the second species, the relative birth rate of the first mature species is increasing, this finally increases the chance of the survival of the first species.
4 Numeric simulations
Now let us consider the following example.
Example 4.1
Let us consider the two species stage-structured commensalism model:
Here we choose \(\alpha =\beta =\delta_{1}=\delta_{2}=\gamma =a_{2}=b _{2}=1\). Hence
It follows from Lemma 2.1 that the boundary equilibrium \(O(0,0)\) of the following system is globally asymptotically stable.
That is, without the cooperation of the second species, the first species will be driven to extinction (Fig. 1 supports this assertion).
-
(1)
Now let us choose \(d=0.25\) in system (4.1), then
$$ (\beta +\delta_{1}) \biggl(\delta_{2}-\frac{db_{2}}{a_{2}} \biggr)-\alpha \beta =0.5>0, $$(4.3)and it follows from Theorem 3.1 that \(A_{2}(0,0,1)\) is globally asymptotically stable. Figure 2–Fig. 4 support this assertion.
-
(2)
Now let us choose \(d=2\) in system (4.1), then
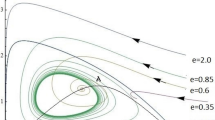
$$ -\alpha \beta -(\beta +\delta_{1}) \biggl(\delta_{2}- \frac{db_{2}}{a_{2}} \biggr)=3>0, $$(4.4)and it follows from Theorem 3.2 that \(A_{4}(\frac{3}{4},\frac{3}{2},1)\) is globally asymptotically stable. Figure 5–Fig. 7 support this assertion.
Dynamic behaviors of system (4.2), the initial conditions \((x_{1}(0), x_{2}(0) )=(0.5,2)\), \((1,2) \), and \((1,0.5)\), respectively
Dynamic behaviors of the first component \(x_{1}(t)\) of system (4.1), here we take \(d=1/4\) and the initial conditions \((x_{1}(0), x_{2}(0),y(0))=(0.5,0.5, 0.5)\), \((0.1, 0.1, 0.1)\), \((1, 1, 1)\), and \((0.3, 0.3, 0.3)\), respectively
ynamic behaviors of the second component \(x_{2}(t)\) of system (4.1), here we take \(d=1/4\) and the initial conditions \((x_{1}(0), x_{2}(0),y(0))=(0.5,0.5, 0.5)\), \((0.1, 0.1, 0.1)\), \((1, 1, 1)\), and \((0.3, 0.3, 0.3)\), respectively
Dynamic behaviors of the third component \(y(t)\) of system (4.1), here we take \(d=1/4\) and the initial conditions \((x_{1}(0), x_{2}(0),y(0))=(0.5,0.5, 0.5)\), \((0.1, 0.1, 0.1)\), \((1, 1, 1)\), and \((0.3, 0.3, 0.3)\), respectively
Dynamic behaviors of the first component \(x_{1}(t)\) of system (4.1), here we take \(d=2\) and the initial conditions \((x_{1}(0), x_{2}(0),y(0))=(0.5,0.5, 0.5)\), \((0.1, 0.1, 0.1), (1, 1, 1)\), and \((2, 2, 2)\), respectively
Dynamic behaviors of the second component \(x_{2}(t)\) of system (4.1), here we take \(d=2\) and the initial conditions \((x_{1}(0), x_{2}(0),y(0))=(0.5,0.5, 0.5)\), \((0.1, 0.1, 0.1)\), \((1, 1, 1)\), and \((2, 2, 2)\), respectively
Dynamic behaviors of the third component \(y(t)\) of system (4.1), here we take \(d=2\) and the initial conditions \((x_{1}(0), x_{2}(0),y(0))=(0.5,0.5, 0.5)\), \((0.1, 0.1, 0.1)\), \((1, 1, 1)\), and \((2, 2, 2)\), respectively
5 Conclusion
Recently, many scholars investigated the dynamic behaviors of the mutualism and commensalism model [1–21]. The traditional Lotka–Volterra commensalism model was studied by many scholars, and in [15], by constructing some suitable Lyapunov function, Han and Chen showed that system (1.2) admits the unique positive equilibrium. However, to this day, still no scholar has proposed and studied the dynamic behaviors of the stage-structured commensalism model. This motivated us to propose system (1.1), which is the most simple commensalism system with stage structure.
In system (1.1), without the cooperation of the second species, depending on the relationship of the coefficients, the species may be driven to extinction or become persistent in the long run. Such dynamic behaviors are different to those of the stage-structured system (1.8), which was introduced by Aeillo and Freedman. We argue that such kind of property (the species could be driven to extinction) is one of the new characters due to the introduction of the stage structure.
For the extinction case, we show that depending on the intensity of cooperation, the species may still be driven to extinction or become persistent. Therefore, the cooperation between the two species is one of the essential factors that lead to the persistence of species. Such a property is quite different to that of the stage-structured cooperative system (1.10), which was proposed by Chen et al. [34]. They showed that the cooperation between species has no influence on the persistence property of the system.
To sum up, to increase the intensity of cooperation between the species is one of the essential methods to avoid the extinction of the endangered species.
References
Yang, K., Miao, Z.S., et al.: Influence of single feedback control variable on an autonomous Holling-II type cooperative system. J. Math. Anal. Appl. 435(1), 874–888 (2016)
Chen, F., Xie, X., et al.: Extinction in two species nonautonomous nonlinear competitive system. Appl. Math. Comput. 274, 119–124 (2016)
Yang, K., Xie, X.D., et al.: Global stability of a discrete mutualism model. Abstr. Appl. Anal. 2014, Article ID 709124 (2014)
Chen, L.J., Xie, X.D.: Feedback control variables have no influence on the permanence of a discrete N-species cooperation system. Discrete Dyn. Nat. Soc. 2009, Article ID 306425 (2009)
Chen, F.D.: Permanence for the discrete mutualism model with time delays. Math. Comput. Model. 47(3–4), 431–435 (2008)
Chen, F.D., Yang, J.H., et al.: On a mutualism model with feedback controls. Appl. Math. Comput. 214, 581–587 (2009)
Chen, L.J., Chen, L.J., et al.: Permanence of a delayed discrete mutualism model with feedback controls. Math. Comput. Model. 50, 1083–1089 (2009)
Xie, X.D., Chen, F.D., et al.: Note on the stability property of a cooperative system incorporating harvesting. Discrete Dyn. Nat. Soc. 2014, Article ID 327823 (2014)
Xie, X.D., Chen, F.D., et al.: Global attractivity of an integrodifferential model of mutualism. Abstr. Appl. Anal. 2014, Article ID 928726 (2014)
Lin, Q.F.: Dynamic behaviors of a commensal symbiosis model with non-monotonic functional response and non-selective harvesting in a partial closure. Commun. Math. Biol. Neurosci. 2018, Article ID 4 (2018)
Han, R., Chen, F., et al.: Global stability of May cooperative system with feedback controls. Adv. Differ. Equ. 2015, Article ID 360 (2015)
Wu, R.X., Li, L., et al.: A Holling type commensal symbiosis model involving Allee effect. Commun. Math. Biol. Neurosci. 2018, Article ID 6 (2018)
Wu, R.X., Li, L., et al.: A commensal symbiosis model with Holling type functional response. Int. J. Math. Comput. Sci. 16, 364–371 (2016)
Yang, L., Xie, X., et al.: Permanence of the periodic predator–prey-mutualist system. Adv. Differ. Equ. 2015, Article ID 331 (2015)
Han, R.Y., Chen, F.D.: Global stability of a commensal symbiosis model with feedback controls. Commun. Math. Biol. Neurosci. 2015, Article ID 15 (2015)
Xie, X.D., Miao, Z.S., Xue, Y.: Positive periodic solution of a discrete Lotka–Volterra commensal symbiosis model. Commun. Math. Biol. Neurosci. 2015, Article ID 2 (2015)
Xue, Y.L., Xie, X.D., et al.: Almost periodic solution of a discrete commensalism system. Discrete Dyn. Nat. Soc. 2015, Article ID 295483 (2015)
Chen, J.H., Wu, R.X.: A commensal symbiosis model with non-monotonic functional response. Commun. Math. Biol. Neurosci. 2017, Article ID 5 (2017)
Deng, H., Huang, X.Y.: The influence of partial closure for the populations to a harvesting Lotka–Volterra commensalism model. Commun. Math. Biol. Neurosci. 2018, Article ID 10 (2018)
Zhao, L., Bin, Q., et al.: Permanence and global stability of a May cooperative system with strong and weak cooperative partners. Adv. Differ. Equ. 2018, Article ID 172 (2018)
Li, T.T., Lin, Q.X., et al.: Positive periodic solution of a discrete commensal symbiosis model with Holling II functional response. Commun. Math. Biol. Neurosci. 2016, Article ID 22 (2016)
Wu, R.: Dynamic behaviors of a nonlinear amensalism model. Adv. Differ. Equ. 2018, Article ID 187 (2018)
Chen, B.: Dynamic behaviors of a commensal symbiosis model involving Allee effect and one party can not survive independently. Adv. Differ. Equ. 2018, Article ID 212 (2018)
Lin, Q.: Allee effect increasing the final density of the species subject to the Allee effect in a Lotka–Volterra commensal symbiosis model. Adv. Differ. Equ. 2018, Article ID 196 (2018)
Lin, Q.: Stability analysis of a single species logistic model with Allee effect and feedback control. Adv. Differ. Equ. 2018, Article ID 190 (2018)
Chen, F.D., Chen, W.L., et al.: Permanence of a stage-structured predator–prey system. Appl. Math. Comput. 219(17), 8856–8862 (2013)
Chen, F.D., Xie, X.D., et al.: Partial survival and extinction of a delayed predator–prey model with stage structure. Appl. Math. Comput. 219(8), 4157–4162 (2012)
Chen, F.D., Wang, H.N., et al.: Global stability of a stage-structured predator–prey system. Appl. Math. Comput. 223, 45–53 (2013)
Lin, Q., Xie, X., et al.: Dynamical analysis of a logistic model with impulsive Holling type-II harvesting. Adv. Differ. Equ. 2018, 112 (2018)
Li, T.T., Chen, F.D., et al.: Stability of a mutualism model in plant–pollinator system with stage-structure and the Beddington–DeAngelis functional response. J. Nonlinear Funct. Anal. 2017, Article ID 50 (2017)
Li, Z., Chen, F.D.: Extinction in periodic competitive stage-structured Lotka–Volterra model with the effects of toxic substances. J. Comput. Appl. Math. 231, 143–153 (2009)
Li, Z., Han, M.A., Chen, F.: Global stability of stage-structured predator–prey model with modified Leslie–Gower and Holling-type II schemes. Int. J. Biomath. 5(6), Article ID 1250057 (2012). https://doi.org/10.1142/S179352451250057X
Li, Z., Han, M., et al.: Global stability of a predator–prey system with stage structure and mutual interference. Discrete Contin. Dyn. Syst., Ser. B 19(1), 173–187 (2014)
Chen, F.D., Xie, X.D., et al.: Dynamic behaviors of a stage-structured cooperation model. Commun. Math. Biol. Neurosci. 2015, Article ID 4 (2015)
Lin, X., Xie, X., et al.: Convergences of a stage-structured predator–prey model with modified Leslie–Gower and Holling-type II schemes. Adv. Differ. Equ. 2016, 181 (2016)
Chen, F.D., You, M.S.: Permanence, extinction and periodic solution of the predator–prey system with Beddington–DeAngelis functional response and stage structure for prey. Nonlinear Anal., Real World Appl. 9(2), 207–221 (2008)
Liu, Y., Xie, X., et al.: Permanence, partial survival, extinction, and global attractivity of a nonautonomous harvesting Lotka–Volterra commensalism model incorporating partial closure for the populations. Adv. Differ. Equ. 2018, Article ID 211 (2018)
Xue, Y.L., Xie, X.D., Lin, Q., Chen, F.: Global attractivity and extinction of a discrete competitive system with infinite delays and single feedback control. Discrete Dyn. Nat. Soc. 2018, Article ID 1893181 (2018). https://doi.org/10.1155/2018/1893181
Song, X., Cai, L., et al.: Ratio-dependent predator–prey system with stage structure for prey. Discrete Contin. Dyn. Syst., Ser. B 4(3), 747–758 (2012)
Wu, H.L., Chen, F.D.: Harvesting of a single-species system incorporating stage structure and toxicity. Discrete Dyn. Nat. Soc. 2009, Article ID 290123 (2009)
Khajanchi, S., Banerjee, S.: Role of constant prey refuge on stage structure predator–prey model with ratio dependent functional response. Appl. Math. Comput. 314, 193–198 (2017)
Aiello, W.G., Freedman, H.I.: A time-delay model of single-species growth with stage structure. Math. Biosci. 101(2), 139–144 (1990)
Xiao, A., Lei, C.Q.: Dynamic behaviors of a non-selective harvesting single species stage structure system incorporating partial closure for the populations. Adv. Differ. Equ. 2018, Article ID 245 (2018). https://doi.org/10.1186/s13662-018-1709-5
Lei, C.Q.: Dynamic behaviors of a stage structure amensalism system with a cover for the first species. Adv. Differ. Equ. 2018, Article ID 272 (2018). https://doi.org/10.1186/s13662-018-1729-1
Zhang, X., Chen, L., Neumann, A.U.: The stage-structured predator–prey model and optimal harvesting policy. Math. Biosci. 168(2), 201–210 (2000)
Acknowledgements
The author is grateful to two anonymous referees for their excellent suggestions, which have greatly improved the presentation of the paper.
Funding
This work is supported by the National Natural Science Foundation of China under Grant (11601085) and the Natural Science Foundation of Fujian Province (2017J01400).
Author information
Authors and Affiliations
Contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that there is no conflict of interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Lei, C. Dynamic behaviors of a stage-structured commensalism system. Adv Differ Equ 2018, 301 (2018). https://doi.org/10.1186/s13662-018-1761-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-018-1761-1