1 Introduction

As was pointed out by Berryman [1], the dynamic relationship between predator and prey has long been and will continue to be one of the dominant themes in both ecology and mathematical ecology due to its universal existence and importance. Already the predator-prey model has been studied by several scholars [2–10]. For example, Das et al. [8] investigated a three species ecosystem consisting of a prey, a predator, and a top predator. They derived the criteria for local and global stability of all the eight equilibrium points by using a Routh-Hurwitz and Lyapunov function. Wu and Li [9] studied the permanence and global attractivity of the discrete predator-prey system with Hassell-Varley-Holling type III functional response. Chen and Chen [10] proposed a ratio-dependent predator-prey model incorporating a prey refuge. They studied the global stability, limit cycle, and Hopf bifurcation of the system.

Mutualism is one of the most important relationships in the real world, for instance, ants prevent herbivores from feeding on plants (see [11]) and ants prevent predators from feeding on aphids (see [12, 13]). As was pointed out by Murray [14]: ‘this area has not been as widely studied as the others even though its importance is comparable to that of predator-prey and competition interactions.’ To this end, Rai and Krawcewicz [15] proposed the following three species predator-prey-mutualist system:

$$\begin{aligned}& \frac{dx}{dt}=\alpha x\biggl(1- \frac{x}{K} \biggr)- \frac{\beta xz}{1+my}, \\& \frac{dy}{dt}=\gamma y \biggl(1- \frac{y}{lx+L_{0}} \biggr), \\& \frac{dz}{dt}=z \biggl(-s+ \frac{c\beta x}{1+my} \biggr), \end{aligned}$$
(1.1)

where \(x(t)\), \(y(t)\), \(z(t)\) denote the densities of prey, mutualist and predator population at any time t, respectively. They applied the equivariant degree method to study the Hopf bifurcation phenomenon of the system.

In this paper, we will study the non-autonomous case of system (1.1), i.e.,

$$\begin{aligned}& \dot{x}=x \biggl(a_{1}(t)-b_{1}(t)x- \frac {c_{1}(t)z}{d_{1}(t)+d_{2}(t)y} \biggr), \\& \dot{y}=y \biggl(a_{2}(t)- \frac{y}{d_{3}(t)+d_{4}(t)x} \biggr), \\& \dot{z}=z \biggl(-a_{3}(t)+ \frac{c_{2}(t)x}{d_{1}(t)+d_{2}(t)y} \biggr), \end{aligned}$$
(1.2)

where x is the density of the prey at time t, y is the density of the mutualist and z is the density of the predator at time t, respectively. \(a_{i}(t)\) (\(i=1,2,3\)), \(d_{j}(t)\) (\(j=1,2,3,4\)), and \(c_{k}(t)\) (\(k=1,2\)) are all continuously positive w-periodic functions. The assumption of periodicity of the parameters is a way to incorporate the periodicity of the environment (e.g. seasonal effects of weather condition, food supplies, temperature, mating habits, harvesting, etc.). For this system, due to the lack of density restriction of the predator species, one could not investigate the stability property of the system by constructing the suitable Lyapunov function. Hence, to investigate the persistent property of the system has become one of the most important topics, and we try to push forward this topic.

We arrange the rest of the paper as follows: In Section 2, we introduce one lemma and state the main results of this paper. The results are proved in Section 3. In Section 4, a suitable example together with its numeric simulation is present to show the feasibility of the main results. We end this paper by a briefly conclusion. For more works on the non-autonomous predator-prey system, one could refer to [16–19] and the references cited therein.

2 Statement of the main results

Let us first consider the logistic equation,

$$ \frac{du(t)}{dt}=u(t) \bigl(\alpha(t)-\beta(t)u(t)\bigr), $$
(2.1)

where \(\alpha(t)\) and \(\beta(t)\) are periodic continuous functions on R with common periodic \(w>0\).

Lemma 2.1

[20]

If \(\beta(t)\geq0\) for all \(t\in R\) and \(\int_{0}^{w}\beta(t)\, dt>0\), then (2.1) has a unique nonnegative w-periodic solution \(u^{*}(t)\) which is globally asymptotically stable, that is, \(u(t)-u^{*}(t)\rightarrow0\) as \(t\rightarrow\infty\) for any positive solution \(u(t)\) of (2.1). Moreover, if \(\int_{0}^{w}\alpha(t)\, dt>0\), then \(u^{*}(t)>0\) for all \(t\in R\) and if \(\int_{0}^{w}\alpha(t)\, dt\leq0\) then \(u^{*}(t)\equiv0\).

Definition 2.2

System (1.2) is said to be permanent if there exist positive constants \(\eta_{i}\), \(M_{i}\), \(i=1, 2, 3\), such that

$$\begin{aligned}& \eta_{1}\leq\liminf_{t\to\infty}x(t)\leq\limsup _{t\to\infty}x(t)\leq M_{1}, \\& \eta_{2}\leq\liminf_{t\to\infty}y(t)\leq\limsup _{t\to\infty}y(t)\leq M_{2}, \\ & \eta_{3}\leq\liminf_{t\to\infty}z(t)\leq\limsup _{t\to\infty}z(t)\leq M_{3} \end{aligned}$$

for any positive solution \((x(t),y(t),z(t))\) of system (1.2).

We first consider the following system:

$$ \dot{u_{1}}=u_{1}\bigl(a_{1}(t)-b_{1}(t)u_{1} \bigr), $$
(2.2)

from Lemma 2.1, (2.2) has a unique nonnegative w-periodic solution \(u_{10}(t)\) which is globally asymptotically stable.

Second, we consider the following system:

$$ \dot{u_{2}}=u_{2} \biggl(a_{2}(t)- \frac{u_{2}}{d_{3}(t)+d_{4}(t)M^{*}} \biggr), $$
(2.3)

where \(M^{*}= \max_{0\leq t\leq w}\{u_{10}(t)+1\}\), from Lemma 2.1, (2.3) also has a unique nonnegative w-periodic solution \(u_{20}(t)\) which is globally asymptotically stable.

As concerns the persistent property of the system (1.2), we have the following result.

Theorem 2.3

System (1.2) is permanent if

$$ \int_{0}^{w} \biggl(-a_{3}(t)+ \frac {c_{2}(t)u_{10}(t)}{d_{1}(t)+d_{2}(t)u_{20}(t)} \biggr)\, dt>0 $$
(2.4)

holds, where \(u_{10}(t)\) and \(u_{20}(t)\) are the unique positive periodic solution of systems (2.2) and (2.3), respectively.

As a direct corollary of Theorem 2 in [21], from Theorem 2.3, we have the following.

Corollary 2.4

Under the assumption that (2.4) holds, system (1.2) admits of at least one positive w-periodic solution.

3 Proof of the main result

We need the following propositions to prove Theorem 2.3.

Proposition 3.1

There exist positive constants \(M_{1}\) and \(M_{2}\), such that

$$ \limsup_{t\to\infty}x(t)\leq M_{1},\qquad \limsup _{t\to\infty}y(t)\leq M_{2} $$
(3.1)

for all solutions of system (1.2).

Proof

Obviously, \(R_{+}^{3}=\{(x, y, z)|x\geq0, y\geq0, z\geq0\}\) is a positively invariant set of system (1.2). Given any solution \((x(t), y(t), z(t))\) of system (1.2), we have

$$ \dot{x}\leq x\bigl(a_{1}(t)-b_{1}(t)x\bigr). $$
(3.2)

By Lemma 2.1, the auxiliary equation

$$ \dot{u_{1}}= u_{1}\bigl(a_{1}(t)-b_{1}(t)u_{1} \bigr) $$
(3.3)

has a unique globally attractive positive w-periodic solution \(u_{10}(t)\). Let \(u_{1}(t)\) is the solution of (3.3) with \(u_{1}(0)=x(0)\), by the comparison theorem, we have

$$ x(t)\leq u_{1}(t),\quad t\geq0. $$
(3.4)

Moreover, from the global attractivity of \(u_{10}(t)\), for every given ε (\(0<\varepsilon<1\)), there exists a \(T_{1}>0\), such that

$$ \bigl\vert u_{1}(t)-u_{10}(t)\bigr\vert < \varepsilon, \quad t\geq T_{1}. $$
(3.5)

Equation (3.4) combined with (3.5) leads to

$$ x(t)< u_{10}(t)+\varepsilon,\quad t>T_{1}. $$
(3.6)

Let \(M_{1}= \max_{0\leq t\leq w}\{u_{10}(t)+\varepsilon\}\), we have

$$ \limsup_{t\to\infty}x(t)\leq M_{1}. $$
(3.7)

Since \(M^{*}= \max_{0\leq t\leq w}\{u_{10}(t)+1\}\), there exists a large enough \(T_{2}\geq T_{1}\) such that for all \(t>T_{2}\), one has

$$ x(t)< M^{*}. $$
(3.8)

From (3.8), we have

$$ \dot{y}\leq y \biggl(a_{2}(t)-\frac{y}{d_{3}(t)+d_{4}(t) M^{*}} \biggr), \quad t\geq T_{2}. $$
(3.9)

By Lemma 2.1, the auxiliary equation

$$ \dot{u_{2}}= u_{2} \biggl(a_{2}(t)- \frac{u_{2}}{d_{3}(t)+d_{4}(t)M^{*}} \biggr) $$
(3.10)

has a unique globally attractive positive w-periodic solution \(u_{20}(t)\). Similarly, we find that there is a constant \(T_{3}>T_{2}\) such that

$$ y(t)< u_{20}(t)+\varepsilon,\quad t>T_{3}. $$
(3.11)

Let \(M_{2}=\max_{0\leq t\leq w}\{u_{20}(t)+\varepsilon\}\), we have

$$ \limsup_{t\to\infty}y(t)\leq M_{2}. $$
(3.12)

This completes the proof of Proposition 3.1. □

Proposition 3.2

There is a universal constant \(\alpha>0\) such that

$$ \limsup_{t\to\infty}z(t)>\alpha. $$
(3.13)

Proof

If (2.4) holds, we can choose the constant \(\varepsilon_{1}>0\) such that

$$ \int_{0}^{w} \biggl(-a_{3}(t)+ \frac{c_{2}(t)(u_{10}(t)-\varepsilon _{1})}{d_{1}(t)+d_{2}(t)(u_{20}(t)+\varepsilon_{1})} \biggr)\, dt>0. $$
(3.14)

For any constant \(\alpha>0\), we consider the following equation:

$$ \frac{dv_{1}}{dt}=v_{1}(t) \biggl(a_{1}(t)- \frac{c_{1}(t)2\alpha }{d_{1}(t)}-b_{1}(t)v_{1}(t) \biggr). $$
(3.15)

Owing to \(\int_{0}^{w}a_{1}(t)\, dt>0\), \(\int_{0}^{w} (a_{1}(t)-\frac {c_{1}(t)2\alpha}{d_{1}(t)} )\, dt>0\) for small enough \(\alpha>0\). By Lemma 2.1, (3.15) has a unique positive w-periodic solution \(v_{1\alpha}^{*}(t)\) which is globally asymptotically stable. Let \(\bar{v}_{1\alpha}(t)\) be the solution of (3.15) with initial condition \(\bar{v}_{1\alpha}(0)=u_{10}(0)\), where \(u_{10}(t)\) is the unique positive periodic solution of (2.2). Hence, for above \(\varepsilon _{1}\), there exists a sufficiently large \(T_{4}>T_{3}\) such that

$$\bigl\vert \bar{v}_{1\alpha}(t)-v_{1\alpha}^{*}(t)\bigr\vert < \frac{\varepsilon_{1}}{4}\quad \mbox{for } t\geq T_{4}. $$

By the continuity of the solution in the parameter, we have \(\bar {v}_{1\alpha}(t)\rightarrow u_{10}(t)\) uniformly in \([T_{4}, T_{4}+w]\) as \(\alpha\rightarrow0\). Hence, for \(\varepsilon_{1}>0\), there exists a \(\alpha_{0}=\alpha_{0}(\varepsilon_{1})>0\) such that

$$\bigl\vert \bar{v}_{1\alpha}(t)-u_{10}(t)\bigr\vert < \frac{\varepsilon_{1}}{4}\quad \mbox{for } t\in[T_{4}, T_{4}+w], 0< \alpha< \alpha_{0}. $$

So, we have

$$\bigl\vert v_{1\alpha}^{*}(t)-u_{10}(t)\bigr\vert < \frac{\varepsilon_{1}}{2} \quad \mbox{for } t\in [T_{4}, T_{4}+w]. $$

Note that \(v_{1\alpha}^{*}(t)\) and \(u_{10}(t)\) are all w-periodic, hence

$$\bigl\vert v_{1\alpha}^{*}(t)-u_{10}(t)\bigr\vert < \frac{\varepsilon_{1}}{2} \quad \mbox{for } t\geq0, 0< \alpha< \alpha_{0}. $$

Choosing a constant \(\alpha_{1}\) (\(0<\alpha_{1}<\alpha_{0}\), \(2\alpha _{1}<\varepsilon_{1}\)), we have

$$ v_{1\alpha_{1}}^{*}(t)\geq u_{10}(t)-\frac{\varepsilon_{1}}{2}, \quad t\geq 0. $$
(3.16)

If \(\limsup_{t\to\infty}z(t)\leq\alpha_{1}\), then there exists \(\phi\in R_{+}^{3}\) such that

$$\limsup_{t\to\infty}z(t, \phi)< \alpha_{1}, $$

where \((x(t, \phi), y(t, \phi), z(t, \phi))\) is the solution of system (1.2) with \(\phi(0)=(\phi_{1}(0), \phi_{2}(0), \phi_{3}(0)) >0\). So, there exists \(T_{5}>T_{4}\) such that

$$ z(t)< 2\alpha_{1}< \varepsilon_{1},\quad t\geq T_{5}. $$
(3.17)

We have

$$ \dot{x}\geq x \biggl(a_{1}(t)-\frac{c_{1}(t)2\alpha _{1}}{d_{1}(t)}-b_{1}(t)x \biggr)\quad \mbox{for } t\geq T_{5}. $$
(3.18)

Let \(v_{1}(t)\) be the solution of (3.15) with \(\alpha=\alpha_{1}\) and \(v_{1}(T_{5})=x(T_{5})\), then

$$x(t)\geq v_{1}(t), \quad t\geq T_{5}. $$

By the global asymptotic stability of \(v_{1\alpha_{1}}^{*}(t)\), for the given \(\varepsilon=\frac{\varepsilon_{1}}{2}\), there exists \(T_{6}\geq T_{5}\), such that

$$\bigl\vert v_{1}(t)-v_{1\alpha_{1}}^{*}(t)\bigr\vert < \frac{\varepsilon_{1}}{2},\quad t\geq T_{6}. $$

So,

$$x(t)\geq v_{1}(t)>v_{1\alpha_{1}}^{*}(t)- \frac{\varepsilon_{1}}{2},\quad t\geq T_{6}, $$

and hence, by using (3.16), it follows that

$$ x(t) > u_{10}(t)-\varepsilon_{1},\quad t\geq T_{6}. $$
(3.19)

From (3.8), there exists \(T_{7}\geq T_{6}\) such that \(y(t)< u_{20}(t)+\varepsilon_{1}\). Therefore, by using (3.17) and (3.19), for \(t\geq T_{7}\) it follows that

$$\dot{z}\geq z(t) \biggl(-a_{3}(t)+\frac{c_{2}(t)(u_{10}(t)-\varepsilon _{1})}{d_{1}(t)+d_{2}(t)(u_{20}(t)+\varepsilon_{1})} \biggr). $$

Integrating the above inequality from \(T_{7}\) to t yields

$$z(t)\geq z( T_{7})\exp \int_{T_{7}}^{t} \biggl(-a_{3}(s)+\frac {c_{2}(s)(u_{10}(s)-\varepsilon _{1})}{d_{1}(s)+d_{2}(s)(u_{20}(s)+\varepsilon_{1})} \biggr)\, ds. $$

Thus, from (3.14) it follows that \(z(t)\rightarrow\infty\) as \(t\rightarrow\infty\). This is a contradiction. This completes the proof of Proposition 3.2. □

Proposition 3.3

There is a universal constant \(\eta_{2}>0\) such that

$$ \liminf_{t\to\infty}y(t)\geq\eta_{2}. $$
(3.20)

Proof

From the second equation of system (1.2) it follows that

$$ \dot{y}\geq y \biggl(a_{2}(t)-\frac{y}{d_{3}(t)} \biggr), $$
(3.21)

and we consider the following equation:

$$ \dot{u}_{3}=u_{3} \biggl(a_{2}(t)- \frac{u_{3}}{d_{3}(t)} \biggr). $$
(3.22)

By Lemma 2.1, (3.22) has a unique positive w-periodic solution \(u_{30}(t)\). Similar to the analysis of (3.4)-(3.7), for ε enough small, without loss of generality, \(\varepsilon< \min_{0\leq t\leq w}{u_{30}(t)}\), we find that there is a constant \(T_{8}>T_{7}\) such that

$$ y(t)\geq u_{30}(t)-\varepsilon>0,\quad t>T_{8}. $$
(3.23)

Letting \(\eta_{2}= \min_{0\leq t\leq w}\{u_{30}(t)-\varepsilon\}\), we have

$$ \liminf_{t\to\infty}y(t)\geq\eta_{2}. $$
(3.24)

This completes the proof of Proposition 3.3. □

Proposition 3.4

There is a universal constant \(\eta_{3}>0\) such that

$$ \liminf_{t\to\infty}z(t)\geq\eta_{3}. $$
(3.25)

Proof

Suppose that (3.25) is not true, then there is a sequence \(\{\phi_{m}\} \in R_{+}^{3}\), such that

$$ \liminf_{t\to\infty}z(t, \phi_{m} )< \frac{\alpha}{ m+1 },\quad m=1,2,\ldots. $$
(3.26)

On the other hand, by Proposition 3.2, we have

$$ \limsup_{t\to\infty}z(t, \phi_{m} )>\alpha,\quad m=1,2, \ldots. $$
(3.27)

Hence, there are time sequences \(\{s_{q}^{m}\}\) and \(\{t_{q}^{m}\}\) satisfying

$$\begin{aligned}& 0< s_{1}^{m}< t_{1}^{m} < s_{2}^{m}< t_{2}^{m} < \cdots < s_{q}^{m}< t_{q}^{m}< \cdots, \\& s_{q}^{m}\rightarrow+\infty,\qquad t_{q}^{m} \rightarrow+\infty \quad \mbox{as } q\rightarrow+\infty \end{aligned}$$

and

$$\begin{aligned}& z\bigl(s_{q}^{m}, \phi_{m}\bigr)=\alpha,\qquad z \bigl(t_{q}^{m}, \phi_{m}\bigr)=\frac{\alpha}{m+1}, \\& \frac{\alpha}{m+1}< z(t, \phi_{m})< \alpha,\quad t\in \bigl(s_{q}^{m}, t_{q}^{m}\bigr). \end{aligned}$$

From the third equation of system (1.2) it follows that

$$ \dot{z}\geq-a_{3}(t)z. $$
(3.28)

Obviously, by integrating (3.28) from \(s_{q}^{m}\) to \(t_{q}^{m}\),

$$z\bigl(t_{q}^{m}, \phi_{m}\bigr)\geq z \bigl(s_{q}^{m}, \phi_{m}\bigr)\exp\int _{s_{q}^{(m)}}^{t_{q}^{(m)}}\bigl(-a_{3}(t)\bigr)\, dt $$

or

$$\int_{s_{q}^{(m)}}^{t_{q}^{(m)}}\bigl(a_{3}(t)\bigr)\, dt \geq\ln(m+1) . $$

Thus, from the boundedness of \(a_{3}(t)\), we have

$$ t_{q}^{(m)}-s_{q}^{(m)}\rightarrow+\infty \quad \mbox{as } m\rightarrow +\infty. $$
(3.29)

By (3.14), there are constants \(P> 0\) and \(\gamma> 0\), such that, for any \(t\geq P\) and \(a\geq0\),

$$ \int_{a}^{a+t} \biggl(-a_{3}(s)+ \frac{c_{2}(s)(u_{10}(s)-\varepsilon _{1})}{d_{1}(s)+d_{2}(s)(u_{20}(s)+\varepsilon_{1})} \biggr)\, ds>\gamma . $$
(3.30)

For any m, q, and \(t\in[s_{q}^{(m)}, t_{q}^{(m)}]\), we have

$$ \dot{x}(t, \phi_{m})\geq x(t, \phi_{m}) \biggl(a_{1}(t)-\frac {c_{1}(t)\alpha}{d_{1}(t)}-b_{1}(t)x(t, \phi_{m}) \biggr). $$
(3.31)

Let \(v_{1}(t)\) be the solution of (3.15) with the initial condition \(v_{1}(s_{q}^{(m)})=\alpha\), then by (3.31), we have \(x(t, \phi _{m})\geq v_{1}(t)\) for all \(t\in[s_{q}^{(m)}, t_{q}^{(m)}]\). By the periodicity of (3.15), it follows that the periodic solution \(v_{1\alpha}^{*}(t)\) is globally uniformly asymptotically stable. Hence, from (3.16), we find that there is a constant \(T_{0}>P\), and \(T_{0}\) is independent on any q and m, such that

$$v_{1}(t)\geq u_{10}(t)-\varepsilon_{1}\quad \mbox{for all } t\geq T_{0}+s_{q}^{(m)}. $$

By (3.29), there is a \(N_{0}>0\) such that \(t_{q}^{(m)}> s_{q}^{(m)}+2T_{0}\) for all \(m\geq N_{0}\). Hence,

$$\begin{aligned}& x(t, \phi_{m}) u_{10}(t)-\varepsilon_{1}, \\& y(t, \phi _{m})< u_{20}(t)+\varepsilon_{1}\quad \mbox{for all } t\in \bigl[s_{q}^{(m)}+T_{0}, t_{q}^{(m)}\bigr], m\geq N_{0}. \end{aligned}$$

Since

$$\dot{z}(t, \phi_{m})\geq z(t, \phi_{m}) \biggl(-a_{3}(t)+\frac {c_{2}(t)(u_{10}(t)-\varepsilon _{1})}{d_{1}(t)+d_{2}(t)(u_{20}(t)+\varepsilon_{1})} \biggr) $$

for all \(t\in[s_{q}^{(m)}+T_{0}, t_{q}^{(m)}]\) and \(m\geq N_{0}\), by integrating from \(s_{q}^{(m)}+T_{0}\) to \(t_{q}^{(m)}\), we obtain

$$\begin{aligned} z\bigl(t_{q}^{(m)}, \phi_{m}\bigr) \geq& z \bigl(s_{q}^{(m)}+T_{0}, \phi_{m}\bigr) \\ &{}\times\exp\int_{s_{q}^{(m)}+T_{0}}^{t_{q}^{(m)}} \biggl(-a_{3}(t)+ \frac {c_{2}(t)(u_{10}(t)-\varepsilon _{1})}{d_{1}(t)+d_{2}(t)(u_{20}(t)+\varepsilon_{1})} \biggr)\, dt. \end{aligned}$$

By (3.30), we have

$$\begin{aligned} \frac{\alpha}{m+1} \geq& \frac{\alpha}{m+1}\exp\int_{s_{q}^{(m)}+T_{0}}^{t_{q}^{(m)}} \biggl(-a_{3}(t)+\frac {c_{2}(t)(u_{10}(t)-\varepsilon _{1})}{d_{1}(t)+d_{2}(t)(u_{20}(t)+\varepsilon_{1})} \biggr)\, dt \\ >& \frac{\alpha}{m+1}, \end{aligned}$$

which is a contradiction. This completes the proof of Proposition 3.4. □

Proposition 3.5

There is a universal constant \(M_{3}>0\) such that

$$ \limsup_{t\to\infty}z(t)\leq M_{3}. $$
(3.32)

Proof

Choose the constant \(M>0\) and small enough ε such that

$$ \int_{0}^{w} \biggl(a_{1}(t)- \frac {c_{1}(t)M}{d_{1}(t)+d_{2}(t)(M_{2}+\varepsilon)} \biggr)\, dt< 0. $$
(3.33)

We first prove that

$$ \liminf_{t\to\infty}z(t)\leq M. $$
(3.34)

If (3.34) is not true, then there is a \(T_{9}\geq T_{8}\) such that \(z(t)>M\) and \(y(t)\leq M_{2}+\varepsilon\) (ε is small enough) for all \(t\geq T_{9}\). Since

$$\dot{x}\leq x \biggl(a_{1}(t)-\frac {c_{1}(t)M}{d_{1}(t)+d_{2}(t)(M_{2}+\varepsilon)}-b_{1}(t)x \biggr) \quad \mbox{for all } t\geq T_{9}. $$

By Lemma 2.1 we easily obtain \(x(t)\rightarrow0\) as \(t\rightarrow \infty\). Choose a constant \(0<\varepsilon_{2}<\eta_{2} \) such that

$$ \int_{0}^{w} \biggl(-a_{3}(t)+ \frac{c_{2}(t)\varepsilon _{2}}{d_{1}(t)+d_{2}(t)(\eta_{2}-\varepsilon_{2})} \biggr)\, dt< 0. $$
(3.35)

Then there is a \(T_{10}>T_{9}>0\) such that \(x(t)\leq\varepsilon_{2}\) and \(y(t)>\eta_{2}-\varepsilon_{2}\) for all \(t\geq T_{10}\), and so

$$ \dot{z}\leq z \biggl(-a_{3}(t)+\frac{c_{2}(t)\varepsilon _{2}}{d_{1}(t)+d_{2}(t)(\eta_{2}-\varepsilon_{2})} \biggr). $$
(3.36)

Integrating the above inequality from \(T_{10}\) to t leads to

$$z(t)\leq z(T_{10})\exp\int_{T_{10}}^{t} \biggl(-a_{3}(s)+\frac {c_{2}(s)\varepsilon_{2}}{d_{1}(s)+d_{2}(s)(\eta_{2}-\varepsilon _{2})} \biggr)\, ds. $$

Hence, we have \(z(t)\rightarrow0\) as \(t\rightarrow\infty\) which is a contradiction. Now, if (3.32) is not true, then there is a sequence \(\{\phi_{m}\} \subset R_{+}^{3}\) such that \(\limsup_{t\to\infty}z(t, \phi_{m})> (2M+1)m \) for all \(m=1,2,\ldots\) . By (3.34), there are time sequences \(\{s_{q}^{m}\}\) and \(\{t_{q}^{m}\}\) satisfying

$$\begin{aligned}& 0< s_{1}^{m}< t_{1}^{m} < s_{2}^{m}< t_{2}^{m} < \cdots < s_{q}^{m}< t_{q}^{m}< \cdots, \\& s_{q}^{m}\rightarrow+\infty,\qquad t_{q}^{m} \rightarrow+\infty \quad \mbox{as } q\rightarrow+\infty \end{aligned}$$

and

$$\begin{aligned}& z\bigl(s_{q}^{m}, \phi_{m}\bigr)=2M,\qquad z \bigl(t_{q}^{m}, \phi_{m}\bigr)=(2M+1)m, \\& 2M< z(t, \phi_{m})< (2M+1)m\quad \mbox{for all } t\in \bigl(s_{q}^{m}, t_{q}^{m}\bigr). \end{aligned}$$

Since there is a \(T_{1}^{(m)}>0\) such that \(x(t, \phi_{m})< M_{1}\) for all \(t\geq T_{1}^{(m)}\), we have

$$\dot{z}(t, \phi_{m}) \leq z(t, \phi_{m}) \biggl(-a_{3}(t)+\frac {c_{2}(t)M_{1}}{d_{1}(t)} \biggr) \quad \mbox{for all } t\geq T_{1}^{(m)}. $$

Obviously, there is a \(K_{1}(m)>0\) such that \(s_{q}^{m}>T_{1}^{(m)}\) for all \(q\geq K_{1}(m)\). Hence, we obtain

$$z\bigl(t_{q}^{m}, \phi_{m}\bigr)\leq z \bigl(s_{q}^{m}, \phi_{m}\bigr)\exp\int _{s_{q}^{(m)}}^{t_{q}^{(m)}} \biggl(-a_{3}(t)+ \frac {c_{2}(t)M_{1}}{d_{1}(t)} \biggr)\, dt \quad \mbox{for all } q\geq K_{1}(m). $$

Consequently,

$$ t_{q}^{(m)}-s_{q}^{(m)}\rightarrow\infty \quad \mbox{as } m\rightarrow\infty , q\geq K_{1}(m). $$
(3.37)

By (3.35), there is a \(p_{1}>0\) such that for any \(t\geq p_{1}\) and \(a\geq0\),

$$\int_{a}^{a+t} \biggl(-a_{3}(s)+ \frac{c_{2}(s)\varepsilon _{2}}{d_{1}(s)+d_{2}(s)(\eta_{2}-\varepsilon_{2})} \biggr)\, ds< 0. $$

By (3.33), there is a \(p_{2}>0\) such that for all \(t\geq p_{2}\) and \(b\geq0\),

$$\int_{b}^{b+t} \biggl(a_{1}(s)- \frac {c_{1}(s)M}{d_{1}(s)+d_{2}(s)(M_{2}+\varepsilon)} \biggr)\, ds< \ln\frac {\varepsilon_{2}}{2M} . $$

By (3.37), there is a \(L>0\) such that \(t_{q}^{(m)}-s_{q}^{(m)}>p_{1}+p_{2}\) for all \(m\geq L\), \(q\geq K_{1}(m)\). For any \(m\geq L\), \(q \geq K_{1}(m)\) and \(t\in[s_{q}^{(m)}+p_{1}+p_{2}, t_{q}^{(m)}]\), we have

$$\begin{aligned} \dot{x}(t, \phi_{m}) \leq& x(t, \phi_{m}) \biggl(a_{1}(t)- \frac {c_{1}(t)2M}{d_{1}(t)+d_{2}(t)(M_{2}+\varepsilon)} \biggr) \\ \leq& x(t, \phi_{m}) \biggl(a_{1}(t)- \frac{c_{1}(t) M}{d_{1}(t)+d_{2}(t)(M_{2}+\varepsilon)} \biggr). \end{aligned}$$

Hence,

$$x(t, \phi_{m})\leq x\bigl(s_{q}^{(m)}, \phi_{m}\bigr)\exp\int_{s_{q}^{(m)}}^{t} \biggl(a_{1}(s)-\frac{c_{1}(s) M}{d_{1}(s)+d_{2}(s)(M_{2}+\varepsilon)} \biggr)\, ds< \varepsilon_{2}. $$

Since

$$\dot{z}(t, \phi_{m})\leq z(t, \phi_{m}) \biggl(-a_{3}(t)+\frac {c_{2}(t)\varepsilon_{2}}{d_{1}(t)+d_{2}(t)(\eta_{2}-\varepsilon _{2})} \biggr),\quad t\in\bigl[s_{q}^{(m)}+p_{1}+p_{2}, t_{q}^{(m)}\bigr]. $$

we obtain

$$\begin{aligned} z\bigl(t_{q}^{(m)}, \phi_{m}\bigr) \leq& z \bigl(s_{q}^{(m)}+p_{1}+p_{2}, \phi_{m}\bigr) \\ &{}\times\exp\int_{s_{q}^{(m)}+p_{1}+p_{2}}^{t_{q}^{(m)}} \biggl(-a_{3}(t)+ \frac{c_{2}(t)\varepsilon_{2}}{d_{1}(t)+d_{2}(t)(\eta _{2}-\varepsilon_{2})} \biggr)\, dt \\ < & (2M+1)m, \end{aligned}$$

which is contradictory with \(z(t_{q}^{(m)}, \phi_{m})=(2M+1)m\). Therefore, there is a constant \(M_{3}>0\) such that (3.32) holds. □

Proposition 3.6

There is a universal constant \(0<\eta<\eta_{2} \) such that

$$ \limsup_{t\to\infty}x(t) > \eta $$
(3.38)

and

$$\int_{0}^{t} \biggl(-a_{3}(s)+ \frac{c_{2}(s)2\eta}{d_{1}(s)+d_{2}(s) \eta_{2} } \biggr)\, ds< 0 $$

hold, where \(\eta_{2}\) is obtained in Proposition  3.3.

Proof

If \(\limsup_{t\to\infty}x(t) \leq \eta\), then by Proposition 3.3, there is a \(T_{11}>T_{10}\) such that \(x(t)<2\eta\) and \(y(t)\geq\eta_{2}-\varepsilon\) (ε is small enough) for all \(t\geq T_{11}\). Since

$$\dot{z}(t)\leq z(t) \biggl(-a_{3}(t)+\frac{c_{2}(t)2\eta }{d_{1}(t)+d_{2}(t)(\eta_{2}-\varepsilon)} \biggr)\quad \mbox{for all } t\geq T_{11}, $$

and since

$$\int_{0}^{t} \biggl(-a_{3}( s)+ \frac{c_{2}(s)2\eta}{d_{1}(s)+d_{2}(s) \eta_{2} } \biggr)\, ds< 0, $$

and for a small enough ε,

$$\int_{0}^{t} \biggl(-a_{3}(s)+ \frac{c_{2}(s)2\eta}{d_{1}(s)+d_{2}(s) (\eta _{2}-\varepsilon) } \biggr)\, ds < 0, $$

by integrating from \(T_{11}\) to t, we can obtain

$$z(t)\leq z(T_{11})\exp\int_{T_{11}}^{t} \biggl(-a_{3}(s)+\frac{c_{2}(s)2\eta }{d_{1}(s)+d_{2}(s)(\eta_{2}-\varepsilon)} \biggr)\, ds. $$

Hence, inequality (3.38) implies \(z(t)\rightarrow0\) as \(t\rightarrow \infty\), which is a contradiction and Proposition 3.6 is proved. □

Proposition 3.7

There is a universal constant \(\eta_{1}>0\) such that

$$ \liminf_{t\to\infty}x(t)> \eta_{1}. $$
(3.39)

Proof

We first choose the constant \(0<\varepsilon_{3}<\eta\) such that

$$ \int_{0}^{w} \biggl(-a_{3}(t)+ \frac{c_{2}(t)\varepsilon _{3}}{d_{1}(t)+d_{2}(t)\eta_{2}} \biggr)\, dt< 0. $$
(3.40)

Here the constants \(\eta_{2} >0\) and \(\eta>0\) are obtained in Propositions 3.3 and 3.6. Suppose that (3.39) is not true. Then there is a sequence \(\{\phi_{m}\}\subset R_{+}^{3}\) such that \(\lim\inf_{t\to\infty}x(t, \phi_{m} )<\frac{\varepsilon_{3}}{m+1}\) for all \(m=1,2,\ldots\) . By Proposition 3.6, there are two time sequences \(\{s_{q}^{(m)}\}\) and \(\{t_{q}^{(m)}\}\) satisfying the following conditions:

$$\begin{aligned} \begin{aligned} &0< s_{1}^{m}< t_{1}^{m} < s_{2}^{m}< t_{2}^{m} < \cdots < s_{q}^{m}< t_{q}^{m}< \cdots, \\ &s_{q}^{m}\rightarrow+\infty, \qquad t_{q}^{m} \rightarrow+\infty \quad \mbox{as } q\rightarrow+\infty, m=1,2,\ldots \end{aligned} \end{aligned}$$

and

$$\begin{aligned}& x\bigl(s_{q}^{m}, \phi_{m}\bigr)= \varepsilon_{3},\qquad x\bigl(t_{q}^{m}, \phi_{m}\bigr)=\frac {\varepsilon_{3}}{m+1}, \\& \frac{\varepsilon_{3}}{m+1} < x(t, \phi_{m})< \varepsilon_{3}\quad \mbox{for all } t\in\bigl(s_{q}^{m}, t_{q}^{m} \bigr). \end{aligned}$$

By Propositions 3.1 and 3.3, there is a \(T^{(m)}>0\) such that \(z(t, \phi_{m})\leq M_{3}\) and \(x(t, \phi_{m})\leq M_{1}\) for all \(t\geq T^{(m)}\), and further there is a \(K^{(m)}>0\) such that \(s_{q}^{m}\geq T^{(m)}\) for all \(q\geq K^{(m)}\). Hence, for any \(t\in[s_{q}^{m}, t_{q}^{m}]\) and \(q\geq K^{(m)}\), we have

$$\dot{x}(t, \phi_{m}) \geq x(t, \phi_{m}) \biggl(a_{1}(t)-b_{1}(t)M_{1}-\frac{c_{1}(t)M_{3}}{d_{1}(t)} \biggr). $$

By integrating from \(s_{q}^{m}\) to \(t_{q}^{m}\), we obtain

$$x\bigl(t_{q}^{m}, \phi_{m}\bigr)\geq x \bigl(s_{q}^{m}, \phi_{m}\bigr)\exp\int _{s_{q}^{(m)}}^{t_{q}^{(m)}} \biggl(a_{1}(t)-b_{1}(t)M_{1}- \frac {c_{1}(t)M_{3}}{d_{1}(t) } \biggr)\, dt. $$

Consequently,

$$\ln(m+1)\leq\int_{s_{q}^{(m)}}^{t_{q}^{(m)}} \biggl(-a_{1}(t)+b_{1}(t)M_{1}+ \frac{c_{1}(t)M_{3}}{d_{1}(t)} \biggr)\, dt\quad \mbox{for all } q\geq K^{(m)}. $$

Hence, we obtain

$$ t_{q}^{(m)} -s_{q}^{(m)}\rightarrow\infty \quad \mbox{as } m\rightarrow\infty , q \geq K^{(m)}. $$
(3.41)

By (3.40), there is a constant \(T_{12}>0\), and \(T_{12}\) is independent on any m and q, such that

$$M_{3}\exp\int_{s_{q}^{(m)}}^{t_{q}^{(m)}} \biggl(-a_{3}(t)+\frac {c_{2}(t)\varepsilon_{3}}{d_{1}(t)+d_{2}(t)(\eta_{2}-\varepsilon)} \biggr)\, dt< \eta_{3}. $$

By (3.41), there is a \(M_{0}>0\) such that \(t_{q}^{(m)}>s_{q}^{(m)}+M_{0}\) for all \(m\geq M_{0}\) and \(q\geq K^{(m)}\). Hence, for any \(t\in[s_{q}^{m}, t_{q}^{m}]\), \(m\geq M_{0}\), and \(q\geq K^{(m)}\), we have \(y(t)\geq\eta_{2}-\varepsilon \) and

$$\dot{z}(t, \phi_{m})\leq z(t, \phi_{m}) \biggl(-a_{3}(t)+\frac {c_{2}(t)\varepsilon_{3}}{d_{1}(t)+d_{2}(t)(\eta_{2}-\varepsilon)} \biggr). $$

By integrating from \(s_{q}^{(m)}\) to \(s_{q}^{(m)}+M_{0}\), we obtain

$$\begin{aligned} \eta_{3} < &z\bigl(s_{q}^{(m)}+M_{0}, \phi_{m}\bigr) \\ \leq& z\bigl(s_{q}^{(m)}, \phi_{m}\bigr)\exp\int _{s_{q}^{(m)}}^{s_{q}^{(m)}+M_{0}} \biggl(-a_{3}(t)+ \frac {c_{2}(t)\varepsilon_{3}}{d_{1}(t)+d_{2}(t)(\eta_{2}-\varepsilon)} \biggr)\, dt < \eta_{3}, \end{aligned}$$

which is a contradiction, and Proposition 3.7 is proved. □

3.1 Proof of Theorem 2.3

The results of Theorem 2.3 now follow from Propositions 3.1-3.7.

4 Example

In this section, we shall give an example to illustrate the feasibility of the main results.

Example

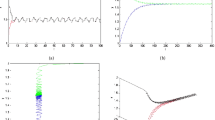
Consider the following predator-prey-mutualist system (see Figure 1):

$$\begin{aligned}& \dot{x}=x \biggl( 3.2-0.3x- \frac{0.6z}{0.8+0.3y} \biggr), \\& \dot{y}=y \biggl( 3.0- \frac{y}{0.5+0.5x} \biggr), \\& \dot{z}=z \biggl(- (0.7-0.1\sin t )+ \frac{0.5x}{0.8+0.3y} \biggr). \end{aligned}$$
(4.1)
Figure 1
figure 1

Dynamic behaviors of the solution \(\pmb{(x(t), y(t), z(t))}\) system ( 4.1 ) with initial conditions \(\pmb{(x(0), y(0),z(0) )=(10, 13, 15),(12, 10, 13)\mbox{ and }(2, 4, 6)}\) , respectively.

Full size image

Corresponding to system (1.2), one has

$$\begin{aligned}& a_{1}(t)=3.2,\qquad b_{1}(t)=0.3,\qquad c_{1}(t)=0.6,\qquad d_{1}(t)=0.8, \\ & d_{2}(t)=0.3,\qquad a_{2}(t)=3.0,\qquad d_{3}(t)=0.5,\qquad d_{4}(t)=0.5, \\ & a_{3}(t)=0.7-0.1\sin t,\qquad c_{2}(t)=0.5 . \end{aligned}$$

One easily sees that

$$\dot{u}_{1}(t)=u_{1}(t) \bigl(3.2-0.3u_{1}(t) \bigr) $$

has a unique positive periodic solution \(u_{10}(t)\approx10.667\). So \(M^{*}=11.667\),

$$\dot{u}_{2}(t)=u_{2}(t) \biggl(3.0- \frac{u_{2}(t)}{0.5+0.5\times 11.667} \biggr) $$

has a unique positive periodic solution \(u_{20}(t)\approx17.503\).

By simple computation, one has

$$\begin{aligned} \begin{aligned} &\int_{0}^{w} \biggl(-a_{3}(t)+ \frac {c_{2}(t)u_{10}(t)}{d_{1}(t)+d_{2}(t)u_{20}(t)} \biggr)\, dt \\ &\quad =\int_{0}^{2 \pi} \biggl(- (0.7-0.1\sin t )+ \frac{0.5\times 10.667}{0.8+0.3\times17.503} \biggr)\, dt\approx1.1394>0. \end{aligned} \end{aligned}$$

Condition (2.4) is satisfied. Thus, corresponding to Theorem 2.3 and Corollary 2.4, we know that system (4.1) is permanent and admits at least one positive 2π-periodic solution.

5 Conclusion

In this paper, we studied a periodic predator-prey-mutualist system. From system (1.2), we see the mutualist species y can reduce the capture rate of the predator species z to the prey species x. By further developing the analysis technique of Teng [20], we obtain a set of conditions which ensure the permanence of system (1.2). Note that \(u_{10}(t)\) and \(u_{20}(t)\) are the globally attractive periodic solution of (2.2) and (2.3), respectively, which, as shown by Lemma 2.1, always exists. Hence, the left side of condition (2.4) implies that if the death rate of the predator species is enough small and the cooperation effect between species x and y is not very strong, the system is permanent.