1 Introduction

With the presentation of new analytical results in recent years, the power of fractional calculus in describing processes and modeling physical events and engineering tools has become clear to everyone. In most published papers we are able to observe different generalized fractional modelings of standard equations in which the Caputo or Riemann–Liouville derivatives or their extensions have been utilized in fractional differential equations (FDEs) and fractional differential inclusions (FDIs) such as pantograph inclusion [1], hybrid thermostat inclusion [2], q-differential inclusion on time scale [3], Langevin inclusion [4], and higher order fractional differential inequalities [5]. One can find many published works on various applications of fractional calculus in different fields of science (see, for example, [6–16]).

In 2016, the authors considered the following mixed initial value problem involving Hadamard derivative and Riemann–Liouville fractional integrals given by

$$ \textstyle\begin{cases} {}^{H }\mathbb{D}^{q} (y(t) - \sum_{i=1}^{m} {}^{RC } \mathbb{I}_{r}^{\sigma _{i}} w_{i} (t, y(t) ) \in \mathfrak{H}( t, y(t)), \quad t \in [1, M], \\ y(1) =0, \end{cases} $$

where \({}^{H }\mathbb{D}^{q}\) denotes the Hadamard fractional derivative of order \(0 < q\leq 1\), \({}^{RC }\mathbb{I}_{r}^{\sigma}\) is the Riemann–Liouville fractional integral of order \(\sigma >0\), \(\sigma \in \{\sigma _{1}, \sigma _{2}, \dots , \sigma _{m}\}\), \(\mathfrak{H}: [1, M ] \times \mathbb{R} \to \mathcal{P}(\mathbb{R})\), \(w_{i} \in C([1, M] \times \mathbb{R}, \mathbb{R})\) with \(w_{i}(1,0)=0\), \(i=1,2,\dots , m\) [17]. In 2017, Ahmad et al. considered the existence and uniqueness of solutions to the initial value problem of Caputo–Hadamard sequential fractional order neutral functional differential equations as follows:

$$ \textstyle\begin{cases} {}^{C }\mathbb{D}^{\sigma _{1}} [ {}^{C }\mathbb{D}^{\sigma _{2}} y(t) - f_{1}(t, y_{t} ) ]= f_{2}(t, y_{t}),& t \in [1, M], \\ y(t) = \phi (t), & t \in [1-r, 1], \\ {}^{C }\mathbb{D}^{\sigma _{2}} y(1) = \eta \in \mathbb{R}, \end{cases} $$

where \({}^{C }\mathbb{D}^{\sigma _{1}}\), \({}^{C }\mathbb{D}^{\sigma _{2}}\) are the Caputo–Hadamard fractional derivatives, \(0 < \alpha , \beta <1\), \(f_{i}: [1, M] \times C([-r, 0], \mathbb{R}) \to \mathbb{R}\) is a given function, \(i=1,2\), and \(\phi \in C([1-r, 1], \mathbb{R})\) [18]. The authors in [19] introduced a new class of boundary value problems consisting of Caputo–Hadamard type fractional differential equations and Hadamard type fractional integral boundary conditions:

$$ \textstyle\begin{cases} ( {}^{C }\mathbb{D}^{\sigma _{1}} + \lambda {}^{C }\mathbb{D}^{ \sigma _{1}-1} ) y(t) = w_{1} ( t, y(t), z(t),{}^{C } \mathbb{D}^{\beta} z(t) ),& 1 < \sigma _{2} \leq 2, \\ ( {}^{C }\mathbb{D}^{\sigma _{2}} + \lambda {}^{C }\mathbb{D}^{ \sigma _{2} -1} ) z(t) = w_{2} ( t, y(t), {}^{C } \mathbb{D}^{\beta} y(t), z(t) ),& 1 < \sigma _{2} \leq 2, \\ y(1) =0, a_{11} \mathbb{I}^{\gamma _{1}} v(\eta _{1}) + a_{12} u(\delta )= K_{1}, & \gamma _{1} >0, 1 < \eta _{1} < \delta , \\ z(1) =0, a_{21} \mathbb{I}^{\gamma _{2}} u(\eta _{2}) + a_{22} v(\delta )= K_{2}, & \gamma _{2} >0, 1 < \eta _{2} < \delta , \end{cases} $$

where \(0 <\beta <1\), \({}^{C }\mathbb{D}^{(.)}\), \(\mathbb{I}^{(.)}\) respectively denote the Caputo–Hadamard fractional derivative and Hadamard fractional integral (to be defined later), \(w_{i}: [0, \delta ] \times \mathbb{R}^{3} \to \mathbb{R}\) is a given appropriate function and \(a_{ij}\), \(K_{i}\) are real constants, here \(i,j=1,2\) [19].

More precisely, in [1], Thabet et al. formulated a version of FDI taken from the pantograph BVP in the sense of Caputo-conformable equipped with three-point RL-conformable integral conditions:

$$ \textstyle\begin{cases} {}^{CC }\mathbb{D}_{r}^{q,\sigma _{1}} y(t) \in \mathfrak{H}( t, \varkappa (t), \varkappa (\lambda ^{\ast}t) ), \quad t \in [r, M], \\\varkappa (r) =0, \\ p_{1} \varkappa (M) + p_{2} {}^{RC }\mathbb{I}_{r}^{q,\sigma _{2}} \varkappa (\zeta ) = \varkappa ^{\ast}. \end{cases} $$

Here, \({}^{CC }\mathbb{D}_{r}^{q,\sigma _{1}}\) indicates the derivative of the Caputo-conformable type of order \(1 < \sigma _{1} < 2\) along with \(0 < q <1\), \({}^{RC }\mathbb{I}_{r}^{q,\sigma _{2}}\) is the integral of the RL-conformable type of order \(\sigma _{2}>0\), \(\zeta \in (r, M)\), \(p_{1}\), \(p_{2}\), \(y^{\ast}\in \mathbb{R}\), \(0 < \lambda <1\), and \(\mathfrak{H}: [r, M] \times \mathbb{R}^{2} \to \mathcal{P} ( \mathbb{R})\) is a multifunction. Also, Baleanu et al. in [2] investigated the hybrid problem caused by the thermostat model

$$ \textstyle\begin{cases} {}^{C}\mathbb{D}_{0}^{q} ( \frac {y(t) }{\varkappa (t, y(t))} ) + w (t, y(t)) =0, \\ \mathbb{D} ( \frac {y(t) }{\varkappa (t, y(t))} ) |_{t=0} =0, \\ \eta {}^{C}\mathbb{D}_{0}^{q-1} ( \frac {y(t) }{\varkappa (t, y(t))} ) |_{t=1} + ( \frac {y(t) }{\varkappa (t, y(t))} ) |_{t= a} =0, \end{cases} $$

so that \({}^{C }\mathbb{D}_{0}^{q}\) is the Caputo derivation of fractional order \(1 < q\leq 2\), \(\mathbb{D} = \frac{\mathrm{d}}{\mathrm{d}t}\) the function \(w : [0,1] \times \mathbb{R} \to \mathbb{R} \) is continuous, \(\varkappa \in C([0,1]\times \mathbb{R}, \mathbb{R} \setminus \{0\} )\), η is a positive real parameter and \(0 \leq a \leq 1\). Furthermore, Samei et al. in [3] discussed the fractional q-differential inclusion

$$ \textstyle\begin{cases} {}^{C }\mathbb{D}_{q}^{\sigma} y(t) \in \mathfrak{H} (t, y(t) , y'(t), {}^{C }\mathbb{D}_{q}^{p_{1}} y(t), \dots , {}^{C } \mathbb{D}_{q}^{p_{m}} y(t) ), \quad t \in [0, 1], \\y(0) + c y''(0) =0, \qquad a_{1}y(\tau )+ a_{2}\varrho (1)=0, \qquad c y'(1) + a_{3} \varrho (1) = 0. \end{cases} $$

Here, \({}^{C }\mathbb{D}_{q}^{\sigma}\) denotes the Caputo fractional quantum derivative of order \(2 < \sigma \leq 3\), \(1< p_{i}\leq 2\), (\(i=1,2,\dots , m\)), \(0 < \tau <1\), \(c = \sum_{j=1}^{m} c_{i}\), \(c_{j} \in \mathbb{R}\), \(\varrho : [0, \infty ) \to [0, \infty )\) defined by

$$ \varrho _{i}(z) = \int _{0}^{z} \varphi \bigl(y(\xi )\bigr) \, \mathrm{d}\xi ,$$

\(\varphi : [0, \infty ) \to [0, \infty )\), \(\mathfrak{H}: [0,1]\times \mathbb{R}^{m+2} \to \mathcal{P}( \mathbb{R})\) is a compact-valued multifunction and \(a_{1}, a_{2}, a_{3} \in \mathbb{R}\). Recently, Rezapour et al. introduced and investigated a new BVP consisting of a generalized fractional integro-Langevin equation with constant coefficient and nonlocal fractional boundary conditions (BCs) given by

$$ \textstyle\begin{cases} {}^{C }\mathbb{D}_{0^{+}}^{q_{1}} [ {}^{C }\mathbb{D}_{0^{+}}^{q_{2}} y(t) - \beta y(t) ] = {}^{RL}\mathbb{I}_{0^{+}}^{p} h( t, y(t)), & t \in [0, 1], \\y(0) =0, \qquad {}^{C }\mathbb{D}_{0^{+}}^{q_{2}} y(0) = 0,& \\ {}^{C }\mathbb{D}_{0^{+}}^{1} y(1) {}^{C }\mathbb{D}_{0^{+}}^{1} y( \tau ) =0,& \tau \in (0,1), \end{cases} $$

where \(0 < q_{1} < 1\), \(1 < q_{2} < 2\), \(p>0\), \(\beta \in \mathbb{R}^{+}\), \({}^{C }\mathbb{D}_{0^{+}}^{\eta}\), (\(\eta \in \{ q_{1}, q_{2}\}\)) and \({}^{RL }\mathbb{I}_{0^{+}}^{p}\) denote the Caputo fractional derivative operators and the Riemann–Liouville fractional integral of orders p and η, respectively, and the function \(h: [0,1] \times \mathbb{R} \to \mathbb{R}\) is continuous [4].

The authors in [5] showed how fractional differential inequalities can be useful to establish the properties of solutions of different problems in biomathematics and flow phenomena. The nonexistence of global solutions to a higher order fractional differential inequality with a nonlinearity involving Caputo fractional derivative has been obtained [5]. On the other hand in [20] the authors analyzed the properties of fractional operators with fixed memory length in the context of Laplace transform of the Riemann–Liouville fractional integral and derivative with fixed memory length [20] on the fractional differential equation

$$ {}_{a }\mathbb{D}_{t^{+}}^{\eta} y(t) \sim {}_{t-L }\mathbb{D}_{t}^{ \eta} y(t), \quad t > a+L.$$

These facts could be used to better explain the motivation behind the present study [20]. Jleli et al. studied the wave inequality with a Hardy potential

$$ \partial _{tt} y - \Delta y + \frac{\lambda}{ \vert x \vert ^{2}} y \geq \vert y \vert ^{p} \quad \text{in } (0, \infty )\times \Omega ,$$

where Ω is the exterior of the unit ball in \(\mathbb{R}^{N}\), (\(N\geq 2\)), \(p>1\), and

$$ \lambda \geq - \biggl(\frac{N-2}{2} \biggr)^{2},$$

under the inhomogeneous boundary condition \(\alpha \frac{\partial y}{\partial x} (t, x) + \beta y(t, x) \geq w(x)\) on \((0, \infty )\times \partial \Omega \), where \(\alpha , \beta \geq 0\) and \((\alpha , \beta ) \neq (0,0)\) [21]. The Caputo–Hadamard derivation operator [22] is another extension of the above operators that many researchers got help from it in their modelings. For instance, we can find the applications of this generalized operator in modeling of the Sturm–Liouville–Langevin problem [23], investigation of the combination synchronization of a Caputo–Hadamard system [24], description of an uncertain BVP‘ [25], studying the proportional Langevin BVP [26], etc.

Our main novelty in this work is to use the Caputo–Hadamard operator for generalizing the standard jerk problem in the form of a fractional inclusion problem. In fact, a jerk system is a simple form of a nonlinear ODE of third order depicted by

$$ \frac {\mathrm{d}^{3}y}{\mathrm{d}t^{3}} = \mathcal{F} \biggl(y, \frac {\mathrm{d}y}{\mathrm{d}t}, \frac {\mathrm{d}^{2}y}{\mathrm{d}t^{2}} \biggr),$$

where, in mechanics, the nonlinear mapping \(\mathcal{F}(\cdot , \cdot , \cdot )\) is equivalent to the 1st-derivative of acceleration. For this reason, it is introduced as a jerk [27, 28].

The mathematical analysis of this generalized system is our main purpose in this work. To do this, we decided to utilize a new family of multi-functions belonging to ϕ-admissibles and ϕ-ψ-contractions for proving theorems based on fixed point methods. Also, those multi-functions that have approximate property for their end points play a fundamental role in our analysis. These items present the novelty and contribution of our work in this regard, because most researchers get help from standard fixed point techniques in their papers. For example, the Leray–Schauder, the Banach principle, Krasnoselskii, degree principle, Schaefer are the most famous of them, and they are applied in more papers including the generalized proportional equation by Das et al. in [29], impulsive implicit problem by Ali et al. in [30], nonlinear ϕ-Hilfer problem on compact domain by Mottaghi et al. in [31], multi-term multi-strip coupled system by Ahmad et al. in [32], ψ-Hilfer system of coupled Langevin equations by Sudsutad et al. in [33], sequential RL-Hadamard–Caputo problem by Ntouyas et al. in [34], sequential post-quantum integro-difference problem by Soontharanon et al. in [35] and Samei in [36–38], Neumann symmetric Hahn problem by Dumrongpokaphan et al. in [39], etc.

By virtue of the idea of a standard jerk equation and extending it to the generalized fractional Caputo–Hadamard settings, we here introduce and study new existence methods based on some special multi-functions to guarantee the existence of solution for the extended fractional jerk inclusion problem illustrated as

$$ \textstyle\begin{cases} ({}^{CH }\mathbb{D}_{1^{+}}^{\iota _{1}} ( {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{2}}({}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}}y) ) )(t) \\\quad \in \mathbb{G} ( t,y(t), {}^{CH }\mathbb{D}_{1^{+}}^{ \iota _{3}}y(t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} ( {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}}y(t) ) ), \\y(1) + y(e) = 0,\qquad {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}} y ( \eta ) = 0,\qquad {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} ( {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}} y (e) ) = 0, \end{cases} $$
(1)

in which \(\iota _{1},\iota _{2},\iota _{3} \in (0,1]\) and \({}^{CH }\mathbb{D}_{1^{+}}^{p}\) displays the derivative operator in the sense of Caputo–Hadamard subject to \(p \in \{ \iota _{1}, \iota _{2}, \iota _{3} \}\) and also \(t\in I := [1,e]\) and \(\eta \in (1,e)\). In addition to these, we have considered the operator \(\mathbb{G}: I \times \mathbb{R}^{3} \rightarrow \mathcal{P}( \mathbb{R})\) as a multi-function in which \(\mathcal{P}(\mathbb{R})\) illustrates all nonempty subsets of \(\mathbb{R}\).

This research is conducted as follows. Section 2 is fundamental and necessary in its nature since it collects definitions and required results. Section 3 is divided into two parts: one is in relation to the existence criterion via fixed points and the second is in relation to the existence criterion via end points. In fact, in Sect. 3.1, some inequalities between multi-functions and contractions and admissible functions play the role to prove the desired results via fixed point notion. Accordingly, Sect. 3.2 is devoted to proving similar results via end points and approximate property for end points. Section 4 discusses an example for simulating and analyzing the results numerically. Section 5 completes our research via conclusions.

2 Preliminaries

Here, we shall review some primitive and fundamental concepts in the direction of used approaches and techniques in the present study. As you will observe, these notions and properties are utilized throughout the paper. The readers can find more details in [22, 40, 41].

Definition 2.1

([40, 41])

Let \(q \geq 0\). Then the Hadamard fractional \(q^{\mathrm{th}}\)-integral of a continuous function \(y:(a,\infty )\to \mathbb{R}\) of order q is formulated by \({}^{H}\mathbb{I}_{a^{+}}^{0} y(t)=y(t) \) and

$$ {}^{H}\mathbb{I}_{a^{+}}^{q} y(t)= \frac{1}{\Gamma (q )} \int _{a}^{t} \biggl( \ln \frac{t}{r} \biggr)^{q-1}y(r) \frac{\mathrm{dr}}{r},\quad q>0.$$

Definition 2.2

([22])

The Caputo–Hadamard fractional \(q^{\mathrm{th}}\)-derivative for \(y \in AC_{\delta}^{n}([a, b], \mathbb{R})\) is illustrated as

$$ {}^{CH }\mathbb{D}_{a^{+}}^{q} y(t)= {}^{H}\mathbb{I}_{a^{+}}^{n-q} \delta ^{n} y(t) = \frac{1}{\Gamma ( n - q )} \int _{a}^{t} \biggl( \ln \frac{t}{r} \biggr)^{n-q-1} \delta ^{n} y(r) \frac{\mathrm{dr}}{r},$$

in which \(n-1 < q < n\) and \(\delta = t \frac {\mathrm{d}}{\mathrm{dt}}\). Note that, for \(q=n\in \mathbb{N}\), we have

$$ {}^{CH }\mathbb{D}_{a^{+}}^{n} y(t) = \delta ^{n} y(t) = \biggl(t \frac {\mathrm{d}}{\mathrm{dt}} \biggr)^{n} y(t), \qquad {}^{CH } \mathbb{D}_{a^{+}}^{0} y(t) = y(t).$$

From here onwards, we denote the abbreviations HF-integral and CHF-derivative for the above fractional operators. To find other information on the CHF-operators, we direct the interested readers to [22].

Lemma 2.3

([22, 40, 41])

Let \(q,p \in \mathbb{R}^{+}\). Then:

  1. (1)

    \({}^{H}\mathbb{I}_{a^{+}}^{q} {}^{H}\mathbb{I}_{a^{+}}^{p} y(t)= {}^{H} \mathbb{I}_{a^{+}}^{ q + p} y(t)\), (Semi-group property for HF-integrals);

  2. (2)

    For \(n-1< q<n\), \(m-1< p< m\) and \(y(t) \in C_{\delta}^{m+n} [a,b]\), we have

    $$ {}^{CH }\mathbb{D}_{a^{+}}^{q} {}^{CH } \mathbb{D}_{a^{+}}^{p} y(t)= {}^{CH } \mathbb{D}_{a^{+}}^{ q + p} y(t),$$

    (Semi-group property for CHF-derivatives);

  3. (3)

    For \(q>p\),

    $$ {}^{CH }\mathbb{D}_{a^{+}}^{p} {}^{H} \mathbb{I}_{a^{+}}^{q} y(t)= {}^{H} \mathbb{I}_{a^{+}}^{ q - p} y(t),$$

    (Composition property for HF-CHF-operators).

Example 2.4

([40, 41])

Let \(q , \iota \in \mathbb{R}^{+}\). For \(y(t) = ( \ln \frac {t}{a} )^{\iota}\), we have

$$ {}^{H}\mathbb{I}_{a^{+}}^{q} y(t) = {}^{H}\mathbb{I}_{a^{+}}^{q} \biggl( \ln \frac {t}{a} \biggr)^{\iota}= \frac{\Gamma (\iota +1)}{\Gamma (q+\iota +1)} \biggl( \ln \frac {t}{a} \biggr)^{q+\iota},\quad \forall t>a. $$

Further, if \(y(t) \equiv c \in \mathbb{R}\), then

$$ {}^{H}\mathbb{I}_{a^{+}}^{q} y(t) = {}^{H}\mathbb{I}_{a^{+}}^{q}c= \frac{c}{\Gamma (q+1)} \biggl( \ln \frac {t}{a} \biggr)^{q},\quad \forall t>a. $$

Lemma 2.5

([22])

Let \(y \in AC_{\delta}^{n}([a, b], \mathbb{R})\) and \(n -1 < q < n\).

$$ {}^{H}\mathbb{I}_{a^{+}}^{q} \bigl({}^{CH } \mathbb{D}_{a^{+}}^{q} y \bigr) (t)= y (t)-\sum _{i=0}^{n-1} \frac{\delta ^{i} y(a)}{i!} \biggl( \ln \frac{t}{a} \biggr)^{i},\quad \forall t>a.$$

For the homogeneous CHF-differential equation \({}^{CH }\mathbb{D}_{a^{+}}^{q} y(t)=0\), its general solution, by virtue of Lemma 2.5, is obtained by

$$ y(t) = s_{0} + s_{1} \biggl( \ln \frac {t}{a} \biggr) + s_{2} \biggl( \ln \frac {t}{a} \biggr)^{2} + \cdots + s_{n-1} \biggl( \ln \frac {t}{a} \biggr)^{n-1},$$

subject to \(s_{i} \in \mathbb{R}\) and \(n = [ q ] + 1\) [22]. Hence

$$\begin{aligned} {}^{H}\mathbb{I}_{a^{+}}^{q} \bigl( {}^{CH }\mathbb{D}_{a^{+}}^{q} y \bigr) (t) & = y(t) + s_{0} + s_{1} \biggl( \ln \frac {t}{a} \biggr) + s_{2} \biggl( \ln \frac {t}{a} \biggr)^{2} \\ & \quad {}+ \cdots + s_{n-1} \biggl( \ln \frac {t}{a} \biggr)^{n-1} \end{aligned}$$

for \(t>a\) [22].

In what follows we give a brief introduction to some special function spaces and multi-valued operators. We assume \((A,\|\cdot \|)\) as a normed space. We mean by \({\mathcal {P}}_{CL}( A )\), \({\mathcal {P}}_{BN}( A )\), \({\mathcal {P}}_{CP}( A )\), and \({\mathcal {P}}_{CV}( A )\) the category of all closed, bounded, compact, and convex sets, respectively, belonging to A.

Definition 2.6

([42])

The (Pompeiu–Hausdorff) metric, displayed by

$$ H_{\rho}: \bigl( \mathcal{P}(A) \bigr)^{2} \to \mathbb{R} \cup \{\infty \},$$

is introduced as

$$ H_{\rho}(W_{1}, W_{2}) = \max \Bigl\{ \sup _{\nu _{1} \in W_{1}}\rho ( \nu _{1},\nu _{2}), \sup _{\nu _{2} \in W_{2}}\rho (W_{1},\nu _{2}) \Bigr\} ,$$

in which ρ is a metric of A and

$$ \rho (W_{1},\nu _{2}) = \inf_{\nu _{1} \in W_{1}} \rho (\nu _{1}, \nu _{2}), \qquad \rho (\nu _{1},W_{2}) = \inf_{\nu _{2} \in W_{2}} \rho (\nu _{1},\nu _{2}).$$

Definition 2.7

([42])

For \(\mathbb{G} : A \to {\mathcal {P}}_{CL} (A)\) and \(y_{1}, y_{2} \in A\), let

$$ H_{\rho}\bigl(\mathbb{G}(y_{1}),\mathbb{G}(y_{2}) \bigr) \leq L \rho (y_{1},y_{2}).$$

Then \(\mathbb{G}\) is called: (1) Lipschitz if \(L > 0\); (2) a contraction if \(L \in (0,1)\).

In the next step, we recall a specific family of multi-functions introduced by Amini-Harandi [42] in 2010 which we utilize in our proofs.

Definition 2.8

([42])

Let A be a metric space and \(\mathbb{G}\) be a multi-valued operator on it. Then

  1. (1)

    \(y \in A\) is an end point of \(\mathbb{G} :A\to \mathcal{P}(A)\) if \(\mathbb{G}y=\{ y\}\).

  2. (2)

    \(\mathbb{G}\) admits the AEP-property (approximate end point property) whenever

    $$ \inf_{v\in A}\sup_{y\in \mathbb{G}v}\rho (v,y)=0.$$

Later, in 2013, Mohammadi, Rezapour, and Shahzad [43] provided another family of multi-functions based on two operators ψ and ϕ which is a generalized structure of a similar notion pertinent to single-valued operators given by Samet et al. [44] in 2012.

Definition 2.9

([43])

Let Ψ be a family of all increasing mappings \(\psi : \mathbb{R}^{\geq 0}\to \mathbb{R}^{\geq 0}\) s.t. \(\forall t>0\), \(\sum_{i=1}^{\infty}\psi ^{i}(t)<\infty \) and \(\psi (t)< t\). Let \(\mathbb{G}: A\to \mathcal{P}(A)\) and \(\phi : A\times A \to \mathbb{R}^{\geq 0}\). In this case:

  1. (1)

    \(\mathbb{G}: A \to \mathcal{P}_{CL,BN}(A)\) is ϕ-ψ-contraction if \(\forall y_{1}, y_{2}\in A\),

    $$ \phi (y_{1},y_{2}) H_{\rho}(\mathbb{G} y_{1}, \mathbb{G} y_{2})\leq \psi \bigl(\rho (y_{1}, y_{2})\bigr). $$
  2. (2)

    \(\mathbb{G}\) is ϕ-admissible if \(\forall y_{1}\in A\) and \(\forall y_{2}\in \mathbb{G}y_{1}\),

    $$ \phi (y_{1},y_{2})\geq 1 \quad \Longrightarrow\quad \phi ( y_{2},y_{3})\geq 1,\quad \forall y_{3}\in \mathbb{G}y_{2}.$$
  3. (3)

    A admits the property \((C_{\phi})\) if for each \(\{ y_{n} \}_{n \geq 1} \subset A\) with \(y_{n}\to y\) and \(\phi (y_{n} , y_{n+1}) \geq 1\),

    $$ \exists \{ y_{n_{i}} \} \subset \{ y_{n} \}, \quad \text{s.t.}\quad \phi (y_{n_{i}}, y)\geq 1, \quad \forall i\in \mathbb{N}.$$

To follow the required arguments on the existence of a solution for the Caputo–Hadamard fractional jerk problem (CHF-jerk problem) (1), we begin this section by introducing a Banach space as follows:

$$ A = \bigl\{ y(t): y(t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}}y(t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{ \iota _{3}}y(t)\bigr) \in C(I, \mathbb{R}) \bigr\} ,$$

equipped with

$$ \Vert y \Vert _{A}=\sup_{t\in I} \bigl\vert y(t) \bigr\vert + \sup_{t\in I} \bigl\vert {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y(t) \bigr\vert + \sup _{t\in I} \bigl\vert {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl( {}^{CH }\mathbb{D}_{1^{+}}^{ \iota _{3}}y(t) \bigr) \bigr\vert $$

for all \(y \in A\).

3 Existence results via fixed-points and end points

Now, in the next proposition, the solution’s structure for the supposed CHF-jerk problem (1) is exhibited in the format of an integral equation.

Proposition 3.1

Let \(\iota _{1},\iota _{2},\iota _{3} \in (0,1]\), \(\eta \in (1,e)\) and \(T \in C(I,\mathbb{R})\). Then the solution of the linear CHF-jerk problem

$$ \textstyle\begin{cases} ( {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{1}} ( {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{2}} ({}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}}y) ) )(t) = T(t),&t\in I, \\ y(1) + y(e) = 0,\qquad {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}} y (\eta ) = 0,& \\ {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} ( {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}} y (e) ) = 0,& \end{cases} $$
(2)

is obtained as

$$\begin{aligned} y(t)&= \frac{1}{\Gamma (\iota _{1}+\iota _{2}+\iota _{3})} \int _{1}^{t} \biggl( \ln \frac{t}{r} \biggr)^{\iota _{1}+\iota _{2}+\iota _{3} -1} T(r) \frac{\mathrm{dr}}{r} \\ &\quad {}- \frac{1}{2\Gamma (\iota _{1}+\iota _{2}+\iota _{3})} \int _{1}^{e} \biggl( \ln \frac{e}{r} \biggr)^{\iota _{1}+\iota _{2}+\iota _{3} -1} T(r) \frac{\mathrm{dr}}{r} \\ &\quad {}+ \frac{F_{1}(t)}{2\Gamma (1 + \iota _{3})\Gamma (\iota _{1} + \iota _{2})} \int _{1}^{\eta} \biggl( \ln \frac{\eta}{r} \biggr)^{\iota _{1} + \iota _{2} -1} T(r) \frac{\mathrm{dr}}{r} \\ &\quad {}+ \frac{F_{2}(t)}{2\Gamma (1+\iota _{2} + \iota _{3} )\Gamma (1 + \iota _{2})\Gamma (1 + \iota _{3})\Gamma (\iota _{1})} \\ & \quad {}\times \int _{1}^{e} \biggl( \ln \frac{e}{r} \biggr)^{\iota _{1} -1} T(r) \frac{\mathrm{dr}}{r}, \end{aligned}$$
(3)

where

$$ \textstyle\begin{cases} F_{1}(t) = 1- 2 ( \ln t )^{\iota _{3}}, \\F_{2}(t) = \Gamma (1+\iota _{2}) \Gamma (1+ \iota _{3}) [ 1- 2 ( \ln t )^{\iota _{2} + \iota _{3}} ] \\\hphantom{F_{2}(t) = } {}- \Gamma (1 + \iota _{2} + \iota _{3}) ( \ln \eta )^{\iota _{2}} [ 1- 2 ( \ln t )^{\iota _{3}} ]. \end{cases} $$
(4)

Proof

Let y satisfy the linear CHF-jerk problem (2). In view of the semi-group property for HF-integrals given in Lemma 2.3, since \(\iota _{1} \in (0,1]\), so by utilizing the HF-integral of order \(\iota _{1}\), we get

$$ {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl( {}^{CH }\mathbb{D}_{1^{+}}^{ \iota _{3}} y \bigr) (t) = \frac{1}{\Gamma (\iota _{1})} \int _{1}^{t} \biggl( \ln \frac{t}{r} \biggr)^{\iota _{1} -1} T(r) \frac{\mathrm{dr}}{r} + c_{0}, $$
(5)

where \(c_{0} \in \mathbb{R}\). Again, utilizing the HF-integral of order \(\iota _{2} \in (0,1]\) to both sides of (5), we get

$$ {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}} y(t) = \frac{1}{\Gamma (\iota _{1} + \iota _{2})} \int _{1}^{t} \biggl( \ln \frac{t}{r} \biggr)^{\iota _{1} + \iota _{2} -1} T(r) \frac{\mathrm{dr}}{r} + c_{0} \frac{ ( \ln t )^{\iota _{2}}}{\Gamma (1+ \iota _{2})} + c_{1}, $$
(6)

where \(c_{1} \in \mathbb{R}\). At last, utilizing the HF-integral of order \(\iota _{3} \in (0,1]\) to both sides of (6), the general series solution of (2) can be derived by

$$\begin{aligned} y(t) & = \frac{1}{\Gamma (\iota _{1} + \iota _{2} + \iota _{3})} \int _{1}^{t} \biggl( \ln \frac{t}{r} \biggr)^{\iota _{1} + \iota _{2} + \iota _{3} -1} T(r) \frac{\mathrm{dr}}{r} \\ & \quad {}+ c_{0} \frac{ ( \ln t )^{\iota _{2} + \iota _{3}}}{\Gamma (1+ \iota _{2} + \iota _{3})} + c_{1} \frac{ ( \ln t )^{\iota _{3}}}{\Gamma (1+ \iota _{3})} + c_{2}, \end{aligned}$$
(7)

where \(c_{2} \in \mathbb{R}\). To obtain the values \(c_{i}\) (\(i=0,1,2\)), we first consider the third boundary condition and (5), and so the coefficient \(c_{0}\) is obtained as

$$ c_{0} = - \frac{1}{\Gamma (\iota _{1} )} \int _{1}^{e} \biggl( \ln \frac{e}{r} \biggr)^{\iota _{1} -1} T(r) \frac{\mathrm{dr}}{r}. $$
(8)

In the sequel, the second boundary condition and the obtained value for \(c_{0}\) in (8) yield

$$ \begin{aligned} c_{1} & = - \frac{1}{\Gamma (\iota _{1} + \iota _{2} )} \int _{1}^{\eta}\biggl( \ln \frac{\eta}{r} \biggr)^{\iota _{1} + \iota _{2} -1} T(r) \frac{\mathrm{dr}}{r} \\ & \quad {}+ \frac{ ( \ln \eta )^{\iota _{2}} }{\Gamma (1 + \iota _{2})\Gamma (\iota _{1})} \int _{1}^{e} \biggl( \ln \frac{e}{r} \biggr)^{\iota _{1} -1} T(r) \frac{\mathrm{dr}}{r}. \end{aligned} $$
(9)

Finally, (8) and (9) and the first boundary condition give

$$\begin{aligned} c_{2} &= - \frac{1}{2\Gamma (\iota _{1} + \iota _{2} + \iota _{3} )} \int _{1}^{e} \biggl( \ln \frac{e}{r} \biggr)^{\iota _{1} + \iota _{2} + \iota _{3} -1} T(r) \frac{\mathrm{dr}}{r} \\ &\quad {}+ \frac{1}{2\Gamma (1+ \iota _{3})\Gamma (\iota _{1} + \iota _{2} )} \int _{1}^{\eta}\biggl( \ln \frac{\eta}{r} \biggr)^{\iota _{1} + \iota _{2} -1} T(r) \frac{\mathrm{dr}}{r} \\ &\quad {}+ \frac{\Gamma (1+ \iota _{2}) \Gamma (1+ \iota _{3}) - \Gamma (1 + \iota _{2} + \iota _{3}) ( \ln \eta )^{\iota _{2}} }{2\Gamma ( 1 + \iota _{2} + \iota _{3})\Gamma (1 + \iota _{2})\Gamma (1+\iota _{3})\Gamma (\iota _{1})} \\ & \quad {}\times \int _{1}^{e} \biggl( \ln \frac{e}{r} \biggr)^{\iota _{1} -1} T(r) \frac{\mathrm{dr}}{r}. \end{aligned}$$
(10)

At this moment, we insert the value of the coefficients \(c_{i}\), by (8)–(10), into (7) and obtain

$$\begin{aligned} y(t)&= \frac{1}{\Gamma (\iota _{1}+\iota _{2}+\iota _{3})} \int _{1}^{t} \biggl( \ln \frac{t}{r} \biggr)^{\iota _{1}+\iota _{2}+\iota _{3} -1} T(r) \frac{\mathrm{dr}}{r} \\ &\quad{}- \frac{1}{2\Gamma (\iota _{1}+\iota _{2}+\iota _{3})} \int _{1}^{e} \biggl( \ln \frac{e}{r} \biggr)^{\iota _{1}+\iota _{2}+\iota _{3} -1} T(r) \frac{\mathrm{dr}}{r} \\ &\quad{}+ \frac{F_{1}(t)}{2\Gamma (1 + \iota _{3})\Gamma (\iota _{1} + \iota _{2})} \int _{1}^{\eta} \biggl( \ln \frac{\eta}{r} \biggr)^{\iota _{1} + \iota _{2} -1} T(r) \frac{\mathrm{dr}}{r} \\ &\quad{}+ \frac{F_{2}(t)}{2\Gamma (1+\iota _{2} + \iota _{3} )\Gamma (1 + \iota _{2})\Gamma (1 + \iota _{3})\Gamma (\iota _{1})} \int _{1}^{e} \biggl( \ln \frac{e}{r} \biggr)^{\iota _{1} -1} T(r) \frac{\mathrm{dr}}{r}, \end{aligned}$$

showing that y satisfies (3) and \(F_{1}(t)\), \(F_{2}(t)\) are continuous functions represented in (4). This ends the proof. □

3.1 Fixed-point and jerk model (1)

In this part, we define the solution to the CHF-jerk problem (1).

Definition 3.2

The function \(y \in C(I, A)\) is named the solution to the supposed CHF-jerk problem (1) whenever it fulfills the given BCs and \(\exists g \in L^{1}(I)\) s.t.

$$ g(t)\in \mathbb{G} \bigl( t,y(t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}}y(t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl( {}^{CH }\mathbb{D}_{1^{+}}^{ \iota _{3}}y(t) \bigr) \bigr)$$

for almost all \(t\in I\) and

$$\begin{aligned} y(t)&= \frac{1}{\Gamma (\iota _{1}+\iota _{2}+\iota _{3})} \int _{1}^{t} \biggl( \ln \frac{t}{r} \biggr)^{\iota _{1}+\iota _{2}+\iota _{3} -1} g(r) \frac{\mathrm{dr}}{r} \\ &\quad {}- \frac{1}{2\Gamma (\iota _{1}+\iota _{2}+\iota _{3})} \int _{1}^{e} \biggl( \ln \frac{e}{r} \biggr)^{\iota _{1}+\iota _{2}+\iota _{3} -1} g(r) \frac{\mathrm{dr}}{r} \\ &\quad {}+ \frac{F_{1}(t)}{2\Gamma (1 + \iota _{3})\Gamma (\iota _{1} + \iota _{2})} \int _{1}^{\eta} \biggl( \ln \frac{\eta}{r} \biggr)^{\iota _{1} + \iota _{2} -1} g(r) \frac{\mathrm{dr}}{r} \\ &\quad {}+ \frac{F_{2}(t)}{2\Gamma (1+\iota _{2} + \iota _{3} )\Gamma (1 + \iota _{2})\Gamma (1 + \iota _{3})\Gamma (\iota _{1})} \int _{1}^{e} \biggl( \ln \frac{e}{r} \biggr)^{\iota _{1} -1} g(r) \frac{\mathrm{dr}}{r}. \end{aligned}$$

\(\forall t\in I\). For each \(y \in A\), we specify selections of \(\mathbb{G}\) as

$$\begin{aligned} \mathit{S}_{\mathbb{G}, y} &= \bigl\{ g \in L^{1}(I) : g(t) \in \mathbb{G} \bigl( t, y(t), {}^{ CH } \mathbb{D}_{1^{+}}^{ \iota _{3}}y(t), \\ & \quad {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y(t) \bigr) \bigr) \text{ (a.e.) } t\in I \bigr\} . \end{aligned}$$

In the sequel, define the multi-function \(K:A\to \mathcal{P}(A)\) by

$$ K(y)= \bigl\{ z\in A: \text{there exists } g\in \mathit{S}_{\mathbb{G}, y} \text{ such that } z(t)= \pi (t) \ \forall t\in I \bigr\} , $$
(11)

for which

$$\begin{aligned} \pi (t)&=\frac{1}{\Gamma (\iota _{1}+\iota _{2}+\iota _{3})} \int _{1}^{t} \biggl( \ln \frac{t}{r} \biggr)^{\iota _{1}+\iota _{2}+\iota _{3} -1} g(r) \frac{\mathrm{dr}}{r} \\ &\quad {}- \frac{1}{2\Gamma (\iota _{1}+\iota _{2}+\iota _{3})} \int _{1}^{e} \biggl( \ln \frac{e}{r} \biggr)^{\iota _{1}+\iota _{2}+\iota _{3} -1} g(r) \frac{\mathrm{dr}}{r} \\ &\quad {}+ \frac{F_{1}(t)}{2\Gamma (1 + \iota _{3})\Gamma (\iota _{1} + \iota _{2})} \int _{1}^{\eta} \biggl( \ln \frac{\eta}{r} \biggr)^{\iota _{1} + \iota _{2} -1} g(r) \frac{\mathrm{dr}}{r} \\ &\quad {}+ \frac{F_{2}(t)}{2\Gamma (1+\iota _{2} + \iota _{3} )\Gamma (1 + \iota _{2})\Gamma (1 + \iota _{3})\Gamma (\iota _{1})} \int _{1}^{e} \biggl( \ln \frac{e}{r} \biggr)^{\iota _{1} -1} g(r) \frac{\mathrm{dr}}{r}. \end{aligned}$$
(12)

By making use of the following theorem relying on some inequalities between special multi-functions such as ϕ-ψ-contractions and ϕ-admissible, we establish the first criterion guaranteeing the existence of solution for the CHF-jerk problem (1).

Theorem 3.3

([43])

Regard the complete metric space \((A,\rho )\), \(\psi \in \Psi \), \(\phi : A \times A \to \mathbb{R}^{\geq 0}\) and \(\mathbb{G}: A \to \mathcal{P}_{CL,BN}(A)\). Assume that:

  1. (1)

    \(\mathbb{G}\) is ϕ-admissible and ϕ-ψ-contraction;

  2. (2)

    \(\phi (y_{0}, y_{1} )\geq 1\) for some \(y_{0} \in A\) and \(y_{1} \in \mathbb{G}y_{0}\);

  3. (3)

    A involves the \((C_{\phi})\)-property.

Then \(\mathbb{G}\) admits a fixed point.

Remark 3.4

For the sake of simplicity, we define

$$\begin{aligned}& \begin{aligned}[t] \check{\Lambda}_{1} &= \frac{ 3 }{2\Gamma (\iota _{1}+\iota _{2}+\iota _{3}+1)} + \frac{ F_{1}^{*} (\ln \eta )^{\iota _{1}+\iota _{2}} }{2\Gamma (1 + \iota _{3})\Gamma (\iota _{1} + \iota _{2}+1)} \\ & \quad {}+ \frac{ F_{2}^{*} }{2\Gamma (1+\iota _{2} + \iota _{3} )\Gamma (1 + \iota _{2})\Gamma (1 + \iota _{3})\Gamma (\iota _{1}+1)}, \end{aligned} \\& \begin{aligned}[t] \check{\Lambda}_{2} &= \frac{1}{ \Gamma (\iota _{1}+\iota _{2}+1)} + \frac{ F_{1}^{**}(\ln \eta )^{\iota _{1}+\iota _{2}} }{2\Gamma (1 + \iota _{3})\Gamma (\iota _{1} + \iota _{2}+1)} \\ & \quad {}+ \frac{ F_{2}^{**} }{2\Gamma (1+\iota _{2} + \iota _{3} )\Gamma (1 + \iota _{2})\Gamma (1 + \iota _{3})\Gamma (\iota _{1}+1)}, \end{aligned} \\& \check{\Lambda}_{3} = \frac{1}{ \Gamma (\iota _{1}+1) } + \frac{ F_{2}^{***} }{2\Gamma (1+\iota _{2} + \iota _{3} )\Gamma (1 + \iota _{2})\Gamma (1 + \iota _{3})\Gamma (\iota _{1}+1)}, \end{aligned}$$
(13)

where for \(t\in I=[1,e]\),

$$ \textstyle\begin{cases} \sup_{t\in I} \vert F_{1}(t) \vert \leq \sup_{t\in I} ( 1 + 2 ( \ln t )^{\iota _{3}} ) = 3 :=F_{1}^{*}>0, \\\sup_{t\in I} \vert F_{2}(t) \vert \leq \sup_{t\in I} ( \Gamma (1+\iota _{2}) \Gamma (1+ \iota _{3}) [ 1 + 2 ( \ln t )^{\iota _{2} + \iota _{3}} ] \\\hphantom{\sup_{t\in I} \vert F_{2}(t) \vert \leq} {}+ \Gamma (1 + \iota _{2} + \iota _{3}) ( \ln \eta )^{ \iota _{2}} [ 1+ 2 ( \ln t )^{\iota _{3}} ] ) \\\hphantom{\sup_{t\in I} \vert F_{2}(t) \vert }\leq 3\Gamma (1+\iota _{2}) \Gamma (1+ \iota _{3}) + 3\Gamma (1 + \iota _{2} + \iota _{3}) ( \ln \eta )^{\iota _{2}} \\\hphantom{\sup_{t\in I} \vert F_{2}(t) \vert }:=F_{2}^{*} >0, \end{cases} $$
(14)

and

$$ \textstyle\begin{cases} \sup_{t\in I} \vert ({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}} F_{1})(t) \vert \leq \sup_{t\in I} ( 2 \Gamma (\iota _{3}+1) ) \\\hphantom{\sup_{t\in I} \vert ({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}} F_{1})(t) \vert } = 2 \Gamma (\iota _{3}+1) :=F_{1}^{**}>0, \\\sup_{t\in I} \vert ({}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}}F_{2})(t) \vert \\\quad \leq \sup_{t\in I} ( 2 \Gamma (1+ \iota _{3}) \Gamma (1+ \iota _{2} + \iota _{3}) ( \ln t )^{\iota _{2} } \\ \qquad {}+ 2\Gamma (1 + \iota _{2} + \iota _{3}) \Gamma (1+\iota _{3}) ( \ln \eta )^{\iota _{2}} ) \\\quad \leq 2\Gamma (1 + \iota _{2} + \iota _{3}) \Gamma (1+\iota _{3}) (1 + ( \ln \eta )^{\iota _{2}} ) :=F_{2}^{**} >0, \end{cases} $$
(15)

and

$$ \textstyle\begin{cases} \sup_{t\in I} \vert {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}}({}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}}F_{1})(t) \vert \leq \sup_{t\in I} ( 0 ) = 0 :=F_{1}^{***}, \\\sup_{t\in I} \vert {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}}({}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}}F_{2})(t) \vert \\\quad \leq \sup_{t\in I} ( 2 \Gamma (1+ \iota _{3}) \Gamma (1+ \iota _{2} + \iota _{3}) \Gamma (1+\iota _{2}) ) \\\quad = 2 \Gamma (1+ \iota _{3}) \Gamma (1+ \iota _{2} + \iota _{3}) \Gamma (1+\iota _{2}) :=F_{2}^{***} >0. \end{cases} $$
(16)

Theorem 3.5

Let \(\mathbb{G}:I \times A^{3} \to \mathcal{P}_{CP}(A)\) be a multifunction and assume the following scenario:

\((\mathcal{H}_{1})\):

The multifunction \(\mathbb{G}\) is bounded and integrable with \(\mathbb{G}(\cdot , y_{1}, y_{2}, y_{3}): I \to \mathcal{P}_{CP}(A)\) is measurable for all \(y_{m} \in A\) (\(m=1,2,3\));

\((\mathcal{H}_{2})\):

There exist \(\kappa \in C(I, [0, \infty ))\) and \(\psi \in \Psi \) s.t.

$$ {H}_{\rho} (\mathbb{G}(t, y_{1}, y_{2}, y_{3}), \mathbb{G}(t, \bar{y}_{1}, \bar{y}_{2}, \bar{y}_{3} ) \leq \kappa (t) \biggl( \frac{\vartheta ^{\star}}{ \Vert \kappa \Vert } \biggr) \psi \Biggl(\sum_{m=1}^{3} \vert y_{m} - \bar{y}_{m} \vert \Biggr) $$
(17)

for all \(t \in I\) and \(y_{m}, \bar{y}_{m} \in A \) (\(m= 1,2,3\)), where \(\sup_{t\in I} \vert \kappa (t) \vert = \Vert \kappa \Vert \),

$$ \vartheta ^{\star}= \frac {1}{ \check{\Lambda}_{1} + \check{\Lambda}_{2}+ \check{\Lambda}_{3} },$$

and \(\check{\Lambda}_{m}\) (\(m=1,2,3\)) are given by (13);

\((\mathcal{H}_{3})\):

A function \(\Omega _{\star}:\mathbb{R}^{3} \times \mathbb{R}^{3} \to \mathbb{R}\) exists such that, for all \(y_{m}, \bar{y}_{m} \in A \) (\(m= 1,2,3\)), we have

$$ \Omega _{\star}\bigl((y_{1}, y_{2}, y_{3}), (\bar{y}_{1},\bar{y}_{2}, \bar{y}_{3} )\bigr) \geq 0;$$
\((\mathcal{H}_{4})\):

If \(\{ y_{\jmath}\}_{\jmath \geq 1} \subset A\) s.t. \(y_{\jmath}\to y\) and

$$\begin{aligned} &\Omega _{\star}\bigl( \bigl(y_{\jmath}(t), {}^{CH } \mathbb{D}_{1^{+}}^{ \iota _{3}}y_{\jmath}(t), {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{2}} \bigl( {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y_{\jmath}(t) \bigr) \bigr), \\ &\quad \bigl(y_{\jmath +1}(t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}}y_{ \jmath +1}(t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y_{\jmath +1}(t) \bigr) \bigr) \bigr) \geq 0, \end{aligned}$$

then \(\exists \{ y_{\jmath _{s}} \}_{s \geq 1} \subset \{y_{\jmath}\}\) exists such that, for all \(t \in I\) and \(s \geq 1\), we have

$$\begin{aligned} &\Omega _{\star}\bigl( \bigl(y_{\jmath _{s}}(t), {}^{CH } \mathbb{D}_{1^{+}}^{ \iota _{3}}y_{\jmath _{s}}(t), {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{2}}\bigl( {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y_{\jmath _{s}}(t) \bigr) \bigr), \\ &\quad \bigl(y(t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}}y(t), {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y(t) \bigr) \bigr) \bigr) \geq 0; \end{aligned}$$
\((\mathcal{H}_{5})\):

There exist a member \(y^{0} \in A\) and \(\mu \in K(y^{0})\) such that, for any \(t \in I\),

$$\begin{aligned} &\Omega \bigl( \bigl(y^{0}(t), {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y^{0}(t), {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{2}} \bigl( {}^{CH } \mathbb{D}_{1^{+}}^{ \iota _{3}}y^{0}(t) \bigr) \bigr), \\ & \quad \bigl(\mu (t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}} \mu (t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH }\mathbb{D}_{1^{+}}^{ \iota _{3}}\mu (t)\bigr) \bigr) \bigr) \geq 0, \end{aligned}$$

where the multifunction \(K: A \to \mathcal{P}(A)\) is specified by (11);

\((\mathcal{H}_{6})\):

For every \(y \in A\) and \(\mu \in K(y)\) with

$$\begin{aligned} &\Omega _{\star}\bigl( \bigl( y(t), {}^{CH } \mathbb{D}_{1^{+}}^{ \iota _{3}}y(t), {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y(t) \bigr) \bigr), \\ & \quad \bigl(\mu (t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}} \mu (t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH }\mathbb{D}_{1^{+}}^{ \iota _{3}}\mu (t) \bigr) \bigr) \bigr) \geq 0, \end{aligned}$$

there exists a member \(\nu \in K(y)\) such that the inequality

$$\begin{aligned} &\Omega _{\star}\bigl( \bigl( \mu (t), {}^{CH } \mathbb{D}_{1^{+}}^{ \iota _{3}}\mu (t), {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}\mu (t) \bigr) \bigr), \\ & \quad \bigl(\nu (t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}} \nu (t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH }\mathbb{D}_{1^{+}}^{ \iota _{3}}\nu (t) \bigr) \bigr) \bigr) \geq 0 \end{aligned}$$

holds for all \(t\in I\).

Then, the CHF-jerk problem (1) owns a solution.

Proof

Definitely, the fixed point of the mapping \(K: A \to \mathcal{P}(A)\) is a solution of the CHF-jerk problem (1). Note that \(S_{\mathbb{G}, y}\) is nonempty. Indeed, the multifunction

$$ t \mapsto \mathbb{G} \bigl(t, y(t), {}^{CH }\mathbb{D}_{1^{+}}^{ \iota _{3}}y(t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y(t)\bigr) \bigr) $$

is both measurable and closed-valued for any \(y \in A\), so \(S_{\mathbb{G}, y} \neq \emptyset \). Firstly, we will claim that \(K(y)\subseteq A\) is closed \(\forall y\in A\). As for, take a sequence \(\{ y_{n} \}_{n \geq 1}\) in \(K(y)\) such that \(y_{n} \to y\) as \(n\to \infty \). For each \(n \geq 1\), there is \(g_{n}\in S_{\mathbb{G}, y}\) such that

$$\begin{aligned} y_{n}(t)&= \frac{1}{\Gamma (\iota _{1}+\iota _{2}+\iota _{3})} \int _{1}^{t} \biggl( \ln \frac{t}{r} \biggr)^{\iota _{1}+\iota _{2}+\iota _{3} -1} g_{n}(r) \frac{\mathrm{dr}}{r} \\ &\quad {}- \frac{1}{2\Gamma (\iota _{1}+\iota _{2}+\iota _{3})} \int _{1}^{e} \biggl( \ln \frac{e}{r} \biggr)^{\iota _{1}+\iota _{2}+\iota _{3} -1} g_{n}(r) \frac{\mathrm{dr}}{r} \\ &\quad {}+ \frac{F_{1}(t)}{2\Gamma (1 + \iota _{3})\Gamma (\iota _{1} + \iota _{2})} \int _{1}^{\eta} \biggl( \ln \frac{\eta}{r} \biggr)^{\iota _{1} + \iota _{2} -1} g_{n}(r) \frac{\mathrm{dr}}{r} \\ &\quad {}+ \frac{F_{2}(t)}{2\Gamma (1+\iota _{2} + \iota _{3} )\Gamma (1 + \iota _{2})\Gamma (1 + \iota _{3})\Gamma (\iota _{1})} \int _{1}^{e} \biggl( \ln \frac{e}{r} \biggr)^{\iota _{1} -1} g_{n}(r) \frac{\mathrm{dr}}{r} \end{aligned}$$

for all \(t\in I\). Since the multifunction \(\mathbb{G}\) has compact values, there is indeed a subsequence of \(\{g_{n} \}_{n \geq 1}\) (following the same notation) that converges to some \(g\in {L}^{1} (I)\). Subsequently, \(g\in S_{\mathbb{G}, y}\) and

$$\begin{aligned} {y}_{n}(t) &\to y(t) \\ &= \frac{1}{\Gamma (\iota _{1}+\iota _{2}+\iota _{3})} \int _{1}^{t} \biggl( \ln \frac{t}{r} \biggr)^{\iota _{1}+\iota _{2}+\iota _{3} -1} g(r) \frac{\mathrm{dr}}{r} \\ &\quad {}- \frac{1}{2\Gamma (\iota _{1}+\iota _{2}+\iota _{3})} \int _{1}^{e} \biggl( \ln \frac{e}{r} \biggr)^{\iota _{1}+\iota _{2}+\iota _{3} -1} g(r) \frac{\mathrm{dr}}{r} \\ &\quad {}+ \frac{F_{1}(t)}{2\Gamma (1 + \iota _{3})\Gamma (\iota _{1} + \iota _{2})} \int _{1}^{\eta} \biggl( \ln \frac{\eta}{r} \biggr)^{\iota _{1} + \iota _{2} -1} g(r) \frac{\mathrm{dr}}{r} \\ &\quad {}+ \frac{F_{2}(t)}{2\Gamma (1+\iota _{2} + \iota _{3} )\Gamma (1 + \iota _{2})\Gamma (1 + \iota _{3})\Gamma (\iota _{1})} \\ & \quad {}\times \int _{1}^{e} \biggl( \ln \frac{e}{r} \biggr)^{\iota _{1} -1} g(r) \frac{\mathrm{dr}}{r} \end{aligned}$$

for all \(t\in I\). As a result, we can deduce that \(y\in K(y)\) and K is closed-valued. The boundedness of \(K(y)\) is obvious from the compactness of multifunction \(\mathbb{G}\). Next, we prove that K is a ϕ-ψ-contraction. To do this, we regard \(\phi :A^{2}\mapsto {\mathbb{R}}_{\geq 0}\) by \(\phi (y, \bar{y})= 1\) whenever

$$\begin{aligned} &\Omega _{\star}\bigl( \bigl(y(t), {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}} y(t), {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{ \iota _{3}}y(t)\bigr) \bigr), \\ & \quad \bigl(\bar{y}(t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}} \bar{y}(t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}\bar{y}(t)\bigr) \bigr) \bigr) \geq 0, \end{aligned}$$

and \(\phi (y, \bar{y})=0\) otherwise, where \(y, \bar{y} \in A\). Consider \(y, \bar{y} \in A\) and \(\ell _{1} \in K(\bar{y})\) and choose \(g_{1}\in S_{\mathbb{G}, \bar{y}}\) such that

$$\begin{aligned} \ell _{1}(t) &= \frac{1}{\Gamma (\iota _{1}+\iota _{2}+\iota _{3})} \int _{1}^{t} \biggl( \ln \frac{t}{r} \biggr)^{\iota _{1}+\iota _{2}+ \iota _{3} -1} g_{1}(r) \frac{\mathrm{dr}}{r} \\ &\quad {}- \frac{1}{2\Gamma (\iota _{1}+\iota _{2}+\iota _{3})} \int _{1}^{e} \biggl( \ln \frac{e}{r} \biggr)^{\iota _{1}+\iota _{2}+\iota _{3} -1} g_{1}(r) \frac{\mathrm{dr}}{r} \\ &\quad {}+ \frac{F_{1}(t)}{2\Gamma (1 + \iota _{3})\Gamma (\iota _{1} + \iota _{2})} \int _{1}^{\eta} \biggl( \ln \frac{\eta}{r} \biggr)^{\iota _{1} + \iota _{2} -1} g_{1}(r) \frac{\mathrm{dr}}{r} \\ &\quad {}+ \frac{F_{2}(t)}{2\Gamma (1+\iota _{2} + \iota _{3} )\Gamma (1 + \iota _{2})\Gamma (1 + \iota _{3})\Gamma (\iota _{1})} \\ & \quad{}\times \int _{1}^{e} \biggl( \ln \frac{e}{r} \biggr)^{\iota _{1} -1} g_{1}(r) \frac{\mathrm{dr}}{r} \end{aligned}$$

for all \(t\in I\). By making use of (17), we get

$$\begin{aligned} \mathbb{H}_{\rho} & \bigl(\mathbb{G} \bigl( t, y(t), {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y(t), {}^{CH } \mathbb{D}_{1^{+}}^{ \iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y(t) \bigr) \bigr), \\ & \quad \mathbb{G} \bigl( \bar{y}(t), {}^{CH } \mathbb{D}_{1^{+}}^{ \iota _{3}}\bar{y}(t), {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{2}} \bigl( {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}\bar{y}(t)\bigr) \bigr) \bigr) \\ & \leq \kappa (t) \biggl( \frac{\vartheta ^{\star}}{ \Vert \kappa \Vert } \biggr) \psi \bigl( \vert y - \bar{y} \vert + \bigl\vert {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}} y - {}^{CH } \mathbb{D}_{1^{+}}^{ \iota _{3}} \bar{y} \bigr\vert \\ & \quad {}+ \bigl\vert {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y \bigr) - {}^{CH }\mathbb{D}_{1^{+}}^{ \iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}\bar{y} \bigr) \bigr\vert \bigr) \end{aligned}$$

with

$$\begin{aligned} &\Omega _{\star}\bigl( \bigl( y(t), {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y(t), {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{ \iota _{3}}y(t) \bigr) \bigr), \\ & \quad \bigl( \bar{y}(t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}} \bar{y}(t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}\bar{y}(t) \bigr) \bigr) \bigr) \geq 0. \end{aligned}$$

Thus, there exists

$$ \wp \in \mathbb{G} \bigl(t, y(t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}}y(t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{ \iota _{3}}y(t) \bigr) \bigr)$$

such that

$$\begin{aligned} \bigl\vert g_{1}(t) - \wp \bigr\vert & \leq \kappa (t) \biggl( \frac{\vartheta ^{\star}}{ \Vert \kappa \Vert } \biggr) \psi \bigl( \vert y - \bar{y} \vert + \bigl\vert {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}}y - {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}\bar{y} \bigr\vert \\ & \quad {}+ \bigl\vert {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}}y \bigr) - {}^{CH }\mathbb{D}_{1^{+}}^{ \iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}\bar{y} \bigr) \bigr\vert \bigr). \end{aligned}$$

Now, consider a mapping \(\mathbb{U}: I \to \mathcal{P}(A)\) defined by

$$\begin{aligned} \mathbb{U}(t) &= \biggl\{ \wp \in A : \bigl\vert g_{1}(t) - \wp \bigr\vert \leq \kappa (t) \biggl( \frac{\vartheta ^{\star}}{ \Vert \kappa \Vert } \biggr) \psi ( \vert y - \bar{y} \vert + \bigl\vert {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y - {}^{CH }\mathbb{D}_{1^{+}}^{ \iota _{3}}\bar{y} \bigr\vert \\ &\quad{}+ \bigl\vert {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y \bigr) - {}^{CH }\mathbb{D}_{1^{+}}^{ \iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}\bar{y} \bigr) \bigr\vert \biggr\} \end{aligned}$$

for any \(t\in I\). Since \(g_{1}\) and

$$\begin{aligned} \mho & = \kappa (t) \biggl( \frac{\vartheta ^{\star}}{ \Vert \kappa \Vert } \biggr) \psi \bigl( \vert y - \bar{y} \vert + \bigl\vert {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}}y - {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}}\bar{y} \bigr\vert \\ & \quad {}+ \bigl\vert {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y \bigr) - {}^{CH }\mathbb{D}_{1^{+}}^{ \iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}\bar{y} \bigr) \bigr\vert \bigr) \end{aligned}$$

are measurable, so the multivalued function

$$ \mathbb{U} (\cdot )\cap \mathbb{G} (\cdot , y(\cdot ), {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y(\cdot ), {}^{CH } \mathbb{D}_{1^{+}}^{ \iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y(\cdot ) \bigr)$$

is also measurable. Now, suppose

$$ g_{2} \in \mathbb{G} (t, y(t), {}^{CH }\mathbb{D}_{1^{+}}^{ \iota _{3}}y(t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y(t) \bigr),$$

so that we have

$$\begin{aligned} \bigl\vert g_{1}(t) - g_{2}(t) \bigr\vert &\leq \kappa (t) \biggl( \frac{\vartheta ^{\star}}{ \Vert \kappa \Vert } \biggr) \psi \bigl( \vert y - \bar{y} \vert + \bigl\vert {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}}y - {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}}\bar{y} \bigr\vert \\ & \quad {}+ \bigl\vert {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y \bigr) - {}^{CH }\mathbb{D}_{1^{+}}^{q_{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}\bar{y} \bigr) \bigr\vert \bigr). \end{aligned}$$

Define \(\ell _{2} \in K(y)\) by

$$\begin{aligned} \ell _{2}(t) &= \frac{1}{\Gamma (\iota _{1}+\iota _{2}+\iota _{3})} \int _{1}^{t} \biggl( \ln \frac{t}{r} \biggr)^{\iota _{1}+\iota _{2}+ \iota _{3} -1} g_{2}(r) \frac{\mathrm{dr}}{r} \\ &\quad {}- \frac{1}{2\Gamma (\iota _{1}+\iota _{2}+\iota _{3})} \int _{1}^{e} \biggl( \ln \frac{e}{r} \biggr)^{\iota _{1}+\iota _{2}+\iota _{3} -1} g_{2}(r) \frac{\mathrm{dr}}{r} \\ &\quad {}+ \frac{F_{1}(t)}{2\Gamma (1 + \iota _{3})\Gamma (\iota _{1} + \iota _{2})} \int _{1}^{\eta} \biggl( \ln \frac{\eta}{r} \biggr)^{\iota _{1} + \iota _{2} -1} g_{2}(r) \frac{\mathrm{dr}}{r} \\ &\quad {}+ \frac{F_{2}(t)}{2\Gamma (1+\iota _{2} + \iota _{3} )\Gamma (1 + \iota _{2})\Gamma (1 + \iota _{3})\Gamma (\iota _{1})} \\ & \quad {}\times \int _{1}^{e} \biggl( \ln \frac{e}{r} \biggr)^{\iota _{1} -1} g_{2}(r) \frac{\mathrm{dr}}{r} \end{aligned}$$

for any \(t\in I\). Then we get the following inequalities as a result.

$$\begin{aligned} & \bigl\vert \ell _{1}(t) - \ell _{2}(t) \bigr\vert \\ &\quad \leq \frac{1}{\Gamma (\iota _{1}+\iota _{2}+\iota _{3})} \int _{1}^{t} \biggl( \ln \frac{t}{r} \biggr)^{\iota _{1}+\iota _{2}+\iota _{3} -1} \bigl\vert g_{1}(r) - g_{2}(r) \bigr\vert \frac{\mathrm{dr}}{r} \\ &\qquad {}+ \frac{1}{2\Gamma (\iota _{1}+\iota _{2}+\iota _{3})} \int _{1}^{e} \biggl( \ln \frac{e}{r} \biggr)^{\iota _{1}+\iota _{2}+\iota _{3} -1} \bigl\vert g_{1}(r) - g_{2}(r) \bigr\vert \frac{\mathrm{dr}}{r} \\ &\qquad{} + \frac{ \vert F_{1}(t) \vert }{2\Gamma (1 + \iota _{3})\Gamma (\iota _{1} + \iota _{2})} \int _{1}^{\eta} \biggl( \ln \frac{\eta}{r} \biggr)^{\iota _{1} + \iota _{2} -1} \bigl\vert g_{1}(r) - g_{2}(z) \bigr\vert \frac{\mathrm{dr}}{r} \\ &\qquad {}+ \frac{ \vert F_{2}(t) \vert }{2\Gamma (1+\iota _{2} + \iota _{3} )\Gamma (1 + \iota _{2})\Gamma (1 + \iota _{3})\Gamma (\iota _{1})} \\ & \qquad{} \times \int _{1}^{e} \biggl( \ln \frac{e}{r} \biggr)^{\iota _{1} -1} \bigl\vert g_{1}(r) - g_{2}(z) \bigr\vert \frac{\mathrm{dr}}{r} \\ &\quad \leq \frac{ (\ln t)^{\iota _{1}+\iota _{2}+\iota _{3}} }{\Gamma (\iota _{1}+\iota _{2}+\iota _{3}+1)} \Vert \kappa \Vert \biggl( \frac{\vartheta ^{\star}}{ \Vert \kappa \Vert } \biggr) \psi \bigl( \Vert y - \bar{y} \Vert \bigr) \\ &\qquad {}+ \frac{1}{2\Gamma (\iota _{1}+\iota _{2}+\iota _{3}+1)} \Vert \kappa \Vert \biggl( \frac{\vartheta ^{\star}}{ \Vert \kappa \Vert } \biggr) \psi \bigl( \Vert y - \bar{y} \Vert \bigr) \\ &\qquad {}+ \frac{ F_{1}^{*} (\ln \eta )^{\iota _{1}+\iota _{2}} }{2\Gamma (1 + \iota _{3})\Gamma (\iota _{1} + \iota _{2}+1)} \Vert \kappa \Vert \biggl( \frac{\vartheta ^{\star}}{ \Vert \kappa \Vert } \biggr) \psi \bigl( \Vert y - \bar{y} \Vert \bigr) \\ & \qquad {}+ \frac{ F_{2}^{*} }{2\Gamma (1+\iota _{2} + \iota _{3} )\Gamma (1 + \iota _{2})\Gamma (1 + \iota _{3})\Gamma (\iota _{1}+1)} \\ & \qquad{} \times \Vert \kappa \Vert \biggl( \frac{\vartheta ^{\star}}{ \Vert \kappa \Vert } \biggr) \psi \bigl( \Vert y - \bar{y} \Vert \bigr) \\ &\quad = \biggl[\frac{ 3 }{2\Gamma (\iota _{1}+\iota _{2}+\iota _{3}+1)} + \frac{ F_{1}^{*} (\ln \eta )^{\iota _{1}+\iota _{2}} }{2\Gamma (1 + \iota _{3})\Gamma (\iota _{1} + \iota _{2}+1)} \\ & \qquad{} + \frac{ F_{2}^{*} }{2\Gamma (1+\iota _{2} + \iota _{3} )\Gamma (1 + \iota _{2})\Gamma (1 + \iota _{3})\Gamma (\iota _{1}+1)} \biggr] \\ & \qquad{} \times \Vert \kappa \Vert \biggl( \frac{\vartheta ^{\star}}{ \Vert \kappa \Vert } \biggr) \psi \bigl( \Vert y - \bar{y} \Vert \bigr) \\ &\quad = \vartheta ^{\star} \check{\Lambda}_{1} \psi \bigl( \Vert y - \bar{y} \Vert \bigr). \end{aligned}$$

Also, we have

$$\begin{aligned} & \bigl\vert {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}}\ell _{1}(t) - {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}} \ell _{2}(t) \bigr\vert \\ &\quad \leq \biggl[ \frac{1}{ \Gamma (\iota _{1}+\iota _{2}+1)} + \frac{ F_{1}^{**}(\ln \eta )^{\iota _{1}+\iota _{2}} }{2\Gamma (1 + \iota _{3})\Gamma (\iota _{1} + \iota _{2}+1)} \\ &\quad\quad{}+ \frac{ F_{2}^{**} }{2\Gamma (1+\iota _{2} + \iota _{3} )\Gamma (1 + \iota _{2})\Gamma (1 + \iota _{3})\Gamma (\iota _{1}+1)} \biggr] \\ &\quad \quad {}\times \Vert \kappa \Vert \biggl( \frac{\vartheta ^{\star}}{ \Vert \kappa \Vert } \biggr) \psi \bigl( \Vert y - \bar{y} \Vert \bigr) \\ &\quad= \vartheta ^{\star} \check{\Lambda}_{2} \psi \bigl( \Vert y - \bar{y} \Vert \bigr) \end{aligned}$$

and

$$\begin{aligned} &\bigl\vert {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}\ell _{1}(t) \bigr) - {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}} \ell _{2}(t)\bigr) \bigr\vert \\ &\quad \leq \biggl[ \frac{1}{ \Gamma (\iota _{1}+1) } \\ &\quad \quad {}+ \frac{ F_{2}^{***} }{2\Gamma (1+\iota _{2} + \iota _{3} )\Gamma (1 + \iota _{2})\Gamma (1 + \iota _{3})\Gamma (\iota _{1}+1)} \biggr] \\ &\quad \quad {}\times \Vert \kappa \Vert \biggl( \frac{\vartheta ^{\star}}{ \Vert \kappa \Vert } \biggr) \psi \bigl( \Vert y - \bar{y} \Vert \bigr) \\ &\quad= \vartheta ^{\star} \check{\Lambda}_{3} \psi \bigl( \Vert y - \bar{y} \Vert \bigr) \end{aligned}$$

for all \(t\in I\). Consequently,

$$\begin{aligned} \Vert \ell _{1} - \ell _{2} \Vert & = \sup _{t\in I} \bigl\vert \ell _{1}(t) - \ell _{2}(t) \bigr\vert + \sup_{t\in I} \bigl\vert {}^{CH }\mathbb{D}_{1^{+}}^{ \iota _{3}}\ell _{1}(t) - {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}} \ell _{2}(t) \bigr\vert \\ &\quad {}+ \sup_{t\in I} \bigl\vert {}^{CH } \mathbb{D}_{1^{+}}^{ \iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}\ell _{1}(t) \bigr) -{}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{ \iota _{3}}\ell _{2}(t)\bigr) \bigr\vert \\ &\leq \vartheta ^{\star} (\check{\Lambda}_{1} + \check{\Lambda}_{2} + \check{\Lambda}_{3}) \psi \bigl( \Vert y - \bar{y} \Vert \bigr) = \psi \bigl( \Vert y - \bar{y} \Vert \bigr). \end{aligned}$$

Accordingly, \(\phi (y, \bar{y}) \mathbb{H}_{\rho} ( K (y), K(\bar{y}) ) \leq \psi (\Vert y - \bar{y} \Vert )\) for all \(y, \bar{y} \in A\). This confirms that K is a ϕ-ψ-contraction. Next, suppose that \(y \in A\) and \(\bar{y} \in K (y)\) s.t. \(\phi (y, \bar{y}) \geq 1\) and

$$\begin{aligned} &\Omega _{\star}\bigl( \bigl( y(t), {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y(t), {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{ \iota _{3}}y(t) \bigr) \bigr), \\ & \quad \bigl( \bar{y}(t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}} \bar{y}(t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}\bar{y}(t) \bigr) \bigr) \bigr) \geq 0, \end{aligned}$$

so there exists \(\wp \in K(\bar{y})\) such that

$$\begin{aligned} &\Omega _{\star}\bigl( \bigl(\bar{y}(t), {}^{CH } \mathbb{D}_{1^{+}}^{ \iota _{3}}\bar{y}(t), {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}\bar{y}(t)\bigr) \bigr), \\ & \quad \bigl(\wp (t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}} \wp (t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH }\mathbb{D}_{1^{+}}^{ \iota _{3}}\wp (t) \bigr) \bigr) \bigr) \geq 0, \end{aligned}$$

which further implies that \(\phi (\bar{y}, \wp ) \geq 1\) and accordingly K is ϕ-admissible. Finally, let \(y^{0} \in A\) and \(\bar{y} \in K(y^{0})\) so that

$$\begin{aligned} &\Omega _{\star}\bigl( \bigl( y^{0}(t), {}^{CH } \mathbb{D}_{1^{+}}^{ \iota _{3}}y^{0}(t), {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{2}} \bigl( {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y^{0}(t) \bigr) \bigr), \\ & \quad \bigl(\bar{y}(t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}} \bar{y}(t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}\bar{y}(t)\bigr) \bigr) \bigr) \geq 0 \end{aligned}$$

for all \(t\in I\). It follows that \(\phi (y^{0}, \bar{y}) \geq 1\). Assume \(\{ y_{\jmath}\}_{\jmath \geq 1} \subset A\) s.t. \(y_{\jmath}\to y\) and \(\phi (y_{\jmath}, y_{\jmath +1}) \geq 1\) for all ȷ. Then we have

$$\begin{aligned} &\Omega _{\star}\bigl( \bigl(y_{\jmath}(t), {}^{CH } \mathbb{D}_{1^{+}}^{ \iota _{3}}y_{\jmath}(t), {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y_{\jmath}(t) \bigr) \bigr), \\ & \quad \bigl(y_{\jmath +1}(t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}}y_{ \jmath +1}(t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y_{\jmath +1}(t) \bigr) \bigr) \bigr) \geq 0. \end{aligned}$$

Then hypothesis \((\mathcal{H}_{4})\) confirms the existence of a subsequence \(\{ y_{\jmath _{s}} \}_{s\geq 1}\) of \(\{ y_{\jmath}\}\) satisfying

$$\begin{aligned} &\Omega _{\star}\bigl( \bigl( y_{\jmath _{s}}(t), {}^{CH } \mathbb{D}_{1^{+}}^{ \iota _{3}}y_{\jmath _{s}}(t), {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y_{\jmath _{s}}(t) \bigr) \bigr), \\ & \quad \bigl( y(t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}}y(t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{ \iota _{3}}y(t) \bigr) \bigr) \bigr) \geq 0 \end{aligned}$$

for all \(t\in I\). Thus, \(\phi (y_{\jmath _{s}}, y) \geq 1\) for all t, and accordingly it possesses the \((C_{\phi})\) condition. Hence, Theorem 3.3 allows that K possesses a fixed point which is a solution for the CHF-jerk inclusion (1). □

3.2 End point and jerk model (1)

Now, in the next place, by utilizing another theorem based on some other special multi-functions containing the AEP-property, we derive the second criterion guaranteeing the existence of solution for the supposed CHF-jerk problem (1).

Theorem 3.6

([42])

Consider \((A,\rho )\) as a complete metric space. Assume:

  1. (1)

    \(\psi \in \Psi \) is u.s.c along with \(\liminf_{t\to \infty}(t-\psi (t))>0\) for \(t>0\);

  2. (2)

    \(\mathbb{G} : A \to \mathcal{P}_{CL,BN}(A)\) admits the property

    $$ H_{\rho}(\mathbb{G} y_{1},\mathbb{G} y_{2})\leq \psi \bigl(\rho (y_{1}, y_{2})\bigr), \quad \forall y_{1}, y_{2} \in A.$$

Then \(\mathbb{G}\) admits one and exactly one end point iff \(\mathbb{G}\) contains the AEP-property.

Theorem 3.7

Take \(\mathbb{G}:I \times A^{3} \to \mathcal{P}_{CP}(A)\). Assume that

\((\mathcal{H}_{7})\):

There exists a nondecreasing and upper semi-continuous mapping \(\psi : \mathbb{R}_{\geq 0} \to \mathbb{R}_{\geq 0}\) which satisfies \(\psi (t) \leq t\), \(\forall t>0\) and \(\liminf_{t \to \infty} (t - \psi (t)) \geq 0\);

\((\mathcal{H}_{8})\):

Multifunction \(\mathbb{G}:I \times A^{3} \to \mathcal{P}_{CP}(A)\) is bounded and integrable such that the map \(\mathbb{G}( \cdot , y_{1}, y_{2}, y_{3}): I \to \mathcal{P}_{CP}(A)\) is measurable for all \(y_{m} \in A \) (\(m=1,2,3\));

\((\mathcal{H}_{9})\):

There is a function \(\kappa \in {C}(I, [0, \infty ))\) s.t.

$$ {H}_{\rho} (\mathbb{G}(t, y_{1}, y_{2}, y_{3}), \mathbb{G}(t, \check{y}_{1}, \check{y}_{2}, \check{y}_{3} ) \leq \kappa (t) \varpi ^{\star} \psi \Biggl(\sum_{m=1}^{3} \vert y_{m} - \check{y}_{m} \vert \Biggr) $$
(18)

for all \(t\in I\) and \(y_{m}, \check{y}_{m} \in A \) (\(m=1,2,3\)), where

$$ \varpi ^{\star}= \frac {1}{\Xi _{1} + \Xi _{2} + \Xi _{3}}, \qquad \Xi _{m} = \Vert \kappa \Vert \check{\Lambda}_{m}\quad (m=1,2,3);$$
\((\mathcal{H}_{10})\):

The AEP-property is valid for the multi-function K.

Then the CHF-jerk problem (1) has a solution.

Proof

We want to establish that the multifunction \(K: A \to \mathcal{P}(A)\) possesses an end point. Initially, we claim that \(K(y)\) is closed \(\forall y\in A\). As the multifunction

$$ t \mapsto \mathbb{G} \bigl( t, y(t), {}^{CH }\mathbb{D}_{1^{+}}^{ \iota _{3}}y(t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y(t) \bigr) \bigr)$$

is both measurable and closed-valued for any \(y \in A\), so the \(\mathbb{G}\) has a measurable selection and \(S_{\mathbb{G}, y} \neq \emptyset \). By using the same procedure as that given in Theorem 3.5, it can be easily deduced that \(K(y)\) is closed-valued. Also, the compactness of \(\mathbb{G}\) ensures the boundedness of \(K(y)\). Next, assume that \(y, \check{y} \in A\) and \(\ell _{1} \in K(\check{y})\) and choose \(g_{1}\in S_{\mathbb{G}, \check{y}}\) such that

$$\begin{aligned} \ell _{1}(t) &= \frac{1}{\Gamma (\iota _{1}+\iota _{2}+\iota _{3})} \int _{1}^{t} \biggl( \ln \frac{t}{r} \biggr)^{\iota _{1}+\iota _{2}+ \iota _{3} -1} g_{1}(r) \frac{\mathrm{dr}}{r} \\ &\quad {}- \frac{1}{2\Gamma (\iota _{1}+\iota _{2}+\iota _{3})} \int _{1}^{e} \biggl( \ln \frac{e}{r} \biggr)^{\iota _{1}+\iota _{2}+\iota _{3} -1} g_{1}(r) \frac{\mathrm{dr}}{r} \\ &\quad {}+ \frac{F_{1}(t)}{2\Gamma (1 + \iota _{3})\Gamma (\iota _{1} + \iota _{2})} \int _{1}^{\eta} \biggl( \ln \frac{\eta}{r} \biggr)^{\iota _{1} + \iota _{2} -1} g_{1}(r) \frac{\mathrm{dr}}{r} \\ &\quad {}+ \frac{F_{2}(t)}{2\Gamma (1+\iota _{2} + \iota _{3} )\Gamma (1 + \iota _{2})\Gamma (1 + \iota _{3})\Gamma (\iota _{1})} \int _{1}^{e} \biggl( \ln \frac{e}{r} \biggr)^{\iota _{1} -1} g_{1}(r) \frac{\mathrm{dr}}{r} \end{aligned}$$

for all \(t\in I\). Also, for all \(y, \check{y} \in A\) and \(t\in I\), we have

$$\begin{aligned} \mathbb{H}_{\rho} & ( \mathbb{G} \bigl( t, y(t), {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y(t), {}^{CH } \mathbb{D}_{1^{+}}^{ \iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y(t) \bigr) \bigr), \\ & \quad \mathbb{G} \bigl(\check{y}(t), {}^{CH } \mathbb{D}_{1^{+}}^{ \iota _{3}}\check{y}(t), {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}\check{y}(t) \bigr) \bigr) \\ & \leq \kappa (t)\varpi ^{\star}\psi \bigl( \bigl\vert y(t) - \check{y}(t) \bigr\vert + \bigl\vert {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}}y(t) - {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}}\check{y}(t) \bigr\vert \\ & \quad {}+ \bigl\vert {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y(t) \bigr) - {}^{CH }\mathbb{D}_{1^{+}}^{ \iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}\check{y}(t) \bigr) \bigr\vert \bigr). \end{aligned}$$

There exists

$$ \grave{\wp} \in \mathbb{G} \bigl(t, y(t), {}^{CH }\mathbb{D}_{1^{+}}^{ \iota _{3}}y(t), {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y(t) \bigr) \bigr)$$

such that

$$\begin{aligned} \bigl\vert g_{1}(t) - \grave{\wp} \bigr\vert &\leq \kappa (t) \varpi ^{\star}\psi \bigl( \bigl\vert y(t) - \check{y}(t) \bigr\vert + \bigl\vert {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y(t) - {}^{CH }\mathbb{D}_{1^{+}}^{ \iota _{3}}\check{y}(t) \bigr\vert \\ &\quad{}+ \bigl\vert {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y(t) \bigr) - {}^{CH }\mathbb{D}_{1^{+}}^{ \iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}\check{y}(t) \bigr) \bigr\vert \bigr). \end{aligned}$$

We give a mapping \(\digamma : I \to \mathcal{P}(A)\) by

$$\begin{aligned} \digamma (t) & = \bigl\{ \grave{\wp} \in A : \bigl\vert g_{1}(t) - \grave{\wp} \bigr\vert \leq \kappa (t) \varpi ^{\star}\psi \bigl( \bigl\vert y(t) - \check{y}(t) \bigr\vert \\ & \quad {}+ \bigl\vert {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}}y(t) - {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}}\check{y}(t) \bigr\vert \\ &\quad {}+ \bigl\vert {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl( {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y(t) \bigr) - {}^{CH }\mathbb{D}_{1^{+}}^{ \iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}\check{y}(t) \bigr) \bigr\vert \bigr) \bigr\} \end{aligned}$$

for any \(t\in I\). Because \(g_{1}\) and

$$\begin{aligned} \Bbbk & = \kappa (t) \varpi ^{\star}\psi \bigl( \vert y - \check{y} \vert + \bigl\vert {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y - {}^{CH }\mathbb{D}_{1^{+}}^{ \iota _{3}}\check{y} \bigr\vert \\ & \quad {}+ \bigl\vert {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y \bigr) - {}^{CH } \mathbb{D}_{1^{+}}^{ \iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}} \check{y} \bigr) \bigr\vert \bigr) \end{aligned}$$

are measurable, thus

$$ \digamma (\cdot )\cap \mathbb{G} \bigl(\cdot , y(\cdot ), {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y(\cdot ), {}^{CH } \mathbb{D}_{1^{+}}^{ \iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y(\cdot ) \bigr) \bigr)$$

is too. Take

$$ g_{2} \in \mathbb{G} \bigl(t, y(t), {}^{CH } \mathbb{D}_{1^{+}}^{ \iota _{3}}y(t), {}^{CH } \mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y(t) \bigr) \bigr),$$

s.t. for all \(t\in I\) we get

$$\begin{aligned} \bigl\vert g_{1}(t) - g_{2}(t) \bigr\vert &\leq \kappa (t) \varpi ^{\star}\psi \bigl( \bigl\vert y(t) - \check{y}(t) \bigr\vert + \bigl\vert {}^{CH }\mathbb{D}_{1^{+}}^{ \iota _{3}}y(t) - {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}}\check{y}(t) \bigr\vert \\ &\quad {}+ \bigl\vert {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}y(t) \bigr) - {}^{CH }\mathbb{D}_{1^{+}}^{ \iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{\iota _{3}}\check{y}(t) \bigr) \bigr\vert \bigr). \end{aligned}$$

Define \(\ell _{2} \in K(y)\) by

$$\begin{aligned} \ell _{2}(t) &= \frac{1}{\Gamma (\iota _{1}+\iota _{2}+\iota _{3})} \int _{1}^{t} \biggl( \ln \frac{t}{r} \biggr)^{\iota _{1}+\iota _{2}+ \iota _{3} -1} g_{2}(r) \frac{\mathrm{dr}}{r} \\ &\quad {}- \frac{1}{2\Gamma (\iota _{1}+\iota _{2}+\iota _{3})} \int _{1}^{e} \biggl( \ln \frac{e}{r} \biggr)^{\iota _{1}+\iota _{2}+\iota _{3} -1} g_{2}(r) \frac{\mathrm{dr}}{r} \\ &\quad {}+ \frac{F_{1}(t)}{2\Gamma (1 + \iota _{3})\Gamma (\iota _{1} + \iota _{2})} \int _{1}^{\eta} \biggl( \ln \frac{\eta}{r} \biggr)^{\iota _{1} + \iota _{2} -1} g_{2}(r) \frac{\mathrm{dr}}{r} \\ &\quad {}+ \frac{F_{2}(t)}{2\Gamma (1+\iota _{2} + \iota _{3} )\Gamma (1 + \iota _{2})\Gamma (1 + \iota _{3})\Gamma (\iota _{1})} \int _{1}^{e} \biggl( \ln \frac{e}{r} \biggr)^{\iota _{1} -1} g_{2}(r) \frac{\mathrm{dr}}{r} \end{aligned}$$

for any \(t\in I\). Using the same techniques that were employed in the proof of Theorem 3.5, we get that

$$\begin{aligned} \Vert \ell _{1} - \ell _{2} \Vert &= \sup _{t\in I} \bigl\vert \ell _{1}(t) - \ell _{2}(t) \bigr\vert + \sup_{t\in I} \bigl\vert {}^{CH }\mathbb{D}_{1^{+}}^{ \iota _{3}}\ell _{1}(t) - {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{3}} \ell _{2}(t) \bigr\vert \\ &\quad {}+ \sup_{t\in I} \bigl\vert {}^{CH } \mathbb{D}_{1^{+}}^{ \iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{ \iota _{3}}\ell _{1}(t) \bigr) - {}^{CH }\mathbb{D}_{1^{+}}^{\iota _{2}} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{ \iota _{3}}\ell _{2}(t) \bigr)\bigr\vert \\ &\leq \varpi ^{\star} (\Xi _{1} + \Xi _{2} + \Xi _{3} ) \psi \bigl( \Vert y - \check{y} \Vert \bigr) = \psi \bigl( \Vert y - \check{y} \Vert \bigr). \end{aligned}$$

We get

$$ {H}_{\rho} \bigl( K (y) , K(\check{y}) \bigr) \leq \psi \bigl( \Vert y - \check{y} \Vert \bigr), \quad \forall y, \check{y} \in A.$$

Hypothesis \((\mathcal{H}_{10})\) gives the approximate property for the end points of K. Hence, due to Theorem 3.6, \(\exists y_{*} \in A\) s.t. \(K(y_{*})= \{ y_{*} \}\). As a result, \(y_{*}\) is a solution of the CHF-jerk problem (1). □

4 Example

We give an example for simulating and analyzing the results numerically.

Example 4.1

We model the following CHF-jerk inclusion BVP by assuming the constant values \(\iota _{1}=0.5\), \(\iota _{2} = 0.7\), \(\iota _{3} = 0.99\) as

$$ \textstyle\begin{cases} ( {}^{CH }\mathbb{D}_{1^{+}}^{0.5} ( {}^{CH }\mathbb{D}_{1^{+}}^{0.7} ({}^{CH }\mathbb{D}_{1^{+}}^{0.99}y) ) )(t) \in [ 0, \frac {1}{4} ( t \vert \sin (y (t)) \vert + t \vert {}^{CH } \mathbb{D}_{1^{+}}^{0.99} y(t) \vert \\\quad {}+ 0.5t \vert \tan ^{-1} ( {}^{CH }\mathbb{D}_{1^{+}}^{0.7} ({}^{CH }\mathbb{D}_{1^{+}}^{0.99} y)(t) ) \vert ) + 2\exp{(t)} ], \\y(1) + y(e) = 0, \qquad {}^{CH }\mathbb{D}_{1^{+}}^{0.99} y (2.69) = 0, \qquad {}^{CH }\mathbb{D}_{1^{+}}^{0.7} ( {}^{CH }\mathbb{D}_{1^{+}}^{0.99} y (e) ) = 0, \end{cases} $$
(19)

where \(t \in I :=[1,e]\), and we choose \(\eta =2.69 \in (1,e)\). Now, consider the multi-function \(\mathbb{G}:I \times A^{3} \to \mathcal{P}_{CP}(A)\) defined by

$$\begin{aligned} \mathbb{G} \bigl( t, y_{1}(t), y_{2}(t), y_{3}(t) \bigr) &= \biggl[ 0, \frac{1}{4} \bigl( t \bigl\vert \sin \bigl(y_{1} (t) \bigr) \bigr\vert \\ & \quad {}+ t \bigl\vert y_{2}(t) \bigr\vert + 0.5t \bigl\vert \tan ^{-1} \bigl( y_{3}(t) \bigr) \bigr\vert \bigr) + 2 \exp{(t)} \biggr], \end{aligned}$$

where

$$ A = \bigl\{ y(t): y(t), {}^{CH }\mathbb{D}_{1^{+}}^{0.99}y(t), {}^{CH }\mathbb{D}_{1^{+}}^{0.7} \bigl({}^{CH } \mathbb{D}_{1^{+}}^{0.99}y(t)\bigr) \in C\bigl([1,e], \mathbb{R} \bigr) \bigr\} .$$

Some calculations, by the above data and using (13), give \(F_{1}^{*}=3\),

$$\begin{aligned} F_{2}^{*}& = 3\Gamma (1+\iota _{2}) \Gamma (1+ \iota _{3}) + 3\Gamma (1 + \iota _{2} + \iota _{3}) ( \ln \eta )^{\iota _{2}} \\ & = 3\Gamma (1.7)\Gamma (1.99) + 3\Gamma (2.69) ( \ln 2.69 )^{0.7} \simeq 7.278176, \end{aligned}$$

\(F_{1}^{**}= 2 \Gamma (1.99)= 1.991626\),

$$\begin{aligned} F_{2}^{**} & = 2\Gamma (1 + \iota _{2} + \iota _{3}) \Gamma (1+\iota _{3}) \bigl(1 + ( \ln \eta )^{\iota _{2}} \bigr) \\ & =2\Gamma (2.69) \Gamma (1.99) \bigl(1 + ( \ln 2.69 )^{0.7} \bigr) \simeq 6.0818, \end{aligned}$$

\(F_{1}^{***}=0\),

$$\begin{aligned} F_{2}^{***}& = 2 \Gamma (1+ \iota _{3}) \Gamma (1+ \iota _{2} + \iota _{3}) \Gamma (1+\iota _{2}) \\ & = 2 \Gamma (1.99) \Gamma (2.69) \Gamma (1.7)\simeq 2.773247, \end{aligned}$$

and

$$\begin{aligned}& \begin{aligned} \check{\Lambda}_{1} &= \frac{ 3 }{2\Gamma (\iota _{1}+\iota _{2}+\iota _{3}+1)} + \frac{ F_{1}^{*} (\ln \eta )^{\iota _{1}+\iota _{2}} }{2\Gamma (1 + \iota _{3})\Gamma (\iota _{1} + \iota _{2}+1)} \\ & \quad {}+ \frac{ F_{2}^{*} }{2\Gamma (1+\iota _{2} + \iota _{3} )\Gamma (1 + \iota _{2})\Gamma (1 + \iota _{3})\Gamma (\iota _{1}+1)} \\ &= \frac{ 3 }{2\Gamma (3.19)} + \frac{ 3 (\ln 2.69)^{1.2}}{ 2\Gamma (1.99)\Gamma (2.2)} \\ & \quad {}+ \frac{ 7.278176}{2\Gamma (2.69)\Gamma (1.7)\Gamma (1.99)\Gamma (1.5)} \\ & \simeq 4.936355, \end{aligned} \\& \begin{aligned} \check{\Lambda}_{2} &= \frac{1}{ \Gamma (\iota _{1}+\iota _{2}+1)} + \frac{ F_{1}^{**}(\ln \eta )^{\iota _{1}+\iota _{2}} }{2\Gamma (1 + \iota _{3})\Gamma (\iota _{1} + \iota _{2}+1)} \\ & \quad {}+ \frac{ F_{2}^{**} }{2\Gamma (1+\iota _{2} + \iota _{3} )\Gamma (1 + \iota _{2})\Gamma (1 + \iota _{3})\Gamma (\iota _{1}+1)} \\ & = \frac{1}{ \Gamma (2.2)} + \frac{ 1.991626(\ln 2.69)^{1.2} }{2\Gamma (1.99)\Gamma (2.2)} \\ & \quad {}+ \frac{ 6.0818 }{2\Gamma (2.69)\Gamma (1.7)\Gamma (1.99)\Gamma (1.5)} \\ & \simeq 4.278391, \end{aligned} \\& \begin{aligned} \check{\Lambda}_{3} &= \frac{1}{ \Gamma (\iota _{1}+1) } + \frac{ F_{2}^{***} }{2\Gamma (1+\iota _{2} + \iota _{3} )\Gamma (1 + \iota _{2})\Gamma (1 + \iota _{3})\Gamma (\iota _{1}+1)} \\ & = \frac{1}{ \Gamma (1.5) } + \frac{ 2.7732476 }{2\Gamma (2.69)\Gamma (1.7)\Gamma (1.99)\Gamma (1.5)} \\ & \simeq 2.256758. \end{aligned} \end{aligned}$$

For each \(y_{m}, \bar{y}_{m} \in \mathbb{R} \) (\(m=1,2,3\)), we have

$$\begin{aligned} &{H}_{\rho} \bigl( \mathbb{G} \bigl(t, y_{1}(t), y_{2}(t), y_{3}(t) \bigr), \mathbb{G} \bigl(t, \bar{y}_{1}(t), \bar{y}_{2}(t), \bar{y}_{3}(t) \bigr) \bigr) \\ &\quad\leq \frac{t}{4} \bigl( \bigl\vert \sin \bigl(y_{1}(t) \bigr)- \sin \bigl(\bar{y}_{1} (t)\bigr) \bigr\vert + \bigl\vert y_{2}(t) - \bar{y}_{2}(t) \bigr\vert \\ &\quad \quad {}+ \bigl\vert \tan ^{-1}\bigl( y_{3}(t)\bigr) - \tan ^{-1}\bigl(\bar{y}_{3} (t) \bigr) \bigr\vert \bigr) \\ &\quad\leq \frac{t}{4} \bigl( \bigl\vert y_{1}(t) - \bar{y}_{1} (t) \bigr\vert + \bigl\vert y_{2}(t) - \bar{y}_{2} (t) \bigr\vert + \bigl\vert y_{3}(t) - \bar{y}_{3} (t) \bigr\vert \bigr) \\ &\quad= \frac{t}{4} \Biggl( \sum_{i=1}^{3} \bigl\vert y_{i}(t) - \bar{y}_{i} (t) \bigr\vert \Biggr) \\ &\quad= \frac{t}{4} \psi \Biggl( \sum_{i=1}^{3} \bigl\vert y_{i}(t) - \bar{y}_{i} (t) \bigr\vert \Biggr) \\ &\quad= \kappa (t)\psi \Biggl( \sum_{i=1}^{3} \bigl\vert y_{i}(t) - \bar{y}_{i} (t) \bigr\vert \Biggr) \\ &\quad\leq \kappa (t)\varpi ^{\star}\psi \Biggl( \sum _{i=1}^{3} \bigl\vert y_{i}(t) - \bar{y}_{i} (t) \bigr\vert \Biggr). \end{aligned}$$

Hence, from the above, it is found a function \(\kappa \in {C}(I, [0, \infty ))\) as \(\kappa (t)=\frac {t}{2}\) for all \(t\in I = [1,e]\). Then

$$ \Vert \kappa \Vert = \sup_{t \in I} \biggl\vert \frac {t}{2} \biggr\vert = \frac {e}{2} \simeq 1.355.$$

Next, define \(\psi : [0, \infty ) \to [0, \infty )\) by \(\psi (t) = \frac {t}{2}\) for (a.e.) \(t >0\). It is simple to verify that

$$ \liminf_{t \to \infty} \bigl(t - \psi (t)\bigr) >0,$$

and \(\psi (t) < t\) for all \(t >0\). Also, we obtain

$$ \varpi ^{\star}= \frac {1}{\Xi _{1} + \Xi _{2} + \Xi _{3}},\quad \Xi _{m} = \Vert \kappa \Vert \check{\Lambda}_{m}\ (m=1,2,3),$$

in which

$$\begin{aligned} \Xi _{1} & \simeq \Vert \kappa \Vert \check{\Lambda}_{1} \simeq 6.688761, \\ \Xi _{2} & \simeq \Vert \kappa \Vert \check{ \Lambda}_{2} \simeq 5.797221, \\ \Xi _{3} & \simeq \Vert \kappa \Vert \check{ \Lambda}_{3} \simeq 3.057907. \end{aligned}$$

Thus

$$ \varpi ^{\star}=\frac {1}{\Xi _{1} + \Xi _{2} + \Xi _{1}} \simeq \frac {1}{15.543889} \simeq 0.064333 $$

for all \(t\in I\). In the sequel, we regard the multi-function \(K: A \to \mathcal{P}(A)\) by

$$ K(y)= \bigl\{ z\in A: \text{there exists } g\in \mathit{S}_{\mathbb{G}, y} \text{ such that } z(t)= \pi (t), \forall t\in I \bigr\} , $$

for which

$$\begin{aligned} \pi (t)&=\frac{1}{\Gamma (2.19)} \int _{1}^{t} \biggl( \ln \frac{t}{r} \biggr)^{1.19} g(r) \frac{\mathrm{dr}}{r} \\ &\quad {}- \frac{1}{2\Gamma (2.19)} \int _{1}^{e} \biggl( \ln \frac{e}{r} \biggr)^{1.19} g(r) \frac{\mathrm{dr}}{r} \\ &\quad {}+ \frac{F_{1}(t)}{2\Gamma (1.99)\Gamma (1.2)} \int _{1}^{\eta} \biggl( \ln \frac{\eta}{r} \biggr)^{0.2} g(r) \frac{\mathrm{dr}}{r} \\ &\quad {}+ \frac{F_{2}(t)}{2\Gamma (2.69)\Gamma (1.7)\Gamma (1.99)\Gamma (0.5)} \int _{1}^{e} \biggl( \ln \frac{e}{r} \biggr)^{-0.5} g(r) \frac{\mathrm{dr}}{r}, \end{aligned}$$
(20)

where

$$ \textstyle\begin{cases} F_{1}(t) = 1- 2 ( \ln t )^{\iota _{3}}= 1- 2 ( \ln t )^{0.99}, \\F_{2}(t) = \Gamma (1+\iota _{2}) \Gamma (1+ \iota _{3}) [ 1- 2 ( \ln t )^{\iota _{2} + \iota _{3}} ] \\\hphantom{F_{2}(t) =} {}- \Gamma (1 + \iota _{2} + \iota _{3}) ( \ln \eta )^{\iota _{2}} [ 1- 2 ( \ln t )^{\iota _{3}} ] \\\hphantom{F_{2}(t)} = \Gamma (1.7) \Gamma (1.99) [ 1- 2 ( \ln t )^{1.69} ] \\\hphantom{F_{2}(t) =} {}- \Gamma (2.69) ( \ln 2.69 )^{0.7} [ 1- 2 ( \ln t )^{0.99} ]. \end{cases} $$
(21)

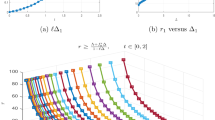
One can see the results of \(F_{1}(t)\), \(F_{2}(t)\) for \(t \in [1, e]\) in Table 1 and can see a graphical representation of them in Fig. 1. As the multi-function K possesses an approximate end point property, hence by using Theorem 3.7, the supposed CHF-jerk problem (19) admits a solution.

Figure 1
figure 1

Graphical representation of \(F_{1}(t)\) and \(F_{2}(t)\) for \(t \in I\)

Full size image
Table 1 Numerical results of \(F_{1}(t)\) and \(F_{2}(t)\) for \(t \in I\)
Full size table

5 Conclusion

In this research work, a generalization of the standard jerk equation in the context of the Caputo–Hadamard differential inclusion (1) was provided, in which we used some inequalities and important properties of multi-valued functions in the framework of the special contractions and admissible mappings. We extracted existence properties of solutions of the mentioned inclusion (1) by applying two different notions of fixed points and end points in functional analysis. This type of the Caputo–Hadamard structure for a jerk problem is a newly-defined FBVP, and we tried to establish our results based on some new non-routine techniques of fixed point and end point theories. With the help of an example, we described our method numerically and graphically. Due to the importance of jerk in the modern physics, it is necessary that we continue our study on the extended models of such physical structures and investigate other qualitative properties of them.