Abstract
Background
Barley, globally the fourth most important cereal, provides food and beverages for humans and feed for animal husbandry. Maximizing grain yield under varying climate conditions largely depends on the optimal timing of flowering. Therefore, regulation of flowering time is of extraordinary importance to meet future food and feed demands. We developed the first barley nested association mapping (NAM) population, HEB-25, by crossing 25 wild barleys with one elite barley cultivar, and used it to dissect the genetic architecture of flowering time.
Results
Upon cultivation of 1,420 lines in multi-field trials and applying a genome-wide association study, eight major quantitative trait loci (QTL) were identified as main determinants to control flowering time in barley. These QTL accounted for 64% of the cross-validated proportion of explained genotypic variance (pG). The strongest single QTL effect corresponded to the known photoperiod response gene Ppd-H1. After sequencing the causative part of Ppd-H1, we differentiated twelve haplotypes in HEB-25, whereof the strongest exotic haplotype accelerated flowering time by 11 days compared to the elite barley haplotype. Applying a whole genome prediction model including main effects and epistatic interactions allowed predicting flowering time with an unmatched accuracy of 77% of cross-validated pG.
Conclusions
The elaborated causal models represent a fundamental step to explain flowering time in barley. In addition, our study confirms that the exotic biodiversity present in HEB-25 is a valuable toolbox to dissect the genetic architecture of important agronomic traits and to replenish the elite barley breeding pool with favorable, trait-improving exotic alleles.
Similar content being viewed by others
Background
Barley is among the oldest crop species human civilization was built on. Approximately 10,500 years ago, barley was domesticated in the Fertile Crescent [1,2], presumably followed by additional independent domestication events in East Asia [3,4]. Domestication and subsequent genetic selection led to gene erosion in most crop species’ gene pools [5,6], threatening future breeding advances. Utilizing the untapped biodiversity, present in wild progenitors is one promising approach to replenish the elite breeding pool with new favorable alleles [6-13]. The enriched diversity may be pivotal to boost the rate of genetic improvement and to cope with the anticipated enhanced effects of biotic and abiotic stresses due to climate change.
In this regard, time of flowering is expected to play a major role in future crop improvement. It is a key trait for the successful completion of a plant’s life cycle and, therefore, it has a strong impact on grain yield [14]. Flowering time indicates the transition from vegetative to reproductive stage, which is mainly influenced by environmental cues like day length (photoperiod) and prolonged exposure to cold temperatures (vernalization). In barley, the day length determining light signal is transmitted from a circadian clock oscillator, with Ppd-H1, a PSEUDO-RESPONSE REGULATOR 7 (PRR7) gene, in its center [15]. Under long day condition, Ppd-H1, through mediation of CONSTANS (CO), promotes the expression of the floral inducer Vrn-H3, a homolog of the Arabidopsis thaliana FLOWERING LOCUS T (FT) gene [16]. On the other hand, Vrn-H2, a zinc-finger CONSTANS, CO-like and TOC1 (CCT)-domain protein (ZCCT1) acts as a repressor of Vrn-H3 [17]. Vrn-H2, in turn, is repressed by Vrn-H1, an APETALA1 family MADS-box transcription factor [18], which is up-regulated during vernalization. Thus, after vernalization, the repression of Vrn-H3 is abolished and flowering is induced. Based on its vernalization requirement, winter barley and spring barley can be distinguished. Spring barley lacks the vernalization requirement due to a deletion of Vrn-H2 [19].
Besides photoperiod and vernalization, there are also genetic mechanisms acting independently of environmental cues, so-called earliness per se [20]. Although several key regulatory cereal genes of flowering time were characterized and finally cloned during the last two decades, still little is known about the genetic architecture underlying flowering time regulation in temperate cereals, as compared to the model species A. thaliana [14,21-23]. So far, a holistic explanation of flowering time in a segregating germplasm population and the accurate prediction of a plant’s time of flowering, based on the combined action and interaction of major genes, is still not fully achieved in cereal species. Furthermore, it is reported that wild barley accessions possess a rich reservoir of beneficial alleles controlling flowering time [7,24,25].
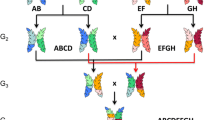
Nested association mapping (NAM) emerged as a multi-parental mapping design to investigate genomic regions with unprecedented genetic resolution and allelic variation by combining the advantages of linkage analysis and association mapping [26]. Hence, it facilitates the elucidation of a trait’s genetic architecture via genome-wide association study (GWAS). Until now, the NAM design was applied to the allogamous species maize and sorghum [26,27]. NAM populations for autogamous species like barley or wheat have not been developed, yet. In maize, the genetic dissection of various agronomic traits, including flowering time, has been investigated [28-34]. However, it was not possible to completely dissect the genetic architecture of flowering time in maize due to its complex inheritance and the multitude of involved small effect QTL. We developed the first NAM population in the autogamous species barley, termed ‘Halle Exotic Barley 25’ (HEB-25). The population results from initial crosses between the spring barley elite cultivar Barke (Hordeum vulgare ssp. vulgare, Hv) and 25 highly divergent exotic barley accessions, contributing an ideal instrument to study biodiversity. The exotic donors comprise 24 wild barley accessions of H. vulgare ssp. spontaneum (Hsp), the progenitor of domesticated barley, and one Tibetian H. vulgare ssp. agriocrithon (Hag) accession. Barke was selected since it was also used as a parent of a barley high-resolution mapping population [35] and as a genetic stock for mutation screening [36]. The exotic donors were selected from Badr et al. [37] to represent a substantial part of the genetic diversity that is present across the Fertile Crescent, where barley domestication occurred. To generate the nested population, F1 plants were backcrossed to Barke and, subsequently, selfed three times (Figure 1). In total, HEB-25 consists of 1,420 BC1S3 lines, divided into 25 HEB families of up to 75 lines per family (Additional file 1).
Development of the nested association mapping population HEB-25. HEB-25 is made of 25 families with 1,420 NAM lines in BC1S3. Per NAM line, one chromosome pair is illustrated as a double bar. Black and colored bars represent chromosome segments originating from Barke and the exotic donor accessions, respectively. At each SNP locus, HEB-25 is expected to segregate into 71.875% homozygous Barke, 6.25% heterozygous and 21.875% homozygous donor genotypes.
In the present study we investigated the genetic architecture of flowering time in barley. For this purpose, the NAM population HEB-25 was grown from 2011 to 2013 in multi-field trials to gather data on flowering time. By combining these data with high-density SNP marker information via genome-wide association studies and genomic prediction models, we could show that flowering time in barley mainly depends on a low number of large-effect QTL and epistatic interactions.
Results and discussion
Characterization of HEB-25
The inheritance of parental segments across the genomes of the 1,420 HEB lines was characterized through genotyping 5,709 informative, genic single nucleotide polymorphism (SNP) markers [35]. Marker saturation was high with an average genetic distance of 0.17 cM and a maximum gap of 11.1 cM between adjacent markers. Linkage disequilibrium (LD) among the 26 parents decayed rapidly (Additional file 2) enabling a high mapping resolution [26]. The SNP data revealed a low degree of genetic similarity between Barke and the donors, ranging from 40 to 54% (Additional file 1). Parents and the HEB-25 population could be clearly separated in a principal component analysis (PCA) (Additional file 3). Also, HEB families could be ordered in the PCA based on their geographical origin. These findings point to the high genetic diversity that is present among HEB-25 and its parents.
Diversity in HEB-25 was also visible phenotypically. During the seasons 2011 through 2013, HEB-25 was cultivated at the Halle University Experimental Field Station to collect flowering time data. The HEB lines flowered on average 68.1 days after sowing with a range from 51.0 to 98.9 days and a standard deviation of 6.5 days (Additional files 4 and 5). The broad variation in flowering time, covering almost 50 days among the 1,420 HEB lines, and a high heritability of 91.6%, as well as the genetic properties of the NAM population provided an excellent starting point to study the genetic architecture of flowering time through GWAS.
Genome-wide association study
For GWAS, we initially applied the multiple linear regression Model-B with step-wise selection of cofactors, as outlined in Liu et al. [38]. Model-B was found most suitable to study traits across multiple related families [39], where a family effect and additional SNPs, selected as cofactors, are included in the model. GWAS revealed eight highly significant major QTL regions controlling flowering time with PBON-HOLM < 1.0 E-10 (Table 1, Figure 2, Additional files 6 and 7). Testing the combined explanatory power of the single peak markers of the eight major QTL revealed a cross-validated explained proportion of genotypic variance (pG, [40]) of 64% (Figure 3). To check if genetic relatedness, as reported elsewhere [41], affects this parameter in HEB-25, we also estimated pG for different sets of eight randomly chosen SNPs, excluding regions with significant QTL. However, since the cross-validated explained pG remained low with an average of 8%, we conclude that genetic relatedness between individual lines does not play a major role in HEB-25. This emphasizes the power and precision of QTL detection in HEB-25, which may be a combined effect of the low extent of LD and the particular mating design, resulting in an elevated rate of chromosomal recombination. Thus, flowering time of barley can be reliably predicted based on eight major QTL. This finding is in contrast to flowering time regulation in the allogamous species maize and sorghum, where only small effect minor QTL were detected [28,42]. The most significant association in HEB-25 (PBON-HOLM = 3.4 E-130) was observed on the short arm of chromosome 2H and explained a pG of 36%. This SNP is directly located within Ppd-H1, the major determinant of photoperiod response in barley under long day condition [15]. Seven further genomic regions of extraordinary high significance were detected on chromosome arms 1HL, 2HS, 3HL, 4HS, 4HL, 5HL, and 7HS. All except one QTL (4HS) could be assigned to known flowering time genes (Table 1, Figure 2 and Additional file 7). Besides Ppd-H1, also the vernalization genes Vrn-H1 and Vrn-H2, as well as the floral inducer Vrn-H3 and its putative paralog HvCEN [43] exhibited highly significant effects. In addition, we could confirm the importance of gibberellic acid (GA) in flowering time regulation [44] through detection of denso [45] and HvELF3 [46,47] as two further major QTL. Both genes are shown to be involved in GA biosynthesis [45,48]. So far, only the QTL on 4HS could not been referenced. This QTL, thus, remains a subject for further genetic investigations.
Genetic architecture of flowering time in HEB-25. Barley chromosomes are indicated as colored bars on the inner circle, centromeres are highlighted as transparent boxes. a) Grey connector lines represent the genetic position of SNPs on the chromosomes. b) Frequency of QTL detection in 100 cross-validation runs via GWAS (0 to 100, grid line spacing: 25); markers with > 50 detections are colored in red. c) Additive effect of the SNP obtained from the BayesCπ genomic prediction model. d) Links in the center of the circle represent significant (PBON-HOLM < 0.05) di-genic interactions between SNP markers via GWAS. Clusters of significant SNP interactions are indicated by different colors. Position of candidate genes, potentially explaining major effects and epistatic effects, correspond to Table 1 and are indicated in blue outside the circle.
Cross-validated proportion of explained genotypic variance (pG) of different applied models. The box-whisker plots depict the variation of explained genotypic variance after 100 cross-validations. The tested QTL models are (i) the single SNP locus Ppd-H1 (Mean pG = 0.36), (ii) GWAS with peak markers, representing the eight major QTL indicated in Table 1 (Mean pG = 0.64), (iii) the whole genome ridge regression best linear unbiased prediction (RR-BLUP, mean pG = 0.71), (iv) the BayesCπ prediction (Mean pG = 0.74), and (v) RR-BLUP including epistasis (Mean pG = 0.77).
The eight major QTL were located with high genetic precision, with four QTL restricted to confidence intervals of less than 0.9 cM (Table 1). In cases where gene-specific SNPs were available (i.e. Ppd-H1 and Vrn-H3), exactly those SNPs revealed the highest significance within the respective QTL window (Additional file 6). The exotic alleles at Ppd-H1 and Vrn-H3 revealed the strongest effects, accelerating flowering time by 9.5 days and delaying flowering time by 4.1 days, respectively. The drastic effects of single QTL outline the high potential of introducing wild barley alleles from HEB-25 in order to adapt flowering time to environmental requirements and to enhance biodiversity in the elite barley breeding pool.
Ppd-H1 haplotype study
As we used bi-allelic SNP markers, additive effects were estimated across the NAM population. Theoretically, there may be up to 26 different alleles present at each locus in HEB-25. Thus, distinct alleles that show contrasting effects between families potentially escaped detection in our SNP-based GWAS. Contrasting effects are illustrated in Figure 4 and, in detail, in Additional file 6. For instance, SNPs at position 46.2 cM on chromosome 3H, which are tightly linked to HvGI [49], revealed opposing effects across HEB families. We tested the potential to integrate SNP haplotypes in the GWAS model for Ppd-H1, which exhibited the largest pG. After re-sequencing the last two exons and three introns of Ppd-H1, twelve haplotypes could be distinguished (Additional file 1). All Hsp donor haplotypes at Ppd-H1 showed a significantly reduced flowering time (Additional file 8 and Figure 5), where a maximum reduction of flowering time was associated with H-6 (−11.1 days compared to elite barley haplotype H-2). Only the Hag haplotype H-45 did not differ from H-2. This finding confirms the presence of haplotype-specific effects present in HEB-25. Consequently, we expect the existence of further haplotype effects for other candidate genes controlling flowering time. The haplotype-based Ppd-H1 model resulted in a slight increase of the cross-validated explained pG from 36% to 38%. This finding implies that modelling haplotype-specific effects for a substantial portion of the barley gene space may result in an improved prediction of flowering time in HEB-25. However, a genome-wide re-sequencing of HEB-25 lines will be required to identify and distinguish those haplotypes.
Visualization of family-wise SNP effects. Barley chromosomes are indicated as inner circle of colored bars, centromeres are highlighted as transparent boxes. Grey connector lines represent the genetic position of SNPs on chromosomes. Each track displays one HEB family (F01 – F25, from inside to outside). The heatmap indicates the difference in days between the donor and Barke genotype. Blue and red colors specify early and late flowering, respectively, caused by the donor genotype. White color indicates no SNP effect or SNPs monomorphic in the respective family. Candidate genes (Table 1) are indicated outside the circle. Black frames highlight their family-specific effects as indicated in Additional file 6.
Box-whisker plots of flowering time BLUEs for Ppd-H1 haplotypes. Green box-whisker-plots display the distribution of flowering time BLUEs of all HEB lines carrying the respective haplotype. Horizontal lines and diamonds indicate median and mean, respectively, for each haplotype. The extension of vertical lines indicates minimum and maximum observations, excluding outliers, which are indicated as circles. The red dotted horizontal line indicates the BLUE of cultivar Barke (68.2 days). H-2 represents the haplotype of the Barke genotype present in HEB lines. All haplotypes except H-45 differ significantly (P < 0.05) from H-2, as indicated by red asterisks. Further information to haplotypes is given in Additional files 1 and 8.
Applying genomic prediction models
To check whether we could further elucidate the genetic architecture of barley flowering time we applied genomic prediction models that considered all markers simultaneously. Genomic prediction evolved in animal breeding as a tool to predict a phenotype based on modelling a large set of SNP data [50]. It is used for selection of improved genotypes based on estimated genomic breeding values. Applying RR-BLUP [51] and BayesCπ [52] models, we could further increase the cross-validated explained pG to 71% and 74%, respectively (Figure 3). These findings are in agreement with comparisons of multiple linear regression and genomic prediction of traits in bi-parental plant populations [53]. However, our pG values substantially exceed the prediction accuracies of genomic prediction models reported in comparable studies [54-56], underlining the tremendous predictive power of HEB-25. Interestingly, compared to GWAS, only a few additional loci had non-zero effects in the BayesCπ model, indicating that flowering time is indeed mainly controlled by the eight major loci detected via GWAS.
We assume that important reasons for the slightly higher explained pG of genomic prediction compared to GWAS are that minor QTL effects and marginally existing genetic relatedness [55,57] among HEB lines may be better modeled in the first case. Furthermore, modeling all makers simultaneously enables a better prediction of flowering time due to the estimation of family-specific QTL effects. This is indicated by the occurrence of opposing additive effects between HEB families alongside tightly linked SNPs (Figure 2 and Additional file 6).
A model including epistasis to maximize the cross-validated explained pG
A final increase of the cross-validated explained pG to an extraordinary high level of 77% was achieved by including di-genic epistatic interactions between significant main effect SNPs in the RR-BLUP model. This finding indicates that epistasis explains a portion of the ‘missing heritability’ [58] of flowering time regulation in barley, whereas in maize it does not [28]. The term ‘missing heritability’ is highly debated in quantitative genetics and refers to the observation that the explained genotypic variance of combined marker effects is usually lower than the heritability of the trait. Epistatic interactions between candidate genes may point to functional relationships and genetic networks [59]. Our findings indicate that the flowering time genes HvGI, Vrn-H2, Vrn-H1 and HvCO1 [60] on chromosomes 3H, 4H, 5H and 7H, respectively, are probably major players of di-genic epistatic interactions in HEB-25. All four genes potentially interact with each other as well as with further genes on additional chromosomes (Figure 2 and Additional file 9). These observations are in agreement with independent studies in barley and A. thaliana where these interacting genes were placed in a day length and temperature depending signaling network that controls flowering time [14,21-23]. It is, thus, likely that the observed interaction between the chromosomal regions in HEB-25 may be a function of the mentioned flowering time genes. As an example we refer to the potential interaction found between Vrn-H1 and Vrn-H2. Epistatic interactions between these loci were already reported [17,61,62] and support the model that Vrn-H2 is a long-day suppressor of flowering, that is itself suppressed by Vrn-H1 following vernalization [63]. Barke is a spring type barley cultivar that lacks the vernalization requirement due to a deletion of Vrn-H2 [19]. Hence, our findings may indicate that the epistatic interaction found between the two regions on chromosomes 4H and 5H is based on the presence (exotic allele) or absence (Barke allele) of Vrn-H2, the target of Vrn-H1. In general, the epistatic interactions detected in HEB-25 may provide hints for the presence of so far unknown functional networks of genes, which assist in fine-tuning flowering time in barley. Studies with knock out lines of these genes may be used to validate the observed interaction effects.
Conclusions
The first barley NAM population HEB-25 provides great opportunities for future research and breeding. The genetic constitution of HEB-25 allows to carry out detailed studies on the genetic architecture of important agronomic traits, as exemplified by flowering time. The present study substantiated that flowering time in barley is primarily determined by large-effect QTL and epistatic interactions. This finding is in contrast to flowering time regulation in the allogamous species maize and sorghum, where only small effect minor QTL were detected [28,42], indicating that the mating system may control the genetic architecture of adaptive traits [28].
In future, the NAM population HEB-25 will be utilized in two directions: On the one hand, HEB-25 may support elucidating the genetic architecture of quantitatively inherited agronomic traits, ultimately resulting in cloning of yet unknown causal genes. On the other hand, HEB-25 will be exploited by breeders to enhance biodiversity of the elite barley gene pool. This may occur through introgression of favorable wild alleles with the aim to sustainably increase yield and stress tolerances against disadvantageous climate conditions like drought, heat and salt.
Methods
Development of the NAM population
The development of the NAM population ‘Halle Exotic Barley 25’ (HEB-25) was initiated in 2007 conducting crosses between the spring barley cultivar Barke (Hordeum vulgare ssp. vulgare) and 25 highly divergent exotic wild barley accessions. The latter were used as pollen donors. Twenty-four accessions, originating from Afghanistan, Iran, Iraq, Israel, Lebanon, Turkey, and Syria (Hordeum vulgare ssp. spontaneum), were selected to maximize the genetic diversity in HEB-25. One further accession, HID380, originating from Tibet, China, was classified as Hordeum vulgare ssp. agriocrithon (Åberg). F1 plants of the initial crosses were backcrossed with Barke as the female parent. Twenty BC1 plants per cross were subsequently selfed three times, using the single seed descent (SSD) technique to generate the next generations. The resulting BC1S3 generation consists of 1,420 individual lines, classified in 25 HEB families with 22 to 75 individual lines per family (Additional file 1). Subsequently, each HEB line was bulk propagated until BC1S3:6 to achieve sufficient seed numbers for field testing. No artificial selection was carried out during the development of HEB-25.
Collecting single nucleotide polymorphism (SNP) data
SNP genotype data were collected at TraitGenetics, Gatersleben, Germany, for all 1,420 individual BC1S3 lines and their corresponding parents with the barley Infinium iSelect 9k chip consisting of 7,864 SNPs [35]. At each locus, three genotypes were differentiated, with an expected BC1S3 segregation ratio of 0.71875 : 0.0625 : 0.21875 for homozygous recipient (i.e. Barke), heterozygous and homozygous donor genotypes, respectively. In total, 1,027 monomorphic SNPs and 1,128 SNPs with high failure rates (i.e. no call in >10% of HEB lines) were excluded from the dataset, resulting in 5,709 informative SNPs for further analyses.
Extraction of genomic DNA
DNA was extracted from leaf tissue of 1,420 single founder HEB plants in generation BC1S3. The subsequent seed propagation of HEB lines was based on these founder HEB plants. For Barke and the wild barley accessions leaf material from three to four plants was used to create bulked samples. The plants were cultivated in a glasshouse and 50 to 100 mg of leaf material was harvested for each sample. DNA was extracted according to the manufacturer’s protocol, using the BioSprint 96 DNA Plant Kit and a BioSprint work station (Qiagen, Hilden, Germany), and finally dissolved in distilled water at approximately 50 ng/μl.
SNP mapping
The chromosomal positions of 3,391 out of 5,709 SNPs were taken from Comadran et al. [35]. The remaining SNPs were fitted next to the mapped SNPs applying chi-square tests of independence. Each non-mapped SNP was compared to each mapped SNP based on genotype segregation across all HEB lines. If two SNPs segregated completely independent from each other, i.e. in case of no linkage disequilibrium (LD), one expects to find all possible genotype combinations according to the product of their single locus genotype frequencies. However, in case of tight linkage, there should be a significant deviation from the expected genotype combination frequencies due to reduced recombination between these markers. Consequently, a high chi-square statistic and a low P-value likely indicate a tight linkage. Therefore, we assigned the position of the SNP with the lowest P-value (minimum: P < 0.001) to the non-mapped SNP under investigation. If there were more than one SNP with the same P-value, the position of the unmapped SNP was defined as the average of the minimum and the maximum position of the respective markers. In this way, all except six of the non-mapped SNPs were placed into the Comadran map.
SNP calling
The differentiation of the HEB genotypes was based on an identity-by-state approach. Based on parental genotype information, the exotic allele could be specified in each segregating family. Thus, HEB lines that showed a homozygous exotic genotype were assigned a value of 2 and HEB lines that showed a homozygous Barke genotype were assigned a value of 0. Consequently, heterozygous HEB lines were assigned a value of 1. If a SNP was monomorphic in one HEB family but polymorphic in a second family, lines of the first HEB family were assigned a genotype value of 0 to keep a full genotype data set, which is a pre-requisite for the subsequent multiple regression analysis. For the same reason, missing genotypes were estimated applying the mean imputation (MNI) approach [64]. For this, each missing SNP value was replaced with the mean of the non-missing values of that SNP in the respective HEB family. Quantitative SNP genotypes were subsequently used for multiple regression analysis.
Evaluation of genetic diversity
SAS 9.4 Software (SAS Institute Inc., Cary, NC, USA) was used to evaluate genetic diversity among parents and progenies of the HEB-25 population. Genetic similarities (GS) between HEB lines and their parents and among HEB lines were calculated with Proc Distance, based on a simple matching comparison between the three possible genotype states across all informative SNPs. In addition, we performed principal component analysis (PCA) using R [65]. First we applied PCA for the 26 parents (the cultivar Barke and 25 wild donors) based on the SNP matrix. The first two PCs explained 51.9 and 4.8% of the variation. Then, all progenies of HEB-25 were projected to the space spanned by the two PCs (Additional file 3) as outlined in detail elsewhere [66].
Linkage disequilibrium (LD)
LD was calculated as r2 [67] between all mapped SNPs with the software package TASSEL [68]. For this purpose, heterozygous genotypes and SNPs with a minor allele frequency < 0.05 were excluded. LD was calculated across the 26 parents of HEB-25. LD decay across intra-chromosomal SNPs was displayed by plotting r2 between SNP pairs against their genetic distance. A second-degree smoothed loess curve [69] was fitted in SAS with Proc Loess. The population-specific baseline r2 was defined as the 95% percentile of the distribution of r2 for unlinked markers [70]. LD decay was defined as the distance, at which this baseline crossed the loess curve.
Ppd-H1 haplotype definition
For sequencing of the Ppd-H1 locus on chromosome 2HS we used the following primers: PP05 (forward) 5′-GTGCAAAGCATAATATCAGTGTCC-3′ and PP04 (reverse) 5′-GGCCAAAGACACAAGAATCAG-3′. These primers amplify the last two exons and three introns of Ppd-H1 covering the CCT domain that contains SNP22, the causal SNP of Ppd-H1 [15]. Identical sequences were grouped into haplotypes. A detailed description of the sequencing is given in Jakob et al. [71].
HEB-25 field trials
Between 2011 and 2013, three field trials were conducted at the ‘Kühnfeld Experimental Station’ of the University of Halle to gather phenotype data on flowering time. In 2011, the field trial was conducted with selfed progenies of BC1S3 lines (so-called BC1S3:4). Sowing occurred in single to five row plots with a length of 1.50 m and a distance of 0.20 m between rows. The number of rows per HEB line and the position inside the field trial depended on the number of available BC1S3:4 seeds. Lines with seed numbers lower than ten were planted in plots with a length of 0.50 m. In 2012 and 2013, the field trials were conducted with the selfed progenies in BC1S3:5 and BC1S3:6, respectively. Two replications per HEB line, arranged in two randomized complete blocks, were cultivated in 2012 and 2013. The plots consisted of two rows (30 seeds each) with a length of 1.50 m and a distance of 0.20 m between rows. All field trials were sown in spring between March and April with fertilization and pest management following local practice.
Phenotypic data
The occurrence of flowering time was recorded as days after sowing, when the first awns were visible (BBCH49 [72]) for 50% of all plants of a plot. We performed a one-step phenotypic data analysis with SAS, using a linear mixed model with effects for genotype (i.e. 1,420 HEB lines), environment (i.e. 3 years) and interaction of genotype and environment. To estimate variance components, all effects were assumed to be random. Broad-sense heritability (h2) was estimated on an entry-mean basis. Best linear unbiased estimates (BLUEs) of flowering time were calculated for each genotype assuming fixed genotype effects.
Genome-wide association study (GWAS)
For GWAS, we applied Model-B as outlined in detail by Liu et al. [38]. This model was found most suitable to carry out GWAS with multiple families [39]. It is based on multiple regression considering an SNP effect and a family effect in addition to cofactors, which control both population structure and genetic background [39]. Cofactor selection was carried out by applying Proc Glmselect in SAS and minimizing the Schwarz Bayesian Criterion [73]. The genome-wide scan for presence of marker-trait associations was implemented in the statistical software R [65], excluding cofactors linked closer than 1 cM to the SNP under investigation. The Bonferroni–Holm procedure [74] was used to adjust marker-trait associations for multiple testing. Significant marker main effects were accepted with PBON-HOLM < 0.05. Additive effects for each SNP were estimated based on regression across but also within families. Significant marker trait associations were grouped to a singled QTL if the significant SNPs were linked by less than 5 cM and revealed additive effects of the same direction, i.e. both exotic alleles increased or decreased flowering time. In addition, a two-dimensional epistasis scan was carried out to identify pairwise marker interactions. For this, the GWAS Model-B was extended to cover a second main SNP effect and the interaction effect between the two SNPs.
Haplotype-based association mapping for Ppd-H1
A haplotype-based association mapping test was implemented in HEB-25 to test for effects of haplotypes at Ppd-H1. We used the same GWAS procedure with cofactor selection as mentioned before. However, bi-allelic SNPs covering the region of Ppd-H1 were replaced by a qualitative variable containing the defined Ppd-H1 haplotype. BLUEs were determined for each haplotype. Subsequently, pairwise comparisons between all haplotype BLUEs were performed using the Tukey-Kramer [75] multiple comparison test.
Genomic prediction
Based on BLUEs of the 1,420 HEB genotypes, two approaches for genomic prediction were applied considering additive effects: ridge regression best linear unbiased prediction (RR-BLUP [51]) and BayesCπ [52]. All statistical procedures for genomic prediction approaches were executed using R. We briefly describe the two models in the following.
Let n be the number of genotypes, m be the number of markers and l be the number of environments. The RR-BLUP model has the form y = 1 n μ + Xg + e, where y is the vector of BLUEs of flowering time scores for all HEB genotypes across environments, 1n denotes the vector of 1’s, μ is the overall mean, g is the vector of marker effects (for SNP markers, allele effects), X is the corresponding design matrix and e is the residual term. In the model we assumed that \( g \sim N\left(0,{\sigma}_g^2\right) \), \( e \sim N\left(0,\ {\sigma}_e^2\right) \), where \( {\sigma}_g^2={\sigma}_G^2/m \) for SNP markers and \( {\sigma}_e^2={\sigma}_R^2/l \). Here \( {\sigma}_G^2 \) and \( {\sigma}_R^2 \) are the genotypic and residual variance components obtained in the mixed model in the phenotypic data analysis. The penalty parameter is \( \lambda =\left({\sigma}_R^2/l\right)/\left({\sigma}_G^2/m\right) \). The estimation of marker effects is then given by the mixed model equations [76].
The basic model of BayesC π is the same as RR-BLUP. However, all parameters are treated as random variables in a Bayesian framework. First, we defined the prior distributions as \( g \sim N\left(0,{\sigma}_g^2\right),\kern1em e \sim N\left(0,\ {\sigma}_e^2\right) \). The prior of μ is a constant. The prior distribution of \( {\sigma}_g^2 \) is assumed to be zero with probability π and a scaled inverse chi-squared distribution with probability (1-π). The probability π is a random variable whose prior distribution is uniform on the interval [0,1]. The prior distribution of \( {\sigma}_e^2 \) is also scaled inverse chi-squared. A Gibbs sampler algorithm was then implemented to infer all the parameters in the model. It was run for 10,000 cycles and the first 1,000 cycles were discarded as burn in. The samples of g from all later cycles were averaged to obtain estimates of the marker effects.
Cross-validation for additive models
The accuracy of the prediction of flowering time by GWAS and the two genomic prediction approaches were evaluated using five-fold cross-validations [77]. In each run of cross-validation, the estimation set included 80% of HEB lines, randomly selected per HEB family, while the remaining 20% of HEB lines were assigned to build the test set. For GWAS, we performed an association mapping scan within the estimation set and recorded the detected significant markers. To determine the cross-validated proportion of explained genotypic variance (pG), we estimated the effects of the significant peak markers within the estimation set and predicted the genotypic value of the lines in the test set [40]. We then calculated the cross-validated pG as the squared Pearson product–moment correlation between predicted and observed genotypic values in the test set standardized with the heritability. The mean pG in 100 cross-validation runs (20 times five-fold cross-validations) was taken as the final record. In addition, the number of significances for each SNP was cumulated across all runs and is referred to as QTL detection rate.
For genomic prediction we estimated the effects for all markers using the estimation set and predicted the genotypic value of the lines in the test set. The cross-validated pG was calculated as in GWAS.
Exploiting additive and additive times additive epistatic effects in genomic prediction
We extended the RR-BLUP based on main effects to model also epistasis for markers with significant main effects in the GWAS. The model is \( y={1}_n\mu +{\displaystyle {\sum}_{i=1}^n{X}_i{g}_i}+{\displaystyle {\sum}_{j<l}\left({X}_j\cdot {X}_l\right)}{f}_{jl}+e \), where y is the vector of BLUEs of flowering time for all HEB genotypes, 1n denotes the vector of 1’s, μ is the overall mean, g i is the main additive effect of the i-th marker, X i is the vector of marker indices, f jl is the epistatic effects of the j- and the l-th marker, X j X l is the point-wise product of the two vectors X j and X l , and e is the vector of residual terms. Note that in the third term of the right hand side of the formula, the sum is not taken over all pairs of markers but only pairs of markers exhibiting a significant additive effect in the GWAS study performed previously. Hence, in different cross-validation runs, different pairs of markers were considered in the model. The model assumptions are similar to the usual RR-BLUP, except treating additive and epistatic effects separately. We assumed \( {g}_i \sim N\left(0,{\sigma}_g^2\right) \), \( {f}_{jl} \sim N\left(0,{\sigma}_f^2\right) \), where \( {\sigma}_g^2={p}_G{\sigma}_G^2/m \), \( {\sigma}_f^2=\left(1-{p}_G\right){\sigma}_G^2/p \). Here P G is the cross-validated proportion of explained genotypic variance for genomic prediction, obtained previously by the RR-BLUP, only considering additive effects, m is the number of markers, p is the number of pairs of markers having significant additive effect. Therefore the penalty parameter λ is different for additive and epistatic effects.
Using the above extended model, for each cross-validation run we estimated the additive effects of all markers and epistatic effects of all pairs of markers exhibiting significant additive effects in GWAS using the estimation set. Then we predicted genotypic values of the lines in the test set and calculated the pG in the same way as outlined above.
Availability of supporting data
Raw data, including data on SNPs, Ppd-H1 haplotypes and GWAS, and all other supporting data are provided as additional files.
Abbreviations
- BC1 :
-
Progeny of F1 after back-crossing with Barke
- BC1S3 :
-
Progeny of BC1 after three rounds of selfing
- BC1S3:x :
-
Progeny of BC1S3 individual after x-3 rounds of bulk propagation
- BLUE:
-
Best linear unbiased estimate
- cM:
-
Centimorgan
- F1 :
-
First generation after initial crosses
- GA:
-
Gibberellic acid
- GS:
-
Genetic similarity
- GWAS:
-
Genome-wide association study
- Hag :
-
Hordeum agriocrithon
- HEB:
-
Halle exotic barley
- HID:
-
Hordeum identity
- Hsp :
-
Hordeum spontaneum
- Hv :
-
Hordeum vulgare
- LD:
-
Linkage disequilibrium
- MNI:
-
Mean imputation
- NAM:
-
Nested association mapping
- PC:
-
Principal component
- PCA:
-
Principal component analysis
- pG :
-
Proportion of explained genotypic variance
- QTL:
-
Quantitative trait locus/loci
- RR-BLUP:
-
Ridge regression best linear unbiased prediction
- SNP:
-
Single nucleotide polymorphism
- SSD:
-
Single seed descent
References
Sakuma S, Salomon B, Komatsuda T. The domestication syndrome genes responsible for the major changes in plant form in the Triticeae crops. Plant Cell Physiol. 2011;52:738–49.
Zohary D, Hopf M, Weiss E. Domestication of Plants in the Old World: The origin and spread of domesticated plants in Southwest Asia, Europe, and the Mediterranean Basin. 4th ed. Oxford: Oxford University Press; 2012.
Morrell PL, Clegg MT. Genetic evidence for a second domestication of barley (Hordeum vulgare) east of the Fertile Crescent. Proc Natl Acad Sci U S A. 2007;104:3289–94.
Dai F, Nevo E, Wu D, Comadran J, Zhou M, Qiu L, et al. Tibet is one of the centers of domestication of cultivated barley. Proc Natl Acad Sci U S A. 2012;109:16969–73.
Tanksley SD, McCouch SR. Seed Banks and Molecular Maps: Unlocking Genetic Potential from the Wild. Science. 1997;277:1063–6.
Zamir D. Improving plant breeding with exotic genetic libraries. Nat Rev Genet. 2001;2:983–9.
Ellis RP, Forster BP, Robinson D, Handley LL, Gordon DC, Russell JR, et al. Wild barley: a source of genes for crop improvement in the 21st century? J Exp Bot. 2000;51:9–17.
Pillen K, Zacharias A, Leon J. Advanced backcross QTL analysis in barley (Hordeum vulgare L.). Theor Appl Genet. 2003;107:340–52.
Wang G, Schmalenbach I, von Korff M, Leon J, Kilian B, Rode J, et al. Association of barley photoperiod and vernalization genes with QTLs for flowering time and agronomic traits in a BC(2)DH population and a set of wild barley introgression lines. Theor Appl Genet. 2010;120:1559–74.
Schmalenbach I, March TJ, Bringezu T, Waugh R, Pillen K. High-Resolution Genotyping of Wild Barley Introgression Lines and Fine-Mapping of the Threshability Locus thresh-1 Using the Illumina GoldenGate Assay. G3 (Bethesda). 2011;1:187–96.
Ma X, Li C, Wang A, Duan R, Jiao G, Nevo E, et al. Genetic diversity of wild barley (Hordeum vulgare ssp. spontaneum) and its utilization for barley improvement. Sci Cold Arid Reg. 2012;4:453–61.
McCouch S, Baute GJ, Bradeen J, Bramel P, Bretting PK, Buckler E, et al. Agriculture: Feeding the future. Nature. 2013;499:23–4.
Schnaithmann F, Kopahnke D, Pillen K. A first step toward the development of a barley NAM population and its utilization to detect QTLs conferring leaf rust seedling resistance. Theor Appl Genet. 2014;127:1513–25.
Cockram J, Jones H, Leigh FJ, O’Sullivan D, Powell W, Laurie DA, et al. Control of flowering time in temperate cereals: genes, domestication, and sustainable productivity. J Exp Bot. 2007;58:1231–44.
Turner A, Beales J, Faure S, Dunford RP, Laurie DA. The pseudo-response regulator Ppd-H1 provides adaptation to photoperiod in barley. Science. 2005;310:1031–4.
Yan L, Fu D, Li C, Blechl A, Tranquilli G, Bonafede M, et al. The wheat and barley vernalization gene VRN3 is an orthologue of FT. Proc Natl Acad Sci U S A. 2006;103:19581–6.
Yan L, Loukoianov A, Blechl A, Tranquilli G, Ramakrishna W, SanMiguel P, et al. The wheat VRN2 gene is a flowering repressor down-regulated by vernalization. Science. 2004;303:1640–4.
Yan L, Loukoianov A, Tranquilli G, Helguera M, Fahima T, Dubcovsky J. Positional cloning of the wheat vernalization gene VRN1. Proc Natl Acad Sci U S A. 2003;100:6263–8.
von Zitzewitz J, Szűcs P, Dubcovsky J, Yan L, Francia E, Pecchioni N, et al. Molecular and structural characterization of barley vernalization genes. Plant Mol Biol. 2005;59:449–67.
Laurie D, Pratchett N, Snape J, Bezant J. RFLP mapping of five major genes and eight quantitative trait loci controlling flowering time in a winter × spring barley (Hordeum vulgare L.) cross. Genome. 1995;38:575–85.
Distelfeld A, Li C, Dubcovsky J. Regulation of flowering in temperate cereals. Curr Opin Plant Biol. 2009;12:178–84.
Jung C, Mueller AE. Flowering time control and applications in plant breeding. Trends Plant Sci. 2009;14:563–73.
Milec Z, Valárik M, Bartoš J, Šafář J. Can a late bloomer become an early bird? Tools for flowering time adjustment. Biotechnol Adv. 2014;32:200–14.
Cockram J, Hones H, O’Sullivan DM. Genetic variation at flowering time loci in wild and cultivated barley. Plant Genet Resour. 2011;9:264–7.
Nevo E, Fu Y-B, Pavlicek T, Khalifa S, Tavasi M, Beiles A. Evolution of wild cereals during 28 years of global warming in Israel. Proc Natl Acad Sci U S A. 2012;109:3412–5.
Yu J, Holland JB, McMullen MD, Buckler ES. Genetic design and statistical power of nested association mapping in maize. Genetics. 2008;178:539–51.
Jordan D, Mace E, Cruickshank A, Hunt C, Henzell R. Exploring and exploiting genetic variation from unadapted sorghum germplasm in a breeding program. Crop Sci. 2011;51:1444–57.
Buckler ES, Holland JB, Bradbury PJ, Acharya CB, Brown PJ, Browne C, et al. The Genetic Architecture of Maize Flowering Time. Science. 2009;325:714–8.
Kump KL, Bradbury PJ, Wisser RJ, Buckler ES, Belcher AR, Oropeza-Rosas MA, et al. Genome-wide association study of quantitative resistance to southern leaf blight in the maize nested association mapping population. Nat Genet. 2011;43:163–8.
Poland JA, Bradbury PJ, Buckler ES, Nelson RJ. Genome-wide nested association mapping of quantitative resistance to northern leaf blight in maize. Proc Natl Acad Sci U S A. 2011;108:6893–8.
Tian F, Bradbury PJ, Brown PJ, Hung H, Sun Q, Flint-Garcia S, et al. Genome-wide association study of leaf architecture in the maize nested association mapping population. Nat Genet. 2011;43:159–62.
Cook JP, McMullen MD, Holland JB, Tian F, Bradbury P, Ross-Ibarra J, et al. Genetic Architecture of Maize Kernel Composition in the Nested Association Mapping and Inbred Association Panels. Plant Physiol. 2012;158:824–34.
Peiffer JA, Romay MC, Gore MA, Flint-Garcia SA, Zhang Z, Millard MJ, et al. The genetic architecture of maize height. Genetics. 2014;196:1337–56.
Wallace J, Larsson S, Buckler E. Entering the second century of maize quantitative genetics. Heredity (Edinb). 2014;112:30–8.
Comadran J, Kilian B, Russell J, Ramsay L, Stein N, Ganal M, et al. Natural variation in a homolog of Antirrhinum CENTRORADIALIS contributed to spring growth habit and environmental adaptation in cultivated barley. Nat Genet. 2012;44:1388–92.
Gottwald S, Bauer P, Komatsuda T, Lundqvist U, Stein N. TILLING in the two-rowed barley cultivar ‘Barke’ reveals preferred sites of functional diversity in the gene HvHox1. BMC Res Notes. 2009;2:258.
Badr A, Muller K, Schafer-Pregl R, El Rabey H, Effgen S, Ibrahim HH, et al. On the origin and domestication history of barley (Hordeum vulgare). Mol Biol Evol. 2000;17:499–510.
Liu W, Gowda M, Steinhoff J, Maurer HP, Würschum T, Longin CFH, et al. Association mapping in an elite maize breeding population. Theor Appl Genet. 2011;123:847–58.
Würschum T, Liu W, Gowda M, Maurer H, Fischer S, Schechert A, et al. Comparison of biometrical models for joint linkage association mapping. Heredity (Edinb). 2012;108:332–40.
Utz HF, Melchinger AE, Schön CC. Bias and sampling error of the estimated proportion of genotypic variance explained by quantitative trait loci determined from experimental data in maize using cross validation and validation with independent samples. Genetics. 2000;154:1839–49.
Gowda M, Zhao Y, Würschum T, Longin CF, Miedaner T, Ebmeyer E, et al. Relatedness severely impacts accuracy of marker-assisted selection for disease resistance in hybrid wheat. Heredity (Edinb). 2014;112:552–61.
Mace E, Hunt C, Jordan D. Supermodels: sorghum and maize provide mutual insight into the genetics of flowering time. Theor Appl Genet. 2013;126:1377–95.
Loscos J, Igartua E, Contreras-Moreira B, Gracia MP, Casas AM. HvFT1 polymorphism and effect – survey of barley germplasm and expression analysis. Front Plant Sci. 2014;5:251.
Mutasa-Göttgens E, Hedden P. Gibberellin as a factor in floral regulatory networks. J Exp Bot. 2009;60:1979–89.
Jia Q, Zhang J, Westcott S, Zhang X-Q, Bellgard M, Lance R, et al. GA-20 oxidase as a candidate for the semidwarf gene sdw1/denso in barley. Funct Integr Genomics. 2009;9:255–62.
Faure S, Turner AS, Gruszka D, Christodoulou V, Davis SJ, von Korff M, et al. Mutation at the circadian clock gene EARLY MATURITY 8 adapts domesticated barley (Hordeum vulgare) to short growing seasons. Proc Natl Acad Sci U S A. 2012;109:8328–33.
Zakhrabekova S, Gough SP, Braumann I, Muller AH, Lundqvist J, Ahmann K, et al. Induced mutations in circadian clock regulator Mat-a facilitated short-season adaptation and range extension in cultivated barley. Proc Natl Acad Sci U S A. 2012;109:4326–31.
Boden SA, Weiss D, Ross JJ, Davies NW, Trevaskis B, Chandler PM, et al. EARLY FLOWERING3 Regulates Flowering in Spring Barley by Mediating Gibberellin Production and FLOWERING LOCUS T Expression. Plant Cell. 2014;26:1557–69.
Dunford RP, Griffiths S, Christodoulou V, Laurie DA. Characterisation of a barley (Hordeum vulgare L.) homologue of the Arabidopsis flowering time regulator GIGANTEA. Theor Appl Genet. 2005;110:925–31.
Meuwissen THE, Hayes BJ, Goddard ME. Prediction of Total Genetic Value Using Genome-Wide Dense Marker Maps. Genetics. 2001;157:1819–29.
Whittaker JC, Thompson R, Denham MC. Marker-assisted selection using ridge regression. Genet Res. 2000;75:249–52.
Habier D, Fernando RL, Kizilkaya K, Garrick DJ. Extension of the Bayesian alphabet for genomic selection. BMC Bioinf. 2011;12:186.
Lorenzana RE, Bernardo R. Accuracy of genotypic value predictions for marker-based selection in biparental plant populations. Theor Appl Genet. 2009;120:151–61.
Guo ZG, Tucker DM, Lu JW, Kishore V, Gay G. Evaluation of genome-wide selection efficiency in maize nested association mapping populations. Theor Appl Genet. 2012;124:261–75.
Guo Z, Tucker DM, Basten CJ, Gandhi H, Ersoz E, Guo B, et al. The impact of population structure on genomic prediction in stratified populations. Theor Appl Genet. 2014;127:749–62.
Zhao Y, Mette MF, Gowda M, Longin CFH, Reif JC. Bridging the gap between marker-assisted and genomic selection of heading time and plant height in hybrid wheat. Heredity (Edinb). 2014;112:638–45.
Habier D, Fernando R, Dekkers J. The impact of genetic relationship information on genome-assisted breeding values. Genetics. 2007;177:2389–97.
Mackay TF. Epistasis and quantitative traits: using model organisms to study gene-gene interactions. Nat Rev Genet. 2013;15:22–33.
von Korff M, Léon J, Pillen K. Detection of epistatic interactions between exotic alleles introgressed from wild barley (H. vulgare ssp. spontaneum). Theor Appl Genet. 2010;121:1455–64.
Griffiths S, Dunford RP, Coupland G, Laurie DA. The evolution of CONSTANS-like gene families in barley, rice, and Arabidopsis. Plant Physiol. 2003;131:1855–67.
Tranquilli G, Dubcovsky J. Epistatic interaction between vernalization genes Vrn-Am1 and Vrn-Am2 in diploid wheat. J Hered. 2000;91:304–6.
Szűcs P, Skinner JS, Karsai I, Cuesta-Marcos A, Haggard KG, Corey AE, et al. Validation of the VRN-H2/VRN-H1 epistatic model in barley reveals that intron length variation in VRN-H1 may account for a continuum of vernalization sensitivity. Mol Genet Genomics. 2007;277:249–61.
Chen A, Dubcovsky J. Wheat TILLING mutants show that the vernalization gene VRN1 down-regulates the flowering repressor VRN2 in leaves but is not essential for flowering. PLoS Genet. 2012;8:e1003134.
Rutkoski JE, Poland J, Jannink J-L, Sorrells ME. Imputation of Unordered Markers and the Impact on Genomic Selection Accuracy. G3 (Bethesda). 2013;3:427–39.
R Development Core Team (2010) R: A language and environment for statistical computing, R Foundation for Statistical Computing. http://www.R-project.org
Xia X, Reif J, Melchinger A, Frisch M, Hoisington D, Beck D, et al. Genetic diversity among CIMMYT maize inbred lines investigated with SSR markers. Crop Sci. 2005;45:2573–82.
Weir BS. Genetic Data Analysis II. Sunderland, MA: Sinauer Associates, Inc.; 1996.
Bradbury PJ, Zhang Z, Kroon DE, Casstevens TM, Ramdoss Y, Buckler ES. TASSEL: software for association mapping of complex traits in diverse samples. Bioinformatics. 2007;23:2633–5.
Cleveland WS. Robust locally weighted regression and smoothing scatterplots. J Am Stat Assoc. 1979;74:829–36.
Breseghello F, Sorrells ME. Association mapping of kernel size and milling quality in wheat (Triticum aestivum L.) cultivars. Genetics. 2006;172:1165–77.
Jakob SS, Rödder D, Engler JO, Shaaf S, Özkan H, Blattner FR, et al. Evolutionary History of Wild Barley (Hordeum vulgare subsp. spontaneum) Analyzed Using Multilocus Sequence Data and Paleodistribution Modeling. Genome Biol Evol. 2014;6:685–702.
Lancashire PD, Bleiholder H, Boom TVD, Langelüddeke P, Stauss R, Weber E, et al. A uniform decimal code for growth stages of crops and weeds. Ann Appl Biol. 1991;119:561–601.
Schwarz G. Estimating the dimension of a model. Ann Stat. 1978;6:461–4.
Holm S. A simple sequentially rejective multiple test procedure. Scand J Stat. 1979;6:65–70.
Kramer CY. Extension of multiple range tests to group means with unequal numbers of replications. Biometrics. 1956;12:307–10.
Henderson CR. Applications of Linear Models in Animal Breeding. Guelph: University of Guelph; 1984.
Hjorth JU. Computer intensive statistical methods: Validation, model selection, and bootstrap. London: Chapman & Hall/CRC; 1993.
Acknowledgements
This work was supported by Deutsche Forschungsgemeinschaft (DFG), Bonn (projects Pi339/7-1 and Pi 339/7-2), and the Interdisciplinary Centre for Crop Plant Research (IZN), Halle. We are grateful to Roswitha Ende, Jana Müglitz, Diana Rarisch, Helga Sängerlaub, Brigitte Schröder, Bernd Kollmorgen and various student assistants for excellent technical help and to TraitGenetics GmbH, Gatersleben, Germany, for genotyping HEB-25 with the Infinium iSelect 9k SNP chip.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
AM planned and conducted the field trials in 2012 and 2013, analyzed the genotype and phenotype data, carried out the GWAS, created the figures, and drafted the manuscript. VD was involved in the development of the HEB-25 population, gathered the genotype data, and planned and conducted the field trial in 2011. YJ performed the genomic prediction and cross-validation approaches. FS was involved in the development of the HEB-25 population. RS performed the re-sequencing of Ppd-H1. ES supervised the field trials. BK supervised the Ppd-H1 re-sequencing. JCR supervised the genomic prediction and cross-validation approaches. KP acquired the funding, supervised the development of the HEB-25 population and all analyses, and drafted the manuscript. All authors read and approved the final manuscript.
Andreas Maurer and Vera Draba contributed equally to this work.
Additional files
Additional file 1:
Genetic constitution of HEB-25: classification of families and donors. Tabular overview of the genetic constitution of HEB-25, classifying the 25 families and donors and containing the Ppd-H1 haplotypes.
Additional file 2:
LD decay of intra-chromosomal markers among HEB-25 parents. Figure showing the LD decay of intra-chromosomal markers among HEB-25 parents by plotting r2 against the genetic marker distance.
Additional file 3:
Principal component analysis for HEB-25 and its parents. Figure showing the relatedness of HEB-25 lines by plotting of the first two principal components of a principal component analysis for HEB-25 and its parents.
Additional file 4:
Distribution of flowering time. Figure showing the frequency distribution of flowering time BLUEs across three field trials and illustrating contrasting phenotypes in the field.
Additional file 5:
Phenotype and genotype data for HEB-25. Table listing the complete phenotype and genotype data of HEB-25 underlying this study as well as marker information.
Additional file 6:
Estimates of single marker GWAS and genomic prediction effects across HEB-25 and within individual HEB families. Table listing the results of GWAS and genomic prediction across HEB-25 and within individual HEB families.
Additional file 7:
GWAS Manhattan plot for flowering time. Figure displaying the GWAS results through plotting the significance and effects of markers in a Manhattan plot.
Additional file 8:
Ppd-H1 haplotype comparison. Two tables contrasting the different Ppd-H1 haplotype effects by comparison of their BLUEs.
Additional file 9:
Significant epistatic interactions via GWAS. Table listing all significant (PBON-HOLM < 0.05) epistatic interactions between SNPs that were obtained via GWAS.
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Maurer, A., Draba, V., Jiang, Y. et al. Modelling the genetic architecture of flowering time control in barley through nested association mapping. BMC Genomics 16, 290 (2015). https://doi.org/10.1186/s12864-015-1459-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s12864-015-1459-7