1 Introduction

The African wild dog is one of the endangered carnivorous species in South Africa. They are mainly distributed in parts of eastern and southern Africa. In the past few decades the habitat of African wild dog has been drastically reduced, and the population quantity has declined significantly [1]. Research suggests that there are many reasons for the sharp decline in the distribution and number of African wild dogs, which may include conflicts with humans, habitat loss, persecution and competition with other predators, genetic diversity of infectious diseases, and inbreeding depression [2]. The scholars analyzed the demographic data of endangered Lycaon pictus in Hluhluwe–Imfolozi Park in South Africa from 1980 to 2004. They found that the African wild dog population has an obvious Allee effect [3]. In 1931, W.C. Allee paid attention to the possibility of a positive relationship between individual aspects of fitness and population density [4]. In other words, when the species has a small population density, the death rate increases, and the birth rate decreases, then the risk of species extinction increases. There are many reasons for this phenomenon. For example, for an individual, it is difficult to seek spouses and difficult to resist enemies and inbreeding depression [5]. Therefore many researches focus on the Allee effect (sparse effect) and have done a lot of work in this direction [6–9].

The Allee effect has been observed in many species, such as plants, marine invertebrates, and mammals [8]. For these species, there exists a minimum survival threshold, which implies that it is not necessary to adopt any measure to intervene when the population density is above this threshold [10]. But once the population density is lower than the survival threshold, some corresponding control measures should be performed according to the state of the target species. So the threshold strategy is also called the state feedback control strategy. This strategy can be precisely described by an impulsive differential equation in mathematics [11].

In recent years, impulsive differential equations have been used in various fields [12–20], such as disease control and pharmacology [21–29], integrated pest management [30–38], microbial culture [38–43], and protection of endangered animals and plants [44–51]. For example, Zhang et al. [10] focused on a predator–prey model with impulsive state feedback control and assuming that the spraying pesticide and releasing the natural enemies are taken at different thresholds. Liang et al. [5] investigated a state-dependent impulsive control model for computer virus propagation under media coverage, and the results show that the media coverage can delay the spread of computer virus. Nie et al. [52] studied different types of chemostat ecosystems of microbial cultures. However, there are few studies on the use of impulsive control strategies to protect the endangered species.

Assume that the model with Allee effect of African wild dog species is as follows:

$$ \frac{dx}{dt}=x \biggl[ r \biggl( 1-\frac{x}{K} \biggr) - \frac{a}{cax+1} \biggr] , $$
(1)

where K is the maximum capacity of the environment, r is the intrinsic growth rate, and \(\frac{a}{cax+1}\) represents the Allee effect caused by mating restrictions. If \(a>\sqrt{\frac{r}{ck}}\), then for system (1), there exists the Allee effect [8]. However, the population number of African wild dogs also depends on the population density at all times in the past. Therefore the investigation of continuous time delay in population dynamics has a great significance. Therefore we consider an African wild dog model with Allee effect and continuous time delay as follows:

$$ \frac{dx}{dt}=x \biggl[ r \biggl( 1-\frac{x}{K} \biggr) - \frac{a}{cax+1}-\omega \int _{-\infty }^{t}e^{-b(t-s)}x(s)\,ds \biggr]. $$
(2)

We assume that \(y(t)=\int _{-\infty }^{t}e^{-b(t-s)}x(s)\,ds\). We think that artificial breeding methods and monitoring the population size can protect the African wild dog. When the population number of African wild dogs reaches the minimum survival threshold h, the release of artificial captivity in the African wild dog population is considered as an effective method of protection. So we consider an African wild dog impulsive feedback control model with Allee effect and continuous time delay as follows:

$$ \textstyle\begin{cases} \left . \textstyle\begin{array}{@{}l@{}} \frac{dx}{dt}=x [ r ( 1-\frac{x}{K} ) -\frac{a}{cax+1}-\omega y ] , \\ \frac{dy}{dt}=x-by, \end{array}\displaystyle \right \}& x>h, \\ \left . \textstyle\begin{array}{@{}l@{}} \triangle x(t)=p,\\ \triangle y(t)=0, \end{array}\displaystyle \right \}& x=h. \end{cases} $$
(3)

In this work, all the parameters are positive, and \(\int _{0}^{\infty }e^{(-s)}\,ds=1\).

The paper is organized is as follows. In Sect. 2, we first analyze qualitatively the singularity of system (3) without impulse effect by the Bendixson–Dulac theory. Then we use the geometric theory of impulsive differential equations to prove the existence of a periodic orbit. The uniqueness of the periodic orbit of model (3) is proved by the monotonicity of subsequent functions. Meanwhile, the geometric properties of subsequent functions are used to prove the stability of the periodic orbit of system (3) in Sect. 3. In Sect. 4, we illustrate the correctness of the results obtained by some numerical simulations. Finally, we conclude our work.

2 Dynamic analysis of system (3)

2.1 Qualitative analysis of system (3)

In this subsection, we first discuss system (3) without impulse. Thus we consider the following system:

$$ \textstyle\begin{cases} x'(t)=x(t) [ r ( 1-\frac{x(t)}{K} ) -\frac{a}{cax(t)+1}-\omega y(t) ] \triangleq P(x,y), \\ y'(t)=x(t)-by(t)\triangleq Q(x,y). \end{cases} $$
(4)

Then, we solve the system

$$ \textstyle\begin{cases} x(t) [ r ( 1-\frac{x(t)}{K} ) -\frac{a}{cax(t)+1}-\omega y(t) ] =0, \\ x(t)-by(t)=0. \end{cases} $$
(5)

Obviously, system (3) has the equilibrium point \(O(0,0)\) and a positive equilibrium point \(E^{*}(x^{*},y^{*})\), where

$$\begin{aligned}& x^{*}=\frac{(rcabK-rb-\omega K)+\sqrt{\Delta }}{2(rcab+\omega caK)}, \\& y^{*}=\frac{(rcabK-rb-\omega K)+\sqrt{\Delta }}{2b(rcab+\omega caK)}, \end{aligned}$$

and

$$ \Delta =(rcabK-rb-\omega K)^{2}+4(rK-aK) \bigl(rcab^{2}+ \omega Kca\bigr). $$

Let

$$ (H_{1}):K< 2x^{*} $$

and

$$ (H_{2}):\sqrt{\frac{r}{cK}}< a< 2b. $$

Theorem 2.1

If \((H_{1})\) holds, then the point \(E^{*}(x^{*},y^{*})\) is locally asymptotically stable.

Proof

The Jacobian matrix at the point \(E^{*}(x^{*},y^{*})\) is

$$\begin{aligned} J=\left ( \textstyle\begin{array}{cc} \displaystyle r-\frac{2rx^{*}}{K}-\frac{a}{(cax^{*}+1)^{2}}-\omega y^{*} & \displaystyle -\omega \\ 1 & \displaystyle -b \end{array}\displaystyle \right ) . \end{aligned}$$

Iif \((H_{1})\) holds, then we have

$$\begin{aligned} {\operatorname{tr}\bigl(J\bigl(E^{*}\bigr)\bigr)} =& r-\frac{2rx^{*}}{K}- \frac{a}{(cax^{*}+1)^{2}}-\omega y-b< 0 \end{aligned}$$

and

$$\begin{aligned} {\operatorname{Det}\bigl(J\bigl(E^{*}\bigr)\bigr)} =& -b \biggl[ r- \frac{2rx^{*}}{K}-\frac{a}{(cax^{*}+1)^{2}}-\omega y \biggr] +\omega >0. \end{aligned}$$

Thus the point \(E^{*}(x^{*},y^{*})\) is a locally asymptotically stable node or focus. □

Theorem 2.2

If \((H_{1})\) and \((H_{2})\) hold, then the point \(E^{*}(x^{*},y^{*})\) is globally asymptotically stable.

Proof

Let \(B=\frac{1}{x}\). Then

$$\begin{aligned} {D} =& \frac{\partial (PB)}{\partial x}+\frac{\partial (QB)}{\partial y} \\ =& -\frac{r}{K}+\frac{ca^{2}}{(cax+1)^{2}}-\frac{b}{x} \\ =& \frac{Kca^{2}x-r(cax+1)^{2}-bK(cax+1)^{2}}{(cax+1)^{2}} \\ =& \frac{-rc^{2}a^{2}x^{3}-2carx^{2}-rx-bKc^{2}a^{2}x^{2}-2cabKx-bK+cKa^{2}x}{(cax+1)^{2}} \\ =& \frac{caKx(a-2b)-rc^{2}a^{2}x^{3}-2carx^{2}-rx-bKc^{2}a^{2}x^{2}-bK}{(cax+1)^{2}}. \end{aligned}$$

Obviously, if \((H_{2})\) holds, then the function

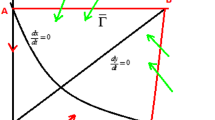
$$ D=\frac{\partial (PB)}{\partial x}+\frac{\partial (QB)}{\partial y}< 0. $$

In other words, system (4) has no limit cycle in \(R_{2}^{+}=\{(x,y)|x\geq 0,y\geq 0\}\), and every solution of system (4) is bounded in \(R_{2}^{+}\). According to the method in [8], the point \(E^{*}(x^{*},y^{*})\) is a globally asymptotically stable focus or node (see Fig. 1).

Figure 1
figure 1

Phase diagram of system (3) with \(r=1\), \(K=5\), \(b=2\), \(a=0.5\), \(\omega =0.1\), \(c=3\)

Full size image

 □

2.2 Dynamic analysis of an order-one periodic orbit of system (3)

2.2.1 System (3) has a unique periodic orbit

In this subsection, we study the existence and uniqueness of an order-one periodic orbit. We assume that the impulsive set \(M=\{(x,y)\in R_{2}^{+}|x=h,y\geq 0\}\) and phase set \(N=\{(x,y)\in R_{2}^{+}|x=h+p,y\geq 0\}\) are straight lines. The trajectory that starts from any point A is denoted by \(f(A,t)\). A positive equilibrium \(E^{*}(x^{*}, y^{*})\) is globally asymptotically stable if conditions \((H_{1})\) and \((H_{2})\) hold.

Theorem 2.3

  1. (1)

    If \(0< h< h+p\leq x^{*}\), then system (3) has no order-one periodic orbit.

  2. (2)

    If \(0< h< x^{*}< h+p< K\), then system (3) has no order-one periodic orbit.

Proof

Case 1. \(0< h< h+p\leq x^{*}\).

If \(0< h< h+p\leq x^{*}\), then the impulsive set M and the phase set N are on the left of the point \(E^{*}(x^{*},y^{*})\). The impulsive set M and the phase set N intersect the x-axis at the points \(M^{\prime}(h,0)\) and \(N^{\prime}(h+p,0)\), respectively. The isoclinic line \(\dot{x}=0\) intersects with the x-axis at the point \(E^{\prime}(\tau ,0)\), where

$$ \tau =\frac{(rKca-r)+\sqrt{\Theta }}{2rca} $$

and

$$ \Theta =(rKca-r)^{2}+4rca(rK-aK). $$

The intersection point of the isoclinic line \(\dot{x}=0\) and the impulsive set M is \(F_{1}(h,y_{F_{1}})\), where

$$ y_{F_{1}}=\frac{(ahc+1)(rK-rh)-aK}{\omega K(ahc+1)}. $$

According to the biological background, we only have to study the dynamic behavior of such a system in the region \(\Phi =\{(x,y)|x\geq h,0< y\leq b_{M}-Kx\}\), where \(b_{M}\) is a sufficiently large constant satisfying \(\frac{d\chi }{dt} |_{\chi =0}<0\).

Let

$$ \chi :Kx+y-b_{M}=0. $$

Then we have

$$\begin{aligned} {\frac{d\chi }{dt} \Big|_{\chi =0}} =& \frac{Kdx}{dt}+\frac{dy}{dt} \\ =& x-b_{M}y+K \biggl[ x\biggl(r-\frac{rx}{K}\biggr)- \frac{a}{cax+1}-\omega y \biggr] \\ =& x+rKx-rx^{2}-\frac{aK}{cax+1}-\omega Ky-b_{M}y \\ =& (1+rK)x-rx^{2}-\frac{aK}{cax+1}-(\omega K+b_{M})y< 0. \end{aligned}$$

This implies that there must exist an intersection point of the trajectory \(f(F_{1},t)\) and the phase set N denoted by \(F(h+p,y_{F})\). The point \(F_{1}\) jumps to the point \(F^{1}\) due to the impulse effect. According to the definition of the subsequent function in [5] and the trajectory tend of system (3), the subsequent function of the point F is

$$ g(F)=y_{F^{1}}-y_{F}< 0. $$

The trajectory \(f(N^{\prime},t)\) will have no intersection point with the impulsive set M. Thus, the trajectory starting from any point located on the segment \(\overline{FN^{\prime}}\subset N\) is attractive to the positive equilibrium point \(E^{*}\) by impulse effect. The orbit starting from any point that is above the point F is also attractive to the point \(E^{*}\) by several impulsive effects at most.

In summary, system (3) has no order-one periodic orbit when \(0< h< h+p\leq x^{*}\) (see Fig. 2).

Figure 2
figure 2

Existence of order-one periodic orbit if \(0< h< h+p\leq x^{*}\)

Full size image

Case 2. \(0< h< x^{*}< h+p< K\)

If \(0< h< x^{*}< h+p< K\) holds, then the point \(E^{*}(x^{*},y^{*})\) is between the impulsive set M and the phase set N. The isoclinic line \(\dot{x}=0\) intersects the impulsive set M at the point \(F_{1}(h,y_{F_{1}})\). The impulsive set M intersects the x-axis at the point \(M^{\prime}(h,0)\), and the intersection point of the phase set N and the x-axis is the point \(N^{\prime}(h+p,0)\).

Thus the orbit \(f(N^{\prime},t)\) tends to the point \(E^{*}(x^{*},y^{*})\), and the trajectory \(f(F_{1},t)\) surely has an intersection point with the phase set N, denoted by \(F(h+p,y_{F})\), where

$$ y_{F}>y^{*}=\frac{(rcabK-rb-\omega K)+\sqrt{\Delta }}{2b(rcab+\omega caK)}. $$

Thus the point \(F_{1}\) will jump to the point \(F^{1}\in N\) by the impulse effect. So the subsequent function of the point F is

$$ g(F)=y_{F^{1}}-y_{F}< 0. $$

Similarly, the orbit that starts from any point on the segment \(\overline{FN^{\prime}}\subset N\) will tend to the positive equilibrium point \(E^{*}(x^{*},y^{*})\), and the trajectory starting from any point above the point F on the phase set N will also be attractive to the point \(E^{*}\) by several impulse effects at most.

Thus, system (3) has no order-one periodic orbit if \(0< h< x^{*}< h+p< K\) (see Fig. 3).

Figure 3
figure 3

Existence of order-one periodic orbit if \(0< h< x^{*}< h+p< K\)

Full size image

 □

Theorem 2.4

If \(0< x^{*}\leq h< h+p< K\), then system (3) has an order-one periodic orbit, and when \(h+p>\frac{\sqrt{\Lambda }+(brkca-\omega r-br)}{2(brca+\omega Kca)}\), the order-one periodic orbit is unique.

Proof

Let \(0< x^{*}\leq h< h+p< K\). Then the positive equilibrium point \(E^{*}\) is on the left of the impulsive set M. The phase set N intersects the isoclinic line \(\dot{x}=0\) and \(\dot{y}=0\) at the points \(P(h+p,y_{P})\) and \(H(h+p,\frac{h+p}{b})\), respectively, where

$$ y_{P}=\frac{-rca(h+p)^{2}+(rKca-r)(h+p)+K(r-a)}{\omega Kca(h+p)+\omega K}. $$

By the asymptotic stability of the point \(E^{*}\) the trajectory \(f(H,t)\) intersects the impulsive set M at the point \(H_{1}\), then it hits the impulsive set M at the point \(H^{1}(h+p,y_{H^{1}})\) on the phase set N. The successor point \(H^{1}\) of the point H is surely under the point H, so \(y_{H^{1}}< y_{H}\). Then the subsequent function of the point H is

$$ g(H)=y_{H^{1}}-y_{H}< 0. $$

The trajectory \(f(P,t)\) hits the impulsive set M at the point \(P_{1}\), then jumps to the point \(P^{1}(h+p,y_{P^{1}})\) by the impulsive effect. The successor point \(P^{1}\) of the point P must be above the point P by the trajectory tend of system (3). Thus the subsequent function of the point P is

$$ g(P)=y_{P^{1}}-y_{P}>0. $$

By [10] there must be a point S between the points H and F such that

$$ g(S)=0, $$

and thus the orbit \(f(S,t)\) is an order-one periodic orbit of system (3) when \(0< x^{*}< h< h+p< K\) (see Fig. 4).

Figure 4
figure 4

Existence and uniqueness of order-one periodic orbit if \(0< x^{*}\leq h< h+p< K\)

Full size image

Now, we prove the uniqueness of the order-one periodic orbit of system (3).

We choose any two points \(G(h+p,y_{G})\) and \(I(h+p,y_{I})\) such that

$$ y_{G}>y_{I}. $$

The intersection point of the trajectory \(f(G,t)\) and the impulsive set M is the point \(G_{1}\). Then the point \(G_{1}\) jumps to the point \(G^{1}\) by impulse effects. The subsequent function of the point G is

$$ g(G)=y_{G^{1}}-y_{G}. $$

The intersection point of the orbit \(f(I,t)\) and the impulsive set M is the point \(I_{1}\),.Then the point \(I_{1}\) jumps to the point \(I^{1}\) by impulse effects. The subsequent function of the point I is

$$ g(I)=y_{I^{1}}-y_{I}. $$

Let the function \(y_{(x,Q_{0})}\) be denoted by the coordinates of an arbitrary point on the trajectory \(f(Q_{0}, t)\), where \(Q_{0}\) is the starting point. According to

$$ y_{G}>y_{I}, $$

we define

$$ y_{G}(x)\triangleq y_{(x,G)},\qquad y_{I}(x)\triangleq y_{(x,I)} $$

and

$$ d_{GI}=y_{G}(x)-y_{I}(x),\quad x\in [h,h+p]. $$

Hence we have

$$\begin{aligned} {d'_{GI}(x)}&= y'_{G}(x)-y'_{I}(x) \\ &= \frac{K(cax+1)}{x} \biggl[ \frac{x-by_{G}}{(rK-rx-\omega y_{G}K)(cax+1)-aK} \\ &\quad {}-\frac{x-by_{I}}{(rK-rx-\omega y_{I}K)(cax+1)-aK} \biggr] \\ &= \frac{K(cax+1)}{x}\phi '(\varsigma ) (y_{G}-y_{I}), \end{aligned}$$

where

$$ \phi (y)=\frac{x-by}{(rK-rx-\omega yK)(cax+1)-aK} $$

and

$$\begin{aligned} {\phi '(y)} =& \frac{-b[(cax+1)(rK-rx-\omega Ky)]+\omega K(cax+1)(x-by)}{[(cax+1)(rK-rx-\omega Ky)-aK]^{2}} \\ =& \frac{-brcaKx+brcax^{2}-brK+brx+\omega Kcax^{2}+\omega Kx}{[(cax+1)(rK-rx-\omega Ky)-aK]^{2}} \\ =& \frac{(brca+\omega Kca)x^{2}+(\omega K+br-brkca)x-brk}{[(cax+1)(rK-rx-\omega Ky)-aK]^{2}} \end{aligned}$$

when

$$ h+p>\frac{\sqrt{\Lambda }+(brkca-\omega r-br)}{2(brca+\omega Kca)}, $$

where

$$ \Lambda =(\omega K+br-brKca)^{2}+4brK(brKa+\omega Kca). $$

Then

$$ \phi '(y)>0, $$

and thus

$$ d'_{GI}>0 $$

for \(x\in [h,h+p]\). In summary, the function \(d_{GI}(x)\) is an increasing function, and

$$ d_{GI}(h+p)>d_{GI}(h). $$

Let

$$\begin{aligned}& d_{1}=d_{GI}(h+p)=y_{G}-y_{I}, \\& d_{2}=d_{GI}(h)=y_{G^{1}}-y_{I^{1}}. \end{aligned}$$

Obviously,

$$ d_{1}>d_{2}. $$

Hence the subsequent function of the points G and I satisfies

$$\begin{aligned} {g(G)-g(I)} =& (y_{G^{1}}-y_{G})-y_{I^{1}}=y_{I} \\ =& -(y_{G}-y_{I})+(y_{G^{1}}-y_{I^{1}}) \\ =& d_{2}-d_{1}< 0. \end{aligned}$$

Thus, the successor function is decreasing monotonously on the phase set N. So there must exist a unique point S such that \(g(S)=0\). This means that the order-one periodic orbit of system (3) is unique. □

3 Stability of the order-one periodic solution

Theorem 3.1

The periodic orbit of system (3) is orbitally asymptotically stable.

Proof

By Theorems 2.3 and 2.4 system (3) has a unique order-one periodic orbit between the points H and F, and \(y_{F}< y_{S}< y_{H}\). Thus \(g(F)>0\) for any \(F\in N\) with \(y_{S}>y_{F}\), \(g(H)<0\) for any \(H\in N\) with \(y_{H}>y_{S}\), and \(g(F)=g(H)=0\) if and only if \(H=F=S\).

Then we choose an arbitrary point \(F^{0}\) on the phase set N. If \(F^{0}\in N/\overline{FS}\), then after several impulse effects, the orbit jumps to the segment \(\overline{FS}\). Hence we assume that \(F^{0}\in \overline{FS}\subset N\). The orbit \(f(F^{0},t)\) hits the impulsive set M at the point \(F_{1}\), then the point \(F_{1}\) jumps to the point \(F^{1}\in N\) after an impulse effect, and

$$ y_{F}< y_{F^{0}}< y_{F_{1}}=y_{F^{1}}< y_{S}. $$

The orbit \(f(F^{1},t)\) intersects the impulsive set M at the point \(F_{2}\), then jumps to the point \(F^{2}\in N\), and

$$ y_{F}< y_{F^{0}}< y_{F^{1}}< y_{F^{2}}< y_{S}. $$

The orbit \(f(F^{2},t)\) hits the impulsive set M at the point \(F_{3}\), then jumps to the point \(F^{3}\in N\), and

$$ y_{F}< y_{F^{0}}< y_{F^{1}}< y_{F^{2}}< y_{F^{3}}< y_{S}. $$

Repeating this process, we get a point sequence \(\{F^{k}\}\), where \(k=0,1,2,\ldots\) , such that

$$ y_{F}< y_{F^{0}}< y_{F^{1}}< \cdots < y_{F^{k}}< \cdots \leq y_{S}. $$

Then the sequence \(F^{k}\parallel _{k=0,1,2,\ldots }\) is an increasing sequence with upper bound \(y_{S}\). According to the monotone bounded theorem, there exists the limit \(\lim_{k\rightarrow \infty }y_{F^{k}}=y_{S'}\), which implies that

$$ g\bigl(S'\bigr)=g\Bigl(\lim_{k\rightarrow \infty }y_{F^{k}} \Bigr)=\lim_{k\rightarrow \infty }g(y_{F^{k}})=\lim_{k\rightarrow \infty }(y_{F^{k+1}}-y_{F^{k}})=0. $$

Since \(g(F)=0\) if and only if \(F=S\), we get \(S'=S\), that is,

$$ \lim_{k\rightarrow \infty }g(y_{F^{K}})=y_{S'}=y_{S}. $$

Similarly, by the same method we obtain a point sequences \(I^{k}\parallel _{k=0,1,2,\ldots }\) such that

$$ y_{S}\leq \cdots < y_{I^{k}}< \cdots < y_{I^{2}}< y_{I^{1}}< y_{I^{0}}< y_{I}. $$

Since \(\{I^{k}\}\) is an decreasing sequence with lower bound \(y_{S}\), by the monotone bounded theorem it has the limit \(\lim_{k\rightarrow \infty }y_{I^{k}}=y_{S'}\), which means that

$$ g\bigl(S'\bigr)=g\Bigl(\lim_{k\rightarrow \infty }y_{I^{k}} \Bigr)=\lim_{k\rightarrow \infty }g(y_{I^{K}})=\lim_{k\rightarrow \infty }(y_{I^{k+1}}-y_{I^{k}})=0. $$

Since \(g(I)=0\) if and only if \(I=S\), we get \(S'=S\), that is, \(y_{I^{k}}=y_{S}\). Then we have

$$ y_{F}< y_{F^{0}}< y_{F^{1}}< \cdots < y_{F^{k}}< \cdots \leq y_{S}\leq \cdots < y_{I^{k}}< \cdots < y_{I^{2}}< y_{I^{1}}< y_{I^{0}}< y_{J}. $$

By the arbitrariness of the points \(I^{0}\) and \(F^{0}\) we have

$$ \lim_{k\rightarrow \infty }y_{I^{k}}=\lim_{k\rightarrow \infty }y_{F^{k}}=y_{S}. $$

In summary, all orbits of system (3) tend to the order-one periodic orbit (see [5]). So the order-one periodic orbit of system (3) is orbitally asymptotically stable and globally attractive (see Fig. 5).

Figure 5
figure 5

Orbital asymptotically stability of the order-one periodic orbit of system (1)

Full size image

 □

Thus our theoretical results show that releasing the African wild dogs in captivity to the wild is effective for protecting African wild dog population with Allee effect and continuous delay. Therefore, when protecting African wild dogs, we can determine the survival threshold, have African wild dogs in captivity, and monitor the wild populations (the initial value). Then, according to the state feedback of wild white-headed langurs, a certain amount of white-headed langurs in captivity will be released to the wild to increase the number of white-headed langurs in the wild, making the population have a normal reproduction to survive. According to the survival threshold and initial value, we can choose different grazing plans.

4 Numerical simulations and conclusion

4.1 Numerical simulations

In this section, we verify the correctness of the results by two examples.

Example 4.1

Let \(r=1\), \(K=5\), \(\omega =0.1\), \(b=2\), \(c=3\), and \(a=0.5\). By calculations we obtain the point \(E^{*}(3.694254177,10847127088)\). Thus system (3) becomes

$$ \textstyle\begin{cases} \left . \textstyle\begin{array}{l} \frac{dx}{dt}=x [ 1 ( 1-\frac{x}{5} ) -\frac{0.5}{1.5x+1}-0.1 y ] , \\ \frac{dy}{dt}=x-2y, \end{array}\displaystyle \right \}& x>h,\\ \left . \textstyle\begin{array}{l} \triangle x(t)=0.8,\\ \triangle y(t)=0, \end{array}\displaystyle \right \}& x=h. \end{cases} $$
(6)

Then we get the following cases.

Case I: Let \(h=2.2\), \(p=0.8\). Then \(0< h< h+p< x^{*}\). See Fig. 6.

Figure 6
figure 6

(a) Phase portrait of system (3) with \(h=2.2\), \(p=0.8\), and the initial point is \(\hbar (3,1.4611)\). (b) (c) Time series of model (3)

Full size image

Case II: Let \(h=3.39\), \(p=0.8\). Then \(0< h< x^{*}< h+p< K\). See Fig. 7.

Figure 7
figure 7

(a) Phase portrait of system (3) with \(h=3.39\), \(p=0.8\), and the initial point is \(\hbar (5,3.35)\). (b) (c)Time series of model (3)

Full size image

Case III: Let \(h=4\), \(p=0.8\). Then \(0< x^{*}< h< h+p< K\). See Fig. 8.

Figure 8
figure 8

(a) Phase portrait of system (3) with \(h=4\), \(p=0.8\), and the initial point is \(\hbar (0.45,2.5)\). (b) (c) Time series of model (3)

Full size image

Example 4.2

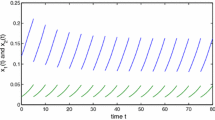
We verify the feasibility of feedback control strategy by a real-life example.

In [8], the authors studied the data from 1980–2004 on a small region population of Lycaon pictus in Hluhluwe–Imfolozi Park (HIP) to analyze the pack and population density dynamics. According to these data in [8], the authors take the annual growth rate of Lycaon pictus is 0–1.47, the carrying capacity K is 2.2–13.3, the parameter a is 0.6–1.3, and c is 0.5–1.2. Thus, we assume that the initial value of the pack is 2. We determine the minimum survival threshold by monitoring the population of Lycaon pictus in the wild; when the population of Lycaon pictus decreases to 1.5, a certain amount of Lycaon pictus in captivity is released to the wild. Let the parameters \(r=1\), \(K=2.5\), \(a=0.7\), \(c=1\), \(\omega =0.1\), and \(b=1\) (see Fig. 9). Numerical simulation shows that the feedback control strategy can effectively protect the Lycaon pictus population.

Figure 9
figure 9

The parameter x denotes the density of Lycaon pictus. The red line denotes the sample path of species with Allee effect and feedback control, and the blue star denotes the experimental data

Full size image

4.2 Conclusion

In this paper, we studied the African wild dogs impulsive state feedback control model with Allee effect and continuous time delay. By the feedback information of the density of African wild dog population from the monitor we can protect the African wild dog population.

First, we carried on the quantitative and qualitative analysis and obtained two conditions \((H_{1})\) and \((H_{2})\). We proved the global asymptotic stability of the positive equilibrium \(E^{*}(x^{*},y^{*})\) by the Bendixson–Dulac theory.

Then we proved that the existence of an order-one periodic orbit of system (3) by the geometric theory of differential equations. We also proved the uniqueness of the order-one periodic orbit of system (3) by the monotonicity of the successor functions and the Lagrange mean value theorem.

Finally, we studied the orbital asymptotic stability of the order-one periodic orbit by the geometric properties of successor functions. Then we proved that the limit exists by the uniqueness of the order-one periodic orbit and the limit existence theorem.

All the results suggest that the release of artificial captive of African wild dogs can effectively protect the African wild dog population with Allee effect. The determination of the value of the survival threshold h involves analyzing the viability of the African wild dog population, which will be our future work.