Skip to main content
SpringerLink
Log in

Periodic solution of a Leslie predator–prey system with ratio-dependent and state impulsive feedback control

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

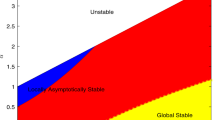
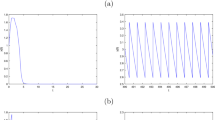
In this paper, a Leslie predator–prey system with ratio-dependent and state impulsive feedback control is investigated by applying the geometry theory of differential equation. When the economic threshold level is under the positive equilibrium, the existence, uniqueness and orbital asymptotical stability of order-1 periodic solution for the system can be obtained. When the economic threshold level is above the positive equilibrium, and the positive equilibrium is a focus point, sufficient conditions of the existence, uniqueness and orbital asymptotical stability of order-1 periodic solution for the system are also acquired. Furthermore, when the positive equilibrium is an unstable focus point, the existence of order-1 periodic solution of the impulsive system can be obtained within limit cycle of the continuous system. The mathematical results can be verified by numerical simulations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21

Similar content being viewed by others

References

  1. Stern, V.M., Smith, R.F., Rosch, V.D.R., Hagen, K.S.: The integrated control concept. Hilgardia 29, 81–101 (1959)

    Article  Google Scholar 

  2. Bainov, D.D., Simeonov, P.S.: Impulsive Differential Equations: Periodic Solutions and Applications. Longman, England (1993)

    MATH  Google Scholar 

  3. Bainov, D.D., Simeonov, P.S.: Impulsive Differential Equations: Asymptotic Properties of the Solutions. World Scientific, Singapore (1995)

    Book  MATH  Google Scholar 

  4. Simenov, P.S., Bainov, D.D.: Orbital stability of the periodic solutions of autonomous systems with impulse effect. Int. J. Syst. Sci. 19, 2561–2585 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  5. Ciesielski, K.: On stability in impulsive dynamical systems. Bull. Polish Acad. Sci. Math. 52, 81–91 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  6. Bonotto, E.M., Federson, M.: Poisson stability for impulsive semidynamical systems. Nonlinear Anal. 71, 6148–6156 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  7. Bonotto, E.M., Federson, M.: Limit sets and the Poincaré–Bendixson theorem in impulsive semidynamical systems. J. Differ. Equ. 244, 2334–2349 (2008)

    Article  MATH  Google Scholar 

  8. Chen, L.S.: Pest control and geometric theory of semi-continuous dynamical system. J. Beihua Univ. (Nat. Sci.) 12, 1–9 (2011)

    Google Scholar 

  9. Chen, L.S.: Theory and application of semi-continuous dynamical system. J. Yulin Normal Univ. (Nat. Sci.) 34, 1–10 (2013)

    Google Scholar 

  10. Liang, Z.Q., Pang, G.P., Zen, X.P., Liang, Y.H.: Qualitative analysis of a predator–prey system with mutual interference and impulsive state feedback control. Nonlinear Dyn. 87, 1495–1509 (2017)

    Article  MathSciNet  Google Scholar 

  11. Sun, S.L., Guo, C.H., Qin, C.: Dynamic behaviors of a modified predator–prey model with state-dependent impulsive effects. Adv. Differ. Equ. 2016, 50 (2016)

    Article  MathSciNet  Google Scholar 

  12. Wang, T.Y., Chen, L.S.: Nonlinear analysis of a microbial pesticide model with impulsive state feedback control. Nonlinear Dyn. 65, 1–10 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  13. He, Z.M.: Impulsive state feedback control of a predator–prey system with group defense. Nonlinear Dyn. 79, 2699–2714 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  14. Xiao, Q.Z., Dai, B.X., Xu, B.X., Bao, L.S.: Homoclinic bifurcation for a general state-dependent Kolmogorov type predator–prey model with harvesting. Nonlinear Anal. RWA 26, 263–273 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  15. Wei, C.J., Chen, L.S.: Periodic solution and heteroclinic bifurcation in a predator–prey system with Allee effect and impulsive harvesting. Nonlinear Dyn. 76, 1109–1117 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  16. Pang, G.P., Chen, L.S.: Periodic solution of the system with impulsive state feedback control. Nonlinear Dyn. 78, 743–753 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  17. Zhao, Z., Pang, L.Y., Song, X.Y.: Optimal control of phytoplankton–fish model with the impulsive feedback control. Nonlinear Dyn. 88, 2003–2011 (2017)

    Article  MathSciNet  Google Scholar 

  18. Leslie, P.H.: Some further notes on the use of matrices in population mathematics. Biometrika 35, 213–245 (1948)

    Article  MathSciNet  MATH  Google Scholar 

  19. Leslie, P.H., Gower, J.C.: The properties of a stochastic model for the predator–prey type of interaction between two species. Biometrika 47, 219–231 (1960)

    Article  MathSciNet  MATH  Google Scholar 

  20. Hsu, S.B., Huang, T.W.: Global stability for a class of predator–prey systems. SIAM J. Appl. Math. 55, 763–783 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  21. Chen, L.J., Chen, F.D.: Global stability of a Leslie–Gower predator–prey model with feedback controls. Appl. Math. Lett. 22, 1330–1334 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  22. Singh, M.K., Bhadauria, B.S., Singh, B.K.: Qualitative analysis of a Leslie–Gower predator–prey system with nonlinear harvesting in predator. Int. J. Eng. Math. 2016, 2741891 (2016)

    Article  Google Scholar 

  23. Feng, P., Kang, Y.: Dynamics of a modified Leslie–Gower model with double Allee effects. Nonlinear Dyn. 80, 1051–1062 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  24. Yang, R.Z., Zhang, C.R.: Dynamics in a diffusive modified Leslie–Gower predator–prey model with time delay and prey harvesting. Nonlinear Dyn. 87, 863–878 (2017)

    Article  MathSciNet  Google Scholar 

  25. Cao, J.Z., Yuan, R.: Bifurcation analysis in a modified Lesile–Gower model with Holling type II functional response and delay. Nonlinear Dyn. 84, 1341–1352 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  26. Murray, J.D.: Mathematical Biology. Springer, Berlin (1989)

    Book  MATH  Google Scholar 

  27. May, R.M.: Stability and Complexity in Ecosystems. Princeton University Press, Princeton (2001)

    MATH  Google Scholar 

  28. Gasull, A., Kooij, R.E., Torregrosa, J.: Limit cycles in the Holling–Tanner model. Publ. Mat. 41, 149–167 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  29. Saez, E., Gonzalez-Olivares, E.: Dynamics of predator–prey model. SIAM J. Appl. Math. 59, 1867–1878 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  30. Song, Z.G., Zhen, B., Xu, J.: Species coexistence and chaotic behavior induced by multiple delays in a food chain system. Ecol. Complex. 19, 9–17 (2014)

    Article  Google Scholar 

  31. Guo, L., Song, Z.G., Xu, J.: Complex dynamics in the Leslie–Gower type of the food chain system with multiple delays. Commun. Nonlinear Sci. Numer. Simul. 19, 2850–2865 (2014)

    Article  MathSciNet  Google Scholar 

  32. Holling, C.S.: Functional response of predators to prey density and its role in mimicry and population regulation. Mem. Entomol. Soc. Can. 97, 1–60 (1965)

    Article  Google Scholar 

  33. Arditi, R., Ginzburg, L.R.: Coupling in predator–prey dynamics: ratio-dependence. J. Theor. Biol. 139, 311–326 (1989)

    Article  Google Scholar 

  34. Abrams, P.A., Ginzburg, L.R.: The nature of predation: prey dependent, ratio-dependent or neither? Trends Ecol. Evol. 15, 337–341 (2000)

    Article  Google Scholar 

  35. Akcakaya, H.R., Arditi, R., Ginzburg, L.R.: Ratio-dependent prediction: an abstraction that works. Ecology 79, 995–1004 (1995)

    Article  Google Scholar 

  36. Liang, Z.Q., Pan, H.W.: Qualitative analysis of a ratio-dependent Holling–Tanner model. J. Math. Anal. Appl. 334, 954–964 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  37. Celik, C.: Stability and hopf bifurcation in a delayed ratio dependent Holling–Tanner type model. Appl. Math. Comput. 255, 228–237 (2015)

    MathSciNet  MATH  Google Scholar 

  38. Saha, T., Chakrabarti, C.: Dynamical analysis of a delayed ratio-dependent Holling–Tanner predator–prey model. J. Math. Anal. Appl. 358, 389–402 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  39. Wang, Q., Zhang, Y.M., Wang, Z.J., Ding, M.M., Zhang, H.Y.: Periodicity and attractivity of a ratio-dependent Leslie system with impulses. J. Math. Anal. Appl. 376, 212–220 (2011)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of PR China (61364020,11361068) and the Major Research Programmes of Yulin Normal University of PR China (2015YJZD02).

Author information

Authors and Affiliations

  1. College of Mathematics and statistics, Guangxi Colleges and Universities Key Lab of Complex System Optimization and Large Data Processing, Yulin Normal University, Yulin, 537000, Guangxi, China

    Zhiqing Liang, Xiaping Zeng, Guoping Pang & Yanhong Liang

Authors
  1. Zhiqing Liang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiaping Zeng
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Guoping Pang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yanhong Liang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zhiqing Liang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liang, Z., Zeng, X., Pang, G. et al. Periodic solution of a Leslie predator–prey system with ratio-dependent and state impulsive feedback control. Nonlinear Dyn 89, 2941–2955 (2017). https://doi.org/10.1007/s11071-017-3637-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-017-3637-4

Keywords

Search

Navigation