Abstract
We discuss the numerical solution of the time-fractional telegraph equation. The main purpose of this work is to construct and analyze stable and high-order scheme for solving the time-fractional telegraph equation efficiently. The proposed method is based on a generalized finite difference scheme in time and Legendre spectral Galerkin method in space. Stability and convergence of the method are established rigorously. We prove that the temporal discretization scheme is unconditionally stable and the numerical solution converges to the exact one with order \(\mathcal {O}(\tau^{2-\alpha}+N^{1-\omega})\), where \(\tau, N \), and ω are the time step size, polynomial degree, and regularity of the exact solution, respectively. Numerical experiments are carried out to verify the theoretical claims.
Similar content being viewed by others
1 Introduction
In recent decades, fractional partial differential equations have attracted increasing interest mainly due to their potential applications in various realms of science and engineering [1–3]. The fractional telegraph equation, as a typical diffusion-wave equation, is commonly used in propagation of electrical signals [4], random walk theory [5], the neutron transport in nuclear reactor [6], and so on.
The fractional telegraph equation has been considered recently by several authors. Liu et al. [7] considered the analytical solution of the time-fractional telegraph equation by the method of separating variables. Momani [8] used the Adomian decomposition method to obtain analytic and approximate solutions of the space- and time-fractional telegraph equations. Huang [9] provided the fractional Green function for the time-fractional telegraph equation by employing the Laplace and Fourier transforms. In [10], an analytical mathematical tool, the homotopy analysis method, is used to solve the time-fractional telegraph equation. Although many valuable works have been conducted on theoretical analysis, the obtained solutions of most fractional telegraph equations are not analytic. Therefore many researchers have studied numerical solution of the fractional telegraph equation. Hosseini et al. [11] implemented a hybrid of the radial basis functions and finite difference scheme to achieve a semidiscrete solution of the time-fractional telegraph equation. Liu et al. [12] present a class of unconditionally stable difference schemes of high order for solving a Riesz space-fractional telegraph equation. Hashemi et al. [13] proposed a simple and accurate numerical scheme for solving the time-fractional telegraph equation. Wang et al. [14] discussed and analyzed an \(H^{1}\)-Galerkin mixed finite element method to look for the numerical solution of time-fractional telegraph equation. Ford et al. [15] considered a finite difference method for the two-parameter fractional telegraph equation and obtained a stability condition of the numerical method. Wei [16] developed a fully discrete local discontinuous Galerkin finite element method for numerical simulation of the time-fractional telegraph equation. Although many authors have studied the numerical solution of the fractional telegraph equation, they did not strictly prove the unconditional stability and convergence in time direction.
In this paper, we study the method resulting from a generalized finite difference method for the temporal discretization and a Legendre spectral Galerkin method for the spatial discretization of the following time-fractional telegraph problem:
where \(0 < \alpha<1\) is a parameter describing the fractional derivative with respect to time, \(\Omega=[a,b]\) is a bounded closed interval in \(\mathbb{R}\), \(\beta, \lambda\) are positive constants in \(\mathbb{R}\), and \(f(x,t), u_{0}(x)\), and \(u_{1}(x)\) are given smooth functions.
The time-fractional derivative in (1.1) uses the Caputo fractional partial derivative of order α defined as follows:
where Γ is the gamma function. Obviously, if \(0<\alpha<1\), then \(1<\alpha+1<2\), so
The rest of the paper is organized as follows. In the next section, the temporal discretization scheme of the time-fractional telegraph equation and its stability and convergence are discussed. In Section 3, we derive a full discretization scheme of the time-fractional telegraph equation and obtain error estimates. Numerical experiments are carried out in Section 4, which verify the effectiveness of our method and support the theoretical analysis. The last section is the concluding remarks.
2 Discretization in time: a generalized finite difference scheme
First, we introduce a generalized finite difference approximation to discretize the time-fractional derivative. Let \(t_{k}: = k \tau, k=0,1,\ldots,K \), where \(\tau= \frac{T}{K}\) is the time step. To motivate the construction of the scheme, we define the sequence \(\{a_{j}\}|_{j=0}^{K}\) as \(a_{j}=\frac{\tau ^{1-\alpha}}{1-\alpha} ((j+1)^{1-\alpha}-j^{1-\alpha} )\) and introduce the following lemmas [17].
Lemma 2.1
Let \(g\in C^{2}[0, t_{k}]\) and \(0< \alpha< 1\). Then
Lemma 2.2
For any \(G=\{G_{1}, G_{2}, G_{3},\dots\}\) and q, we have
To motivate the construction of the time-discrete scheme, we use the following functions:
Introduce the following notation:
Then we have
and there exists a constant \(C_{1}\) such that \(|r_{1}^{k-1/2}|\leq C_{1}\tau^{2}\) for all \(1\leq k\leq K\).
By Lemma 2.1 we have
and there exist constants \(C_{2}\) and\(C_{3}\) such that \(|r_{2}^{k-1/2}|\leq C_{2}\tau^{2-\alpha}\) and \(|r_{3}^{k-1/2}|\leq C_{3}\tau^{2-\alpha}\).
where
with
Dropping the truncation error \(R^{k-1/2}\) in (2.6), we can easily get the the variation (weak) formulation of (1.1): Find \(u^{k}(x)\in H_{0}^{1}(\Omega)\) such that, for all \(v\in H_{0}^{1}(\Omega)\),
For the semidiscrete problem, we have the following result.
Theorem 2.1
The semidiscrete problem (2.8) is unconditionally stable in the sense that, for all \(\tau \geq 0\),
where \(n=1,2,\ldots,K\), and \(C=\frac{\max\{\beta, \gamma\}}{\min\{ \beta , \gamma\}}+\frac{2T^{1-\alpha}}{\min\{\beta, \gamma\}\Gamma (2-\alpha )}+ \frac{\Gamma(1-\alpha)T^{1+\alpha}}{\min\{\beta, \gamma\}}\) is a constant.
Proof
Taking \(v = \delta_{t} u^{k-1/2}+u^{k-1/2}\) in (2.8), we have
We first sum both sides of (2.9) for k from 1 to n, and then, using Lemma 2.2 and the Cauchy-Schwarz inequality for the first term of the left-hand side of (2.9), we obtain
The third term can be written as
Similarly, the second term can be written as
Using the Young inequality for the right-hand side of (2.9), we have
From (2.10)-(2.13) we get the following relation:
Denoting \(A:=\max\{\beta, \gamma\}\) and \(B:=\min\{\beta,\gamma\} \), we have
Multiplying both sides of this inequality at \(\frac{2\tau}{B}\), we obtain
The proof is completed. □
Theorem 2.2
Let \(u(x,t)\) (\(\{u^{k}=u(t_{k})\}_{k=0}^{K}\)) be the exact solution of (1.1), and \(\{u_{\varsigma}^{k}\}_{k=0}^{K}\) be the solution of variation (weak) formulation (2.8). Then we have the following error estimate:
Proof
Denoting \(\rho^{k}=u^{k}-u_{\varsigma}^{k}\), we obtain
Taking \(v=\delta_{t}\rho^{k-1/2}+\rho^{k-1/2}\) in (2.17) yields
Summing up for k from 1 to n and using Lemma 2.2, we obtain
In addition, similarly to the proof of Theorem 2.1, we can write the following relations:
and
From (2.19)-(2.22) we obtain the following relation:
From (2.7) we can find a constant \(C':=\frac{2C_{1}}{\Gamma (2-\alpha)}+C_{2}+C_{3}\) such that \(\vert R^{k-1/2} \vert \leq C'\tau^{2-\alpha}\). Similarly to (2.16), we obtain
Letting \(C=\frac{T^{1+\alpha}\Gamma(1-\alpha)}{B}{C^{\prime}}^{2}\), the theorem is proved. □
3 Full discretization
To simplify the notation, let \(\Omega=(-1,1)\). The Galerkin spectral discretization proceeds by approximating the solution by polynomials of high degree. To this end, we denote by \(P_{N}(\Omega)\) the space of all polynomials of degree ≤N with respect x. Then the discrete space, denoted by \(P_{N}^{0}(\Omega)\), is defined as follows: \(P_{N}^{0}(\Omega ):=H_{0}^{1}(\Omega)\cap P_{N}(\Omega)\).
Now we consider the spectral Galerkin discretization to problem (1.1) as follows. Find \(u_{N}^{k}(x)\in P_{N}^{0}(\Omega)\) such that, for all \(v_{N}(x)\in P_{N}^{0}(\Omega)\),
For all \(\{u_{N}^{k}\}|_{k=0}^{K}\), the well-posed problem (3.1) is guaranteed by the well-known Lax-Milgram lemma. In this section, we would like to derive an error estimation for the full-discrete solution \(\{u_{N}^{k}\}|_{k=0}^{K}\). Let \(\pi_{N}^{1}\) be the \(H^{1}\)-orthogonal projection operation from \(H_{0}^{1}(\Omega)\) into \(P_{N}^{0}(\Omega )\), where
The following projection estimation is well known:
Lemma 3.1
Let \(\{u_{\varsigma}^{k}\}_{k=0}^{K}\) be the solution of the semidiscrete problem (2.8). Then there exists a constant C such that
where
Proof
Using the triangle inequality, Lemma 3.1, and relation (3.3), we easily obtain that \(\vert R_{N} \vert \leq C(N^{1-\omega}+\tau ^{2-\alpha})\), where C depends on the norm of \(\{u_{\varsigma}^{k}\}_{k=0}^{K}\). □
Theorem 3.1
Let \(\{u_{\varsigma}^{k}\}_{k=0}^{K}\) be the solution of the semidiscrete problem (2.8), and \(\{u_{N}^{k}\}_{k=0}^{K}\) be the solution of the full-discrete problem (3.1). Suppose that \(\{u_{\varsigma}^{k}\}_{k=0}^{K} \in H^{\omega}(\Omega)\cap H_{0}^{1}(\Omega), \omega>1\). Then there exists a constant C such that
Proof
Subtracting (3.1) from (2.8) and using (3.2) give
To simplify the function, we let \(\phi_{N}^{k}=\pi _{N}^{1}u_{\varsigma }^{k}-u_{N}^{k}\). Taking \(v_{N}=\delta_{t}\phi_{N}^{k-1/2}+\phi _{N}^{k-1/2}\) yields
Similarly to the proof of Theorem 2.1, we can write the following relations:
Similarly to (2.16) we obtain
From the triangle inequality and (3.2) we obtain
The proof of the theorem is completed. □
Theorem 3.2
Let \(u(x,t)\) (\(\{u^{k}=u(t_{k})\}_{k=0}^{K}\)) be the exact solution of (1.1), and \(\{u_{N}^{k}\}_{k=0}^{K}\) be the solution of the full-discrete problem (3.1). Suppose that \(\{u^{k}\}_{k=0}^{K} \in H^{\omega}(\Omega)\cap H_{0}^{1}(\Omega), \omega>1\). Then there exists a constant C such that
Proof
From Theorem 2.2, Theorem 3.1, and the triangle inequality we obtain
where \(\{u_{\varsigma}^{k}\}_{k=0}^{K}\) is the solution of the semidiscrete problem (2.8). □
4 Numerical examples
4.1 Implementation
Before numerical experiments, in this subsection, we briefly introduce an implementation.
Let \(L_{i}(x)\) be the ith-degree Legendre polynomial. They are mutually orthogonal in \(L^{2}(\Omega)\), that is,
where \(\delta_{ij}\) is the Kronecker delta symbol.
We define (see [18])
One useful property of the Legendre polynomials is
which gives the relation
It is easy to verify that, for \(N\geq2\),
Let us denote
Then, scheme (3.1) leads to the following linear system: For \(k=1,2,\ldots,K\),
Using the orthogonality of Legendre polynomials, we can easily determine that the matrix M is pentadiagonal and P is diagonal. We easily obtain:
Hence, at each time step, we obtain a system of linear algebraic equations with different right-hand-side vectors. The matric in the left-hand side of (4.7) is banded, and the linear system (4.7) can be easily solved.
4.2 Numerical results
In this subsection, we carry out two numerical experiments and present some results to confirm our theoretical statements. The main purpose is to check the convergence behavior of the numerical solution with respect to the time step size τ and polynomial degree N used in the calculation. Here, all the calculations are carried out in Matlab.
Example 1
Consider the time-fractional telegraph equation (1.1) in \([-1,1]\times[0,1]\) with \(\beta=\lambda=1\) and the exact solution:
It can be checked that the corresponding forcing term, initial condition, and boundary condition are respectively
We solve this example using the proposed method with several values of \(\tau, N\), and α.
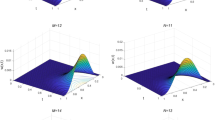
When \(\alpha=0.6\), as an example, the graphs of the exact solution and the numerical solution with \(\tau=\frac{1}{1{,}000}\) and \(N=48\) are shown in Figure 1.
Example 1 . Graphs of the exact solution (left panel) and the numerical solution (right panel).
Figure 2 (left) shows the plot of the absolute \(L_{\infty}, L_{2}, H_{1}\) errors as functions of the time step size for \(N=24\) via \(\alpha=0.3\). Figure 2 (right) shows the plot of the absolute \(L_{\infty}, L_{2}, H_{1}\) errors as functions of polynomial degree N for \(\tau=\frac{1}{20{,}000}\) via \(\alpha=0.1\).
Example 1 . Graphs of error as a function of the time step size τ (left panel) and the polynomial degree N (right panel).
Table 1 lists some numerical results when \(N=24\) (the degree of Lagrange polynomial), which shows that the convergence order of presented scheme in temporal direction is \(O(\tau^{2-\alpha})\), where \(\alpha=0.1, 0.5, 0.9\). Table 2 presents the errors in \(H_{1}\)-norm and the convergence orders of presented scheme in space direction with \(\tau=\frac{1}{20{,}000}\) and \(\alpha=0.1, 0.3\), respectively.
Example 2
The proposed method also can be used to solve another kind of time-fractional telegraph equation:
with exact solution
It can be checked that the corresponding forcing term, initial condition, and boundary condition are respectively
Figure 3 (left) shows the plot of the absolute \(L_{\infty}, L_{2}, H_{1}\) errors as functions of the time step size for \(N=24\) via \(\alpha=0.7\). Figure 3 (right) shows the plot of the absolute \(L_{\infty}, L_{2}, H_{1}\) errors as functions of polynomial degree N for \(\tau=\frac{1}{20{,}000}\) via \(\alpha=0.6\).
Example 2 . Graphs of error as functions of the time step size τ (left panel) and the polynomial degree N (right panel).
Table 3 lists some numerical results when \(N=24\) (the degree of Lagrange polynomial) and \(\alpha=0.2, 0.4, 0.6, 0.8\), respectively, which shows that the time convergence order of the case \(0< \alpha< 0.5\) is \(\mathcal{O}(\tau^{2-2\alpha})\) and the time convergence order of the case \(0.5< \alpha< 1\) is \(\mathcal{O}(\tau ^{3-2\alpha})\). Table 4 presents the errors in \(H_{1}\)-norm and the convergence order of presented scheme in space direction with \(\tau=\frac{1}{20{,}000}\) and \(\alpha=0.1, 0.2, 0.6, 0.7\), respectively.
5 Concluding remarks
In this paper, we have proposed a new numerical method for the time-fractional telegraph equation with convergence order \(\mathcal {O}(\tau^{2-\alpha}+N^{1-\omega})\) in \(H_{1}\)-norm by combining the generalized finite difference method and spectral Galerkin method, and we have rigorously proved the stability and convergence of this method. By Example 1 we have verified the theoretical results. It is demonstrated that this method is an effective and high-accuracy numerical scheme for solving the time-fractional telegraph equation (1.1). Example 2 shows that the proposed method also can solve the other kind of time-fractional telegraph equation with convergence order \(\mathcal{O}(\tau^{2-2\alpha}+N^{1-\omega})\) when \(0<\alpha<0.5\) and convergence order \(\mathcal{O}(\tau^{3-2\alpha}+N^{1-\omega})\) when \(0.5<\alpha<1\).
References
Podlubny, I: Fractional Differential Equations. Mathematics in Science and Engineering, vol. 198. Academic Press, San Diego (1999)
Kilbas, AA, Srivastava, HM, Trujillo, JJ: Theory and Applications of Fractional Differential Equations. Elsevier, New York (2006)
Samko, SG, Kilbas, AA, Marichev, O: Integrals and Derivatives of Fractional Order and Some of Their Applications. Nauka i Tekhnika, Minsk (1987)
Jordan, P, Puri, A: Digital signal propagation in dispersive media. J. Appl. Phys. 85(3), 1273-1282 (1999)
Banasiak, J, Mika, JR: Singularly perturbed telegraph equations with applications in the random walk theory. J. Appl. Math. Stoch. Anal. 11(1), 9-28 (1998)
Vyawahare, VA, Nataraj, P: Fractional-order modeling of neutron transport in a nuclear reactor. Appl. Math. Model. 37(23), 9747-9767 (2013)
Chen, J, Liu, F, Anh, V: Analytical solution for the time-fractional telegraph equation by the method of separating variables. J. Math. Anal. Appl. 338(2), 1364-1377 (2008)
Momani, S: Analytic and approximate solutions of the space-and time-fractional telegraph equations. Appl. Math. Comput. 170(2), 1126-1134 (2005)
Huang, F: Analytical solution for the time-fractional telegraph equation. J. Appl. Math. 2009, Article ID 890158 (2009). doi:10.1155/2009/890158
Das, S, Vishal, K, Gupta, P, Yildirim, A: An approximate analytical solution of time-fractional telegraph equation. Appl. Math. Comput. 217(18), 7405-7411 (2011)
Hosseini, VR, Chen, W, Avazzadeh, Z: Numerical solution of fractional telegraph equation by using radial basis functions. Eng. Anal. Bound. Elem. 38, 31-39 (2014)
Chen, S, Jiang, X, Liu, F, Turner, I: High order unconditionally stable difference schemes for the Riesz space-fractional telegraph equation. J. Comput. Appl. Math. 278, 119-129 (2015)
Hashemi, M, Baleanu, D: Numerical approximation of higher-order time-fractional telegraph equation by using a combination of a geometric approach and method of line. J. Comput. Phys. 316, 10-20 (2016)
Wang, J, Zhao, M, Zhang, M, Liu, Y, Li, H: Numerical analysis of an \(H^{1}\)-Galerkin mixed finite element method for time fractional telegraph equation. Sci. World J. 2014, Article ID 371413 (2014)
Ford, NJ, Rodrigues, MM, Xiao, J, Yan, Y: Numerical analysis of a two-parameter fractional telegraph equation. J. Comput. Appl. Math. 249, 95-106 (2013)
Wei, L, Dai, H, Zhang, D, Si, Z: Fully discrete local discontinuous Galerkin method for solving the fractional telegraph equation. Calcolo 51(1), 175-192 (2014)
Sun, Z, Wu, X: A fully discrete difference scheme for a diffusion-wave system. Appl. Numer. Math. 56(2), 193-209 (2006)
Shen, J: Efficient spectral-Galerkin method I. Direct solvers of second-and fourth-order equations using Legendre polynomials. SIAM J. Sci. Comput. 15(6), 1489-1505 (1994)
Acknowledgements
The authors are grateful for the referee’s helpful suggestions and comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Funding
This work is supported by the National Nature Science Foundation of China, No. 11371289.
Abbreviations
Not applicable.
Availability of data and materials
Not applicable.
Competing interests
The authors declare that they have no competing interests.
Consent for publication
Both authors read and approved the final manuscript.
Authors’ contributions
All authors contributed equally to the writing of the paper.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Wang, Y., Mei, L. Generalized finite difference/spectral Galerkin approximations for the time-fractional telegraph equation. Adv Differ Equ 2017, 281 (2017). https://doi.org/10.1186/s13662-017-1348-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-017-1348-2