Abstract
This paper presents a novel adaptive finite-time tracking control scheme for nonlinear systems. During the design process of control scheme, the unmodeled dynamics in nonlinear systems are taken into account. The radial basis function neural networks (RBFNNs) are adopted to approximate the unknown nonlinear functions. Meanwhile, based on RBFNNs, the assumptions with respect to unmodeled dynamics are also relaxed. This paper provides a new finite-time stability criterion, making the adaptive tracking control scheme more suitable in the practice than traditional methods. Combining RBFNNs and the backstepping technique, a novel adaptive controller is designed. Under the presented controller, the desired system performance is realized in finite time. Finally, a numerical example is presented to demonstrate the effectiveness of the proposed control method.
Similar content being viewed by others
1 Introduction
In recent years, the adaptive control of nonlinear systems has achieved remarkable breakthroughs by combining with the backstepping technology [1–24]. Many of the technical limitations in traditional adaptive control, such as matching condition and relative-degree constraint, can be eliminated by an adaptive backstepping control scheme. Fuzzy logic systems and neural networks (NNs) provide useful tools for designing control schemes of uncertain nonlinear systems, because of their capability of nonlinear approximation [7, 25–52]. One of the breakthroughs in neural networks control is the introduction of adaptive algorithms for tuning the weighs of NNs [53]. However, the application of this method is limited by the large computation. This phenomenon is due mainly to the fact that the number of adaptive parameters is always affected by the nodes of the neural network. This problem has been resolved by the adaptive control scheme proposed in [54] to a certain extent. In [54], the key technique to relaxing the limitation lies in employing norms of unknown neural weight vectors as the estimated parameters. It is also well known that the applicability of the adaptive backstepping control method is limited by unmodeled dynamics existing in many practical nonlinear systems. Consequently, adaptive control for nonlinear systems with unmodeled dynamics has been given widely attention in the past several years [55, 56].
Unmodeled dynamics are caused by many factors, such as measuring errors, modeling errors and uncertain perturbations. The traditional adaptive control methods are not suitable in the presence of unmodeled dynamics. There are two possible ways to eliminate the influence of unmodeled dynamics. The first way is to introduce a dynamics signal to dominate the dynamics perturbation. In [57], K-filters and dynamic signal are introduced to estimate the unmeasured states and deal with the dynamic uncertainties, respectively. This method also was employed in nonlinear systems with fuzzy dead zone and dynamic uncertainties based on fuzzy adaptive algorithm [58]. The second avenue is to make the assumption with respect to unmodeled dynamics satisfying a lower triangular condition [59, 60]. The control laws designed in [59] did not require an extra dynamic signal to prove Lagrange stability. The same method was also employed in nonlinear systems with many types of uncertainties, such as unknown dead-zone inputs, time-varying delay uncertainties, unknown dynamic disturbances [60]. However, the control schemes proposed in the above literature can only achieve desired system performance when the time tends to infinity. In practical engineering, it is necessary to ensure that the performance of the system can be realized in finite time.
Finite-time control has received much attention because it can provide many benefits such as strong robustness and better disturbance resistance capability [3, 4, 61]. The Lyapunov theory of finite-time stability for nonlinear systems has been clearly established by several authors [62, 63]. It is necessary to point out that the nonlinear functions in these systems all meet the linear growth condition. However, in practice, the nonlinear functions are often completely unknown for the constraints of the modeling method or unknown dynamic disturbances. In this case, the linear growth condition might not be satisfied. To eliminate this limitation, a new finite-time stability criterion was proposed in [64]. However, the controller proposed in [64] cannot be applied to the nonlinear system with unmodeled dynamics. In other words, there is still some room for improvement in making the finite-time control scheme implemented more efficiently. These facts motivate us to provide a new finite-time adaptive backstepping control scheme for uncertain nonlinear system with unmodeled dynamics. In contrast with the existing literature, the control scheme in this note offers the following benefits.
(1) The traditional adaptive neural or fuzzy control strategies can only guarantee the system performance when time tends to infinity. These existing adaptive fuzzy control methods are not suitable for the finite-time tracking control for uncertain nonlinear system. Based on the Lyapunov theory of finite-time stability of nonlinear systems, this paper constructs a neural network controller which can ensure the tracking performance of the system in finite time. Therefore, to a certain extent, the control strategy proposed in this paper is more meaningful than the control methods presented in [1, 2, 5, 56] in the practical application fields.
(2) During the design process of control scheme, the unmodeled dynamics are considered. Meanwhile, based on RBFNNs, the assumptions with respect to unmodeled dynamics are also relaxed. Moreover, in the presence of unknown dynamic disturbances and unmodeled dynamics, finite-time control can provide many benefits such as strong robustness and better disturbance resistance capability.
(3) The classical stability criteria draw a conclusion on finite-time stability based on inequality \(\dot{V}\leq-a_{0}V^{\wp}\) with \(a_{0}>0\) and \(0<\wp<1\). In contrast with the existing finite-time control methods, the corresponding approximation errors in this paper will result in a positive constant \(d_{0}\) appearing in the right side of the inequality \(\dot{V}\leq-a_{0}V^{\wp}\). These facts motivate us to provide a novel criterion of finite-time stability, say \(\dot{V}\leq-a_{0}V^{\wp}+d_{0}\) with \(d_{0}>0\). With the new adaptive control scheme based on the novel criterion of finite-time stability proposed in this article, the nonlinear functions can be completely unknown and they are only required to be continuous. Consequently, in contrast with the existing finite-time control methods in [62–64], the control method in this note is more adaptable to the realistic systems.
The paper is organized as follows. The control problem of the nonlinear system with unmodeled dynamics is formulated in Sect. 2. The main results are presented in Sect. 3, where the adaptive neural networks controller is presented to achieve the control objective in finite time. Simulation results are presented in Sect. 4. The paper ends with the conclusion in Sect. 5.
2 Preliminaries and problem formulation
2.1 System description
The nonlinear systems with unmodeled dynamics in this paper can be expressed as follows:
where \(\bar{x}_{i}=[x_{1},\dots,x_{i}]^{T}\), \(f_{i}\) denotes unknown smooth nonlinear function, u represents the control input, \(z_{1}=x_{1}-y_{d}\) and \(y_{d}\) denotes the desired trajectory. Unmodeled dynamics are represented by \(s(t) \in R^{\breve{n}}\), while \(x=[x_{1},x_{2},\ldots ,x_{n}]^{T}\) denotes part of the measured states. \(p_{i}(t,s,x)\) (\(i=1,\ldots,n\)) are the uncertain dynamic disturbances. In this paper, it is assumed that \(p_{i}(t,s,x)\) are unknown Lipschitz continuous functions.
In this article, the adaptive neural networks controller u is proposed, so that the control performance can be guaranteed in finite time.
Definition 1
([65])
The solution \(\{z(t), t\geq0\}\) of \(\dot{z}=f(z,\nu)\) is semi-globally uniformly finite-time bounded (SGUFB), if for all \(z(t_{0})=z_{0} \in\Omega_{0}\) (some compact set containing the origin), there exist \(\epsilon>0\) and a settling time \(T(\epsilon, z_{0})<\infty\), such that \(\|z(t)\|< \epsilon \), for all \(t \geq t_{0} + T\).
Assumption 1
Assume that the desired trajectory \(y_{d}=y_{d}^{(0)}\) and its kth time derivative \(y_{d}^{(k)}\) (\(1\leq k \leq n\)) are continuous and bounded.
Assumption 2
Consider \(\dot{s}=\varphi(t,s,z_{1})\) and \(p_{i}(t,s,x)\) in (1). Suppose that:
-
The equilibrium \(s=0\) of \(\dot{s}=\varphi(t,s,0)-\varphi(t,0,0)\) is globally exponentially stable equilibrium point, and there is a Lyapunov function \(V_{\varphi}(t,s)\) that satisfies
$$\begin{aligned}& k_{1}\|s\|^{2} \leq V_{\varphi}(t,s) \leq k_{2}\|s\|^{2} , \end{aligned}$$(2)$$\begin{aligned}& \frac{\partial{V_{\varphi}}}{\partial{t}}+\frac{\partial{V_{\varphi }}}{\partial{s}}\bigl(\varphi(t,s,0)- \varphi(t,0,0)\bigr) \leq-k_{3}\|s\|^{2} , \end{aligned}$$(3)$$\begin{aligned}& \bigg|\frac{\partial{V_{\varphi}}}{\partial{s}}\bigg| \leq k_{4}\|s\| , \end{aligned}$$(4)$$\begin{aligned}& \big\| \varphi(t,0,0)\big\| \leq k_{5}, \quad\forall t\geq0 , \end{aligned}$$(5)where \(k_{1}\), \(k_{2}\), \(k_{3}\), \(k_{4}\) and \(k_{5}\) are unknown positive constants.
-
φ and \(p_{i}\) (\(i=1,\ldots,n\)) satisfy the inequalities
$$\begin{aligned}& \big\| \varphi(t,s,z_{1})-\varphi(t,s,0)\big\| \leq e_{0}\rho_{0}\bigl(\|z_{1}\|\bigr) , \end{aligned}$$(6)$$\begin{aligned}& \big\| p_{i}(t,s,x)\big\| \leq e_{i} \sigma_{i1}\bigl(\|\bar{x}_{i}\|\bigr)+e_{i}\|s\|\sigma _{i2}(\bar{x}_{i}),\quad i=1,\ldots,n , \end{aligned}$$(7)where \(e_{0}\) and \(e_{i}\) (\(i=1,\ldots,n\)) are unknown positive constants, \(\rho_{0}(\|z_{1}\|) \in C_{1}\) is unknown continuous function, \(\rho_{0}(0)=0\), \(\sigma_{i1}(\|\bar{x}_{i}\|)\) and \(\sigma_{i2}(\bar {x}_{i})\) are unknown positive continuous functions.
Remark 1
Assumption 2 is similar to assumptions used in [59, 66]. However, in this article, \(\rho_{0}\), \(\sigma_{i1}\) and \(\sigma_{i2}\) can be completely unknown. To a certain extent, the control method in this note is more adaptable to realistic systems, in contrast with [59].
Lemma 1
([67])
For \({a}_{\jmath}\in{R}\), \(\jmath=1,\ldots ,M\), \(0<\varrho\leq1\), we have
Lemma 2
([68])
For \(\forall(x_{0},y_{0})\in R^{2}\) and positive constants μ, ρ, λ, the following inequality holds:
Lemma 3
Consider the system
Let \(V(z)\in C^{1}\) satisfy the inequality
where \(c_{0}\), ℘ and \(d_{0}\) are constants. Then the solution of the nonlinear system \(\dot{z}=f(z,\nu)\) is semi-globally uniformly finite-time bounded (SGUFB).
Proof
It follows from (11) that
Let \(\Omega_{z}=\{z|V^{\wp}(z)\leq\frac{d_{0}}{(1-\zeta)c_{0}}\}\) and \(\tilde{\Omega}_{z}=\{z|V^{\wp}(z)>\frac{d_{0}}{(1-\zeta)c_{0}}\}\).
Let \(z(t)\in\tilde{\Omega}_{z}\). Then we have
Therefore
Hence
Let
where \(z(0)\) denotes the initial value of \(z(t)\). Then one has \({z}_{t}\in\Omega_{z}\) for \(\forall{T}\geq{T}_{r}\). If \({z}_{t}\in\Omega _{z}\), \({z}_{t}\) does not exceed the set \(\Omega_{z}\). In conclusion, the solution of the nonlinear system \(\dot{z}=f(z,\nu)\) is SGUFB. □
Remark 2
It is difficult to achieve the asymptotic stability of the nonlinear system in the presence of uncertain perturbations. The system performance we can expect to realize is that the solution of the system is bounded in finite time and the bound can be sufficiently small.
2.2 RBF neural networks
In the following design, the radial basis function neural networks (RBFNNs) will be utilized to approximate the unknown function \(f(\zeta )\) defined on some compact set \(\Omega\in R^{p}\). \(\Re(\zeta)=[\Re _{1}(\zeta), \Re_{2}(\zeta), \ldots, \Re_{\kappa}(\zeta)]^{T}\) is the basis function vector and \(h^{T}=[h_{1}, h_{2}, \ldots, h_{\kappa}]^{T}\) denotes the weight vector. In this research, the following Gaussian basis function \(\Re_{i}(\zeta)\) will be utilized:
where κ is the neural networks node number, \(\iota_{i}=[\iota _{i1}, \iota_{i2}, \ldots, \iota_{ip}]^{T}\) denotes the center of the receptive field and \(\omega_{i}\) represents the width of the Gaussian function.
Lemma 4
([69])
Let \(f(\zeta)\) be a continuous function defined on a compact set Ω. Then, for \(\forall \varepsilon>0\), there exists a neural network \({h^{*}}^{T}\Re(\zeta)\) such that
where \({h^{*}}=\arg\min_{h\in R^{\kappa}}\{\sup_{\zeta\in\Omega}|f(\zeta )-h^{T}\Re(\zeta)|\}\) and \(\epsilon(\zeta) \leq\varepsilon\).
3 Adaptive tracking controller design and stability analysis
3.1 Controller design
In this section we propose a novel adaptive backstepping controller in which the uncertain nonlinear function is approximated by RBFNNs.
The controller design is based on the coordinate transformation as follows:
where \(\xi_{k-1}\) denotes an intermediate controller, which will be established later.
Before the design procedure, we define a positive constant as follows:
Obviously, \(\tau_{k}\) is an unknown positive constant because \(\| h_{k}^{*}\|\) is unknown. Define \(\hat{\tau}_{k}\) as the estimate of \(\tau _{k}\), and \(\check{\tau}_{k}=\tau_{k}-\hat{\tau}_{k}\). The control law is defined as
where \(l_{n}>0\), \(0<\wp<1\), \(\mu_{n}\) are design parameters.
The adaptive laws are designed as
where \(q_{k}\), \(\mu_{k}\) and \(\zeta_{k}\) are positive constants.
3.2 Stability analysis
Theorem 1
Consider the uncertain nonlinear system with unmodeled dynamics (1). If the state feedback controller is designed as (20) and the adaptive laws are designed as (21), then all the signals in the system are SGUFB for any bounded initial conditions and the tracking error converges to a small neighborhood of the origin.
Proof
Step 1. Consider a Lyapunov function candidate
where \(\gamma_{0}\) is a positive constant and \(V_{\varphi}(t,s)\) is given in Assumption 2. In the light of Assumption 2, the time derivative of \(V_{\varphi}(t,s)\) along the solutions of (1) satisfies
According to Lemma 2, one has
and
Now, by substituting (23)–(25) into (22) we obtain
According to Assumption 2 and Lemma 2, we also obtain
and
where \(\alpha_{{i}1}\) and \(\beta_{{i}1}\) \(({i}=1,2,\ldots,n)\) are design parameters.
Now consider the Lyapunov function candidate \(V_{1}\)
Differentiating (29) with respect to time and using (27)–(28) yield
where
Obviously, \(\hat{f}_{1}\) is an unknown function because \(\sigma_{11}\), \(\sigma_{12}\) and \(f_{1}\) are unknown. According to Lemma 4, for \(\forall \varepsilon_{1}> 0\), there is a RBFNN \({h^{*}}_{1}^{T}\Re_{1}\) such that
where \(X_{1} = [y, y_{d}, \dot{y}_{d}]^{T}\). Based on Lemma 4 and (19), one has
Choose the virtual control signal as
where ℘ and \(l_{1}\) are design parameters. Substituting (21), (33) and (34) into (30) yields the following:
Step m (\(2 \leq m \leq n-1\)). Let \(V_{m-1}=V_{m-2}+\frac {1}{2}z_{m-1}^{2}+\frac{1}{2q_{m-1}}\breve{\tau}_{m-1}^{2}\), where \(q_{m-1}>0\) are design parameters. Assuming that \(V_{m-1}\) satisfies the following inequality:
where \(\Delta_{i}=\frac{\beta_{{i}1}^{2}e^{2}_{i}}{2}+\frac{\alpha _{{i}1}^{2}e^{4}_{i}}{2}\) (\(1 \leq{i} \leq n\)).
Consider the Lyapunov function candidate
Establish the virtual control signal as
where ℘ and \(l_{m}\) are design parameters. Differentiating \(\xi_{m-1}\) with respect to time yields
where \(\Xi_{m-1}=\sum_{\jmath=1}^{m-1}(\frac{\partial{\xi }_{m-1}}{\partial{\dot{\hat{\tau}}}_{\jmath}}+\frac{\partial{\xi }_{m-1}}{\partial{y^{(\jmath-1)}_{d}}}y^{(\jmath)}_{d})\).
Differentiating \(V_{m}\) with respect to time and using (39) yield
where
Obviously, \(\hat{f}_{m}\) is an unknown function. According to Lemma 4, for \(\forall\varepsilon_{m}> 0\), there is a RBFNN \({h^{*}}_{m}^{T}\Re_{m}\) such that
where \(X_{m}=[\bar{x}_{m}^{T},\xi_{m-1},\bar{y}_{d}^{(m)},\bar{\dot{\hat{\tau }}}_{m}]^{T}\). Based on Lemma 4 and (19), one has
where
Substituting (21), (38), (41) and (42) into (40) yields the following:
Step n. Consider the Lyapunov function candidate
where \(q_{n-1},q_{n} > 0\). Establish the control signal as (20).
Differentiating \(\xi_{n-1}\) with respect to time yields
where \(\Xi_{n-1}=\sum_{\jmath=1}^{n-1}(\frac{\partial{\xi }_{n-1}}{\partial{\dot{\hat{\tau}}}_{\jmath}}+\frac{\partial{\xi }_{n-1}}{\partial{y^{(\jmath-1)}_{d}}}y^{(\jmath)}_{d})\).
Differentiating \(V_{n}\) with respect to time and using (45) yield
where
Obviously, \(\hat{f}_{n}\) is an unknown function. According to Lemma 4, for \(\forall\varepsilon_{n}> 0\), there is a RBFNN \({h^{*}}_{n}^{T}\Re_{n}\) such that
where \(X_{n}=[\bar{x}_{n}^{T},\xi_{n-1},\bar{y}_{d}^{(n)},\bar{\dot{\hat{\tau }}}_{n}]^{T}\). Based on Lemma 2, one has
Performing in the same way as in step m, one has
where \(\hat{l}=\min_{\jmath=1,\ldots,n}\{{{l}_{\jmath}}\}\).
Nothing that \(\check{\tau}_{\jmath}=\tau_{\jmath}-\hat{\tau}_{\jmath}\), the following inequality holds for \(\jmath=1,\ldots,n\):
where â is a positive constant satisfying \(\hat{a}\geq\frac {1}{2}\), and \({\eta}_{\jmath}=\frac{\zeta_{i}}{{q}_{i}}\).
According to Lemma 1 and Lemma 2, we get
and
where \(\bar{c}_{0}=-2^{\wp}c_{0}\), \(c_{0}=\min\{\hat{l},\frac {k_{3}}{(2^{n}\gamma)^{\wp}}\}\) and
Define a positive constant \(\varsigma_{0}=\frac{\bar{d}_{0}}{(1-\zeta_{0})\bar {c}_{0}}\), where \(\zeta_{0}\) is a constant which satisfies \(0<\zeta_{0}<1\).
Let
where \(V_{n}(X(0))\) represents the initial of \(V_{n}(X)\) with \(X=[\bar {x}_{n}^{T},\xi_{n-1},\bar{y}_{d}^{(n)},\bar{\dot{\hat{\tau}}}_{n}]^{T}\). Then according to Lemma 3, the time to reach the set \(X(t)\in\Omega_{z}\), is bounded as \(T_{r}\) where \(\Omega_{z}=\{X|V_{n}^{\wp}(X)\leq\frac{\bar {d}_{0}}{(1-\zeta_{0})\bar{c}_{0}}\}\). Consequently, all signals in the resulting system are SGUFB. □
4 Simulation example
In this section, an example will be used to expound our design scheme and verify the results obtained.
The nonlinear system with unmodeled dynamics is given as
where \(s(t)\) represents the unmodeled dynamics, \(p_{1}=s^{2}+0.5{x}_{1}\sin {t}\) and \(p_{2}=5s^{2}+0.2\cos(0.5{x}_{2})\). The reference signal is chosen as \(y_{d}=\sin(\frac{1}{2}t)+0.5\sin (\frac{3}{2}t)\).
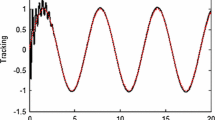
The intermediate control function, adaptive laws and control law are, respectively, chosen as (20), (21), (34). The related simulation parameters are selected as \(\mu_{1}=0.3\), \(\mu_{2}=0.36\), \(l_{1}=0.1\), \(l_{2}=0.1\), \(\wp=0.8\), \(\zeta _{1}=0.01\) and \(\zeta_{2}=0.05\). Choose the initial conditions as \({x}_{1}(0)=0.6\), \({x}_{2}(0)=10\), \(s(0)=0\), \(\hat{\tau}_{1}(0)=1\) and \(\hat{\tau}_{2}(0)=12\). Gaussian basis function \(\Re_{\jmath}(X_{\jmath})\) is chosen as (16), where \(X_{1}=[{x}_{1},y_{d},\dot{y_{d}}]^{T}\) and \(X_{2}=[{x}_{1},{x}_{2},\xi_{1},\dot {y}_{d},\ddot{y}_{d},\dot{\hat{\tau}}_{1},\dot{\hat{\tau}}_{2}]^{T}\). The results of the simulation are shown in Figs. 1, 2, 3, 4.
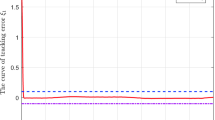
In order to give some suggestions in choosing the design parameter ℘, we select \(\wp=0.99\), while the rest of parameters remain the same. Compared with the existing control strategies, a previous adaptive fuzzy control scheme proposed in [29] is also utilized to control this system with the above controller parameter. The simulation results are shown in Figs. 5, 6, 7. From Figs. 5, 6, we see that the tracking errors converge to a small neighborhood of the origin in finite time \(T_{r}\approx1.7\) and \(T_{r}\approx2.2\), respectively. It can be seen from Figs. 5, 6, 7 that the control system with the developed finite-time adaptive neural controller has a smaller tracking error.
y and \(y_{d}\) with the controller in [29]
5 Conclusion
In this paper, the issue of finite-time control for a class of uncertain nonlinearity systems with unmodeled dynamics is investigated. During the design process of the adaptive NN control scheme, the unmodeled dynamics are considered. The proposed adaptive NN control can guarantee that all the signals in the closed-loop system are semi-globally uniformly finite-time bounded.
References
Tong, S.C., Sun, K.K., Sui, S.: Observer-based adaptive fuzzy decentralized optimal control design for strict feedback nonlinear large-scale systems. IEEE Trans. Fuzzy Syst. 26(2), 569–584 (2018)
Wang, F., Chen, B., Liu, X.P., Lin, C.: Finite-time adaptive fuzzy tracking control design for nonlinear systems. IEEE Trans. Fuzzy Syst. (2017). https://doi.org/10.1109/TFUZZ.2017.2717804
Wang, F., Zhang, X.Y., Chen, B., Lin, C., Li, X.H., Zhang, J.: Adaptive finite-time tracking control of switched nonlinear systems. Inf. Sci. 421, 126–135 (2017)
Wang, F., Chen, B., Lin, C., Zhang, J., Meng, X.: Adaptive neural network finite-time output feedback control of quantized nonlinear systems. IEEE Trans. Cybern. (2017). https://doi.org/10.1109/TCYB.2017.2715980
Wang, F., Liu, Z., Zhang, Y., Chen, C.L.P.: Adaptive fuzzy control for a class of stochastic pure-feedback nonlinear systems with unknown hysteresis. IEEE Trans. Fuzzy Syst. 24(1), 140–152 (2016)
Liu, Y.J., Tong, S.C.: Barrier Lyapunov functions for Nussbaum gain adaptive control of full state constrained nonlinear systems. Automatica 76, 143–152 (2017)
Zhang, S.Q., Meng, X.Z., Zhang, T.H.: Dynamics analysis and numerical simulations of a stochastic non-autonomous predator–prey system with impulsive effects. Nonlinear Anal. Hybrid Syst. 26, 19–37 (2017)
Wang, J.M., Cheng, H.D., Li, Y., Zhang, X.N.: The geometrical analysis of a predator–prey model with multi-state dependent impulses. J. Appl. Anal. Comput. 8(2), 427–442 (2018)
Guo, R., Zhang, Z., Liu, X., Lin, C.: Existence, uniqueness, and exponential stability analysis for complex-valued memristor-based BAM neural networks with time delays. Appl. Math. Comput. 311, 100–117 (2017)
Wang, J., Cheng, H., Liu, H., et al.: Periodic solution and control optimization of a prey–predator model with two types of harvesting. Adv. Differ. Equ. (2018). https://doi.org/10.1186/s13662-018-1499-9
Li, Y., Cheng, H., Wang, J., et al.: Dynamic analysis of unilateral diffusion Gompertz model with impulsive control strategy. Adv. Differ. Equ. (2018). https://doi.org/10.1186/s13662-018-1484-3
Li, X.P., Lin, X.Y., Lin, Y.Q.: Lyapunov-type conditions and stochastic differential equations driven by G-Brownian motion. J. Math. Anal. Appl. 439(1), 235–255 (2016)
Zou, Y.M., He, G.P.: On the uniqueness of solutions for a class of fractional differential equations. Appl. Math. Lett. 74, 68–73 (2017)
Cui, Y.J., Ma, W.J., Sun, Q., Su, X.W.: New uniqueness results for boundary value problem of fractional differential equation. Nonlinear Anal., Model. Control 23(1), 31–39 (2018)
Bian, F.F., Zhao, W.C., Song, Y., Yue, R.: Dynamical analysis of a class of prey–predator model with Beddington–DeAngelis functional response, stochastic perturbation, and impulsive toxicant input. Complexity 2017, Article ID 3742197 (2017)
Wang, Z., Wang, X.H., Li, Y.X., Huang, X.: Stability and Hopf bifurcation of fractional-order complex-valued single neuron model with time delay. Int. J. Bifurc. Chaos (2017). https://doi.org/10.1142/S0218127417502091
Yu, H., Xia, X.H.: Adaptive leaderless consensus of agents in jointly connected networks. Neurocomputing 241(7), 64–70 (2017)
Tu, Z.Z., Yu, H., Xia, X.H.: Decentralized finite-time adaptive consensus of multiagent systems with fixed and switching network topologies. Neurocomputing 219, 59–67 (2017). https://doi.org/10.1016/j.neucom.2016.09.013
Chen, F.T., Yu, H., Xia, X.: Output consensus of multi-agent systems with delayed and sampled-data. IET Control Theory Appl. 11(5), 632–639 (2017)
Li, C.D., Gao, J.L., Yi, J.Q., Zhang, G.Q.: Analysis and design of functionally weighted single-input-rule-modules connected fuzzy inference systems. IEEE Trans. Fuzzy Syst. 26(1), 56–71 (2018)
Li, Y.M., Tong, S.C.: Fuzzy adaptive control design strategy of nonlinear switched large-scale systems. IEEE Trans. Syst. Man Cybern. Syst. (2017). https://doi.org/10.1109/TSMC.2017.2703127
Li, Y.M., Tong, S.C.: Adaptive neural networks prescribed performance control design for switched interconnected uncertain nonlinear systems. IEEE Trans. Neural Netw. Learn. Syst. (2017). https://doi.org/10.1109/TNNLS.2017.2712698
Li, Y.M., Ma, Z.Z., Tong, S.C.: Adaptive fuzzy fault-tolerant control of non-triangular structure nonlinear systems with error-constraint. IEEE Trans. Fuzzy Syst. (2017) https://doi.org/10.1109/TFUZZ.2017.2761323
Tong, S.C., Li, Y.M.: Adaptive fuzzy output feedback control for switched nonlinear systems with unmodeled dynamics. IEEE Trans. Cybern. 47(2), 295–305 (2017)
Wang, H.Q., Liu, W.X., Qiu, J.B., Liu, P.X.P.: Adaptive fuzzy control for a class of strong interconnected nonlinear systems with unmodeled dynamics. IEEE Trans. Fuzzy Syst. 26(2), 836–846 (2018). https://doi.org/10.1109/TFUZZ.2017.2694799
Wang, H.Q., Liu, P.X.P., Li, S., Wang, D.: Adaptive neural output-feedback control for a class of non-lower triangular nonlinear systems with unmodeled dynamics. IEEE Trans. Neural Netw. Learn. Syst. (2017). https://doi.org/10.1109/TNNLS.2017.2716947
Niu, B., Li, H., Qin, T., Karimi, H.R.: Adaptive NN dynamic surface controller design for nonlinear pure-feedback switched systems with time-delays and quantized input. IEEE Trans. Syst. Man Cybern. Syst. (2017). https://doi.org/10.1109/TSMC.2017.2696710
Chi, M.N., Zhao, W.C.: Dynamical analysis of multi-nutrient and single microorganism chemostat model in a polluted environment. Adv. Differ. Equ. (2018). https://doi.org/10.1186/s13662-018-1573-3
Zhang, T.P., Xia, M., Yi, Y.: Adaptive neural dynamic surface control of strict-feedback nonlinear systems with full state constraints and unmodeled dynamics. Automatica 81, 232–239 (2017)
Song, Q.L., Dong, X.Y., Bai, Z.B., Chen, B.: Existence for fractional Dirichlet boundary value problem under barrier strip conditions. J. Nonlinear Sci. Appl. 10, 3592–3598 (2017)
Li, F., Meng, X.Z., Cui, Y.J.: Nonlinear stochastic analysis for a stochastic SIS epidemic model. J. Nonlinear Sci. Appl. 10, 5116–5124 (2017)
Zhang, L.L., Lei, Y., Wang, Y., Chen, B.: Stabilization of time-varying and disturbed complex dynamical networks with different-dimensional nodes and uncertain nonlinearities. Asian J. Control 19(6), 2143–2154 (2017)
Zhang, L.L., Lei, Y., Wang, Y., et al.: Generalized outer synchronization between non-dissipatively coupled complex networks with different-dimensional nodes. Appl. Math. Model. 55, 248–261 (2018)
Liu, F., Wu, H.X.: Regularity of discrete multisublinear fractional maximal functions. Sci. China Math. 60(8), 1461–1476 (2017)
Cui, G., Wang, Z., Zhuang, G., et al.: Adaptive decentralized NN control of large-scale stochastic nonlinear time-delay systems with unknown dead-zone inputs. Neurocomputing 158, 194–203 (2015)
Sun, Y., Chen, B., Lin, C., et al.: Adaptive neural control for a class of stochastic non-strict-feedback nonlinear systems with time-delay. Neurocomputing 214, 750–757 (2016)
Guo, R.N., Zhang, Z.Y., Liu, X.P., Lin, C., Wang, H.X., Chen, J.: Exponential input-to-state stability for complex-valued memristor-based BAM neural networks with multiple time-varying delays. Neurocomputing 275, 2041–2054 (2018)
Liu, Y.J., Lu, S.M., Tong, S.C., Chen, X.K., Chen, C.L.P., Li, D.J.: Adaptive control-based barrier Lyapunov functions for a class of stochastic nonlinear systems with full state constraints. Automatica 87, 83–93 (2018)
Liu, Y.J., Gong, M.Z., Tong, S.C., Chen, C.L.P., Li, D.J.: Adaptive fuzzy output feedback control for a class of nonlinear systems with full state constraints. IEEE Trans. Fuzzy Syst. (2018). https://doi.org/10.1109/TFUZZ.2018.2798577
Li, C.D., Ding, Z.X., Zhao, D.B., Yi, J.Q., Zhang, G.Q.: Building energy consumption prediction: an extreme deep learning approach. Energies 10(10), Article ID 1525 (2017)
Sun, Y.M., Chen, B., Lin, C., Wang, H.H., Zhou, S.W.: Adaptive neural control for a class of stochastic nonlinear systems by backstepping approach. Inf. Sci. 369, 748–764 (2016)
Wang, F., Chen, B., Lin, C., Li, X.H.: Distributed adaptive neural control for stochastic nonlinear multiagent systems. IEEE Trans. Cybern. 47(7), 1795–1803 (2017)
Sun, Y.M., Chen, B., Lin, C., et al.: Finite-time adaptive control for a class of nonlinear systems with nonstrict feedback structure. IEEE Trans. Cybern. (2017). https://doi.org/10.1109/TCYB.2017.2749511
Li, Y., Tong, S., Li, T.: Observer-based adaptive fuzzy tracking control of MIMO stochastic nonlinear systems with unknown control direction and unknown dead-zones. IEEE Trans. Fuzzy Syst. 23(4), 1228–1241 (2015)
Xing, L., Wen, C., Liu, Z., Su, H., Cai, J.: Event-triggered adaptive control for a class of uncertain nonlinear systems. IEEE Trans. Autom. Control 62(4), 2071–2076 (2017)
Xing, L., Wen, C., Zhu, Y., Su, H., Liu, Z.: Output feedback control for uncertain nonlinear systems with input quantization. Automatica 65, 191–202 (2016)
Zhang, W.H., An, X.Y.: Finite-time control of linear stochastic systems. Int. J. Innov. Comput. Inf. Control 4(3), 689–696 (2008)
Xin, Y.M., Li, Y.X., Huang, X.: Consensus of third-order nonlinear multi-agent systems. Neurocomputing 159(1), 84–89 (2015)
Zou, L., Wang, Z.D., Gao, H.J., et al.: Finite-horizon H-infinity consensus control of time-varying multiagent systems with stochastic communication protocol. IEEE Trans. Cybern. 47(8), 1830–1840 (2017)
Zhang, L., Zhu, Y., Zheng, W.X.: Synchronization and state estimation of a class of hierarchical hybrid neural networks with time-varying delays. IEEE Trans. Neural Netw. Learn. Syst. 27(2), 459–470 (2016)
Zhang, L., Zhu, Y., Zheng, W.X.: State estimation of discrete-time switched neural networks with multiple communication channels. IEEE Trans. Cybern. 47(4), 1028–1040 (2017)
Zhu, Y., Zhong, Z., Zheng, W.X., Zhou, D.: HMM-based H-infinity filtering for discrete-time Markov jump LPV systems over unreliable communication channels. IEEE Trans. Syst. Man Cybern. Syst. (2017). https://doi.org/10.1109/TSMC.2017.2723038
Zhang, T., Ge, S.S., Hang, C.C.: Adaptive neural network control for strict-feedback nonlinear systems using backstepping design. Automatica 36(12), 1835–1846 (2000)
Liu, F., Xue, Q., Yabuta, K.: Rough maximal singular integral and maximal operators supported by subvarieties on Triebel–Lizorkin spaces. Nonlinear Anal. 171, 41–72 (2018)
Liu, F.: Continuity and approximate differentiability of multisublinear fractional maximal functions. Math. Inequal. Appl. 21(1), 25–40 (2018)
Bai, Z.B., Chen, Y.Q., Lian, H.R., Sun, S.J.: On the existence of blow up solutions for a class of fractional differential equations. Fract. Calc. Appl. Anal. 17(4), 1175–1187 (2014)
Wang, N.N., Zhang, T.P., Yi, Y., Wang, Q.: Adaptive control of output feedback nonlinear systems with unmodeled dynamics and output constraint. J. Franklin Inst. 354(13), 5176–5200 (2017)
Wang, F., Liu, Z., Zhang, Y., Chen, X., Chen, C.L.P.: Adaptive fuzzy dynamic surface control for a class of nonlinear systems with fuzzy dead zone and dynamic uncertainties. Nonlinear Dyn. 79(3), 1693–1709 (2015)
Jiang, Z.P., Hill, D.J.: A robust adaptive backstepping scheme for nonlinear systems with unmodeled dynamics. IEEE Trans. Autom. Control 44(9), 1705–1711 (1999)
Shi, X.C., Xu, S.Y., Li, Y.M., Chen, W.M., Chu, Y.M.: Robust adaptive control of strict-feedback nonlinear systems with unmodelled dynamics and time-varying delays. Int. J. Control 90(2), 334–347 (2016)
Su, C., Stepanenko, Y., Svoboda, J., Leung, T.: Robust adaptive control of a class of nonlinear systems with unknown backlash-like hysteresis. IEEE Trans. Autom. Control 45(12), 2427–2432 (2000)
Bhat, S.P., Bernstein, D.S.: Continuous finite-time stabilization of the translational and rotational double integrators. IEEE Trans. Autom. Control 43(5), 678–682 (1998)
Bhat, S.P., Bernstein, D.S.: Finite-time stability of continuous autonomous systems. SIAM J. Control Optim. 38(3), 751–766 (2000)
Zhu, Z., Xia, Y.Q., Fu, M.Y.: Attitude stabilization of rigid spacecraft with finite-time convergence. Int. J. Robust Nonlinear Control 21(6), 686–702 (2011)
Huang, S.P., Xiang, Z.G.: Adaptive finite-time stabilization of a class of switched nonlinear systems using neural networks. Neurocomputing 173, 2055–2061 (2016)
Khalil, H.: Nonlinear Systems, 2nd edn. Prentice Hall, Upper Saddle River (1996)
Hardy, G., Littlewood, J., Polya, G.: Inequalities. Cambridge University Press, Cambridge (1952)
Qian, C., Lin, W.: Non-Lipshitz continuous stabilizers for nonlinear systems with uncontrollable unstable linearization. Syst. Control Lett. 42(3), 185–200 (2001)
Park, J., Sandberg, I.W.: Universal approximation using radial-basis-function network. Neural Comput. 3(2), 246–257 (1991)
Acknowledgements
This work is supported partially by the National Natural Science Foundation of China (Grant No. 61503223, 61402265), in part by the Project of Shandong Province Higher Educational Science and Technology Program (J15LI09), in part by China Postdoctoral Science Foundation-funded project 2016M592140, partially by Shandong innovation postdoctoral program 201603066, partially by the SDUST Research Fund (2014TDJH102) and partially by SDUST Innovation Fund for Graduate Students (SDKDYC180347).
Author information
Authors and Affiliations
Contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Lv, W., Wang, F. & Li, Y. Adaptive finite-time tracking control for nonlinear systems with unmodeled dynamics using neural networks. Adv Differ Equ 2018, 159 (2018). https://doi.org/10.1186/s13662-018-1615-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-018-1615-x