1 Introduction

Mathematical inequalities play an important role in many fields of mathematical analysis and applications, especially for differential systems [1–5]. Recently, the inequalities techniques have been widely used to impulsive differential systems [6–10], stochastic differential systems [11–16] and impulsive stochastic differential systems [17–20], thus some new and interesting results have been obtained.

In the last few decades, infectious diseases have brought a series of troubles and great pain to millions of families. Many suitable measures are implemented to prevent the outbreak of infectious diseases. Various mathematical models are essential tools to study the spread of infectious diseases. Epidemiological models can analyze the underlying mechanisms which influence the expansion of infectious diseases. Let us assume that all individuals are divided into three compartments: \(S(t)\) represents susceptible individuals who are susceptible to the disease; \(I(t)\) represents infected individuals who are infected by the disease; and \(R(t)\) represents recovered individuals who hold temporary immunity acquired from a disease, namely, after recovery, individuals lose immunity and move into the susceptible individuals. This is called SIRS model [21]. In most epidemic models, the bilinear incidence rate \(\lambda S(t)I(t)\) is extensively used. Therefore, the dynamics of the SIRS epidemic model can be expressed by the following system of ordinary differential equations:

$$ \textstyle\begin{cases} \frac{\mathrm {d}{S}(t)}{\mathrm {d}t}=d N(t)-d S(t)-\lambda S(t)I(t)+ \nu R(t), \\ \frac{\mathrm {d}{I}(t)}{\mathrm {d}t}=\lambda S(t)I(t)-(d+r) I(t), \\ \frac{\mathrm {d}{R}(t)}{\mathrm {d}t}=r I(t)-(d+\nu) R(t), \end{cases} $$
(1)

where the parameters λ, d, ν and r are positive constants. Here, \(N(t)=S(t)+I(t)+R(t)\) represents all individuals, λ is the rate of transmission per contact, d represents the diseased death rate and also represents the rate of recruitment of individuals, ν represents the rate at which recovered individuals lose immunity and return to the susceptible individuals, r is the recovery rate of the infected individuals. Many researchers have studied several different SIRS epidemic models in the literature [21–25].

In epidemiological models, many different types of incidence rate play an important role. In 1986, Liu et al. [26] introduced a general incidence rate

$$ Sf(I)=\frac{\lambda S I^{p}}{1+\alpha I^{q}} $$
(2)

into the SIRS epidemic model. Here, \(\lambda I^{p}\) is infection force of the disease and \(\frac{1}{1+\alpha I^{q}}\) represents inhibition effect. The general incidence rate is more reasonable than the bilinear incidence rate because the general incidence rate takes into account the crowding effect and behavioral change of the infective individuals and prevents the unboundedness of the contact rate occurring by choosing suitable parameters. We notice that when \(p=1\) and \(\alpha=0\) or \(q=0\), the general incidence rate (2) changes into the bilinear incidence rate. In recent years, a number of researchers [27–31] have investigated the nonlinear transmission laws more than the bilinear transmission laws. In 1992, Hethcote et al. [32] studied a standard incidence rate

$$ Sf(I)=\frac{\lambda S I}{S+I+R} $$
(3)

in the continuous-time SIRS epidemic model. In this paper, the authors analyzed the stability of the disease-free equilibrium and the endemic equilibrium for the SIRS model.

To prevent the spread of the infectious disease, many researchers [33–36] began to investigate a treatment function in the epidemic models. In 2004, Wang et al. [37] introduced a constant treatment function

$$\begin{aligned} T(I)= \textstyle\begin{cases} \beta,&I>0, \\ 0,& I=0 \end{cases}\displaystyle \end{aligned}$$

into the \(SIR\) epidemic model. The authors found that to eradicate the disease, it is unnecessary to take such a large treatment capacity, and proved that disease spread may depend on a certain range of the initial parameters. In 2006, Wang [38] introduced a piecewise linear treatment function

$$\begin{aligned} T(I)= \textstyle\begin{cases} \beta I,&0\leq I\leq I_{0}, \\ m,& I\geq I_{0} \end{cases}\displaystyle \end{aligned}$$

into the \(SIR\) model and proved that a backward bifurcation existed in this model. In 2011, Eckalbar et al. [39] adopted a quadratic treatment function

$$ T(I)=\max\bigl\{ \beta I-gI^{2}, 0\bigr\} ,\quad \beta, g>0 $$

into the \(SIR\) epidemic model and found four equilibria at most. Recently, the saturated treatment function has been frequently used in classical epidemic models. In 2008, Zhang et al. [40] introduced a saturated treatment function

$$ T(I)=\frac{\beta I}{1+\alpha I} $$
(4)

into the \(SIR\) model, where \(\beta>0\), \(\alpha\geq0\). β is the cure rate and α represents the extent to which the infected effect delays the treatment. In [40], authors found that the valid methods for the control of disease were providing the patients timely treatment, enhancing the cure efficiency and decreasing the infective coefficient. According to (1), (3) and (4), in [41], Gao et al. took into account the SIRS epidemic model with standard incidence rate and saturated treatment function as follows:

$$\begin{aligned} \textstyle\begin{cases} \frac{\mathrm {d}{S}(t)}{\mathrm {d}t}= \Lambda-d S(t)-\frac{\lambda S(t)I(t)}{N(t)}+\nu R(t), \\ \frac{\mathrm {d}{I}(t)}{\mathrm {d}t}= \frac{\lambda S(t)I(t)}{N(t)}-(d+r)I(t)-\frac{ \beta I(t)}{1+\alpha I(t)}, \\ \frac{\mathrm {d}{R}(t)}{\mathrm {d}t}= r I(t)-(d+\nu) R(t)+\frac{ \beta I(t)}{1+\alpha I(t)}, \end{cases}\displaystyle \end{aligned}$$

where Λ is the recruitment rate of susceptible individuals, d represents only the diseased death rate, \(N(t)\equiv S(t)+I(t)+R(t)\) represents the total population size, other parameters have the same meaning as the ones above.

On the other hand, any systems are inevitably affected by various environmental noises, such as white noise, which are important components in an ecosystem. In 2001, May [42] showed that according to environmental fluctuation, the population birth and death rate, transmission coefficient and other parameters exhibit random perturbations to a lesser or greater extent. Consequently, we assume that the environmental fluctuation affects not only the standard incidence rate but also the saturated treatment rate of the disease, so that

$$ \lambda\rightarrow\lambda+\sigma_{1}\dot{B}_{1}(t), \quad \quad \beta \rightarrow\beta+\sigma_{2}\dot{B}_{2}(t), $$

where \(B_{1}(t)\) and \(B_{2}(t)\) represent standard Brownian motions with \(B_{1}(0)=0\) and \(B_{2}(0)=0\), \(\sigma^{2}_{1}\) and \(\sigma^{2}_{2}\) denote the intensities of white noise. In recent years, many researchers [14, 43–52] have introduced stochastic environmental perturbations into deterministic population models to analyze the effects of environmental noise.

Motivated by the above work, we obtain the following stochastic SIRS epidemic model with standard incidence rate and saturated treatment function:

$$ \textstyle\begin{cases} \mathrm {d}{S}(t)= [ \Lambda-d S(t)- \frac{\lambda S(t)I(t)}{N(t)}+\nu R(t) ] \,\mathrm {d}t-\frac{\sigma _{1} S(t)I(t)}{N(t)}\,\mathrm {d}B_{1}(t), \\ \mathrm {d}{I}(t)= [ \frac{\lambda S(t)I(t)}{N(t)}-(d+r)I(t)-\frac{ \beta I(t)}{1+\alpha I(t)} ] \,\mathrm {d}t+ \frac{\sigma_{1} S(t)I(t)}{N(t)}\,\mathrm {d}B_{1}(t)-\frac{\sigma_{2}I(t)}{1+ \alpha I(t)}\,\mathrm {d}B_{2}(t), \\ \mathrm {d}{R}(t)= [ r I(t)-(d+\nu) R(t)+\frac{\beta I(t)}{1+ \alpha I(t)} ] \,\mathrm {d}t+\frac{\sigma_{2}I(t)}{1+\alpha I(t)} \,\mathrm {d}B_{2}(t). \end{cases} $$
(5)

This paper is organized as follows. In Section 2, we first introduce preliminary knowledge and give some notations and lemmas. Furthermore, we prove the existence of a global positive solution for the corresponding limiting SIRS epidemic system. Moreover, we explore sufficient conditions for the persistence in mean and extinction of the stochastic SIRS epidemic system. In Section 3, we give a summary of the main results and a series of numerical simulations to illustrate the theoretical results.

2 Main results

The main purpose of our study is to investigate the threshold dynamics of the stochastic SIRS epidemic model which governs the extinction and permanence of the epidemic disease by applying the techniques of a series of stochastic inequalities.

2.1 Preliminary knowledge

In the section, we give some notations and lemmas which can be used for our main theoretical results. To this end, throughout this paper, unless otherwise specified, we let \((\Omega, \mathcal{F}, \{{\mathcal{F} _{t}}\}_{t\geq0}, \mathbb{P})\) stand for a complete probability space with a filtration \(\{{\mathcal{F}_{t}}\}_{t\geq0}\) satisfying the usual conditions (i.e., it is increasing and right continuous while \(\mathcal{F}_{0}\) contains all \(\mathbb{P}\)-null sets). For convenience, for an integrable function \(f(t)\) on \(\mathbb{R}_{+}=[0,+\infty)\), we define \(\langle f(t) \rangle= \frac{1}{t}\int_{0}^{t} f(s) \,\mathrm {d}s\).

Generally speaking, an n-dimensional stochastic differential equation is expressed as follows:

$$ \mathrm {d}X(t)=F\bigl(t,X(t)\bigr)\,\mathrm {d}t+G\bigl(t,X(t)\bigr) \,\mathrm {d}B(t). $$
(6)

Here, \(F(t,x)\) represents a function defined in \([0, +\infty)\times \mathbb{R}^{n}\) and \(G(t,x)\) represents an \(n\times m\) matrix, \(F(t,x)\) and \(G(t,x)\) satisfy the locally Lipschitz conditions in x. \(B(t)\) represents an m-dimensional standard Brownian motion defined on the complete probability space. \(C^{2,1}(\mathbb{R}^{n} \times[0, +\infty),\mathbb{R}_{+})\) is a family of all nonnegative functions \(V(x,t)\) which are defined on \(\mathbb{R}^{n}\times[0, + \infty)\) such that this family of functions are continuously twice differentiable on x and continuously once differentiable on t. In [53], Mao defined a differential operator \(\mathcal{L}\) for the stochastic differential equation (6):

$$\begin{aligned} \mathcal{L}=\frac{\partial}{\partial t} +\sum^{n}_{i=1}F_{i}(x,t) \frac{ \partial}{\partial x_{i}} +\frac{1}{2}\sum^{n}_{i,j=1} \bigl[G^{T}(x,t)G(x,t)\bigr]_{i,j} \frac{\partial ^{2}}{\partial x_{i}\partial x_{j}}. \end{aligned}$$

Applying \(\mathcal{L}\) to a function \(V(x,t)\in C^{2,1}(\mathbb{R} ^{n}\times[0, +\infty),\mathbb{R}_{+})\), we get

$$\begin{aligned} \mathcal{L}V(x,t)=V_{t}(x,t)+V_{x}(x,t)F(x,t) + \frac{1}{2}\operatorname{trace}\bigl[G^{T}(x,t)V _{xx}(x,t)G(x,t) \bigr], \end{aligned}$$

where \(V_{t}(x,t)=\frac{\partial V}{\partial t}\), \(V_{x}(x,t)=(\frac{ \partial V}{\partial x_{1}},\frac{\partial V}{\partial x_{2}},\ldots, \frac{\partial V}{\partial x_{n}})\) and \(V_{xx}(x,t)=(\frac{\partial ^{2}V}{\partial x_{i}\partial x_{j}})_{n\times n}\). By Itô’s formula, when \(x(t)\in\mathbb{R}^{n}\), we have

$$ \mathrm {d}V(x,t)=\mathcal{L}V(x,t)\,\mathrm {d}t+V_{x}(x,t)G(x,t) \,\mathrm {d}B(t). $$

Definition 2.1

([54])

The definitions of extinction and persistence in mean are given as follows:

  1. (i)

    The population \(X(t)\) is said to be extinct when \(\lim_{t\rightarrow+\infty}X(t)=0\);

  2. (ii)

    The population \(X(t)\) is said to be persistent in mean when \(\liminf_{t\rightarrow+\infty}\langle X(t)\rangle>m\), where m is a positive constant.

The following inequalities can be used frequently in the sequel.

Lemma 2.1

(Burkholder–Davis–Gundy inequality [53])

Let \(f(t)\in C ^{2}(\mathbb{R}_{+}; \mathbb{R}^{n\times m})\) (\(C^{2}(\mathbb{R}_{+}; \mathbb{R}^{n\times m})\) be the family of processes \(\{f(t)\}_{t \geq0}\) such that, for every \(T> 0\), \(\{f(t)\}_{0\leq t\leq T}\in C ^{2}([0, T]; \mathbb{R}^{n\times m})\), where \(C^{2}([0, T]; \mathbb{R}^{n\times m})\) represents the family of \(R^{n\times m}\)-valued \({\mathcal{F}_{t}}\)-adapted processes \(\{f(t)\}_{0\leq t\leq T}\) such that \(\int_{0}^{T} \vert f(t) \vert ^{2}\,dt< \infty\)). For every \(t\geq0\), we define

$$\begin{aligned} M(t)= \int_{0}^{t} f(\theta)\,\mathrm {d}B(\theta), \quad \quad A(t)= \int_{0}^{t} \bigl\vert f(\theta) \bigr\vert ^{2}\,\mathrm {d}\theta. \end{aligned}$$

Thus, for any \(\eta>0\), there are two positive constants \(c_{\eta}\) and \(C_{\eta}\) such that

$$ c_{\eta}\mathbf{E} \bigl\vert A(t) \bigr\vert ^{\frac{\eta}{2}}\leq \mathbf{E} \Bigl( \sup_{0 \leq\theta\leq t} \bigl\vert M(\theta) \bigr\vert ^{\eta} \Bigr) \leq C_{\eta} \mathbf{E} \bigl\vert A(t) \bigr\vert ^{\frac{\eta}{2}},\quad t\geq0, $$

where \(c_{\eta}\) and \(C_{\eta}\) only depend on η.

Lemma 2.2

(Chebyshev’s inequality [53])

For all \(c> 0\), \(\eta> 0\) and \(X\in L^{\eta}\), the following inequality holds:

$$ \mathbb{P} \bigl\{ \xi: \bigl\vert X(\xi) \bigr\vert \geq c \bigr\} \leq \frac{ \mathbf{E} \vert X \vert ^{\eta}}{c^{\eta}}. $$

Lemma 2.3

(Doob’s martingale inequality [53])

Let X be a submartingale taking nonnegative real values, either in discrete or continuous time. That is, for all times s and t having \(s< t\), we have

$$\begin{aligned} X_{s}\leq\mathbf{E}[X_{t}| \mathcal{F}_{s}]. \end{aligned}$$

Then, for any constant \(c> 0\),

$$\begin{aligned} \mathbb{P} \Bigl[ \sup_{0\leq t \leq T}X_{t}\geq c \Bigr] \leq \frac{ \mathbf{E}[ \vert X_{T} \vert ]}{c}, \end{aligned}$$

where \(\mathbb{P}\) denotes the probability measure on the sample space Ω of the stochastic process \(X: [0, T]\times\Omega\rightarrow [0, +\infty]\) and E denotes the expected value with respect to the probability measure \(\mathbb{P}\).

According to the biological meanings, we know that variables \(S(t)\), \(I(t)\) and \(R(t)\) of system (5) should be nonnegative when \(t\geq0\). Before we prove that the global positive solution of system (5) is existent and unique, we firstly investigate the following Lemma 2.4.

Lemma 2.4

For the positive solution \((S(t), I(t), R(t))\) of system (5) with any initial value \((S(0), I(0), R(0))\in\mathbb{R}^{3}_{+}\), we have

$$\begin{aligned} \max \Bigl\{ \limsup_{t\rightarrow+\infty}S(t), \limsup_{t\rightarrow+\infty}I(t), \limsup_{t\rightarrow+\infty}R(t) \Bigr\} \leq\frac{\Lambda}{d}. \end{aligned}$$

Proof

For system (5), computing the sum of three equations yields

$$\begin{aligned} \frac{\mathrm {d}(S(t)+I(t)+R(t))}{\mathrm {d}t}=\Lambda-d\bigl(S(t)+I(t)+R(t)\bigr). \end{aligned}$$

Then we obtain

$$\begin{aligned} \lim_{t\rightarrow+\infty} \bigl(S(t)+I(t)+R(t) \bigr)= \frac{\Lambda}{d}. \end{aligned}$$

It is easy to see that

$$\begin{aligned} \limsup_{t\rightarrow+\infty}S(t)\leq\frac{\Lambda}{d}, \quad\quad \limsup _{t\rightarrow+\infty}I(t)\leq\frac{\Lambda}{d}, \quad\quad \limsup _{t\rightarrow+\infty}R(t)\leq\frac{\Lambda}{d}, \end{aligned}$$

and \(S(t)\geq0\), \(I(t)\geq0\), \(R(t)\geq0\).

This completes the proof of Lemma 2.4. □

According to Lemma 2.4, we can know that at any equilibrium \(E^{\ast}=(S^{\ast},I^{\ast},R^{\ast})\) of system (5), \(N^{\ast}\equiv S^{\ast}+I^{\ast}+R^{\ast}\equiv \frac{\Lambda}{d}\), then

$$ \Omega= \biggl\{ \bigl(S(t),I(t),R(t) \bigr):S(t)\geq0,I(t)\geq0,R(t) \geq0,S(t)+I(t)+R(t)\equiv\frac{\Lambda}{d} \biggr\} $$

is a positively invariant region for the system. Therefore, we only consider the dynamics of system (5) in Ω.

The set Ω is a positive invariant region for system (5), thus we assume the population size has reached limiting value; in other words, \(N(t)\equiv\frac{\Lambda}{d}\equiv S(t)+I(t)+R(t)\), and we obtain \(R(t)\equiv\frac{\Lambda}{d}-S(t)-I(t)\). Obviously, system (5) can be reduced to the following system:

$$ \textstyle\begin{cases} \mathrm {d}{S}(t)= [\Lambda-dS(t)-\frac{\lambda \,dS(t)I(t)}{ \Lambda} +\nu (\frac{\Lambda}{d}-S(t)-I(t) ) ]\,\mathrm {d}t -\frac{d\sigma_{1} S(t)I(t)}{\Lambda}\,\mathrm {d}B_{1}(t), \\ \mathrm {d}{I}(t)= [\frac{\lambda \,dS(t)I(t)}{\Lambda}-(d+r)I(t) -\frac{\beta I(t)}{1+\alpha I(t)} ]\,\mathrm {d}t +\frac{d\sigma_{1} S(t)I(t)}{ \Lambda}\,\mathrm {d}B_{1}(t) -\frac{\sigma_{2}I(t)}{1+\alpha I(t)} \,\mathrm {d}B_{2}(t). \end{cases} $$
(7)

Therefore, system (7) is equivalent to system (5). Next, we prove the existence and uniqueness of the global positive solution of system (7).

Lemma 2.5

For any given initial value \((S(0), I(0))\in\mathbb{R}_{+}^{2}\), model (7) has a unique positive solution \((S(t), I(t))\) on \(t\geq0\), and the solution remains in \(\mathbb{R}_{+}^{2}\) with probability 1, namely \((S(t), I(t))\in\mathbb{R}_{+}^{2}\) for all \(t\geq0\) almost surely.

Proof

Since all the coefficients of system (7) satisfy the local Lipschitz condition, for any initial value \((S(0), I(0))\in \mathbb{R}_{+}^{2}\), there exists a unique local solution \((S(t), I(t))\) on \([0, \tau_{e})\), where \(\tau_{e}\) represents the explosion time. Then \(\tau_{e}=+\infty\) demonstrates that the solution of system (7) is global. Therefore, we let \(k_{0}\geq1\) be a sufficiently large constant for every component of \((S(0), I(0))\) all lying within the interval \([\frac{1}{k_{0}},k_{0}]\times[\frac{1}{k _{0}},k_{0}]\). For each integer \(k>k_{0}\), we define the stopping time as follows:

$$ \tau_{k}=\inf \biggl\{ t\in[0, \tau_{e}):\min\bigl\{ \bigl(S(t), I(t)\bigr) \bigr\} \leq \frac{1}{k}\text{ or }\max\bigl\{ \bigl(S(t), I(t)\bigr)\bigr\} \geq k \biggr\} . $$

Throughout this paper, we let \(\inf\emptyset=\infty\) (as usual ∅ denotes the empty set). It is easy to see that \(\tau_{k}\) is increasing as \(k\rightarrow+\infty\). We set \(\tau_{\infty}=\limsup_{k\rightarrow+\infty}\tau_{k}\), obviously \(\tau_{\infty}\leq\tau_{e}\) a.s. If we can show that \(\tau_{\infty }=+\infty\) a.s., then we can obtain that \(\tau_{e}=+\infty\). Next, we only need to show \(\tau_{\infty}=+\infty\) a.s. Assuming this assertion is not true, there exist a constant \(T>0\) and \(\varepsilon\in(0, 1)\) such that \(\mathbb{P}\{\tau_{\infty}\leq T\}>\varepsilon\). Thus, there exists an integer \(k_{1}\geq k_{0}\) such that

$$ \mathbb{P}\{\tau_{k}\leq T\}>\varepsilon \quad \text{for all } k\geq k_{1}. $$
(8)

We define a \(C^{2}\)-function V: \(\mathbb{R}_{+}^{2}\rightarrow \mathbb{R}_{+}\) by

$$\begin{aligned} V\bigl(S(t),I(t)\bigr)=\bigl(S(t)-1-\ln S(t)\bigr)+\bigl(I(t)-1-\ln I(t)\bigr). \end{aligned}$$

Applying Itô’s formula leads to

$$\begin{aligned} \mathrm {d}V\bigl(S(t),I(t)\bigr)=\mathcal{L}V\bigl(S(t),I(t)\bigr)\,\mathrm {d}t + \frac{d \sigma_{1}(I(t)-S(t))}{\Lambda}\,\mathrm {d}B_{1}(t) -\frac{\sigma_{2}(I(t)-1)}{1+ \alpha I(t)} \,\mathrm {d}B_{2}(t), \end{aligned}$$

where

$$\begin{aligned} \mathcal{L}V\bigl(S(t),I(t)\bigr) =& \biggl(1-\frac{1}{S(t)} \biggr) \biggl[\Lambda-d S(t)-\frac{ \lambda \,d S(t) I(t)}{\Lambda}+\nu \biggl(\frac{\Lambda}{d}-S(t)-I(t) \biggr) \biggr] \\ &{}+ \biggl(1-\frac{1}{I(t)} \biggr) \biggl[\frac{\lambda \,d S(t) I(t)}{\Lambda }-(d+r)I(t) - \frac{\beta I(t)}{1+\alpha I(t)} \biggr] \\ &{}+\frac{1}{2} \biggl[ \frac{d^{2}\sigma_{1}^{2}I^{2}(t)}{\Lambda^{2}} +\frac{d ^{2}\sigma_{1}^{2}S^{2}(t)}{\Lambda^{2}} + \frac{\sigma_{2}^{2}}{(1+ \alpha I(t))^{2}} \biggr] \\ =&\Lambda-d S(t)-\frac{\lambda \,d S(t) I(t)}{\Lambda} +\nu \biggl(\frac{ \Lambda}{d}-S(t)-I(t) \biggr)-\frac{\Lambda}{S(t)}+d +\frac{\lambda \,d I(t)}{ \Lambda} \\ &{}-\frac{\nu (\frac{\Lambda}{d}-S(t)-I(t) )}{S(t)} +\frac{ \lambda \,d S(t) I(t)}{\Lambda} -(d+r)I(t)-\frac{\beta I(t)}{1+\alpha I(t)}- \frac{\lambda \,d S(t)}{\Lambda} \\ &{}+d+r+\frac{\beta}{1+\alpha I(t)} +\frac{d^{2}\sigma_{1}^{2}I^{2}(t)}{2 \Lambda^{2}} +\frac{d^{2}\sigma_{1}^{2}S^{2}(t)}{2\Lambda^{2}} + \frac{ \sigma_{2}^{2}}{2(1+\alpha I(t))^{2}} \\ \leq&\Lambda+\frac{\nu\Lambda}{d}+2d+\lambda+r+\beta+\sigma _{1}^{2}+ \frac{\sigma_{2}^{2}}{2} \\ \leq&K, \end{aligned}$$

where K is a positive constant which is independent of \(S(t)\), \(I(t)\) and t.

Therefore, we can have

$$ \mathrm {d}V\bigl(S(t),I(t)\bigr)\leq K\,\mathrm {d}t+ \frac{d\sigma_{1}(I(t)-S(t))}{ \Lambda}\,\mathrm {d}B_{1}(t) -\frac{\sigma_{2}(I(t)-1)}{1+\alpha I(t)} \,\mathrm {d}B_{2}(t). $$
(9)

Integrating (9) from 0 to \(T\wedge\tau_{k}=\min\{T, \tau _{k}\}\) and taking expectation on both sides yield

$$\begin{aligned} \mathbf{E}V\bigl(S(T\wedge\tau_{k}),I(T\wedge\tau_{k}) \bigr)\leq V\bigl(S(0),I(0)\bigr) +K\mathbf{E}(T\wedge\tau_{k}), \end{aligned}$$

then

$$ \mathbf{E}V\bigl(S(T\wedge\tau_{k}),I(T\wedge \tau_{k})\bigr)\leq V\bigl(S(0),I(0)\bigr) +K T. $$
(10)

Set \(\Omega_{k}=\{\tau_{k}\leq T\}\), from inequality (8), we can know that \(\mathbb{P}(\Omega_{k})\geq\varepsilon\). And for all \(\omega\in\Omega_{k}\), there exists at least one of \(S(\tau_{k}, \omega)\), \(I(\tau_{k}, \omega)\) which equals either k or \(\frac{1}{k}\). Thus, we get \(V(S(\tau_{k}, \omega),I(\tau_{k}, \omega))\) is no less than either

$$ k-1-\ln k\text{ or }\frac{1}{k}-1-\ln\frac{1}{k}= \frac{1}{k}-1+ \ln k. $$

As a result, we can have

$$ V\bigl(S(T\wedge\tau_{k}),I(T\wedge \tau_{k})\bigr)\geq(k-1-\ln k)\wedge\biggl( \frac{1}{k}-1+\ln k \biggr). $$
(11)

Combining equations (10) and (11), we can have

$$\begin{aligned} \begin{aligned} V\bigl(S(0),I(0)\bigr)+K T&\geq\mathbf{E} \bigl[ {1}\Omega_{k}( \omega)V\bigl(S(T \wedge\tau_{k}),I(T\wedge\tau_{k})\bigr) \bigr] \\ &\geq\varepsilon(k-1- \ln k)\wedge\biggl(\frac{1}{k}-1+\ln k\biggr), \end{aligned} \end{aligned}$$

where \({1}\Omega_{k}\) denotes the indicator function of \(\Omega_{k}\). When \(k\rightarrow+\infty\), we obtain

$$ +\infty>V\bigl(S(0),I(0)\bigr)+K T=+\infty, $$

which is a contradiction. Thus, we obtain that \(\tau_{\infty}=+ \infty\) a.s.

This completes the proof of Lemma 2.5. □

Lemma 2.6

Let \((S(t),I(t))\) be a solution of system (7) with any initial value \((S(0),I(0))\in\mathbb{R}_{+}^{2}\), then

$$\begin{aligned}& \lim_{t\rightarrow+\infty}\frac{1}{t} \int_{0}^{t}\frac{d\sigma_{1}S( \theta)}{\Lambda}\,\mathrm {d}B_{1}( \theta)=0, \quad\quad \lim_{t\rightarrow+\infty}\frac{1}{t} \int_{0}^{t}\frac{\sigma_{2}}{1+ \alpha I(\theta)}\,\mathrm {d}B_{2}( \theta)=0, \\& \lim_{t\rightarrow+\infty}\frac{1}{t} \int_{0}^{t}\frac{\sigma_{2}I( \theta)}{1+\alpha I(\theta)}\,\mathrm {d}B_{2}( \theta)=0, \quad\quad \lim_{t\rightarrow+\infty}\frac{1}{t} \int_{0}^{t}\frac{\sigma_{2}}{ \alpha}\,\mathrm {d}B_{1}( \theta)=0. \end{aligned}$$

Proof

We let \(M_{1}(t)=\int_{0}^{t}\frac{d\sigma_{1}S(\theta)}{\Lambda} \,\mathrm {d}B_{1}(\theta)\) and \(\eta> 2\). Making use of Lemma 2.1 for the Burkholder–Davis–Gundy inequality and the results of Lemma 2.4, we can get

$$ \begin{aligned} \mathbf{E} \Bigl[ \sup_{0\leq\theta\leq t} \bigl\vert M_{1}( \theta ) \bigr\vert ^{ \eta} \Bigr] &\leq C_{\eta}\mathbf{E} \biggl[ \int_{0}^{t} \frac{d^{2} \sigma^{2}_{1}S^{2}(\theta)}{\Lambda^{2}} \,\mathrm {d}\theta \biggr] ^{\frac{\eta}{2}} \leq t^{\frac{\eta}{2}}C_{\eta}\mathbf{E} \biggl[ \sup_{0\leq\theta\leq t}\frac{d^{\eta}\sigma^{\eta}_{1}S^{\eta}( \theta)}{\Lambda^{\eta}} \biggr] \\ &\leq t^{\frac{\eta}{2}}C_{\eta} \sigma_{1}^{\eta}. \end{aligned} $$

Here, we set ϵ be an arbitrary positive constant. Thus, applying Lemma 2.2 for Chebyshev’s inequality yields

$$ \begin{aligned} \mathbb{P} \Bigl\{ \xi:\sup_{k\delta\leq t\leq(k+1)\delta} \bigl\vert M _{1}(t) \bigr\vert ^{\eta}> (k\delta)^{1+\epsilon+\frac{\eta }{2}} \Bigr\} &\leq\frac{\mathbf{E}( \vert M_{1}((k+1)\delta) \vert ^{\eta })}{(k\delta)^{1+ \epsilon+\frac{\eta}{2}}} \leq\frac{\sigma^{\eta}_{1}C_{\eta}[(1+k) \delta]^{\frac{\eta}{2}}}{(k\delta)^{1+\epsilon+\frac{\eta}{2}}} \\ &\leq\frac{2^{\frac{\eta}{2}}\sigma^{\eta}_{1}C_{\eta}}{(k\delta)^{1+ \epsilon}}. \end{aligned} $$

Using Lemma 2.3 for Doob’s martingale inequality and the Borel-Cantelli lemma in [53], for almost every \(\xi \in\Omega\), we always get that

$$ \sup_{k\delta\leq t\leq(k+1)\delta} \bigl\vert M_{1}(t) \bigr\vert ^{\eta} \leq(k\delta)^{1+\epsilon+\frac{\eta}{2}} $$
(12)

satisfies for all except finitely some k. Thus, there is a positive number \(k_{0}(\xi)\), for almost every \(\xi\in\Omega\), inequality (12) holds when \(k\geq k_{0}(\xi)\). Therefore, when both \(k\geq k_{0}(\xi)\) and \(k\delta\leq t\leq(k+1)\delta\) hold, for almost all \(\xi\in\Omega\), we get

$$ \frac{\ln \vert M_{1}(t) \vert ^{\eta}}{\ln t}\leq\frac {(1+\epsilon+\frac{ \eta}{2})\ln(k\delta)}{\ln(k\delta)}=1+\epsilon+\frac{\eta}{2}. $$

Thus, it is easy to see that

$$ \limsup_{t\rightarrow+\infty}\frac{\ln \vert M_{1}(t) \vert }{\ln t}\leq\frac{1+ \epsilon+\frac{\eta}{2}}{\eta}. $$

Let \(\epsilon\rightarrow0\), we can have that

$$ \limsup_{t\rightarrow+\infty}\frac{\ln \vert M_{1}(t) \vert }{\ln t}\leq \frac{1}{2}+ \frac{1}{\eta}\quad \textit{a.s.} $$

So, for an arbitrary small positive constant ζ (\(\zeta< \frac{1}{2}-\frac{1}{\eta}\)), there is a constant \(T(\xi)\) and a set \(\Omega_{\zeta}\) such that \(\mathbb{P}(\Omega_{\zeta})\geq1-\zeta \). Furthermore, for \(t\geq T(\xi)\), \(\xi\in\Omega_{\zeta}\), we have

$$ \ln \bigl\vert M_{1}(t) \bigr\vert \leq \biggl( \frac{1}{2}+\frac {1}{\eta}+\zeta \biggr) \ln t. $$

As a result, we get

$$ \limsup_{t\rightarrow+\infty}\frac{M_{1}(t)}{t}\leq \limsup _{t\rightarrow+\infty}\frac{t^{\frac{1}{2}+\frac{1}{\eta}+ \zeta}}{t}=0 \quad \textit{a.s.} $$

On the other hand, we know

$$ \limsup_{t\rightarrow+\infty}\frac{ \vert M_{1}(t) \vert }{t}\geq0\quad \textit{a.s.} $$

To sum up

$$ \lim_{t\rightarrow+\infty}\frac{ \vert M_{1}(t) \vert }{t}=0\quad \textit{a.s.} $$

That is to say,

$$ \lim_{t\rightarrow+\infty}\frac{M_{1}(t)}{t}= \lim_{t\rightarrow+\infty} \frac{1}{t} \int_{0}^{t}\frac{d\sigma_{1}S( \theta)}{\Lambda}\,\mathrm {d}B_{1}( \theta)=0\quad \textit{a.s.} $$

Making use of the same argument, we let \(M_{2}(t)=\int_{0}^{t}\frac{ \sigma_{2}}{1+\alpha I(\theta)}\,\mathrm {d}B_{2}(\theta)\), then we can get

$$ \limsup_{t\rightarrow+\infty} \frac{\langle M_{2},M_{2}\rangle_{t}}{t} \leq \limsup _{t\rightarrow+\infty}\frac{1}{t} \int_{0}^{t}\sigma^{2}_{2} \,\mathrm {d}\theta=\sigma^{2}_{2}< +\infty\quad \textit{a.s.} $$

Using the strong law of large numbers, we can obtain

$$ \lim_{t\rightarrow+\infty}\frac{M_{2}(t)}{t}=0\quad \textit{a.s.}, $$

i.e.,

$$ \lim_{t\rightarrow+\infty}\frac{M_{2}(t)}{t}= \lim_{t\rightarrow+\infty} \frac{1}{t} \int_{0}^{t}\frac{\sigma_{2}}{1+ \alpha I(\theta)}\,\mathrm {d}B_{2}( \theta)=0\quad \textit{a.s.} $$

Let \(M_{3}(t)=\int_{0}^{t}\frac{\sigma_{2}I(\theta)}{1+\alpha I( \theta)}\,\mathrm {d}B_{2}(\theta)\), then we can get

$$ \limsup_{t\rightarrow+\infty} \frac{\langle M_{3},M_{3}\rangle_{t}}{t} \leq \limsup _{t\rightarrow+\infty}\frac{1}{t} \int_{0}^{t}\frac{\sigma ^{2}_{2}}{\alpha^{2}}\,\mathrm {d}\theta= \frac{\sigma^{2}_{2}}{\alpha ^{2}}< +\infty\quad \textit{a.s.} $$

Using the strong law of large numbers, we can obtain

$$ \lim_{t\rightarrow+\infty}\frac{M_{3}(t)}{t}=0 \quad \textit{a.s.}, $$

i.e.,

$$ \lim_{t\rightarrow+\infty}\frac{M_{3}(t)}{t}= \lim_{t\rightarrow+\infty} \frac{1}{t} \int_{0}^{t}\frac{\sigma_{2}I( \theta)}{1+\alpha I(\theta)}\,\mathrm {d}B_{2}( \theta)=0\quad \textit{a.s.} $$

Let \(M_{4}(t)=\int_{0}^{t}\frac{\sigma_{2}}{\alpha}\,\mathrm {d}B_{2}( \theta)\), then we can get

$$ \limsup_{t\rightarrow+\infty} \frac{\langle M_{4},M_{4}\rangle_{t}}{t} = \limsup _{t\rightarrow+ \infty}\frac{1}{t} \int_{0}^{t}\frac{\sigma^{2}_{2}}{\alpha^{2}} \,\mathrm {d}\theta= \frac{\sigma^{2}_{2}}{\alpha^{2}}< +\infty\quad \textit{a.s.} $$

Using the strong law of large numbers, we can obtain

$$ \lim_{t\rightarrow+\infty}\frac{M_{4}(t)}{t}=0\quad \textit{a.s.}, $$

i.e.,

$$ \lim_{t\rightarrow+\infty}\frac{M_{4}(t)}{t}= \lim_{t\rightarrow+\infty} \frac{1}{t} \int_{0}^{t}\frac{\sigma_{2}}{ \alpha}\,\mathrm {d}B_{2}( \theta)=0 \quad \textit{a.s.} $$

The proof of Lemma 2.6 is complete. □

2.2 Extinction

When we study an epidemic model, extinction and persistence in mean are two important properties. In this subsection, we explore the conditions which lead to the extinction of epidemic system (7) under stochastic disturbances.

Next, we explore the conditions for the extinction of the epidemic disease of stochastic system (7).

Theorem 2.1

Let \((S(t),I(t))\) be the solution of system (7) with any initial value \((S(0),I(0))\in\mathbb{R}^{2}_{+}\). When one of the following conditions holds:

  1. (i)

    \(R_{1}=\frac{\lambda^{2}}{2(d+r)\sigma_{1} ^{2}}+\frac{\beta^{2}}{2(d+r) \sigma_{2}^{2}}< 1\),

  2. (ii)

    \(\lambda\geq\sigma_{1}^{2}\) and \(R_{2}=\frac{2(\lambda-d-r)(d+\alpha\Lambda)^{2}}{\sigma_{1}^{2} (d+ \alpha\Lambda)^{2}+d^{2}\sigma_{2}^{2}}-\frac{2d\beta(d+\alpha \Lambda)}{\sigma_{1}^{2}(d+\alpha\Lambda)^{2}+d^{2}\sigma_{2}^{2}}< 1\),

  3. (iii)

    \(\lambda< \sigma_{1}^{2}\) and \(R_{3}=\frac{ \lambda^{2}(d+\alpha\Lambda)}{2\sigma_{1}^{2}[d\beta+(d+r)(d+ \alpha\Lambda)]}-\frac{d^{2}\sigma_{2}^{2}}{2[d\beta(d+\alpha \Lambda)+(d+r) (d+\alpha\Lambda)^{2}]}< 1\),

  4. (iv)

    \(\lambda\geq\sigma_{1}^{2}\) and \(R_{4}=\frac{2 \lambda}{\sigma_{1}^{2}+2(d+r)}+\frac{\beta^{2}}{\sigma_{2}^{2}[ \sigma_{1}^{2}+2(d+r)]}<1\),

then

$$ \lim_{t\rightarrow+\infty}S(t)=\frac{\Lambda}{d}, \quad\quad \lim _{t\rightarrow+\infty}I(t)=0. $$

Proof

Making use of Itô’s formula to the second equation of the stochastic differential system (7), we get

$$\begin{aligned} \mathrm {d}\ln I(t) =&\frac{1}{I(t)} \biggl[ \biggl( \frac{\lambda \,d S(t)I(t)}{ \Lambda}-(d+r)I(t) -\frac{\beta I(t)}{1+\alpha I(t)} \biggr)\,\mathrm {d}t + \frac{d\sigma_{1} S(t)I(t)}{\Lambda}\,\mathrm {d}B_{1}(t) \\ &{}-\frac{\sigma_{2}I(t)}{1+\alpha I(t)}\,\mathrm {d}B_{2}(t) \biggr] + \frac{1}{2} \biggl(-\frac{1}{I^{2}(t)} \biggr) \biggl[\frac{d^{2}\sigma^{2} _{1} S^{2}(t)I^{2}(t)}{\Lambda^{2}} +\frac{\sigma^{2}_{2}I^{2}(t)}{(1+ \alpha I(t))^{2}} \biggr]\,\mathrm {d}t \\ =& \biggl(\frac{\lambda \,d S(t)}{\Lambda}-(d+r) -\frac{\beta}{1+\alpha I(t)}-\frac{d^{2}\sigma^{2}_{1} S^{2}(t)}{2\Lambda^{2}} - \frac{\sigma ^{2}_{2}}{2(1+\alpha I(t))^{2}} \biggr)\,\mathrm {d}t \\ &{}+\frac{d\sigma_{1} S(t)}{\Lambda}\,\mathrm {d}B_{1}(t) -\frac{\sigma _{2}}{1+\alpha I(t)} \,\mathrm {d}B_{2}(t) \\ =& \biggl[-\frac{d^{2}\sigma_{1}^{2}}{2\Lambda^{2}} \biggl(S^{2}(t) -\frac{2 \lambda\Lambda}{d\sigma_{1}^{2}}S(t) \biggr) \\ &{}-\frac{\sigma_{2}^{2}}{2} \biggl(\frac{1}{(1+\alpha I(t))^{2}}+\frac{2\beta}{\sigma^{2}_{2}(1+ \alpha I(t))} \biggr)-(d+r) \biggr]\,\mathrm {d}t \\ &{}+\frac{d\sigma_{1} S(t)}{\Lambda}\,\mathrm {d}B_{1}(t) -\frac{\sigma _{2}}{1+\alpha I(t)} \,\mathrm {d}B_{2}(t) \\ =& \biggl[-\frac{d^{2}\sigma_{1}^{2}}{2\Lambda^{2}} \biggl(S(t) -\frac{ \lambda\Lambda}{d\sigma_{1}^{2}} \biggr)^{2}-\frac{\sigma_{2}^{2}}{2} \biggl(\frac{1}{1+\alpha I(t)}+ \frac{\beta}{\sigma^{2}_{2}} \biggr)^{2}+\frac{ \lambda^{2}}{2\sigma^{2}_{1}} + \frac{\beta^{2}}{2\sigma_{2}^{2}}-(d+r) \biggr]\,\mathrm {d}t \\ &{}+\frac{d\sigma_{1} S(t)}{\Lambda}\,\mathrm {d}B_{1}(t) -\frac{\sigma _{2}}{1+\alpha I(t)} \,\mathrm {d}B_{2}(t). \end{aligned}$$
(13)

Case (i): When \(R_{1}=\frac{\lambda^{2}}{2(d+r)\sigma _{1}^{2}}+\frac{\beta^{2}}{2(d+r) \sigma_{2}^{2}}< 1\) holds, integrating both sides of inequality (13) from 0 to t gives

$$\begin{aligned} \ln I(t) =&-\frac{d^{2}\sigma_{1}^{2}}{2\Lambda^{2}} \int_{0}^{t} \biggl(S(\theta)-\frac{\lambda\Lambda}{d\sigma_{1}^{2}} \biggr)^{2} \,\mathrm {d}\theta-\frac{\sigma_{2}^{2}}{2} \int_{0}^{t} \biggl(\frac{1}{1+ \alpha I(\theta)}+ \frac{\beta}{\sigma^{2}_{2}} \biggr)^{2}\,\mathrm {d}\theta \\ &{}- \biggl(d+r-\frac{\lambda^{2}}{2\sigma^{2}_{1}} -\frac{\beta^{2}}{2 \sigma_{2}^{2}} \biggr)t+M_{1}(t)-M_{2}(t)+ \ln I(0) \\ \leq&- \biggl(d+r-\frac{\lambda^{2}}{2\sigma^{2}_{1}} -\frac{\beta^{2}}{2 \sigma_{2}^{2}} \biggr)t+M_{1}(t)-M_{2}(t)+\ln I(0), \end{aligned}$$
(14)

where \(M_{1}(t)=\int_{0}^{t}\frac{d\sigma_{1}S(\theta)}{\Lambda} \,\mathrm {d}B_{1}(\theta)\) and \(M_{2}(t)=\int_{0}^{t}\frac{\sigma_{2}}{1+ \alpha I(\theta)}\,\mathrm {d}B_{2}(\theta)\).

Dividing both sides of inequality (14) by t yields

$$\begin{aligned} \frac{\ln I(t)}{t} \leq&- \biggl(d+r-\frac{\lambda^{2}}{2\sigma^{2} _{1}} - \frac{\beta^{2}}{2\sigma_{2}^{2}} \biggr)+\frac{M_{1}(t)}{t}-\frac{M _{2}(t)}{t} + \frac{\ln I(0)}{t}. \end{aligned}$$
(15)

The functions \(M_{1}(t)\) and \(M_{2}(t)\) are known as the local continuous martingale with \(M_{1}(0)=0\) and \(M_{2}(0)=0\). Applying Lemma 2.6, we can know

$$ \lim_{t\rightarrow+\infty}\frac{M_{1}(t)}{t}=0, \quad\quad \lim _{t\rightarrow+\infty}\frac{M_{2}(t)}{t}=0\quad \textit{a.s.} $$

Making use of the condition \(R_{1}=\frac{\lambda^{2}}{2(d+r)\sigma _{1}^{2}}+\frac{\beta^{2}}{2(d+r) \sigma_{2}^{2}}< 1\) and taking the limit superior of both sides of inequality (15), we can get

$$\begin{aligned} \limsup_{t\rightarrow+\infty}\frac{\ln I(t)}{t}\leq- \biggl(d+r- \frac{ \lambda^{2}}{2\sigma^{2}_{1}} -\frac{\beta^{2}}{2\sigma_{2}^{2}} \biggr)=(d+r) (R_{1}-1)< 0, \end{aligned}$$

which implies \(\lim_{t\rightarrow+\infty}I(t)=0\).

Case (ii): When both \(\lambda\geq\sigma_{1}^{2}\) and \(R_{2}=\frac{2(\lambda-d-r)(d+\alpha\Lambda)^{2}}{\sigma_{1}^{2} (d+ \alpha\Lambda)^{2}+d^{2}\sigma_{2}^{2}}-\frac{2d\beta(d+\alpha \Lambda)}{\sigma_{1}^{2}(d+\alpha\Lambda)^{2}+d^{2}\sigma_{2}^{2}}< 1\) hold, according to inequality (13), we can get

$$\begin{aligned} \mathrm {d}\ln I(t) \leq& \biggl[-\frac{d^{2}\sigma_{1}^{2}}{2\Lambda ^{2}} \biggl(S(t) -\frac{\lambda\Lambda}{d\sigma_{1}^{2}} \biggr)^{2} +\frac{ \lambda^{2}}{2\sigma^{2}_{1}} - \frac{d^{2}\sigma_{2}^{2}}{2(d+\alpha \Lambda)^{2}} -\frac{d\beta}{d+\alpha\Lambda}-(d+r) \biggr] \,\mathrm {d}t \\ &{}+\frac{d\sigma_{1} S(t)}{\Lambda}\,\mathrm {d}B_{1}(t) -\frac{\sigma _{2}}{1+\alpha I(t)} \,\mathrm {d}B_{2}(t). \end{aligned}$$
(16)

Since \(\lambda\geq\sigma_{1}^{2}\), the variable \(S(t)\) in inequality (16) takes its maximum value on the interval \([0, \frac{ \Lambda}{d}]\) at \(\frac{\Lambda}{d}\), thus we have

$$\begin{aligned} \mathrm {d}\ln I(t) \leq& \biggl[-\frac{\sigma_{1}^{2}}{2}+\lambda- \frac{d ^{2}\sigma_{2}^{2}}{2(d+\alpha\Lambda)^{2}} -\frac{d\beta}{d+ \alpha\Lambda}-(d+r) \biggr]\,\mathrm {d}t \\ &{}+\frac{d\sigma_{1} S(t)}{\Lambda}\,\mathrm {d}B_{1}(t) -\frac{\sigma _{2}}{1+\alpha I(t)} \,\mathrm {d}B_{2}(t). \end{aligned}$$
(17)

Integrating both sides of inequality (17) from 0 to t and dividing both sides by t, we obtain

$$\begin{aligned} \begin{aligned}[b] \frac{\ln I(t)}{t} &\leq \biggl[-\frac{\sigma_{1}^{2}}{2}+\lambda- \frac{d ^{2}\sigma_{2}^{2}}{2(d+\alpha\Lambda)^{2}} -\frac{d\beta}{d+ \alpha\Lambda}-(d+r) \biggr] \\ &\quad{} +\frac{M_{1}(t)}{t} - \frac{M_{2}(t)}{t}+\frac{ \ln I(0)}{t}. \end{aligned} \end{aligned}$$
(18)

Using the condition \(R_{2}=\frac{2(\lambda-d-r)(d+\alpha\Lambda)^{2}}{ \sigma_{1}^{2} (d+\alpha\Lambda)^{2}+d^{2}\sigma_{2}^{2}}-\frac{2d \beta(d+\alpha\Lambda)}{\sigma_{1}^{2}(d+\alpha\Lambda)^{2}+d ^{2}\sigma_{2}^{2}}< 1\), by Lemma 2.6 and taking the limit superior of both sides of inequality (18), one has

$$\begin{aligned} \limsup_{t\rightarrow+\infty}\frac{\ln I(t)}{t} \leq& - \biggl[ \biggl( \frac{ \sigma_{1}^{2}}{2}+ \frac{d^{2}\sigma_{2}^{2}}{2(d+\alpha\Lambda)^{2}} \biggr)- \biggl(\lambda - \frac{d \beta}{d+\alpha\Lambda}-d-r \biggr) \biggr] \\ =&\frac{1}{2} \biggl( \sigma_{1}^{2}+ \frac{d^{2}\sigma_{2}^{2}}{(d+ \alpha\Lambda)^{2}} \biggr) (R_{2}-1)< 0, \end{aligned}$$

which implies \(\lim_{t\rightarrow+\infty}I(t)=0\).

Case (iii): When both \(\lambda< \sigma_{1}^{2}\) and \(R_{3}=\frac{\lambda^{2}(d+\alpha\Lambda)}{2\sigma_{1}^{2}[d\beta+(d+r)(d+ \alpha\Lambda)]}-\frac{d^{2}\sigma_{2}^{2}}{2[d\beta(d+\alpha \Lambda)+(d+r) (d+\alpha\Lambda)^{2}]}< 1\) hold, since \(\lambda< \sigma_{1}^{2}\), the variable \(S(t)\) in inequality (16) takes its maximum value on the interval \([0, \frac{\Lambda}{d}]\) at \(\frac{\lambda\Lambda}{d\sigma_{1}^{2}}\), so we have

$$\begin{aligned} \begin{aligned}[b] \mathrm {d}\ln I(t)&\leq \biggl[\frac{\lambda^{2}}{2\sigma^{2}_{1}} - \frac{d ^{2}\sigma_{2}^{2}}{2(d+\alpha\Lambda)^{2}} -\frac{d\beta}{d+ \alpha\Lambda}-(d+r) \biggr]\,\mathrm {d}t \\ &\quad{} + \frac{d\sigma_{1} S(t)}{ \Lambda}\,\mathrm {d}B_{1}(t) -\frac{\sigma_{2}}{1+\alpha I(t)} \,\mathrm {d}B_{2}(t). \end{aligned} \end{aligned}$$
(19)

Integrating both sides of inequality (19) from 0 to t and dividing both sides by t, we can obtain

$$\begin{aligned} \frac{\ln I(t)}{t} \leq \biggl[\frac{\lambda^{2}}{2\sigma^{2}_{1}} - \frac{d ^{2}\sigma_{2}^{2}}{2(d+\alpha\Lambda)^{2}} -\frac{d\beta}{d+ \alpha\Lambda}-(d+r) \biggr]+\frac{M_{1}(t)}{t} - \frac{M_{2}(t)}{t}+\frac{ \ln I(0)}{t}. \end{aligned}$$
(20)

Applying the condition \(R_{3}=\frac{\lambda^{2}(d+\alpha\Lambda)}{2 \sigma_{1}^{2}[d\beta+(d+r)(d+\alpha\Lambda)]}-\frac{d^{2}\sigma _{2}^{2}}{2[d\beta(d+\alpha\Lambda)+(d+r) (d+\alpha\Lambda)^{2}]}< 1\), by Lemma 2.6 and taking the limit superior of both sides of inequality (20), we get

$$\begin{aligned} \limsup_{t\rightarrow+\infty}\frac{\ln I(t)}{t} \leq& \biggl[ \frac{ \lambda^{2}}{2\sigma^{2}_{1}} -\frac{d^{2}\sigma_{2}^{2}}{2(d+\alpha \Lambda)^{2}} -\frac{d\beta}{d+\alpha\Lambda}-(d+r) \biggr] \\ =&\biggl(\frac{d\beta}{d+\alpha\Lambda}+d+r\biggr) (R_{3}-1)< 0, \end{aligned}$$

which implies \(\lim_{t\rightarrow+\infty}I(t)=0\).

Case (iv): When both \(\lambda\geq\sigma_{1}^{2}\) and \(R_{4}=\frac{2\lambda}{\sigma_{1}^{2}+2(d+r)}+\frac{\beta^{2}}{\sigma _{2}^{2}[\sigma_{1}^{2}+2(d+r)]}<1\) hold, since \(\lambda\geq\sigma _{1}^{2}\), the variable \(S(t)\) in inequality (13) takes its maximum value on the interval \([0, \frac{\Lambda}{d}]\) at \(\frac{ \Lambda}{d}\), thus one has

$$\begin{aligned} \mathrm {d}\ln I(t) \leq& \biggl[-\frac{d^{2}\sigma_{1}^{2}}{2\Lambda ^{2}} \biggl( \frac{\Lambda}{d} - \frac{\lambda\Lambda}{d\sigma_{1}^{2}} \biggr)^{2}-\frac{\sigma_{2} ^{2}}{2} \biggl(\frac{1}{1+\alpha I(t)}+\frac{\beta}{\sigma^{2}_{2}} \biggr)^{2}+ \frac{\lambda^{2}}{2\sigma^{2}_{1}} +\frac{\beta^{2}}{2 \sigma_{2}^{2}}-(d+r) \biggr]\,\mathrm {d}t \\ &{}+\frac{d\sigma_{1} S(t)}{\Lambda}\,\mathrm {d}B_{1}(t) -\frac{\sigma _{2}}{1+\alpha I(t)} \,\mathrm {d}B_{2}(t) \\ =& \biggl[-\frac{\sigma_{1}^{2}}{2} \biggl(1+\frac{\lambda^{2}}{\sigma_{1} ^{4}} - \frac{2\lambda}{\sigma_{1}^{2}} \biggr) - \frac{\sigma_{2}^{2}}{2} \biggl(\frac{1}{1+\alpha I(t)}+ \frac{\beta}{ \sigma^{2}_{2}} \biggr)^{2}+\frac{\lambda^{2}}{2\sigma^{2}_{1}} + \frac{ \beta^{2}}{2\sigma_{2}^{2}}-(d+r) \biggr]\,\mathrm {d}t \\ &{}+\frac{d\sigma_{1} S(t)}{\Lambda}\,\mathrm {d}B_{1}(t) -\frac{\sigma _{2}}{1+\alpha I(t)} \,\mathrm {d}B_{2}(t) \\ =& \biggl[-\frac{\sigma_{1}^{2}}{2}+\lambda-\frac{\sigma_{2}^{2}}{2} \biggl( \frac{1}{1+\alpha I(t)}+\frac{\beta}{\sigma^{2}_{2}} \biggr)^{2} + \frac{ \beta^{2}}{2\sigma_{2}^{2}}-(d+r) \biggr]\,\mathrm {d}t \\ &{}+\frac{d\sigma_{1} S(t)}{\Lambda}\,\mathrm {d}B_{1}(t) -\frac{\sigma _{2}}{1+\alpha I(t)} \,\mathrm {d}B_{2}(t) \\ \leq& \biggl(-\frac{\sigma_{1}^{2}}{2}+\lambda+\frac{\beta^{2}}{2 \sigma_{2}^{2}}-(d+r) \biggr) \,\mathrm {d}t +\frac{d\sigma_{1} S(t)}{\Lambda }\,\mathrm {d}B_{1}(t) -\frac{\sigma_{2}}{1+\alpha I(t)} \,\mathrm {d}B_{2}(t). \end{aligned}$$
(21)

Integrating both sides of inequality (21) from 0 to t and dividing both sides by t yield

$$\begin{aligned} \frac{\ln I(t)}{t} \leq \biggl(-\frac{\sigma_{1}^{2}}{2}+\lambda+ \frac{ \beta^{2}}{2\sigma_{2}^{2}}-(d+r) \biggr)+\frac{M_{1}(t)}{t} -\frac{M _{2}(t)}{t}+ \frac{\ln I(0)}{t}. \end{aligned}$$
(22)

Applying the condition \(R_{4}=\frac{2\lambda}{\sigma _{1}^{2}+2(d+r)}+\frac{ \beta^{2}}{\sigma_{2}^{2}[\sigma_{1}^{2}+2(d+r)]}<1\), by Lemma 2.6 and taking the limit superior of both sides of inequality (22), we get

$$\begin{aligned} \limsup_{t\rightarrow+\infty}\frac{\ln I(t)}{t} \leq& \biggl(- \frac{ \sigma_{1}^{2}}{2}+\lambda+\frac{\beta^{2}}{2\sigma_{2}^{2}}-(d+r) \biggr) \\ =&\biggl(d+r+\frac{\sigma_{1}^{2}}{2}\biggr) (R_{4}-1)< 0, \end{aligned}$$

which implies \(\lim_{t\rightarrow+\infty}I(t)=0\).

Since \(\lim_{t\rightarrow+\infty}I(t)=0\), we have assumed the population size has reached limiting value. Further we consider the limit system of stochastic differential system (7)

$$ \mathrm {d}S(t)= \biggl[\Lambda-d S(t) +\nu \biggl(\frac{\Lambda}{d}-S(t) \biggr) \biggr]\,\mathrm {d}t. $$

It is easy to see that \(\lim_{t\rightarrow+\infty}S(t)=\frac{\Lambda }{d}\). This completes the proof of Theorem 2.1. □

2.3 Persistence in mean

The conditions of the extinction for system (7) have been obtained. In this subsection, we investigate the conditions which lead to the persistence in mean of epidemic system (7) under the stochastic disturbances, which implies the infectious disease is prevalent.

Theorem 2.2

Let \((S(t),I(t))\) be the solution of system (7) with any initial value \((S(0),I(0))\in\mathbb{R}^{2}_{+}\). When both the conditions \(\frac{d\lambda}{\alpha\Lambda}\geq d+\nu\) and

$$ \widetilde{R}=\frac{\alpha\Lambda(d+\nu)[2\lambda-2d-2r -(\sigma _{1}^{2}+\sigma_{2}^{2})]}{2d\beta\lambda}>1 $$

hold, then the epidemic disease \(I(t)\) is persistent in mean; in other words,

$$ 0< \frac{\beta}{\alpha(\nu+d+r)}(\widetilde{R}-1)\leq \liminf_{t\rightarrow+\infty}\bigl\langle I(t)\bigr\rangle \leq \limsup_{t\rightarrow+\infty}\bigl\langle I(t)\bigr\rangle \leq\frac{\Lambda }{d}. $$

Proof

For system (7), computing the sum of two equations yields

$$\begin{aligned} \mathrm {d}\bigl(S(t)+I(t) \bigr) =& \biggl[\Lambda-d S(t)+ \frac{\nu\Lambda }{d} -\nu S(t)-\nu I(t)-(d+r)I(t)-\frac{\beta I(t)}{1+\alpha I(t)} \biggr] \,\mathrm {d}t \\ &{}-\frac{\sigma_{2}I(t)}{1+\alpha I(t)}\,\mathrm {d}B_{2}(t) \\ \geq& \biggl[\Lambda+\frac{\nu\Lambda}{d} -(d+\nu) S(t)-(\nu+d+r)I(t)- \frac{ \beta}{\alpha} \biggr]\,\mathrm {d}t \\ &{}- \frac{\sigma_{2}I(t)}{1+\alpha I(t)}\,\mathrm {d}B_{2}(t). \end{aligned}$$
(23)

Integrating both sides of inequality (23) from 0 to t and dividing both sides by t, we obtain

$$\begin{aligned} \begin{aligned}[b] \frac{1}{t}\bigl[S(t)-S(0)+I(t)-I(0)\bigr]&\geq \biggl( \Lambda+\frac{\nu\Lambda }{d}-\frac{\beta}{\alpha} \biggr)-(d+\nu) \bigl\langle S(t) \bigr\rangle -( \nu+d+r)\bigl\langle I(t)\bigr\rangle \\ &\quad{} -\frac{M_{3}(t)}{t}, \end{aligned} \end{aligned}$$
(24)

where \(M_{3}(t)=\int_{0}^{t}\frac{\sigma_{2}I(\theta)}{1+\alpha I( \theta)}\,\mathrm {d}B_{2}(\theta)\).

Taking the limit of both sides of inequality (24) and by Lemma 2.6, we can get

$$\begin{aligned} 0\geq \biggl(\Lambda+\frac{\nu\Lambda}{d}-\frac{\beta}{\alpha} \biggr) -(d+\nu)\lim _{t\rightarrow+\infty}\bigl\langle S(t)\bigr\rangle -( \nu+d+r)\lim _{t\rightarrow+\infty}\bigl\langle I(t)\bigr\rangle , \end{aligned}$$

i.e.,

$$\begin{aligned} \lim_{t\rightarrow+\infty}\bigl\langle S(t)\bigr\rangle \geq \biggl(\frac{ \Lambda}{d}-\frac{\beta}{\alpha(d+\nu)} \biggr) -\frac{\nu+d+r}{d+ \nu}\lim _{t\rightarrow+\infty}\bigl\langle I(t)\bigr\rangle . \end{aligned}$$
(25)

Next, we define a \(C^{2}\)-function V: \(\mathbb{R}_{+}^{2}\rightarrow \mathbb{R}_{+}\) by

$$\begin{aligned} V\bigl(S(t),I(t)\bigr)=\frac{1}{\alpha}\ln I(t)+I(t)+S(t). \end{aligned}$$

Applying Itô’s formula results in

$$\begin{aligned} \mathrm {d}V\bigl(S(t),I(t)\bigr)=\mathcal{L}V\bigl(S(t),I(t) \bigr)\,\mathrm {d}t +\frac{d \sigma_{1}S(t)}{\alpha\Lambda}\,\mathrm {d}B_{1}(t) - \frac{\sigma_{2}}{ \alpha}\,\mathrm {d}B_{2}(t), \end{aligned}$$
(26)

where

$$\begin{aligned} \mathcal{L}V\bigl(S(t),I(t)\bigr) =& \biggl[\Lambda-d S(t)-\frac{d\lambda S(t) I(t)}{ \Lambda}+ \nu \biggl(\frac{\Lambda}{d}-S(t)-I(t) \biggr) \biggr] \\ &{}+\frac{1+\alpha I(t)}{\alpha} \biggl[\frac{d\lambda S(t)}{\Lambda }-(d+r)-\frac{ \beta}{1+\alpha I(t)} \biggr] \\ &{}-\frac{d^{2}\sigma_{1}^{2}S^{2}(t)}{2\alpha\Lambda^{2}} -\frac{ \sigma_{2}^{2}}{2\alpha(1+\alpha I(t))^{2}} \\ =& \biggl(\Lambda+\frac{\nu\Lambda}{d}-\frac{d+r+\beta}{\alpha} \biggr) + \biggl( \frac{d\lambda}{\alpha\Lambda}-d-\nu \biggr)S(t) \\ &{}-(\nu+d+r)I(t)-\frac{d^{2}\sigma_{1}^{2}S^{2}(t)}{2\alpha\Lambda ^{2}} -\frac{\sigma_{2}^{2}}{2\alpha(1+\alpha I(t))^{2}} \\ \geq& \biggl(\Lambda+\frac{\nu\Lambda}{d}-\frac{d+r+\beta}{\alpha } \biggr) + \biggl( \frac{d\lambda}{\alpha\Lambda}-d-\nu \biggr)S(t) \\ & {} -(\nu+d+r)I(t)-\frac{\sigma_{1}^{2}}{2\alpha} -\frac{\sigma_{2} ^{2}}{2\alpha} \\ =& \biggl(\Lambda+\frac{\nu\Lambda}{d}-\frac{d+r+\beta}{\alpha} -\frac{ \sigma_{1}^{2}+\sigma_{2}^{2}}{2\alpha} \biggr) + \biggl(\frac{d\lambda}{ \alpha\Lambda}-d-\nu \biggr)S(t) \\ &{} -(\nu+d+r)I(t). \end{aligned}$$

Integrating both sides of inequality (26) from 0 to t and dividing both sides by t, we get

$$\begin{aligned} \frac{1}{t} \biggl(\frac{1}{\alpha}\ln I(t)+I(t)+S(t) \biggr) \geq& \biggl(\Lambda+\frac{\nu\Lambda}{d}-\frac{d+r+\beta}{\alpha} -\frac{ \sigma_{1}^{2}+\sigma_{2}^{2}}{2\alpha} \biggr) + \biggl(\frac{d\lambda}{ \alpha\Lambda}-d-\nu \biggr)\bigl\langle S(t)\bigr\rangle \\ & {} -(\nu+d+r)\bigl\langle I(t)\bigr\rangle +\frac{M_{1}(t)}{\alpha t} - \frac{M _{4}(t)}{t} \\ & {} +\frac{1}{t} \biggl(\frac{1}{\alpha}\ln I(0)+I(0)+S(0) \biggr), \end{aligned}$$

i.e.,

$$\begin{aligned} (\nu+d+r)\bigl\langle I(t)\bigr\rangle \geq& \biggl(\Lambda+ \frac{\nu\Lambda }{d}-\frac{d+r+\beta}{\alpha} -\frac{\sigma_{1}^{2}+\sigma_{2}^{2}}{2 \alpha} \biggr) + \biggl( \frac{d\lambda}{\alpha\Lambda}-d-\nu \biggr) \bigl\langle S(t)\bigr\rangle + \frac{M_{1}(t)}{\alpha t} \\ & {} -\frac{M_{4}(t)}{t} -\frac{\ln I(t)-\ln I(0)}{\alpha t}- \frac{I(t)-I(0)}{t} - \frac{S(t)-S(0)}{t} \\ \geq& \textstyle\begin{cases} (\Lambda+\frac{\nu\Lambda}{d}-\frac{d+r+\beta }{\alpha} -\frac{ \sigma_{1}^{2}+\sigma_{2}^{2}}{2\alpha} ) + (\frac{d\lambda}{ \alpha\Lambda}-d-\nu )\langle S(t)\rangle+\frac{M_{1}(t)}{ \alpha t} \\ \quad{} -\frac{M_{4}(t)}{t} +\frac{\ln I(0)}{\alpha t}-\frac{I(t)-I(0)}{t} - \frac{S(t)-S(0)}{t},\quad \hspace{21pt} 0< I(t)< 1; \\ (\Lambda+\frac{\nu\Lambda}{d}-\frac{d+r+\beta}{\alpha} -\frac{ \sigma_{1}^{2}+\sigma_{2}^{2}}{2\alpha} ) + (\frac{d\lambda}{ \alpha\Lambda}-d-\nu )\langle S(t)\rangle+\frac{M_{1}(t)}{ \alpha t} \\ \quad{} -\frac{M_{4}(t)}{t} -\frac{\ln I(t)-\ln I(0)}{\alpha t}- \frac{I(t)-I(0)}{t} -\frac{S(t)-S(0)}{t},\quad 1\leq I(t), \end{cases}\displaystyle \end{aligned}$$
(27)

where \(M_{1}(t)=\int_{0}^{t}\frac{d\sigma_{1}S(\theta)}{\Lambda} \,\mathrm {d}B_{1}(\theta)\) and \(M_{4}(t)=\int_{0}^{t}\frac{\sigma_{2}}{ \alpha}\,\mathrm {d}B_{2}(\theta)\).

Taking the limit of both sides of inequality (27), by Lemma 2.6, we have

$$\begin{aligned} \begin{aligned}[b] (\nu+d+r)\lim_{t\rightarrow+\infty}\bigl\langle I(t)\bigr\rangle &\geq \biggl( \Lambda+\frac{\nu\Lambda}{d}-\frac{d+r+\beta}{\alpha} - \frac{ \sigma_{1}^{2}+\sigma_{2}^{2}}{2\alpha} \biggr) \\ &\quad{} + \biggl(\frac{d\lambda}{ \alpha\Lambda}-d-\nu \biggr) \lim _{t\rightarrow+\infty}\bigl\langle S(t) \bigr\rangle . \end{aligned} \end{aligned}$$
(28)

From inequality (25) and inequality (28), and assuming that the condition \(\frac{d\lambda}{\alpha\Lambda}\geq d+\nu\) holds, then we can obtain

$$\begin{aligned}& (\nu+d+r)\lim_{t\rightarrow+\infty}\bigl\langle I(t)\bigr\rangle \\& \quad \geq \biggl(\Lambda+\frac{\nu\Lambda}{d}-\frac{d+r+\beta}{\alpha} -\frac{ \sigma_{1}^{2}+\sigma_{2}^{2}}{2\alpha} \biggr) \\& \quad \quad {} + \biggl(\frac{d\lambda}{\alpha\Lambda}-d-\nu \biggr) \biggl[ \biggl(\frac{ \Lambda}{d}- \frac{\beta}{\alpha(d+\nu)} \biggr) -\frac{\nu+d+r}{d+ \nu}\lim_{t\rightarrow+\infty}\bigl\langle I(t)\bigr\rangle \biggr] \\& \quad = \Lambda+\frac{\nu\Lambda}{d}-\frac{d+r+\beta}{\alpha} -\frac{ \sigma_{1}^{2}+\sigma_{2}^{2}}{2\alpha}+ \frac{\lambda}{\alpha} -\frac{ \lambda d\beta}{\alpha^{2}\Lambda(d+\nu)}- \frac{(d+\nu)\Lambda}{d} +\frac{\beta}{\alpha} \\& \quad \quad {} - \biggl[ \frac{\lambda d(\nu+d+r)}{\alpha\Lambda(d+\nu)}-(\nu +d+r) \biggr] \lim_{t\rightarrow+\infty} \bigl\langle I(t)\bigr\rangle , \end{aligned}$$

i.e.,

$$\begin{aligned} \lim_{t\rightarrow+\infty}\bigl\langle I(t)\bigr\rangle \geq& \biggl[ \frac{2 \lambda-2d-2r-(\sigma_{1}^{2}+\sigma_{2}^{2})}{2\alpha} -\frac{ \lambda d\beta}{\alpha^{2}\Lambda(d+\nu)} \biggr] \cdot\frac{\alpha \Lambda(d+\nu)}{\lambda d(\nu+d+dr)} \\ =&\frac{\beta}{\alpha(\nu+d+r)} \biggl[ \frac{\alpha\Lambda(d+ \nu)[2\lambda-2d-2r -(\sigma_{1}^{2}+\sigma_{2}^{2})]}{2d\beta \lambda}-1 \biggr] \\ :=&\frac{\beta}{\alpha(\nu+d+r)}(\widetilde{R}-1). \end{aligned}$$
(29)

When the condition \(\widetilde{R}=\frac{\alpha\Lambda(d+\nu)[2 \lambda-2d-2r -(\sigma_{1}^{2}+\sigma_{2}^{2})]}{2d\beta\lambda}>1\) holds, taking the inferior limit of both sides of (29) yields

$$\begin{aligned} \liminf_{t\rightarrow+\infty}\bigl\langle I(t)\bigr\rangle \geq \frac{\beta}{ \alpha(\nu+d+r)}(\widetilde{R}-1)>0. \end{aligned}$$

By Lemma 2.4, we know \(\limsup_{t\rightarrow+\infty}I(t) \leq\frac{\Lambda}{d}\), then \(\limsup_{t\rightarrow+\infty}\langle I(t)\rangle\leq\frac{\Lambda}{d}\). Therefore, we get

$$ 0< \frac{\beta}{\alpha(\nu+d+r)}(\widetilde{R}-1)\leq \liminf_{t\rightarrow+\infty}\bigl\langle I(t)\bigr\rangle \leq \limsup_{t\rightarrow+\infty}\bigl\langle I(t)\bigr\rangle \leq\frac{\Lambda }{d}. $$

This completes the proof of Theorem 2.2. □

3 Conclusions and numerical simulations

In this paper, we investigate the stochastic SIRS epidemic model with standard incidence rate and saturated treatment function. We first prove the existence and uniqueness of a global positive solution for the corresponding limiting system (7). Then we investigate the persistence in mean and extinction of the stochastic SIRS epidemic system by using the Lyapunov method and the techniques of a series of stochastic inequalities. The biological significance of our results shows that the ability of the epidemic model to adapt to the external environment disturbance is limited, and the external environment disturbances may have important effect on the stability of the SIRS epidemic system. When the perturbations in the environment are small enough, the stability of the stochastic SIRS epidemic system cannot be destroyed, while large disturbances occurring in the environment can lead to the extinction of epidemic diseases. Therefore, this shows that the environmental distributions are advantageous to controlling infectious diseases. Our results significantly improve and generalize the corresponding results in recent literature. The developed theoretical methods and stochastic inequalities techniques can be applied to explore the high-dimensional nonlinear stochastic differential systems.

Next, we give some numerical simulations to illustrate our theoretical results. The discrete equations of system (7) are described by

$$\begin{aligned}& \begin{aligned} S_{n+1}&=S_{n} + \biggl[ \Lambda-d S_{n}- \frac{d\lambda S_{n}I_{n}}{ \Lambda}+\nu\biggl(\frac{\Lambda}{d}-S_{n}-I_{n} \biggr) \biggr] \Delta t \\ &\quad {}-\sigma_{1}\frac{d S_{n}I_{n}}{\Lambda}\sqrt{\Delta t} W_{1n} - \frac{ \sigma_{1}^{2}}{2}\frac{d S_{n}I_{n}}{\Lambda} \bigl(W_{1n}^{2}-1 \bigr)\Delta t, \end{aligned} \\& \begin{aligned} I_{n+1}&=I_{n} + \biggl[ \frac{d\lambda S_{n}I_{n}}{\Lambda}-(d+r)I_{n}- \frac{ \beta I_{n}}{1+\alpha I_{n}} \biggr] \Delta t \\ &\quad {}+\sigma_{1}\frac{d S_{n}I_{n}}{\Lambda}\sqrt{\Delta t} W_{1n} + \frac{ \sigma_{1}^{2}}{2}\frac{d S_{n}I_{n}}{\Lambda} \bigl(W_{1n}^{2}-1 \bigr)\Delta t \\ &\quad {}-\sigma_{2}\frac{I_{n}}{1+\alpha I_{n}}\sqrt{\Delta t} W_{2n} - \frac{ \sigma_{2}^{2}}{2}\frac{I_{n}}{1+\alpha I_{n}}\bigl(W_{2n}^{2}-1\bigr) \Delta t, \end{aligned} \end{aligned}$$

where \(W_{1n}\), \(W_{2n}\), \(n=1,2,\ldots\) , are independent Gaussian random variables \(N(0, 1)\). Here, we let \(\Delta t=0.01\).

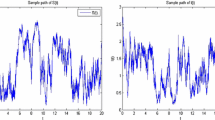
In the following figures, we let \(S(0)=0.1\), \(I(0)=0.1\), \(\alpha=0.3\), \(\beta=0.01\), \(\lambda=0.7\), \(d=0.5\), \(\Lambda=0.1\), \(r=0.07\), \(\nu=0.5\), and the step size \(\Delta t=0.01\).

Figure 1(a) is the deterministic model of stochastic system (7) with \(\sigma_{1}=\sigma_{2}=0\). Figure 1(b) shows the stochastic epidemic system (7) with \(\sigma_{1}=0.7\) and \(\sigma_{2}=0.1\). By computation, we get that

$$ R_{1}=\frac{\lambda^{2}}{2(d+r)\sigma_{1}^{2}}+\frac{\beta^{2}}{2(d+r) \sigma_{2}^{2}}=0.886< 1, \quad\quad \lim_{t\rightarrow+\infty}S(t)=\frac{ \Lambda}{d}=0.2, \quad\quad \lim _{t\rightarrow+\infty}I(t)=0, $$

which satisfy case (i) of Theorem 2.1. For Figure 2(a) with \(\sigma_{1}=0.5\) and \(\sigma_{2}=0.2\), we get that

$$\begin{aligned}& \lambda=0.7\geq0.25=0.5^{2}=\sigma_{1}^{2}, \\& R_{2}=\frac{2(\lambda -d-r)(d+\alpha\Lambda)^{2}}{\sigma_{1}^{2} (d+\alpha\Lambda)^{2}+d ^{2}\sigma_{2}^{2}}-\frac{2d\beta(d+\alpha\Lambda)}{\sigma_{1}^{2}(d+ \alpha\Lambda)^{2}+d^{2}\sigma_{2}^{2}}=0.8443< 1, \end{aligned}$$

and

$$ \lim_{t\rightarrow+\infty}S(t)=\frac{\Lambda}{d}=0.2,\quad\quad \lim _{t\rightarrow+\infty}I(t)=0, $$

which satisfy case (ii) of Theorem 2.1. For Figure 2(b) with \(\sigma_{1}=0.85\) and \(\sigma_{2}=0.3\), we get that

$$\begin{aligned}& \lambda=0.7< 0.7225=0.85^{2}=\sigma_{1}^{2}, \\& R_{3}=\frac{\lambda^{2}(d+\alpha\Lambda)}{2\sigma_{1}^{2}[d\beta+(d+r)(d+ \alpha\Lambda)]}-\frac{d^{2}\sigma_{2}^{2}}{2[d\beta(d+\alpha \Lambda)+(d+r) (d+\alpha\Lambda)^{2}]}=0.5161< 1, \end{aligned}$$

and

$$ \lim_{t\rightarrow+\infty}S(t)=\frac{\Lambda}{d}=0.2,\quad\quad \lim _{t\rightarrow+\infty}I(t)=0, $$

which satisfy case (iii) of Theorem 2.1. For Figure 3(a) with \(\sigma_{1}=0.7\) and \(\sigma_{2}=0.3\), we get that

$$ \lambda=0.7\geq0.49=0.7^{2}=\sigma_{1}^{2},\quad \quad R_{4}=\frac {2\lambda }{\sigma_{1}^{2}+2(d+r)}+\frac{\beta^{2}}{\sigma_{2}^{2}[\sigma_{1} ^{2}+2(d+r)]}=0.85958< 1, $$

and

$$ \lim_{t\rightarrow+\infty}S(t)=\frac{\Lambda}{d}=0.2,\quad\quad \lim _{t\rightarrow+\infty}I(t)=0, $$

which satisfy case (iv) of Theorem 2.1.

Figure 1
figure 1

Time sequence diagram: (a) the deterministic epidemic model, (b) the stochastic epidemic system (7) for case (i) of Theorem 2.1

Full size image
Figure 2
figure 2

Time sequence diagram of stochastic system (7): (a) case (ii) of Theorem 2.1, (b) case (iii) of Theorem 2.1

Full size image
Figure 3
figure 3

Time sequence diagram of stochastic system (7): (a) case (iv) of Theorem 2.1, (b) case of Theorem 2.2

Full size image

According to Figures 1(b), 2(a), 2(b) and 3(a), the disease \(I(t)\) in the stochastic epidemic system (7) is extinct. Comparing Figure 1(a) with Figures 1(b), 2(a), 2(b) and 3(a), we can see that when the environmental fluctuations are large enough, they can lead to the extinction of disease. Thus, the random fluctuations are beneficial to the control of epidemic diseases. This is consistent with our conclusion in Theorem 2.1.

For Figure 3(b), we let \(\sigma_{1}=\sigma_{2}=0.03\). By computation, we get that

$$ \frac{d\lambda}{\alpha\Lambda}=11.6\geq1=d+\nu, \quad\quad \widetilde{R}= \frac{ \alpha\Lambda(d+\nu)[2\lambda-2d-2r -(\sigma_{1}^{2}+\sigma_{2} ^{2})]}{2d\beta\lambda}=1.10657>1, $$

which satisfies the conditions of Theorem 2.2. Comparing Figure 1(a) with Figure 3(b), when the white noises are small, the stochastic epidemic system (7) is persistent in mean. This is consistent with our conclusion in Theorem 2.2.

Obviously, the numerical simulation results are consistent with the conclusions of our theorems.

To sum up, our main results are summarized as follows:

  1. I.

    Extinction

    When one of the following conditions holds:

    1. (i)

      \(R_{1}=\frac{\lambda^{2}}{2(d+r)\sigma_{1}^{2}}+\frac{ \beta^{2}}{2(d+r) \sigma_{2}^{2}}< 1\),

    2. (ii)

      \(\lambda\geq\sigma_{1}^{2}\) and \(R_{2}=\frac{2(\lambda-d-r)(d+\alpha\Lambda)^{2}}{\sigma_{1}^{2} (d+ \alpha\Lambda)^{2}+d^{2}\sigma_{2}^{2}}-\frac{2d\beta(d+\alpha \Lambda)}{\sigma_{1}^{2}(d+\alpha\Lambda)^{2}+d^{2}\sigma_{2}^{2}}< 1\),

    3. (iii)

      \(\lambda< \sigma_{1}^{2}\) and \(R_{3}=\frac{\lambda ^{2}(d+\alpha\Lambda)}{2\sigma_{1}^{2}[d\beta+(d+r)(d+\alpha \Lambda)]}-\frac{d^{2}\sigma_{2}^{2}}{2[d\beta(d+\alpha\Lambda)+(d+r) (d+\alpha\Lambda)^{2}]}< 1\),

    4. (iv)

      \(\lambda\geq\sigma_{1}^{2}\) and \(R_{4}=\frac{2 \lambda}{\sigma_{1}^{2}+2(d+r)}+\frac{\beta^{2}}{\sigma_{2}^{2}[ \sigma_{1}^{2}+2(d+r)]}<1\),

    then

    $$ \lim_{t\rightarrow+\infty}S(t)=\frac{\Lambda}{d},\quad\quad \lim _{t\rightarrow+\infty}I(t)=0. $$
  2. II.

    Persistence in mean

    When both conditions \(\frac{d\lambda}{\alpha\Lambda}\geq d+\nu\) and

    $$ \widetilde{R}=\frac{\alpha\Lambda(d+\nu)[2\lambda-2d-2r -(\sigma _{1}^{2}+\sigma_{2}^{2})]}{2d\beta\lambda}>1 $$

    hold, then the epidemic disease \(I(t)\) is persistent in mean; in other words,

    $$ 0< \frac{\beta}{\alpha(\nu+d+r)}(\widetilde{R}-1)\leq \liminf_{t\rightarrow+\infty}\bigl\langle I(t)\bigr\rangle \leq \limsup_{t\rightarrow+\infty}\bigl\langle I(t)\bigr\rangle \leq\frac{\Lambda }{d}. $$