1 Introduction

Recently, the following nonlinear density-dependent mortality Nicholson’s blowflies system with patch structure:

$$\begin{aligned} x_{i }'(t) =&-a_{ii}(t)+b_{ii}(t)e^{-x_{i }(t)}+ \sum_{j=1,j \neq i}^{n} \bigl(a_{ij}(t)-b_{ij}(t)e^{-x_{j}(t)} \bigr) \\ &{}+\sum_{j=1}^{m}\beta _{ij}(t)x_{i} \bigl(t-\tau _{ij}(t) \bigr)e^{- \gamma _{ij}(t)x_{i}(t-\tau _{ij}(t))}, \quad i \in Q:=\{1,2,\ldots ,n\}, \end{aligned}$$
(1.1)

has been used in [1, 2] to describe the dynamics of recruitment-delayed model with the Rickers-type birth function and the harvesting strategy Type II (cyrtoid). In the ith patch, \(a_{ii}(t)-b_{ii}(t)e^{-x_{i }(t)}\) is a nonlinear density-dependent mortality term which represents the death rate of the current population level \(x_{i }(t)\); the birth rate function \(\beta _{ij}(t)x_{i}(t-\tau _{ij}(t))e^{-\gamma _{ij}(t)x _{i}(t-\tau _{ij}(t))}\) depends on maturation delays \(\tau _{ij}(t)\) and the maximum reproduction rate \(\frac{1}{\gamma _{ij}(t)}\); for \(i, j\in Q\) and \(j\neq i\), \(a_{ij}(t)-b_{ij}(t)e^{-x_{j}(t)} \) denote cooperative connection weights of the populations ith and jth patch [2–6].

Because the almost-periodic oscillation is an important dynamic characteristic in population dynamics, more attention has been paid to the almost-periodic problems for delayed Nicholson’s blowflies equation and and its variants [7–9]. Furthermore, a recent study in [10] established the existence and global stability of almost-periodic solutions for Nicholson’s blowflies system (1.1) involving a positive constant \(M>\kappa \) obeying

$$\begin{aligned}& \gamma _{ij} (t ) M \leq \widetilde{\kappa } , \quad \mbox{for all } t \in \mathbb{R}, i\in Q, j\in I=\{1,2,\ldots ,m\}, \end{aligned}$$
(1.2)
$$\begin{aligned}& \sup_{t\in \mathbb{R}} \Biggl\{ -a_{ii}(t)+b_{ii}(t)e^{-M}+ \sum_{j=1,j\neq i}^{n}a_{ij}(t) + \sum_{j=1}^{m} \frac{\beta _{ij}(t)}{\gamma _{ij}(t)} \frac{1}{e} \Biggr\} < 0, \end{aligned}$$
(1.3)
$$\begin{aligned}& \inf_{t\in \mathbb{R},s\in [0,\kappa ]} \Biggl\{ -a_{ii}(t)+b_{ii}(t)e ^{-s} +\sum_{j=1,j\neq i}^{n} \bigl(a_{ij}(t)-b_{ij}(t) \bigr) +\sum _{j=1}^{m}\frac{\beta _{ij}(t)}{\gamma _{ij}(t)}se^{-s} \Biggr\} >0, \end{aligned}$$
(1.4)
$$\begin{aligned}& \sup_{t\in \mathbb{R}} \Biggl\{ -b_{ii}(t)e^{-M} +\sum_{j=1,j \neq i}^{n}b_{ij}(t)e^{-\kappa }+ \frac{1}{e^{2}}\sum_{j=1}^{m} \beta _{ij}(t) \Biggr\} < 0, \end{aligned}$$
(1.5)

where

$$ \kappa \in (0, 1),\qquad \frac{1-\kappa }{e^{\kappa }}=\frac{1}{e^{2}},\qquad \widetilde{\kappa }\in (1, +\infty ), \qquad \kappa e^{-\kappa }= \widetilde{\kappa } e^{-\tilde{\kappa }},\qquad i\in Q . $$
(1.6)

Alas, the additional assumptions (1.2)–(1.5) are all defined on \(\mathbb{R}\), which are evidently not in accord with the biological interpretation in the considered systems. Apparently, according to the biological background of (1.2) in [8, 9], one needs to relax the above additional assumptions as follows:

$$\begin{aligned}& M \limsup_{t\rightarrow +\infty } \gamma _{ij} (t ) \leq \widetilde{\kappa } , \end{aligned}$$
(1.7)
$$\begin{aligned}& \sup_{t\in [t_{0}, + \infty )} \Biggl\{ -a_{ii}(t)+b_{ii}(t)e^{-M}+ \sum_{j=1,j\neq i}^{n}a_{ij}(t)+ \sum_{j=1}^{m} \frac{ \beta _{ij}(t)}{\gamma _{ij}(t)} \frac{1}{e} \Biggr\} < 0, \end{aligned}$$
(1.8)
$$\begin{aligned}& \inf_{ s\in [0,\kappa ]}\liminf_{t \rightarrow + \infty } \Biggl\{ -a_{ii}(t)+b_{ii}(t)e^{-s} +\sum _{j=1,j\neq i}^{n} \bigl(a_{ij}(t)-b _{ij}(t) \bigr) +\sum_{j=1}^{m} \frac{\beta _{ij}(t)}{\gamma _{ij}(t)}se ^{-s} \Biggr\} >0, \end{aligned}$$
(1.9)
$$\begin{aligned}& \lim \sup_{t\rightarrow +\infty } \Biggl\{ -b_{ii}(t)e^{-M}+ \sum_{j=1,j\neq i}^{n}b_{ij}(t)e^{-\kappa } +\frac{1}{e^{2}} \sum_{j=1}^{m} \beta _{ij}(t) \Biggr\} < 0, \end{aligned}$$
(1.10)

for all \(i\in Q \), \(j\in I\).

Inspired by the above analysis, in this paper, under the weaker assumptions (1.7)–(1.10), we develop a novel approach to demonstrate the global stability of positive asymptotically almost-periodic solutions for system (1.1).

This paper is organized as follows: In Sect. 2, some necessary preparations are provided. In Sect. 3, the existence and global convergence of asymptotically almost-periodic solutions are demonstrated by developing an approach based on differential inequality techniques coupled with the Lyapunov function method. To verify our theoretical findings, a numerical experiment is carried out in Sect. 4. And concluding remarks are stated in Sect. 5.

2 Preliminary results

Notations

\(\mathbb{R}^{+}=[0, +\infty )\), and \(C_{+}= \prod_{i=1}^{n}C([-\sigma _{i}, 0], \mathbb{R} ^{+})\). For \(\mathbb{J} ,\mathbb{J}_{1}, \mathbb{J}_{2}\subseteq \mathbb{R}\), define

$$ W_{0} \bigl(\mathbb{R}^{+}, \mathbb{J} \bigr)= \Bigl\{ \nu :\nu \in C \bigl(\mathbb{R}^{+}, \mathbb{J} \bigr), \lim _{t\rightarrow +\infty }\nu (t)=0 \Bigr\} , $$

and let \(\operatorname{BC}(\mathbb{J}_{1},\mathbb{J}_{2} )\) be the set of bounded and continuous functions from \(\mathbb{J}_{1}\) to \(\mathbb{J}_{2} \). Also, we label the set of all almost-periodic functions from \(\mathbb{R}\) to \(\mathbb{J} \) by \(\operatorname{AP}(\mathbb{R},\mathbb{J} )\). The collection of the asymptotically almost-periodic functions will be labeled by \(\operatorname{AAP}(\mathbb{R},\mathbb{J} )\). For more details on the above definitions, we refer the readers to [8, 9, 11, 12].

It will be supposed that

$$ \sigma _{i}=\max_{ j\in I}{\sup _{t\in \mathbb{R}}\tau _{ij}(t)}>0,\qquad \liminf _{t\rightarrow +\infty }\gamma _{ij}(t) \geq 1,\quad i \in Q, j\in I $$
(2.1)

which is a weaker condition than the \(\inf_{t\in \mathbb{R}} \gamma _{ij}(t) \geq 1\) adopted in [7, 10]. For \(x=(x_{1},\ldots ,x _{n}) \in \mathbb{R}^{n}\), define \(|x|=(|x_{1}|,\ldots ,|x_{n}|) \) and \(\|x\|=\max_{ i\in Q}|x_{i}|\).

Throughout this paper, we assume that \(a_{ii}, b_{ii}, \gamma _{ ij} \in \operatorname{AAP}(\mathbb{R}, (0, +\infty )) \), \(a_{ij}\ (i \neq j), b_{ij}\ (i\neq j)\), \(\beta _{ ij}, \tau _{ ij} \in \operatorname{AAP}(\mathbb{R}, \mathbb{R}^{+})\) and

$$ a_{ ij} =a ^{h}_{ ij}+a ^{g}_{ ij} ,\qquad b _{ ij}=b ^{h}_{ ij}+b ^{g}_{ ij},\qquad \beta _{ ij}=\beta _{ ij}^{h}+\beta _{i j}^{g},\qquad \gamma _{ ij}=\gamma _{ ij} ^{h}+\gamma _{ ij}^{g}, \qquad \tau _{ ij}=\tau _{ ij}^{h}+\tau _{i j}^{g} , $$

where \(a_{ii}^{h}, b_{ii}^{h}, \gamma _{ ij}^{h} \in \operatorname{AP}( \mathbb{R}, (0, +\infty )) \), \(a_{ij}^{h}\ (i\neq j), b_{ij}^{h}\ (i \neq j), \beta _{ ij}^{h}, \tau _{ ij}^{h} \in \operatorname{AP}( \mathbb{R}, \mathbb{R}^{+}) \), \(a^{g}_{ij}, b^{g}_{ij}, \beta _{ ij}^{g}, \gamma _{i j}^{g}, \tau _{i j}^{g}\in W _{0}(\mathbb{R}^{+}, \mathbb{R}^{+} )\), and \(i\in Q\), \(j\in I\).

In what follows, we need to set up a nonlinear almost-periodic differential system:

$$\begin{aligned} x_{i }'(t) =&-a_{ii}^{h}(t)+b^{h}_{ii}(t)e^{-x_{i }(t)}+ \sum_{j=1,j\neq i}^{n} \bigl(a_{ij}^{h}(t)-b_{ij}^{h}(t)e^{-x_{j}(t)} \bigr) \\ &{}+\sum_{j=1}^{m}\beta _{ij}^{h}(t)x_{i} \bigl(t-\tau _{ij}^{h}(t) \bigr)e ^{-\gamma _{ij}^{h}(t)x_{i}(t-\tau _{ij}^{h}(t))},\quad i \in Q . \qquad (1.1)^{h} \end{aligned}$$

With the biological meaning in mind, we consider the initial condition:

$$ x_{i}(t_{0}+\theta ) =\varphi _{i}( \theta ), \quad \theta \in [-\sigma _{i}, 0], \varphi =(\varphi _{1},\ldots ,\varphi _{n} ) \in C_{+} \quad \mbox{and}\quad \varphi _{i}(0)>0,\quad i \in Q. $$
(2.2)

Lemma 2.1

Let \(x(t; t_{0}, \varphi )\)be a solution of the initial value problem \((1.1)^{h}\)and (2.2). Assume that there exists a positive constant \(M>\kappa \)such that (1.7), (1.9) and

$$ \sup_{t\in [t_{0}, + \infty )} \Biggl\{ -a_{ii}^{h}(t)+b_{ii}^{h}(t)e ^{-M} +\sum_{j=1,j\neq i}^{n}a_{ij}^{h}(t)+ \sum_{j=1} ^{m} \frac{\beta _{ij}^{h}(t)}{\gamma _{ij}^{h}(t)} \frac{1}{e} \Biggr\} < 0,\quad i \in Q, $$
(2.3)

hold. Then, \(x (t )=x(t; t_{0}, \varphi )\)exists on \([t_{0}, + \infty )\), and there is a \(t _{\varphi }\in [t_{0}, +\infty )\)such that

$$ \kappa < x_{i} (t ) < M \quad \textit{for all } t\in [t _{\varphi }, +\infty ), i\in Q. $$
(2.4)

Proof

First, we state that

$$ x_{i}(t)>0 \quad \mbox{for all } t\in \bigl[t_{0}, \eta ( \varphi ) \bigr), i \in Q, $$
(2.5)

where \([t_{0},\eta (\varphi ))\) is the maximal right existence interval of \(x(t )\). Suppose that, on the contrary, we can take \(i_{0}\in Q\) and \(\bar{t }_{i_{0}}\in (t_{0}, \eta (\varphi ))\) such that

$$ x_{i_{0}}(\bar{t }_{i_{0}})=0,\qquad x_{j}(t)>0 \quad \mbox{for all } t\in [t_{0} , \bar{t}_{i_{0}}), j \in Q . $$

Apparently, \((1.1)^{h}\) and (2.3) yield

$$\begin{aligned} 0 \geq &x_{i_{0}}'(\bar{t }_{i_{0}}) \\ = &-a_{i_{0}i_{0}}^{h}(\bar{t }_{i_{0}})+b_{i_{0}i_{0}}^{h}( \bar{t } _{i_{0}})e^{-x_{i_{0}}(\bar{t }_{i_{0}})} +\sum _{j=1,j\neq i _{0}}^{n} \bigl(a_{i_{0}j}^{h}( \bar{t }_{i_{0}})-b_{i_{0}j}^{h}( \bar{t } _{i_{0}})e^{-x_{j}(\bar{t }_{i_{0}})} \bigr) \\ &{}+\sum_{j=1}^{m}\beta _{ i_{0}j}^{h}(\bar{t }_{i_{0}})x_{i _{0}} \bigl(\bar{t }_{i_{0}}-\tau _{i_{0}j}^{h}(\bar{t }_{i_{0}}) \bigr)e^{- \gamma _{i_{0}j}^{h}(\bar{t }_{i_{0}}) x_{i_{0}}(\bar{t }_{i_{0}}- \tau _{i_{0}j}^{h}(\bar{t }_{i_{0}}))} \\ \geq &-a_{i_{0}i_{0}}^{h}(\bar{t }_{i_{0}})+b_{i_{0}i_{0}}^{h}( \bar{t }_{i_{0}}) +\sum_{j=1,j\neq i_{0}}^{n} \bigl(a_{i_{0}j}^{h}(\bar{t } _{i_{0}})-b_{i_{0}j}^{h}( \bar{t }_{i_{0}}) \bigr) \\ > & 0, \end{aligned}$$

a contradiction. This yields the stated results.

Now, we demonstrate that \(x(t)\) is bounded on \([t_{0},\eta (\varphi ))\). For \(t\in [t_{0}-\sigma _{i},\eta (\varphi )) \) and \(i\in Q\), we define

$$ M_{i}(t)=\max \Bigl\{ \xi :\xi \leq t, x_{i}(\xi )= \max_{t_{0}-\sigma _{i}\leq s\leq t}x_{i}(s) \Bigr\} . $$

Suppose that \(x (t)\) is unbounded on \([t_{0},\eta (\varphi ))\). Then, we can choose \(i^{*}\in Q\) and a strictly monotone increasing sequence \(\{\zeta _{n}\}_{n=1}^{+\infty }\) such that

$$ \textstyle\begin{cases} x_{i^{*}}(M_{i^{*}}(\zeta _{n}))=\max_{j\in Q}\{x_{j}(M_{j}( \zeta _{n}))\}, \\ \lim_{n\rightarrow +\infty } x_{i^{*}}(M_{i^{*}}(\zeta _{n}))=+ \infty ,\qquad \lim_{n\rightarrow +\infty }\zeta _{n} =\eta (\varphi ) , \end{cases} $$
(2.6)

and then

$$ \lim_{n\rightarrow +\infty }M_{i^{*}}(\zeta _{n}) =\eta (\varphi) . $$

By virtue of the fact that \(\sup_{u\geq 0}ue^{-u}=\frac{1}{e}\), it follows from \((1.1)^{h}\) and (2.6) that

$$\begin{aligned} 0 \leq &x_{i^{*}}' \bigl(M_{i^{*}}(\zeta _{n}) \bigr) \\ = &-a_{ i^{*} i^{*} }^{h} \bigl(M_{i^{*}}(\zeta _{n}) \bigr)+b_{i^{*} i^{*}}^{h} \bigl(M _{i^{*}}(\zeta _{n}) \bigr)e^{-x_{i^{*}}(M_{i^{*}}(\zeta _{n}))} \\ &{}+\sum_{j=1,j\neq i^{*} }^{n} \bigl(a_{ i^{*} j}^{h} \bigl(M_{i^{*}}( \zeta _{n}) \bigr)-b_{ i^{*} j}^{h} \bigl(M_{i^{*}}(\zeta _{n}) \bigr)e^{-x_{j}(M_{i^{*}}( \zeta _{n}))} \bigr) \\ &{}+\sum_{j=1}^{m} \frac{\beta _{i^{*}j}^{h}(M_{i^{*}}(\zeta _{n}))}{\gamma _{i^{*}j}^{h}(M_{i^{*}}(\zeta _{n}))} \gamma _{i^{*}j} ^{h} \bigl(M_{i^{*}}(\zeta _{n}) \bigr) x_{i^{*}} \bigl(M_{i^{*}}(\zeta _{n})-\tau _{i^{*}j} ^{h} \bigl(M_{i^{*}}(\zeta _{n}) \bigr) \bigr) \\ &{} \times e^{-\gamma _{i^{*}j}^{h}(M_{i^{*}}(\zeta _{n})) x_{i^{*}}(M _{i^{*}}(\zeta _{n})-\tau _{i^{*}j}^{h}(M_{i^{*}}(\zeta _{n})))} \\ \leq &-a_{ i^{*} i^{*} }^{h} \bigl(M_{i^{*}}(\zeta _{n}) \bigr)+b_{i^{*} i^{*}} ^{h} \bigl(M_{i^{*}}(\zeta _{n}) \bigr)e^{-x_{i^{*}}(M_{i^{*}}(\zeta _{n}))} \\ &{} +\sum_{j=1,j\neq i^{*} }^{n} \bigl(a_{ i^{*} j}^{h} \bigl(M_{i^{*}}( \zeta _{n}) \bigr)-b_{ i^{*} j}^{h} \bigl(M_{i^{*}}( \zeta _{n}) \bigr)e^{-x_{i^{*}}(M_{i ^{*}}(\zeta _{n}))} \bigr) \\ &{}+\sum_{j=1}^{m} \frac{\beta _{i^{*}j}^{h}(M_{i^{*}}(\zeta _{n}))}{\gamma _{i^{*}j}^{h}(M_{i^{*}}(\zeta _{n}))}\frac{1}{e} ,\quad \mbox{for all } M_{i^{*}}(\zeta _{n})>t_{0}. \end{aligned}$$

According to (2.3), taking \(n\rightarrow +\infty \) leads to

$$\begin{aligned} 0 \leq & \lim_{n \rightarrow +\infty } \Biggl[ -a_{ i^{*} i^{*} }^{h} \bigl(M _{i^{*}}(\zeta _{n}) \bigr) +\sum _{j=1,j\neq i^{*} }^{n} a_{ i^{*} j} ^{h} \bigl(M_{i^{*}}(\zeta _{n}) \bigr) + \sum _{j=1}^{m}\frac{\beta _{i^{*}j} ^{h}(M_{i^{*}}(\zeta _{n}))}{\gamma _{i^{*}j}^{h}(M_{i^{*}}(\zeta _{n}))} \frac{1}{e} \Biggr] \\ \leq & \sup_{ t\in [t_{0}, + \infty )} \Biggl[ -a_{ i^{*} i^{*} } ^{h}(t) +\sum_{j=1,j\neq i^{*} }^{n} a_{ i^{*} j}^{h}(t) + \sum_{j=1}^{m} \frac{\beta _{i^{*}j}^{h}(t)}{\gamma _{i^{*}j}^{h}(t)}\frac{1}{e} \Biggr] \\ < &0, \end{aligned}$$

which is absurd and implies that \(x(t)\) is bounded on \([t_{0},\eta ( \varphi ))\). By Theorem 2.3.1 in [13], we easily show \(\eta (\varphi )=+\infty \).

Next, we validate that (2.4) is true. Designate \(i^{l}, i^{L}\in Q\) such that

$$ l=\liminf_{t\rightarrow +\infty }x_{i^{l}}(t)=\min _{i \in Q}\liminf_{t\rightarrow +\infty }x _{i}(t ), \qquad L= \limsup_{t\rightarrow +\infty }x_{i^{L}}(t)= \max_{i \in Q}\limsup_{t\rightarrow +\infty }x _{i}(t ). $$

By the fluctuation lemma [14, Lemma A.1], we can select two sequences \(\{t_{k}^{*}\}_{k=1}^{+\infty }\) and \(\{t_{k}^{**}\}_{k=1}^{+\infty }\) satisfying

$$ \lim_{k\rightarrow +\infty }t_{k}^{*}= +\infty , \qquad \lim_{k\rightarrow +\infty }x_{i^{l}} \bigl(t_{k}^{*} \bigr) = l ,\quad \mbox{and}\quad \lim_{k\rightarrow +\infty }x'_{i^{l}} \bigl(t_{k}^{*} \bigr) = 0, $$
(2.7)

and

$$ \lim_{k\rightarrow +\infty }t_{k}^{**}= +\infty , \qquad \lim_{k\rightarrow +\infty }x _{i^{L}} \bigl(t_{k}^{**} \bigr) = L , \quad \mbox{and}\quad \lim_{k\rightarrow +\infty } x' _{i^{L}} \bigl(t_{k}^{**} \bigr) = 0, $$
(2.8)

respectively. From the almost-periodicity of \((1.1)^{h}\), we can take a subsequence of \(\{ k \}_{k\geq 1} \), still denoted by \(\{ k \}_{k \geq 1} \), such that

$$\begin{aligned}& \lim_{k \rightarrow + \infty } a_{i^{l}j} ^{h} \bigl(t_{k}^{*} \bigr) ,\qquad \lim _{k \rightarrow + \infty } b_{i^{l}j} ^{h} \bigl(t_{k}^{*} \bigr) , \qquad \lim _{k \rightarrow + \infty } \beta _{i ^{l}q} ^{h} \bigl(t_{k}^{*} \bigr) ,\qquad \lim _{k \rightarrow + \infty } \gamma _{i^{l}q} ^{h} \bigl(t_{k}^{*}\bigr) , \\& \lim_{k \rightarrow + \infty } x_{j}\bigl(t_{k}^{*} \bigr) ,\qquad \lim_{k \rightarrow + \infty } x_{i^{l}}\bigl(t_{k}^{*}- \tau _{i^{l} q} ^{h} \bigl(t_{k}^{*} \bigr)\bigr) , \qquad \lim_{k \rightarrow + \infty } a_{i ^{L}j} ^{h}\bigl(t_{k}^{**}\bigr) , \qquad \lim _{k \rightarrow + \infty } b _{i^{L}j}^{h} \bigl(t_{k}^{**}\bigr) , \\& \lim_{k \rightarrow + \infty } \beta _{i^{L}q} ^{h}\bigl(t_{k}^{**} \bigr) , \qquad \lim_{k \rightarrow + \infty } \gamma _{i^{L}q}^{h} \bigl(t_{k}^{**}\bigr) , \qquad \lim_{k \rightarrow + \infty } x_{j}\bigl(t_{k}^{**} \bigr) \quad \mbox{and} \quad \lim_{k \rightarrow + \infty } x_{i^{L}} \bigl(t_{k}^{**}- \tau _{i^{L} q}^{h} \bigl(t_{k}^{**}\bigr)\bigr) \end{aligned}$$

exist for all \(j\in Q\), \(q\in I\). Furthermore, by taking limits, we have from (2.3) and (2.8) that

$$\begin{aligned}& \sup_{t\in [t_{0}, + \infty )} \Biggl\{ -a_{i^{L}i^{L}}^{h}(t)+b _{i^{L}i^{L}}^{h}(t)e^{-M} +\sum _{j=1,j\neq i^{L}}^{n}a_{i^{L}j} ^{h}(t) +\sum_{j=1}^{m} \frac{\beta _{i^{L}j}^{h}(t)}{ \gamma _{i^{L}j}^{h}(t)}\frac{1}{e} \Biggr\} \\& \quad < 0 \\& \quad = \lim_{k \rightarrow + \infty }x_{i^{L}}' \bigl(t_{k}^{**} \bigr) \\& \quad = -\lim_{k \rightarrow + \infty }a_{i^{L} i^{L}}^{h} \bigl(t_{k} ^{**} \bigr) +\lim_{k \rightarrow + \infty }b_{i^{L} i^{L}}^{h} \bigl(t _{k}^{**} \bigr)e^{-L} \\& \qquad {} +\sum_{j=1,j\neq i^{L} }^{n} \Bigl(\lim _{k \rightarrow + \infty }a_{ i^{L} j}^{h} \bigl(t_{k}^{**} \bigr) - \lim_{k \rightarrow + \infty }b_{ i^{L} j}^{h} \bigl(t_{k}^{**} \bigr)e ^{-\lim _{k \rightarrow + \infty } x_{j}(t_{k}^{**} ) } \Bigr) \\& \qquad {} + \sum_{j=1}^{m}\lim _{k \rightarrow + \infty }\frac{ \beta _{i^{L}j}^{h}(t_{k}^{**})}{\gamma _{i^{L}j}^{h}(t_{k}^{**})} \lim_{k \rightarrow + \infty } \gamma _{i^{L}j}^{h} \bigl(t_{k}^{**} \bigr) x _{i^{L}} \bigl(t_{k}^{**}-\tau _{i^{L}j}^{h} \bigl(t_{k}^{**} \bigr) \bigr) \\& \qquad {} \times e^{-\lim _{k \rightarrow + \infty }\gamma _{i^{L}j} ^{h}(t_{k}^{**})\lim _{k \rightarrow + \infty }x_{i^{L}}(t_{k} ^{**}-\tau _{i^{L}j}^{h}(t_{k}^{**}))} \\& \quad \leq -\lim_{k \rightarrow + \infty }a_{i^{L} i^{L}}^{h} \bigl(t _{k}^{**} \bigr) +\lim_{k \rightarrow + \infty }b_{i^{L} i^{L}}^{h} \bigl(t _{k}^{**} \bigr)e^{-L} \\& \qquad {} +\sum_{j=1,j\neq i^{L} }^{n} \Bigl(\lim _{k \rightarrow + \infty }a_{ i^{L} j}^{h} \bigl(t_{k}^{**} \bigr) - \lim_{k \rightarrow + \infty }b_{ i^{L} j}^{h} \bigl(t_{k}^{**} \bigr)e ^{-L} \Bigr)+ \sum _{j=1}^{m}\lim_{k \rightarrow + \infty } \frac{ \beta _{i^{L}j}^{h}(t_{k}^{**})}{\gamma _{i^{L}j}^{h}(t_{k}^{**})} \frac{1}{e} \\& \quad \leq \lim_{k \rightarrow + \infty } \Biggl[ -a_{i^{L} i^{L}}^{h} \bigl(t _{k}^{**} \bigr) + b_{i^{L} i^{L}}^{h} \bigl(t_{k}^{**} \bigr)e^{-L} +\sum _{j=1,j\neq i^{L} }^{n} a_{ i^{L} j}^{h} \bigl(t_{k}^{**} \bigr) + \sum _{j=1}^{m} \frac{\beta _{i^{L}j}^{h}(t_{k}^{**})}{\gamma _{i^{L}j} ^{h}(t_{k}^{**})} \frac{1}{e} \Biggr] \\& \quad \leq \sup_{t\in [t_{0}, + \infty )} \Biggl\{ -a_{i^{L}i^{L}}^{h}(t)+b _{i^{L}i^{L}}^{h}(t)e^{-L} +\sum _{j=1,j\neq i^{L}}^{n}a_{i^{L}j} ^{h}(t) +\sum_{j=1}^{m} \frac{\beta _{i^{L}j}^{h}(t)}{ \gamma _{i^{L}j}^{h}(t)}\frac{1}{e} \Biggr\} , \end{aligned}$$

which entails that

$$ \textstyle\begin{cases} L< M,\qquad l\leq \lim_{k \rightarrow + \infty } x_{j}(t_{k}^{*} )< M, \\ l\leq \lim_{k \rightarrow + \infty } \gamma _{i^{l}q}^{h} (t _{k}^{*})\lim_{k \rightarrow + \infty } x_{i^{l}}(t_{k}^{*}- \tau _{i^{l} q} (t_{k}^{*}))\leq \widetilde{\kappa } , \end{cases}\displaystyle \quad \mbox{where } j\in Q, q\in I. $$
(2.9)

Next, we show that \(l>\kappa \). By way of contradiction, we assume that \(0\leq l \leq \kappa \). With the help of (1.6), (1.9), (2.7), and (2.9), we gain

$$\begin{aligned} 0 =&\lim_{k \rightarrow + \infty }x_{i^{l}}' \bigl(t_{k}^{*} \bigr) \\ \geq & -\lim_{k \rightarrow + \infty }a_{i^{l} i^{l}}^{h} \bigl(t _{k}^{*} \bigr) +\lim_{k \rightarrow + \infty }b_{i^{l} i^{l}}^{h} \bigl(t _{k}^{*} \bigr)e^{-l} +\sum _{j=1,j\neq i^{l} }^{n} \Bigl(\lim _{k \rightarrow + \infty }a_{ i^{l} j}^{h} \bigl(t_{k}^{*} \bigr) -\lim_{k \rightarrow + \infty }b_{ i^{l} j}^{h} \bigl(t_{k}^{*} \bigr)e^{-l} \Bigr) \\ &{}+ \sum_{j=1}^{m} \frac{\lim_{k \rightarrow + \infty } \beta _{i^{l}j}^{h}(t_{k}^{* })}{\lim_{k \rightarrow + \infty } \gamma _{i^{l}j}^{h}(t_{k}^{*})} \lim_{k \rightarrow + \infty } \gamma _{i^{l}j} ^{h} \bigl(t_{k}^{*} \bigr) x_{i^{l}} \bigl(t_{k}^{*}-\tau _{i^{l} j} ^{h} \bigl(t_{k}^{*} \bigr) \bigr)e^{- \lim _{k \rightarrow + \infty } \gamma _{i^{l}j} ^{h} (t_{k}^{*}) x_{i^{l}}(t_{k}^{*}-\tau _{i^{l} j} ^{h} (t_{k}^{*}))} \\ \geq & -\lim_{k \rightarrow + \infty }a_{i^{l} i^{l}}^{h} \bigl(t _{k}^{*} \bigr) +\lim_{k \rightarrow + \infty }b_{i^{l} i^{l}}^{h} \bigl(t _{k}^{*} \bigr)e^{-l} +\sum _{j=1,j\neq i^{l} }^{n} \Bigl(\lim _{k \rightarrow + \infty }a_{ i^{l} j}^{h} \bigl(t_{k}^{*} \bigr) -\lim_{k \rightarrow + \infty }b_{ i^{l} j}^{h} \bigl(t_{k}^{*} \bigr)e^{-l} \Bigr) \\ &{}+ \sum_{j=1}^{m} \frac{\lim_{k \rightarrow + \infty } \beta _{i^{l}j}^{h}(t_{k}^{* })}{\lim_{k \rightarrow + \infty } \gamma _{i^{l}j}^{h}(t_{k}^{* })} le^{- l} \\ \geq &\liminf_{t \rightarrow + \infty } \Biggl\{ -a_{i^{l}i^{l}}^{h}(t)+b _{i^{l}i^{l}}^{h}(t)e^{-l} +\sum _{j=1,j\neq i^{l}}^{n} \bigl(a_{i ^{l}j}^{h}(t)-b_{i^{l}j}^{h}(t) \bigr) +\sum_{j=1}^{m} \frac{ \beta _{i^{l}j}^{h}(t)}{\gamma _{i^{l}j}^{h}(t)}l e^{-l} \Biggr\} \\ =&\liminf_{t \rightarrow + \infty } \Biggl\{ -a_{i^{l}i^{l}} (t)+b _{i^{l}i^{l}} (t)e^{-l} +\sum_{j=1,j\neq i^{l}}^{n} \bigl(a_{i^{l}j} (t)-b_{i^{l}j} (t) \bigr) +\sum _{j=1}^{m}\frac{\beta _{i^{l}j} (t)}{ \gamma _{i^{l}j} (t)}l e^{-l} \Biggr\} \\ \geq & \inf_{ s\in [0,\kappa ]}\liminf_{t \rightarrow + \infty } \Biggl\{ -a_{i^{l}i^{l}} (t)+b_{i^{l}i^{l}} (t)e^{-s} +\sum _{j=1,j\neq i^{l}}^{n} \bigl(a_{i^{l}j} (t)-b_{i^{l}j} (t) \bigr) +\sum_{j=1}^{m} \frac{\beta _{i^{l}j} (t)}{\gamma _{i^{l}j} (t)}se^{-s} \Biggr\} \\ >&0 , \end{aligned}$$

which results in a contradiction. This entails that \(l >\kappa \). Hence, from \(L< M\), we can choose \(t_{\varphi }>t_{0}\) such that

$$ \kappa < x_{i}(t;t_{0},\varphi )< M \quad \mbox{for all } t\geq t_{\varphi }, i\in Q. $$

The proof is now completed. □

By using a similar argument as in Lemma 2.1, we can show the following lemma:

Lemma 2.2

Let \(x(t; t_{0}, \varphi )\)be a solution of the initial value problem (1.1) and (2.2). Suppose that there exists a positive constant \(M>\kappa \)such that (1.7), (1.8), and (1.9) hold. Then, \(x (t )=x(t; t_{0}, \varphi )\)exists on \([t_{0}, +\infty )\),

$$ \kappa < \min_{i\in Q}\liminf_{t\rightarrow +\infty }x _{i}(t )\leq \max_{i\in Q}\limsup _{t\rightarrow +\infty }x _{i}(t ) < M, $$

and there is \(t _{\varphi }^{*}\in [t_{0}, +\infty )\)such that

$$ \kappa < x_{i} (t ) < M \quad \textit{for all } t\in \bigl[t _{\varphi }^{*}, +\infty \bigr), i\in Q. $$
(2.10)

Lemma 2.3

Suppose that \(M>\kappa \)satisfies (1.7), and (1.9), (1.10) and (2.3) hold. Moreover, assume that \(x(t)= x(t; t_{0}, \varphi ) \)is a solution of equation \((1.1)^{h}\)and (2.2). Then, for any \(\epsilon > 0\), we can make a relatively dense subset \(P_{\epsilon }\)of \(\mathbb{R}\)with the property that, for each \(\delta \in P_{ \epsilon }\), there exists \(T=T(\delta )>0\)satisfying

$$ \bigl\Vert x(t+\delta )-x(t) \bigr\Vert < \frac{\epsilon }{2 },\quad \textit{for all } t> T. $$
(2.11)

Proof

By virtue of Lemma 2.1, with the help of (1.10), (2.1) and the fact that \(b^{g}_{ij}, \beta _{ ij}^{g} \in W_{0}(\mathbb{R} ^{+}, \mathbb{R}^{+} )\), we can pick \(T_{1}>\max \{0, t_{\varphi } \}\) and ζ to satisfy that, \(\mbox{ for all } t\geq T_{1}\),

$$ \gamma _{ij}^{h}(t) x _{i} \bigl(t -\tau _{ij}^{h}(t) \bigr) > \kappa ,\qquad -b_{ii} ^{h}(t)e^{-M}+\sum _{j=1,j\neq i}^{n}b_{ij}^{h}(t)e^{-\kappa } +\frac{1}{e ^{2}}\sum_{j=1}^{m} \beta _{ij}^{h}(t)< -\zeta , $$

which results in that there exist two constants \(\eta >0 \) and \(\lambda \in (0, 1]\) such that

$$ \sup_{t\in [T_{1}, +\infty ) } \Biggl\{ - \bigl[b_{ii}^{h}(t)e^{-M} -\lambda \bigr]+\sum_{j=1,j\neq i}^{n}b_{ij}^{h}(t)e^{-\kappa } + \sum_{j=1}^{m} \beta _{ij}^{h}(t)\frac{1}{e^{2}}e^{\lambda \sigma _{i}} \Biggr\} < -\eta . $$
(2.12)

Label

$$ x_{i}(t)\equiv x_{i}(t_{0}-\sigma _{i}), \quad \mbox{for all } t\in (- \infty ,t_{0}- \sigma _{i}], i\in Q, $$
(2.13)

and

$$\begin{aligned} A _{i}(\delta ,t) =& \bigl[b_{ii}^{h}(t+ \delta )-b_{ii}^{h}(t) \bigr]e^{-x_{i}(t+ \delta )}-\sum _{j=1,j\neq i}^{n} \bigl[b_{ij}^{h}(t+ \delta )-b_{ij} ^{h}(t) \bigr]e^{-x_{j}(t+\delta )} \\ &{}+\sum_{j=1}^{m} \bigl[\beta _{ij}^{h}(t+\delta )-\beta _{ij}^{h}(t) \bigr]x _{i} \bigl(t+\delta -\tau _{ij}^{h}(t+ \delta ) \bigr)e^{-\gamma _{ij}^{h}(t+\delta )x_{i}(t+\delta -\tau _{ij}^{h}(t+\delta ))} \\ &{}+\sum_{j=1}^{m}\beta _{ij}^{h}(t) \bigl[x_{i} \bigl(t+\delta - \tau _{ij} ^{h}(t+\delta ) \bigr)e^{-\gamma _{ij}^{h}(t+\delta )x_{i}(t+\delta -\tau _{ij}^{h}(t+\delta ))} \\ &{}-x_{i} \bigl(t-\tau _{ij}^{h}(t)+ \delta \bigr)e^{-\gamma _{ij}^{h}(t+\delta )x _{i}(t-\tau _{ij}^{h}(t)+\delta )} \bigr] \\ &{}+\sum_{j=1}^{m}\beta _{ij}^{h}(t) \bigl[x_{i} \bigl(t-\tau _{ij}^{h}(t)+ \delta \bigr)e^{-\gamma _{ij}^{h}(t+\delta )x_{i}(t-\tau _{ij}^{h}(t)+\delta )} \\ &{}-x_{i} \bigl(t-\tau _{ij}^{h}(t)+ \delta \bigr)e^{-\gamma _{ij}^{h}(t)x_{i}(t- \tau _{ij}^{h}(t)+\delta )} \bigr]- \bigl[a_{ii}^{h}(t+ \delta )-a_{ii}^{h}(t) \bigr] \\ &{}+\sum_{j=1,j\neq i}^{n} \bigl[a_{ij}^{h}(t+\delta )-a_{ij}^{h}(t) \bigr], \quad \mbox{for all } t\in \mathbb{R}, i\in Q . \end{aligned}$$
(2.14)

The boundedness of the right-hand side of \((1.1)^{h}\) and (2.13) entails that \(x (t)\) is uniformly continuous on \(\mathbb{R}\). Therefore, for any \(\epsilon >0\), we can take a small enough constant \(\epsilon ^{*}>0\) such that

$$ \textstyle\begin{cases} \vert a_{ij} ^{h}(t)-a ^{h}_{ij}(t+\delta ) \vert < \epsilon ^{*},\qquad \vert b^{h} _{ij}(t)-b^{h}_{ij}(t+\delta ) \vert < \epsilon ^{*}, \\ \vert \beta _{ ij}^{h}(t)-\beta _{ ij}^{h} (t+\delta ) \vert < \epsilon ^{*} ,\qquad \vert \gamma _{ ij}^{h}(t)-\gamma _{ ij}^{h}(t+\delta ) \vert < \epsilon ^{*},\qquad \vert \tau _{ ij}^{h}(t)-\tau _{ ij}^{h}(t+\delta ) \vert < \epsilon ^{*}, \end{cases} $$

and it follows that

$$ \bigl\vert A _{i}(\delta ,t) \bigr\vert < \frac{1}{2 }\eta \epsilon , $$
(2.15)

where \(t\in \mathbb{R}\), \(i\in Q\), \(j\in I\).

Furthermore, for \(\epsilon ^{*}>0\), from the uniformly almost-periodic family theory in [12, p. 19, Corollary 2.3], one can make a relatively dense subset \(P_{\epsilon ^{*}}\) of \(\mathbb{R}\) such that

$$ \textstyle\begin{cases} \vert a_{ij} ^{h}(t)-a ^{h}_{ij}(t+\delta ) \vert < \epsilon ^{*},\qquad \vert b_{ij} ^{h}(t)-b_{ij}^{h}(t+\delta ) \vert < \epsilon ^{*}, \\ \vert \beta _{ ij}^{h}(t)-\beta _{ ij}^{h} (t+\delta ) \vert < \epsilon ^{*} , \\ \vert \gamma _{ ij}^{h}(t)-\gamma _{i j}^{h}(t+\delta ) \vert < \epsilon ^{*},\qquad \vert \tau _{ ij}^{h}(t)-\tau _{ ij}^{h}(t+\delta ) \vert < \epsilon ^{*}, \end{cases}\displaystyle \quad \delta \in P_{\epsilon ^{*}}, $$
(2.16)

where \(t \in \mathbb{R}\), \(i\in Q\), \(j\in I\).

Relabeling \(P_{\epsilon }=P_{\epsilon ^{*}}\), for any \(\delta \in P _{\epsilon }\), from (2.15) and (2.16), we have

$$ \bigl\vert A _{i}(\delta ,t) \bigr\vert < \frac{1}{2 }\eta \epsilon ,\quad \mbox{for all } t \in \mathbb{R}, i\in Q . $$
(2.17)

Let \(\varLambda _{0}\geq \max \{|t_{0}|+T_{1}+ \max_{i\in Q}\sigma _{i} , |t_{0}|+T_{1}+ \max_{i\in Q}\sigma _{i}-\delta \} \). For \(t\in \mathbb{R}\), label

$$ u(t)= \bigl(u_{1}(t),u_{2}(t),\ldots ,u_{n}(t) \bigr) ,\qquad u_{i}(t)=x_{i}(t+ \delta )-x_{i}(t), $$

and

$$ U(t)= \bigl(U_{1}(t),U_{2}(t),\ldots ,U_{n}(t) \bigr) , \qquad U_{i}(t)=e^{\lambda t}u_{i}(t), $$

where \(i\in Q\). Let \(i_{t}\) be such an index that

$$ \bigl\vert U_{i_{t}}(t) \bigr\vert = \bigl\Vert U(t) \bigr\Vert . $$
(2.18)

Then, for all \(t\geq \varLambda _{0}\), we gain

$$\begin{aligned} u_{i}'(t) =&b_{ii}^{h}(t) \bigl[e^{-x_{i}(t+\delta )}-e^{-x_{i}(t)} \bigr]- \sum _{j=1,j\neq i}^{n}b_{ij}^{h}(t) \bigl[e^{-x_{j}(t+\delta )} -e ^{-x_{j}(t)} \bigr] \\ &{}+\sum_{j=1}^{m}\beta _{ij}^{h}(t) \bigl[x_{i} \bigl(t-\tau _{ij}^{h}(t)+ \delta \bigr)e^{-\gamma _{ij}^{h}(t)x_{i}(t-\tau _{ij}^{h}(t)+\delta )} \\ &{}-x_{i} \bigl(t-\tau _{ij}^{h}(t) \bigr)e^{-\gamma _{ij}^{h}(t)x_{i} (t-\tau _{ij} ^{h}(t))} \bigr]+ A_{i}(\delta ,t). \end{aligned}$$
(2.19)

From (2.4), (2.19) and the inequalities

$$ \bigl(e^{-x}- e^{-y} \bigr)\operatorname{sgn}(x-y ) \leq -e^{-M} \vert x -y \vert \quad \mbox{for all } x,y\in [\kappa , M] , $$
(2.20)

and

$$ \bigl\vert \alpha e^{-\alpha }-\beta e^{-\beta } \bigr\vert \leq \frac{1}{e^{2}} \vert \alpha -\beta \vert \quad \mbox{where } \alpha ,\beta \in [\kappa , +\infty ) , $$
(2.21)

we obtain

$$\begin{aligned}& D^{-} \bigl( \bigl\vert U_{i_{s}}(s) \bigr\vert \bigr)\big|_{s=t} \\& \quad \leq \lambda e^{\lambda t} \bigl\vert u_{i_{t}}(t) \bigr\vert +e^{\lambda t} \Biggl\{ b_{i_{t}i _{t}}^{h}(t) \bigl[e^{-x_{i_{t}}(t+\delta )}-e^{-x_{i_{t}}(t)} \bigr] \operatorname{sgn} \bigl(x _{i_{t}}(t+\delta )-x_{i_{t}}(t) \bigr) \\& \qquad {}+\sum_{j=1,j\neq i_{t}}^{n}b_{i_{t}j}^{h}(t) \bigl\vert e^{-x_{j}(t+ \delta )}-e^{-x_{j}(t)} \bigr\vert +\sum _{j=1}^{m}\beta _{i_{t}j}^{h}(t) \\& \qquad {}\times \bigl\vert x_{i_{t}} \bigl(t-\tau _{i_{t}j}^{h}(t)+\delta \bigr)e^{-\gamma _{i_{t}j} ^{h}(t)x_{i_{t}}(t-\tau _{i_{t}j}^{h}(t)+\delta )} -x_{i_{t}} \bigl(t- \tau _{i_{t}j}^{h}(t) \bigr)e^{-\gamma _{i_{t}j}^{h}(t)x_{i_{t}}(t-\tau _{i _{t}j}^{h}(t))} \bigr\vert \\& \qquad {}+ \bigl\vert A_{i_{t}}(\delta ,t) \bigr\vert \Biggr\} \\& \quad = \lambda e^{\lambda t} \bigl\vert u_{i_{t}}(t) \bigr\vert +e^{\lambda t} \Biggl\{ b_{i_{t}i _{t}}^{h}(t) \bigl[e^{-x_{i_{t}}(t+\delta )}-e^{-x_{i_{t}}(t)} \bigr] \operatorname{sgn} \bigl(x _{i_{t}}(t+\delta )-x_{i_{t}}(t) \bigr) \\& \qquad {}+\sum_{j=1,j\neq i_{t}}^{n}b_{i_{t}j}^{h}(t) \bigl\vert e^{-x_{j}(t+ \delta )}-e^{-x_{j}(t)} \bigr\vert +\sum _{j=1}^{m} \frac{\beta _{i_{t}j} ^{h}(t)}{\gamma _{i_{t}j}^{h}(t)} \\& \qquad {}\times \bigl\vert \gamma _{i_{t}j}^{h}(t)x_{i_{t}} \bigl(t-\tau _{i_{t}j}^{h}(t)+ \delta \bigr)e^{-\gamma _{i_{t}j}^{h}(t)x_{i_{t}}(t-\tau _{i_{t}j}^{h}(t)+ \delta )} \\& \qquad {} -\gamma _{i_{t}j}^{h}(t)x_{i_{t}} \bigl(t-\tau _{i_{t}j}^{h}(t) \bigr)e^{- \gamma _{i_{t}j}^{h}(t)x_{i_{t}}(t-\tau _{i_{t}j}^{h}(t))} \bigr\vert + \bigl\vert A_{i_{t}}( \delta ,t) \bigr\vert \Biggr\} \\& \quad \leq \lambda e^{\lambda t} \bigl\vert u_{i_{t}}(t) \bigr\vert +e^{\lambda t} \Biggl\{ -b_{i _{t}i_{t}}^{h}(t)e^{-M } \bigl\vert u_{i_{t}}(t) \bigr\vert +\sum _{j=1,j\neq i_{t}} ^{n}b_{i_{t}j}^{h}(t)e^{-\kappa } \bigl\vert u_{j}(t) \bigr\vert \\& \qquad {}+\sum_{j=1}^{m} \beta _{i_{t}j}^{h}(t) \frac{1}{e^{2}} \bigl\vert u_{i _{t}} \bigl(t-\tau _{i_{t}j}^{h}(t) \bigr) \bigr\vert + \bigl\vert A_{i_{t}}(\delta ,t) \bigr\vert \Biggr\} \\& \quad = - \bigl[b_{i_{t}i_{t}}^{h}(t)e^{-M }- \lambda \bigr] \bigl\vert U_{i_{t}}(t) \bigr\vert +\sum _{j=1,j\neq i_{t}}^{n}b_{i_{t}j}^{h}(t)e^{-\kappa } \bigl\vert U_{j}(t) \bigr\vert \\& \qquad {}+\sum_{j=1}^{m}\beta _{i_{t}j}^{h}(t) \frac{1}{e^{2}} e^{ \lambda \tau _{i_{t} j}^{h}(t)} \bigl\vert U_{i_{t}} \bigl(t-\tau _{i_{t}j}^{h}(t) \bigr) \bigr\vert +e ^{\lambda t} \bigl\vert A_{i_{t}}(\delta ,t) \bigr\vert \quad \mbox{for all }t\geq \varLambda _{0}. \end{aligned}$$
(2.22)

Let

$$ E(t)=\sup_{-\infty < s\leq t} \bigl\{ e^{\lambda s} \bigl\Vert u (s) \bigr\Vert \bigr\} . $$

It is obvious that \(e^{\lambda t} \|u (t) \| \leq E(t)\), and \(E(t)\) is non-decreasing.

Now, the remaining proof will be divided into two steps.

Step 1. If \(E(t)> e^{\lambda t} \|u (t) \|\) for all \(t\geq \varLambda _{0}\), we assert that

$$ E(t)\equiv \bigl\Vert U( \varLambda _{0}) \bigr\Vert \quad \mbox{for all } t\geq \varLambda _{0}. $$
(2.23)

In the contrary case, one can pick \(\varLambda _{1}> \varLambda _{0}\) such that \(E(\varLambda _{1})> E( \varLambda _{0})\). Because

$$ e^{\lambda t} \bigl\Vert u (t) \bigr\Vert \leq E( \varLambda _{0})\quad \mbox{for all } t \leq \varLambda _{0}, $$

there must exist \(\beta ^{*} \in ( \varLambda _{0}, \varLambda _{1})\) such that

$$ e^{\lambda \beta ^{*}} \bigl\Vert u \bigl(\beta ^{*} \bigr) \bigr\Vert = E(\varLambda _{1})\geq E \bigl(\beta ^{*} \bigr), $$

which contradicts the fact that \(E(\beta ^{*})>e^{\lambda \beta ^{*}} \|u (\beta ^{*}) \|\) and proves the above assertion. Then, we can make \(\varLambda _{2}>\varLambda _{0}\) satisfying

$$ \bigl\Vert u (t) \bigr\Vert \leq e^{-\lambda t}E(t)= e^{-\lambda t}E( \varLambda _{0})< \frac{ \varepsilon }{2}\quad \mbox{for all } t\geq \varLambda _{2}. $$
(2.24)

Step 2. If there exists \(\varsigma \geq \varLambda _{0}\) such that \(E(\varsigma )= e^{\lambda \varsigma } \|u (\varsigma ) \| \), we can have from (2.22) and the definition of \(E(t)\) that

$$\begin{aligned} 0 \leq &D^{-} \bigl( \bigl\vert U_{i_{s}}(s) \bigr\vert \bigr)\big|_{s=\varsigma } \\ \leq & - \bigl[b_{i_{\varsigma }i_{\varsigma }}^{h}(\varsigma )e^{-M }- \lambda \bigr] \bigl\vert U_{i_{\varsigma }}(\varsigma ) \bigr\vert +\sum_{j=1,j\neq i_{\varsigma }}^{n} b_{i_{\varsigma }j}^{h}(\varsigma )e^{-\kappa } \bigl\vert U_{j}(\varsigma ) \bigr\vert \\ &{}+\sum_{j=1}^{m}\beta _{i_{\varsigma }j}^{h}(\varsigma ) \frac{1}{e ^{2}} e^{\lambda \tau _{i_{\varsigma }j}^{h}(\varsigma )} \bigl\vert U_{i_{\varsigma }} \bigl(\varsigma -\tau _{i_{\varsigma }j}^{h}(\varsigma ) \bigr) \bigr\vert +e^{\lambda \varsigma } \bigl\vert A_{i_{\varsigma }}(\delta ,\varsigma ) \bigr\vert \\ \leq & \Biggl\{ - \bigl[b_{i_{\varsigma }i_{\varsigma }}^{h}(\varsigma )e^{-M }- \lambda \bigr] +\sum_{j=1,j\neq i_{\varsigma }}^{n}b_{i_{\varsigma }j}^{h}( \varsigma )e^{-\kappa } \\ &{}+\sum_{j=1}^{m}\beta _{i_{\varsigma }j}^{h}(\varsigma ) \frac{1}{e ^{2}} e^{\lambda \tau _{i_{\varsigma }j}^{h}(\varsigma )} \Biggr\} E(\varsigma ) + \frac{1}{2}\eta \varepsilon e^{\lambda \varsigma } \\ < &-\eta E(\varsigma )+ \frac{1}{2}\eta \varepsilon e^{\lambda \varsigma }, \end{aligned}$$
(2.25)

which leads to

$$ e^{\lambda \varsigma } \bigl\Vert u (\varsigma ) \bigr\Vert =E(\varsigma )< \frac{ \varepsilon }{2} e^{\lambda \varsigma }, \quad \mbox{and}\quad \bigl\Vert u ( \varsigma ) \bigr\Vert < \frac{\varepsilon }{2}. $$
(2.26)

For any \(t>\varsigma \) satisfying \(E(t )= e^{\lambda t } \|u (t ) \| \), by the same method as that in the derivation of (2.26), we can show

$$ e^{\lambda t } \bigl\Vert u (t ) \bigr\Vert < \frac{\varepsilon }{2} e^{\lambda t } \quad \mbox{and}\quad \bigl\Vert u (t ) \bigr\Vert < \frac{\varepsilon }{2}. $$
(2.27)

In addition, if \(E(t )> e^{\lambda t } \|u (t ) \| \) and \(t>\varsigma \), one can pick \(\varLambda _{3}\in [\varsigma , t)\) such that

$$ E(\varLambda _{3} )= e^{\lambda \varLambda _{3}} \bigl\Vert u (\varLambda _{3} ) \bigr\Vert \quad \mbox{and}\quad E(s)> e^{\lambda s } \bigl\Vert u (s ) \bigr\Vert \quad \mbox{for all } s \in (\varLambda _{3}, t], $$

which, together with (2.26) and (2.27), indicates that

$$ \bigl\Vert u (\varLambda _{3}) \bigr\Vert < \frac{\varepsilon }{2}. $$
(2.28)

With a similar reasoning as that in the proof of Step 1, we can validate that

$$ E(s)\equiv E(\varLambda _{3}) \quad \mbox{is a constant for all } s \in ( \varLambda _{3}, t], $$

which, together with (2.28), implies that

$$ \bigl\Vert u (t ) \bigr\Vert < e^{-\lambda t }E(t)= e^{-\lambda t }E( \varLambda _{3})= \bigl\Vert u ( \varLambda _{3}) \bigr\Vert e^{-\lambda (t-\varLambda _{3}) }< \frac{\varepsilon }{2}. $$

Finally, from the above discussion we infer that there exists \(\hat{\varLambda }>\max \{\varsigma , \varLambda _{0}, \varLambda _{2} \}\) obeying

$$ \bigl\Vert u (t ) \bigr\Vert \leq \frac{\varepsilon }{2}< \varepsilon\quad \mbox{for all } t>\hat{\varLambda }, $$
(2.29)

which finishes the proof of Lemma 2.3. □

3 Main result

Theorem 3.1

Let \(M>\kappa \)satisfy (1.7), (1.8), (1.9), (1.10) and (2.3). Then, for system \((1.1)^{h}\), there exists exactly one positive almost-periodic solution \(x^{*}(t)\), and every solution of (1.1) with initial condition (2.2) converges to \(x^{*}(t)\)as \(t\rightarrow +\infty \), which is asymptotically almost-periodic on \(\mathbb{R}^{+}\).

Proof

Let \(v(t) \) be a solution of system \((1.1)^{h}\) with the initial function φ satisfying (2.2),

$$ v_{i}(t)\equiv v_{i}(t_{0}-\sigma _{i}), \quad \textit{for all } t\in (- \infty ,t_{0}- \sigma _{i}], i\in Q. $$

We also define

$$\begin{aligned} B _{i}( q,t) =& \bigl[b_{ii}^{h}(t+t_{q})-b_{ii}^{h}(t) \bigr]e^{-v_{i}(t+t_{q})} -\sum_{j=1,j\neq i}^{n} \bigl[b_{ij}^{h}(t+t_{q})-b_{ij}^{h}(t) \bigr]e ^{-v_{j}(t+t_{q})} \\ &{}+\sum_{j=1}^{m} \bigl[\beta _{ij}^{h}(t+t_{q})-\beta _{ij}^{h}(t) \bigr]v _{i} \bigl(t+t_{q}-\tau _{ij}^{h}(t+t_{q}) \bigr) e^{-\gamma _{ij}^{h}(t+t_{q})v _{i}(t+t_{q}-\tau _{ij}^{h}(t+t_{q}))} \\ &{}+\sum_{j=1}^{m}\beta _{ij}^{h}(t) \bigl[v_{i} \bigl(t+t_{q}-\tau _{ij}^{h}(t+t _{q}) \bigr)e^{-\gamma _{ij}^{h}(t+t_{q}) v_{i}(t+t_{q}-\tau _{ij}^{h}(t+t _{q}))} \\ &{}-v_{i} \bigl(t-\tau _{ij}^{h}(t)+t_{q} \bigr)e^{-\gamma _{ij}^{h}(t+t_{q})v_{i}(t- \tau _{ij}^{h}(t)+t_{q})} \bigr] \\ &{}+\sum_{j=1}^{m}\beta _{ij}^{h}(t) \bigl[v_{i} \bigl(t-\tau _{ij}^{h}(t)+t _{q} \bigr)e^{-\gamma _{ij}^{h}(t+t_{q}) v_{i}(t-\tau _{ij}^{h}(t)+t_{q})} \\ &{}-v_{i} \bigl(t-\tau _{ij}^{h}(t)+t_{q} \bigr)e^{-\gamma _{ij}^{h}(t)v_{i}(t-\tau _{ij}^{h}(t)+t_{q})} \bigr]- \bigl[a_{ii}^{h}(t+t_{q})-a_{ii}^{h}(t) \bigr] \\ &{}+\sum_{j=1,j\neq i}^{n} \bigl[a_{ij}^{h}(t+t_{q})-a_{ij}^{h}(t) \bigr],\quad \mbox{for all } t\in \mathbb{R}, i\in Q . \end{aligned}$$
(3.1)

where \(\{t_{q}\}_{q\geq 1}\subseteq \mathbb{R} \) is a sequence. Then

$$\begin{aligned} v' _{i}(t+t_{q}) =& -a^{h}_{ii}(t)+b^{h}_{ii}(t)e^{-v_{i}(t+t_{q})} + \sum_{j=1,j\neq i}^{n} \bigl(a_{ij}^{h}(t)-b_{ij}^{h}(t)e^{-v_{j}(t+t _{q})} \bigr) \\ &{} +\sum_{j=1}^{m}\beta _{ij}^{h}(t) v_{i} \bigl(t-\tau _{ij}^{h} (t) +t_{q} \bigr)e^{-\gamma _{ij}^{h}(t) v_{i}(t-\tau _{ij}^{h}(t)+t_{q})}+B_{ i } (q, t) , \end{aligned}$$
(3.2)

for all \(t+t_{q}\geq t_{0}\), \(i\in Q\). By using a similar proof as in Lemma 2.3, we can take \(\{t_{q}\}_{q\geq 1}\) such that

$$ \bigl\vert B_{ i} (q, t) \bigr\vert < \frac{1}{q} \quad \mbox{for all } i, q, t. $$
(3.3)

Based on Arzela–Ascoli Lemma coupled with the fact that the function sequence \(\{v(t+t_{q})\} _{q\geq 1} \) is uniformly bounded and equiuniformly continuous, we can choose a subsequence \(\{t_{q_{j}}\} _{j\geq 1}\) of \(\{t_{q}\}_{q\geq 1}\), such that \(\{v(t+t_{q_{j}})\} _{j\geq 1}\) (for convenience, we still denote it by \(\{v(t+t_{q})\} _{q\geq 1}\)) uniformly converges to a continuous function \(x^{*}(t)=(x ^{*}_{1}(t),x^{*}_{2}(t),\ldots ,x^{*}_{n}(t)) \) on any compact set of \(\mathbb{R}\). Then, Lemma 2.1 gives us

$$ \kappa < \min_{i\in Q}\liminf_{t\rightarrow +\infty }v _{i}(t )\leq x^{*}_{i} (t ) \leq \max _{i\in Q}\limsup_{t\rightarrow +\infty }v _{i}(t ) < M \quad \mbox{for all } t \in \mathbb{R}, i\in Q, $$
(3.4)

and

$$ \textstyle\begin{cases} -a^{h}_{ij}(t)+b^{h}_{ij}(t)e^{-v_{j}(t+t_{q})}\quad \Rightarrow\quad -a_{ij} ^{h}(t)+b_{ij}^{h}(t)e^{-x^{*}_{j} (t )}, \\ \sum_{j=1}^{m}\beta _{ij}^{h}(t) v_{i} (t-\tau _{ij}^{h} (t) +t _{q} )e^{-\gamma _{ij}^{h}(t) v_{i}(t-\tau _{ij}^{h}(t)+t_{q})} \\ \quad \Rightarrow\quad \sum_{j=1}^{m}\beta _{ij}^{h}(t) x^{*}_{i} (t- \tau _{ij}^{h} (t) )e^{-\gamma _{ij}^{h}(t) x^{*}(t-\tau _{ij}^{h}(t) )}, \end{cases}\displaystyle \quad \mbox{as } q\rightarrow +\infty , $$
(3.5)

on any compact set of \(\mathbb{R}\) for all \(i, j\in Q\), where “⇒” denotes “uniformly converge”. Thus, for \(i\in Q\), (3.2), (3.3) and (3.5) imply that \(\{v'_{i} (t+t_{q})\}_{q\geq 1}\) uniformly converges to

$$\begin{aligned}& -a^{h}_{ii}(t)+b^{h}_{ii}(t)e^{-x^{*}_{i} (t )} +\sum_{j=1,j\neq i}^{n} \bigl(a_{ij}^{h}(t)-b_{ij}^{h}(t)e^{-x_{j}^{*}(t )} \bigr) \\& \quad {} +\sum^{m}_{j=1}\beta _{ ij}^{h}(t) x^{*}_{i} \bigl(t-\tau _{ij}^{h}(t) \bigr)e ^{-\gamma _{ ij}^{h}(t)x^{*} (t-\tau ^{h}_{ ij}(t))} \end{aligned}$$

on any compact set of \(\mathbb{R}\). This suggests that \(x^{*}(t)\) is a solution of \((1.1)^{h}\) and

$$\begin{aligned} \bigl(x^{*}_{i}(t) \bigr)' =& -a^{h}_{ii}(t)+b^{h}_{ii}(t)e^{-x^{*}_{i} (t )} + \sum_{j=1,j\neq i}^{n} \bigl(a_{ij}^{h}(t)-b_{ij}^{h}(t)e^{-x_{j} ^{*}(t )} \bigr) \\ & +\sum^{m}_{j=1}\beta _{ ij}^{h}(t) x^{*}_{i} \bigl(t-\tau _{ij}^{h}(t) \bigr)e ^{-\gamma _{ ij}^{h}(t)x^{*} (t-\tau ^{h}_{ ij}(t))}, \quad \mbox{for all } t\in \mathbb{R}, i\in Q . \end{aligned}$$
(3.6)

Furthermore, from Lemma 2.3, for any \(\epsilon >0\), we can get a relatively dense subset \(P_{\epsilon }\) of \(\mathbb{R}\) with the property that, for each \(\delta \in P_{\epsilon }\), there exists \(T=T(\delta )>0\) satisfying

$$ \bigl\Vert v (s+t_{q}+\delta )-v (s+t_{q}) \bigr\Vert < \frac{\epsilon }{2}, \quad \mbox{for all } s+t_{q}> T, $$

and

$$ \lim_{q\rightarrow +\infty } \bigl\Vert v (s+t_{q}+\delta )-v (s+t_{q}) \bigr\Vert = \bigl\Vert x^{*} (s +\delta )-x^{*} (s) \bigr\Vert \leq \frac{\epsilon }{2}< \epsilon \quad \mbox{for all } s\in \mathbb{R}, $$

which implies that \(x^{*}(t)\) is a positive almost-periodic solution of \((1.1)^{h}\).

Now, we show that all solutions of (1.1) converge to \(x^{*}(t)\) as \(t\rightarrow +\infty \). Let \(x(t) \) be an arbitrary solution of system (1.1) with the initial value φ satisfying (2.2). Define \(y(t)=x(t) -x^{*}(t)\), add the definition of \(x_{i}(t)\) with \(x_{i}(t)\equiv x _{i}( t_{0}-\sigma _{i})\) for all \(t\in (-\infty , t_{0}-\sigma _{i}]\), and let

$$\begin{aligned} F_{i} ( t) = & - \bigl[ \bigl( \bigl(a^{h}_{ii}(t)+a^{g}_{ii}(t) \bigr)+ \bigl(b^{h}_{ii}(t)+b^{g}_{ii}(t) \bigr)e ^{-x_{i}(t)} \bigr)- \bigl( a^{h}_{ii}(t) + b^{h}_{ii}(t) e^{-x_{i}(t)} \bigr) \bigr] \\ &{}+\sum_{j=1,j\neq i}^{n} \bigl[ \bigl(a_{ij}^{h}(t)+a_{ij}^{h}(t) - \bigl(b_{ij} ^{h}(t)+b_{ij}^{g}(t) \bigr)e^{-x_{j}(t)} \bigr)- \bigl( a_{ij}^{h}(t) - b_{ij}^{h}(t) e^{-x_{j}(t)} \bigr) \bigr] \\ &{}+\sum^{m}_{j=1} \bigl[ \bigl( \beta _{ ij}^{h}(t)+\beta _{ ij}^{g}(t) \bigr)x_{i} \bigl(t- \bigl(\tau _{ij}^{h}(t)+ \tau _{ij}^{g}(t) \bigr) \bigr))e^{-(\gamma _{ ij}^{h}(t)+\gamma _{ ij}^{g}(t))x_{i} (t-(\tau _{ij}^{h}(t)+\tau _{ij}^{g}(t)))} \\ &{}-\beta _{i j}^{h}(t)x_{i} \bigl(t- \tau _{ij}^{h}(t) \bigr)e^{-\gamma _{ ij}^{h}(t)x _{i} (t-\tau ^{h}_{i j}(t))} \bigr]. \end{aligned}$$

Then

$$\begin{aligned} y'_{i} (t) =& b^{h}_{ii}(t) \bigl[e^{-x_{i}(t)}-e^{-x^{*}_{i}(t)} \bigr]-\sum _{j=1,j\neq i}^{n} b_{ij}^{h}(t) \bigl[e^{-x_{j}(t)}- e^{-x_{j} ^{*}(t)} \bigr] \\ &{}+\sum^{m}_{j=1}\beta _{i j}^{h}(t) \bigl[x_{i} \bigl(t-\tau ^{h}_{ ij}(t) \bigr)e^{- \gamma _{ ij}^{h}(t)x_{i} (t-\tau _{ ij}^{h}(t))} \\ &{}-x_{i}^{*} \bigl(t-\tau _{ij}^{h}(t) \bigr)e^{-\gamma _{ ij}^{h}(t)x_{i}^{*} (t- \tau ^{h}_{ ij}(t))} \bigr]+ F_{i} ( t), \quad \mbox{for all } t \geq t_{0}, i \in Q. \end{aligned}$$
(3.7)

For any \(\epsilon >0\), in view of the global existence and uniform continuity of x and the fact that \(a_{ij}^{g}, b_{ij}^{g}, \beta _{ ij}^{g}, \gamma _{i j}^{g}, \tau _{ ij}^{g} \in W_{0}(\mathbb{R}^{+}, \mathbb{R}^{+} )\), we can choose a constant \(T_{\varphi }^{**}>\max \{T_{1}, t_{\varphi }^{*}\}\) such that

$$ \bigl\vert F_{i} ( t) \bigr\vert < \eta \frac{\epsilon }{2 }, \quad \mbox{for all } t>T_{ \varphi }^{**}. $$
(3.8)

Set

$$ G(t)=\sup_{-\infty < s\leq t} \bigl\{ e^{\lambda s} \bigl\Vert y (s) \bigr\Vert \bigr\} ,\quad \mbox{for all } t \in \mathbb{R}, $$

and let \(i_{t}\) be such an index that

$$ e^{\lambda t} \bigl\vert y_{i_{t}}(t) \bigr\vert = \bigl\Vert e^{\lambda t}y(t) \bigr\Vert . $$

By virtue of (1.7), (2.1), (3.4) and Lemma 2.2, one can find \(T_{\varphi , x^{*} }>T_{\varphi }^{**}\) such that

$$ \kappa < x _{i} (t ), x^{*}_{i} (t ), \gamma _{ij}^{h} (t) x _{i} \bigl(t - \tau _{ij}^{h}(t) \bigr) \leq \widetilde{\kappa }\quad \mbox{for all } t>T _{\varphi , x^{*} }, i\in Q. $$
(3.9)

With the help of (2.20), (2.21), (3.7) and (3.9), we gain

$$\begin{aligned}& D^{-} \bigl(e^{\lambda s} \bigl\vert y_{i_{s}}(s) \bigr\vert \bigr)\big|_{s=t} \\& \quad \leq - \bigl[b_{i_{t}i_{t}}^{h}(t)e^{-M }- \lambda \bigr] e^{\lambda t} \bigl\vert y_{i _{t}}(t) \bigr\vert +\sum_{j=1,j\neq i_{t}}^{n}b_{i_{t}j}^{h}(t)e^{- \kappa } e^{\lambda t} \bigl\vert y_{j}(t) \bigr\vert \\& \qquad {} +\sum_{j=1}^{m}\beta _{i_{t}j}^{h}(t) \frac{1}{e^{2}} e^{ \lambda \tau _{i_{t} j}^{h}(t)} e^{\lambda (t-\tau _{i_{t}j}^{h}(t))} \bigl\vert y _{i_{t}} \bigl(t-\tau _{i_{t}j}^{h}(t) \bigr) \bigr\vert \\& \qquad {}+e^{\lambda t} \bigl\vert F_{i_{t}}( t) \bigr\vert \quad \mbox{for all } t\geq T_{\varphi , x ^{*} }, i\in Q. \end{aligned}$$
(3.10)

Then, from (2.12), (3.8) and (3.10), by employing a similar approach as when proving Lemma 2.3, we know that there is a constant \(\widetilde{T} \geq T_{\varphi , x^{*} }\) such that

$$ \bigl\Vert y (t) \bigr\Vert < \frac{\epsilon }{2 } \quad \mbox{for all } t \geq \widetilde{T}, $$

which yields

$$ \lim_{t\rightarrow +\infty } x(t)=x^{*}(t) \quad \mbox{and} \quad x(t) \in \operatorname{AAP} \bigl(\mathbb{R},\mathbb{R}^{n} \bigr). $$

It follows from the uniqueness of the limit function that \((1.1)^{h}\) has exactly one positive almost-periodic solution \(x^{*}(t)\). The proof is complete. □

Remark 3.1

If the assumptions in Lemma 2.3 are satisfied, according to Lemmas 2.1 and 2.3, by utilizing a similar argument as in Theorem 3.1 of [10], one can show that the solution \(x(t; t_{0}, \varphi )\) of \((1.1)^{h}\) converges exponentially fast to \(x ^{* }(t )\) as \(t\rightarrow +\infty \). Here, all assumptions in (1.7)–(1.10) are weaker than those in (1.2)–(1.5), and one can easily find that all conclusions about \((1.1)^{h}\) in [10] are special cases of Theorem 3.1 in this paper. Evidently, for \(n=1\), (1.9) is weaker than

$$ \inf_{ t\in [t_{0}, +\infty ), s\in [0,\kappa ]} \Biggl\{ -a_{11}(t)+b _{11}(t)e^{-s} +\sum_{j=1}^{m} \frac{\beta _{1j}(t)}{\gamma _{1j}(t)}se^{-s} \Biggr\} >0, $$

which has been considered as fundamental in the most recently paper [9]. This implies that the results in [9] are also special cases of this present article.

4 An example

In this section, a numerical example is presented to justify the effectiveness of the proposed asymptotically almost-periodic stability results. The simulation is performed by using Matlab software.

Example 4.1

Consider the following class of nonlinear density-dependent mortality Nicholson’s blowflies system subject to asymptotically almost-periodic environments:

$$ \textstyle\begin{cases} x_{1} '(t) = -e^{-(1+0.08 \vert \sin \sqrt{2}t \vert )}+(1+0.001\sin t)e^{-x _{1}(t)} \\ \hphantom{x_{1} '(t) = {}}{} +0.1e^{-(1+0.08\sin ^{2}\sqrt{2}t)}+\frac{1}{20+ \vert t \vert } \\ \hphantom{x_{1} '(t) = {}}{} -(0.1+0.0001\cos t+\frac{1}{20.5+ \vert t \vert })e^{-x_{2}(t)} \\ \hphantom{x_{1} '(t) = {}}{} +\frac{1+\cos ^{2}t}{2000}x_{1}(t-2\sin ^{2} t-\frac{1}{1+t^{2}}) \\ \hphantom{x_{1} '(t) = {}}{} \times e^{-(0.001+\frac{ \vert t \vert + \vert \sin t \vert }{10+ \vert t \vert })x_{1}(t-2\sin ^{2} t-\frac{1}{1+t ^{2}})} \\ \hphantom{x_{1} '(t) = {}}{} +\frac{1+\cos ^{2} 2t}{2000}x_{1}(t-2 \vert \cos t \vert -\frac{2}{1+t^{2}}) \\ \hphantom{x_{1} '(t) = {}}{} \times e^{-(0.002+\frac{ \vert t \vert + \vert \sin 2t \vert }{10+ \vert t \vert })x_{1}(t-2 \vert \cos t \vert -\frac{2}{1+t ^{2}})} , \\ x_{2} '(t) = -e^{-(1+0.08 \vert \cos \sqrt{2}t \vert )}+(1+0.001\cos t)e^{-x _{2}(t)} \\ \hphantom{x_{2} '(t) = {}}{} +0.1e^{-(1+0.08\cos ^{2}\sqrt{2}t)}+\frac{1}{21+ \vert t \vert } \\ \hphantom{x_{2} '(t) = {}}{} -(0.1+0.0001\sin t+\frac{1}{20.2+ \vert t \vert })e^{-x_{1}(t)} \\ \hphantom{x_{2} '(t) = {}}{} +\frac{1+\sin ^{2}t}{2000}x_{2}(t-2\sin ^{2} t- \frac{t^{2}}{20+t ^{4}}) \\ \hphantom{x_{2} '(t) = {}}{} \times e^{-(0.003+\frac{ \vert t \vert + \vert \sin 3t \vert }{10+ \vert t \vert })x_{2}(t-2\sin ^{2} t- \frac{t^{2}}{20+t^{4}})} \\ \hphantom{x_{2} '(t) = {}}{} +\frac{1+\sin ^{2} 2t}{2000}x_{2}(t-2\cos ^{4} t- \frac{t^{2}}{30+t ^{4}}) \\ \hphantom{x_{2} '(t) = {}}{} \times e^{-(0.0015+\frac{ \vert t \vert + \vert \sin 4t \vert }{10+ \vert t \vert })x_{2}(t-2\cos ^{4} t- \frac{t^{2}}{30+t^{4}})} . \end{cases} $$
(4.1)

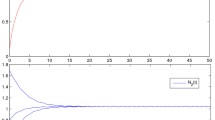
It is easy to obtain that \(\widetilde{\kappa }\approx 1.342276\), \(\kappa \approx 0.7215355\). Setting \(M=1.31\), one can verify that system (4.1) satisfies all the assumptions adopted in Theorem 3.1. Consequently, all solutions of (4.1) are asymptotically almost-periodic functions on \(\mathbb{R}^{+}\), and converge to the same almost-periodic function as \(t\rightarrow +\infty \). This fact can be revealed in Fig. 1.

Figure 1
figure 1

Trajectories of system (4.1) involving differential initial values

Full size image

Remark 4.1

It should be mentioned that system (4.1) is not almost-periodic, and

$$ \inf_{t\in \mathbb{R}^{+}}\gamma _{ij} (t ) < 0.05, $$

so that it does not satisfy \(\inf_{t\in \mathbb{R}}\gamma _{ij}(t) \geq 1\) which was adopted as fundamental in [7, 10]. In particular, the results in [1–6, 8, 9, 15–46] give no conclusion about the problem of asymptotically almost-periodic dynamics of Nicholson’s blowflies models involving such a patch structure. Hence, all results in [1–10] and [15–62] cannot be straightforwardly employed to validate that all solutions of (4.1) converge globally to the almost-periodic function.

5 Conclusions

In this article, we addressed the asymptotic almost-periodicity in the nonlinear density-dependent mortality Nicholson’s blowflies system with patch structures. With some delicate applications of differential inequality techniques, some sufficient conditions on the global convergence were obtained to reveal that all solutions of the considered systems are convergent to the same almost-periodic function when \(t\rightarrow +\infty \). In addition, the approach developed here is applicable in studying the asymptotic almost-periodic dynamics of other nonlinear density-dependent mortality population dynamic systems involving asymptotic almost-periodic environments.