1 Introduction

Recently, Berezansky and Braverman [1] pointed out that several important classes of infinite dimensional dynamical systems arising from biological and medical sciences are special cases of the following general scalar delay differential equation:

$$ x '(t)=\sum^{m}_{j=1}F_{j} \bigl(t, x\bigl(t-\tau_{1}(t)\bigr),\ldots,x\bigl(t- \tau_{l}(t)\bigr)\bigr)-G\bigl(t, x(t)\bigr),\quad t \geq t_{0}, $$
(1.1)

where m and l are positive integers. Here G is considered to be instantaneous mortality, \(F_{j}\) (\(j\in I:=\{1,2,\ldots, m\}\)) describes the feedback controls depending on the values of the stable variable with respective delays \(\tau_{1}(t) \), \(\tau_{2}(t),\ldots,\tau_{l}(t) \). Clearly, (1.1) includes the following nonlinear density-dependent mortality Nicholson’s blowflies model:

$$ x' (t)= -\frac{a(t)x(t)}{b(t)+x(t)} +\sum _{j=1}^{m}\beta_{j}(t) x \bigl(t-h_{j} (t) \bigr)e^{-\gamma_{j}(t) x(t-g_{j}(t))}, \quad t \geq t_{0}, $$
(1.2)

which in the case \(h_{j}\equiv g_{j}\) coincide with the classical models [2–6]. In particular, the nonlinear density-dependent mortality term, \(\frac{a(t)x(t)}{b(t)+x(t)}\) is referred to as population mortality, \(\beta_{j}(t) x (t-h_{j} (t) )e^{-\gamma_{j}(t) x(t-g_{j}(t))}\) designates the time-dependent birth function with maturation delay \(h_{ j}(t)\) and incubation delay \(g_{ j}(t)\), and gets the maximum reproduces rate \(\frac{1}{\gamma_{ j}(t)}\), and \(j\in I \).

For the past decade or so, for the special case of (1.2) with \(h_{j}\equiv g_{j}\) (\(j\in I\)), not only the dynamic behaviors of time-delay Nicholson’s blowflies models, such as existence, persistence, oscillation, periodicity and stability, but also the variants of the models have aroused current research interest, and some useful results have been obtained in the existing papers; for example, see [7–15]. In addition, it is proved that more than one delay involved in the identical nonlinear function \(F_{j}\) can cause chaotic oscillations in [1], and an example is given to represent that two delays, rather than one delay, can produce a continuous oscillation. As a matter of fact, when more than one delay occurs, the delay feedback function \(F_{j}\) should be regarded as a multi-variable function. This will make it more difficult to study the dynamic behaviors of (1.1) and (1.2).

On the other hand, it is of great practical significance to investigate the dynamic behaviors of a Nicholson’s blowflies model with patch structure. Consequently, the scalar equation (1.1) can be naturally generalized as the following nonlinear density-dependent mortality Nicholson’s blowflies model with patch structure:

$$\begin{aligned} x_{i }'(t) =&-\frac{a_{ii}(t)x_{i }(t)}{b_{ii}(t)+x_{i }(t) } +\sum _{j=1,j\neq i}^{n} \frac{a_{ij}(t)x_{j }(t)}{b_{ij}(t)+x_{j }(t) } \\ &{}+\sum_{j=1}^{m} \beta_{ij}(t)x_{i}\bigl(t-\tau_{ij}(t) \bigr)e^{- \gamma_{ij}(t)x_{i}(t-\sigma_{ij}(t))}, \quad i \in Q:=\{1,2,\ldots ,n\}, \end{aligned}$$
(1.3)

which in the classical case \(\tau_{ij}\equiv\sigma_{ij}\) (\(i \in Q\), \(j\in I\)) has been widely studied in the literature of the past [16–20]. In the ith patch, \(\frac{a_{ii}(t)x_{i }(t)}{b_{ii}(t)+x_{i }(t) }\) labels the death rate of the the current population level \(x_{i }(t)\); \(\beta_{ij}(t)x_{i}(t-\tau_{ij}(t))e^{-\gamma_{ij}(t)x_{i}(t- \sigma_{ij}(t))}\) designates the time-dependent birth function which requires maturation delays \(\tau_{ij}(t)\) and incubation delays \(\sigma_{ij}(t)\), and gets the maximum reproduction rate \(\frac{1}{\gamma_{ij}(t)}\); for \(i, j\in Q\) and \(j\neq i\), the weight function \(\frac{a_{ij}(t)x_{j }(t)}{b_{ij}(t)+x_{j }(t) } \) designates the population cooperative connection between jth patch and ith patch.

It should be mentioned that, up to now, the models (1.1), (1.2) and (1.3) relate to the global stability analysis of two or more delays are very few [1, 21–24]. For the special case of (1.2) with \(h_{j}\equiv g_{j}\) (\(j\in I\)), some delay-independent criteria ensuring the global asymptotic stability have been established in [25]. More precisely, the author in [25] obtained the global asymptotical stability of (1.2) on \(C([-\tau, 0], (0, +\infty)) \) and under the following assumptions:

$$ \max_{ j \in I}\gamma_{j}^{+} \leq1 , \qquad \sup_{t \in R} \sum_{j=1}^{m} \frac{\beta_{j} (t )}{ \gamma_{j} (t ) } < \frac{a ^{-}}{\max\{1, b^{+} \}}, \qquad \limsup _{t\rightarrow+\infty} \sum_{j=1}^{m} \frac{\beta_{j}(t )}{\gamma_{j} (t )} \frac{1}{e}< \frac{a^{-} }{b^{+ }+1}, $$
(1.4)

where \(\tau:=\max\{\max_{1\leq j \leq m} g_{j}^{+}, \max_{1\leq j \leq m} h_{j}^{+} \} >0 \), and \(g^{+}\) and \(g^{-}\) be defined as

$$ g^{+}=\sup_{t\in[t_{0}, +\infty)}g(t), \qquad g^{-}= \inf_{t\in[t_{0}, +\infty)}g(t) . $$

The deficiency is that we can find some errors in the process of proving the main consequence in [25]. In fact, as pointed in [26], in lines 3–4 of page 856 in [25], letting \(t\rightarrow\eta(\varphi)\) cannot result in \(\limsup_{t\rightarrow+\infty} \sum_{j=1}^{m} \frac{\beta_{j }(t)}{\gamma_{j}(t)a(t)} \frac{1}{e} \geq1 \) because of the fact that \(\eta(\varphi)=+\infty\) has not been proved. This suggests that the above-described literature leaves space for improvement.

Based on the above considerations, we study a nonlinear density-dependent mortality Nicholson’s blowflies system involving multiple pairs of time-varying delays described in (1.3). We shall establish a delay-independent criterion to ensure the global asymptotic stability of (1.3) without \(\tau_{ij}\equiv\sigma_{ij}\) (\(i\in Q\), \(j\in I\)), which has not been investigated till now. Moreover, our consequences generalize and improve all known consequences in [25, 26], and the error mentioned above has been corrected in Lemma 2.1.

For convenience, we suppose that \(a_{ii}\), \(b_{ii}\), \(\gamma_{ij}:\mathbb{R}\rightarrow(0, +\infty) \), \(a_{ij}\) (\(i \neq j\)), \(b_{ij}\) (\(i \neq j\)), \(\beta_{ij} , \tau_{ij}, \sigma_{ij}:\mathbb{R}\rightarrow[0, +\infty)\) for all \(i\in Q\), \(j\in I \) are bounded and continuous functions, and we denote

$$ r_{i}=\max\Bigl\{ \max_{ j \in I}{ \tau_{ij}^{+}}, \max_{ j \in I}{ \sigma_{ij}^{+}}\Bigr\} , \qquad \tau=\max _{ i \in Q}r_{i}, \qquad C_{+}= \prod _{i=1}^{n}C\bigl([-r_{i}, 0], [0, +\infty)\bigr). $$

For \(x=(x_{1},\ldots,x_{n}) \in\mathbb{R}^{n}\) and \(\varphi\in\prod_{i=1}^{n}C([-r_{i}, 0], [0, +\infty))\), define \(|x|=(|x_{1}|,\ldots,|x_{n}|) \), \(\Vert x\Vert_{\infty}=\max_{ i\in Q}|x_{i}|\), and \(\Vert\varphi\Vert =\max_{ i\in Q}\{\max_{t\in[-r_{i}, 0]}| \varphi_{i}(t)|\}\). Furthermore, it will be considered the following admissible initial conditions:

$$ x_{i}(t_{0}+\theta) =\varphi_{i}(\theta), \qquad \theta\in[-r_{i}, 0],\qquad \varphi\in C_{+}^{0}= \bigl\{ \varphi\in C_{+}| \varphi_{i}(0)>0, i \in Q\bigr\} . $$
(1.5)

We denote \(x(t; t_{0}, \varphi) \) as a solution of (1.3) with the initial value problem (1.5), and let \([t_{0}, \eta(\varphi))\) be the maximal right-interval of existence of \(x(t; t_{0}, \varphi) \). Moreover, by employing the local Lipschitz property of the right side function with regard to the nonnegative function space, we find that \(x(t; t_{0}, \varphi)\) exists and is unique.

2 Preliminary results

We first present the global existence of solutions for (1.3) with the admissible initial value problem (1.5).

Lemma 2.1

For all\(i\in Q\), \(j\in I\), assume that

$$ \limsup_{t\rightarrow+\infty} \Biggl[\sum_{j=1,j\neq i }^{n} \frac{a_{i j}(t)}{a_{i i }(t)} +\sum_{j=1}^{m} \frac{\beta_{i j }(t)}{a_{i i }(t)\gamma_{ i j}(t)} \frac{1}{e}\Biggr]< 1 $$
(2.1)

and

$$ \sigma_{ij}(t)\geq\tau_{ij}(t) \quad\textit{and} \quad \lim_{t \rightarrow+\infty}\bigl( \sigma_{ij}(t)- \tau_{ij}(t)\bigr) e^{\int_{t_{0}}^{t}[ \sum_{j=1,j\neq i }^{n} a_{i j}(v)+\sum_{j=1}^{m} \beta_{ij} (v)]\,dv}=0 $$
(2.2)

hold. Then, the solution\(x (t)=x(t; t_{0}, \varphi)\)is positive and bounded for all\(t\in[t_{0}, +\infty)\).

Proof

We first assert that

$$ x_{i}(t)>0 \quad\text{for all } t\in\big[t_{0}, \eta( \varphi)\big), i \in Q. $$
(2.3)

Suppose to the contrary that Eq. (2.3) does not hold, then there exist \(\omega\in Q\) and \(\bar{t }_{\omega}\in(t_{0}, \eta(\varphi))\) such that

$$ x_{\omega}(\bar{t }_{\omega})=0,\qquad x_{j}(t)>0 \quad \text{for all } t\in[t_{0} , \bar{t }_{\omega}), j\in Q . $$

Based on the fact that

$$ \textstyle\begin{cases} x_{\omega} (t_{0})=\varphi_{w} (0)>0, \\ x_{\omega} '(t) \geq - \frac{a _{\omega\omega}(t)}{b _{\omega\omega}(t) }x_{\omega} (t) +\sum_{j=1}^{m} \beta_{ \omega j} (t)x_{ \omega} (t-\tau_{\omega j} (t))e^{- \gamma_{\omega j} (t) x_{ \omega} (t- \sigma_{\omega j} (t))},\quad t\in[t_{0} , \bar{t }_{\omega}), \end{cases} $$

we obtain

$$\begin{aligned} 0 =& x_{\omega} (\bar{t }_{\omega}) \\ \geq& e^{-\int_{t_{0}}^{\bar{t }_{\omega}} \frac{a _{\omega\omega}(u)}{b _{\omega\omega}(u)}\,du}x_{\omega}(t_{0}) \\ &{} +e^{-\int_{t_{0}}^{\bar{t }_{\omega}} \frac{a _{\omega\omega}(u)}{b _{\omega\omega}(u)}\,du} \int_{t_{0}}^{ \bar{t }_{\omega}} e^{ \int_{t_{0}}^{s} \frac{a _{\omega\omega}(v)}{b _{\omega\omega}(v)}\,dv}\sum _{j=1}^{m} \beta_{ \omega j} (s)x_{ \omega} \bigl(s-\tau_{\omega j} (s)\bigr)e^{- \gamma_{\omega j} (s) x_{ \omega} (s- \sigma_{\omega j} (s))} \,ds \\ > & 0, \end{aligned}$$

which is a contradiction and results in the above assertion.

Now, we show that \(\eta(\varphi)=+\infty\). For all \(i\in Q\) and \(t\in[t_{0}, \eta(\varphi))\), define \(y_{i}(t)=\max\{1, \max_{t_{0}-r_{i} \leq s\leq t} x_{i} (s) \}\), we obtain

$$\begin{aligned} x_{i }'(t) \leq\sum_{j=1,j\neq i}^{n} a_{ij}(t) +\sum_{j=1}^{m} \beta_{ij}(t)x_{i}\bigl(t-\tau_{ij}(t)\bigr) \leq\Biggl[\sum_{j=1,j\neq i}^{n} a_{ij}(t) +\sum_{j=1}^{m} \beta_{ij}(t)\Biggr]y_{i}(t ) \end{aligned}$$

and

$$\begin{aligned} x _{i} (t) \leq& x _{i}(t_{0}) + \int_{t_{0}}^{t} \Biggl[\sum _{j=1,j \neq i}^{n} a_{ij}(v) +\sum _{j=1}^{m}\beta_{ij}(v)\Biggr] y _{i}(v)\,dv \\ \leq& \max\bigl\{ 1, \Vert \varphi \Vert \bigr\} + \int_{t_{0}}^{t}\Biggl[\sum _{j=1,j\neq i}^{n} a_{ij}(v) +\sum _{j=1}^{m}\beta_{ij}(v)\Biggr] y _{i}(v)\,dv, \end{aligned}$$

which suggests that

$$\begin{aligned} y _{i} (t)\leq\max\bigl\{ 1, \Vert \varphi \Vert \bigr\} + \int_{t_{0}}^{t}\Biggl[\sum _{j=1,j\neq i}^{n} a_{ij}(v) +\sum _{j=1}^{m}\beta_{ij}(v)\Biggr] y _{i}(v)\,dv, \quad\forall t \in[t_{0}, \eta(\varphi)), i\in Q. \end{aligned}$$

Hence, by the Gronwall–Bellman inequality, we obtain

$$\begin{aligned} x _{i} (t)\leq y_{i} (t)\leq\max\bigl\{ 1, \Vert \varphi \Vert \bigr\} e^{\int _{t_{0}}^{t}[\sum_{j=1,j\neq i}^{n} a_{ij}(v) +\sum_{j=1}^{m}\beta_{ij}(v)]\,dv} , \quad\forall t\in[t_{0}, \eta(\varphi)), i\in Q. \end{aligned}$$

It follows from Theorem 2.3.1 in [27] that \(\eta(\varphi)=+\infty\), and then

$$ x _{i} (t)\leq y _{i} (t)\leq\max\bigl\{ 1, \Vert \varphi \Vert \bigr\} e^{\int _{t_{0}}^{t}[\sum_{j=1,j\neq i}^{n} a_{ij}(v) +\sum_{j=1}^{m}\beta_{ij}(v)]\,dv} , $$
(2.4)

for all \(t\in[t_{0}, +\infty)\), \(i\in Q\).

Furthermore, for each \(t\in[t_{0}-r_{i}, +\infty) \), we define

$$ M_{i}(t)=\max\Bigl\{ \xi:\xi\leq t, x _{i}(\xi)=\max _{t_{0}-r_{i} \leq s\leq t} x_{i} (s)\Bigr\} . $$

Next, we show that \(x _{i}(t)\) is bounded on \([t_{0}, +\infty)\) for all \(i\in Q\). Otherwise, we can choose \(i_{0}\in Q\) such that

$$ \lim_{t\rightarrow+\infty}x_{i_{0}} \bigl(M_{i_{0}}(t) \bigr)=+ \infty, \quad\text{and}\quad \lim_{t\rightarrow+\infty }M_{i_{0}}(t)=+ \infty. $$
(2.5)

Note that, for \(t\ge t_{0}\), it follows that

$$\begin{aligned} x_{i_{0}}'(s) \le& \sum_{j=1,j\neq i_{0}}^{n} a_{i_{0}j}(s) +\sum_{j=1}^{m} \beta_{i_{0}j}(s) x_{i_{0}}\bigl(M_{i_{0}}(t)\bigr) \\ \le& \Biggl[\sum_{j=1,j\neq i_{0}}^{n} a_{i_{0}j}(s) +\sum_{j=1}^{m} \beta_{i_{0}j}(s)\Biggr]y_{i_{0}}\bigl(M_{i_{0}}(t) \bigr), \end{aligned}$$
(2.6)

for all \(s\in[t_{0}, t]\) and \(t\in[t_{0}, + \infty)\). This, combined with (1.3), (2.2), (2.3), (2.4) and the fact that \(\sup_{w\ge0} we^{-w}=\frac{1}{e}\), gives us

$$\begin{aligned} 0 \leq& x_{i_{0}} '\bigl(M_{i_{0}}(t)\bigr) \\ \leq& - \frac {a_{i_{0}i_{0}}(M_{i_{0}}(t))x_{i_{0}}(M_{i_{0}}(t))}{b_{i_{0}i_{0} }(M_{i_{0}}(t)) +x_{i_{0}}(M_{i_{0}}(t))} +\sum_{j=1,j\neq i_{0}}^{n} a_{i_{0}j}\bigl(M_{i_{0}}(t)\bigr) \\ &{}+\sum_{j=1}^{m} \beta_{i_{0}j }\bigl(M_{i_{0}}(t)\bigr) x_{i_{0}} \bigl(M_{i_{0}}(t)-\sigma_{i_{0}j} \bigl(M_{i_{0}}(t) \bigr)\bigr)e^{-\gamma_{i_{0}j}(M_{i_{0}}(t)) x_{i_{0}}(M_{i_{0}}(t)-\sigma_{i_{0}j}(M_{i_{0}}(t)))} \\ & {}+\sum_{j=1}^{m} \beta_{i_{0}j }\bigl(M_{i_{0}}(t)\bigr) \int_{M_{i_{0}}(t)- \sigma_{i_{0}j} (M_{i_{0}}(t))}^{M_{i_{0}}(t)-\tau_{i_{0}j} (M_{i_{0}}(t))}x_{i_{0}} '(s)\,ds e^{-\gamma_{i_{0}j}(M_{i_{0}}(t)) x_{i_{0}}(M_{i_{0}}(t)- \sigma_{i_{0}j} (M_{i_{0}}(t)))} \\ \leq& a_{i_{0}i_{0}}\bigl(M_{i_{0}}(t)\bigr)\Biggl[- \frac{ x_{i_{0}}(M_{i_{0}}(t))}{b_{i_{0}i_{0} }(M_{i_{0}}(t)) +x_{i_{0}}(M_{i_{0}}(t))} +\sum_{j=1,j\neq i_{0}}^{n} \frac{a_{i_{0}j}(M_{i_{0}}(t))}{a_{i_{0}i_{0}}(M_{i_{0}}(t))} \\ &{}+\sum_{j=1}^{m} \frac{\beta_{i_{0}j }(M_{i_{0}}(t))}{a_{i_{0}i_{0}}(M_{i_{0}}(t))\gamma_{i_{0}j}(M_{i_{0}}(t))} \gamma_{i_{0}j}\bigl(M_{i_{0}}(t) \bigr)x_{i_{0}} \bigl(M_{i_{0}}(t)-\sigma_{i_{0}j} \bigl(M_{i_{0}}(t)\bigr)\bigr) \\ &{} \times e^{-\gamma_{i_{0}j}(M_{i_{0}}(t)) x_{i_{0}}(M_{i_{0}}(t)- \sigma_{i_{0}j}(M_{i_{0}}(t)))}\Biggr] \\ &{} +\sum_{j=1}^{m} \beta_{i_{0}j }\bigl(M_{i_{0}}(t)\bigr) \int_{M_{i_{0}}(t)- \sigma_{i_{0}j} (M_{i_{0}}(t))}^{M_{i_{0}}(t)-\tau_{i_{0}j} (M_{i_{0}}(t))}\Biggl[ \sum _{j=1,j\neq i_{0}}^{n} a_{i_{0}j}(s) +\sum _{j=1}^{m} \beta_{i_{0}j}(s) \Biggr]y_{i_{0}}\bigl(M_{i_{0}}(t)\bigr)\,ds \\ \leq& a_{i_{0}i_{0}}\bigl(M_{i_{0}}(t)\bigr)\Biggl[- \frac{ x_{i_{0}}(M_{i_{0}}(t))}{b_{i_{0}i_{0} }(M_{i_{0}}(t)) +x_{i_{0}}(M_{i_{0}}(t))} +\sum_{j=1,j\neq i_{0}}^{n} \frac{a_{i_{0}j}(M_{i_{0}}(t))}{a_{i_{0}i_{0}}(M_{i_{0}}(t))} \\ &{}+\sum_{j=1}^{m} \frac{\beta_{i_{0}j }(M_{i_{0}}(t))}{a_{i_{0}i_{0}}(M_{i_{0}}(t))\gamma_{i_{0}j}(M_{i_{0}}(t))} \frac{1}{e}\Biggr] \\ &{} +\sum_{j=1}^{m} \beta_{i_{0}j }\bigl(M_{i_{0}}(t)\bigr) \bigl[ \sigma_{i_{0}j} \bigl(M_{i_{0}}(t)\bigr)-\tau_{i_{0}j} \bigl(M_{i_{0}}(t)\bigr) \bigr]e^{ \int_{t_{0}}^{M_{i_{0}}(t)}[\sum_{j=1,j\neq i_{0}}^{n} a_{i_{0}j}(v) +\sum_{j=1}^{m}\beta_{i_{0}j}(v)]\,dv} \\ &{}\times\Biggl[\sum_{j=1,j\neq i_{0}}^{n} a_{i_{0}j} ^{+} +\sum_{j=1}^{m} \beta_{i_{0}j} ^{+}\Biggr]\max\bigl\{ 1, \Vert \varphi \Vert \bigr\} \end{aligned}$$

and

$$\begin{aligned} 0 \leq& \Biggl[- \frac{ x_{i_{0}}(M_{i_{0}}(t))}{b_{i_{0}i_{0} }(M_{i_{0}}(t)) +x_{i_{0}}(M_{i_{0}}(t))} +\sum_{j=1,j\neq i_{0}}^{n} \frac{a_{i_{0}j}(M_{i_{0}}(t))}{a_{i_{0}i_{0}}(M_{i_{0}}(t))} \\ &{}+\sum_{j=1}^{m} \frac{\beta_{i_{0}j }(M_{i_{0}}(t))}{a_{i_{0}i_{0}}(M_{i_{0}}(t))\gamma_{i_{0}j}(M_{i_{0}}(t))} \frac{1}{e}\Biggr] \\ &{} +\frac{1}{a_{i_{0}i_{0}}(M_{i_{0}}(t))}\sum_{j=1}^{m} \beta_{i_{0}j }\bigl(M_{i_{0}}(t)\bigr) \bigl[ \sigma_{i_{0}j} \bigl(M_{i_{0}}(t)\bigr)-\tau_{i_{0}j} \bigl(M_{i_{0}}(t)\bigr) \bigr] \\ &{}\times e^{\int_{t_{0}}^{M_{i_{0}}(t)}[\sum_{j=1,j\neq i_{0}}^{n} a_{i_{0}j}(v) +\sum_{j=1}^{m}\beta_{i_{0}j}(v)]\,dv}\Biggl[\sum_{j=1,j\neq i_{0}}^{n} a_{i_{0}j} ^{+} +\sum_{j=1}^{m} \beta_{i_{0}j} ^{+}\Biggr]\max\bigl\{ 1, \Vert \varphi \Vert \bigr\} , \end{aligned}$$
(2.7)

where \(M_{i_{0}}(t)>2\tau+t_{0}\).

Letting \(t\rightarrow+\infty\), from the facts

$$ \lim_{t\rightarrow+\infty}\bigl[\sigma_{i_{0}j} (t)- \tau_{i_{0}j} (t) \bigr]e^{\int_{t_{0}}^{t}[\sum_{j=1,j\neq i_{0}}^{n} a_{i_{0}j}(v) +\sum_{j=1}^{m}\beta_{i_{0}j}(v)]\,dv}=0\quad \text{and}\quad \lim_{t\rightarrow+\infty}M_{i_{0}}(t)=+\infty, $$

Equation (2.7) yields

$$ 0 \leq-1 + \limsup_{t\rightarrow+\infty} \Biggl[\sum _{j=1,j \neq i_{0}}^{n} \frac{a_{i_{0}j}(t)}{a_{i_{0}i_{0}}(t)} +\sum _{j=1}^{m} \frac{\beta_{i_{0}j }(t)}{a_{i_{0}i_{0}}(t)\gamma_{i_{0}j}(t)} \frac{1}{e}\Biggr]< 0, $$

which is a contradiction and proves that \(x (t)\) is bounded for all \(t\in[t_{0}, +\infty)\). The proof is complete. □

3 Global asymptotic stability for (1.3)

Theorem 3.1

For all\(i\in Q\), \(j \in I\), let (2.2) and

$$ \left . \textstyle\begin{array}{ll} \max_{ i\in Q, j \in I} \limsup_{t\rightarrow+ \infty} \gamma_{ij}(t) \leq1, \\ \sup_{t\in[t_{0}, +\infty)}\max\{1, b_{i i }(t ) \}[ \sum_{j=1,j\neq i }^{n} \frac{a_{i j}(t ) }{a_{i i }(t ) b_{i j}(t )} +\sum_{j=1}^{m} \frac{\beta_{i j}(t )}{a_{i i }(t )}]< 1, \\ \limsup_{t\rightarrow+\infty} [1+b_{i i}(t )][\sum_{j=1,j\neq i }^{n} \frac{a_{i j}(t)}{a_{i i }(t) } +\sum_{j=1}^{m} \frac{\beta_{i j }(t)}{a_{i i }(t)\gamma_{ij}(t) }\frac{1}{e} ]< 1, \\ \limsup_{t\rightarrow+\infty} \max\{1, b_{i i }(t ) \}[ \sum_{j=1,j\neq i }^{n} \frac{a_{i j}(t)}{a_{i i }(t)b_{i j}(t )}e +\sum_{j=1}^{m} \frac{\beta_{i j }(t)}{a_{i i }(t)\gamma_{ij}(t) } ]< 1, \end{array}\displaystyle \right \} $$
(3.1)

be satisfied. Then the zero equilibrium point of (1.3) is globally asymptotically stable on\(C_{+}^{0} \).

Proof

Denote \(x(t; t_{0}, \varphi)\) by \(x (t)\). From Lemma 2.1, we find that the set of \(\{x(t; t_{0}, \varphi): t\in[t_{0}, +\infty)\}\) is bounded, and \(0\leq\limsup_{t\rightarrow+\infty} x_{i} (t ) <+\infty\) for all \(i\in Q\).

We first claim that the zero equilibrium point is stable. Without loss of generality, let \(0<\epsilon<1\) satisfy

$$ \sup_{t\in[t_{0}, +\infty)}\max\bigl\{ 1, b_{i i }(t ) \bigr\} \Biggl[ \sum_{j=1,j\neq i }^{n} \frac{a_{i j}(t ) }{a_{i i }(t ) b_{i j}(t )} +\sum_{j=1}^{m} \frac{\beta_{i j}(t )}{a_{i i }(t )}\Biggr] < e^{-\epsilon},\quad i\in Q . $$
(3.2)

Choose \(0<\delta<\epsilon\), we claim that, for \(\|\varphi\|<\delta\),

$$ x_{i}(t)=x_{i}(t; t_{0}, \varphi)< \epsilon \quad \text{for all } t \in[t_{0}, +\infty) \text{ and } i\in Q . $$
(3.3)

In the contrary case, there exist \(t_{*}\in(t_{0}, +\infty)\) and \(i_{*}\in Q\) such that

$$ x_{i_{*}}(t_{*})=\epsilon, \qquad x_{j}(t)< \epsilon \quad \text{for all } t\in [t_{0}-\sigma_{j}, t_{*}) \text{ and } j\in Q. $$
(3.4)

Note the fact that

$$ b_{i}(t)+x < \max\bigl\{ 1, b_{i}(t) \bigr\} e^{ x}\quad \text{for all } (t, x) \in[t_{0}, +\infty) \times(0, +\infty) \text{ and } i\in Q, $$
(3.5)

and from Eqs. (1.3), (3.2) and (3.4) we have the result that

$$\begin{aligned} 0 \leq& x_{i_{*}}'(t_{*}) \\ = & - \frac{a_{i_{*}i_{*}}(t_{*})\epsilon}{b_{i_{*}i_{*}}(t_{*})+\epsilon} +\sum_{j=1,j\neq i_{*}}^{n} \frac{a_{i_{*}j}(t_{*})x_{j}(t_{*})}{b_{i_{*}j}(t_{*})+x_{j}(t_{*})} \\ &{}+\sum_{j=1}^{m} \beta_{i_{*}j}(t_{*})x_{i_{*}} \bigl(t_{*}- \tau_{i_{*}j}(t_{*}) \bigr)e^{-\gamma_{i_{*}j}(t_{*})x_{i_{*}}(t_{*}- \sigma_{i_{*}j}(t_{*}))} \\ \leq& - \frac{a_{i_{*}i_{*}}(t_{*})}{\max\{1, b_{i_{*}i_{*}}(t_{*}) \}}\epsilon e^{-\epsilon} +\sum _{j=1,j \neq i_{*}}^{n} \frac{a_{i_{*}j}(t_{*})\epsilon}{b_{i_{*}j}(t_{*})} \\ &{}+\sum_{j=1}^{m} \beta_{i_{*}j}(t_{*})x_{i_{*}} \bigl(t_{*}- \tau_{i_{*}j}(t_{*}) \bigr)e^{-\gamma_{i_{*}j}(t_{*})x_{i_{*}}(t_{*}- \sigma_{i_{*}j}(t_{*}))} \\ = & a_{i_{*}i_{*}}(t_{*}) \Biggl\{ - \frac{1}{\max\{1, b_{i_{*}i_{*}}(t_{*}) \}} \epsilon e^{-\epsilon} +\sum_{j=1,j \neq i_{*}}^{n} \frac{a_{i_{*}j}(t_{*})\epsilon}{a_{i_{*}i_{*}}(t_{*}) b_{i_{*}j}(t_{*})} \\ &{}+\sum_{j=1}^{m} \frac{\beta_{i_{*}j}(t_{*})}{a_{i_{*}i_{*}}(t_{*})}x_{i_{*}}\bigl(t_{*}- \tau_{i_{*}j}(t_{*})\bigr)e^{-\gamma_{i_{*}j}(t_{*})x_{i_{*}}(t_{*}- \sigma_{i_{*}j}(t_{*}))} \Biggr\} \\ < & \frac{a_{i_{*}i_{*}}(t_{*})}{\max\{1, b_{i_{*}i_{*}}(t_{*}) \}} \Biggl\{ - e^{-\epsilon} +\max\bigl\{ 1, b_{i_{*}i_{*}}(t_{*}) \bigr\} \\ & {}\times\Biggl[\sum_{j=1,j\neq i_{*}}^{n} \frac{a_{i_{*}j}(t_{*}) }{a_{i_{*}i_{*}}(t_{*}) b_{i_{*}j}(t_{*})} +\sum_{j=1}^{m} \frac{\beta_{i_{*}j}(t_{*})}{a_{i_{*}i_{*}}(t_{*})}\Biggr] \Biggr\} \epsilon \\ \leq& \frac{a_{i_{*}i_{*}}(t_{*})}{\max\{1, b_{i_{*}i_{*}}(t_{*}) \}} \Biggl\{ - e^{-\epsilon} +\sup _{t\in[t_{0}, +\infty)}\max\bigl\{ 1, b_{i_{*}i_{*}}(t ) \bigr\} \\ &{} \times\Biggl[\sum_{j=1,j\neq i_{*}}^{n} \frac{a_{i_{*}j}(t ) }{a_{i_{*}i_{*}}(t ) b_{i_{*}j}(t )} +\sum_{j=1}^{m} \frac{\beta_{i_{*}j}(t )}{a_{i_{*}i_{*}}(t )}\Biggr] \Biggr\} \epsilon \\ < & 0, \end{aligned}$$

which is absurd and proves (3.3). Therefore, the zero equilibrium point is stable.

Next, we just need to prove that \(u =\max_{i\in Q}\limsup_{t\rightarrow+\infty} x _{i}(t ) =0\). From the fluctuation lemma [28, Lemma A.1], one can pick a sequence \(\{t_{k} \} _{k\geq1}\) and \(i^{*}\in Q\) such that

$$ t_{k}\to+\infty,\qquad x_{i^{*}} (t_{k}) \to u,\qquad x_{i^{*}} '(t_{k}) \to0\quad \text{as }k\to+\infty. $$

Moreover, from the boundedness of the coefficient and delay functions in (1.3), we can suppose that, for \(j\in I\),

$$\begin{aligned}& \begin{aligned}&\lim_{k \rightarrow+ \infty} a_{i^{*}j}(t_{k}) =a_{i^{*}j}^{*} \in\bigl[ a_{i^{*}j}^{-} , a_{i^{*}j}^{+} \bigr],\qquad \lim_{k \rightarrow+ \infty } b_{i^{*}j}(t_{k}) =b_{i^{*}j}^{*} \in\bigl[ b_{i^{*}j}^{-} , b_{i^{*}j}^{+} \bigr], \\ &\lim_{k \rightarrow+ \infty} \beta_{i^{*}j}(t_{k})= \beta_{i^{*}j}^{*} \in\bigl[ \beta_{i^{*}j}^{-} , \beta_{i^{*}j}^{+} \bigr], \\ &\lim_{k \rightarrow+ \infty} \gamma_{i^{*}j}(t_{k})= \gamma_{i^{*}j}^{*} \in\bigl[ \gamma_{i^{*}j}^{-} , \gamma_{i^{*}j}^{+} \bigr],\qquad \lim _{k \rightarrow+ \infty} \tau_{i^{*}j}(t_{k})= \tau_{i^{*}j}^{*} \in\bigl[ \tau_{i^{*}j}^{-} , \tau_{i^{*}j}^{+} \bigr], \\ &\lim_{k \rightarrow+ \infty} \sigma_{i^{*}j}(t_{k})= \sigma_{i^{*}j}^{*} \in\bigl[\sigma_{i^{*}j}^{-} , \sigma_{i^{*}j}^{+} \bigr],\qquad \lim _{k \rightarrow+ \infty}\gamma_{i^{*}j}(t_{k}) x_{i^{*}} \bigl(t_{k}-\sigma_{i^{*}j} (t_{k})\bigr)= \mu_{i^{*}j}^{*} \in[ 0, u ], \\ &\lim_{k \rightarrow+ \infty}\bigl(b_{i^{*}i^{*}}(t_{k}) +1\bigr) \Biggl(\sum_{j=1,j\neq i^{*}}^{n} \frac{a_{i^{*}j} (t_{k})}{a_{i^{*}i^{*}} (t_{k})}+ \sum_{j=1}^{m} \frac{\beta_{i^{*}j } (t_{k})}{a_{i^{*}i^{*}} (t_{k})\gamma_{i^{*}j} (t_{k})} \frac{1}{e} \Biggr) \\ &\quad =\bigl(b_{i^{*}i^{*}}^{*} +1\bigr) \Biggl(\sum _{j=1,j\neq i^{*}}^{n} \frac{a_{i^{*}j} ^{*}}{a_{i^{*}i^{*}} ^{*}}+ \sum _{j=1}^{m} \frac{\beta_{i^{*}j } ^{*}}{a_{i^{*}i^{*}} ^{*}\gamma_{i^{*}j} ^{*}} \frac{1}{e} \Biggr) \\ &\quad \leq \limsup_{t\rightarrow+\infty}\bigl(b_{i^{*}i^{*}}(t ) +1 \bigr) \Biggl( \sum_{j=1,j\neq i^{*}}^{n} \frac{a_{i^{*}j} (t )}{a_{i^{*}i^{*}} (t )}+ \sum_{j=1}^{m} \frac{\beta_{i^{*}j } (t )}{a_{i^{*}i^{*}} (t )\gamma_{i^{*}j} (t )} \frac{1}{e} \Biggr)< 1 , \end{aligned} \end{aligned}$$
(3.6)

and

$$\begin{aligned}& \lim_{k \rightarrow+ \infty}\max\bigl\{ 1, b_{i^{*}i^{*}} (t_{k}) \bigr\} \Biggl(\sum_{j=1,j\neq i^{*}}^{n} \frac{a_{i^{*}j} (t_{k})}{a_{i^{*}i^{*}} (t_{k})b_{i^{*}j} (t_{k})}e +\sum_{j=1}^{m} \frac{\beta_{i^{*}j } (t_{k})}{a_{i^{*}i^{*}}(t_{k}) \gamma_{i^{*}j} (t_{k})} \Biggr) \\& \quad =\max\bigl\{ 1, b_{i^{*}i^{*}}^{*}\bigr\} \Biggl(\sum _{j=1,j\neq i^{*}}^{n} \frac{a_{i^{*}j} ^{*}}{a_{i^{*}i^{*}} ^{*}b_{i^{*}j} ^{*}}e +\sum _{j=1}^{m} \frac{\beta_{i^{*}j } ^{*}}{a_{i^{*}i^{*}} ^{*}\gamma_{i^{*}j} ^{*}} \Biggr) \\& \quad \leq \limsup_{t\rightarrow+\infty}\max\bigl\{ 1, b_{i^{*}i^{*}} (t )\bigr\} \Biggl(\sum_{j=1,j\neq i^{*}}^{n} \frac{a_{i^{*}j} (t )}{a_{i^{*}i^{*}} (t )b_{i^{*}j} (t )}e +\sum_{j=1}^{m} \frac{\beta_{i^{*}j } (t )}{a_{i^{*}i^{*}}(t ) \gamma_{i^{*}j} (t )} \Biggr)< 1 . \end{aligned}$$
(3.7)

Furthermore, from (1.3), (2.2), (2.4), we get

$$\begin{aligned} x _{i^{*}}'(t_{k}) = & - \frac {a_{i^{*}i^{*}}(t_{k})x_{i^{*}}(t_{k})}{b_{i^{*}i^{*}}(t_{k})+x_{i^{*}}(t_{k})} +\sum_{j=1,j\neq i^{*}}^{n} \frac{ a_{i^{*}j}(t_{k})x_{j}(t_{k})}{b_{i^{*}j}(t_{k})+x_{j}(t_{k})} \\ & {}+\sum_{j=1}^{m} \beta_{i^{*}j }(t_{k}) x_{i^{*}} \bigl(t_{k}- \sigma_{i^{*}j} (t_{k}) \bigr)e^{-\gamma_{i^{*}j}(t_{k}) x_{i^{*}}(t_{k}- \sigma_{i^{*}j}(t_{k}))} \\ &{} +\sum_{j=1}^{m} \beta_{i^{*}j }(t_{k}) \int_{t_{k}- \sigma_{i^{*}j}(t_{k})}^{t_{k}-\tau_{i^{*}j}(t_{k})}x _{i^{*}}'(s) \,ds e^{-\gamma_{i^{*}j}(t_{k}) x_{i^{*}}(t_{k}-\sigma_{i^{*}j}(t_{k}))} \\ \leq& a_{i^{*}i^{*}}(t_{k}) \Biggl\{ - \frac{x_{i^{*}}(t_{k})}{b_{i^{*}i^{*}}(t_{k})+x_{i^{*}}(t_{k})} + \sum_{j=1,j\neq i^{*}}^{n} \frac{ a_{i^{*}j}(t_{k})x_{j}(t_{k})}{ a_{i^{*}i^{*}}(t_{k})[b_{i^{*}j}(t_{k})+x_{j}(t_{k})]} \\ &{} +\sum_{j=1}^{m} \frac{\beta_{i^{*}j }(t_{k})}{a_{i^{*}i^{*}}(t_{k})\gamma_{i^{*}j}(t_{k})} \gamma _{i^{*}j}(t_{k})x_{i^{*}} \bigl(t_{k}-\sigma_{i^{*}j} (t_{k}) \bigr)e^{-\gamma_{i^{*}j}(t_{k}) x_{i^{*}}(t_{k}- \sigma_{i^{*}j}(t_{k}))} \\ & {}+\sum_{j=1}^{m} \frac{\beta_{i^{*}j }(t_{k})}{a_{i^{*}i^{*}}(t_{k})} \int_{t_{k}- \sigma_{i^{*}j}(t_{k})}^{t_{k}-\tau_{i^{*}j}(t_{k})}\Biggl[\sum _{j=1,j \neq i^{*}}^{n} a_{i^{*}j}(s) +\sum _{j=1}^{m}\beta_{i^{*}j}(s) \Biggr]y_{i^{*}}(t_{k} )\,ds \Biggr\} \\ \leq& a_{i^{*}i^{*}}(t_{k}) \Biggl\{ - \frac{x_{i^{*}}(t_{k})}{b_{i^{*}i^{*}}(t_{k})+x_{i^{*}}(t_{k})} + \sum_{j=1,j\neq i^{*}}^{n} \frac{ a_{i^{*}j}(t_{k})x_{j}(t_{k})}{ a_{i^{*}i^{*}}(t_{k})[b_{i^{*}j}(t_{k})+x_{j}(t_{k})]} \\ &{} +\sum_{j=1}^{m} \frac{\beta_{i^{*}j }(t_{k})}{a_{i^{*}i^{*}}(t_{k})\gamma_{i^{*}j}(t_{k})} \gamma _{i^{*}j}(t_{k})x_{i^{*}} \bigl(t_{k}-\sigma_{i^{*}j} (t_{k}) \bigr)e^{-\gamma_{i^{*}j}(t_{k}) x_{i^{*}}(t_{k}- \sigma_{i^{*}j}(t_{k}))} \\ & {}+\sum_{j=1}^{m} \frac{\beta_{i^{*}j }(t_{k})}{a_{i^{*}i^{*}}(t_{k})} \bigl(\sigma_{i^{*}j}(t_{k})- \tau_{i^{*}j}(t_{k}) \bigr) \\ & {}\times e^{\int_{t_{0}}^{t_{k}}[\sum_{j=1,j\neq i^{*}}^{n} a_{i^{*}j}(v) +\sum_{j=1}^{m}\beta_{i^{*}j}(v)]\,dv} \Biggl(\sum_{j=1,j\neq i^{*}}^{n} a_{i^{*}j} ^{+} +\sum_{j=1}^{m} \beta_{i^{*}j} ^{+}\Biggr) \max\bigl\{ 1, \Vert \varphi \Vert \bigr\} \Biggr\} \end{aligned}$$

and

$$\begin{aligned}& \frac{1}{a_{i^{*}i^{*}}(t_{k})}x_{i^{*}} '(t_{k}) \\& \quad \leq - \frac{x_{i^{*}}(t_{k})}{b_{i^{*}i^{*}}(t_{k})+x_{i^{*}}(t_{k})} + \sum_{j=1,j\neq i^{*}}^{n} \frac{ a_{i^{*}j}(t_{k})x_{j}(t_{k})}{ a_{i^{*}i^{*}}(t_{k})[b_{i^{*}j}(t_{k})+x_{j}(t_{k})]} \\& \qquad {} +\sum_{j=1}^{m} \frac{\beta_{i^{*}j }(t_{k})}{a_{i^{*}i^{*}}(t_{k})\gamma_{i^{*}j}(t_{k})}\gamma _{i^{*}j}(t_{k})x_{i^{*}} \bigl(t_{k}-\sigma_{i^{*}j} (t_{k}) \bigr)e^{-\gamma_{i^{*}j}(t_{k}) x_{i^{*}}(t_{k}- \sigma_{i^{*}j}(t_{k}))} \\& \qquad {} +\sum_{j=1}^{m} \frac{\beta_{i^{*}j }(t_{k})}{a_{i^{*}i^{*}}(t_{k})} \bigl(\sigma_{i^{*}j}(t_{k})- \tau_{i^{*}j}(t_{k}) \bigr) \\& \qquad {} \times e^{\int_{t_{0}}^{t_{k}}[\sum_{j=1,j\neq i^{*}}^{n} a_{i^{*}j}(v) +\sum_{j=1}^{m}\beta_{i^{*}j}(v)]\,dv} \Biggl(\sum_{j=1,j\neq i^{*}}^{n} a_{i^{*}j} ^{+} +\sum_{j=1}^{m} \beta_{i^{*}j} ^{+}\Biggr) \max\bigl\{ 1, \Vert \varphi \Vert \bigr\} , \end{aligned}$$
(3.8)

where \(t_{k}>2\tau+t_{0}\). If \(u\geq1\), from (2.2), (3.1), (3.6), (3.8) and the facts that \(\frac{u}{b _{ii}^{*}+u}\geq\frac{1}{b_{ii} ^{*}+1}\) and \(\sup_{u\geq0} ue^{- u}=\frac{1}{ e}\), letting \(k\rightarrow+\infty\) leads to

$$\begin{aligned} 0 \leq&-\frac{1}{b_{i^{*}i^{*}}^{*} +1} +\sum_{j=1,j\neq i^{*}}^{n} \frac{a_{i^{*}j} ^{*}u}{a_{i^{*}i^{*}} ^{*}(b_{i^{*}j} ^{*}+u)} +\sum_{j=1}^{m} \frac{\beta_{i^{*}j } ^{*}}{a_{i^{*}i^{*}} ^{*}\gamma_{i^{*}j} ^{*}} \frac{1}{e} \\ < &\frac{1}{b_{i^{*}i^{*}}^{*} +1} \Biggl[-1 +\bigl(b_{i^{*}i^{*}}^{*} +1\bigr) \Biggl( \sum_{j=1,j\neq i^{*}}^{n} \frac{a_{i^{*}j} ^{*}}{a_{i^{*}i^{*}} ^{*}}+ \sum_{j=1}^{m} \frac{\beta_{i^{*}j } ^{*}}{a_{i^{*}i^{*}} ^{*}\gamma_{i^{*}j} ^{*}} \frac{1}{e} \Biggr)\Biggr] < 0, \end{aligned}$$

which is a contradiction and we have the result that \(0\leq u<1\).

If \(0< u< 1\), from (2.2), (3.1), (3.5), (3.7), (3.8) and the fact that

$$ xe^{-x}\quad \text{is monotonously increasing on } [0, 1] , $$

we have

$$\begin{aligned}& \frac{1}{a_{i^{*}i^{*}}(t_{k})}x_{i^{*}} '(t_{k}) \\& \quad \leq \frac{1}{\max\{1, b_{i^{*}i^{*}}(t_{k})\} } \Biggl\{ - x_{i^{*}}(t_{k})e^{-x_{i^{*}}(t_{k})} +\max\bigl\{ 1, b_{i^{*}i^{*}}(t_{k})\bigr\} \Biggl[\sum _{j=1,j\neq i^{*}}^{n} \frac{ a_{i^{*}j}(t_{k})x_{j}(t_{k})}{ a_{i^{*}i^{*}}(t_{k}) b_{i^{*}j}(t_{k}) } \\& \qquad {} +\sum_{j=1}^{m} \frac{\beta_{i^{*}j }(t_{k})}{a_{i^{*}i^{*}}(t_{k})\gamma_{i^{*}j}(t_{k})}\gamma _{i^{*}j}(t_{k})x_{i^{*}} \bigl(t_{k}-\sigma_{i^{*}j} (t_{k}) \bigr)e^{-\gamma_{i^{*}j}(t_{k}) x_{i^{*}}(t_{k}- \sigma_{i^{*}j}(t_{k}))} \\& \qquad {} +\sum_{j=1}^{m} \frac{\beta_{i^{*}j }(t_{k})}{a_{i^{*}i^{*}}(t_{k})} \bigl(\sigma_{i^{*}j}(t_{k})- \tau_{i^{*}j}(t_{k}) \bigr)e^{\int_{t_{0}}^{t_{k}}[\sum_{j=1,j \neq i^{*}}^{n} a_{i^{*}j}(v) +\sum_{j=1}^{m}\beta_{i^{*}j}(v)]\,dv} \\& \qquad {} \times\Biggl(\sum_{j=1,j\neq i^{*}}^{n} a_{i^{*}j} ^{+} + \sum_{j=1}^{m} \beta_{i^{*}j} ^{+}\Biggr) \max\bigl\{ 1, \Vert \varphi \Vert \bigr\} \Biggr] \Biggr\} ,\quad \text{where } t_{k}>2 \tau+t_{0}, \end{aligned}$$

and then

$$\begin{aligned} 0 \leq& -u e^{-u} +\max\bigl\{ 1, b_{i^{*}i^{*}}^{*} \bigr\} \Biggl(\sum_{j=1,j \neq i^{*}}^{n} \frac{a_{i^{*}j} ^{*}}{a_{i^{*}i^{*}} ^{*}b_{i^{*}j} ^{*}}u +\sum_{j=1}^{m} \frac{\beta_{i^{*}j } ^{*}}{a_{i^{*}i^{*}} ^{*}\gamma_{i^{*}j} ^{*}} \mu^{*}_{i^{*}j} e^{ -\mu^{*}_{ i^{*}j}} \Biggr) \\ < & \Biggl[-1 +\max\bigl\{ 1, b_{i^{*}i^{*}}^{*}\bigr\} \Biggl(\sum_{j=1,j\neq i^{*}}^{n} \frac{a_{i^{*}j} ^{*}}{a_{i^{*}i^{*}} ^{*}b_{i^{*}j} ^{*}}e +\sum_{j=1}^{m} \frac{\beta_{i^{*}j } ^{*}}{a_{i^{*}i^{*}} ^{*}\gamma_{i^{*}j} ^{*}} \Biggr)\Biggr]ue^{-u} \\ < & 0, \end{aligned}$$

which is absurd and proves that \(u=0\). The proof is complete. □

Remark 3.1

Obviously, for the scalar equation (1.2), all the results of [25, 26] are special cases in Theorem 3.1 because the adopted assumptions are weaker.

4 A numerical example

This section presents a numerical example to illustrate the applicability of the analytical results derived in this article.

Example 4.1

Consider the following equations:

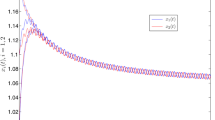
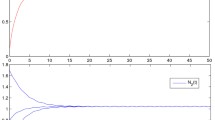
$$ \textstyle\begin{cases} x'_{1} (t) = -\frac{(2+\cos t)x_{1}(t)}{3+x_{1}(t)}+ \frac{\frac{1}{10}(1+\cos t)x_{2}(t)}{2+x_{2}(t)} \\ \hphantom{x'_{1} (t) =}{}+\frac{1}{60}(1+\sin^{2}t)x_{1}(t-2e^{|\arctan t|})e^{- (1+ \frac{100}{1+t^{2}})x_{1}(t-2e^{|\arctan t|}-100e^{-1.5t})} \\ \hphantom{x'_{1} (t) =}{}+ \frac{1}{80}(1+\sin^{2}2t)x_{1}(t-2e^{| \arctan2t|})e^{- (1+\frac{200}{1+t^{2}}) x_{1}(t-2e^{|\arctan 2t|}-150e^{-1.5t})}, \\ x'_{2} (t) = -\frac{(2+\sin t)x_{2}(t)}{4+x_{2}(t)}+ \frac{\frac{1}{20}(1+\cos2t)x_{1}(t)}{2+x_{1}(t)} \\ \hphantom{x'_{2} (t) =}{}+\frac{1}{130}(1+\cos^{2}t)x_{2}(t-2e^{|\arctan4t|})e^{- (1+ \frac{100}{1+t^{2}})x_{2}(t-2e^{|\arctan4t|}-100e^{-1.4t})} \\ \hphantom{x'_{2} (t) =}{}+ \frac{1}{150}(1+\cos^{4}2t)x_{2}(t-2e^{| \arctan4t|})e^{- (1+\frac{200}{1+t^{2}}) x_{2}(t-2e^{|\arctan 4t|}-145e^{-1.45t})}. \end{cases} $$
(4.1)

Obviously, it is elementary to check that the assumptions (2.2) and (3.1) are satisfied in (4.1). Therefore, by Theorem 3.1, we find that \((0, 0)\) is a globally asymptotically stable equilibrium point on \(C_{+}^{0} =\{\varphi\in C([-(2e^{ \frac{\pi}{2}}+150), 0], [0, + \infty)) \times C([-(2e^{\frac{\pi}{2}}+145), 0], [0, +\infty)) \text{ and } \varphi_{i}(0)>0, i=1,2\}\). Figure 1 reveals the above consequences through a numerical solution of different initial values.

Figure 1
figure 1

Numerical solutions \(x(t)\) on system (4.1). Numerical solutions \(x(t)\) to Example 4.1 with initial values: \(( \sin t+1,-\cos t-3,\cos t,\sin t)\), \((2\cos t+2, 3\sin t-1,-2\sin t,3 \cos t)\), \((-3\sin t-2,-4\sin t+3,-3\cos t,-4\cos t)\).

Full size image

Remark 4.1

It should be pointed out that the global asymptotic stability on the patch structure Nicholson’s blowflies systems with nonlinear density-dependent mortality terms and multiple pairs of time-varying delays has not been touched in the previous literature. As in [16–26] and [29–74], the authors still do not make a point of the global asymptotic stability on the Nicholson’s blowflies systems involving multiple pairs of time-varying delays, and we also mention that none of the consequences in [16–26] and [29–97] can obtain the convergence of the zero equilibrium point in (4.1).

5 Conclusions

In the present manuscript, we studied nonlinear density-dependent mortality Nicholson’s blowflies systems with patch structure, in which the delays are time-varying and come in multiple pairs. Here, we develop a method based on differential inequality techniques combining the application of the fluctuation lemma to obtain some sufficient conditions for the global asymptotic stability of the given system. The derived results of this manuscript complement some earlier publications to some extent. To the best of our knowledge, it is the first time one deals with this aspect. In addition, the method used in this paper provides a possible method for studying the global asymptotic stability of other patch structure population dynamic models with multiple pairs of different time-varying delays.