Abstract
We study positive almost periodic solutions for a delayed Nicholson’s blowflies system with nonlinear density-dependent mortality terms and patch structure. By applying the differential inequality technique and the Lyapunov functional, we derive sufficient conditions for the existence and global exponential stability of positive almost periodic solutions. We also give an example and its numerical simulations to support the theoretical effectiveness.
Similar content being viewed by others
1 Introduction
To describe the population of Australian sheep-blowfly and agree well with the experimental data of Nicholson [1], Gurney et al. [2] proposed the following famous Nicholson’s blowflies equation
Here, is the size of the population at time t, p is the maximum per capita daily egg production, is the size at which the population reproduces at its maximum rate, δ is the per capita daily adult death rate, and τ is the generation time. The results on the dynamics behavior of this equation and its modifications are abundant [3–21] and systematically collected and compared by Berezansky et al. [22]. In the real world phenomena, since the almost periodic variation of the environment plays a crucial role in many biological and ecological dynamical systems and is more frequent and general than the periodic variation of the environment, some influential theory and results have been obtained in [23, 24]. Furthermore, there have been extensive results on the problem of the existence of positive almost periodic solutions for Nicholson’s blowflies equation without nonlinear density-dependent mortality term in the literature [25–27] which are considered only with a linear density-dependent mortality term. Recently, considering that new fishery models with nonlinear density-dependent mortality rates are successfully applied, Berezansky et al. [22] presented the following Nicholson’s blowflies model with a nonlinear density-dependent mortality term:
where P is a positive constant and the function D might have one of the following forms: or with positive constants a, b. Up to present, several authors in [28–35] have researched the permanence and existence of positive periodic and almost periodic solutions for model (1.2) and its generalized model. Moreover, Wang [36] studied the exponential extinction for the following delayed Nicholson’s blowflies system with nonlinear density-dependent mortality terms and patch structure:
where
However, as far as we know, there exist few works on the global exponent stability of positive almost periodic solutions for a Nicholson’s blowflies system with nonlinear density-dependent mortality terms and patch structure. Motivated by the above arguments, in this paper, we investigate the existence and global exponential stability of positive almost periodic solutions for the following delayed Nicholson’s blowflies system with nonlinear density-dependent mortality terms and patch structure:
where and are continuous almost periodic functions with , . It is easy to see that (1.4) is a special case of (1.3) with .
It is convenient and simple to introduce some notations. Given a bounded continuous function f defined on R, we denote and as
It will be assumed that and, without loss of generality (after scaling), that , , . Let be the set of all (nonnegative) real vectors, we will use to denote a column vector, in which the symbol denotes the transpose of a vector. We let denote the absolute-value vector given by and define . Denote and as a Banach space equipped with the supremum norm defined by for all (or ). If is defined on with , and , then we define as , where for all and .
It is biologically reasonable to assume that only positive solutions of model (1.4) are meaningful and therefore admissible. So we consider the admissible initial conditions
Define a continuous map by setting
Then f is a locally Lipschitz map with respect to , which ensures the existence and uniqueness of the solution of (1.4) with admissible initial conditions (1.5).
We denote () for a solution of the initial value problem (1.4) and (1.5). Also, let be the maximal right-interval of existence of .
The remaining part of this paper is structured as follows. We devote Section 2 to some definitions and lemmas on the bounded set and almost periodicity for system (1.4) which help to deduce the existence, uniqueness and global exponential stability of positive almost periodic solutions in Section 3. In Section 4 an example and its numerical simulations are provided to verify our results obtained in the previous sections.
2 Preliminary results
As it is easy to analyze the property of functions and in the range , one can get that there exist only and such that
The following definitions and lemmas will be used to prove our main results in Section 3.
Let be continuous in t. is said to be almost periodic on if for any , the set is relatively dense, i.e., for any , it is possible to find a real number such that for any interval with length , there exists a number in this interval such that . From the theory of almost periodic functions in [23, 24], it follows that for any , it is possible to find a real number ; for any interval with length , there exists a number in this interval such that
for all , and .
Lemma 2.1 Suppose that there exists a positive constant M such that
Then every solution of (1.4) and (1.5) is positive and bounded on and . Moreover, there exists such that
Proof Let . Firstly, we assert that
With the reduction to absurdity, assume that there exist and such that
Calculating the derivative of , (1.4), the second inequalities of (2.4) and (2.7) imply that
which is paradoxical and implies that (2.6) holds.
Next we show that is bounded on . For each , , we define
In the contrary case, suppose that there exists such that is unbounded on . Then, observe as , we get
On the other hand,
Hence, together with the reality that and (1.4), we have
Taking results in
which is absurd and implies that is bounded on . From Theorem 2.3.1 in [37], we easily obtain .
Another step is to prove that there exists such that
Otherwise, there exists such that
which together with the first inequalities of (2.4) and (2.6) implies that
It leads to
Thus
which contradicts (2.6). Hence (2.9) holds. We now prove that
Suppose, for the sake of contradiction, that there exist and such that
Calculating the derivative of , together with the fact that , (1.4), the first inequalities of (2.4) and (2.11) imply that
which is a contradiction and implies that (2.10) holds.
Finally, we show that for all . By a way of contradiction, we assume that there exists such that . By the fluctuation lemma [[38], Lemma A.1.], there exists a sequence such that
Since is bounded and equicontinuous, by the Ascoli-Arzelà theorem, there exists a subsequence, still denoted by itself for simplicity of notation, such that
Moreover,
Without loss of generality, we assume that all , , , and are convergent to , , , and , respectively, and , . This can be achieved because of almost periodicity. Then by (1.5) and (2.3) we arrive at
It follows from
that (taking limits)
which is a contradiction. This proves that for all . Hence, from (2.10), we can choose such that
The proof is now completed. □
Lemma 2.2 Suppose that (2.3) and (2.4) hold, and
Moreover, let be a solution of equation (1.4) with initial condition (1.5) and is bounded continuous on , . Then, for any , there exists such that every interval contains at least one number δ for which there exists satisfies
Proof For all , define continuous functions by setting
Then, from (2.12), we obtain
which implies that there exist two constants and such that
For , , we add the definition of with . Set
By Lemma 2.1, the solution is bounded and
which implies that the right-hand side of (1.4) is also bounded, and is a bounded function on , . Thus, in view of the fact that for , , we obtain that is uniformly continuous on R. From (2.2), for any ε, there exists such that every interval contains δ for which
Let and denote , where , . Then, for all , we have
Set
Let be such an index that
Calculating the upper left derivative of along with (2.18), together with (2.1), (2.15), (2.16), (2.19) and the inequalities
and
we get
which is held under the following fact:
Let
It is obvious that and is non-decreasing. Now, we distinguish two cases to finish the proof.
Case one.
We claim that
Assume, by a way of contradiction, that (2.26) does not hold. Then there exists such that . Since
there must exist such that
which contradicts (2.25) and implies that (2.26) holds. It follows that there exists such that
Case two. There is such that . Then, in view of (2.14), (2.17) and (2.23), we have
which yields that
For any , with the same approach as that in deriving of (2.29), we can show
if . On the other hand, if and , we can choose such that
which together with (2.30) yields
With a similar argument as that in the proof of case one, we can show that
which implies that
In summary, there must exist such that holds for all . This completes the proof. □
3 Main results
In this section, we establish sufficient conditions for the existence and global exponential stability of positive almost periodic solutions of (1.4).
Theorem 3.1 Suppose that all conditions in Lemma 2.2 are satisfied. Then system (1.4) has at least one positive almost periodic solution . Moreover, is globally exponentially stable, i.e., there exist constants , and such that
Proof Let be a solution of equation (1.4) with initial conditions satisfying the assumptions in Lemma 2.2. We also add the definition of with for all , . Set
where is any sequence of real numbers. By Lemma 2.1, the solution is bounded and
which implies that the right-hand side of (1.4) is also bounded, and () are bounded functions on . Thus, in view of the fact that for all , , we obtain that () are uniformly continuous on R. Then, from the almost periodicity of , , , and , we can select a sequence such that
for all and , .
Since () is uniformly bounded and equi-uniformly continuous, by the Arzelà-Ascoli lemma and the diagonal selection principle, we can choose a subsequence of such that (for convenience, we still denote it by , ) uniformly converges to a continuous function () on any compact set of R, and
Now, we prove that is a solution of (1.4). In fact, for any and , from (3.3), we have
where , . Consequently, (3.5) implies that
Therefore, is a solution of (1.4).
Next we prove that is an almost periodic solution of (1.4). From Lemma 2.2, for any , there exists such that every interval contains at least one number δ for which there exists satisfies
Then, for any fixed , we can find a sufficiently large positive integer such that for any ,
Let , we obtain
which implies that is an almost periodic solution of system (1.4).
Finally, we prove that is globally exponentially stable.
Let and , where , , . Then
It follows from Lemma 2.1 that there exists such that
We consider the Lyapunov functional
For all and , calculating the upper left derivative of along with the solution of (3.9), we have
In the sequel, we claim that
Contrarily, there must exist and such that
Since
together with (2.20)-(2.22), (3.10), (3.12) and (3.14), we get
Thus,
which contradicts (2.14). Hence (3.13) holds. It follows that
This completes the proof. □
4 An example
In this section, we give an example and numerical simulations to explain the results obtained in the previous sections.
Example 4.1 Consider the following Nicholson’s blowflies system with nonlinear density-dependent mortality terms and patch structure:
Obviously, , , , , , , , , , , , . Let , from (2.1), we obtain , , and
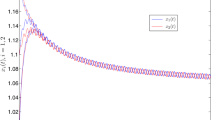
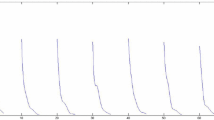
which imply that the Nicholson’s blowflies system (4.1) satisfies (2.2), (2.3) and (2.11). Therefore, system (4.1) has a positive almost periodic solution which is globally exponentially stable with the exponential convergent rate . The numerical simulationsin Figure 1 strongly support the consequence.
Remark 4.1 To the best of our knowledge, few authors have considered the problems of the global exponential stability of positive almost periodic solutions for a Nicholson’s blowflies system with nonlinear density-dependent mortality terms and patch structure. It is clear that all the results in [25–35] and the references therein cannot be applicable to prove that all the solutions of (4.1) converge exponentially to the positive almost periodic solution. This implies that the results of this paper are essentially new.
References
Nicholson AJ: An outline of the dynamics of animal populations. Aust. J. Zool. 1954, 2: 9-25. 10.1071/ZO9540009
Gurney WSC, Blythe SP, Nisbet RM: Nicholson’s blowflies revisited. Nature 1980, 287: 17-21. 10.1038/287017a0
So J, Yu JS: Global attractivity and uniform persistence in Nicholson’s blowflies. Differ. Equ. Dyn. Syst. 1994, 2: 11-18.
Kulenović MRS, Ladas G, Sficas Y: Global attractivity in Nicholson’s blowflies. Appl. Anal. 1992, 43: 109-124. 10.1080/00036819208840055
Kulenović MRS, Ladas G: Linearized oscillations in population dynamics. Bull. Math. Biol. 1987, 49(5):615-627. 10.1007/BF02460139
Feng Q, Yan J: Global attractivity and oscillation in a kind of Nicholson’s blowflies. J. Biomath. 2002, 17: 21-26.
Gyori I, Ladas G: Oscillation Theory of Delay Differential Equations with Applications. Clarendon Press, New York; 1991.
Gyori I, Trofimchuk S: On the existence of rapidly oscillatory solutions in the Nicholson blowflies equation. Nonlinear Anal. 2002, 48: 1033-1042. 10.1016/S0362-546X(00)00232-7
Giang D, Lenbury Y, Seidman T: Delay effects of population growth. J. Math. Anal. Appl. 2005, 305: 631-643. 10.1016/j.jmaa.2004.12.018
Kulenović MRS, Ladas G, Sficas Y: Global attractivity in population dynamics. Comput. Math. Appl. 1989, 18: 925-928. 10.1016/0898-1221(89)90010-2
Kulenović MRS, Ladas G: Linearized oscillations in population dynamics. Bull. Math. Biol. 1987, 49: 615-627. 10.1007/BF02460139
Kuang Y Mathematics in Science and Engineering 191. In Delay Differential Equations with Applications in Population Dynamics. Academic Press, Boston; 1993.
Liz E: Four theorems and one conjecture on the global asymptotic stability of delay differential equation. In The First 60 Years of Nonlinear Analysis of Jean Mawhin. Word Scientific, River Edge; 2004:117-129.
Wei J, Li M: Hopf bifurcation analysis in a delayed Nicholson blowflies equation. Nonlinear Anal. 2005, 60(7):1351-1367. 10.1016/j.na.2003.04.002
Li M, Yan J: Oscillation and global attractivity of generalized Nicholson’s blowfly model. In Differential Equations and Computational Simulations. Word Scientific, River Edge; 2000:196-201. (Chengdu, 1999)
Saker S, Agarwal S: Oscillation and global attractivity in a periodic Nicholson’s blowflies model. Math. Comput. Model. 2002, 35: 719-731. 10.1016/S0895-7177(02)00043-2
Li J: Global attractivity in Nicholson’s blowflies. Appl. Math. J. Chin. Univ. Ser. B 1996, 11: 425-434. 10.1007/BF02662882
Chen Y: Periodic solutions of delayed periodic Nicholson’s blowflies models. Can. Appl. Math. Q. 2003, 11: 23-28.
Braverman E, Kinzebulatov D: Nicholson’s blowflies equation with a distributed delay. Can. Appl. Math. Q. 2006, 14: 107-128.
Li J, Du C: Existence of positive periodic solutions for a generalized Nicholson blowflies model. J. Comput. Appl. Math. 2008, 221: 226-233. 10.1016/j.cam.2007.10.049
Li WT, Fan YH: Existence and global attractivity of positive periodic solutions for the impulsive delay Nicholson’s blowflies model. J. Comput. Appl. Math. 2007, 201: 55-68. 10.1016/j.cam.2006.02.001
Berezansky L, Braverman E, Idels L: Nicholson’s blowflies differential equations revisited: main results and open problems. Appl. Math. Model. 2010, 34: 1405-1417. 10.1016/j.apm.2009.08.027
Fink AM Lecture Notes in Mathematics 377. In Almost Periodic Differential Equations. Springer, Berlin; 1974.
He CY: Almost Periodic Differential Equation. Higher Education Publishing House, Beijing; 1992. (in Chinese)
Chen W, Liu B: Positive almost periodic solution for a class of Nicholson’s blowflies model with multiple time-varying delays. J. Comput. Appl. Math. 2011, 235: 2090-2097. 10.1016/j.cam.2010.10.007
Wang W, Wang L, Chen W: Existence and exponential stability of positive almost periodic solution for Nicholson-type delay systems. Nonlinear Anal., Real World Appl. 2011, 12: 1938-1949. 10.1016/j.nonrwa.2010.12.010
Long F: Positive almost periodic solution for a class of Nicholson’s blowflies model with a linear harvesting term. Nonlinear Anal., Real World Appl. 2012, 13: 686-693. 10.1016/j.nonrwa.2011.08.009
Wang W: Positive periodic solutions of delayed Nicholson’s blowflies models with a nonlinear density-dependent mortality term. Appl. Math. Model. 2012, 36: 4708-4713. 10.1016/j.apm.2011.12.001
Hou X, Duan L, Huang Z: Permanence and periodic solutions for a class of delay Nicholson’s blowflies models. Appl. Math. Model. 2012, 2012: 1537-1544.
Liu B, Gong S: Permanence for Nicholson-type delay systems with nonlinear density-dependent mortality terms. Nonlinear Anal., Real World Appl. 2011, 12: 1931-1937. 10.1016/j.nonrwa.2010.12.009
Chen W: Permanence for Nicholson-type delay systems with patch structure and nonlinear density-dependent mortality terms. Electron. J. Qual. Theory Differ. Equ. 2012., 2012: Article ID 73
Chen W, Wang L: Positive periodic solutions of Nicholson-type delay systems with nonlinear density- dependent mortality terms. Abstr. Appl. Anal. 2012., 2012: Article ID 843178 10.1155/2012/843178
Chen Z: Periodic solutions for Nicholson-type delay system with nonlinear density-dependent mortality terms. Electron. J. Qual. Theory Differ. Equ. 2013., 2013: Article ID 1
Liu B: Almost periodic solutions for a delayed Nicholson’s blowflies model with a nonlinear density-dependent mortality term. Adv. Differ. Equ. 2014., 2014: Article ID 72 10.1186/1687-1847-2014-72
Xu YL: Existence and global exponential stability of positive almost periodic solutions for a delayed Nicholson’s blowflies model. J. Korean Math. Soc. 2014, 51: 473-493. 10.4134/JKMS.2014.51.3.473
Wang W: Exponential extinction of Nicholson’s blowflies system with nonlinear density-dependent mortality terms. Abstr. Appl. Anal. 2012., 2012: Article ID 302065 10.1155/2012/302065
Hale JK, Verduyn Lunel SM: Introduction to Functional Differential Equations. Springer, New York; 1993.
Smith HL: An Introduction to Delay Differential Equations with Applications to the Life Sciences. Springer, New York; 2011.
Acknowledgements
We would like to thank the anonymous reviewer for their suggestions to improve the manuscript. This work was supported by the National Natural Science Foundation of China (Grant No. 11301341, 11201184), Innovation Program of Shanghai Municipal Education Commission (Grant No. 13YZ127), and Shanghai Fiscal Special Fund (Grant No. A4-4902-13-12).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
The authors declare that the study was realized in collaboration with the same responsibility. Both authors read and approved the final version.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Chen, W., Wang, W. Almost periodic solutions for a delayed Nicholson’s blowflies system with nonlinear density-dependent mortality terms and patch structure. Adv Differ Equ 2014, 205 (2014). https://doi.org/10.1186/1687-1847-2014-205
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2014-205