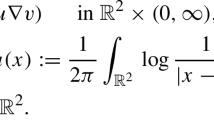Almost periodic solutions for a delayed Nicholson’s blowflies model with a nonlinear density-dependent mortality term

Abstract

A delayed Nicholson’s blowflies model with a nonlinear density-dependent mortality term is studied in this paper. Some sufficient conditions are obtained to guarantee the existence and global exponential stability of positive almost periodic solutions of this model. An example with numerical simulations is given to illustrate our main results.

MSC: 34C25, 34K13.

1 Introduction

In population dynamics, the classic Nicholson’s blowflies equation developed by Gurney et al. [1] takes the following form:

$$x^{\prime }(t)=Px(t-\tau )e^{-\alpha x(t-\tau )}-\gamma x(t),$$

where $x(t)$ denotes the population of sexually mature adults at time t, P is the maximum possible per capita egg production rate, $1/\alpha$ is the population size at which the whole population reproduces at its maximum rate, τ is the generation time, and the mortality rate γ is assumed to be a constant. Such an assumption is reasonable for populations at low densities, but may not be valid any more when the populations are at high densities. A straightforward extension thus assumes that the mortality rate is density-dependent, for instance, Berezansky et al. [2] proposed the following Nicholson’s blowflies equation:

$$x^{\prime }(t)=-D(x(t))+Px(t-\tau )e^{-x(t-\tau )},$$

(1.1)

where the nonlinear density-dependent mortality function $D(x)$ might have one of the following forms: $D(x)=\frac{ax}{b+x}$ or $D(x)=a-b{e}^{-x}$ with positive constants $a,b>0$.

Since variable coefficients and delays in differential equations of population and ecology problems are much more realistic in the real world, (1.1) has been often generalized as follows:

$$x^{\prime }(t)=-D(t,x(t))+P(t)x(t-\tau )e^{-x(t-\tau (t))},$$

(1.2)

where coefficients and delays are time-varying with $D(t,x)=\frac{a(t)x}{b(t)+x}$ or $D(t,x)=a(t)-b(t)e^{-x}$. Moreover, the dynamic behaviors on the existence of positive solutions, periodic solutions, persistence, permanence, oscillation and stability of Nicholson’s blowflies model (1.2) and its analogous equations have been studied extensively. We refer the reader to [3–9] and the references cited therein. On the other hand, the variation of the environment plays an important role in many biological and ecological dynamical systems. Fink [10] and He [11] pointed out that periodically varying environment and almost periodically varying environment are foundations for the theory of nature selection. Compared with periodic effects, almost periodic effects are more frequent. Hence, the effects of almost periodic environment on evolutionary theory have been the object of intensive analysis by numerous authors, and some of these results on Nicholson’s blowflies model without nonlinear density-dependent mortality term can be found in [12–14]. In particular, these results were obtained by using exponential dichotomy theory on almost periodic differential equations or functional differential equations with linear part. However, there is not any linear part in Nicholson’s blowflies model with a nonlinear density-dependent mortality term. Thus, many classical and traditional approaches fail to almost periodic problems on (1.2). Therefore, a new method must be sought to investigate the existence and stability of positive almost periodic solutions of (1.2).

Motivated by the above discussions, in this paper, we employ a novel method to establish some criteria on the existence and global exponential stability of almost periodic solutions for the nonlinear density-dependent mortality Nicholson’s blowflies model given by

$$x^{\prime }(t)=-a(t)+b(t)e^{-x(t)}+\sum _{j=1}^m{\beta }_j(t)x(t-{\tau }_j(t))e^{-{\gamma }_j(t)x(t-{\tau }_j(t))},$$

(1.3)

where $a,b,{\beta }_j,{\gamma }_j:R\to (0,+\mathrm{\infty })$ and ${\tau }_j:R\to [0,+\mathrm{\infty })$ are almost periodic functions, and $j=1,2,\dots ,m$.

For convenience, we introduce some notations. In the following part of this paper, given a bounded continuous function g defined on R, let $g^{+}$ and $g^{-}$ be defined as

$$g^{+}=\underset{t\in R}{sup}g(t),g^{-}=\underset{t\in R}{inf}g(t).$$

It will be assumed that

$$r=\underset{1\le j\le m}{max}{\tau }_j^{+},a^{-}>0,b^{-}>0,{\beta }_j^{-}>0,{\gamma }_j^{-}\ge 1,j=1,2,\dots ,m.$$

(1.4)

Throughout this paper, let $R_{+}$ denote a nonnegative real number space, $C=C([-r,0],R)$ be the continuous functions space equipped with the usual supremum norm $\parallel \cdot \parallel$, and let $C_{+}=C([-r,0],R_{+})$. If $x(t)$ is continuous and defined on $[-r+t_0,\sigma )$ with $t_0,\sigma \in R$, then we define $x_t\in C$, where $x_t(\theta )=x(t+\theta )$ for all $\theta \in [-r,0]$.

It is biologically reasonable to assume that only positive solutions of model (1.3) are meaningful and therefore admissible. Much can be learned by considering admissible initial conditions

$$x_{t_0}=\phi ,\phi \in C_{+}\text{and}\phi (0)>0.$$

(1.5)

Define a continuous map $f:R\times C_{+}\to R$ by setting

$$f(t,\phi )=-a(t)+b(t)e^{-\phi (0)}+\sum _{j=1}^m{\beta }_j(t)\phi (-{\tau }_j(t))e^{-{\gamma }_j(t)\phi (-{\tau }_j(t))}.$$

Then f is a locally Lipschitz map with respect to $\phi \in C_{+}$, which ensures the existence and uniqueness of the solution of (1.3) with admissible initial conditions (1.5).

We denote by $x_t(t_0,\phi )(x(t;t_0,\phi ))$ an admissible solution of admissible initial value problem (1.3) and (1.5). Also, let $[t_0,\eta (\phi ))$ be the maximal right-interval of the existence of $x_t(t_0,\phi )$.

Since the function $\frac{1-x}{e^x}$ is decreasing with the range $[0,1]$, it follows easily that there exists a unique $\kappa \in (0,1)$ such that

$$\frac{1-\kappa }{e^{\kappa }}=\frac{1}{e^2}.$$

(1.6)

Obviously,

$$\underset{x\ge \kappa }{sup}\left|\frac{1-x}{e^x}\right|=\frac{1}{e^2}.$$

(1.7)

Moreover, since $x{e}^{-x}$ increases on $[0,1]$ and decreases on $[1,+\mathrm{\infty })$, let $\tilde{\kappa }$ be the unique number in $(1,+\mathrm{\infty })$ such that

$$\kappa e^{-\kappa }=\tilde{\kappa }{e}^{-\tilde{\kappa }}.$$

(1.8)

The remainder of this paper is organized as follows. In Section 2, we give some definitions and lemmas, which tell us that some kinds of solutions to (1.3) are bounded. These results play an important role in Section 3 to establish the existence of almost periodic solutions of (1.3). Here we also study the local exponential stability of almost periodic solutions. The paper concludes with an example to illustrate the effectiveness of the obtained results by numerical simulation.

2 Preliminary results

In this section, we shall first recall some basic definitions, lemmas which are used in what follows.

Definition 2.1 (see [10, 11])

A continuous function $u:R\to R$ is said to be almost periodic on R if, for any $ϵ>0$, the set $T(u,ϵ)=\{\delta :|u(t+\delta )-u(t)|<ϵ\text{ for all }t\in R\}$ is relatively dense, i.e., for any $ϵ>0$, it is possible to find a real number $l=l(ϵ)>0$ with the property that, for any interval with length $l(ϵ)$, there exists a number $\delta =\delta (ϵ)$ in this interval such that $|u(t+\delta )-u(t)|<ϵ$ for all $t\in R$.

From the theory of almost periodic functions in [10, 11], it follows that for any $ϵ>0$, it is possible to find a real number $l=l(ϵ)>0$; for any interval with length $l(ϵ)$, there exists a number $\delta =\delta (ϵ)$ in this interval such that

$$\{\begin{array}{l}|a(t+\delta )-a(t)|<ϵ,|b(t+\delta )-b(t)|<ϵ,|{\beta }_j(t+\delta )-{\beta }_j(t)|<ϵ,\\ |{\tau }_j(t+\delta )-{\tau }_j(t)|<ϵ,|{\gamma }_j(t+\delta )-{\gamma }_j(t)|<ϵ\end{array}$$

(2.1)

for all $t\in R$ and $j=1,2,\dots ,m$.

Lemma 2.1 Suppose that there exists a positive constant M such that

$${\gamma }_j^{+}\le \frac{\tilde{\kappa }}{M},j=1,2,\dots ,m,$$

(2.2)

$$\begin{array}{l}{sup}_{t\in R}\{-a(t)+b(t)e^{-M}+{\sum }_{j=1}^m\frac{{\beta }_j(t)}{{\gamma }_j(t)}\frac{1}{e}\}<0,\\ {inf}_{t\in R,s\in [0,\kappa ]}\{-a(t)+b(t)e^{-s}+{\sum }_{j=1}^m\frac{{\beta }_j(t)}{{\gamma }_j(t)}s{e}^{-s}\}>0.\end{array}\}$$

(2.3)

Then the set of $\{x_t(t_0,\phi ):t\in [t_0,\eta (\phi ))\}$ is bounded, and $\eta (\phi )=+\mathrm{\infty }$. Moreover, there exists $t_{\phi }>t_0$ such that

$$\kappa <x(t;t_0,\phi )<M\mathit{\text{for all }}t\ge t_{\phi }.$$

(2.4)

Proof Let $x(t)=x(t;t_0,\phi )$. We first claim:

$$x(t)>0\text{for all }t\in [t_0,\eta (\phi )).$$

(2.5)

Suppose, for the sake of contradiction, that there exists $\overline{t}\in (t_0,\eta (\phi ))$ such that

$$x(\overline{t})=0,x(t)>0\text{for all }t\in [t_0,\overline{t}).$$

It follows that $x^{\prime }(\overline{t})\le 0$. But

$$\begin{array}{rcl}{x}^{\prime }(\overline{t})& =& -a(\overline{t})+b(\overline{t})e^{-x(\overline{t})}+\sum _{j=1}^m{\beta }_j(\overline{t})x(\overline{t}-{\tau }_j(\overline{t}))e^{-{\gamma }_j(\overline{t})x(\overline{t}-{\tau }_j(\overline{t}))}\\ \ge & -a(\overline{t})+b(\overline{t})\ge \underset{t\in R,s\in [0,\kappa ]}{inf}\{-a(t)+b(t)e^{-s}+\sum _{j=1}^m\frac{{\beta }_j(t)}{{\gamma }_j(t)}s{e}^{-s}\}\\ >& 0.\end{array}$$

This contradiction means that $x(t)>0$ for all $t\in [t_0,\eta (\phi ))$.

For each $t\in [t_0-r,\eta (\phi ))$, we define

$$M(t)=max\{\xi :\xi \le t,x(\xi )=\underset{t_0-r\le s\le t}{max}x(s)\}.$$

We now show that $x(t)$ is bounded on $[t_0,\eta (\phi ))$. In the contrary case, observe that $M(t)\to \eta (\phi )$ as $t\to \eta (\phi )$, we have

$$\underset{t\to \eta (\phi )}{lim}x(M(t))=+\mathrm{\infty }.$$

(2.6)

On the other hand,

$$x(M(t))=\underset{t_0-r\le s\le t}{max}x(s)\text{and so}{x}^{\prime }(M(t))\ge 0,\text{where }M(t)>t_0.$$

Thus, in view of the fact that ${sup}_{u\ge 0}u{e}^{-u}=\frac{1}{e}$, we get

$$\begin{array}{rcl}0& \le & x^{\prime }(M(t))\\ =& -a(M(t))+b(M(t))e^{-x(M(t))}\\ +\sum _{j=1}^m\frac{{\beta }_j(M(t))}{{\gamma }_j(M(t))}{\gamma }_j(M(t))x(M(t)-{\tau }_j(M(t)))e^{-{\gamma }_j(M(t))x(M(t)-{\tau }_j(M(t)))}\\ \le & -a(M(t))+b(M(t))e^{-x(M(t))}+\sum _{j=1}^m\frac{{\beta }_j(M(t))}{{\gamma }_j(M(t))}\frac{1}{e},\text{where }M(t)>t_0.\end{array}$$

Letting $t\to \eta (\phi )$ leads to

$$0\le \underset{t\to \eta (\phi )}{\overline{lim}}[-a(t)+\sum _{j=1}^m\frac{{\beta }_j(t)}{{\gamma }_j(t)}\frac{1}{e}]\le \underset{t\in R}{sup}\{-a(t)+b(t)e^{-M}+\sum _{j=1}^m\frac{{\beta }_j(t)}{{\gamma }_j(t)}\frac{1}{e}\}<0,$$

which is a contradiction and implies that $x(t)$ is bounded on $[t_0,\eta (\phi ))$. From Theorem 2.3.1 in [15], we easily obtain $\eta (\phi )=+\mathrm{\infty }$.

We next show that there exists $t^{\mathrm{\#}}\in [t_0,+\mathrm{\infty })$ such that

$$x\left(t^{\mathrm{\#}}\right)<M.$$

(2.7)

Otherwise,

$$x(t)\ge M\text{for all }t\in [t_0,+\mathrm{\infty }),$$

which together with (2.3) implies that

$$\begin{array}{rcl}{x}^{\prime }(t)& =& -a(t)+b(t)e^{-x(t)}+\sum _{j=1}^m\frac{{\beta }_j(t)}{{\gamma }_j(t)}{\gamma }_j(t)x(t-{\tau }_j(t))e^{-{\gamma }_j(t)x(t-{\tau }_j(t))}\\ \le & -a(t)+b(t)e^{-M}+\sum _{j=1}^m\frac{{\beta }_j(t)}{{\gamma }_j(t)}\frac{1}{e}\\ <& 0\text{for all }t\ge t_0.\end{array}$$

This yields that

$$\begin{array}{rcl}x(t)& =& x(t_0)+{\int }_{t_0}^t{x}^{\prime }(s)ds\\ \le & x(t_0)+\underset{t\in R}{sup}\{-a(t)+b(t)e^{-M}+\sum _{j=1}^m\frac{{\beta }_j(t)}{{\gamma }_j(t)}\frac{1}{e}\}(t-t_0),\mathrm{\forall }t\ge t_0.\end{array}$$

Thus

$$\underset{t\to +\mathrm{\infty }}{lim}x(t)=-\mathrm{\infty },$$

which contradicts with (2.5). Hence, (2.7) holds. In the sequel, we prove that

$$x(t)<M\text{for all }t\in [t^{\mathrm{\#}},+\mathrm{\infty }).$$

(2.8)

Suppose, for the sake of contradiction, that there exists $\tilde{t}\in (t^{\mathrm{\#}},+\mathrm{\infty })$ such that

$$x(\tilde{t})=M,x(t)<M\text{for all }t\in [t^{\mathrm{\#}},\tilde{t}).$$

(2.9)

Calculating the derivative of $x(t)$, together with the fact that ${sup}_{x\in R}x{e}^{-x}=\frac{1}{e}$, (1.3), (2.3) and (2.9) imply that

$$\begin{array}{rcl}0& \le & x^{\prime }(\tilde{t})\\ =& -a(\tilde{t})+b(\tilde{t})e^{-x(\tilde{t})}+\sum _{j=1}^m\frac{{\beta }_j(\tilde{t})}{{\gamma }_j(\tilde{t})}{\gamma }_j(\tilde{t})x(\tilde{t}-{\tau }_j(\tilde{t}))e^{-{\gamma }_j(\tilde{t})x(\tilde{t}-{\tau }_j(\tilde{t}))}\\ \le & -a(\tilde{t})+b(\tilde{t})e^{-M}+\sum _{j=1}^m\frac{{\beta }_j(\tilde{t})}{{\gamma }_j(\tilde{t})}\frac{1}{e}\\ <& 0.\end{array}$$

This contradiction yields that (2.8) holds.

We finally show that $l={lim\hspace{0.17em}inf}_{t\to \mathrm{\infty }}x(t)>\kappa$. By way of contradiction, we assume that $0\le l\le \kappa$. By the fluctuation lemma [[16], Lemma A.1], there exists a sequence ${\{t_k\}}_{k\ge 1}$ such that

$$t_k\to +\mathrm{\infty },x(t_k)\to \underset{t\to \mathrm{\infty }}{lim\hspace{0.17em}inf}x(t),x^{\prime }(t_k)\to 0\text{as }k\to +\mathrm{\infty }.$$

Since $\{x_{t_k}\}$ is bounded and equicontinuous, by the Ascoli-Arzelá theorem, there exists a subsequence, still denoted by itself for simplicity of notation, such that

$$x_{t_k}\to {\phi }^{\ast }\text{for some }{\phi }^{\ast }\in C_{+}.$$

Moreover,

$${\phi }^{\ast }(0)=l\le {\phi }^{\ast }(\theta )\le M\text{for }\theta \in [-r,0).$$

Without loss of generality, we assume that all $a(t_k)$, $b(t_k)$, ${\beta }_j(t_k)$, ${\tau }_j(t_k)$ and ${\gamma }_j(t_k)$ are convergent to $a^{\ast }$, $b^{\ast }$, ${\beta }_j^{\ast }$, ${\tau }_j^{\ast }$ and ${\gamma }_j^{\ast }$, respectively. This can be achieved because of almost periodicity. Then (1.4) and (2.2) lead to

$$l\le {\gamma }_j^{\ast }{\phi }^{\ast }(-{\tau }_j^{\ast })\le {\gamma }_j^{\ast }M\le \tilde{\kappa },j=1,2,\dots ,m.$$

It follows from

$$x^{\prime }(t_k)=-a(t_k)+b(t_k)e^{-x(t_k)}+\sum _{j=1}^m\frac{{\beta }_j(t_k)}{{\gamma }_j(t_k)}{\gamma }_j(t_k)x(t_k-{\tau }_j(t_k))e^{-{\gamma }_j(t_k)x(t_k-{\tau }_j(t_k))}$$

that (taking limits)

$$\begin{array}{rcl}0& =& -a^{\ast }+b^{\ast }{e}^{-l}+\sum _{j=1}^m\frac{{\beta }_j^{\ast }}{{\gamma }_j^{\ast }}{\gamma }_j^{\ast }{\phi }^{\ast }(-{\tau }_j^{\ast })e^{-{\gamma }_j^{\ast }{\phi }^{\ast }(-{\tau }_j^{\ast })}\\ \ge & -a^{\ast }+b^{\ast }{e}^{-l}+\sum _{j=1}^m\frac{{\beta }_j^{\ast }}{{\gamma }_j^{\ast }}l{e}^{-l}\\ \ge & \underset{t\in R,s\in [0,\kappa ]}{inf}\{-a(t)+b(t)e^{-s}+\sum _{j=1}^m\frac{{\beta }_j(t)}{{\gamma }_j(t)}s{e}^{-s}\}\\ >& 0,\end{array}$$

a contradiction. This proves that $l>\kappa$. Hence, from (2.8), we can choose $t_{\phi }>t_0$ such that

$$\kappa <x(t;t_0,\phi )<M\text{for all }t\ge t_{\phi }.$$

This ends the proof of Lemma 2.1. □

Lemma 2.2 Suppose that (2.2) and (2.3) hold, and

$$\underset{t\in R}{sup}\{-b(t)e^{-M}+\frac{1}{e^2}\sum _{j=1}^m{\beta }_j(t)\}<0.$$

(2.10)

Moreover, assume that $x(t)=x(t;t_0,\phi )$ is a solution of equation (1.3) with the initial condition (1.5) and ${\phi }^{\prime }$ is bounded continuous on $[-r,0]$. Then, for any $ϵ>0$, there exists $l=l(ϵ)>0$ such that every interval $[\alpha ,\alpha +l]$ contains at least one number δ for which there exists $N>0$ satisfying

$$|x(t+\delta )-x(t)|\le ϵ\mathit{\text{for all }}t>N.$$

(2.11)

Proof Define a continuous function $\mathrm{\Gamma }(u)$ by setting

$$\mathrm{\Gamma }(u)=\underset{t\in R}{sup}\{-[b(t)e^{-M}-u]+\sum _{j=1}^m{\beta }_j(t)\frac{1}{e^2}{e}^{ur}\},u\in [0,1].$$

(2.12)

Then we have

$$\mathrm{\Gamma }(0)=\underset{t\in R}{sup}\{-b(t)e^{-M}+\sum _{j=1}^m{\beta }_j(t)\frac{1}{e^2}\}<0,$$

which implies that there exist two constants $\eta >0$ and $\lambda \in (0,1]$ such that

$$\mathrm{\Gamma }(\lambda )=\underset{t\in R}{sup}\{-[b(t)e^{-M}-\lambda ]+\sum _{j=1}^m{\beta }_j(t)\frac{1}{e^2}{e}^{\lambda r}\}<-\eta <0.$$

(2.13)

For $t\in (-\mathrm{\infty },t_0-r]$, we add the definition of $x(t)$ with $x(t)\equiv x(t_0-r)$. Set

$$\begin{array}{rcl}ϵ(\delta ,t)& =& [b(t+\delta )-b(t)]e^{-x(t+\delta )}\\ +\sum _{j=1}^m[{\beta }_j(t+\delta )-{\beta }_j(t)]x(t+\delta -{\tau }_j(t+\delta ))e^{-{\gamma }_j(t+\delta )x(t+\delta -{\tau }_j(t+\delta ))}\\ +\sum _{j=1}^m{\beta }_j(t)[x(t+\delta -{\tau }_j(t+\delta ))e^{-{\gamma }_j(t+\delta )x(t+\delta -{\tau }_j(t+\delta ))}\\ -x(t-{\tau }_j(t)+\delta )e^{-{\gamma }_j(t+\delta )x(t-{\tau }_j(t)+\delta )}]\\ +\sum _{j=1}^m{\beta }_j(t)[x(t-{\tau }_j(t)+\delta )e^{-{\gamma }_j(t+\delta )x(t-{\tau }_j(t)+\delta )}-x(t-{\tau }_j(t)+\delta )e^{-{\gamma }_j(t)x(t-{\tau }_j(t)+\delta )}]\\ -[a(t+\delta )-a(t)],t\in R.\end{array}$$

(2.14)

By Lemma 2.1, the solution $x(t)$ is bounded and

$$\kappa <x(t)<M\text{for all }t\ge t_{\phi },$$

(2.15)

which implies that the right-hand side of (1.3) is also bounded, and $x^{\prime }(t)$ is a bounded function on $[t_0-r,+\mathrm{\infty })$. Thus, in view of the fact that $x(t)\equiv x(t_0-r)$ for $t\in (-\mathrm{\infty },t_0-r]$, we obtain that $x(t)$ is uniformly continuous on R. From (2.1), for any $ϵ>0$, there exists $l=l(ϵ)>0$ such that every interval $[\alpha ,\alpha +l]$, $\alpha \in R$, contains δ for which

$$|ϵ(\delta ,t)|\le \frac{1}{2}\eta ϵ\text{for all }t\in R.$$

(2.16)

Let $N_0\ge max\{t_0,t_0-\delta ,t_{\phi }+r,t_{\phi }+r-\delta \}$. For $t\in R$, denote

$$u(t)=x(t+\delta )-x(t).$$

Then, for all $t\ge N_0$, we get

$$\begin{array}{rcl}\frac{du(t)}{dt}& =& b(t)[e^{-x(t+\delta )}-e^{-x(t)}]\\ +\sum _{j=1}^m{\beta }_j(t)[x(t-{\tau }_j(t)+\delta )e^{-{\gamma }_j(t)x(t-{\tau }_j(t)+\delta )}-x(t-{\tau }_j(t))e^{-{\gamma }_j(t)x(t-{\tau }_j(t))}]\\ +ϵ(\delta ,t).\end{array}$$

(2.17)

From (1.7), (2.14), (2.17) and the inequalities

$$\begin{array}{rcl}(e^{-s}-e^{-t})sgn(s-t)& =& -e^{-(s+\theta (t-s))}|s-t|\\ \le & -e^{-M}|s-t|,\text{where }s,t\in [\kappa ,M],0<\theta <1\end{array}$$

(2.18)

and

$$\begin{array}{rcl}|s{e}^{-s}-t{e}^{-t}|& =& \left|\frac{1-(s+\theta (t-s))}{e^{s+\theta (t-s)}}\right||s-t|\\ \le & \frac{1}{e^2}|s-t|,\text{where }s,t\in [\kappa ,+\mathrm{\infty }),0<\theta <1,\end{array}$$

(2.19)

we obtain

$$\begin{array}{c}{D}^{-}\left(e^{\lambda s}\right|u(s)\left|\right){|}_{s=t}\hfill \\ \le \lambda e^{\lambda t}|u(t)|+e^{\lambda t}\{b(t)[e^{-x(t+\delta )}-e^{-x(t)}]sgn(x(t+\delta )-x(t))\hfill \\ +|\sum _{j=1}^m{\beta }_j(t)[x(t-{\tau }_j(t)+\delta )e^{-{\gamma }_j(t)x(t-{\tau }_j(t)+\delta )}-x(t-{\tau }_j(t))e^{-{\gamma }_j(t)x(t-{\tau }_j(t))}]+ϵ(\delta ,t)|\}\hfill \\ =\lambda e^{\lambda t}|u(t)|+e^{\lambda t}\{b(t)[e^{-x(t+\delta )}-e^{-x(t)}]sgn(x(t+\delta )-x(t))\hfill \\ +|\sum _{j=1}^m\frac{{\beta }_j(t)}{{\gamma }_j(t)}[{\gamma }_j(t)x(t-{\tau }_j(t)+\delta )e^{-{\gamma }_j(t)x(t-{\tau }_j(t)+\delta )}-{\gamma }_j(t)x(t-{\tau }_j(t))e^{-{\gamma }_j(t)x(t-{\tau }_j(t))}]\hfill \\ +ϵ(\delta ,t)\left|\right\}\hfill \\ \le \lambda e^{\lambda t}|u(t)|+e^{\lambda t}\{-b(t)e^{-M}|u(t)|+\sum _{j=1}^m{\beta }_j(t)\frac{1}{e^2}|u(t-{\tau }_j(t))|+|ϵ(\delta ,t)\left|\right\}\hfill \\ =-[b(t)e^{-M}-\lambda ]e^{\lambda t}|u(t)|\hfill \\ +\sum _{j=1}^m{\beta }_j(t)\frac{1}{e^2}{e}^{\lambda {\tau }_j(t)}{e}^{\lambda (t-{\tau }_j(t))}\left|u(t-{\tau }_j(t))\right|\hfill \\ +e^{\lambda t}|ϵ(\delta ,t)|\text{for all }t\ge N_0.\hfill \end{array}$$

(2.20)

Let

$$U(t)=\underset{-\mathrm{\infty }<s\le t}{sup}\left\{e^{\lambda s}\right|u(s)\left|\right\}.$$

(2.21)

It is obvious that $e^{\lambda t}|u(t)|\le U(t)$ and $U(t)$ is non-decreasing.

Now, we distinguish two cases to finish the proof.

Case one.

$$U(t)>e^{\lambda t}|u(t)|\text{for all }t\ge N_0.$$

(2.22)

We claim that

$$U(t)\equiv U(N_0)\text{is a constant for all }t\ge N_0.$$

(2.23)

Assume, by way of contradiction, that (2.23) does not hold. Then there exists $t_1>N_0$ such that $U(t_1)>U(N_0)$. Since

$$e^{\lambda t}|u(t)|\le U(N_0)\text{for all }t\le N_0,$$

there must exist $\beta \in (N_0,t_1)$ such that

$$e^{\lambda \beta }|u(\beta )|=U(t_1)\ge U(\beta ),$$

which contradicts (2.22). This contradiction implies that (2.23) holds. It follows that there exists $t_2>N_0$ such that

$$|u(t)|\le e^{-\lambda t}U(t)=e^{-\lambda t}U(N_0)<ϵ\text{for all }t\ge t_2.$$

(2.24)

Case two. There is $t_0^{\ast }\ge N_0$ such that $U(t_0^{\ast })=e^{\lambda t_0^{\ast }}|u(t_0^{\ast })|$. Then, in view of (2.13) and (2.20), we get

$$\begin{array}{rcl}0& \le & D^{-}\left(e^{\lambda s}\right|u(s)\left|\right){|}_{s=t_0^{\ast }}\\ \le & -[b\left(t_0^{\ast }\right)e^{-M}-\lambda ]e^{\lambda t_0^{\ast }}\left|u\left(t_0^{\ast }\right)\right|\\ +\sum _{j=1}^m{\beta }_j\left(t_0^{\ast }\right)\frac{1}{e^2}{e}^{\lambda {\tau }_j(t_0^{\ast })}{e}^{\lambda (t_0^{\ast }-{\tau }_j(t_0^{\ast }))}\left|u(t_0^{\ast }-{\tau }_j\left(t_0^{\ast }\right))\right|+e^{\lambda t_0^{\ast }}\left|ϵ(\delta ,t_0^{\ast })\right|\\ \le & \{-[b\left(t_0^{\ast }\right)e^{-M}-\lambda ]+\sum _{j=1}^m{\beta }_j\left(t_0^{\ast }\right)\frac{1}{e^2}{e}^{\lambda r}\}U\left(t_0^{\ast }\right)+\frac{1}{2}\eta ϵe^{\lambda t_0^{\ast }}\\ <& -\eta U\left(t_0^{\ast }\right)+\eta ϵe^{\lambda t_0^{\ast }},\end{array}$$

(2.25)

which yields that

$$e^{\lambda t_0^{\ast }}\left|u\left(t_0^{\ast }\right)\right|=U\left(t_0^{\ast }\right)<ϵe^{\lambda t_0^{\ast }}\text{and}\left|u\left(t_0^{\ast }\right)\right|<ϵ.$$

(2.26)

For any $t>t_0^{\ast }$, with the same approach as that in deriving of (2.26), we can show

$$e^{\lambda t}|u(t)|<ϵe^{\lambda t}\text{and}|u(t)|<ϵ$$

(2.27)

if $U(t)=e^{\lambda t}|u(t)|$.

On the other hand, if $U(t)>e^{\lambda t}|u(t)|$ and $t>t_0^{\ast }$, we can choose $t_0^{\ast }\le t_3<t$ such that

$$U(t_3)=e^{\lambda t_3}|u(t_3)|\text{and}U(s)>e^{\lambda s}|u(s)|\text{for all }s\in (t_3,t],$$

which, together with (2.27), yields

$$|u(t_3)|<ϵ.$$

With a similar argument as that in the proof of case one, we can show that

$$U(s)\equiv U(t_3)\text{is a constant for all }s\in (t_3,t],$$

(2.28)

which implies that

$$|u(t)|<e^{-\lambda t}U(t)=e^{-\lambda t}U(t_3)=|u(t_3)|e^{-\lambda (t-t_3)}<ϵ.$$

In summary, there must exist $N>max\{t_0^{\ast },N_0,t_2\}$ such that $|u(t)|\le ϵ$ holds for all $t>N$. The proof of Lemma 2.2 is now complete. □

3 Main results

In this section, we establish sufficient conditions on the existence and global exponential stability of almost periodic solutions of (1.3).

Theorem 3.1 Under the assumptions of Lemma  2.2, equation (1.3) has at least one positive almost periodic solution $x^{\ast }(t)$. Moreover, $x^{\ast }(t)$ is globally exponentially stable, i.e., there exist constants $K_{\phi ,x^{\ast }}$ and $t_{\phi ,x^{\ast }}$ such that

$$|x(t;t_0,\phi )-x^{\ast }(t)|<K_{\phi ,x^{\ast }}{e}^{-\lambda t}\mathit{\text{for all }}t>t_{\phi ,x^{\ast }}.$$

Proof Let $v(t)=v(t;t_0,{\phi }^v)$ be a solution of equation (1.3) with initial conditions satisfying the assumptions in Lemma 2.2. We also add the definition of $v(t)$ with $v(t)\equiv v(t_0-r)$ for all $t\in (-\mathrm{\infty },t_0-r]$. Set

$$\begin{array}{rcl}ϵ(k,t)& =& [b(t+t_k)-b(t)]e^{-v(t+t_k)}\\ +\sum _{j=1}^m[{\beta }_j(t+t_k)-{\beta }_j(t)]v(t+t_k-{\tau }_j(t+t_k))e^{-{\gamma }_j(t+t_k)v(t+t_k-{\tau }_j(t+t_k))}\\ +\sum _{j=1}^m{\beta }_j(t)[v(t+t_k-{\tau }_j(t+t_k))e^{-{\gamma }_j(t+t_k)v(t+t_k-{\tau }_j(t+t_k))}\\ -v(t-{\tau }_j(t)+t_k)e^{-{\gamma }_j(t+t_k)v(t-{\tau }_j(t)+t_k)}]\\ +\sum _{j=1}^m{\beta }_j(t)[v(t-{\tau }_j(t)+t_k)e^{-{\gamma }_j(t+t_k)v(t-{\tau }_j(t)+t_k)}\\ -v(t-{\tau }_j(t)+t_k)e^{-{\gamma }_j(t)v(t-{\tau }_j(t)+t_k)}]-[a(t+t_k)-a(t)],t\in R,\end{array}$$

(3.1)

where $\{t_k\}$ is any sequence of real numbers. By Lemma 2.1, the solution $v(t)$ is bounded and

$$\kappa <v(t)<M\text{for all }t\ge t_{{\phi }^v},$$

(3.2)

which implies that the right-hand side of (1.3) is also bounded, and $v^{\prime }(t)$ is a bounded function on $[t_0-r,+\mathrm{\infty })$. Thus, in view of the fact that $v(t)\equiv v(t_0-r)$ for $t\in (-\mathrm{\infty },t_0-r]$, we obtain that $v(t)$ is uniformly continuous on R. Then, from the almost periodicity of a, b, ${\tau }_j$, ${\gamma }_j$ and ${\beta }_j$, we can select a sequence $\{t_k\}\to +\mathrm{\infty }$ such that

$$\begin{array}{l}|a(t+t_k)-a(t)|\le \frac{1}{k},|b(t+t_k)-b(t)|\le \frac{1}{k},|{\tau }_j(t+t_k)-{\tau }_j(t)|\le \frac{1}{k},\\ |{\beta }_j(t+t_k)-{\beta }_j(t)|\le \frac{1}{k},|{\gamma }_j(t+t_k)-{\gamma }_j(t)|\le \frac{1}{k},|ϵ(k,t)|\le \frac{1}{k}\end{array}\}$$

(3.3)

for all j, t.

Since ${\{v(t+t_k)\}}_{k=1}^{+\mathrm{\infty }}$ is uniformly bounded and equiuniformly continuous, by the Arzelá-Ascoli lemma and the diagonal selection principle, we can choose a subsequence $\{t_{k_j}\}$ of $\{t_k\}$ such that $v(t+t_{k_j})$ (for convenience, we still denote it by $v(t+t_k)$) uniformly converges to a continuous function $x^{\ast }(t)$ on any compact set of R, and

$$\kappa \le x^{\ast }(t)\le M\text{for all }t\in R.$$

(3.4)

Now, we prove that $x^{\ast }(t)$ is a solution of (1.3). In fact, for any $t\ge t_0$ and $\mathrm{\Delta }t\in R$, from (3.3), we have

$$\begin{array}{c}{x}^{\ast }(t+\mathrm{\Delta }t)-x^{\ast }(t)\hfill \\ =\underset{k\to +\mathrm{\infty }}{lim}[v(t+\mathrm{\Delta }t+t_k)-v(t+t_k)]\hfill \\ =\underset{k\to +\mathrm{\infty }}{lim}{\int }_t^{t+\mathrm{\Delta }t}\{-a(\mu +t_k)+b(\mu +t_k)e^{-v(\mu +t_k)}\hfill \\ +\sum _{j=1}^m{\beta }_j(\mu +t_k)v(\mu +t_k-{\tau }_j(\mu +t_k))e^{-{\gamma }_j(\mu +t_k)v(\mu +t_k-{\tau }_j(\mu +t_k))}\}d\mu \hfill \\ =\underset{k\to +\mathrm{\infty }}{lim}{\int }_t^{t+\mathrm{\Delta }t}\{-a(\mu )+b(\mu )e^{-v(\mu +t_k)}\hfill \\ +\sum _{j=1}^m{\beta }_j(\mu )v(\mu +t_k-{\tau }_j(\mu ))e^{-{\gamma }_j(\mu )v(\mu +t_k-{\tau }_j(\mu ))}+ϵ(k,\mu )\}d\mu \hfill \\ ={\int }_t^{t+\mathrm{\Delta }t}\{-a(\mu )+b(\mu )e^{-x^{\ast }(\mu )}\hfill \\ +\sum _{j=1}^m{\beta }_j(\mu )x^{\ast }(\mu -{\tau }_j(\mu ))e^{-{\gamma }_j(\mu )x^{\ast }(\mu -{\tau }_j(\mu ))}\}d\mu +\underset{k\to +\mathrm{\infty }}{lim}{\int }_t^{t+\mathrm{\Delta }t}ϵ(k,\mu )d\mu \hfill \\ ={\int }_t^{t+\mathrm{\Delta }t}\{-a(\mu )+b(\mu )e^{-x^{\ast }(\mu )}+\sum _{j=1}^m{\beta }_j(\mu )x^{\ast }(\mu -{\tau }_j(\mu ))e^{-{\gamma }_j(\mu )x^{\ast }(\mu -{\tau }_j(\mu ))}\}d\mu ,\hfill \end{array}$$

(3.5)

where $t+\mathrm{\Delta }t\ge t_0$. Consequently, (3.5) implies that

$$\frac{d}{dt}\{x^{\ast }(t)\}=-a(t)+b(t)e^{-x^{\ast }(t)}+\sum _{j=1}^m{\beta }_j(t)x^{\ast }(t-{\tau }_j(t))e^{-{\gamma }_j(t)x^{\ast }(t-{\tau }_j(t))}.$$

(3.6)

Therefore, $x^{\ast }(t)$ is a solution of (1.3).

Secondly, we prove that $x^{\ast }(t)$ is an almost periodic solution of (1.3). From Lemma 2.2, for any $ϵ>0$, there exists $l=l(ϵ)>0$ such that every interval $[\alpha ,\alpha +l]$ contains at least one number δ for which there exists $N>0$ satisfying

$$|v(t+\delta )-v(t)|\le ϵ\text{for all }t>N.$$

(3.7)

Then, for any fixed $s\in R$, we can find a sufficient large positive integer $N_1>N$ such that for any $k>N_1$,

$$s+t_k>N,|v(s+t_k+\delta )-v(s+t_k)|\le ϵ.$$

(3.8)

Let $k\to +\mathrm{\infty }$, we obtain

$$|x^{\ast }(s+\delta )-x^{\ast }(s)|\le ϵ,$$

which implies that $x^{\ast }(t)$ is an almost periodic solution of equation (1.3).

Finally, we prove that $x^{\ast }(t)$ is globally exponentially stable.

Let $x(t)=x(t;t_0,\phi )$ and $y(t)=x(t)-x^{\ast }(t)$, where $t\in [t_0-r,+\mathrm{\infty })$. Then

$$\begin{array}{rcl}{y}^{\prime }(t)& =& b(t)[e^{-x(t)}-e^{-x^{\ast }(t)}]\\ +\sum _{j=1}^m{\beta }_j(t)[x(t-{\tau }_j(t))e^{-{\gamma }_j(t)x(t-{\tau }_j(t))}-x^{\ast }(t-{\tau }_j(t))e^{-{\gamma }_j(t)x^{\ast }(t-{\tau }_j(t))}].\end{array}$$

(3.9)

It follows from Lemma 2.1 that there exists $t_{\phi ,x^{\ast }}>t_0$ such that

$$\kappa \le x(t),x^{\ast }(t)\le M\text{for all }t\in [t_{\phi ,x^{\ast }}-r,+\mathrm{\infty }).$$

(3.10)

We consider the Lyapunov functional

$$V(t)=|y(t)|e^{\lambda t}.$$

(3.11)

Calculating the upper left derivative of $V(t)$ along the solution $y(t)$ of (3.9), we have

$$\begin{array}{rcl}{D}^{-}(V(t))& \le & b(t)[e^{-x(t)}-e^{-x^{\ast }(t)}]sgn(x(t)-x^{\ast }(t))e^{\lambda t}\\ +\sum _{j=1}^m{\beta }_j(t)|x(t-{\tau }_j(t))e^{-{\gamma }_j(t)x(t-{\tau }_j(t))}\\ -x^{\ast }(t-{\tau }_j(t))e^{-{\gamma }_j(t)x^{\ast }(t-{\tau }_j(t))}|e^{\lambda t}+\lambda |y(t)|e^{\lambda t}\text{for all }t>t_{\phi ,{\phi }^{\ast }}.\end{array}$$

(3.12)

We claim that

$$\begin{array}{rcl}V(t)& =& |y(t)|e^{\lambda t}\\ <& e^{\lambda t_{\phi ,x^{\ast }}}\left(\underset{t\in [t_0-r,t_{\phi ,x^{\ast }}]}{max}\right|x(t)-x^{\ast }(t)|+1)\\ :=& K_{\phi ,x^{\ast }}\text{for all }t>t_{\phi ,x^{\ast }}.\end{array}$$

(3.13)

Contrarily, there must exist $t_{\ast }>t_{\phi ,x^{\ast }}$ such that

$$V(t_{\ast })=K_{\phi ,x^{\ast }}\text{and}V(t)<K_{\phi ,x^{\ast }}\text{for all }t\in [t_0-r,t_{\ast }).$$

(3.14)

Since

$$\kappa \le {\gamma }_j(t_{\ast })x(t_{\ast }-{\tau }_j(t_{\ast })),{\gamma }_j(t_{\ast })x^{\ast }(t_{\ast }-{\tau }_j(t_{\ast }))\le {\gamma }_j^{+}M\le \tilde{\kappa },j=1,2,\dots ,m.$$

Together with (2.18), (2.19), (3.12) and (3.14), we obtain

$$\begin{array}{rcl}0& \le & D^{-}(V(t_{\ast }))\\ \le & b(t_{\ast })[e^{-x(t_{\ast })}-e^{-x^{\ast }(t_{\ast })}]sgn(x(t_{\ast })-x^{\ast }(t_{\ast }))e^{\lambda t_{\ast }}\\ +\sum _{j=1}^m{\beta }_j(t_{\ast })|x(t_{\ast }-{\tau }_j(t_{\ast }))e^{-{\gamma }_j(t_{\ast })x(t_{\ast }-{\tau }_j(t_{\ast }))}\\ -x^{\ast }(t_{\ast }-{\tau }_j(t_{\ast }))e^{-{\gamma }_j(t_{\ast })x^{\ast }(t_{\ast }-{\tau }_j(t_{\ast }))}|e^{\lambda t_{\ast }}+\lambda |y(t_{\ast })|e^{\lambda t_{\ast }}\\ \le & -b(t_{\ast })e^{-M}|y(t_{\ast })|e^{\lambda t_{\ast }}+\sum _{j=1}^m{\beta }_j(t_{\ast })|x(t_{\ast }-{\tau }_j(t_{\ast }))e^{-{\gamma }_j(t_{\ast })x(t_{\ast }-{\tau }_j(t_{\ast }))}\\ -x^{\ast }(t_{\ast }-{\tau }_j(t_{\ast }))e^{-{\gamma }_j(t_{\ast })x^{\ast }(t_{\ast }-{\tau }_j(t_{\ast }))}|e^{\lambda t_{\ast }}+\lambda |y(t_{\ast })|e^{\lambda t_{\ast }}\\ =& -[b(t_{\ast })e^{-M}-\lambda ]|y(t_{\ast })|e^{\lambda t_{\ast }}+\sum _{j=1}^m\frac{{\beta }_j(t_{\ast })}{{\gamma }_j(t_{\ast })}|{\gamma }_j(t_{\ast })x(t_{\ast }-{\tau }_j(t_{\ast }))e^{-{\gamma }_j(t_{\ast })x(t_{\ast }-{\tau }_j(t_{\ast }))}\\ -{\gamma }_j(t_{\ast })x^{\ast }(t_{\ast }-{\tau }_j(t_{\ast }))e^{-{\gamma }_j(t_{\ast })x^{\ast }(t_{\ast }-{\tau }_j(t_{\ast }))}|e^{\lambda t_{\ast }}\\ \le & -[b(t_{\ast })e^{-M}-\lambda ]|y(t_{\ast })|e^{\lambda t_{\ast }}+\sum _{j=1}^m{\beta }_j(t_{\ast })\frac{1}{e^2}\left|y(t_{\ast }-{\tau }_j(t_{\ast }))\right|e^{\lambda (t_{\ast }-{\tau }_j(t_{\ast }))}{e}^{\lambda {\tau }_j(t_{\ast })}\\ \le & \{-[b(t_{\ast })e^{-M}-\lambda ]+\sum _{j=1}^m{\beta }_j(t_{\ast })\frac{1}{e^2}{e}^{\lambda r}\}{K}_{\phi ,x^{\ast }}.\end{array}$$

Thus,

$$0\le -[b(t_{\ast })e^{-M}-\lambda ]+\sum _{j=1}^m{\beta }_j(t_{\ast })\frac{1}{e^2}{e}^{\lambda r},$$

which contradicts with (2.13). Hence, (3.13) holds. It follows that

$$|y(t)|<K_{\phi ,x^{\ast }}{e}^{-\lambda t}\text{for all }t>t_{\phi ,x^{\ast }}.$$

This completes the proof of Theorem 3.1. □

4 Example

In this section, we present an example and its numerical simulation to check the validity of results we obtained in the previous sections.

Example 4.1 Consider the following Nicholson’s blowflies model with a nonlinear density-dependent mortality term:

$$\begin{array}{rcl}{x}^{\prime }(t)& =& -e^{-(1+0.08{cos}^2\sqrt{2}t)}+(1+0.001cos\sqrt{3}t)e^{-x(t)}\\ +\frac{1+{cos}^{2}t}{2\text{,}000}x(t-2e^{{sin}^{4}t})e^{-x(t-2e^{{sin}^{4}t})}\\ +\frac{1+{cos}^{2}2t}{2\text{,}000}x(t-2e^{{cos}^{4}t})e^{-x(t-2e^{{cos}^{4}t})}.\end{array}$$

(4.1)

Obviously, $r=2e$, $a^{-}=e^{-1.08}$, $a^{+}=e^{-1}$, $b^{-}=0.999$, $b^{+}=1.001$, ${\beta }_j^{-}=0.0005$, ${\beta }_j^{+}=0.001$, ${\gamma }_j^{-}={\gamma }_j^{+}=1$, $j=1,2$. Let $M=1.3$, from (1.6) and (1.8), we get

$$\begin{array}{c}\kappa \approx 0.7215355,\tilde{\kappa }\approx 1.342276,\hfill \\ a^{-}=e^{-1.08}>1.001e^{-1.3}+2\times \frac{0.001}{e}=b^{+}{e}^{-M}+\sum _{j=1}^2\frac{{\beta }_j^{+}}{e{\gamma }_j^{-}},\hfill \\ a^{+}=e^{-1}\approx 0.3678794<b^{-}{e}^{-\kappa }=0.999e^{-\kappa }\approx 0.999e^{-0.7215355}\approx 0.4855194\hfill \end{array}$$

and

$$b^{-}{e}^{-M}=0.999e^{-1.3}\approx 0.272>\frac{1}{e^2}\sum _{j=1}^m{\beta }_j^{+}=0.002e^{-2}\approx 0.00027\text{for all }t\in R,$$

which implies that the Nicholson’s blowflies model (4.1) satisfies the assumptions of Theorem 3.1. Hence, equation (4.1) has a unique positive almost periodic solution $x^{\ast }(t)$, which is globally exponentially stable with the exponential convergent rate $\lambda \approx 0.01$. The numerical simulation in Figure 1 strongly supports the conclusion.

Figure 1

Numerical solution $\mathit{x}\mathbf{(}\mathit{t}\mathbf{)}$ of equation ( 4.1 ) for initial value $\mathit{\phi }\mathbf{(}\mathit{s}\mathbf{)}\mathbf{\equiv }\mathbf{2}$ , $\mathit{s}\mathbf{\in }\mathbf{[}\mathbf{-}\mathbf{2}\mathit{e}\mathbf{,}\mathbf{0}\mathbf{]}$ .

Remark 4.1 To the best of our knowledge, few authors have studied the problems of positive almost periodic solutions of Nicholson’s blowflies delayed systems with nonlinear density-dependent mortality terms. It is clear that the results in [11–13] and the references therein cannot be applicable to system (4.1) to prove the global exponential stability of a positive almost periodic solution. Moreover, one can find that the main results of [17] are restricted to considering the Nicholson’s blowflies delayed systems with the nonlinear density-dependent mortality term $\frac{a(t)x}{b(t)+x}$ and give no opinions about $a(t)-b(t)e^{-x}$. This implies that the results of the present paper are new and complement previously known results.