1 Introduction

Issues concerning wormholes in space-time as a solution and the occurrence of these phenomena are a problem that has been widely investigated. Since this paper will treat a phenomenological issue in wormhole space-times, we refer to various phenomenological works on wormhole space-times, including gravitational lensing [1,2,3,4,5,6,7,8], shadows [9,10,11], observation [12], the Casimir effect [13], teleportation [14], the collision of two particles [15], and the creation of a traversable wormhole [16].

Today, many studies are actively investigating wormholes in space-time. This is because it was recently found that the Einstein–Rosen (ER) bridge [17] gives some type of Einstein–Podolsky–Rosen (EPR) pair [18,19,20,21], which plays a very important role in the literature on the information paradox [22]. It would be also its reason that there are common features and behaviors between AdS\(_2\) wormholes and the SYK models, from which currently we can perform various interesting studies [23,24,25,26].

Also, there are studies to construct a graphene wormhole in the material physics from some brane configurations in superstring theory [27, 28]. From these studies, Chern-Simon current in the graphene wormhole is studied in [29].

In the present study, we consider the Morris–Thorne traversable wormhole (traversable wormhole) [30] in a situation in which a gas fills its whole space-time, where it is assumed that a Bose–Einstein condensate (BEC) can be formed at some temperature in this gas. Then, we point out that a state analogous to the Josephson junction is always formed at any temperature except zero in the vicinity of its throat.

For this, we first analyze the critical Unruh temperature of the gas with regard to the BEC in the Rindler space, then check that it agrees with the critical temperature obtained in the flat Euclidean space.

We do this to check that our analytical method is valid for obtaining the critical temperature of the BEC in curved space-times. Our analytical method in curved space-time is actually different from the traditional one in the flat Euclidean space [31] to treat curved space-times. However, since the accelerated system is equivalent to an inertial system with the same temperature as the Unruh temperature, the critical Unruh temperature obtained in the Rindler space should agree with that in the flat Euclidean space.

Then, considering the same gas in the traversable wormhole, we analyze its critical temperature with respect to BEC in the vicinity of its throat.

Here, it is known that generally, the effective potential always diverges, and a BEC is not formed in the flat Euclidean space, if the number of its spatial dimensions is two or less. Then, since the spatial part of the vicinity of the throat in the traversable wormhole space-time becomes effectively one-dimensional, we can expect that the critical temperature of a BEC in the vicinity of the throat is always zero (if the critical temperature is zero, the state is considered always to be in the normal state).

Then,

  • If the critical temperature is always zero in the vicinity of the throat, since the throat exists in a form to separate the wormhole space-time from the other side of the wormhole space-time, the normal state also always appears in a form to separate the wormhole space-time from the other side of the wormhole space-time, as in Fig. 1.

  • The far region of the wormhole space-time is asymptotically flat space-time. Therefore, the critical temperature of BEC in the far region is given by the one calculated in the flat space-time.

  • Then, by extrapolation of the results between the throat region and the far region, we can obtain an expectation that a state analogous to the Josephson junction is always formed at any temperature except zero in the vicinity of the throat.

Fig. 1
figure 1

Penrose diagram for the (t, r) part of the traversable wormhole space-time. The dotted line represents the throat of the wormhole. The yellow and blue parts represent the normal and superconductor states that we expect to appear, respectively. As the normal state appears in a form to separate the space-time, we can expect that a state analogous to the Josephson junction is formed in the vicinity of the throat

Full size image

Since this could be considered a gravitational phenomenology, it would be interesting. It would also be interesting because we can consider the possibility that the Josephson current flows from one side of the wormhole to the other side. Of course, the wave function of the current may be damped when it tunnels, and the Josephson current does not exist in practice. However, this is the subject of future work, and we cannot currently make any explicit claims on this point from the analysis in this study. We discuss this in Sect. 5.

The wormholes we consider in this study are the ER bridge and the traversable wormhole space-time. Then, first, some hard tidal force exists in both of these near-throat regions. We will not consider this problem in this study. In what follows, we point out some other problems in each of these.

The ER bridge is given by patching the part of the event horizon of two Schwarzschild black holes together; therefore, it is no different from the Schwarzschild black hole if it is viewed from the outside. The fact that everything is sucked into the horizon in the vicinity of the horizon may then be a problem in our consideration for the formation of the Josephson junction and current in the ER bridge.

The traversable wormhole is free from this problem, but it needs the exotic matter (some matter to have some negative energy density) [39] so that the traversable wormhole space-time can be the solution of the Einstein equation. We explicitly show this in Sect. 4.2. This is a critical problem, as it means that the matter should be tachyonic and cannot exist; therefore, the traversable wormhole space-time cannot be the solution and cannot be realized. The ER bridge is free from this problem, as it is given using a stable solution, the Schwarzschild black hole. For some recent studies on exotic matter and the attempt to make it into a solution, see [49,50,51,52,53,54,55,56]. In this study, we consider the traversable wormhole with knowledge of this problem.

The paper is organized as follows. We analyze the critical Unruh temperature of the gas with respect to the BEC in the Rindler space in Sect. 2, in the Euclidean space in Sect. 3, and in the traversable wormhole space-time in Sect. 4. Then, in Sect. 5, we point out that a state analogous to the Josephson junction is formed in the vicinity of its throat. In Sect. 6, we obtain the phase structure for the BEC/normal state transition in the ER bridge. In Sect. 7, we summarize the results of this study and discuss examples in which phenomenology analogous to our Josephson junction is formed in other systems. In Appendix B, we note some points in the mechanism for the formation of BEC in this study.

2 Critical temperature of BEC in accelerating system

2.1 Rindler coordinates and Unruh temperature

As a theoretical model, we consider a gas that completely fills the Minkowski space-time and performs a uniformly accelerating motion with acceleration a in one direction. The space-time of such a gas is given by the Rindler coordinate system. We denote its coordinates as \((\eta ,\rho ,y,z)\); then, using these, its squared line element can be written as

$$\begin{aligned} \mathrm{d}s^2 = \rho ^2 \mathrm{d}\eta ^2 - \mathrm{d}\rho ^2 - dx_\perp ^2, \end{aligned}$$
(1)

where (y, z) are common with those in the Minkowski coordinates, and we use the notation \(x_\perp \equiv (y,z)\) in what follows. Note that we do not take a sphere coordinates, but plane coordinates, for the \(x_\perp \)-direction. \((\eta ,\rho )\) are related to the Minkowski coordinates (t, x) by the following relations:

$$\begin{aligned} (t,x) = a^{-1}\big ( \sinh \eta ,\, \cosh \eta \big ) = \rho \left( \sinh \eta ,\, \cosh \eta \right) . \end{aligned}$$
(2)

The gas in the Rindler coordinate system can be considered to be at the following Unruh temperatures:

$$\begin{aligned} T_U= a/2\pi =1/2\pi \rho , \end{aligned}$$
(3)

where \(\rho = 1/a\), as can be seen from (2).

We can see from (3) that locating at different \(\rho \) means having a different Unruh temperature. Therefore, we should be cautious as to the physical meaning when we perform the \(\rho \)-integral and so on. For this point, see [32]. Snd finally we can see that the particles comprising the gas should locate at smaller \(\rho \), as these are close to the trailing endpoint of the gas to maintain its original figure. Therefore, we will finally analyze the critical Unruh temperature by separating the effective potential by each \(\rho \).

2.2 Hamiltonian in finite density, probability amplitude and Euclideanization

We start with the following Lagrangian density for the complex scalar field for the particles comprising the gas that we mention in Sect. 2.1 that fills the whole space:

$$\begin{aligned} {{\mathcal {L}}} = \, g^{\mu \nu } \partial _\mu \phi ^* \partial _\nu \phi - m^2 \phi ^* \phi , \end{aligned}$$
(4)

where \(\phi =\frac{1}{\sqrt{2}}(\phi _1+i \phi _2)\) (\(\phi _{1,2}\) are real scalar fields, and indices \(\mu \), \(\nu \) and \(g^{\mu \nu }\) refer to the Rindler coordinates (\(\eta \), \(\rho \), \(x_\perp \)) and the matrices in (1).

We define \((\pi , \pi ^*)\) as the canonical momenta for (\(\phi ^*\), \(\phi \)), and (\(\bar{\pi }\), \(\bar{\pi }^*\)) as those with lower indices:

$$\begin{aligned} (\pi , \pi ^*)&\equiv \left( \frac{\partial {{\mathcal {L}}}}{\partial (\partial _\eta \phi ^*)},\frac{\partial {{\mathcal {L}}}}{\partial (\partial _\eta \phi )}\right) =(g^{\eta \eta } \partial _\eta \phi , g^{\eta \eta } \partial _\eta \phi ^*), \nonumber \\ (\bar{\pi },\bar{\pi }^*)&\equiv (g_{\eta \eta }\pi ,g_{\eta \eta }\pi ^*) =(\partial _\eta \phi , \partial _\eta \phi ^*). \end{aligned}$$
(5)

Corresponding to \(\phi =\frac{1}{\sqrt{2}}(\phi _1+i \phi _2)\), \(\pi _{1,2}\) and \(\bar{\pi }_{1,2}\) are defined as

$$\begin{aligned} \displaystyle \pi _{1,2} \equiv g^{\eta \eta }\partial _\eta \phi _{1,2}, \quad \bar{\pi }_{1,2} \equiv g_{\eta \eta }\pi _{1,2}=\partial _\eta \phi _{1,2}. \end{aligned}$$
(6)

With these, the Hamiltonian density associated with the Lagrangian density (4) is given as

$$\begin{aligned} {{\mathcal {H}}}&= \pi \,\partial _\eta \phi + \pi ^* \,\partial _\eta \phi ^* - {{\mathcal {L}}} \nonumber \\&= \pi ^* \bar{\pi } - g^{ij} \partial _i \phi ^* \partial _j \phi +m^2 \phi ^* \phi , \end{aligned}$$
(7)

where \(i,j=\rho ,x_\perp \). Then, we can write the Hamiltonian in the grand canonical ensemble, \({{\mathcal {H}}} - \mu _R \, q\), as

$$\begin{aligned} {{\mathcal {H}}} - \mu _R \, q=&\, \frac{1}{2} \big (g^{\eta \eta }\big (\bar{\pi }_1 \bar{\pi }_1+\bar{\pi }_2 \bar{\pi }_2\big )\nonumber \\&-g^{ij}(\partial _i \phi _1\partial _j \phi _1+\partial _i \phi _2\partial _j \phi _2) + m^2 \big (\phi _1^2+\phi _2^2 \big )\big )\nonumber \\&-\mu _R (\pi _2 \phi _1-\pi _1 \phi _2), \end{aligned}$$
(8)

where \(\mu _R\) is the chemical potential and \(q \equiv -i \, g^{\eta \eta }(\phi \,\partial _\eta \phi ^*-\phi ^*\,\partial _\eta \phi )\) is the particle density.

With (8), we can write the probability amplitude as

(9)

where \(\mathrm{I}\) represents the whole Rindler wedge I, \(\gamma _R \equiv \sqrt{-\det g_{\mu \nu }}\), and we perform the following redefinitions for the canonical momenta:

$$\begin{aligned}&\bar{\pi }_1 - (\partial _\eta \phi _1 - \mu _R \,\phi _2) \rightarrow \bar{\pi }_1, \end{aligned}$$
(10a)
$$\begin{aligned}&\bar{\pi }_2 - (\partial _\eta \phi _2 + \mu _R \,\phi _1) \rightarrow \bar{\pi }_2. \end{aligned}$$
(10b)

\({{\mathcal {C}}}_R \) is given as

$$\begin{aligned} {{\mathcal {C}}}_R \equiv \int {{\mathcal {D}}} \pi _1 {{\mathcal {D}}} \pi _2 \exp \big [ i \int _{\Omega _\mathrm{I}} d^4x \, \gamma _R \, g_{\eta \eta } ( (\pi _1)^2+(\pi _2)^2 ) \big ]. \end{aligned}$$
(11)

Since \({{\mathcal {C}}}_R\) is some number irrelevant to \(\mu _R\), and we finally take the derivative with regard to \(\mu _R\) to obtain the e.v. of the particle density, we can ignore \({{\mathcal {C}}}_R\) in our analysis in what follows.

We perform Euclideanization:

$$\begin{aligned} \eta \rightarrow -i \tau . \end{aligned}$$
(12)

At this time,

$$\begin{aligned}&(\pi _\alpha ,\bar{\pi }_\alpha ) \rightarrow i(\pi _\alpha ,\bar{\pi }_\alpha ), \end{aligned}$$
(13a)
$$\begin{aligned}&q \rightarrow iq, \end{aligned}$$
(13b)
$$\begin{aligned}&\mathrm{d}s^2 \rightarrow -\rho ^2 \mathrm{d}\tau ^2-d \rho ^2,\quad 0 \le \tau < 2 \pi , \end{aligned}$$
(13c)
$$\begin{aligned}&g_{\eta \eta } \rightarrow g_{\tau \tau },\quad g_{\tau \tau }=g_{\eta \eta }, \end{aligned}$$
(13d)

where there is no change in the content between \(g_{\tau \tau }\) and \(g_{\eta \eta }\) except for the notations. Therefore, we can see that the period of the imaginary time \(\beta _R \) is \(2\pi \), so the momenta in the \(\eta \)-direction can be written as

$$\begin{aligned} 2\pi n /\beta _R= n \equiv \omega _n \quad (\beta _R=2\pi ). \end{aligned}$$
(14)

Under the Euclideanization (12) with (13), Z in (9) can be rewritten as

$$\begin{aligned} Z&= \int {{\mathcal {D}}} \phi _1 {{\mathcal {D}}} \phi _2 \exp \Bigg [ -\frac{1}{2} \int d^3 x \int _0^{\beta _R} \mathrm{d}\tau \,\gamma _R \,\nonumber \\&\quad \times \left( \begin{array}{cc} \phi _1&\phi _2 \end{array} \right) \left( \begin{array}{cc} \hat{G}_R+M_R^2 &{} -2ig^{\tau \tau }\mu _R \, \partial _\eta \\ 2ig^{\tau \tau }\mu _R \,\partial _\eta &{} \hat{G}_R+M_R^2 \end{array} \right) \left( \begin{array}{c} \phi _1 \\ \phi _2 \end{array} \right) \Bigg ], \end{aligned}$$
(15)

where \( \hat{G}_R \equiv \, -g^{\tau \tau } \partial _\tau \partial _\tau + \gamma _R^{-1} g^{ij} \partial _i (\gamma _R\partial _j)\) and \(M_R^2 \equiv m^2 - g^{\tau \tau }\mu _R^2\).

2.3 Description for BEC and upper limit of chemical potential

In order to express the fields in the superconducting state, we separately rewrite \(\phi _{1,2}\) as the e.v. part and the original \(\phi _{1,2}\) as the following [31]:

$$\begin{aligned} \phi _1 \, \equiv&\, \sqrt{2} \, \alpha \, \cos \Theta + \tilde{\phi }_1, \end{aligned}$$
(16a)
$$\begin{aligned} \phi _2 \, \equiv&\, \sqrt{2} \, \alpha \, \sin \Theta + \tilde{\phi }_2. \end{aligned}$$
(16b)

where \(\alpha \) and \(\Theta \) represent the absolute value and the phase of e.v., and

$$\begin{aligned} \alpha \left\{ \begin{array}{l} = 0 \quad \text {corresponds to the normal state,} \\ \not = 0 \quad \text {corresponds to the BEC state.} \\ \end{array} \right. \end{aligned}$$
(17)

Rewriting Z in (15) and employing the expressions in (16), we can obtain the following Z:

$$\begin{aligned} Z&= \exp \left[ -\alpha ^2\beta _R V_\perp \int \mathrm{d}\rho \gamma _R \, M_R^2\right] \nonumber \\&\quad \times \int {{\mathcal {D}}} \tilde{\phi }_1 {{\mathcal {D}}} \tilde{\phi }_2 \exp \left[ - \frac{1}{2} \int _0^\infty d \rho \int _{-\infty }^\infty d^2 x_\perp \int _0^{\beta _R} \mathrm{d}\tau \, \gamma _R \right. \nonumber \\&\quad \left. \times \left( \begin{array}{cc} \tilde{\phi }_1&\tilde{\phi }_2 \end{array} \right) \left( \begin{array}{cc} \hat{G}_R+M_R^2 &{} 2ig^{\tau \tau }\mu _R \,\partial _\eta \\ -2ig^{\tau \tau }\mu _R \,\partial _\eta &{} \hat{G}_R+M_R^2 \end{array} \right) \left( \begin{array}{c} \tilde{\phi }_1 \\ \tilde{\phi }_2 \end{array} \right) \right] , \end{aligned}$$
(18)

where \(V_\perp \equiv \int dx_\perp ^2 = \int dk_\perp ^2\).

Now let us look at the contribution from the zero mode in the pass-integral part in (18), which we can write as

$$\begin{aligned} \int {{\mathcal {D}}} \tilde{\phi }_1 {{\mathcal {D}}} \tilde{\phi }_2 \exp \left[ - \frac{ M_R^2 }{2} (\tilde{\phi }_1^2 + \tilde{\phi }_2^2) \right] ^{V_I}, \end{aligned}$$
(19)

where the configurations generated by \(\int {{\mathcal {D}}} \tilde{\phi }'_1 {{\mathcal {D}}} \tilde{\phi }'_2\) are only the constant configurations irrelevant to the coordinates, and \(V_I\) means \(\int _0^\infty d \rho \int _{-\infty }^\infty d^2 x_\perp \int _0^{\beta _R} \mathrm{d}\tau \, \gamma _R \). Then we can see that (20) can converge when \(M_R^2\) is positive, and diverge when \(M_R^2\) is negative or zero. Therefore, we can write

$$\begin{aligned} Z \text {in }(18) \left\{ \begin{array}{l} \text {converges for }M_R^2>0, \\ \text {diverges for }M_R^2\le 0. \end{array} \right. \end{aligned}$$
(20)

From (20), we can see that there is an upper bound for the value that the chemical potential can take as

$$\begin{aligned} \mu _R^c = m/\sqrt{g^{\eta \eta }}=m/a. \end{aligned}$$
(21)

Here, we explain how the BEC is formed in our system. When decreasing the Unruh temperature from some high temperature (therefore, \(\alpha \) is 0), keeping the e.v. of the particle density constant, it turns out that the chemical potential should rise (see (58)). However, as in (21), there is an upper limit for the value that the chemical potential can take. Therefore, finally, \(\alpha \) should start to have some finite value to keep the e.v. of the particle density constant. Similarly, at some lower Unruh temperature, \(\alpha \) becomes finite and BEC is formed. (For further description of this issue, see Appendix B.)

2.4 Effective potential (1)

We can diagonalize the shoulder in Z in (18) as

$$\begin{aligned} Z =&\exp \left[ -\alpha ^2\beta _R V_\perp \int _0^\infty \mathrm{d}\rho \gamma _R M_R^2\right] \int {{\mathcal {D}}} \tilde{\phi }'_1 {{\mathcal {D}}} \tilde{\phi }'_2 \exp \nonumber \\&\quad \times \Bigg [- \frac{1}{4} \int _0^\infty \mathrm{d}\rho \int _{-\infty }^\infty d^2 x_\perp \int _0^{\beta _R} \mathrm{d}\tau \, \gamma _R\nonumber \\&\quad \times \left( \begin{array}{cc} \tilde{\varphi }'{}^*&\tilde{\varphi }' \end{array} \right) \left( \begin{array}{cc} \hat{G}_{R+} + M_R^2 &{} 0 \\ 0 &{} \hat{G}_{R-} + M_R^2 \end{array} \right) \left( \begin{array}{c} \tilde{\varphi }' \\ \tilde{\varphi }'{}^* \end{array} \right) \bigg ], \end{aligned}$$
(22)

where \(\hat{G}_{R\pm } \equiv \hat{G}_R \pm 2g^{\eta \eta }\mu _R\) and \( \frac{1}{\sqrt{2}} \left( \begin{array}{c} \tilde{\varphi }' \\ \tilde{\varphi }'{}^* \end{array} \right) \equiv U^{-1} \left( \begin{array}{c} \tilde{\phi }_1 \\ \tilde{\phi }_2 \end{array} \right) \). U is given as \(\frac{1}{\sqrt{2}} \left( \begin{array}{cc} i &{} -i \\ 1 &{} 1 \end{array} \right) \). The difference that arises in the path-integral measure by the transformation U is just some constant, which we can ignore.

We express \(\phi _\alpha \) \((\alpha =1,2)\) by the plane-wave expansion for the \(x_\perp \)-directions, keeping the \(\rho \)-direction as

$$\begin{aligned} \tilde{\phi }_{\alpha }(\rho ,\eta ,x^\perp )&= \frac{1}{(2\pi )^2\beta _R} \sum _{n=-\infty }^\infty \nonumber \\&\quad \times \int dk_\perp ^2 \tilde{\varphi }_{\alpha ,n} (\rho ,k_\perp ) e^{-i(\omega _n \eta \,+\,k_\perp x^\perp )}. \end{aligned}$$
(23)

Then \(\hat{G}_0 \equiv \frac{1}{2}(\hat{G}_{R+} + \hat{G}_{R-}+2 M_R^2)\) in Z in (22) is given asFootnote 1

$$\begin{aligned} \hat{G}_0 \rightarrow G_0&= g^{\tau \tau } \omega _n^2 + \gamma _R^{-1} g^{\rho \rho } \partial _\rho (\gamma _R\partial _\rho ) + g^{\perp \perp } k_\perp ^2+M_R^2\nonumber \\&\equiv G_R+M_R^2 \end{aligned}$$
(26)

with \((\partial _\eta ,\partial _\perp ) \rightarrow -i(\omega _n, k_\perp )\); \( \gamma _R^{-1} g^{\rho \rho } \partial _\rho (\gamma _R \partial _\rho )\) is still the operator. As a result, Z in (22) can be given as

$$\begin{aligned} Z&= \exp \left[ -\alpha ^2\beta _R V_\perp \int _0^\infty \mathrm{d}\rho \gamma _R M_R^2\right] \int {{\mathcal {D}}} \tilde{\phi }'_{1,n} {{\mathcal {D}}} \tilde{\phi }'_{2,n} \exp \nonumber \\&\quad \times \Bigg [- \frac{1}{2\beta _R} \sum _{n=-\infty }^\infty \int _0^\infty \mathrm{d}\rho \int _{-\infty }^\infty d^2 k_\perp \, \gamma _R (G_R+M_R^2) \nonumber \\&\quad \times ( (\tilde{\phi }'_{1,n}(\rho ,k_\perp ))^2 + (\tilde{\phi }'_{2,n}(\rho ,k_\perp ))^2 ) \Bigg ], \end{aligned}$$
(27)

where the formula \(\beta ^{-1}\int _0^\beta \mathrm{d}\tau e^{i(\omega _m-\omega _n)}=\delta _{mn}\) has been used. Then, performing the functional integral for \(\tilde{\phi }'_{\alpha ,n}\), we can obtain the following Z:

$$\begin{aligned} Z&= \exp \left[ -\alpha ^2\beta _R V_\perp \int \mathrm{d}\rho \gamma _R M_R^2\right] \prod _{n=-\infty }^\infty \prod _\rho \mathrm{Det}\nonumber \\&\quad \times \left( \frac{\pi \Delta \rho \, \gamma _R}{2\beta _R} (G_R+M_R^2)\right) ^{-1}, \end{aligned}$$
(28)

where from (26) to (27) we have rewritten the integral \(\int \mathrm{d}\rho \) as \(\sum _\rho \Delta \rho \) (\(\rho \) takes all the real numbers from 0 to \(\infty \)), and \(\mathrm{Det}\) is the one with regard to the \(k_\perp \)-space for each \(\rho \), where we have written the reason for why we separate by each \(\rho \) in Sect. 2.1.

Defining the free energy \(F_R\) as \(Z=\exp (-\beta _R F_R )\),

$$\begin{aligned} F_R =&\, \alpha ^2 V_\perp \int _0^\infty \mathrm{d}\rho \gamma _R M_R^2 + \frac{1}{\beta _R} \sum _{n=-\infty }^\infty \sum _\rho \mathrm{Tr}\, \mathrm{Log} \nonumber \\&\quad \times (G_R+M_R^2), \end{aligned}$$
(24)

where we have ignored \({{\mathcal {N}}} \, \mathrm{Log}(\frac{\pi \Delta \rho \, \gamma _R}{2\beta _R})\) (where \({{\mathcal {N}}}=\mathrm{Dim}(n) \times \mathrm{Dim}(\rho ) \times \mathrm{Dim}(k_\perp )\)), as it is irrelevant to \(\mu _R\). We can express \(F_R\) in (28) as

$$\begin{aligned} F_R =&\, \alpha ^2 V_\perp \int _0^\infty \mathrm{d}\rho \gamma _R M_R ^2 + \frac{V_\perp }{\beta _R} \sum _{n=-\infty }^\infty \sum _\rho \gamma _R\nonumber \\&\times \int \frac{dk_\perp ^2}{(2\pi )^2} \int _0^{M_R^2}\mathrm{d}\Delta ^2 \widetilde{D}_{\Delta ^2}(\rho ,n, k_\perp ), \end{aligned}$$
(29)

where

$$\begin{aligned} \widetilde{D}_{\Delta ^2}(\rho , k_\eta ,k_\perp )&\equiv \left( G_R + \Delta ^2 \right) ^{-1}\nonumber \\&= \Bigg ( g^{\tau \tau } \omega _n^2 + \gamma _R^{-1} g^{\rho \rho } \partial _\rho (\gamma _R \partial _\rho ) + g^{\perp \perp } k_\perp ^2 \nonumber \\&\quad + \Delta ^2\Bigg )^{-1}. \end{aligned}$$
(30)

In (29), we have ignored \(\mathrm{Log} \, G_R\), as it is irrelevant to \(\mu _R\)Footnote 2. Further, \(\widetilde{D}_{\Delta ^2}(\rho , k_\eta ,k_\perp )\) in (29) includes some operator, but for now we suppose that it is some numbers.

We consider expressing \(F_R/V_\perp \) for each \(\rho \) as \(\Gamma _R^{(\rho )}\) as

$$\begin{aligned} \Gamma _R^{(\rho )}&= \alpha ^2 \gamma _R M_R ^2 +\frac{1}{\beta _R } \sum _{n=-\infty }^\infty \gamma _R \int _{-\infty }^\infty \frac{\mathrm{d}k^2}{(2\pi )^2} \nonumber \\&\quad \times \int ^{M_R^2}_0 \mathrm{d}\Delta ^2 \, \widetilde{D}_{\Delta ^2}(\omega _n,\rho ,k). \end{aligned}$$
(33)

2.5 \(\widetilde{D}_{\Delta ^2}(\omega _n,\rho ,k)\)

\(\widetilde{D}_{\pm ,\Delta ^2}(\rho , \omega _n,k_\perp )\) in (30) is given as some operator. In this section, we obtain its expression as numbers. For this purpose, we define \(\widetilde{D}_{\pm ,\Delta ^2}(\rho , \omega _n,k_\perp )\) as

$$\begin{aligned} D_{\Delta ^2}(x-x')&=\int \frac{\mathrm{d}^3k}{(2\pi )^3} \, \widetilde{D}_{\Delta ^2}(\rho -\rho ',k_\eta ,k_\perp ) \,\nonumber \\&\quad \times e^{i\,(\omega _n \, (\eta -\eta ') - k_\perp (x_\perp -x_\perp '))}. \end{aligned}$$
(34)

\(D_{\Delta ^2}(x-x')\) should satisfy the following identity:

$$\begin{aligned}&( g^{\tau \tau } \omega _n^2 + \gamma _R^{-1} g^{\rho \rho } \partial _\rho (\gamma _R \partial _\rho )\nonumber \\&\quad + g^{\perp \perp } k_\perp ^2 + \Delta ^2 ) D_{\Delta ^2}(x-x') =\gamma _R^{-1} \delta ^4(x-x'), \end{aligned}$$
(35)

where the operator in l.h.s. in (34) is taken from (29). From (34), we can obtain the relation that \(\widetilde{D}_{\pm ,\Delta ^2}\) should satisfy as

$$\begin{aligned}&\big (\,\hat{{{\mathcal {F}}}} {-} \omega _n^2\,\big ) \,\widetilde{D}_{\pm ,\Delta ^2}(\rho -\rho ',k_\eta ,k_\perp ) = -\rho \, \delta (\rho -\rho '), \nonumber \\&\hat{{{\mathcal {F}}}} \equiv \rho ^2 \partial _\rho ^2+ \rho \, \partial _\rho - \rho ^2\kappa ^2, \quad \kappa ^2 \equiv (k_\perp ^2+\Delta ^2). \end{aligned}$$
(31)

Based on (35), we obtain \(\widetilde{D}_{\Delta ^2}(\rho -\rho ',k_\eta ,k_\perp )\) in what follows.

To obtain \(\widetilde{D}_{\Delta ^2}(\rho -\rho ',k_\eta ,k_\perp ) \), we focus on the fact that \(\hat{{{\mathcal {F}}}}\) is the operator of the following eigenvalue equation with eigenvalue \((i\lambda )^2\):

$$\begin{aligned}&\hat{{{\mathcal {F}}}} \,\Theta _\lambda (\rho \kappa ) = (i \lambda )^2 \, \Theta _\lambda (\rho \kappa ), \nonumber \\&\Theta _\lambda (\rho \kappa )\equiv C_\lambda K_{i \lambda }(\rho \kappa ),\quad C_\lambda \equiv \frac{1}{\pi }\sqrt{2\lambda \sinh (\pi \lambda )}, \end{aligned}$$
(36)

where \(K_\alpha (x)\) is the modified Bessel function of the second kind, and \(\Theta _\lambda (\rho ,k)\) satisfies the following normalized orthogonal relationFootnote 3:

$$\begin{aligned} \int _0^\infty \frac{\mathrm{d}\rho }{\rho } \, \Theta _{\lambda '}(\rho \kappa ) \, \Theta _\lambda (\rho \kappa )=\delta (\lambda '-\lambda ). \end{aligned}$$
(37)

\(\lambda \) is a real number; therefore, \(\Theta _\lambda (\rho \kappa )\) can form a set of an infinite-dimensional orthogonal system. Then, by taking \(\Theta _\lambda (\rho \kappa )\) as a set of the orthogonal bases, let us formally write \(\widetilde{D}_{\pm ,\Delta ^2}(\rho -\rho ',k_\eta ,k_\perp )\) in the expanded form as

$$\begin{aligned} \widetilde{D}_{\Delta ^2}(\rho -\rho ',k_\eta ,k_\perp ) =\int _0^\infty \mathrm{d}\lambda \, f_{\lambda } \, \Theta _\lambda (\rho \kappa ), \end{aligned}$$
(38)

where \(f_{\lambda ,\pm }\) are the coefficients of each independent direction, \(\Theta _\lambda (\rho \kappa )\), specified by \(\lambda \), which are to be obtained in what follows.

To obtain \(f_{\lambda }(\omega ,\rho ')\), we consider two quantities, \(\langle \widetilde{D}_{\Delta ^2} | \hat{{{\mathcal {F}}}} | \Theta _\lambda (\rho \kappa ) \rangle \) and \(\langle \Theta _\lambda (\rho \kappa ) | \hat{{{\mathcal {F}}}} | \widetilde{D}_{\Delta ^2} \rangle \), which should be equivalent to each other; however, each of these expressions can be given as

$$\begin{aligned} \int _0^\infty \frac{\mathrm{d}\rho }{\rho } \, \widetilde{D}_{\Delta ^2} \, \hat{{{\mathcal {F}}}} \, \Theta _\lambda (\rho \kappa )&= -\lambda ^2 \int _0^\infty \frac{\mathrm{d}\rho }{\rho } \, \widetilde{D}_{\Delta ^2} \, \Theta _\lambda (\rho \kappa ), \end{aligned}$$
(39a)
$$\begin{aligned} \int _0^\infty \frac{\mathrm{d}\rho }{\rho } \, \Theta _\lambda (\rho \kappa ) \, \hat{{{\mathcal {F}}}} \widetilde{D}_{\Delta ^2}&= {\omega _n^2} \int _0^\infty \frac{\mathrm{d}\rho }{\rho } \, \Theta _\lambda (\rho \kappa ) \widetilde{D}_{\Delta ^2} \nonumber \\&\quad - \Theta _\lambda (\rho '\kappa ), \end{aligned}$$
(39b)

where we have used (36) and (35). From the condition (39a)–(39b) = 0 whereFootnote 4

$$\begin{aligned} (39a) - (39b) = \big ( -\lambda ^2{-}\omega _n^2 \big ) \, f_{\lambda } + \Theta _\lambda (\rho '\kappa ), \end{aligned}$$
(42)

\(f_{\lambda ,\pm }(\rho -\rho ',k_\eta ,k_\perp )\) can be determined as

$$\begin{aligned} f_{\lambda }=\frac{\Theta _\lambda (\rho '\kappa )}{\lambda ^2{+}\omega _n^2}. \end{aligned}$$
(43)

Using (42) in (38), we can write \(\widetilde{D}_{\Delta ^2}\) as

$$\begin{aligned} \widetilde{D}_{\Delta ^2} (\rho -\rho ',k_\eta ,k_\perp )&=\int _0^\infty \mathrm{d}\lambda \, \frac{\Theta _\lambda (\rho '\kappa )\Theta _\lambda (\rho \kappa )}{\lambda ^2{+}\omega _n^2}\nonumber \\&=\int _0^\infty \mathrm{d}\lambda \, \frac{C_\lambda ^2 K_{i \lambda }(\rho '\kappa )K_{i \lambda }(\rho \kappa )}{\lambda ^2{+}\omega _n^2}. \end{aligned}$$
(44)

This expression does not include operators, which in principle is some numbers.

2.6 Effective potential (2)

In the previous section we obtained some concrete expression of \(\widetilde{D}_{\Delta ^2}(\rho -\rho ',k_\eta ,k_\perp )\) as in (43). Using it, we can write \(\Gamma ^{(\rho )}_R\) in (32) asFootnote 5,

$$\begin{aligned} \Gamma ^{(\rho )}_R = \alpha ^2 \gamma _R M_R^2 +\frac{\gamma _R}{2\pi ^3} \int _0^\infty \mathrm{d}\lambda \, \cosh (\pi \lambda ) \int _0^\infty \mathrm{d}k k\, \Psi , \end{aligned}$$
(45a)

where

$$\begin{aligned} \Psi&\equiv \int ^{M_R^2}_0 \mathrm{d}\Delta ^2 \, K_{i\lambda }^2(\kappa \rho ),\nonumber \\&\qquad (\kappa ^2 \equiv k_\perp ^2+\Delta ^2, \quad M_R^2 \equiv m^2 - g^{\eta \eta }\mu _R^2). \end{aligned}$$
(40)

To perform the derivative with regard to \(\mu _R\), we pick up the \(\mu _R\)-dependent parts in \(\Psi \) by expanding it around \(\mu _R=0\)Footnote 6 as

$$\begin{aligned} \Psi =&\, \Psi \Big |_{\mu _R=0} + \frac{\partial \Psi }{\partial \mu _R} \Big |_{\mu _R=0} \,\mu _R + \frac{1}{2}\frac{\partial ^2 \Psi }{\partial \mu _R^2} \Big |_{\mu _R=0} \,\mu _R^2 + {{\mathcal {O}}}(\mu _R^4) \nonumber \\ =&\, \Psi _0- a^2 K_{i\lambda }^2(\kappa \rho ) \Big |_{\Delta ^2=M^2} \, \mu _R^2 + {{\mathcal {O}}}(\mu _R^4) \end{aligned}$$
(49a)

whereFootnote 7,

$$\begin{aligned} \Psi _0&\equiv \int _0^{m^2} d \Delta ^2 \, K_{i\lambda }^2(\kappa \rho ) , \end{aligned}$$
(49c)
$$\begin{aligned} \frac{\partial \Psi }{\partial \mu _R} \bigg |_{\mu _R=0}&= \frac{\partial M_R^2}{\partial \mu _R} \frac{\partial \Psi }{\partial M_R^2} \bigg |_{\mu _R=0} = 0, \end{aligned}$$
(50)
$$\begin{aligned} \frac{1}{2}\frac{\partial ^2 \Psi }{\partial \mu _R^2} \bigg |_{\mu _R=0}&= \frac{1}{2}\frac{\partial }{\partial \mu _R} \bigg (\frac{\partial M_R^2}{\partial \mu _R} \frac{\partial \Psi }{\partial M_R^2} \,\bigg )\bigg |_{\mu _R=0} \nonumber \\&= -a^2 K_{i\lambda }^2(\kappa \rho ) \Big |_{\Delta ^2=m^2}. \end{aligned}$$
(46)

With (47), we can write \(\Gamma ^{(\rho )}_R\) in (44) as

$$\begin{aligned} \Gamma ^{(\rho )}_R&= \alpha ^2\gamma _R M_R^2 + \frac{\gamma _R}{2\pi ^3} \int _0^\infty \mathrm{d}\lambda \, \cosh (\pi \lambda ) \int _0^\infty dk k\,\nonumber \\&\quad \times \left( \Psi _0 -a^2\mu _R^2 \, K_{i\lambda }^2(\kappa \rho )\Big |_{\Delta ^2=m^2} \right) . \end{aligned}$$
(48)

We are going to finally assign the critical value \(\mu _R^c=m/a_c\) in (20) to \(\mu _R\) in (47), then take the leading order in the expansion of \(\mu _R^c\). For this, we now use two symbols, \(\mu _R\) and \(\mu _R'\):

  • \(\mu _R\): chemical potential on which the derivative with respect to \(\mu _R\) can act; finally the value \(m/a_c\) is assigned,

  • \(\mu _R'\): just a symbol for the value \(m/a_R^c\), on which the derivative with respect to \(\mu _R\) does not act.

Then, \(\Psi _0\) and \(a^2\mu _R^2 \, K_{i\lambda }^2(\kappa \rho )\Big |_{\Delta ^2=m^2}\) can be expanded with regard to \(\mu _R'\) as

$$\begin{aligned} \Psi _0&= a_c^2 \, K_{i \lambda }^{2}(k/a_c)\,{\mu _R'}^2 +{{\mathcal {O}}}(\mu _R'{}^{4}), \end{aligned}$$
(51a)
$$\begin{aligned} a_c^2\mu _R^2 \, K_{i\lambda }^2(\kappa \rho )\Big |_{\Delta ^2=m^2}&= a_c^2\mu _R^2\,(K_{i \lambda }^2(k/a_c)+{{\mathcal {O}}}(\mu _R'{}^2)). \end{aligned}$$
(51b)

Using (51), we can obtain \(\Gamma ^{(\rho )}_R\) at the critical moment given by (47) as

$$\begin{aligned} \Gamma ^{(\rho )}_R= \alpha ^2a_c^{-1}M_R^2+\frac{a_c^3}{4\pi ^2} (\mu _R'{}^2-\mu _R^2)\int ^\infty _0 \mathrm{d}\lambda \lambda \coth (\pi \lambda ), \end{aligned}$$
(52)

where we have used \(\displaystyle \int ^\infty _0 dkk K_{i\lambda }^2(k/a_c)\) is given as \(\frac{a_c^2\pi \lambda }{2\sinh \pi \lambda }\).  

Let us evaluate the \(\lambda \)-integral in (52).

$$\begin{aligned} \int ^\infty _0 \mathrm{d}\lambda \lambda \coth (\pi \lambda ). \end{aligned}$$
(53)

First, we can see that (53) is divergent if it is evaluated as it is. Therefore, we consider doing some regularization toward (53)Footnote 8. For this purpose, we consider pulling out some constant in \(\coth (\pi \lambda )\). Therefore, expressing \(\coth (\pi \lambda )\) as

$$\begin{aligned} \coth (\pi \lambda )= 1+\frac{2}{e^{2 \pi \lambda }-1}, \end{aligned}$$
(54)

we exclude “1”. Then, once putting the upper limit of the integral as \(\Lambda \), we perform the integral, and we obtain as

$$\begin{aligned}&\int ^{\Lambda }_0 \mathrm{d}\lambda \lambda (\coth (\pi \lambda )-1) \nonumber \\&\quad = -\frac{1}{12} -\Lambda ^2 +\frac{\Lambda \log (1-e^{2 \pi \Lambda })}{\pi }+\frac{\text {Li}_2(e^{2 \pi \Lambda })}{2 \pi ^2}, \end{aligned}$$
(55)

where \(\Lambda \rightarrow \infty \) finally. Then, excluding “\(-\frac{1}{12}\)” in (55), we take the \(\Lambda \) to \(\infty \). As a result we obtain as

$$\begin{aligned} \lim _{\Lambda \rightarrow \infty } \left( -\Lambda ^2+\frac{\Lambda \log (1-e^{2 \pi \Lambda })}{\pi }+\frac{\text {Li}_2(e^{2 \pi \Lambda })}{2 \pi ^2}\right) =\frac{1}{6}. \end{aligned}$$
(56)

Then, using this result, we can give the effective potential \(\Gamma _R^{(\rho )}\) as

$$\begin{aligned} \Gamma _R^{(\rho )}= \alpha ^2a_c^{-1}M_R^2+\frac{a_c^3}{24\pi ^2}(\mu _R'{}^2-\mu _R^2). \end{aligned}$$
(57)

2.7 Critical Unruh temperature for BEC

We can obtain the e.v. of the particle density according to \(d_R = - \partial \Gamma _R^{(\rho )}/\partial \mu _R\) as

$$\begin{aligned} d_R = 2\alpha ^3 a_c \mu _R + \frac{a_c^3}{12\pi ^2}\mu _R, \end{aligned}$$
(58)

From (58), we can see that if we decrease the Unruh temperature from some high temperature, fixing the e.v. of the particle density to some constant, the value of the chemical potential should increase.

Let us consider reaching the critical Unruh temperature by decreasing the acceleration gradually from some high accelerations where BEC is not formed. Then, from the explanation under (21), we can obtain the critical acceleration from (58) asFootnote 9

$$\begin{aligned} a^c = 2 \, \pi \,\sqrt{3d_R/m}, \end{aligned}$$
(59)

where \(\alpha =0\) and \(\mu _c = m/a^c\) are assigned in (58). Using the relation between the Unruh temperature and acceleration, \(a=2\pi T_U\), we can obtain the critical Unruh temperature as \(T_U = \sqrt{3d_R/m}\). This result is consistent with the critical temperature for BEC obtained from the different analytical method in the \(D=1+3\) flat Euclidean space at finite temperature [31].

3 Critical Unruh temperature of BEC in flat Euclidean space at finite temperature

In this section, we obtain the critical temperature in the \(D=1+3\) flat Euclidean space at finite temperature from our analysis in the previous section just by exchanging the space-time for the \(D=1+3\) flat Euclidean space at finite temperature.

Therefore, as the calculation method in this section is basically the same as that in the previous section, in this section we describe only the points in the case of the \(D=1+3\) flat Euclidean space at finite temperature.

3.1 Exchanging the background space for Euclidean space

First, we exchange the Rindler space (1) for the flat \(D=1+3\) Euclidean space at finite temperature, which can be done by (1) putting \(\rho \) to 1, then (2) Euclideanizing the \(\eta \)-direction as (12), then periodizing it by the arbitrary period \(\beta _E\). The (1) in which these two manipulations are performed can be written as

$$\begin{aligned} \mathrm{d}s_E^2 = -\rho ^2 \mathrm{d}\tau ^2 - \mathrm{d}\rho ^2 - \mathrm{d}x_\perp ^2, \end{aligned}$$
(60)

where the \(\tau \)-direction is periodic with the arbitrary period \(\beta _E\).

3.2 Effective potential

Employing (60), we proceed with the analysis in the previous section. Then, the following \(\Gamma _E\) can be obtained instead of (32):

$$\begin{aligned} \Gamma _E =&\,\, \alpha ^2M_E^2+ \frac{2}{\pi ^2\beta _E} \int _{-\infty }^\infty \frac{\mathrm{d}k^2_\perp }{(2\pi )^2} \nonumber \\&\times \int _0^\infty \mathrm{d}\lambda \, \lambda \, \sinh (\pi \lambda ) \sum _{n=-\infty }^\infty \frac{1}{\lambda ^2-\omega _n^2} \Psi _E, \end{aligned}$$
(61)

where

$$\begin{aligned} \omega _n&\equiv \frac{2\pi }{\beta _E}n, \quad \Psi _E \equiv \int ^{M_E^2}_0 \mathrm{d}\Delta ^2 \, K_{i\lambda }^2(\kappa ), \nonumber \\&\quad (\kappa ^2 \equiv k_\perp ^2+\Delta ^2, \quad M_E^2 \equiv m^2 - \mu _E^2), \end{aligned}$$
(62)

and \(K_\alpha (x)\) represent the Bessel function of the second kind, and as for \(\omega _n\), we use the same notation as that in the previous section.

From \(M_E^2\) above, we can see that the upper bound of the value of the chemical potential in the case of the flat \(D=1+3\) Euclidean space at finite temperature is given as

$$\begin{aligned} \mu _E^c=m. \end{aligned}$$
(63)

Expanding (61) to the second order of the value of the critical chemical potential in the same way we did in Sect. 2.6, we can obtain the following \(\Gamma _E\):

$$\begin{aligned} \Gamma _E = \, \alpha ^2M_E^2+ \frac{1}{4\pi ^2} \int _0^\infty \mathrm{d} \lambda \, \lambda \, \coth \left( \frac{\beta _E \lambda }{2}\right) (\mu _E'^2-\mu _E^2), \end{aligned}$$
(64)

where \(\mu _E'\) has the same meaning as that in Sect. 2.6, but in the current case, \(\mu _E'\) is given by m corresponding to (63).

Now, we evaluate \(\displaystyle \int _0^\infty \mathrm{d}\lambda \, \lambda \, \coth (\beta _E \lambda /2)\) in (64). If we performed the integration as it is, it would be divergent. Hence, we perform some regularization. As \(\coth x\) can be rewritten as \(\displaystyle 1+{2}/(e^{2x}-1)\), we subtract the constant “1” as some regularization, then evaluate it as \(\displaystyle \int _0^\infty \mathrm{d}\lambda \, \lambda \, ( \coth (\beta _E \lambda /2)-1)=2\pi ^2/3\beta _E^2\). Using this, we can obtain the following \(\Gamma _E\):

$$\begin{aligned} \Gamma _E = \, \alpha ^2M_E^2+ \frac{1}{6\beta _E^2} (\mu _E'^2-\mu _E^2). \end{aligned}$$
(65)

3.3 Critical temperature

From (65), calculating the density according to \(d_E=-\frac{\partial \Gamma _E}{\partial \mu _E}\), then putting \(\alpha =0\) and \(\mu _E^c=m\) corresponding to the critical moment, we can obtain the relation between the temperature and density at the critical moment as

$$\begin{aligned} T_E^c=\sqrt{3d_E/m}. \end{aligned}$$
(66)

This agrees with the critical temperature for BEC in the \(D=1+3\) flat Euclidean space at finite temperature in [31]; however, our method of obtaining this result is different from [31].

4 BEC in the traversable wormhole space-time

4.1 Traversable wormhole space-time

In this section, we consider the traversable wormhole given by considering two of the following space-times,

$$\begin{aligned} \mathrm{d}s^2 = \mathrm{d}t^2 - \frac{\mathrm{d}r^2}{1-v^2/r^2}-r^2(\mathrm{d}\theta ^2+\sin ^2 \theta \mathrm{d}\phi ^2), \end{aligned}$$
(67)

then attaching the parts of \(r=v\) of these [39]. Therefore, the position of the throat is located at \(r=v\) and the range of r on one side of the wormhole space-time is

$$\begin{aligned} v \le r \le \infty , \quad (\text {the throat is located at r=v}). \end{aligned}$$
(68)

In order for the wormhole (67) to be a solution of the Einstein equation, the exotic matter violating the null energy condition is needed [39]; however, we do not consider it in this study.

4.2 On the fact that matter with negative energy density is needed

(67) leads to the following Einstein tensor:

$$\begin{aligned} R_{\mu \nu }-\frac{g_{\mu \nu }}{2}R= \left( \begin{array}{cccc} -\frac{v^2}{r^4} &{} 0 &{} 0 &{} 0 \\ 0 &{} \frac{v^2}{r^2 \left( v^2-r^2\right) } &{} 0 &{} 0 \\ 0 &{} 0 &{} \frac{v^2}{r^2} &{} 0 \\ 0 &{} 0 &{} 0 &{} \frac{v^2 \sin ^2 \theta }{r^2} \\ \end{array} \right) . \end{aligned}$$
(69)

From the result above, we can see that the energy density of our scalar field should be negative, which means that our scalar field is tachyonic. However, since such tachyonic matter cannot exist, (67) cannot be a solution. Therefore, (67) will not be realized. This study treats (67) with this knowledge.

Indeed, this problem is general in the context of the traversable wormhole space-time. For recent studies on this, see Sect. 1.

4.3 Probability amplitude and its Euclideanization

In the case that the wormhole (67) is taken as our space-time, the probability amplitude corresponding to (7) is given as

(70)

where \(i=r,\theta ,\phi \) and \(j_{\mu \nu }\) refer to the metrics in (67) and \(\gamma _w \equiv \sqrt{-\det j_{\mu \nu }}\). \({{\mathcal {C}}}_w\) is ignorable as well as Sect. 2.2.

We perform the Euclideanization,

$$\begin{aligned} t \rightarrow -i \tau . \end{aligned}$$
(71)

At this time,

$$\begin{aligned}&(\pi _\alpha ,\bar{\pi }_\alpha ) \rightarrow i(\pi _\alpha ,\bar{\pi }_\alpha ) , \end{aligned}$$
(72a)
$$\begin{aligned}&\mathrm{d}t^2 \rightarrow -\mathrm{d}\tau ^2, \end{aligned}$$
(72b)
$$\begin{aligned}&j_{tt} \rightarrow j_{\tau \tau } \quad (j_{tt}=j_{\tau \tau }), \end{aligned}$$
(72c)

Therefore, the momenta in the \(\tau \)-direction can be written as

$$\begin{aligned} 2\pi n /\beta _w \equiv \omega _n. \end{aligned}$$
(73)

We write \(\phi _\alpha \) (\(\alpha =1,2\)) as

$$\begin{aligned} \phi _{\alpha }(\tau ,r,\theta ,\phi ) = \frac{1}{\beta _w} \sum _{n=-\infty }^\infty \varphi _{\alpha ,n} (r,\theta ,\phi ) e^{-i\omega _n \tau }, \quad (\alpha =1,2) \end{aligned}$$
(74)

As a result, Z in (70) can be written as

$$\begin{aligned} Z&= \int {{\mathcal {D}}} \phi _1 {{\mathcal {D}}} \phi _2 \exp \Bigg [ -\frac{1}{2} \int d^3 x \int _0^{\beta } \mathrm{d}\tau \,\gamma _w \, \nonumber \\&\quad \times \left( \begin{array}{cc} \phi _1&\phi _2 \end{array} \right) \left( \begin{array}{cc} \hat{G}_w+M_w^2 &{} -2ig^{\tau \tau } \mu _w \, \partial _\tau \\ 2ij^{\tau \tau } \mu _w \, \partial _\tau &{} \hat{G}_w+M_w^2 \end{array} \right) \left( \begin{array}{c} \phi _1 \\ \phi _2 \end{array} \right) \Bigg ], \end{aligned}$$
(75)

where \( \hat{G}_w \equiv \, -j^{\tau \tau } \partial _\tau \partial _\tau + \gamma _w^{-1} j^{ij} \partial _i (\gamma _w \partial _j)\) and \(M_w^2 \equiv m^2 - g^{\tau \tau }\mu _0^2\). From the \(M_w^2\) above, we can see that the upper bound of the value of the chemical potential in the case of the traversable wormhole at finite temperature is

$$\begin{aligned} \mu _w^c=m. \end{aligned}$$
(76)

4.4 Effective potential in the near-throat geometry

In the same way as (16), putting \(\phi _\alpha \) (\(\alpha =1,2\)) as

$$\begin{aligned} \phi _\alpha&\equiv \sqrt{2} \, \alpha \, \cos \Theta + \tilde{\phi }_\alpha , \end{aligned}$$
(77a)
$$\begin{aligned} \phi _\alpha&\equiv \sqrt{2} \, \alpha \, \sin \Theta + \tilde{\phi }_\alpha , \end{aligned}$$
(77b)

then proceeding with the calculation from (75) in the same way as in Sect. 2.4, we can obtain the following Z:

$$\begin{aligned} Z&= \exp [-\alpha ^2\beta _w V_3 M_w^2] \int {{\mathcal {D}}} \tilde{\phi }'_{1,n} {{\mathcal {D}}} \tilde{\phi }'_{2,n} \exp \Bigg [ - \frac{1}{2\beta _w }\nonumber \\&\quad \times \sum _{n=-\infty }^\infty \int _0^\infty \mathrm{d}r \int _{-\infty }^\infty d^2 k_\perp \, \gamma _w \hat{G}_w (\tilde{\phi }_{1,n}^2 + \tilde{\phi }_{2,n}^2 ) \Bigg ], \end{aligned}$$
(78)

where \(V_3 \equiv \int dx^3 \gamma _w\).

We switch our viewpoint from the entire region from \(r=0\) to \(\infty \) to only the vicinity of the throat. Therefore, replacing the r in \(\gamma _w \hat{G}_w\) in (78) with \(v+r\), we take \(\gamma _w \hat{G}_w\) in (78) up to \(r^0\)-order as

$$\begin{aligned} \gamma _w \hat{G}_w&= \frac{v^{5/2} \sin \theta }{\sqrt{2r}} (-\partial _\tau ^2+M_w^2)\nonumber \\&\quad -\frac{\sqrt{v} \sin \theta }{\sqrt{2r}}(v\partial _r -\hat{L}^2) +{{\mathcal {O}}}(r^0), \end{aligned}$$
(79)

then expand it to \(r^0\) order, and where \(\hat{L}^2\) is the squared angular-momentum operator:

$$\begin{aligned} \hat{L}^2\equiv -\left( \frac{\partial _\theta (\sin \theta \partial _\theta )}{\sin \theta }+\frac{\partial _\phi ^2}{\sin \theta ^2}\right) . \end{aligned}$$
(80)

Also, \(V_3 \) is given as

$$\begin{aligned} V_3=\frac{v^{5/2}\sin \theta }{\sqrt{2r}}+{{\mathcal {O}}}(r^0). \end{aligned}$$
(81)

In what follows, we proceed with our analysis by focusing on this near-throat geometry, where the r in what follows refers to from 0 to \(\infty \), but where the points are in the near-throat geometry.

We perform the expansion for the (\(\theta ,\phi \))-directions of \(\phi _\alpha \) (\(\alpha =1,2\)) with the spherical harmonics as

$$\begin{aligned} \tilde{\phi }_{\alpha ,n}(r,\theta ,\phi ) = \frac{1}{\beta } \sum _{n=-\infty }^\infty \sum _{l,m} e^{-i\omega _n \tau }\tilde{\varphi }_{\alpha ,n,l,m} (r) Y^l_m(\theta ,\phi ). \end{aligned}$$
(82)

Then, proceeding with the calculation from (78) the same way as in Sect. 2.4, we can obtain the free energy, \(Z=\exp (-\beta _w F_w)\), as

$$\begin{aligned} F_w&= \, \alpha ^2 M_w^2 \frac{4\pi v^{5/2}}{\sqrt{2}}\int \frac{dr}{\sqrt{r}} + \frac{1}{\beta _w} \sum _{n=-\infty }^\infty \sum _r \sum _{l,m} \int _0^{M_w^2}\nonumber \\&\quad \times \mathrm{d}\Delta ^2 H_{\Delta ^2}(r,n,l), \end{aligned}$$
(83)

where r in the summation takes all the real numbers from 0 to \(\infty \), and

$$\begin{aligned} H_{\Delta ^2}(r,n,l) \equiv \frac{1}{\omega _n^2-v\partial _r+l(l+1)+\Delta ^2}. \end{aligned}$$
(84)

We finally obtain the critical temperature at some points where r is near 0, so we take the contribution at each r in (83) as

$$\begin{aligned} \Gamma _w =&\, \alpha ^2 M_w^2 \frac{4\pi v^{5/2}}{\sqrt{2r}} + \frac{1}{\beta } \sum _{n=-\infty }^\infty \sum _{l,m} \int _0^{M_w^2}\mathrm{d}\Delta ^2 H_{\Delta ^2}(r,n,l), \end{aligned}$$
(85)

where r in (85) takes some values near 0.

4.5 \(H_{\Delta ^2}(r,n,l)\)

\(H_{\Delta ^2}(r,n,l)\) in (84) can be defined as the one satisfying the following equation:

$$\begin{aligned} (\omega _n^2-v\partial _r+l(l+1)+v^2\Delta ^2)H_{\Delta ^2}(r,n,l)=\gamma _w^{-1}\delta (r) \end{aligned}$$
(86)

where \(\gamma _w^{-1}=\frac{\sqrt{2 r} }{v^{5/2}\sin \theta }+{{\mathcal {O}}}(r)\). Performing the Fourier expansion for the r-direction in \(\tilde{D}_{\Delta ^2}(r,n,l)\) and \(\delta (r)\) as

$$\begin{aligned} H_{\Delta ^2}(r,n,l)&=\frac{1}{2\pi }\int _{-\infty }^\infty dk \tilde{J}_{\Delta ^2} (k) e^{-ikr}, \nonumber \\ \quad \delta (r)&=\frac{1}{2\pi }\int _{-\infty }^\infty dk e^{-ikr}, \end{aligned}$$
(87)

it can be seen that \(\tilde{J}(k)\) is given as

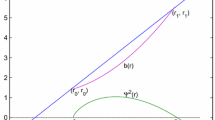
$$\begin{aligned} \tilde{J}_{\Delta ^2}(k)&= \frac{\gamma _w^{-1}|_{r=r_0}}{iv(k-ik_0)} \quad (r_0 \,\text {is taken to 0 from the positive}), \nonumber \\ k_0&\equiv \frac{1}{v}(l(l+1)+v^2\Delta ^2+v^2\omega _n^2), \end{aligned}$$
(88)

where \(r_0\) is taken to some values near 0, and \(ik_0\) is located in the upper half-plane in the complex plane (see Fig. 2).

Now that we have obtained \(\tilde{J}_{\Delta ^2}(k)\) as in (88), we evaluate \(\tilde{H}_{\Delta ^2}(r,n,l)\) in (87). We use the residue theorem for this, and then we can see that

$$\begin{aligned}&\bullet \quad \text {when }r > 0,\text { the contribution from the path of}\\&\quad \left\{ \begin{array}{l} \text {the upper semi circle, }C_+,\text { is }\infty ,\\ \text {the lower semi circle, }C_-,\text { is }0, \end{array} \right. \\&\bullet \quad \text {when }r < 0,\text { the contribution from the path of}\\&\quad \left\{ \begin{array}{l} \text {the upper semi circle, }C_+,\text { is }0,\\ \text {the lower semi circle, }C_-,\text { is }\infty , \end{array} \right. \\&\bullet \quad \text {when }r = 0,\text { the contribution from the paths of }\\&\quad C_\pm \text { are }\infty , \end{aligned}$$

where \(C_\pm \) and the position of \(k_0\) are sketched in Fig. 2.

Fig. 2
figure 2

This figure represents the paths of \(C^\pm \) and the position of the pole \(ik_0\) to calculate \(H_{\Delta ^2}(r,n,l)\) in (87) using the residue theorem

Full size image

Finally, we can obtain as

$$\begin{aligned} \tilde{H}_{\Delta ^2}(r,n,l)&= e^{\frac{r}{v}(\Delta ^2+l(l+1)+\omega _n^2)} - \frac{\sqrt{2r_0}}{v^{7/2}\sin \theta }\Theta (-r)\nonumber \\&= e^{\frac{r}{v}(\Delta ^2+l(l+1)+\omega _n^2)}, \end{aligned}$$
(89)

where \(\Theta (-r)\) is the step function (it is 1 or 0 for negative or positive r), and our \(r_0\) is some positive values near 0.  

Now we have obtained \(\tilde{D}_{\Delta ^2}(r,n,l)\) as in (89). Then, in (85), performing the integration with regard to \(\Delta ^2\) , we can obtain the following \(\Gamma _w\):

$$\begin{aligned} \Gamma _w&= \alpha ^2 M_w^2 \frac{4\pi v^{5/2}}{\sqrt{2r}}+ \frac{v}{\beta _w r} \nonumber \\&\quad \times \sum _{n=-\infty }^\infty \sum _{l,m} \left( -e^{\frac{r}{v} (l(l+1)+\omega _n^2)} + e^{\frac{r}{v} (l(l+1)+M^2+\omega _n^2)}\right) . \end{aligned}$$
(90)

4.6 Particle density and critical temperature in the vicinity of the throat

From (90), according to \(d_w=-\mathrm{d}\Gamma _w/\mathrm{d}\mu _w\), we can obtain the e.v. of the particle density as

$$\begin{aligned} d_w= \frac{2\mu _w}{\beta _w} \sum _{n=-\infty }^\infty \sum _{l,m} e^{\frac{r}{v} (l(l+1)+m^2-\mu _w^2+\omega _n^2)} \end{aligned}$$
(91)

where considering that we close from some high temperatures to the critical temperature, we have put \(\alpha \) to 0 as well as Sect. 2.7 and 3.3.

Now, we obtain the critical temperature in the vicinity of the throat. For this purpose, we first expand \(d_w\) in (91) around \(r=0\). Then, we apply \(\mu _w^c=m\). At this time, the temperature is at the critical temperature, so we can write \(\beta _w\) as \(\beta _w^c\). Then, we can write (91) as

$$\begin{aligned} d_w=\frac{2m}{\beta ^c_w}\sum _{n=-\infty }^\infty \sum _{l,m} \left( 1+\frac{2 m}{v}(l(l+1)+\omega _n^2)r\right) +{{\mathcal {O}}}(r^2). \end{aligned}$$
(92)

Then, after treating the summations \( \sum _{n=-\infty }^\infty \sum _{l,m}\) in (92) as \(\sum _{n=-N_0}^{N_0}\sum _{l=0}^{L_0}(2l+1)\) (\(N_0\) and \(L_0\) are taken to infinity finally), we evaluate these summations. Then, we can obtain the critical temperature as

$$\begin{aligned} T_w^c&=\frac{d_w}{2 (L_0+1)^2 (2 m N_0+m)} -\frac{ (2 \pi ^2 d^2 N_0(N_0+1)+3 L_0 (L_0+2) (L_0+1)^4 (2 m N_0+m)^2}{12 v(L_0+1)^6 (2 m N_0+m)^3}d_w \, r+{{\mathcal {O}}}(r^2). \end{aligned}$$
(93)

We can see that this \(T_w^c\) goes to 0 when \(N_0\) and \(L_0\) are sent to \(\infty \).

5 Phase structure of the normal/BEC states in the traversable wormhole space-time and Josephson junction formed in the vicinity of its throat

5.1 Phase structure

In the previous section, we found that the critical temperature for BEC in the gas filling the whole space-time is always zero in the vicinity of the throat, as in (93). On the other hand, the far region of our wormhole (67) is asymptotically flat, and we found that the critical temperature for the BEC in \(D=3+1\) Euclidean flat space-time at finite temperature is finite, as in (66). Therefore, summing up these results:

  • \(T^c_w =0\) at \(r \sim v\) (vicinity of the throat),

  • \(T^c_w=(66)\) at \(r=\infty \) (far flat region).

By extrapolating between these two results, we can sketch a phase structure as shown in Fig. 3.

Fig. 3
figure 3

Sketch of the phase structure for the critical temperature with respect to the BEC in the gas on one side of the wormhole space-time. Left and right red solid lines represent the critical temperatures in the vicinity of the throat and the far region that we have analytically obtained, respectively. The red dotted line is the interpolation between these. From this sketch, we can see that a state analogous to the Josephson junction can be formed in the vicinity of the throat at some low temperature

Full size image

From Fig. 3, we can see that a state analogous to the Josephson junction is always formed at any temperature except zero in the vicinity of the throat.

Then, the question of whether or not the Josephson current is flowing in the vicinity of the throat would arise, which we discuss in the next section.

5.2 On the Josephson current flowing in the vicinity of the throat

The typical scales for the largeness of the Josephson junction and Josephson current in laboratories would be roughly

$$\begin{aligned} \text {1[nm]}-[\mu \text {m}]\quad \text { and }\quad 1[\mu \text {A}]-[\text {mA}]. \end{aligned}$$
(94)

Then, since the Josephson current is a kind of tunneling, it is considered that the Josephson current would be more damped by the exponential as the width of the vicinity of the throat increasesFootnote 10. Therefore, if the width of the normal state in the vicinity of the throat were larger than the scale in (94), the Josephson current could not occur in practice. Contrarily, if it were in the scale of (94), the Josephson current in the magnitude in (94) might appear (though it depends on the property of the space-time playing the role of the normal state through which the Josephson current flows).

To address this problem, we have to analyze the width of the normal state in the vicinity of the throat and how much the wave function is damped when it tunnels. Currently, we cannot make any explicit claims about this from the analysis in this paper. Normally, since the wormhole is the astronomical object, the width of the normal state is much larger than (94). Therefore, the wave function of the Josephson current might be damped when it goes through the normal state in the vicinity of the throat and would be effectively zero.

However, we cannot exclude the possibility that it is not damped much for some effect of the curved space. Actually, there is a thought that the Hawking radiation is a kind of tunneling [57]. If the Hawking radiation exists, the Josephson current might also exist as the same tunneling phenomenon.

One approach to this issue is to analyze the thermal de Broglie wavelength in the curved space-time. Giving the final answer to this problem is one of our future works.

6 BEC in ER bridge

6.1 Phase structure

As such, the traversable wormhole cannot be the solution, although our result obtained in Sect. 5 would be interesting. Therefore, in this section, we consider the phase structure for the BEC/normal state transition in another wormhole, the ER bridge.

Since the ER bridge can be obtained by attaching two Schwarzschild black hole space-times, it can be a solution, and its near-horizon geometry is given by the vicinity of the horizon of the Schwarzschild black hole. Then, it is known that the near-horizon geometry of the Schwarzschild black hole is mathematically equivalent to the Rindler space, and we can numerically identify the Unruh temperature by the Hawking temperature.

Therefore, since the critical acceleration is given as (59), we can see the that critical Hawking temperature will be given as

$$\begin{aligned} T_\mathrm{H}^c=\sqrt{3d_R/m}. \end{aligned}$$
(96)

On the other hand, since the far region of the ER bridges is the flat space-time, and the critical temperature in the flat space-time was obtained as in (66), un the discussion in this section, \(d_R\) and \(d_E\) can be taken to mean the same.

Then, we can obtain the phase structure as in Fig. 3. However, since (66) and (96) are equivalent to each other, the phase structure is trivial (in which just a horizontal line is drawn), and we can know this without seeing it. Therefore, we will skip showing it.

6.2 On the finitely obtained critical Hawking temperature

That the critical Hawking temperature can be finitely obtained as in (96) may appear strange, if we consider two facts, that (1) in the type of model (9), it is known that BEC is never formed in D = 3 or lessFootnote 11 and (2) the vicinity of the throat would effectively become one-dimensional, as only the rr-component of the metric increases there.

However, this is wrong, since the vicinity of the throat of the ER bridge never becomes one-dimensional. We can understand this from the fact that we can write the squared line element in the vicinity of the throat of the ER bridge for the (t, r)-part like

$$\begin{aligned} \mathrm{d}s_\mathrm{BH}^2=e^{\zeta /r_\mathrm{H}}(\mathrm{d}t^2-\mathrm{d}\zeta ^2), \end{aligned}$$
(97)

where we have applied \(r=r_\mathrm{H}(1+e^{\zeta /r_\mathrm{H}})\) (r is the quantity a little bit larger than \(r_\mathrm{H}\)) to \(\mathrm{d}s_\mathrm{BH}^2=(1-r_\mathrm{H}/r)\mathrm{d}t^2-(1-r_\mathrm{H}/r)^{-1}dr^2\) . From this, we can see that the squared line element in the vicinity of the throat of the ER bridge will be still four dimensional and never become one dimensional.

On the other hand, in the case of the traversable wormhole, the vicinity of its throat effectively becomes one-dimensional. Therefore, we can understand our result in (93).

7 Summary

In this study, we have investigated the phase structure for the BEC/normal state transition in the ER bridge and traversable wormhole space-time filled by some gas to form BEC up to a certain temperature.

The first idea to start this work is something like the consideration we mentioned in Sect. 6.2, and we discuss the points in the mechanism for the formation of the BEC in this study in Appendix B.

As a result, in the case of the traversable wormhole, we have found that the critical temperature of the gas for BEC is zero in the vicinity of its throat. Then, based on that result, we have pointed out that a state analogous to the Josephson junction is always formed in the vicinity of its throat. This is a theoretically expected gravitational phenomenon and the result obtained in this study.

However, the traversable wormhole space-time has negative energy density and cannot be a solution as long as we do not modify the gravitational theory or do not devise any special ways as shown in Sect. 4.2. This is a critical problem from the standpoint of the realizability of the Josephson junction in this study. To solve this problem, we have to make the traversable wormhole space-time into a solution.

As for this attempt, we have referred to some works in the last part of Sect. 1. Of course, this problem would be basically very difficult, as can be known from the uniqueness theorem, and it seems that any clear solutions have not yet been obtained. Although the current situation is as such, the author has his own idea for this problem. It is not to use the exotic matter, and its fundamental idea would be different from any ideas of the studies conducted to date. The author is going to give it a try in the near future.

If we could make this into a solution, we could reach the stage to discuss the realizability of the Josephson junction in this study, at which we should care about the following two practical problems: (1) the effect of the strong tidal force on the existence of our Josephson junction formed at the vicinity of the throat (here, there is no very strong gravitational force, as there is no event horizon in the traversable wormhole), and (2) how to actually create the situation where the space is filled by the gas (this would be no problem if we could assume the existence of the gas from the beginning).

If we could finally resolve these problems, we might consider our Josephson junction realistically. At this time, we also discuss examples in which phenomenology analogous to our Josephson junction is formed in other systems. We discuss these below.

Normally, in that case (namely, when there is a gravitational phenomenology and one considers whether there is some phenomenology analogous to it in other systems), one would turn to the condensed matter physics and AdS/CFT, so let us discuss these one by one. (In addition, we finally also discuss “an example where our Josephson junction can be used as an effective model for the inflation cosmology”.)

Then, first remember that this study is a gravitational phenomenology arising in some gas on a strongly curved space-time. Therefore, the key effect in the phenomenology in this study is the strong gravitational effect making it difficult for the system to form a BEC. Therefore, when a S-N-S state is formed in some material, we could consider it as the analogous phenomenology, if any effect analogous to the strong gravitational effect or the effect itself works in its formation.

Here, we refer to [27, 28] in Sect. 1. However, honestly, the author cannot understand these works, so the author will write the following discussion in the range the author can say.

Basically, it seems that they use the same technology as that used in [59] (see Fig. 1 in this), so let us suppose that there is no technical problems in these. Then, looking at their fundamental issues in the work, the author cannot read off the following two points: (1) their superconductor is supposed to always exist from the beginning or it is the one to be formed up to some parameters, and (2) the system formed in these is S-N-S or not (if the wormhole part is superconducting, it would be probably be S or N-S-N and not S-N-S).

Therefore, the author can say that if their system were S-N-S and it was formed by some effect analogous to the strong gravitational effect or the effect itself, their S-N-S would be “an example of the formation of a Josephson junction analogous to our Josephson junction”. This is all that the author can currently say with regard to the phenomenology analogous to our Josephson junction in condensed matter physics. Next, let us consider how the AdS/CFT would be if the gravity side is given by the four- or five-dimensional asymptotically AdS traversable wormhole space-times.

However, since there are technically various unclear points in the AdS/CFT, the author cannot say anything definite about this in this study (where we have given some references for the AdS/CFT between AdS\(_2\) wormholes and SYK models in Sect. 1). Also, the author has no clear thought about how its gauge/gravity would be at present. However, since the AdS/CFT by the traversable wormhole space-time would be intriguing, it would be meaningful to investigate its correspondence relation. If any correspondences can be confirmed, we should investigate the correspondence of the S-N-S state. If it could be confirmed, it would be considered as “an example where our Josephson junction is formed in another system”, since it can be considered that our Josephson junction is formed in the CFT side.

By the way, let us mention that it seems that it would be possible to obtain the traversable wormhole space-time regardless of the values of the cosmological constant if it comes to the five dimension (c.f. [60]). This is because the uniqueness theorem is a theorem in four dimension.

In the two cases mentioned above, it seems that any meaningful things are not stated, so let us discuss “an example where our Josephson junction can be used as an effective model”. If it can be finally confirmed that it can work well, we may consider it “an example in which phenomenology analogous to our Josephson junction is formed in other systems”.

As one of the interesting examples in which our Josephson junction would play a very intriguing role, the author considers some scalar-gravity system (the scalar field is supposed to form BSE up to a temperature, c.f. [61]) on the following Euclidean five-dimensional traversable wormhole space-time (\(ds_2^4\) part is represented in Fig. 4):

$$\begin{aligned} \mathrm{d}s_5^2 = \mathrm{d}t_E^2 + \mathrm{d}s_4^2, \quad \text {where} \quad \mathrm{d}s_4^2 \equiv \frac{dr^2}{1-v^2/r^2}+r^2\mathrm{d}\Omega _3^2, \end{aligned}$$
(98)

as an effective model for the expanding early universe including the previous universe collapsing to the beginning of the current universe; the space-time given by (98) corresponds to the shape of the space time for the two universes joined by the throat part corresponding to the beginning of the current universe. Postponing the explanation for the practical points in (98) to the next paragraph, we first say that it seems we could get the five-dimensional traversable wormhole space-time as a solution (c.f. the text written in two paragraphs above and [60]).

Fig. 4
figure 4

The image of the \(ds^4\) part of the traversable wormhole space-time given by (98) to be used as the effective early cosmological model in the idea written in the body text, which has been obtained based on the program in “Trying to plot a wormhole; getting bad results” in https://mathematica.stackexchange.com/. The curved surface in this figure corresponds to the four-dimensional space-time we exist; blue circle represents its \(S^3\) spatial space (\(\Omega ^3\)-direction), and red direction is r-direction and parametrizes the time development of that \(S^3\) spatial space (therefore, r-direction shrinks and grows as time grows in the previous and current universes). Here, throat part is the \(S^3\) space at \(r = v\), which corresponds to the three-dimensional space at the beginning of the current cosmology. We can see it is not singular, therefore it is considered that the space at the beginning of the cosmology is regularized, which is the point in our idea using the traversable wormhole space time given by (98). In this figure, \(t_E\)-direction is not included; it is originally the time-direction, which is now being \(S_1\) compactified into the imaginary direction and prescribes the temperature of the four-dimensional space depicted in this figure. Therefore, the four-dimensional space depicted in this figure is supposed to be at some temperature. It would be interesting if the boundary between the superconductor and normal phases in our study can relate to Big Bang (at this time, the superconductor region corresponds to the inflation era). Here, note that the large r-region corresponds to the space times for the far future and past (in the previous universe), which are given by the flat space time, not being in the form of Big Crunch, in our model

Full size image

In (98), the \(S^3\)-direction given by \(r^2\mathrm{d}\Omega _3^2\) corresponds to the three-dimensional spatial part we exist, and the r-direction parametrizes the time development of that \(S^3\) space (therefore, r-direction shrinks and grows as time grows in the previous and current universes). The \(t_E\)-direction is the original time-direction, which is now being \(S^1\) compacted into the imaginary direction and prescribes the temperature of the four-dimensional part of \(\mathrm{d}s_4^2\) (c.f. [62]).

Therefore, the space given by the \(\mathrm{d}s_4^2\) part corresponds to the four-dimensional space-time we exist which is applied to the curved surface in Fig. 4, and is at some temperature determined by the period of the \(t_E\)-direction. The scalar field to form the BEC up to the temperature also exists on the curved surface in Fig. 4.

The three-dimensional space at the beginning of the current universe corresponds to the throat part at \(r=v\) in (98), which is not singular, therefore it is considered that the space-time at the beginning of the cosmology is regularized in this model. This point is one of the points in this model as the effective model for cosmology.

Our Josephson junction is supposed to be formed in the vicinity of the beginning of the cosmology, where we have discussed how the Josephson current will be in the range the author can say at present at present as in Sect. 5.2. It would be interesting if the boundary between the superconductor and normal phases in our study can relate to Big Bang, which is another point in this model (at this time, the superconductor region corresponds to the inflation era).

Note that the space times of the far future and past (in the previous universe) given by the large r-region are the flat space time, which are not in the form of Big Crunch, in our model by (98).

In conclusion, supposing we could get the five-dimensional traversable wormhole space-time as a solution and clear the practical problems mentioned above, it would be interesting to examine whether or not the effective model above could reproduce the picture of the early cosmology described by the standard cosmology and give the solutions for the unsettled problems in our current cosmology (c.f. [63]).

The result in this study means that the state of the gas is changed from the normal state to the superconductor state at some point in the space. Investigating where it is and how it is are a future problem. In addition, it is a future problem to study whether or not the Josephson junction in this study can be formed even if we consider the very strong tidal force in the vicinity of the throat of the wormhole.

An interesting problem obtained from this study is how the curvature of the space-time affects the thermal phase transition. One approach to this issue is to analyze the thermal de Broglie wavelength [64] in the curved space-time.