1 Introduction

Wormholes are handles or tunnels in spacetime connecting different regions of our Universe or different universes altogether. That wormholes could be actual structures suitable for interstellar travel was first proposed by Morris and Thorne [1]. Such a wormhole could be described by the static spherically symmetric line element [1]

$$\begin{aligned} \mathrm{d}s^{2}=-\mathrm{e}^{2\Phi (r)}\mathrm{d}t^{2}+\frac{\mathrm{d}r^2}{1-b(r)/r}+r^{2}(\mathrm{d}\theta ^{2}+\sin ^{2}\theta \, \mathrm{d}\phi ^{2}),\nonumber \\ \end{aligned}$$
(1)

using units in which \(c=G=1\). Here \(\Phi = \Phi (r)\) is called the redshift function, which must be everywhere finite to avoid an event horizon. The function \(b=b(r)\) helps determine the spatial shape of the wormhole and is therefore called the shape function. The spherical surface \(r=r_0\) is the throat of the wormhole and must satisfy the following conditions: \(b(r_0)=r_0,b(r)<r\) for \(r>r_0\), and \(b'(r_0)<1\), now usually called the flare-out condition. This condition refers to the flaring out of the embedding diagram pictured in Ref. [1]. The flare-out condition can only be satisfied by violating the null energy condition.

The Einstein field equations in the orthonormal frame, \(G_{\hat{\mu }\hat{\nu }}=8\pi T_{\hat{\mu }\hat{\nu }}\), yield the following simple interpretation for the components of the stress-energy tensor: \(T_{\hat{t}\hat{t}}= \rho (r)\), the energy density, \(T_{\hat{r}\hat{r}}=p_r\), the radial pressure, and \(T_{\hat{\theta }\hat{\theta }}= T_{\hat{\phi }\hat{\phi }}=p_t\), the lateral pressure. For the theoretical construction of the wormhole, Morris and Thorne then proposed the following strategy: retain complete control over the geometry by specifying the functions b(r) and \(\Phi (r)\) to obtain the desired properties of the wormhole. The problem with this strategy is that it relies on the engineering team to manufacture or search for those materials or fields that yield the required stress-energy tensor.

This purely geometric approach can be supplemented by an appropriate equation of state, an example of which is \(p=\omega \rho ,\omega <-1\), representing phantom dark energy [2–5]. The energy density may also be known for physical reasons, as in the case of the Navarro–Frenk–White density profile for dark matter [6, 7]

$$\begin{aligned} \rho (r)=\frac{\rho _s}{\frac{r}{r_s} \left( 1+\frac{r}{r_s}\right) ^2}, \end{aligned}$$
(2)

where \(r_s\) is the characteristic scale radius and \(\rho _s\) is the corresponding density.

In this paper we consider another equation of state, \(p=-A/\rho ,A>0\), representing Chaplygin gas or, more generally, \(p=-A/\rho ^{\alpha },0<\alpha \le 1\), called generalized Chaplygin gas [8–12]. Cosmologists became interested in this model when it was shown that the Chaplygin gas is a candidate for unifying dark matter and dark energy. To see this, consider the energy conservation equation \(\dot{\rho }=-3\dot{a} (\rho +p)/a\) in a flat FLRW spacetime and then substitute \(p=-A/\rho ^{\alpha }\). The result is

$$\begin{aligned} \rho =\left( A+\frac{B}{a^{3(\alpha +1)}} \right) ^{1/(\alpha +1)}, \end{aligned}$$
(3)

where B is an integration constant. It is seen that \(\rho \sim a^{-3}\) at early times, implying that \(\rho \) behaves like matter, while in later times it behaves like a cosmological constant \((\rho \equiv \text {constant})\).

In a cosmological setting one would normally assume a homogeneous distribution of matter. It was pointed out in Ref. [13], however, that the generalized Chaplygin equation of state is that of a polytropic gas with a negative polytropic index. Thus inhomogeneous structures may arise from a density fluctuation in the cosmological background. Also, a Born–Infeld phantom gravastar has been constructed by replacing the interior de Sitter solution with the Chaplygin gas equation of state [14]. A similar problem arises with another type of dark energy, phantom dark energy. Here Sushkov and Kim [15] have shown that away from the throat the radial and transverse pressures converge fairly quickly. Accordingly, we will follow Refs. [10, 11] and assume that the equation of state is

$$\begin{aligned} p_r=-\frac{A}{\rho ^{\alpha }}. \end{aligned}$$
(4)

The tangential pressure can be determined from the Einstein field equations.

To obtain a complete wormhole solution, we are going to make the additional assumption that our spacetime admits a one-parameter group of conformal motions, i.e., conformal Killing vectors, discussed next.

2 Conformal Killing vectors

As noted above, we assume that our spacetime admits a one-parameter group of conformal motions, which are motions along which the metric tensor of a spacetime remains invariant up to a scale factor. In other words, there exists a set of conformal Killing vectors such that

$$\begin{aligned} {\mathcal {L}}_{\xi }g_{\mu \nu }=g_{\eta \nu }\, \xi ^{\eta }_{;\mu }+g_{\mu \eta }\,\xi ^{\eta }_{; \nu }=\psi (r)\,g_{\mu \nu }, \end{aligned}$$
(5)

where the left-hand side is the Lie derivative of the metric tensor and \(\psi (r)\) is the conformal factor. The vector \(\xi \) characterizes the conformal symmetry since the metric tensor \(g_{\mu \nu }\) is conformally mapped into itself along \(\xi \). The assumption of conformal symmetry has led to numerous new solutions, as well as new geometric and kinematical insights [16–22].

Given a noncommutative-geometry background, exact solutions of traversable wormholes admitting conformal motions are discussed in Ref. [23]. Two earlier studies assumed a non-static conformal symmetry [24, 25].

As in Ref. [23], we use the following form of the metric to discuss conformal symmetry:

$$\begin{aligned} \mathrm{d}s^2=-\mathrm{e}^{\nu (r)}\mathrm{d}t^2+\mathrm{e}^{\lambda (r)} \mathrm{d}r^2+r^2(\mathrm{d}\theta ^2+\sin ^2\theta \, \mathrm{d}\phi ^2). \end{aligned}$$
(6)

The Einstein field equations are

$$\begin{aligned}&\mathrm{e}^{-\lambda } \left[ \frac{\lambda ^\prime }{r} - \frac{1}{r^2} \right] +\frac{1}{r^2}= 8\pi \rho ,\end{aligned}$$
(7)
$$\begin{aligned}&\mathrm{e}^{-\lambda } \left[ \frac{1}{r^2}+\frac{\nu ^\prime }{r}\right] -\frac{1}{r^2}= 8\pi p_r, \end{aligned}$$
(8)

and

$$\begin{aligned} \frac{1}{2} \mathrm{e}^{-\lambda } \left[ \frac{1}{2}(\nu ^\prime )^2+ \nu ^{\prime \prime } -\frac{1}{2}\lambda ^\prime \nu ^\prime + \frac{1}{r}({\nu ^\prime - \lambda ^\prime })\right] =8\pi p_t. \end{aligned}$$
(9)

Equation (9) can actually be obtained from the conservation of the stress-energy tensor, i.e., \(T^{\mu \nu }_{;\nu }=0\). So we need to use only Eqs. (7) and (8).

To discuss the assumption of conformal symmetry in Eq. (5), we follow Herrera and Ponce de León [16] and restrict the vector field by requiring that \(\xi ^{\alpha }U_{\alpha }=0\), where \(U_{\alpha }\) is the four-velocity of the perfect fluid distribution. The assumption of spherical symmetry then yields \(\xi ^0=\xi ^2=\xi ^3=0\) [16]. Equation (5) now produces the following results:

$$\begin{aligned}&\xi ^1 \nu ^\prime =\psi ,\end{aligned}$$
(10)
$$\begin{aligned}&\xi ^1 = \frac{\psi r}{2}, \end{aligned}$$
(11)

and

$$\begin{aligned} \xi ^1 \lambda ^\prime +2\,\xi ^1 _{,1}=\psi . \end{aligned}$$
(12)

These equations, in turn, yield

$$\begin{aligned} \mathrm{e}^\nu =C r^2 \end{aligned}$$
(13)

and

$$\begin{aligned} \mathrm{e}^\lambda = \left( \frac{a}{\psi }\right) ^2, \end{aligned}$$
(14)

where C and a are integration constants. In order to make use of these equations, it is convenient to write Eqs. (7) and (8) in the following forms:

$$\begin{aligned} \frac{1}{r^2}\left( 1 - \frac{\psi ^2}{a^2} \right) -\frac{2\psi \psi ^\prime }{a^2r}= 8\pi \rho \end{aligned}$$
(15)

and

$$\begin{aligned} \frac{1}{r^2}\left( \frac{3\psi ^2}{a^2}-1 \right) = 8\pi p_r. \end{aligned}$$
(16)

3 The solution

To obtain a wormhole solution, we start with the equation of state (4), \(p_r=-A/\rho ^{\alpha }\), and substitute Eqs. (15) and (16) to obtain

$$\begin{aligned} \frac{1}{8\pi }\frac{1}{r^2}\left( \frac{3\psi ^2}{a^2}-1\right) = -\frac{A}{\left\{ \frac{1}{8\pi }\left[ \frac{1}{r^2}\left( 1-\frac{\psi ^2}{a^2} \right) -\frac{2\psi \psi '}{a^2r} \right] \right\} ^{\alpha }}.\nonumber \\ \end{aligned}$$
(17)

This equation can be put into a more transparent form by noting that \(2\psi \psi '=(\psi ^2)'\) and eliminating the negative sign:

$$\begin{aligned} \frac{1}{8\pi }\frac{1}{r^2} \left( 1{-}\frac{3\psi ^2}{a^2}\right) {=} \frac{A}{\left\{ \frac{1}{8\pi }\left[ \frac{1}{r^2}\left( 1{-}\frac{\psi ^2}{a^2} \right) -\frac{(\psi ^2)'}{a^2r} \right] \right\} ^{\alpha }}. \end{aligned}$$
(18)

Now observe that since A and \(\rho ^{\alpha }\) are positive, the left side is also positive, allowing us to raise each side to the power \(1/\alpha \). We can thereby obtain

$$\begin{aligned} (\psi ^2)'{=}\frac{1}{r}\left[ a^2{-}\psi ^2 {-}\left( \frac{Aa^{2(\alpha +1)} (8\pi )^{\alpha +1}r^{2(\alpha {+}1)}}{a^2-3\psi ^2} \right) ^{1/\alpha }\right] .\nonumber \\ \end{aligned}$$
(19)

Before considering a possible solution, observe that by comparing Eqs. (1) and (6), we have in view of Eq. (14),

$$\begin{aligned} b(r)=r(1-\mathrm{e}^{-\lambda })= r\left( 1-\frac{\psi ^2}{a^2}\right) . \end{aligned}$$
(20)

So to obtain b(r), Eq. (19) must be solved for \(\psi ^2(r)\). To satisfy the condition \(b(r_0)=r_0\), we must have \(\psi ^2(r_0)=0\), which becomes the initial condition for Eq. (19). Moreover, since \(1-3\psi ^2/a^2>0\) by Eq. (18), we also have \(1-\psi ^2/a^2>0\), so that \(b(r)>0\).

To check the flare-out condition \(b'(r_0)<1\), we obtain from Eqs. (20) and (19),

$$\begin{aligned} \left. b'(r)=1-\frac{\psi ^2}{a^2}- r\frac{(\psi ^2)'}{a^2}\right| _{r=r_0} =A(8\pi )^{\alpha +1}r_0^{2(\alpha +1)}<1. \end{aligned}$$

So to meet the flare-out condition, the constant A from the Chaplygin equation of state must satisfy the inequality

$$\begin{aligned} A<\frac{1}{(8\pi r_0^2)^{\alpha +1}}, \end{aligned}$$
(21)

which agrees with Refs. [10, 11].

Now we turn our attention to Eq. (19), recalling the initial condition \(\psi ^2(r_0)=0\). Since this equation does not have a closed-form solution, we will use a numerical approach. To do so, we choose an arbitrary value for \(r=r_0\) and some values of A and \(\alpha \) that satisfy the above conditions. It becomes apparent immediately that the solution for b(r) is independent of the integration constant a. The reason for this can be seen by writing Eqs. (19) and (20) in the following respective forms:

$$\begin{aligned} \left[ \left( \frac{\psi }{a}\right) ^2\right] ' {=}\frac{1}{r} \left[ 1{-}\left( \frac{\psi }{a}\right) ^2 -\left( \frac{A(8\pi )^{\alpha {+}1} r^{2(\alpha +1)}}{1-3(\psi /a)^2} \right) ^{1/\alpha }\right] \nonumber \\ \end{aligned}$$
(22)

and

$$\begin{aligned} b(r)=r\left[ 1-\left( \frac{\psi }{a} \right) ^2\right] . \end{aligned}$$
(23)

So the solutions of Eqs. (19) and (22) have the same qualitative forms. (In other words, by rescaling \(\psi \), the constant a could be eliminated.)

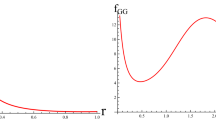
The plots for \(\psi ^2\) and b(r), using some typical values of the parameters, are shown in Fig. 1. For any particular choice of A, the function \(\psi ^2\) becomes zero for some \(r=r_1\) and hence negative for \(r>r_1\). Since the corresponding function \(\psi \) is now imaginary, \(b=b(r)\) is undefined for \(r>r_1\). (Observe that \(b(r_1)=r_1\), as shown in Fig. 1; also, \(b(r)<r\) for \(r_0<r<r_1\).)

Fig. 1
figure 1

\(\psi ^2\) and b are defined on the interval \([r_0, r_1]\)

Full size image

We conclude that the wormhole material is confined to some interval \([r_0, r_1]\). This conclusion is consistent with Refs. [10, 11], which state that the dimensions of the wormhole cannot be arbitrarily large.

As a final comment, while the length of the interval \([r_0, r_1]\) is independent of a, it does depend on A: the closer A is to the upper limit \(1/(8\pi r_0^2)^{\alpha +1}\), the closer \(b'(r_0)\) is to unity and hence the smaller the interval \([r_0, r_1]\); this behavior can also be seen from Fig. 1.

4 The redshift function

We see from Eq. (13), \(\mathrm{e}^{\nu }=Cr^2\), that the wormhole spacetime cannot be asymptotically flat. Normally one would now introduce an extra requirement by stating that the wormhole material has to be cut off at some r and joined to an exterior Schwarzschild solution,

$$\begin{aligned} \mathrm{d}s^{2}= & {} -\left( 1-\frac{2M}{r}\right) \mathrm{d}t^{2} \nonumber \\&+\frac{\mathrm{d}r^2}{1-2M/r} +r^{2}(\mathrm{d}\theta ^{2}+\sin ^{2}\theta \, \mathrm{d}\phi ^{2}). \end{aligned}$$
(24)

Since the need for a cut-off is already known from the previous section, we are not dealing with a new requirement. Unfortunately, the previous cut-off at \(r=r_1\) cannot be used here because \(b(r_1)=r_1\). Instead, we need to choose some \(r=r_2<r_1\). We can therefore complete the wormhole solution by noting that

$$\begin{aligned} M=\frac{1}{2}b(r_2). \end{aligned}$$

So for \(\mathrm{e}^{\nu }=Cr_2^2\), we have \(Cr_2^2 =1-2M/r_2\) and the integration constant becomes

$$\begin{aligned} C=\frac{1}{r_2^2} \left( 1-\frac{b(r_2)}{r_2}\right) . \end{aligned}$$

The need for a cut-off at \(r=r_2<r_1\), due to the coordinate singularity at \(r=r_1\), is consistent with Refs. [26, 27], which consist of a detailed investigation of the Tolman–Oppenheimer–Volkoff equations for Chaplygin and generalized Chaplygin gas, respectively. The main conclusion in these studies is much more general in the sense that the scalar curvature was found to become singular at some finite distance; moreover, the Universe is not asymptotically flat. That our wormhole spacetime cannot be arbitrarily large was also shown in Ref. [10] without relying on conformal symmetry. However, in the present study, conformal symmetry is needed to determine the redshift function (to obtain a complete wormhole solution) but not for the wormhole solutions in Refs. [26, 27].

5 Conclusion

For the theoretical construction of a traversable wormhole, Morris and Thorne proposed the following strategy: retain complete control over the geometry by choosing functions \(\Phi (r)\) and b(r) that yield the desired properties, thereby leaving the components of the stress-energy tensor unspecified. In this paper we obtained a complete wormhole solution by (1) adopting the equation of state \(p_r=-A/\rho ^{\alpha }\) representing a generalized Chaplygin gas and (2) assuming that the wormhole admits a one-parameter group of conformal motions. These two assumptions complement each other via the requirement that the wormhole spacetime must be cut off at some \(r=r_2\) and joined to an exterior vacuum solution.