How appropriate are the gravitational entropy proposals for traversable wormholes?

Abstract

In this paper we have examined the validity of some proposed definitions of gravitational entropy (GE) in the context of traversable wormhole solutions of the Einstein field equations. Here we have adopted two different proposals of GE and checked for their applicability in the case of these wormholes. The first one is the phenomenological approach proposed by Rudjord et al [Phys. Scr. 77:055901, 2008] and expanded by Romero et al in [Int. J. Theor. Phys. 51:925, 2012], which is a purely geometric method of measuring gravitational entropy. The latter one is the Clifton-Ellis-Tavakol (CET) proposal [Class. Quantum Grav. 30:125009, 2013] for the gravitational entropy which arises in relativistic thermodynamics, and is based on the Bel-Robinson tensor, that represents the effective super-energy-momentum tensor of free gravitational fields. Considering some of the Lorentzian traversable wormholes along with the Brill solution for NUT wormholes and the AdS wormholes, we have evaluated the gravitational entropy for these systems. Incidentally, the application of the CET proposal can provide unique gravitational entropies for spacetimes of Petrov type D and N only, whereas the geometric method can be applied to almost every kind of spacetime, although it has no relation with thermodynamics. For any traversable wormhole to be physically realistic, it should have a viable GE. We found that the GE proposals do give us a consistent measure of GE in several of them. This means that the existence of a viable gravitational entropy strictly depends on its definition.

Appendix: Some additional notes

In this section we will briefly analyse the case of two more traversable wormholes. These are additional case studies to support our conclusions, but less significant from the point of view of the observed features.

1.1 Appendix-I: Traversable AdS wormhole

The following metric represents a stationary NUT wormhole with a negative cosmological constant with a nonlinear sigma model as source, which was illustrated in [44]:

$$\begin{aligned} ds^2=dz^2+\dfrac{\rho ^2(z)}{4}\left[ -Q^2(d\tau +cos\theta d\phi )^2 +(d\theta ^2+sin^2\theta d\phi ^2) \right] , \end{aligned}$$

(71)

where $\rho (z)=\sqrt{{3(K-8)}/{4\vert \Lambda \vert }} \cosh \left( {\vert \Lambda \vert ^{1/2}}z/{\sqrt{3}}\right) ,$ and $Q^2= {K}/{4}.$ In addition to this, $\Lambda <0$ if the system has to satisfy the Einstein equations. Here Q is the NUT parameter and must be an even integer for the solution to be single-valued [62]. The asymptotic NUT-AdS regions with $z\rightarrow \pm \infty$ are connected by this wormhole at the throat $z=0$. This spacetime has no curvature singularities and is locally regular, and is therefore an object of our interest in this paper.

The determinant of the metric for the traversable AdS wormhole is given by the following:

$$\begin{aligned} g=-{\frac{27\, \left( K-8 \right) ^{3} \left( \cosh \left( 1/3\,\sqrt{ \left| \Lambda \right| }\sqrt{3}z \right) \right) ^{6}{K}^{2} \left( \sin \left( \theta \right) \right) ^{2}}{65536\, \left( \left| \Lambda \right| \right) ^{3}}}. \end{aligned}$$

(72)

Consequently the Weyl curvature scalar square is given by the following:

$$\begin{aligned} W={\frac{4\, \left( {K}^{2}+16 \right) ^{2}{\Lambda }^{2}}{27\, \left( \cosh \left( 1/3\,\sqrt{ \left| \Lambda \right| }\sqrt{3}z \right) \right) ^{4} \left( K-8 \right) ^{2}}}. \end{aligned}$$

(73)

The Kretschmann curvature scalar ($\tilde{K}$) for the AdS wormhole is given by the equation:

$$\begin{aligned} \tilde{K}&= \frac{11\,{\Lambda }^{2}}{36\, \left( \cosh \left( 1/3\,\sqrt{ \left| \Lambda \right| }\sqrt{3}z \right) \right) ^{4} \left( K-8 \right) ^{2}}\nonumber \\&\quad \times \Bigg [ {\frac{96\, \left( \cosh \left( 1/3\,\sqrt{ \left| \Lambda \right| }\sqrt{3}z \right) \right) ^{4} \left( K-8\right) ^{2}}{11}}\nonumber \\&\quad - {\frac{ \left( 8\,K-64 \right) \left( {K}^{2}+12 \,K-32 \right) \left( \cosh \left( 1/3\,\sqrt{ \left| \Lambda \right| }\sqrt{3}z \right) \right) ^{2}}{11}}\nonumber \\&\quad +{K}^{4}+ {\frac{8\,{K }^{3}}{11}}+{\frac{368\,{K}^{2}}{11}}-{\frac{256\,K}{11}}+{\frac{ 3072}{11}} \Bigg ]. \end{aligned}$$

(74)

Fig. 11

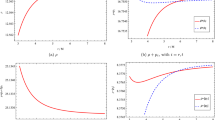
a Variation of $P_{1}^2$ for traversable AdS wormhole with z and the parameter $\Lambda$. b Variation of $P_{2}$ for traversable AdS wormhole with z and the parameter $\Lambda$. In both the cases the NUT parameter is $K = 16$. Here the blue region represents high positive values and it gradually decreases through the yellow region to the white colored region

Fig. 12

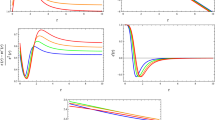
Variation of entropy density s of AdS traversable wormhole with z for different parameters. Here we have considered only the radial contribution as defined in (8). Also the definition of gravitational entropy density is calculated using $P_{1}$

Fig. 13

Variation of entropy density s of AdS traversable wormhole with z for different parameters. We have considered both the radial and angular contribution (9) and the gravitational entropy density is calculated using $P_{1}$

• 1. Weyl scalar proposal: From the above expressions, the ratio of the two curvature scalars is obtained along straightforward calculations, and is given below:

  $$\begin{aligned} P_{1}&= \frac{4\,\sqrt{33}}{33}\Bigg [ \left( {K}^{2}+16 \right) ^{2} \Bigg ( {\frac{96\, \left( \cosh \left( 1/3\,\sqrt{ \left| \Lambda \right| }\sqrt{3}z \right) \right) ^{4} \left( K-8 \right) ^{2}}{11}} \nonumber \\&\quad - {\frac{ \left( 8\,K-64 \right) \left( {K}^{2}+12\,K-32 \right) \left( \cosh \left( 1/3\,\sqrt{ \left| \Lambda \right| }\sqrt{3}z \right) \right) ^{2}}{11}}\nonumber \\&\quad + {K}^{4}+{\frac{8\,{K}^{3}}{11}}+{\frac{368\,{K}^{2}}{11}}-{\frac{256\,K}{11}}+{\frac{3072}{11}} \Bigg ) ^{- 1}\Bigg ]^{\frac{1}{2}}. \end{aligned}$$

  (75)

  The ratio of curvature scalars, i.e. $P_{1}^2$, is given in the expression (75). For the sake of clarity, it is also illustrated graphically in Fig.11(a).

  In Figs. 12 and 13 we have shown the variation of gravitational entropy density with different parameters. In both these cases, $P_{1}$ is being used for the calculations. In Fig.12 we have only taken the contribution of the radial component while determining the gravitational entropy density and in Fig. 13 both the radial and angular contributions are taken into account.

  In Fig. 12a the variation of the gravitational entropy density of AdS wormhole is shown with angular orientation $\theta$, where we have fixed the other parameters as $\Lambda =$-$0.1,\,K=16$. In this case we see no change as we did not include the angular contribution into our analysis. Next in Fig. 12b, the variation with the parameter K is being studied for $\Lambda =$-$0.1,\,{\theta ={\pi }/{4} }$. As the value of K increases, so does the value of gravitational entropy density. In the last figure Fig. 12c, the variation of the gravitational entropy density of traversable AdS wormhole is shown with various negative values of cosmological constant $\Lambda$ for the fixed parameter values as $K=16,\,{\theta ={\pi }/{4} }$. Here we can clearly observe that with increasing negative value of the cosmological constant the peak value of the gravitational entropy density increases. Fig. 13 shows these variations with a higher sensitivity including both the radial and angular contributions in the entropy density. Fig. 13a shows the variation with the angular orientation while fixing the other parameters at $\Lambda =$-$0.1,\,K=16$. Here each angular orientation gives different gravitational entropy unlike the previous case. Figure 13b gives us the nature of variation of entropy density with K when we fix $\Lambda =-0.1,\, {\theta ={\pi }/{4} }$. In Fig. 13c the dependence of gravitational entropy density on the cosmological constant is being depicted, where we have chosen our free parameters as $K=16,\,{\theta ={\pi }/{4} }$. Here the overall dependence remains the same but the extra contribution from the angular components in the gravitational entropy density makes it non zero at the throat region unlike in the previous case, which means that the gravitational entropy density is continuous through the wormhole throat. As we know that the $g_{t\phi }$ component is also nonzero in the metric of AdS traversable wormhole, therefore the alternative definition of the gravitational entropy using $P_{2}$ must be applied to see how the result differs from the former case. The graphical representation of $P_{2}$ is shown in Fig. 11b.

  Consequently in Figs. 14 and 15 we have used $P_{2}$ as the definition and used the radial contribution only to draw the graphs (in Fig. 14), and in the later figures both the contributions of radial and angular components have been considered.

  In Fig. 14a we have chosen $\Lambda =-0.1, K=16$ to show the variation with the angular orientation while in FIG. 14b, the values $\Lambda =-0.1,\,{\theta ={\pi }/{4} }$ are fixed to show the variation with the parameter K. Similar to the case for $P_{1}$, here too there are no changes in Fig. 14a while the variations in Fig. 14b are also similar to that of $P_{1}$ except that the graphs are way more compact, i.e. the gravitational entropy density is localized in a much more smaller region when we consider $P_{2}$. Figure 14c shows the variation of gravitational entropy density with the negative values of cosmological constant with the fixed parameters as $K=16,\,{\theta ={\pi }/{4} }$ where we find that the magnitude of s increases with increasing negative values of the cosmological constant $\Lambda$.

  Figure 15a shows the variation with $\theta$ for $\Lambda =-0.1, K=16$. The introduction of the angular component changes the entropy density drastically for higher values of the angular orientation $\theta$. If we fix $\Lambda =-0.1,\, {\theta ={\pi }/{4} }$ as constants, then we obtain Fig. 15b, which shows the variation with K. Finally Fig. 15c shows the variation with $\Lambda$ for the fixed parameter $K=16,\,{\theta ={\pi }/{4} }$. The introduction of the angular component reduces the gravitational entropy density from a double peaked one to a single peaked function but the overall evenness with respect to the radius is not lost.

  In general, the gravitational entropy density increases near the throat region when we consider both the radial and angular contribution for our analysis. Therefore we can say that the procedure involving the $P_{2}$, which includes both the radial and angular contribution, is more suitable for the analysis of gravitational entropy in this case.

Fig. 14

Variation of entropy density s of AdS traversable wormhole with z for different parameters. Here we have considered only the radial contribution as in (8). The gravitational entropy density is calculated using $P_{2}$

Fig. 15

Variation of entropy density s of AdS traversable wormhole with z for different parameters. Here we have considered both the radial and angular contribution (9), and the gravitational entropy density is calculated using $P_{2}$

Fig. 16

Embedding diagram of Maldacena wormhole ansatz

1.2 Appendix-II: Maldacena wormhole ansatz

Very recently Maldacena and Milekhin have discussed humanly traversable wormholes [63], where they have proposed a hypothetical connecting wormhole between two oppositely charged magnetic blackholes. This is an interesting situation, worth analysing. The metric is given by

$$\begin{aligned} ds^2=r_{e}^2[-(\rho ^2+1)d\tau ^2+\dfrac{d\rho ^2}{(\rho ^2+1)}+(d\theta ^2+\sin ^2\theta d\phi ^2)], \qquad \,\,\,\,\, -\rho _{c}\le \rho \le \rho _{c} \end{aligned}$$

(76)

where $\rho ={l(r-r_{e})}/{r_{e}^2}$ for $\rho>>1$, $l=t/\tau$, and $r-r_{e}<<r_{e}$ are the interrelations connecting the coordinates of (76) and (77). Beyond the limit of $\rho =\pm \rho _{c}$ of the wormhole region, the geometry is of two extremal magnetic blackholes. In Fig. 16 the wormhole is connecting two extremal magnetically charged black holes given by the following black hole metric (77):

$$\begin{aligned} ds^2=-fdt^2+\dfrac{dr^2}{f}+r^2(d\theta ^2+sin^2\theta d\phi ^2), \end{aligned}$$

(77)

where $A= ({q}/{2}) \cos \theta d\phi$; $\ell _{p}\equiv \sqrt{G_{4}}$; $r_{e}\equiv ({\sqrt{\pi }q\ell _{p}}) /{g_{4}}$; $M_{e}={r_{e}}/{G_{4}}$; $f=\left( 1-{r_{e}}/{r}\right) ^2$. Here q is the magnetic charge which is an integer, and $M_{e}$ is the mass of the BH at extremality. In the near horizon region, $r_{e}$ sets the radius of curvature and also the size of the 2-sphere. At the extremal limit as $r\rightarrow r_{e}$, an infinite throat develops. Using the principal null tetrads we can easily get the following value of the Weyl scalar:

$$\begin{aligned} \Psi _{2}=\dfrac{r_{e}(r_{e}-r)}{r^4} . \end{aligned}$$

Using the CET proposal we obtain the gravitational energy density of the BH as:

$$\begin{aligned} \rho _{grav}=\dfrac{\alpha }{4\pi }\left| \dfrac{r_{e}(r_{e}-r)}{r^4}\right| . \end{aligned}$$

(78)

Similarly the gravitational temperature can be computed as

$$\begin{aligned} T_{grav}=\dfrac{1}{2\pi }\left| \dfrac{r_{e}}{r^2}\right| . \end{aligned}$$

(79)

Finally the ratio of gravitational energy density to gravitational temperature for this BH is given by

$$\begin{aligned} \dfrac{\rho _{grav}}{T_{grav}}=\frac{\alpha }{2}\left| \dfrac{(-r+r_{e})}{r^2}\right| . \end{aligned}$$

(80)

For the sake of completeness, and to check the validity of CET proposal, we can compute the gravitational entropy of this BH on a surface with radius R as:

$$\begin{aligned} S_{grav}=\int _{0}^{R}\int _{0}^{\pi }\int _{0}^{2\pi }\frac{\alpha }{2} \left| \dfrac{(-r+r_{e})}{r^2}\right| \dfrac{r^2 \sin \theta }{(1-\frac{r_{e}}{r})}dr d\theta d\phi =\alpha \pi R^2 . \end{aligned}$$

(81)

Thus the CET gravitational entropy of the magnetized extremal BH is directly proportional to the horizon area, conforming with the definition of Hawking-Bekenstein entropy. Moreover, the ratio for the curvature scalars for the BH is given by the following expression:

$$\begin{aligned} P_{1}^2=\dfrac{6(-r+r_{e})^2}{7r_{e}^2-12r_{e}r+6r^2} . \end{aligned}$$

(82)

Next we calculate the Weyl scalar proposal gravitational entropy density for the connecting wormhole, which turns out to be: $s=k_{s}\vert \nabla .\Psi \vert =0$. Surprisingly, we find that the gravitational entropy of such wormholes vanishes in this proposal. This shows that either the proposal itself is not valid in this case, or the wormhole itself is nonphysical in nature.

Similarly for the CET proposal of gravitational entropy the gravitational energy density of the connecting wormhole is found to vanish, raising questions on the physical viability of such WHs. The relevant expressions are given below:

$$\begin{aligned} \rho _{grav}=0; \,\,\,\, T_{grav}=\dfrac{1}{2\pi }\left| \dfrac{\rho }{r_{e}\sqrt{1+\rho ^2}} \right| ;\,\,\,\,\, s_{grav}=0 \,\,(\rho \ne 0). \end{aligned}$$

(83)

As the gravitational entropy is zero even in the CET proposal, we can say that it conforms to our analysis of the extremal magnetic BHs. As $r\rightarrow r_{e}$, the ratio of curvature scalars in (82) reduces to zero, indicating a zero gravitational entropy density for the Weyl proposal. In this limit, for the CET proposal the gravitational energy density in (78) also reduces to zero and the temperature in (79) becomes $\sim \left| {1}/{2\pi r_{e}} \right|$, which matches with the wormhole gravitational temperature in the limit $\rho>>1$. Consequently the ratio in (80) becomes zero in this limit, thereby matching with the wormhole counterpart. The interesting point to note here is that the gravitational temperature is nonzero, but at $\rho =0$. Thus at $\rho =0$ we may still have a finite entropy, as in that case the ratio of gravitational energy density to gravitational temperature assumes the mathematical form 0/0 , but these proposals are not yet equipped to address such cases.