A new class of compact stellar model compatible with observational data

Abstract

In this work, a physically reasonable metric potential $g_{rr}$ and a specific choice of the anisotropy has been utilized to obtain closed-form solutions of the Einstein field equation for a spherically symmetric anisotropic matter distribution. This class of solution has been used to develop viable models for observed pulsars. Smooth matching of interior spacetime metric with the exterior Schwarzschild metric and utilizing the condition that radial pressure is zero across the boundary leads us to determine the model parameters. A particular pulsar $4U1820-30$ having current estimated mass and radius ($mass=1.58 M_\odot$ and $radius=9.1$ km) has been allowed for testing the physical acceptability of the developed model. The gross physical nature of the observed pulsar has been analyzed graphically. The stability of the model is also discussed given causality conditions, adiabatic index and generalized Tolman–Oppenheimer–Volkov (TOV) equation under the forces acting on the system. To show that this model is compatible with observational data, few more pulsars have been considered, and all the requirements of a realistic star are highlighted. Additionally, the mass-radius (M–R) relationship of compact stellar objects analyzed for this model. The maximum mass for the presented model is $\approx 4M_\odot$ which is compared with the realization of Rhoades and Ruffini (Phys Rev Lett 32:324, 1974).

1 Introduction

Stars at the end of their stellar evolution, after exhausting all its nuclear fuel end up with the formation of compact objects. Compact relativistic stars, being one of the fascinating entities known in the Universe, have astonished all astrophysicists among the world. Neutron stars, a class of compact object are supported by neutron degeneracy pressure against the pull of gravity. White dwarf the other type of compact objects supported by electron degeneracy pressures against the gravity. The first exact solution representing the vacuum exterior gravitational field of static spherically symmetric compact object in hydrostatic equilibrium was obtained by Schwarzschild in the year 1916 [2]. Since then the exact solutions describing static compact stellar configurations has continuously been investigated. The interior geometry, and hence the complete structure of the stellar object depends on the nature of the matter composition. The quest of the exact solution of the Einstein field equation regarding the modelling of the realistic compact stellar object has been an intense area of relativistic astrophysics. Though the Einstein gravity replaces classical gravity long ago, however, it got tremendous importance to govern the study of the compact stellar object only after the discovery of quasars in the 1960s. Compact objects have the mass to radius ratio between $10^{-5}$ to 1 and are the natural laboratories which provide extreme conditions like high gravity and density for test bed of Einstein general relativity.

To study the equilibrium structure of the compact stellar object one requires the proper nature of the nuclear equation of states (EoS), i.e., how the pressure linked with density of the matter. With the help of EoS, the physical properties of a compact star can be studied by solving the Tolman–Oppenheimer–Volkov (TOV) equation, the general relativistic equations of stellar structures. Uncertainty in the knowledge of nuclear EoS leads to uncertainty in the prediction of Mass-radius relation and limiting the mass of neutron stars. However, in the absence of the information of particle interactions in extreme density, the researchers often use the alternative approach of assuming specific form of geometry or the fall off behaviour of density, pressure or the matter source.

In general relativity, the studies of compact stellar structure assumes the characterization of the matter distribution to be isotropic in nature, i.e., perfect fluid, which has equal radial ($p_r$) and tangential ($p_t$) pressures. Though in a compact object, the pressures in radial and transverse directions may not be equal and the difference of radial pressure and tangential pressure produces anisotropy. The effects of pressure anisotropy on the stellar objects are evident in different investigations for the neutral or charged stellar objects. In 1933, Leimatre projected the first anisotropic model [3] exclusively by $p_t$ and constant energy density ($\rho$). From the work of Mak and Harko [4, 5] it is evident that on reaching a maximum at the surface, within the interior of the star anisotropy radial decreases and at the centre of the fluid sphere the anisotropy is expected to vanish.

The different factors are identified for assuming the compact star as anisotropic rather than isotropic. In the high-density regime ($> 10^{15}\hbox { g/cc}$) of compact stars where the nuclear interactions must be treated relativistically, there may develop anisotropy inside the stellar objects as shown by Ruderman [6] and Canuto [7]. In relativistic stars, anisotropy might occur due to the existence of a solid core or type 3A superfluid as pointed out by Kippenhahn and Weigert [8]. Strong magnetic fields can also regard as a source of anisotropic pressure inside a compact object as discussed by Weber [9]. Anisotropy may also develop due to the slow rotation of fluids [10]. A mixture of perfect and a null fluid may also be formally described as an anisotropic fluid [11]. The existence of anisotropy in astrophysical objects may have various reasons such as viscosity, different kinds of phase transitions [12], pion condensation [13] and the presence of strong electromagnetic field [14]. The factors contributing to the pressure anisotropy have also been discussed by Dev and Gleiser [15, 16] and Gleiser and Dev [17]. Ivanov [18] pointed out that influences of shear, electromagnetic field, etc. on self-bound systems can be absorbed if the system is considered to be anisotropic. Self-bound systems composed of scalar fields, the so-called ‘boson stars’ are naturally anisotropy [19]. Wormholes [20] and gravastars [21, 22] are also considered as anisotropic as well. Bowers and Liang [23] first applied the anisotropic model on the equilibrium configuration of a relativistic compact star like neutron stars. In fact, it was Bowers and Lang who indicated that anisotropy might have non-negligible effects on some parameters such as equilibrium mass and surface redshift. A review of the origins and effects of local anisotropy in astrophysical objects may also be found in Refs. [24, 25]. In 1975, Heinzmann and Hillebrandt have considered fully relativistic anisotropic superdense neutron star models and have established that there is no limiting mass of a neutron star for arbitrarily large anisotropy. However, the maximum mass of the neutron star was still past $3-4M_\odot$ [26]. Hillebrandt et al. [27] have discussed the stability of fully relativistic anisotropic neutron star and found that there exists a stability criterion just like that are obtained in isotropic models.

Several anisotropic models have been investigated by incorporating anisotropic pressure in the stress-energy tensor of the material composition. Exact solutions corresponding to static spherically symmetric anisotropic matter distributions have been developed and analyzed by Bayin [28], Krori et al. [29], Bondi [30, 31], Barreto [32], Barreto et al. [33], Coley and Tupper [34], Martínez et al. [35], Singh et al. [36], Hernández et al. [37], Dev and Gleiser [15, 17], Harko and Mak [38], Patel and Mehta [39], Lake [40], Böhmer and Harko [41, 42], Esculpi et al. [43], Khadekar and Tade [44], Karmakar et al. [45], Abreu et al. [46], Ivanov [47], Herrera et al. [48], Mak and Harko [49], Sharma and Mukherjee [50], Harko and Mak [51], Herrera et al. [52], amongst others. By introducing an algorithm, new exact solutions of an anisotropic fluid distribution have proposed by Maharaj and Maartens [53]. Utilizing the Maharaj and Maartens algorithm, Gokhroo and Mehra [54] and Chaisi and Maharaj [55, 56] have developed and studied new anisotropic fluid models. General algorithms for generating static anisotropic solutions was also found by Lake [57]. Thomas and co-workers [58,59,60] have proposed models of gravitationally bound systems in equilibrium with an anisotropic fluid distribution. Assuming a linear EoS, Sharma and Maharaj [61] provided an exact analytic solution for the compact anisotropic matter distributions. Thirukkanesh and Maharaj [62] have also analyzed an anisotropic fluid distribution to obtain a new class of exact solutions. For example, using the Finch and Skea [63] ansatz for the metric potential $g_{rr}$, Sharma and Ratanpal [64] have reported a static spherically symmetric compact anisotropic star model which admits a quadratic EoS. Pandya et al. [65] have developed a new class of solutions of static spherically symmetric anisotropic system by generalizing the Finch and Skea ansatz. The model proposed by Sharma and Ratanpal [64] is a sub-class of the solutions provided by Pandya et al. [65]. Bhar et al. [66] studied the static spherically symmetric relativistic anisotropic compact object considering the Tolman VII solution as one of the metric potentials. A new anisotropic model of a strange star admitting the Chaplygin equation of state was proposed by Bhar [67].

In the present work, we have developed a model describing a static spherically symmetric anisotropic matter distribution. To develop the model a particular form of the metric potential $g_{rr}$ has been utilized. By assuming a particular form of the anisotropy, the other metric potential has been solved in simple analytic form. All the physical parameters are shown to well behaved and regular inside the anisotropic star which implies a realistic description of astrophysical compact objects. The maximum mass has been estimated by producing mass-radius relation graphically from our model.

This paper has been organized as follows: In Sect. 2, the basic Einstein field equations governing the anisotropic system of the compact object has been presented. In Sect. 3, by assuming the metric potential $g_{rr}$ and a particular anisotropic profile, the relevant field equations have been solved to develop a new model. The physical requirements of a realistic compact star are stated in Sect. 4. In Sect. 5, the exterior Schwarzschild space-time is matched with the interior and corresponding boundary conditions have laid down analytically. The various relevant physical parameters are derived analytically in Sect. 6. The recently observed data of a pulsar are shown to validate this model in Sect. 7 with some graphical representation. Stability of the model has been discussed in Sect. 8. Finally, some concluding remarks and discussions have been made in Sect. 9.

2 Einstein field equations

We write the line element describing the interior space-time of a spherically symmetric star in standard coordinates $x^0 = t$, $x^1=r$, $x^2 = \theta$, $x^3 = \phi$ as

$$\begin{aligned} ds_{-}^2 = -A_{0}^2(r)dt^2 + B_{0}^2(r)dr^2 + r^2(d\theta ^2 + \sin ^2\theta d\phi ^2),\nonumber \\ \end{aligned}$$

(1)

where $A_{0}(r)$ and $B_{0}(r)$ the gravitational potential are yet to be determined.

We assume that the matter distribution of the stellar interior is anisotropic in nature and described by an energy-momentum tensor of the form

$$\begin{aligned} T_{\alpha \beta } = (\rho + p_t)u_{\alpha } {u_\beta } + p_{t} g_{\alpha \beta } + (p_r - p_t)\chi _{\alpha } \chi _{\beta }, \end{aligned}$$

(2)

where $\rho$ represents the energy-density, $p_r$ and $p_t$, respectively denote fluid pressures along the radial and transverse directions, $u^\alpha$ is the 4-velocity of the fluid and $\chi ^\alpha$ is a unit space-like 4-vector along the radial direction so that $u^\alpha u_\alpha = -1$, $\chi ^\alpha \chi _\beta =-1$ and $u^\alpha \chi _\beta =0$.

The Einstein field equations governing the evolution of the system is then obtained as (we set $G = c = 1$)

$$\begin{aligned} 8\pi \rho= & {} \left[ \frac{1}{r^2}-\frac{1}{r^2 B_0^2}+\frac{2B_0'}{r B_0^3}\right] , \end{aligned}$$

(3)

$$\begin{aligned} 8\pi p_r= & {} \left[ -\frac{1}{r^2}+\frac{1}{B_0^2 r^2}+\frac{2A_0'}{r A_0B_0^2}\right] ,\end{aligned}$$

(4)

$$\begin{aligned} 8\pi p_t= & {} \left[ \frac{A_0''}{A_0B_0^2} + \frac{A_0'}{rA_0B_0^2} - \frac{B_0'}{r B_0^3} - \frac{A_0'B_0'}{A_0 B_0^3}\right] . \end{aligned}$$

(5)

In Eqs. (3)–(5), a ‘prime’ denotes differentiation with respect to r.

Making use of Eqs. (4) and (5), we define the anisotropic parameter of the stellar system as

$$\begin{aligned} \Delta (r)&= 8\pi (p_t-p_r)\nonumber \\&= \left[ \frac{A_0''}{A_0B_0^2} - \frac{A_0'}{r A_0B_0^2} - \frac{B_0'}{r B_0^3} \frac{A_0'B_0'}{A_0B_0^3} - \frac{1}{r^2B_0^2} + \frac{1}{r^2}\right] .\nonumber \\ \end{aligned}$$

(6)

The anisotropic force is defined as $\frac{2 \Delta }{r}$ will be repulsive or attractive in nature depending upon whether $p_t>p_r$ or $p_t<p_r$. The mass contained within a radius r of the sphere is defined as

$$\begin{aligned} m(r)= \frac{1}{2}\int _0^r\omega ^2 \rho (\omega )d\omega . \end{aligned}$$

(7)

3 Generating a new model

To develop a physically reasonable model of the stellar configuration, we assume that the metric potential $g_{rr}$ is given by

$$\begin{aligned} B_0^2 (r) = \frac{1}{\left( 1 -\frac{r^2}{R^2}\right) ^4}, \end{aligned}$$

(8)

where R is the curvature parameter describing the geometry of the configuration having a dimension of length and it will be determined from the matching conditions. This choice of metric potential assures that the function $B^2_0(r)$ is finite, continuous and well defined within stellar interior range. Also $B^2_0(r)=1$ for $r=0$ ensures that it is finite at the center. Again, the metric is regular at the center since $(B^2_0(r))'_{r=0}=0$. So the system of equations given by Eqs. (3)–(6) is the system of four equations in six variables ($\rho$, $p_r$, $p_t$, $\Delta (r)$, $A_0(r)$, $B_0(r)$). With this choice of $B_0(r)$ Eq. (6) then reduces to

$$\begin{aligned} \Delta (r)= & {} \frac{(3 r^7 - 8 r^5 R^2 + 6 r^3 R^4) A_0(r)}{r R^8 A_0(r)}\nonumber \\&+ \frac{(r^2 - R^2)^3 \left( (3 r^2 + R^2)r (r^2 - R^2) A''_0(r)\right) }{r R^8 A_0(r)}. \end{aligned}$$

(9)

On rearranging Eq. (9) we get

$$\begin{aligned}&\frac{A_0''(r)}{A_0(r)}+\frac{(3 r^2+R^2)A_0'(r)}{r(r^2-R^2)A_0(r)}+\frac{(3 r^6 - 8 r^4 R^2 + 6 r^2 R^4)}{(r^2-R^2)^4}\nonumber \\&\qquad =\frac{\Delta (r) R^8}{(r^2-R^2)^4}. \end{aligned}$$

(10)

Now the above Eq. (10) can be solved for $A_0(r)$ if $\Delta (r)$ is specified in particular form. To make the equation easily integrable it is assumed that

$$\begin{aligned} \Delta (r)=\frac{(3 r^6 - 8 r^4 R^2 + 6 r^2 R^4)}{R^8}. \end{aligned}$$

(11)

The above choice for anisotropy is physically reasonable, as at the center ($r=0$) anisotropy is vanishes as expected. This feature will be explained graphically in Sect. 6. It is to be marked that we have considered anisotropy in the polynomial form as

$$\begin{aligned} \Delta = X_1(r^2)^3 + X_2(r^2)^2 + X_3(r^2), \end{aligned}$$

i.e. up to order 6 of Taylor Series for $\Delta$ in terms of r. Similar polynomial form of anisotropy ($\Delta =\sum _{i} X_i r^i$) can be found to study charged anisotropic system in several literatures [68,69,70,71]. The isotropic condition can be regained by choosing arbitrary constants to zero in their work. Maharaj et al. [68] and Sunzu et al. [69] found new exact solutions to the Einstein-Maxwell system of equations of a charged anisotropic matter distribution by assuming the anisotropy in the polynomial form $\Delta =\sum _{i=0}^{3} X_i r^i$. Anisotropy in the form $\Delta =\sum _{i=1}^{3} X_i r^i$ can be found in the work of Sunzu et al. [70] for describing charged anisotropic stars. Anisotropy, $\Delta =\sum _{i=1}^{5} X_i r^i$ have been discussed by Sunzu et al. [71] and anisotropy in the form of $\Delta =X_3 r^3+ X_4 r^4$ is also fashioned in the work of Sunzu and Mahali [72]. As a limitation of our model, we can not generate the isotropic pressure condition from the specified anisotropic form.

Also, this choice provides a solution for Eq. (10) in closed form. Substituting Eqs. (11) in (10), we obtain,

$$\begin{aligned} A''_0(r)+\frac{(3 r^2+R^2)}{r(r^2-R^2)} A'_0(r)=0. \end{aligned}$$

(12)

We obtain a simple solution of the Eq. (12)

$$\begin{aligned} A_0(r)=\frac{C}{2(R^2-r^2)}+D, \end{aligned}$$

(13)

where C and D are integration constants will be obtained from the boundary conditions. With the choices of the metric potentials the matter density, radial pressure, transverse pressure and mass are obtained as

$$\begin{aligned} 8\pi \rho= & {} \frac{(-9 r^6+28 r^4 R^2 -30 r^2 R^4+12 R^6)}{R^8}, \end{aligned}$$

(14)

$$\begin{aligned} 8\pi p_r= & {} \frac{C(-3 r^6+ 8r^4 R^2-6 r^2 R^4)}{R^8(C+2 D(R^2-r^2))} \nonumber \\&- \frac{D(r^8-5 r^6 R^2+10 r^4 R^4-10 r^2 R^6+4 R^8)}{R^8(C+2 D(R^2-r^2))}, \end{aligned}$$

(15)

$$\begin{aligned} 8\pi p_t= & {} 8\pi p_r+ \Delta \nonumber \\= & {} \frac{-8 D(r^2-R^2)^4}{R^8\left( C+2 D(R^2-r^2)\right) }, \end{aligned}$$

(16)

$$\begin{aligned} m(r)= & {} \frac{(-r^9 + 4 r^7 R^2 - 6 r^5 R^4 + 4 r^3 R^6)}{2 R^8}. \end{aligned}$$

(17)

4 Physical requirements

For a physically viable stellar model, should satisfy the following conditions throughout the stellar configuration:

• (i) The gravitational potentials $A_0(r)$, $B_0(r)$ and the matter variables $\rho$, $p_r$, $p_t$ should be well defined at the center and regular as well as singularity free throughout the interior of the star.

• (ii) The energy density $\rho$ should be positive throughout the stellar interior i.e., $\rho \ge 0$. Its value at the center of the star should be positive finite and monotonically decreasing towards the boundary inside the stellar interior, mathematically $\frac{d\rho }{d r}\le 0$.

• (iii) The radial pressure $p_r$ and the tangential pressure $p_t$ must be positive inside the fluid configuration i.e., $p_r \ge 0$, $p_t \ge 0$. The gradient of the pressure must be negative inside the stellar body, i.e., $\frac{dp_r}{dr} < 0$, $\frac{dp_t}{dr} < 0$. At the stellar boundary $r=b$ the radial pressure $p_r$ should vanish but the tangential pressure $p_t$ may not zero at the boundary. At the centre both the pressures are equal which means the anisotropy should vanish at the centre, $\Delta (r=0)=0$.

• (iv) For an anisotropic fluid sphere fulfillment of the either of one energy conditions refers to the following inequalities in every point inside the fluid sphere are required:

  • (1) Weak energy condition (WEC): $p_r + \rho> 0,~ \rho > 0$,

  • (2) Null energy condition (NEC): $p_r + \rho> 0,~ \rho > 0$,

  • (3) Strong energy condition (SEC): $\rho + p_r \ge 0$; $\rho + p_t \ge 0$; $\rho - p_r - 2 p_t \ge 0$.

  • (4) Dominant energy conditions (DEC): $\rho \ge p_r$ and $\rho \ge p_t$.

• (v) Causality condition has to be satisfied to be realistic model i.e. the speed of sound must be smaller than 1 (assuming the speed of light $c=1$) in the interior of the star, i.e., $0 \le \frac{dp_r}{d\rho } \le 1$, $0 \le \frac{dp_t}{d\rho } \le 1$.

• (vi) The interior metric functions should match smoothly to the exterior Schwarzschild space-time metric at the boundary.

• (vii) For a stable model, the adiabatic index should be greater than $\frac{4}{3}$.

• (viii) Herrera [73] cracking method to study the stability of anisotropic stars suggests that a viable model should also satisfy $-1<v_t^2-v_r^2<0$, where $v_r$ and $v_t$ are it’s radial and transverse speed respectively.

5 Exterior space-time and boundary conditions

The exterior space-time for a not radiating star is empty and is described by the exterior Schwarzschild solution which is

$$\begin{aligned} ds^{2}= & {} -\left( 1-\frac{2m}{r}\right) dt^{2}+\left( 1-\frac{2m}{r}\right) ^{-1}dr^{2}\nonumber \\&+r^{2}\left( d\theta ^{2}+\sin ^{2}\theta d\phi ^{2} \right) , \end{aligned}$$

(18)

where $r>2m$, m being the total mass of the stellar object.

The interior spacetime metric (1) must be matched to the exterior Schwarzschild spacetime metric Eq. (18) at the boundary of the star $r=b$. The continuity of the metric functions across the boundary $r=b$ yields

$$\begin{aligned} A^2_0(b)= & {} \left( 1-\frac{2 m}{b}\right) , \end{aligned}$$

(19)

$$\begin{aligned} B^2_0(b)= & {} \left( 1-\frac{2 m}{b}\right) ^{-1}. \end{aligned}$$

(20)

Radial pressure drops to zero at a finite value of the radial parameter r, defined as the radius of the star. Hence the radius of the star can be obtained by utilizing the condition $p_r(r=b)=0$.

The above boundary conditions determine the constants which are

$$\begin{aligned} R= & {} \sqrt{\frac{b^2}{1-(1-\frac{2 m}{b})^{\frac{1}{4}}}}, \end{aligned}$$

(21)

$$\begin{aligned} C= & {} -\frac{[1+(1-\frac{2 m}{b})^{\frac{1}{4}}][1+(1-\frac{2 m}{b})^{\frac{1}{2}}] b^2}{2[-1+(1-\frac{2 m}{b})^{\frac{1}{4}}]}, \end{aligned}$$

(22)

$$\begin{aligned} D= & {} -\frac{(1-\frac{2 m}{b})^{\frac{3}{4}}[3 m+2 (-1+(1-\frac{2 m}{b})^{\frac{3}{4}})b]}{2[-1+(1-\frac{2 m}{b})^{\frac{1}{4}}](b-2 m)}. \end{aligned}$$

(23)

6 Physical analysis

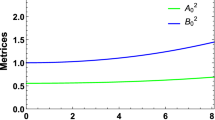
• 1. The gravitational potentials in this model satisfy, $A^2_0(0)=(\frac{C}{2 R^2}+D)^2=constant$, $B^2_0(0)=1$, i.e., finite at the center ($r=0$) of the stellar configuration. Also one can easily check that $(A^2_0(r))'_{r=0}=(B^2_0(r))'_{r=0}=0$. These imply that the metric is regular at the center and well behaved throughout the stellar interior.

• 2. The central density, central radial pressure and central tangential pressure in this case are:

  $$\begin{aligned} \rho (0)= & {} \frac{12}{R^2}, \\ p_r(0)= & {} \frac{-8 D }{(C+2 D R^2)}, \\ p_t(0)= & {} \frac{-8 D }{(C+2 D R^2)}. \end{aligned}$$

  Note that the density is always positive as R is a positive quantity. The radial pressure and tangential pressure at the centre are equal which means pressure anisotropy vanishes at the center. The radial and tangential pressure at the center will be non-negative if one choose the model parameters satisfying the conditions $D<0$ and $C> 2 D R^2$ or $D>0$ and, $C< 2 D R^2$. Also according to Zeldovich’s condition, $p_r/\rho$ must be $\le 1$ at the centre. Therefore,

  $$\begin{aligned} \frac{-8 D R^2}{12(C+2DR^2)}\le 1 . \end{aligned}$$

  Using above equation along with the central pressure leads to the inequality $|\frac{C}{D}| \ge \frac{5 R^2}{6}$.

• 3. The gradient of energy density, radial pressure and tangential pressure are respectively obtained as:

  $$\begin{aligned} \frac{d\rho }{dr}= & {} \frac{(-54 r^5+112 r^3 R^2 -60 r R^4)}{R^8}, \end{aligned}$$

  (24)
  $$\begin{aligned} \frac{dp_r}{dr}= & {} \frac{2 r C^2(-9 r^4+16 r^2 R^2-6 R^4)}{R^8(C+2 D(R^2-r^2))^2}\nonumber \\&+ \frac{8 C D r (r^2-R^2)(r^4-2 R^4)}{R^8(C+2 D(R^2-r^2))^2}\nonumber \\&+\frac{8 D r(r^2-R^2)^2(3 r^4-8 r^2 R^2+6 R^4))}{R^8(C+2 D(R^2-r^2))^2}, \end{aligned}$$

  (25)
  $$\begin{aligned} \frac{dp_t}{dr}= & {} \frac{32 D r (r^2-R^2)^3(-2C +3 D(r^2-R^2))}{R^8(C+2 D(R^2-r^2))^2}. \end{aligned}$$

  (26)

  The gradient of the density, radial pressure and tangential pressure are negative inside the stellar body are shown graphically in the next section.

• 4. The radial and transverse velocity of sound ($c=1$) are obtained as

  $$\begin{aligned} v^2_{sr}= & {} \frac{dp_r}{d\rho }=\frac{- 4 C D (r^2-R^2)(r^4-2 R^4)}{(27 r^4-56 r^2 R^2+30 R^4)(C+2 D(R^2-r^2))^2}\nonumber \\&+ \frac{C^2(9 r^4-16 r^2 R^2+6 R^4)}{(27 r^4-56 r^2 R^2+30 R^4)(C+2 D(R^2-r^2))^2}\nonumber \\&-\frac{4 D^2(r^2-R^2)^2(3 r^4-8 r^2 R^2+6 R^4)}{(27 r^4-56 r^2 R^2+30 R^4)(C+2 D(R^2-r^2))^2}, \end{aligned}$$

  (27)
  $$\begin{aligned} v^2_{st}= & {} \frac{dp_t}{d\rho }=\frac{16 D(r^2-R^2)^3(2 C-3 D r^2+3 D R^2)}{(27 r^4-56 r^2 R^2+30 R^4)(C+2 D(R^2-r^2))^2}.\nonumber \\ \end{aligned}$$

  (28)

  In this model the speed of sound are smaller than 1 in the interior of the star, i.e., $0 \le \frac{dp_r}{d\rho } \le 1$, $0 \le \frac{dp_t}{d\rho } \le 1$ which has been shown graphically in the next section. Based on the ‘cracking’ method to study the stability of anisotropic stars proposed by Herrera [73], Abreu et al. [46] proved that the region of an anisotropic fluid sphere is stable where $1 \le v^2_{st} - v^2_{sr} \le 0$ is potentially stable. Our model is shown to be stable considering this condition.

• 5. Energy condition: The energy conditions for an anisotropic fluid sphere implies the positive values of the terms $\rho + p_r \ge 0$, $\rho + p_t \ge 0$ and $\rho - p_r - 2 p_t \ge 0$, throughout the stellar interior. These quantities are shown to remain positive throughout the compact sphere graphically in the next section.

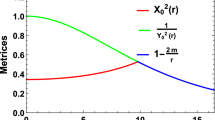
• 6. The smooth matching of the interior metric function with that of the Schwarzschild exterior at the boundary is shown graphically in the next section.

• 7. Equation of state (EoS) parameter: Equation of state parameter is given by

  $$\begin{aligned} \omega _r=\frac{p_r}{\rho };\quad \omega _t=\frac{p_t}{\rho }. \end{aligned}$$

  (29)

  To be non-exotic in nature the value of $\omega$ should lie within 0 and 1. Our model is shown to satisfies the condition $0\le \omega _r\le 1$, $0\le \omega _t\le 1$.

7 Compatibility with observational data

7.1 Discussions around $4U1820-30$

The physical acceptability of this model has been examined by plugging the masses and radii of observed pulsars as input parameters. In order to validate our model, we have considered the pulsar $4 U 1820-30$ whose estimated mass and radius are $M = 1.58 ~M_{\odot }$ and $b=9.1$ km, respectively [74]. Using these values of mass and radius as an input parameter, the boundary conditions have been utilized to determine the constants as $C=785.818$, $D=-0.234$ and $R=22.451$. Making use of these values of constants and plugging the values of G and c in the expressions, various physical variables have been plotted graphically.

Regular and well-behaved nature of all the relevant physically meaningful quantities imply that all the requirements of a realistic star are satisfied in this model. Figures 1 and 2 depict the regularity of the metric potentials considering the pulsar $4U1820-30$.

Fig. 1

Metric potential $A_0(r)^2$

Fig. 2

Metric potential $B_0(r)^2$

Figure 3 shows the variation of gradients which are negative throughout the stellar configuration ensures the decreasing nature of density, radial and transverse pressures.

Fig. 3

Gradient of pressures and density for $4U1820-30$

Figure 4 shows that the density decrease from its maximum value at the center towards its boundary.

Fig. 4

Density for the pulsar $4U1820-30$

Variation of radial and tangential pressures has been plotted in Fig. 5, which are also radially decreasing outwards from its maximum value at the center and in case of radial pressure it drops to zero at the boundary as it should be but the tangential pressure remains non zero at the boundary.

Fig. 5

Radial and transverse pressure for the pulsar $4U1820-30$

Radial variation of anisotropy has been shown in Fig. 6 which is zero as center as expected and is maximum at the surface.

Fig. 6

Anisotropy $\Delta$ for the pulsar $4U1820-30$

In Figs. 7 and 8, the sound speed in radial and transverse directions have been plotted against the radial parameter which ensures the non-violations of causality condition in the interior of the star.

Fig. 7

Radial velocity of sound against ‘r’ for $4U1820-30$

Fig. 8

Transverse velocity of sound against ‘r’ for $4U1820-30$

The energy conditions are plotted in Fig. 9, which are positive throughout the stellar configuration as required for a physically meaningful stellar model.

Fig. 9

Energy conditions plotted against radius ‘r’ for the pulsar $4U1820-30$

Figures 10 and 11 depicted the smooth matching of the interior and exterior metrices at the boundary.

Fig. 10

Matching of $A_0(r)^2$ with Schwarzschild interior

Fig. 11

Matching of $B_0(r)^2$ with Schwarzschild exterior

The relationship between the thermodynamic parameters energy density and pressure which reflects the nature of the equation of state (EoS) of the matter distribution of a given pulsar is plotted in Fig. 12 which shows an almost linear relationship.

Fig. 12

EoS for the pulsar $4U1820-30$

In Fig. 12, we have plotted the data for $\rho$ and $p_r$ across the range of the radius for the pulsar $4U1820-30$. We estimated that best fitted relation between $\rho$ and $p_r$ is given by the expression $0.410478 x - 194.495$ which is illustrated in Fig. 13. Though we have not prescribed any EoS of the anisotropic matter distribution for modelling the compact object, it is observed that linear EoS holds good for our model.

Fig. 13

Best fit curve

The mass function is given in Eq. (17) is monotonically increasing the function of r and $m(0)=0$ as depicted in Fig. 14.

Fig. 14

Mass function corresponding to ‘r’ for the pulsar $4U1820-30$

For the compactness of a model ($u(r)=m(r)/r$) limit condition need to be satisfied as suggested by Buchdahl [75]. The ratio of mass to the radius should lie within the range $\frac{2 M}{r}<\frac{8}{9}$ [75]. It can be easily checked that $\frac{m(r)}{r}=0.25611 < \frac{4}{9}=0.44$, i.e. Buchdahl conditions are being satisfied with this model.

The surface redshift is

$$\begin{aligned} z=\left( 1-\frac{2 M}{R}\right) ^{-\frac{1}{2}}-1. \end{aligned}$$

(30)

In Fig. 15 the radial variation of the surface redshift is plotted.

According to Bohmer and Harko [76], the surface red shift should always be $\le 5$. The surface redshift of this model is 0.159.

Fig. 15

Surface red shift z for the pulsar $4U1820-30$

For a given value of the surface density ($\rho (r=b) = 1.5\times 10^{15}~$g $\hbox {cm}^{-3}$), we have also obtained the mass–radius ($M-R$) relationship in our model shown in Fig. 16.

Fig. 16

$M-R$ relation for $4U1820-30$. Here $M_{max}=4.0971$ when $r=12.94$

Upper bound to the maximum mass for a neutron star, which is obtained by integrating Oppenheimer–Volkoff equation for density EoS [77], is approximately $3.2M_\odot$ [1]. For uniform density spheres where causality is not inherent, this limit in general relativity $\approx 5.2 M_\odot$ [78]. The equation of State (EoS) parameter as is shown in Figs. 12 and 17 lies between 0 and 1.

Fig. 17

EoS parameter $\omega _t$ for $4U1820-30$

Table 1 Values of model parameters

7.2 Discussions around other Pulsars

To show that this model has a wide range of applicability for highly compact stars, we have also analyzed the validity of our model by considering some well-known pulsars such as RX J $1856-37$ ($\hbox {Mass}=0.9 \pm 0.2 M_{\odot }$, Radius$\approx 6\hbox { km}$) [79], EXO $1785-248$ ($\hbox {Mass}=1.3 \pm 0.2 M_{\odot }$, $\hbox {Radius}=8.849 \pm 0.4\hbox { km}$)[80], Her X-1 ($\hbox {Mass}=0.85 \pm 0.15 M_{\odot }$, $\hbox {Radius}=8.1 \pm 0.41\hbox { km}$) [81], PSR J $1614-2230$ ($\hbox {Mass}=1.97 \pm 0.04 M_{\odot }$, $\hbox {Radius}=9.69 \pm 0.2\hbox { km}$), Cen X-3 ($\hbox {Mass}=1.49 \pm 0.08 M_{\odot }$, $\hbox {Radius}=9.178 \pm 0.13\hbox { km}$) and $4U 1608-52$ ($\hbox {Mass}=1.74 \pm 0.14 M_{\odot }$, $\mathrm{Radius}=9.52 \pm 0.15\hbox { km}$).

Table 2 Values of physical quantities

The estimated masses and radii of these pulsars have been used to determine the corresponding model parameters C, D and R as given in Table 1. Making use of these values, in Table 2, we have calculated the values of the physically reasonable parameters which are sufficient to justify the requirements of a physically realistic star. Note that we have used $()|_0$ and $()|_R$ to denote the evaluated values of the physical parameters at the center and surface of the star, respectively. From Table 2 it is clear that central density is greater than the surface density for all of the listed compact objects, which shows that the density of a compact star is maximum at the centre and decrease towards the surface as one of the important criteria for a compact star. Also, radial pressure is zero at the boundary for all the compact object since we have used this condition to determine the model parameters along with the matching of the interior metric potentials at the boundary with that of the Schwarzschild exterior. Here, radial velocity and transverse velocity of the sound for these pulsars at the centre as well as at the surface is less than 1, satisfying the casuality condition throughout the stellar interior. Also, $\rho - p_r - 2 p_t \ge 0$ for all the compact object at the centre as well as at the surface indicates that the strong energy condition is satisfied throughout the stellar configuration. It can be seen from Table 2 that this presented model satisfy Buchdahl condition as well as surface redshift condition for other pulsars as $z_s\le 2$. So a wide range of compact object can be accommodated in this presented model.

8 Stability analysis of the model

8.1 Stability under three different forces

A star remains in static equilibrium under the forces namely, gravitational force, hydrostatics force and anisotropic force. This condition is formulated mathematically as TOV equation by Tolman–Oppenheimer–Volkoff which is

$$\begin{aligned} -\frac{M_G}{r} (\rho +p_r)\frac{A_0(r)}{B_0(r)}-\frac{dp_r}{dr}+\frac{2}{r}(p_t-p_r)=0, \end{aligned}$$

(31)

where $M_G(r)$ is the gravitational mass of the star within the radius r, can be derived from the Tolman–Whittaker formula and Einstein’s field equations and is defined by

$$\begin{aligned} {M_G}(r)=\frac{r B_0(r) A'_0(r)}{A^2_0(r)}. \end{aligned}$$

(32)

Using the expression of $M_G(r)$ in Eq. (31) we obtain

$$\begin{aligned} -\frac{A_0'(r)}{A_0(r)}(\rho +p_r)-\frac{dp_r}{dr}+\frac{2}{r}(p_t-p_r)=0. \end{aligned}$$

(33)

The above equation is equivalent to

$$\begin{aligned} F_g + F_h + F_a = 0, \end{aligned}$$

(34)

where

$$\begin{aligned} F_g= & {} -\frac{A_0'(r)}{A_0(r)}(\rho +p_r), \end{aligned}$$

(35)

$$\begin{aligned} F_h= & {} -\frac{dp_r}{dr}, \end{aligned}$$

(36)

$$\begin{aligned} F_a= & {} \frac{2}{r}(p_t-p_r), \end{aligned}$$

(37)

represents the gravitational, hydrostatics and anisotropic forces respectively.

The expression for $F_g$, $F_h$ and $F_a$ can be written as,

$$\begin{aligned} F_g= & {} -\frac{8 C r(r^2-R^2)^2(3 C-4 D r^2+4 D R^2)}{R^8(C-2 D r^2+2 D R^2)^2}, \end{aligned}$$

(38)

$$\begin{aligned} F_h= & {} -\left[ \frac{2 r C^2(-9 r^4+16 r^2 R^2-6 R^4)}{R^8(C+2 D (R^2-r^2))^2}\right. \nonumber \\&+ \frac{8 C D r (r^2-R^2)(r^4-2 R^4)}{R^8(C+2 D (R^2-r^2))^2}\nonumber \\&\left. + \frac{ 8 D r (r^2-R^2)^2(3 r^4-8 r^2 R^2+6 R^4))}{R^8(C+2 D (R^2-r^2))^2}\right] , \end{aligned}$$

(39)

$$\begin{aligned} F_a= & {} \frac{2 r}{R^8}(3 r^4 - 8 r^2 R^2 + 6 R^4). \end{aligned}$$

(40)

The three different forces are plotted in Fig. 18. The figure shows that hydrostatics and anisotropic force are positive and is dominated by the gravitational force which is negative to keep the system in static equilibrium.

Fig. 18

Different types of forces as function of radial coordinate ‘r’ for the pulsar $4U1820-30$

8.2 Adiabatic index

The adiabatic index which is defined as

$$\begin{aligned} \Gamma =\frac{\rho +p}{p}\frac{dp}{d\rho }, \end{aligned}$$

(41)

is related to the stability of a relativistic anisotropic stellar configuration. A Newtonian isotropic sphere will be in stable equilibrium if the adiabatic index $\Gamma > \frac{4}{3}$ as per Heintzmann and Hillebrandth’s concept [26] and for $\Gamma =\frac{4}{3}$, isotropic sphere will be in neutral equilibrium. Based on some recent works of Chan et al. [82] one can demand the following condition for the stability of a relativistic anisotropic sphere

$$\begin{aligned} \Gamma > \gamma , \end{aligned}$$

(42)

where

$$\begin{aligned} \gamma =\frac{4}{3}-\left[ \frac{4(p_r-p_t)}{3|p'_r| r}\right] _{max}, \end{aligned}$$

(43)

and $\Gamma > \frac{4}{3}$. In Fig. 19, we have plotted $\Gamma _r$, $\Gamma _t$, $\gamma$ respectively. clearly, it can be seen that values of $\Gamma _r$ and $\Gamma _t$ are greater than $\gamma$ throughout the stellar interior and hence the stability condition is fulfilled.

Finally, it is to be noted that the adiabatic index $\gamma$ is a local characteristic of a specific EoS and depends on the interior fluid density.

Fig. 19

Adiabatic index for the pulsar $4U1820-30$

8.3 Causality condition

For a physically acceptable model of relativistic anisotropic star the radial and transverse velocity speed of sound must be smaller than $1(c=1)$ in the interior of the star, i.e., $0 \le \frac{dp_r}{d\rho } \le 1$, $0 \le \frac{dp_t}{d\rho } \le 1$. This condition is known as causality condition and are verified in Figs. 7 and 8.

Based on Herrera cracking method, Abreu et al. [46] proved that the region of an anisotropic fluid sphere where $1 \le v^2_{st} - v^2_{sr} \le 0$ is potentially stable which is shown graphically in Fig. 20.

Fig. 20

Variation of $|{v_{st}^2-v_{sr}^2}|$ against the r for $4U1820-30$

9 Discussions

In this work, a static spherically symmetric anisotropic fluid model has been developed by assuming a physically reasonable metric potential and a particular form of the anisotropy. The presented solution satisfies all the physical criterion of a physically well behaved compact object. All the physical quantities are regular and well behaved throughout the stellar interior. Energy density, radial pressure and transverse pressure are decreasing functions towards the surface of the star. Here anisotropy is finite, continuous and monotonically increasing function of the radial coordinate ‘r’ away from the stellar centre i.e. anisotropic force is repulsive in nature. Similar profile for anisotropy can be found in the work of Sunzu et al. [69]. The model is shown to remain stable in hydrostatic equilibrium against different forces. The developed model has been shown to fit a wide range of recently observed values of masses and radii of pulsars. The mass-radius relation is also explored here. The maximum mass for the model is 4.0971 and it is obtained for $r=12.9416$, which is stable as the mass $\le 5 M_\odot$ [1].

The above model can be of significant study for modelling of astrophysical objects with a wide variety of masses and radii. The developed model can be analyzed further by using different metric potentials, a different measure of anisotropy for new results.