1 Introduction

The study of nature and the internal structure of compact objects, i.e. white dwarfs, neutron stars, black holes etc. is one of the fascinating realms of Astrophysics. In the General Theory of Relativity (GTR), since the astrophysical configurations primarily follow the local solutions of Einstein field equations, obtaining one for spherically symmetric perfect fluid solutions has been studied massively by researchers across the world. The launchpad for examining the exact solutions for spherically symmetric structures was provided in 1916 by the astounding work of Schwarzschild in obtaining the first exterior solution [2] and the interior solution [3] considering a uniform density sphere. Owing to the extreme core density (\(>10^{15}\) gm/cc), neutron stars provide one of the best laboratories in the Universe to appraise many astrophysical models in the strong gravitational field regime [4, 5] and are one of the most enigmatic stellar remnants with an incredibly dense core and sturdy crust, enough to hold up long-lived bulges that could produce potentially large ripples in the space, known as gravitational waves [6]. The discovery of the first pulsar in the year 1968 by Hewish et al. [7] which was identified as a rotating neutron star, changed the course of investigating neutron stars, although Tolman [8] and Oppenheimer and Volkoff [9] developed a relativistic theory of neutron stars even before its actual discovery.

Due to the high non-linearity of the Einstein field equations, several factors need to be taken care of for compact stellar modelling. Among many other factors, the role of pressure anisotropy (difference of the pressures) needs to be considered due to the extreme and unusual conditions reigning in the interior of compact objects [10]. Later, Leimatre [11] examined the first anisotropic model entirely with tangential pressure and constant density. In 1972, Ruderman [12] theoretically observed that predominantly because of its high density (\(>10^{15}\) gm/cc) filled interior, the radial pressure may not be equal to the tangential pressure in massive stellar objects. It is well known that anisotropy can occur in any astrophysical object due to several factors: very high magnetic field [13,14,15,16,17,18,19,20], pion condensation [21], phase transitions [22], relativistic nuclear interactions [23], crystallization of the core [24], superfluid core [25,26,27], viscosity [28,29,30,31]. In recent times, Herrera [32] suggested that due to the association of various physical processes with highly compact objects, anisotropic stress cannot be ignored in the interior of a relativistic compact star. The relativistic compact object-like neutron star configuration with anisotropic pressure was first modelled by Bowers and Liang [33]. The Bowers–Liang model is primarily based on the following assumptions: (i) the anisotropy should vanish quadratically at the origin. (ii) the anisotropy should depend non-linearly on the radial pressure, and (iii) the anisotropy is gravitationally induced [34]. Their study also claimed that the anisotropy might have non-negligible effects on the surface redshift and the equilibrium mass. A heuristic procedure to obtain interior solutions of Einstein’s equations for anisotropic matter from any known solutions for the isotropic matter was studied by Cosenza et al. [35].

Several investigations have been conducted extensively for anisotropic compact stellar objects, some of the remarkable works are: the effect of the pressure anisotropy on the maximum mass and the surface redshift is analysed in the Vaidya–Tikekar model by Karmarkar et al. [36], and it is shown that in the presence of anisotropic pressure, maximum compactness can be observed and also the red-shift and the mass increase inside the structure, Dev and Gleiser [37] studied the properties of spherically symmetric gravitationally bound stellar objects with the anisotropic matter distribution and showed how drastically anisotropy might impact the structure and the properties of a star, possible causes for the appearance of local anisotropy (unequal principal stresses) in self-gravitating systems and its main consequences are studied by Herrera and Santos [38].

There are several known processes to solve the Einstein field equations. Among all other prospects of obtaining an analytic solution of the field equations, the simplest is to assume that without the inclusion of electric charge, the material content is isotropic, \(p_r = p_t\). However, the inclusion of anisotropy changes the number of unknown variables to five (namely density \(\rho \), radial pressure \(p_r\), transverse pressure \(p_t\) and two unknown metric potentials and with an electric charge, the number rises to six), then it is necessary to prescribe more information [39]. Another recipe to obtain the solution is by imposing a specific equation of state (EoS) or by making use of geometric constraints on the specific spacetime geometry. This EoS links the main thermodynamic functions of the fluid i.e., the energy density and pressure (in the radial and tangential directions), and that describes the microphysical processes of the system and it is estimated to be a linear relationship between those physical observables. For a given EoS, the physical properties of a neutron star can be analyzed by solving the Tolman-Oppenheimer-Volkov equations. The simple linear form of EoS in the MIT Bag model is assumed by many authors for studying compact stellar modelling, [40,41,42,43,44,45,46,47,48,49] to name a few. Many investigators have also assumed a quadratic form of EoS to model compact stars [50,51,52,53]. Additionally, Chaplygin EoS [54], modified Chaplygin EoS [55], and Van der Waals type EoS [56] are also considered for representing compact stellar models with the anisotropic fluid. However, since the equation of state of a compact star is not very clear yet, so by starting with EoS, one generally lands on numerical methods leading to graphical results that lack the analysis of the local properties of the matter close to the centre of such relativistic stars. Thus, most researchers prefer to obtain the exact solutions of the concerned Einstein’s field equations using ad-hoc methods such as assuming one of the metric potentials. The other metric potential is obtained using some additional conditions on the metric. Motivated by this convention, the current work assumes the metric potential \(g_{rr}\) in the form of \((1 + a r^2)^2\) where \(a>0\) is the model parameter. One can easily see the metric potential resembles the form of a modified Finch–Skea metric where the Finch–Skea metric is of the form \((1 + \frac{r^2}{R^2})\), \(R >0\) being the curvature parameter. The beauty of the Finch–Skea metric [57] is that it is well-behaved, and it fulfills the criteria to be a static spherically symmetric perfect fluid solution as suggested by Delgaty and Lake [58] and also has been shown to be consistent with the Walecka theory [59] for cold condensed stars. Moreover, the Finch–Skea metric is found to be consistent with studying neutron stars, especially investigating the central densities of the neutron star in the relativistic mean-field theory [60]. Recently, the Finch–Skea metric has been studied in the background of mimetic gravity also [61]. One of the fascinating features of our obtained solution is the codependency of the metric potentials. Although it does not take the form of some known approaches such as embedding class one method, conformally flat geometry and conformal motion, the link equations respectively being, \(e^\nu = \left( A + B \int \sqrt{e^\lambda - 1} dr \right) ^2\), \(e^\nu = C^2 r^2 \cosh ^2 \left( \int \frac{e^{\lambda /2}}{r}dr + D \right) \) and \(e^\nu = c^2 r^2 exp\left( \frac{-2k}{B} \int \frac{e^{\lambda /2}}{r}dr\right) \) where A, B, C, D, c and k are constants. However, the obtained solution and hence the model is found to be stable under several conditions. Several studies have been conducted using the Finch–Skea ansatz and modified Finch–Skea ansatz for modelling anisotropic compact stellar structure [62,63,64,65,66,67,68,69,70,71,72,73].

The study of rotating compact objects, in the context of the general theory of relativity, is extremely significant as it might generate information about unknown EoS at such high densities [74]. Recent studies conducted by Neutron Star Interior Composition Explorer (NICER) have placed constraints on the masses and radii of X-ray pulsar PSR J\(0740+6620\) [75,76,77]. The study of slowly rotating compact objects in the framework of general relativity was pioneered by Hartle [78] in 1967 when his work provided the calculation for equilibrium configurations of slowly rotating stars to the second order in the angular velocity. Hartle considered the fluid interior to be characterized by one parameter EoS. Using specific EoSs, Hartle–Thorne [79] studied equilibrium configurations of rigidly rotating white dwarfs and neutron stars. Later using Hartle’s method, Chandrasekhar and Miller [80] studied the slow rotation of the homogeneous masses, which are characterized by constant energy density. They found that the ellipticity of the configuration, for varying radius but constant mass and angular momentum, displays the maximum value at \(\frac{\text {radius of the star} (b)}{\text {Schwarzschild radius} (b_S)} \approx 2.4\). Additionally, they found that for stars having radius \(b = \frac{9}{8} b_S\), the quadrupole mass moment is very close to the value associated with the Kerr metric to second order in the angular velocity. Motivated by these, Posada [81] investigated the surface and integral properties of a slowly rotating Schwarzschild star in the unstudied region of \(b_S< b < \frac{9}{8}\). Recently, the Hartle–Thorne equations for slowly rotating relativistic masses, Posada and Stuchlìk studied the slowly rotating Tolman VII fluid sphere, at second order in the angular velocity [82]. A lot of literature can be found in recent times that delve into approximating slowly rotating compact configurations [83,84,85,86,87].

The layout of the present paper is given as: Sect. 2 offers a brief highlight on the Einstein field equation and the novel solution thus obtained describing the anisotropic configuration. The expressions for the model parameter from the smooth matching conditions at the boundary are discussed in Sect. 3. The physical analysis and the stability analysis for the obtained model are described in Sects. 4 and 5 respectively. The nature of mass–radius, compactness and the equation of state is described in Sect. 6. Considering the slow rotating structure, we have studied the nature of the angular momentum and the moment of inertia with respect to the radius and central density in Sect. 7. Finally, the compatibility of our model with some other known compact objects is illustrated in Sect. 8 and the concluding remarks are given in Sect. 9.

2 Novel class of solutions of the Einstein field equations

The Einstein field equation is given by

$$\begin{aligned} \mathcal {R}_{\alpha \beta } - \frac{1}{2}g _{\alpha \beta } \mathcal {R} = \frac{8 \pi G}{c^4} T_{\alpha \beta }, \end{aligned}$$
(1)

where \(\mathcal {R}_{ij}\), \(g_{ij}\), \(\mathcal {R}\) and \(T_{ij}\) are Ricci tensor, metric tensor, Ricci scalar and energy–momentum tensor respectively. Also, G represents the gravitational constant and c is the speed of light. Now for the matter distribution of the stellar interior to be anisotropic in nature, the energy–momentum tensor is described as that of a perfect fluid and it is considered in the form,

$$\begin{aligned} T_{\alpha \beta } = \bigg (\rho + \frac{p_t}{c^2}\bigg )u_{\alpha } {u_\beta } - p_{t} g_{\alpha \beta } + (p_r - p_t)\chi _{\alpha } \chi _{\beta }, \end{aligned}$$
(2)

where \(\rho \) represents the energy density, \(p_r\) and \(p_t\), respectively denote fluid pressures along the radial and transverse directions, \(u^\alpha \) is the 4-velocity of the fluid and \(\chi ^\alpha \) is a unit space-like 4-vector along the radial direction. Since we considered the configuration of our system to be in a comoving coordinate system we have the following relations for the 4-vectors,

$$\begin{aligned} u^\alpha u_\alpha = 1;~ \chi ^\alpha \chi _\alpha =-1;~ u^\alpha \chi _\alpha =0. \end{aligned}$$
(3)

The energy–momentum tensor can always be brought in the diagonal form \(T_{\alpha \beta } =diag(\rho c^2,-p_r,-p_t,-p_t)\). To describe the space-time of the interior of a spherically symmetric star with zero angular momentum in Schwarzschild coordinates i.e. in (\(t,r, \theta , \phi \)) coordinates we choose the line element to be of the form as the following,

$$\begin{aligned} ds^2 = -X_{0}^2(r)dt^2 + Y_{0}^2(r)dr^2 + r^2(d\theta ^2 + \sin ^2\theta d\phi ^2), \end{aligned}$$
(4)

where \(X_{0}(r)\) and \(Y_{0}(r)\) are the gravitational potentials and these metric functions are functions of the radial coordinate r only.

Thus the spherically symmetric line element Eq. (4) then provides the Einstein field equations governing the evolution of the system (we set \(c = 1\)) as follows:

$$\begin{aligned} \frac{8\pi G}{c^2} \rho= & {} \left[ \frac{1}{r^2}-\frac{1}{r^2 Y_0^2}+\frac{2Y_0'}{r Y_0^3}\right] , \end{aligned}$$
(5)
$$\begin{aligned} \frac{8\pi G}{c^4} p_r= & {} \left[ -\frac{1}{r^2}+\frac{1}{Y_0^2 r^2}+\frac{2X_0'}{r X_0Y_0^2}\right] , \end{aligned}$$
(6)
$$\begin{aligned} \frac{8\pi G}{c^4} p_t= & {} \left[ \frac{X_0''}{X_0Y_0^2} + \frac{X_0'}{rX_0Y_0^2} - \frac{Y_0'}{r Y_0^3} - \frac{X_0'Y_0'}{X_0 Y_0^3}\right] , \end{aligned}$$
(7)

where ‘prime’ in Eqs. (5)–(7) denotes differentiation with respect to the radial coordinate r. The system of field equations Eqs. (5)–(7) are highly non-linear as it consists of three equations and five unknowns (\(\rho ,~ p_r,~ p_t,~ X_0,~ Y_0\)) so to find the exact solutions, any two of them can be chosen freely. One of the methods of obtaining exact solutions is to specify one metric potential and using another assumption (specific equation of state or embedding condition etc.), we obtain another one. In the present work, we are motivated to investigate the metric potential in this form considering it as a \(g_{rr}\) metric and it is given by,

$$\begin{aligned} Y^2_0 (r) = (1 + a r^2)^2, \end{aligned}$$
(8)

where \(a > 0\) is the model parameter. A similar kind of metric potential was considered by Das et al. [88] for relativistic anisotropic stellar models with spherically symmetric matter distribution in the Einstein Gauss–Bonnet (EGB) gravity. The metric is finite, continuous and well-defined within the stellar structure. \(Y_0^2 (r =0)=1\) depicts the finite nature and the non-singularity of the metric potential at the centre of the stellar configuration. Also, \(\left( Y_0^2(r)\right) '_{r = 0}= 0\) represents the regularity of metric potentials at the centre. The anisotropic parameter of the stellar system \(\Delta \) is defined as the difference between two pressures [89] given in Eqs. (6) and (7),

$$\begin{aligned} \Delta (r)= & {} \frac{8\pi G}{c^4} (p_t-p_r) \nonumber \\= & {} \frac{X_0''}{X_0Y_0^2} - \frac{X_0'}{r X_0Y_0^2} - \frac{Y_0'}{r Y_0^3} - \frac{X_0'Y_0'}{X_0Y_0^3}- \frac{1}{r^2Y_0^2} + \frac{1}{r^2} \nonumber \\= & {} \frac{ a r \left\{ a r \left( a r^2+3\right) X_0(r)+r X_0''(r)-3 X_0'(r)\right\} }{ \left( a r^2+1\right) ^3 X_0(r)} \nonumber \\{} & {} + \frac{r X_0''(r)-X_0'(r)}{r \left( a r^2+1\right) ^3 X_0(r)}. \end{aligned}$$
(9)

It is well known that anisotropy \(\Delta (r)\) is assumed to vanish at the interior of a stable stellar configuration i.e. \(p_r(r) = p_t(r)\). The anisotropic force which is defined as \(2 \Delta /r\) will be repulsive or attractive in nature depending upon whether \(p_t>p_r\) or \(p_t<p_r\).

On rearranging Eq. (9) we get

$$\begin{aligned}{} & {} \frac{X_0''(r)}{X_0(r)}- \frac{(1+ 3 a^2 r)X_0'(r)}{r (a^2 r + 1)X_0(r)} \nonumber \\{} & {} =\frac{r \Delta (r) ( a r^2 + 1)^3 - a^2 r^3 (a r^2 + 3)}{r( a^2 r + 1 )}. \end{aligned}$$
(10)

Now the Eq. (10) can be solved for \(X_0(r)\) if \(\Delta (r)\) is specified in a particular form. The anisotropy factor needs to be taken in such a way that the regularity at the centre is satisfied and the factor becomes a monotonically increasing function of the radial coordinate ‘r’ [90]. The increasing trend of anisotropy generally yields a well-behaved solution. We are considering anisotropy in a polynomial form such that the regularity and the monotonically increasing condition are satisfied and at the same time Eq. (10) can be easily integrable.

Thus we consider the second assumption by imposing that the component \(g_{tt}\) has no contribution to the anisotropy parameter, so,

$$\begin{aligned} \Delta (r)=\frac{a^2 r^2 \left( a r^2+3\right) }{\left( a r^2+1\right) ^3}. \end{aligned}$$
(11)

The above choice for anisotropy is physically reasonable, as at the centre (\(r=0\)) anisotropy vanishes as expected. Also \(\frac{d\Delta (r)}{dr}\) is positive throughout the stellar structure as r is positive, which makes \(\Delta (r)\) a monotonically increasing function. Now this choice of anisotropy provides a solution to Eq. (10) in closed form. Substituting Eq. (11) in Eq. (10), we obtain,

$$\begin{aligned} \frac{X_0''(r)}{X'_0(r)}-\frac{\left( 3 a r^2+1\right) }{r(a r^2+1)}=0. \end{aligned}$$
(12)

We obtain a simple solution of the Eq. (12) in the form

$$\begin{aligned} X_0(r)= \frac{C r^2}{4} \left( a r^2+2 \right) + D, \end{aligned}$$
(13)

where C and D are integration constants and which will be obtained from the boundary conditions. Interestingly one can observe that both the obtained metric potentials are codependent and their link equation is given as,

$$\begin{aligned} Y^2_0 = 1+ \frac{4a}{C}(X_0 - D). \end{aligned}$$
(14)

So one can argue that the line element takes the form of,

$$\begin{aligned} ds^2= & {} -X_{0}^2(r)dt^2 + \left[ 1+ \frac{4a}{C}(X_0(r) - D)\right] dr^2 + r^2(d\theta ^2 \nonumber \\{} & {} + \sin ^2\theta d\phi ^2). \end{aligned}$$
(15)

With the choices of these metric potentials the matter density, radial pressure, transverse pressure and mass function are now obtained as

$$\begin{aligned} \frac{8\pi G}{c^2}\rho= & {} \frac{a \left[ a r^2 \left( a r^2+3\right) +6\right] }{\left( a r^2+1\right) ^3}, \end{aligned}$$
(16)
$$\begin{aligned} \frac{8\pi G}{c^4} p_r= & {} \frac{8 C- a C r^2 \{ 4 - a r^2 (ar^2 + 4)\} - 4 a D (a r^2 + 2)}{\left( a r^2+1\right) ^2 \left( a C r^4+2 C r^2+4 D\right) },\nonumber \\ \end{aligned}$$
(17)
$$\begin{aligned} \frac{8\pi G}{c^4} p_t= & {} \frac{2 C \left[ 3 a r^2 \left( a r^2+2\right) +4\right] -8 a D}{\left( a r^2+1\right) ^3 \left[ C r^2 \left( a r^2+2\right) +4 D\right] }. \end{aligned}$$
(18)

Moreover, the mass contained within a radius r of the sphere is defined as

$$\begin{aligned} m(r)= & {} 4\pi \int _0^r \omega ^2 \rho (\omega )d\omega \nonumber \\= & {} \frac{1}{2} a r^3 \frac{2 + a r^2}{(1+ a r^2)^2}. \end{aligned}$$
(19)

3 Matching conditions at the stellar boundary

Since the Schwarzschild solution is the unique spherically symmetric solution of the vacuum Einstein field equations, so a spherically symmetric gravitational field in empty space outside a spherical star must be static and asymptotically flat. Now the continuity of the first fundamental form states that the interior solution must match smoothly to the vacuum exterior Schwarzschild solution at the boundary, provided the mass remains the same as above [91]. Here the exterior space-time for a non-radiating star can be described by Schwarzschild metric and it is given as

$$\begin{aligned} ds^2= & {} -\left( 1-\frac{2M}{r}\right) dt^2 + \left( 1-\frac{2M}{r}\right) ^{-1}dr^2 + r^2(d\theta ^2 \nonumber \\{} & {} + \sin ^2\theta d\phi ^2), \end{aligned}$$
(20)

where \(r>2\,M\), M being the mass of the stellar. This continuity of the metrices across the boundary leads to

$$\begin{aligned} X_0^2(b)=\left( 1-\frac{2M}{b}\right) ~~~~\text{ and }~~~~Y_0^2(b)=\left( 1-\frac{2M}{b}\right) ^{-1}. \end{aligned}$$
(21)
Fig. 1
figure 1

Smooth matching of the metric potentials \(X_0^2(r)\) and \(Y_0^2(r)\) at the boundary of the star

Full size image

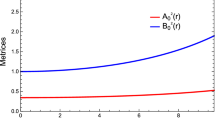
Furthermore, the continuity of the second fundamental form at the boundary states that the radial pressure drops to zero at a finite value of r. This value is known as the radius of the star, thus from the condition \(p_r(r=b)=0\), one can easily find the radius of the star (Fig. 1). Hence from the juxtaposition of both first and second boundary conditions for the spacetime and curvature, the model constants are determined in terms of mass and radius of the star as,

$$\begin{aligned} a= & {} \frac{b-2 M -\sqrt{b(b-2 M )}}{b^2(2 M -b)},\nonumber \\ C= & {} \frac{M}{b^3}, \nonumber \\ D= & {} \frac{M \left[ b+ 9 \sqrt{b(b - 2 M)}\right] - 2 M^2 - 4 b \sqrt{b(b - 2M)}}{4b (2 M - b)}.\nonumber \\ \end{aligned}$$
(22)

The matching of metric potentials has been demonstrated in Fig. 1.

4 Physical analysis of the obtained solution

This section dives into the analysis of the physical features of the obtained result. For the graphical representation we have chosen the pulsar 4U1608-52 with the mass \(=1.57^{+0.30}_{-0.29} ~M\odot \) and radius \(=9.8 \pm 1.8\) km [1] and the values of the constants are found to be \(a = 0.00392534\), \(C= 0.00246044\) and \(D= 0.5858\). For the sake of calculation, we have considered the geometrized units as (\(G = c = 1\)). The detailed discussions around some of the important physical features are given below:

4.1 Regularity of the metric

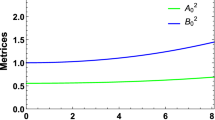
The gravitational potentials for our model satisfy, \(X^2_0(0)=D=constant\), \(Y^2_0(0)=1\), i.e. both the metric potentials are finite at the centre (\(r=0\)). Also, we have \((X^2_0(r))'_{r=0}=(Y^2_0(r))'_{r=0}=0\), illustrates the regularity of the metric at the centre and well-behaved nature throughout the stellar interior (Fig. 2).

Fig. 2
figure 2

Variation of the metric potentials \(X_0^2(r)\) and \(Y_0^2(r)\) with respect to r

Full size image

At the centre and throughout the structure, the matter variables should be regular and well-defined for a physically acceptable model. Thus for a stable model, the density \(\rho \), radial pressure \(p_r\) and the tangential pressure \(p_t\) should be positive inside the star and \(\rho (0)\), \(p_r(0)\) and \(p_t(0)\) should be finite at the centre. Figure 3 shows that the density is positive throughout and the density decreases from its maximum value at the center towards its boundary. Moreover, the central density seems to be increased for the higher value of the model parameter a. It is evident from the Figs. 4 and 5 that our model satisfies the regularity of main thermodynamic variables.

The radial and tangential pressures are also radially decreasing outwards its boundary from its maximum value at the centre. The radial pressure vanishes at the boundary but the tangential pressure remains non-zero at the boundary. A similar nature of transverse pressure can be seen in [92].

Additionally, the central density, central radial pressure and central tangential pressure in this case are given as

$$\begin{aligned} \rho (0) = 6 a,~~~p_r(0)=p_t(0) = \frac{2}{D} (C - a D). \end{aligned}$$

Since a is a positive quantity central density is always positive. The absence of anisotropy at the centre i.e. similarity of \(p_r(0)\) and \(p_t(0)\) can be seen in our model. However, the anisotropy is increasing within the configuration as shown in Fig. 6 indicating the direction of anisotropic force to be outward, which proves the existence of a repulsive force resulting in more compact objects using anisotropic force rather than using isotropic force [93]. Using Zeldovich Condition for density and pressure of stable configuration we have, \(\frac{p_r}{\rho }\le 1\) at the center i.e. \(\frac{C}{D}\le 4 a\).

Fig. 3
figure 3

Radially symmetric profiles of the energy density (MeV/fm\(^3\)) is depicted corresponding to the compact star 4U1608-52

Full size image
Fig. 4
figure 4

Radially symmetric profiles of the radial pressure (MeV/fm\(^3\)) is depicted corresponding to the compact star 4U1608-52

Full size image
Fig. 5
figure 5

Radially symmetric profiles of the transverse pressure (MeV/fm\(^3\)) is depicted corresponding to the compact star 4U1608-52

Full size image
Fig. 6
figure 6

Variation of anisotropy \(\Delta \) against the radial coordinate r

Full size image

4.2 Gradient

Any model is considered to be a viable model of anisotropic compact star if the energy density and the pressure are maximum at the centre and are decreasing monotonically towards the surface of the star i.e. \(\left( \frac{d\rho }{dr}\right) _{r=0}=0=\left( \frac{dp}{dr} \right) _{r=0}\) and \(\left( \frac{d^2\rho }{dr^2}\right) _{r=0}<0\), \(\left( \frac{d^2 p}{dr^2}\right) _{r=0}<0\) such that the gradients are negative within \(0~<r~<~b\), b being the radius of the star. Here the gradient of energy density, radial pressure and tangential pressure are respectively obtained as follows,

$$\begin{aligned} \frac{d\rho }{dr}= & {} -\frac{2 a^2 r \left( a^2 r^4+4 a r^2+15\right) }{\left( a r^2+1\right) ^4}, \nonumber \\ \frac{dp_r}{dr}= & {} \frac{2 r \left[ 16 a^2 D^2 \left( a r^2+3\right) +8 a C D \left( a^3 r^6+5 a^2 r^4+2 a r^2-4\right) +C^2 \left( a^5 r^{10}+7 a^4 r^8-8 a^3 r^6-60 a^2 r^4-64 a r^2-16\right) \right] }{\left( a r^2+1\right) ^3 \left( C r^2 \left( a r^2+2\right) +4 D\right) ^2}, \nonumber \\ \frac{dp_t}{dr}= & {} -\frac{4 r \left[ -8 a C D \left( a^2 r^4+2 a r^2-2\right) -48 a^2 D^2+C^2 \left( 9 a^4 r^8+36 a^3 r^6+56 a^2 r^4+40 a r^2+8\right) \right] }{\left( a r^2+1\right) ^4 \left( C r^2 \left( a r^2+2\right) +4 D\right) ^2}. \end{aligned}$$
(23)

The gradient of the density and radial pressure are shown to be negative inside the stellar body in Fig. 7 throughout the structure. However, the gradient of the tangential pressure is seen to be non-negative in the configuration.

Fig. 7
figure 7

Variation of the gradient of the radial pressure and the density against the radial coordinate r

Full size image

4.3 Energy conditions

Fig. 8
figure 8

Variation of different energy conditions plotted against radial coordinate r

Full size image
Fig. 9
figure 9

Static equilibrium under three different forces

Full size image

The framework of General Relativity allows us to describe energy conditions as the local inequalities that process a relation between energy density \(\rho \) and pressures \((p_r,~p_t)\) with some certain constraints. So a physically viable structure needs to satisfy some energy conditions throughout the stellar interior. Although there are various ways to calculate energy conditions, the focus mainly revolves around Null Energy Condition (NEC), Weak Energy Condition (WEC), Strong Energy Condition (SEC), Dominant Energy Condition (DEC) and Trace Energy Condition (TEC), defined as follows

$$\begin{aligned} NEC_r&: \rho (r) + p_r(r)\ge 0,~~ NEC_t : \rho (r) + p_t(r)\ge 0,\nonumber \\ WEC_r&: \rho (r)\ge 0,~~ \rho (r) + p_r(r)\ge 0,\nonumber \\ WEC_t&: \rho (r)\ge 0,~~ \rho (r) + p_t(r)\ge 0,\nonumber \\ DEC_r&: \rho (r) - |p_r(r)|\ge 0,~~ DEC_t : \rho (r) - |p_t(r)|\ge 0,\nonumber \\ SEC&: \rho (r) + p_r(r) + 2p_t(r)\ge 0, \nonumber \\ TEC&: \rho (r) - p_r(r) - 2p_t(r)\ge 0. \end{aligned}$$
(24)

For positive density and pressures, NECs and WECs are bound to satisfy. So graphically we only have plotted both the DECs, SEC and TEC in Fig. 8 and found that these energy conditions are satisfied simultaneously by the presented solutions. Now to obtain the bound on the model parameters let us check the nature of TEC at the centre.

$$\begin{aligned} 0 \le TEC|_{r =0} \implies \frac{C}{D} \le 2 a. \end{aligned}$$

5 Stability analysis for the obtained solution

5.1 Stability under three forces

The stability of any star under hydrostatic equilibrium is analysed through the equation known as TOV equation [8, 9] followed by the name of Tolman–Oppenheimer–Volkoff. This TOV equation states that any viable model must be stable under three different forces viz. gravitational force, hydrostatics force and anisotropic force and mathematically the resultant forces must be zero throughout the star. TOV equation defines the internal structure of a spherically symmetric compact stellar body and in the presence of anisotropy it is defined as,

$$\begin{aligned} -\frac{M_G}{r}(\rho +p_r)\frac{X_0(r)}{Y_0(r)}-\frac{dp_r}{dr}+\frac{2}{r}(p_t-p_r)=0, \end{aligned}$$
(25)

where \(M_G(r)\) is the effective gravitational mass and it can be derived with the help of Tolman–Whittaker mass formula given as,

$$\begin{aligned} M_G(r) = \frac{rY_0(r)X'_0(r)}{X_0(r)^2}. \end{aligned}$$
(26)

Using the expression of \(M_G(r)\) in Eq. (26) we obtain the expression as,

$$\begin{aligned} -\frac{X'_0(r)}{X_0(r)}(\rho +p_r)-\frac{dp_r}{dr}+\frac{2}{r}(p_t-p_r)=0, \end{aligned}$$
(27)

Equivalently Eq. (27) can be written as,

$$\begin{aligned} F_g+F_h+F_a=0, \end{aligned}$$
(28)

where \(F_g, F_h, F_a\) are gravitational force, hydrostatics force and anisotropic force respectively. Thus, the expressions for gravitational force, hydrostatics force and anisotropic force can be represented as,

$$\begin{aligned} F_g = -\frac{X'_0(r)}{X_0(r)}(\rho +p_r),~~ F_h =-\frac{dp_r}{dr},~~ F_a = \frac{2}{r}(p_t-p_r), \end{aligned}$$

respectively. For this model, the expressions for the several different forces are as follows,

$$\begin{aligned} F_g= & {} -\frac{16 C r \left[ C \left( 3 a^2 r^4+6 a r^2+2\right) +4 a D\right] }{\left( a r^2+1\right) ^2 \left[ C r^2 \left( a r^2+2\right) +4 D\right] ^2},\nonumber \\ F_h= & {} -\frac{2 r \left[ 16 a^2 D^2 \left( a r^2+3\right) +8 a C D \left( a^3 r^6+5 a^2 r^4+2 a r^2-4\right) +C^2 \left( a^5 r^{10}+7 a^4 r^8-8 a^3 r^6-60 a^2 r^4-64 a r^2-16\right) \right] }{\left( a r^2+1\right) ^3 \left( C r^2 \left( a r^2+2\right) +4 D\right) ^2}, \nonumber \\ F_a= & {} \frac{2 a^2 r \left( a r^2+3\right) }{\left( a r^2+1\right) ^3}. \end{aligned}$$
(29)

The variation of the several forces against the radial coordinate is depicted in Fig. 9 and it can be seen that gravitational force is negative, dominating in nature and is balanced by the combined effect of hydrostatic forces and anisotropic forces to keep the system in equilibrium.

5.2 Herrera cracking method

Fig. 10
figure 10

Variation of sound velocity in the radial direction with the radial coordinate r

Full size image

In an attempt to understand the (un)stability of any anisotropic compact stellar objects, one of the important tests is to check the overturning or the cracking of the model. The general idea is that at both sides of the cracking point, the fluid elements are accelerated with respect to each other. For self-gravitating compact objects, the concept of cracking for anisotropic matter distribution is first studied by Herrera [94]. The cracking condition suggests that for any stellar model to be physically acceptable, the radial sound speed needs to satisfy the causality condition i.e. \(v_{r}^2 \le 1\) (taking \(c = 1\) and \(v = \frac{dp}{d\rho }\)). Also, Le Chatelier’s principle suggests the sound speed to be positive i.e. \(v_r > 0\). Now the expression for radial sound speed is given as

$$\begin{aligned} \frac{dp_r}{d\rho }= & {} -\frac{\left( a r^2+1\right) }{a^2 \left( a^2 r^4+4 a r^2+15\right) \left[ C r^2 \left( a r^2+2\right) +4 D\right] ^2}\nonumber \\{} & {} \times \Bigg [16 a^2 D^2 \left( a r^2+3\right) +8 a C D \left( a^3 r^6+5 a^2 r^4+2 a r^2-4\right) \nonumber \\{} & {} + C^2 \left( a^5 r^{10}+7 a^4 r^8-8 a^3 r^6-60 a^2 r^4-64 a r^2-16\right) \Bigg ], \nonumber \\ \frac{dp_t}{d\rho }= & {} \frac{2 \left[ -8 a C D \left( a^2 r^4+2 a r^2-2\right) -48 a^2 D^2+C^2 \left( 9 a^4 r^8+36 a^3 r^6+56 a^2 r^4+40 a r^2+8\right) \right] }{a^2 \left( a^2 r^4+4 a r^2+15\right) \left[ C r^2 \left( a r^2+2\right) +4 D\right] ^2}. \end{aligned}$$
(30)

The fulfillment of the causality condition for our model is shown in Fig. 10. Moreover, Abreu et al. [95] modified Herrera’s cracking concept to determine the stability of compact objects by introducing a range for potentially stable (or unstable) anisotropic compact structures. As per their study, a potentially stable model should follow the inequality \(-1 \le v_{t}^2 - v_{r}^2 \le 0\) provided no sign change of \(v_{t}^2 - v_{r}^2\) within the stellar radius. Since the inequality \(-1 \le v_{t}^2 - v_{r}^2 \le 0\) also holds for our model as shown in Fig. 11 so the model is concluded to fulfill Herrera’s cracking concept. Furthermore, to obtain the bound on the model parameter we obtain the value of sound speed at the centre. Using causality condition at the centre of the stellar structure leads to the following inequality:

$$\begin{aligned} C (C + 2 a D ) \le 18 a^2 D^2. \end{aligned}$$

5.3 Adiabatic index

Another basic test to examine the stability of stars is stability against the adiabatic index. The nature of the equation of state can be described by the adiabatic index for a fixed energy density. Thus the stability of relativistic as well as non-relativistic compact stars depends on the adiabatic index. Now, for relativistic anisotropic structure, the adiabatic index \(\Gamma \) is described as the ratio of two specific heats and is defined as [96]

$$\begin{aligned} \Gamma = \frac{\rho +p}{p}\frac{dp}{d\rho }, \end{aligned}$$
(31)

where \(\frac{dp}{d\rho }\) is the velocity of sound in units of the velocity of light. For a stellar structure to be stable, Bondi [97] suggested for the Newtonian sphere the stability condition to be \(\Gamma > {4 \over 3}\) and for neutral equilibrium the stability condition becomes \(\Gamma = {4 \over 3}\). Heintzmann and Hillebrandth [98] included the anisotropy for a stellar sphere to be in equilibrium and obtained the adiabatic index \(\Gamma \) must be \(>\frac{4}{3}\). Later some corrections were done by Chan et al. [96] for the case of relativistic fluid and it is expressed as

$$\begin{aligned} \Gamma < \frac{4}{3} \left[ \frac{4}{3} \frac{p_{t0} - p_{r0}}{r |p'_{r0}|} + \frac{8 \pi }{3} \frac{r \rho _0 p_{r0}}{|p'_{r0}|} \right] _{max}, \end{aligned}$$
(32)
Fig. 11
figure 11

Variation of the difference of sound speeds with radial coordinate r

Full size image

where \(\rho _0\), \(p_{r0}\) and \(p_{t0}\) are the initial density, radial and tangential pressures respectively in unperturbed equilibrium. Here the first term on the right-hand side of Eq. (32) corresponds to anisotropy and the second term represents the relativistic corrections to the Newtonian perfect fluid. Now critical value for the adiabatic index was introduced to tackle the instability occuring from the correction term. This critical value depends on the compactness factor (\(u(r) \equiv \frac{m(r)}{r}\)) and mathematically it is expressed as \(\Gamma \ge \Gamma _{crit}\) where \(\Gamma _{crit} = \frac{4}{3} + \frac{19 u}{21}\). We have checked the stability under the adiabatic index for our model graphically in Fig. 12. Since due to the presence of anisotropy, the growth of instability might be slowed down which eventually leads to a gravitational collapse in the radial direction [99], so we have plotted only \(\Gamma _r\) and it shows that values of \(\Gamma _r\) are greater than \({4 \over 3}\) throughout the stellar configuration.

Fig. 12
figure 12

Variation of the adiabatic index with radial coordinate r

Full size image

6 Mass–radius for the model

6.1 Equation of state

One of the key aspects of studying compact stars is its equation of state (EoS). EoS primarily connects the radial pressure of the model to its density and it follows \(p \equiv p(\rho )\). The pressure-density relationship for the model is shown in Fig. 13.

Fig. 13
figure 13

Variation of the radial pressure with the density

Full size image

In the context of the pulsar 4U1608-52, the best fit for the EoS of our model becomes \(p_r = 0.050886 \rho - 17.318\) as shown in Fig. 14.

Fig. 14
figure 14

Linear fit (black dashed line) are shown for the pulsar 4U1608-52

Full size image

6.2 Compactness and surface redshifts

Fig. 15
figure 15

Variation of mass function with radial coordinate r is increasing in nature

Full size image

Quite naturally the stability of any stellar model depends on its mass and radius (Fig. 15). Thus the stellar stability can be checked through a dimensionless ratio (mass to radius), known as the compactness factor. Mathematically the ratio \(\frac{2 m}{r}\) should be less than \(\frac{8}{9}\) to be a stable compact structure. This limit, known as Buchdhal limit [100], was suggested for a spherically symmetric isotropic fluid sphere. However the same can apply to the anisotropic sphere as suggested by several works on compact stars. Additionally, the gravitational interior redshift is given as

$$\begin{aligned} z=\left( 1-\frac{2M}{r} \right) ^{-1/2}-1. \end{aligned}$$
(33)

From Eq. (33) it is evident that interior redshift increases with the increase of \({M \over r}\). Since the compactness of a star satisfies Buchdahl’s condition there should exist an upper bound for gravitational redshifts. For any self-gravitating compact object, the surface redshifts \(z_b\) should be less than universal bounds when different energy conditions hold [101]. Specifically for anisotropic fluid, the upper limit for the surface redshifts become 5.211 and 3.842 in the presence of DEC and SEC respectively [102].

6.3 Mass–radius relationship

The dynamic stability of any viable model can be examined by observing its mass to radius relation. The mass of any compact object opposing the gravitational collapse must be within the allowable mass for any stable structure [4]. For the present model, we have chosen the surface density as \(\rho (r =b) = 4 \times 10^{14}\) gm/cc to obtain the mass–radius relationship in Fig. 16. In Fig. 16 we have plotted some known compact stars in the mass–radius plot which are best fit for our model namely SAX J1748.9-2021 (mass = \(1.81^{+0.25}_{-0.37} M_\odot \) and radius = \(11.7 \pm 1.7\) km), 4U1820-30 (mass = \(1.46 \pm 0.21 M_\odot \) and radius = \(11.1 \pm 1.8\) km), Vela X-1 (mass = \(1.77 \pm 0.08 M_\odot \) and radius = 10.654 km), Her X - 1 (mass = \(0.85 \pm 0.15 M_\odot \) and radius = 8.1 km) and GW\(170817-1\) (mass = \(1.45 M_\odot \) and radius = 11.9 km).

Fig. 16
figure 16

Mass–radius relationship for the model

Full size image

   For our model, it can be seen that our model allows maximum mass to be \(3.841 M_\odot \) with the radius 12.4 km. This model slightly exceeds the maximum allowable mass for a neutron star, \(\approx 3.2 M_\odot \) as suggested by Rhodes and Ruffini [103] implying a more compact neutron star (Fig. 17).

6.4 Zeldovich–Harrison–Novikov condition

Any compact structure is considered to be stable if the mass of the configuration increases with the increase of central density. Mathematically any stable structure satisfies \(\frac{dM(\rho (0))}{\rho (0)} > 0\). This stability criterion is known as Zeldovich–Harrison–Novikov Condition [104, 105]. Although this condition is necessary one not a sufficient condition.

Fig. 17
figure 17

Central density–radius relationship for the model

Full size image

   For our model, it is to be found,

$$\begin{aligned} M(\rho (0))= & {} \frac{1}{2} \frac{\rho (0)b^3 (2 + \rho (0) b^2)}{(1 + \rho (0) b^2)^2}, \nonumber \\ \frac{d M(\rho (0))}{d \rho (0)}= & {} \frac{b^3}{(1 + \rho (0) b^2)^3}. \end{aligned}$$
(34)

We have plotted mass vs central density plot in Fig. 18 and it is seen that mass is increasing with the increase of its central density. Thus our model satisfies the Zeldovich–Harrison–Novikov stability criteria. Additionally, we have also plotted the radius vs central density plot in Fig. 17.

Fig. 18
figure 18

Central density-mass relationship for the model

Full size image

7 Slow rotating effect

Unlike Newtonian theory, the inertial frames within a general-relativistic fluid do not remain stationary relative to distant stars [106]. Instead, the local inertial frames are carried along by the rotation of the fluid. This phenomenon, rooted in general relativity, was initially explored by Thirring in 1918 [107] and later examined in greater depth by Brill and Cohen in 1966 [108], shedding light on its relationship with Mach’s principle. Accurately determining the rate of rotation becomes crucial for establishing equilibrium among gravitational, pressure, and centrifugal forces. We now investigate the effects of a slow rotation on these configurations.

7.1 Moment of inertia and time period

Recent studies on the masses and radii of X-ray radio pulsars are flourishing aspects of observational astrophysics and obtaining moment of inertia plays a vital role in the modelling of radio pulsars. Using Nuclear Spectroscopic Telescope Array mission (NuSTAR) data, investigations on the X-ray pulsars 1E 1145.1-6141 [109], IGR J19294+1816 [110] have been studied in the recent past. Moment of inertia is more sensitive to the EoS compared to other physical properties. With the change of soft EoS to the stiff one, theoretically the maximum mass of the star increases by a factor of two, however, the maximum moment of inertia increases by a factor of seven [111]. Thus it is relevant to study the moment of inertia of a static system considering it as a slow rotating one. Now let us study the stability of our model considering a slow rotating system. One of the important features is to observe the moment of inertia as it contains the square of the radius. This means for a given mass, the moment of inertia of a star is sensitive towards the stiffness of the equation of state. It is examined by Bejger–Haensel [112]’s famous formula that transforms a static system into a rotating one. The formula is given by

$$\begin{aligned} I = \frac{2}{5} (1 + x) M b^2, \end{aligned}$$
(35)

where the parameter x is given by \(x = (M/M_\odot )\)(km/b).

Fig. 19
figure 19

Moment of inertia with respect to mass for the model

Full size image

   For the present work, taking the surface density \(\rho (r =b) = 4 \times 10^{14}\) gm/cc, we have plotted the moment of inertia vs mass plot in the Fig. 19. The maximum mass here is found to be \(3.815 M_\odot \) with the corresponding moment of inertia of 515.5  km\(^3\). The decline of the maximum mass of the model is about 0.68%. Since the difference of mass between non-rotating and slow-rotating models at this rotation rate is of the order of about 1% or less, it can be concluded the softening of the equation of state without any strong high density due to hyperonization or phase transition to an exotic state [113].

For any non-rotating structure, time period can be given as

$$\begin{aligned} \tau \approx 0.82 \sqrt{\frac{M_\odot }{M}} \left( \frac{b}{10~km}\right) ^{\frac{3}{2}} ~ms. \end{aligned}$$
(36)

Now the variation of time period for the model with its mass is given in Fig. 20 and the time period for the maximum allowable mass for our model is 1.87 ms.

Fig. 20
figure 20

Profile for time period for the model

Full size image

7.2 Moment of inertia vs central density relationship

Fig. 21
figure 21

Nature of moment of inertia against the central density

Full size image

Now we observe the moment of inertia in terms of the static mass and the square of the static radius as a function of the central density. Figure 21 depicts the nature of the moment of inertia against the central density. It is seen that with the increase of central density, the moment of inertia decreases. Studies have shown that for higher central densities, a moment of inertia for static structure is almost similar to that of rotating one [114, 115]. For our model, the moment of inertia decreases as some of the studies have suggested [114].

7.3 Angular momentum-central density relationship

Let us now observe the nature of the angular momentum of the model with the respect to central density. Figure 22 depicts that with the increase of central density, the angular momentum also increases. However, for our model, the angular momentum is seen to be fixed around 0.28 kg m\(^2\)/s .

Fig. 22
figure 22

Variation of angular momentum with the central density

Full size image

7.4 Angular momentum–radius relationship

Another aspect of a slow-rotating structure is its nature of angular momentum with the radius of the structure. We have studied in Fig. 23, the profile of the angular momentum considering the structure as a rotating one. Here angular momentum is seen to increase with the increase of the radius of the configuration.

Fig. 23
figure 23

Variation of angular momentum with the radius

Full size image

   Additionally, Fig. 24 depicts the best fit for the angular momentum-radius curve and the best fit is found to be \(exp[0.328 b +3.186]\).

Fig. 24
figure 24

Best fit for Fig. 23

Full size image

   Studying all the aforementioned profiles considering the slowly rotating structure for the model, one can write the spacetime for Kerr Metric in the form [116],

$$\begin{aligned} ds^2= & {} -X_{0}^2(r)dt^2 + Y_{0}^2(r)dr^2 + r^2(d\theta ^2 + \sin ^2\theta d\phi ^2) \nonumber \\{} & {} + \frac{4J}{r} \sin ^2 \theta d\phi dt, \end{aligned}$$
(37)

where J can be approximated to be \(exp[0.328 r +3.186]\).

This angular momentum causes the dragging of inertial frames and the metric given in Eq. (37) describes the gravitational field of the slowly rotating equilibrium compact objects.

8 Compatibility of the model with some known stars

Let us investigate some important physical features and thus the compatibility of the model with some known compact objects. In Table 1, we have estimated the masses of the known objects and thus compared the obtained radius with the known one. Also, compactness and surface redshifts are computed to test the stability of our model. For tabular calculation, additionally, we have considered an arbitrary massive neutron star having mass \(2.6~M_\odot \) and radius 15.5 km [117].

Table 1 Mass and radius of some known compact objects
Full size table

In Table 1 it can be seen that for massive stars with radii (\(>12\) km), the compactness factor fails to fall under the prescribed limit. After checking the compatibility of masses and radii of some of the known pulsars, we now check some of the physical features of the model compatible with these pulsars. Some of the thermodynamical properties, namely density, sound speeds, and TEC: \(\rho - p_r - 2p_t\) are calculated in Table 2, both at the centre and at the surface. In Table 2, \(|_0\) and \(|_b\) denote the value of these properties at the centre and the surface respectively.

Table 2 Thermodynamic variables of the model
Full size table

9 Concluding remarks

Our present work focuses on a simple anisotropic solution that fulfils all the primary criteria of a compact stellar structure. We start off by selecting a specific form of metric potential \(Y_0^2(r)\). Imposing the additional condition on \(g_{tt}\) we obtain the specific form of anisotropy which leads us to an exact solution. This solution is then matched with the Schwarzschild exterior spacetime at the boundary to get the expressions for the model parameters. We have examined the obtained solutions for their physical regularity and stability under some important key features. For graphical illustration, we have considered the pulsar 4U1608-52 with its current estimated data (mass \(=1.57^{+0.30}_{-0.29} ~M\odot \) and radius \(=9.8 \pm 1.8~km\) [1]). Some of the observations regarding our results are as follows:

  • Regularity of the metric and matter variables: We have studied the metrices and the physical matter variables \(\rho ,~p_r,~p_t\) graphically in Figs. 2, 3, 4 and 5 and the metric potentials and the matter variables are found to be well-behaved and well-defined for the model. Also, the anisotropy for the model increases throughout the structure as shown in Fig. 6 which forms a base for our model to be a stable configuration.

  • Negative gradients of matter variables: The derivatives of radial pressure and density are found to be negative throughout the stellar structure. However, the transverse pressure gradient is seen to be non-negative in the configuration. Although right before reaching the surface (at 8.2 km), the transverse pressure gradient becomes negative for the rest of the configuration as seen in Fig. 7.

  • Fulfillment of energy conditions: For any physically acceptable model, their density and pressures undergo some bounds, known as energy conditions. Several different energy conditions viz. DEC, WEC, NEC, SEC, and TEC are studied for the model analytically. Graphically, we have checked DEC, SEC and TEC in Fig. 8 and each energy condition is satisfied inside the stellar structure. Additionally, we have tested TEC for various known compact stars (both low mass and high mass) in tabular form in Table 2.

  • Stability under TOV equation: Effects of different forces on the model for its stability are shown graphically in Fig. 9, and it can be seen that the dominant gravitational force is counterbalanced by the amalgamation of hydrostatic and anisotropic forces.

  • Causality condition: The model satisfies the causality condition (see Fig. 10) as the variation of the radial sound speed is less than 1. To check the potentially (un)stable region for any anisotropic model, the cracking method is undoubtedly one of the important conditions for stability. However, the model is shown to be in a potentially stable region \((-1,0)\) as seen in Fig. 11 as suggested by Abreu et al. [95].

  • Stability under adiabatic index: The nature of the adiabatic index for the model is plotted in Fig. 12 and it shows that the adiabatic index in radial direction becomes greater than both \(\frac{4}{3}\) and also the critical value of the adiabatic index from approximately 4.2 km. From the centre to the radius of 4.2 km, the model does not fall under the limit.

  • Best fit for the EoS: Equation of state of any stellar structure is an important aspect in checking the properties of the configuration. The relationship between density and pressure is depicted in Fig. 13, which shows the linear relationship. The linear relationship between pressure and density is shown in Fig. 14 and the best fit is expressed as \(p_r = 0.050886 \rho -17.318 \).

  • Compactness and surface redshifts: We have investigated the mass function for the model graphically in Fig. 15, and it can be seen it is an increasing function of r, and it attains maximum value at the surface. Compactness and surface redshifts are calculated in tabular form for some known compact stars in Table 1. One interesting feature of the model can be observed from Table 1 is that for massive stars with radii (\(> 12\) km), the compactness factor fails to be under 0.44 as suggested by Buchdahl [100].

    Additionally, the surface redshifts for several different stellar objects are seen to follow the upper bound ( \(<~2\)) in Table 1.

  • Discussions about central density: We have checked Harrison Zeldovich Novikov stability criteria by observing the nature of the mass and central density profile, and it is found that the mass of the model increases with the increase of central density (see Fig. 18). Additionally, the relationship between the angular momentum and central density has also been observed in Fig. 22 and the model is seen to fulfill increasing angular momentum with the increase of central density. However, the value of angular momentum later becomes fixed around 0.28 kg m\(^2\)/s.

  • Moment of inertia and time period: Considering the surface density \(\rho (r =b)= 4 \times 10^{14}~gm/cc\), we have studied the mass–radius relation for the model. The graph is plotted in Fig. 16, and it can be seen that the model assumes the maximum mass to be \(3.84 M_\odot \) corresponding to the radius 12.4 km. Additionally, we have plotted some known compact objects in Fig. 16 for comparison and here the pulsars SAX J 1748.9-2021 and 4U1820-30 are seen to be best fitted with the mass–radius plot of our model.

    One of the highlights of the present work is the observation of the structure as a rotating one. Using the Bejger–Haensel formula we have studied the nature of the moment of inertia of the model and hence obtain a graphical moment of inertia to mass relationship in Fig. 19. Here the maximum allowable mass is 0.68% less than that of our obtained maximum mass indicating the softening of the equation of state of the model. Furthermore, the time period of rotation considering the slow rotating configuration is obtained to be 1.87 ms for our model as seen in Fig. 20.

  • Discussions around angular momentum: We have studied the profile of angular momentum for the model with respect to central density (Fig. 22). Here the angular momentum is seen to increase with the increase of central density. However, for our model, the angular momentum is seen to be fixed around 0.28 kg m\(^2\)/s. We have also investigated the angular momentum against the radius. Figure 23 depicts the nature of angular momentum with radius and it is seen to be increasing with the increasing radius. Additionally, Fig. 24 depicts the best fit for the angular momentum–radius curve and the best fit is found to be \(exp[0.328 b +3.186]\) and this angular momentum causes the dragging of the inertial frames in the system. The Kerr metric considering the slowly rotating structure is given in Eq. (37).

Another captivating fact regarding our model can be inferred by comparing the work of Pandya et al. [118]. Applying the bounds on the model parameter one can get the following,

$$\begin{aligned} p|_{r =0}> 0&\implies \frac{6 C}{D}> \rho _0, \nonumber \\ Zeldovich ~Condition&\implies \frac{3 C}{2 D} \le \rho _0, \nonumber \\ SEC|_0> 0&\implies \frac{4 C}{D} \le \rho _0, \nonumber \\ DEC|_0 > 0&\implies \frac{3 C}{2 D}< \rho _0, \nonumber \\ Herrera ~Cracking&\implies \frac{\sqrt{19} C}{18 D} + \frac{c}{18 D} < \rho _0, \nonumber \end{aligned}$$

where \(\rho _0 = 6 a\) being the central density. Compiling all the feasible conditions given above, the accepted bound for our model turns out to be \(\frac{\sqrt{19} C}{18 D} + \frac{c}{18 D}< \rho _0 < \frac{6 C}{D} \). Additionally, all the stability analyses vouch for the acceptability of the model. It can be seen that the model depicts a stable model with \(n =2\). Since Pandya et al. [118] have studied the upper limit for the stable model to be \(n \le \frac{4}{\sqrt{3}}\), the present work can be considered as an extension of this paper with an extra feature that that the obtained angular momentum causes the dragging of inertial frames of the slowly rotating equilibrium compact objects.

Hence, keeping in mind all of the above discussions it can be concluded that a new class of model can be described by the metric potentials. The fulfilment of several important physical features and stability analysis support the model to be a physically acceptable one.