Study of compact objects: a new analytical stellar model

Abstract

In this paper, we obtain analytical solutions of Einstein field equations for a spherically symmetric anisotropic matter distributions. For this purpose physically meaningful metric potential corresponds to $g_{rr}$ and a particular choice of the anisotropy has been utilized to obtain the solutions in closed form. This class of solution has been used to characterized observed pulsars from different aspects. Smooth matching of interior spacetime metric with the exterior Schwarzschild metric and in addition with the condition of vanishing radial pressure across the boundary leads us to determine the model parameters. Pulsar $4U1820-30$ with its current estimated data for mass and radius (Mass $=1.58 M_\odot$ and radius $=9.1$ km) has been allowed for testing the physical acceptability of our developed model. We have graphically analyzed the gross physical features of the observed pulsar. The stability of the model is also discussed under the conditions of causality, adiabatic index and generalized Tolman–Oppenheimer–Volkov (TOV) equation under the forces acting on the system. Few more pulsars with their have been considered, to show that this model is compatible with observational data, and all the requirements of a realistic star are highlighted. Mass-radius (M–R) relationship have been generated for our model. The impact of anisotropy on the gross physical features of stars have been explored with the graphical presentation.

1 Introduction

Finding out a non-singular, regular and well-behaved solution for Einstein’s equations that would be used to understand the properties of highly dense relativistic stars, is an active field of research. The solutions describing relativistic stars can be broadly classified as isotropic and anisotropic. In isotropic solutions the radial and transverse pressures are considered to be same but in solutions with the considerations of local anisotropy, the radial and transverse pressures are taken unequal. The origin and nature of local anisotropy in relativistic stars were thoroughly reviewed by Herrera and Santos [1]. In [1] a number of reasons were pointed out for the origin of anisotropy in compact stars. Let us take a look into some reasons relevant to the present study. Existence as a mixture of two or more isotropic fluids within the compact star might lead to anisotropy development within the star. Secondly, slow rotation of the star may give rise to local anisotropy due to the effect of centrifugal force. Thirdly, highly dense matter content within the compact star tend to be viscous. The viscous matter might generate local anisotropy. Apart from this, in [2], Herrera observed three principal factors responsible for the development of pressure anisotropy inside a spherically symmetric star. They are:

• the effect of Weyl tensor

• the shear

• the “dissipative” effects which reveals itself through the heat flux.

It is pointed out in [2] that even a spherically symmetric system which is initially isotropic, may develop anisotropy during its evolution due to these physical factors. It is highly probable that this anisotropy would not vanish in the final equilibrium state of the system. In fact, there is no known physical process inside a compact star that can reverse the anisotropy in pressure developed during its dynamical evolution. Thus, principal pressures within the compact star should, in general, be unequal. Jeans [3] studied anisotropy in the distribution of stars in a galaxy having spherical symmetry. However, Lemaitre [4] was the first to mention local anisotropy in a general relativistic system. There are good number of publications investigating the anisotropic solutions for relativistic stars since the seminal endeavour by Bowers and Liang [5]. After a year, Heintzmann and Hillebrandt [6] reported that for “arbitrarily large anisotropy” the mass of a neutron star has no upper limit while obeying the stability constraints under small perturbation limit. Barraco et al. [7] also found that the Buchdahl limit for isotropic fluid spheres, is violated for anisotropic fluid distribution. Mak et al. [8] proposed a model of anisotropic star generalizing Einstein’s field equations to D $(D \ge 4)$ dimensions. In another paper [9], they obtained exact solution for anisotropic star assuming some suitable forms of anisotropy. They also found out exact solution for charged anisotropic strange star considering conformal symmetry in yet another paper [10]. They calculated the radius and mass of the modelled strange quark star to be 9.46 km and $2.86 M_{\odot }.$ The mass of the quark matter reported to be $1.772 M_{\odot }.$ Gleiser and Dev [11] gave a new exact solution for anisotropic star and investigated the stability of the star using Chandrasekhar’s method of perturbation. Many researchers modelled quark star or strange star taking anisotropic pressure [12,13,14,15,16,17,18,19,20]. There are instances of other choices of equations of state. Recently, Kumar and Bharti [21] reviewed large number of static spherically symmetric anisotropic solutions of the Einstein- Maxwell system and classified the solutions. Interested readers may refer to this excellent review to get updated on various categories of anisotropic solutions in literature. There are a number of models of compact star with the consideration of local anisotropy that exploits well-known Karmakar’s condition [22, 23]. There are anisotropic solutions where conformal symmetry is assumed within the star [15, 24, 25]. Thirukkanesh et al. [26] explored the possibility of anisotropic superdense star with Vaidya Tikekar metric for some chosen forms of anisotropy function. Assuming Newton’s constant to be a function of radial coordinate, Panotopoulos et al. [27] obtained anisotropic solution for the interior of a relativistic star. Bhar et al. [28] examined several physical features of anisotropic solution of static spherically symmetric relativistic stars under general theory of relativity. Azmat and Zubair [29] considered Drugapal V solution for charged fluid sphere and extended it for anisotropic spherical distribution under the consideration of gravitational decoupling through Minimum Geometric Deformation. Das et al. [30] in their model of anisotropic compact star found out the anisotropy function which is physically possible. They also calculated the tidal love number of the star. In a similar approach, Parida et al. [31] explored the impact of tidal love number, $k_2,$ on the equation of state parameter of the matter content of the anisotropic star so as to constrain the mass–radius relationship for the star. Bhar [32] studied interior solutions of anisotropic star under f(Q) gravity. The solutions conform to all the conditions of physical viability. Anisotropic solutions are studied in other modified theories of gravity [33,34,35]. Rincón et al. [36] studied the role of complexity factor on the physical features of anisotropic stars considering a generalized Chaplygin equation of state. It is apparent from the foregoing review of literature that physical possibilities of anisotropic stars are extensively explored by the researchers. However, the effect of anisotropy on the physical features of the star are yet to be investigated completely. In the present paper, we have explored the effect of anisotropy parameter on all the physically relevant quantities of the star in order to understand what role it actually plays on the stellar structure. Solving Einstein’s equations for anisotropic fluid, we calculate the parameter values for pulsar $4U1820-30.$ With this parameter values, we predict possible equation of state for the pulsar. This approach may be important for opening up prospects of further observation of these astrophysical objects.

The plan of the paper is as follows. In the next Sect. 2 we present Einstein Field Equations and the Energy-Momentum tensor. In Sect. 3 we obtained exact analytical solution of the system of equations and generating functions have been discussed. In Sect. 4 unknown parameters are calculated with the help of the matching conditions. In Sect. 5 qualitative aspects of the model are analysed. In next section (Sect. 6) the model is applied for the observed compact object $4U 1820 - 30.$ In Sect. 7 we extensively analysed the stability features of the model. The paper ends with a discussion in Sect. 8 of the salient results of the present study.

2 Einstein field equations

In the usual Schwarzschild coordinates the geometry inside the spherically symmetric body can be described by the following metric:

$$\begin{aligned} ds_{-}^2 = -A_{0}^2(r)dt^2 + B_{0}^2(r)dr^2+ r^2(d\theta ^2 + \sin ^2\theta d\phi ^2),\nonumber \\ \end{aligned}$$

(1)

where all the metric potentials depend only on the radial coordinate. We assume the star to be spherically symmetric and constituted of anisotropic matter. The energy–momentum tensor corresponding to this matter distribution is

$$\begin{aligned} T_{\alpha \beta } = (\rho + p_t)u_{\alpha } {u_\beta } + p_{t} g_{\alpha \beta }+ (p_r - p_t)\chi _{\alpha } \chi _{\beta }, \end{aligned}$$

(2)

where $\rho$ represents the energy-density, $p_r$ and $p_t,$ respectively denote fluid pressures along the radial and transverse directions, $u^\alpha$ is the 4-velocity of the fluid and $\chi ^\alpha$ is a unit space-like 4-vector along the radial direction so that $u^\alpha u_\alpha = -1,$ $\chi _\alpha \chi _\beta =-1$ and $u^\alpha \chi _\beta =0 .$

The Einstein field equations governing the evolution of the system is then obtained as (we set $G = c = 1$)

$$\begin{aligned} 8\pi \rho= & {} \left[ \frac{1}{r^2}-\frac{1}{r^2 B_0^2}+\frac{2B_0'}{r B_0^3}\right] , \end{aligned}$$

(3)

$$\begin{aligned} 8\pi p_r= & {} \left[ -\frac{1}{r^2}+\frac{1}{B_0^2 r^2}+\frac{2A_0'}{r A_0B_0^2}\right] , \end{aligned}$$

(4)

$$\begin{aligned} 8\pi p_t= & {} \left[ \frac{A_0''}{A_0B_0^2} + \frac{A_0'}{rA_0B_0^2} - \frac{B_0'}{r B_0^3} - \frac{A_0'B_0'}{A_0 B_0^3}\right] . \end{aligned}$$

(5)

In Eqs. (3)–(5), a ‘prime’ denotes differentiation with respect to r.

Making use of Eqs. (4) and (5), we define the anisotropic parameter of the stellar system as

$$\begin{aligned} \varDelta (r)= & {} 8\pi (p_t-p_r) \nonumber \\= & {} \left[ \frac{A_0''}{A_0B_0^2} - \frac{A_0'}{r A_0B_0^2} - \frac{B_0'}{r B_0^3} \frac{A_0'B_0'}{A_0B_0^3} - \frac{1}{r^2B_0^2} + \frac{1}{r^2}\right] .\nonumber \\ \end{aligned}$$

(6)

The anisotropic force is defined as $\frac{2 \varDelta }{r}$ will be repulsive or attractive in nature depending upon whether $p_t>p_r$ or $p_t<p_r.$ The mass enclosed within a radius r of the sphere is defined as

$$\begin{aligned} m(r)= \frac{1}{2}\int _0^r\omega ^2 \rho (\omega )d\omega . \end{aligned}$$

(7)

3 A physically acceptable model

A physically reasonable model of a star demands the metric potentials to be regular at the center $(r = 0).$ Keeping that requirement in mind, we choose the metric potential $g_{rr}$ in the following form

$$\begin{aligned} B_0^2 (r) = \frac{1}{a r^4-b r^2+1}, \end{aligned}$$

(8)

where a and b are the curvature constants having a dimension of $L^{-4}$ and $L^{-2}$ respectively and it will be determined from the junction conditions at the surface of the star. With this choice of $B_0(r)$ Eq. (6) then reduces to

$$\begin{aligned} \varDelta (r) =\frac{a r^3 A_0(r){+}(a r^4{-}1)A0'(r){+}r (1{-}b r^2{+} a r^4) A_0''(r)}{r A_0(r)}. \end{aligned}$$

(9)

On rearranging Eq. (9) we get

$$\begin{aligned} \frac{A_0''(r)}{A_0(r)}+\frac{(a r^4-1)A_0'(r)}{r(1-b r^2+ a r^4)A_0(r)}= \frac{\varDelta (r) -a r^2}{(1-b r^2+ a r^4)}.\nonumber \\ \end{aligned}$$

(10)

Now the above Eq. (8) can be solved for $A_0(r)$ if $\varDelta (r)$ is specified in particular form. One way to make the equation easily integrable is to assume a suitable form of anisotropy as

$$\begin{aligned} \varDelta (r)=a r^2. \end{aligned}$$

(11)

The above choice for anisotropy is physically reasonable, as at the center $(r=0)$ anisotropy vanishes as expected. This feature will be explained graphically in Sect. 6. Herrera and Santos [1] showed that anisotropy of this form may arise within compact stars due to slow rotation. Also, this choice provides a solution for Eq. (10) in closed form. Substituting Eq. (11) in Eq. (8), we obtain,

$$\begin{aligned} A''_0(r)+\frac{(a r^4-1)}{r(1-b r^2+ a r^4)} A'_0(r)=0. \end{aligned}$$

(12)

We obtain a simple solution of the Eq. (12)

$$\begin{aligned} A_0(r)=\frac{C_1 \log \left( 2 \sqrt{a} \sqrt{a r^4-b r^2+1}+2 a r^2-b\right) }{2 \sqrt{a}}+C_2, \end{aligned}$$

(13)

where $C_1$ and $C_2$ are integration constants that can be obtained from the boundary conditions. With the choices of the metric potentials the matter density, radial pressure, transverse pressure and mass are obtained as

$$\begin{aligned} 8\pi \rho =&3 b - 5 a r^2, \end{aligned}$$

(14)

$$\begin{aligned} 8\pi p_r =&\frac{4 \sqrt{a} C_1 \sqrt{a r^4-b r^2+1}}{C_1 \log \left( 2 \sqrt{a} \sqrt{a r^4-b r^2+1}+2 a r^2-b\right) +2 \sqrt{a} C_2} \nonumber \\&+ a r^2-b, \end{aligned}$$

(15)

$$\begin{aligned} 8\pi p_t =&8\pi p_r+ \varDelta \nonumber \\ =&\frac{4 \sqrt{a} C_1 \sqrt{a r^4-b r^2+1}}{C_1 \log \left( 2 \sqrt{a} \sqrt{a r^4-b r^2+1}+2 a r^2-b\right) +2 \sqrt{a} C_2}\nonumber \\&+2 a r^2-b, \end{aligned}$$

(16)

$$\begin{aligned} m(r) =&\frac{1}{2} r^3 \left( b-a r^2\right) . \end{aligned}$$

(17)

It is possible to show that the solution obtained in this model can be expressed in terms of two generating functions. For this purpose we followed the work by Herrera et al. [37]. With the substitution of $A_0^2(r) = e^{\int (2 z(r) - \frac{2}{r} ) \, dr}$ in the Einstein field Equations, they found out the expression of $g_{rr}$ as

$$\begin{aligned} g_{rr} = \frac{z^2(r) e^{\int \left( \frac{4}{r^2z(r)}+2 z(r) \right) dr}}{r^2\left[ F - 2 \int \frac{z(r)\left( 1 + \varDelta (r) r^2 \right) e^{\int \left( \frac{4}{r^2 z(r)} + 2 z(r) \right) dr}}{r^8} dr \right] }, \end{aligned}$$

where F is an arbitrary integrating constant and other physical quantities in terms of the functions z(r) and $\varDelta (r).$ They pointed out that these two functions as the generating functions for complete description of any static solution of an anisotropic fluid distribution. For the present model, we have

$$\begin{aligned} z(r) = \frac{\nu '(r)}{2} + \frac{1}{r} \end{aligned}$$

(18)

or equivalently,

$$\begin{aligned} z(r) =\frac{1}{r}+\frac{A'_0(r)}{A_0(r)} = \frac{2 \sqrt{a} C_1 r}{\sqrt{a r^4-b r^2+1} \left( C_1 \log \left( 2 \sqrt{a} \sqrt{a r^4-b r^2+1}+2 a r^2-b\right) +2 \sqrt{a} C_2\right) }, \end{aligned}$$

(19)

and

$$\begin{aligned} \varDelta (r)= \left( \frac{b R^3-2 M}{R^5} \right) r^2. \end{aligned}$$

(20)

When compared to Eq. (11), we immediately get the value of the parameter $a =(bR^3 - 2M)/R^5.$ Note that both generating functions z and $\varDelta (r)$ are always positive. Here z is decreasing in nature where as $\varDelta (r)$ is always increasing with radial coordinate.

The physical parameters can also be expressed in terms of generating functions.

$$\begin{aligned} 4 \pi p_r= & {} \frac{z(r-2 m)+m/r-1}{r^2},\end{aligned}$$

(21)

$$\begin{aligned} 4 \pi p_t= & {} (1-2m/r)\left( z'+z^2-\frac{z}{r}+\frac{1}{r^2}\right) \nonumber \\{} & {} +z\left( \frac{m}{r^2}-\frac{m'}{r}\right) ,\end{aligned}$$

(22)

$$\begin{aligned} 4 \pi \rho= & {} \frac{m'}{r^2} , \end{aligned}$$

(23)

where the mass function m(r) is related as

$$\begin{aligned} e^{-\lambda } =1- \frac{2m(r)}{r}. \end{aligned}$$

(24)

4 Matching conditions at the surface of the star

Since the star static, and hence non-radiating, the exterior of the star should be empty. Thus, the exterior space-time is described by the Schwarzschild metric.

$$\begin{aligned} ds^{2}= & {} -\left( 1-\frac{2m}{r}\right) dt^{2}+\left( 1-\frac{2m}{r}\right) ^{-1}dr^{2}\nonumber \\{} & {} +r^{2}\left( d\theta ^{2}+\sin ^{2}\theta d\phi ^{2} \right) , \end{aligned}$$

(25)

where $r>2m,$ m being the total mass of the stellar object. The matching conditions that must be considered are:

$$\begin{aligned}{} & {} \left( g_{rr}\right) _{interior} = \left( g_{rr}\right) _{exterior}, \end{aligned}$$

(26)

$$\begin{aligned}{} & {} \left( g_{tt}\right) _{interior} = \left( g_{tt}\right) _{exterior}, \end{aligned}$$

(27)

$$\begin{aligned}{} & {} p_{r}(r = R) = 0. \end{aligned}$$

(28)

The continuity of the metric functions across the boundary $r=R$ yields

$$\begin{aligned} A^2_0(R)= & {} \left( 1-\frac{2 m}{R}\right) , \end{aligned}$$

(29)

$$\begin{aligned} B^2_0(R)= & {} \left( 1-\frac{2 m}{R}\right) ^{-1}. \end{aligned}$$

(30)

The boundary conditions (26), (27), (28) determine the constants which are

$$\begin{aligned}{} & {} a= \frac{b R^3-2 M}{R^5}, \end{aligned}$$

(31)

$$\begin{aligned}{} & {} C_1=\frac{M}{R^3}. \end{aligned}$$

(32)

$$\begin{aligned}{} & {} C_2=\frac{M \sqrt{\frac{b R^3-2 M}{R}} \log \left( 2 \sqrt{1-\frac{2 M}{R}} \sqrt{\frac{b R^3-2 M}{R^5}}+b-\frac{4 M}{R^3}\right) -2 \sqrt{1-\frac{2 M}{R}} \left( b R^3-2 M\right) }{4 M-2 b R^3}. \end{aligned}$$

(33)

Note from Eq. (31), that the value of a obtained the boundary conditions is in conformity to the value obtained from the generating function formalism.

5 Qualitative analysis of the physical features of the model

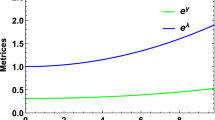
• 1. Regularity of the metric potentials: The gravitational potentials in this model must be finite at the center of the star for the solution to be well-behaved. In our model, we have chosen a form for $B_{0}(r)$ which is regular at the center of the star, i.e., $B^2_0(0)=1.$ However, we have derived the metric potential $A_{0}(r).$ At $r = 0,$ $A_{0}(r)$ is also finite $A^2_0(0)=(\frac{C_1 \log \left( 2 \sqrt{a}-b\right) }{2 \sqrt{a}}+C_2)^2=constant.$ Also, one can easily check that $(A^2_0(r))'_{r=0}=(B^2_0(r))'_{r=0}=0.$ It is apparent from Eqs. (10) and (13) that metric potentials are finite and positive inside the star. These imply that the metric is regular at the center and well-behaved throughout the stellar interior.

• 2. Nature of pressure and density at the center: The central density, central radial pressure and central tangential pressure required to be finite and non-negative. In the present model, the values at the center are:

  $$\begin{aligned} \rho (0)= & {} 3 b, \\ p_r(0)= & {} \frac{4 \sqrt{a} \text {C1}}{\text {C1} \log \left( 2 \sqrt{a}-b\right) +2 \sqrt{a} \text {C2}}-b, \\ p_t(0)= & {} \frac{4 \sqrt{a} \text {C1}}{\text {C1} \log \left( 2 \sqrt{a}-b\right) +2 \sqrt{a} \text {C2}}-b. \end{aligned}$$

  Note that the density is always positive as b is a positive quantity. The pressure in both directions are finite and constant. The radial pressure and tangential pressure at the centre are equal which readily indicates the vanishing of pressure anisotropy at the center. The radial and tangential pressure at the center will be non-negative if one choose the model parameters satisfying the matching conditions mentioned in Sect. 6. Also the variation of mass and radius of the star against central density have been plotted in Figs. 15 and 16. The plots show a maximum possible mass $2.06M_{\odot }$ for the star corresponding to the central density $1.23 \times 10^{18}~\text {g-m}^{-3}.$

• 3. Pressure and density throughout the star: The gradient of energy density, radial pressure and tangential pressure are required to be negative inside the star. These physical quantities should be positive and monotonically decreasing functions for a physically reasonable model of compact star. In our model, we get the gradients of these quantities as follows:

  $$\begin{aligned}{} & {} \frac{d\rho }{dr} = -10 a r,\nonumber \\{} & {} \frac{d p_r}{dr} = 2 \sqrt{a} \left( -\frac{4 \sqrt{a} C_1^2 r}{\left( C_1 \log \left( 2 \sqrt{a} \sqrt{a r^4-b r^2+1}+2 a r^2-b\right) +2 \sqrt{a} C_2\right) ^2} \right) \nonumber \\{} & {} +2 \sqrt{a} \left( \frac{C_1\left( 4 a r^3-2 b r\right) }{\sqrt{a r^4-b r^2+1} \left( C_1 \log \left( 2 \sqrt{a} \sqrt{a r^4-b r^2+1}+2 a r^2-b\right) +2 \sqrt{a} C_2\right) } +\sqrt{a} r \right) , \nonumber \\{} & {} \frac{dp_t}{dr} = - \left( \frac{8 a C_1^2 r}{\left( C_1 \log \left( 2 \sqrt{a} \sqrt{a r^4-b r^2+1}+2 a r^2-b\right) +2 \sqrt{a} C_2\right) ^2}\right) \nonumber \\{} & {} -\left( \frac{4 \sqrt{a} C_1 r \left( b-2 a r^2\right) }{\sqrt{a r^4-b r^2+1} \left( C_1 \log \left( 2 \sqrt{a} \sqrt{a r^4-b r^2+1}+2 a r^2-b\right) +2 \sqrt{a} C_2\right) }\right) +4 a r. \end{aligned}$$

  (34)

  The gradient of the density, radial pressure and tangential pressure are negative inside the stellar body are shown graphically in the next section. Moreover, the plots of the density and pressure show that all these quantities are positive inside the star and monotonically decreasing within the star.

• 4. Equation of state parameter: The equation of state parameter is given by the ratio of the pressure to density. It conveys significant information regarding the nature of the constituent matter of the star. The maximum mass the compact star also, depends on this parameter. Zeldovich indicated that this parameter, i.e., $p/\rho$ must be $\le 1$ throughout the star. Equation of state parameters are given by

  $$\begin{aligned} \omega _r=\frac{p_r}{\rho };~ \omega _t=\frac{p_t}{\rho }. \end{aligned}$$

  (35)

  To be non-exotic in nature the value of $\omega$ should lie within 0 and 1. Our model is shown to satisfies the condition $0\le \omega _r\le 1,$ $0\le \omega _t\le 1.$

• 5. Causality Condition: The radial and transverse velocity of sound $(c=1)$ are obtained as

  $$\begin{aligned} v^2_{sr}= & {} \frac{1}{5 \sqrt{a} r} \left[ \frac{4 \sqrt{a} C_1^2 r}{\left( C_1 \log \left( 2 \sqrt{a} \sqrt{a r^4-b r^2+1}+2 a r^2-b\right) +2 \sqrt{a} C_2\right) ^2}\right] -\frac{1}{5 \sqrt{a} r}\nonumber \\{} & {} \times \left[ \frac{C_1 \left( 4 a r^3-2 b r\right) }{\sqrt{a r^4-b r^2+1} \left( C_1 \log \left( 2 \sqrt{a} \sqrt{a r^4-b r^2+1}+2 a r^2-b\right) +2 \sqrt{a} C_2\right) }- \sqrt{a} r \right] ,\nonumber \\ v^2_{st}= & {} \frac{1}{10 a r} \left[ \frac{8 a C_1^2 r}{\left( C_1 \log \left( 2 \sqrt{a} \sqrt{a r^4-b r^2+1}+2 a r^2-b\right) +2 \sqrt{a} C_2\right) ^2}\right] -\frac{1}{10 a r}\nonumber \\{} & {} \times \left[ \frac{4 \sqrt{a} C_1 r \left( b-2 a r^2\right) }{\sqrt{a r^4-b r^2+1} \left( C_1 \log \left( 2 \sqrt{a} \sqrt{a r^4-b r^2+1}+2 a r^2-b\right) +2 \sqrt{a} C_2\right) }- 4 a r \right] .\qquad \qquad \qquad \qquad \qquad \qquad \qquad \end{aligned}$$

  (36)

  For a physically acceptable model of relativistic anisotropic star the radial and transverse velocity speed of sound must be smaller than $1(c=1)$ in the interior of the star, i.e., $0 \le \frac{dp_r}{d\rho } \le 1 ,$ $0 \le \frac{dp_t}{d\rho } \le 1 .$ This condition is known as causality condition and is verified graphically in the next section.

• 6. Energy Conditions: The classical energy conditions are helpful in predicting the nature of the matter inside the compact star. Generally, the energy conditions are:

  • (a) Null Energy Condition (NEC): $\rho + p_{i} \ge 0$

  • (b) Weak Energy Condition (WEC): $\rho + p_{i} = 0,$ $\rho \ge 0.$

  • (c) Strong Energy Condition (SEC): $\rho + p_{i} \ge 0,$ $\rho + \varSigma p_{i} = 0.$

  Qualitatively, it can be concluded that the matter is normal, if all the energy conditions mentioned above are satisfied. We have plot these expressions against the radial distance for the star $4U1820-30$ in the next section. The plot remains positive everywhere within the star.

• 7. Moment of Inertia: Expression for Moment of inertia of compact astrophysical objects taking into consideration the effect of General Relativity is remarkably different from the expression for solid sphere given in mechanics. Using slow rotation approximation proposed by Hartle [38], a number of attempts have been made for deriving an approximate expression for the moment of inertia of a compact star [39,40,41]. We use the approximate expression for moment of inertia of strange star provided in [42].

  $$\begin{aligned} {\mathcal {I}} = 0.4\left( 1 + \xi \right) M R^2, \end{aligned}$$

  (37)

  where $\xi = \frac{M}{R}\frac{\text {km}}{M_{\odot }}$ is the dimensionless compactness parameter [43]. This value of moment of inertia is valid up to the maximum mass of the star. In the next section, we have plot ${\mathcal {I}}$ against the mass of the star (see Fig. 13). The plot clearly shows a maximum value for the moment of inertia for mass $2.04M_{\odot }.$ Interesting to note that this value of mass is almost of the same value as the maximum mass of the star as obtained from the M–R diagram (see Fig. 12).

  The maximum rotational frequency of a compact star was given by [44] in the following form

  $$\begin{aligned} \varOmega = {\mathcal {C}} \left( \frac{M}{M_{\odot }}\right) ^{\frac{1}{2}} \left( \frac{R}{10~\text {km}}\right) ^{-\frac{3}{2}}, \end{aligned}$$

  (38)

  where ${\mathcal {C}}$ is a constant. R and M are maximum allowable radius and mass of the star. Das et al. [45] used this approximate value to calculate the time period of the model star. We use their value to study the variation of the time period of the star with mass (Fig. 14). The plot shows a maximum value of the time period corresponding to the mass $2.04M_{\odot }.$

6 Validity of the model with observational data

6.1 A particular pulsar $4U1820-30$

The physical acceptability of this model has been examined by plugging the masses and radii of observed pulsars as input parameters. In order to validate our model, we have considered the pulsar $4 U 1820-30$ whose estimated mass and radius are $M = 1.58 ~M_{\odot }$ and $R=9.1~\text {km},$ respectively [46]. Using these values of mass and radius as an input parameter, the boundary conditions have been utilized to determine the constants as $C_1=0.00309,$ $C_2=3.52$ and $a=0.000015877$ by assuming $b=0.0075.$ Making use of these values of constants and plugging the values of G and c in the expressions, various physical variables have been plotted graphically.

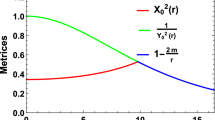
Regular and well-behaved nature of all the relevant physically meaningful quantities imply that all the requirements of a realistic star are satisfied in this model. Figure 1 depict the regularity of the metric potentials considering the pulsar $4U1820-30.$

Fig. 1

Metric potentials $A_0(r)^2$ and $B_0(r)^2$

Figure 2 shows the variation of gradients which are negative throughout the stellar configuration ensures the decreasing nature of density, radial and transverse pressures.

Fig. 2

Gradient of pressures and density for the pulsar $4U1820-30$

Figure 3 shows that the density decrease from its maximum value at the center towards its boundary.

Fig. 3

Energy density profile for the pulsar $4U1820-30$

Variation of radial and tangential pressures has been plotted in Fig. 4, which are also radially decreasing outwards from its maximum value at the center and in case of radial pressure it drops to zero at the boundary as it should be but the tangential pressure remains non zero at the boundary.

Fig. 4

Radial and transverse pressure profile for the pulsar $4U1820-30$

Radial variation of anisotropy has been shown in Fig. 5 which is zero at center as expected and is maximum at the surface.

Fig. 5

Anisotropic pressure profile for the pulsar $4U1820-30$

In Fig. 6, the sound speed in radial and transverse directions have been plotted against the radial parameter which ensures the non-violations of causality condition in the interior of the star.

Fig. 6

Radial and transverse velocities of sound against ’r’ for $4U1820-30$

The energy conditions are plotted in Fig. 7, which are positive throughout the stellar configuration as required for a physically meaningful stellar model.

Fig. 7

Energy conditions plotted against radius ‘r’ for the pulsar $4U1820-30$

Figure 8 depicted the smooth matching of the interior and exterior metrices at the boundary.

Fig. 8

Matching of $A_0(r)^2$ and $B_0(r)^2$ with the exterior

The relationship between the thermodynamic parameters energy density and pressure which reflects the nature of the equation of state (EoS) of the matter distribution of a given pulsar is plotted in Fig. 9 which shows an almost linear relationship. One can note that we have not assumed any EoS to develop the model though able to extract the nature between the density and pressure. The equation of State (EoS) parameter as is shown in Fig. 10 lies between 0 and 1.

Fig. 9

EoS for the model

Fig. 10

Equation of state parameter for the pulsar $4U1820-30$

The mass function is given in Eq. (17) is monotonically increasing the function of r and $m(0)=0$ as depicted in Fig. 11.

Fig. 11

Mass function corresponding to ‘r’ for the pulsar $4U1820-30$

For a given value of the surface density $(\rho (r=R) = 4.7\times 10^{14}$ g-cm$^{-3}$), we have also obtained the mass–radius $(M{-}R)$ relationship in our model shown in Fig. 12. The maximum mass allowed in this model is $2 M_\odot$ (Figs. 13, 14, 15, 16).

Fig. 12

$M{-}R$ relation

Fig. 13

Variation of the moment of inertia with mass

Fig. 14

Variation of the time period with mass

Fig. 15

Variation of the mass with central density

Fig. 16

Variation of radius with the central density

6.2 A wide range of pulsars

To show that this model has a wide range of applicability for highly compact stars, we have also analyzed the validity of my model by considering some well-known pulsars such as RX J $EXO 1785-248,$ PSR J $1614-2230,$ Cen X-3 and $4U 1608-52$ [47].

The estimated masses and radii of these pulsars have been used to determine the corresponding model parameters as given in Table 1. Making use of these values, in Table 2, we have calculated the values of the physically reasonable parameters which are sufficient to justify the requirements of a physically realistic star. Note that we have used $()|_0$ and $()|_R$ to denote the evaluated values of the physical parameters at the center and surface of the star, respectively. Additionally, mass–radius and other parameters of some other stars are discussed in Table 1. It can be seen from Table 2 that this presented model satisfy Buchdahl condition as well as surface redshift condition for other pulsars also.

Table 1 Values of model parameters

Table 2 Values of physical quantities

7 Stability analysis of the model

7.1 Stability under TOV criterion

A star maintain its static equilibrium state under the forces namely, gravitational force, hydrostatics force and anisotropic force. This condition is formulated mathematically as TOV equation by Tolman–Oppenheimer–Volkoff which is

$$\begin{aligned} -\frac{M_G}{r} (\rho +p_r)\frac{A_0(r)}{B_0(r)}-\frac{dp_r}{dr}+\frac{2}{r}(p_t-p_r)=0, \end{aligned}$$

(39)

where $M_G(r)$ is the gravitational mass of the star within the radius r,  can be derived from the Tolman–Whittaker formula and Einstein’s field equations and is defined by

$$\begin{aligned} M_G (r)=\frac{r B_0(r) A'_0(r)}{A^2_0(r)}. \end{aligned}$$

(40)

Using the expression of $M_G(r)$ in Eq. (39) we obtain

$$\begin{aligned} -\frac{A_0'(r)}{A_0(r)}(\rho +p_r)-\frac{dp_r}{dr}+\frac{2}{r}(p_t-p_r)=0. \end{aligned}$$

(41)

The above equation is equivalent to

$$\begin{aligned} F_g + F_h + F_a = 0, \end{aligned}$$

(42)

where

$$\begin{aligned} F_g= & {} -\frac{A_0'(r)}{A_0(r)}(\rho +p_r), \end{aligned}$$

(43)

$$\begin{aligned} F_h= & {} -\frac{dp_r}{dr}, \end{aligned}$$

(44)

$$\begin{aligned} F_a= & {} \frac{2}{r}(p_t-p_r), \end{aligned}$$

(45)

represents the gravitational, hydrostatics and anisotropic forces respectively.

The expression for $F_g,$ $F_h$ and $F_a$ can be written as,

$$\begin{aligned} F_g= & {} -\frac{4 \sqrt{a} C_1 r }{\sqrt{1 - b r^2 + a r^4} (2 \sqrt{a} C_2 + C_1 \log {(-b + 2 a r^2 + 2 \sqrt{a} \sqrt{1 - b r^2 + a r^4})})^2} \left[ 2 \sqrt{a} (b C_2 - 2 a C_2 r^2\right. \nonumber \\{} & {} + C_1 \sqrt{1 - b r^2 + a r^4}) +\left. C_1 (b - 2 a r^2) \log {(-b + 2 a r^2 + 2 \sqrt{a} \sqrt{1 - b r^2 + a r^4}})\right] , \end{aligned}$$

(46)

$$\begin{aligned} F_h= & {} -2 a r +\frac{8 a C_1^2 r}{(2 \sqrt{a} C_2 + C_1 \log {(-b + 2 a r^2 + 2 \sqrt{a} \sqrt{1 - b r^2 + a r^4})})^2}\nonumber \\{} & {} +\left. \frac{4 \sqrt{a} C_1 r (b - 2 a r^2)}{\sqrt{1 - b r^2 + a r^4} (2 \sqrt{a} C_2 + C_1 \log {(-b + 2 a r^2 + 2 \sqrt{a} \sqrt{1 - b r^2 + a r^4})})}, \right. \end{aligned}$$

(47)

$$\begin{aligned} F_a= & {} 2 a r. \end{aligned}$$

(48)

The three different forces are plotted in Fig. 17. The figure shows that hydrostatics and anisotropic force are positive and is dominated by the gravitational force which is negative to keep the system in static equilibrium.

Fig. 17

Different types of forces as function of radial coordinate r for the pulsar $4U1820-30$

7.2 Adiabatic index

The adiabatic index which is defined as

$$\begin{aligned} \varGamma =\frac{\rho +p}{p}\frac{dp}{d\rho }, \end{aligned}$$

(49)

is related to the stability of a relativistic anisotropic stellar configuration. A Newtonian isotropic sphere will be in stable equilibrium if the adiabatic index $\varGamma > \frac{4}{3}$ as per Heintzmann and Hillebrandt’s concept [6] and for $\varGamma =\frac{4}{3},$ isotropic sphere will be in neutral equilibrium. Based on some recent works of Chan et al. [48] one can demand the following condition for the stability of a relativistic anisotropic sphere

$$\begin{aligned} \varGamma > \gamma , \end{aligned}$$

(50)

where

$$\begin{aligned} \gamma =\frac{4}{3}-\left[ \frac{4(p_r-p_t)}{3|p'_r| r}\right] _{max}, \end{aligned}$$

(51)

and $\varGamma > \frac{4}{3}.$ In Fig. 18, we have plotted $\varGamma _r,$ $\varGamma _t,$ $\gamma$ respectively. clearly, it can be seen that values of $\varGamma _r$ and $\varGamma _t$ are greater than $\gamma$ throughout the stellar interior and hence the stability condition is fulfilled.

Finally, it is to be noted that the adiabatic index $\gamma$ is a local characteristic of a specific EoS and depends on the interior fluid density.

Fig. 18

Adiabatic index for the pulsar $4U1820-30$

7.3 Cracking condition

Based on the cracking method to study the stability of anisotropic stars proposed by Herrera [49], Abreu et al. [50] proved that the region of an anisotropic fluid sphere is stable where $-1 \le v^2_{t} - v^2_{r} \le 0$ is potentially stable which is shown graphically in Fig. 19.

Fig. 19

Variation of ${v_{t}^2-v_{r}^2}$ against r for $4U1820-30$

Fig. 20

Comparison of density profile with different b against r for $4U1820-30$

8 Discussions

In this study, we derived an analytic exact solution to the field equations for a spherically symmetric matter distribution taking the local anisotropic pressure into account in the framework of general relativity. The solution obtained assuming a specific metric and imposing a specific form of anisotropy potential has been shown to be non-singular, regular and well-behaved and could describe relativistic compact stellar objects.

Our analysis considered some well-known pulsars such as $4U1820-30,$ RX J $EXO 1785-248,$ PSR J $1614-2230,$ Cen X-3 and $4U 1608-52$ with their recent observational data we determined the different model parameters in Table 1 and then utilizing the model parameters the physical features of the stars displayed in Table 2 where these values of physically reasonable parameters are sufficient to justify the requirements of a physically realistic star refers a stable configuration. Matching of the interior solutions with that of the exterior on any hypersurface along with the condition of the vanishing radial pressure at the boundary refers to Darmois matching conditions. The satisfaction of TOV-equation shows that the combined effect of $F_h$ and $F_a$ balances $F_g,$ so that total force is essentially zero at all points inside a star, refers to hydrodynamical stable equilibrium configuration and satisfaction of causality guarantees that the solution is physically viable. It should be mentioned here that we have considered the transverse pressure dominates over the radial pressure $(p_t > p_r)$ for the construction of the stellar model. The model is unstable by the change in sign of the anisotropic parameter $(p_r > p_t)$ where radial pressure wins over tangential pressure.

We have analyzed the effects of anisotropy on the physical parameters e.g., density, radial pressure, transverse pressure, mass, and EoS of a star. The effects of variation of anisotropy by tuning the model parameter b and hence the overall effects of anisotropy on the gross physical features have been shown graphically in this study. The central density picks a higher value but the surface density tends to lower value with the increase of b (Fig. 20). Figures 21 and 22 show that the radial and transverse pressure increases through the interior of the star with an increase of b,  hence with an increase of anisotropy. Figure 23 shows that anisotropy increases with an increase of model parameter b.

Fig. 21

Comparison of radial pressure profile with different b against r for $4U1820-30$

Fig. 22

Comparison of transverse pressure profile with different b against r for $4U1820-30$

Fig. 23

Comparison of anisotropy profile with different b against r for $4U1820-30$

Fig. 24

Linear fitting of the EoS profile with different b

Fig. 25

EoS profile with different b

In general, the standard approach for constructing a stellar model is to prescribe an equation of state (EoS) describing the matter’s interior. In our present approach, we have not suggested any EoS but still our model predicts an almost linear pressure-density relationship. We have chosen well-behaved forms of $g_{rr}$ and the anisotropic factor. These choices also play a role on the behavior of the EoS. We have calculated the best fit for the EoS corresponding to pulsar $4U1820-30$ by using the least squares technique. Figure 24 demonstrates graphically the best fit for the EoS. It is found that the approximation for the best-fitted relation is given as $p_r=-290.6+0.58 \rho .$ The EoS relating energy density and pressure shows almost the same linear behaviour but with the increase of b equation soften lowering the slope value (Fig. 25).

We have also analyzed the mass–radius $(M {-} R)$ relationship for a specific surface density $(\rho (r=R) = 4.7\times 10^{14}~\text {g}~\text {cm}^{-3})$ for our model which in general, is obtained from the TOV equations with a given EoS. In the present study, in the absence of any prescribed EoS corresponding to the matter composition, the $M{-}R$ relationship has been generated for a given surface density. We note that the maximum mass allowed in our model is $M_{max} = 2.05 ~M_{\odot }$ corresponding to radius $R=10.85$ km which is in well agreement with the recent measurements. In the Fig. 12, $\frac{2M}{R}$ is 0.56 which is $< 8/9,$ thus satisfy the Buchdahl condition. Recently, Alho et al. [51] investigated the Buchdahl bound for static spherically symmetric solutions. The Buchdahl bound on compactness $(\frac{2M}{R})$ might be arbitrarily close to the Black hole limit $(= 1)$ for elastic material with no limit on the speed of wave propagation. However, they reported the bound to be $\le 0.924$ for solutions with subluminal wave propagation speed. Our result is in conformity to their result. Also Fig. 26 shows the mass–radius $(M{-}R)$ plot with different b clearly indicates impacts of anisotropy on the M–R plot. It is noted that with the increase of anisotropic parameter b, the maximum mass is allowed to pick higher values. In a study Ratanpal et al. [52] discussed the impact of the charge on the M–R relationship in developing the stellar model in the background of Finch–Skea geometry. In their study, it is revealed that a stellar configuration tends to accommodate more mass with the increase of the electromagnetic field. Our results arrived at the same findings if we consider that a charge fluid distribution has an anisotropic interpretation.

Fig. 26

M–R profile with different b

Considering the star to be a slow rotating one for a fixed surface density, the moment of inertia has been plotted against mass which shows the maximum mass to be $1.84~M_{\odot }.$ Again the variation of the time period of rotation with its mass indicates the time period for the maximum allowable mass for our model is 1.1 ms.

The model developed here can be significantly studied to accommodate astrophysical objects with a wide range of masses and radii. These results can be applied to provide a mechanism for constraining anisotropy to fine-tune with observational data of different millisecond pulsars. The study of the effects of electromagnetic fields in addition to anisotropy is another area that we would also like to take up in our future investigation.