1 Introduction

For over forty years, the discussion of the black holes and Anti de Sitter (AdS) spacetime has remained an active field of inquiry in modern theoretical physics [1,2,3,4]. Of particular interest are the thermodynamic properties of AdS black holes, which, through the generalized first law of black hole thermodynamics, can be derived from the correspondence between the cosmological constant in the AdS spacetime and the pressure in the common thermodynamic system. Later investigations include the comparison between the state parameter of black holes and the van der Waals equation, the critical phenomena at the critical point, as well as the phase transitions with different spacetime parameters [5,6,7,8]. Recently, there has also been flourishing interest in the subject of dark energy (DE) [9,10,11,12,13,14,15], which has opened up an interesting possibility to deeply understand the quasi-de Sitter spacetime in the early inflation period [16,17,18,19]. On the other hand, the inclusion of cosmological constant (or vacuum energy density) in the study of de Sitter spacetime is very similar to the case of dark energy in modern cosmology. In particular, if the simplest candidate for the uniformly distributed dark energy is considered to be in the form of cosmological constant, our universe will naturally evolve into a new de Sitter phase. Therefore, in order to construct the overall evolution history of the Universe, it is necessary to better understand the classical and quantum properties of de Sitter spacetime.

In the paradigm of de Sitter spacetime, the black hole horizon and the cosmological horizon are always considered to be different thermodynamic systems with different radiation temperatures [20,21,22]. However, under such circumstance, de Sitter spacetime does not satisfy the requirements of thermodynamic equilibrium stability, which makes it difficult to investigate the thermodynamics of Anti de Sitter (AdS) black holes. Moreover, in initial works it was always assumed that the entropy of de Sitter spacetime is the sum of the entropy of the black hole horizon and the cosmological horizon [23], on the base of which the effective temperature and pressure can be derived from the first law of thermodynamics [24,25,26,27,28,29,30]. However, recent development on the thermodynamics of AdS black holes shows that the interaction between the two horizons could bring a multitude of interesting possibilities. More specifically, when the state parameters of charged AdS black holes satisfy certain conditions, the radiation temperature (as well as the effective temperature) of two horizons will be equal to each other [31,32,33]. Such constraint condition was extensively discussed in the recent analysis of lukewarm black holes [34], with certain conditions satisfied by the charge of spacetime. On the other hand, as is well known, the parameters describing the charged AdS black hole thermodynamic system are not only related to the state parameters, but also electromagnetic parameters like the charge and electric potential. For instance, due to the additional hair parameters in higher dimensional hairy black holes, Refs. [35, 36] proposed that the hairy black hole solutions become far richer than those predicted in General Relativity. Extensions of this work to the thermodynamic properties of AdS hairy black hole with negative cosmological constant (\(\varLambda <0\)) have yielded more exotic results [2, 37,38,39,40,41,42,43,44], i.e., the hair parameters can have significant effects on the phase transition, while Van der Waals-like phase transition could also exist in AdS hairy black holes. Motivated by such recent developments of black hole thermodynamics, several questions arise: Considering the interaction between the black hole horizon and the cosmological horizon, does the Van der Waals-like phase transition still exist in AdS hairy black holes? More importantly, is it possible to quantify the effects of hair parameter q on the phase transition? The investigation of the above two problems is the main motivation of our analysis.

In this paper, concentrating on the correlation between the state parameters of the black hole’s horizon and the cosmological horizon, we will study the thermodynamic properties of de Sitter spacetime, and provide the effective thermodynamic quantity of electrically charged hairy black hole (ECBH) spacetime. Then we obtain the entropy correction term and the corresponding effective thermodynamic quantity caused by the interaction between the state parameters of the two horizons. Finally, in the framework of the well-known Ehrenfest method, we summarize the classification of phase transition in de Sitter spacetime, discuss the conditions on which the stability and phase transition of de Sitter spacetime could take place, and try to quantify the effects of hair parameter q on the phase transition. The units of \({G=h=k_{B}=c=1}\) are used throughout this work.

2 Higher dimensional hairy black holes

A number of analytic solutions of Einstein–Maxwell-\(\varLambda \) theory conformally coupled to a scalar field in higher dimensions were discussed in Refs. [45,46,47,48]. In what follows we focus on the exact solution of electrically charged hairy black hole in five dimensions, the action of which is given by

$$\begin{aligned} I = \frac{1}{k}\int {{d^5}y\sqrt{ - g} } \left[ {R - 2\varLambda - \frac{1}{4}{F^2} + k{L_m}(\phi ,\nabla \phi )} \right] \end{aligned}$$
(1)

where

$$\begin{aligned} \begin{aligned} L_m&= {b_0}{\phi ^{15}} + {b_1}{\phi ^7}{S_{\mu \nu }}^{\mu \nu }+ {b_2}{\phi ^{ - 1}}({S_{\mu \gamma }}^{\mu \gamma }{S_{\nu \delta }}^{\nu \delta }\\&\quad - 4{S_{\mu \gamma }}^{\nu \gamma }{S_{\nu \delta }}^{\mu \delta } + {S_{\mu \nu }}^{\gamma \delta }{S^{\nu \mu }}_{\gamma \delta }) \end{aligned} \end{aligned}$$
(2)

with the coupling constants of conformal field theory (\(b_0, b_1, b_2\)) and

$$\begin{aligned} \begin{aligned} {S_{\mu \nu }}^{\gamma \delta }&= {\phi ^2}{R_{\mu \nu }}^{\gamma \delta } - 12\delta _{[\mu }^{[\gamma }\delta _{\nu ]}^{\delta ]}{\nabla _\rho }\phi {\nabla ^\rho }\phi \\&\quad - 48\phi \delta _{[\mu }^{[\gamma }{\nabla _{\nu ]}}{\nabla ^{\delta ]}}\phi + 18\delta _{[\mu }^{[\gamma }{\nabla _{\nu ]}}\phi {\nabla ^{\delta ]}}\phi \end{aligned} \end{aligned}$$
(3)

The five-dimensional solution to Eq. (1) is given by [49]

$$\begin{aligned} d{s^2} = - f(r)d{t^2} + {f^{- 1}(r)}d{r^2} + {r^2}d\varOmega _{(k)3}^2 \end{aligned}$$
(4)

where the metric function is obtained as follows

$$\begin{aligned} f(r) = k - \frac{m}{{{r^2}}} - \frac{q}{{{r^3}}} + \frac{{{e^2}}}{{{r^4}}} - \frac{\varLambda }{6}{r^2} \end{aligned}$$
(5)

and \(d\varOmega _{(k)3}^2\) is the line element on a three-dimensional surface of constant positive, zero, or negative curvature. The constant k characterizes the geometric property of hypersurface, which takes values \(k=0\) for flat, \(k=-1\) for negative curvature, and \(k=1\) for positive curvature, respectively. Moreover, e represents the electric charge, m denotes the mass parameter of the solution, and \(\varLambda \) is the cosmological constant. Note that q is given in terms of coupling constants of the scalar field [50, 51]

$$\begin{aligned} q = \frac{{64\pi }}{5}\varepsilon k{b_1}{\left( {\frac{{ - 18k{b_1}}}{{5{b_0}}}} \right) ^{3/2}} \end{aligned}$$
(6)

where \(\varepsilon =- 1,0,1\) and there exists an additional constraint to ensure the existence of this black hole solution (\(10{b_0}{b_2} = 9b_1^2\)). Therefore, one can straightforwardly obtain the value of q as \(0, \pm \left| q \right| \). Now we should make some comments on the physical meaning of the parameter q. At first sight an expectation would be that it represents the scalar charges in the first law of thermodynamics, especially for hairy black holes in AdS spacetime [52, 53]. The new interpretation of the role of scalar charges played in the first law of thermodynamics can also be found in Refs. [35, 40, 54]. However, it should be noted that the hair parameter q is not defined as the conserved charge corresponding to some symmetry—its value may vary with the scalar field coupling parameters [50]. More specifically, in order to develop the consistency between the first law of black hole thermodynamics and the Smarr relation [51], the coupling parameters should be treated as dynamical variables, which means that q is extended to be a continuous and real parameter in the Smarr relation.

In addition, the scalar field configuration takes the form of

$$\begin{aligned} \phi (r) = \frac{n}{{{r^{1/3}}}}, n = \varepsilon {\left( { - \frac{{18k{b_1}}}{{5{b_0}}}} \right) ^{1/6}} \end{aligned}$$
(7)

and the Maxwell gauge potential reads

$$\begin{aligned} {A_\mu } = \sqrt{3} \frac{e}{{{r^2}}}\delta _\mu ^0 \end{aligned}$$
(8)

where the field strength is obtained as \({F_{\mu \nu }} = {\partial _\mu }{A_\nu } - {\partial _\nu }{A_\mu }\). When \(\varLambda >0\) , the positions of black hole horizon \({r_ + }\) and cosmic horizon \({r_c}\) are determined with \(f(r)=0\).

Fig. 1
figure 1

The characteristic behavior of f(r) as a function of x for \(m=0.5, 0.8, 1.0\). The other parameters are fixed at \(\varLambda =1\), \(k=1\) ,\(e=0.2\), and \(q=-0.2\)

Full size image
Fig. 2
figure 2

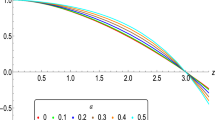
The same as Fig. 1, but with different value of e (the other parameters are fixed at \(\varLambda =1\), \(k=1\), \(m=1\), and \(q=-0.2\))

Full size image

Based on the above equations, the \(f(r)- r\) diagrams could be derived by taking different value of m, q, and e. Firstly we consider the spherical case (i.e., \(k=+1\) and \(\varLambda \mathrm{{ = 1}}\)) which are explicitly illustrated in Figs. 1, 2, and 3. We find that, when the parameters characterizing the ECBH spacetime satisfy certain conditions, the spacetime will exhibit the black hole horizon and the cosmological horizon, i.e., there exit three real roots for the equation \(f(r)=0\): the largest one is the cosmological horizon (CEH) at \(r_c\), followed by the outer horizon (BEH) of black hole at \(r=r_+\), and the smallest is the inner (Cauchy) horizon of the black hole. More importantly, the difference between the the cosmological horizon and the outer horizon of black hole (\(|r_c-r_+|\)) will significantly increase with the value of q, which demonstrates the non-negligible effect of this hair parameter in Fig. 3. Now one interesting question arises: considering the possible existence of planar hairy black holes [38, 55] and first-order phase transitions in AdS spacetime [42] once the ground state is correctly identified, is it possible to study the thermodynamic behavior of hairy dS black holes with \(k=0\)? To answer this question, we have studied the behavior of the metric function for planar black holes with \(k=0\) and hyperbolic black holes with \(k=-1\). The final results show that, only in the spherical case both of the black hole horizon and the cosmological horizon can be derived. Therefore, we dedicate the following sections to the exploration of the thermodynamic behavior for spherical black holes with \(k=+1\).

Fig. 3
figure 3

The same as Fig. 1, but with different value of q (the other parameters are fixed at \(\varLambda =1\), \(k=1\), \(e=0.2\), and \(m=1\))

Full size image

In what follows we will concentrate on the conserved quantities at the black hole horizon and cosmological horizon, which are derived with the counterterm method extensively used both in de Sitter and Anti-de Sitter spacetime [55,56,57,58]. We know that some thermodynamic quantities are associated with the cosmological horizon as

$$\begin{aligned} \begin{aligned}&M = \frac{{3{\omega _3}(k)}}{{16\pi }}m, Q = - \frac{{{\omega _3}(k)\sqrt{3} }}{{16\pi }}e, P =-\frac{\varLambda }{{8\pi }},\\&{S_c} = {\omega _3}(k)\left( {\frac{{r_c^3}}{4} - \frac{5}{8}q} \right) , {V_c} = \frac{{{\omega _3}(k)}}{4}r_c^4,\\&{T_c} = - \frac{1}{{\pi r_c^4}}\left( {\frac{{kr_c^3}}{2} + \frac{q}{4} - \frac{{{e^2}}}{{2{r_c}}} - \frac{\varLambda }{6}r_c^5} \right) . \end{aligned} \end{aligned}$$
(9)

and the first law of thermodynamics for the cosmological horizon following form [56, 57]

$$\begin{aligned} dM = - {T_c}d{S_c} + {V_c}dP + {\varPhi _c}dQ + {K_c}dq \end{aligned}$$
(10)

where

$$\begin{aligned} {K_c} = - \frac{{{\omega _3}(k)\varLambda }}{{192r_c^5}}\left( {20r_c^6 - 12\frac{{r_c^4}}{\varLambda }(5k - 3) - \frac{{30}}{\varLambda }q{r_c} + \frac{{60{e^2}}}{\varLambda }} \right) \end{aligned}$$
(11)

For the black hole horizon, the associated thermodynamic quantities can be written as

$$\begin{aligned} \begin{aligned}&{S_ + } = {\omega _3}(k)\left( {\frac{{r_ + ^3}}{4} - \frac{5}{8}q} \right) , {V_ + } = \frac{{{\omega _3}(k)}}{4}r_ + ^4,\\&{T_ + } = \frac{1}{{\pi r_ + ^4}}\left( {\frac{{kr_ + ^3}}{2} + \frac{q}{4} - \frac{{{e^2}}}{{2{r_ + }}} - \frac{\varLambda }{6}r_ + ^5} \right) \end{aligned} \end{aligned}$$
(12)

while the thermodynamic quantities of black hole horizon satisfy the first law of thermodynamics [55, 58]

$$\begin{aligned} dM = {T_ + }d{S_ + } + {V_ + }dP + {\varPhi _ + }dQ + {K_ + }dq \end{aligned}$$
(13)

where

$$\begin{aligned} {K_ + } = - \frac{{{\omega _3}(k)\varLambda }}{{192r_ + ^5}}\left( {20r_ + ^6 - 12\frac{{r_ + ^4}}{\varLambda }(5k - 3) - \frac{{30}}{\varLambda }q{r_ + } + \frac{{60{e^2}}}{\varLambda }} \right) \end{aligned}$$
(14)

It is fairly straightforward to show that there exits only the black hole horizon in the case of \(P =-\frac{\varLambda }{8\pi }>0\). In addition, the situation is significantly more interesting in the case of \(q<0\). More recently, Refs. [50, 51, 51] studied the second-order phase transition of hairy black holes in the AdS spacetime, and furthermore derived the critical thermodynamic quantities as: \(r_c=(-5q)^{1/3}\), \(T_c=-\frac{3(-5q)^{2/3}}{20\pi q}\), and \(P_c=\frac{9}{200\pi }(-\frac{\sqrt{5}}{9})^{2/3}\), and the ratio of the critical values \(10P_cr_c=3T_c\). Therefore, compared with the well-known thermodynamic properties in the charged case [1,2,3,4], the parameter q plays a very similar role in the phase transition of hairy black holes, just as the electric charge Q in the scenario of charged black holes.

Moreover, for \(f({r_{ + ,c}}) = 0\) we can derive

$$\begin{aligned} m= & {} \frac{{kr_c^2{x^2}}}{{(1 + {x^2})}} - \frac{q}{{{r_c}}}\frac{{(1 - {x^5})}}{{x(1 - {x^4})}} + \frac{{{e^2}}}{{r_c^2}}\frac{{(1 - {x^6})}}{{{x^2}(1 - {x^4})}} \end{aligned}$$
(15)
$$\begin{aligned} \frac{\varLambda }{6}= & {} \frac{k}{{r_c^2(1 + {x^2})}} + \frac{q}{{r_c^5}}\frac{{1 - x}}{{x(1 - {x^4})}} - \frac{{{e^2}}}{{r_c^6}}\frac{1}{{{x^2}(1 + {x^2})}} \end{aligned}$$
(16)

On the other hand, taking \(T = {T_ + } = {T_c}\), the combination of Eqs. (9) and (12) will generate

$$\begin{aligned} \frac{\varLambda }{6} = \frac{k}{{2r_c^2x}} + \frac{q}{{4r_c^5{x^4}}}\frac{{(1 + {x^4})}}{{\left( {1 + x} \right) }} - \frac{{{e^2}}}{{2r_c^6}}\frac{{(1 + {x^5})}}{{{x^5}\left( {1 + x} \right) }} \end{aligned}$$
(17)

where \(x = {r_ + }/{r_c}\). Thus, when the temperature of the black hole horizon is equal to that of the cosmological horizon, the electric charge of the system satisfies the following expression

$$\begin{aligned} \begin{aligned} \frac{{{e^2}}}{{{r_c}}}&= k\frac{{{x^4}r_c^3}}{{(1 + x + 3{x^2} + {x^3} + {x^4})}} \\&\quad +q\frac{{x(1 + 2x + 4{x^2} + 2{x^3} + {x^4})}}{{2\left( {1 + x} \right) (1 + x + 3{x^2} + {x^3} + {x^4})}} \end{aligned} \end{aligned}$$
(18)

with the radiation temperature of the two horizons derived from Eqs. (12)–(14):

$$\begin{aligned} \begin{aligned} T&= {T_ + } = {T_c}\\&= \frac{{(1 - {x^2})(1 + x)(1 + {x^2})}}{{2\pi (1 + {x^2})(1 + x + 3{x^2} + {x^3} + {x^4}){r_c}}}\\&\quad \times \left( k + \frac{{q(2 - x + 3{x^2} - 3{x^3} + {x^4} - 2{x^5})}}{{2xr_c^3{{(1 + x)}^2}(1 - {x^2})(1 + {x^2})}} \right) \end{aligned} \end{aligned}$$
(19)
Fig. 4
figure 4

The \(T(x)-x\) diagram when the parameter q is fixed at \(-0.1, -0.2,\) and \(-0.3\), respectively

Full size image

In order to have a better illustration, the \(T(x) - x\) diagram of the electrically charged hairy black holes was displayed in Fig. 4 for the specific cases with \({r_c} = 1\), which highlights the salient features of the q parameter. We see that, the maximum value of T(x) and the allowed region of \(T(x)>0\) will increase with the value of q, while the radiation temperature in the spacetime will approach zero (\(T \rightarrow 0\)) when the two horizons coincide (\(x \rightarrow 1\)).

Fig. 5
figure 5

The same as Fig. 4, but for the metric function f(x) and entropy S(x)

Full size image

3 The effective thermodynamic quantity of spacetime

Now, considering the interaction between the black hole horizon and the cosmological horizon, we can derive the effective thermodynamic quantities and the corresponding first law of black hole thermodynamics as [59]

$$\begin{aligned} dM = {T_{{ eff}}}dS - {P_{{ eff}}}dV + {\phi _{{ eff}}}dQ + {K_{{ eff}}}dq \end{aligned}$$
(20)

with the thermodynamic volume defined as [16]

$$\begin{aligned} V = {V_c} - {V_ + } = \frac{{{\omega _3}(k)}}{4}r_c^4(1 - {x^4}) \end{aligned}$$
(21)

Note that the entropy S is an explicit function of the horizon position. In particular, when x approaches zero (\(x\rightarrow 0\)), there exits only the cosmological horizon with the corresponding entropy \(S_c=\omega _3(k)(\frac{r_c^3}{4}-\frac{5}{8}q)\), while with the absence of cosmological constant (\(\varLambda =0\)), there exits only the black hole horizon with the entropy of \(S_+=\omega _3(k)(\frac{r_+^3}{4}-\frac{5}{8}q)\). In this analysis, considering the interaction between the two spacetime horizons and the external entropy generated by such interaction (\(S_{ex}\)), the entropy of ECBH spacetime can be written as

$$\begin{aligned} S = {S_ + } + {S_c} + {S_{ex}} = {\omega _3}(k)r_c^3(1 + {x^3} + f(x)) - \frac{{5{\omega _3}(k)}}{4}q \end{aligned}$$
(22)

where the undefined function f(x) represents the extra contribution from the correlation between the two horizons [60].

Inserting Eq. (15) into Eqs. (20)–(22), the effective temperature of ECBH spacetime is obtained as

$$\begin{aligned} \begin{aligned} T_{{ eff}}&= \frac{3}{{2\pi r_c^4A(x)}}\left[ q\frac{{(1 - 4{x^4} + 4{x^5} - {x^9})}}{{2{x^2}(1 - {x^4})}}\right. \\&\quad \left. +kr_c^3x\frac{{(1 - {x^2} + {x^4})}}{{(1+{x^2})}}-\frac{{{e^2}}}{{{r_c}}}\frac{{(1 - 2{x^4} + 2{x^6} - {x^{10}})}}{{{x^3}(1 - {x^4})}} \right] \end{aligned} \end{aligned}$$
(23)

where

$$\begin{aligned} A(x) = \left[ {(3{x^2} + f'(x))(1 - {x^4}) + 3{x^3}(1 + {x^3} + f(x))} \right] \ \end{aligned}$$
(24)

and the combination of Eqs. (18) and (23) will lead to the effective temperature of ECBH spacetime

$$\begin{aligned} \begin{aligned} {\bar{T}_{{ eff}}}&= \frac{{3(1 - {x^2}){x^2}(1 + x)(1 + {x^5})}}{{2\pi (1 - {x^4})(1 + x + 3{x^2} + {x^3} + {x^4})r_c^4A(x)}}\Bigg [ {kr_c^3} +q\\&\quad {\frac{{(2 - x + 3{x^2} - 3{x^3} + {x^4} - {x^6} + 3{x^7} - 3{x^8} + {x^9} - 2{x^{10}})}}{{2x{{(1 + x)}^2}(1 + {x^5})(1 - {x^2})(1 + {x^2})}}} \Bigg ] \end{aligned} \end{aligned}$$
(25)

One should note that, when the radiation temperature of the black hole horizon is equal to that of the cosmological horizon, the effective temperature \(\bar{T}_{{ eff}}\) of ECBH spacetime should be the same as the radiation temperature, i.e.,

$$\begin{aligned} \bar{T}_{{ eff}} = T \end{aligned}$$
(26)
Fig. 6
figure 6

The behavior of the effective temperature as a function of x. a For different e (q is fixed at − 0.2), b for different q (e is fixed at 0.2)

Full size image

The radiation temperature can be rewritten as

$$\begin{aligned} \begin{aligned} T&= \frac{{(1 - {x^2})(1 + x)}}{{2\pi (1 + x + 3{x^2} + {x^3} + {x^4})r_c^4}}\Bigg [ {kr_c^3} \\&\quad +{\frac{{q(2 - x + 3{x^2} - 3{x^3} + {x^4} - {x^6} + 3{x^7} - 3{x^8} + {x^9} - 2{x^{10}})}}{{2x(1 - {x^2}){{(1 + x)}^2}(1 + {x^2})(1 + {x^5})}}} \Bigg ] \end{aligned} \end{aligned}$$
(27)

Then we can calculate the expression of A(x) from Eq. (25) and find it to be

$$\begin{aligned} A(x) = \frac{{3{x^2}(1 + {x^5})}}{{(1 - {x^4})}} \end{aligned}$$
(28)

Now the combination of Eqs. (24) and (28) will generate

$$\begin{aligned} f'(x) + \frac{{3{x^3}}}{{1 - {x^4}}}f(x) = - \frac{{3{x^3}(1 - {x^3} - 2{x^4})}}{{{{(1 - {x^4})}^2}}} \end{aligned}$$
(29)

with the corresponding solution of

$$\begin{aligned} f(x) = \frac{{11}}{7}{(1 - {x^4})^{3/4}} - \frac{{11 - x(11 + 3{x^3})(1 + {x^3})}}{{7(1 - {x^4})}} \end{aligned}$$
(30)

In Fig. 5 we display the behavior of f(x) and S(x) with different value of q parameter.

Table 1 Summary of the highest effective temperature \(T_{{ eff}}^{c}\) and the corresponding x for different curves in Fig. 6
Full size table

Furthermore, we get the effective temperature of ECBH spacetime from Eqs. (23) and (28)

$$\begin{aligned} \begin{aligned} T_{{ eff}}&= \frac{1}{{2\pi {r_c}{x^2}(1 + {x^5})}}\Bigg [ {kx(1 - {x^2})(1 - {x^2} + {x^4})} \\&\quad +\frac{q}{{r_c^3}}\frac{{(1 - 4{x^4} + 4{x^5} - {x^9})}}{{2{x^2}}} { - \frac{{{e^2}}}{{r_c^4}}\frac{{(1 - 2{x^4} + 2{x^6} - {x^{10}})}}{{{x^3}}}} \Bigg ] \end{aligned} \end{aligned}$$
(31)

Similarly, in order to clearly see the effect of relevant parameters on the effective temperature, we illustrate an example of the \({T_{{ eff}}} - x\) diagram with different value of e and q, which are explicitly shown in Fig. 6 (by fixing \(k=1\) and \({r_c}=1\)). The corresponding numerical results can be seen in Table 1. It is obvious that different values of q and e may lead to different effective temperature of ECBH spacetime, as can be seen from Fig. 6. More specifically, when q is fixed, the maximum value of the effective temperature of the system will decrease with e, while the allowed region with \({T_{{ eff}}}\) lager than zero is also reduced. Such tendency can also be seen from the behavior of the effective temperature as a function of x, in term of different q.

On the other hand, the effective pressure of ECBH spacetime can be derived from Eq. (20), which is given by

$$\begin{aligned} {P_{{ eff}}} = \frac{{16\pi }}{{3\omega _3^2(k)r_c^2{x^2}(1 + {x^5})(1 - {x^4})}}P(x,{r_c},q,e) \end{aligned}$$
(32)

where

$$\begin{aligned}&P(x,{r_c},q,e) \nonumber \\&\quad ={x^4}\frac{{(1 + {x^5})}}{{(1 - {x^4})}}\left[ {2k(1 - {x^2}) + \frac{q}{{r_c^3}}\frac{{(1 - {x^5})}}{{{x^3}}}- \frac{{2{e^2}}}{{r_c^4}}\frac{{(1 - {x^6})}}{{{x^4}}}} \right] \nonumber \\&\qquad + x\left[ {\frac{{11}}{7}{{(1 - {x^4})}^{3/4}} - \frac{{4(1 + {x^4})(1 - x + {x^2}) - 11{x^3}}}{{7(1 - x)(1 + {x^2})}}} \right] \nonumber \\&\qquad \times \left[ {2k(1 - {x^2})1 - {x^2} + {x^4}) + \frac{q}{{r_c^3}}\frac{{(1 - 4{x^4} + 4{x^5} - {x^9})}}{{{x^3}}}} \right. \nonumber \\&\qquad - \left. {\frac{{{e^2}}}{{r_c^4}}\frac{{2(1 - 2{x^4} + 2{x^6} -{x^{10}})}}{{{x^4}}}} \right] \end{aligned}$$
(33)

The effective potential of ECBH spacetime can be written as

Fig. 7
figure 7

The same as Fig. 6, but for the behavior of the effective pressure \(P_{{ eff}}\)

Full size image
Fig. 8
figure 8

The \(S-T_{{ eff}}\) diagram with different \(\phi _{{ eff}}\) (while q is fixed at − 0.2) and different q (while \(\phi _{{ eff}}\) is fixed at 0.2)

Full size image
$$\begin{aligned} {\phi _{{ eff}}} = {\left( {\frac{{\partial M}}{{\partial Q}}} \right) _{S,V,q}} = \frac{{32\pi Q}}{{\omega (k)r_c^2}}\frac{{(1 - {x^6})}}{{(1 - {x^4})}} = - \frac{{2\sqrt{3} e}}{{r_c^2}}\frac{{(1 - {x^6})}}{{(1 - {x^4})}} \end{aligned}$$
(34)

By taking different value of q and e (with k fixed at 1), we analyze the behavior of the effective pressure \({P_{{ eff}}}\) in Fig. 7, from which one could clearly see the effect of these parameters on the effective pressure of ECBH spacetime. Notice that the maximum value of the effective pressure \({P_{{ eff}}}\) and its positive region (\({P_{{ eff}}}>0\)) will decrease with e and q, which is quite similar to the behavior of effective temperature shown in Fig. 6. Meanwhile, concerning different value of \({\phi _{{ eff}}}\) and q (with \(k = 1\)), we can obtain the correlation between the entropy S and the effective temperatue \(T_{{ eff}}\) presented in Fig. 8. For comparison, the value of \({S_0}\) and \(T_{{ eff}}^0\) at the phase transition point is also displayed in Table 2.

Now we will focus on the thermodynamic properties of ECBH spacetime in the vicinity of \(T_{{ eff}}^0\) and \({S_0}\). As can be clearly seen from the results presented in Fig. 8, when the effective temperature is lower than \(T_{{ eff}}^0\), there exist two different entropy for one specific effective temperature. Thus, considering the strong correlation between entropies and phases, \(T_{{ eff}}<T_{{ eff}}^0\) is a two-state coexistence region, which can be classified first-order phase transition in the framework of the well known Ehrenfest classification of phase transitions [61]. When the effective temperature approaches \(T_{{ eff}}^0\), the difference between the two entropies will significantly decrease, which indicates that at the phase transition point (\(T_{{ eff}}=T_{{ eff}}^0\)), the AdS black holes will transform from one-order phase transition to second-order phase transition. On the other hand, the heat capacity \(C_Q\) will diverge at the phase transition point, as can be seen from the slope of the yielded \(S-T\) curves for the thermodynamic system. We remark here that, the allowed region of the first-order phase is strongly dependent on the value of q, i.e., the effective temperature of the second-order phase will dramatically increase with the q parameter, which gives birth to an enlarged region of the first-order phase. Meanwhile, it is interesting to understand whether the presence of the scalar field will change the phase diagram. Comparing the two cases illustrated in Fig. 8, one could easily find that the scalar field plays a similar role as the q parameter. More specifically, the decrease of the effective potential \(\phi _{{ eff}}\) could significantly influence the effective temperature of the second-order phase, and thus contribute to the absence of the first-order phase transitions.

Table 2 Summary of the value of \({S_0}\) and \(T_{{ eff}}^0\) at the phase transition point for different q and e parameter
Full size table
Fig. 9
figure 9

Heat capacity \({C_{{\phi _{{ eff}}}}}\) varying with effective temperature \({T_{{ eff}}}\) and entropy S, for the case of \(k=1\), \({\phi _{{ eff}}}=0.2\) and \(q=-0.2\). Note the phase transition of ECBH spacetime occurs when the effective temperature is less than \(T_{{ eff}}^0=0.0356\)

Full size image
Fig. 10
figure 10

The same as Fig. 9, but for the behavior of the Gibbs function G

Full size image

For the case of \({r_c} = 1\), the heat capacity with equal \({\phi _{{ eff}}}\) can be expressed as

$$\begin{aligned} {C_{{\phi _{{ eff}}}}} = {T_{{ eff}}}{\left( {\frac{{\partial S}}{{\partial {T_{{ eff}}}}}} \right) _{{\phi _{{ eff}}}}} \end{aligned}$$
(35)

where

$$\begin{aligned} {T_{{ eff}}}= & {} \frac{1}{{2\pi {r_c}{x^2}(1 + {x^5})}}\Bigg [ {kx(1 - {x^2})(1 - {x^2} + {x^4})} \nonumber \\&+ \frac{q}{{r_c^3}}\frac{{(1 - 4{x^4} + 4{x^5} - {x^9})}}{{2{x^2}}} \nonumber \\&{ - \phi _{{ eff}}^2\frac{{(1 - 2{x^4} + 2{x^6} - {x^{10}}){{(1 - {x^4})}^2}}}{{12{x^3}{{(1 - {x^6})}^2}}}} \Bigg ] \end{aligned}$$
(36)
$$\begin{aligned} S= & {} {S_ + } + {S_c} + {S_{ex}} = {\omega _3}(k)r_c^3(1 + {x^3} + f(x)) - \frac{{5{\omega _3}(k)}}{4}q \end{aligned}$$
(37)
$$\begin{aligned}&{C_{{\phi _{{ eff}}}}} = {T_{{ eff}}}{\left( {\frac{{\partial S}}{{\partial {T_{{ eff}}}}}} \right) _{{\phi _{{ eff}}}}} = {T_{{ eff}}}{\left( {\frac{{dS(x)}}{{d{T_{{ eff}}}(x)}}} \right) _{{\phi _{{ eff}}}}} \end{aligned}$$
(38)

In term of the thermodynamic quantities discussed above, the extended Gibbs free energy for our system is given by

$$\begin{aligned} G = M - {T_{{ eff}}}S - {\phi _{{ eff}}}Q \end{aligned}$$
(39)

provided the mass of the electrically charged hairy black hole [62]

$$\begin{aligned} \begin{aligned} M&= \frac{{3{\omega _3}(k)}}{{16\pi }}r_c^2\\&\quad \times \left( {\frac{{k{x^2}}}{{(1 + {x^2})}} - \frac{q}{{r_c^3}}\frac{{(1 - {x^5})}}{{x(1 - {x^4})}} + \phi _{{ eff}}^2\frac{{(1 - {x^4})}}{{12{x^2}(1 - {x^6})}}} \right) \end{aligned} \end{aligned}$$
(40)

Now, it is worthwhile commenting on the correlation between the corresponding Gibbs function and the effective temperature. Taking \(k = 1\), \({\phi _{{ eff}}} = 0.2\) and \(q = - 0.2\), we obtain the \({C_{{\phi _{{ eff}}}}} - {T_{{ eff}}}\), \({C_{{\phi _{{ eff}}}}} - S\), \(G - S\), and \(G - {T_{{ eff}}}\) graphs presented in Figs. 9 and 10. One could note that when the effective temperature is less than \(T_{{ eff}}^0 = 0.03560\), there exist two different Gibbs function for one certain effective temperature. Meanwhile, the ECBH spacetime will exhibit the smallest Gibbs function G under the isothermal and isobaric conditions (with fixed \({\phi _{{ eff}}}\) and \(T_{{ eff}}\)). More interestingly, following the Gibbs principle of minimum free energy, any fluctuation of the spacetime could generate possible phase transition, i.e., an arbitrary state of phase 2 may change to the state of phase 1 under the isothermal and isobaric conditions, which, in the framework of Ehrenfest’s classification method, satisfies the requirements of zero-order phase transition [61]. Such classification of general types of transition between phases of matter, introduced by Paul Ehrenfest in 1933, lies at a crossroads in the thermodynamical study of critical phenomena. Therefore, similar to the case of AdS spacetime [50, 63,64,65,66,67,68], through a zero-order phase transition our Universe may transform from an initially unstable phase to a stable phase, which can be interpreted as a confinement/deconfinement phase transition in dual quark gluon plasma [69], superfluidity, and superconductivity [70,71,72].

In the next we will explore the phase structure of hairy black hole solutions in the framework of Ehrenfest’s scheme.

Fig. 11
figure 11

Entropy (S) with different \(\alpha \) and \({k_T}\) (for the charged hairy black holes with \(q=-0.2\) and \({\phi _{{ eff}}}=0.2\))

Full size image

4 Phase transition and Ehrenfest’s equations

As is well known, the classification of phase transition using Ehrenfests scheme is a very elegant technique in the standard thermodynamics [73,74,75,76]. However, it is still not widely explored in the context of black hole thermodynamics, in spite of some attempts made in Ref. [16] and further discussed in Ref. [17]. Therefore, it is rewarding to classify the phase transitions in electrically charged hairy black holes by Ehrenfest’s scheme. Let us start by reviewing the \(S-T_{{ eff}}\) graph shown in Fig. 8. Considering the fact that the entropy S is indeed a continuous function of temperature \(T_{{ eff}}\), the possible existence of a first-order phase transition could be ruled out [77]. However, turning to the infinite divergence of specific heat close to the critical point \(T = T_0\), the onset of a higher-order (continuous) phase transition is strongly supported, which is also supported by the behavior of the \(C_{\varPhi _{{ eff}}} - S\) graph shown in Fig. 9.

Moreover, concerning the first law of thermodynamics in term of the thermodynamic quantities of ECBH spacetime (Eq. 20), the state parameters of ECBH spacetime are corresponding to those of general thermodynamic systems, i.e., \(V \leftrightarrow Q\) and \(P \leftrightarrow - {\phi _{{ eff}}}\). Therefore, the Ehrenfest’s equations in ECBH spacetime can be rewritten as

$$\begin{aligned} - {\left( {\frac{{\partial {\phi _{{ eff}}}}}{{\partial {T_{{ eff}}}}}} \right) _S}= & {} \frac{{{C_{2{\phi _{{ eff}}}}} - {C_{1{\phi _{{ eff}}}}}}}{{T_{{ eff}}^c{Q^c}({\alpha _2} - {\alpha _1})}} = \frac{{\varDelta {C_{{\phi _{{ eff}}}}}}}{{T_{{ eff}}^c{Q^c}\varDelta \alpha }} \end{aligned}$$
(41)
$$\begin{aligned} - {\left( {\frac{{\partial {\phi _{{ eff}}}}}{{\partial {T_{{ eff}}}}}} \right) _Q}= & {} \frac{{{\alpha _2} - {\alpha _1}}}{{{k_{T2}} - {k_{T1}}}} = \frac{{\varDelta \alpha }}{{\varDelta {k_T}}} \end{aligned}$$
(42)

where \({k_T}\) is the analog of isothermal compressibility, and \(\alpha \) is the analog of volume expansion coefficient given by

$$\begin{aligned} \alpha = \frac{1}{Q}{\left( {\frac{{\partial Q}}{{\partial {T_{{ eff}}}}}} \right) _{{\phi _{{ eff}}}}} = - \frac{1}{Q}{\left( {\frac{{\partial Q(x)}}{{d{T_{{ eff}}}(x)}}} \right) _{{\phi _{{ eff}}}}} \end{aligned}$$
(43)

Note that \(\alpha \) can be obtained from the above expression, in combination with the derivative of Eq. (36) and the transformation of Eq. (34):

$$\begin{aligned} Q = {\phi _{{ eff}}}\frac{{\omega (k)r_c^2}}{{32\pi }}\frac{{(1 - {x^4})}}{{(1 - {x^6})}} \end{aligned}$$
(44)

while in the case of constant \({\phi _{{ eff}}}\) and \({r_c} = 1\), the analog of isothermal compressibility can be derived from Eqs. (31) and (34):

$$\begin{aligned} \begin{aligned} {k_T}&= \frac{1}{Q}{\left( {\frac{{\partial Q}}{{\partial {\phi _{{ eff}}}}}} \right) _{{T_{{ eff}}}}}\\&= \frac{1}{Q}\frac{{{{\left( {\frac{{\partial {T_{{ eff}}}}}{{\partial x}}} \right) }_Q}}}{{{{\left( {\frac{{\partial {T_{{ eff}}}}}{{\partial x}}} \right) }_Q}{{\left( {\frac{{\partial {\phi _{{ eff}}}}}{{\partial Q}}} \right) }_x} - {{\left( {\frac{{\partial {T_{{ eff}}}}}{{\partial Q}}} \right) }_x}{{\left( {\frac{{\partial {\phi _{{ eff}}}}}{{\partial x}}} \right) }_Q}}} \end{aligned} \end{aligned}$$
(45)

In Fig. 11, we plot the change of the entropy S with the analog of isothermal compressibility and volume expansion coefficient, for the special case of \(q =-0.2\) and \({\phi _{{ eff}}} = 0.2\)). One can clearly see from the plot that the phase transition of the thermodynamic system of ECBH spacetime appears at \(S = {S_0} = 55.0477\), \({T_{{ eff}}}=T_{{ eff}}^0=0.3560\), \({\phi _{{ eff}}}=0.2\), which satisfies the requirements of thermodynamic second-order phase transition in the \({C_{{\phi _{{ eff}}}}} - S\), \(\alpha - S\), \({k_T} - S\) and \(G - {T_{{ eff}}}\), \(G - S\) diagrams [78, 79].

Following the same direction, given the analogy between the thermodynamic state variables and black hole parameters, the Maxwell relation provide the following expressions as

$$\begin{aligned} \begin{aligned} - {\left( {\frac{{\partial {\phi _{{ eff}}}}}{{\partial {T_{{ eff}}}}}} \right) _S} = {\left( {\frac{{\partial S}}{{\partial Q}}} \right) _{{\phi _{{ eff}}}}}, \\ - {\left( {\frac{{\partial {\phi _{{ eff}}}}}{{\partial {T_{{ eff}}}}}} \right) _Q} = {\left( {\frac{{\partial S}}{{\partial Q}}} \right) _{{T_{{ eff}}}}} \end{aligned} \end{aligned}$$
(46)

and

$$\begin{aligned} \begin{aligned} -{\left[ {{{\left( {\frac{{\partial {\phi _{{ eff}}}}}{{\partial {T_{{ eff}}}}}} \right) }_S}} \right] ^c} = {\left[ {{{\left( {\frac{{\partial S}}{{\partial Q}}} \right) }_{{\phi _{{ eff}}}}}} \right] ^c},\\{\left[ { - {{\left( {\frac{{\partial {\phi _{{ eff}}}}}{{\partial {T_{{ eff}}}}}} \right) }_Q}} \right] ^c} = {\left[ {{{\left( {\frac{{\partial S}}{{\partial Q}}} \right) }_{{T_{{ eff}}}}}} \right] ^c} \end{aligned} \end{aligned}$$
(47)

Here the footnote c denotes the value of physical quantities at the critical point. Then substituting Eqs.  (47) into (41)–(42), one may straightforwardly get

$$\begin{aligned} \begin{aligned} \frac{{\varDelta {C_{{\phi _{{ eff}}}}}}}{{T_{{ eff}}^c{Q^c}\varDelta \alpha }} = {\left[ {{{\left( {\frac{{\partial S}}{{\partial Q}}} \right) }_{{\phi _{{ eff}}}}}} \right] ^c},\\ \frac{{\varDelta \alpha }}{{\varDelta {k_T}}} = {\left[ {{{\left( {\frac{{\partial S}}{{\partial Q}}} \right) }_{{T_{{ eff}}}}}} \right] ^c} \end{aligned} \end{aligned}$$
(48)

The critical point is determined through

$$\begin{aligned} \begin{aligned}&{\left( {\frac{{\partial {\phi _{{ eff}}}}}{{\partial Q}}} \right) _{{T_{{ eff}}}}} = 0, \\&{\left( {\frac{{{\partial ^2}{\phi _{{ eff}}}}}{{\partial {Q^2}}}} \right) _{{T_{{ eff}}}}} = 0 \end{aligned} \end{aligned}$$
(49)

and it is convenient to rescale some quantities of Eq. (45) in the following way:

$$\begin{aligned} {\left( {\frac{{\partial {\phi _{{ eff}}}}}{{\partial Q}}} \right) _{{T_{{ eff}}}}}= & {} \frac{{{{\left( {\frac{{\partial {T_{{ eff}}}}}{{\partial x}}} \right) }_Q}{{\left( {\frac{{\partial {\phi _{{ eff}}}}}{{\partial Q}}} \right) }_x} - {{\left( {\frac{{\partial {T_{{ eff}}}}}{{\partial Q}}} \right) }_x}{{\left( {\frac{{\partial {\phi _{{ eff}}}}}{{\partial x}}} \right) }_Q}}}{{{{\left( {\frac{{\partial {T_{{ eff}}}}}{{\partial x}}} \right) }_Q}}}\nonumber \\= & {} 0 \end{aligned}$$
(50)
$$\begin{aligned} {\left( {\frac{{\partial S}}{{\partial Q}}} \right) _{{\phi _{{ eff}}}}}= & {} - {\left( {\frac{{\partial {\phi _{{ eff}}}}}{{\partial Q}}} \right) _x}{\left( {\frac{{\partial x}}{{\partial {\phi _{{ eff}}}}}} \right) _Q}\frac{{dS(x)}}{{dx}}, \end{aligned}$$
(51)
$$\begin{aligned} {\left( {\frac{{\partial S}}{{\partial Q}}} \right) _{{T_{{ eff}}}}}= & {} - {\left( {\frac{{\partial {T_{{ eff}}}}}{{\partial Q}}} \right) _x}{\left( {\frac{{\partial x}}{{\partial {T_{{ eff}}}}}} \right) _Q}\frac{{dS(x)}}{{dx}} \end{aligned}$$
(52)

Two further comments should be made based on the above calculations. First of all, as is implied from the combination of Eqs. (50)–(52):

$$\begin{aligned} {\left[ {{{\left( {\frac{{\partial S}}{{\partial Q}}} \right) }_{{\phi _{{ eff}}}}}} \right] ^c} = {\left[ {{{\left( {\frac{{\partial S}}{{\partial Q}}} \right) }_{{T_{{ eff}}}}}} \right] ^c} \end{aligned}$$
(53)

our analysis demonstrates the validity of the Ehrenfest equations at the critical point [77]. More interestingly, the Prigogine–Defay (PD) ratio

$$\begin{aligned} \varPi = \frac{{\varDelta {C_{{\phi _{{ eff}}}}}\varDelta {k_T}}}{{T_{{ eff}}^c{Q^c}{{(\varDelta \alpha )}^2}}} = 1 \end{aligned}$$
(54)

which can be calculated from the combination of Eqs. (48) and (53), agrees very well with the previous results derived in the AdS spacetime [80]. Such quantity contains information about possible phase transitions in the system and allows us to uncover a rich phase structure for electrically charged hairy black holes [80].

5 Conclusion and discussion

The subject of black hole thermodynamics continues to be one of great importance in gravitational physics. Over the past forty years many of the studies in this field have concentrated on the thermodynamics of de Sitter spacetime, in which the black hole horizon and the cosmological horizon are always considered to be different thermodynamic systems with different radiation temperatures [20,21,22]. In this paper, in the framework of de Sitter spacetime satisfying the first thermodynamics law, we discuss the effective thermodynamic quantities of higher dimensional electrically charged hairy black holes, by considering the interaction between the black hole horizon and the cosmological horizon. Here we summarize our main conclusions in more detail:

  • Considering the correlation between the black hole horizon and the cosmological horizon, we obtain the effective temperature and the total entropy of the spacetime. Our results show that the interaction between the two horizons, which is only determined by the position of the horizons, could significantly contribute to the total entropy of de Sitter spacetime.

  • As can be clearly seen from the \(S(x)-x\), \({T_{{ eff}}}-x\) diagrams (shown in Figs. 5 and 6) and the expression of heat capacity \(C = {T_{{ eff}}}\left( {\frac{{\partial S(x)}}{{\partial {T_{{ eff}}}(x)}}} \right) \), the ECBH spacetime is thermodynamically unstable when \(1 \ge x > {x_c}\). However, we cannot expect the existence of such ECBH black holes in the Universe, considering the fact that there exist only ECBH black holes satisfying the condition of \({x_0}< x < {x_c}\) [81].

  • The investigation of the thermodynamic quantities of such spacetime indicates that, under certain conditions both zero-order and second-order phase transition will appear. However, one could also note the absence of first-order phase transition in the electrically charged hairy black holes, which is different from the case in AdS spacetime [66, 67].

  • Turning to the classification of phase transition in Ehrenfest’s equations, our findings indicate that the possible existence of first-order phase transitions can be ruled out, while the onset of higher-order (continuous) phase transitions is strongly supported in the thermodynamic system of ECBH spacetime. More interestingly, our analysis demonstrates the validity of the Ehrenfest equations at the critical point, and furthermore indicates the similarity of Prigogine–Defay (PD) ratio between ECBH spacetime and AdS spacetime [80].

  • Therefore, our analysis in this paper has theoretically revealed the conditions of phase transition and thermodynamic stability in de Sitter spacetime, which, to some extent, may contribute to the construction of the overall evolution history of the Universe, as well as the classical and quantum properties of the de Sitter spacetime.