1 Motivation

In the backgrounds of string theory and brane world cosmologies, there have been predicted that spacetimes possess extra dimensions. This motivates extending gravity theory to higher spacetime dimensions. The Einstein tensor cannot be regarded as the most prevalent conserved symmetric quantity when higher dimensional geometries are taken into consideration. The Lovelock gravity theory (LGT) is the most intriguing adaptation of general relativity (GR) in extra dimensions [1]. One of the remarkable properties of LGT is its reduction to GR in four spacetime dimensions. This theory’s gravitational field equations only have derivatives of metric up to the second order, hence its quantization is ghost-free [2]. The investigation of Lovelock black holes has recently received renewed interest since LGT of order two, commonly known as Gauss–Bonnet gravity, is also observed in the low energy limit of string theory [2,3,4]. The action describing LGT can be written as

$$\begin{aligned} {\mathcal {I}}_G=\int d^dx\sqrt{-g}\sum _{k=0}^{k_{max}}\alpha _k{\mathcal {L}}_k. \end{aligned}$$
(1.1)

Here, g is the determinant of the metric tensor, \(\alpha _k\) are arbitrary coupling parameters, and \({\mathcal {L}}_k\)’s represent the Euler densities corresponding to the 2k-dimensional manifolds which can be defined as

$$\begin{aligned} {\mathcal {L}}_k=\frac{1}{2^k}\delta ^{\mu _1\nu _1\ldots \mu _{k}\nu _{k}}_{\sigma _1\lambda _1\ldots \sigma _{k}\lambda _{k}}R^{\sigma _1\lambda _1}_{\mu _1\nu _1}\ldots R^{\sigma _k\lambda _k}_{\mu _k\nu _k}, \end{aligned}$$
(1.2)

where \(k_{max}=[\frac{d-1}{2}]\) in which the brackets stand for the integer part of \((d-1)/2.\) Furthermore, \(\delta ^{\mu _1\nu _1\ldots \mu _{k}\nu _{k}}_{\sigma _1\lambda _1\ldots \sigma _{k}\lambda _{k}}\) is the generalized Kronecker delta, and \(R^{\sigma \lambda }_{\alpha \beta }\) are the components of the Riemannian tensor.

Although LGT includes the majority of Einstein’s presumptions, there exist some limitations to this gravity theory as well. For instance, it is impossible to uniquely determine the time development of fields in higher dimensional spacetimes. In other words, for a particular surface at initial time \(t=t_0,\) the dynamical equations do not specify all the values of the field at times greater than \(t_0.\) This lack of uniqueness results from the nonlinear terms of velocities that appear in the action [5, 6]. Additionally, the action includes additional \([(d+1)/2]\) arbitrary parameters along with the cosmological constant \(\Lambda \) and Newtonian constant G [7]. The inclusion of these arbitrary parameters makes it challenging to extract an explicit black hole solution. Thus, the investigations regarding the physical properties of the black holes become complicated. Apart from these difficulties, some other effects brought by these parameters have also been pointed out. They are: (1) the equations of motion provide at most \((d-1)/2\) dissimilar solutions, (2) each of which may have horizons for both positive and negative energy, and (3) the entropy density does not rise with the horizon radius, which results the non-satisfaction of the second law of black hole thermodynamics. All these issues point towards the need for a special selection of arbitrary parameters. In light of this, Bañados, Teitelboim and Zanelli made appropriate parameter choices and found an explicit solution to the gravitational field equations. Based upon this choice, a new special case of LGT, called the dimensionally continued gravity (DCG), was developed [7]. In Refs. [7,8,9,10], different spherically symmetric solutions describing static black holes of DCG are derived. Additionally, thermodynamic properties of these dimensionally continued black holes are probed as well [7,8,9,10,11,12,13,14].

The illustrious no-hair theorems imply that asymptotically flat black holes with conformal scalar hair do not exist in the framework of GR [15, 16]. The four-dimensional asymptotically flat hairy black holes were discovered but the configuration of a scalar field on the event horizon was not well-defined [17]. Additionally, it is claimed that the higher dimensional geometries cannot support the existence of hairy black holes [18]. Three- and four-dimensional conformal hairy black hole solutions with \(\Lambda \ne 0\) have recently been found [19,20,21,22,23,24]. Note that the configuration of a conformal scalar field is convergent everywhere for these gravitating objects. Because of no-go results, it was previously believed that higher dimensional hairy black holes did not exist [25]. It is worth noting that the no hair theorem was not originally applied to conformally coupled theories, but rather to minimally coupled scalar fields with self-interaction (subject to certain restrictions). In fact, the theorem was precisely avoided by using the conformally coupled model to relax the scalar field’s behaviour on the horizon. Hence, the hairy black holes in diverse dimensions could be investigated since it has been demonstrated that gravity can be non-minimally coupled with the real scalar field [26, 27]. Introducing the constituent

$$\begin{aligned} S^{\sigma \lambda }_{\mu \nu }= & {} \psi ^2R^{\sigma \lambda }_{\mu \nu }-2\delta ^{[\sigma }_{[\mu } \delta ^{\lambda ]}_{\nu ]}\nabla _{\beta }\psi \nabla ^{\beta }\psi -4\psi \delta ^{[\sigma }_{[\mu }\nabla _{\nu ]}\nabla ^{\lambda ]}\psi \nonumber \\{} & {} +8\delta ^{[\sigma }_{[\mu }\nabla _{\nu ]}\psi \nabla ^{\lambda ]}\psi . \end{aligned}$$
(1.3)

which transforms homogeneously as \(S^{\gamma \alpha }_{\mu \nu }\rightarrow \Omega ^{-4}S^{\gamma \alpha }_{\mu \nu }\) under the conformal transformations i.e. \(g_{\rho \sigma }\rightarrow \Omega ^2g_{\rho \sigma }\) and \(\psi \rightarrow \psi ,\) one can construct the following conformal invariant action

$$\begin{aligned}{} & {} {\mathcal {I}}_s=\int d^dx\sqrt{-g}\sum _{k=0}^{k_{max}}\nonumber \\{} & {} \quad \times \bigg (b_k\psi ^{d-4k}\delta ^{\mu _1\nu _1\ldots \mu _{k}\nu _k}_{\sigma _1\lambda _1\ldots \sigma _k\lambda _k}S^{\sigma _1\lambda _1}_{\mu _1\nu _1}\ldots S^{\sigma _{k}\lambda _{k}}_{\mu _{k}\nu _{k}}\bigg ), \end{aligned}$$
(1.4)

where \(g_{\mu \nu }\) and \(\psi \) are, respectively, the metric tensor and the scalar field, and \(b_k\) are the conformal coupling parameters.

It is worth noting that the linearized form of gravity theory described by Eq. (1.4) is free of ghosts. When \(k=1,\) the potential associated with the scalar field of action (1.4) becomes \(V(\psi )=\frac{\lambda }{4!}\psi ^4.\) This makes the non-minimal coupling term equal to \((-1/12)R\psi ^2\) where R is the Ricci scalar [27, 28]. Different hairy black hole solutions within this set-up were found in Refs. [27,28,29,30,31,32]. The conformal scalar field \(\psi \) associated with these black hole solutions is not only well-defined in the exterior of the black hole but converges on the outer horizon as well. It is believed that the presence of a conformal scalar field produces unavoidable effects on the stability of the black hole systems [29, 30]. Hairy black hole solutions of DCG with nonlinear electromagnetic sources were recently derived and their thermodynamic properties have also been explored [33,34,35]. Recently, the hairy black holes in the context of quartic quasi-topological gravity and power law model of Yang–Mills field have also been investigated [36].

At present time, numerous experimental observations showed that our Universe goes through a phase of accelerated expansion. A plausible explanation is that the Universe expands due to the gravitationally self-repulsive dark energy. According to current cosmological observational data, our Universe is composed of 4.9% baryon matter, 68.3% dark energy, and 26.8% dark matter [37,38,39,40]. Due to this dominance of dark matter and dark energy in our Universe, it is quite motivating to investigate the effects of these mysterious things on the physical properties of black holes. One of the important candidates for the mysterious dark energy is quintessence and can be exemplified through the equation of state \(p_{quint} = \omega \rho _{quint},\) in which \(p_{quint}\) and \(\rho _{quint}\) are, respectively, the pressure and density whereas the parameter \(\omega _q\) ranges in the interval \(-1< \omega _q < -1/3\) [41,42,43,44,45]. There has been a lot of interest in examining how quintessence affects spherically symmetric black holes. Kiselev [46], for instance, developed the generalized Schwarzschild solution with quintessence. The effects of quintessence on the charged, Nariai, and higher dimensional black holes were also covered in Refs. [47,48,49,50]. Quasi-normal modes [51, 52], thermodynamic properties [53,54,55,56] and shadows [57, 58] of the black holes influenced by quintessence were also studied. The generalization of Kiselev solutions with axially symmetric backgrounds was also obtained in Refs. [59, 60]. Recent studies have also looked into a number of charged and uncharged Lovelock black holes with quintessence [61,62,63,64,65]. Additionally, under the combined influence of string clouds and quintessential dark energy, Lovelock black holes with scalar hair are explored in Ref. [66].

Looking intently at the dominance of the dark sector, it is proposed that the unified dark fluid (hybrid of dark matter and dark energy) is mainly contributing to this sector. The Chaplygin gas [67] and generalized Chaplygin gas [68, 69] are two of the unified dark fluid models that are frequently used for the exploration of accelerated expansion of the Cosmos [70,71,72]. The intriguing characteristic of the Chaplygin-like dark fluid is that it dynamically exhibits dark matter behaviour in the early time, and it behaves as dark energy in the late time. Recently, charged Lovelock black holes in a unified dark fluid model have been studied [73]. Moreover, Lovelock black holes sourced by power-Yang–Mills field and unified dark fluid have also been studied [74]. Note that the Chaplygin-like dark fluid in the surrounding of these black holes was characterized by the equation of state \(p_{df}=-B/\rho _{df}.\) Here, the quantities \(p_{df}\) and \(\rho _{df}\) are the pressure and energy density, respectively, of the unified dark fluid while B is a positive constant. Inspired by the above background, in this work we have considered the Chaplygin-like dark fluid as a matter source and worked out the dimensionally continued hairy black hole solutions. Furthermore, the effects of this unified dark fluid on the thermodynamic and physical characteristics of these objects are also studied. Furthermore, Lovelock black holes within this set-up are also briefly studied.

Our paper follows the following outline. The solution describing dimensionally continued hairy black holes surrounded by Chaplygin-like dark fluid is derived in Sect. 2. In Sect. 3, we look into the thermodynamics of these hairy black holes. Moreover, Sect. 4 provides a brief discussion of the Hawking radiation linked with the dimensionally continued black holes. In Sect. 5, we discuss the topological black holes of LGT supported by Chaplygin-like dark fluid. We conclude our paper with some remarks in Sect. 6.

2 Dimensionally continued black holes sourced by conformal scalar field and Chaplygin-like dark fluid

The d-dimensional action function of Lovelock-scalar gravity including matter sources can be given as

$$\begin{aligned} I= & {} \frac{1}{16\pi G}\int d^dx\sqrt{-g}\left[ \sum _{k=0}^{k_{max}}\frac{1}{2^k}\delta ^{\mu _1\nu _1\ldots \mu _{k}\nu _{k}}_{\sigma _1\lambda _1\ldots \sigma _{k}\lambda _k} \right. \nonumber \\{} & {} \times \left. \bigg (\alpha _k R^{\sigma _1\lambda _1}_{\mu _1\nu _1}\ldots R^{\sigma _{k}\lambda _{k}}_{\mu _{k}\nu _{k}} \right. \nonumber \\{} & {} \left. +16\pi G b_k\psi ^{d-4k}S^{\sigma _1\lambda _1}_{\mu _1\nu _1}\ldots S^{\sigma _{k}\lambda _{k}}_{\mu _{k}\nu _{k}}\bigg )+4\pi G{\mathcal {L}}_M\right] , \end{aligned}$$
(2.1)

where \({\mathcal {L}}_M\) denotes the matter’s Lagrangian density and \(\alpha _k\) are arbitrary Lovelock parameters. This will lead to a special class of LGT, i.e., DCG if the arbitrary parameters \(\alpha _k\)’s are considered as [7, 11, 33,34,35]

$$\begin{aligned} \alpha _k=\left( \begin{array}{c} n-1 \\ k \end{array} \right) \frac{(d_1-2k)!}{d_2!l^{-2(k+1-n)}}, \end{aligned}$$
(2.2)

in which the cosmological constant and the parameter l are related by \(\Lambda =-d_1d_2/2l^2\) and a positive integer n is related to the dimensionality parameter d by \(d=2n+2\) in even and \(d=2n+1\) in odd dimensional spacetimes. Note that in the above equation and throughout our work, we are using \(d_k=d-k\) for simplicity. It is important to mention that this theory corresponds to the Born–Infeld gravity for \(d=2n+2\) and to the Chern–Simons gravity for \(d=2n+1\) [7,8,9]. From the action (2.1) and relation (2.2), it is obvious that the parameters that remain within this theory are only G and l. Using the action principle one can derive the equations of motion as

$$\begin{aligned}{} & {} \sum _{k=0}^{k_{max}}\frac{\alpha _k}{2^{k+1}}\delta ^{\alpha \sigma _1\lambda _1\ldots \sigma _k\lambda _{k}}_{\beta \kappa _1\rho _1\ldots \kappa _k\rho _{k}} R^{\kappa _1\rho _1}_{\sigma _1\lambda _1}\ldots R^{\kappa _{k}\rho _{k}}_{\sigma _{k}\lambda _{k}}\nonumber \\{} & {} \quad =-16\pi G{\mathcal {T}}^{(M)\alpha }_{\beta }-16\pi G{\mathcal {T}}^{(S)\alpha }_{\beta }, \end{aligned}$$
(2.3)

where \({\mathcal {T}}^{(M)\alpha }_{\beta }\) is the matter tensor

$$\begin{aligned} {\mathcal {T}}^{(M)}_{\alpha \beta }=-\frac{2}{\sqrt{-g}}\frac{\delta {\mathcal {I}}_M}{\delta g^{\alpha \beta }}. \end{aligned}$$
(2.4)

Note that \({\mathcal {I}}_M\) is the action that describes the matter sources, for instance, unified dark fluid. Similarly, the contribution of a scalar field is described by the matter tensor

$$\begin{aligned} {\mathcal {T}}^{(S)\alpha }_{\beta }=\sum _{k=0}^{k_{max}} \frac{b_k}{2^{k+1}}\psi ^{d-4k}\delta ^{\alpha \sigma _1\lambda _1\ldots \sigma _k\lambda _{k}}_{\beta \kappa _1\rho _1\ldots \kappa _k\rho _{k}}S^{\kappa _1\rho _1}_{\sigma _1\lambda _1}\ldots S^{\kappa _k\rho _{k}}_{\sigma _{k}\lambda _{k}}. \end{aligned}$$
(2.5)

The equations of motion associated with the conformal scalar field can be obtained as

$$\begin{aligned} \sum _{k=0}^{k_{max}}(d-2k)\frac{b_k}{2^k}\psi ^{d_1-4k}\delta ^{\sigma _1\lambda _1\ldots \sigma _{k}\lambda _k}_{\kappa _1\rho _1\ldots \kappa _{k}\rho _k}S^{\kappa _1\rho _1}_{\sigma _1\lambda _1}\ldots S^{\kappa _{k}\rho _{k}}_{\sigma _{k}\lambda _{k}}=0. \end{aligned}$$
(2.6)

By enforcing Eq. (2.6), one can verify that the matter tensor (2.5) is trace-free. This shows the conformal invariance of the real scalar field \(\psi .\)

Now assume the metric ansatz for the d-dimensional spacetime as

$$\begin{aligned} ds^2=-f(r)dt^2+\frac{dr^2}{f(r)}+r^2d\Upsilon ^{2}_{d_2}, \end{aligned}$$
(2.7)

where \(d\Upsilon ^{2}_{d_2}\) refers to a line element of the \(d_2\)-dimensional hypersurface of constant curvature \(d_2d_3\kappa \) and can be explicitly expressed as

$$\begin{aligned}{} & {} d\Upsilon ^2_{d_2}\nonumber \\{} & {} \quad =\left\{ \begin{array}{ll} d\theta _1^2+\sum _{j=2}^{d-2}\prod _{l=1}^{j-1}\sin ^2\theta _l d\theta _j^2, &{} \quad \kappa =1,\\ d\theta _1^2+\sinh ^2\theta _1d\theta _2^2+\sinh ^2\theta _1\sum _{j=3}^{d-2}\\ \prod _{l=2}^{j-1}\sin ^2\theta _ld\theta ^2_j, &{} \quad \kappa =-1,\\ \sum _{j=1}^{d-2}d\phi _j^2, &{} \quad \kappa =0. \end{array}\right. \nonumber \\ \end{aligned}$$
(2.8)

Suppose that the unified dark fluid has a nonlinear equation of state, i.e., \(p_{df}=-B/\rho _{df},\) in which B is a constant. Then by using Eq. (2.7), one can define the matter tensor of the Chaplygin-like dark fluid as

$$\begin{aligned}&{\mathcal {T}}^{(M) t}_{t}=\Psi (r), \nonumber \\&{\mathcal {T}}^{(M) i}_{t}=0,\nonumber \\&{\mathcal {T}}^{(M) j}_{i}=\Xi (r)\frac{r_ir^j}{r_kr^k}+\Pi (r)\delta ^{j}_{i}. \end{aligned}$$
(2.9)

Taking isotropic average over the angles

$$\begin{aligned}{}[r_ir^j]_{A}=\frac{r_kr^k \delta ^{j}_{i}}{d_1}, \end{aligned}$$
(2.10)

one may find

$$\begin{aligned}{}[{\mathcal {T}}^{(M) j}_{i}]_{A}=\bigg (\frac{\Xi (r)}{d_1}+\Pi (r)\bigg )\delta ^{j}_{i}=p_{df}(r)\delta ^{j}_{i}=-\frac{B}{\rho _{df}(r)}.\nonumber \\ \end{aligned}$$
(2.11)

Implementing the assumption of staticity and spherical symmetry, \({\mathcal {T}}^{(M) t}_{t}={\mathcal {T}}^{(M) r}_{r}=-\rho _{df}(r),\) on (2.11) one obtains

$$\begin{aligned} {\mathcal {T}}^{(M)t}_t= & {} {\mathcal {T}}^{(M)r}_r=\Psi (r)=-\rho _{df}(r), \nonumber \\ \Xi (r)= & {} -\frac{d_1\rho _{df}}{d_2}+\frac{d_1B}{d_2\rho _{df}},\nonumber \\ \Pi (r)= & {} \frac{\rho _{df}}{d_2}-\frac{d_1B}{d_2\rho _{df}}. \end{aligned}$$
(2.12)

Similarly, the other components of Eq. (2.9) are determined as

$$\begin{aligned}{} & {} {\mathcal {T}}^{(M) \theta _1}_{\theta _1}={\mathcal {T}}^{(M) \theta _2}_{\theta _2}=\cdots ={\mathcal {T}}^{(M) \theta _{d_2}}_{\theta _{d_2}}\nonumber \\{} & {} \quad =\frac{1}{d_2}\rho _{df}(r)-\frac{d_1B}{d_2\rho _{df}(r)}. \end{aligned}$$
(2.13)

By defining the configuration of a scalar field as

$$\begin{aligned} \psi (r)=\frac{X}{r}, \end{aligned}$$
(2.14)

one can show that this form satisfies Eq. (2.6) if the equations

$$\begin{aligned} \sum _{k=1}^{k_{max}}kb_k\frac{d_1!}{(d_1-2k)!}\kappa ^{k-1}X^{2-2k}=0, \end{aligned}$$
(2.15)

and

$$\begin{aligned} \sum _{k=1}^{k_{max}}b_k\frac{d_1!(d^2-d+4k^2)}{(d_1-2k)!}\kappa ^{k}X^{-2k}=0, \end{aligned}$$
(2.16)

are true. Since it is a system of two equations in one unknown X so one of them should be a constraint on the conformal coupling parameters \(b_k.\)

Using Eqs. (2.12)–(2.13) and conservation of energy–momentum, it is possible to obtain the first order differential equation for energy density \(\rho _{df}\) as

$$\begin{aligned} \rho _{df}'(r)+\frac{d_1}{r}\rho _{df}(r)=\frac{Bd_1}{r\rho _{df}}, \end{aligned}$$
(2.17)

which possesses the solution

$$\begin{aligned} \rho _{df}(r)=\bigg (B+\frac{S^2}{r^{2d_1}}\bigg )^{1/2}. \end{aligned}$$
(2.18)

Here, prime denotes the derivative with respect to r,  and \(S^2\) with positive S serves as the integration constant. It can be observed that the energy density (2.18) appears in a form identical to that derived in Refs. [73, 74]. Moreover, it can also be understood from Eq. (2.18) that for higher values of the coordinate r,  energy density tends to value \(\sqrt{B}.\) This indicates that far away from the gravitational source, Chaplygin-like dark fluid behaves like the cosmological constant.

Thus, by putting Eq. (2.2), metric ansatz (2.7), the energy–momentum tensor of the Chaplygin-like dark fluid (2.12)–(2.13) with the value of \(\rho _{df}\) in Eq. (2.18), and Eqs. (2.14)–(2.16) for the conformal scalar field \(\psi (r)\) in Eq. (2.3), the following independent equation of motion describing dimensionally continued gravitational field is derived

$$\begin{aligned} \frac{d}{dr}\bigg [r^{d_1}\bigg (\frac{\kappa -f(r)}{r^2}{+}\frac{1}{l^2}\bigg )^{n-1}\bigg ]= & {} \frac{32\pi Gr^{d_2}}{d_1d_2}\bigg (B{+}\frac{S^2}{r^{2d_1}}\bigg )^{1/2}\nonumber \\{} & {} -\frac{32\pi G{\mathcal {H}}}{d_1r^2}, \end{aligned}$$
(2.19)

where

$$\begin{aligned} {\mathcal {H}}=\sum _{k=0}^{k_{max}}b_k\frac{d_2!\kappa ^{k}X^{d-2k}}{(d_2-2k)!}. \end{aligned}$$
(2.20)

By solving the above Eq. (2.19) one can get the solution

$$\begin{aligned} f(r)= & {} \kappa +\frac{r^2}{l^2}-r^2\bigg [\frac{16\pi G M}{V_{d_2}r^{d_1}}+\frac{\delta _{d,2n-1}}{r^{d_1}}+\frac{32\pi G {\mathcal {H}}}{r^d}\nonumber \\{} & {} +\frac{32\pi G}{d_1^2d_2}\bigg (B+\frac{S^2}{r^{2d_1}}\bigg )^{1/2}\nonumber \\{} & {} -\frac{32\pi G S}{d_2d_1^2r^{d_1}}sinh^{-1}\bigg (\frac{S}{\sqrt{B}r^{d_1}}\bigg )\bigg ]^{\frac{1}{n-1}}, \end{aligned}$$
(2.21)

where \(V_{d_2}\) denotes the volume of the \(d_2\)-dimensional hyper-surface.

Fig. 1
figure 1

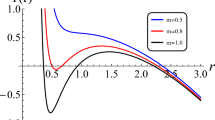
Plot of f(r) (Eq. (2.21)) for fixed values \(l=2,\) \(M=1,\) \(\delta _{d,2n-1}=0.3,\) \(V_{d_2}=100,\) \(B=0.5,\) \(S=1\) and \({\mathcal {H}}=1\)

Full size image
Fig. 2
figure 2

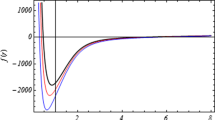
Plot of f(r) (Eq. (2.21)) for fixed values \(l=2,\) \(M=0.5,\) \(\delta _{d,2n-1}=0.3,\) \(V_{d_2}=100,\) \(n=2,\) \(d=5\) and \({\mathcal {H}}=1\)

Full size image
Fig. 3
figure 3

Plot of f(r) (Eq. (2.21)) for fixed values \(l=2,\) \(M=0.5,\) \(\delta _{d,2n-1}=0.3,\) \(V_{d_2}=100,\) \(n=2,\) \(d=5,\) \(B=0.05\) and \(S=0.5\)

Full size image

The integration constant M in Eq. (2.21) symbolizes the black hole’s mass whereas \(\delta _{d,2n-1}\) takes those values for which the event horizon shrinks to a point in the limit \(M\rightarrow 0\) [8, 11, 33,34,35]. The way that solution (2.21) behaves in various dimensions of spacetime is demonstrated in Fig. 1. The black hole’s horizons correspond to the points at which the solution intersects with the r-axis. It is noted that the black hole possesses one non-extreme horizon for any fixed values of the parameters l,  M,  \(\delta _{d,2n-1},\) B,  S,  and \({\mathcal {H}}.\) Hence, the solution (2.21) can be regarded as the Schwarzschild-like solution of DCG in the presence of a unified dark fluid. Similarly, Fig. 2 displays the plots of f(r) for various values of the parameters B and S in five-dimensional spacetimes. One can see that these parameters largely affect the behaviour of the solution in the exterior spacetime of the black hole. It should be noted that in the absence of a conformal scalar field, i.e when \({\mathcal {H}}\) vanishes, one will get a new class of non-hairy black holes of DCG. This corresponds to the case \({\mathcal {H}}=0\) in Fig. 3. Additionally, one can see that the event horizon’s radius becomes larger when the parameter \({\mathcal {H}}\) increases. Since the equations associated with a conformal scalar field, i.e., (2.15)–(2.16) are not valid in four-dimensional spacetimes, so, the above family of black hole solutions with scalar hair is well-defined only for \(d>4.\) This behaviour of the hairy black holes surrounded by the dark fluid is similar to those which were introduced in the backgrounds of electromagnetic fields, quintessence, and the cloud of strings [33,34,35, 66].

The Ricci and Kretschmann scalars associated with the ansatz (2.13) are described, respectively, by

$$\begin{aligned} R=\bigg [d_2d_3\bigg (\frac{\kappa -f(r)}{r^2}\bigg )-f''(r)-\frac{2d_2}{r}f'(r)\bigg ], \end{aligned}$$
(2.22)

and

$$\begin{aligned} {\mathcal {K}}=\bigg [2d_2d_3\bigg (\frac{\kappa -f(r)}{r^2}\bigg )^2- \big (f''(r)\big )^2+\frac{2d_2}{r^2}\big (f'(r)\big )^2\bigg ].\nonumber \\ \end{aligned}$$
(2.23)

Using the metric function (2.21) and its derivatives one can show that both of the above invariants are not convergent in the vicinity of \(r=0.\) Hence, the metric function (2.21) is portraying the existence of the higher dimensional black hole.

3 Thermodynamic properties of dimensionally continued black holes

Here, we want to figure out the basic thermodynamic quantities and inspect the impacts of Chaplygin-like dark fluid on the black hole’s thermodynamic stability. From the stipulation \(f(r_+)=0,\) it is easy to illustrate the finite mass as

$$\begin{aligned} M= & {} \frac{V_{d_2}d_2r^{d_1}_+}{16\pi G}\bigg [\bigg (\frac{1}{r_+^2}+\frac{1}{l^2}\bigg )^{n-1}- \frac{\delta _{d,2n-1}}{r_+^{d_1}}-\frac{32\pi G {\mathcal {H}}}{d_1r_+^{d}}\nonumber \\{} & {} -\frac{32\pi G}{d_2d_1^2} \sqrt{B+\frac{S^2}{r_+^{2d_1}}}+\frac{32\pi G S}{d_2d_1^2r_+^{d_1}}\sinh ^{-1}\bigg (\frac{S}{B^{1/2}r_+^{d_1}}\bigg )\bigg ]. \nonumber \\ \end{aligned}$$
(3.1)

Note that, we have considered the topological parameter \(\kappa \) equal to 1. The other cases, i.e., \(\kappa =-1,0\) can be argued correspondingly.

By implementing the definition of surface gravity, one may express Hawking temperature [75] as

$$\begin{aligned} T_H=\frac{1}{2\pi }\bigg (-\frac{1}{2}(\nabla _{\beta }{\mathfrak {X}}_{\gamma }) (\nabla ^{\gamma }{\mathfrak {X}}^{\beta })\bigg )^{\frac{1}{2}}, \end{aligned}$$
(3.2)

where \({\mathfrak {X}}_{\beta }\) denotes the temporal Killing vector field. Thus, one may find out the temperature as

$$\begin{aligned} T_{H}= & {} \frac{1}{4\pi }\bigg [\frac{(d_{2n}+1)}{(n-1)r_+}+\frac{d_1r_+}{(n-1)l^2}\nonumber \\{} & {} +\frac{(r_+^2+l^2)^{2-n}}{(n-1)l^{4-2n}r_+^{4-2n}}\bigg (\frac{32\pi G{\mathcal {H}}}{d_1r_+^{d_1}}\nonumber \\{} & {} -\frac{32\pi G r_+\big (B+\frac{S^2}{r_+^{2d_1}}\big )^{1/2}}{d_1d_2}\bigg )\bigg ]. \end{aligned}$$
(3.3)
Fig. 4
figure 4

Plot of the Hawking temperature \(T_H\) (Eq. (3.3)) as a function of \(r_+.\) The values of the other parameters are set to \(l=2,\) \(B=0.5,\) \(V_{d-2}=100,\) \(S=1.0,\) \(32\pi G=1\) and \({\mathcal {H}}=1\)

Full size image
Fig. 5
figure 5

Plot of the Hawking temperature \(T_H\) (Eq. (3.3)) as a function of horizon radius for several values of B and S. The particular values i.e. \(l=2,\) \(n=2,\) \(V_{d-2}=100,\) \(d=5,\) \(32\pi G=1,\) and \({\mathcal {H}}=1\) are also used

Full size image
Fig. 6
figure 6

Plot of the Hawking temperature \(T_H\) (Eq. (3.3)) as a function of horizon radius for several values of \({\mathcal {H}}.\) The particular values i.e. \(l=2,\) \(n=2,\) \(V_{d-2}=100,\) \(d=5,\) \(32\pi G=1,\) \(B=1.5,\) and \(S=1\) are also used

Full size image

The behaviour of the Hawking temperature \(T_H\) for various values of the dimensionality parameter and particular values of parameters B,  S and l can be demonstrated from Fig. 4. Correspondingly, Figs. 5 and 6 illustrate the effects of Chaplygin-like dark fluid and conformal scalar field on \(T_H\) in five-dimensional spacetime. One can observe that first the temperature of the hairy black hole decreases with the increase of \(r_+.\) However, after reaching its minimum value, it starts strictly increasing with the increase of horizon radius. Furthermore, the value \({\mathcal {H}}=0\) in Fig. 6 corresponds to the temperature of a non-hairy black hole. Here, the point at which the temperature vanishes defines horizon of the extremal black hole. Since we are studying the black holes of DCG, the area law should be disobeyed in general [76, 77]. In this regard, the entropy can be estimated from the Hamiltonian formalism [78,79,80]. The generalization to this formulation in the background of higher curvature gravities can be made from the employment of Wald’s method [81, 82]. Hence, the entropy associated with our solution (2.21) can be worked out as

$$\begin{aligned} S= & {} \frac{\Sigma _{d_2}}{4G}\sum _{k=1}^{k_{max}}\frac{kb_kd_2!X^{d-2k}}{(d-2k)!}\nonumber \\{} & {} + \frac{(n-1)\Sigma _{d_2}r_+^{d_{2n}+2}(r_+^2+l^2)^{n-1}}{4G(d_{2n}+2)l^{2n-2}}\nonumber \\{} & {} \times F_1\bigg (\bigg [1,\frac{d}{2}\bigg ],\bigg [\frac{d_{2n}+4}{2}\bigg ], \frac{-r_+^2}{l^2}\bigg ), \end{aligned}$$
(3.4)

where \(F_1\) refers to the Gaussian hypergeometric function. It is important to keep in mind that in the entropy given above, the effect of Chaplygin-like fluid originates from the event horizon radius \(r_+\) via Eq. (3.1). Once more, this behaviour resembles the Lovelock black holes discovered in Refs. [33,34,35, 61,62,63,64,65, 73, 74]. By considering the conformal parameters as extensive thermodynamic variables, one can generalize the first law as

$$\begin{aligned} dM=T_HdS+\sum _{k=0}^{k_{max}}{\mathcal {B}}^{(k)}db_k, \end{aligned}$$
(3.5)

with

$$\begin{aligned} T_H=\frac{\partial M}{\partial S}, \end{aligned}$$
(3.6)

and

$$\begin{aligned} {\mathcal {B}}^{(k)}=-\frac{d_2\Sigma _{d_2}}{r_+} \sum _{k=0}^{k_{max}}\frac{d_2!X^{d_{2k}}}{(d_{2}-2k)!}-\frac{\Sigma _{d_2} T_H}{4}\sum _{k=1}^{k_{max}}\frac{d_2!kX^{d_{2k}}}{d_{2k}!}.\nonumber \\ \end{aligned}$$
(3.7)

Our calculations show that Eq. (3.6) yields the same expression of temperature as Eq. (3.3). Thus, the first law is verified. In order to test the local thermodynamic stability, it is crucial to check the behaviour of heat capacity which can be defined as

$$\begin{aligned} C_H=T_{H}\frac{dS}{dT_H}. \end{aligned}$$
(3.8)

Consequently, from temperature (3.3) and Wald entropy (3.4) one can obtain

$$\begin{aligned} C_H=\frac{\bigg (\frac{d_{2n}+1}{r_+(n-1)}+\frac{d_1r_+}{(n-1)l^2}+ {\mathcal {Z}}_1\bigg )\bigg ((n-1)V_{d_2}r_+^{d+1}\big (\frac{1}{l^2}+ \frac{1}{r_+^2}\big )^n({\mathcal {N}}_1-{\mathcal {N}}_2)\bigg )}{4G(d_{2n}+2)(d_{2n}+4)(r_+^2+l^2)^2\bigg (\frac{d_1}{(n-1)l^2}- \frac{d_{2n}+1}{(n-1)r_+^2}+{\mathcal {Z}}_2-{\mathcal {Z}}_3\bigg )},\nonumber \\ \end{aligned}$$
(3.9)

where

$$\begin{aligned} {\mathcal {Z}}_1(r_+)= & {} \frac{2}{(n-1)}\bigg (\frac{1}{l^2}+\frac{1}{r_+^2} \bigg )^{2-n}\bigg (\frac{16\pi G{\mathcal {H}}}{d_1r_+^{d_1}}\nonumber \\{} & {} -\frac{16\pi Gr_+\big (B+\frac{S^2}{r_+^{2d_1}}\big )^{1/2}}{d_1d_2}\bigg ), \end{aligned}$$
(3.10)
$$\begin{aligned} {\mathcal {Z}}_2(r_+)= & {} \frac{4(n-2)\bigg (16\pi Gd_2{\mathcal {H}}-16\pi Gr_+^d\big (B+\frac{S^2}{r_+^{2d_1}}\big )^{1/2}\bigg )}{(n-1)d_1d_2r_+^{d+2} \big (\frac{1}{l^2}+\frac{1}{r_+^2}\big )^{n-1}},\nonumber \\ \end{aligned}$$
(3.11)
$$\begin{aligned} {\mathcal {Z}}_3(r_+)= & {} \frac{32\pi Gr_+^{2n-4}l^{2n-4}}{(n-1)(r_+^2+l^2)^{n-2}} \bigg [\frac{{\mathcal {H}}}{r_+^d}+\frac{1}{d_1d_2}\sqrt{B+\frac{S^2}{r_+^{2d_1}}}\nonumber \\{} & {} -\frac{S^2}{d_2r_+^{2d_1}}\bigg (B+\frac{S^2}{r_+^{2d_1}}\bigg )^{-1/2}\bigg ], \end{aligned}$$
(3.12)
$$\begin{aligned} {\mathcal {N}}_1(r_+)= & {} l^2(d_{2n}+4)(r_+^2d+(d_{2n}+2)l^2)\nonumber \\{} & {} \times F_1 \bigg (\bigg [1,\frac{d}{2}\bigg ],\bigg [\frac{d_{2n}+4}{2}\bigg ],\frac{-r_+^2}{l^2}\bigg ), \end{aligned}$$
(3.13)

and

$$\begin{aligned}{} & {} {\mathcal {N}}_2(r_+)=2dr_+^2(l^2+r^2_+)\nonumber \\{} & {} \quad \times F_1\bigg (\bigg [2,\frac{d+2}{2}\bigg ], \bigg [\frac{d_{2n}+6}{2}\bigg ],\frac{-r_+^2}{l^2}\bigg ), \end{aligned}$$
(3.14)
Fig. 7
figure 7

Dependence of specific heat \(C_H\) (Eq. (3.9)) on the event horizon in different dimensional spacetimes. The other parameters are fixed as \(l=2,\) \(32\pi G=1,\) \(B=1.5,\) \(V_{d_2}=100,\) \(S=5,\) and \({\mathcal {H}}=1\)

Full size image
Fig. 8
figure 8

Dependence of specific heat \(C_H\) (Eq. (3.9)) on the event horizon for various values of B and S. The particular values of the other parameters are selected as \(l=2,\) \(32\pi G=1,\) \(n=2,\) \(V_{d_2}=1,\) \(d=5\) and \({\mathcal {H}}=1\)

Full size image
Fig. 9
figure 9

Dependence of specific heat \(C_H\) (Eq. (3.9)) on the event horizon for various values of \({\mathcal {H}}.\) The other parameters are fixed as \(l=2,\) \(32\pi G=1,\) \(B=1.5,\) \(V_{d_2}=100,\) \(S=5,\) and \(d=5\)

Full size image

Figure 7 illustrates the possibility of stable black holes in various dimensions. The horizon radii of unstable black holes match the values of \(r_+\) that give negative heat capacity. Alternatively, the horizon radii of locally stable black holes are those values of \(r_+\) that give non-negative \(C_H.\) The first order phase transition occurs when this quantity vanishes. Similarly, the second order phase transitions correspond to the divergence of the heat capacity. Additionally, Figs. 8 and 9 show how Chaplygin-like dark fluid and scalar fields are dependent on local stability. The curve corresponding to \({\mathcal {H}}=0\) describes the behaviour of heat capacity associated with the non-hairy black hole. It is concluded that the heat capacity possesses no divergences when the impact of scalar field vanishes. Using Eqs. (3.1)–(3.4), one can obtain Gibb’s free energy density as

$$\begin{aligned} G(r_+)= & {} \frac{V_{d_2}d_2r_+^{d_1}}{2}\bigg [\bigg (\frac{1}{r_+^2}+ \frac{1}{l^2}\bigg )^{n-1}-\frac{\delta _{d,2n-1}}{r_+^{d_1}}+{\mathfrak {W}}(r_+)\bigg ]\nonumber \\{} & {} -\frac{V_{d_2}}{16\pi }\times \bigg (\frac{d_{2n}+1}{(n-1)r_+}+\frac{d_1r_+}{(n-1)l^2} +{\mathcal {Z}}_1(r_+)\bigg )\bigg [{\mathcal {H}}_{\psi }\nonumber \\{} & {} +\frac{(n-1)r_+^{d_{2n}+2}}{4l^{2n-2}(d_{2n}+2)}\nonumber \\{} & {} \times \big (r_+^2+l^2\big )^{n-1}F_1\bigg (\bigg [1,\frac{d}{2}\bigg ], \bigg [\frac{d_{2n}+4}{2}\bigg ],\frac{-r_+^2}{l^2}\bigg )\bigg ],\nonumber \\ \end{aligned}$$
(3.15)

where

$$\begin{aligned} {\mathcal {H}}_{\psi }=\sum _{k=1}^{k_{max}}\frac{kb_kd_2!X^{d-2k}}{(d-2k)!}, \end{aligned}$$
(3.16)

and

$$\begin{aligned} {\mathfrak {W}}(r_+)= & {} \frac{32\pi S}{d_2d_1^2r_+^{d_1}}\sinh ^{-1}\bigg ( \frac{S}{B^{1/2}r_+^{d_1}}\bigg )-\frac{32\pi }{d_2d_1^2}\sqrt{B+\frac{S^2}{r_+^{2d_1}}}\nonumber \\{} & {} -\frac{32\pi {\mathcal {H}}}{d_1r_+^d}. \end{aligned}$$
(3.17)
Fig. 10
figure 10

Plot of Gibb’s energy (Eq. (3.15)) vs \(r_+\) for several values of d. The other parameters are fixed as \(l=2,\) \(B=0.05,\) \(V_{d_2}=100,\) \(S=1,\) \({\mathcal {H}}_{\psi }=1\) and \({\mathcal {H}}=1\)

Full size image
Fig. 11
figure 11

Plot of Gibb’s energy (Eq. (3.15)) for various values of B and S. The other parameters are fixed as \(l=2,\) \(d=5,\) \(V_{d_2}=100,\) \(n=2,\) \({\mathcal {H}}_{\psi }=1\) and \({\mathcal {H}}=1\)

Full size image
Fig. 12
figure 12

Plot of Gibb’s energy (Eq. (3.15)) for various values of \({\mathcal {H}}.\) The other parameters are fixed as \(l=2,\) \(d=5,\) \(V_{d_2}=100,\) \(n=2,\) \({\mathcal {H}}_{\psi }=1,\) \(B=0.05\) and \(S=1\)

Full size image

It should be noted that we have set the value of gravitational constant G equal to unity during the calculation of \(G(r_+).\) Gibb’s free energy density plays a vital role in the investigation of global stability. The behaviour of this quantity dependent on \(r_+\) for different values of dimensionality parameter can be seen from Fig. 10. Those points at which \(G(r_+)\) is less than zero are the horizon radii of globally stable black holes. Hence, black holes with a smaller values of \(r_+\) enjoy global stability while larger objects are globally unstable. Correspondingly, Figs. 11 and 12 show the dependence of dark fluid and conformal scalar field on the global stability of a five-dimensional black hole system. It can be understood from these figures that the region of global stability becomes smaller when the values of the parameters B and S increase. However, this region becomes larger when \({\mathcal {H}}\) grows in magnitude. Moreover, Gibb’s energy with \({\mathcal {H}}=0\) shows that the non-hairy black hole sourced by Chaplygin-like dark fluid is globally unstable.

4 Hawking radiation

Now, we want to discuss the thermal radiations emitted from the hairy black holes described by Eq. (2.21). From the result obtained through WKB method [83,84,85], the tunnelling probability of the particle emitted from the black hole is given by

$$\begin{aligned} \gamma \sim \exp {\bigg (-2Im{\mathcal {Z}}\bigg )}. \end{aligned}$$
(4.1)

Here \(Im{\mathcal {Z}}\) refers to the action’s imaginary part that describes the trajectory of an emitting particle. One may define the transformation [86]

$$\begin{aligned} dT=dt+\frac{1}{f(r)}\sqrt{\frac{r_+}{r}}dr, \end{aligned}$$
(4.2)

where \(r_+\) is the outer horizon radius of the hairy black hole (2.21). Hence, one may write the metric (2.7) in the form as

$$\begin{aligned} ds^2= & {} -f(r)dT^2+2\sqrt{\frac{r_+}{r}}dTdr+\frac{(r-r_+)}{r}\frac{dr^2}{f(r)}\nonumber \\{} & {} +r^2d\Upsilon ^{2}_{d_2}. \end{aligned}$$
(4.3)

One can see that the coordinate singularity \(r=r_+\) is now absent in this particular representation of the spacetime. The radial geodesics of a massless particle can be determined from

$$\begin{aligned} \frac{dr}{dT}= \frac{f(r)}{\big (1+\sqrt{\frac{r_+}{r}}\big )}. \end{aligned}$$
(4.4)

The action’s imaginary part \(Im{\mathcal {Z}}\) can be expressed as [87,88,89,90,91,92]

$$\begin{aligned} Im{\mathcal {Z}}{} & {} =Im\int _{T_i}^{T_f}LdT=Im\int _{r_i}^{r_f}{\mathcal {P}}_rdr\nonumber \\{} & {} =Im\int _{r_i}^{r_f}\int _{0}^{{\mathcal {P}}_r}d{\mathcal {P}}_rdr. \end{aligned}$$
(4.5)

Note that the quantity \({\mathcal {P}}_r\) refers to the canonical momentum correlated with r. Therefore, from the equation \(\frac{dr}{dT}=\frac{dH}{dP_r}|_r=\frac{dM}{dP_r},\) one can write

$$\begin{aligned} Im{\mathcal {Z}}=\int _{M}^{M-\zeta }\int _{r_i}^{r_f}\frac{1+\sqrt{r_+/r}}{f(r)}drdM. \end{aligned}$$
(4.6)

Here, M is the black hole’s initial mass, and \(M-\zeta \) is the mass that has been lowered as a result of the radiating particle with energy \(\zeta .\) Since the aforementioned integrand has a simple pole at \(r=r_+,\) so the value of the integral can be determined as

$$\begin{aligned} Im{\mathcal {Z}}{} & {} =-2\pi \int _{M}^{M-\eta }\frac{1}{f'(r_+)}dM\nonumber \\{} & {} =-\int _{r_{+,i}}^{r_{+,f}}\frac{1}{2 T_H(r_+)}M'(r_+)dr_+, \end{aligned}$$
(4.7)

where primes indicate differentiation with respect to \(r_+.\) Substituting the temperature \(T_H(r_+)\) from Eq. (3.3) and

$$\begin{aligned} M'(r_+)= & {} \frac{d_2V_{d_2}}{16\pi G}\bigg [d_2r_+^{d_2}\bigg (\frac{1}{r_+^2}+\frac{1}{l^2}\bigg )^{n-1}\nonumber \\{} & {} - \frac{(2n-2)r_+^{d_{2n}}}{l^{2n-4}(r_+^2+l^2)^{2-n}}\nonumber \\{} & {} +\frac{32\pi G H}{(d-1)r_+^2}-\frac{32\pi G d_1r_+^{d_2}}{d_2d_1^2}\sqrt{B+\frac{S^2}{r_+^{2d_1}}}\bigg ], \end{aligned}$$
(4.8)

one may find

$$\begin{aligned} Im{\mathcal {Z}}= & {} -\frac{(n-1)\Sigma _{d_2}r_{+}^{d_{2n}+2}(r_+^2+l^2)^{n-1}}{8 G(d-2n+2)l^{2n-2}}\nonumber \\{} & {} \times F_1\bigg (\bigg [1,\frac{d}{2}\bigg ],\bigg [\frac{d-2n+4}{2}\bigg ],\frac{-r_+^2}{l^2}\bigg )\Bigg |^{r_{+f}}_{r_{+i}}. \end{aligned}$$
(4.9)

Since the terms of entropy (3.4) containing X and conformal coupling parameters \(b_k\) are independent of \(r_+,\) so we can conclude from (4.9) that

$$\begin{aligned} Im{\mathcal {Z}}=-\frac{\Delta S}{2}. \end{aligned}$$
(4.10)

Hence, the tunnelling probability (4.1) of the radiated particle is determined by

$$\begin{aligned} \gamma \sim \exp {(\Delta S)}. \end{aligned}$$
(4.11)

This demonstrates how the probability is connected to the entropy change before and after the emission i.e. \(\Delta S=S(M-\zeta )-S(M).\) This result is in agreement with the Hawking radiations of black holes explored in Refs. [62, 63, 65]. However, in our case the event horizon \(r_+\) is dependent on the parameters of Chaplygin-like dark fluid and conformal scalar field through Eq. (3.1). It is important to note that when the parameters \(b_k\) are constants then the standard first law \(dM=T_HdS\) is satisfied.

5 Hairy black holes sourced by Chaplygin-like dark fluid in Lovelock-scalar gravity

Here, we focus on the scalar hairy black holes of LGT. Recall that the Chaplygin-like dark fluid is also considered as matter source of gravitational field. By substituting the energy–momentum tensor components of the Chaplygin-like dark fluid (2.12)–(2.13) with the value of \(\rho _{df}\) in (2.18) and (2.14)–(2.16) for the function \(\psi (r)\) into Eqs. (2.3), the following differential equation of motion for the Lovelock polynomial can be derived

$$\begin{aligned}{} & {} \frac{d}{dr}\bigg [r^{d_1}P\bigg (\frac{\kappa -f(r)}{r^2}\bigg )\bigg ]=\frac{32\pi G}{d_2}r^{d_2}\bigg (B+\frac{S^2}{r^{2d_1}}\bigg )^{\frac{1}{2}}\nonumber \\{} & {} \quad -\frac{32\pi G {\mathcal {H}}}{r^2}, \end{aligned}$$
(5.1)

where

$$\begin{aligned} P\bigg (\frac{\kappa -f(r)}{r^2}\bigg )=\sum _{k=0}^{k_{max}}{\overline{\alpha }}_k \bigg (\frac{\kappa -f(r)}{r^2}\bigg )^k, \end{aligned}$$
(5.2)

in which we have considered the arbitrary parameters \({\overline{\alpha }}_k\) for simplicity. These parameters are related to the Lovelock parameters \(\alpha _k\) through relations

$$\begin{aligned}&{\overline{\alpha }}_0=\frac{\alpha _0}{d_1d_2},\nonumber \\&{\overline{\alpha }}_1=1,\nonumber \\&{\overline{\alpha }}_k=\prod _{i=3}^{2k}d_i\alpha _k. \end{aligned}$$
(5.3)

Note that, the general formula for the \({\overline{\alpha }}_k\) holds only for \(k\ge 2.\) By integrating Eq. (5.1) one may easily find that the f(r) satisfies the following polynomial equation

$$\begin{aligned}{} & {} P\bigg (\frac{\kappa -f(r)}{r^2}\bigg )\nonumber \\{} & {} \quad =\frac{16\pi G M}{d_2V_{d_2}r^{d_1}}+\frac{32\pi G H}{r^d}+\frac{32\pi G}{d_2d_1}\bigg (B+\frac{S^2}{r^{2d_1}}\bigg )^{\frac{1}{2}}\nonumber \\{} & {} \qquad -\frac{32\pi G S}{d_1d_2r^{d_1}}\sinh ^{-1}\bigg (\frac{S}{\sqrt{B}r^{d_1}}\bigg ). \end{aligned}$$
(5.4)

Associated with the above Eq. (5.4), it is easy to get the finite black hole’s mass as

$$\begin{aligned} M= & {} \frac{d_2V_{d_2}}{16\pi G}\bigg [\sum _{k=o}^{k_{max}}{\overline{\alpha }}_k\kappa ^kr_+^{d_1-2k}\nonumber \\{} & {} -\frac{32\pi G {\mathcal {H}}}{r_+}-\frac{32\pi G r_+^{d_1}}{d_1d_2}\bigg (B+\frac{S^2}{r_+^{2d_1}}\bigg )^{\frac{1}{2}}\nonumber \\{} & {} +\frac{32\pi G S}{d_1d_2}\sinh ^{-1}\bigg (\frac{S}{\sqrt{B}r_+^{d_1}}\bigg )\bigg ]. \end{aligned}$$
(5.5)

In the same way, the Hawking temperature corresponding to Lovelock black hole in this setup can be found as

$$\begin{aligned} T_{H}(r_+)= & {} \frac{1}{4\pi {\mathfrak {S}}(r_+)}\bigg [\sum _{k=0}^{k_{max}}\frac{{\overline{\alpha }}_k\kappa ^k(d_1-2k)}{r_+^{2k+1}}+\frac{32\pi G {\mathcal {H}}}{r_+^{d+1}}\nonumber \\{} & {} -\frac{32\pi G}{d_2r_+}\bigg (B+\frac{S^2}{r_+^{2d_1}}\bigg )^{\frac{1}{2}}\bigg ], \end{aligned}$$
(5.6)

where \({\mathfrak {S}}(r_+)\) is given by

$$\begin{aligned} {\mathfrak {S}}(r_+)=\sum _{k=1}^{k_{max}}\frac{k{\overline{\alpha }}_k\kappa ^{k-1}}{r_+^{2k}}. \end{aligned}$$
(5.7)

Again one can find the entropy with the help of Wald’s formalism in the form

$$\begin{aligned} S=\frac{d_2V_{d_2}}{4G}\sum _{k=1}^{k_{max}}k\kappa ^{k-1}\bigg (\frac{{\overline{\alpha }}_k}{d-2k}r_+^{d-2k}+\frac{b_kd_3!X^{d-2k}}{(d-2k)!}\bigg ). \nonumber \\ \end{aligned}$$
(5.8)

From the above expressions of temperature (5.6) and entropy (5.8), one can express the heat capacity as

$$\begin{aligned} C_H=\frac{d_2V_{d_2}{\mathcal {B}}_2(r_+){\mathfrak {S}}(r_+) \sum _{k=1}^{k_{max}}k\kappa ^{k-1}{\overline{\alpha }}_kr_+^{d_1-2k}}{4{\mathfrak {S}}(r_+){\mathcal {B}}_1(r_+)+8{\mathcal {B}}_2(r_+) \sum _{k=1}^{k_{max}}\frac{k^2{\overline{\alpha }}_k\kappa ^{k-1}}{r_+^{2k+1}}}, \end{aligned}$$
(5.9)

where

$$\begin{aligned} {\mathcal {B}}_1(r_+)= & {} -\sum _{k=0}^{k_{max}}\frac{(2k+1)(d_1-2k) {\overline{\alpha }}_k\kappa ^k}{r_+^{2(k+1)}}-\frac{32\pi G H(d+1)}{r_+^{d+2}}\nonumber \\{} & {} +\frac{32\pi G}{d_2r_+^2}\bigg (B+\frac{S^2}{r_+^{2d_1}}\bigg )^{\frac{1}{2}}\nonumber \\{} & {} +\frac{32\pi G d_1S^2}{d_2r_+^{2d}}\bigg (B+\frac{S^2}{r_+^{2d_1}}\bigg )^{\frac{-1}{2}}, \end{aligned}$$
(5.10)

and

$$\begin{aligned} {\mathcal {B}}_2(r_+)= & {} \sum _{k=0}^{k_{max}}\frac{{\overline{\alpha }}_k \kappa ^k(d_1-2k)}{r_+^{2k+1}}+\frac{32\pi G {\mathcal {H}}}{r_+^{d+1}}\nonumber \\{} & {} -\frac{32\pi G}{d_2r_+}\bigg (B+\frac{S^2}{r_+^{2d_1}}\bigg )^{\frac{1}{2}}. \end{aligned}$$
(5.11)

The Lovelock polynomial equation (5.4) is very significant because it provides solutions that describe hairy black holes surrounded by Chaplygin-like dark fluid in a general LGT. For instance, by selecting the coupling parameters such that \({\overline{\alpha }}_2\ne 0\) and \({\overline{\alpha }}_k=0\) for \(k\ge 3,\) one can obtain the black hole solution in Gauss–Bonnet gravity as follows

$$\begin{aligned} f_{\pm }(r)=\kappa +\frac{r^2}{2{\overline{\alpha }}_2}\bigg [1\pm \sqrt{\aleph (r)}\bigg ], \end{aligned}$$
(5.12)

where

$$\begin{aligned} \aleph (r)= & {} 1-4{\overline{\alpha }}_2{\overline{\alpha }}_0+4{\overline{\alpha }}_2{\overline{\alpha }}_0\bigg [\frac{16\pi G M}{d_2V_{d_2}r^{d_1}}+\frac{32\pi G {\mathcal {H}}}{r^d}\nonumber \\{} & {} +\frac{32\pi G}{d_1d_2}\sqrt{B+\frac{S^2}{r^{2d_1}}}\nonumber \\{} & {} -\frac{32\pi G S}{d_1d_2r^{d_1}}\sinh ^{-1} \bigg (\frac{S}{\sqrt{B}r^{d_1}}\bigg )\bigg ]. \end{aligned}$$
(5.13)

Similarly, the solution that describes third-order Lovelock black holes within this set-up can be found as

$$\begin{aligned} f(r)=\kappa +\frac{r^2}{{\overline{\alpha }}_2}\bigg [1-\root 3 \of {{\mathcal {U}}(r)}\bigg ], \end{aligned}$$
(5.14)

where

$$\begin{aligned} {\mathcal {U}}(r)= & {} 1-\frac{d_1d_2{\overline{\alpha }}_0{\overline{\alpha }}_2}{2}+\frac{48\pi G M{\overline{\alpha }}_2}{d_2V_{d_2}r^{d_1}}+\frac{96\pi G{\mathcal {H}}{\overline{\alpha }}_2}{r^d}\nonumber \\{} & {} +\frac{96\pi G{\overline{\alpha }}_2}{d_1d_2}\sqrt{B+\frac{S^2}{r^{2d_1}}}\nonumber \\{} & {} -\frac{96\pi GS}{d_1d_2r^{d_1}}\sinh ^{-1}\bigg (\frac{S}{\sqrt{B}r^{d_1}}\bigg ). \end{aligned}$$
(5.15)

It is important to note that in the computation of the above solution, we have enforced the restriction \({\overline{\alpha }}_3={\overline{\alpha }}^2/3\) on the arbitrary coupling parameters. However, one can also construct a solution of the Lovelock field equations exclusive of this restriction on the coupling parameters.

6 Closing remarks

In this study, we investigated the d-dimensional hairy black holes sourced by unified dark fluid in the context of LGT. Firstly, we explored the new topological black holes of DCG in the presence of Chaplygin-like dark fluid and conformally coupled scalar field. It is shown that the parameters describing the strength of the dark fluid affect the horizon structure of our black hole solution (2.21). Besides, we also investigated the thermodynamic properties of these dimensionally continued black holes. Associated with the metric function (2.21) we compute the mass of the hairy black hole, Hawking temperature, and heat capacity as a function of the event horizon. It is evident that these thermodynamic quantities are impacted by the dark fluid and the scalar field. However, the entropy is not explicitly affected by the presence of dark fluid. In this manner, the dark fluid behaves like quintessential dark energy and indirectly influences the entropy due to the value of the horizon radius through Eq. (3.1). In order to keep things simple, we only looked into the thermodynamic properties of the dimensionally continued black holes when the topological parameter \(\kappa \) is equal to unity. One may consider the cases of other horizon topologies for the investigation of stability in a similar way. We illustrated graphically the behaviour of Hawking temperature and specific heat capacity for fixed values of B,  S,  l,  and \({\mathcal {H}}\) in different dimensional geometries. The positivity of the specific heat shows that the hairy black holes specified by (2.21) with associated values of \(r_+\) are locally stable. On the other hand, those values of \(r_+\) which keep correspondence with the negative \(C_H\) are the event horizons of unstable black holes. One can also observe that there exist values of \(r_+\) on which the heat capacity can be zero or singular. Hence, both first and second order phase transitions are happening for these thermodynamical systems. Similarly, the dependence of Chaplygin-like dark fluid on the temperature and heat capacity can be visualized from Figs. 5 and 8. It is concluded that both the parameters B and S can affect the local stability of the hairy black holes. Furthermore, the impact of conformal scalar field on the local stability can be observed from Fig. 9. We conclude that the divergent points of heat capacity shift to the right when the parameter \({\mathcal {H}}\) increases. On the other hand, the heat capacity of non-hairy black holes surrounded by dark fluid has no singular points and thus there are no second order phase transition for these objects. We also determine how the dimensionality parameter d and dark fluid affect the way Gibb’s free energy behaves as a function of horizon radius. The black hole with an associated value of \(r_+\) is shown to be globally stable if Gibb’s energy is negative. The smaller black holes are demonstrated to be globally stable, but the larger ones are unstable. Additionally, it can be seen that the sizes of the globally stable black holes shrink when the parameters B and S increase simultaneously (Figs. 10 and 11). Furthermore, the effect of scalar field on the global stability of hairy black holes can be analyzed in Fig. 12. It is observed that there exists a point \(r_a\) at which Gibb’s energy changes sign from negative to positive. The hairy black hole with horizon radius less than \(r_a\) is globally stable. One can see that the radius \(r_a\) increases when the parameter \({\mathcal {H}}\) grows in magnitude. We also briefly looked at the Hawking radiation phenomena, which demonstrates the relationship between tunnelling probability and the difference in entropy. This behaviour resembles the other Einstein and Lovelock black holes [63, 65].

Finally, the topological solutions of general Lovelock gravity sourced by the conformal scalar field and Chaplygin-like dark fluid are also explored. We arrive at a polynomial equation that can produce the solutions characterizing new Lovelock black holes. The thermodynamic quantities for these black holes have also been worked out. It is significant to observe that for \({\mathcal {H}}=0\) or \(b_k=0,\) Eq. (2.21) characterizes a new family of non-hairy black holes of dimensionally continued gravity sourced by Chaplygin-like dark fluid. Additionally, the metric function (2.21) and the polynomial equation (5.4) describe, respectively, the neutral hairy black holes of DCG and general LGT when \(B=S=0.\)

Studying the critical behaviour, particle dynamics and greybody factors in this setup may lead to interesting insights. The study of charged black holes and black strings in the configuration of dark fluid could also be quite intriguing.