1 Introduction

The best-known theory for describing the mechanism behind superconductivity from a microscopic perspective is the BCS theory proposed by Bardeen, Cooper and Schrieffer. According to BCS theory, the condensation of Cooper pairs into a boson-like state, at low temperature, is responsible for an infinite conductivity in the solid state system [1]. However, when the temperature increases, the Cooper pair decouples and thus the BCS theory is unable to explain the mechanism of superconductivity for high temperature superconductors [1]. The correspondence between gravity in an anti-de Sitter (AdS) spacetime and Conformal Field Theory (CFT) living on the boundary of the spacetime provides a powerful tool for calculating correlation functions in a strongly interacting field theory using a dual classical gravity description [2]. According to the AdS/CFT duality proposal an n-dimensional conformal field theory on the boundary is equivalent to gravity theory in \((n+1)\)-dimensional AdS bulk [2,3,4,5,6,7]. The dictionary of AdS/CFT duality implies that each quantity in the bulk has a dual on the boundary. For example, the energy-momentum tensor \(T_{\mu \nu }\) on the boundary corresponds to the bulk metric \(g_{\mu \nu }\) [3, 4]. Based on this duality, Hartnoll et al. proposed a model for a holographic superconductor in 2008 [5]. Their motivation was to shed light on the problem of high temperature superconductors. According to the theory of holographic superconductors, we need a hairy black hole on the gravity side to describe a superconductor on its boundary. During the past decade, the investigation of the holographic superconductor has got a lot of attention (see e.g. [6,7,8,9,10,11,12,13,14,15,16,17,18, 20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37]).

On the other hand, BTZ (Bandos–Teitelboim–Zanelli) black holes, the well-known solutions of general relativity in \((2+1)\)-dimensional spacetime, provide a simplified model to investigate some conceptual issues in black hole thermodynamics, quantum gravity, string theory, gauge theory and the AdS/CFT correspondence [38,39,40,41,42]. It has been shown that the quasinormal modes in this spacetime coincide with the poles of the correlation function in the dual CFT. This gives quantitative evidence for AdS/CFT [43]. In addition, BTZ black holes play a crucial role for improving our perception of gravitational interaction in low-dimensional spacetimes [44]. These kinds of solutions have been studied from different point of views [45,46,47,48].

Holographic superconductors dual to asymptotic BTZ black holes have been explored widely (see e.g. [19, 49,50,51,52,53,54,55,56,57,58,59]). In order to construct the \((1+1)\)-dimensional holographic superconductors one should employ the AdS\(_{3}\)/CFT\(_{2}\) correspondence. In [49], the \((1+1)\)-dimensional holographic superconductors were explored in the probe limit and its distinctive features in both normal and superconducting phases were investigated. Employing the variational method of the Sturm–Liouville eigenvalue problem, the one-dimensional holographic superconductors have been analytically studied in [50,51,52]. It is also interesting to study the \((1+1)\)-dimensional holographic superconductor away from the probe limit by considering the backreaction. In [53], the effects of the backreaction have been studied for s-wave linearly charged one-dimensional holographic superconductors.

Holographic superconductors have also been studied extensively in the presence of nonlinear electrodynamics (see e.g. [24, 25, 28,29,30,31,32,33, 36, 37]). The most famous nonlinear electrodynamics is Born–Infeld electrodynamics. This model was presented for the first time to solve the problem of the divergence of the electrical field at the position of a point particle [60,61,62,63,64]. It was later showed that this model could be reproduced by string theory. In the present work, we would like to extend the investigation of the \((1+1)\)-dimensional holographic superconductors by taking into account the nonlinear Born–Infeld (BI) electrodynamics, as our gauge field. Furthermore, we will study the effects of backreaction on our holographic superconductors. We perform our investigation both analytically and numerically and shall compare the result of two methods. Our analytical approach is based on the Sturm–Liouville variational method. In the latter study, we find the relation between the critical temperature and the chemical potential. Moreover, in order to study our holographic superconductors numerically, we use the shooting method. We show that the analytical results are in good agreement with numerical ones, which implies that the Sturm–Liouvile variation method is still powerful enough for studying the \((1+1)\)-dimensional holographic superconductor.

The structure of our paper is as follows. In Sect. 2, the basic field equations of one-dimensional holographic superconductors with backreaction in the presence of BI nonlinear electrodynamics is introduced. In Sect. 3, we describe the procedure of an analytical study of the one-dimensional holographic superconductor based on Sturm–Liouvile method and obtain the relation between the critical temperature and the chemical potential. In Sect. 4, the numerical approach to the study of our holographic superconductors will be presented. Finally, we summarize our results in Sect. 5.

2 Basic field equations

The action of three-dimensional AdS gravity in the presence of a gauge and a scalar field is given by

$$\begin{aligned} S= & {} \frac{1}{2\kappa ^{2}}\int \mathrm{d}^{3}x\sqrt{-g}\left( R+\frac{2}{l^{2}} \right) \nonumber \\&+\int \mathrm{d}^{3}x\sqrt{-g} [ \mathcal {L}(\mathcal {F})-|\nabla \psi -iqA\psi |^{2}-m^{2}|\psi |^{2}],\nonumber \\ \end{aligned}$$
(1)

where m and q are the mass and the charge of the scalar field, \(\kappa ^{2}={8\pi G_{3}}\) and \(G_{3}\) is the three-dimensional Newton gravitation constant. Also, g, R and l are the metric determinant, Ricci scalar and AdS radius, respectively. In (1), \(\mathcal {F}=F_{\mu \nu }F^{\mu \nu }\) where \(F_{\mu \nu }=\nabla _{[\mu }A_{\nu ]}\) is the electrodynamics field tensor and \(A_{\mu }\) is the vector potential. \( \mathcal {L}(\mathcal {F})\) stands for the Lagrangian density of the BI nonlinear electrodynamics defined as

$$\begin{aligned} \mathcal {L}(\mathcal {F})=\frac{1}{b}\left( 1-\sqrt{1+\frac{b\mathcal {F}}{2}} \right) , \end{aligned}$$
(2)

where b is the nonlinear parameter. When \(b\rightarrow 0\), \(\mathcal {L}\) reduces to \(-F_{\mu \nu }F^{\mu \nu }/{4}\), which is the standard Maxwell Lagrangian [5]. Variation of the above action with respect to the scalar field \(\psi \), the gauge field \(A_{\mu }\) and the metric \(g_{\mu \nu }\) yields the following equations of motion:

$$\begin{aligned} 0= & {} \left( \nabla _{\mu }-i{q}A_{\mu }\right) \left( \nabla ^{\mu }-i{q} A^{\mu }\right) \psi -m^{2}\psi , \end{aligned}$$
(3)
$$\begin{aligned} 0= & {} \nabla ^{\mu }\left( 4\mathcal {L}_{\mathcal {F}}F_{\mu \nu }\right) \nonumber \\&-i{q}\left[ -\psi ^{*}(\nabla _{\nu }-i{q}A_{\nu })\psi +\psi (\nabla _{\nu }+i{q}A_{\nu })\psi ^{*}\right] \,, \end{aligned}$$
(4)
$$\begin{aligned} 0= & {} \frac{1}{2\kappa ^{2}}\left[ R_{\mu \nu }-g_{\mu \nu }\left( \frac{R}{2} +\frac{1}{l^{2}}\right) \right] +2F_{ac}F_{b}{}^{c}\mathcal {L}_{\mathcal {F}} \nonumber \\&-\frac{g_{\mu \nu }}{2}\left[ \mathcal {L}(\mathcal {F})-m^{2}|\psi |^{2}-{ |\nabla \psi -i{q}A\psi |^{2}}\right] \nonumber \\&-\frac{1}{2}\left[ (\nabla _{\mu }\psi -i{q}A_{\mu }\psi )(\nabla _{\nu }\psi ^{*}+i{q}A_{\nu }\psi ^{*})+\mu \leftrightarrow \nu \right] ,\nonumber \\ \end{aligned}$$
(5)

where \(\mathcal {L}_{\mathcal {F}}=\partial \mathcal {L}/\partial {\mathcal {F}}\).

Since we would like to consider the effect of the backreaction on the holographic superconductor, we take a metric ansatz as follows [53]:

$$\begin{aligned} {\mathrm{d}s}^{2}=-f(r)\mathrm{e}^{-\chi (r)}{\mathrm{d}t}^{2}+\frac{{\mathrm{d}r}^{2}}{f(r)}+\frac{r^{2}}{l^{2}} {\mathrm{d}x}^{2}. \end{aligned}$$
(6)

The Hawking temperature of the three-dimensional black hole on the outer horizon \(r_{+}\) (where \(r_{+}\) is the horizon radius obtained as the largest root of \(f(r_{+})=0\)) may be obtained through the use of the general definition of the surface gravity [65],

$$\begin{aligned} T=\frac{\kappa _\mathrm{{sg}}}{2\pi }=\frac{1}{2\pi }\sqrt{-\frac{1}{2}(\nabla _{\mu }\chi _{\nu })(\nabla ^{\mu }\chi ^{\nu })}, \end{aligned}$$

where \(\kappa _\mathrm{{sg}}\) is the surface gravity and \(\chi =\partial /\partial t\) is the null Killing vector of the horizon. Taking \(\chi ^{\nu }=(-1,0,0)\), we have \(\chi _{\nu }=(f(r_{+})\mathrm{e}^{-\chi (r_{+})},0,0)\) and hence on the horizon where \(f(r_{+})=0\), we find \((\nabla _{\mu }\chi _{\nu })(\nabla ^{\mu }\chi ^{\nu })=-\frac{1}{2}\left[ f^{\prime }(r_{+})\right] ^{2}\mathrm{e}^{-\chi (r_{+})}\). Thus, the temperature is obtained:

$$\begin{aligned} T=\frac{\mathrm{e}^{-\chi (r_{+})/2}f^{^{\prime }}(r_{+})}{4\pi }. \end{aligned}$$
(7)

We also choose the scalar and the gauge fields as [5]

$$\begin{aligned} A_{\mu }=(\phi (r),0,0), \,\quad \psi =\psi (r). \end{aligned}$$
(8)

Substituting (6) and (8) into the field Eqs. (3)–(5), we arrive at

$$\begin{aligned} 0= & {} \psi ^{\prime \prime }+\psi ^{\prime }\left[ \frac{1}{r}+\frac{ f^{\prime }}{f}-\frac{\chi ^{\prime }}{2}\right] +\psi \left[ \frac{ q^{2}\phi ^{2}{\mathrm {e}}^{\chi }}{f^{2}}-\frac{m^{2}}{f}\right] , \end{aligned}$$
(9)
$$\begin{aligned} 0= & {} \phi ^{\prime \prime }+\phi ^{\prime }\left[ -\frac{b\mathrm{e}^{\chi }\phi ^{\prime 2}}{r}+\frac{\chi ^{\prime }}{2}+\frac{1}{r}\right] \nonumber \\&- \frac{2q^{2}\psi ^{2}\phi }{f}\left[ 1-b\mathrm{e}^{\chi }\phi ^{\prime 2}\right] ^{3/2}, \end{aligned}$$
(10)
$$\begin{aligned} 0= & {} f^{\prime }-\frac{2r}{l^{2}} +2\kappa ^{2}r \bigg [ \frac{q^{2}\mathrm{e}^{\chi }\psi ^{2}\phi ^{2}}{f}+f\psi ^{\prime 2}+m^{2}\psi ^{2} \nonumber \\&-\frac{1}{b}+\frac{1}{b\sqrt{1-b\mathrm{e}^{\chi }\phi ^{\prime 2}}} \bigg ] , \end{aligned}$$
(11)
$$\begin{aligned} 0= & {} \chi ^{\prime }+4\kappa ^{2}r\left[ \frac{q^{2}\phi ^{2}\psi ^{2}{ \mathrm {e}}^{\chi }}{f^{2}}+\psi ^{\prime 2}\right] , \end{aligned}$$
(12)

where the prime denotes the derivative with respect to r. Note that in the presence of the nonlinear BI electrodynamics equations (9) and (12) do not change compared to the linear Maxwell case. In the limiting case where \(b\rightarrow 0\) the equations of motion (10) and (11) turn into the corresponding equations of the one-dimensional holographic superconductor with a Maxwell field [53]. The field Eqs. (9)–(12) enjoy the symmetries

$$\begin{aligned} q\rightarrow q/a,\phi \rightarrow a\phi , \psi \rightarrow a\psi , \nonumber \\ \kappa \rightarrow \kappa /a, b\rightarrow b/a^{2}, \end{aligned}$$
(13)
$$\begin{aligned} l\rightarrow al, r\rightarrow ar, q\rightarrow q/a, \nonumber \\ m\rightarrow m/a, b\rightarrow a^{2}b. \end{aligned}$$
(14)

Hereafter, we set q and l equal to unity by virtue of these symmetries. The behavior of our model functions for large r (near the boundary) read

$$\begin{aligned} \chi \rightarrow 0,\ \ \ f(r)\sim r^{2}, \nonumber \\ \phi \sim \rho +\mu \ln (r),\ \ \ \psi \sim \psi _{-}r^{-\Delta _{-}}+\psi _{+}r^{-\Delta _{+}}, \end{aligned}$$
(15)

where \(\mu \) and \(\rho \) are the chemical potential and the charge density of the field theory on the boundary and \(\Delta _{\pm }=1\pm \sqrt{1+m^{2}}\), which implies \(m^{2}\ge -1\). Actually, \(\chi \) could be a constant near the boundary but by using the symmetry of the field equation, \(\mathrm {e}^{\chi }\rightarrow a^{2}\mathrm {e}^{\chi },\) \(\phi \rightarrow \phi /a\), it could be set to zero there. We consider \(\psi _{-}\) and \(\psi _{+}\) as the source and the dual of the order parameter, respectively. One may think that either \(\psi _{+}\) or \(\psi _{-}\) can be dual to the expectation value of the condensation operator (or order operator) \(\left\langle O\right\rangle \), while the other is dual to its source. However, in general this is not the case. While \(\psi _{+} \) can always be dual to \(\left\langle O\right\rangle \), \(\psi _{-}\) can be dual to it only if \(-1\le m^{2}<0\) where \(\Delta _{-}\) is positive. We give \(\psi _{-}\) the role of source and \(\psi _{+}\) the role of the expectation value of the order parameter \( \left\langle O_{+}\right\rangle \) in this work. Since we seek for study the effects of b and \(\kappa \) on our holographic superconductors and different values of the scalar field mass do not influence this behavior qualitatively, we consider \(m^{2}=0\) in this work. With this choice, we have \(\Delta _{+}=2\), \(\Delta _{-}=0\) and thus

$$\begin{aligned} \psi \sim \psi _{-}+\frac{\psi _{+}}{r^{2}}, \end{aligned}$$
(16)

near the boundary. We set \(\psi _{-}=0\) at the boundary and consider \(\psi _{+}\) as the dual of order parameter \(\left\langle O_{+}\right\rangle \). In Appendix A, we present the calculation for \( \left\langle O_{+}\right\rangle \) and show that it is proportional to \(\psi _{+}\) and the other parameters do not appear in its formula explicitly. It is remarkable that the asymptotic solution for \(\psi \) given in Eq. (16) does not depend on the type of electrodynamics and thus for the Maxwell case in three dimensions the solution is the same as in Eq. (16). However, the solution depends on the spacetime dimensions. This is due to the fact that the equation for \( \psi \) given in (9) is independent of the type of electrodynamics but depends on the spacetime dimensions and the mass parameter m [34, 53, 66].

The next step is to solve the coupled nonlinear field equations (9)–(12) simultaneously and obtain the behavior of the model functions. Then we could figure out the behavior of different parameters of holographic superconductor, specially the order parameter \(\langle O_{+}\rangle \) and the critical temperature, by using these functions. In this work, we use both analytical and numerical methods for studying the holographic superconductor. For analytical study, we perform the Sturm–Liouville method, while for numerical study, we use the shooting method.

3 Sturm–Liouville method

In this section, we employ the Sturm–Liouville eigenvalue problem to investigate analytically the phase transition of the one-dimensional s-wave holographic superconductor in the presence of BI nonlinear electrodynamics. In addition, we calculate the relation between the critical temperature \( T_\mathrm{{c}}\) and the chemical potential \(\mu \) near the horizon. Furthermore, we study the effect of backreaction and BI nonlinear electrodynamics on the critical temperature. For future convenience, we define a new variable \( z=r_{+}/r\) \((\in \left[ 0,1\right] )\). With this new coordinate, the field equations (9)–(12) could be rewritten as

$$\begin{aligned} 0= & {} \psi ^{\prime \prime }+\psi ^{\prime }\left[ \frac{f^{\prime }}{f}- \frac{\chi ^{\prime }}{2}+\frac{1}{z}\right] +\psi \left[ \frac{ r_{+}^{2}\mathrm{e}^{\chi }\phi ^{2}}{z^{4}f^{2}}-\frac{m^{2}r_{+}^{2}}{z^{4}f}\right] , \nonumber \\\end{aligned}$$
(17)
$$\begin{aligned} 0= & {} \phi ^{\prime \prime }+\phi ^{\prime }\left[ \frac{bz^{3}\mathrm{e}^{\chi }\phi ^{\prime 2}}{r_{+}^{2}}+\frac{\chi ^{\prime }}{2}+\frac{1}{z}\right] -\frac{ 2r_{+}^{2}\psi ^{2}\phi }{z^{4}f}\Upsilon ^{\frac{3}{2}}, \end{aligned}$$
(18)
$$\begin{aligned} 0= & {} f^{\prime }+\frac{2r_{+}^{2}}{z^{3}}+\frac{2r_{+}^{2}\kappa ^{2}}{z^{3}} \nonumber \\&\times \left[ \frac{1}{b} (1-\Upsilon ^{-\frac{1}{2}}) -\frac{ z^{4}f\psi ^{\prime 2}}{r_{+}^{2}}-\frac{\mathrm{e}^{\chi }\psi ^{2}\phi ^{2}}{f} -m^{2}\psi ^{2}\right] , \nonumber \\ \end{aligned}$$
(19)
$$\begin{aligned} 0= & {} \chi ^{\prime }-4\kappa ^{2}\left[ \frac{r_{+}^{2}\mathrm{e}^{\chi }\psi ^{2}\phi ^{2}}{z^{3}f^{2}}+z\psi ^{\prime 2}\right] , \end{aligned}$$
(20)

where \(\Upsilon =1-bz^{4}\mathrm{e}^{\chi }\phi ^{\prime 2}/r_{+}^{2}\) and now the prime indicates the derivative with respect to z. Since in the vicinity of critical temperature the order parameter is small, we can consider it as an expansion parameter

$$\begin{aligned} \epsilon \equiv \langle O_{i} \rangle , \end{aligned}$$

where \(i=+\) or −. We focus on solutions for small values of condensation parameter \(\epsilon \), therefore we can expand the model functions as

$$\begin{aligned} \psi\approx & {} \epsilon \psi _{1}+\epsilon ^{3}\psi _{3}+\epsilon ^{5}\psi _{5}+\cdots , \\ \phi\approx & {} \phi _{0}+\epsilon ^{2}\phi _{2}+\epsilon ^{4}\phi _{4}+\cdots , \\ f\approx & {} f_{0}+\epsilon ^{2}f_{2}+\epsilon ^{4}f_{4}+\cdots , \\ \chi\approx & {} \epsilon ^{2}\chi _{2}+\epsilon ^{4}\chi _{4}+\cdots , \end{aligned}$$

where \(\epsilon \ll 1\) near the critical temperature. Moreover, by considering \(\delta \mu _{2}>0\), the chemical potential can be expressed as

$$\begin{aligned} \mu =\mu _{0}+\epsilon ^{2}\delta \mu _{2}+ \cdots \rightarrow \epsilon \thickapprox \Bigg (\frac{\mu -\mu _{0}}{\delta \mu _{2}}\Bigg )^{1/2}. \end{aligned}$$

During a phase transition, \(\mu _\mathrm{{c}}=\mu _{0}\), thus the order parameter vanishes. Meanwhile, the critical exponent \(\beta =\frac{1}{2}\) is in good agreement with the mean field theory result.

At zeroth order of \(\epsilon \), the gauge field equation of motion (18) reduces to

$$\begin{aligned} \phi ^{\prime \prime }+\frac{\phi ^{\prime }}{z}+\frac{bz^{3}\phi ^{\prime 3} }{r_{+}^{2}}=0, \end{aligned}$$
(21)

which could be rewritten as a first order Bernoulli differential equation by taking \(\phi ^{\prime }\) as a new function [67]. Therefore, one obtains

$$\begin{aligned} \phi ^{\prime }=\frac{\lambda r_{+}}{z\sqrt{b\lambda ^{2}z^{2}+1}} \end{aligned}$$
(22)

for small values of b where we define \(\lambda =\mu /r_{+}\) and fix the integration constants by looking at the behavior of \(\phi \) near the boundary given in (15). Integrating (22) and using the fact that \(\phi (z=1)=0\),Footnote 1 we can obtain

$$\begin{aligned} \phi _{0}(z)= & {} \int _{1}^{z}\frac{\lambda r_{+}}{z}\left( 1-\frac{1}{2} b\lambda ^{2}z^{2}\right) \,\mathrm{d}z \nonumber \\= & {} \lambda r_{+}\log (z)-\frac{1}{4}b\lambda ^{3}r_{+} ( z^{2}-1). \end{aligned}$$
(23)

When \(b=0\) the above equation reduces to the one of [50]. Note that at the zeroth order with respect to \(\epsilon \), \(\psi _{0}=\chi _{0}=0\). Substituting (22) in (19), the equation for f at zeroth order with respect to \(\epsilon \) has the following form:

$$\begin{aligned} f_{0}(z)= & {} r_{+}^{2}g(z), \nonumber \\ g(z)= & {} \frac{1}{z^{2}}-1+\frac{1}{8}b\kappa ^{2}\lambda ^{4}\left( 1-z^{2}\right) +\kappa ^{2}\lambda ^{2}\log (z). \end{aligned}$$
(24)

The asymptotic behavior of the scalar field \(\psi \) was given in (15). Near the boundary, we define the function F(z) so that

$$\begin{aligned} \psi (z)=\frac{\left\langle O_{i}\right\rangle z^{\triangle _{i}}}{\sqrt{2} r_{+}^{\triangle _{i}}}F(z). \end{aligned}$$
(25)

Inserting Eq. (25) in Eq. (17) yields

$$\begin{aligned}&F^{\prime \prime }(z)+F^{\prime }(z)\left[ \frac{g^{\prime }(z)}{g(z)}+ \frac{2\Delta }{z}+\frac{1}{z}\right] \nonumber \\&\quad +F(z)\left[ \frac{\Delta g^{\prime }(z)}{zg(z)}-\frac{m^{2}}{z^{4}g(z)}+ \frac{\Delta ^{2}}{z^{2}}\right] \nonumber \\&\quad -\frac{F(z)}{2z^{4}g(z)^{2}}[ \lambda ^{2}\log (z) ( b\lambda ^{2}r_{+} ( z^{2}-1) -2\log (z)) ] =0.\nonumber \\ \end{aligned}$$
(26)

We can rewrite this equation in the Sturm–Liouville form as

$$\begin{aligned} \left[ T(z)F^{\prime }(z)\right] ^{\prime }+P(z)T(z)F(z)+\lambda ^{2}Q(z)T(z)F(z)=0, \end{aligned}$$
(27)

where the functions T, P, Q are defined as

$$\begin{aligned} T(z)=z^{2\Delta +1}\left[ \frac{1}{z^{2}}-1+\frac{1}{8}b\kappa ^{2}\lambda ^{4}\left( 1-z^{2}\right) +\kappa ^{2}\lambda ^{2}\log (z)\right] , \end{aligned}$$
(28)
$$\begin{aligned} P(z)=\frac{\Delta }{z}\left( \frac{g^{\prime }(z)}{g(z)}+\frac{\Delta }{z} \right) -\frac{m^{2}}{z^{4}g(z)}, \end{aligned}$$
(29)
$$\begin{aligned} Q(z)=-\frac{\log (z)\left( b\lambda ^{2}r_{+}\left( z^{2}-1\right) -2\log (z)\right) }{2z^{4}g(z)^{2}}. \end{aligned}$$
(30)

We can consider the trial function \(F(z)=1-\alpha z^{2}\), which satisfies the required boundary conditions \(F(0)=1\) and \(F^{^{\prime }}(0)=0\). Then the eigenvalue problem could be solved for (27) by minimizing the expression

$$\begin{aligned} \lambda ^{2}=\frac{\int _{0}^{1}T ( F^{\prime 2}-PF^{2}) \mathrm{d}z}{ \int _{0}^{1}TQF^{2}\mathrm{d}z}, \end{aligned}$$
(31)

with respect to \(\alpha \). For the backreaction parameter, we could use the iteration method and define [68]

$$\begin{aligned} \kappa _{n}=n\Delta \kappa ,\ \ \ n=0,1,2,\ldots , \end{aligned}$$
(32)

where \(\Delta \kappa =\kappa _{n+1}-\kappa _{n}\). Here, we take \(\Delta \kappa =0.05\). Since we are interested in finding the effects of nonlinearity on backreaction up to the order \(\kappa ^{2}\), we have

$$\begin{aligned} \kappa ^{2}\lambda ^{2}={\kappa _{n}}^{2}\lambda ^{2}={\kappa _{n}} ^{2}(\lambda ^{2}|_{\kappa _{n-1}})+O[(\Delta \kappa )^{4}], \end{aligned}$$
(33)

where we take \(\kappa _{-1}=0\) and \(\lambda ^{2}|_{\kappa _{-1}}=0\). We shall also retain the linear terms with respect to the nonlinearity parameter b, and therefore

$$\begin{aligned} b\lambda ^{2}=b\left( \lambda ^{2}|_{b=0}\right) +\mathcal {O}(b^{2}). \end{aligned}$$
(34)

Then the minimum eigenvalue of Eq. (31) can be obtained. At the critical point, the temperature is defined as (see Eq. (7) and note that at zeroth order with respect to \(\epsilon \), \(\chi \) is zero.)

$$\begin{aligned} T_\mathrm{{c}}=\frac{f^{\prime }\left( r_{+c}\right) }{4\pi }. \end{aligned}$$
(35)

Using Eqs. (11) and (23), we obtain

$$\begin{aligned} f^{\prime }\left( r_{+c}\right) =2r_{+c}+\frac{2\kappa ^{2}r_{+c}}{b}\left[ 1-\frac{1}{\sqrt{1-b\phi ^{\prime }\left( r_{+c}\right) {}^{2}}}\right] , \end{aligned}$$
(36)

and thus

Table 1 Analytical results of \({T_\mathrm{{c}}}/{\mu }\) for different values of backreaction and nonlinearity parameters.
Full size table
Fig. 1
figure 1

The behavior of the condensation parameter as a function of the temperature for different values of backreaction

Full size image
Fig. 2
figure 2

The behavior of the condensation parameter as a function of the temperature for different values of the nonlinearity parameter b

Full size image
$$\begin{aligned} T_\mathrm{{c}}= & {} \frac{1}{4\pi }(\frac{\mu }{\lambda })[2-\kappa _{n}^{2}(\lambda ^{2}|_{\kappa _{n-1}}) \nonumber \\&-\frac{3}{4}b\kappa _{n}^{2}(\lambda ^{4}|_{\kappa _{n-1},b=0})+b\kappa _{n}^{2}(\lambda ^{4}|_{\kappa _{n-1},b=0})]. \end{aligned}$$
(37)

As an example, if \(b=\kappa ^{2}=0\) we have

$$\begin{aligned} \lambda ^{2}=\dfrac{\frac{2}{3}\alpha ^{2}-\frac{4}{3}\alpha +1}{-\frac{ 251\alpha ^{2}}{864}+\frac{9\alpha }{16}+\frac{\alpha ^{2}\zeta (3)}{4}- \frac{\alpha \zeta (3)}{2}+\frac{\zeta (3)}{4}-\frac{1}{4}}. \end{aligned}$$

Inserting \(\alpha =0.759\), \(\lambda _\mathrm{{min}}^{2}=13.76\) and \(T_\mathrm{{c}}=0.429\mu \). The latter result perfectly agrees with [50].

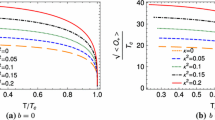
The values of \(T_\mathrm{{c}}/\mu \) for different backreaction and nonlinearity parameters are listed in Table 1. As shown, the effect of increasing the backreaction parameter \(\kappa \) for a fixed value of nonlinearity parameter b follows the same trend as raising b for a fixed value of \( \kappa \). In both cases, the critical temperature \(T_\mathrm{{c}}\) diminishes by the growth of the backreaction or nonlinearity parameters. It shows that the presence of backreaction and Born–Infeld nonlinear electrodynamics makes the scalar hair harder to form. In the next section, we will re-study the problem numerically using the shooting method.

4 Shooting method

In this section, we will study our holographic superconductor numerically. In order to do this, we use the shooting method [8]. In this method, the boundary values are found by setting appropriate initial conditions. So, for doing this, we need to know the behavior of the equations of motion both at horizon and at the boundary. Using a Taylor expansion at the horizon around \(z=1\), we get

$$\begin{aligned} f(z)= & {} f_{1}\left( 1-z\right) +f_{2}\left( 1-z\right) {}^{2}+\cdots , \end{aligned}$$
(38)
$$\begin{aligned} \phi (z)= & {} \phi _{1}\left( 1-z\right) +\phi _{2}\left( 1-z\right) {}^{2}+\cdots , \end{aligned}$$
(39)
$$\begin{aligned} \psi (z)= & {} \psi _{0}+\psi _{1}\left( 1-z\right) +\psi _{2}\left( 1-z\right) {}^{2}+\cdots , \end{aligned}$$
(40)
$$\begin{aligned} \chi (z)= & {} \chi _{0}+\chi _{1}\left( 1-z\right) +\chi _{2}\left( 1-z\right) {}^{2}+\cdots . \end{aligned}$$
(41)

Note that \(\phi =0\) at horizon, otherwise it will be ill-defined there. In our procedure, we find all coefficients in terms of \(\phi _{1}\), \(\psi _{0}\) and \(\chi _{0}\) by using the equations of motion. Varying them at the horizon, we try to get \(\psi _{-}=\chi =0\) at the boundary. So, the values of \(\psi _{+}\) and \(\mu \) are obtained. In addition, we will set \(r_{+}=1\) by virtue of the equations of motion’s symmetry,

$$\begin{aligned} r\rightarrow ar,f\rightarrow a^{2}f,\phi \rightarrow a\phi . \end{aligned}$$

Performing a numerical solution, we can find the values of \(T_\mathrm{{c}}/\mu \) for different backreaction and nonlinearity parameters. In order to compare the latter results with the analytical ones, we list both of them next to each other in Table 1. It is obvious that there is a reasonable agreement between the results of both methods. Moreover, in Table 1, the results of [53] for \(b=0\) have been recovered for different values of the backreaction parameter. As one could see in this table, increasing the backreaction parameter for a fixed value of b decreases the critical temperature. This means that larger values of the backreaction parameter make the condensation harder to form. Similarly, for a fixed value of \( \kappa \), increasing the nonlinearity of the electrodynamic model makes scalar hair harder to form because it diminishes the critical temperature.

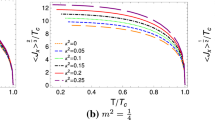
Figures 1 and 2 give information about the effect of the backreaction and nonlinear electrodynamics on condensation. All curves follow a same trend. As \(b\rightarrow 0\), we regain the results of the Maxwell case presented in [53]. As the figures show, the condensation gap increases by making the backreaction and nonlinearity parameters larger, while the other one is fixed. So, it can be understood that it is harder to form a superconductor. This is in agreement with the results obtained from the behavior of the critical temperature before.

5 Summary and discussion

In this work, by using the Sturm–Liouville eigenvalue problem, we analytically investigated the properties of the \((1+1)\)-dimensional holographic superconductor developed in a BTZ black hole background in the presence of BI nonlinear electrodynamics. We have relaxed the probe limit and further assumed that the gauge and scalar fields do backreact on the background metric. We determined the critical temperature for different values of backreaction and nonlinear parameters. We have continued our study by using the numerical shooting method and confirmed that the analytical results are in agreement with the numerical approach. We observed that the formation of scalar hair is harder in the presence of BI nonlinear electrodynamics and backreaction and it becomes harder and harder to form by increasing the strength of either the nonlinear or the backreaction parameters.

Finally, it would be of interest to extend this procedure for other nonlinear electrodynamics like the Power-Maxwell version and logarithmic cases and investigate the effects of nonlinear electrodynamics on the critical temperature and condensation operator of one-dimensional holographic superconductors. These issues are now under investigation and the results will appear elsewhere.