1 Introduction

In 1911 Kamerlingh Onnes discovered that the electrical resistance of mercury completely disappeared at temperatures a few degrees above absolute zero [1]. This phenomenon became known as superconductivity. He was awarded the Nobel Prize in physics in 1913 for his investigations of the properties of matter at low temperatures, which led, inter alia, to the production of liquid helium. Since the discovery of Kamerlingh Onnes, the studies on the superconductors have become an active field of research and a lot of papers have appeared in the literature to explain the mechanism of superconductivity. The aim was to explain the zero resistance of the materials from a microscopic point of view. The great step in this direction was made in 1957 by Bardeen, Cooper and Schrieffer who described superconductivity as a microscopic effect caused by a condensation of Cooper pairs into a boson-like state. They were also awarded the Nobel Prize in physics 1972 for their jointly developed theory of superconductivity, usually called the BCS theory. The BCS theory, however, requires only that the potential be attractive, regardless of its origin. In the BCS framework, superconductivity is a macroscopic effect which results from the condensation of Cooper pairs. It was the first widely accepted theory that explained superconductivity at low temperatures. Based on this theory superconductivity occurs because of condensation of Cooper pairs (including electrons with different spins and momenta) at low temperature. According to the angular momentum of Cooper pairs, we can classify superconductors as s-wave \((\ell =0)\), p-wave \((\ell =1)\), d-wave \( (\ell =2)\) etc. [2]. Since the Cooper pairs are decoupled at higher temperatures, the BCS theory has been argued to be inadequate to fully explain the mechanism of high temperature superconductivity [3]. In order to shed some light on the problem of high temperature superconductivity the Anti de Sitter/Conformal Field Theory (AdS/CFT) correspondence was taken into account [4, 5]. AdS/CFT duality relates the strong coupling conformal field theory living on the boundary in d-dimensions to a weak coupling gravity in (\(d+1\))-dimensional spacetime in the bulk. Through AdS/CFT, each quantity in the bulk has a dual on the boundary [4,5,6,7,8,9]. In 2008, Hartnoll et al. proposed a holographic s-wave superconductor model based on the gauge/gravity duality [5]. In his holographic model, Hartnoll assumed that there is a phase transition from a black hole with no hair (normal phase) to a hairy one (superconducting phase) below the critical temperature. Through this process, the system faces spontaneous U(1) symmetry breaking. Many studies of holographic superconductors have appeared in the past decade (see e.g. [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37] and the references therein).

The holographic p-wave superconductors can be studied by condensation of a charged vector field in the bulk which is the dual of a vector order parameter in the boundary, which can also be considered as the condensation of a 2-form field in the boundary. For this type of holographic superconductor, the formation of vector hair below the critical temperature is observed. Various models of holographic p-wave superconductors have been proposed. In [38] a p-wave superconductors was proposed by using an SU(2) Yang–Mills field in the bulk and one of the gauge degrees of freedom which is dual to spin-1 order parameter in the field theory. Also, p-wave type superconductivity may have arisen by the condensation of a 2-form field [39] and a massive spin-1 vector in the bulk [40, 41]. Holographic p-wave superconductors have been widely investigated in the literature (see e.g. [42,43,44,45,46,47,48]).

On the other side, holographic superconductors have also been explored when the bulk spacetime is a three-dimensional black hole. The Einstein field equations admit a three-dimensional solution known as BTZ (Bandos–Teitelboim–Zanelli) black holes. BTZ black holes have several crucial effects on the improvement in string theory [49,50,51,52,53]. The corresponding superconductor living on the boundary of BTZ black hole is one dimensional. Using the probe brane construction, holographic p-wave superconductors were investigated in [54]. One-dimensional holographic p-wave superconductors coupled to a massive complex vector field and in the probe limit were explored in [2]. It was argued that below a certain critical temperature, there is a formation of a vector hair around the black hole [2]. It is worth noting that in order to analyze one-dimensional holographic superconductor on the boundary of the three-dimensional spacetime, one needs to apply \(\hbox {AdS}_{{3}}\)/\(\hbox {CFT}_{{2}}\) duality [55]. One-dimensional holographic s-wave and p-wave superconductors were investigated analytically and numerically from different points of view (see e.g. [56,57,58,59,60,61,62,63,64,65,66,67]). All investigations of the (\(1+1\))-dimensional holographic p-wave superconductors are restricted to the case where the vector and gauge fields do not backreact on the background geometry. In the present work, we would like to extend the study of the holographic p-wave superconductors by considering the effects of the vector and gauge fields on the background of spacetime and disclose the effects of the backreaction on the properties of the superconductor.

We shall employ the Sturm–Liouville eigenvalue problem for the analytical calculation and the shooting method for the numerical investigations. For each method, the relation between critical temperature and chemical potential and critical exponent are investigated. We shall also compare the analytical results with the numerical data.

This paper is outlined now. In Sect. 2, we present the basic field equations and the boundary conditions of the (\(1+1\))-dimensional backreacting holographic p-wave superconductors. In Sect. 3, by using the Sturm–Liouville variational method, we obtain a relation between the critical temperature and the chemical potential. We also apply the shooting method and study the problem numerically and confirm that the analytical results are compatible with the numerical data. In Sect. 4, we calculate the critical exponent both analytically and numerically. The last section is devoted to closing remarks.

2 Basic field equations and boundary conditions

As mentioned, our study is based on the \(\hbox {AdS}_{{3}}\)/\(\hbox {CFT}_{{2}}\) duality. Due to this model, we have a spontaneous local/global U(1) symmetry breaking in the bulk/at the boundary. The action which can describe a charged massive spin-1 field \(\rho _{\mu }\) with charge q and mass m in (\(2+1\))-dimensional Einstein–Maxwell theory with a negative cosmological constant is given by

$$\begin{aligned}&S =\frac{1}{2\kappa ^{2}}\int d^{3}x\sqrt{-g}\left( R+\frac{2}{l^{2}} \right) +\int d^{3}x\sqrt{-g}{\mathcal {L}}_{m}, \nonumber \\&{\mathcal {L}}_{m} = -\dfrac{1}{4}F_{\mu \nu }F^{\mu \nu }-\frac{1}{2} \rho _{\mu \nu }^{\dagger }\rho ^{\mu \nu }-m^{2}\rho _{\mu }^{\dagger }\rho ^{\mu }+iq\gamma \rho _{\mu }\rho _{\nu }^{\dagger }F^{\mu \nu }, \nonumber \\ \end{aligned}$$
(1)

where g, R and l are the metric determinant, Ricci scalar and AdS radius, respectively. \(\kappa ^{2}=8\pi G_{3}\), in which \(G_{3}\) characterizes the three-dimensional Newton gravitation constant in the bulk. Also, by considering \(A_{\mu }\) as the vector potential, the strength of the Maxwell field reads \(F_{\mu \nu }=\nabla _{\mu }A_{\nu }-\nabla _{\nu }A_{\mu }\). In addition, \(\rho _{\mu \nu }=D_{\mu }\rho _{\nu }-D_{\nu }\rho _{\mu }\) where \(D_{\mu }=\nabla _{\mu }-iqA_{\mu }\). A nonlinear interaction between \(\rho _{\mu }\) with \(\gamma \) (the magnetic moment) and \(A_{\mu }\) is described by the last term in the above action. Since we consider the case without external magnetic field, this term plays no role.

We obtain the equations of motion for matter and gravitational fields by varying the action (1) with respect to the metric \(g_{\mu \nu }\), the gauge field \(A_{\mu }\) and the vector field \( \rho _{\mu }\). We find

$$\begin{aligned}&\frac{1}{2\kappa ^{2}}\left[ R_{\mu \nu }-g_{\mu \nu }\left( \frac{R}{2}+ \frac{1}{l^{2}}\right) \right] =\frac{1}{2}F_{\mu \lambda }F_{\nu }{}^{\lambda }\nonumber \\&\quad +\frac{1}{2}{\mathcal {L}}_{m}g_{\mu \nu }+\frac{1}{2}\left[ \rho ^{\dagger }{}_{\mu \lambda }\rho _{\nu }^{\lambda }+m^{2}\rho ^{\dagger }{}_{\mu }\rho _{\nu }\right. \nonumber \\&\quad \left. -i\gamma qF_{\nu }^{\lambda }\left( \rho _{\mu }\rho ^{\dagger }{}_{\lambda }-\rho ^{\dagger }{}_{\mu }\rho _{\lambda }\right) +\mu \leftrightarrow \nu \right] , \end{aligned}$$
(2)
$$\begin{aligned}&\nabla ^{\nu }F_{\nu \mu }=iq\left( \rho ^{\nu }\rho ^{\dagger }{}_{\nu \mu }-\rho ^{\nu \dagger }\rho _{\nu \mu }\right) \nonumber \\&\quad +iq\gamma \nabla ^{\nu }\left( \rho _{\nu }\rho ^{\dagger }{}_{\mu }-\rho ^{\dagger }{}_{\nu }\rho _{\mu }\right) , \end{aligned}$$
(3)
$$\begin{aligned}&D^{\nu }\rho _{\nu \mu }-m^{2}\rho _{\mu }+iq\gamma \rho ^{\nu }F_{\nu \mu }=0. \end{aligned}$$
(4)

The boundary value of \(\rho _{\mu }\) is the origin of a charged vector operator, its expectation value playing the role of order parameter in the boundary theory. When the temperature decreases below the critical value, the normal phase becomes unstable and the vector hair which corresponds to superconducting phase appears.

In order to study the one-dimensional holographic p-wave superconductor in the presence of backreaction, we take the following metric for the background geometry:

$$\begin{aligned} {{\text {d}}s}^{2}=-f(r)e^{-\chi (r)}{{\text {d}}t}^{2}+\frac{{dr}^{2}}{f(r)}+r^{2}{{\text {d}}x}^{2}, \end{aligned}$$
(5)

with the following choices for the vector and gauge fields:

$$\begin{aligned} \rho _{\nu }{\text {d}}x^{\nu }=\rho _{x}(r){\text {d}}x,\ \ \ A_{\nu }{\text {d}}x^{\nu }=\phi (r){\text {d}}t. \end{aligned}$$
(6)

The Hawking temperature of this black hole is given by [67]

$$\begin{aligned} T=\frac{e^{-\chi (r_{+})/2}f^{^{\prime }}(r_{+})}{4\pi }. \end{aligned}$$
(7)

Substituting the metric (5) and Eq. (6) in the field equations (2) and (3), we arrive at

$$\begin{aligned}&\phi ^{\prime \prime }(r)+\left[ \frac{1}{2}\chi ^{\prime }(r)+\frac{1}{r} \right] \phi ^{\prime }(r)-\frac{2q^{2}\rho _{{x}}(r)^{2}\phi (r)}{ r^{2}f(r)}=0, \end{aligned}$$
(8)
$$\begin{aligned}&\rho ^{\prime \prime }_{x}(r)+\left[ \frac{f^{\prime }(r)}{f(r)}- \frac{1}{2}\chi ^{\prime }(r)-\frac{1}{r}\right] \rho ^{\prime } _{x}(r)\nonumber \\&\quad +\left[ \frac{q^{2}e^{\chi (r)}\phi (r)^{2}}{f(r)^{2}}-\frac{m^{2}}{f(r)} \right] \rho _{x}(r)=0, \end{aligned}$$
(9)
$$\begin{aligned}&f^{\prime }(r)-\frac{2r}{l^{2}}+\frac{2\kappa ^{2}}{r}\left[ \frac{q^{2} {\rho _{x}}(r)^{2}e^{\chi (r)}\phi (r)^{2}}{f(r)}\right. \nonumber \\&\quad \left. +f(r)\rho ^{\prime 2}_{x}+m^{2}\rho _{x}(r)^{2}+\frac{r^{2}}{2}e^{\chi (r)}\phi ^{\prime 2}\right] =0, \end{aligned}$$
(10)
$$\begin{aligned}&\chi ^{\prime }(r)+\frac{4\kappa ^{2}}{r}\left[ \frac{q^{2}{\rho _{x}} (r)^{2}e^{\chi (r)}\phi (r)^{2}}{f(r)^{2}}+{\rho ^{\prime } _{x}}^2 \right] =0. \end{aligned}$$
(11)

Here, the prime denotes a derivative with respect to r. If we consider the probe limit (\(\kappa \rightarrow 0\)), the equations of motion (8) and (9) reduce to the corresponding equations in [2]. In the following, we set q and l equal to unity by using the symmetries

$$\begin{aligned}&q\rightarrow q/a,\quad \phi \rightarrow a\phi ,\quad \rho _{x}\rightarrow a\rho _{x},\ \ \ \kappa \rightarrow \kappa /a, \end{aligned}$$
(12)
$$\begin{aligned}&l\rightarrow al,\quad r\rightarrow ar,\quad q\rightarrow q/a,\ \ \ m\rightarrow m/a. \end{aligned}$$
(13)

The asymptotic behavior \((r\rightarrow \infty )\) of the solutions is given by

$$\begin{aligned}&\phi (r)\sim \rho +\mu \ln (r),\ \ f(r)\sim r^{2},\ \ \chi (r)\rightarrow 0,\nonumber \\&\quad \rho _{x}(r)\sim \frac{\rho _{x_{-}}}{r^{-m}}+\frac{\rho _{x_{+}}}{ r^{m}}, \end{aligned}$$
(14)

in which \(\mu \) and \(\rho \) are chemical potential and charge density, respectively. Note that in (14), the value of \(\chi \) has been set to zero by virtue of the symmetry,

$$\begin{aligned} e^{\chi }\rightarrow a^{2}e^{\chi },\quad t\rightarrow at,\quad \phi \rightarrow \phi /a. \end{aligned}$$
(15)

The asymptotic behavior of the vector field \(\rho _{x}(r)\) is in agreement with the result of [68]. Here, the Breitenlohner–Freedman (BF) bound is \(m^{2}\ge 0\). In this limit, \(\rho _{x_{-}}\) plays the role of the source and \(\rho _{x_{+}}\) known as x-component of the expectation value of the order parameter \(\langle J_{x}\rangle \). In the next sections, we will analyze the properties of the one-dimensional backreacting holographic p-wave superconductor analytically and numerically.

3 Superconductivity phase transition

In this section, we are going to investigate the phase transition and critical temperature of (\(1+1\))-dimensional backreacting holographic p-wave superconductors. We address the relation between critical temperature \(T_{c}\) and chemical potential \(\mu \) as well as the effect of backreaction parameter on \( T_{c}\) in the vicinity of transition point.

3.1 Analytical approach

For the analytical approach, we employ the Sturm–Liouville eigenvalue problem. To do this we use the coordinate transformation \(z=r_{+}/r\) where \(0\leqslant z\leqslant 1\). In the new coordinates, the field equations (8)–(11) turn into

$$\begin{aligned}&\phi ^{\prime \prime }(z)+\left( \frac{\chi ^{\prime }(z)}{2}+\frac{1}{z} \right) \phi ^{\prime }(z)-\frac{2\rho _{x}(z)^{2}\phi (z)}{z^{2}f(z)}=0, \end{aligned}$$
(16)
$$\begin{aligned}&\rho _{x}^{\prime \prime }(z)+\left( -\frac{1}{2}\chi ^{\prime }(z)+\frac{ f^{\prime }(z)}{f(z)}+\frac{3}{z}\right) \rho _{x}^{\prime }(z)\nonumber \\&\quad +\rho _{x}(z)\left( \frac{r_{+}^{2}e^{\chi (z)}\phi (z)^{2}}{z^{4}f(z)^{2}}-\frac{ m^{2}r_{+}^{2}}{z^{4}f(z)}\right) =0, \end{aligned}$$
(17)
$$\begin{aligned}&f^{\prime }(z)+\frac{2r_{+}^{2}}{l^{2}z^{3}}-2\kappa ^{2}\left( \frac{ e^{\chi (z)}\phi (z)^{2}\rho _{x}(z){}^{2}}{zf(z)}+\frac{z^{3}f(z)\rho _{x}^{\prime 2}}{r_{+}^{2}}\right. \nonumber \\&\quad \left. +\frac{m^{2}\rho _{x}(z){}^{2}}{z}+\frac{z}{2} e^{\chi (z)}\phi ^{\prime 2}\right) =0, \end{aligned}$$
(18)
$$\begin{aligned}&\chi ^{\prime }(z)-4\kappa ^{2}\left( \frac{e^{\chi (z)}\phi (z)^{2}\rho _{x}(z){}^{2}}{ zf^{2}(z)}+\frac{z^{3}\rho _{x}^{\prime }(z)^{2}}{r_{+}^{2}}\right) =0. \end{aligned}$$
(19)

Here, the prime indicates the derivative with respect to z. Near the critical temperature, the expectation value of \(\langle J_{x}\rangle \) is small, so we can take it as an expansion parameter

$$\begin{aligned} \epsilon \equiv \left\langle J_{x}\right\rangle . \end{aligned}$$

Since in the vicinity of critical temperature \(\epsilon \ll 1\), we focus on solutions for small values of the condensation parameter \(\epsilon \). Therefore, we can expand the model functions as

$$\begin{aligned}&\rho _{x}\approx \epsilon \rho _{x_{1}}+\epsilon ^{3}\rho _{x_{3}}+\epsilon ^{5}\rho _{x_{5}}+\cdots , \end{aligned}$$
(20)
$$\begin{aligned}&\phi \approx \phi _{0}+\epsilon ^{2}\phi _{2}+\epsilon ^{4}\phi _{4}+\cdots , \end{aligned}$$
(21)
$$\begin{aligned}&f\approx f_{0}+\epsilon ^{2}f_{2}+\epsilon ^{4}f_{4}+\cdots , \end{aligned}$$
(22)
$$\begin{aligned}&\chi \approx \epsilon ^{2}\chi _{2}+\epsilon ^{4}\chi _{4}+\cdots . \end{aligned}$$
(23)

Furthermore, we have a similar expression for the chemical potential which can be expressed as

$$\begin{aligned} \mu =\mu _{0}+\epsilon ^{2}\delta \mu _{2}+\cdots \rightarrow \epsilon \thickapprox \Bigg (\frac{\mu -\mu _{0}}{\delta \mu _{2}}\Bigg )^{1/2}, \end{aligned}$$
(24)

where \(\delta \mu _{2}>0\). Thus, near the phase transition point (\(\mu _{c}=\mu _{0}\)) the order parameter \(\epsilon \) vanishes. In addition, we obtain the mean field value of the critical exponent: \(\beta =1/2\).

The equation of motion for the gauge field (16) at zeroth order of \(\epsilon \) is given by

$$\begin{aligned} \phi ^{\prime \prime }(z)+\frac{\phi ^{\prime }(z)}{z}=0. \end{aligned}$$
(25)

The solution of this equation reads

$$\begin{aligned} \phi (z)=\lambda r_{+}\log (z),\ \ \ \lambda =\frac{\mu }{r_{+}}. \end{aligned}$$
(26)

Combining the solutions (26) with Eq. (18), the equation for f(z), at zeroth order of \(\epsilon \), can be obtained:

$$\begin{aligned} f^{\prime }(z)+\frac{2r_{+}^{2}}{z^{3}}-\frac{\kappa ^{2}\lambda ^{2}r_{+}^{2}}{z}=0, \end{aligned}$$
(27)

which has the solutions

$$\begin{aligned} f(z)=\frac{r_{+}^{2}g(z)}{z^{2}},\quad g(z)=1-z^{2}+\kappa ^{2}\lambda ^{2}z^{2}\log (z). \end{aligned}$$
(28)

Near the boundary, the vector field can be defined by

$$\begin{aligned} \rho _{x}(z)=\frac{\langle J_{x}\rangle }{\sqrt{2}r_{+}^{\Delta }}z^{\Delta }F(z). \end{aligned}$$
(29)

Inserting Eqs. (28) and (29) in Eq. (17) yields

$$\begin{aligned}&F^{\prime \prime }(z)+F^{\prime }(z)\left( \frac{g^{\prime }(z)}{g(z)}+\frac{ 2\Delta }{z}+\frac{1}{z}\right) \nonumber \\&\quad +F(z)\left( \frac{\Delta g^{\prime }(z)}{ zg(z)}-\frac{m^{2}}{z^{2}g(z)}+\frac{\Delta ^{2}}{z^{2}}\right) \nonumber \\&\quad +\frac{ F(z)\left( \lambda ^{2}\kappa ^{2}\log ^{2}(z)\right) }{g(z)^{2}}=0. \end{aligned}$$
(30)

If we define some new functions, see below, we can rewrite Eq. (30) in the Sturm–Liouville form:

$$\begin{aligned} \left[ T(z)F^{\prime }(z)\right] ^{\prime }+P(z)T(z)F(z)+\lambda ^{2}Q(z)T(z)F(z)=0, \nonumber \\ \end{aligned}$$
(31)

where

$$\begin{aligned}&T(z) = z^{2\Delta +1}g(z),\quad P(z)=\left[ \frac{\Delta g^{\prime }(z)}{zg(z)}-\frac{m^{2}}{z^{2}g(z)}+\frac{\Delta ^{2}}{z^{2}}\right] ,\nonumber \\&Q(z)=\frac{\log ^{2}(z)}{g(z)^{2}}. \end{aligned}$$
(32)

Next, we define the trial function \(F(z)=1-\alpha z^{2}\), which is satisfied in the boundary conditions \(F(0)=1\) and \(F^{^{\prime }}(0)=0\). By minimizing the following expression with respect to \(\alpha \), Eq. (31) will be solved:

$$\begin{aligned} \lambda ^{2}=\frac{\int _{0}^{1}T\left( F^{\prime 2}-PF^{2}\right) {\text {d}}z}{ \int _{0}^{1}TQF^{2}{\text {d}}z}. \end{aligned}$$
(33)

With the help of the iteration method, the definition of the backreacting parameter is [69]

$$\begin{aligned} \kappa _{n}=n\Delta \kappa ,\ \ \ n=0,1,2,\ldots ,\ \ \Delta \kappa =\kappa _{n+1}-\kappa _{n}. \end{aligned}$$
(34)

Here, \(\Delta \kappa =0.05\). In addition, we have

$$\begin{aligned} \kappa ^{2}\lambda ^{2}={\kappa _{n}}^{2}\lambda ^{2}={\kappa _{n}} ^{2}(\lambda ^{2}|_{\kappa _{n-1}})+O[(\Delta \kappa )^{4}], \end{aligned}$$
(35)

where \(\kappa _{-1}=0\) and \(\lambda ^{2}|_{\kappa _{-1}}=0\). At the critical point, at zeroth order with respect to \(\epsilon \), the critical temperature is defined asFootnote 1

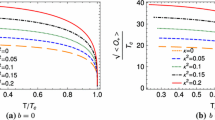
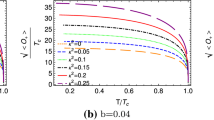
$$\begin{aligned} T_{c}=\frac{f^{\prime }\left( r_{+c}\right) }{4\pi }=r_{+c}\left( \frac{2-{ \kappa }^{2}\lambda ^{2}}{4\pi }\right) =\frac{\mu }{\lambda }\left( \frac{2- {\kappa }_{n}^{2}\lambda ^{2}|_{\kappa _{n-1}}}{4\pi }\right) . \end{aligned}$$
(36)

The analytical results of \(T_{c}/\mu \) for different values of mass and backreaction parameters are shown in Table 1. According to these results, enlarging the values of mass have the same effect as increasing the backreaction parameter on \(T_{c}/\mu \) and makes it smaller. Thus, it makes condensation harder to form.

3.2 Numerical method

We employ the shooting method [10] to numerically investigate the properties of the (\(1+1\))-dimensional holographic p-wave superconductor developed in a BTZ black hole background, when the gauge and vector fields backreact on the background geometry. For this purpose, we must know the behavior of the model functions both at horizon and boundary. By using a Taylor expansion around the horizon we arrive at

$$\begin{aligned}&f(z) = f_{1}\left( 1-z\right) +f_{2}\left( 1-z\right) {}^{2}+\cdots , \end{aligned}$$
(37)
$$\begin{aligned}&\phi (z)=\phi _{1}\left( 1-z\right) +\phi _{2}\left( 1-z\right) {}^{2}+\cdots , \end{aligned}$$
(38)
$$\begin{aligned}&\rho _{x}(z)=\rho _{x_{0}}+\rho _{x_{1}}\left( 1-z\right) +\rho _{x_{2}}\left( 1-z\right) {}^{2}+\cdots , \end{aligned}$$
(39)
$$\begin{aligned}&\chi (z)=\chi _{0}+\chi _{1}\left( 1-z\right) +\chi _{2}\left( 1-z\right) {}^{2}+\cdots . \end{aligned}$$
(40)

We impose the boundary condition \(\phi (z=1)\), which is motivated by the fact that the gauge field \(A_{\nu }\) has a finite norm at the horizon. In this method, all coefficients will be defined in terms of \(\phi _{1}\), \( \rho _{x_{0}}\) and \(\chi _{0}\). The desirable state is \(\rho _{x_{-}}(\infty )=\chi (\infty )=0\). This will be obtained by varying \(\phi _{1}\), \(\rho _{x_{0}}\) and \(\chi _{0}\) at the horizon. Furthermore, we can set \(r_{+}=1\) by virtue of the equations of motion’s symmetry

$$\begin{aligned} r\rightarrow ar,\quad f\rightarrow a^{2}f,\quad \phi \rightarrow a\phi . \end{aligned}$$
(41)
Table 1 Analytical and numerical results of \({T_{c}}/{\mu }\) for different values of backreaction and mass parameters
Full size table
Fig. 1
figure 1

The behavior of the condensation parameter as a function of the temperature for different values of backreaction

Full size image

This method leads one to find the values of \(T_{c}/\mu \) for different masses and backreaction parameters. In order to compare the numerical and analytical results, data are given in Table 1. The results of the Sturm–Liouville method are confirmed by numerical data. The effects of mass and backreaction parameters on the behavior of condensation are shown in Fig. 1. We see that all curves follow the same behavior. As is clear from Fig. 1, enhancing the values of mass and backreaction parameter causes the gap in the curves to be larger and thus it makes the formation of condensation harder. As a result, the critical temperature decreases with increasing the backreaction and mass parameters.

4 Critical exponents

In this section we calculate the expectation value of \(\langle J_{x}\rangle \) in the boundary theory near the critical temperature for the one-dimensional holographic p-wave superconductor in the presence of backreaction. Furthermore, we compute the values of the critical exponents both analytically and numerically.

Table 2 Analytical and numerical results of \(\gamma \) for different values of the backreaction and mass parameters
Full size table
Fig. 2
figure 2

The behavior of \(\log \langle J_{x}\rangle /T_{c}^{\Delta +1}\) as a function of \(\log \left( 1-T/T_{c}\right) \) with slope of 1 / 2 for different values of mass and backreaction parameters

Full size image

4.1 Analytical approach

We focus on the behavior of the gauge field in the vicinity of the critical temperature. In this limit, the field equation (16) turns into

$$\begin{aligned} \phi ^{\prime \prime }(z)+\frac{\phi ^{\prime }(z)}{z}-\frac{2\rho _{x}(z)^{2}\phi (z)}{z^{2}f(z)}=0. \end{aligned}$$
(42)

Because of nonzero value of the condensation in the vicinity of the critical temperature, we have an extra term in the above equation in comparison with the field equation in the previous section. Inserting Eqs. (28) and (29) in Eq. (42) we have

$$\begin{aligned} \phi ^{\prime \prime }(z)+\frac{\phi ^{\prime }(z)}{z}=\frac{\langle J_{x}\rangle ^{2}z^{2\Delta }}{r_{+}^{2\Delta +2}g(z)}F(z)^{2}\phi (z). \end{aligned}$$
(43)

Using the fact that the value of \(\frac{\langle J_{x}\rangle ^{2}}{ r_{+}^{2\Delta +2}}\) is small in the \(T\sim T_{c}\) limit, we assume that Eq. (43) has the following answer:

$$\begin{aligned} \frac{\phi (z)}{r_{+}}=\lambda \log (z)+\frac{\langle J_{x}\rangle ^{2}}{ r_{+}^{2\Delta +2}}\eta (z),\ \ \ \lambda =\frac{\mu }{r_{+}}. \end{aligned}$$
(44)

Since at the horizon \(\phi (z=1)=0\), we have \(\eta (1)=0\). Substituting the above equation in Eq. (43) up to \(\frac{\langle J_{x}\rangle ^{2}}{ r_{+}^{2\Delta +2}}\) order, we arrive at

$$\begin{aligned} \eta ^{\prime \prime }(z)+\frac{\eta ^{\prime }(z)}{z}=\frac{\lambda z^{2\Delta }\log (z)}{g(z)}F(z)^{2}. \end{aligned}$$
(45)

Multiplying both sides of Eq. (45) by z and integrating from \(z=0\) to \(z=1\), we get

$$\begin{aligned}&\int _{0}^{1}d\left( z\eta ^{\prime }(z)\right) =\eta ^{\prime }(1)=\lambda \int _{0}^{1}\frac{z^{2\Delta +1}\log (z)}{1-z^{2}+\kappa ^{2}\lambda ^{2}z^{2}\log (z)}\nonumber \\&\quad \times F(z)^{2}\,{\text {d}}z=\lambda {\mathcal {A}}, \end{aligned}$$
(46)

where

$$\begin{aligned} {\mathcal {A}}\equiv \int _{0}^{1}\frac{z^{2\Delta +1}\log (z)}{1-z^{2}+\kappa ^{2}\lambda ^{2}z^{2}\log (z)}F(z)^{2}\,{\text {d}}z. \end{aligned}$$
(47)

Combining Eqs. (14) and (44) and taking into account the fact that the first term on the rhs of Eq. (44) is the solution of \(\phi (z)\) at the critical point, and the second term is a correction term, we can write near the critical point

$$\begin{aligned} \frac{\rho }{r_{+}}+\frac{\mu }{r_{+}}\log (z)=+\frac{\mu }{r_{+c}}\log (z)+ \frac{\langle J_{x}\rangle ^{2}}{r_{+c}^{2\Delta +2}}\eta (z). \end{aligned}$$
(48)

Now, we use the coordinate transformation \( z\rightarrow Z+1\); then by expanding the resulting equation around \(Z=0\) we get

$$\begin{aligned}&\frac{\rho }{r_{+}}+\frac{\mu }{r_{+}}\left( Z-\frac{Z^{2}}{2}+\cdots \right) =+\frac{\mu }{ r_{+c}}\left( Z-\frac{Z^{2}}{2}+\cdots \right) \nonumber \\&\quad +\frac{\langle J_{x}\rangle ^{2}}{r_{+c}^{2\Delta +2}}\left( \eta (1)+Z\eta ^{\prime }(1)+\cdots \right) . \end{aligned}$$
(49)

Comparing the coefficients Z on the two sides of Eq. (49) and using Eq. (46) we find

$$\begin{aligned} \frac{\mu }{r_{+}}=\frac{\mu }{r_{+c}}\left( 1+\frac{\langle J_{x}\rangle ^{2}}{r_{+c}^{2\Delta +2}}{\mathcal {A}}\right) . \end{aligned}$$
(50)

Near the critical point we have \(T\sim T_{c}\), and thus using Eq. (36), we can find the equation of \(r_{+}\):

$$\begin{aligned} r_{+}=\frac{4\pi T}{\left( 2-\kappa ^{2}\lambda ^{2}\right) }, \end{aligned}$$
(51)

Inserting Eqs. (36) and (51) in Eq. (50) and taking the absolute values of the resulting equation, we arrive at

$$\begin{aligned} \langle J_{x}\rangle =\gamma T_{c}^{\Delta +1}\sqrt{1-\frac{T}{T_{c}}}, \end{aligned}$$
(52)

where

$$\begin{aligned} \gamma =\frac{1}{\sqrt{\left| {\mathcal {A}}\right| }}\left( \frac{4\pi }{2-\kappa ^{2}\lambda ^{2}}\right) ^{\Delta +1}. \end{aligned}$$
(53)

Based on the above equation, it is obvious that the critical exponent \(\beta =1/2\) is in a perfect agreement with the mean field theory. Since the value of \(\beta \) is independent of the effect of backreaction, we have the second order phase transition for all values of the backreaction parameter. The analytical results are shown in Table 2. Increasing the values of the mass and backreaction parameters causes larger values of the condensation parameter. Therefore, the larger values of the mass and the backreacting of the gauge and vector fields on the background geometry make the condensation harder to form.

4.2 Numerical method

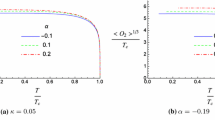
Based on the behavior of condensation near the critical temperature, which is obtained by using analytical approach (i.e. Eq. (52)), we have

$$\begin{aligned} \log \left( \frac{\langle J_{x}\rangle }{T_{c}^{\Delta +1}}\right) =\log (\gamma )+\frac{1}{2}\log \left( 1-\frac{T}{T_{c}}\right) . \end{aligned}$$
(54)

In Fig. 2, the behavior of \(\log \langle J_{x}\rangle /T_{c}^{\Delta +1}\) as a function of \(\log \left( 1-T/T_{c}\right) \) for different values of the backreaction and mass parameters was shown. The slope of the curves is 1 / 2, which is in agreement with mean field theory and shows that we face a second order phase transition—the same as in the analytical approach. In addition, this value of the critical exponent is independent of the backreaction parameter. Using Eq. (54), it is obvious that the intercept of the curves represents the values of \(\log \gamma \) numerically. In order to compare the analytical and numerical values of \(\gamma \), the results are listed in Table 2. The best agreement between the values of \(\gamma \) from these two approaches appears in \(m^{2}=1/16\) and for larger values of mass we observe a poorer match. In addition, the values of \(\gamma \) increase for larger values of the backreaction parameter. The same results are obtained in analytical method.

5 Closing remarks

In this paper, we analyzed a holographic p-wave superconductor model in a three-dimensional Einstein–Maxwell theory in the presence of a negative cosmological constant and a vector field when the gauge and vector fields backreact on the background geometry. In order to study the problem analytically, we employ the Sturm–Liouville eigenvalue problem, while the numerical data were obtained with the help of the shooting method. We analytically calculated the relation between the critical temperature and the chemical potential for different values of the mass and backreaction parameters. These data were confirmed by numerical results. We found that increasing the values of the mass and backreaction parameters makes the condensation harder to form and thus the critical temperature decreases. In addition, the critical exponent of this system has also been obtained both analytically and numerically. Based on these investigations, we face a second order phase transition. Furthermore, the obtained critical exponent value \(\beta ={1}/{2}\) follows the mean field theory value. Since the nonlinear electrodynamics gives much information in comparison with the Maxwell case, it is worthwhile to consider the effect of nonlinearity on the physical properties of holographic p-wave superconductors. We leave this issue for future investigations.