1 Introduction

The AdS / CFT duality provides a correspondence between a strongly coupled conformal field theory (CFT) in d-dimensions and a weakly coupled gravity theory in (\(d+1\))-dimensional anti-de Sitter (AdS) spacetime [1,2,3]. Since it is a duality between two theories with different dimensions, it is commonly called holography. The idea of holography has been employed in condensed matter physics to study various phenomena such as superconductors [4,5,6,7,8]. For describing the properties of low temperature superconductors, the BCS theory can work very well [9, 10]. However, this theory fails to describe the mechanism of high temperature superconductor. In latter regime, the holography was suggested to study the properties of superconductors [11, 12]. Hortnol et al. have represented the first model of holographic superconductors [11, 12]. After that, holographic superconductors have attracted a lot of attention and investigated from different point of views [4, 13,14,15,16].

BTZ black holes play a significant role in many of recent developments in string theory [17,18,19]. BTZ-like solutions are dual of (\(1+1\) )-dimensional holographic systems such as one-dimensional holographic superconductors. Distinctive features of normal and superconducting phases of one-dimensional systems have been studied studied in [20]. The latter study was done in probe limit. Considering the effects of backreaction, the properties of one-dimensional holographic superconductors have been studied both numerically [21, 22] and analytically [23, 24].

It is interesting to investigate the effect of nonlinear electrodynamic models on holographic systems including holographic superconductors [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44]. Nonlinear models carry more information than the usual Maxwell case and also are considered as a possible way for avoiding the singularity of the point-like charged particle at the origin [45,46,47,48,49]. The oldest nonlinear electrodynamic model is Born-Infeld (BI) model. There are also two BI-like nonlinear electrodynamics namely logarithmic [33, 50, 51] and exponential [40, 52, 53] electrodynamics. It has been found that the exponential electrodynamics has stronger effect on the condensation than other models [54].

In the present work, we will study the one-dimensional holographic superconductors both analytically and numerically in the presence of exponential electrodynamics. To bring rich physics in holographic model, we consider the backreaction of the scalar and gauge fields on the metric background [55,56,57,58,59,60,61]. To perform the analytical study, we employ the Sturm–Liouville eigenvalue problem. We will study the effects of nonlinear exponential electrodynamics model as well as backreaction on critical temperature. We shall also use the numerical shooting method to investigate the features of our holographic superconductors and make comparison between analytical and numerical results.

This paper is organized as follows: In next section, we introduce the action and basic field equations governing (\(1+1\))-dimensional holographic superconductors in the presence of exponential electrodynamics. In Sect. 3, we study the properties of holographic superconductors applying the analytical method based on Sturm–Liuoville eigenvalue problem. In Sect. 4, we study holographic superconductors numerically by employing the shooting method. We also compare our numerical and analytical results. Finally, in last section we will summarize our results.

2 Holographic set-up

To study a (\(1+1\))-dimensional holographic superconductor, we consider a (\( 2+1\))-dimensional bulk action of AdS gravity coupled to a charged scalar field \(\psi \)

$$\begin{aligned} S= & {} \frac{1}{2\kappa ^{2}}\int d^{3}x\sqrt{-g}\left( R+\frac{2}{l^{2}}\right) \nonumber \\&+\int d^{3}x\sqrt{-g}\left[ L\left( F\right) -|\nabla \psi -iqA\psi |^{2}-m^{2}|\psi |^{2}\right] , \nonumber \\ \end{aligned}$$
(1)

where g is the determinant of metric, R is Ricci scalar, l is the AdS radius, A is electromagnetic potential and \(F=F_{\mu \nu }F^{\mu \nu }\) in which \(F_{\mu \nu }=\nabla _{[\mu }A_{\mu ]}\). In action (1), \(\kappa ^{2}=8\pi G_{3}\) where \(G_{3}\) is the (\(2+1\))-dimensional Newtonian constant and m and q represent the mass and charge of scalar field, respectively. \(L\left( F\right) \) stands for the Lagrangian of electrodynamics model. (\(1+1\))-dimensional holographic superconductors in the presence of linear Maxwell electrodynamics presented by \(L\left( F\right) =-F/4\) have been studied in [21, 62]. The linear model is an idealization of reality. In principle, other powers of F may play role. There are different nonlinear electrodynamics models which exhibit the electrodynamics interaction. In this paper, we suppose that electrodynamics interaction is governed by exponential nonlinear electrodynamics model [52]

$$\begin{aligned} L\left( F\right) =\frac{1}{4b}\left( {\mathrm {e}}^{-bF}-1\right) , \end{aligned}$$
(2)

where b determines the nonlinearity. For small values of b, Lagrangian ( 2) recovers the linear Maxwell Lagrangian. The parameter \(\kappa \) in (1) also determines the backreaction. When \(\kappa \) goes to zero, we are in the probe limit, meaning that the gravity part of action (1) is stronger than the matter field part. Physically, this implies that the gauge and matter fields do not back react on the metric background. In superconducting language, implies that the Cooper pairs have negligible interaction with background system. In the presence of backreaction, the dual black hole solution may be given by the ansatz

$$\begin{aligned} ds^{2}=-f(r){\mathrm {e}}^{-\chi (r)}dt^{2}+\frac{dr^{2}}{f(r)}+\frac{r^{2}}{ l^{2}}dx^{2}. \end{aligned}$$
(3)

The Hawking temperature of above black hole solution is given by

$$\begin{aligned} T=\frac{f^{\prime }(r_{+}){\mathrm {e}}^{-\chi (r_{+})}}{4\pi }, \end{aligned}$$
(4)

where \(r_{+}\) is event horizon which could be obtained as the greatest root of \(f(r)=0\). Varying the action (1) with respect to \(\psi \), \(A_{\nu }\) and \(g_{\mu \nu }\), the field equations read, respectively,

$$\begin{aligned} 0= & {} \left( \nabla _{\mu }-i{q}A_{\mu }\right) \left( \nabla ^{\mu }-i{q} A^{\mu }\right) \psi -m^{2}\psi \,, \end{aligned}$$
(5)
$$\begin{aligned} 0= & {} \nabla ^{\mu }\left( 4L_{F}F_{\mu \nu }\right) \nonumber \\&-i{q}\left[ -\psi ^{*}(\nabla _{\nu }-i{q}A_{\nu })\psi +\psi (\nabla _{\nu }+i{q}A_{\nu })\psi ^{*}\right] \,, \end{aligned}$$
(6)
$$\begin{aligned} 0= & {} \frac{1}{2\kappa ^{2}}\left[ R_{\mu \nu }-g_{\mu \nu }\left( \frac{R}{2} +\frac{1}{l^{2}}\right) \right] +2F_{ac}F_{b}{}^{c}L_{F} \nonumber \\&-\frac{g_{\mu \nu }}{2}\left[ L\left( F\right) -m^{2}|\psi |^{2}-{|\nabla \psi -i{q}A\psi |^{2}}\right] \nonumber \\&-\frac{1}{2}\left[ (\nabla _{\mu }\psi -i{q}A_{\mu }\psi )(\nabla _{\nu }\psi ^{*}+i{q}A_{\nu }\psi ^{*})+\mu \leftrightarrow \nu \right] , \nonumber \\ \end{aligned}$$
(7)

where \(L_{F}=\partial L/\partial F\). Adopting the ansatz \(A_{\mu }=\phi (r)\delta _{\mu }^{0}\) and \(\psi =\psi (r)\), field Eq. (5)–(7) lead to

$$\begin{aligned} 0= & {} \psi ^{\prime \prime }+\psi ^{\prime }\left[ \frac{1}{r}+\frac{ f^{\prime }}{f}-\frac{\chi ^{\prime }}{2}\right] +\psi \left[ \frac{ q^{2}\phi ^{2}{\mathrm {e}}^{\chi }}{f^{2}}-\frac{m^{2}}{f}\right] , \end{aligned}$$
(8)
$$\begin{aligned} 0= & {} \phi ^{\prime \prime }+\phi ^{\prime }\left( \frac{1}{r}+\frac{\chi ^{\prime }}{2}\right) \nonumber \\&-{\frac{2{q}^{2}\psi ^{2}\phi }{{\mathrm {e}^{2b\phi ^{\prime 2}{\mathrm {e} ^{\chi }}}}f}+2b\phi ^{\prime 2}{\mathrm {e}^{\chi }}\left( 2\phi ^{\prime \prime }+\phi ^{\prime }\chi ^{\prime }\right) }, \end{aligned}$$
(9)
$$\begin{aligned} 0= & {} f^{\prime }+{\frac{\kappa ^{2}r}{2b}}\left[ 1+{\mathrm {e}^{2b\phi ^{\prime 2}{\mathrm {e}^{\chi }}}}\left( 4b\phi ^{\prime 2}{\mathrm {e}^{\chi } }-1\right) \right] \nonumber \\&+2\,\kappa ^{2}r\left[ {\frac{q^{2}\phi ^{2}\psi ^{2}{\mathrm {e}^{\chi }}}{ f}}+\left( m\psi \right) ^{2}+\psi ^{\prime 2}f\right] -{\frac{2r}{{l}^{2}}}, \end{aligned}$$
(10)
$$\begin{aligned}&\nonumber \\ 0= & {} \chi ^{\prime }+4\kappa ^{2}r\left[ \frac{q^{2}\phi ^{2}\psi ^{2}{ \mathrm {e}}^{\chi }}{f^{2}}+\psi ^{\prime 2}\right] . \end{aligned}$$
(11)

where the prime denotes the derivative with respect to r. Obviously, the above equations reduce to the corresponding equations in Ref. [21] when \(b\rightarrow 0\) while in the absence of the backreaction (\(\kappa \rightarrow 0\)), Eqs. (22) and (23) reduce to ones in Ref. [54]. By virtue of symmetries of field equations (22)–(25)

$$\begin{aligned}&q\rightarrow q/a, \, \phi \rightarrow a\phi , \, \psi \rightarrow a\psi , \nonumber \\&\kappa \rightarrow \kappa /a, \, b\rightarrow b/a^{2}, \end{aligned}$$
(12)
$$\begin{aligned}&l\rightarrow al, \, r\rightarrow ar, \, q\rightarrow q/a, \nonumber \\&m\rightarrow m/a, \, b\rightarrow a^{2}b, \end{aligned}$$
(13)

one can set \(q=l=1\). In the following sections, we will study the superconding phase transition both analytically and numerically.

3 Analytical study

The behaviors of model functions governed by field equations (22)–(25) near the boundary \(r\rightarrow \infty \) areFootnote 1

$$\begin{aligned}&\chi (r)\rightarrow 0,\qquad f(r)\sim r^{2}, \nonumber \\&\phi (r)\sim \rho +\mu \ln (r),\qquad \psi (r)\sim \frac{\psi _{-}}{ r^{\Delta _{-}}}+\frac{\psi _{+}}{r^{\Delta _{+}}}, \end{aligned}$$
(14)

where \(\mu \) and \(\rho \) are chemical potential and charge density of dual field theory and \(\Delta _{\pm }=1+\sqrt{1\pm m^{2}}\). The superconducting phase transition is characterized by growing the expectation value of order parameter \(\left\langle O\right\rangle \) as temperature decreases. In normal phase, \(\left\langle O\right\rangle \) vanishes. According to holographic dictionary, the expectation value of order parameter \(\left\langle O\right\rangle \) is dual to \({\psi _{+}}\) or \({\psi _{-}}\) while the other one can be considered as the source. Therefore, near the critical point \( \left\langle O_{\pm }\right\rangle \) is small and one can define it as

$$\begin{aligned} \epsilon \equiv \left\langle O_{i}\right\rangle , \end{aligned}$$
(15)

where \(i=+\) or −. Since \(\epsilon \) is so small, we can expand the model functions as [7, 55, 63, 64]Footnote 2

$$\begin{aligned} f= & {} f_{0}+\epsilon ^{2}f_{2}+\epsilon ^{4}f_{4}+\cdots , \end{aligned}$$
(16)
$$\begin{aligned} \chi= & {} \epsilon ^{2}\chi _{2}+\epsilon ^{4}\chi _{4}+\cdots , \end{aligned}$$
(17)
$$\begin{aligned} \psi= & {} \epsilon \psi _{1}+\epsilon ^{3}\psi _{3}+\epsilon ^{5}\psi _{5}+\cdots , \end{aligned}$$
(18)
$$\begin{aligned} \phi= & {} \phi _{0}+\epsilon ^{2}\phi _{2}+\epsilon ^{4}\phi _{4}+\cdots . \end{aligned}$$
(19)

Also we can expand the chemical potential as [7]

$$\begin{aligned} \mu =\mu _{0}+\epsilon ^{2}\delta \mu _{2}+..., \end{aligned}$$
(20)

where \(\delta \mu _{2}>0\). Thus, the order parameter as a function of chemical potential can be obtained as

$$\begin{aligned} \epsilon \approx \frac{(\mu -\mu _{0})^{1/2}}{\delta \mu _{2}}. \end{aligned}$$
(21)

When \(\mu \rightarrow \mu _{0}\), phase transition occurs and the order parameter is zero at the critical value \(\mu _{c}=\mu _{0}\). Above equation also indicates the critical exponent \(\beta =1/2\) which is the same as the universal result from the mean field theory. Hereafter, we define the dimensionless coordinate \(z=r_{+}/r\) instead of r,  since it is easier to work with it. In terms of this new coordinate, \(z=0\) and \(z=1\) correspond to the boundary and horizon respectively. The field equations (22)–(25) can be rewritten in terms of z as

$$\begin{aligned} 0= & {} \psi ^{\prime \prime }+\left[ \frac{1}{z}+\frac{f^{\prime }}{f}-\frac{ \chi ^{\prime }}{2}\right] \psi ^{\prime }+\frac{r_{+}^{2}}{z^{4}}\left[ \frac{q^{2}\phi ^{2}{\mathrm {e}}^{\chi }}{f^{2}}-\frac{m^{2}}{f}\right] \psi , \end{aligned}$$
(22)
$$\begin{aligned} 0= & {} \phi ^{\prime \prime }+\left( \frac{\chi ^{\prime }}{2}+\frac{1}{z} \left[ \frac{1+4\Upsilon }{1+2\Upsilon }\right] \right) \phi ^{\prime } - \frac{2q^{2}r_{+}^{2}\psi ^{2}}{z^{4}f}\left( \frac{{\mathrm {e}}^{-\Upsilon } }{1+2\Upsilon }\right) \phi , \nonumber \\\end{aligned}$$
(23)
$$\begin{aligned} 0= & {} f^{\prime }-{\frac{\kappa ^{2}{r_{+}}^{2}}{2bz^{3}}}\left[ 1+{\mathrm {e} ^{\Upsilon }}\left( {2\Upsilon }-1\right) \right] \nonumber \\&-\frac{2\kappa ^{2}{r_{+}^{2}}}{z^{3}}\left[ \frac{q^{2}\phi ^{2}{\psi ^{2} }{\mathrm {e}^{\chi }}}{f}+m^{2}\psi ^{2}\right] +{\frac{2{r_{+}^{2}}}{z^{3}}} , \end{aligned}$$
(24)
$$\begin{aligned} 0= & {} \chi ^{\prime }-\frac{4\kappa ^{2}r_{+}^{2}}{z^{3}}\left[ \frac{ q^{2}\phi ^{2}\psi ^{2}{\mathrm {e}}^{\chi }}{f^{2}}+\frac{z^{4}\psi ^{\prime 2}}{r_{+}^{2}}\right] , \end{aligned}$$
(25)

where \(\Upsilon =2bz^{4}{\mathrm {e}}^{\chi }\phi ^{\prime 2}/{r_{+}}^{2}\). The field equation of \(\phi \) (Eq. (23)) at zeroth order with respect to \(\epsilon \) reduces to

$$\begin{aligned} \phi ^{\prime \prime }(z)+\frac{\phi ^{\prime }(z)(r_{+}^{2}+8{b}{z^{4}}\phi ^{\prime 2}(z))}{z(r_{+}^{2}+4{b}{z^{4}}\phi ^{\prime 2}(z))}=0. \end{aligned}$$
(26)

The solution of above equation reads

$$\begin{aligned} \phi (z)=\int _{1}^{z}\frac{r_{+}\sqrt{L_{W}(\frac{4bz^{2}C_{0}^{2}}{{r_{+}} ^{2}})}}{2{z^{2}}\sqrt{b}}dz, \end{aligned}$$
(27)
Table 1 Analytical results of \({T_{c}}/{\mu }\) for different values of \(\kappa \) and b
Full size table

where \(C_{0}\) is an integration constant and \(L_{W}(x)=LambertW(x)\) is the Lambert function which satisfies [65]

$$\begin{aligned} L_{W}(x){\mathrm {e}}^{L_{W}(x)}=x, \end{aligned}$$
(28)

and can be expanded as

$$\begin{aligned} L_{W}(x)=x-x^{2}+\frac{3}{2}x^{3}-\frac{8}{3}x^{4}. \end{aligned}$$
(29)

Expanding Eq. (27) for small b and keeping the terms up to first order of b we find

$$\begin{aligned} \phi (z)=C_{1}+C_{0}\ln (z)+\frac{C_{0}^{3}}{r_{+}^{2}}(1-z^{2})b+O\left( b^{2}\right) . \end{aligned}$$
(30)

Comparing the above equation with Eq. (14), we find \(C_{0}=-\mu \) . Also, \(C_{1}=0\), since at the horizon \(\phi (r_{+})=0\). Inserting \(C_{0}\) into Eq. (30) we have

$$\begin{aligned} \phi _{0}(z)=\lambda r_{+}\left[ -\ln (z)+\lambda ^{2}(z^{2}-1)b\right] , \quad {b}\lambda ^{2}<1, \end{aligned}$$
(31)

where \(\lambda =\mu /r_{+}\). Substituting \(\phi (z)\) into the field equation (24), we find the metric function at zeroth order with respect to \( \epsilon \), \(f_{0}(z)=r_{+}^{2}g(z)\) where

$$\begin{aligned} g(z)=\left( \frac{1}{z^{2}}-1+\kappa ^{2}\lambda ^{2}\ln (z)+\frac{1}{2} \kappa ^{2}\lambda ^{4}b(1-z^{2})\right) . \end{aligned}$$
(32)

Note that at the horizon \(f_{0}(1)=0\). The asymptotic behavior of scalar field \(\psi \) near the boundary (\(z=0\)) is given by Eq. (14). In order to match this behavior near the boundary, we introduce a trial function F(z) as \(\psi (z)=\left\langle O_{i}\right\rangle \left( z/r_{+}\right) ^{\Delta _{i}}F(z)\) which satisfies the boundary condition \( F(0)=1\) and \(F^{\prime }(0)=0\). Inserting the functions obtained above and the trial function F(z) into Eq. (22), one receives

$$\begin{aligned}&F^{\prime \prime }(z)+F^{\prime }(z)\left[ \frac{2\Delta +1}{z}+\frac{ g^{\prime }(z)}{g(z)}\right] \nonumber \\&+\left[ -\frac{m^{2}}{g(z)z^{4}}+\frac{\Delta ^{2}}{z^{2}}+\frac{\Delta g^{\prime }(z)}{zg(z)}\right] F(z)+ \nonumber \\&+\frac{q^{2}\lambda ^{2}F(z)}{g(z)^{2}}\left[ \frac{{\ln (z)}^{2}}{z^{4}}- \frac{2\lambda ^{2}{b}{\ln (z)}}{z^{2}}+\frac{2\lambda ^{2}{b}{\ln (z)}}{ z^{4}}\right] =0. \end{aligned}$$
(33)

It is a matter of calculations to show that the above equation satisfies the following second order Sturm–Liouville equation [66]

$$\begin{aligned} \left[ T(z)F^{\prime }(z)\right] ^{\prime }-Q(z)F(z)+\lambda ^{2}P(z)F(z)=0, \end{aligned}$$
(34)

where

$$\begin{aligned} T(z)= & {} {g(z)}z^{2\Delta +1}, \end{aligned}$$
(35)
$$\begin{aligned} P(z)= & {} \frac{q^{2}T(z)}{g^{2}(z)}\left[ \frac{{\ln (z)}^{2}}{z^{4}}-\frac{ 2\lambda ^{2}{b}{\ln (z)}}{z^{2}}+\frac{2\lambda ^{2}{b}{\ln (z)}}{z^{4}} \right] , \nonumber \\\end{aligned}$$
(36)
$$\begin{aligned} Q(z)= & {} -T(z)\left[ -\frac{m^{2}}{g(z)z^{4}}+\frac{\Delta ^{2}}{z^{2}}+\frac{ \Delta g^{\prime }(z)}{zg(z)}\right] . \end{aligned}$$
(37)

Considering the trial function as \(F(z)=1-\alpha z^{2}\) and using the Sturm–Liouville eigenvalues problem, the eigenvalues of Eq. (34) can be obtained by minimizing

$$\begin{aligned} \lambda ^{2}=\frac{\int _{0}^{1}{dz}T(z)\left[ F^{\prime 2}(z)+Q(z)F^{2}(z) \right] }{\int _{0}^{1}{dz}.T(z)P(z)F^{2}(z)}, \end{aligned}$$
(38)

with respect to \(\alpha \) [67]. Here, we use a perturbative expansion \( b\lambda ^{2}\) up to the first order of b

$$\begin{aligned} b\lambda ^{2}=b(\lambda ^{2}|_{b=0})+O(b^{2}). \end{aligned}$$
(39)

For backreaction parameter, we use iteration method and take

$$\begin{aligned} \kappa _{n}=n\Delta \kappa ,\qquad \ n=0,1,2,3,\ldots , \end{aligned}$$
(40)

where \(\Delta \kappa =\kappa _{n+1}-\kappa _{n}\). Here we chose \(\Delta \kappa =0.005\). So, the effect of the nonlinear corrections on the backreaction term can be obtained as

$$\begin{aligned} \kappa ^{2}\lambda ^{2}={\kappa _{n}}^{2}\lambda ^{2}={\kappa _{n}} ^{2}(\lambda ^{2}|_{\kappa _{n-1}})+O[(\Delta \kappa )^{4}]. \end{aligned}$$
(41)

By taking \(\kappa _{-1}=0\) and \(\lambda ^{2}|_{\kappa _{-1}}=0\), the minimum eigenvalue of Eq. (38) can be calculated. To calculate the critical temperature, we obtain the latter value by variation of Eq. (38) with respect to \(\alpha \) where the other parameters such as \(b,\kappa ,m,q,\ldots \) are fixed. Using the definition of T (Eq. (4)), the critical temperature is given by \(T_{c}=f^{\prime }(r_{+})/4\pi \) whereFootnote 3

$$\begin{aligned} f^{\prime }(r_{+})={{2{r_{+}}}}-{\frac{\kappa ^{2}{r_{+}}}{2b}}\left[ 1+{ \mathrm {e}^{2b\phi _{0}^{\prime 2}(r_{+})}}\left( 4b\phi _{0}^{\prime 2}(r_{+})-1\right) \right] ,\nonumber \\ \end{aligned}$$
(42)

and \(r_{+}=\mu /\lambda \) so we have

$$\begin{aligned} T_{c}=\frac{1}{4\pi }\frac{\mu }{\lambda }\left[ 2-{\kappa _{n}}^{2}(\lambda ^{2}|_{\kappa _{n-1}})+3b{\kappa _{n}}^{2}(\lambda ^{4}|_{\kappa _{n-1},b=0}) \right] . \end{aligned}$$
(43)

As an example, for \(b=0.01\) and \(\kappa =0\) the Eq. (38) reduce to

$$\begin{aligned} \lambda ^{2}=\frac{0.667\alpha ^{2}-1.333\alpha +1}{0.0276-0.0165\alpha +0.0035\alpha ^{2}}, \end{aligned}$$
(44)

which has a minimum \(\lambda _{\min }=21.6337\), with respect to \(\alpha \), at \(\alpha =0.8258\) and thus according to Eq. (43) we achieve \( T_{c}=0.03421\mu \). We employ the iteration method to obtain the critical temperature for different values of \(\kappa \) and b.

In Table 1, we present our results. This table shows that by increasing nonlinear parameter (b), the value of \(T_{c}\) decreases. As it can be understood from this table, for a fixed value of b, with increasing the backreaction parameter \(\kappa \), the value of the critical temperature decreases. We also reproduce the results of the linear Maxwell case without backreaction (i.e. \(b\rightarrow 0\) and \(\kappa \rightarrow 0\)) presented in [23].

Table 2 Numerical results of \({T_{c}}/{\mu }\) for different values of \(\kappa \) and b
Full size table

4 Numerical study

Fig. 1
figure 1

The behavior of order parameter versus temperature for \(m^{2}=0\)

Full size image
Fig. 2
figure 2

The behavior of order parameter versus temperature for \(m^{2}=0\)

Full size image

In this section, we employ the shooting method [4] to numerically investigate the superconducting phase transition. Besides setting q and l to unity, we also set \(r_{+}=1\) in the numerical calculation which may be justified by virtue of the field equation symmetry [21]

$$\begin{aligned} r\rightarrow ar, \, f\rightarrow a^{2}f, \, \phi \rightarrow a\phi , \end{aligned}$$

First, we expand Eqs. (22)–(25) near black hole horizon (\(z=1\))

$$\begin{aligned} \psi\approx & {} \psi (1)+\psi ^{\prime }(1)(1-z)+\frac{\psi ^{{\prime }{ \prime }}}{2}(1-z)^{2}+\cdots , \end{aligned}$$
(45)
$$\begin{aligned} \phi\approx & {} \phi ^{\prime }(1)(1-z)+\frac{\phi ^{{\prime }{\prime }}}{2} (1-z)^{2}+\cdots , \end{aligned}$$
(46)
$$\begin{aligned} f\approx & {} f^{\prime }(1)(1-z)+\frac{f^{{\prime }{\prime }}}{2} (1-z)^{2}+\cdots , \end{aligned}$$
(47)
$$\begin{aligned} \chi\approx & {} \chi (1)+\chi ^{\prime }(1)(1-z)+\frac{\chi ^{{\prime }{ \prime }}}{2}(1-z)^{2}+\cdots . \end{aligned}$$
(48)

In above equations, we have imposed \(f(1)=\phi (1)=0\).Footnote 4 In our numerical process, we will find \(\psi (1)\), \(\phi ^{\prime }(1)\) and \(\chi (1)\) such that the desired values for boundary parameters in Eq. (14) are attained. At boundary, one can set either \(\psi _{-} \) or \(\psi _{+}\) to zero as source and find the value of the other one as the expectation value of order parameter \(\left\langle O\right\rangle \). We will focus on \(m^{2}=0\) case for our numerical calculations. For this case, the behavior of \(\psi \) near boundary is (see Eq. (14))

$$\begin{aligned} \psi (z)\approx \psi _{-}+{\psi _{+}}{z^{2}}. \end{aligned}$$
(49)

We consider \(\psi _{+}\) as holographic dual to the order parameter \( \left\langle O_{+}\right\rangle \) at the boundary field theory.

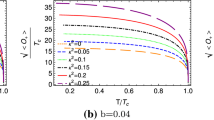
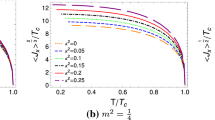
Table 3 Analytical and numerical results of \({T_{c}}/{\mu }\) for different values of \(\kappa \) and b
Full size table

In Table 2, our numerical results for critical temperature with different values of backreaction parameter \(\kappa \) and nonlinear parameter b are presented. In the Maxwell limit (\(b\rightarrow 0)\), our numerical results reproduce the ones of [21]. It can be seen that in the absence of nonlinearity effect, the critical temperature decreases as \(\kappa \) increases [21]. In the presence of nonlinearity parameter i.e. for any nonvanishing value of b, it can be found that as \(\kappa \) enhances, the critical temperature \(T_{c}\) decreases. Similar behavior can be found for different values of b when \(\kappa \) is fixed. As the nonlinear parameter b becomes larger, the critical temperature decreases i.e. the condensation process becomes harder. This behavior have been reported previously in [68] for (\(2+1\))-dimensional holographic superconductors too. Figures 1 and 2 confirm above results. As it can be seen from Fig. 1, the scalar hair forms harder as \(\kappa \) increases i.e. the gap in graph of \(\left\langle O_{+}\right\rangle \) becomes larger. The latter means that the condensation of the operator \(\left\langle O_{+}\right\rangle \) starts at larger values for stronger values of backreaction parameter. It shows that the scalar hair can be formed more difficult when the backreaction is stronger. Figure 2 shows the same effect for nonlinearity parameter b. We compare the analytical and numerical results in Table 3. Table 3 shows that there is a good agreement between analytical and numerical results for small values of \( \kappa \) and b. For larger values of these parameters, analytical and numerical results separate more from each other.

5 Conclusion

In this work, we have studied the properties of one-dimensional holographic superconductor in the presence of nonlinear exponential electrodynamics. We have also considered the backreaction effect of scalar and gauge fields on the background metric. We have performed both analytical and numerical methods for studying our superconductors. To investigate the problem analytically, we have used the Sturm–Lioville while our numerical study was based on shooting method. It was shown that the enhancement in both nonlinearity of electrodynamics model as well as the backreaction causes the superconducting phase more difficult to be appeared. This result is reflected in two ways from our data. From one side, we observed that the increasement in the effects of nonlinearity and backreaction makes the critical temperature of superconductor lower. From another side, for larger values of nonlinear and backreaction parameters, the gap in condensation parameter is larger which in turn exhibits that the condensation is formed harder. We have also observed that, for small values of backreaction parameter \(\kappa \) and nonlinear parameter b, the analytic results are in a good agreement with numerical ones whereas for larger values they separate more from each other.

Finally, we would like to stress that in this work, we have only studied the basic properties of one-dimensional backreacting holographic s-wave superconductors in the presence of exponential nonlinear electrodynamics. It is also interesting to investigate other characteristics of these systems such as the behaviour of real and imaginary parts of conductivity or optical features. One may also consider \((1+1)\)-dimensional p-wave and d-wave holographic superconductors in the background of BTZ black holes and disclose the effects of nonlinearity as well as backreaction on the the phase transition and conductivity of these models. These issue are now under investigations and the result will be appeared soon.