1 Introduction

There are various modern materials which play an extremely vital role in the improvement of our way of life. Some of these materials are used in modern cars and airplanes to make them lighter, safer and more fuel-efficient than their predecessors. Nano-composites materials are one of those modern materials. A nano-composite substance is consisting of a matrix or curing phase and nano-particles in powder form/suspension/dispersion to develop the characteristics of the basic material.

The addition of nanoparticles to a polymer medium can advance its performance. The strategy of adding nano-particles into another mixture is very valuable in cropping high-performance composites. Various nanoparticles like carbon nanotubes, graphene, molybdenum disulfide, etc. are being frequently applied as reinforcing materials to fabricate strong eco-friendly nanocomposites for cartilage tissue. The inclusion of such types of nano-particles in the polymer at a very low concentration shows a significant development in the compressive properties of nanocomposites.

The nanofluid character to transfer convective heat mainly depends on the thermal and physical parameters of the base fluid and suspended nanoparticles, the shape, and the dimension of nanoparticles, the volume ratio of suspended nanoparticles and the flow structure. The above properties make nanofluid very useful in various real-life applications such as residential, commercial, transportation and industrial sectors. Thermal stability in a nano liquid layer consistently heated below was considered by Tzou [1, 2]. He has used the transport equations derived by Buongiorno [3] and found that the joint performance of thermophoresis of nanoparticles and the Brownian movement has destabilizing effect. Nield and Kuznetsov [4] revisited the thermal stability in a horizontal nano-fluid layer by introducing various dimensionless numbers. The Rayleigh–Benard stability in a nano-liquid layer was considered by Dhananjay et al. [5].

The effect of various parameters on thermal instability in the nanofluid layer was studied by various authors in the literature. Yadav et al. [6] measured the rotation effect on the stability of a nano-liquid layer. They showed that the rotation stabilizes the system for a specific collection of values of various nanofluid parameters. The thermal stability in a nano-liquid porous layer was considered by Nield and Kuznetsov [7]. In this problem, they have used Darcy’s model. They (Kuznetsov and Nield [8]) extended this problem by taking Brinkman’s model. The impact of the porous medium on the convection of nanofluid was solved by Bhadauria and Agarwal [9, 10]. The outcome of the double-diffusive phenomenon on the thermal instability in a nano-liquid layer was performed by Nield and Kuznetsov [11]. They were using a Galerkin approach up to one-term and obtained that the stability boundaries. The consequence of swirl on the thermal stability in a horizontal porous layer of nano-liquid was considered by Chand and Rana [12] and showed that porosity and has destabilizing nature in the case of stationary convection. Sheikholeslami et al. [13] have studied the problem of heat transfer of nanoparticles employing innovative turbulator considering entropy generation. Also the problem of heat transfer of nanoparticles employing innovative turbulator considering entropy generation is considered by Sheikholeslami et al. [14]. Shankar et al. [15] have discussed the MHD instability of pressure-driven fow of a non-Newtonian fluid. Faraz et al. [16] also considered MHD impacts on an axisymmetric Casson nanofluid and studied the heat transfer over a sheet. Sheu [17] considered the linear thermal stability in a viscoelastic nanofluid layer. Kumar and Awasthi [18] performed triple-diffusive phenomenon on the stability of a nano-liquid layer. Awasthi et al. [19] considered the impact of triple-diffusive phenomenon on the Maxwell fluid layer when heat source was present.

In recent years, nano-composites materials have gained a lot of interest because of their use in research, industry and the community. The polymer nanocomposites are a mixture of an organic polymer and inorganic nano-particle. These composites have achieved much more attention because of their exceptional properties emerging from the mixture of organic and inorganic hybrid materials. If we combine the functionalities of both components, and the nanostructure of the particles, nano-composites are anticipated to show new and enhanced properties. The resultant nano-composites have various potential applications in automotive, optoelectronics, biomedical, sensors, etc. Various papers on experimental analysis on nano-composite material are available in the literature. This is the first attempt to study the mathematical stability analysis of nano-composite materials.

The thermal stability in a composite horizontal nano-liquid layer is not examined yet to the best of our knowledge. Therefore an effort has been made to explore the onset of thermal convection in a composite nano-liquid layer heated from below. The following assumptions have been taken for the mathematical treatment of the considered problem.

  1. 1.

    The nano-liquid is taken as Newtonian as well as incompressible and the laminar flow is considered.

  2. 2.

    The surface charge technology is used to suspend the nanoparticles in the base liquid.

  3. 3.

    The liquid and the nanoparticles are not reacting chemically during the thermal convection.

  4. 4.

    There is no force between both the nano-particles suspensions.

  5. 5.

    The density in each term of the nanofluid momentum equation is considered to be invariable except in the external force term while other thermophysical parameters of nano-liquid (viscosity, specific heat, thermal conductivity, etc.) are assumed to be constant (Boussinesq hypothesis).

  6. 6.

    Both types of nanoparticles and the base fluid phase are assumed to be in thermal balance state.

  7. 7.

    In this study, the spherical nano-particles are measured.

  8. 8.

    The effect of radioactive heat transport between the sides of the rigid boundary is neglected as it is exceptionally small.

2 Problem formulation

In this study, the dimensional parameters are represented adding asterisks; meanwhile, the non-dimensional variables are with no asterisks. Here \(z\)-axis is taken as vertically upward and therefore, the gravitational force will be \(- g\hat{\varvec{k}}\). A horizontal layer of composite nano-fluid (a base fluid suspended with two different types of nano-particles) restricted between the perfectly insulating planes \(z^{*} = d\) and \(z^{*} = 0\) (Fig. 1). The temperature at the plane \(z^{*} = d\) is assumed to be \(T_{0}^{ * }\); meanwhile, the temperature at \(z^{*} = 0\) is \(T_{0}^{*} + \Delta T^{*}\) and \(\Delta T^{*} \ll T_{0}^{*}\). The composite nano-fluid mixture is considered to be homogeneous and will be in the local thermal equilibrium state. The Oberbeck–Boussinesq approximation will be used to linearize the equations.

Fig. 1
figure 1

Schematic diagram of the problem

Full size image

The flow of composite nano-fluid layer is governed by Tzou [2] and Buongiorno [3].

$$\nabla \cdot \varvec{u}^{*} = 0 ,$$
(1)
$$\rho \left( {\frac{{\partial u^{*} }}{{\partial t^{*} }} + (u^{*} \cdot \nabla^{*} )u^{*} } \right) = \mu \nabla^{*2} u^{*} - \nabla^{*} p^{*} + \left[ {\begin{array}{*{20}l} {\phi_{1}^{*} \rho_{{p_{1} }} + \phi_{2}^{*} \rho_{{p_{2} }} + (1 - \phi_{1}^{*} - \phi_{2}^{*} )\rho } \hfill \\ {\left( {1 - \beta_{T} (T^{*} - T_{0}^{*} )} \right)} \hfill \\ \end{array} } \right] ,$$
(2)
$$\begin{aligned} \rho c\left( {\frac{{\partial T^{*} }}{{\partial t^{*} }} + (\varvec{u}^{*} \cdot \nabla^{*} )T^{*} } \right) & = \kappa \nabla^{*2} T^{*} + \left( {\rho c} \right)_{{p_{1} }} \left[ {D_{{B_{1} }} \nabla^{*} \phi_{1}^{*} \cdot \nabla^{*} T^{*} + \left( {D_{{T_{1} }} /T_{0}^{*} } \right)\nabla^{*} T^{*} \cdot \nabla^{*} T^{*} } \right] \\ & \quad + \left( {\rho c} \right)_{{p_{2} }} \left[ {D_{{B_{2} }} \nabla^{*} \phi_{2}^{*} \cdot \nabla^{*} T^{*} + \left( {D_{{T_{2} }} /T_{0}^{*} } \right)\nabla^{*} T^{*} \cdot \nabla^{*} T^{*} } \right] \\ \end{aligned} ,$$
(3)
$$\frac{{\partial \phi_{1}^{*} }}{{\partial t^{*} }}\; + \;(\varvec{u}^{*} \cdot \nabla^{*} )\phi_{1}^{*} = D_{{B_{1} }} \nabla^{*2} \phi_{1}^{*} + \left( {D_{{T_{1} }} /T_{0}^{*} } \right)\nabla^{*2} T^{*} .$$
(4)
$$\frac{{\partial \phi_{2}^{*} }}{{\partial t^{*} }}\; + \;(\varvec{u}^{*} \cdot \nabla^{*} )\phi_{2}^{*} = \;D_{{B_{2} }} \nabla^{*2} \phi_{1}^{*} + \left( {D_{{T_{2} }} /T_{0}^{*} } \right)\nabla^{*2} T^{*} .$$
(5)

Here the nanofluid velocity is taken as \(\varvec{u}^{*} (m/s) = (u^{*} ,\,v^{*} ,\,w^{*} )\); \(t^{*} (s)\) is the time; \(T^{*} (^{0} K)\) is the temperature of nanofluid; \(\beta_{T} (^{0} K^{ - 1} )\) is the thermal volumetric coefficient; \(\phi_{1}^{*} ,\,\phi_{2}^{*}\) are the nano-particle volume fractions; \(\mu (N\,s/m^{2} )\) is the viscosity; \(D_{{B_{1} }} ,\,D_{{B_{2} }} (m^{2} /s)\) are the Brownian diffusion coefficients; \(D_{{T_{1} }} ,\,D_{{T_{2} }} (m^{2} /s)\) are the thermophoretic diffusion coefficients; \(\rho_{{p_{1} }} ,\rho_{{p_{2} }} (Kg/m^{3} )\) are the nano-particles mass density; \(\kappa (W/mK)\) is the thermal conductivity of the nanofluid. Also, we assumed that the nano-particles volume fractions are invariable on both the boundaries. The conditions on the boundary are defined as;

$$\left. {w^{*} = 0,\frac{{\partial w^{*} }}{{\partial z^{*} }} + \lambda_{1} d\frac{{\partial^{2} w^{*} }}{{\partial z^{*2} }} = 0,T^{*} = T_{0}^{*} + \Delta T^{*} ,\phi_{1}^{*} = \phi_{10}^{*} ,\phi_{2}^{*} = \phi_{20}^{*} } \right\}\quad {\text{at}}\;z^{*} = 0$$
(6)
$$\left. {w^{*} = 0,\frac{{\partial w^{*} }}{{\partial z^{*} }} - \lambda_{2} d\frac{{\partial^{2} w^{*} }}{{\partial z^{*2} }} = 0,T^{*} = T_{0}^{*} ,\phi_{1}^{*} = \phi_{11}^{*} ,\phi_{2}^{*} = \phi_{21}^{*} } \right\}\quad {\text{at}}\;z^{*} = d$$
(7)

where \(d\) is the dimensional layer depth while \(\lambda_{1}\) and \(\lambda_{2}\) are the parameters which acquire the value zero for rigid boundary and infinity for a free boundary.

We admit that in a number of contexts, the selection of boundary conditions forced on \(\phi_{1}^{*}\) and \(\phi_{2}^{*}\) is somewhat subjective. It might be claimed that on the boundaries, zero particle flux is more practical, but then someone may not found the steady solution for base state heat equations (we have calculated and got a contradiction) and hence, to find the analytical solution for considered problem it is essential to restrict the base state profile for \(\phi_{1}^{*} ,\,\,\phi_{2}^{*}\) and so our preference of conditions is fairly realistic.

Now, we introduce the non-dimensional variables \((u,v,w),\,\,(x,y,z),\,\,t,\,\,p,\,\phi_{1} ,\,\,\phi_{2} ,\,T\) is defined as \((u,v,w) = (u^{*} ,v^{*} ,w^{*} )d/\alpha_{f} ,\)\((x,y,z) = (x^{*} ,y^{*} ,z^{*} )/d\), \(t = t^{*} \alpha_{f} /d^{2}\), \(p = p^{*} d^{2} /\mu \alpha_{f}\), \(\phi_{1} = \left( {\phi_{1}^{*} - \phi_{10}^{*} } \right)/\left( {\phi_{11}^{*} - \phi_{10}^{*} } \right)\), \(\phi_{2} = \left( {\phi_{2}^{*} - \phi_{20}^{*} } \right)/\left( {\phi_{21}^{*} - \phi_{20}^{*} } \right)\), \(T = \left( {T^{*} - T_{0}^{*} } \right)/\Delta T^{*}\), where \(\alpha_{f} = \kappa /\rho c\) is the nanofluid thermal diffusivity \(\left( {m^{2} /s} \right)\). The non-dimensional form of the Eqs. (1)–(5) can be stated that

$$\nabla \cdot \varvec{u} = 0,$$
(8)
$$\frac{1}{\Pr }\left( {\frac{{\partial \varvec{u}}}{\partial t} + (\varvec{u} \cdot \nabla )\varvec{u}} \right) = RaT\hat{e}_{z} - Rn_{1} \phi_{1} \hat{e}_{z} - Rn_{2} \phi_{2} \hat{e}_{z} - Rm\hat{e}_{z} - \nabla p + \nabla^{2} \varvec{u}\text{,}$$
(9)
$$\frac{\partial T}{\partial t} + (\varvec{u} \cdot \nabla )T = \nabla^{2} T + \frac{{N_{{B_{1} }} }}{{Ln_{1} }}\nabla \phi_{1} \cdot \nabla T + \frac{{N_{{A_{1} }} N_{{B_{1} }} }}{{Ln_{1} }}\nabla T \cdot \nabla T + \frac{{N_{{B_{2} }} }}{{Ln_{2} }}\nabla \phi_{2} \cdot \nabla T + \frac{{N_{{A_{2} }} N_{{B_{2} }} }}{{Ln_{2} }}\nabla T \cdot \nabla T,$$
(10)
$$\frac{{\partial \phi_{1} }}{\partial t}\; + \;(\varvec{u} \cdot \nabla )\phi_{1} = \;\frac{1}{{Ln_{1} }}\nabla^{2} \phi_{1} + \frac{{N_{{A_{1} }} }}{{Ln_{1} }}\nabla^{2} T$$
(11)
$$\frac{{\partial \phi_{2} }}{\partial t}\; + \;(\varvec{u} \cdot \nabla )\phi_{2} = \;\frac{1}{{Ln_{2} }}\nabla^{2} \phi_{2} + \frac{{N_{{A_{2} }} }}{{Ln_{2} }}\nabla^{2} T .$$
(12)

The dimensionless conditions will be

$$\left. {T = 1,w = 0,\phi_{1} = 0,\frac{\partial w}{\partial z} + \lambda_{1} d\frac{{\partial^{2} w}}{{\partial z^{2} }} = 0,\phi_{2} = 0} \right\}\quad {\text{at}}\;z = 0$$
(13)
$$\left. {T = 0,w = 0,\phi_{1} = 1,\frac{\partial w}{\partial z} - \lambda_{2} d\frac{{\partial^{2} w}}{{\partial z^{2} }} = 0,\phi_{2} = 1} \right\}\quad {\text{at}}\;z = 1$$
(14)

The non-dimensional variables used above are defined as; the Prandtl number, \(\Pr = \mu /\rho \alpha_{f}\); the thermo-nanofluid Lewis numbers, \(Ln_{1} = \alpha_{f} /D_{{B_{1} }}\), \(Ln_{2} = \alpha_{f} /D_{{B_{2} }}\); the thermal Rayleigh number, \(Ra = \frac{{\rho g\beta_{T} d^{3} \Delta T^{*} }}{{\mu \alpha_{f} }}\); the basic density Rayleigh number, \(Rm = \left[ {\rho_{{p_{1} }} \phi_{10}^{*} + \rho_{{p_{2} }} \phi_{20}^{*} + \rho \left( {1 - \phi_{10}^{*} - \phi_{20}^{*} } \right)} \right]gd^{3} /\mu \alpha_{f}\); the nano-particle concentration Rayleigh numbers, \(Rn_{1} = \left[ {\left( {\rho_{{p_{1} }} - \rho } \right)\left( {\phi_{11}^{*} - \phi_{10}^{*} } \right)} \right]gd^{3} /\mu \alpha_{f}\) and \(Rn_{2} = \left[ {\left( {\rho_{{p_{2} }} - \rho } \right)\left( {\phi_{21}^{*} - \phi_{20}^{*} } \right)} \right]gd^{3} /\mu \alpha_{f}\); the modified diffusivity ratios, \(N_{{A_{1} }} = D_{{T_{1} }} \Delta T^{*} /D_{{B_{1} }} T_{0}^{*} \left( {\phi_{11}^{*} - \phi_{10}^{*} } \right)\) and \(N_{{A_{2} }} = D_{{T_{2} }} \Delta T^{*} /D_{{B_{2} }} T_{0}^{*} \left( {\phi_{21}^{*} - \phi_{20}^{*} } \right)\) and the modified particle-density increments \(N_{{B_{1} }} = \left( {\rho c} \right)_{{p_{1} }} \left( {\phi_{11}^{*} - \phi_{10}^{*} } \right)/\rho c\) and \(N_{{B_{2} }} = \left( {\rho c} \right)_{{p_{2} }} \left( {\phi_{21}^{*} - \phi_{20}^{*} } \right)/\rho c\).

As small thermal gradients in the nano-particles dilute suspension are considered, we neglect the terms, which are the product of \(\phi_{1}\) and \(\phi_{2}\) with \(T\) for linearization of Eq. (9) following the concept of Oberbeck–Boussinesq approximation.

3 Basic state

The base state of a composite nanofluid layer is considered to be time-independent and the given by the expressions;

$$\varvec{u} = (0,0,0),\;\;T = T_{b} (z),\;\;p = p_{b} (z),\;\;\phi_{1} = \phi_{1b} (z),\;\;\phi_{2} = \phi_{2b} (z).$$
(15)

Equations (8)–(14) take the form with the above values

$$0 = - \frac{d}{dz}p_{b} + RaT_{b} - Rn_{1} \phi_{1b} - Rn_{2} \phi_{2b} - Rm,$$
(16)
$$\frac{{d^{2} T_{b} }}{{dz^{2} }} + \frac{{N_{{B_{1} }} }}{{Ln_{1} }}\left( {\frac{{d\phi_{1b} }}{dz}.\frac{{dT_{b} }}{dz}} \right) + \frac{{N_{{A_{1} }} N_{{B_{1} }} }}{{Ln_{1} }}\left( {\frac{{dT_{b} }}{dz}} \right)^{2} + \frac{{N_{{B_{2} }} }}{{Ln_{2} }}\left( {\frac{{d\phi_{2b} }}{dz}.\frac{{dT_{b} }}{dz}} \right) + \frac{{N_{{A_{2} }} N_{{B_{2} }} }}{{Ln_{2} }}\left( {\frac{{dT_{b} }}{dz}} \right)^{2} = 0,$$
(17)
$$\frac{{d^{2} \phi_{1b} }}{{dz^{2} }} + N_{{A_{1} }} \frac{{d^{2} T_{b} }}{{dz^{2} }} = 0.$$
(18)
$$\frac{{d^{2} \phi_{2b} }}{{dz^{2} }} + N_{{A_{2} }} \frac{{d^{2} T_{b} }}{{dz^{2} }} = 0.$$
(19)
$$T_{b} (0) = 1,\;\;\phi_{1b} (0) = 0,\;\;\phi_{2b} (0) = 0,\;\;T_{b} (1) = 0,\;\;\phi_{1b} (0) = 1\;\;{\text{and}}\;\;\phi_{1b} (0) = 1.$$
(20)

Infrequently cases of nano-fluid layers, \(\frac{{Ln_{1} }}{{\phi_{11}^{*} - \phi_{10}^{*} }}\) and \(\frac{{Ln_{2} }}{{\phi_{21}^{*} - \phi_{20}^{*} }}\) are very large and are of order \(10^{5} - 10^{6}\) (Buongiorno [3]) and in addition the nano-particle fraction decrement \(\left( {\phi_{11}^{*} - \phi_{10}^{*} } \right)\) and \(\left( {\phi_{11}^{*} - \phi_{10}^{*} } \right)\) are characteristically not smaller than \(10^{ - 3}\) and therefore, we get a conclusion that \(Ln_{1}\) and \(Ln_{2}\) are large and is of order \(10^{2} - 10^{3}\). It can also be observed that \(N_{{A_{1} }}\) and \(N_{{A_{2} }}\) will be lesser than 10.

Using the above approximation, the base solution can be written as follows;

$$T_{b} (z) = 1 - z,\;\;\phi_{1b} (z) = z\;\;{\text{and}}\;\;\phi_{2b} (z) = z.$$
(21)

4 Perturbed state

The small perturbations are imposed on the basic state of the composite nanofluid layer, the parameters become \(\varvec{u} = \varvec{u}(0,0,0) + \varvec{u}(u^{{\prime }} ,v^{{\prime }} ,w^{{\prime }} )\), \(\phi_{1} = \phi_{1b} + \phi_{1}^{{\prime }}\), \(p = p_{b} + p^{{\prime }}\), \(T = T_{b} + T^{{\prime }}\) and \(\phi_{2} = \phi_{2b} + \phi_{2}^{{\prime }}\). Here prime quantities are the quantities in a perturbed state.

The linear stability is analyzed in the present study and therefore, the nonlinear terms have been neglected. The linear governing equations are as:

$$\nabla \cdot \varvec{u}^{{\prime }} = 0,$$
(22)
$$\frac{1}{\Pr }\frac{{\partial \varvec{u}^{{\prime }} }}{\partial t}\; = - \;\nabla p^{{\prime }} \; + \;\nabla^{2} \varvec{u}^{{\prime }} \; + RaT^{{\prime }} \hat{e}_{z} - Rn_{1} \phi_{1}^{{\prime }} \hat{e}_{z} - Rn_{2} \phi_{2}^{{\prime }} \hat{e}_{z} ,$$
(23)
$$\frac{{\partial T^{{\prime }} }}{\partial t}\; - \;w^{{\prime }} \; = \;\nabla^{2} T^{{\prime }} + \frac{{N_{{B_{1} }} }}{{Ln_{1} }}\left( {\frac{{\partial T^{{\prime }} }}{\partial z} - \frac{{\partial \phi_{1}^{{\prime }} }}{\partial z}} \right) - \frac{{2N_{{A_{1} }} N_{{B_{1} }} }}{{Ln_{1} }}\frac{{\partial T^{{\prime }} }}{\partial z} + \frac{{N_{{B_{2} }} }}{{Ln_{2} }}\left( {\frac{{\partial T^{{\prime }} }}{\partial z} - \frac{{\partial \phi_{2}^{{\prime }} }}{\partial z}} \right) - \frac{{2N_{{A_{2} }} N_{{B_{2} }} }}{{Ln_{2} }}\frac{{\partial T^{{\prime }} }}{\partial z},$$
(24)
$$\frac{{\partial \phi_{1}^{'} }}{\partial t} + w^{{\prime }} = \frac{1}{{Ln_{1} }}\nabla^{2} \phi_{1}^{{\prime }} + \frac{{N_{{A_{1} }} }}{{Ln_{1} }}\nabla^{2} T^{{\prime }} .$$
(25)
$$\frac{{\partial \phi_{2}^{{\prime }} }}{\partial t} + w^{{\prime }} = \frac{1}{{Ln_{2} }}\nabla^{2} \phi_{2}^{{\prime }} + \frac{{N_{{A_{2} }} }}{{Ln_{2} }}\nabla^{2} T^{{\prime }} .$$
(26)

With conditions at the boundaries;

$$w^{{\prime }} = 0,\;\;\frac{{\partial w^{{\prime }} }}{\partial z} + \lambda_{1} \frac{{\partial^{2} w^{{\prime }} }}{{\partial z^{2} }} = 0,\;\;T^{{\prime }} = 0,\;\;\phi_{1}^{{\prime }} = 0\;\;{\text{and}}\;\;\phi_{2}^{{\prime }} = 0\;{\text{at}}\;z = 0$$
(27)

and

$$w^{{\prime }} = 0,\frac{{\partial w^{{\prime }} }}{\partial z} - \lambda_{2} \frac{{\partial^{2} w^{{\prime }} }}{{\partial z^{2} }} = 0,\;\;T^{{\prime }} = 0,\;\;\phi_{1}^{{\prime }} = 0\;\;{\text{and}}\;\;\phi_{2}^{{\prime }} = 0\;{\text{at}}\;z = 1.$$
(28)

The factor \(Rm\) is only an element of the necessary static pressure gradient in the above equations. For a regular fluid, the numbers \(Rn\), \(N_{{A_{1} }} ,N_{{A_{2} }} ,N_{{B_{1} }}\) and \(N_{{B_{2} }}\) will vanish and second term in L.H.S in Eq. (24) is missing because \(d\phi_{1b} /dz = 0\) and \(d\phi_{2b} /dz = 0\).

Taking curl twice on (23), we can eliminate \(p'\) and get

$$\frac{1}{\Pr }\frac{\partial }{\partial t}\;\nabla^{2} w^{{\prime }} = Ra\nabla_{H}^{2} T^{{\prime }} + \nabla^{4} w^{{\prime }} - Rn_{1} \nabla_{H}^{2} \phi_{1}^{'} - Rn_{2} \nabla_{H}^{2} \phi_{2}^{'} .$$
(29)

Here \(\nabla_{H}^{2}\) is the Laplacian operator. Here we get a boundary value problem in the linear form constituted by Eqs. (24)–(26), (29) and conditions (27), (28). This boundary value problem will be solved by a normal mode procedure. Now writing the in the form as follows;

$$\left[ {T^{\prime},w,\phi_{1}^{'} ,\phi_{2}^{'} } \right] = \left[ {\varTheta (z),W(z),\varPhi_{1} (z),\varPhi_{2} (z)} \right]\exp \{ nt\} \exp \{ ik_{x} x\; + \;ik_{y} y\} ,$$
(30)

where \(n\) which is a complex value, in general, is called frequency of a disturbance. The wavenumbers \(k_{x}\) and \(k_{y}\) will produce the resultant wave number \(k\; = \;(k_{x}^{\,2} \; + \;k_{y}^{\,2} )^{\,1/2}\). Using Eq. (34) in the Eqs. (33) and (27)–(30), we get

$$\frac{n}{\Pr }\left( {D^{2} - k^{2} } \right)\;W = - Rak^{2} \varTheta + Rn_{1} k^{2} \varPhi_{1} + Rn_{2} k^{2} \varPhi_{2} + \left( {D^{2} - k^{2} } \right)^{2} \;W,$$
(31)
$$W + \left( {D^{2} - k^{2} - n + \frac{{N_{{B_{1} }} }}{{Ln_{1} }}D - \frac{{2N_{{A_{1} }} N_{{B_{1} }} }}{{Ln_{1} }}D + \frac{{N_{{B_{2} }} }}{{Ln_{2} }}D - \frac{{2N_{{A_{2} }} N_{{B_{2} }} }}{{Ln_{2} }}D} \right)\;\varTheta - \frac{{N_{{B_{1} }} }}{{Ln_{1} }}D\varPhi_{1} - \frac{{N_{{B_{2} }} }}{{Ln_{2} }}D\varPhi_{2} = 0,$$
(32)
$$W - \left( {\frac{1}{{Ln_{1} }}\left( {D^{2} - k^{2} } \right) - n} \right)\;\varPhi_{1} - \frac{{N_{{A_{1} }} }}{{Ln_{1} }}\left( {D^{2} - k^{2} } \right)\varTheta = 0,$$
(33)
$$W - \left( {\frac{1}{{Ln_{2} }}\left( {D^{2} - k^{2} } \right) - n} \right)\;\varPhi_{2} - \frac{{N_{{A_{2} }} }}{{Ln_{2} }}\left( {D^{2} - k^{2} } \right)\varTheta = 0,$$
(34)

Both free boundaries are considered here for stability analysis. Therefore the conditions are

$$W = 0,\;\;\varTheta = 0,\;\;D^{2} W = 0,\;\;\varPhi_{1} = 0\;\;{\text{and}}\;\;\varPhi_{2} = 0\;\;{\text{at}}\;z = 0\;{\text{and}}\;z = 1.$$
(35)

The solutions of the Eqs. (35)–(39) taken as

$$W = W_{0} Sin\pi z,\;\;\varTheta = \varTheta_{0} Sin\pi z,\;\;\varPhi_{1} = \varPhi_{10} Sin\pi z,\;\;\varPhi_{2} = \varPhi_{20} Sin\pi z.$$
(36)

Substituting Eq. (36) into Eqs. (31)–(34) and integrating from \(z = 0\) and \(z = 1\), we have the following matrix equation

$$\left[ \begin{aligned} \delta^{4} + \frac{n}{\Pr }\delta^{2} \,\,\,\,\,\, - Rak^{2} \,\,\,\,\,\,\,\,\,\,\,\,\,\,Rn_{1} k^{2} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,Rn_{2} k^{2} \hfill \\ 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \left( {\delta^{2} + n} \right)\,\,\,\,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0 \hfill \\ 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{N_{{A_{1} }} }}{{Ln_{1} }}\delta^{2} \,\,\,\,\,\,\,\,n + \frac{{\delta^{2} }}{{Ln_{1} }}\,\,\,\,\,\,\,\,\,\,\,\,\,\,0 \hfill \\ 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{N_{{A_{2} }} }}{{Ln_{2} }}\delta^{2} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,n + \frac{{\delta^{2} }}{{Ln_{2} }} \hfill \\ \end{aligned} \right]\left[ \begin{aligned} W_{0} \hfill \\ \varTheta_{0} \hfill \\ \varPhi_{1} \hfill \\ \varPhi_{2} \hfill \\ \end{aligned} \right] = 0 .$$
(37)

Here \(\delta^{2} = \pi^{2} + k^{2}\) is the total wave number. The nontrivial solution of the homogeneous Eqs. (37) produces

$$Ra = \frac{{\left( {n + \delta^{2} } \right)}}{{k^{2} }}\left( {\delta^{4} + \frac{{n\delta^{2} }}{\Pr }} \right) - \frac{{\left( {Ln_{1} \left( {n + \delta^{2} } \right) + \delta^{2} N_{{A_{1} }} } \right)Rn_{1} }}{{(nLn_{1} + \delta^{2} )}}\, - \frac{{\left( {Ln_{2} \left( {n + \delta^{2} } \right) + \delta^{2} N_{{A_{2} }} } \right)Rn_{2} }}{{(nLn_{2} + \delta^{2} )}},$$
(38)

Now, we put \(n = i\omega\) in Eq. (38) and we obtain

$$Ra = \Delta_{1} + i\omega \Delta_{2} .$$
(39)

Here

$$\Delta_{1} = \frac{{\delta^{2} }}{{k^{2} }}\left( {\delta^{4} - \frac{{\omega^{2} }}{\Pr }} \right) - \frac{{\left( {\delta^{4} \left( {Ln_{1} + N_{{A_{1} }} } \right) + \omega^{2} Ln_{1}^{2} } \right)Rn_{1} }}{{(\delta^{4} + \omega^{2} Ln_{1}^{2} )}} - \frac{{\left( {\delta^{4} \left( {Ln_{2} + N_{{A_{2} }} } \right) + \omega^{2} Ln_{2}^{2} } \right)Rn_{2} }}{{(\delta^{4} + \omega^{2} Ln_{2}^{2} )}},$$
(40)

and

$$\Delta_{2} = \delta^{2} \left[ {\frac{{\delta^{2} }}{{k^{2} }}\left( {1 + \frac{1}{\Pr }} \right) + \frac{{\left( {Ln_{1}^{2} + Ln_{1} \left( {N_{{A_{1} }} - 1} \right)} \right)Rn_{1} }}{{(\delta^{4} + \omega^{2} Ln_{1}^{2} )}} + \frac{{\left( {Ln_{2}^{2} + Ln_{2} \left( {N_{{A_{2} }} - 1} \right)} \right)Rn_{2} }}{{(\delta^{4} + \omega^{2} Ln_{2}^{2} )}}} \right],$$
(41)

The Rayleigh number \(Ra\) should be real. Therefore, it can be concluded from the Eq. (39) that either \(\omega = 0\) (steady-state, exchange of stabilities) or \(\Delta_{2} = 0\) (\(\omega \ne 0,\) overstability or oscillatory onset).

5 Stationary convection

Stationary onset refers to \(\omega = 0\) and Rayleigh number will be

$$Ra^{st} = \frac{{\delta^{6} }}{{k^{2} }} - \left( {Ln_{1} + N_{{A_{1} }} } \right)Rn_{1} - \left( {Ln_{2} + N_{{A_{2} }} } \right)Rn_{2} ,$$
(42)

The size of critical cell for the onset of thermal instability is achieved from \(\frac{\partial }{\partial k}Ra = 0\).

$$k_{c} = \pi /\sqrt 2 ,$$
(43)

Thus, for steady onset, the consequent critical thermal Rayleigh number will become

$$Ra^{st} = \frac{{27\pi^{4} }}{4} - \left( {Ln_{1} + N_{{A_{1} }} } \right)Rn_{1} - \left( {Ln_{2} + N_{{A_{2} }} } \right)Rn_{2} ,$$
(44)

For \(Rn_{2} = 0\), Eq. (44) become

$$Ra^{st} = \frac{{27\pi^{4} }}{4} - \left( {Ln_{1} + N_{{A_{1} }} } \right)Rn_{1} .$$
(45)

This equation is same as the equation given by Sheu (2011). Also, It should be noted that Eq. (42) is not a function of Prandtl number.

6 Oscillatory convection

For oscillatory onset, \(\Delta_{2} = 0\) and \(\omega \ne 0\), which gives the expression

$$b_{2} (\omega^{2} )^{2} + b_{1} (\omega^{2} ) + b_{0} = 0.$$
(46)

Here

$$\begin{aligned} b_{2} & = \delta^{2} Ln_{1}^{2} Ln_{2}^{2} (1 + \Pr ), \\ b_{1} & = \delta^{6} (Ln_{1}^{2} + Ln_{2}^{2} )(1 + \Pr ) + k^{2} Ln_{1}^{2} Ln_{2}^{2} \Pr \left( {Rn_{1} + Rn_{2} } \right) + k^{2} Ln_{1} Ln_{2}^{2} \Pr (N_{{A_{1} }} - 1)Rn_{1} \\ & \quad + k^{2} Ln_{1}^{2} Ln_{2} \Pr (N_{{A_{2} }} - 1)Rn_{2} , \\ b_{0} & = \delta^{10} (1 + \Pr ) + k^{2} \delta^{4} \Pr \left( {Ln_{1}^{2} Rn_{1} + Ln_{2}^{2} Rn_{2} } \right) + k^{2} \delta^{4} Ln_{1} \Pr (N_{{A_{1} }} - 1)Rn_{1} \\ & \quad + k^{2} \delta^{4} Ln_{2} \Pr (N_{{A_{2} }} - 1)Rn_{2} . \\ \end{aligned}$$

If Eq. (46) does not admit the positive value of \(\omega^{2}\), oscillatory instability is not possible.

In other words, we can say Oscillatory convection is possible only when \(Le_{1} ,Le_{2} > 1\).

Thus from Eqs. (39) and (40), oscillatory Rayleigh number is given by

$$Ra^{osc} = \frac{{\delta^{2} }}{{k^{2} }}\left( {\delta^{4} - \frac{{\omega^{2} }}{\Pr }} \right) - \frac{{\left( {\delta^{4} \left( {Ln_{1} + N_{{A_{1} }} } \right) + \omega^{2} Ln_{1}^{2} } \right)Rn_{1} }}{{(\delta^{4} + \omega^{2} Ln_{1}^{2} )}} - \frac{{\left( {\delta^{4} \left( {Ln_{2} + N_{{A_{2} }} } \right) + \omega^{2} Ln_{2}^{2} } \right)Rn_{2} }}{{(\delta^{4} + \omega^{2} Ln_{2}^{2} )}},$$
(47)

Here \(\omega^{2}\) is given by Eq. (46). If no positive value of \(\omega^{2}\) existing, no oscillatory convection is achievable. This outcome is analogous to Sheu (2011). If we are able to find two positive values of \(\omega^{2}\) then the least value of (47) gives the oscillatory Rayleigh number for \(\omega^{2}\). If there is only one positive value of \(\omega^{2}\) then by substituting this positive value into (47), we get the oscillatory Rayleigh number.

7 Case of overstability

In this section, we check the chance of occurrence of overstability. As we are looking to calculate the Rayleigh number for stability taking pure oscillations and therefore, it is acceptable to calculate the situation that the Eq. (46) will produce a solution containing real \(\omega\). The three values of \(\omega^{2}\) (\(\omega\) being real) will be positive.

The addition of the roots of Eq. (46) will be \(- \,(b_{0} /b_{2} )\) and this will be positive. At the same time, one can observe that \(b_{2}\) is always positive; meanwhile, \(b_{0}\) will be positive if \(N_{{A_{1} }} > 1\) and \(N_{{A_{2} }} > 1\). Hence these inequalities are acceptable conditions for the non-occurrence of overstability.

8 Results and discussion

In this section, we describe our results numerically. The stationary thermal Rayleigh number for composite nanofluid is given by Eq. (42) and the oscillatory thermal Rayleigh number is achieved analytically using Eq. (47) where \(\omega^{2}\) is given by Eq. (46). From Eq. (42), it is obvious that both oscillatory Rayleigh number and stationary Rayleigh number for composite nanofluid do not depend on \(N_{{B_{1} }}\) and \(N_{{B_{2} }}\) because the effect of \(N_{{B_{1} }}\) and \(N_{{B_{2} }}\) in Eq. (32) is eliminated due to orthogonal functions. The thermal energy equations do not contain the impact of Brownian motions and thermophoresis. The Brownian motions and thermophoresis contribute directly in the expressing the conservation of nanoparticles equation. Therefore, the temperature and nanoparticle densities are combined in a specific way so that the instability is approximately purely an event happening due to buoyancy and nanoparticle motions.

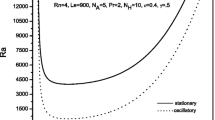
Figure 2 demonstrates the comparison between the Rayleigh numbers of ordinary nanofluid and composite nanofluid for \(Ln_{1} = 100\), \(Ln_{2} = 100\), \(N_{{A_{1} }} = 5\), \(N_{{A_{2} }} = 5\), \(Rn_{1} = 0.5\) and \(Rn_{2} = 0.5\). Here positive values of \(Rn_{1}\) and \(Rn_{2}\) mean that a top-heavy distribution is considered. It is noticed that Rayleigh number for composite nanofluid is more than the Rayleigh number of ordinary nanofluid. This shows that mixture of two different nanoparticles more stabilizes the stationary convection as compare of the single nanoparticles in case of top-heavy distribution. In Fig. 3, the comparison between the Rayleigh numbers of ordinary nanofluid and composite nanofluid for \(Ln_{1} = 100\), \(Ln_{2} = 100\), \(N_{{A_{1} }} = 5\), \(N_{{A_{2} }} = 5\), \(Rn_{1} = - 0.5\) and \(Rn_{2} = - 0.5\) is made. Here negative values of \(Rn_{1}\) and \(Rn_{2}\) mean that a bottom-heavy distribution is considered. It has been observed that Rayleigh number for composite nanofluid is less than the Rayleigh number of ordinary nanofluid. This shows that mixture of two different nanoparticles destabilizes the stationary convection as compare of the single nanoparticles in case of basement-heavy distribution.

Fig. 2
figure 2

Neutral stability curve for Rayleigh number \(Ln_{1} = 100\), \(Ln_{2} = 100\), \(N_{{A_{1} }} = 5\), \(N_{{A_{2} }} = 5\), \(Rn_{1} = 0.5\) and \(Rn_{2} = 0.5\)

Full size image
Fig. 3
figure 3

Neutral stability curve for Rayleigh number \(Ln_{1} = 100\), \(Ln_{2} = 100\), \(N_{{A_{1} }} = 5\), \(N_{{A_{2} }} = 5\), \(Rn_{1} = - 0.5\) and \(Rn_{2} = - 0.5\)

Full size image

Figure 4 displays the neutral curves for various values of the first thermo-nanofluid Lewis number \(Ln_{1}\) with fixed values of remaining parameters. Note that the stationary Rayleigh number decreases with increasing the first thermo-nanofluid Lewis number. Thus, the first thermo-nanofluid Lewis number has destabilizing nature for the stationary convection in case of top-heavy distribution while it stabilizes the stationary convection in case of basement-heavy distribution. Figure 5 exhibits the neutral curves for various values of the second thermo-nanofluid Lewis number \(Ln_{2}\) with fixed values of remaining parameters. It is observed that the stationary Rayleigh number decreases with increasing the second thermo-nanofluid Lewis number. Thus, the second thermo-nanofluid Lewis number destabilizes the stationary convection in case of top-heavy distribution while it stabilizes the stationary convection in case of basement-heavy distribution.

Fig. 4
figure 4

Neutral stability curve for Rayleigh number for various values of \(Ln_{1}\) \(Ln_{2} = 100\), \(N_{{A_{1} }} = 5\), \(N_{{A_{2} }} = 5\), \(Rn_{1} = 0.5\) and \(Rn_{2} = 0.5\)

Full size image
Fig. 5
figure 5

Neutral stability curve for Rayleigh number for various values of \(Ln_{2}\) \(Ln_{1} = 100\), \(N_{{A_{1} }} = 5\), \(N_{{A_{2} }} = 5\), \(Rn_{1} = 0.5\) and \(Rn_{2} = 0.5\)

Full size image

Figure 6 demonstrates the neutral curves for various values of the first modified diffusivity ratio \(N_{{A_{1} }}\) with fixed values of the remaining parameters. Note that the stationary Rayleigh number decreases with increasing the first modified diffusivity ratio. Thus, the first modified diffusivity ratio has destabilizing nature for the stationary convection in case of top-heavy distribution while it stabilizes the stationary convection in case of basement-heavy distribution. Figure 7 displays the neutral curves for various values of the second modified diffusivity ratio \(N_{{A_{2} }}\) with fixed values of the remaining parameters. Note that the stationary Rayleigh number decreases with increasing the second modified diffusivity ratio. Thus, second modified diffusivity ratio has destabilizing nature for the stationary convection in case of top-heavy distribution while it stabilizes the stationary convection in case of basement-heavy distribution.

Fig. 6
figure 6

Neutral stability curve for Rayleigh number for various values of \(N_{{A_{1} }}\) \(Ln_{1} = 100\), \(Ln_{2} = 100\), \(N_{{A_{2} }} = 5\), \(Rn_{1} = 0.5\) and \(Rn_{2} = 0.5\)

Full size image
Fig. 7
figure 7

Neutral stability curve for Rayleigh number for various values of \(N_{{A_{2} }}\) \(Ln_{1} = 100\), \(Ln_{2} = 100\), \(N_{{A_{1} }} = 5\), \(Rn_{1} = 0.5\) and \(Rn_{2} = 0.5\)

Full size image

Note that the stationary convection is achievable for both basement-heavy as well as top-heavy distributions of nanoparticles. Also, the Rayleigh number is lesser for top-heavy distribution than that of the basement-heavy distribution of nanoparticles.

9 Conclusions

Linear stability investigation in a horizontal composite nanofluid layer is made for free–free boundaries taking normal mode procedure. The key conclusions are:

  1. 1.

    Instability is unaffected by Brownian motions and thermophoresis. It is merely a phenomenon due to the coupling of buoyancy and nano-particles conservation.

  2. 2.

    The first and second thermo-nanofluid Lewis numbers have destabilizing nature for the stationary convection in case of top-heavy distribution while it stabilizes the stationary convection in case of basement-heavy distribution.

  3. 3.

    Concentration Rayleigh’s number makes the stationary convection destabilize. It is also found that stationary convection is achievable for both basement-heavy and top-heavy nano-particles distribution.

  4. 4.

    The Oscillatory convection is not possible if both first and second thermo-nanofluid Lewis numbers \(\le 1\).

  5. 5.

    The critical Rayleigh number does not change with the modified particle-density increment \(N_{{B_{1} }}\) and \(N_{{B_{2} }}\).

  6. 6.

    The acceptable conditions for the non-occurrence of over-stability are \(N_{{A_{1} }} > 1\) and \(N_{{A_{2} }} > 1\).