1 Introduction

The study of non-Newtonian fluids flow and their characteristics is of great importance for authors due to their remarkable applications in industrial products and procedures. These fluids have non-linear relation between stress and rate of strain while Newtonian fluid model has a linear relations mode. Examination of flow field and its characteristics in these fluids is quite difficult as compared to Newtonian fluids. In general, flow of such fluids is not possible to explain by single constitutive equation. Hence, different governing equations are presented to handle the diversity of such fluids. Metzner and Otto [1], presented a brief description about the shear rate of a non-Newtonian fluid and importance of its rheological behavior. He also examined the relationship between impeller speed and the shear rate of the fluid. Parand [2], explored a numerical computational technique to find out the behavior of non-Newtonian boundary layer flow.

Casson fluid model is one of the most popular non-Newtonian fluid model in order to express flow curves for blood. It is most realistic fluid model due to its practical implications in bio medical field and polymer processing. For practical purposes, it provides a convenient means for evaluating the two characteristics; Cason viscosity and the apparent yield stress. Casson [3], initially presented this model to describe the flow curves of suspensions of pigments in the preparation of printing inks. Later, Scott Blair [4], discovered that the model could describe flow curves of blood. The idea was further verified by [5, 6], and the model has received much attention of researchers in order to elaborate blood flow curves. Makinde et al. [7], explored the impacts of Lorentz force and heat transmission of MHD Casson fluid flow over a thermally stratified melting horizontal surface. Gireesha et al. [8] studied Cason Nanofluid with buoyancy forces and thermal radiation over stretching sheet. They utilized shooting technique along with Runge–Kutta method to achieve the numerical solution. Hari Krishna et al. [9] presented impacts of chemical reaction on Casson fluid flow with permeable stretching sheet. Makinde et al. [10] examined Cattaneo–Christov heat flux on Casson nanofluid flow past a stretching cylinder. Ibrahim and Makinde [11] explored MHD flow of Casson nanofluid on stretchable surface convective boundary and slip effects in the neighborhood of stagnation point. In past few decades, vast amount of literature is produced on the subject of heat transmission in the Casson fluid flow and numerous cases of fluid flows have been discussed including boundary layer flows [12,13,14,15,16].

Recent advancements in heat transfer phenomena have led to the development of nano fluids which are homogenous mixtures of base fluids suspended with metallic or non-metallic elements of diameter less than 100 nm. Usually, the base fluids such as engine oils, water, organic liquids, ethylene glycol mixtures, etc. exhibit low thermal conductivity. A suspension of small particles/fiber as nanometer sized in a base fluid can be enhanced in carrier of liquid properties (thermal conductivity, viscosity, density, mass diffusivity) and is regarded as nanofluid the metallic nanoparticles commonly used for nano-fluids are copper \(\left( {\text{Cu}} \right)\), silver \(\left( {\text{Ag}} \right)\), gold \(\left( {\text{Au}} \right)\) whereas the non-metallic nanoparticles are oxides such as aluminum oxide \(\left( {{\text{Al}}_{2} {\text{O}}_{3} } \right)\), copper oxide \(\left( {\text{Cuo}} \right)\), zinc oxide \(\left( {\text{Zno}} \right)\), titanium dioxide \(\left( {{\text{Tio}}_{2} } \right)\) and numerous forms of carbons. The terminology of nano-fluids was initially introduced by [17]. The significance of these fluids is observed due to their high heat transmission and cooling ability with very low gravitational settling in fluid flows. In recent decades, vast amount of literature is generated on the subject of heat transmission in nano-fluids and numerous cases of fluid flows have been discussed including boundary layer flows [18,19,20,21,22].

Mixed convection phenomena occur when forced and natural convection mechanisms act together to transfer heat. In past decade many authors have reported on convective heat transmission over stretching/shrinking surfaces due to their applications in engineering including thermal insulation, solar collector and atmospheric boundary-layer flows. The pioneer study on mixed-convection fluid flow was reported by [23], they explored heat transformation effects about non-isothermal body subjected to a non-uniform free stream velocity [24], and examined the behavior of free-convection magneto-hydro-dynamics boundary layer flow of an incompressible electrically conducting fluid in a porous media. Comprehensive studies are reported to investigate the mixed convection flow and heat transmission over unsteady radially stretching/shrinking sheet [25, 26].

Extension in the boundary-layer theory is a quite challenging task. This difficulty is caused by the diversity of non-Newtonian fluids in their constitutive behavior and their elastic and viscous properties. B.C. Sakidis gave the idea of axisymmetric flow and examined the behavior of solid surfaces on boundary layer flow [27]. After this theoretical investigation, various aspects of stretching surfaces which involve flow and heat transmission phenomena were explored by different researchers and a considerable quantity of literature is produced [28,29,30,31,32,33]. The studies reported above considered the steady flow. However, unsteadiness becomes an essential component of study in various engineering procedures in the case when flow depends upon time. Unsteady flow over impulsively stretched sheet at time \(t = 0\) with varying velocity was investigated by [34]. A good amount of literature is produced on unsteady flows to investigate the heat transmission phenomena in the studies [35,36,37,38]. Presented unsteady axisymmetric flow of nano-fluid over a radially contracting sheet in the presence of magnetic field and partial slip [39]. Proposed the series solution of unsteady axisymmetric flow and heat transfer over a radially stretching sheet [40]. The case of time-dependent radially contracting surface with heat transmission was discussed by [41]. Examined the non-similar solution of third grade fluid flow with radially stretching sheet [42]. Studied the MHD flow behavior and heat transmission past a permeable stretching sheet with slip conditions [43]. Moreover, Explored homogeneous/heterogeneous reactions and melting heat transmission impacts in the MHD flow by a contracting sheet with variable thickness [44]. MHD stagnation point flow of Jeffrey fluid by a radially stretching surface with viscous dissipation and Joule heating was investigated by [45].

The purpose of present study is to explore MHD Axisymmetric Casson nanofluid free convection flow and heat transfer over unsteady radially stretching sheet attend very less attention. To the best of our knowledge, the proposed scheme of work have not yet been discussed and the results obtained here are new. The suitable transmutations are utilized to transform partial differential equations into ordinary differential equations which are solved via Keller-box finite difference method. A decline in velocity and temperature is observed with a rise in Casson parameter. Moreover, the fluid velocity initially decreases with the rise in unsteadiness parameter while temperature decreases significantly (Fig. 1).

Fig. 1
figure 1

Physical model and coordinate system

Full size image

2 Mathematical formulation

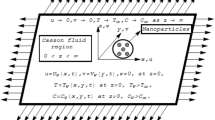
Consider a two-dimensional laminar incompressible magneto-hydrodynamic unsteady flow of an electrically-conducting Cason nanofluid from a radially stretching sheet. The flow occurs because of the unsteady stretching of the surface in the radial direction with velocity \(U_{w} = \frac{ar}{1 - ct}\) is the stretching velocity \(r\) and \(z\) are components of velocity. We suppose temperature of the form \(T_{w} = T_{\infty } + \frac{br}{1 - ct}\) is the wall temperature,\(T_{\infty }\) is the ambient fluid temperature with \(T_{w} > T_{\infty }\) where a, b and c are constant. Here \(a > 0,\,\,b \ge 0\,\,and\,\,c \ge 0\) are constants having dimension 1/times (t), where \(t\) stands for time such that the product \(ct < 1\). In this analysis the velocity and the temperature field is taken \(v = [(u(r,z,t),0,w(r,z,t))],\,\,\,T = T(r,z,t)\).

The governing equations of flow are as under [41, 46],

$$\frac{\partial u}{\partial r} + \frac{u}{r} + \frac{\partial w}{\partial z} = 0$$
(1)
$$\frac{\partial u}{\partial t} + u\frac{\partial u}{\partial r} + w\frac{\partial u}{\partial z} = \upsilon \left( {1 + \frac{1}{\beta }} \right)\left( {\frac{{\partial^{2} u}}{{\partial z^{2} }}} \right) - \frac{{\sigma B^{2} }}{\rho }u + g\beta_{T} (T - T_{\infty } )$$
(2)
$$\begin{aligned} & \frac{\partial T}{\partial t} + u\frac{\partial T}{\partial r} + w\frac{\partial T}{\partial z} = \frac{k}{{(\rho c_{p} )_{f} }}\frac{{\partial^{2} T}}{{\partial z^{2} }} + \tau \left\{ {D_{B} \left( {\frac{\partial C}{\partial r}.\frac{\partial T}{\partial z}} \right) + \frac{{D_{T} }}{{T_{ \infty } }}\left( {\frac{\partial T}{\partial z}} \right)^{2} } \right\} \\ & \quad + \frac{\mu }{{(\rho c_{p} )_{f} }}\left( {1 + \frac{1}{\beta }} \right)\left( {\frac{\partial u}{\partial z}} \right)^{2} + \frac{{\sigma B^{2} }}{{(\rho c_{p} )_{f} }}u^{2} \\ \end{aligned}$$
(3)
$$\frac{\partial C}{\partial t} + u\frac{\partial C}{\partial r} + w\frac{\partial C}{\partial z} = D_{B} \frac{{\partial^{2} C}}{{\partial z^{2} }} + \frac{{D_{T} }}{{T_{ \infty } }}\frac{{\partial^{2} T}}{{\partial z^{2} }}$$
(4)

The boundary constraints are followed as [41, 46]:

$$u = U_{w} ,\quad w = W_{0} ,\quad T = T_{w} = T_{\infty } + \frac{br}{1 - ct},\quad C = C_{w} ,\quad at\quad z = 0$$
(5)
$$u \to 0,\,\,T \to T_{\infty } \,,\,C \to C_{\infty } \,as\,\,z \to \infty .$$
(6)

\(u\) and \(v\) are velocity components of in r–z coordinates system. \(\beta ,\sigma ,g,\beta_{T} ,D_{B} ,D_{T} ,\rho ,c_{p} ,k\) Casson fluid parameter, electrical conductivity, gravity force of acceleration, volumetric coefficient of thermal expansion, effect of Brownian motion, effect of Thermophoresis, the fluid density, the specific heat at constant pressure, and the thermal conductivity of the fluid respectively. \(W_{0} = - 2\left( {\frac{{\nu U_{w} }}{r}} \right)^{1/2}\) expresses the mass transformation parameter with \(W_{0} > 0\) and \(W_{0} < 0\) are, suction and injection respectively. Following transforming function are used to dimensionless the Eqs. (1)–(6) as [41]:

$$\varPsi ( {\text{r,z)}} = -\, r^{2} U_{w} \text{Re}^{{ - \frac{1}{2}}} f(\eta ),\quad \eta = \frac{z}{r}\text{Re}^{{\frac{1}{2}}} ,\quad \theta (\eta ) = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }},\quad {\text{and}}\quad \varphi (\eta ) = \frac{{C - C_{\infty } }}{{C_{w} - C_{\infty } }}$$
(7)

Here “Stokes” function can be expressed as \(\psi (r,z)\) with \(u = \frac{ - 1}{r}\frac{\partial \psi }{\partial z}\,and\,w = \frac{1}{r}\frac{\partial \psi }{\partial r}.\)\(U_{w} = \frac{ar}{1 - ct}\) is the stretching velocity with \(r\) and z-components follows as:

$$u = f^{\prime}(\eta ),\,\,\,and\,\,w = - 2U_{w} \text{Re}^{1/2} f(\eta ),$$
(8)

Reynolds number is defined as \(\text{Re}_{r} = \frac{{rU_{w} }}{v}\), we get the following equations in dimensionless form, the Eqs. (2)–(4) following as:

$$\left( {1 + \frac{1}{\beta }} \right)f^{\prime\prime\prime} - Mf^{\prime} + 2ff^{\prime\prime} - \left( {f^{\prime}} \right)^{2} - \alpha \left[ {f^{\prime} + \frac{1}{2}\eta f^{\prime\prime}} \right] + \lambda \theta = 0$$
(9)
$$\begin{aligned} & \frac{1}{\Pr }\theta^{\prime\prime} + 2f\theta^{\prime} - f^{\prime}\theta - Mf^{\prime} + N_{b} \theta^{\prime}\phi^{\prime} + N_{t} \left( {\theta^{\prime}} \right)^{2} + Ec\left( {1 + \frac{1}{\beta }} \right)f^{''2} \\ & \quad + MEcf^{'2} - \alpha \left[ {\theta + \frac{1}{2}\eta \theta^{\prime}} \right] = 0 \\ \end{aligned}$$
(10)
$$\phi^{\prime\prime} + \frac{{N_{t} }}{{N_{b} }}\theta^{\prime\prime} - Sc\left[ {\alpha \left\{ {\phi + \frac{1}{2}\eta \phi^{\prime\prime}} \right\} + f^{\prime}\phi - 2f\phi^{\prime}} \right] = 0$$
(11)

the boundary constraints used in Eqs. (5) and (6) are transformed as [41]:

$$\begin{aligned} & f\left( \eta \right) = S,f^{\prime}\left( \eta \right) = 1,\theta \left( \eta \right) = 1,\phi \left( \eta \right) = 1,\,when\,\eta = 0 \\ & \quad f^{\prime}\left( \infty \right) = 0,\theta \left( \infty \right) = 0,\phi \left( \infty \right) = 0,as\,\eta \to \infty \\ \end{aligned}$$
(12)

In Eqs. (9)–(11) the parameters are \(\Pr = \frac{{\mu c_{p} }}{k}\), \(\alpha = \frac{a}{c}\), \(M = \frac{{\sigma B^{2} }}{{\rho_{f} }}\), \(N_{b} = \frac{{\tau (C_{w} - C_{\infty } )D_{B} }}{\upsilon }\), \(N_{t} = \frac{{\tau (T_{w} - T_{\infty } )D_{T} }}{{\upsilon T_{\infty } }}\), \(Sc = \frac{\nu }{{D_{B} }}\), \(\lambda = \frac{Gr}{{Re^{2} }}\), \(Gr = \frac{{g\beta (T_{w} - T_{\infty } )r^{3} }}{{\nu^{2} }}\), \(Ec = \frac{{u_{w}^{2} }}{{c_{p} (T_{w} - T_{\infty } )}}\), and \(S,\{ S > 0,S < 0\}\) represent Prandtl, Unsteady, magnetic field flux, Brownian motion, Thermophoresis, Schmidt number, mixed convection parameter, Grashof, Eckert number and the mass transfer for mass suction and injection respectively.The physical quantities like skin coefficient \(C_{f}\), local Nusselt number \(Nu\) and Sherwood number \(Sh\) are defined as:

$$C_{f} = \frac{{\tau_{w} }}{{\frac{1}{2}\rho U^{2} }},\quad N_{u} = \frac{{rp_{w} }}{{K(T_{w} - T_{\infty } )}}\quad and\quad Sh = \frac{{rq_{m} }}{{D_{B} (C_{w} - C_{\infty } )}}$$
(13)

where \(\tau_{w}\) is the skin friction along the r direction, the heat and mass transfer from the surfaces \(p_{w}\) and \(q_{m}\) are given by

$$\tau_{w} = \left( {\mu_{B} + \frac{{P_{y} }}{{\sqrt {2\pi c} }}} \right)\left( {\frac{\partial u}{\partial z}} \right)_{z = 0} ,\quad p_{w} = - k\left( {\frac{\partial T}{\partial z}} \right)_{z = 0} \quad and\quad q_{m} = - D_{B} \left( {\frac{\partial C}{\partial y}} \right)_{z = 0} .$$
(14)

The dimension free variables explained in Eqs. (7), (8) and these well-quantities as:

$$\text{Re}_{r}^{1/2} C_{f} = \left( {1 + \frac{1}{\beta }} \right)f^{\prime\prime}(0),\quad \text{Re}_{r}^{ - 1/2} Nu = - \theta^{\prime}(0)\quad and\quad \text{Re}_{r}^{ - 1/2} Sh = - \varphi^{\prime}\left( 0 \right).$$
(15)

2.1 Finite difference solutions

In this method, first of all, the new variables \(U,\,V,\,G,\,P,\,W\) and \(Q\) are introduced to convert Eqs. (10)–(12) into a set of first order differential equations.

A net on \(\eta\) is then introduced which is defined as follow

$$\eta_{0} = 0,\eta_{j} = \eta_{j - 1} + h_{j} ,\quad j = 1,2,3, \ldots ,J$$
(16)

The variable quantities (\(P,G,Q,f,U,V,W\)) at different points on the net \(\eta_{j}\) are then estimated by (\(P_{j}^{n}\), \(G_{j}^{n}\), \(Q_{j}^{n}\)\(f_{j}^{n}\), \(U_{j}^{n}\), \(V_{j}^{n}\), \(W_{j}^{n}\)) and \(g_{j}^{n}\) is also exerted for quantities halfway between net points

$$\begin{aligned} & \eta_{j} = \frac{1}{2}\left( {\eta_{j} + \eta_{j - 1} } \right) \\ & \quad g_{j}^{n - 1/2} = \frac{1}{2}\left( {g_{j}^{n} + g_{j}^{n - 1} } \right) \\ \end{aligned}$$
(17)

We substitute the finite difference estimation of the derivatives in the first order set of differential equations along with the boundary conditions. Now Newton’s quasi-linearization method is employed to linearize the system of discretized equations involving \(7J + 7\) unknowns of the form \(f_{j}^{n}\), \(U_{j}^{n}\), \(V_{j}^{n}\), \(G_{j}^{n}\), \(P_{j}^{n}\), \(W_{j}^{n}\), \(Q_{j}^{n}\) and Keller-box elimination technique is utilized to attain the solution of these equations.

To begin the procedure, we recommend a set of estimated profiles for \(f,U,V,G,P,W\) and \(Q\) which are implemented in Keller box scheme with accuracy of 2nd order to move step by step. This repetitive process cease at the final velocity, temperature and concentration functions when the difference in calculating these functions in the successive procedure is less than \(10^{ - 5}\), i.e. \(\delta f_{i} \le 10^{ - 5}\). We consider \(\eta_{j} = \sinh (\frac{j}{a})\) attaining the rapid convergence and hence making the computations time and space economical.

3 Results and discussion

MHD Axisymmetric Casson nanofluid free convection flow and heat transmission over unsteady radially stretching sheet is proposed. The impacts of different parameters on flow features are sketched graphically and results of study are tabulated and argued briefly. The governing transport Eqs. (9)–(11) have been solved by utilizing KBM (Keller Box Method) and sketched in the Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 and 13. The numerical problem is comprised of three dependent thermos-fluid-dynamic-variable \(\left( {f,\,\theta ,\,\phi } \right)\) and eight multi-physical control parameters \(\Pr ,{\text{Sc}},\beta ,M,N_{b} ,N_{t} \alpha ,\lambda\). The effects of stream wise space variables \(\eta\) are also explored. A comparison of numerically obtained results is established for reduced Nusselt number with existing works for \(M = \lambda = {\text{Sc}} = N_{t} = N_{b} = 0,\beta = \infty\). Tables 1, 2 and 3 show a well justifying comparisons of our results and [41, 47] results for \(f^{\prime\prime}(0)\) and \(- \theta (0)\).

Fig. 2
figure 2

Variation of \(\beta\) Casson fluid parameter at a velocity profile, b temperature profiles and c concentration profiles against \(\eta\)

Full size image
Fig. 3
figure 3

Variation of \(M\) (MHD) parameter at a velocity profile, b temperature profiles and c concentration profiles against \(\eta\)

Full size image
Fig. 4
figure 4

Variation of \(\alpha\) unsteady parameter at a velocity profile, b temperature profiles and c concentration profiles against \(\eta\)

Full size image
Fig. 5
figure 5

Variation of \(\lambda\) mixed convection parameter at a velocity profile, b temperature profiles and c concentration profiles against \(\eta\)

Full size image
Fig. 6
figure 6

Variation of \(S\) mass suction at a velocity profile, b temperature profiles and c concentration profiles against \(\eta\)

Full size image
Fig. 7
figure 7

Variation of \(S\) injection at a velocity profile, b temperature profiles and c concentration profiles against \(\eta\)

Full size image
Fig. 8
figure 8

Variation of \(\Pr\) Prandtl number at a temperature profiles and b concentration profiles against \(\eta\)

Full size image
Fig. 9
figure 9

Variation of \(N_{t} ,N_{b}\) at a temperature profiles and b concentration profiles against \(\eta\)

Full size image
Fig. 10
figure 10

Variation of Sc Schmidt number at c concentration profiles against \(\eta\)

Full size image
Fig. 11
figure 11

Variation of Pr at a skin coefficient \(C_{f}\), b local Nusselt number Nu, and c Sherwood number Sh at \(\lambda\)

Full size image
Fig. 12
figure 12

Variation of \(N_{b} = N_{t}\) at a skin coefficient \(C_{f}\), b local Nusselt number Nu, and c Sherwood number Sh at \(\lambda\)

Full size image
Fig. 13
figure 13

Variation of Sc at a skin coefficient \(C_{f}\), b local Nusselt number Nu, and c Sherwood number Sh at \(\lambda\)

Full size image
Table 1 Comparison of results for \(f^{\prime\prime}(0)\) when \(M = \lambda = Sc = N_{t} = N_{b} = 0,\quad \beta = \infty\) for different values
Full size table
Table 2 Comparison of results for \(\, - \theta^{\prime}(0)\) when \(M = \lambda = Sc = N_{t} = N_{b} = 0,\,\,\beta = \infty\) for different values
Full size table
Table 3 The numerical values of the skin friction coefficient for different values of physical parameter \(\lambda = Sc = N_{t} = N_{b} = 0,\,\,\beta = \infty .\) are fixed
Full size table

Table 4 presents the variations of \(f^{\prime\prime}(0),\)\(-\, \theta^{\prime}(0)\) and \(- \,\phi^{\prime}(0)\), for various values of influential flow parameters. A decline in Nusselt number is witnessed while Sherwood number increase with the rise in \(\Pr\) and \(Sc\). The variations in Nusselt number can be demonstrated on the basis that by increasing the values of \(N_{b}\) or \(N_{t}\) results a rise in thermal boundary layer and thus a reduction of Nusselt number. However, the Sherwood number augments significantly with the rise in \(N_{b}\) and \(N_{t}\).

Table 4 Variations in \(f^{\prime\prime}(0),\, - \theta^{\prime}(0)\), and \(- \phi^{\prime}(0)\), for various values of the flow parameters
Full size table

3.1 Velocity profile

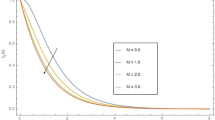
Figure 2a shows that when we increase the Casson fluid parameter β, it changes the fluid nature from non-Newtonian to Newtonian. As momentum diffusivity of non-Newtonian fluid is faster as compare to Newtonian fluid, therefore both radial velocity and momentum boundary layer shows reduction with rising values of parameter β. Similar patterns for unsteady fluid flow can be seen in [41]. Figure 3a illustrates the impacts of parameter \(M\) on the dimension free velocity. It can be noticed that higher values of \(M\) offers a resistive force to an electrically conducting fluid which as a consequence slow down the movement and hence a decline in velocity is observed. Figure 4a exhibits a decline in velocity profile and boundary layer thickness with the rise in value of unsteady parameter α. It is noticed that increase in value of \(\alpha\) slow down the movement of boundary layer thickness and hence a decline in velocity is observed. Figure 6a reveals a reduction in both profiles with the rise in suction parameter (S > 0) while Fig. 7a displays an opposite behavior with decreasing values of injection parameter (S < 0). Figure 5a illustrates that there is a direct relationship between mixed Convection parameter λ and velocity profile. Figure 9a indicates an elevation in both profiles with the enhancement in thermophoresis parameter \(N_{t}\) and Brownian motion \(N_{b}\).

The fluctuations of the shear stress, is delineated in Fig. 11a for different \(\Pr\) values. The local skin friction increases alongside the increase in \(\lambda\) value. It is because of the positive correlation between the fluid velocity and buoyancy force, which elevates the wall shear stress leading to increase the coefficient of skin-friction. For a unique \(\lambda\) with increasing \(\Pr\), the coefficient of skin-friction decrease. Figure 12a shows that rise in the values of \(N_{b}\) and \(N_{t}\), results a decrease in the shear stress. There is an increase skin friction coefficient with the rising values of suction parameter and can be seen in Fig. 13a. From Fig. 14a, it is shown that there is a decline in skin friction coefficient with the increasing values of Magnetic parameter.

Fig. 14
figure 14

Variation of \(M\) at a skin coefficient \(C_{f}\), b local Nusselt number Nu, and c Sherwood number Sh at \(\lambda\)

Full size image

3.2 Temperature profile

Figure 4b shows that rise in unsteady parameter α results a decline of dimension-less temperature profile and thermal boundary layer thickness. Figure 5b exhibits that the higher values of radially stretching bouncy force reduces the thermal boundary layer thickness and temperature profile. A noticeable decrease in temperature along the boundary layer with rise in \(\lambda\) values is witnessed due to which the fluid flow regime is cooled most effectively at stretchable sheet and gets hot as we move along the stretchable surface boundary upwards. Figure 6b shows reduction in thermal boundary layer thickness because of elevation in mass suction parameter (S > 0). Figure 8a depicts the radial temperature profile in which the boundary layer thickness is reduced with the rise in Prandtl number Pr. Casson fluid includes in the present investigation exhibits great viscosity and Prandtl number is used to increase the rate of cooling in conducting flows. This is because the Pr number is defined as the ratio between momentum and thermal diffusivity. In the present investigation Pr = 20 is very suitable for cooling purposes.

Figure 2b demonstrates that thermal boundary layer and temperature shoot up with higher values of β. Figure 3b display the similar impact on both profiles with magnetic parameter \(M\). Figure 7a illustrate a rise in boundary layer thickness with the injection parameter S < 0. Figure 8a exhibits that by increasing in \(\Pr\) values consequently diminishes the temperature. Hence the Prandtl number can be utilized to raise the cooling rate in conducting flows. Fig  9a shows the impacts of Brownian motion and Thermophoresis on temperature distribution profile. As \(N_{b} ,N_{t}\) start increasing at a point, the temperature is increased. Consequently the boundary layer thickness rises with the rise in values of \(N_{b} ,\,N_{t}\).

It is noted that the velocity tends to increase due to increased buoyancy force and causes the wall shear stress to increase and thus there is an increase in heat transfer at the sheet and it can be been in Fig. 11b. We observe that with the increase in both \(N_{b}\) and \(N_{t}\), \(- \theta '(0)\) decreases Fig. 12b. This behavior can be explained in the sense that increasing the Brownian motion or that of thermophoresis parameters cause to decrease the Nusselt number. Figure 13b shows that skin friction coefficient decreases when suction increases. It is observed in Fig. 14b, an increase in Magnetic parameter decrease the Nusselt Number.

3.3 Concentration profile

Figure 2c displays an elevation in concentration profile and concentration boundary layer thickness with higher values of Casson fluid parameter \(\beta\).The effect of dimensionless magnetic parameter \(M\) on concentration profile is sketched in Fig. 3c. It demonstrates that concentration profile is higher with higher values of \(M\). Figure 4c exhibits the relationship between unsteady parameter α and concentration profile. It depicts that concentration profile decreases with the rise in unsteady parameter α. Figure 5c elucidates that concentration profile and thickness of concentration boundary layer augment with an elevation in values of \(\lambda\). Figure 6c shows a sharp decline in concentration profile due to increase in mass suction parameter \(S > 0\) but Fig. 7c shows opposite behavior in case of injection parameter \(S < 0\). It enhances value of nanoparticle volume fraction. The relation between Prandtl number \(\Pr\) and nanoparticle volume fraction concentration profile is displayed in Fig. 8b. It narrates that higher value of Prandtl number increases the nano-particle concentration. It is witnessed that concentration profile increase away from the wall but decreases close to the wall. The same situations can be witnessed in case of Brownian motion and the Thermophoresis \(N_{b} ,\,N_{t}\) in Fig. 9b. Figure 10a indicates that Schmidt number Sc reduces the nanoparticle volume fraction concentration profile.

From Fig. 11c it is observed that the rate of mass transfer decreases with the increase of \(\Pr\). The Sherwood number increases with increasing values of \(N_{b}\) and \(N_{t}\), it can be seen in Fig. 12c. From Fig. 13a–c show that skin friction coefficient decreases, Nusselt number increases and Sheerwood number decrease with the increase of suction parameter. Figure 14c shows that an increase in Magnetic parameter decreases the rate of mass transfer.

4 Conclusions

Unsteady axisymmetric Casson fluid flow of free convection with nano-particles over a radially stretching surface is studied. The numerical results are sketched, examined and argued briefly. The solution mainly relies on the nanoparticle volume fraction, linear radially stretching parameter, and the Prandtl number. Present results are compared with the previous work done by Shahzad et al. [41] and a good agreement is found. It is noticed that the insertion of nanoparticles into the base fluid of current investigation is able to change the flow pattern.

The major results of study are as under:

  1. 1.

    Rise in Casson fluid parameter \(\beta\) creates resistance in the flow of fluid due to which fluid velocity is decreased.

  2. 2.

    Velocity profile augments with the rise in MHD parameter \(M\).

  3. 3.

    Decline in velocity, temperature and concentration profile is witnessed with the rise in unsteady parameter and hence the heat and mass transmission is reduced.

  4. 4.

    Free convection and velocity varies directly.

  5. 5.

    Decrease in the suction parameter \(S > 0\) reduces the velocity, temperature and concentration profile closed to the wall.

  6. 6.

    The rise in the injection parameter causes a rise in velocity and concentration profile but a sharp enhancement in temperature profile.

  7. 7.

    Temperature profile declines with the rise in \(\Pr\), while concentration profile initially increases and then decrease continuously.

  8. 8.

    By increasing the Brownian motion parameter and Thermophoresis, the temperature of the fluid rises but concentration profile decreases in start and then start increasing.

  9. 9.

    Reduction in concentration profile is noted with the rise in \({\text{Sc}}\) parameter.