Abstract
Supergranulation is a fluid-dynamical phenomenon taking place in the solar photosphere, primarily detected in the form of a vigorous cellular flow pattern with a typical horizontal scale of approximately 30–35 Mm, a dynamical evolution time of 24–48 h, a strong 300–400 m/s (rms) horizontal flow component and a much weaker 20–30 m/s vertical component. Supergranulation was discovered more than 60 years ago, however, explaining its physical origin and most important observational characteristics has proven extremely challenging ever since, as a result of the intrinsic multiscale, nonlinear dynamical complexity of the problem concurring with strong observational and computational limitations. Key progress on this problem is now taking place with the advent of twenty-first-century supercomputing resources and the availability of global observations of the dynamics of the solar surface with high spatial and temporal resolutions. This article provides an exhaustive review of observational, numerical and theoretical research on supergranulation, and discusses the current status of our understanding of its origin and dynamics, most importantly in terms of large-scale nonlinear thermal convection, in the light of a selection of recent findings.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The story of solar supergranulation started in Oxford in 1953 when Avril B. Hart reported the existence of a “noisy” fluctuating velocity field on top of the mean solar equatorial rotation speed that she was attempting to measure (Hart 1954). It is in fact very probable that this “noise” was detected as early as 1915 by Plaskett (1916). In a second article, Hart (1956) confirmed her initial discovery and gave an accurate estimate of 26 Megameters (Mm, or 1000 km) for the typical horizontal length scale of these “velocity fluctuations” (sic). Supergranulation was subsequently recognised as a characteristic, and essentially statistically steady dynamical feature of the surface of the quiet Sun (the majority of the solar surface characterized by relatively weak and statistically homogeneous magnetic fields) after the seminal publication by Leighton et al. (1962) of the first Doppler images of the solar surface (also resulting in the first detection of the 5-min solar acoustic oscillations). This work was soon supplemented by another paper by Simon and Leighton (1964) establishing a strong spatial correlation between supergranulation and the magnetic network of the quiet Sun.
More than 60 years after its initial discovery, there remains a significant theoretical uncertainty about how supergranulation originates, what makes it particularly stand out among other solar surface motions, what its exact interactions with solar surface magnetic fields and solar rotation are, whether it is a universal feature of solar type stars or of stellar surface convection, and whether it plays a role in the local or global solar dynamo process. As will become clear in this review, these difficulties stem both from a combination of observational and numerical limitations and from the intrinsic dynamical complexity of the problem. In recent years, however, the solar physics community has gained unprecedented access to a large amount of high-resolution data collected by space observatories, and to large supercomputers that allow for increasingly realistic numerical simulations of the problem, so that a clear resolution of these questions now look increasingly possible. The main purpose of this document is to support this ongoing effort with a large review of observational, theoretical, and phenomenological research on this problem, with a particular emphasis on some of the latest findings.
The review is divided into six parts including this introduction. The next section provides some introductory material on the physics of convection in the Sun and on the essence of the supergranulation problem (Sect. 2). Section 3 is dedicated to observational results. Section 4 reviews classical convection models and phenomenological turbulence arguments historically put forward to explain the origin of supergranulation. Numerical simulations of the problem are reviewed in Sect. 5. Section 6, finally, offers a recap of the main observational results, a discussion of the physics and dynamical phenomenology of supergranulation in the light of our current theoretical, numerical and observational knowledge, and a brief outlook on desirable and expected future research on the problem.
2 The supergranulation puzzle
2.1 The dynamical landscape of the quiet Sun
2.1.1 The solar convection zone
The outer 30% in radius of the Sun are commonly referred to as the solar convection zone [SCZ, see, e.g., dedicated reviews by Miesch (2005) and Nordlund et al. (2009)]. In this region, the solar luminosity (heat flux) originating in the nuclear fusion reactions taking place in the core cannot be evacuated by microscopic heat diffusion alone, but is instead essentially transported by fluid motions driven by thermal buoyancy. Physically, the strong non-adiabatic radiative cooling of the surface layers, like the top cold plate of a convection experiment, imposes a strong negative entropy gradient in the first hundred kilometers below the surface. This gradient is likely very small at larger depth due to the efficiency of the convective mixing of entropy. Internal structure calculations taking into account the ionisation properties of the gas and using local convective transport prescriptions suggest that this gradient remains weakly superadiabatic down to the depth of \({\sim }\,0.3\,R_\odot \), marking the transition with an internal radiative zone. There is still some uncertainty about the precise entropy stratification of the SCZ though, and, as we shall discuss in detail in Sect. 5.3.4, this question may be an important piece of the supergranulation puzzle. Finally, the SCZ, unlike the standard fluid Rayleigh–Bénard convection system, is strongly stratified in density: the density ratio between the bottom and top of the SCZ is of the order of \(10^6\) (see Stix 2004).
With the notable exception of the solar differential rotation, which is accurately determined by helioseismic inversions, the internal dynamics of the SCZ is not very well constrained observationally (Hanasoge et al. 2012; Gizon and Birch 2012; Toomre and Thompson 2015; Greer et al. 2015). While there are many promising ongoing efforts to better characterize this dynamics (some of them will be reviewed in Sect. 3), much of the information we have still comes from observations of the photosphere and chromosphere. Historically, it is important to remember that it is this surface view which has defined the terms of the supergranulation problem.
2.1.2 Granulation
The most prominent, and best understood dynamical feature visible at the surface of the quiet Sun is a photospheric intensity and cellular flow pattern called granulation, which paves the entire surface of the quiet Sun and is characterized by an intensity contrast of around 15%, typical horizontal length scales ranging from \({\sim }\) 0.5 to 2 Mm (Rieutord et al. 2010), typical velocities ranging from 0.5 to 1.5 km/s (Title et al. 1989), and a typical lifetime/renovation time of 5–10 min. Granulation is driven by buoyancy and radiative effects in the thermal boundary layer formed in the strongly superadiabatic surface region of the SCZ where the solar plasma becomes optically thin (see Fig. 2). The dynamical features of granulation are well reproduced by numerical simulations of radiative hydrodynamics (Stein and Nordlund 1998; Nordlund et al. 2009).
2.1.3 Supergranulation
As mentioned in the introduction, the existence of supergranulation, a dynamical cellular flow pattern paving the surface of the Sun with a typical horizontal scale of 30–35 Mm, was first established through Doppler measurements of solar surface flows. This phenomenon is clearly illustrated by the Doppler image of the solar disc shown in Fig. 1. The much weaker signal at the disc centre indicates that supergranulation flows are essentially horizontal. The quest to understand what drives these flows (and why they occur primarily at this particular scale) is the central theme of this review. From a theoretical point of view, this question may look relatively easy at first glance: in most fluid systems, there are usually just a few important physical processes at work, and as a result only a small number of special scales can be formed from dimensional and phenomenological analysis. We will, however, shortly find out that, all “simple” known facts considered, supergranulation essentially resists a straightfoward analysis of this kind. In particular, we will see that while a thermal convective origin of supergranulation has long been, and remains the most obvious and credible explanation, understanding the exact nature and dynamics of the process in detail is extremely challenging in practice.
2.1.4 Mesogranulation
Mesogranulation has for a long time been thought to be a distinct dynamical feature of solar surface convection taking place at intermediate horizontal scales between the granulation (1 Mm) and the supergranulation (30 Mm) scales. It was first reported as such by November et al. (1981), who identified a prominent pattern of vertical motions with a typical horizontal scale of the order of 8 Mm in time-averaged Doppler images, see also November and Simon (1988), Title et al. (1989), Chou et al. (1992) and Ginet and Simon (1992). However, several other observational studies (Wang 1989; Chou et al. 1991; Straus et al. 1992), including one by Hathaway et al. (2000) using high-resolution Doppler data from the SOHO space observatory, found no evidence for a local maximum in the power spectrum of solar convection (the scale-by-scale distribution of energy) at such scales.
While the topic remained controversial for a while (Roudier et al. 1999; Rieutord et al. 2000; Shine et al. 2000; Lawrence et al. 2001), a variety of observational characterizations of the solar power spectrum derived from high-resolutions, space-based observations with the SDO observatory over periods of time of the order of 24 h have now clearly confirmed the lack of a distinctive spectral bump at mesogranulation scales (Williams and Pesnell 2011; Hathaway et al. 2015; Rincon et al. 2017). Observational analyses of magnetic field distributions at the solar surface in the mesogranulation range also appear to support this conclusion (Yelles Chaouche et al. 2011; Berrilli et al. 2014). Several authors had also previously made the case that mesogranulation, understood as a singular dynamical feature, was simply a ghost feature artificially generated by averaging procedures (Matloch et al. 2009; Rieutord et al. 2010). As early as 1994, one of the authors of the original mesogranulation study, November (1994), wrote that the term “mesogranulation” was misleading and instead suggested to interpret this feature as “the vertical component of the supergranular convection”, while Straus and Bonaccini (1997) argued that mesogranulation was a mere powerful extension of granulation at large scales. Overall, it is clear that there is a lot of dynamics taking place at scales intermediate between granulation and supergranulation, but it does not seem that the dynamics at any particular scale in that range particularly stands out. To avoid any possible misunderstanding, we will, henceforth, refer to this range of scales as the mesoscale range, without necessarily implying that there is anything physically special about it.
2.2 Physical scales in turbulent solar convection
Having identified various dynamical phenomena taking place at the top of the SCZ, is it now possible to come up with intuitive physical explanations of their origin within the framework of thermal convection theory? An important point here is that convection in the SCZ is evidently strongly turbulent and nonlinear. Global Reynolds numbers \(\textit{Re}=LV{/}\nu \), based on either the full vertical extent of the convective layer, or thermodynamic scales heights below the surface, and on typical convective velocities estimated from either surface measurements or mixing length theory, range from \(10^{10}\) to \(10^{13}\) in the SCZ. To fix ideas, laboratory experiments on turbulent convection are currently limited to \(\textit{Re}< 10^7\) (e.g., Niemela et al. 2000). We may then ask what kind of scales can be baked in this kind of dynamical environment.
2.2.1 Injection scale
The injection range of a turbulent flow is the typical range of scales at which kinetic energy is injected into the system by either a natural or artificial forcing process. In turbulent convection, this injection of kinetic energy is due to the work of the buoyancy force. Within the framework of classical phenomenological turbulent convection theories (the exact relevance of which for the problem at hand will be discussed in Sect. 6), the scale most representative of the injection range is called the Bolgiano scale \(L_B\) (Bolgiano 1959, 1962; Oboukhov 1959; L’vov 1991; Chillá et al. 1993; Rincon 2006). It can be shown, based on purely dimensional arguments and scaling considerations for heat transport in turbulent convection, to be almost always of the same order (up to some order one prefactor) as the local typical scale height (Rincon 2007 see also Kumar et al. 2014). In an incompressible thermal convection experiment, this corresponds to the distance between the hot and cold plates, but in the strongly stratified SCZ, a more sensible estimate is the local pressure or density scale height \(H_p\) or \(\hbox {H}_\rho \). Close to the surface, the Bolgiano scale is, therefore, roughly of the order of a Megameter, comparable to the typical scale of granulation \(L_\mathrm {G}\), but significantly smaller than the scale of supergranulation \(L_\mathrm {SG}\).
As we go deeper in the SCZ, the typical density and pressure scale heights become larger and, therefore, so should the Bolgiano scale. As a result, the Bolgiano scale in the SCZ is expected to increase with depth, ranging from 1 Mm close to the surface to 100 Mm close at the bottom of the SCZ. From a physical point of view, we can think of convection in the stratified SCZ as being driven by cold, low entropy plumes of fluid sinking from the surface and expanding self-similarly throught the nearly isentropic convection zone (Rieutord and Zahn 1995). These large-scale plumes undergo secondary instabilities along their descending trajectories, producing a turbulent mixture of vorticity filaments (see, e.g., Rast 1998; Clyne et al. 2007; Stein et al. 2009, and Fig. 2).

Image credits: Mark Rast, see Clyne et al. (2007)
Left: the entropy profile as a function of depth, as estimated by numerical simulations or one-dimensional structure models. Right: numerical vizualisation a cool plume diving from the surface. As it penetrates into the isentropic background, the plume increases both its mass and momentum flux by turbulent entrainment (represented by curly arrows) and expands horizontally.
2.2.2 Dissipation scales
As we are considering the turbulent motions of a non-ideal MHD fluid with finite viscosity and finite magnetic and thermal diffusivities, there are also three distinctive dissipation scales in the problem at hand: the viscous dissipation scale \(\ell _\nu \), the magnetic dissipation scale \(\ell _\eta \) and the thermal dissipation scale \(\ell _\kappa \). All of them are depth-dependent in the inhomogeneous SCZ.
A rough estimate for the viscous dissipation scale \(\ell _\nu \) can be obtained from the Kolmogorov phenomenology of turbulence (Frisch 1995) via the expression \(\ell _\nu \sim \textit{Re}^{-3/4}L\), where L stands for the injection scale and \(\textit{Re}=LV{/}\nu \), V being the typical velocity at the injection scale. In the SCZ, where \(\nu \sim 10^{-3}\,\hbox {m}^2{/}\hbox {s}\) (Rieutord 2008), we find \(\ell _\nu \sim 10^{-3}\) m at the surface, taking \(L\sim L_\mathrm {G}\sim 1\) Mm and \(V\sim 1\) km/s for the the typical granulation scale and velocity. At the bottom of the SCZ, where the injection scale is much larger, one can estimate similarly that \(\ell _\nu \sim 0.1\) m. Hence, \(\ell _\nu \) is everywhere extremely small compared to the resolution of current observations and to the dynamical scales of interest.
In MHD, the relative value of the magnetic dissipation scale \(\ell _\eta \) with respect to the viscous scale \(\ell _\nu \) depends on the ordering of the dissipation coefficients of the fluid (see e.g. Schekochihin et al. 2007). When the magnetic diffusivity \(\eta \) is much larger than the kinematic viscosity \(\nu \), as is the case in the Sun, one may use \(\ell _\eta {/}\ell _\nu \sim \textit{Pm}^{-3/4}\) (Moffatt 1961), where \(\textit{Pm}=\nu {/}\eta \) is the magnetic Prandtl number, and we have again assumed a Kolmogorov scaling for the velocity field. The magnetic diffusivity in the subsurface layers of the Sun is \(\eta \sim 10^2\,\hbox {m}^2{/}\hbox {s}\) (Spruit 1974; Rieutord 2008), hence \(\textit{Pm}\sim 10^{-5}\) and \(\ell _\eta \sim 100\) m close to the surface (see also Pietarila Graham et al. 2009). This is also small compared to the resolution of current observations and to the dynamical scales of interest. Close to the bottom of the SCZ, \(\textit{Pm}\sim 10^{-1}{-}10^{-2}\), so \(\ell _\eta \sim 1\) m.
Finally, we have the thermal dissipation scale \(\ell _\kappa \), which is the largest of the three dissipation scales in the solar context. In the SCZ, the thermal diffusivity \(\kappa \) is everywhere much larger than the kinematic viscosity \(\nu \), so the thermal Prandtl number \(\textit{Pr}=\nu {/}\kappa \) is very small. Under these conditions, we may estimate \(\ell _\kappa \) from the expression \(\ell _\kappa {/}\ell _\nu \sim \textit{Pr}^{-3/4}\), once again assuming a Kolmogorov scaling for the velocity field. Thermal diffusion in the Sun is directly supported by photons and, thus, depends strongly on the opacity of the fluid and, therefore, on depth. In the deep SCZ, \(\textit{Pr}\sim 10^{-4}\)–\(10^{-6}\), so \(\ell _\kappa \sim 500\) m. In the optically thin surface layers, on the other hand, \(\ell _\kappa \) is much larger, and comparable to the scale of granulation \(L_\mathrm {G}\sim 1\) Mm. As explained earlier, thermal cooling is a key ingredient of granulation. The typical granulation scale and flow turnover time can in fact be explained as a the result of a balance between the advection time and cooling times of buoyant, high-entropy fluid particles. To summarise, the ordering of the characteristic spatial scales close to the solar surface is (a similar ordering holds for timescales):
2.3 What about supergranulation?
While there is a clear coincidence between some of these scales and the scale of granulation, we see that we cannot as easily construct a scale comparable to that of supergranulation at the solar surface from the standard phenomenology of turbulent MHD convection. Of course, we have argued that the injection scale of turbulent convection should increase self-similarly with depth in the stratified SCZ. We are, therefore, in principle allowed to speculate that supergranulation could be associated with convective motions originating deeper into the SCZ (say at \({\sim }\,30\) Mm). But in that case we are still left with the question of finding a process that would single out this particular depth physically, among the available continuum of injection scales. At the minimum, we have to conclude that understanding the origin, and determining what sets the scale of supergranulation from phenomenological considerations, requires a somewhat more sophisticated line of thinking than that outlined above.
Absent a straightforward answer (and given the historical difficulties to simulate numerically the dynamics in the corresponding range of scale, as will be explained in Sect. 5), many different potential clues and explanations, including the effects of changes in chemical composition or ionisation, the effects of shear, rotation or/and magnetic fields on convection, or nonlinear dynamical effects such as inverse cascades, have long been sought through either observational detection programmes or more or less rigorous theoretical proposals and models. These different lines of research will be reviewed and discussed at length in Sects. 3 and 4, but it is important at this stage to acknowledge that none of them has led a comprehensive, predictive and falsifiable theoretical explanation of supergranulation so far. On the other hand, we will see that drastic improvements of both observational capacities and computing power over the last 10 years are now leading to the emergence of new observational and numerical evidence strongly supporting the idea that the supergranulation scale at the solar surface is a special scale at which the dynamics is indeed first and foremost driven by buoyancy forces. The possible physics phenomenologies seemingly underlying these various results will be discussed in detail in Sect. 6.
3 Observational characterization
This section offers a wide review of the observational characterization of supergranulation. After an introduction of the principal methods of detection/inference of solar surface flows (Sect. 3.1), we review the numerous observational characterization of the scale of supergranulation (Sect. 3.2), measurements of supergranulation-scale intensity variations (Sect. 3.3), the inferred depth of the pattern (Sect. 3.2.4) and its interactions with rotation (Sect. 3.4) and magnetic fields (Sect. 3.5).
3.1 Flow measurement methods
Supergranulation is first and foremost detected in the form of a flow at the surface of the quiet Sun. Three methods are currently used to measure the corresponding velocity field: Doppler imaging, granule tracking and local helioseismology.
3.1.1 Doppler imaging
Doppler imaging is the oldest technique used to monitor supergranulation (the first detection by Hart (1954) was on a Doppler signal). A SOHO/MDI Doppler view of supergranulation has already been shown in the previous section in Fig. 1. Dopplergrams only provide the line-of-sight component of the velocity field. Therefore, except at the disc centre or at the solar limb, this signal consists in a mixture of the horizontal and vertical velocity field components. As already mentioned in the previous section, one clearly notices that the supergranulation velocity field is mainly horizontal, as the signal almost disappears near the disc centre. Doppler imaging of solar surface motions has been tremendously developed since Hart (1954), and is a key component of many modern space solar observatories, such as SOHO, SDO and Hinode.
3.1.2 Correlation and structure tracking
Another way to measure the velocity field at the photospheric level is by tracking structures visible at the surface. The idea is that small-scale structures such as granules (see Sect. 2.1.2 below) are simply advected by large-scale flows. Three variations of this technique are used: the local correlation tracking (LCT), the coherent structure tracking (CST) and the ball-tracking (BT). LCT determines the motion of features on an image by maximising the correlation between small sub-images (November and Simon 1988). CST identifies coherent intensity structures in the image by a segmentation process and then measures their displacement (e.g., Roudier et al. 1999; Rieutord et al. 2007; Tkaczuk et al. 2007). BT follows the displacement of floating balls over the intensity surface of images. The motion of the floating balls follows the mean motion of granules; this is presumably more effective computationally speaking than LCT and CST (Potts et al. 2004).
The principles and accuracy of granule tracking with LCT or CST have been tested by Rieutord et al. (2001) using synthetic data extracted from numerical simulations. Flows at scales larger than 2.5 Mm are well reproduced by the displacements of granules. At shorter scales, the random motion of granules (which are dynamical structures) generates a noise that blurs the signal. This 2.5 Mm lower limit has been confirmed by Rieutord et al. (2010) using Hinode/SOT observations. The 2.5 Mm resolution is significantly smaller than the supergranulation scale, therefore, these methods are well adapted to derive the horizontal components of the supergranulation flow. Unlike Doppler imaging, they do not suffer from a projection effect, but only measure the horizontal component of the flow. We will see a bit later that a combination of Doppler and tracking techniques now appears to make it possible to separate the horizontal and vertical components of the flow (albeit in a limited range of scales). An example of the horizontal velocity fields using this technique applied to ground-based sequences of wide-field images obtained at Pic du Midi is shown in Fig. 3.

Image reproduced with permission from Rieutord et al. (2008), copyright by ESO
The supergranulation horizontal velocity field as obtained by granule tracking.

Images reproduced with permission from a Williams et al. (2014), copyright by Springer; b Rincon et al. (2017), copyright by ESO; c Greer et al. (2015), copyright by AAS
Kinetic energy and velocity spectra of photospheric and subphotospheric flows derived using three different methods. a Global spherical harmonics spectra of the line-of-sight Doppler velocity field obtained with SOHO/MDI and SDO/HMI. The supergranulation peak around \(\ell =120\) (SOHO) and \(\ell =130\) (SDO) is clearly visible. The granulation peak expected around \(\ell =3000\) is eroded and effectively shifted to larger scales (\(\ell \sim 1500\)) due to time-averaging. b Global spherical harmonics power spectra of the three components of the surface velocity field (radial \(E_r\), spheroidal \(E_S\), toroidal \(E_T\)) inferred from a combined CST tracking/Doppler analysis of 24 h of SDO/HMI data. The inset shows the vertical scale height of the flow inferred from the ratio between the amplitudes of the horizontal and vertical velocity, as a function of horizontal scale. c Global spherical harmonics spectrum of the subphotospheric horizontal velocity field at different depths (full lines), derived from a local helioseismic ring-diagram analysis. The peak scale of the flows shifts towards larger scales with increasing depth. Note also that the sign of the vertical velocity gradient changes around \(\ell =30\)–40 in this inversion (the vertical amplitude of the flow seems to increase with depth at large scales, while it decreases at smaller scales).
3.1.3 Local helioseismology
Helioseismology uses the propagation of acoustic or surface gravity waves (f-modes) to determine the velocity of the medium over which they propagate. If the wave velocity is c and that of the fluid is V, a plane wave travelling downstream shows a velocity \(V+c\) whereas the one travelling upstream moves with a velocity \(V-c\). The sum of the two measured velocities gives that of the fluid. However, the phase velocity of the waves is not directly measurable: the observable quantity is the local oscillation of the fluid which results from the superposition of many travelling waves. A proper filtering is thus needed to select the desired wave; this operation requires a true machinery. The reader is referred to the reviews of Gizon and Birch (2005), Hanasoge and Sreenivasan (2014) and Hanasoge et al. (2016) for more detailed presentation of these techniques in the context of subsurface solar convective dynamics. Let us here simply recall some basic information about their output: the spatial resolution at which velocity fields can be measured is around 5 Mm, and the time resolution for time–distance helioseismology is around 8 h. While this is lower than what can be achieved with other methods, this technique provides the only means to probe the vertical dependence of the velocities and the subphotospheric dynamics. Typically, vertical variations can be evaluated down to 10–15 Mm below the surface, but the accuracy of measurements deeper than 10 Mm is still debated. A comparison between the tracking and helioseismic reconstructions of large-scale solar surface flows, showing good agreement between the two, can be found for instance in Švanda et al. (2007) and Greer et al. (2016).
3.1.4 Power spectra of solar surface flows
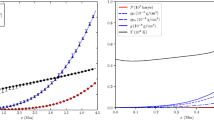
Given a local or global velocity field map obtained by one of the means described above, power spectra (scale-by-scale distribution of kinetic energy in Fourier or spherical harmonics space) are one of the most important tools to characterize the properties of the surface and subsurface dynamics of the solar photosphere. These include spectra of full-disc Doppler velocity maps obtained by SOHO/MDI (Hathaway et al. 2000, 2002) and SDO/HMI data (Williams and Pesnell 2011; Williams et al. 2014; Hathaway et al. 2015) and spectra of horizontal velocity fields derived from tracking applied to photometric ground-based wide-field data (Rieutord et al. 2008), Hinode/SOT data (Rieutord et al. 2010), SDO/HMI data (Langfellner et al. 2015a), or from helioseismic inversions of flows based on SDO/HMI Doppler data (Greer et al. 2016). A selection of recently published spherical harmonics spectra derived from SDO/HMI data using different kinds of flow measurements covering large areas of the solar disc is shown in Fig. 4. Figure 4a shows a spectrum of the Doppler (line of sight) velocity field as measured by the SOHO/MDI and SDO/HMI Michelson imagers (Williams and Pesnell 2011). Figure 4b shows the spectra of the three components of the photospheric velocity field, determined from a new technique combining CST (tracking) and Doppler velocity fields reduced from SDO/HMI data (Rincon et al. 2017). Finally, Fig. 4c shows the velocity spectra of subsurface flows determined from a ring-diagram analysis of SDO/HMI data (Greer et al. 2015).
3.2 The scales and structure of supergranulation
3.2.1 Horizontal spatial scale and morphology
Several techniques are used to measure the horizontal scale of supergranulation flows. The most popular one by far is to estimate the peak scale of power spectra such as those shown in Fig. 4. All studies of this kind basically find a peak scale value of 30–36 Mm, corresponding to \(\ell =120\)–140 spherical harmonics, with a typical width of 20–75 Mm. The comparison shown in Fig. 4a between SOHO/MDI spectra and SDO/HMI spectra computed for the same observation period suggests that the lower spatial resolution of SOHO/MDI leads to a 10%-larger estimate for the size of supergranules (Williams et al. 2014).
A detailed analysis of the plots of Rincon et al. (2017) in Fig. 4b reveals that the spectra of the horizontal and vertical components of the flow are very different. The supergranulation peak around \(\ell =120\) is essentially associated with horizontal spheroidal motions corresponding to diverging/converging flows. This dominance of the spheroidal spectrum over the toroidal/vortical spectrum of horizontal flows attests of the predominantly cellular structure of supergranulation motions. The weaker radial velocity spectrum increases monotically with decreasing scale down to the 2.5–5 Mm resolution of the velocity map used in the studyFootnote 1 and only shows a tentative inflexion at the supergranulation scale (a similar conclusion applies to the toroidal/vortical component). This trend of the radial velocity field to increase with scale down to the spatial resolution of the data has also been observed using a different flow-component determination method based on a differentiation of Doppler maps (Hathaway et al. 2015). The very different radial and horizontal velocity spectra reflect the strong anisotropy of the flow. We will shortly argue that this result can be used to infer some information about the vertical scale height of the velocity field. Finally, the helioseismic data analysis shown in Fig. 4c reveals the interesting, albeit perhaps not entirely surprising result that the scale of the spectral peak increases monotonically with increasing depth, as one would expect from the self-similarity argument described in Sect. 2.
Other non-spectral techniques have been used to measure the horizontal scale of supergranulation. In their seminal work, Leighton et al. (1962) and Simon and Leighton (1964) calculated the auto-correlation length of Dopplergrams, and found 32 Mm. Other authors, like DeRosa et al. (2000) and DeRosa and Toomre (2004), used local correlation tracking to determine the horizontal flows from the Doppler signal of SOHO/MDI and identified supergranules with horizontal divergences. From these data, they derived a rather small “diameter” in the 12–20 Mm range. Using a similar technique, Meunier et al. (2007c) found a mean value for supergranule diameters around 30 Mm. As underlined in these papers, the exact size of supergranules very much depends on the smoothing procedure used in the data processing. Another technique consists in estimating the supergranulation scale from horizontal flow divergence maps derived from local helioseismic analysis (this quantity is directly associated with the difference between wave travel times in seismology and is, therefore, more readily accessible than the velocity field itself). Using this technique on SOHO/MDI data, Del Moro et al. (2004) computed the statistics of the sizes of supergranules and found a mean diameter at 27 Mm, with a peak in the distribution at 30 Mm. Similar results have been obtained by Hirzberger et al. (2008) using an even larger set of data (collecting more than \(10^5\) supergranules).
Finally, several authors have used tesselation algorithms or threshold-based identification techniques to capture individual supergranulation cells and subsequently study their geometrical properties and spatial arrangement. Such techniques have mostly been applied to maps of the chromospheric network (e.g., Hagenaar et al. 1997; Schrijver et al. 1997; Berrilli et al. 1998; Chatterjee et al. 2017), whose relationship to supergranulation is further described in Sect. 3.5.1, and tend to give slightly smaller size estimates.
3.2.2 Time scale and lifetime
As with horizontal spatial scales, there are several ways in which the time scale of supergranulation can be measured. Historically, many such measurements rely on the statitics of coherent cellular structures. Worden and Simon (1976) suggested a supergranulation lifetime of 36 h. Later, Wang and Zirin (1989) showed that supergranulation lifetime estimates depended strongly on the choice of tracer or proxy. They obtained 20 h using Dopplergrams, 2 days using direct counting techniques of supergranulation cells and 10 h using the tracking of magnetic structures (see also Sect. 3.5). Here again, SOHO/MDI data have dramatically increased the statistics and thus the quality of the determinations. Using a wavelet analysis of MDI data, Parfinenko et al. (2014) found a time scale of 1.3 days, while Hirzberger et al. (2008) report a lifetime around 1.6–1.8 days using helioseismic techniques. These latter estimates are somewhat longer than the others, but they rely on very long time series and large statistics enabling a better representation of long-living supergranules. A recent SDO/HMI helioseismic analysis by Greer et al. (2016) finds a very similar coherence time of supergranules in the first few Megameters below the surface, but also concludes that the pattern visible at the surface at any given time may subsequently propagate down to the base of the near surface shear layer over a scale of a month. We will come back to this result when we discuss the influence of rotation on supergranulation.
3.2.3 Velocity scales
A typical horizontal velocity associated with supergranules can be quickly derived from the ratio between the horizontal spatial scales and time scales given above. Taking 30 Mm for the former and 1.7 days for the latter leads to a velocity of 205 m/s, in reasonable agreement with more direct inferences of the supergranulation velocity field from observations: the original work of Hart (1954) inferred 170 m/s, Simon and Leighton (1964) mentioned 300 m/s and more Hathaway et al. (2002) evaluated this amplitude at \({\sim }\,360\) m/s from SOHO/MDI Dopplergrams.
A quantitative way to estimate the magnitude of the supergranulation velocity field is through the spectral density of kinetic energy E(k) describing the relation between the scale and amplitude of the flow. The dimensional value of the spectral density of horizontal kinetic energy \(E_h(k)\) was for instance derived by Rieutord et al. (2010) from granule tracking velocity measurements using Hinode/SOT data. The spectral power density at supergranulation scales is 500 \(\hbox {km}^3{/}\hbox {s}^2\), which is larger than that at granulation scales.Footnote 2 This energy density is related (dimensionally) to the velocity at scale \(\lambda =2\pi /k\) by the relation \(V_\lambda =\sqrt{kE_h(k)}\). This leads to \(V_{\uplambda =36\,\hbox {Mm}}\simeq 300\) m/s, consistent with the direct Doppler measurements of the velocity field at supergranulation scales.
It has been known from Dopplergrams for very long that the supergranulation flow field is largely dominated by its horizontal component. The 300–400 m/s estimates above refer to this component. The vertical component of supergranulation flows is much smaller and has proven much harder to measure, notably because the corresponding signal is mixed with the much stronger 5 min signal of acoustic solar oscillations, and polluted by the presence of magnetic field concentrations at supergranule boundaries, where up and downflows tend to be localized (see Sect. 3.5 below). November (1989, 1994) advocated that this vertical component was in fact the mesogranulation that he detected some years before on radial velocities at disc centre (November et al. 1981). The rms value of this quantity was then estimated to be 60 m/s. This quantity was more precisely evaluated using the SOHO/MDI data. Hathaway et al. (2002) derived an estimate of 30 m/s while Duvall and Birch (2010) found a very low rms value around 4 m/s with upwelling velocities of 10 m/s. Similarly, power spectra of line-of-sight velocities from Hinode/SOT data derived by Rieutord et al. (2010) point to a rms vertical velocity of 10 m/s at the scale of supergranulation, however, with low statistics. The recent global analysis of SDO/HMI surface data by Rincon et al. (2017) aiming at disentangling the three components of the velocity and the corresponding spectra (Fig. 4b), points to a value of no more than 20–30 m/s for the radial/vertical velocity field at supergranulation scales. Only an upper bound can be inferred from such surface measurements as it is very difficult to isolate the weak signal from this slow flow component in the data. Recent helioseismic measurements by Greer et al. (2016) point to a typical vertical flow field of the order 40 m/s in the first few Mm below the surface. Whatever the exact value, the results show that the vertical amplitude of the flow is at best ten times smaller than the horizontal one, emphasizing once again the strong anisotropy of the supergranulation flow.
3.2.4 Depth and vertical structure
A typical scale height of subsonic flows in the supergranulation to mesogranulation range can be indirectly estimated from velocities measured at the photospheric level using the anelastic equation of mass conservation
where the index h refers to the horizontal quantities and z. This equation can also be expressed as \(v_h{/}\lambda _h\sim v_z{/}\lambda _z\), where \(\lambda _h\) is the horizontal scale and \(\lambda _z\) stands for the smallest of the density scale height and typical vertical scale of variation of the flow. We see that a separate measurement of the vertical and horizontal velocities at given horizontal scale allows for an estimation of the corresponding vertical scale of the flow. Combining Dopplergrams and correlation tracking inferences, November (1994) argued that the supergranulation flow should disappear at depths larger than 2.4 Mm below the visible surface. Rieutord et al. (2010) performed the same kind of calculation using divergences and velocity fields derived from Hinode data, and found a vertical velocity scale height of \({\sim }\,1\) Mm, indicating a very shallow structure. Finally, in their recent global spectral analysis of the different components of the flow using SDO/HMI data, Rincon et al. (2017) found that \(\lambda _z\) is approximately constant and of the order of 2.5 Mm in the horizontal range extending from the supergranulation scale down to a few Mm (see inset in Fig. 4b). The conclusion that the flow has a relatively small vertical scale of variation below the surface appears to be an inescapable consequence of the measurements of a large horizontal to vertical surface velocity ratio. This result, however, does not imply that there is no flow below that depth.
There is obviously only so much one can do with surface measurements to study the vertical structure of supergranulation. Fortunately, the advent of local helioseismology in the late 1990s has made it possible to start probing supergranulation-scale flows at optically-thick levels. Using MDI data, Duvall et al. (1997), detected flows at supergranulation scales only in the first few Mm below the surface. Duvall Jr (1998) further estimated that the depth of supergranulation was 8 Mm. Zhao and Kosovichev (2003), on the other hand, found converging flows at 10 Mm and estimated the supergranulation depth to be 15 Mm. Woodard (2007) reported a detection of a flow pattern down to 5 Mm corresponding to the deepest layers accessible with their data set. Using Hinode data, Sekii et al. (2007) found that a supergranulation pattern, monitored for 12 h in a small field of \(80\times 40\,\hbox {Mm}^2\), does not persist at depths larger than 5 Mm. The existence of a return flow at depths larger than 5 Mm was also suggested in that period but remained unclear (Duvall Jr 1998; Zhao and Kosovichev 2003). There is a large scatter in these early results, and a lot of ambiguity in what they really represent.
The helioseismic determination of the vertical extent and structure of supergranulation remains a work in progress and a difficult task. Various discussions of the early shortcomings, difficulties and artefacts associated with the development of helioseismic imaging of subsurface flows can be found in Braun and Lindsey (2003), Lindsey and Braun (2004) and Gizon and Birch (2005) and more recently in Švanda (2015) and Bhattacharya and Hanasoge (2016). But, as these difficulties are progressively eliminated, helioseismic techniques are now increasingly playing a key role in the study and understanding of supergranulation, and new helioseismic analyses of subsurface flows have now been conducted with SDO/HMI data. Duvall and Hanasoge (2013) and Duvall et al. (2014) found suprisingly high-speed supergranular flows at a depth \({\sim }\,2\) Mm, namely vertical upflows of 240 m/s at a depth of 2.3 Mm and horizontal flows of 700 m/s at a depth 1.6 Mm. Such high values have, however, been challenged by subsequent studies by DeGrave and Jackiewicz (2015) and Greer et al. (2015, 2016). This tension may be due to the fact that Duvall and Hanasoge (2013) and Duvall et al. (2014) used a large skip distances and imaged vertical flows, and also averaged over a larger number of supergranules, while the local methods used in other studies typically image horizontal flows using moderate skip distances. Greer et al. (2016) also find an instantaneous correlation depth of \(\sim \) 7 Mm for the supergranulation pattern, but suggests that the pattern actually propagates down to the bottom of the near surface shear layer over a month at a vertical speed of the order of 40 m/s. This propagation may help to explain some of the deeper earlier estimates for the depth of supergranulation. Note however that these determinations of the correlation depth of flows may be affected by the details of helioseismic inversion procedures, as suggested by the analysis of DeGrave et al. (2014b). Finally, Greer et al. (2016) suggest that supergranules “form[s] at the surface and rains downward, imprinting [their] pattern in deeper layers”. They also find that the pattern does not take the form of a cellular flow like in the laminar picture of Rayleigh–Bénard convection, but is rather dominated by downflows. As mentioned earlier, the spectral analysis of helioseismically determined convective flows by Greer et al. (2015) (Fig. 4c) also suggests a monotonic increase of the energetically dominant horizontal scale of fluctuations with depth.
3.3 Intensity variations in supergranules
The surface thermal signature of supergranulation appears to be quite small. Early measurements suggested that the intensity contrast between the border and the centre of supergranules probably does not exceed a few percents in the infrared (Worden 1975). The photometric intensity contrast at supergranulation scales in white light images is also much smaller and ambiguous than that of granulation, which has been shown to be up to 27% at a wavelength of 450 nm (Wedemeyer-Böhm and Rouppe van der Voort 2009). Several early studies (Beckers 1968; Frazier 1970; Foukal and Fowler 1984; Lin and Kuhn 1992) found an increase of intensity at the edge of supergranulation cells, corresponding to a negative correlation between the supergranulation horizontal divergence maps and intensity maps. These early results may naively tend to rule out a convective origin for supergranulation but are subject to caution. First, supergranulation vertices are strongly correlated with magnetic bright points (see Sect. 3.5 below). To circumvent this difficulty, Rast (2003a) considered only areas with low magnetic fields and found a small decrease of intensity at the edge of supergranules. The problem was reconsidered in detail by Meunier et al. (2007b, 2008) using MDI intensity maps. There too, the influence of the magnetic network was carefully eliminated. In contrast to most previous studies, they report a very small but significant intensity decrease from the centre to the edge of supergranulation cells (in the range 0.8–2.8 K). This conclusion was also reached by Goldbaum et al. (2009) using a different methodology. In addition, Meunier et al. (2008) noticed that the radial temperature profile at the surface of a supergranule is very similar to that of a simulated granule. Using SDO/HMI continuum intensity maps centered around 617 nm, (Langfellner et al. 2016) recently derived a new estimate at \(\varDelta T=1.1\pm 0.1\) K of the temperature drop between centre and edge of supergranules, in line with the preceding results.
While such contrats are relatively weak, it has been argued that they remain consistent with a convective origin of supergranulation (Goldbaum et al. 2009). Also, the many complexities of radiative transfer at the surface, including strongly temperature-dependent opacities (Nordlund et al. 2009), imply that small surface intensity contrasts cannot alone easily be accepted as smoking-gun evidence for weak buoyancy/entropy driving below the surface. Helioseismic analysis (e.g., Duvall et al. 1997) notably seem to point to larger relative temperature contrasts of the order of a few percents below the surface. We will also see in Sect. 5 that a strong buoyancy driving is observed at scales larger than granulation in large-scale simulations, but does not generally translate into a strong surface intensity pattern in simulations incorporating realistic radiative physics.
3.4 Effects of rotation
The influence of the global rotation \(\varOmega \) of the Sun on the dynamics of a structure of size L and typical velocity V is measured by the Rossby number:
The second expression uses the lifetime of the structure \(\tau =L/V\). In numbers, taking \(\tau _{\mathrm {SG}}=1.7\) days and a rotation period of 25–30 days leads to \(\textit{Ro}_{\mathrm {SG}}\sim 2{-}3\). This is not a large value, indicating that the Coriolis acceleration should affect the dynamics of supergranules. Such an effect has been reported by Gizon and Duvall (2003), who showed (Fig. 5a) that the correlation between vertical vorticity and horizontal divergence of supergranules changes sign at the equator: it is negative in the northern hemisphere and positive in the southern one. Hence, supergranules, while essentially consisting of cells of diverging flows, behave like weak anticyclones (the vertical vorticity of anticyclones changes sign at the equator, see Fig. 5b). These anticyclones are surrounded by cyclonic vorticity associated with downward flows; because these downdrafts have a somewhat smaller scale, the cyclonic vorticity is less conspicuous in measurements than the anticyclonic contribution of supergranules, but it has actually been singled out in the work of Komm et al. (2007). A recent study of Langfellner et al. (2015b) applying both time–distance helioseismology and local correlation tracking to SDO/HMI data has recently confirmed these conclusions with spatially-resolved measurements of the supergranulation vorticity. They find a typical vortical flow component of the order of 10 m/s in the diverging core of supergranules, much weaker than the diverging horizontal flow component itself. This result is consistent with the weakness of the toroidal flow component with respect to the spheroidal flow component found in the spectral analysis of Rincon et al. (2017).
a Correlation between the horizontal divergence and vertical vorticity of the supergranulation flow as a function of latitude. Image reproduced with permission from Gizon and Duvall (2003), copyright by ESA. b Schematic view of anticyclones at the surface of the rotating Sun
Early studies of the rotational properties of supergranulation focused on the rotation rate of the supergranulation pattern (Duvall 1980; Snodgrass and Ulrich 1990). Using Dopplergrams, they found, surprisingly, that supergranulation is rotating 4% faster than the plasma. This phenomenon is usually referred to as the superrotation of supergranules. Superrotation was seemingly confirmed by Duvall and Gizon (2000) using the time–distance technique applied to f-modes detected with SOHO/MDI, and Beck and Schou (2000) estimated that the supergranulation rotation rate is larger than the solar rotation rate at any depth probed by helioseismology.
Analysing time series of divergence maps inferred from time–distance helioseismology applied to MDI data, Gizon et al. (2003) further found that the supergranulation pattern had wave-like properties with a typical period of 6–9 days, quite longer than the lifetime of individual supergranules. They also found that the power spectrum of the supergranulation signal close to the equator presented a power excess in the prograde direction (with a slight equatorwards deviation in both hemispheres), thus explaining the anomalous superrotation rate of the pattern. The dispersion relation for the supergranulation “wave” appears to be only weakly dependent on latitude (Gizon and Duvall 2004). Schou (2003) seemingly confirmed these findings with direct Doppler shift measurements and found that wave motions were mostly aligned with the direction of propagation of the pattern. These results brought interesting new light on the supergranulation phenomenon and led to the conjecture that supergranulation could be a manifestation of oscillatory convection, a typical property of convection in the presence of rotation and/or magnetic fields (see Sect. 4). This interpretation of the observed power spectrum in terms of oscillations was, however, questioned by Rast et al. (2004) and Lisle et al. (2004), who instead suggested an explanation in terms of two superimposed steady flow components identified as mesogranulation and supergranulation advected by giant cell circulations. According to Gizon and Birch (2005), this interpretation is not supported by observations. They argued that the finding of Lisle et al. (2004) that supergranules tend to align in the direction of the Sun’s rotation axis under the influence of giant cells can be explained naturally in terms of wave dynamics. North–South alignments of supergranules have also been found in the polar regions by Nagashima et al. (2011) using local helioseismology with Hinode/SOT data. A recent study by Langfellner et al. (2018) using both time–distance helioseismology on SDO/HMI data and correlation tracking appears to further confirm the results of Gizon et al. (2003) on the wave-like oscillatory properties of the dynamics in the range of scales \(50<\ell <120\) comparable to or slightly larger than the supergranulation scale.
Going back to surface measurements, Hathaway et al. (2006) argued that the supergranulation pattern superrotation inferred from Doppler shifts was due to projection effects on the line-of-sight signal. Using correlation tracking of divergence maps derived from intensity maps (Meunier et al. 2007c) and comparing it with direct Doppler tracking, Meunier and Roudier (2007) confirmed the existence of projection effects with the latter method, but found that the supergranulation pattern inferred from divergence maps was still superrotating, albeit at smaller angular velocities than those inferred by Duvall (1980) and Snodgrass and Ulrich (1990). More recently, Hathaway (2012) found that supergranules of increasingly larger size seem to accurately track the solar rotation rate at increasingly larger depths, down \(\sim \) 50 Mm. This latter estimate is quite large compared to the coherence length (7 Mm) inferred by Greer et al. (2016) but is consistent with the high speed vertical flows suggested by the Duvall et al. (2014) analysis. Also, Greer et al. (2016) note that the 7 Mm estimate is deceptive because of the slow downwards propagation of the supergranulation pattern diagnosed in their helioseismic analysis, and notably argue that the slow propagation speed is consistent with a propagation of the pattern down to the base of the near surface shear layer on a timescale comparable to the solar rotation period. This suggests that supergranulation is in dynamical interaction with the subsurface differential rotation layer down to 30–50 Mm deep, and may actually play an important role in the dynamical establishment of this layer.
For the sake of completeness, let us finally mention the observations by Kuhn et al. (2000) of small-scale 100 m-high “hills” at the solar surface, which they interpreted as Rossby waves. It has been argued (Williams et al. 2007) that these structures simply result from the vertical convective motions associated with supergranules.
3.5 Effects of magnetic fields
As explained in Sect. 2.2, the magnetic dissipation scale at the solar surface is \(\ell _\eta \sim 100\) m or slightly less. Hence, convection at the solar surface is strongly coupled to the Sun’s magnetic dynamics at all observable scales, including that of supergranulation. The aim of this section is to review the breadth of observational results on the interactions between the two. We first look at the correlations between supergranulation and the magnetic network and review the main properties of internetwork fields, whose dynamics is directly related to the formation of the magnetic network. We then review studies of the dependence of supergranulation on the global solar magnetic cycle, and of its interactions with active regions.
3.5.1 Supergranulation and the magnetic network
The discovery of the chromospheric network in \(\hbox {Ca}^{+}\) K spectroheliograms (the K-line of \(\hbox {Ca}^+\) at 393.4 nm) such as shown in Fig. 6 dates back to Deslandres (1899). The first comparative analyses between magnetograms, spectroheliograms and Dopplergrams by Leighton et al. (1962) and Simon and Leighton (1964) revealed a strong correlation between the chromospheric network, the magnetic field distribution of the quiet Sun and supergranulation. For this reason, both magnetograms and spectroheliograms have been used as a proxy to study supergranulation (e.g., Lisle et al. 2000; Del Moro et al. 2007; Tian et al. 2010), but it should be kept in mind that the dynamical interactions between magnetic fields and supergranulation are actually still not well understood (this problem will be discussed in Sect. 6).

Image reproduced with permission from Roudier et al. (2009), copyright by ESO
Distribution of magnetic field intensity (grey scale levels) on the supergranulation boundaries. The black dots show the final positions of floating corks that have been advected by the velocity field computed from the average motion of granules. The distribution of corks closely matches that of the magnetic field.
The magnetic network refers to a distribution of magnetic field concentrations (associated with bright points in spectroheliograms) with typical field strengths of the order of 1 kG (see reviews by Solanki 1993; de Wijn et al. 2009), primarily located on the boundaries of supergranules (Simon et al. 1988), in downflow areas. Several differences between supergranulation and the magnetic network have been noticed, including a 2% relative difference in the rotation rate of the two patterns (see Snodgrass and Ulrich 1990 and Sect. 3.4 above). The magnetic network is not regularly distributed on the boundaries of supergranulation cells but rather concentrates into localized structures (see Fig. 7). Estimates of the lifetime and size of supergranules inferred from magnetograms or spectroheliograms are significantly smaller than those based on direct velocimetric measurements (Wang and Zirin 1989; Schrijver et al. 1997; Hagenaar et al. 1997). For instance, Hagenaar et al. (1997), using correlations of maps of the chromospheric network, obtained a typical size of 16 Mm. As far as the horizontal velocities are concerned, the tracking of magnetic network elements gives values around 350 m/s, close to the estimates derived from granule tracking (Lisle et al. 2000). The spatial distribution of magnetic network fields can be reconstructed quite well by letting passive magnetic elements be advected by the surface flow field (Krijger and Roudier 2003; Roudier et al. 2009). Moreover, tagging the granules and following their evolution and motion leads to the so-called Trees of Fragmenting Granules in a space-time diagram, a structure whose spatial boundaries also neatly match part of the boundary of the embodying supergranule (Roudier et al. 2016; Malherbe et al. 2018).
These results show that the formation of the magnetic network is related to the large-scale dynamics of the surface (see Orozco Suárez et al. 2012; Giannattasio et al. 2014; Berrilli et al. 2014). The magnetic field-flow interaction occurs over a wide range of scales extending up to the 35 Mm supergranulation scale, and several studies with the Swedish Solar Telescope at La Palma observatory indicate that strong correlations between flows at scales comparable to or smaller than mesoscales (i.e., significantly smaller than supergranulation) and intense magnetic elements exist (Domínguez Cerdeña 2003; Domínguez Cerdeña et al. 2003). A study by Roudier et al. (2009), combining spectropolarimetric and photometric Hinode measurements, also established a very clear correlation between the motions at mesoscales and those of the magnetic network (see also de Wijn and Müller 2009). Note finally that the network formation process may be influenced by an East–West anisotropy now detected in supergranules (see Langfellner et al. 2015a; Roudier et al. 2016).
3.5.2 Internetwork fields
One of the important advances on solar magnetism in the last two decades has been the detection of quiet Sun magnetic fields at scales much smaller than that of granulation (e.g., Domínguez Cerdeña et al. 2003; Berger et al. 2004; Trujillo Bueno et al. 2004; Rouppe van der Voort et al. 2005; Lites et al. 2008). The ubiquity of these fields and their energetics suggest that the dynamics of internetwork fields could also be a piece of the supergranulation puzzle. The following summary is not meant to be exhaustive. For a more detailed presentation, we refer the reader to the reviews of de Wijn et al. (2009) and Stenflo (2013). Internetwork fields refer to mixed-polarity fields that populate the interior of supergranules. Their strength is on average thought to be much weaker than that of network fields, but magnetic bright points are also observed in the internetwork, (e.g., Muller 1983; Nisenson et al. 2003; de Wijn et al. 2005; Lites et al. 2008). Besides, network and internetwork fields are known to be in permanent interaction (e.g., Martin 1988). In fact, in the light of nowadays high-resolution observations and numerical MHD simulations (see Sect. 5.3.6), the historical distinction between network and internetwork fields cannot be easily justified on dynamical grounds, as the two appear to be part of a complex multiscale dynamics involving some local dynamical intensification process. Internetwork magnetism was originally discovered by Livingston and Harvey (1971, 1975) and subsequently studied by many authors (e.g., Martin 1988; Keller et al. 1994; Lin 1995) at resolutions not exceeding 1” (730 km). Observations with the solar telescope at La Palma observatory revealed the existence of such fields at scales comparable and even smaller than the granulation scale (Domínguez Cerdeña et al. 2003; Roudier and Muller 2004; Rouppe van der Voort et al. 2005). Studies based on Hinode observations (Orozco Suárez et al. 2007; Lites et al. 2008) reported magnetic field variations at scales comparable to or smaller than 100 km.
The strength of internetwork fields, their distribution at granulation and subgranulation scales and their preferred orientation are still a matter of debate. Almost every possible field-strength value in the 5–500 G range can be found in literature (Martin 1988; Keller et al. 1994; Lin 1995; Domínguez Cerdeña et al. 2003; Trujillo Bueno et al. 2004; Lites et al. 2008). This wide dispersion is explained by several factors. Zeeman spectropolarimetry, one of the most frequently used tools to study solar magnetism, is affected by cancellation effects when the magnetic field reverses sign at scales smaller than the instrument resolution (Trujillo Bueno et al. 2004; de Wijn et al. 2009). Hence, very small-scale fields can partially escape detection via this method. Zeeman spectropolarimetry estimates of the average field strength based on Hinode observations (Lites et al. 2008) are 11 G for longitudinal fields and 60 G for transverse fields (horizontal fields at disc centre), but wide excursions from these average values are detected and the observed signatures may also be compatible with stronger, less space-filling magnetic fields. Using Hanle spectropolarimetry, Trujillo Bueno et al. (2004) report an average field strength of 130 G, with stronger fields in the intergranular lanes and much weaker fields in the bright centres of granules. The discrepancy between Hanle and Zeeman estimates can be reduced using techniques that circumvent cancellation effects, though, leading to estimates of 60–80 G (Danilovic et al. 2010, 2016a, b).
Some Zeeman estimates seem to indicate that small-scale internetwork fields have a tendency to be horizontal (Orozco Suárez et al. 2007; Bommier et al. 2007; Lites et al. 2008), sometimes even bridging over granules, but other studies have come to the opposite conclusion that internetwork fields are mostly isotropic (Martínez González et al. 2008; Asensio Ramos 2009; Bommier et al. 2009). Using Zeeman and Hanle diagnostics in a complementary way, López Ariste et al. (2010) came to the conclusion that internetwork fields are mostly isotropic and highly disordered, with a typical magnetic energy containing scale of 10 km. We again refer the reader to Stenflo (2013) for a more detailed review of this problem. The isotropy properties of the field also seem to be dependent on the depth at which they are probed (Schüssler and Vögler 2008; Rempel 2014), and conditional on the amplitude of the signal polarization (Lites et al. 2017).
Finally, at the scale of supergranulation, it has been pointed out that regions of supergranulation up-welling (i.e., of positive divergence) can be very quiet and have very little flux emergence (Martínez González et al. 2012; Stangalini 2014). One possible explanation is that supergranulation-scale diverging flows somewhat hinder small-scale dynamo action, but this observation may also be a simple consequence of the fast sweeping of the magnetic fields peppered by the small-scale dynamo to the boundaries of supergranules.
3.5.3 Magnetic power spectrum of the quiet photosphere
The scale-by-scale distribution of magnetic energy and the power spectrum of magnetic fields in the quiet photosphere may also give us clues on MHD dynamics in the subgranulation to supergranulation range. Several authors have notably argued that solar magnetic fields, from the global solar scales to the smallest scales available to observations, may have a fractal or multifractal structure (Lawrence et al. 1995; Komm 1995; Nesme-Ribes et al. 1996; Meunier 1999; Janßen et al. 2003; Stenflo and Holzreuter 2002, 2003a, b; Abramenko 2005).
Studies of the magnetic power spectrum of the quiet Sun are currently mostly limited to the line-of-sight component of the magnetic field. Most spectra available in literature have been obtained from either ground-based observations, SOHO / MDI and Hinode magnetograms. The power spectrum of magnetic energy at scales below 1 Mm has recently been studied by Stenflo (2012), Katsukawa and Orozco Suárez (2012) and Danilovic et al. (2016a) using Hinode/SOT data. These different studies find a rather slow decay of the magnetic energy (\({\sim }\,k^{-0.7}\)–\(k^{-1.4}\)) at subgranulation scales suggestive of vigorous magnetic dynamics at such scales. At the larger scales of most interest here, the magnetic power spectrum is rather flat, but shows a maximum in the meso to supergranulation-scale range. The spectrum appears to have a relatively shallow negative slope below 10–20 Mm, (e.g., Lee et al. 1997; Abramenko et al. 2001; Harvey et al. 2007; McAteer et al. 2010; Longcope and Parnell 2009). There have unfortunately been very few studies of supergranulation-scale magnetic fields with SDO/HMI so far. A raw comparison of Hinode/SOT, SOHO/MDI and SDO/HMI magnetic spectra obtained in this range of scale has been made by Abramenko et al. (2011).
3.5.4 Supergranulation variations over the solar cycle
In view of the association between supergranulation and the magnetic network, it is natural to wonder if and how the size of supergranules varies with solar activity. Early studies did not directly focus on supergranulation flows but rather on the cycle-dependence of the magnetic network itself. Singh and Bappu (1981) studied spectroheliograms spanning a period of seven solar maxima and found the typical size of the chromospheric network to be smaller at the maxima than at the minima of the cycle. A similar conclusion was reached by Kariyappa and Sivaraman (1994), Berrilli et al. (1999) and Raju and Singh (2002), but Wang (1988) and Münzer et al. (1989) both reported an increase of network cell sizes in regions of stronger magnetic activity instead. Using MDI magnetograms spanning the first half of Cycle 23, Meunier (2003) found an increase of the size of magnetic elements at supergranulation-like scales with solar activity [Berrilli et al. (1999) also used data obtained at the beginning of Cycle 23 close to the activity minimum]. However, in the upper solar atmosphere (quiet chromosphere and transition region) there is a clear decrease of the supergranular scale when the magnetic cycle decreases McIntosh et al. 2011; Chatterjee et al. 2017. These somehow contradicting results show that magnetic tracers must be used with care for this kind of measurements. The results are sensitive to the thresholds used to identify the various field components (e.g. network or internetwork), and disentangling these effects is difficult.
Other studies have attempted to use proxies independent of magnetic tracers of supergranulation to measure its size, notably velocity features like positive divergences. DeRosa and Toomre (2004), using two data sets obtained at periods of different levels of magnetic activity, found smaller supergranulation cell sizes in the period of high activity. A similar conclusion was reached by Meunier et al. (2008). Meunier et al. (2007a) found a decrease of the typical cell sizes with increasing field strength within supergranules, but noted that larger supergranulation cells were associated with stronger network fields at their boundaries. Hence, it seems that a negative or a positive correlation can be obtained, depending on whether the level of magnetic activity is defined with respect to internetwork or network fields. Meunier et al. (2007a) also reported the absence of large supergranulation cells for supergranules with large internetwork magnetic field strengths, suggesting that internetwork fields (whose existence is most likely rooted in a small-scale dynamo mechanism independent of the solar cycle) do have a dynamical influence on supergranules. We refer the reader to Meunier et al. (2007a) for a more exhaustive discussion of the previous results and of the possible shortcomings and biases of the various methods.
The last marked and long minimum that occurred in 2008 between solar cycles 23 and 24, prompted Williams and Pesnell (2011) to compare the characteristic time scale, length scale and velocities of supergranulation with the ones of the preceding minimum in 1996. Only slight differences have been found. Finally, on the helioseismic side, the dispersion relation for the supergranulation oscillations found by Gizon et al. (2003) appears to be only weakly dependent on the phase of the solar cycle (Gizon and Duvall 2004). However, the same authors reported a decrease in the lifetime and power anisotropy of the pattern from solar minimum to solar maximum. Overall, it is therefore fair to say that a possible dependence of supergranulation on the solar cycle, if any, appears to be relatively weak, and does not appear to drastically affect its dynamics.
3.5.5 Supergranulation and flows in active regions
Let us finally consider the properties of surface flows at scales comparable to supergranulation within active regions and in the vicinity of sunspots. The reason for doing this is twofold. First, we may wonder how supergranulation evolves locally during the formation or decay of an active region. Second, the properties of flows around sunspots may give us some hints of the effect of strong magnetic flux concentrations on the flow dynamics in the quiet Sun.
Information regarding the first point remains scarce. Rieutord et al. (2010) reported the disappearance of the supergranulation spectral peak in the kinetic energy power spectrum of solar convection during the emergence of two magnetic pores. While the pores (of a size comparable to that of a granule) are emerging, the supergranulation flow becomes very weak just like if the surrounding magnetic flux associated with the pores had a significant impact on the flow. A related observation by Hindman et al. (2009) shows that the fairly regular tiling of the surface of the quiet Sun associated with supergranulation is somewhat disorganised and washed away within magnetic active regions.
As far as the second point is concerned, many studies in the past have focused on the detection and characterisation of intrinsic flows associated with sunspot regions (see Solanki (2003) and Thomas and Weiss (2008) for exhaustive descriptions of sunspot structure and dynamics) and significant observational progress has been made on this problem in recent years thanks to local helioseismology (Lindsey et al. 1996; Gizon et al. 2000; Zhao et al. 2001, 2004, 2010; Haber et al. 2001, 2004; Braun and Lindsey 2003; Hindman et al. 2009; Komm et al. 2011, 2012; Kosovichev 2012; Jain et al. 2016; Löptien et al. 2017). The general picture seems to be as follows [Hindman et al. (2009), but see also DeGrave et al. (2014a) for a discussion of the possible limitations of helioseismic techniques in sunspots]: an annular outflow called the moat flow (Sheeley 1969) is observed at the surface, close to the sunspot. There is a corresponding return flow at depths smaller than 2 Mm, so the moat circulation is fairly shallow. In contrast, further away from the sunspot umbra, larger-scale circulations characterized by a surface inflow and a deep (\({>}\,10\) Mm) outflow are inferred from helioseismic inversions.
The structure of the moat flow has been probed using the Doppler signal (Sheeley and Bhatnagar 1971; Sheeley 1972), the tracking of surface features, such as granules (Muller and Mena 1987; Shine et al. 1987) or small-scale magnetic elements (Sheeley 1972; Harvey and Harvey 1973; Hagenaar and Shine 2005), and with helioseismology (Gizon et al. 2000). The outflow appears to have properties similar to those of supergranulation (see notably Brickhouse and Labonte 1988), albeit with a larger velocity \({\sim }\,1\) km/s. It remains unclear whether this strong-field dynamical behaviour has anything in common with supergranulation though. The outflow in this case is centred on a strong field region whereas it is the supergranulation inflow vertices that coincide with magnetic flux concentrations in the quiet Sun (see, e.g., Requerey et al. 2018).
4 Classical fluid theory and phenomenological models
4.1 Context
The big problem with understanding supergranulation has always been the important challenges that its numerical simulation and formal theoretical description present. Until the mid-2000s and the advent of the first large-scale 3D numerical simulations, our computing arsenal was too limited to probe almost any aspect of the multiscale dynamical nonlinear complexity of large-scale solar surface dynamics, leaving theoretical astrophysicists almost naked with just linear or weakly nonlinear theories from the 1960–1990 era at hand, plus a few generic hand-waving turbulence concepts from the same period. All the classical phenomenological models of supergranulation from this “pre-numerics era” are extremely simplified, qualitative and speculative. Most of them have consequently proven unfalsifiable and, as we shall see with the review of numerical results in the next section, are in fact most likely too idealized. To be fair, similar limitations have plagued research on many, if not all nonlinear astrophysical fluid dynamics problems. It also has to be recognized that such models are not devoid of meaningful physical insights either, and have played an important role in shaping the generic astrophysical fluid dynamical phenomenological landscape over the years. This section is, therefore, perhaps best understood as a testimony of the historical development of the many different possible phenomenological scenarios for supergranulation dynamics. Modern numerical developments, and ongoing theoretical discussions inspired by them as well as by some of the observational results reviewed in the previous section, will be reviewed in Sects. 5 and 6.
The classical phenomenological models of supergranulation are essentially of two types: those which assume that supergranulation is rooted in thermal convection (i.e., it is driven by thermal buoyancy) and rely on classical fluid convection theory, and those which do not and rely on more general phenomenological concepts of turbulent dynamics. In the following, we therefore first briefly introduce the rotating MHD Rayleigh–Bénard problem (Sect. 4.2), which provides the simplest mathematical description of rotating magnetoconvection in a fluid. While this system is not entirely adequate to describe convection in the strongly stratified SCZ and close to the optically thin surface (Nordlund 1982), it is sufficient for the purpose of discussing the generic phenomenology of linear and turbulent convection, most classical convection models of supergranulation, as well as some aspects of the nonlinear dynamics observed in the simulations that will be reviewed in the next section. We then review different simple “linearized” thermal convection models of supergranulation (Sect. 4.3), and other possible fluid dynamical mechanisms involving nonlinear turbulent interactions and collective dynamics of smaller-scale turbulence (Sect. 4.4).
4.2 Rotating, MHD Rayleigh–Bénard convection
4.2.1 Formulation
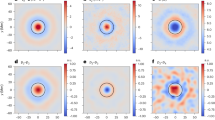
The simplest mathematical formulation of the dynamical problem of thermal fluid convection is the Rayleigh–Bénard problem describing convection between two differentially heated horizontal plates, each held at a fixed temperature. This model is derived under the Boussinesq approximation, which amounts to assuming that the flow is highly subsonic and that density perturbations \(\delta \rho \) to a uniform and constant background density \(\rho _o\) are negligible everywhere except in the buoyancy term \(\delta \rho \,{\mathbf {g}}\), where \({\mathbf {g}}=-g\mathbf {e}_z\) stands for the gravity (Chandrasekhar 1961). The equilibrium background state is a linear temperature profile with temperature decreasing from the bottom to the top of the layer. Anticipating discussions of the effects of rotation and magnetic fields on supergranulation, we consider the case of an electrically conducting fluid threaded by a mean vertical magnetic field denoted by \(\mathbf {B}_o=B_o\mathbf {e}_z\) and rotating around a vertical axis, with a rotation rate \(\varvec{\Omega }=\varOmega \,\mathbf {e}_z\). This set-up is pictured in Fig. 8.
In nondimensional form, the equations for momentum and energy conservation, the induction equation, the equations for mass conservation and magnetic field solenoidality read
where the momentum equation has been written in the rotating frame, lengths are measured in terms of the thickness of the convection layer d, times are defined with respect to the thermal diffusion time \(\tau _{\kappa }=d^2{/}\kappa \) (\(\kappa \) is the thermal diffusivity), the total magnetic field \(\mathbf {B}\) is expressed in terms of the Alfvén speed \(V_A=B_o{/}\sqrt{\rho _o\mu _o}\), temperature deviations \(\theta \) to the initial linear temperature profile are measured in terms of the background temperature difference \(\varDelta T=T_{\mathrm {top}}-T_{\mathrm {bot}}\) between the two horizontal plates enclosing the fluid in the vertical direction. Nondimensional velocity and pressure fluctuations are denoted by \(\mathbf {u}\) and p respectively. This set of equations is to be complemented by appropriate boundary conditions, most commonly fixed temperature or fixed thermal flux conditions on the temperature, no-slip or stress-free conditions on velocity perturbations, and perfectly conducting or insulating boundaries for the magnetic field. Note that the diffusive non-dimensionalization of the fluid equations used above is a matter of convention. This formulation is faithful to the historical development of the linear theory of rotating magnetoconvection pioneered by Chandrasekhar (1961), and has been central to the formulation of classical theories of many stellar convective phenomena ranging from supergranulation to sunspot dynamics (Thomas and Weiss 2008; Weiss and Proctor 2014).
Several dimensionless numbers appear in the equations above, starting with the Rayleigh number
where \(\alpha \) is the thermal expansion coefficient of the fluid defined according to \(\delta \rho {/}\rho _o=-\alpha \, \theta \). Here, \(N^2=\alpha \varDelta T g/d < 0\) is the square of the Brunt–Väisälä frequency (negative for a convectively unstable layer) and \(\tau _{\nu }=d^2{/}\nu \) is the viscous diffusion time, so the Rayleigh number measures the relative effects of the convection “engine”, buoyancy, and of the “brakes”, namely viscous friction and heat diffusion. The second important parameter above is the Chandrasekhar number
which is a measure of the relative importance of magnetic tension (\(\tau _A=d/V_A\) is the Alfvén crossing time) on the flow in comparison to magnetic diffusion (\(\eta \) is the magnetic diffusivity, \(\tau _\eta =d^2{/}\eta \) is the typical magnetic diffusion time) and viscous friction. The relative importance of the Coriolis force in comparison to viscous friction is measured by the Taylor number,
Finally, \(\textit{Pr}=\nu {/}\kappa \) and \(\textit{Pm}=\nu {/}\eta \), where \(\eta \) is the magnetic diffusivity, stand for the thermal and magnetic Prandtl numbers (see Sect. 2.2).
4.2.2 Linear theory
In the simplest non-rotating hydrodynamic case (\(\textit{Ta}=Q=0\), no induction), when the Rayleigh number is less than a critical value \({\textit{Ra}}_\mathrm{crit}\) that depends on the particular choice of boundary conditions, diffusive processes dominate over buoyancy: the hydrostatic solution is stable, i.e., any velocity or temperature perturbations decays. For \({\textit{Ra}}> Ra_\mathrm{crit} \), convection sets in as a linear instability and perturbations grow exponentially in the form of convection rolls or hexagons with a horizontal spatial periodicity \(\lambda \) comparable to the convective layer depth d in most cases. For stress-free, fixed temperature boundary conditions, \(Ra_\mathrm{crit}=27\pi ^4/4\simeq 657\) and \(\lambda _\mathrm{crit}/d=2\sqrt{2}\), while for rigid, fixed-temperature boundary conditions, \(Ra_\mathrm{crit}\simeq 1707\) and \(\lambda _\mathrm{crit}/d\simeq 2\) (the width of a individual convection roll is \(\lambda /2\)). Some effects of magnetic fields and rotation on linear stability are discussed in the next paragraphs.
4.2.3 Turbulent renormalization of transport coefficients
\({\textit{Ra}}\) and \(\textit{Ta}\) computed from microscopic transport coefficients (Sect. 2.2) are extremely large numbers in the SCZ. Convective dynamics, therefore, takes place very far from the actual convective linear instability threshold (\({\textit{Ra}}/Ra_\mathrm{crit}\sim 10^{15}\)–\(10^{20}\)). Therefore, using linear theory in this context to predict the dominant scale of convection, for instance, does not a priori seem appropriate. Is it possible to deal with this problem simply theoretically? A common argument is that the viscous, thermal and magnetic diffusive transport properties of the plasma at large scales are effectively set by the underlying vigorous turbulence driven in the highly supercritical regime, so that transport coefficients should be renormalized. In the context of large-scale solar convection, turbulent transport coefficients may for instance be estimated from the typical scale and velocity of granulation, \(\nu _T\sim L_GV_G\). The phenomenological rationale for doing this is that fluid systems driven strongly out-of-equilibrium react dynamically in a way that effectively brings them back close to their stability threshold by mixing the fluid in a way that smoothes out unstable free-energy gradients. If we accept that the renormalized turbulent \({\textit{Ra}}\) (and perhaps also Q and \(\textit{Ta}\)) should be close to its value at the stability threshold, then it makes sense to use the simpler mathematical toolkits of linear and weakly nonlinear analysis to describe the large-scale dynamics, rather than solve the full, strongly nonlinear problem.
As we are about to see, linear and weakly non-linear models of convection have proven very convenient and popular in the solar context, mostly because they are solvable. Howevever, keep in mind that they are at best only a quick, very approximate fix to make for the lack of a better available dynamical theory of turbulence and adequate numerics, and are ultimately fundamentally unsatisfying. In particular, their idealized nature implies that we have almost no control over their accuracy in the dynamical regimes of interest, apart from an order of magnitude estimate of turbulent transport coefficients. While these models may be suggestive of qualitative trends or effects, their actual predictive power is quite limited.
4.3 Laminar convection theories of supergranulation
Following its discovery in the 1950s and further studies in the 1960s, supergranulation was rapidly thought to have a convective origin, very much like the solar granulation. Many theoretical models relying on the basic “convection cell” phenomenology described in Sect. 4.2 have been devised to explain the apparently discrete-scales regime of the dynamics of the solar surface (namely the scales of granulation and supergranulation, but also that of mesogranulation, see Sect. 2.1.4). We will discuss a few flavours of these laminar convection models, keeping in mind the important caveats of the previous subsection.
4.3.1 Multiple mode convection
The simplest proposal for the emergence of a set of special scales is that of multiple steady linear or weakly nonlinearly interacting modes of thermal convection forced at different depths. The first theoretical argument of this kind is due to Simon and Leighton (1964), who suggested that supergranulation-scale motions corresponded to simple convection cells driven at the depth of \(\hbox {He}^{++}\) recombination and just advecting granulation-scale convection. Schwarzschild (1975) invoked an opacity break, \(\hbox {He}^{+}\) and H\({^+}\) recombinations as the drivers of supergranulation-scale convection. Simon and Weiss (1968) and Vickers (1971) suggested that deep convection in the Sun had a multilayered structure composed of deep, giant cell circulations extending from the bottom of the convection zone to 40 Mm deep, topped by a shallower circulation pattern corresponding to supergranulation. Bogart et al. (1980) attempted to match a linear combination of convective eigenmodes to the solar convective flux but did not find that supergranulation came out as a preferred scale of convection in this quasilinear framework.
Antia et al. (1981) argued that turbulent viscosity and diffusivity should be taken into account in linear calculations, as they alter the growth and scales of the most unstable modes of convection (but note that this assumption was already implicit in the laminar scenarios described above). In their linear calculation with microscopic viscosity and thermal diffusivity coefficients replaced by their turbulent counterparts, granulation and supergranulation show up as the two most unstable harmonics of convection. Calibrating the amplitudes of a linear superposition of convective modes to match mixing-length estimates of the solar convective flux in the spirit of Bogart et al. (1980), Antia and Chitre (1993) further argued that they could reproduce the main characteristics of the power spectrum of solar surface convection.
Gierasch (1985) devised a one-dimensional energy model for the upper solar convection zone from which he argued that turbulent dissipation takes place and deposits thermal energy at preferred depths, thereby intensifying convection at granulation and supergranulation scales. On this subject, we also mention the work of Wolff (1995), who calculated that the damping of r-modes in the Sun should preferentially deposit heat 50 Mm below the surface as a result of the ionisation profile in the upper solar convection zone. He then argued that this process might lead to convective intensification at similar horizontal scales.
4.3.2 Effects of temperature boundary conditions
A somewhat different phenomenological proposal was made by van der Borght (1974). He considered the case of steady finite-amplitude thermal convection cells in the presence of fixed heat flux boundary conditions imposed at the top and bottom of the layer, and showed that the convection pattern in this framework has much smaller temperature fluctuations than in the standard Rayleigh–Bénard model with fixed temperature boundary conditions. This is interesting in the context of the supergranulation problem, considering that intensity fluctuations at supergranulation scales are somewhat elusive (see Sect. 3.3).
Fixed heat flux boundary conditions naturally favour marginally stable convection cells with infinite horizontal extent compared to the layer depth, or convection cells with a very large but finite horizontal extent when a weak modulation of the heat flux is allowed for (Sparrow et al. 1964; Hurle et al. 1967; van der Borght 1974; Busse and Riahi 1978; Chapman and Proctor 1980; Depassier and Spiegel 1981). This case is, therefore, very different from the standard Rayleigh–Bénard case with fixed temperature boundary conditions, which gives rise to cells with aspect ratio of order unity. The interesting qualitative feature of this boundary-condition effect is that it naturally selects very flat, anisotropic convection cells and, therefore, alleviates the need to invoke convection at depths comparable to the typical horizontal scale of supergranulation.
4.3.3 Oscillatory convection and the relative role of dissipative processes
The discovery by Gizon et al. (2003) that supergranulation has wave-like properties (Sect. 3.4) paved the way for new theoretical speculations. In particular, it offered an opportunity to revive the interest for theories of oscillatory convection dating back to the work of Chandrasekhar (1961). Such a behaviour requires the presence of an extra restoring force acting on the convective motions driven by buoyancy. This force can be provided by Coriolis effects (rotation) or magnetic field tension. The existence of oscillatory solutions is known to depend very strongly on how various dissipative processes (viscous friction, thermal diffusion and ohmic diffusion) compete in the flow. This is usually measured or parametrized in terms of the thermal Prandtl number \(\textit{Pr}=\nu {/}\kappa \), where \(\nu \) is the kinematic viscosity and \(\kappa \) is the thermal diffusivity, the magnetic Prandtl number \(\textit{Pm}=\nu {/}\eta \), where \(\eta \) is the magnetic diffusivity, and the “third” Prandtl number \(\zeta =\eta {/}\kappa =\textit{Pr}{/}\textit{Pm}\). In the Sun, \(\textit{Pr}\sim 10^{-4}{-}10^{-10}\), \(\textit{Pm}\sim 10^{-2}{-}10^{-5}\) (see Sect. 2.2) and \(\zeta \ll 1\) at the photosphere.
4.3.4 Convection, rotation and shear
As mentioned in Sect. 3.4, supergranulation-scale flows are weakly influenced by the global solar rotation. In the presence of a vertical rotation vector, overstable oscillatory convection is preferred to steady convection provided that \(\textit{Pr}\) is small (Chandrasekhar 1961). Physically, an oscillation is only possible if inertial motions are not significantly damped viscously on the thermalization timescale of rising and sinking convective blobs. Busse (2004, 2007) suggested on the basis of a local Cartesian analysis that the drift of supergranulation could be a signature of weakly nonlinear thermal convection rotating about an inclined axis and found a phase velocity consistent with the data of Gizon et al. (2003), assuming an eddy viscosity prescription consistent with solar estimates (based on the typical sizes and velocity of granulation). Earlier work on the linear stability of a rotating spherical Boussinesq fluid layer heated by internal heat sources showed that the most rapidly growing perturbations are oscillatory and form a prograde drifting pattern of convection cells at low Prandtl number in high Taylor number regimes corresponding physically to large rotation (Zhang and Busse 1987).
Related to this issue is the influence of differential rotation, or shear, on supergranulation. Green and Kosovichev (2006) considered the possible role of the solar subsurface shear layer (Schou et al. 1998) by looking at the effect of a vertical shear flow on the onset of convection in a strongly stratified Cartesian layer using linear theory, and found that steady convective modes become travelling when a weak shear is added. Earlier studies had found that this behaviour is possible either at low \(\textit{Pr}\) (Kropp and Busse 1991) or if some generic form of top-down symmetry breaking is present in the system (Matthews and Cox 1997). As a linear shear flow alone does not break this symmetry, it is likely that density stratification plays an important role in obtaining the result. Green and Kosovichev (2006) also found that the derived phase speeds of the travelling pattern were significantly smaller than those inferred from the observations by Gizon et al. (2003).
Note that the relative orientations and amplitudes of rotation, shear and gravity are fundamental parameters in the sheared rotating convection problem. The results (e.g., the pattern phase velocity and wavelength) of local Cartesian theoretical models of supergranulation incorporating solar-like rotation effects are, therefore, expected to depend significantly on latitude. This is a problem with local laminar models of sheared rotating convection, because in practice there is no conclusive observational evidence for a very strong latitudinal dependence of the scales or propagation of supergranulation (see Sect. 3.4). Laminar spherical models do not necessarily suffer from this problem to the same extent, as they predict global modes with a well-defined phase velocity.
4.3.5 Convection and magnetic fields
The presence of magnetic fields in convection can have diverse consequences, the most obvious of which is a coercive effect on convective motions through magnetic tension. Such a coercive effect on the scale of supergranulation was actually discussed very quickly after its discovery. Much of the discussion at the time involved an equipartition argument (e.g. Parker 1963, 1974; Simon and Leighton 1964; Clark and Johnson 1967; Simon and Weiss 1968; Frazier 1970, 1976). Many flux concentrations in the network are actually well above equipartition with the supergranulation flow field. Using the typical value for the velocity field at supergranulation scales given in Sect. 3.2.3 and an order of magnitude estimate for the plasma density in the first 1 Mm below \(\tau =1\), we see that for the kinetic and magnetic energy densities to be comparable in the supergranulation peak range, an rms magnetic field strength of 100 G is required:
Hence, the magnetic energy density of strong network elements with kG fields appears to be roughly 100 times larger than that of the supergranulation flow. This result first suggests that supergranulation-scale motions cannot alone generate these flux concentrations. Partial evacuation of density and vigorous localized motions such as granulation-scale motions seem to be required to obtain superequipartition fields (Webb and Roberts 1978; Spruit 1979; Spruit and Zweibel 1979; Unno and Ando 1979; Proctor 1983; Hughes and Proctor 1988; Bushby et al. 2008). Now, the question is whether such strong, but very localized and inhomogeneous fields can have a strong dynamical impact on the flow. Obviously, numerical simulations provide the best way to test this, but some “effective” phenomenological theories have also been considered in this context. An interesting proposal of this kind is due to Longcope et al. (2003), whose (theoretical) calculations suggest that the dynamical feedback of a distribution of magnetic fibrils embedded into the solar plasma physically translates into a large-scale viscoelasticity.
The forementioned idea of large-scale convection with fixed heat flux boundaries was also further carried out with the addition of a uniform vertical magnetic field threading the convective layer. Contrary to the hydrodynamic case for which zero-wavenumber neutral (zero growth-rate) solutions are preferred linearly, convection cells with a long but finite horizontal extent dominate in the magnetised case, provided that the magnetic field exceeds some threshold amplitude. The horizontal scale of the convection pattern in this model is controlled directly by the typical strength of the magnetic field. Murphy (1977) was the first to suggest that this model might be relevant to supergranulation, and the linear problem in the Boussinesq approximation was solved by Edwards (1990). Rincon and Rieutord (2003) and Rincon (2004) further solved the fully compressible linear problem numerically and revisited it in the context of supergranulation. Using typical solar values as an input for their model parameters (density scale height, turbulent viscosity etc.), it was shown that the average magnetic field strength (measured in the nondimensional equations by the Chandrasekhar number Q) required for compressible magnetoconvection with fixed heat flux to preferentially “select” supergranulation-scale convection was a rather reasonable 100 G (Sect. 3.5.1).
Magnetoconvection in a uniform vertical magnetic field is also known to preferentially be oscillatory at onset provided that \(\zeta \ll 1\) (e.g., Chandrasekhar 1961; Proctor and Weiss 1982), a phenomenon known as magnetic overstability. This is also possible for non-vertical magnetic fields (e.g., Matthews et al. 1992; Hurlburt et al. 1996; Thompson 2005, and references therein). Physically, field lines can only be bent significantly by convective motions and act as a spring if they do not slip too much through the moving fluid, which requires, in this context, that the magnetic diffusivity of the fluid be small enough in comparison to its thermal diffusivity. Since \(\zeta \ll 1\) in the quiet photosphere, oscillatory magnetoconvection represents a possible option to explain the wavy behaviour of supergranulation. On this topic, Green and Kosovichev (2007) built on the work of Green and Kosovichev (2006) by considering the linear theory of sheared magnetoconvection in a uniform horizontal (toroidal) field shaped by the subsurface shear layer. They found that the phase speed of the travelling waves increases in comparison to the hydrodynamic case studied by Green and Kosovichev (2006) and argue that the actual phase speed measured by Gizon et al. (2003) can be obtained for a reasonable uniform horizontal field strength of 300 G.
Yet another possible magnetic feedback mechanism is provided by the interactions between magnetic fields and radiation. Observations, theory and simulations suggest that magnetic concentrations tend to depress the opacity surfaces of the photosphere, which in turn is thought to channel radiation outwards (Spruit 1976; Vögler 2005), and it has been argued that strong magnetic concentrations at network scales may thereby alter the convection process at supergranulation scale and consequently single this scale out in the energy spectrum.
4.3.6 Dissipative effects
Finally, it is known both theoretically and experimentally that even in the absence of any effect such as magnetic couplings, rotation or shear, the value of the thermal Prandtl number can significantly affect the scales and time evolution of convection, both in the linear and nonlinear regimes. Its value notably controls the threshold of secondary oscillatory instabilities of convection rolls (Busse 1972). At very low Prandtl numbers, Thual (1992) showed that a rich dynamical behaviour associated with the interactions between the primary convection mode and the secondary oscillatory instability takes place close to the convection threshold. This includes travelling and standing wave convection. Overall, most theoretical studies of supergranulation to date have been either ideal (no dissipation) or for \(\textit{Pr}\sim \textit{Pm}\sim 1\). For this reason, some important thermal effects relevant to supergranulation-scale convection may well have been overlooked until now. Note that this limitation also applies to most numerical simulations.
4.4 Large-scale instabilities, inverse cascades and collective interactions
A few other qualitative arguments and models have been put forward to explain the origin of supergranulation besides thermal convection scenarios. The generic proposal of these arguments is that supergranulation could emerge from collective nonlinear interactions of small-scale structures such as granules, for instance through a large-scale instability reminiscent of inverse-cascade scenarios in flows with specific spatial symmetries.
4.4.1 Rip currents and large-scale instabilities
The first work along this line of thought is due to Cloutman (1979), who proposed to explain the origin of supergranulation using the physical picture of rip currents on the beaches of oceans: the repeated breaking of waves on beaches induces rip currents flowing parallel to the coast line. On the Sun, he qualitatively associated breakers with the rising flows of granules breaking into the stably stratified upper photosphere. This idea provides an illustration of a broader phenomenological suggestion by Rieutord et al. (2000) that the collective interaction of solar granules may give rise to a large-scale instability at supergranulation scales. The idea finds its root in theoretical work on energy localization processes in nonlinear lattices (Dauxois and Peyrard 1993) and large-scale instabilities (“negative eddy viscosity instabilities”) of flows with particular spatial symmetries, such as the Kolmogorov flow (Meshalkin and Sinai 1961; Sivashinsky and Yakhot 1985) or the decorated hexagonal flow (Gama et al. 1994). Asymptotic theory on simple prescribed vortical flows can be performed under the assumption of scale separation (Dubrulle and Frisch 1991) between the basic periodic flow and the large-scale instability mode. In such theories, the sign and amplitudes of the turbulent viscosities is found to be a function of the Reynolds number. For instance, an asymptotic theory based on a large aspect ratio expansion was developed by Newell et al. (1990) for thermal convection. In this problem, large-scale instabilities take on the form of a slow, long-wavelength modulation of convection roll patterns. Their evolution is governed by a phase diffusion equation with tensorial viscosity. In the case of negative effective parallel diffusion (with respect to the rolls orientation), the Eckhaus instability sets in, while the zigzag instability is preferred in the case of negative effective perpendicular diffusion. In relation with our earlier discussion of the renormalization of transport coefficients, note that phase-instabilities like this one provide a very clear and quantitative example as to why postulating a generic positive turbulent diffusion to parametrize the effects of small-scale motions on large-scale dynamics is not always appropriate.
4.4.2 Plume and fountain interactions
Yet another phenomenological dynamical argument put forward to explain the origin of supergranulation is that the pattern results from the collective interaction of “plumes” (buoyantly driven rising or sinking flows). Plumes can be either laminar or turbulent, however, turbulent structures have by far received most of the attention because of their numerous applications (see Turner 1986). The first numerical simulations of strongly stratified convection at high enough Reynolds numbers (e.g., Stein and Nordlund 1989; Rast and Toomre 1993) quite clearly showed the importance of vigorous sinking plumes in turbulent convection, and the results prompted Rieutord and Zahn (1995) to study the fate of these downdrafts in some mathematical detail. Unlike the downflows computed in early simulations, solar plumes are turbulent structures, which entrain the surrounding fluid (see Fig. 2). As Rieutord and Zahn (1995) pointed it out, the mutual entrainment and merging of these plumes naturally leads to an increase of the horizontal scale as one proceeds deeper.
Toy models have been elaborated in this context to investigate the properties of “n-body” dynamical advection-interactions between plumes. For instance, Rast (2003b) developed a model in which a two-dimensional flow described by a collection of individual divergent horizontal flows (“fountains”) mimicking granules is evolved under a simple set of rules governing the merging of individual elements into larger fountains and their repulsion [this description was inspired by an earlier kinematic model of flows in exploding granules by Simon et al. (1991)]. For some parameters typical of the solar granulation “fountains”, he argued that the clustering scales of the flow after a long evolution of the system resembled that of mesogranulation and supergranulation. A similar model incorporating simplified magnetic field dynamics was designed by Crouch et al. (2007). They observed some magnetic field organisation and polarity enhancement at scales similar to that of supergranulation in the course of the evolution of the model. While they may help to form an intuition of large-scale dynamical interactions in turbulent convection, the main caveat with models like this, of course, is that they are not rooted in the actual fluid dynamical equations.
5 Numerical modelling
Our understanding of turbulent convection in general, and solar convection in particular, has made huge progress over the last 40 years thanks to numerical simulations. The numerical study of solar convection was limited to granulation scales for a long time, but there has finally been some important progress on supergranulation-scale dynamics over the last 15 years. The first part of this section provides an introduction to the potential and limitations of numerical modelling, and describes a few important results on the Rayleigh–Bénard problem and granulation-scale solar convection relevant to our discussion of supergranulation. We then review the main achievements (and difficulties) of numerical simulations of supergranulation-scale dynamics, and discuss their implications for our current understanding of the problem.
5.1 Introduction to convection simulations
5.1.1 General potential and limitations
Numerical simulations are the most important tool that we have to probe and explore the nonlinear dynamics of hydrodynamic turbulent flows and other complex fluid physics such a radiation hydrodynamics or MHD. They are not a panacea though and face many limitations of their own, including in the solar physics context. In particular, the finite capacities of computers make it completely impossible for any type of simulation, even today, to approach dissipative flow regimes characteristic of the solar surface and to span all the range of time and spatial scales involved in the problem. It should, therefore, be constantly kept in mind when discussing numerical simulations of solar convection (and more generally of laboratory and astrophysical turbulence) that we are not actually “simulating the Sun”, but rather a fairly quiet toy model of it. This being said, large-enough simulations can give us important insights into semi-quantitative trends about the nonlinear dynamics, statistics and self-organization of turbulent flows, which is exactly the kind of information needed to address the supergranulation problem.
5.1.2 Turbulent Rayleigh–Bénard convection versus Navier–Stokes turbulence
Despite its simplicity compared to the actual strongly stratified solar convection problem (which also involves radiation), the problem of incompressible, non-rotating turbulent convection in the Rayleigh–Bénard framework introduced in Sect. 4.2 is very important in the context of this review, because it contains both buoyancy effects and all the nonlinearities underlying the typical turbulent dynamics of a fluid. Numerical simulations of this problem can, therefore, tell us a lot about the generic dynamics of turbulent convection in the absence of any other diverting physical effect.
The Boussinesq equations are very similar to the forced Navier–Stokes equations: the main difference between the two is that the forcing term in the Rayleigh–Bénard problem is not an external body force, but is determined self-consistently from the time-evolution of the temperature fluctuations. Both experimental and numerical evidence at order one thermal Prandtl number strongly suggest that the basic phenomenology of Rayleigh–Bénard turbulence at vertical and horizontal scales smaller than the vertical extent of the domain considered should be similar to that of Navier–Stokes turbulence in the inertial-range (Rincon 2006; Lohse and Xia 2010; Kumar et al. 2014). In particular, the dynamics becomes increasingly isotropic at smaller scales. To a very good first approximation, the numerical issues and requirements to simulate the Rayleigh–Bénard problem at very high Rayleigh numbers are, therefore, the same as those pertaining to the simulation of forced Navier–Stokes turbulence at high Reynolds numbers. In particular, a strong scale separation between the vertical size of the numerical domain and the grid size is required to simulate the turbulent cascade properly. High-resolution simulations using spectral methods (Canuto et al. 2006) remain the most adequate tool to reach highly-supercritical regimes. The highest-supercritical simulations to date (\({\textit{Ra}}{/}{\textit{Ra}}_\mathrm{crit}\sim 10^{11}\), see Verzicco and Camussi 2003; Amati et al. 2005; Lohse and Xia 2010) require numerical spectral resolutions of the order of \({\sim }\,512^3\) to \({\sim }\,1000^3\) grid points to simulate turbulent convection in numerical domains of comparable vertical and horizontal size (order one aspect ratios). This is significant even by today’s computing standards. An extra difficulty of the turbulent Rayleigh–Bénard problem, compared to standard Navier–Stokes turbulence in a periodic box, is the need to resolve very fine thermal boundary layers at the top and bottom boundaries. These transition layers scale as a fractional power of \({\textit{Ra}}{/}{\textit{Ra}}_\mathrm{crit}\) and, therefore, become increasingly difficult to resolve at high \({\textit{Ra}}\).
A critical implication of these strong numerical constraints in the context of supergranulation modelling is that simulations of turbulent convection at very high Rayleigh numbers are still restricted to fairly low aspect ratios (the ratio between the horizontal and vertical extents of the domain), typically one-half or one. Simulations of turbulent convection dynamics at horizontal scales signicantly larger than the vertical size of the domain are possible but currently limited to mildly supercritical, soft turbulence regimes, typically \({\textit{Ra}}\sim 10^{5}\)–\(10^7\) (\({\textit{Ra}}{/}{\textit{Ra}}_\mathrm{crit}\sim 10^{3}\)–\(10^5\)). Most simulations are also currently limited to Prandtl numbers of order unity, which makes it difficult to investigate the effect of scale separations between the various dissipation scales of the problem.
5.1.3 Solar convection models
Numerical simulations of astrophysical convection are similar in many ways to Rayleigh–Bénard simulations and are, therefore, plagued by the same numerical limitations. But they also include a variety of extra physical effects relevant to the particular solar context, which are not present in the Rayleigh–Bénard, adding a further layer of complexity. This includes strong vertical density stratification, mild compressibility (up to Mach number of order one), radiative transfer in the surface layers, and the lack of a well-defined rigid bottom boundary. The first direct numerical simulations of strongly stratified convection date back from the 1970s (Graham 1975), and the first numerical study of stratified convection incorporating radiative transfer effects is due to Nordlund (1982). Since then, numerical studies of astrophysical convection have split into two “families” of models that define the main trends in the field nowadays.
“Idealized simulations” rely on simple models of stratified atmospheres such as polytropes, and implement the standard incompressible, anelastic or compressible fluid equations, including explicit viscosity, thermal and magnetic diffusivities in a domain usually bounded by walls in the vertical direction (just as in the Rayleigh–Bénard problem). These simulations do not explicitly incorporate radiative transfer but instead rely on thermal diffusion in the entropy equation to model its effects. This is of course not totally appropriate in the optically thin surface layers, and makes it difficult to directly compare the results with solar observations of light intensity. Idealized simulations, on the other hand, are usually very good at describing the nonlinear dynamics in highly-supercritical regimes. They often rely on numerical spectral methods, which remain the gold standard in simulations of incompressible homogeneous turbulence (Vincent and Meneguzzi 1991; Ishihara et al. 2009), but also face a few problems when it comes to the simulation of compressible flows: for instance, they cannot capture shocks easily. This is not a major issue at mild \({\textit{Ra}}\) where the dynamics is quite subsonic, but becomes a problems as \({\textit{Ra}}\) increases (Cattaneo et al. 1991). A popular approach used in global spherical convection simulations (Clune et al. 1999) is to solve the anelastic equations instead of the fully compressible problem. This approach filters out sound waves, thereby removing a bunch of numerical problems and constraints.
“Realistic” simulations of solar convection (Nordlund et al. 2009), on the other hand, aim at maximum astrophysical realism by taking into account not only the stratified flow dynamics but also other important physical processes in the solar context such as radiative transfer, huge solar-like density stratifications and realistic equations of state including Helium and Hydrogen ionisations. Unlike idealized simulations, they usually ignore the explicit physical dissipative processes like viscosity and instead rely on grid dissipation or hyper-dissipation to avoid numerical blow-up. These features, coupled to the use of “handmade” open boundary conditions, makes this kind of simulations more realistic to solar physics studies, in the sense that some of the physics simulated is closer to that in the SCZ, and their results can be directly compared with solar observations. However, grid-based methods also generically offer less control over dissipative processes and are usually more dissipative for a given numerical resolution than spectral methods in simulations of homogeneous turbulence characterized by space-filling fine-scale gradients. This limitation does not appear to be an important issue for simulations of solar granulation for which thermal radiation, which is well-accounted for in such simulations, plays an overwhelming dynamical role. But, as we shall see in Sect. 5.2.1, understanding the large-scale dynamics requires to understand not only the thermal physics, but also how dynamical nonlinearities play out. Idealized simulations offer an exact control over the supercriticality of the system and can reach slightly more asymptotic regimes at comparable resolution. A second potential problem of realistic simulations is that they could be in the wrong dissipative regimes, simply because they do not take into account rigorously the disparity of time and length scales of different dissipative processes. This may notably be an issue when addressing MHD effects in solar convection.
5.2 Small-scale simulations
We will now review a few turbulent convection simulations in “small” order-one aspect ratio domains but whose results are also directly relevant to the question of supergranulation-scale dynamics.
5.2.1 Turbulent Rayleigh–Bénard convection
Turbulent convection dynamics in increasingly supercritical Rayleigh–Bénard simulations in a slender cylindrical cell of aspect ratio one-half (for \(\textit{Pr}=0.7\) and up to \({\textit{Ra}}=10^{11}\)) is illustrated in Fig. 9. The figure shows temperature snapshots in vertical planes and underlines two very important points. First, there is a very marked evolution of the dynamical pattern from moderate to very large \({\textit{Ra}}\). An asymptotic large \({\textit{Ra}}\) regime is not attained even at \({\textit{Ra}}=10^{11}\). Such a value is way smaller than the \({\textit{Ra}}\) in the SCZ, but also way larger than \({\textit{Ra}}\) in any current simulation of solar convection! This illustrates the problem of accessing asymptotic dynamical regimes in numerical simulations. Second, two large-scale circulations emerge from the small-scale turbulent fluctuations as \({\textit{Ra}}\) increase. These so-called thermal winds are also observed in laboratory experiments on convection (e.g., Krishnamurti and Howard 1981; Sano et al. 1989; Niemela et al. 2001; Xi et al. 2004, and references therein). As we will see in Sect. 5.3.3, these structures are essentially buoyant but they do not necessarily correspond to the most unstable linear convection mode in the problem. They are instead a consistent outcome of the nonlinear self-organization of the buoyant dynamics. It is clear that these large-scale thermal winds are strongly constrained laterally in low aspect ratio geometries, and are likely to take more horizontal space in larger aspect ratio domains. This is a very important point in the context of supergranulation, and will also be discussed in Sect. 5.3.3.

Image reproduced with permission from Verzicco and Camussi (2003), copyright by CUP
Snapshots of temperature fluctuations in a vertical plane, from numerical simulations of Rayleigh–Bénard convection in a slender cylindrical cell at \(\textit{Pr}=0.7\) and Rayleigh-numbers a \(2\times 10^7\), b \(2\times 10^9\), c \(2\times 10^{11}\).
5.2.2 Stratified convection simulations at granulation scales
The first realistic three-dimensional simulation of small-scale solar surface convection of Nordlund (1982) mentioned earlier was followed by improved version at higher resolutions (Stein and Nordlund 1989, 1998). These studies primarily focused on understanding the thermal structure and observational properties of granulation. Stein and Nordlund (1989) notably found that convective granulation-scale plumes in a stratified atmosphere merged into larger plumes at larger depth, producing increasingly large convective patterns deeper and deeper. The results also demonstrated the influence of stratification on the horizontal extent of granules and on the typical plasma velocity within granules.
Early idealized two-dimensional simulations of stratified convection by Graham (1975), Chan et al. (1982) and Hurlburt et al. (1984) had already revealed an asymmetry between up and downflows in two-dimensional simulations of compressible convection in a stratified medium. The physical origin of this phenomenon, known as buoyancy braking, was explicited by Massaguer and Zahn (1980). This kind of simulations were later expanded to Rayleigh numbers up to 1000 times supercritical in two dimensions (Chan and Sofia 1989, 1996), and to three dimensions by Cattaneo et al. (1991). The results of these early idealized small-scale simulations are qualitatively in line with those of Stein and Nordlund (1989) as far as the deep, large-scale dynamics is concerned. This suggests that an explicit modelling of physical processes such as radiative transfer is not essential to study the turbulent dynamics and scale-interactions. These simulations also showed that the presence or absence of a solid bottom wall may be important, as the former tends to generate more shear and large-scale recirculations in deep layers.
Readers interested in the particular problem of granulation-scale convection modelling will find much more detailed information in the reviews by Nordlund et al. (2009) and Asplund et al. (2009). As explained earlier, the surface features of granulation-scale convection are much better understood with realistic simulations which are specifically tailored for this purpose. However, these simulations are also very dissipative, and it still remains a bit unclear whether this kind of modelling can faithfully describe turbulent convection in strongly nonlinear, supercritical regimes typical of the large-scale dynamics of in the SCZ.
5.3 Large-scale simulations
5.3.1 Global versus local simulations
In the 1980s and 1990s, global (spherical) and local numerical simulations of solar-like convection were respectively limited to the study of global-scale convection dynamics (giant cells and larger) and granulation-scale dynamics. The numerical study of the dynamics at scales larger than that of individual granules, but smaller than global solar scales, only became possible in the early 2000s. It is interesting in retrospect to recall as a short anecdotal digression the following optimistic citation extracted from an article of Nordlund (1985): “There is a need for numerical simulations at the scale of supergranulation [...] This is probably feasible with present day computers and numerical methods.”
There are two different possible approaches to the simulation of supergranulation-scale dynamics: local Cartesian simulations (taking a small patch of the solar surface and ignoring curvature effects) and global simulations in a spherical shell. In the local approach, the horizontal box size of the largest simulations to date (i.e., the largest horizontal scale of the simulations) is roughly a few times the horizontal scale of supergranulation (Lord et al. 2014; Cossette and Rast 2016). While numerical resolutions of 512–1024 grid points in each spatial direction are now routinely achievable, simulating the dynamics at 100 Mm horizontal scales still requires to somewhat sacrifice the resolution of dynamical processes at scales of the order \({\sim }\,100\) km only mildly smaller than that of granulation, and way above the actual viscous dissipative cut-off at the solar surface in any case. Note also that the dynamics at supergranulation scales in this kind of set-up remains slightly constrained by (usually periodic) lateral boundary conditions.
Global spherical simulations can model the dynamics at scales significantly larger than supergranulation, but their problem is that the smallest scales included in even the latest-generation simulations of this kind are of the order of a few Mm, only mildly smaller than scale of supergranulation. Hence, the supergranulation-scale dynamics in these simulations is much more dissipative than in local simulations. This is a significant issue because, as shown in Sect. 3.2, the turbulent spectrum of solar surface convection shows that supergranulation is located at the large-scale edge of the injection range of turbulence, not in the dissipation range. The dominant physical processes in these different regimes are obviously very different. Another potentially very important weakness of global simulations in this context is the usually very crude way in which they deal with the thermodynamic surface boundary layer at the photospheric transition. As we shall see, the thermodynamic structure in the first few Megameters below the surface now increasingly appears to play a significant role in setting the horizontal scale of supergranulation-scale dynamics.

Image reproduced with permission from DeRosa et al. (2002), copyright by AAS
Radial velocity snapshots at various depths in global simulations of convection in shallow spherical shells, down to supergranulation scales.
5.3.2 Global spherical simulations
Global spherical simulations of turbulent convection started to appear more than 40 years ago. The first numerical model of 2D Boussinesq convection in a spherical shell is due to Gilman (1975), who used it to study the influence of rotation on convection, the problem of large-scale circulations in the solar convection zone, and that of the interactions between supergranulation and rotation (e.g., Gilman and Foukal 1979). Spherical convection modelling was soon extended to the anelastic approximation by Gilman and Glatzmaier (1981) and Glatzmaier (1984, 1985), and to the fully compressible fluid equations by Valdettaro and Meneguzzi (1991). Most simulations in spherical geometry use the expansions of the fields on spherical harmonics up to a given resolution \(L_\mathrm{max}\) (the \(\ell \) order of the smallest scale spherical harmonic). The early simulations were restricted to fairly laminar regimes and very large solar scales, namely \(L_\mathrm{max}=32\) or, in terms of smallest resolved horizontal scale, \(\lambda = 2\pi R_\odot /L_\mathrm{max} \simeq 130\,\mathrm{Mm}\), which is much larger than the scale of supergranulation (36 Mm, or \(\ell =120\), see Sect. 3.2).
The first dedicated attempt to study supergranulation-scale dynamics through global spherical simulations is due to DeRosa (2001), DeRosa and Toomre (2001) and DeRosa et al. (2002), who carried out idealized three-dimensional hydrodynamic simulations in thin spherical shells with a horizontal resolution of \(L_{\max }=340\), corresponding to a smallest resolved horizontal scale of 13 Mm; they used the popular high-resolution three-dimensional spherical simulations ASH code (Clune et al. 1999). The simulations exhibit structures at scales larger and comparable to that of supergranulation (see Fig. 10). However, it was difficult to diagnose why supergranulation scales would play a special role (except for being in the dissipative range) in these simulations, and the fact that the grid was so close to the supergranulation scale prevented them from drawing any robust conclusion regarding the physical origin of supergranulation. Simulations of solar-like convective shells by Miesch et al. (2008) at higher spherical harmonics resolution (\(L_{\max }=682\)) have further revealed the presence of intense cyclonic downdrafts at scales comparable to those of giant cells, a very likely signature of interactions between large-scale convection and rotation such as described in Sect. 3.4. Looking at the spectrum of these simulations though, it is clear that supergranulation scales are still located close to the dissipative range.
a Radial velocity, b radial (vertical) velocity spectrum and c latitudinal (horizontal) velocity spectrum at \(r/R_\odot =0.99\) (case H0 in black) in global simulations (Hotta et al. 2014) (cases H1 and H2 only extend up to \(r/R_\odot =0.96\) and have smaller density contrasts). The qualitative behaviour of both spectra is very similar to the surface radial and spheroidal spectra derived from observations by Rincon et al. (2017) (black and blue in Fig. 4b)
Even at the highest resolutions that can be achieved today in global simulations, not all the relevant dynamical range required to quantitatively address the problem of the dynamics in the supergranulation to subgranulation range can be simulated adequately. However, there has been some qualitative progress in that direction recently. A new set of numerical simulations of non-rotating convection by Hotta et al. (2014) with a grid resolution of just a few Mm appears to resolve vigorous convective dynamics at scales smaller than supergranulation. Some results appear to be in good qualitative agreement with observations (Fig. 11). For instance, the kinetic energy spectra of the different flow components close to the surface appear to follow the exact same trends as the observational trends reported by Rincon et al. (2017), with the horizontal velocity spectrum peaking at large scales and the radial velocity spectrum increases monotonically down to the grid scale, with just a kink at the peak scale of horizontal motions. Convective motions in these simulations extend down to depths of at least \(0.2\,R_\odot \), with the radial velocity progressively increasing and peaking at a similar scale as horizontal motions at increasing depths. The results also strongly suggest that the very strong anisotropy of supergranulation peak-scale flows observed at the surface is a surface effect shaped by the strong subsurface pressure and density gradients, and is somehow only the tip of the subsurface convection iceberg.
An important difference with observations in the simulations of Hotta et al. (2014), though, is that the peak scale of horizontal motions is a few hundred Mm, significantly larger than that of supergranulation. We will soon encounter this scale-mismatch issue again in local simulations, and will subsequently discuss different physical factors possibly affecting the peak scale of the spectrum.
5.3.3 Large-scale turbulent convection in local Cartesian simulations
Large-scale local Cartesian simulations are also limited in terms of dynamical regimes, but not quite as much as global ones when it comes to the study of the dynamics at scales comparable to or smaller than supergranulation. On current supercomputers, this family of models can typically describe the nonlinear dynamics from scales slightly larger than supergranulation scales (100 Mm) to subgranulation scales (typically 10–100 km).
A strong feature of all three-dimensional, large-scale idealized simulations using bottom and top wall boundaries is a pattern of vigorous large-scale dynamical circulations, topped by a smaller granulation-like pattern in the surface thermal boundary layer. This is shown in Fig. 12 (left). These circulations are very likely the counterpart in large-scale simulations of the thermal winds of aspect ratio unity seen in simulations and experiments (Sect. 4.2). They were quickly dubbed “mesoscale structures” in the solar physics context when they were first reported, because their typical scale was larger than the scale of the granulation pattern, yet their peak size was not quite as large as that of supergranulation (relative to granulation). This was also a period when the question of the existence of mesogranulation (Sect. 2.1.4) as a separate physical phenomenon was widely debated. As we will shortly see, it now seems increasingly clear that these structures are to a large extent the counterpart of supergranulation in the particular regime and geometry of these simulations. These dynamical structures were first reported by Cattaneo et al. (2001) in large-scale Boussinesq simulations with an aspect ratio up to 20 and a Rayleigh number \(5\times 10^5\) (roughly 1000 times supercritical), and were also later observed in several other Boussinesq studies (Hartlep et al. 2003; Parodi et al. 2004; von Hardenberg et al. 2008; Pandey et al. 2018). Their typical correlation time in large-aspect ratio simulations is much longer than the typical turnover time in the granulation boundary layer, and their kinetic energy is also much larger than that contained in the superficial granulation-scale motions. Cattaneo et al. (2001), in the spirit of the turbulence concepts described in Sect. 4.4, speculated that they may be the result of a nonlinear inverse cascade or large-scale secondary instability of smaller-scale convective flows.
Comparison between horizontal temperature maps in an idealized simulation of large-scale compressible convection in a stratified polytropic atmosphere (left, aspect ratio 42, see Rincon et al. (2005) for details) and horizontal temperature maps in a realistic simulation of large-scale solar-like convection (right, aspect ratio 10, see Rieutord et al. (2002) for details). Top: \(z=0.99\,d\) and at optical depth \(\tau =1\) respectively (surface). Middle: half-depth of the numerical domain. Bottom: bottom of the numerical domain. The emergence of the granulation pattern in the surface layers is clearly visible in both types of simulations, on top of a larger-scale mesoscale dynamics extending down to deeper layers
The nonlinear dynamics and origin of these structures was investigated in more detail by Rincon et al. (2005) using fully compressible idealized simulations with rigid walls, \(Ra=3\times 10^5\) and a modest density stratification, but with a very wide aspect ratio \({\sim }\,42\). The main conclusion of the analysis was that these large-scale flows dominate the kinetic energy spectrum and are effectively driven by thermal buoyancy. The organization of such powerful flows at such scales was found to be the result of a dynamical interplay between the linear convection injection process and turbulent cascade and transport processes. What happens is the following (Rincon 2004; Rincon et al. 2005): there is initially a broadband spectrum of linearly unstable convection modes (\({\sim }\,100\)) in the simulation, but in the early stages kinetic energy growth is much faster at the most unstable scales of the system, whose horizontal scale is comparable to the vertical scale of the system. This is of course expected from linear analysis. Once in the nonlinear regime, however, the injection of kinetic energy through thermal buoyancy is observed to continuously drift to larger horizontal scales, with nonlinear interactions cascading down the injected power down to smaller scales. This dynamics is illustrated in Figs. 13 and 14. Physically, the smaller-scale turbulence associated with the early dynamical saturation of the most unstable modes acts as a turbulent diffusion for the still-developing larger-scale structures. Ultimately, the dominant scale appears to be set by a balance between the rate of energy injection by buoyancy (set by the Rayleigh number) and the rate of turbulent dissipation associated with all the saturated smaller-scale modes. Interestingly, both laminar “quasi-linear” convection and nonlinear interactions arguments described in Sect. 4 are phenomenologically relevant to this detailed numerical analysis, albeit not in a straightforward way. In particular, while nonlinear interactions play a big role in the dynamics, the large-scale structures are definitely not driven by them and are, therefore, not due to inverse cascading or large-scale nonlinear instability.

Image from Rincon (2004), Chap. 4.3, p. 85
From left to right and top to bottom: dynamical evolution of the spectra of temperature fluctuations \(E_\theta (k)\) and kinetic energy fluctuations E(k) as a function of time and integer horizontal wave number k and time t (measured in vertical thermal diffusion units) in the large-aspect ratio idealized simulation of turbulent convection with mild density stratification shown in Fig. 12 (left), \(Ra=3\times 10^5\) and \(Pr=0.3\). \(k=1\) corresponds to the horizontal size of the domain and \(k=42\) to the vertical size of the domain. The peak scale of the spectra (\(k\simeq 7\) towards the end of the simulation, much larger than the vertical size of the domain) correspond to the large-scale thermal structures visible in Fig. 12.

Image reprpoduced with permission from Rincon et al. (2005), copyright by ESO
Spectral-space energy budgets as a function of integer horizontal wavenumber k in the large-aspect ratio simulations of turbulent convection described in Figs. 12 (left) and 13. Here, F(k) is the buoyancy forcing term, T(k) is the nonlinear transfer (cascade) term, and D(k) is the dissipation term. The dominant balance in the peak injection range is between the positive buoyancy forcing term and the negative nonlinear transfer term, indicating that the large-scale dissipative structures seen in Fig. 12 (left) are powered by buoyancy. This injected power is dissipated by turbulent viscous dissipation mediated through spectral space by smaller-scale turbulent convective motions.
As striking as it is in idealized simulations, the dynamics described above, including the observation of a kinetic energy peak at scales much larger than the most unstable linear scales, was much less obvious in the first corresponding largish-aspect ratio realistic simulations. An increase of the typical horizontal size of convective structures with depth was for instance observed in aspect ratio 10 “realistic” hydrodynamic simulations by Rieutord et al. (2002) (Fig. 12 (right)), but no strong evidence was reported for particularly vigorous flows at scales larger than that of granulation close to the surface (but only a spectrum of light intensity at the surface, peaking at granulation scale, was documented). Several possible explanations have been put forward for this seeming discrepancy: one is that the small-scale dynamics is not vigorous enough in these simulations, or is simply sufficiently different given the presence of radiative transfer that the dynamics is somewhat different from that in idealized simulations. Another possibility is that boundary conditions play a key role in the dynamical scale selection process, as most realistic simulations have an open bottom boundary condition and a strongly stratified atmosphere. It was notably pointed out by Nordlund et al. (1994) that using “wall-type” boundary conditions, as is standard in idealized simulations, can significantly alter the shape of the convective pattern, because walls allow for a return flow after convective plumes smash down at the bottom. It may also be that particular “idealized” (!) implementations of open bottom boundary conditions used in most realistic (!) simulations artificially suppress or quench large-scale convective motions that would be present in the general case.
5.3.4 State-of-the-art local hydrodynamic Cartesian simulations
The first realistic numerical simulations including supergranulation scales are due to Benson et al. (2006), Georgobiani et al. (2007) and Stein et al. (2009). The latter used a 96 Mm wide and 20 Mm deep three-dimensional numerical box but, just like Rieutord et al. (2002), they found a monotonic smooth increase of the size of convective structures with depth, and no or very little power enhancement at supergranulation scales in the surface power spectrum. Similarly to Spruit et al. (1990), they subsequently argued that there was no reason why a particular scale should pop-up in the continuum of scales present in the simulation (see Nordlund et al. (2009) and Georgobiani et al. (2007) for representations of the power spectra of the simulations). A gradual monotonic increase of the convection scale with depth was also reported in an independent numerical study by Ustyugov (2008) in a 60 Mm wide and 20 Mm deep three-dimensional box. The physics of ionisation of helium and hydrogen were included in the model of Stein et al. (2009), which allowed them to test for the first time the first theoretical proposal for the origin of the supergranulation by Simon and Leighton (1964) described in Sect. 4.3. Considering the gradual large-scale decrease of energy in the power spectrum of their simulations, they concluded that the existence of recombination layers of ionised elements cannot by itself explain supergranulation. This conclusion was further confirmed by Lord et al. (2014) using simulations in a box of size \(196\times 196 \times 49\,\hbox {Mm}^3\) (the latter paper contains an interesting discussion of the slightly surprising actual effects of ionisation in the problem).
The latest realistic local simulations of Lord et al. (2014) appear to show a clear excess of kinetic energy at large scales (see Fig. 15, red line), just like idealized simulations. The reasons for this seemingly new convergence of the large-scale dynamical properties of convection in realistic and idealized simulations (assuming there was ever a big difference between the two) have not yet been clearly discussed to the best of our knowledge. Interestingly, a lot of the discussion in Lord et al. (2014), as well as in subsequent studies (e.g., Featherstone and Hindman 2016; Karak et al. 2018), is now focused on there being too much energy at large scales in simulations in comparison to the solar case. They notably point out that much of the heat flux is carried by the largest-scale flows in their simulations, which demonstrate that these flows are strongly buoyantly driven, just like the large-scale dynamics in idealized simulations described earlier.
Overall, it seems like all realistic and global simulations currently overestimate the peak scale of convection and convective velocities at large-scales in comparison to the solar case, while idealized simulations such as that of Cattaneo et al. (2001) and Rincon et al. (2005) underestimate them. Interestingly, Lord et al. (2014) manage to reproduce the Sun’s kinetic energy spectrum by using an artificial mechanism to carry the whole solar flux below a critical depth (here 10 Mm). The consequence of this prescription is to suppress the flux-transporting motions at the largest scales of the box, resulting in the emergence of a peak scale in the kinetic energy spectrum comparable to that of supergranulation. This result strongly suggests that understanding the asymptotic subtleties of deeper-scale convection in the Sun is very important for a quantitative theory of supergranulation. Cossette and Rast (2016; see also Kessar et al. 2018) have recently followed up on this idea with a series of idealized convection simulations in a strongly stratified atmosphere composed of different, prescribed superadiabatic surface layers matched to an adiabatic interior. They find that the vertical scale of the entropy jump at the surface, which sets the entropy deficit of sinking buoyant plumes (or “entropy rain”, see Brandenburg 2016), has a major effect on the peak “supergranulation” scale of the convection spectrum. We will frame these results in the context of a larger theoretical discussion in Sect. 6.

Image reproduced with permission from Lord et al. (2014), copyright by AAS
Kinetic energy spectra in the radiative hydrodynamics simulations of Lord et al. (2014) (solid red line). The spectrum obtained by reducing artificially the velocities in the deep layers is shown in dotted blue line. The vertical line marks the scale of the largest modes driven in the simulation. The black dashed line corresponds to solar spectra obtained from SDO/HMI data and coherent structure tracking (black dashed line).
While some of the results reviewed above suggest a strong, purely non-rotating, hydrodynamic dependence of the supergranulation scale on the modelling of the thermodynamic structure and heat flux of the whole system, rotation and magnetic fields have also long been thought to play a role in the supergranulation problem (see Sect. 4). What do simulations tell us about these interactions?
5.3.5 Simulations with rotation
As explained in Sect. 3.4, there is an increasing sense that a rotational connexion between the subsurface shear layer and large-scale convection at scales comparable to or larger than supergranulation exists in the Sun. Only a few local simulations have specifically addressed the issue of the interactions between supergranulation and rotation. In an early attempt at simulating this problem in the Boussinesq approximation in a numerical box elongated in the horizontal direction, Hathaway (1982) found that the presence of a tilted rotation axis and generate a subsurface shear layer. The local dynamics of angular momentum transport in turbulent convection has since been studied at much higher numerical resolution (e.g., Brummell et al. 1996, 1998; Käpylä et al. 2004; Brandenburg 2007) and, while the focus of these papers is not specifically on supergranulation, Brandenburg (2007) argued that the travelling-wave properties of supergranulation (Sect. 3.4) could be due to the radial subsurface shear. In a related study, Egorov et al. (2004) reported a good agreement between the divergence-vorticity correlations obtained from simulations of rotating convection and those inferred from observations of the supergranulation flow field.
Based on new high-resolution global spherical simulations dedicated to the supergranulation problem, Featherstone and Hindman (2016) have recently argued that Coriolis effects may effectively quench large-scale, low Rossby number convection in the SCZ, resulting in a reduction of both large-scale heat transport and of the peak scale of convection at the surface, as observed in the simulations of Lord et al. (2014) with artificial heat-flux reduction. This effect might also be indirectly connected to the non-rotating scale-selection effect put forward by Cossette and Rast (2016), in the sense that the effects of rotation on convective heat fluxes can also indirectly affect the internal and subsurface thermal structure on which the peak scale of the convection spectrum depends.
5.3.6 MHD simulations
Just like rotation, magnetic fields have long been recognized to play a non-negligible dynamical role in solar convection. Many (mostly local) large-scale local simulations have now been devoted to the study of MHD convection at scales comparable to supergranulation and to the process of network formation. These can be subdivided into magnetoconvection simulations in an imposed mean magnetic field or with a magnetic flux introduced “by hand” at the beginning of the run, and turbulent dynamo simulations, in which the magnetic field is spontaneously generated by the turbulent convection flow starting from an infinitesimal seed field.
In the absence of a mean field threading the convection layer, small-scale disordered magnetic fields consistently generated by small-scale turbulent dynamo action get organized into a network of ribbons and point-like magnetic flux concentrations, much like in the quiet Sun (Cattaneo 1999; Emonet and Cattaneo 2001; Vögler and Schüssler 2007; Bushby and Favier 2014; Rempel 2014; Danilovic et al. 2016a). The typical scale at which this “network” forms in simulations corresponds to that of the large-scale energetic motions described earlier. A similar phenomenology is observed in magnetoconvection simulations in a weak mean (vertical or horizontal) field (Ustyugov 2006, 2008, 2009; Stein et al. 2011). This process is illustrated in Fig. 16, which shows a large-scale realistic simulation of magnetoconvection with an imposed 50 G vertical field (Ustyugov 2009). Only in the presence of a strong mean vertical field is the peak horizontal scale of these turbulent convective motions strongly constrained and reduced by magnetic tension (Tao et al. 1998; Cattaneo et al. 2003). The field strengths required are generally stronger than observed in most of the quiet Sun, but this kind of effect may be particularly noticeable in polar regions (e.g. Tsuneta et al. 2008).
While an essentially passive magnetic field phenomenology provides the simplest explanation for the observed correlation between supergranulation and the solar magnetic network, we argued in Sect. 4.3.5 that a distribution of spatially-intermittent magnetic fields organized into strongly inhomogeneous structures (such as observed both in simulations and observations) may dynamically affect convection. Numerical evidence for this remains limited, but Ustyugov (2009) notably found that local concentrations of strong magnetic flux seem to play an important role in the scale-selection process in his simulations of network formation with a weak but uniform mean field and may, therefore, exert a significant dynamical feedback on supergranulation. The simulation of Hotta et al. (2015) also provides an example on how small-scale turbulent field may affect convection and entropy mixing throughout the convection zone. Other possible MHD effects briefly described in Sect. 4.3.5 and in the discussion section of the first published edition of this review (Rieutord and Rincon 2010) remain more speculative and have not been conclusively detected in simulations so far.

Image reprpoduced with permission from Ustyugov (2009), copyright by ASP
Horizontal maps of a temperature and b vertical magnetic field fluctuations in the surface layers of local realistic simulations of large-scale MHD convection.
6 Discussion and outlook
The physical and dynamical complexity of the supergranulation problem is quite extraordinary: vigorous turbulent small-scale and large-scale flows in a strongly stratified atmosphere, ionisation physics, rotation, shear and tortuous magnetic-field geometries at all observable scales. It is, therefore, perhaps not suprising that both observers and theoreticians have struggled for many decades after the initial historical observational discoveries to identify and describe the essential processes underlying this phenomenon. As shown in the previous sections, research on the problem as strongly intensified in the last 15 years. This progress has largely been driven by massive improvements in observational capacities and analysis techniques, as well as in computing power. Before we discuss the emergent dynamical picture and outline a few desirable and expected directions of future research, let us first offer a compact recap of the current observational knowledge on the problem against which theoretical and numerical models have to be confronted. A pictorial representation of the results is also provided in Fig. 17.
A schematic view of the supergranulation phenomenon as currently constrained by observations. \(\lambda \) is the scale where the horizontal kinetic energy spectral density is maximum. d is the diameter of “coherent structures” (supergranules). The red and blue patches depict the warm and cold regions of the flow. I.N.B denotes the internetwork magnetic field (the dichotomy between network and internetwork fields is probably not quite as clear as indicated in this drawing). The vertical structure and extent of the dynamics remains one of the main unknowns in this cartoon
6.1 Summary of observations
Supergranulation is a pattern of vigorous, mostly cellular-like flows in the quiet solar photosphere and subphotospheric layers, detected through Doppler measurements, structure tracking, and helioseismic analyses. The typical range of horizontal length scales of supergranulation flows at the photosphere is 20–70 Mm, with a peak at 36 Mm corresponding to the peak scale of the horizontal kinetic energy spectrum of solar surface flows. This result is clearly established in Fig. 4 of Sect. 3. Surface flows in the meso to supergranulation range of scales are strongly anisotropic. A clear distinction must be made between the horizontal and vertical components of the flow at the photospheric level the horizontal, cell-like component of the flow (300–400 m/s) is more than ten times more vigorous than the vertical upflow and downflow components (20–30 m/s) detected respectively it the center and periphery of supergranules, and the kinetic energy spectra of each component look very different. The spectrum of the vertical component, unlike the horizontal spectrum, may have a kink, but does not peak at supergranulation scales. Instead, it increases down to granulation scales.
These different observations strongly suggest that supergranulation-scale dynamics is the dynamical manifestation of a vigorous turbulent energy-injection mechanism, which has many (but not unambiguously all) of the observational hallmarks of thermal convection. Different observations suggest that supergranules are slightly warmer at their centre, but with a temperature drop smaller than 3 K at the surface, possibly larger below the surface. Our understanding of the structure of subsurface flows in the supergranulation range remains a bit fuzzy, but several recent measurements seem to point to the existence of dynamics at scales comparable to or larger than that of supergranulation down to the bottom of the near-surface shear layer, albeit with a shallow vertical scale-height of variation close to the surface, of the order of 2–7 Mm.
Different studies suggest that supergranulation is influenced by the global solar rotation, and may itself play an important role in the establishement of the near-surface shear layer of the SCZ. Finally, flows in the meso to supergranulation-scale range are strongly correlated with the solar magnetic network and have a strong influence of the distribution and advection of small-scale magnetic fields up to network scales. Whether supergranulation itself is constrained by magnetic forces cannot be easily asserted with observations, although a few observations suggests that the emergence of active regions, and stronger fields in general, may dynamically affect it.
6.2 Physics and dynamical phenomenology of supergranulation
There has been ample progress in the last 10–15 years in our understanding of the phenomenology of the dynamics of the solar surface in the range of scales relevant to the supergranulation problem thanks to numerical simulations. At the very least, there now appears to be much more numerical evidence than 10 years ago that supergranulation is buoyantly-driven, and is in fact the energetically dominant convection scale on the large-scale side of the injection range of the photospheric convection spectrum. Simulations also increasingly show that the detailed dynamical picture is significantly more complex than the classical laminar picture of convection described in Sect. 4, although interestingly enough, the nonlinear organization of the dynamics in the turbulent regime (illustrated for instance by the broadband convection spectra in Fig. 4 and the large-scale nonlinear dynamics in the simulations described in Sect. 5.3.3) appears to result in large-scale, vigorous coherent motions reminiscent of laminar convection.
Brute force observational and numerical progress on the problem has recently been accompanied with several potentially-testable theoretical developments and arguments regarding the phenomenology of turbulence and convection at scales larger than granulation (Lord et al. 2014; Cossette and Rast 2016; Featherstone and Hindman 2016; Rincon et al. 2017). It was recently argued by Rincon et al. (2017) on the basis of the strong anisotropy of photospheric flows in the supergranulation to granulation range that an appropriate description of convection dynamics at the surface in this range of scales requires a generalization of the classical isotropic Bolgiano–Oboukhov theory of turbulent convection (Bolgiano 1959, 1962; Oboukhov 1959) to the regime \(kH\ll 1\), where k is the horizontal wavenumber of fluctuations and H is a typical scale height (the distance between plates in the Rayleigh–Bénard experiment, or a thermodynamic scale height in the stratified problem). A tentative generalized theory of this kind can be derived using three key dynamical assumptions: a dominant dynamical balance between buoyancy forces and inertial terms in the momentum equation (as diagnosed in idealized simulations, see Sect. 5.3.3), a constant flux of thermal variance in spectral space in a well-mixed, nearly adiabatic turbulent convection layer and a typical “frustrated” vertical scale of variations of fluctuations independent of their horizontal scale and of the order of H. The first two assumptions are part of the standard Bolgiano–Oboukhov phenomenology, but the latter is specific to the anisotropic regime \(kH\ll 1\). Crucially, the theory predicts that the horizontal kinetic energy spectrum continues to increase at scales larger than granulation and the Bolgiano scale, while the vertical kinetic energy decreases with increasing scale, in broad agreement with observations. This result provides a possible partial way out of the problem raised in Sect. 2 of the mismatch between the supergranulation scale and the Bolgiano injection convection scale: the theory suggests that the latter is just a lower bound on the scale of the injection range, and that an anisotropic, buoyancy-driven nonlinear Bolgiano-like injection regime is possible at horizontal scales larger than the typical vertical scale height of the domain (this regime has never been investigated in laboratory experiments to the best of our knowledge). Finally, the theory also predicts an increase of temperature fluctuations with increasing horizontal scale. This is in relative tension with the relatively weak photospheric light intensity contrasts measurements reported in this range of scales at the solar surface, but is on the other hand quite consistent with a variety of numerical results, notably those of Rincon et al. (2005), Lord et al. (2014) and Cossette and Rast (2016) discussed in Sect. 5.
These preliminary theoretical predictions, considered jointly with the observation of a maximum in the kinetic energy spectrum at scales much larger than granulation, raise several key questions: what sets the scale of this maximum dynamically? why is supergranulation so prominent as a flow pattern but not as a temperature pattern at the photospheric level, and what is the spectrum of thermal fluctuations below the photosphere? Numerical simulations are slowly getting to a place where a much better understanding of the interactions and balance between different relevant linear and nonlinear dynamical processes in this range of scale becomes possible and these questions can be adressed. A closely related issue is to reconcile the peak scales and amplitudes of the observed solar convection spectrum (the actual supergranulation scale) with the dynamics of either global or local simulations. In particular, why does the solar dynamics appear to have so little power on large scales?
In the light of the numerical results reviewed in Sect. 5, there are at least three remaining credible possibilities as to what sets the peak scale of the convection spectrum and supergranulation: the internal thermodynamic structure and the magnitude and thickness of the entropy jump in the surface thermal boundary layer, which are directly constrained by the production of heat in the Sun (Cossette and Rast 2016; Rincon et al. 2017; Kessar et al. 2018), the interaction between slow, large-scale convection and rotation (Featherstone and Hindman 2016), and the dynamical interactions between convection and magnetic fields (Ustyugov 2009; Stein et al. 2011, see also discussion in Rieutord and Rincon 2010). The question of the amplitude of thermal fluctuations at supergranulation scales has recently been discussed by Cossette and Rast (2016) and Rincon et al. (2017).
6.3 Outlook
There are many reasons to be cautiously optimistic about future breakthroughs on the supergranulation problem, and it seems increasingly possible that a robust phenomenology and even perhaps a consistent nonlinear theory of large-scale convection in the SCZ can be constructed in the next decade.
a Global distribution of 24-h-positive time FTLEs of solar surface flows (in inverse hour units) computed from horizontal velocity field maps derived from October 8, 2010 SDO data (one of the quietest periods of solar activity since the launch of SDO). The green circle diameter is 30 Mm. b Local distribution of FTLEs of solar surface flows computed from horizontal velocity field maps derived from August, 2007 Hinode data, (red: positive-time FTLEs, blue: negative-time FTLEs).
From an observational point of view, there has been a strong revival of supergranulation studies in the last 10 years with the launch of Hinode and more recently SDO, and important progress has been made on the characterization of both surface and subsurface dynamics. Particularly encouraging are the ongoing efforts to improve the characterization of subsurface dynamics with localhelioseismology, and the newly acquired capability to study the surface dynamics from a global perspective with either tracking or Doppler techniques (or both) thanks to the highly-sampled SDO/HMI data. More observational results of this kind are expected in the forthcoming years. These should hopefully be accompanied with a better convergence between different techniques and research groups, thereby enriching and consolidating the existing corpus of observational constraints. Among many other things, a better heloiseismic characterization of subsurface thermal fluctuations at supergranulation scales and smaller scales would be extremely valuable for this problem, and so would be a better, less controversial characterization of large-scale convection flows in subsurface layers and in the deeper SCZ. There is still a lot of fuzziness and disagreement between different groups on these questions and more work is required to settle them. The good news is that only a fraction of SDO capacities seems to have been exploited so far on this front. The potential of SDO has also almost not been exploited to look for new observational clues of a possible dynamical relationship between large-scale flows and magnetic fields in the quiet Sun. There seems to be a lot of room left for new discoveries on this front too.
In-depth numerical investigations of the different dynamical scenarios described in the previous paragraph at even higher-resolutions are also almost certainly going to be carried out in the forthcoming years, but making significant further progress is going to be challenging. First of all, as explained in Sect. 5, the actual thermodynamic profiles and entropy jumps established by turbulent mixing in simulations are less extreme than in the SCZ because the simulated regimes are not quite as asymptotic as in the Sun. Finally, the dynamical influence of magnetic fields in the problem is also not easy to understand considering the complex geometry and potentially insidious effects of solar magnetic fields. It is not even clear that all the aspects of the MHD problem have yet been properly recognized [see, e.g., recent discussion by Karak et al. (2018)]. Some of these issues may be very difficult to address numerically, given the difficulty to simulate MHD in the low magnetic Prandtl regime typical of the SCZ (Schekochihin et al. 2007; Vögler and Schüssler 2007; Pietarila Graham et al. 2009; Rempel 2014).
Progress on the supergranulation problem is not only interesting and important in itself, but also from the perspective of understanding the global solar dynamo, turbulent generation of solar magnetic fields, and coronal heating. To emphasize this clearly and open the subject for future discussions, we show in Fig. 18 solar surface distributions of finite time Lyapunov exponents (FTLE) computed from recent Lagrangian tracer analyses of global and local maps of horizontal photospheric velocity fieds derived from Hinode and SDO observations using CST tracking. Such FTLE calculations, introduced in the context of solar coronal heating by Yeates et al. (2012) and Chian et al. (2014), characterize the Lagrangian transport properties of flows and make it possible to image transport barriers, i.e., regions of accumulation or rarefaction of passive tracers such as passive magnetic fields, in the form of Lagrangian Coherent Structures (LCS). These concepts have already found many applications in other fields of physics such as oceanography and atmospheric sciences (e.g., Lekien et al. 2005; Lehahn et al. 2007; Lekien and Ross 2010). These two computations reveal that the Sun is paved with supergranulation-scale lagrangian coherent structures, and strikingly illustrate the Lagrangian process of magnetic network formation. Based on this kind of analysis, it is clear that supergranulation-scale convection plays a major role in the global and local structuration and dynamics of solar magnetic fields at the interface between the solar interior and corona.
To conclude this review, let us note that solar surface convection is one of the very few time and spatially-resolved examples of extremely nonlinear dynamical fluid astrophysical phenomena. As we are increasingly approaching a position where a detailed understanding and characterization of this phenomenon seems possible, it is certainly worth emphasizing that everything we can learn about it is likely to be strongly relevant and illuminating from a much broader astrophysical and fundamental fluid dynamics perspective.
Notes
Consistent use of the component-separation method combining CST and Doppler velocities requires downgrading the Doppler data to the 2.5 Mm CST resolution (Rincon et al. 2017).
At granulation scales, the spectral power density is less than 300 \(\hbox {km}^3{/}\hbox {s}^2\). We recall that granules have a much larger typical velocity than supergranules though, of the order 1–2 km/s (Sect. 2.1.2). The difference comes from the definition of the spectral power density at wavenumber k, \(E(k)\sim k^{-1}V_k^2\), which introduces an extra k factor.
References
Abramenko VI (2005) Multifractal analysis of solar magnetograms. Sol Phys 228:29–42. https://doi.org/10.1007/s11207-005-3525-9
Abramenko V, Yurchyshyn V, Wang H, Goode PR (2001) Magnetic power spectra derived from ground and space measurements of the solar magnetic fields. Sol Phys 201:225–240. https://doi.org/10.1023/A:1017544723973
Abramenko VI, Yurchyshyn VB, Goode PR (2011) Magnetic and kinetic power spectra as a tool to probe the turbulent dynamo. ArXiv e-prints arXiv:1112.2750
Amati G, Koal K, Massaioli F, Sreenivasan KR, Verzicco R (2005) Turbulent thermal convection at high Rayleigh numbers for a Boussinesq fluid of constant Prandtl number. Phys Fluids 17(12):121701. https://doi.org/10.1063/1.2140023
Antia HM, Chitre SM (1993) Discrete cellular scales of solar convection. Sol Phys 145:227–239. https://doi.org/10.1007/BF00690653
Antia HM, Chitre SM, Pandey SK (1981) Granulation and supergranulation as convective modes in the solar envelope. Sol Phys 70:67–91. https://doi.org/10.1007/BF00154392
Asensio Ramos A (2009) Evidence for quasi-isotropic magnetic fields from Hinode quiet-Sun observations. Astrophys J 701:1032–1043. https://doi.org/10.1088/0004-637X/701/2/1032
Asplund M, Grevesse N, Sauval AJ, Scott P (2009) The chemical composition of the Sun. Annu Rev Astron Astrophys 47:481–522. https://doi.org/10.1146/annurev.astro.46.060407.145222
Beck JG, Schou J (2000) Supergranulation rotation. Sol Phys 193:333–343
Beckers JM (1968) Photospheric brightness differences associated with the solar supergranulation. Sol Phys 5:309–322. https://doi.org/10.1007/BF00147143
Benson D, Stein R, Nordlund Å (2006) Supergranulation scale convection simulations. In: Leibacher J, Stein RF, Uitenbroek H (eds) Solar MHD theory and observations: a high spatial resolution perspective. ASP conference series, vol 354. Astronomical Society of the Pacific, San Francisco, p 92
Berger TE, Rouppe van der Voort LHM, Löfdahl MG, Carlsson M, Fossum A, Hansteen VH, Marthinussen E, Title A, Scharmer G (2004) Solar magnetic elements at 0.1 arcsec resolution. General appearance and magnetic structure. Astron Astrophys 428:613–628. https://doi.org/10.1051/0004-6361:20040436
Berrilli F, Florio A, Ermolli I (1998) On the geometrical properties of the chromospheric network. Sol Phys 180:29–45. https://doi.org/10.1023/A:1005023819431
Berrilli F, Ermolli I, Florio A, Pietropaolo E (1999) Average properties and temporal variations of the geometry of solar network cells. Astron Astrophys 344:965–972
Berrilli F, Scardigli S, Del Moro D (2014) Magnetic pattern at supergranulation scale: the void size distribution. Astron Astrophys 568:A102. https://doi.org/10.1051/0004-6361/201424026
Bhattacharya J, Hanasoge SM (2016) Strategies in seismic inference of supergranular flows on the Sun. Astrophys J 826:105. https://doi.org/10.3847/0004-637X/826/2/105
Bogart RS, Gierasch PJ, MacAuslan JM (1980) Linear modes of convection in the solar envelope. Astrophys J 236:285–293. https://doi.org/10.1086/157745
Bolgiano R Jr (1959) Turbulent spectra in a stably stratified atmosphere. J Geophys Res 64:2226–2229. https://doi.org/10.1029/JZ064i012p02226
Bolgiano R (1962) Structure of turbulence in stratified media. J Geophys Res 67(16):3015. https://doi.org/10.1029/JZ067i008p03015
Bommier V, Landi Degl’Innocenti E, Landolfi M, Molodij G (2007) UNNOFIT inversion of spectro-polarimetric maps observed with THEMIS. Astron Astrophys 464:323–339. https://doi.org/10.1051/0004-6361:20054576
Bommier V, Martínez González M, Bianda M, Frisch H, Asensio Ramos A, Gelly B, Landi Degl’Innocenti E (2009) The quiet Sun magnetic field observed with ZIMPOL on THEMIS. I. The probability density function. Astron Astrophys 506:1415–1428. https://doi.org/10.1051/0004-6361/200811373
Brandenburg A (2007) Near-surface shear layer dynamics. In: Kupka F, Roxburgh I, Chan K (eds) Convection in astrophysics. IAU symposium, vol 239. Cambridge University Press, Cambridge, pp 457–466. https://doi.org/10.1017/S1743921307000919
Brandenburg A (2016) Stellar mixing length theory with entropy rain. Astrophys J 832:6. https://doi.org/10.3847/0004-637X/832/1/6
Braun DC, Lindsey C (2003) Helioseismic imaging of the farside and the interior. In: Sawaya-Lacoste H (ed) GONG+ 2002. Local and global helioseismology: the present and future. ESA special publication, vol SP-517. ESA Publications Division, Noordwijk, pp 15–22
Brickhouse NS, Labonte BJ (1988) Mass and energy flow near sunspots. I. Observations of moat properties. Sol Phys 115:43–60. https://doi.org/10.1007/BF00146229
Brummell NH, Hurlburt NE, Toomre J (1996) Turbulent compressible convection with rotation. I. Flow structure and evolution. Astrophys J 473:494. https://doi.org/10.1086/178161
Brummell NH, Hurlburt NE, Toomre J (1998) Turbulent compressible convection with rotation. II. Mean flows and differential rotation. Astrophys J 493:955. https://doi.org/10.1086/305137
Bushby PJ, Favier B (2014) Mesogranulation and small-scale dynamo action in the quiet Sun. Astron Astrophys 562:A72. https://doi.org/10.1051/0004-6361/201322993
Bushby PJ, Houghton SM, Proctor MRE, Weiss NO (2008) Convective intensification of magnetic fields in the quiet Sun. Mon Not R Astron Soc 387:698–706. https://doi.org/10.1111/j.1365-2966.2008.13276.x
Busse FH (1972) The oscillatory instability of convection rolls in a low Prandtl number fluid. J Fluid Mech 52:97–112. https://doi.org/10.1017/S0022112072002988
Busse FH (2004) On thermal convection in slowly rotating systems. Chaos 14:803–808. https://doi.org/10.1063/1.1774413
Busse FH (2007) Convection in the presence of an inclined axis of rotation with applications to the Sun. Sol Phys 245:27–36. https://doi.org/10.1007/s11207-007-9015-5
Busse FH, Riahi N (1978) Nonlinear convection in a layer with nearly insulating boundaries. J Fluid Mech 86:243–256
Canuto C, Hussaini MY, Quarteroni A, Zang TA (2006) Spectral methods: fundamentals in single domains. Scientific computation. Springer, Berlin. https://doi.org/10.1007/978-3-540-30726-6
Cattaneo F (1999) On the origin of magnetic fields in the quiet photosphere. Astrophys J Lett 515:L39–L42. https://doi.org/10.1086/311962
Cattaneo F, Brummell NH, Toomre J, Malagoli A, Hurlburt NE (1991) Turbulent compressible convection. Astrophys J 370:282–294. https://doi.org/10.1086/169814
Cattaneo F, Lenz D, Weiss N (2001) On the origin of the solar mesogranulation. Astrophys J Lett 563:L91–L94. https://doi.org/10.1086/338355
Cattaneo F, Emonet T, Weiss N (2003) On the interaction between convection and magnetic fields. Astrophys J 588:1183–1198. https://doi.org/10.1086/374313
Chan KL, Sofia S (1989) Turbulent compressible convection in a deep atmosphere. IV. Results of three-dimensional computations. Astrophys J 336:1022–1040. https://doi.org/10.1086/167072
Chan KL, Sofia S (1996) Turbulent compressible convection in a deep atmosphere. V. Higher order statistical moments for a deeper case. Astrophys J 466:372. https://doi.org/10.1086/177516
Chan KL, Sofia S, Wolff CL (1982) Turbulent compressible convection in a deep atmosphere. I. Preliminary two-dimensional results. Astrophys J 263:935–943. https://doi.org/10.1086/160561
Chandrasekhar S (1961) Hydrodynamic and hydromagnetic stability. Clarendon, Oxford
Chapman CJ, Proctor MRE (1980) Nonlinear Rayleigh-Bénard convection between poorly conducting boundaries. J Fluid Mech 101:759–782. https://doi.org/10.1017/S0022112080001917
Chatterjee S, Mandal S, Banerjee D (2017) Variation of supergranule parameters with solar cycles: results from century-long Kodaikanal digitized Ca II K data. Astrophys J 841:70. https://doi.org/10.3847/1538-4357/aa709d
Chian ACL, Rempel EL, Aulanier G, Schmieder B, Shadden SC, Welsch BT, Yeates AR (2014) Detection of coherent structures in photospheric turbulent flows. Astrophys J 786:51. https://doi.org/10.1088/0004-637X/786/1/51
Chillá F, Ciliberto S, Innocenti C, Pampaloni E (1993) Boundary layer and scaling properties in turbulent thermal convection. Nuovo Cimento D 15:1229–1249. https://doi.org/10.1007/BF02451729
Chou D, Labonte BJ, Braun DC, Duvall TL Jr (1991) Power spectra of solar convection. Astrophys J 372:314–320. https://doi.org/10.1086/169977
Chou D, Chen C, Ou K, Wang C (1992) Power spectra of median- and small-scale solar convection. Astrophys J 396:333–339. https://doi.org/10.1086/171719
Clark AJ, Johnson HK (1967) Magnetic-field accumulation in supergranules. Sol Phys 2:433–440. https://doi.org/10.1007/BF00146491
Cloutman LD (1979) The supergranulation: solar rip currents? Astron Astrophys 74:L1–L3
Clune TC, Elliott JR, Miesch MS, Toomre J (1999) Computational aspects of a code to study rotating turbulent convection in spherical shells. Parallel Comput 25:361. https://doi.org/10.1016/S0167-8191(99)00009-5
Clyne J, Mininni P, Norton A, Rast MP (2007) Interactive desktop analysis of high resolution simulations: application to turbulent plume dynamics and current sheet formation. New J Phys 9:301. https://doi.org/10.1088/1367-2630/9/8/301
Cossette JF, Rast MP (2016) Supergranulation as the largest buoyantly driven convective scale of the Sun. Astrophys J Lett 829:L17. https://doi.org/10.3847/2041-8205/829/1/L17
Crouch AD, Charbonneau P, Thibault K (2007) Supergranulation as an emergent length scale. Astrophys J 662:715–729. https://doi.org/10.1086/515564
Danilovic S, Schüssler M, Solanki SK (2010) Probing quiet Sun magnetism using MURaM simulations and Hinode/SP results: support for a local dynamo. Astron Astrophys 513:A1. https://doi.org/10.1051/0004-6361/200913379
Danilovic S, Rempel M, van Noort M, Cameron R (2016a) Observed and simulated power spectra of kinetic and magnetic energy retrieved with 2D inversions. Astron Astrophys 594:A103. https://doi.org/10.1051/0004-6361/201527917
Danilovic S, van Noort M, Rempel M (2016b) Internetwork magnetic field as revealed by two-dimensional inversions. Astron Astrophys 593:A93. https://doi.org/10.1051/0004-6361/201527842
Dauxois T, Peyrard M (1993) Energy localization in nonlinear lattices. Phys Rev Lett 70:3935–3938. https://doi.org/10.1103/PhysRevLett.70.3935
de Wijn AG, Müller D (2009) On the relationship between magnetic field and mesogranulation. In: Lites B, Cheung M, Magara T, Mariska J, Reeves K (eds) The Second Hinode Science Meeting: beyond discovery-toward understanding. ASP conference series, vol 415. Astronomical Society of the Pacific, San Francisco, p 211. arXiv:0902.1967
de Wijn AG, Rutten RJ, Haverkamp EMWP, Sütterlin P (2005) DOT tomography of the solar atmosphere. IV. Magnetic patches in internetwork areas. Astron Astrophys 441:1183–1190. https://doi.org/10.1051/0004-6361:20053373. arXiv:0706.2008
de Wijn AG, Stenflo JO, Solanki SK, Tsuneta S (2009) Small-scale solar magnetic fields. Space Sci Rev 144:275–315. https://doi.org/10.1007/s11214-008-9473-6. arXiv:0812.4465
DeGrave K, Jackiewicz J (2015) Helioseismic investigation of modeled and observed supergranule structure. Sol Phys 290:1547–1568. https://doi.org/10.1007/s11207-015-0693-0
DeGrave K, Jackiewicz J, Rempel M (2014a) Time-distance helioseismology of two realistic sunspot simulations. Astrophys J 794:18. https://doi.org/10.1088/0004-637X/794/1/18
DeGrave K, Jackiewicz J, Rempel M (2014b) Validating time-distance helioseismology with realistic quiet-Sun simulations. Astrophys J 788:127. https://doi.org/10.1088/0004-637X/788/2/127
Del Moro D, Berrilli F, Duvall TL Jr, Kosovichev AG (2004) Dynamics and structure of supergranulation. Sol Phys 221:23–32. https://doi.org/10.1023/B:SOLA.0000033363.15641.8f
Del Moro D, Giordano S, Berrilli F (2007) 3D photospheric velocity field of a supergranular cell. Astron Astrophys 472:599–605. https://doi.org/10.1051/0004-6361:20077595
Depassier MC, Spiegel EA (1981) The large-scale structure of compressible convection. Astron J 86:496–512. https://doi.org/10.1086/112908
DeRosa ML (2001) Dynamics in the upper solar convection zone. PhD thesis, University of Colorado at Boulder, Boulder
DeRosa ML, Toomre J (2001) Numerical simulations of supergranular scales of convection in shallow spherical shells. In: Wilson A, Pallé PL (eds) SOHO 10/GONG 2000 workshop: helio- and asteroseismology at the dawn of the millennium. ESA special publication, vol SP–464. ESA Publications Division, Noordwijk, pp 595–600
DeRosa ML, Toomre J (2004) Evolution of solar supergranulation. Astrophys J 616:1242–1260. https://doi.org/10.1086/424920
DeRosa M, Duvall TL Jr, Toomre J (2000) Near-surface flow fields deduced using correlation tracking and time-distance analyses. Sol Phys 192:351–361. https://doi.org/10.1023/A:1005269001739
DeRosa ML, Gilman PA, Toomre J (2002) Solar multiscale convection and rotation gradients studied in shallow spherical shells. Astrophys J 581:1356–1374. https://doi.org/10.1086/344295
Deslandres H (1899) Organisation de l’enregistrement quotidien de la Chromosphère entière du Soleil à l’observatoire de Meudon. Premieres résultats. C R Acad Sci 129:1222–1225
Domínguez Cerdeña I (2003) Evidence of mesogranulation from magnetograms of the Sun. Astron Astrophys 412:L65–L68. https://doi.org/10.1051/0004-6361:20034617
Domínguez Cerdeña I, Sánchez Almeida J, Kneer F (2003) Inter-network magnetic fields observed with sub-arcsec resolution. Astron Astrophys 407:741–757. https://doi.org/10.1051/0004-6361:20030892
Dubrulle B, Frisch U (1991) Eddy viscosity of parity-invariant flow. Phys Rev A 43:5355–5364. https://doi.org/10.1103/PhysRevA.43.5355
Duvall TL Jr (1980) The equatorial rotation rate of the supergranulation cells. Sol Phys 66:213–221. https://doi.org/10.1007/BF00150578
Duvall TL Jr (1998) Recent results and theoretical advances in local helioseismology. In: Korzennik S, Wilson A (eds) SOHO 6/GONG 98: structure and dynamics of the interior of the Sun and Sun-like stars. ESA special publication, vol SP-418. ESA Publications Division, Noordwijk, pp 581–585
Duvall TL Jr, Birch AC (2010) The vertical component of the supergranular motion. Astrophys J Lett 725:L47–L51. https://doi.org/10.1088/2041-8205/725/1/L47
Duvall TL Jr, Gizon L (2000) Time-distance helioseismology with \(f\) modes as a method for measurement of near-surface flows. Sol Phys 192:177–191. https://doi.org/10.1023/A:1005239503637
Duvall TL Jr, Hanasoge SM (2013) Subsurface supergranular vertical flows as measured using large distance separations in time-distance helioseismology. Sol Phys 287:71–83. https://doi.org/10.1007/s11207-012-0010-0
Duvall TL Jr, Kosovichev AG, Scherrer PH, Bogart RS, Bush RI, de Forest C, Hoeksema JT, Schou J, Saba JLR, Tarbell TD, Title AM, Wolfson CJ, Milford PN (1997) Time-distance helioseismology with the MDI instrument: initial results. Sol Phys 170:63–73. https://doi.org/10.1023/A:1004907220393
Duvall TL Jr, Hanasoge SM, Chakraborty S (2014) Additional evidence supporting a model of shallow, high-speed supergranulation. Sol Phys 289:3421–3433. https://doi.org/10.1007/s11207-014-0537-3
Edwards JM (1990) On the influence of the thermal and magnetic boundary conditions on the linear theory of magnetoconvection. Geophys Astrophys Fluid Dyn 55:1–17. https://doi.org/10.1080/03091929008208942
Egorov P, Rüdiger G, Ziegler U (2004) Vorticity and helicity of the solar supergranulation flow-field. Astron Astrophys 425:725–728. https://doi.org/10.1051/0004-6361:20040531
Emonet T, Cattaneo F (2001) Small-scale photospheric fields: observational evidence and numerical simulations. Astrophys J Lett 560:L197–L200. https://doi.org/10.1086/324315
Featherstone NA, Hindman BW (2016) The emergence of solar supergranulation as a natural consequence of rotationally constrained interior convection. Astrophys J Lett 830:L15. https://doi.org/10.3847/2041-8205/830/1/L15
Foukal P, Fowler L (1984) A photometric study of heat flow at the solar photosphere. Astrophys J 281:442–454. https://doi.org/10.1086/162115
Frazier EN (1970) Multi-channel magnetograph observations. II. Supergranulation. Sol Phys 14:89–111. https://doi.org/10.1007/BF00240163
Frazier EN (1976) The photosphere–magnetic and dynamic state. Philos Trans R Soc London, Ser A 281:295–303. https://doi.org/10.1098/rsta.1976.0027
Frisch U (1995) Turbulence: the legacy of A. Cambridge University Press, Cambridge, N. Kolmogorov
Gama S, Vergassola M, Frisch U (1994) Negative eddy viscosity in isotropically forced two-dimensional flow: linear and nonlinear dynamics. J Fluid Mech 260:95–126. https://doi.org/10.1017/S0022112094003459
Georgobiani D, Zhao J, Kosovichev AG, Benson D, Stein RF, Nordlund Å (2007) Local helioseismology and correlation tracking analysis of surface structures in realistic simulations of solar convection. Astrophys J 657:1157–1161. https://doi.org/10.1086/511148
Giannattasio F, Stangalini M, Berrilli F, Del Moro D, Bellot Rubio L (2014) Diffusion of magnetic elements in a supergranular cell. Astrophys J 788:137. https://doi.org/10.1088/0004-637X/788/2/137
Gierasch PJ (1985) On the energetics of the solar supergranulation. Astrophys J 288:795–800. https://doi.org/10.1086/162849
Gilman PA (1975) Linear simulations of Boussinesq convection in a deep rotating spherical shell. J Atmos Sci 32:1331–1352. https://doi.org/10.1175/1520-0469(1975)0321331:LSOBCI2.0.CO;2
Gilman PA, Foukal PV (1979) Angular velocity gradients in the solar convection zone. Astrophys J 229:1179–1185. https://doi.org/10.1086/157052
Gilman PA, Glatzmaier GA (1981) Compressible convection in a rotating spherical shell. I. Anelastic equations. II. A linear anelastic model. III. Analytic model for compressible vorticity waves. Astrophys J Suppl Ser 45:335–388. https://doi.org/10.1086/190714
Ginet GP, Simon GW (1992) On the evidence for mesogranules in solar power spectra. Astrophys J 386:359–363. https://doi.org/10.1086/171022
Gizon L, Birch AC (2005) Local helioseismology. Living Rev Sol Phys 2:6. https://doi.org/10.12942/lrsp-2005-6
Gizon L, Birch AC (2012) Helioseismology challenges models of solar convection. Proc Natl Acad Sci USA 109:11896–11897. https://doi.org/10.1073/pnas.1208875109
Gizon L, Duvall TL Jr (2003) Supergranulation supports waves. In: Sawaya-Lacoste H (ed) GONG+ 2002. Local and global helioseismology: the present and future. ESA special publication, vol SP-517. ESA Publications Division, Noordwijk, pp 43–52
Gizon L, Duvall TL Jr (2004) Solar-cycle variations in the spectrum of supergranulation. In: Stepanov AV, Benevolenskaya EE, Kosovichev AG (eds) Multi-wavelength investigations of solar activity. IAU symposium, vol 223. Cambridge University Press, Cambridge, pp 41–44
Gizon L, Duvall TL Jr, Larsen RM (2000) Seismic tomography of the near solar surface. J Astrophys Astron 21:339. https://doi.org/10.1007/BF02702420
Gizon L, Duvall TL Jr, Schou J (2003) Wave-like properties of solar supergranulation. Nature 421:43–44. https://doi.org/10.1038/nature01287
Glatzmaier GA (1984) Numerical simulations of stellar convective dynamos. I. The model and method. J Comput Phys 55:461–484. https://doi.org/10.1016/0021-9991(84)90033-0
Glatzmaier GA (1985) Numerical simulations of stellar convective dynamos. II. Field propagation in the convection zone. Astrophys J 291:300–307. https://doi.org/10.1086/163069
Goldbaum N, Rast MP, Ermolli I, Sands JS, Berrilli F (2009) The intensity profile of the solar supergranulation. Astrophys J 707:67–73. https://doi.org/10.1088/0004-637X/707/1/67
Graham E (1975) Numerical simulation of two-dimensional compressible convection. J Fluid Mech 70:689–703. https://doi.org/10.1017/S0022112075002297
Green CA, Kosovichev AG (2006) Traveling convective modes in the Sun’s subsurface shear layer. Astrophys J Lett 641:L77–L80. https://doi.org/10.1086/503773
Green CA, Kosovichev AG (2007) Magnetic effect on wavelike properties of solar supergranulation. Astrophys J Lett 665:L75–L78. https://doi.org/10.1086/521101
Greer BJ, Hindman BW, Featherstone NA, Toomre J (2015) Helioseismic imaging of fast convective flows throughout the near-surface shear layer. Astrophys J 803:L17. https://doi.org/10.1088/2041-8205/803/2/L17
Greer BJ, Hindman BW, Toomre J (2016) Helioseismic imaging of supergranulation throughout the Sun’s near-surface shear layer. Astrophys J 824:128. https://doi.org/10.3847/0004-637X/824/2/128
Haber DA, Hindman BW, Toomre J, Bogart RS, Hill F (2001) Daily variations of large-scale subsurface flows and global synoptic flow maps from dense-pack ring-diagram analyses. In: Wilson A, Pallé PL (eds) SOHO 10/GONG 2000 workshop: helio- and asteroseismology at the dawn of the millennium. ESA special publication, vol SP-464. ESA Publications Division, Noordwijk, pp 209–212
Haber DA, Hindman BW, Toomre J, Thompson MJ (2004) Organized subsurface flows near active regions. Sol Phys 220:371–380. https://doi.org/10.1023/B:SOLA.0000031405.52911.08
Hagenaar HJ, Shine RA (2005) Moving magnetic features around sunspots. Astrophys J 635:659–669. https://doi.org/10.1086/497367
Hagenaar HJ, Schrijver CJ, Title AM (1997) The distribution of cell sizes of the solar chromospheric network. Astrophys J 481:988. https://doi.org/10.1086/304066
Hanasoge SM, Sreenivasan KR (2014) The quest to understand supergranulation and large-scale convection in the Sun. Sol Phys 289:3403. https://doi.org/10.1007/s11207-014-0471-4
Hanasoge SM, Duvall TL Jr, Sreenivasan KR (2012) Anomalously weak solar convection. Proc Natl Acad Sci USA 109:11928–11932. https://doi.org/10.1073/pnas.1206570109
Hanasoge S, Gizon L, Sreenivasan KR (2016) Seismic sounding of convection in the Sun. Annu Rev Fluid Mech 48:191. https://doi.org/10.1146/annurev-fluid-122414-034534
Hart AB (1954) Motions in the Sun at the photospheric level. IV. The equatorial rotation and possible velocity fields in the photosphere. Mon Not R Astron Soc 114:17. https://doi.org/10.1093/mnras/114.1.17
Hart AB (1956) Motions in the Sun at the photospheric level. VI. Large-scale motions in the equatorial region. Mon Not R Astron Soc 116:38. https://doi.org/10.1093/mnras/116.1.38
Hartlep T, Tilgner A, Busse FH (2003) Large scale structures in Rayleigh-Bénard convection at high Rayleigh numbers. Phys Rev Lett 91(6):064501. https://doi.org/10.1103/PhysRevLett.91.064501
Harvey K, Harvey J (1973) Observations of moving magnetic features near sunspots. Sol Phys 28:61–71. https://doi.org/10.1007/BF00152912
Harvey JW, Branston D, Henney CJ, Keller CU (2007) Seething horizontal magnetic fields in the quiet solar photosphere. Astrophys J Lett 659:L177–L180. https://doi.org/10.1086/518036. arXiv:astro-ph/0702415
Hathaway DH (1982) Nonlinear simulations of solar rotation effects in supergranules. Sol Phys 77:341–356. https://doi.org/10.1007/BF00156116
Hathaway DH (2012) Supergranules as probes of solar convection zone dynamics. Astrophys J Lett 749:L13. https://doi.org/10.1088/2041-8205/749/1/L13
Hathaway DH, Beck JG, Bogart RS, Bachmann KT, Khatri G, Petitto JM, Han S, Raymond J (2000) The photospheric convection spectrum. Sol Phys 193:299–312. https://doi.org/10.1023/A:1005200809766
Hathaway DH, Beck JG, Han S, Raymond J (2002) Radial flows in supergranules. Sol Phys 205:25–38
Hathaway DH, Williams PE, Cuntz M (2006) Supergranule superrotation identified as a projection effect. Astrophys J 644:598–602. https://doi.org/10.1086/498842
Hathaway DH, Teil T, Norton AA, Kitiashvili I (2015) The Sun’s photospheric convection spectrum. Astrophys J 811:105. https://doi.org/10.1088/0004-637X/811/2/105
Hindman BW, Haber DA, Toomre J (2009) Subsurface circulations within active regions. Astrophys J 698:1749–1760. https://doi.org/10.1088/0004-637X/698/2/1749
Hirzberger J, Gizon L, Solanki SK, Duvall TL Jr (2008) Structure and evolution of supergranulation from local helioseismology. Sol Phys 251:417–437. https://doi.org/10.1007/s11207-008-9206-8
Hotta H, Rempel M, Yokoyama T (2014) High-resolution calculations of the solar global convection with the reduced speed of sound technique. I. The structure of the convection and the magnetic field without the rotation. Astrophys J 786:24. https://doi.org/10.1088/0004-637X/786/1/24
Hotta H, Rempel M, Yokoyama T (2015) Efficient small-scale dynamo in the solar convection zone. Astrophys J 803:42. https://doi.org/10.1088/0004-637X/803/1/42
Hughes DW, Proctor MRE (1988) Magnetic fields in the solar convection zone: magnetoconvection and magnetic buoyancy. Annu Rev Fluid Mech 20:187–223. https://doi.org/10.1146/annurev.fl.20.010188.001155
Hurlburt NE, Toomre J, Massaguer JM (1984) Two-dimensional compressible convection extending over multiple scale heights. Astrophys J 282:557–573. https://doi.org/10.1086/162235
Hurlburt NE, Matthews PC, Proctor MRE (1996) Nonlinear compressible convection in oblique magnetic fields. Astrophys J 457:933. https://doi.org/10.1086/176786
Hurle DTJ, Jakeman E, Pike ER (1967) On the solution of the Bénard problem with boundaries of finite conductivity. Proc R Soc London, Ser A 296:469–475. https://doi.org/10.1098/rspa.1967.0039
Ishihara T, Gotoh T, Kaneda Y (2009) Study of high-Reynolds number isotropic turbulence by direct numerical simulation. Annu Rev Fluid Mech 41:165–180. https://doi.org/10.1146/annurev.fluid.010908.165203
Jain K, Tripathy SC, Ravindra B, Komm R, Hill F (2016) Horizontal flows in active regions from ring-diagram and local correlation tracking methods. Astrophys J 816:5. https://doi.org/10.3847/0004-637X/816/1/5
Janßen K, Vögler A, Kneer F (2003) On the fractal dimension of small-scale magnetic structures in the Sun. Astron Astrophys 409:1127–1134. https://doi.org/10.1051/0004-6361:20031168
Käpylä PJ, Korpi MJ, Tuominen I (2004) Local models of stellar convection: Reynolds stresses and turbulent heat transport. Astron Astrophys 422:793–816. https://doi.org/10.1051/0004-6361:20035874
Karak BB, Miesch M, Bekki Y (2018) Consequences of high effective Prandtl number on solar differential rotation and convective velocity. Phys Fluids 30:046602. https://doi.org/10.1063/1.5022034. arXiv:1801.00560
Kariyappa R, Sivaraman KR (1994) Variability of the solar chromospheric network over the solar cycle. Sol Phys 152:139–144. https://doi.org/10.1007/BF01473196
Katsukawa Y, Orozco Suárez D (2012) Power spectra of velocities and magnetic fields on the solar surface and their dependence on the unsigned magnetic flux density. Astrophys J 758:139. https://doi.org/10.1088/0004-637X/758/2/139
Keller CU, Deubner F, Egger U, Fleck B, Povel HP (1994) On the strength of solar intra-network fields. Astron Astrophys 286:626–634
Kessar M, Hughes DW, Kersale E, Mizerski KA, Tobias SM (2018) Scale selection in the stratified convection of the solar photosphere. ArXiv e-prints arXiv:1802.01309
Komm RW (1995) Wavelet analysis of a magnetogram. Sol Phys 157:45–50. https://doi.org/10.1007/BF00680608
Komm R, Howe R, Hill F, Miesch M, Haber D, Hindman B (2007) Divergence and vorticity of solar subsurface flows derived from ring-diagram analysis of MDI and GONG data. Astrophys J 667:571–584. https://doi.org/10.1086/520765
Komm R, Howe R, Hill F (2011) Subsurface velocity of emerging and decaying active regions. Sol Phys 268:407–428. https://doi.org/10.1007/s11207-010-9692-3
Komm R, Howe R, Hill F (2012) Vorticity of subsurface flows of emerging and decaying active regions. Sol Phys 277:205–226. https://doi.org/10.1007/s11207-011-9920-5
Kosovichev AG (2012) Local helioseismology of sunspots: current status and perspectives. Sol Phys 279:323–348. https://doi.org/10.1007/s11207-012-9996-6
Krijger JM, Roudier T (2003) Photospheric flows measured with TRACE. II. Network formation. Astron Astrophys 403:715–723. https://doi.org/10.1051/0004-6361:20030387
Krishnamurti R, Howard LN (1981) Large-scale flow generation in turbulent convection. Proc Natl Acad Sci USA 78:1981–1985. https://doi.org/10.1073/pnas.78.4.1981
Kropp M, Busse FH (1991) Thermal convection in differentially rotating systems. Geophys Astrophys Fluid Dyn 61:127–148. https://doi.org/10.1080/03091929108229040
Kuhn JR, Armstrong JD, Bush RI, Scherrer P (2000) Rossby waves on the Sun as revealed by solar ‘hills’. Nature 405:544–546. https://doi.org/10.1038/35014530
Kumar A, Chatterjee AG, Verma MK (2014) Energy spectrum of buoyancy-driven turbulence. Phys Rev E 90:023016. https://doi.org/10.1103/PhysRevE.90.023016
Langfellner J, Gizon L, Birch AC (2015a) Anisotropy of the solar network magnetic field around the average supergranule. Astron Astrophys 579:L7. https://doi.org/10.1051/0004-6361/201526422
Langfellner J, Gizon L, Birch AC (2015b) Spatially resolved vertical vorticity in solar supergranulation using helioseismology and local correlation tracking. Astron Astrophys 581:A67. https://doi.org/10.1051/0004-6361/201526024
Langfellner J, Birch AC, Gizon L (2016) Intensity contrast of the average supergranule. Astron Astrophys 596:A66. https://doi.org/10.1051/0004-6361/201629281
Langfellner J, Birch AC, Gizon L (2018) Evolution and wave-like properties of the average solar supergranule. ArXiv e-prints arXiv:1805.12522
Lawrence JK, Cadavid AC, Ruzmaikin AA (1995) Multiplicative cascade models of multifractal solar magnetic fields. Phys Rev E 51:316–324. https://doi.org/10.1103/PhysRevE.51.316
Lawrence JK, Cadavid AC, Ruzmaikin A (2001) Mesogranulation and turbulence in photospheric flows. Sol Phys 202:27–39. https://doi.org/10.1023/A:1011813925550
Lee J, Chae J, Yun HS, Zirin H (1997) Power spectra of solar network and non-network fields. Sol Phys 171:269–282. https://doi.org/10.1023/A:1004904406126
Lehahn Y, D’Ovidio F, Lévy M, Heifetz E (2007) Stirring of the northeast Atlantic spring bloom: a Lagrangian analysis based on multisatellite data. J Geophys Res 112:C08005. https://doi.org/10.1029/2006JC003927
Leighton RB, Noyes RW, Simon GW (1962) Velocity fields in the solar atmosphere. I. Preliminary report. Astrophys J 135:474. https://doi.org/10.1086/147285
Lekien F, Ross SD (2010) The computation of finite-time Lyapunov exponents on unstructured meshes and for non-Euclidean manifolds. Chaos 20(1):017505. https://doi.org/10.1063/1.3278516
Lekien F, Coulliette C, Mariano AJ, Ryan EH, Shay LK, Haller G, Marsden J (2005) Pollution release tied to invariant manifolds: a case study for the coast of Florida. Physica D 210:1–20. https://doi.org/10.1016/j.physd.2005.06.023
Lin H (1995) On the distribution of the solar magnetic fields. Astrophys J 446:421. https://doi.org/10.1086/175800
Lin H, Kuhn JR (1992) Precision IR and visible solar photometry. Sol Phys 141:1–26. https://doi.org/10.1007/BF00155900
Lindsey C, Braun DC (2004) Principles of seismic holography for diagnostics of the shallow subphotosphere. Astrophys J Suppl Ser 155:209–225. https://doi.org/10.1086/424736
Lindsey C, Braun DC, Jefferies SM, Woodard MF, Fan Y, Gu Y, Redfield S (1996) Doppler acoustic diagnostics of subsurface solar magnetic structure. Astrophys J 470:636. https://doi.org/10.1086/177895
Lisle J, DeRosa M, Toomre J (2000) New approach to study extended evolution of supergranular flows and their advection of magnetic elements. Sol Phys 197:21–30. https://doi.org/10.1023/A:1026556721220
Lisle JP, Rast MP, Toomre J (2004) Persistent north-south alignment of the solar supergranulation. Astrophys J 608:1167–1174. https://doi.org/10.1086/420691
Lites BW, Kubo M, Socas-Navarro H, Berger T, Frank Z, Shine R, Tarbell T, Title A, Ichimoto K, Katsukawa Y, Tsuneta S, Suematsu Y, Shimizu T, Nagata S (2008) The horizontal magnetic flux of the quiet-Sun internetwork as observed with the Hinode spectro-polarimeter. Astrophys J 672:1237–1253. https://doi.org/10.1086/522922
Lites BW, Rempel M, Borrero JM, Danilovic S (2017) Are internetwork magnetic fields in the solar photosphere horizontal or vertical? Astrophys J 835:14. https://doi.org/10.3847/1538-4357/835/1/14
Livingston W, Harvey J (1971) The Kitt Peak magnetograph. IV: 40-channel probe and the detection of weak photospheric fields. In: Howard R (ed) Solar magnetic fields. IAU symposium, vol 43. D. Reidel, Dordrecht, p 51. https://doi.org/10.1007/978-94-010-3117-2_6
Livingston WC, Harvey J, (1975) A new component of solar magnetism–the inner network fields. Abstracts of papers presented at the SPD meeting, held 19–23, (Jan 1975) at Boulder. Colorado, Bulletin of the American Astronomical Society 7:346
Lohse D, Xia KQ (2010) Small-scale properties of turbulent Rayleigh-Bénard convection. Annu Rev Fluid Mech 42:335. https://doi.org/10.1146/annurev.fluid.010908.165152
Longcope DW, Parnell CE (2009) The number of magnetic null points in the quiet Sun corona. Sol Phys 254:51–75. https://doi.org/10.1007/s11207-008-9281-x
Longcope DW, McLeish TCB, Fisher GH (2003) A viscoelastic theory of turbulent fluid permeated with fibril magnetic fields. Astrophys J 599:661–674. https://doi.org/10.1086/379280
López Ariste A, Manso Sainz R, Asensio Ramos A, Martinéz Gonzaléz MJ, Malherbe JM, Gelly B (2010) The nature of solar internetwork magnetic fields: constraints from Hanle and Zeeman diagnostics. Unpublished
Löptien B, Birch AC, Duvall TL Jr, Gizon L, Proxauf B, Schou J (2017) Measuring solar active region inflows with local correlation tracking of granulation. Astron Astrophys 606:A28. https://doi.org/10.1051/0004-6361/201731064. arXiv:1705.08833
Lord JW, Cameron RH, Rast MP, Rempel M, Roudier T (2014) The role of subsurface flows in solar surface convection: modeling the spectrum of supergranular and larger scale flows. Astrophys J 793:24. https://doi.org/10.1088/0004-637X/793/1/24
L’vov VS (1991) Spectra of velocity and temperature fluctuations with constant entropy flux of fully developed free-convective turbulence. Phys Rev Lett 67:687–690. https://doi.org/10.1103/PhysRevLett.67.687
Malherbe JM, Roudier T, Stein R, Frank Z (2018) Dynamics of trees of fragmenting granules in the quiet Sun: Hinode/SOT observations compared to numerical simulation. Sol Phys 293:4. https://doi.org/10.1007/s11207-017-1225-x
Martin SF (1988) The identification and interaction of network, intranetwork, and ephemeral-region magnetic fields. Sol Phys 117:243–259. https://doi.org/10.1007/BF00147246
Martínez González MJ, Asensio Ramos A, López Ariste A, Manso Sainz R (2008) Near-IR internetwork spectro-polarimetry at different heliocentric angles. Astron Astrophys 479:229–234. https://doi.org/10.1051/0004-6361:20078500
Martínez González MJ, Manso Sainz R, Asensio Ramos A, Hijano E (2012) Dead calm areas in the very quiet Sun. Astrophys J 755:175. https://doi.org/10.1088/0004-637X/755/2/175
Massaguer JM, Zahn J (1980) Cellular convection in a stratified atmosphere. Astron Astrophys 87:315–327
Matloch L, Cameron R, Schmitt D, Schüssler M (2009) Modelling of solar mesogranulation. Astron Astrophys 504:1041–1055. https://doi.org/10.1051/0004-6361/200811200
Matthews P, Cox S (1997) Linear stability of rotating convection in an imposed shear flow. J Fluid Mech 350:271–293. https://doi.org/10.1017/S0022112097006903
Matthews PC, Hurlburt NE, Proctor MRE, Brownjohn DP (1992) Compressible magnetoconvection in oblique fields–linearized theory and simple nonlinear models. J Fluid Mech 240:559–569. https://doi.org/10.1017/S002211209200020X
McAteer RTJ, Gallagher PT, Conlon PA (2010) Turbulence, complexity, and solar flares. Adv Space Res 45:1067–1074. https://doi.org/10.1016/j.asr.2009.08.026. arXiv:0909.5636
McIntosh SW, Leamon RJ, Hock RA, Rast MP, Ulrich RK (2011) Observing evolution in the supergranular network length scale during periods of low solar activity. Astrophys J Lett 730:L3. https://doi.org/10.1088/2041-8205/730/1/L3
Meshalkin LD, Sinai I (1961) Investigation of the stability of a stationary solution of a system of equations for the plane movement of an incompressible viscous fluid. Prikl Mat Mekh 25(6):1140–1143
Meunier N (1999) Fractal analysis of Michelson Doppler Imager magnetograms: a contribution to the study of the formation of solar active regions. Astrophys J 515:801–811. https://doi.org/10.1086/307050
Meunier N (2003) Statistical properties of magnetic structures: their dependence on scale and solar activity. Astron Astrophys 405:1107–1120. https://doi.org/10.1051/0004-6361:20030713
Meunier N, Roudier T (2007) The superrotation of solar supergranules. Astron Astrophys 466:691–696. https://doi.org/10.1051/0004-6361:20066790
Meunier N, Roudier T, Tkaczuk R (2007a) Are supergranule sizes anti-correlated with magnetic activity? Astron Astrophys 466:1123–1130. https://doi.org/10.1051/0004-6361:20066644
Meunier N, Tkaczuk R, Roudier T (2007b) Intensity variations inside supergranules. Astron Astrophys 463:745–753. https://doi.org/10.1051/0004-6361:20066314
Meunier N, Tkaczuk R, Roudier T, Rieutord M (2007c) Velocities and divergences as a function of supergranule size. Astron Astrophys 461:1141–1147. https://doi.org/10.1051/0004-6361:20065625
Meunier N, Roudier T, Rieutord M (2008) Supergranules over the solar cycle. Astron Astrophys 488:1109–1115. https://doi.org/10.1051/0004-6361:20078835
Miesch MS (2005) Large-scale dynamics of the convection zone and tachocline. Living Rev Sol Phys 2:1. https://doi.org/10.12942/lrsp-2005-1
Miesch MS, Brun AS, DeRosa ML, Toomre J (2008) Structure and evolution of giant cells in global models of solar convection. Astrophys J 673:557–575. https://doi.org/10.1086/523838
Moffatt HK (1961) The amplification of a weak applied magnetic field by turbulence in fluids of moderate conductivity. J Fluid Mech 11:625–635. https://doi.org/10.1017/S0022112061000779
Muller R (1983) The dynamical behavior of facular points in the quiet photosphere. Sol Phys 85:113–121. https://doi.org/10.1007/BF00148262
Muller R, Mena B (1987) Motions around a decaying sunspot. Sol Phys 112:295–303. https://doi.org/10.1007/BF00148783
Münzer H, Schröter EH, Wöhl H, Hanslmeier A (1989) Pole-equator-difference of the size of the chromospheric Ca II-K-network in quiet and active solar regions. Astron Astrophys 213:431–435
Murphy JO (1977) The effect of a magnetic field on the onset of thermal convection when constant flux boundary conditions apply. Proc Astron Soc Australia 3:164. https://doi.org/10.1017/S132335800001523X
Nagashima K, Zhao J, Kosovichev AG, Sekii T (2011) Detection of supergranulation alignment in polar regions of the Sun by helioseismology. Astrophys J Lett 726:L17. https://doi.org/10.1088/2041-8205/726/2/L17
Nesme-Ribes E, Meunier N, Collin B (1996) Fractal analysis of magnetic patterns from Meudon spectroheliograms. Astron Astrophys 308:213–218
Newell AC, Passot T, Souli M (1990) The phase diffusion and mean drift equations for convection at finite Rayleigh numbers in large containers. J Fluid Mech 220:187–252. https://doi.org/10.1017/S0022112090003238
Niemela JJ, Skrbek L, Sreenivasan KR, Donnelly RJ (2000) Turbulent convection at very high Rayleigh numbers. Nature 404:837–840
Niemela JJ, Skrbek L, Sreenivasan KR, Donnelly RJ (2001) The wind in confined thermal convection. J Fluid Mech 449:169–178. https://doi.org/10.1017/S0022112001006310
Nisenson P, van Ballegooijen AA, de Wijn AG, Sütterlin P (2003) Motions of isolated G-band bright points in the solar photosphere. Astrophys J 587:458–463. https://doi.org/10.1086/368067
Nordlund Å (1982) Numerical simulations of the solar granulation. I. Basic equations and methods. Astron Astrophys 107:1–10
Nordlund Å (1985) Solar convection. Sol Phys 100:209–235. https://doi.org/10.1007/BF00158429
Nordlund Å, Galsgaard K, Stein RF (1994) Magnetoconvection and magnetoturbulence. In: Rutten RJ, Schrijver CJ (eds) Solar surface magnetism. NATO ASI Series C, vol 433. Kluwer Academic, Dordrecht, p 471. https://doi.org/10.1007/978-94-011-1188-1_37
Nordlund Å, Stein RF, Asplund M (2009) Solar surface convection. Living Rev Sol Phys 6:2. https://doi.org/10.12942/lrsp-2009-2
November LJ (1989) The vertical component of the supergranular convection. Astrophys J 344:494–503. https://doi.org/10.1086/167818
November LJ (1994) Inferring the depth extent of the horizontal supergranular flow. Sol Phys 154:1–17. https://doi.org/10.1007/BF00676773
November LJ, Simon GW (1988) Precise proper-motion measurement of solar granulation. Astrophys J 333:427–442. https://doi.org/10.1086/166758
November LJ, Toomre J, Gebbie KB, Simon GW (1981) The detection of mesogranulation on the Sun. Astrophys J Lett 245:L123–L126. https://doi.org/10.1086/183539
Oboukhov AM (1959) The influence of hydrostatic forces on the structure of the temperature field turbulent flow. Dokl Akad Nauk SSSR 125:1246–1248
Orozco Suárez D, Bellot Rubio LR, del Toro Iniesta JC, Tsuneta S, Lites BW, Ichimoto K, Katsukawa Y, Nagata S, Shimizu T, Shine RA, Suematsu Y, Tarbell TD, Title AM (2007) Quiet-Sun internetwork magnetic fields from the inversion of Hinode measurements. Astrophys J Lett 670:L61–L64. https://doi.org/10.1086/524139
Orozco Suárez D, Katsukawa Y, Bellot Rubio LR (2012) The connection between internetwork magnetic elements and supergranular flows. Astrophys J Lett 758:L38. https://doi.org/10.1088/2041-8205/758/2/L38
Pandey A, Scheel JD, Schumacher J (2018) Turbulent superstructures in Rayleigh–Bénard convection. Nature Commun 9:2118. https://doi.org/10.1038/s41467-018-04478-0. arXiv:1801.04478
Parfinenko LD, Efremov VI, Solov’ev AA (2014) Supergranulation velocity field from the MDI (SOHO) data. Geomagn Aeron 54:1026–1031. https://doi.org/10.1134/S0016793214080143
Parker EN (1963) Kinematical hydromagnetic theory and its application to the low solar photosphere. Astrophys J 138:552. https://doi.org/10.1086/147663
Parker EN (1974) Hydraulic concentration of magnetic fields in the solar photosphere. I. Turbulent pumping. Astrophys J 189:563–568. https://doi.org/10.1086/152835
Parodi A, von Hardenberg J, Passoni G, Provenzale A, Spiegel EA (2004) Clustering of plumes in turbulent convection. Phys Rev Lett 92(19):194503. https://doi.org/10.1103/PhysRevLett.92.194503
Pietarila Graham J, Danilovic S, Schüssler M (2009) Turbulent magnetic fields in the quiet Sun: implications of Hinode observations and small-scale dynamo simulations. Astrophys J 693:1728–1735. https://doi.org/10.1088/0004-637X/693/2/1728
Plaskett HH (1916) A variation in the solar rotation. Astrophys J 43:145. https://doi.org/10.1086/142239
Potts HE, Barrett RK, Diver DA (2004) Balltracking: an highly efficient method for tracking flow fields. Astron Astrophys 424:253–262. https://doi.org/10.1051/0004-6361:20035891
Proctor MRE (1983) Amplification of magnetic fields by compressible convection. In: Stenflo JO (ed) Solar and stellar magnetic fields: origins and coronal effects. IAU symposium, vol 102. Reidel, Dordrecht, pp 301–304
Proctor MRE, Weiss NO (1982) Magnetoconvection. Rep Prog Phys 45:1317–1379. https://doi.org/10.1088/0034-4885/45/11/003
Raju KP, Singh J (2002) Dependence of supergranular length-scales on network magnetic fields. Sol Phys 207:11–16. https://doi.org/10.1023/A:1015585010078
Rast MP (1998) Compressible plume dynamics and stability. J Fluid Mech 369:125–149
Rast MP (2003a) Supergranulation: new observation, possible explanation. In: Sawaya-Lacoste H (ed) GONG+ 2002. Local and global helioseismology: the present and future. ESA special publication, vol SP-517. ESA Publications Division, Noordwijk, pp 163–172
Rast MP (2003b) The scales of granulation, mesogranulation, and supergranulation. Astrophys J 597:1200–1210. https://doi.org/10.1086/381221
Rast MP, Toomre J (1993) Compressible convection with ionization. II. Thermal boundary-layer instability. Astrophys J 419:240. https://doi.org/10.1086/173478
Rast MP, Lisle JP, Toomre J (2004) The spectrum of the solar supergranulation: multiple nonwave components. Astrophys J 608:1156–1166. https://doi.org/10.1086/420690
Rempel M (2014) Numerical simulations of quiet Sun magnetism: on the contribution from a small-scale dynamo. Astrophys J 789:132. https://doi.org/10.1088/0004-637X/789/2/132
Requerey IS, Ruiz Cobo B, Gošić M, Bellot Rubio LR (2018) Persistent magnetic vortex flow at a supergranular vertex. Astron Astrophys. https://doi.org/10.1051/0004-6361/201731842. arXiv:1712.01510
Rieutord M (2008) The solar dynamo. C R Physique 9:757–765. https://doi.org/10.1016/j.crhy.2008.07.008
Rieutord M, Rincon F (2010) The Sun’s supergranulation. Living Rev Sol Phys 7:2. https://doi.org/10.12942/lrsp-2010-2
Rieutord M, Zahn J (1995) Turbulent plumes in stellar convective envelopes. Astron Astrophys 296:127
Rieutord M, Roudier T, Malherbe JM, Rincon F (2000) On mesogranulation, network formation and supergranulation. Astron Astrophys 357:1063–1072
Rieutord M, Roudier T, Ludwig H, Nordlund Å, Stein R (2001) Are granules good tracers of solar surface velocity fields? Astron Astrophys 377:L14–L17. https://doi.org/10.1051/0004-6361:20011160
Rieutord M, Ludwig H, Roudier T, Nordlund Å, Stein R (2002) A simulation of solar convection at supergranulation scale. Nuovo Cimento C 25:523
Rieutord M, Roudier T, Roques S, Ducottet C (2007) Tracking granules on the Sun’s surface and reconstructing velocity fields. I. The CST algorithm. Astron Astrophys 471:687–694. https://doi.org/10.1051/0004-6361:20066491
Rieutord M, Meunier N, Roudier T, Rondi S, Beigbeder F, Parès L (2008) Solar supergranulation revealed by granule tracking. Astron Astrophys 479:L17–L20. https://doi.org/10.1051/0004-6361:20079077
Rieutord M, Roudier T, Rincon F, Malherbe J, Meunier N, Berger T, Frank Z (2010) On the power spectrum of solar surface flows. Astron Astrophys 512:A4. https://doi.org/10.1051/0004-6361/200913303. arXiv:0911.3319
Rincon F (2004) Large-scale dynamics of convection in the solar photosphere. PhD thesis, Université Paul Sabatier—Toulouse III. https://tel.archives-ouvertes.fr/tel-00008710
Rincon F (2006) Anisotropy, inhomogeneity and inertial-range scalings in turbulent convection. J Fluid Mech 563:43–69. https://doi.org/10.1017/S0022112006000917
Rincon F (2007) Theories of convection and the spectrum of turbulence in the solar photosphere. In: Kupka F, Roxburgh I, Chan K (eds) Convection in astrophysics. IAU symposium, vol 239. Cambridge University Press, Cambridge, pp 58–63. https://doi.org/10.1017/S1743921307000117
Rincon F, Rieutord M (2003) Stability of a compressible fluid layer in a magnetic field: a simple model for supergranulation. In: Combes F, Barret D, Contini T, Pagani L (eds) SF2A-2003: Semaine de l’Astrophysique Francaise, p 103
Rincon F, Lignières F, Rieutord M (2005) Mesoscale flows in large aspect ratio simulations of turbulent compressible convection. Astron Astrophys 430:L57–L60. https://doi.org/10.1051/0004-6361:200400130
Rincon F, Roudier T, Schekochihin AA, Rieutord M (2017) Supergranulation and multiscale flows in the solar photosphere. Global observations vs. a theory of anisotropic turbulent convection. Astron Astrophys 599:A69. https://doi.org/10.1051/0004-6361/201629747
Roudier T, Muller R (2004) Relation between families of granules, mesogranules and photospheric network. Astron Astrophys 419:757–762. https://doi.org/10.1051/0004-6361:20035739
Roudier T, Rieutord M, Malherbe JM, Vigneau J (1999) Determination of horizontal velocity fields at the Sun’s surface with high spatial and temporal resolution. Astron Astrophys 349:301–311
Roudier T, Rieutord M, Brito D, Rincon F, Malherbe JM, Meunier N, Berger T, Frank Z (2009) Mesoscale dynamics on the Sun’s surface from HINODE observations. Astron Astrophys 495:945–952. https://doi.org/10.1051/0004-6361:200811101
Roudier T, Malherbe JM, Rieutord M, Frank Z (2016) Relation between trees of fragmenting granules and supergranulation evolution. Astron Astrophys 590:A121. https://doi.org/10.1051/0004-6361/201628111
Rouppe van der Voort LHM, Hansteen VH, Carlsson M, Fossum A, Marthinussen E, van Noort MJ, Berger TE (2005) Solar magnetic elements at 0.1 arcsec resolution. II. Dynamical evolution. Astron Astrophys 435:327–337. https://doi.org/10.1051/0004-6361:20042561
Sano M, Wu XZ, Libchaber A (1989) Turbulence in helium-gas free convection. Phys Rev A 40:6421–6430. https://doi.org/10.1103/PhysRevA.40.6421
Schekochihin AA, Iskakov AB, Cowley SC, McWilliams JC, Proctor MRE, Yousef TA (2007) Fluctuation dynamo and turbulent induction at low magnetic Prandtl numbers. New J Phys 9:300. https://doi.org/10.1088/1367-2630/9/8/300
Schou J (2003) Wavelike properties of solar supergranulation detected in Doppler shift data. Astrophys J Lett 596:L259–L262. https://doi.org/10.1086/379529
Schou J, Antia HM, Basu S, Bogart RS, Bush RI, Chitre SM, Christensen-Dalsgaard J, di Mauro MP, Dziembowski WA, Eff-Darwich A, Gough DO, Haber DA, Hoeksema JT, Howe R, Korzennik SG, Kosovichev AG, Larsen RM, Pijpers FP, Scherrer PH, Sekii T, Tarbell TD, Title AM, Thompson MJ, Toomre J (1998) Helioseismic studies of differential rotation in the solar envelope by the solar oscillations investigation using the Michelson Doppler Imager. Astrophys J 505:390–417. https://doi.org/10.1086/306146
Schrijver CJ, Hagenaar HJ, Title AM (1997) On the patterns of the solar granulation and supergranulation. Astrophys J 475:328. https://doi.org/10.1086/303528
Schüssler M, Vögler A (2008) Strong horizontal photospheric magnetic field in a surface dynamo simulation. Astron Astrophys 481:L5–L8. https://doi.org/10.1051/0004-6361:20078998
Schwarzschild M (1975) On the scale of photospheric convection in red giants and supergiants. Astrophys J 195:137–144. https://doi.org/10.1086/153313
Sekii T, Kosovichev AG, Zhao J, Tsuneta S, Shibahashi H, Berger TE, Ichimoto K, Katsukawa Y, Lites B, Nagata S, Shimizu T, Shine RA, Suematsu Y, Tarbell TD, Title AM (2007) Initial helioseismic observations by Hinode/SOT. PASJ 59:637. https://doi.org/10.1093/pasj/59.sp3.S637
Sheeley NR Jr (1969) The evolution of the photospheric network. Sol Phys 9:347–357. https://doi.org/10.1007/BF02391657
Sheeley NR Jr (1972) Observations of the horizontal velocity field surrounding sunspots. Sol Phys 25:98–103. https://doi.org/10.1007/BF00155747
Sheeley NR Jr, Bhatnagar A (1971) Two-dimensional observations of the velocity fields in and around sunspots. Sol Phys 19:338–346. https://doi.org/10.1007/BF00146062
Shine RA, Title AM, Tarbell TD, Topka KP (1987) White light sunspot observations from the Solar Optical Universal Polarimeter on Spacelab-2. Science 238:1264–1267. https://doi.org/10.1126/science.238.4831.1264
Shine RA, Simon GW, Hurlburt NE (2000) Supergranule and mesogranule evolution. Sol Phys 193:313–331. https://doi.org/10.1023/A:1005207625696
Simon GW, Leighton RB (1964) Velocity fields in the solar atmosphere. III. Large-scale motions, the chromospheric network, and magnetic fields. Astrophys J 140:1120. https://doi.org/10.1086/148010
Simon GW, Weiss NO (1968) Supergranules and the hydrogen convection zone. Z Astrophys 69:435
Simon GW, Title AM, Topka KP, Tarbell TD, Shine RA, Ferguson SH, Zirin H, Team SOUP (1988) On the relation between photospheric flow fields and the magnetic field distribution on the solar surface. Astrophys J 327:964–967. https://doi.org/10.1086/166253
Simon GW, Title AM, Weiss NO (1991) Modeling mesogranules and exploders on the solar surface. Astrophys J 375:775–788. https://doi.org/10.1086/170242
Singh J, Bappu MKV (1981) A dependence on solar cycle of the size of the \(\text{ Ca }^{+}\) network. Sol Phys 71:161–168. https://doi.org/10.1007/BF00153615
Sivashinsky G, Yakhot V (1985) Negative viscosity effect in large-scale flows. Phys Fluids 28:1040–1042. https://doi.org/10.1063/1.865025
Snodgrass HB, Ulrich RK (1990) Rotation of Doppler features in the solar photosphere. Astrophys J 351:309–316. https://doi.org/10.1086/168467
Solanki SK (1993) Small-scale solar magnetic fields: an overview. Space Sci Rev 63:1–188. https://doi.org/10.1007/BF00749277
Solanki SK (2003) Sunspots: an overview. Astron Astrophys Rev 11:153–286. https://doi.org/10.1007/s00159-003-0018-4
Sparrow EM, Goldstein RJ, Jonsson VK (1964) Thermal instability in a horizontal fluid layer: effect of boundary conditions and non-linear temperature profile. J Fluid Mech 18:513–528. https://doi.org/10.1017/S0022112064000386
Spruit HC (1974) A model of the solar convection zone. Sol Phys 34:277–290. https://doi.org/10.1007/BF00153665
Spruit HC (1976) Pressure equilibrium and energy balance of small photospheric fluxtubes. Sol Phys 50:269–295. https://doi.org/10.1007/BF00155292
Spruit HC (1979) Convective collapse of flux tubes. Sol Phys 61:363–378. https://doi.org/10.1007/BF00150420
Spruit HC, Zweibel EG (1979) Convective instability of thin flux tubes. Sol Phys 62:15–22. https://doi.org/10.1007/BF00150128
Spruit HC, Nordlund Å, Title AM (1990) Solar convection. Annu Rev. Astron Astrophys 28:263–301. https://doi.org/10.1146/annurev.aa.28.090190.001403
Stangalini M (2014) Photospheric supergranular flows and magnetic flux emergence. Astron Astrophys 561:L6. https://doi.org/10.1051/0004-6361/201322831
Stein RF, Nordlund Å (1989) Topology of convection beneath the solar surface. Astrophys J Lett 342:L95–L98. https://doi.org/10.1086/185493
Stein RF, Nordlund Å (1998) Simulations of solar granulation. I. General properties. Astrophys J 499:914. https://doi.org/10.1086/305678
Stein RF, Georgobiani D, Schafenberger W, Nordlund Å, Benson D (2009) Supergranulation scale convection simulations. In: Stempels E (ed) Cool stars, stellar systems and the Sun (15th Cambridge workshop). AIP conference proceedings, vol 1094. American Institute of Physics, Melville, NY, pp 764–767. https://doi.org/10.1063/1.3099227
Stein RF, Lagerfjärd A, Nordlund Å, Georgobiani D (2011) Solar flux emergence simulations. Sol Phys 268:271–282. https://doi.org/10.1007/s11207-010-9510-y
Stenflo JO (2012) Scaling laws for magnetic fields on the quiet Sun. Astron Astrophys 541:A17. https://doi.org/10.1051/0004-6361/201218939
Stenflo JO (2013) Solar magnetic fields as revealed by Stokes polarimetry. Astron Astrophys Rev 21:66. https://doi.org/10.1007/s00159-013-0066-3
Stenflo JO, Holzreuter R (2002) Empirical view of magnetoconvection. In: Sawaya-Lacoste H (ed) SOLMAG 2002. Proceedings of the magnetic coupling of the solar atmosphere euroconference. ESA special publication, vol SP-505. ESA Publications Division, Noordwijk, pp 101–104
Stenflo JO, Holzreuter R (2003a) Distribution of magnetic fields at scales beyond the spatial resolution limit. In: Pevtsov AA, Uitenbroek H (eds) Current theoretical models and future high resolution solar observations: preparing for ATST. ASP conference series, vol 286. Astronomical Society of the Pacific, San Francisco, p 169
Stenflo JO, Holzreuter R (2003b) Flux tubes or fractal distributions–on the nature of photospheric magnetic fields. Astron Nachr 324:397. https://doi.org/10.1002/asna.200310144
Stix M (2004) The Sun: an introduction, 2nd edn. Astronomy and Astrophysics Library, Springer, Berlin
Straus T, Bonaccini D (1997) Dynamics of the solar photosphere. I. Two-dimensional spectroscopy of mesoscale phenomena. Astron Astrophys 324:704–712
Straus T, Deubner FL, Fleck B (1992) Is mesogranulation a distinct regime of convection? Astron Astrophys 256:652–659
Švanda M (2015) Issues with time-distance inversions for supergranular flows. Astron Astrophys 575:A122. https://doi.org/10.1051/0004-6361/201425203
Švanda M, Zhao J, Kosovichev AG (2007) Comparison of large-scale flows on the Sun measured by time-distance helioseismology and local correlation tracking. Sol Phys 241:27–37. https://doi.org/10.1007/s11207-007-0333-4
Tao L, Weiss NO, Brownjohn DP, Proctor MRE (1998) Flux separation in stellar magnetoconvection. Astrophys J Lett 496:L39. https://doi.org/10.1086/311240
Thomas JH, Weiss NO (2008) Sunspots and starspots, Cambridge Astrophysics Series, vol 46. Cambridge University Press, Cambridge
Thompson SD (2005) Magnetoconvection in an inclined magnetic field: linear and weakly non-linear models. Mon Not R Astron Soc 360:1290–1304. https://doi.org/10.1111/j.1365-2966.2005.09127.x
Thual O (1992) Zero-Prandtl-number convection. J Fluid Mech 240:229–258. https://doi.org/10.1017/S0022112092000089
Tian H, Potts HE, Marsch E, Attie R, He JS (2010) Horizontal supergranule-scale motions inferred from TRACE ultraviolet observations of the chromosphere. Astron Astrophys 519:A58. https://doi.org/10.1051/0004-6361/200913254
Title AM, Tarbell TD, Topka KP, Ferguson SH, Shine RA, Team SOUP (1989) Statistical properties of solar granulation derived from the SOUP instrument on Spacelab 2. Astrophys J 336:475–494. https://doi.org/10.1086/167026
Tkaczuk R, Rieutord M, Meunier N, Roudier T (2007) Tracking granules on the Sun’s surface and reconstructing velocity fields. II. Error analysis. Astron Astrophys 471:695–703. https://doi.org/10.1051/0004-6361:20066492
Toomre J, Thompson MJ (2015) Prospects and challenges for helioseismology. Space Sci Rev 196:1. https://doi.org/10.1007/s11214-015-0147-x
Trujillo Bueno J, Shchukina N, Asensio Ramos A (2004) A substantial amount of hidden magnetic energy in the quiet Sun. Nature 430:326–329. https://doi.org/10.1038/nature02669. arXiv:astro-ph/0409004
Tsuneta S, Ichimoto K, Katsukawa Y, Lites BW, Matsuzaki K, Nagata S, Orozco Suárez D, Shimizu T, Shimojo M, Shine RA, Suematsu Y, Suzuki TK, Tarbell TD, Title AM (2008) The magnetic landscape of the Sun’s polar region. Astrophys J 688:1374–1381. https://doi.org/10.1086/592226
Turner JS (1986) Turbulent entrainment: the development of the entrainment assumption, and its application to geophysical flows. J Fluid Mech 173:431–471. https://doi.org/10.1017/S0022112086001222
Unno W, Ando H (1979) Instability of a thin magnetic tube in the solar atmosphere. Geophys Astrophys Fluid Dyn 12:107–115. https://doi.org/10.1080/03091927908242679
Ustyugov SD (2006) Magnetohydrodynamic simulation of solar supergranulation. In: Zank GP, Pogorelov NV (eds) Numerical modeling of space plasma flows. ASP conference series, vol 359. Astronomical Society of the Pacific, San Francisco, p 226
Ustyugov SD (2008) Large eddy simulation of solar photosphere convection with realistic physics. In: Howe R, Komm RW, Balasubramaniam KS, Petrie GJD (eds) Subsurface and atmospheric influences on solar activity. ASP conference series, vol 383. Astronomical Society of the Pacific, San Francisco, p 43
Ustyugov SD (2009) Realistic magnetohydrodynamical simulations of local solar supergranulation. In: Dikpati M, Arentoft T, González Hernández I, Lindsey C, Hill F (eds) GONG 2008/SOHO 21. Solar-stellar dynamos as revealed by helio- and asteroseismology. ASP conference series, vol 416. Astronomical Society of the Pacific, San Francisco, p 427
Valdettaro L, Meneguzzi M (1991) Compressible magnetohydrodynamics in spherical geometry. In: Tuominen I, Moss D, Rüdiger G (eds) The Sun and cool stars: activity, magnetism, dynamos (IAU colloqium 130). Lecture notes in physics, vol 380. Springer, Berlin, p 80
van der Borght R (1974) Nonlinear thermal convection in a layer with imposed energy flux. Aust J Phys 27:481–493. https://doi.org/10.1071/PH740481
Verzicco R, Camussi R (2003) Numerical experiments on strongly turbulent thermal convection in a slender cylindrical cell. J Fluid Mech 477:19–49. https://doi.org/10.1017/S0022112002003063
Vickers GT (1971) On the formation of giant cells and supergranules. Astrophys J 163:363. https://doi.org/10.1086/150776
Vincent A, Meneguzzi M (1991) The spatial structure and statistical properties of homogeneous turbulence. J Fluid Mech 225:1–20. https://doi.org/10.1017/S0022112091001957
Vögler A (2005) On the effect of photospheric magnetic fields on solar surface brightness. Results of radiative MHD simulations. Mem Soc Astron Ital 76:842
Vögler A, Schüssler M (2007) A solar surface dynamo. Astron Astrophys 465:L43–L46. https://doi.org/10.1051/0004-6361:20077253
von Hardenberg J, Parodi A, Passoni G, Provenzale A, Spiegel EA (2008) Large-scale patterns in Rayleigh-Bénard convection. Phys Lett A 372:2223–2229. https://doi.org/10.1016/j.physleta.2007.10.099
Wang H (1988) On the relationship between magnetic fields and supergranule velocity fields. Sol Phys 117:343–358. https://doi.org/10.1007/BF00147252
Wang H (1989) Do mesogranules exist? Sol Phys 123:21–32. https://doi.org/10.1007/BF00150009
Wang H, Zirin H (1989) Study of supergranules. Sol Phys 120:1–17. https://doi.org/10.1007/BF00148532
Webb AR, Roberts B (1978) Vertical motions in an intense magnetic flux tube. II. Convective instability. Sol Phys 59:249–274. https://doi.org/10.1007/BF00951833
Wedemeyer-Böhm S, Rouppe van der Voort L (2009) On the continuum intensity distribution of the solar photosphere. Astron Astrophys 503:225–239. https://doi.org/10.1051/0004-6361/200911983
Weiss NO, Proctor MRE (2014) Magnetoconvection. Cambridge monographs on mechanics. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511667459
Williams PE, Pesnell WD (2011) Comparisons of supergranule characteristics during the solar minima of cycles 22/23 and 23/24. Sol Phys 270:125–136. https://doi.org/10.1007/s11207-011-9718-5
Williams PE, Hathaway DH, Cuntz M (2007) Solar Rossby wave “hills” identified as supergranules. Astrophys J Lett 662:L135–L138. https://doi.org/10.1086/519456
Williams PE, Pesnell WD, Beck JG, Lee S (2014) Analysis of supergranule sizes and velocities using Solar Dynamics Observatory (SDO)/Helioseismic Magnetic Imager (HMI) and Solar and Heliospheric Observatory (SOHO)/Michelson Doppler Imager (MDI) dopplergrams. Sol Phys 289:11–25. https://doi.org/10.1007/s11207-013-0330-8
Wolff C (1995) Oscillation-convection coupling: cause of supergranulation. Astrophys J 443:423–433. https://doi.org/10.1086/175535
Woodard MF (2007) Probing supergranular flow in the solar interior. Astrophys J 668:1189–1195. https://doi.org/10.1086/521391
Worden SP (1975) Infrared observations of supergranule temperature structure. Sol Phys 45:521–532. https://doi.org/10.1007/BF00158467
Worden SP, Simon GW (1976) A study of supergranulation using a diode array magnetograph. Sol Phys 46:73–91. https://doi.org/10.1007/BF00157555
Xi H, Lam S, Xia K (2004) From laminar plumes to organized flows: the onset of large-scale circulation in turbulent thermal convection. J Fluid Mech 503:47–56. https://doi.org/10.1017/S0022112004008079
Yeates AR, Hornig G, Welsch BT (2012) Lagrangian coherent structures in photospheric flows and their implications for coronal magnetic structure. Astron Astrophys 539:A1. https://doi.org/10.1051/0004-6361/201118278
Yelles Chaouche L, Moreno-Insertis F, Martínez Pillet V, Wiegelmann T, Bonet JA, Knölker M, Bellot Rubio LR, del Toro Iniesta JC, Barthol P, Gandorfer A, Schmidt W, Solanki SK (2011) Mesogranulation and the solar surface magnetic field distribution. Astrophys J Lett 727:L30. https://doi.org/10.1088/2041-8205/727/2/L30
Zhang K, Busse FH (1987) On the onset of convection in rotating spherical shells. Geophys Astrophys Fluid Dyn 39:119–147. https://doi.org/10.1080/03091928708208809
Zhao J, Kosovichev AG (2003) On the inference of supergranular flows by time–distance helioseismology. In: Sawaya-Lacoste H (ed) GONG+ 2002. Local and global helioseismology: the present and future. ESA special publication, vol SP-517. ESA Publications Division, Noordwijk, pp 417–420
Zhao J, Kosovichev AG, Duvall TL Jr (2001) Investigation of mass flows beneath a sunspot by time-distance helioseismology. Astrophys J 557:384–388. https://doi.org/10.1086/321491
Zhao J, Kosovichev AG, Duvall TL Jr (2004) On the relationship between the rotational velocity and the field strength of solar magnetic elements. Astrophys J Lett 607:L135–L138. https://doi.org/10.1086/421974
Zhao J, Kosovichev AG, Sekii T (2010) High-resolution helioseismic imaging of subsurface structures and flows of a solar active region observed by Hinode. Astrophys J 708:304–313. https://doi.org/10.1088/0004-637X/708/1/304
Acknowledgements
We would like to thank our many collaborators and colleagues, most importantly Thierry Roudier, for sustaining our interest in the supergranulation problem over the years, and for sharing their insights on solar convection and magnetism with us. We are also grateful to the referees of the 2010 and 2018 versions of this review for their detailed reading and comments on the long manuscript, and for pointing out several relevant references that we had overlooked.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is a revised version of https://doi.org/10.12942/lrsp-2010-2.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Rincon, F., Rieutord, M. The Sun’s supergranulation. Living Rev Sol Phys 15, 6 (2018). https://doi.org/10.1007/s41116-018-0013-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s41116-018-0013-5
Keywords
Article history
Latest
The Sun’s supergranulation- Published:
- 10 September 2018
- Received:
- 14 February 2018
- Accepted:
- 05 July 2018
DOI: https://doi.org/10.1007/s41116-018-0013-5
Original
The Sun’s Supergranulation- Published:
- 01 December 2010
DOI: https://doi.org/10.12942/lrsp-2010-2