Students’ Understanding of the Economic Interpretation of the Derivative in the Context of Marginal Cost

Abstract

Many disciplines make use of mathematical concepts. However, there are often discrepancies between the way mathematical concepts are understood and taught in mathematics and the way they are used in other disciplines. The literature suggests that such discrepancies might make it hard for students in mathematics service courses to make a connection between the mathematical concepts taught and the way they are used in the students’ major disciplines. We investigated this hypothesis for one specific example in mathematics for economics students – the derivative and its interpretation commonly used in economics as the amount of change when increasing the production by one unit. We conducted an interview study investigating to what extent economics students can make a connection between the mathematical concept of the derivative and this common economic interpretation of the derivative. This study provides empirical evidence that it is actually difficult for economics students to make this connection, even though it was covered in their calculus course. In particular, the study reveals difficulties students have when trying to make this connection, which could be addressed in teaching.

Introduction

Mathematics plays a crucial role in many disciplines. Students enrolled in such disciplines should therefore gain a thorough understanding of the mathematical concepts that play an important role in their major discipline (see e.g. Alpers et al. (2013) for engineering). However, there are sometimes discrepancies between the way mathematical concepts are understood in mathematics and how they are used in the students’ major discipline (Alpers, 2017, 2018; Hochmuth et al., 2014). It is therefore important that students can make a connection between the understanding of the mathematical concepts acquired in their mathematics courses and the way these are used in their major discipline.

However, if students can actually make such a connection has not thus far been investigated explicitly. We investigated this issue for economics students and the notion of the derivative. We selected this concept because it plays an important role in economics, for example in marginal analysis (Ruffin & Gregory, 1990), and there are discrepancies between the way the concept is understood in mathematics and the way it is used in economics, as the following definition of marginal cost from the economic textbook by Wöhe and Döring (2013) illustrates (p. 300–301, translated by the authors):

The marginal cost C' is the additional cost of the last unit. The marginal cost for the 33rd unit can be determined easily by subtracting the total cost for 32 units from the total cost for 33 units. The marginal cost is the slope of the cost function. It can be determined by taking the derivative of the cost function $C\hbox{'}=\frac{dC}{dx}$.

In this definition, the derivative is identified with the additional cost of the last unit without further explanation. Similar interpretations of the derivative – mostly as the additional cost of the next unit – can also be found in other economics textbooks, including English-language textbooks (Pindyck & Rubinfeld, 2013; Stiglitz & Walsh, 2002; Varian, 2006). Such an interpretation might confuse students because it does not directly correspond to any of the usual representations and interpretations of the derivative like slope or rate of change, which they have learned at school or in their calculus courses at university. It even contradicts these at first glance: the derivative f ' (x) is a rate and not an amount, and its numerical value is usually not equal to the difference f(x + 1) − f(x) or f(x) − f(x − 1). Hence, in calculus courses for economics students, this economic interpretation of the derivative should be discussed, so that students can make a connection between their understanding of the mathematical concept of the derivative and this common economic interpretation, which also relies on specific assumptions that we will explain later.

We investigated in an interview study to what extent this is achieved in current teaching. This study is part of the first author’s Ph.D.-project about economics students’ understanding of the derivative, under the supervision of the second author at the Centre for Higher Mathematics Education in Germany (khdm) (Feudel, 2019; Feudel & Biehler, 2021). In this project, we first developed on the basis of didactic and economics literature a framework that aimed at describing an understanding of the derivative that might be desirable for economics students after their calculus course. We then investigated, by analyzing mathematics textbooks for economics students, to what extent this understanding is actually conveyed. Finally, we investigated the understanding economics students acquired in their calculus course by analyzing answers in the students’ final exam and by conducting an additional interview study. We want to present the latter here as it directly focuses on the problem to make a connection between the mathematical concept of the derivative and its common economic interpretation.

The study aims at providing detailed insights on the extent to which students in service courses can make a connection between the way mathematical concepts are understood in mathematics and their usage in the students’ major (academic) discipline for one example – the derivative – that is essential for economics students to comprehend. Hence, unlike research conducted in the past illustrating that it might be hard for students to make such a connection due to different practices in mathematics and the students’ major discipline (Alpers, 2017, 2018; Hochmuth et al., 2014), our study provides empirical evidence that making such a connection is actually not trivial for students. Furthermore, the research reveals difficulties students have when trying to make such a connection. Finally, our study also extends the knowledge concerning students’ understanding of the derivative to economics students that have been rarely investigated thus far.

Literature Review and Embedding of the Research

Students’ Difficulties in the Understanding of the Derivative Concept

A substantial amount of research has been conducted on students’ difficulties in the understanding of the derivative concept. First, it is known that students have difficulties in linking its different representations with each other (Hähkiöniemi, 2006; Viholainen, 2005; Zandieh, 2000), in particular the symbolic representation, which is the formal definition of the derivative, with the graphical and verbal representations that assign a meaning to it (Orton, 1983; Viholainen, 2005; vom Hofe, 1998).

More relevant for our research, however, is that students have a lot of problems in interpreting the derivative in contexts. Beichner (1994) has already shown that students often cannot connect a function and its rate of change in kinematics contexts correctly. Typical errors are the graph-as-picture error, the slope/height confusion, or the assumption that the graph of a function equals the graph of its rate of change (Beichner, 1994). Similar problems have been found in many other studies (for example Carlson et al., 2010; Çetin, 2009; Nemirovsky & Rubin, 1992).

An important reason documented in the literature that can lead to these problems is an insufficient understanding of rate. Byerley et al. (2016), for example, showed in a study with mathematics teachers that many of these could assign a meaning to the slope $\frac{\Delta y}{\Delta x}=3.04$ on the basis of Δx = 1, but not for arbitrary Δx ≠ 1. This problem can result from a conception of slope that Byerley et al. (2016) called “chunky”: an understanding of slope as the change Δy if a fixed change of Δx is given. Thompson (1994) had also uncovered evidence of such a conception earlier in a study that examined how a student developed a conception of speed: the first stage of the student’s speed conception was that speed is a distance traveled in a given amount of time. Similar conceptions of rate may also underlie the common economic interpretation of the derivative as the amount of change when increasing the production by one unit, which we will discuss in the next section. However, such a conception of rate can lead to problems in assigning a meaning to difference quotients $\frac{f\left(x+h\right)-f(x)}{h}$ for arbitrary h < 1 during the limiting process h → 0, and hence to the derivative as the limit of such quotients.

Students’ understanding of the derivative in economic contexts has, however, been rarely examined. Wilhelm and Confrey (2003) showed that students cannot easily transfer their knowledge concerning rate of change from a motion context to a money context. In their study, they asked students in an interview to relate distance–time graphs with speed–time graphs on one day, and to relate a total amount of money with daily transactions on a later day. The result was that some of the students who could properly distinguish between a function and its rate of change in a motion context failed to do so in the money context. Mkhatshwa and Doerr (2015) furthermore showed, in a study investigating economics students reasoning when solving optimization problems, that students talked about economic quantities like the marginal cost C' (x) as an amount of change (as the definition from the economics textbook by Wöhe and Döring (2013) mentioned in the introduction also suggests). They in particular used the unit “dollars”. This suggests that students might not have a precise understanding of the connection between the derivative C' (x) and its common economic interpretation as the cost of the next unit. This claim has also been backed up by our own research. An analysis of tasks from economics students’ final calculus exam at the University of Paderborn suggests that many students did not have a deep understanding of this connection (Feudel & Biehler, 2021). In one task, for instance, in which they had to interpret the derivative of a profit function, 51.4% of the students stated an interpretation as an additional profit, but the interpretations of only 26.1% were fully adequate. The others had flaws in the formulation. For example, they did not mention that the derivative just yields an approximation of the profit of the next unit, although this was emphasized in the calculus course.

The study by Mkhatshwa and Doerr (2015), and our own analysis of tasks from economics students’ final calculus exam at the University of Paderborn, suggest that many economic students might not have a precise understanding of the common economic interpretation of the derivative and of its connection to the mathematical concept. The interview study we present here explicitly examines this hypothesis with some participants of the calculus course at the University of Paderborn just mentioned. Its results support the hypothesis and reveal specific difficulties students might have when trying to connect the mathematical concept of the derivative with its common economic interpretation, which could be addressed in teaching.

The Influence of Contexts on Students’ Learning of Mathematical Concepts and Possible Problems

The literature suggests that learning mathematical concepts also depends on the contexts in which these are used (Damlamian et al., 2013). In particular, several studies indicate that the understanding of such concepts by students of other disciplines is influenced by the way these are used in the students’ major discipline (Bingolbali & Monaghan, 2008; Bingolbali et al., 2007; Maull & Berry, 2000; Mkhatshwa & Doerr, 2015).

Maull and Berry (2000), for example, investigated engineering students’ associations regarding key mathematical concepts, and compared these with associations of mathematics students. They drew up a questionnaire, in which students had to rank different associations presented according to how well they were present to them. The questionnaires were given to different groups: to engineering students at the entry to university, at the end of their first year, and in their final year, as well as to mathematics students at the same points in time. They found that, at entry to university, the associations of engineering and mathematics students did not differ, while the associations tended to differ more as the students progressed in their study program. With regard to the derivative, for example, advanced engineering students ranked associations related to rate of change on average higher than the other groups. Maull and Berry (2000) suggested that this ranking difference was due to the way the derivative was used in the engineering students’ major subject.

The influence of the students’ major discipline on their understanding of the derivative became even more explicit in a study by Bingolbali and Monaghan (2008). They investigated engineering and mathematics students’ understanding of the derivative and the development thereof in their calculus course by administering a pre-test, a post-test, and a delayed post-test to both groups of students. In the pre-test, there were no differences in the students’ performance. In the post-tests, the engineering students performed better on items focusing on rate of change while the mathematics students performed better on items including tangents. Furthermore, Bingolbali and Monaghan (2008) posed one additional item in the delayed post-test, in which they presented to the students two ways of thinking about the derivative: as slope or rate of change. They then asked the students to decide which way was closer to their own “derivative definition” and to provide a reason for their choice. While most mathematics students chose the slope, the majority of the engineering students chose the rate of change. Many of the engineering students argued that understanding the derivative as a rate of change is closer to applications occurring in their major subject. Some students even argued explicitly that this is the way the derivative is considered in their department. Hence, this study suggests explicitly that the way mathematical concepts are used in the students’ major discipline influences their learning and understanding of the concepts.

One special challenge that might make it particularly difficult for students of other disciplines to gain an understanding of mathematical concepts is that sometimes there are even discrepancies between the way concepts are understood in mathematics and the way they are used in the students’ major discipline. This phenomenon is documented in the literature with respect to several examples.

Alpers (2018) illustrated this phenomenon for the concept of continuity and its use in engineering by analyzing a textbook of technical mechanics (Gross et al., 2013). In this book, continuity is not defined. Instead, its counterpart, discontinuity, is touched upon by means of functions having jumps or holes at isolated points. This is not consistent with the mathematical point of view, in which a function can be discontinuous even at every point, and in which a function is continuous if and only if it is continuous at every point of its domain (Heuser, 2003). A second example, documented in Alpers (2017), refers to the concept of differential. By analyzing textbooks that covered engineering statics, he found that these books treated differentials as quantities – a conception of differentials that is normally not taught in mathematics courses. A third example was investigated by Hochmuth et al. (2014), who examined the role of the delta distribution in signal analysis. There, it is understood as a pointwise limit of functions describing rectangle impulses (with the value ∞ at x = 0), although from a mathematical point of view the delta-distribution has to be viewed as a limit of distributions.

That even a whole discourse relying on mathematical concepts might be different in other disciplines was discovered by González-Martín and Gomes (2017), who looked at how the concept of the integral is used in electrical engineering. By analyzing the textbook by Beer et al. (2012), they showed that important results in the book were derived mainly from pictures on the basis of the geometric properties of specific situations.

In all these cases, it might be difficult for students to connect their knowledge of the mathematical concepts taught in their mathematics courses to the way these are used in their major discipline. This might result in gaps when students are trying to make sense of the mathematics used in their major discipline (Christensen, 2008). However, there exists no empirical data if students really do have difficulties in making this connection. Our research aims at addressing this gap.

Theoretical Framework of the Study

We use a framework that we developed within the Ph.D.-project mentioned above that examined economics students’ understanding of the derivative. This framework describes an understanding of the derivative that is mathematically acceptable on the one hand, but which also takes into account the way the derivative is used in economics. This framework serves as a reference for the investigation of students’ understanding that we present here.

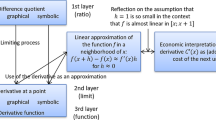
We developed the framework on the basis of the mathematics education literature about students’ understanding of the derivative, in particular Zandieh (2000) and Greefrath et al. (2016), and through an analysis of the way the derivative is used in economics textbooks, and how the textbooks justify this use (Pindyck & Rubinfeld, 2013; Reiß, 2007; Varian, 2006; Wiese, 1999; Wöhe & Döring, 2013). Its theoretical basis is the construct of concept image by Tall and Vinner (1981) that they define as “the total cognitive structure associated with the concept that includes all mental pictures, associated properties, and processes” (p. 152). Details of the framework’s development can be found in Feudel and Biehler (2021). The framework is displayed in Fig. 1. The left part is Zandieh’s model describing an understanding of the mathematical concept of the derivative (Zandieh, 2000). The right part contains the common economic interpretation, and the center illustrates the connection between these two. We will now describe the latter two in detail.

Fig. 1

Framework that describes an understanding of the derivative in mathematics for economics that is mathematically acceptable, but also considers the way the derivative is used in economics

If C : [0, ∞) → [0, ∞) is a cost function (where C(x) represents the cost for the production of x units), the derivative C' (x), called marginal cost, is commonly interpreted in economics as the additional cost of the next unit (Schierenbeck & Wöhle, 2003). However, if one takes this interpretation literally, it would be represented by a different mathematical object, namely C(x + 1) − C(x). There are two essential differences between the derivative C' (x) and the additional cost of the next unit. First, the derivative is a rate while the additional cost of the next unit is an amount. This becomes visible in the different units of C' (x) and the additional cost. If the production output is measured in units of production and the cost is measured in euros, the unit of C' (x) is euros per unit of production, while the additional cost is expressed in euros. Hence, an interpretation of C' (x) as the additional cost of the next unit even contradicts an understanding of the derivative as a rate of change at first glance. However, as already mentioned, Thompson (1994) showed in the speed context that the first stage in the development of a conception of rate is to conceive of it as the amount of change resulting from a fixed change in the independent variable. Similar views might lie behind the interpretation of the derivative C' (x) as the additional cost of the next unit. But one needs to be aware of the different units, which might not be obvious to students because the derivative is rarely considered as a quantity in formal university mathematics, not even in some mathematics textbooks for economics students like that of Hoy et al. (2011).

The second important difference between C' (x) and the additional cost of the next unit is a numerical one. This numerical difference is not small for prototypical functions students know from school, like f(x) = x², f(x) = e^x or f(x) = sin(x), and an interpretation of f ' (x) as f(x + 1) − f(x) would have been considered as incorrect there.

Nevertheless, there is a connection between the derivative C' (x) and the additional cost of the next unit: the approximation C(x + h) − C(x) ≈ C' (x) ⋅ h for h ≈ 0. The idea behind this approximation is to use the derivative as a linear approximation of the original cost function in a neighborhood of x, which is one important approach to the derivative (Greefrath et al., 2016).

Assigning h = 1 in the approximation above then leads to the common economic interpretation of the derivative as the cost of the next unit. This assignation is often justified in economic textbooks with the argument that one unit is considered as so small in economics that the error between C' (x) and C(x + 1) − C(x) is negligible (Reiß, 2007). Reiß also uses the term marginal unit to emphasize that one unit is small in the context considered. However, this justification seems a bit brief because it does not take into account those properties of economic functions that are important for an insignificance of the error between C' (x) and the additional cost of the next unit. These become visible in the book “Microeconomics” by Wiese (1999), pp. 47–48:

For many of the functions we want to consider, it does not make a big difference if we consider the difference quotient [with Δx = 1] or the derivative. For small changes, they are almost equal, and for linear functions, even perfect.

Hence, it is assumed in economics that the functions considered are almost linear within several units. In particular, one unit is assumed to be so small in the context that the functions considered are almost linear within [x; x + 1].

Possible Relationships of our Model to Other Theoretical Constructs

As already mentioned, our model was based on the theoretical construct of concept image by Tall and Vinner (1981), since the model describes associations that bridge the way the derivative is understood in mathematics to the way it is practically used in economics (for details see (Feudel & Biehler, 2021)). However, it can also be related to other constructs from the education literature.

The first one is the notion of representation, as different representations of the derivative (symbolic, graphic, verbal) are part of Zandieh’s model describing an understanding of the mathematical concept (Zandieh, 2000), which is also the left part of our model (see Fig. 1). However, Zandieh (2000) does not consider these as different registers of semiotic representations in the sense of Duval (2006), but as different ways the mathematical community thinks about the derivative in various contexts (p. 105). Nevertheless, the representations in the model can also be related to the different registers by Duval (2006), and being able to switch between these is essential for an understanding of the mathematical concept of the derivative (Kendal & Stacey, 2003; Zandieh, 2000).

The second theoretical construct our model can be related to is boundary-crossing, which plays an important role in research on transfer (Tuomi-Gröhn & Engeström, 2003). The construct was especially used to investigate boundaries, defined as sociocultural differences that give rise to discontinuities in interaction and action (Akkerman & Bakker, 2011), between school and work. According to Engeström et al. (1995), boundary crossing takes place when “experts face the challenge of negotiating and combining ingredients from different contexts to achieve hybrid solutions” (p. 319). This is similar to the challenge economics students face when trying to make sense of how the derivative is used in their major discipline, particularly due to differences between the mathematical concept and its typical interpretation in economics. Our theoretical model then proposes one way of thinking about these two for bridging the differences (without abandoning them, which is one important feature of boundary-crossing (Akkerman & Bakker, 2011)). However, the model only describes their connection for an individual student from a cognitive perspective, while the construct of boundary-crossing is broader, as it views the individual as part of several communities of practice.

Use of the Model in the Study

We used the model just described as the theoretical framework for the empirical study we are presenting here with the following research question:

To what extent are economics students able to make a connection between the mathematical concept of the derivative and its economic interpretation after their calculus course?

Hereby, our theoretical framework describing an understanding of the derivative that is mathematically acceptable on the one hand, but that also considers the way the derivative is used in economics, serves as a reference for the analysis of the connections the students could make.

External Conditions of the Study

Institutional Setting

The study took place with students of a two-semester course “Mathematics for economics students” at a medium-size university in Germany (University of Paderborn). The course consisted of two lectures (90 min each) and one accompanying tutorial (90 min) each week. In the latter, the students had to solve problems in groups. Furthermore, problem sheets were distributed weekly, whose solutions could be handed in. In the following week, solutions to these problems were presented in a “grand tutorial” in the lecture hall. The course was taught by a mathematician who had been teaching it for many years. The first semester of the course covered logic, set theory, and calculus of single-variable functions, while the second semester covered linear algebra.

The teaching was traditional in that new content was introduced in the lecture first, and practiced in the tutorials afterwards. However, the lecturer did not only try to teach content but also techniques of mathematical working (Dietz, 2012; Feudel & Dietz, 2019). To support the students in acquiring an understanding of the mathematical concepts taught (like the derivative), he advised them to immerse themselves with examples, non-examples, visualizations, as well as relevant statements involving the concept and its applications. The students were also required to provide such in the final exam. The students were hence not only expected to carry out procedures but also to build an understanding of the mathematical concepts taught.

Content Taught Concerning the Derivative Concept

The content taught concerning the derivative was typical compared to what can be found in mathematics textbooks for economics students, including English-language textbooks in common use like Sydsæter and Hammond (2012) or Hoy et al. (2011). The concept of the derivative and its economic interpretation were explicitly covered in two lectures, which the first author observed, and in which he took detailed notes about the content taught. We will now describe these two lectures in detail.

First Lecture – Introduction of the Mathematical Concept of Derivative

The concept was defined formally as the limit of the difference quotient. Simultaneously, the geometric representation as the slope of the tangent line and the verbal representation as rate of change were introduced. Hereby, the transition from the difference quotient to the derivative was discussed in all three representations. Afterwards, the differentiation rules were presented, but not proven.

Second Lecture – Treatment of the Economic Interpretation of the Derivative

The lecturer first defined the notion of a marginal function (in German: “Grenzfunktion”) as the derivative of an economic function like a cost function without any meaning in the context (unlike the English term marginal, the German prefix “Grenz-” only refers to the mathematical notion of “limit”). Afterwards, he derived the unit of such marginal functions for the example of the marginal cost C' (x) by means of the formal definition of the derivative. He argued that, if the production output x is measured in units of production (ME) and C(x) is measured in units of money (GE), then the unit of the difference quotient would be $\frac{GE}{ME}$. Since the unit does not change when taking the limit, the unit of C' (x) needs to be $\frac{GE}{ME}$ as well.

The lecturer then posed the question of how to interpret $C\hbox{'}(11)=0.7\ \frac{\mathrm{GE}}{\mathrm{ME}}$ of a cost function C in an economics context. To answer this, he derived the formula ΔC ≈ C^′(x) ⋅ Δx for Δx ≈ 0 from the formal definition of the derivative. By assigning Δx = 1, he then derived the following interpretation of $C\hbox{'}(11)=0.7\ \frac{\mathrm{GE}}{\mathrm{ME}}$:

If one increases the production output from 11 units by one unit , the costs grow by approximately 0.7 units of money.

Hereby, he emphasized that C' (11) usually does not yield the accurate cost of the next unit, but that the error is small if one unit is small in the context given. To illustrate this statement, he visualized the relationship between ΔC and the approximation C^′(x) ⋅ Δx on the board with the tangent line for a convex cost function C.

On this drawing, he then explained that the error between ΔC and C^′(x) ⋅ Δx in the approximation ΔC ≈ C^′(x) ⋅ Δx decreases if Δx becomes smaller. He then argued that for Δx → 0 the approximation becomes “asymptotically accurate” in the following way, which is also given in his mathematics textbook for economics students (Dietz, 2012) (p. 267):

The approximation ΔC ≈ C^′(x) ⋅ Δx transforms for Δx → 0 into a fictive equation dC = C' (x)dx, in which dC and dx are called differentials that should be understood as fictive infinitely small quantities.

He then introduced a second interpretation of $C\hbox{'}(11)=0.7\ \frac{\mathrm{GE}}{\mathrm{ME}}$ on the basis of the equation dC = C' (x)dx:

If one increases the output from 11 units by a marginal unit, the costs grow by 0.7 marginal units.

This alternative interpretation based on differentials as infinitely small quantities is rather unusual in mathematics for economics students. It is, for example, not found in common mathematics textbooks for economics students like Sydsæter and Hammond (2012), in which differentials are introduced as variables (see for example Thompson and Dreyfus (2017) for a description of this conception). A conception of differentials as infinitely small quantities is, however, common in physics and engineering (e.g. in Stroppe (2012)). By introducing this conception for interpreting C' (x) in the context of economics, the lecturer wanted to stress that the increment dx must be extremely small for an insignificance of the error when approximating the additional cost by C' (x)dx.

Accompanying Exercises

We want to restrict the description to two tasks that explicitly focused on the connection between the derivative and its economic interpretation. These are:

• 1) State an economic interpretation of C' (5) of the cost function C with C(x) = 8x² + 10x + 700 (x is measured in tons of oil, C(x) in 100€).

• 2) Estimate the cost at a production output of 45 units of another cost function, for which it is known only that C(43) = 19 GE and $C\hbox{'}(43)=1.4\ \frac{GE}{ME}$.

The first task was discussed in the tutorials. After this discussion, the tutors put the following economic interpretations of C' (5) on the board:

• 1. If one increases the production from 5t of oil by one ton, the costs grow by approximately 9000€.

• 2. If one increases the production from 5t by a marginal unit, the costs grow by 90 marginal units.

Furthermore, the tutors emphasized that the accurate result for the cost of the next ton is represented by C(6) − C(5) = 9800€.

The second task was posed on the weekly problem sheets that the students could submit for later feedback. The solution provided used the (local) linear approximation C(45) ≈ C(43) + 2 ⋅ C^′(43).

Comparison of the Content Taught with our Theoretical Framework

Although the course was not designed on the basis of our theoretical framework in Fig. 1, all the framework’s components were covered. In the first lecture, the mathematical concept was introduced with its three layers (ratio, limit, function) in the three representations (symbolic, graphical, verbal), which are represented in the left part of the framework (Fig. 1). In the second lecture, the economic interpretation of the derivative and its connection to the mathematical concept via local linear approximation were taught (right and center part in Fig. 1). In particular, it was discussed that C' (x) does not yield the accurate additional cost of the next unit. The connection between these two was made in the lecture via the formula ΔC ≈ C^′(x) ⋅ Δx for Δx ≈ 0 on the symbolic level (derived from the definition of the derivative), and on the graphical level with the help of the tangent line as represented in the framework (see arrows in Fig. 1). What remained implicit were assumptions made in economics that explain why C' (x) is commonly nevertheless simply interpreted as the additional cost of the next unit (without approximately), namely that the functions considered are assumed to be almost linear within several units.

Instead, the lecturer introduced an alternative interpretation of C' (x) as the (accurate) additional cost of the next marginal unit, which can also be found in some economics textbooks, like that of Reiß (2007), emphasizing that the increment in x must be extremely small for an insignificance of the error between the accurate additional cost and the approximation relying on the derivative.

Methodology of the Study

We designed and conducted interviews to investigate the extent to which the students could make a connection between the mathematical concept of the derivative and its economic interpretation after their calculus course.

Design of the Interviews

For being able to make a connection between the derivative C' (x) of a cost function and its economic interpretation in the sense of our theoretical framework (Fig. 1) the students should:

• I. know that the common economic interpretation of C' (x) as the additional cost of the next unit is accurately represented by C(x + 1) − C(x), which differs from C' (x) numerically and in the unit,

• II. be able to connect C' (x) and the cost of the next unit on a mathematical level via local linear approximation, for example via the approximation C(x + h) − C(x) ≈ C^′(x) ⋅ h for h ≈ 0,

• III. be aware that the common economic interpretation of C' (x) relies on the assumption that h = 1 is so small in the context that the error between C' (x) and C(x + 1) − C(x) is negligible because the functions considered in economics are almost linear within several units.

It was explicitly taught in the calculus course that C' (x) only yields an approximation of the additional cost C(x + 1) − C(x). Furthermore, C' (x) and C(x + 1) − C(x) were connected via local linear approximation on the graphical and the symbolic level as in our framework. What remained implicit was the difference in the unit and assumption III. explaining the assignation of h = 1 in economics.

To find out the extent to which the students could make this connection, and at which points difficulties arose, we divided the interview into four phases:

• Phase 1. Introductory phase aiming to remind the students of the concept of the marginal cost

• Phase 2. Discussion of differences between C' (x) and its common economic interpretation as the additional cost of the next unit

• Phase 3. Connection between C' (x) and the additional cost of the next unit on the graphical level

• Phase 4. Connection between C' (x) and the additional cost of the next unit on the symbolic level

Each of the phases started off with a task. These were:

• 1. Consider the cost function C with the equation: $C(x)=\frac{1}{1000}{x}^3-\frac{1}{4}{x}^2+21x+500$ (x ≥ 0). The variable x is given in units of production, the cost C(x) is given in €. Determine the marginal cost at a production output of x = 100 units. What is the unit of the marginal cost?

• 2. Is the derivative C' (x) the same as the additional cost when increasing the production from x units of production by one unit? Justify your answer.

• 3. Justify with the picture (Fig. 2) why the values of C' (x) and C(x + 1) − C(x) of the function from task 1 are almost identical (for x = 100).

  Fig. 2

  

  Graph of the cost function for task 3

• 4. Justify with the definition of the derivative why it is often assumed in economics that the numerical values of C' (x) and C(x + 1) − C(x) are almost identical.

The interview was carried out as a semi-structured interview lasting about half an hour. The students were first asked to find solutions to the tasks by themselves. There was no explicit time restriction, but if they could not find solutions by themselves they received prompts, so that difficulties at different points of the solution process became evident. The tasks 1,3, and 4 were provided on a sheet of paper, and the students were encouraged to take notes illustrating their solution. These notes were also collected. However, the main focus was on the students’ oral explanations of the solutions.

Description of the Phases and A Priori Analysis of the Corresponding Tasks

In the following, we present an a priori analysis with the intended solutions to the tasks, anticipated difficulties and possible prompts that might help students to overcome these difficulties.

1st phase (Introduction): The phase began with the task to determine the marginal cost of the cost function C with $C(x)=\frac{1}{1000}{x}^3-\frac{1}{4}{x}^2+21x+500$ (x ≥ 0) at a production output of x = 100 with the production output given in ME (units of production) and the cost in €. This phase aimed at finding out, what the students first associated with marginal cost – the derivative or the additional cost of the next unit – and if their calculation method was coherent with the unit. The derivative yields the result $C\hbox{'}(100)=1\ \frac{\text{\EUR}}{\mathrm{ME}}$. Its unit could be justified with the definition of the derivative or by using the interpretation of the derivative as a rate of change. On the contrary, the additional cost of the next unit is determined by C(101) − C(100) = 1.051€. Its unit could be justified by mentioning that the unit of costs is € (this unit is also suggested by the name marginal cost).

Prompts in the 1st Phase

We expected that every student could at least remember one of the two conceptions of marginal cost to determine it, so we did not develop specific prompts for this phase.

2nd phase (Discussion of differences between C' (x) and the additional cost of the next unit): This phase aimed at finding out if the students were aware of differences between C' (x) and the additional cost of the next unit. To achieve this, we confronted them with an alternative definition of marginal cost. If they had solved task 1 with the derivative, the following definition from the economics textbook by Pindyck and Rubinfeld (2009) was presented to them (p. 325):

The marginal cost at a production output x is the additional cost that results from increasing the production by a further unit.

If they had solved task 1 by means of calculating the cost difference, they were reminded that marginal cost was defined as C' (x) in their calculus course.

In both cases, the interviewer then posed the following question to initiate a discussion about differences between C' (x) and the additional cost of the next unit:

Is the derivative C ' (x) the same as the additional cost while increasing the production from x units of production by one unit?

We chose to present the derivative C' (x) and its economic interpretation as the additional cost of the next unit as two different definitions of the marginal cost to provoke a stronger cognitive conflict.

According to what was taught in the calculus course (see section 4.2), the students might mention the following differences between C' (x) and the additional cost of the next unit:

• 1) The additional cost of the next unit accurately corresponds to the difference C(x + 1) − C(x) on the mathematical level.

• 2) The numerical values of C' (x) and the additional cost of the next unit differ.

• 3) The units differ.

Prompts in the 2nd Phase

If the students did not mention these differences by themselves, the interviewer gave prompts that aimed at guiding them to the differences. Due to limited space, we will not present all the prompts here (for details see Feudel (2019)). The most important ones were:

• Posing a task to determine the additional cost when increasing the production from 10 units by one unit for the function in Fig. 3 graphically if the students used the derivative in task 1.

• Asking the students to determine the marginal cost on the basis of the derivative if they used the cost difference in task 1.

  Fig. 3

  

  Graph of the task to determine the additional cost when increasing the production from 10 units by one unit

• Asking for the unit if one takes literally the definition of the marginal cost as the additional cost of the next unit.

3rd phase (Discussion of the connection between C' (x) and C(x + 1) − C(x) on the graphical level): This phase aimed at finding out if the students could make a connection between C' (x) and the additional cost of the next unit (possibly with new insights from phase 2 about differences) on the graphical level. The task of this phase was to justify graphically for the function of task 1 (the graph was provided, see Fig. 2), why the error between C' (100) and C(101) − C(100) was small. A possible solution might be that C' (100) represents the slope of the tangent line at x = 100. This slope approximately equals the slope of the secant line through (100, C(100)) and (101, C(101)), which is numerically equal to the cost of the next unit. And since the function in Fig. 2 is almost linear within [100; 101], this error is small. Students might also argue directly that the value of C' (100) represents the increase on the tangent line, which is close to the graph of the original function at x = 101.

Prompts in the 3rd Phase

To bring all students into the discussion of why the error between C' (100) and C(101) − C(100) is small for the function given in Fig. 2, prompts could be provided. The two prompts we had thought of in advance were to remind the students of:

• 1) The geometric interpretation of the derivative as the slope of the tangent line, and

• 2) The method for the determination of the slope of a linear function with gradient triangles.

4th phase (Discussion of the connection between C' (x) and C(x + 1) − C(x) on the symbolic level): This phase aimed at finding out if the students could connect C' (x) and the additional cost of the next unit on the symbolic level. The task of this phase was to justify with the definition of the derivative why it is often assumed in economics that C' (x) and C(x + 1) − C(x) are almost equal. According to what was taught in the calculus course, it can be expected that students derive the approximation C(x + h) − C(x) ≈ C^′(x) ⋅ h for h  ≈ 0 from the definition of the derivative, and then argue that it is often assumed in economics that h = 1 is small in the context (see section 4.2).

Prompts in the 4th Phase

The planned prompt in this phase was to provide the students with the formal definition of the derivative if they could not remember or reconstruct it.

Data Collection

Eight participants in the second semester of the course “Mathematics for economics students” described in section 4.1 (the first semester covered calculus) volunteered to take part in the study. All participants had completed the mathematics course with calculus described in section 4 and had passed its final exam successfully. Besides the mathematics course, the participants had completed an introductory course in business administration in their first semester, and attended an introductory course in economics in their second. The latter especially included a section that covered cost theory. The literature used there was exactly the microeconomics textbook by Pindyck and Rubinfeld (2009), that we also referred to in our interviews when presenting the alternative definition of marginal cost as the additional cost of the next unit (hence, this topic was taught in the students’ courses).

Although we could not gather data about students’ performance in their mathematics and economics courses due to data protection considerations, it can be assumed that the volunteering participants were a special sample of students: students, who had at least some understanding of the derivative (the theme “derivative” was announced in advance) and who were willing to talk about it. Both characteristics were important for the interview: the students needed at least some idea of how to determine the marginal cost in task 1 to get the interview started, and the progress of the interviews depended greatly on the communication between participants and interviewer. However, it turned out during the interviews that there were also some participants with a very weak understanding of the derivative. Hence, the data also included some variation regarding students’ understanding of the derivative and the connection to its economic interpretation.

The interviews were conducted and recorded on video by the first author. As previously mentioned, students’ notes from the tasks were also collected.

Data Analysis

The interviews were first transcribed. We then analyzed the transcripts using sequential interpretation (Krummheuer et al., 1999) aiming to reconstruct students’ understanding of the connection between the derivative and its economic interpretation in the context of marginal cost on the basis of students’ individual statements. We interpreted these statements on the basis of four guiding questions relating to different aspects of this connection described in our theoretical framework (an example illustrating the method is shown in Fig. 4):

• Q1. What conception of marginal cost do students associate with the notion of marginal cost first?

• Q2. To what extent are students aware of the differences between the derivative C' (x) and the additional cost of the next unit?

• Q3. To what extent can students make a connection between C' (x) and C(x + 1) − C(x) on the graphical level, and what problems occur?

  Fig. 4

  

  Illustration of the interpretation method with an excerpt of the interview with the student Holger

• Q4. To what extent can students make a connection between C' (x) and C(x + 1) − C(x) on the symbolic level, and what problems occur?

To ensure the validity of the interpretations, the two authors discussed all interpretations intensively and took great care not to over-interpret by backing all their interpretations up with the original transcript (see Fig. 4).

Results of the Study

We will now present the results of two students in detail – Holger, who could not make a connection between the derivative and its economic interpretation, and Lisa, who could make such a connection. For the other six students, we will present summaries according to our guiding questions. These summaries were drawn up using the same methods as for Holger and Lisa. However, we can explain our detailed analysis process only for two cases due to limited space.

Holger’s Understanding of Marginal Cost

Phase I (Introduction)

Holger solved the task of this phase (determination of the marginal cost at the production output of x = 100 for the cost function $C(x)=\frac{1}{1000}{x}^3-\frac{1}{4}{x}^2+21x+500$, the cost is expressed in €) with the derivative, and got the correct numerical result C' (100) = 1. However, he did not mention a unit. After having been asked explicitly, he responded “euros”, but could not justify his answer. He simply mentioned that since the total cost is given in euros, the marginal cost is as well (maybe due to its being named as cost).

Phase 2 (Discussion of Differences between C' (x) and the Additional Cost of the Next Unit)

Since Holger had solved task 1 with the derivative, he was now confronted with the alternative definition of marginal cost as the additional cost of the next unit from the book by Pindyck and Rubinfeld (2009), and asked if this definition also describes the derivative C' (x). After reading this definition carefully, he concluded that it describes the same, but was not sure.

For the recognition of differences, he then got the task to determine the additional cost when raising the production from 10 units by a further unit graphically (Fig. 3). This initiated the following dialogue:

H: You would have to imagine the derivative. Then you would see the additional cost. The derivative is nothing else than the slope at a point. If we take any point.

I: Here is one explicitly given. We search for it at a particular point.

H: Here is one given, 10 units of production. So, we have that the total cost is 21. Now we need the cost if one more is produced. Well, but we do not need this because if we are at 11 the cost is 22 point something. So, the additional cost has to be one point, yes 1.1.

Hence, Holger recognized that he did not need the derivative to determine the additional cost of the next unit, and that it can be determined by C(x + 1) − C(x). Furthermore, it became obvious that Holger knew the geometric interpretation of the derivative as the slope at a point that is often used at school (Greefrath et al., 2016). However, he did not associate the tangent line, which is essential to connect C' (x) and C(x + 1) − C(x) on the graphical level.

For the comparison of C' (x) and C(x + 1) − C(x) he was then asked to also determine the derivative graphically. Since he claimed that a graphical determination of C' (x) does not lead to an accurate result, he was then asked to actually calculate the additional cost of the next unit for the function of task 1. He now got C(101) − C(100) = 1.051 (he did not mention units) compared to C' (100) = 1.

Holger recognized the numerical difference in his calculation, and then saw that the graph of the function (Fig. 2) also does not increase exactly by one between x = 100 and x = 101. But instead of questioning the identity of C' (x) and C(x + 1) − C(x) he said:

H: This [the difference] is probably due to rounding.

After having been told that no rounding is involved, he faced a conflict he could not resolve. He then received the prompt to think about the meaning of the derivative on the graphical level (because he had already shown that he knew its geometric interpretation as slope), and he found a resolution:

H: Oh, that’s the reason why it is not accurate! The origin of the derivative was to determine the slope at a point. To achieve this, you take one point left and one point right of it, which have the same distance, and the slope in between. Afterwards, you try to make this distance as small as possible, as you could think of, but we cannot reach the one point, but in our mind, we want to reach it. And I assume this very small rounding mistake, no, not rounding mistake, but this small difference is because you do not reach the point exactly.

Hence, Holger thought that C' (100) did not yield the accurate additional cost because the derivative does not yield the “true slope at the point”. It later became even explicit that he considered C' (x) as the slope of a secant through (x − h, C(x − h)) and (x + h, C(x + h)) with a “minimal h“. This indicates that Holger considered the limit as part of the limiting process and not as the object “slope at a point”. Hence, he had a strong process conception of the limit, but did not properly relate it to the limiting object, which is important for understanding the derivative concept (Zandieh, 2000). This led to an erroneous conclusion regarding the cause of the error between C' (x) and C(x + 1) − C(x).

Phase 3 (Discussion of the Connection between C' (x) and C(x + 1) − C(x) on the Graphical Level)

Since Holger had already seen the small difference between C' (100) and C(101) − C(100) on the graphical level for the function of task 1 (Fig. 2), the interviewer asked if he knew a function with a larger error between C' (x) and C(x + 1) − C(x). After some thought Holger recognized that both should be identical for linear functions. After having been asked why, he answered:

H: For linear functions, the slope is always identical at each point.

I: Yes.

H: And hence, we also have an accurate slope. This is the problem for all curved functions because the slope always changes, and then between these two points, it is more difficult to determine the slope.

This accords with Holger’s earlier comments. He thought that the derivative C' (x) is represented by the slope of a secant through (x − h, C(x − h)) and (x + h, C(x + h)) with a very small h. However, since this slope still changes as h changes for nonlinear functions, the “true slope at x” cannot be accurately determined with the derivative, which he regarded wrongly as part of the limiting process.

Phase 4 (Discussion of the Connection between C' (x) and C(x + 1) − C(x) on the Symbolic Level)

The task was to justify with the definition of the derivative why it is often assumed in economics that the difference between C' (x) and C(x + 1) − C(x) is small.

Holger did not know the definition of the derivative, so it was given to him. But Holger ignored it, and instead focused on the equation of the function from task 1 $\left(C(x)=\frac{1}{1000}{x}^3-\frac{1}{4}{x}^2+21x+500\right)$, which he regarded as a prototype for a cost function. He then argued as follows:

H: This [the small error] is due to the always small coefficient [the leading coefficient in the polynomial].

He then argued that a small leading coefficient induces a “low curvature”, and hence a small error between C' (x) and C(x + 1) − C(x). However, his argument concerning the leading coefficient is not correct.

The interviewer then emphasized that Holger had not yet used the definition of the derivative (as was required in the task, see section 5.1), but Holger was not able to do so.

Summary of Holger’s Interview According to the Four Guiding Questions

First associations regarding marginal cost in the calculation task (Q1): Holger first associated the marginal cost with the derivative C' (100) for its calculation. The unit he mentioned was the unit of the total cost (€). This is not the unit of C' (100), but of the common interpretation of the derivative in economics as the additional cost of the next unit.

Awareness of differences between C' (x) and the additional cost of the next unit (Q2): Holger first identified the two. During the interview, he recognized that the additional cost of the next unit is represented by the cost difference C(x + 1) − C(x), which also differs numerically from C' (x). However, he did not draw adequate conclusions due to a misconception regarding the limit concept: he considered C' (x) as part of the limiting process and thought that C' (x) does not yield the accurate additional cost of the next unit because the corresponding limit yields the slope of a secant line through (x − h, C(x  −h)) and (x + h, C(x + h)) “with a minimal h”, and not the “true slope at x”.

Connection between C' (x) and C(x + 1) − C(x) on the graphical level (Q3): Holger could not make an adequate connection between these two on the graphical level as represented in our framework, although he knew the interpretation of the derivative as slope at a point. However, he did not associate the tangent line, which is indispensable for connecting these two on the graphical level via local linear approximation as in our framework (Fig. 1). Instead, he used the misconception regarding the limit just described to explain the error between C' (100) and C(101) − C(100) for the function from task 1, and why there is no such error for linear functions (which he recognized correctly).

Connection between C' (x) and C(x + 1) − C(x) on the symbolic level (Q4): Holger first did not know the definition of the derivative. After it had been given to him, he could not work with it, but instead tried to explain why C' (x) and C(x + 1) − C(x) are often identified in economics with the equation of the function from the first task $C(x)=\frac{1}{1000}{x}^3-\frac{1}{4}{x}^2+21x+500$. His argument that the small leading coefficient induces a low curvature and therefore a small error, however, was not correct. Hence, he could not connect C' (x) and C(x + 1) − C(x) via the linear approximation C(x + h) − C(x) ≈ C' (x) ⋅ h for h ≈ 0 on the symbolic level as in our framework.

Lisa’s Understanding of Marginal Cost

Phase I (Introduction)

Lisa solved the introductory task to determine the marginal cost for a cost function at the production output of x = 100 with $C\hbox{'}(100)=1\ \frac{\text{\EUR}}{ME}$. Her unit “€ per unit of production” was also the correct unit for the derivative.

Phase 2 (Discussion of Differences between C' (x) and the Additional Cost of the Next Unit)

Lisa was now confronted with the alternative definition of the marginal cost as the additional cost of the next unit. On the question of whether these are also given by the derivative, she immediately replied that she had recognized this conflict before:

L: Yes, I really thought about this last semester. In the economic subjects, we really learn it this way. We use the derivative and have to interpret the coefficients of “Stata” [a statistic software], I don’t know if you know it. No, ok. Nevertheless, we have to interpret these coefficients in econometrics. … And I always had to say: If you increase x by one unit, y increases by these many units, eh? This is really the case!

She then referred to her mathematics lecture as follows:

L: But I have, since I had mathematics last semester, I always thought that you learn it differently in mathematics. In mathematics, you say: “if you increase x by one marginal unit, y increases by these many marginal units.”

Lisa mentioned the interpretation of C' (x) as the (accurate) additional cost of the next marginal unit, as taught in the calculus course (see section 4.2).

On the question of what a marginal unit actually is, Lisa tried to distinguish it from one unit with the graph of the function (Fig. 2). She first illustrated one unit and determined the additional cost of this unit graphically with the difference C(101) − C(100). Meanwhile, she also recognized the numerical difference to $C\hbox{'}(100)=1\ \frac{\text{\EUR}}{\mathrm{ME}}$. Lisa then explained what she considered to be a marginal unit:

L: And a marginal unit I imagine as very, very small. Here I would go a very, very little bit to the right and then a very little, little bit upwards.

Hence, for Lisa, a marginal unit was not a fictive infinitely small quantity, as was taught in the calculus course (see section 4.2), but a very tiny, yet still finite quantity.

The interviewer then prompted her by asking if the additional cost for such a tiny unit would not be almost equal to zero. She then replied:

L: This has to do with the slope you have. For the derivative, you calculate the slope of the tangent line. The slope of the tangent line is what you calculate, isn’t it?

I: Right, the slope of the tangent line, yes.

L: Yes, and this is also what I get if you increase x by a marginal unit, starting at 100. [Pause] Eh no, what do I get? No, if you increase x by one marginal unit, the marginal cost still increases by one. I think the slope still remains one, right?

These statements indicate how Lisa connects the derivative C' (x) with the cost of a marginal unit. C' (x) represents the slope of the tangent line at x = 100, which equals 1. But if the amount by which the production is raised is just a marginal unit (a tiny amount, which we will now label as dx), the cost function still increases with the same slope as the tangent line. Therefore, the derivative C' (x) can be used to determine the additional cost for such a tiny dx via C' (x)dx. This coincides with the idea taught in the calculus course that the linear approximation ΔC ≈ C^′(x) ⋅ Δx “becomes accurate” for Δx → 0. Furthermore, Lisa recognized the difference in the unit between C' (x) and an additional cost after being asked about which unit additional costs are measured in.

Phase 3 (Discussion of the Connection between C' (x) and C(x + 1) − C(x) on the Graphical Level)

The interviewer first asked Lisa if she knew of a function with a larger error between C(x + 1) − C(x) and C' (x) than the function from task 1 (for the graph see Fig. 2). She responded that these two are numerically equal for linear functions, and then suspected that economists assume linearity when interpreting C' (x) simply as the additional cost of the next unit. After the interviewer’s remark that the function from task 1 was not in fact linear (Fig. 2), she recognized that the central assumption in economics is that the functions considered are almost linear within several units:

L: Oh, yes. But you only have an excerpt of a function from 97 to 104. And in this range, it almost looks linear. If we would scale differently and look at the whole function, it would be totally different.

This statement and Lisa’s remarks in phase 2, in which she stated that the cost function increases with the same slope as for the tangent line (= C' (x)) for very a tiny dx, suggest that she was able to make a connection between C' (x) and C(x + 1) − C(x) via local linear approximation on the graphical level. She also recognized the central assumption in economics that the functions considered are almost linear within some units so that the error between C' (x) and C(x + 1) − C(x) is small.

Phase 4 (Discussion of the Connection between C' (x) and C(x + 1) − C(x) on the Symbolic Level)

Lisa first reconstructed the formal definition of the derivative $f\hbox{'}(x)=\underset{h\to 0}{\lim}\frac{f\left(x+h\right)-f(x)}{h}$ by herself (on the basis of Fig. 2, in which she drew gradient triangles). She then compared it with C(x + 1) − C(x) and recognized that instead of taking the limit, the value of h is assigned to 1. She justified this assignation with the argument that h < 1 does not make sense in discrete contexts:

L: Yes. They more likely say that they want to increase the production by one and not by a marginal unit. Yes, probably because sometimes you do not want to produce marginal units if you produce something like a pen.

Overall, Lisa could connect C' (x) and C(x + 1) − C(x) on the symbolic level and present a plausible reason for their identification in economics (although the argument only works for discrete contexts).

Summary of Lisa’s Interview According to the Four Guiding Questions

First associations regarding marginal cost in the calculation task (Q1): Lisa first associated the derivative C' (100) with the marginal cost. The unit she mentioned ($\frac{\text{\EUR}}{\mathrm{ME}}$) also suited the derivative.

Awareness of differences between C ' (x) and the additional cost of the next unit (Q2): Lisa knew that C' (x) does not usually yield the accurate additional cost of the next unit, and that the latter is represented by C(x + 1) − C(x) on the mathematical level. She also recognized the difference in the unit after having been asked in what unit “additional cost” would be measured. But she claimed that the derivative C' (x) can be used to determine the additional cost of a very tiny amount dx (which she called “marginal unit”) because the original cost function increases with the same slope within such a tiny dx. This suggests that she had absorbed the idea from the calculus course that the linear approximation ΔC ≈ C^′(x)Δx for Δx ≈ 0 “becomes accurate” for Δx → 0.

Connection between C' (x) and C(x + 1) − C(x) on the graphical level (Q3): Lisa knew that C' (x) represents the slope of the tangent line and was able to determine C(x + 1) − C(x) on the graphical level. She also recognized that the error between these two is small if the function is almost linear within several units, which is often assumed in economics. Hence, she could make a connection between C' (x) and C(x + 1) − C(x) on the graphical level via the tangent line as in our framework in Fig. 1.

Connection between C' (x) and C(x + 1) − C(x) on the symbolic level (Q4): Lisa could also connect these two on the symbolic level. She was able to reconstruct the formal definition of the derivative by herself and recognized that one gets the cost difference C(x + 1) − C(x) by assigning h = 1 in the difference quotient instead of taking the limit. She then justified this assignation in economics with the plausible practical argument that h < 1 may not make sense in economics in discrete contexts.

Summaries of the Other Students’ Understanding of Marginal Cost

The summaries of the other students’ understanding of the connection between the mathematical concept of the derivative and its economic interpretation according to our four guiding questions are shown in Tables 1 and 2. The summaries of the results of questions Q1 and Q2 are shown in Table 1, and the ones for questions Q3 and Q4 appear in Table 2.

Table 1 Summary of the results of the other six participants according to the guiding questions Q1 and Q2

Table 2 Summary of the results of the other six participants according to the guiding questions Q3 and Q4

Summary and Discussion

Summary and Contribution of our Research to the Research Domain

Previous research has shown that there are often discrepancies between the way mathematical concepts are understood in mathematics and the way they are used in other disciplines (see section 2.2), which might make it hard for students of mathematics service courses to make a connection between the mathematical concepts taught in their mathematics courses and the way these concepts are used in the students’ major discipline. Our study now provides empirical evidence for one specific example – the concept of the derivative and its interpretation commonly used in economics – that this really is the case. The study in particular reveals difficulties the students experienced when trying to make such a connection.

Only two of the eight participants of our interview study (Lisa and Johannes) could make a connection between the derivative C' (x) of a cost function and its common economic interpretation as the additional cost of the next unit via local linear approximation, as represented in our theoretical framework (Fig. 1), by themselves, even though this connection had been covered in the participants’ calculus course. The other six participants were not able to do so by themselves:

• Holger, Detlef, Karl, and Veronika just considered the derivative C' (x) as identical with the additional cost of the next unit at the beginning of the interview, although it was emphasized in the calculus course that this is not the case.

• Ralf did not consider these as equal, but could not state differences.

• Susanne argued that taking the derivative yields another function, but could not explain differences between C' (x) and the additional cost of the next unit on a conceptual level.

During the interview and with the help of the interviewer’s prompts (see section 5.1), the following difficulties occurred while the students were trying to make a connection between C' (x) and its common economic interpretation as the additional cost of the next unit:

• Except for Lisa and Johannes, the students did not know the formal definition of the derivative and could not make sense of it after it had been given to them, which is important for the connection between C' (x) and its interpretation as the additional cost of the next unit via the local linear approximation C(x + h) − C(x) ≈ C^′(x) ⋅ h for h ≈ 0 on the symbolic level.

• Holger, Ralf, Karl, and Detlef did not associate the tangent line within the geometric interpretation of the derivative as slope (they only associated “slope at a point”), which is important for connecting C' (x) and the additional cost of the next unit via local linear approximation on the graphical level.

• Holger had misconceptions regarding the concept of limit that lead to erroneous conclusions concerning the reason for the numerical difference between C' (x) and C(x + 1) − C(x).

• Susanne did not even know any meaning of the derivative.

• Only Lisa, Ralf, and Johannes were able to present a plausible argument for why economists often simply interpret the derivative as the cost of the next unit, even though these are not equal.

These points suggest two general types of difficulty regarding the connection of a mathematical concept and the way it is used in another discipline. The first four of these points are gaps in students’ understanding of aspects of the mathematical concept that are important for making this connection. The last point is the problem that students might not comprehend why there is a certain practice of the concept’s use in their major discipline and are not aware of underlying assumptions.

Consequences for Teaching

We now discuss consequences for teaching based on three key problems found in our study (Fig. 5) concerning the connection between the way mathematical concepts are understood in mathematics and the way they are used in other disciplines.

Fig. 5

Students’ difficulties concerning the connection between a mathematical concept and the way it is used in their major discipline

Ad I in Fig. 5

One possibility for making students aware of discrepancies between the way a mathematical concept is understood in mathematics and the way it is used in the students’ major discipline can be to induce cognitive conflicts that might result from these discrepancies (just like in the interview). In our case, one could, for example, confront the students directly with the common economic interpretation of C' (x) as the additional cost of the next unit by asking them explicitly if it actually corresponds to the derivative C' (x), and encouraging them to discuss differences if it does not. This might lead to a cognitive conflict so that students might be more attentive to the lecturer’s explanations about this common economic interpretation of the derivative and its connection to the mathematical concept.

Ad II. In Fig. 5

It is crucial to first identify and then try to address gaps in students’ understanding of the mathematical concept that are important for making a connection to its use in the students’ major discipline. In our case, the problem that students did not associate the tangent line, which is important for the connection between C' (x) and its interpretation as the additional cost of the next unit on the graphical level, might be addressed by tying the geometric interpretation of the derivative as slope always to the tangent line in the course (and maybe even to define it this way), for example by setting tasks to determine derivatives graphically. The problem that students had no understanding of the definition of the derivative, which is important for connecting C' (x) with its interpretation as the additional cost of the next unit on the symbolic level, could be addressed by initially trying to connect the formal definition of the derivative to an interpretation as rate of change in contexts that directly correspond to it, for example instantaneous velocity in kinematics.

Ad III. In Fig. 5

It might be promising to discuss in mathematics courses explicitly why mathematical concepts are used in a certain way in the students’ major discipline, including relevant assumptions that explain prevalent usage. In our case, for example, this means making explicit that the common economic interpretation of the derivative as the additional cost of the next unit relies on the specific assumption that the functions considered in economics are almost linear within several units, and in particular within [x; x + 1]. Of course, this does not necessarily have to be done by the lecturer; students could also try to come up with such explanations during discussions.

Outlook for Further Research

The results of our study also yield several starting points for future research. A first point can be to develop a teaching scenario that guides more students to a deeper understanding of the economic interpretation of the derivative and its connection to the mathematical concept by trying to address the problems mentioned in Fig. 5.

A second point concerns the notion of marginal unit used by the two students who were able to make a connection between the derivative C' (x) and its common economic interpretation by themselves (and many students used it to interpret the derivative in their final calculus exam (Feudel & Biehler, 2021)). It could therefore be fruitful to investigate what the students actually meant with this notion to judge if the use of this notion might help students to better understand the connection between the mathematical concept of the derivative and its economic interpretation. Furthermore, since this notion is related to differentials, an investigation of economics students’ understanding of this notion might also contribute to an investigation of students’ understanding of differentials, which is an important theme in mathematics education research, for example in connection with other disciplines like physics (Hu & Rebello, 2013) or with alternative approaches to the concept of limit (Ely, 2019).

A third point concerns the generalization of our results as we only investigated one specific mathematical concept. Further examples from other disciplines might help to find out about the extent, to which the two major problems our participants had when trying to make a connection between the mathematical concept and its use in their major discipline (gaps in understanding of the mathematical concept, and gaps in the comprehension of why there is a certain usage of the concept in their major discipline including underlying assumptions) occur in general among students in mathematics service courses.

A last point for future research concerns the theoretical perspective for investigating students’ connections between mathematics and their major discipline. Due to our choice of the theoretical framework, our perspective was a cognitive one. This allowed us to uncover specific cognitive difficulties individual students had when trying to make a connection between mathematics and economics in the case of one particular concept, which might be addressed in teaching. However, perspectives that consider further aspects of learning, for example sociocultural perspectives, might point the way to more general results regarding students’ connections between different practices in mathematics and their major discipline.