1 Introduction

This paper has three main goals. First, we propose a novel conceptual framework tailored for modeling the meaning of mathematical concepts in university-level mathematics, addressing their rigorous nature and relationships with related concepts. This requires extending existing frameworks that relate to secondary school mathematics or less rigorous college-level mathematics. Second, within this conceptual framework, we present a model of meaning for the concepts of total differentiability and total derivative that provides a variety of possible interpretations and aspects. Third, we use this model of meaning as a tool for analyzing German textbooks on the topic. This analysis sheds light on different semantic approaches to presenting the topic, providing valuable insights both theoretically for understanding teaching approaches and practically for advising instructors and learners in selecting textbooks based on their intended purpose.

While numerous frameworks exist for understanding the 1D derivative at high school and college levels, there is a notable gap in frameworks for the multidimensional case, particularly in the context of rigorous university-level mathematics, while we consider it necessary to have these frameworks to meaningfully discuss higher mathematics education. We focus on teaching the concept of the total derivative in German “Analysis II” courses for mathematics majors. These are courses that mathematics students usually take in their second semester after taking “Analysis I.” While “Analysis I” deals mostly with sequences, series, functions, continuity, differentiability, and integrals in real numbers, “Analysis II” focuses on metric spaces, topological concepts, differentiability in the multidimensional case, and, often, ordinary differential equations. Both courses are rigorous and proof-oriented from the start, and do not focus on calculations. Studies on the specific educational context of Analysis II courses are rare, with a notable exception being Lankeit and Biehler (2019) investigating students’ understanding of relations of differentiability concepts in the multivariate case.

Our work aids understanding of teaching and learning in advanced university mathematics courses, thus aligning with the focus of this special issue. Moreover, our research provides insights for designing innovations related to this mathematical content and offers a useful framework for analyzing other advanced content.

A model of meaning provides a frame for scholarly discussion about which facets of meaning are critical to student understanding. The choice of facets of meaning for a particular course depends on its goals and participants.

Unlike calculus, which has a well-established tradition of subject matter didactics, Analysis I and II courses lack comprehensive analyses of differentiability concepts, especially in higher dimensions. Building on Biehler’s (2005) emphasis on the need for a systematic approach to reconstructing the meanings of mathematical concepts, we provide a thorough examination of the total derivative and total differentiability. We analyze its various meanings in different contexts and its relations to related concepts. While our meaning model is not yet widely adopted, we aim to validate it by comparing it to a selection of German Analysis II textbooks.

2 Literature review

Approaches to subject matter analyses

There is a long tradition of subject matter analyses for conceptualizing mathematical concepts with the aim to “make mathematics accessible and understandable to the learner based on an analysis of the subject matter with mathematical means” (Hußmann et al., 2016, p. 2). These analyses form the basis for the design of teaching and learning scenarios (e.g., Hußmann & Prediger, 2016; vom Hofe, 1998) and the study of learner comprehension (Bikner-Ahsbahs, 2001). In the French tradition of “didactical engineering” (Artigue, 1994), an extensive analysis of the material precedes the design of instructional situations. In addition, such analyses can be used to examine textbooks (Weigand, 1993) or to categorize task difficulties (Kleine et al., 2005). Hußmann and Prediger (2016) introduced the distinction between formal and semantic levels in subject matter analysis. The formal level includes the formal presentation and logical structure of mathematical objects, including definitions, theorems, and proofs. In contrast, the semantic level addresses “sense and meanings – e.g. by big ideas and basic mental models – of the mathematical topic to be learnt and epistemological aspects of the structure between them” (Hußmann & Prediger, 2016, p. 37).

Frameworks for the 1D derivative

For school and college calculus teaching, several frameworks for understanding the 1D derivative on a semantic level have been developed. These frameworks include those based on mental models (“Grundvorstellungen”, Greefrath et al. (2016)), on the notions of concept definition and concept image (e.g., Hartter, 1995), on ways of thinking (Aydın & Ubuz, 2015) or on forms of representation (Kendal & Stacey, 2003), and the theoretical framework of Zandieh (2000). These have been used to examine students’ conceptions of the derivative or for specifying which facets of the concept students should learn. Zandieh’s framework has also been used to critically analyze curriculum materials to assess the potential of such materials for learning various meaning facets of derivatives. Zandieh (2000, p. 11) emphasizes: “The derivative framework of this paper is meant to describe what the mathematical community means by the concept of derivative at the first-year calculus level. The same structures may also be used to describe the parts of an individual’s concept image that coincide with the mathematical community’s concept of derivative.” The claim that a community shares a particular meaning model is a strong claim, which, in principle, requires empirical evidence (which Zandieh does not provide).

Studies on multidimensional derivatives

Limited research exists on concepts of derivatives in the multidimensional case, mostly for functions \({\mathbb{R}}^{2}\to {\mathbb{R}}\) (cf. Martínez-Planell & Trigueros, 2021), and none of the available research formulates concise meaning models for the concepts of derivatives and differentiability, because each study has its own goal and researchers have not considered the need for such a model. Tall (1992) proposes an alternative way of teaching differentials in two and three dimensions by focusing on visual representations and a “locally straight approach.” Martínez-Planell et al., (2015, 2017) and Trigueros et al. (2018) present genetic decompositions for the concepts of tangent plane, differential, partial derivative, and directional derivative for functions \({\mathbb{R}}^{2}\to {\mathbb{R}}\), using visual representations of function graphs. Harel (2021) critiques the teaching of the total derivative concept in US colleges based on textbook and class analysis. Weber (2012) examines students’ understanding of “rate of change in space” for functions \({\mathbb{R}}^{2}\to {\mathbb{R}}\). Halverscheid and Müller (2013) present initial ideas for mental models of multidimensional derivative concepts: Jacobian matrix as best approximation, gradient as slope in the direction of the steepest rise, and directional derivative as a one-dimensional derivative along a vector. Physics education papers, including Bajracharya et al. (2019), Roundy et al. (2015), and Van den Eynde et al. (2022), provide insights into partial derivatives and their application in physics contexts. For example, Roundy et al. (2015) adapt Zandieh’s framework to partial derivatives in physics, incorporating experimental measurements and numerical representations. Bajracharya et al. (2019) discuss aspects critical for physics students’ robust understanding of partial derivatives, while Van den Eynde et al. (2022) investigate how physics students approach the heat equation.

3 Research questions

The following research questions are addressed in this paper:

  1. 1.

    How can we formulate a comprehensive model of meaning of the concepts of derivative and differentiability in rigorous university mathematics, emphasizing the role of concept definitions, rigorous proofs of conceptual properties, and the interconnected network of related mathematical concepts?

  2. 2.

    In the context of the proposed meaning model, how do the interpretations and contextual factors of the concepts of derivative and differentiability differ from those in secondary and college-level mathematics, and how can these interpretations be updated for multidimensional scenarios?

After introducing our model of meaning, we will use it as a tool for textbook analysis to answer the following research questions:

  1. 3.

    Which of the definition variants for total differentiability and total derivative are used as definitions in the selected textbooks? Is the equivalence to other “definition variants” stated, and if so, how? What is the role of partial derivatives in the definition? How are connections of the definition variants to the 1D derivative treated?

  2. 4.

    How do the different textbooks treat the facets of meaning, including facets arising from the relation to other differentiability concepts, in the presented contexts of interpretation?

In addition to providing insights into the landscape of textbooks on the total derivative, we also want to illustrate and substantiate our model of meaning. Therefore, we will also discuss how our model of meaning is useful for analyzing textbooks.

4 The framework for describing meaning facets: The model of meaning

Our meaning model describing facets of meaning for differentiability concepts should satisfy the following requirements:

  1. (a)

    It should take into account the nature of rigorous university mathematics, with more emphasis on the central role of concept definitions, rigorous proofs of conceptual properties and relations, and networks of concepts.

  2. (b)

    It should reflect the complexity of the concepts as compared to the secondary and college level, with more emphasis on differentiability and not only on the derivative, and the different notions of differentiability in the multidimensional context (total, partial, directional).

  3. (c)

    It should include the contexts of interpretation proposed in the secondary and college level models, which may need to be updated in the multidimensional case.

  4. (d)

    It should include meaning facets of the derivative concept in the one-dimensional case in the rigorous Analysis I context, on which a course must or can build, being aware that meanings may not always “generalize” easily, but may involve a discontinuous restructuring.

For our conceptual framework, we build on the notion of formal and semantic level from Hußmann and Prediger (2016). Addressing criterion (a), important first elements of our model of meaning are “definition variants”, building the bridge from the formal to the semantic level. On the formal level, the definition of a concept must be explicitly emphasized. Then, theorems can be formulated and proved to show that other properties are mathematically equivalent to the definition and thus could have been used as the definition as well. In our model of meaning, we include these different ways of formulating the definition and call them “definition variants” when they are mathematically equivalent but conceptually different enough to evoke different associations. Following Richenhagen (1985), we distinguish definition variants for objects (such as the total derivative) into constructive and relational-descriptive. A “constructive” variant provides explicit information on how to derive the defined object (e.g., “A = …”), while relational-descriptive variants define the object by specifying abstract properties. For each definition variant, we analyze whether it is constructive or relational-descriptive, and how differentiability concepts in the multidimensional case relate to the definitions in the 1D case.

The definition variants, combined with mathematical theory on the formal level, form the basis for the analysis of meaning facets. We distinguish between concept-immanent facets and those arising from the network of related concepts, including continuity and the other concepts of differentiability, recognizing that the meaning of a concept is based on its relation to other concepts (Sierpinska et al., 2002), thus satisfying requirement (b). In our model, meaning facets are categorized across various contexts of interpretation. To identify relevant contexts, we analyzed existing meaning models for the 1D derivative (Aydın & Ubuz, 2015; Greefrath et al., 2016; Kendal & Stacey, 2003; Tall, 1996; Zandieh, 2000) to meet criterions (c) and (d). While not explicitly structured in this way, these models contain interpretations of the 1D derivative in diverse contexts, including mathematics-immanent aspects from analysis (e.g., verbalizing the differential quotient as a local or instantaneous rate of change (Greefrath et al., 2016; Kendal & Stacey, 2003; Zandieh, 2000), derivative as an amplification factor (Greefrath et al., 2016), or using the derivative for optimization problems or qualitative function description (Aydın & Ubuz, 2015)) and elemental algebra (e.g., term manipulation by specific rules (Kendal & Stacey, 2003)), interpretations regarding function graphs and their slopes (Aydın & Ubuz, 2015; Greefrath et al., 2016; Kendal & Stacey, 2003; Tall, 1996; Zandieh, 2000) or approximation (Greefrath et al., 2016; Tall, 1996), and using the derivative to model real-world phenomena (Greefrath et al., 2016; Kendal & Stacey, 2003; Zandieh, 2000).

In the few papers addressing concepts of derivatives in the multidimensional case, we find the following interpretations: the idea of local rate of change with respect to partial and directional derivatives (Bajracharya et al., 2019; Roundy et al., 2015; Van den Eynde et al., 2022; Weber, 2012; Harel, 2021), interpretations regarding function graphs and tangent planes (Halverscheid & Müller, 2013; Harel, 2021; Martínez-Planell et al., 2015, 2017; Tall, 1992; Trigueros et al., 2018), and approximation with or without reference to the function graph (Halverscheid & Müller, 2013; Harel, 2021; Martínez-Planell et al., 2015, 2017; Tall, 1992; Trigueros et al., 2018). The aforementioned physics education papers (Bajracharya et al., 2019; Roundy et al., 2015; Van den Eynde et al., 2022) emphasize real-world applications of partial derivatives.

Consequently, our model of meaning for concepts of derivatives and differentiability incorporates the following distinct “contexts of interpretation”: geometric, analytic-algebraic, approximation, and real-world models. The geometric context includes interpretations in the Cartesian coordinate system with respect to function graphs and notions such as “tangent” or tangent (hyper)plane or tangent space, as well as all “classical” geometric notions such as straight lines and planes. It is further subdivided into abstract-geometric, which deals with function graphs, and real-geometric, where abstract-geometric interpretations are applied to real-world hilly landscapes. Although not explicitly mentioned in previous studies, we find this transfer intriguing when discussing functions \({\mathbb{R}}^{2}\to {\mathbb{R}}\), drawing from learners’ experiences with the 3D space they inhabit. The analytic-algebraic context deals with inner-mathematical properties, motivations, and relations not covered by other interpretation contexts. This includes the interpretation as a “local rate of change”, unless explicit real-world applications are mentioned. “Approximation” means using the derivative for local approximations. The “real-world models” context includes the application of the concept to real-world situations, such as in physics, for example for modeling temperature distribution in space. While included, this context is rudimentary, reflecting its limited emphasis in standard Analysis II courses in Germany, where real-world applications are typically not extensively covered.

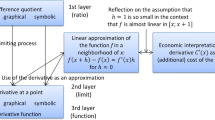
This leads to our model of meaning, illustrated in Fig. 1. It addresses epistemological aspects, since it is concerned with thinking about the concepts of differentiability. However, it does not aim to cover all historical aspects that led to the development of these concepts. In particular, we omit coverage of differentials in the sense of Leibniz and related practices, which are relevant in physics and engineering textbooks, but not in the rigorous context of Analysis II courses tailored for mathematics majors that we focus on.

Fig. 1
figure 1

Overview of the model of meaning

Full size image

5 Model of meaning for the total derivative and total differentiability

In this section, we present various definition variants for total differentiability and total derivative, motivating them by their connections to the 1D case. This is a result of our subject matter analysis and is not given in this particular form in any textbook. We then formulate facets of the meaning of these concepts in the different contexts of interpretation, taking into account their relations to other relevant concepts. Our analysis focuses specifically on concept definitions and initial theoretical aspects at the introduction of these concepts, and excludes facets of meaning that may arise from subsequent applications of the concepts in the course, such as the implicit function theorem. It is important to note that the meanings of mathematical concepts remain open and evolve with each advance in theory development.

We use the following two definition variants, similar to the two “aspects” introduced by Greefrath et al. (2016), for the 1D derivative as a reference:

  • (A1) “Let \(D\subseteq {\mathbb{R}}\) open, \(f:D\to {\mathbb{R}}\) a function, \(\xi \in D.\) Then, \(f\) is differentiable in \(\xi\) if the limit \({f}'\left(\xi \right):=\underset{h\to 0}{{\text{lim}}}\frac{f\left(\xi +h\right)-f\left(\xi \right)}{h}\) exists. In this case, the limit is called the derivative of \(f\) in \(\xi\).”

This definition is a constructive one because it shows how to obtain the derivative as the limit of the quotient of changes in function value and argument. This is the definition most common at secondary level. The local linear approximation definition is a relational-descriptive one:

  • (A2) “Let \(D\subseteq {\mathbb{R}}\) open, \(f:D\to {\mathbb{R}}\) a function, \(\xi \in D.\) Then, \(f\) is differentiable in \(\xi\) if a real number \(a\in {\mathbb{R}}\) and a mapping \(\varphi :{\mathbb{R}}\to {\mathbb{R}}\) exist such that \(f\left(\xi +h\right)=f\left(\xi \right)+a\cdot h+\varphi (h)\) and \(\underset{h\to 0}{{\text{lim}}}\frac{\varphi \left(h\right)}{h}=0\). If a number \(a\) with these properties exists, it is unique and is called the derivative of \(f\) in \(\xi\), written as \(f'(\xi )\).”

5.1 Definition variants (and their “motivations” and connections to the 1D case)

Knowing the two definition variants for the 1D derivative, one can try to formulate a generalization for the multidimensional case. In the 1D case, the derivative of a function at a point is a real number that is defined constructively by the limit (A1) or in a relational-descriptive way by a local linear approximation (A2). For the generalization, the first step could be to look at the components of the function. A function \(f: {\mathbb{R}}^{n}\to {\mathbb{R}}^{m}\) consists of \(m\) functions \({f}_{i}:{\mathbb{R}}^{n}\to {\mathbb{R}}~(f=\left(\begin{array}{c}{f}_{1}\\ \dots \\ {f}_{m}\end{array}\right))\). After explaining what a derivative of a function \({\mathbb{R}}^{n}\to {\mathbb{R}}\) is, one could define that \(f\) is differentiable if and only if all \({f}_{i}\) are differentiable, building the derivative of \(f\) from the derivatives of \({f}_{i}\) as “components.” Continuing the “component-wise strategy,” one could define component-wise “partial” derivatives and differentiability by using differential quotients analogous to (A1) for the respective components: \(\frac{\partial f}{\partial {x}_{i}}\left(\xi \right)=\underset{h\to 0}{{\text{lim}}}\frac{f\left(\xi +h{e}_{i}\right)-f\left(\xi \right)}{h}\). This definition gives \(n\) real numbers which are the partial derivatives (or, for a function \({\mathbb{R}}^{n}\to {\mathbb{R}}^{m}\), \(n\cdot m\) real numbers). If one wanted to have only one object, one could formally write the \(n\) partial derivatives in a \(1\times n\)-matrix or a vector (or an \(n\)-tuple without embedding it in any mathematical structure). This notion of differentiability is called partial differentiability in contemporary mathematics (cf. e.g., Duistermaat & Kolk, 2004, p. 47ff.), and it is important to understand why this notion, and thus the component-wise strategy, is not considered a satisfactory generalization of differentiability in one dimension. A first indication of the shortcomings of this notion is that partial differentiability does not imply continuity – an important relation in the 1D case. This can be seen for example by the function \(f:{\mathbb{R}}^{2}\to {\mathbb{R}},f\left(x,y\right)=\left\{\begin{array}{ll}\frac{xy}{{x}^{2}+{y}^{2}}, &\left(x,y\right)\ne \left(\mathrm{0,0}\right),\\ 0, &\left(x,y\right)=\left(\mathrm{0,0}\right),\end{array}\right.\) which is partially differentiable but not continuous in \(\left(\mathrm{0,0}\right).\) In addition, it can be shown by looking for instance at the function \(f:{\mathbb{R}}^{2}\to {\mathbb{R}},f\left(x,y\right)=\left\{\begin{array}{ll}x, &\text{if } y=0,\\ y, &\text{if } x=0,\\ 1,&\text{else},\end{array}\right.\) that knowing the function value and the partial derivatives at one point only provides information about the behavior of change of the function when only one component is changed: This given example function is partially differentiable at \(\xi =(\mathrm{0,0})\) with partial derivatives \(\frac{\partial f}{\partial x}\left(\mathrm{0,0}\right)=\frac{\partial f}{\partial y}\left(\mathrm{0,0}\right)=0\), but this gives no information about the function at any point \(\left(a,b\right)\) with \(a\ne 0\) and \(b\ne 0\), even for very small \(a\) and \(b\). In fact, the function is obviously not even continuous at \((\mathrm{0,0})\). Many other functions can be constructed like this (cf. Heuser, 1992, p. 252).

Therefore, the object containing all partial derivatives is not necessarily suitable to approximate the function locally. Thus, an additional property is needed to ensure suitability for local approximation. Using these partial derivatives, one could define total differentiability and the total derivative in the following way:

(*) “A function \(f:{\mathbb{R}}^{n}\to {\mathbb{R}}^{m}\) is totally differentiable at \(\xi \in {\mathbb{R}}^{n}\) if it is partially differentiable at \(\xi\) and the Jacobian matrix \({J}_{f}(\xi )\in {\mathbb{R}}^{m\times n}\) containing the partial derivatives yields the condition \(\underset{{h}\to 0}{{\text{lim}}}\frac{f\left(\xi +h\right)-f\left(\xi \right)-{J}_{f}\left(\xi \right)\cdot h}{\left|\left|h\right|\right|}=0\). In this case, the Jacobian matrix \({J}_{f}\left(\xi \right)\) is called the total derivative of \(f\) at \(\xi\), written as \(Df\left(\xi \right)\).”

This is a constructive definition variant of the total derivative. It can be shown formally that this definition implies continuity. The fact that this matrix can be used to approximate the function locally is given by the limit expression. In a relational-descriptive way, it is possible and common to define total differentiability and the total derivative in a similar way without using the partial derivatives:

(**) “A function \(f:{\mathbb{R}}^{n}\to {\mathbb{R}}^{m}\) is totally differentiable at \(\xi \in {\mathbb{R}}^{n}\) if there exists a matrix \({A}_{\xi }\in {\mathbb{R}}^{{\text{m}}\times {\text{n}}}\) such that \(\underset{{h}\to 0}{{\text{lim}}}\frac{f\left(\xi +h\right)-f\left(\xi \right)-{A}_{\xi }\cdot h}{\left|\left|h\right|\right|}=0.\) If it exists, this matrix \({A}_{\xi }\) is unique and is called the total derivative of \(f\) at \(\xi\), written as \(Df\left(\xi \right)\).”

The fact that the matrix in this definition is unique is not a priori clear and has to be proved on the formal level. The uniqueness can be shown by proving that the matrix components must be the partial derivatives.

Every matrix \(A\) can be interpreted as the transformation matrix of the linear transformation \(v\mapsto A\cdot v\). In many textbooks and lectures, it is common to define the total derivative at a point not as a matrix but as a linear mapping. This is a radical change from the 1D case where \({f}'(\xi)\) is a real number. Defining the total derivative as a linear mapping instead of as a matrix for the multidimensional case may seem rather complicated and not very comprehension-inducing at first glance, but it has several advantages. The first is that not only can the total derivative be used to approximate the function locally by a linear mapping, but the total derivative is then the linear mapping used to approximate the function: \(f\left(\xi +h\right)-f\left(\xi \right)\approx {A}_{\xi }(h)\). The tangent plane can then be defined as the graph of this linear mapping (shifted so that the point \(\left(\xi ,f\left(\xi \right)\right)\) corresponds to the origin). Another advantage – considering further generalization of the concept – is that a linear mapping can be defined without using a specific vector space basis, which is helpful when considering functions \(V\to W\) with arbitrary Banach spaces \(V, W\) (finite or infinite dimensional).

This leads to the following definition, which looks quite similar to the last one (**) at first sight, but may evoke different associations:

“A function \(f:{\mathbb{R}}^{n}\to {\mathbb{R}}^{m}\) is totally differentiable at \(\xi \in {\mathbb{R}}^{n}\) if there exists a linear mapping \({A}_{\xi }:{\mathbb{R}}^{n}\to {\mathbb{R}}^{m}\) such that \(\underset{{{h}}\to 0}{{\text{lim}}}\frac{f\left(\xi +h\right)-f\left(\xi \right)-{A}_{\xi }\left(h\right)}{\left|\left|h\right|\right|}=0.\) If it exists, this linear mapping \({A}_{\xi }\) is unique and is called the total derivative of \(f\) at \(\xi\), written as \(Df\left(\xi \right)\).”

On the other hand, it is possible to start from definition variant (A2) from the 1D case. Here, a natural generalization would be to formally copy the definition and replace \({\mathbb{R}}\) by \({\mathbb{R}}^{n}\) and \({\mathbb{R}}^{m}\), respectively, which then leads to a matrix \(A\in {\mathbb{R}}^{m\times n}\) instead of a real number \(a\), and \(\left|\left|h\right|\right|\) in the denominator:

(***) “A function \(f:{\mathbb{R}}^{n}\to {\mathbb{R}}^{m}\) is totally differentiable at \(\xi \in {\mathbb{R}}^{n}\) if there exist a matrix \({A}_{\xi }\in {\mathbb{R}}^{{\text{m}}\times {\text{n}}}\) and a function \({\varphi }_{\xi }:{\mathbb{R}}^{n}\to {\mathbb{R}}^{m}\) such that \(f\left(\xi +h\right)=f\left(\xi \right)+{A}_{\xi }\cdot {\text{h}}+{\varphi }_{\xi }\left(h\right)\) and \(\underset{h\to 0}{{\text{lim}}}\frac{{\mathrm{\varphi }}_{\xi }\left(h\right)}{\left|\left|h\right|\right|}=0\). If it exists, this matrix \({A}_{\xi }\) is unique and is called the total derivative of \(f\) at \(\xi\), written as \(Df\left(\xi \right)\).”

Here – as in definition variant (A2) for the 1D case – an “error function” \({\varphi }_{\xi }\) is introduced. In the former definition variant (**), the expression \(\underset{{{h}}\to 0}{{\text{lim}}}\frac{f\left(\xi +h\right)-f\left(\xi \right)-{A}_{\xi }\cdot h}{\left|\left|h\right|\right|}=0\) combines the two equations \(f\left(\xi +h\right)=f\left(\xi \right)+{A}_{\xi }\cdot {\text{h}}+{\varphi }_{\xi }\left(h\right)\) and \(\lim\limits_{h\to 0}\frac{{\mathrm{\varphi }}_{\xi }\left(h\right)}{\left|\left|h\right|\right|}=0\). Writing the equation \(f\left(\xi +h\right)=\dots\) and using this error function works more clearly toward the approximation property of the total derivative. As above, this definition variant could also be formulated with a linear mapping instead of a matrix. The error function \({\varphi }_{\xi }\) could also be introduced in the definition variant with partial derivatives.

We have now identified several aspects in which the definition variants can differ. We summarize these and give our naming scheme for the definition variants in Table 1, where each row denotes a new aspect. Some aspects concern total differentiability (TD), while others concern the total derivative (A).

Table 1 Naming scheme for definition variants
Full size table

Thus, definition variant (*) is called \(T{D}_{2sM}{A}_{2M}\) and (***) is \(T{D}_{1cM}{A}_{1xM}\), the “x” being d, p or r, depending on how the uniqueness of the total derivative is shown. There are also additional possibilities for definition variants, for example using directional derivatives, which are not included in this paper.

5.2 Facets of meaning

In this section, we present various facets of the meaning of the total derivative in different contexts, thus addressing the semantic level.

Analytic-algebraic context

Depending on the definition variant, the total derivative is seen either as a matrix or as a linear mapping. If a relational-descriptive definition variant is used, it must first be proved that the total derivative of a given function at a point is unique. The constructive definition variants using partial derivatives provide the “recipe” for obtaining the total derivative, while it remains open at first how to compute it given a relational-descriptive definition. One strategy is to identify the linear part in the term \(f\left(\xi +h\right)-f(\xi )\). Another possibility is to use the relation to partial derivatives: It can be shown that total differentiability implies partial differentiability, and the entries of the matrix of the total derivative are exactly the partial derivatives. Partial derivatives can be easily computed using techniques from the 1D case. The matrix containing the partial derivatives can even exist if the function is not totally differentiable, so it is important to check that it is indeed the total derivative. This can be done in two ways: Either it can be shown that \(\underset{h\to 0}{{\text{lim}}}\frac{f\left(\xi +h\right)-f\left(\xi \right)-{J}_{f}\left(\xi \right)\cdot h}{\left|\left|h\right|\right|}=0\) (the condition known from definition variant (\(T{D}_{2..}\)), which is a necessary and sufficient condition) or that all partial derivatives are continuous (\({C}^{1}\)-criterion, not necessary, but sufficient condition, cf. e.g., Duistermaat & Kolk, 2004, p. 49). These are applications of theorems about the relation between total and partial differentiability, which must be proved formally. Here, we see how this connection can be used to compute and thus handle the object “total derivative” more easily. An important interpretation of the 1D derivative is that it is the local rate of change. The total derivative can be thought of as the matrix containing the local rates of change in the respective components and as the mapping that maps each vector \(v\in {\mathbb{R}}^{n}\) to the local rate of change in that direction, which is given by the directional derivative \({D}_{v}f\left(\xi \right)=\underset{h\to 0}{{\text{lim}}}\frac{f\left(\xi +hv\right)-f\left(\xi \right)}{h}\). In this way, the relation between total and directional derivative provides an additional interpretation for the total derivative. As mentioned when introducing the definition variants, total differentiability implies continuity as in the 1D case. Thus, one could colloquially say that total differentiability ensures that the function does not “change too much” in a neighborhood of the point in question.

Approximation context

Most of the meaning models developed for the 1D derivative do not emphasize the approximation interpretation, although Harel (2021) calls this the central interpretation of the total derivative. The total derivative at \(\xi\) is (or can be used to define) the linear function that approximates the difference of the function values near \(\xi\): \(f\left(\xi +h\right)-f\left(\xi \right)\approx {A}_{\xi }(h)\). The sign “\(\approx\)” can be specified by the error function \({\varphi }_{\xi }\) that is introduced in the definition variants “\(T{D}_{.c.}.\)” All of the definition variants allow this interpretation easily, the ones with “c” by stating the term \(f\left(\xi +h\right)=f\left(\xi \right)+{A}_{\xi }\left(h\right)+{\varphi }_{\xi }(h)\), those with “s” by expressing the limit condition \(\underset{h\to 0}{{\text{lim}}}\frac{f\left(\xi +h\right)-f\left(\xi \right)-{A}_{\xi }\cdot h}{\left|\left|h\right|\right|}=0\), indicating that the relative error in writing \(f\left(\xi +h\right)\approx f\left(\xi \right)+{A}_{\xi }\cdot h\) is small. However, the interpretation as an approximation is more obvious in the “c” definition variants.

Geometric context

Analogous to the 1D case, the approximation interpretation can be transferred to the geometric context, where total differentiability implies the graph’s resemblance to a non-vertical plane near \(\xi\), the tangent plane. For functions \({\mathbb{R}}^{n}\to {\mathbb{R}}^{m}\) with \(n+m>3\), the graph cannot be easily visualized. An analog to the tangent plane can still be defined using the total derivative: The tangent space (sometimes still called tangent plane) is an \(n\)-dimensional affine subspace of \({\mathbb{R}}^{m+n}\) and can be understood as the graph of the total derivative shifted so that the point \((\xi , f\left(\xi \right))\) corresponds to the origin (if defined as a linear mapping) or as the set \(\{\left(h,f\left(\xi \right)+{J}_{f}\left(\xi \right)\cdot \left(h-\xi \right)\right)|h\in {\mathbb{R}}^{n}\}\). The matrix \({J}_{f}(\xi )\) contains the “slopes” of the tangent plane in the directions of the respective coordinate axes; for the case \({\mathbb{R}}^{2}\to {\mathbb{R}}\) these are the slopes of the lines obtained by intersecting the tangent plane with the planes parallel to the \(xz\)- and \(yz\)-planes. The geometric context can also be used to explain the relationship between total and directional differentiability: If all directional derivatives of \(f\) at \(\xi\) exist, then tangents to the graph exist in all directions. These tangents do not necessarily form a plane – only if the mapping \(v\mapsto {D}_{v}f\left(\xi \right)\) is linear. If this plane is indeed the tangent plane, \(f\) is totally differentiable at \(\xi\). The real-geometric interpretation is a transfer of this phenomenon to the three-dimensional real world: If the function \(f:{\mathbb{R}}^{2}\to {\mathbb{R}}\) gives the height depending on a point in two coordinates, the graph of \(f\) models a hilly landscape. Then its total differentiability means that the described landscape has no sharp “edges” and does not become “approximately vertical” anywhere, since it looks locally like non-vertical planes everywhere. There is another geometric interpretation of the total derivative \(Df(\xi )\) using the composition of \(f\) with a curve \(\gamma :I\to U\subseteq {\mathbb{R}}^{n}\) with \(\gamma \left(0\right)=\xi\) and \({\gamma }'\left(0\right)=h\in {\mathbb{R}}^{n}\): The composite curve  \(\widetilde{\gamma }=f\circ \gamma\) then has  \(\widetilde{\gamma }\left(0\right)=f(\xi )\) and \({\widetilde{\gamma }}'\left(0\right)=Df(\xi )(h)\). This can be interpreted as follows: If \(x\) moves from \(\xi\) with instantaneous velocity \(h\), then \(f(x)\) moves from \(f(\xi )\) with instantaneous velocity \(Df(\xi )(h)\). Using this curve \(\gamma\), we introduced a notion of time to illustrate the meaning of the total derivative. The directional derivative can then be seen as a special case of this, where \(\gamma\) is a straight line (\(\gamma \left(t\right)=\xi +t\cdot v\)). For functions \({\mathbb{R}}^{n}\to {\mathbb{R}}\), the vector obtained by transposing the matrix \({J}_{f}\left(\xi \right)\) is called the gradient, which provides an additional interpretation: The gradient indicates the direction in which the graph increases the most, and its absolute value is the corresponding slope.

Real-world model

There are many applications for functions \({\mathbb{R}}^{n}\to {\mathbb{R}}^{m}\), for example \(f:{\mathbb{R}}^{3}\to {\mathbb{R}}\) could model the temperature at each point of a room. In this case, the different components of the total derivative, the partial derivatives, can be interpreted as local rates of change in the respective directions. The total derivative can be used to approximate quantities in a small neighborhood, and the linear approximation itself can then be used for other applications, such as linearizing vector fields to simplify working with differential equations. The standard application from the 1D case, instantaneous velocity, is inappropriate for \(n>1\) because it requires the argument to be time, and there cannot be more than one time dimension in a sensible way.

6 Method and selection of the textbooks

Textbooks play a crucial role in teaching math concepts. In German university math lectures, there are no mandatory textbooks, but recommended ones for further reading. Lecturers often draw on multiple resources, including various textbooks, making textbook analyses vital for understanding teaching and learning conditions.

Harel (2021) conducted a rare textbook analysis of the total derivative in U.S. multivariable calculus courses. He found that four out of six textbooks lacked a definition for the total derivative, instead focusing on the tangent plane and briefly mentioning linear approximation. The other two provided a definition but rarely worked with it, considering it too abstract. Harel stresses the importance of linearization, which is often overlooked in teaching. In German “Analysis” courses and textbooks, we anticipate a different approach, expecting a formal definition of the total derivative, but questions remain about how semantic facets and relations to other differentiability concepts are treated.

Our analysis includes three “Analysis II” textbooks in our textbook analysis: (F) (Forster, 2008), (G) (Grieser, 2019), and (H) (Heuser, 1992). Two of these are commonly used in Germany: (F) serves as a standard concise companion book, while (H) is often recommended as a reference for more in-depth understanding. (G) is not yet a published textbook, but a lecturer’s script (published online and soon to be published as a book); however, even though it is not yet in print, we decided to include it in our analysis due to its particularly rich presentation of the topic with a focus on fostering understanding, which we felt would enrich our sample.

Our analysis focuses on the mathematical intentions of the textbooks (Pepin & Haggarty, 2001) using a “vertical analysis” approach (Charalambous et al., 2010) with Bowen’s (2009) method for document analysis. For this, we first selected the relevant chapters, including only those that introduce the different differentiation concepts and initial theories about them. Thus, we excluded sections dealing with higher derivatives, manifolds, Taylor’s theorem, the implicit function theorem, etc. (even though they may contain facets of meaning for the total derivative as well). We then divided the relevant chapters into individual segments: theorems, proofs, definitions, remarks, examples, and accompanying text (which we further subdivided into smaller sections of meaning if necessary).

For RQ 3, we first identified the definition of the total derivative that is given in each textbook and decided which type of definition variant is presented. We then searched all other segments for the use of definition variants and for explicit links to the 1D case and to partial derivatives.

For RQ 4, we coded for each segment whether there is a comment on the total derivative on the semantic level, such as a comment on interpretations, usefulness, or motivation, and then decided which context of interpretation it would fall into (see our model of meaning above). We present these results by summarizing all statements about the total derivative on the semantic level, structured into the different contexts of interpretation, and give citations from the textbooks when necessary.

7 Results of the textbook analysis

7.1 RQ 3: Definition variants in the textbooks

Table 2 provides an overview of the definition variants we found in the three textbooks. The detailed analysis follows.

Table 2 Overview of definition variants used in the textbooks
Full size table

We identified 24 relevant pages in book (F). Total differentiability is defined using definition variant \(T{D}_{1cL}\), but the linear mapping is not yet called “total derivative”, since its uniqueness is not clear at first. A remark afterward explains that every linear mapping can be identified with the corresponding transformation matrix. Shortly after, a theorem states that total differentiability implies partial differentiability and that the components of the matrix are uniquely determined by the partial derivatives (which are defined one chapter earlier). If the function is totally differentiable, the matrix from the definition, which is the matrix consisting of the partial derivatives, is called “differential” (a name sometimes used instead of “total derivative”). Thus, the definition for total differentiability and total derivative given by (F) is the variant \(T{D}_{1cL}{A}_{1pM}\). \(T{A}_{2M}\) is also mentioned. The definition is not motivated by the 1D derivative; there is only a remark on the formal level stating that for \(m=n=1\) the definition is equivalent to the usual 1D-differentiability, referring to a theorem in the corresponding Analysis I book, which proves the equivalence of (A1) and (A2).

In book (G) we identified and analyzed 21 relevant pages. (G) begins the chapter on differentiation in the multidimensional case with the question of how to generalize a definition for the 1D derivative. He starts with the definition of the 1D derivative in form (A1) and notes that this cannot be easily generalized and reformulates the definition in another form (which can be characterized as a form between (A1) and (A2)). This leads to the definition of total differentiability and total derivative in the form \(T{D}_{1sL}{A}_{1dL}\). The total derivative is defined before the uniqueness is shown in a remark afterward, using only the definition. Partial derivatives are not defined before the definition of total differentiability and are not used to show the uniqueness of the total derivative. The remark also states that the definition could also be formulated by defining a “rest function” \(r\left(h\right)=f\left(a+h\right)-f\left(a\right)-L(h)\), thus also mentioning \(T{D}_{1cL}\), and that a linear mapping can be expressed by its transformation matrix, implicitly giving a definition variant \(T{A}_{..M}\). In addition, it is mentioned fleetingly in the same remark that the uniqueness could be shown using the connection to directional derivatives (\(T{A}_{1rL}\)). Later, when partial derivatives are defined, (G) also mentions that the total derivative can be computed using partial derivatives by giving the corresponding theorem, so the equivalence to \(T{A}_{2M}\) is also shown.

In book (H) we found and analyzed 33 relevant pages. Like (F), (H) starts with a chapter on partial derivatives. An interesting intermediate step follows: \({C}^{1}\)-functions are defined as partially differentiable functions with continuous partial derivatives, and their change behavior is analyzed. A theorem shows that for \({C}^{1}\)-functions, the partial derivatives can be used to approximate the function locally. The book begins the chapter on total differentiability with a discussion of this approximation property, calling it “characteristic for real differentiable functions” (Heuser, 1992, p. 259, translated by the authors). Then a definition for total differentiability of type \(T{D}_{1cM}\) is given. After that, (H) states: “In the 1D case, this definition of differentiability leads to the one given earlier […] In this case, \(A\) is the one-element matrix \(({f}'\left(\xi \right))\), which, of course, can be readily identified with the derivative \(f'(\xi )\). This suggests the idea of calling \(A\) a derivative in the general case as well. Before doing so, we have to be sure that A is unique” (Heuser, p.259, translated by the authors). The uniqueness is shown using the connection to partial derivatives, as in (F), before the total derivative is defined as the matrix from the definition of total differentiability, with the remark that it is now known that the entries of this matrix are the partial derivatives. Therefore, the full definition of total differentiability and the total derivative given in (H) is of the type \(T{D}_{1cM}{A}_{1pM}\), with a mention of \(T{A}_{2M}\). Furthermore, (H) states in a remark that thanks to the connection between matrices and linear mappings, the definition could also have been formulated using a mapping (which is further explored in a chapter on differentiation in arbitrary Banach spaces), so the possibility of using a definition variant of type \(T{D}_{..L}{A}_{..L}\) is mentioned but not further explored.

As expected, our results differ from Harel’s (2021) findings: The definition of total differentiability and the total derivative is given and used in all of the books.

The three books differ in many respects. (F) and (H) define partial derivatives first and use them to show uniqueness of the total derivative while (G) introduces partial derivatives later and proves uniqueness using only the definition of total differentiability. It is worth noting that (G) defines total differentiability and the total derivative, leaving the uniqueness of the total derivative open at first and proving it later. A notable aspect is that (H) introduces \({C}^{1}\)-functions and their change behavior as a motivation for the definition of total differentiability. None of the books defines total differentiability by using partial differentiability with an additional property (like definition variants \(T{D}_{2..}\)), even though (F) and (H) have discussed partial derivatives before. The total derivative is defined in a relational-descriptive way in all the books. (F) and (H) state immediately after the definition that it is also the matrix containing the partial derivatives. (G) also states this fact, but much later. It is interesting that (F) defines total differentiability by requiring the existence of a linear mapping with certain properties, but then defines the total derivative as a matrix. All three books mention a definition variant with an error function, although in (G) this is not in the highlighted definition but in a remark afterward. This may be because they are easier to handle on the formal level, or because the approximation property is more obvious this way. This is only speculation, since the books do not comment on their chosen definition variants on a meta-level. There are two different ways of connecting the definition to the 1D case: (F) only shows on the formal level that for \(n=m=1\) the total derivative is the 1D derivative, while (G) and (H) also use the 1D case for motivation and point out similarities and differences.

7.2 RQ 4: Facets of meaning in different contexts of interpretation in the textbooks

There are very few comments on the semantic level in book (F) in the analyzed segments. The only time that concept-immanent facets of the meaning of the total derivative are mentioned is in the introduction to the chapter on total differentiability in the following way:

“In this section we define the total differentiability of functions from open subsets of \({\mathbb{R}}^{n}\) into \({\mathbb{R}}^{m}\) as a certain approximability by linear mappings. In contrast to partial differentiability, one does not need to refer to the separate coordinates in the process; moreover, a totally differentiable function is automatically continuous.” (Forster, 2008, p. 62, translated by the authors)

Here, a meaning facet in the approximation context is given (“certain approximability”). In addition, the fact that continuity will be implied and the absence of the need for references to separate coordinates as a distinction from partial differentiability are emphasized. Regarding facets of meaning from the concept of networks, (F) formulates as a theorem on the formal level that total differentiability implies partial differentiability with the matrix entries of the total derivative being the partial derivatives. In a subsequent remark it is explained that this ensures the uniqueness of the total derivative.

In contrast, book (G) provides very rich interpretations. Concerning the analytic-algebraic context, the idea of the local rate of change is mentioned: After giving the definition of the total derivative, (G) asks whether an interpretation as a local rate of change as in the 1D case is possible. It then states that the connection to directional derivatives will help to answer this question, but the answer is not formulated explicitly and is left to the reader. The relation to directional derivatives, and, as a special case of them, partial derivatives is also explicitly mentioned as a way to compute the total derivative. The approximation context is also mentioned in a remark:

“This can also be formulated as follows: The change in the function value \(f\left(x\right)\) depends almost linearly on the change in the \(x\)-value (from \(a\) to \(a+h\)). Here, ‘almost linearly’ means: linear, plus a term that converges faster than linearly to 0 for \(h\to 0\). The total derivative \(D{f}_{a}\) is then the linear part.” (Grieser, 2019, p. 44f., translated by the authors)

This remark is given after reformulating the definition as \(T{D}_{1cL}\). The idea of approximation is then used for a heuristic argument for proving the chain rule. The geometric idea of the tangent plane permeates the chapter. The attempt to generalize the idea of tangents from 1D derivative to the multidimensional case is expressed in the introduction, where the illustrative notion of a tangent plane is introduced as a generalization. Later, the tangent plane is formally defined as the graph of the total derivative. This idea is recurrently used in arguments about total differentiability of example functions. It is mentioned that the Jacobian matrix contains the “slopes” of the tangent plane. Another geometric interpretation of the total derivative, the idea of the transformation of a curve (described above), is also mentioned. Regarding the interpretation in real-world models, there is a section listing different real-world situations that could be modeled by functions \({\mathbb{R}}^{n}\to {\mathbb{R}}^{m}\) and the meaning of the total derivative in these contexts, for example, the air pressure depending on the location (for which the meaning of the gradient – related to the total derivative – as the direction of the strongest increase is thematized), or different vector fields (e.g., gravity, magnetic fields), for which the book states that the total derivative is then used for a linearization, which can help in solving differential equations, but it does not go into detail about the meaning of the total derivative in this context.

In book (H), partial derivatives are first defined, then the change behavior and approximation properties of \({C}^{1}\)-functions are discussed. This approximation property is used to motivate and define total differentiability. The motivation for looking at more than partial derivatives given by (H) before addressing \({C}^{1}\)-functions is the desire to analyze the change behavior of the function when changes occur in multiple directions, which is motivated by interpretations in real-world models:

“For a given function \(f(x,y)\), one is usually not only interested in controlling its behavior parallel to the coordinate axes, but rather one may be interested in knowing how \(f(x,y)\) changes when \(x\) and \(y\) vary simultaneously. Consider the problem of describing the steady-state temperature distribution in a thin plate […]. Here, one would first arbitrarily […] define a \(xy\)-coordinate system and then express the temperature at the point \((x,y)\) by \(f(x,y)\). If one knows the temperature at the point \((\xi ,\eta )\) then one will not only be interested in being able to follow its course from \((\xi ,\eta )\) parallel to the coordinate axes, which have not the slightest thing to do with the physical problem.” (Heuser, 1992, p. 252, translated by the authors)

The relationship between total and partial derivatives is later used to deduce that the matrix from the definition is indeed unique and can be determined by the partial derivatives. The approximation interpretation is given explicitly: The total derivative is introduced with the idea of approximating a function with “especially easy,” that is, linear, functions, with reference to the theorem about approximation of \({C}^{1}\)-functions, and explicitly mentioning that change in different directions should be possible (in contrast to partial derivatives). The tangent plane is not introduced. A geometric interpretation is given only for other concepts of derivatives: partial derivative as slope of the tangent of a curve, gradient as the direction of greatest ascent, etc. Real-world models are considered throughout the sections on partial derivatives, especially in exercises at the end of the chapters (e.g., concerning fluid mechanics or oscillating strings). The idea of a function modeling temperature on a thin plate is used to motivate that partial derivatives are not enough (see above). The approximation idea is also applied to real-world models in problems for \({C}^{1}\)-functions, such as propagating uncertainty in a harmonic oscillator. These problems are given before the total derivative is defined; after that, no explicit real-world applications are presented.

In summary, we found some of the facets of meaning from our model of meaning in the respective textbooks, but none of the textbooks mentions all of them. All of the textbooks address the approximation property (which Harel (2021) argues to be the most important facet of meaning). It is interesting to note that (G) first reformulates the definition in the definition variant \(T{D}_{1cL}\) before referring to the approximation facet. This supports our thesis that definition variants “c” (using an “error function”) are better suited to illustrate the approximation context. Meaning facets from the geometric context seem to be less common, with only (G) introducing the idea of tangent planes. However, (G) emphasizes the geometric interpretation and uses it for motivation and heuristic arguments. All three books comment on the relations of total differentiability to other concepts on the semantic level: by comparing total differentiability to partial differentiability ((H)), by providing uniqueness of the total derivative ((F), (H)), by providing a way to compute the total derivative ((G) explicitly, (F) and (H) implicitly), and by providing an additional interpretation ((G)). Sometimes a meaning facet is implied but not explicitly stated: (G) asks whether the total derivative can be interpreted using the concept of local rate of change and declares that the question can be answered using the relation between total and directional derivative, but does not explicitly state that the total derivative is the function that maps each vector to the local rate of change in the direction of that vector. (F) has very few remarks on the semantic level. Its focus on the formal level makes it well suited as a reference book but rather inappropriate for building a rich concept image.

8 Discussion

We have introduced a comprehensive model of meaning for total differentiability and the total derivative, offering nuanced interpretations in different contexts while emphasizing relationships with other related concepts. In agreement with Sierpinska et al. (2002), we argue that considering these relationships significantly enhances the understanding of the concept.

Thus, we have contributed to the field by not only presenting a subject matter analysis of a topic in higher mathematics, but also by providing a conceptual framework (resulting in the model of meaning) that could be used to conduct a subject matter analysis of any topic in higher mathematics, provided that relevant contexts of interpretation – which may differ for other topics – are first identified. Although our model does not explicitly refer to ATD or activity theory, we believe that it could be integrated into these theoretical approaches as a valuable reference.

However, our model has limitations. Tailored to mathematics majors, it may not capture facets that are more relevant to other disciplines like engineering or physics, such as Leibniz’s differentials. Moreover, it does not aspire to be a historically accurate account of the origin of the concept of the total derivative. In addition, we developed our model with a focus on a rather small area of the introduction of the concept of total differentiability, focusing on definitions and initial theory, such as connections to other differentiability concepts. We therefore excluded, for example, the analysis of optimal points, Taylor series, or the implicit function theorem, all of which are of course related to the concept of total derivative, or further generalizations such as the Fréchet derivative. In our opinion, it is a characteristic of university mathematics that meaning models can never be complete in the sense that no more facets could be added.

We have shown how our model serves as a tool for analyzing textbooks, providing a special, content-oriented lens for this analysis. We focused on different definition variants and found that the total derivative is always defined in a relational-descriptive way, its uniqueness is often shown using partial derivatives, and an “error function” is usually introduced. We searched for meaning facets on the semantic level in the textbooks and sorted them into the contexts of interpretation that we found to be relevant from a literature review. In doing so, we were open to other remarks on the semantic level that would not fit into any of our contexts but we did not find any such remarks, indicating that our model covers the important areas. Our textbook analysis, although limited to three textbooks, provides insights into different approaches to presenting the topic, revealing differing scopes of “semantic presentation” (ranging from very few remarks on the semantic level in (F) to some in (H) and many in (G)).

The model’s rich and structured presentation of meaning facets makes it versatile, being suitable for reflection on or design of lectures, normative decisions about student learning objectives, and the development of tests or interviews to assess student understanding and concept images.

The model is not a prescription for direct implementation in lectures; rather, it serves as a frame of reference that shows different possibilities of facets of meaning that could be addressed. The design of a specific lecture always depends on circumstances such as the audience. Further research is needed to determine the effectiveness of specific facets and explanations for different types of learners.