Students’ Understanding of the Derivative Concept in the Context of Mathematics for Economics

Abstract

The derivative concept plays a major role in economics. However, its use in economics is very heterogeneous, sometimes inconsistent, and contradicts students’ prior knowledge from school. This applies in particular to the common economic interpretation of the derivative as the amount of change while increasing the production by one unit. Hence, in calculus courses for economics students, learners should acquire an understanding of the derivative that is mathematically acceptable and connected to their prior knowledge, but which also takes into account its practical use in economics. In this paper we first develop a theoretical model describing such an understanding of the derivative for economics students. We then present an exploratory study investigating the extent to which economics students have such an understanding after their calculus course. The results indicate that many of them might not have acquired this kind of understanding, in particular concerning the common economic interpretation of the derivative. The study furthermore yields possible gaps in students’ understanding and possible misconceptions.

Zusammenfassung

Die Ableitung spielt in der Ökonomie eine wesentliche Rolle. Der dortige Umgang mit ihr ist aber sehr heterogen, teilweise inkonsistent und widersprüchlich zum Vorwissen der Studierenden zur Ableitung aus der Schule. Dies trifft insbesondere auf die in der Ökonomie oft verwendete Interpretation der Ableitung als Zuwachs der Funktion bei Erhöhung der Produktion um eine Einheit zu. Daher sollten Studierende der Ökonomie in ihren mathematischen Lehrveranstaltungen ein Verständnis der Ableitung erwerben, welches mathematisch akzeptabel ist und an ihr Vorwissen anknüpft, das aber auch den praktischen Umgang mit ihr in der Ökonomie mitberücksichtigt. In diesem Beitrag entwickeln wir zunächst ein Modell, das ein solches Verständnis theoretisch beschreibt. Anschließend stellen wir eine explorative Studie vor, in der wir untersucht haben, inwieweit Studierende über ein solches Verständnis der Ableitung nach ihrem Kurs der Mathematik für Wirtschaftswissenschaftler verfügen. Deren Ergebnisse lassen vermuten, dass viele Studierende nach dem Kurs nicht über ein entsprechendes Verständnis verfügen, insbesondere in Bezug auf die oben beschriebene ökonomische Deutung der Ableitung. Sie liefert außerdem Hinweise auf mögliche Verständnislücken und Fehlvorstellungen.

1 Introduction and Problem Statement

The concept of the derivative plays a major role in economics, for example in marginal analysis investigating the effect of small changes from the current state of a production. To understand the way the derivative is used in economic contexts, students must in particular be able to interpret the derivative. The literature shows that this is difficult for students, not only for students of economics (Beichner 1994; Hahn and Prediger 2008; Hoffkamp 2011). Furthermore, understanding the way the derivative is practically used in economics presents a special challenge for economics students due to inconsistencies regarding its meaning, as the following definition of marginal cost in the economics textbook by Wöhe and Döring (2013) illustrates (pp. 300–301, translated by the authors):

Marginal cost $C^{\prime}$ is the additional cost of the last unit. The marginal cost for the 33rd unit can be determined easily by subtracting the total cost for 32 units from the total cost for 33 units. The marginal cost is the slope of the cost function. It can be determined by taking the derivative of the cost function $C^{\prime}=\frac{dC}{dx}$.

This definition suggests that the derivative at a point is identical to the additional cost of the last unit (the book also uses the unit €). Such an identification without explanation sometimes leads to inconsistencies or statements appearing wrong at first glance, like the equation $C\left(7\right)=\sum _{i=1}^{7}C^{\prime}\left(i\right)$ for a cost function with $C(0)=0$ (Wöhe et al. 2013), where in fact it is not the derivative that is used but rather its interpretation as the cost of the last unit. A similar handling of the derivative is also found in other economics textbooks, including English textbooks (Pindyck and Rubinfeld 2013; Stiglitz and Walsh 2002; Varian 2006). This usage might confuse students, particularly because it contradicts their knowledge concerning the derivative that they have learned in school. Therefore, it should be taken up in the students’ calculus courses and connected to their prior knowledge with the aim that economics students acquire an understanding of the derivative that is mathematically correct, but which also considers the way the derivative is used in economics.

To what extent this is achieved in current teaching was investigated in the first author’s PhD project under the supervision of the second author at the Centre for Higher Mathematics Education in Germany (khdm) (Feudel 2019). In this PhD project we first developed—on the basis of didactic and economic literature—a theoretical model that aims at describing an understanding of the derivative that might be desirable for economics students after their calculus course. Then we investigated the understanding actually taught by analyzing mathematics textbooks for economics students. Finally, we investigated the understanding economics students acquired in their calculus course with two empirical studies: an exploratory study with all students who completed a one-semester calculus course at the University of Paderborn, and an additional interview focusing on certain problems of students’ understanding that became visible in the data obtained from the exploratory study.

In this paper, we present the theoretical model describing a possible adequate understanding of the derivative for economics students, as this is the theoretical basis for our whole research. Afterwards, we present the exploratory study investigating the understanding economics students actually acquired in their calculus course at university. The study yields first quantitative data on economics students’ understanding of the derivative and its economic interpretation. In particular, it illustrates possible problems in their understanding that can be investigated in detail later. Hence, our research aims at extending the knowledge concerning students’ understanding of the derivative with a focus on economics students who have been rarely considered until now in mathematics education research.

2 Literature Review on Students’ Understanding of the Derivative—Theoretical Models and Empirical Results

2.1 Theoretical Models for Describing an Understanding of the Derivative Concept

Different models have been suggested in the mathematics education literature that aim at describing an understanding of the derivative concept. In the following, we want to describe two prominent models we have built our research on. A review of further models can be found in Feudel (2019).

2.1.1 Zandieh’s Matrix Model to Describe an Understanding of the Derivative

We first present a model by Zandieh (2000), which is often used in mathematics education research at college level (Carlson et al. 2002; Hähkiöniemi 2006; Roorda et al. 2007). She based her model on the construct of concept image by Tall and Vinner (1981). According to them, an understanding of a mathematical concept is not characterized by only knowing its concept definition. It is also characterized by the so-called concept image (p. 152):

The concept image represents the total cognitive structure associated with a concept which includes all the mental pictures and associated properties and processes.

While Vinner (1991) restricted the construct to nonverbal associations, Tall (2010) had a wider view of this construct. According to him, the concept image covers all associations, and may also include personal verbal characterizations and contextual interpretations of a concept. This concept image may be consistent or in conflict with the concept definition provided externally.

In her model, Zandieh aims at describing the concept image of the derivative of the mathematical community. She developed this description on the basis of how the derivative is used in mathematics textbooks, by mathematicians and by mathematics graduate students. Zandieh then defines an individual’s understanding of the derivative as the overlap of the student’s concept image with the concept image of the mathematical community. Hence, by using the mathematical community’s concept image as a reference, she also uses the construct concept image normatively.

Her description of the mathematical community’s concept image is represented by a matrix (Table 1). The rows ratio, limit, function, which she calls layers of the derivative, contain the three steps from a function $f$ to its derivative function $f^{\prime}$, and refer to the concepts these layers are based on. She calls each of these layers a process-object pair (based on the idea of process-object duality of mathematical concepts by Sfard (1991)) because these layers can be understood either as a process or as an object, whereby a process understanding usually precedes an object understanding.

Table 1 Zandieh’s model describing an understanding of the derivative. (Zandieh 2000, p. 106)

The columns contain different representations of these layers. These representations are not meant as different registers of semiotic representations (Duval 2006), but as “ways in which we think of the concept of derivative”: as the slope of the tangent line in graphical situations, as the velocity in kinematic situations, as the limit of the difference quotient in symbolic calculations, and as the rate of change of the dependent variable with respect to a change in the independent variable in a functional relationship. In particular, “verbal representation” in Zandieh’s model just means an interpretation of the derivative as “rate of change of the dependent variable with respect to change in the independent variable” (p. 110), and not a verbal interpretation in any other sense. She also uses the term “contexts” instead of representations. The definition of the derivative as the limit of the difference quotient is part of Zandieh’s model within the symbolic representation. Its existence (differentiability) is, however, not discussed. This role of the definition reflects that the model is aimed at college-level calculus and not at the Real Analysis level, which is comparable to Analysis I for mathematics majors in Germany.

2.1.2 A Model Based on Aspects and Grundvorstellungen

A second model in the literature to describe an understanding of the derivative was put forward by Greefrath et al. (2016). It is based on the notions of aspect and Grundvorstellung. The notion of Grundvorstellung has a long tradition in German didactics of mathematics, also with regard to the derivative concept (Blum and Kirsch 1979; Danckwerts and Vogel 2010; Kirsch 1979; vom Hofe 1992, 1995; vom Hofe and Blum 2016). A detailed description of this notion and its development can be found in vom Hofe and Blum (2016). Greefrath et al. (2016) define a Grundvorstellung of a concept as “a conceptual interpretation that gives it a meaning” (p. 101). Grundvorstellungen, as normative notions, should be part of the student’s concept image (Greefrath et al. 2016, p. 103). Greefrath et al. (2016) newly added the construct of aspect, which they call “a subdomain of the concept that can be used to characterize it on the basis of mathematical content”. Each aspect can be converted into a possible concept definition (p. 103).

Concerning the derivative, two relevant aspects are mentioned by Greefrath et al. (2016): (1) limit of the difference quotient, and (2) local linearization. To give these aspects a meaning, Greefrath et al. (2016) mention the following Grundvorstellungen of the derivative: (1) local rate of change, (2) tangent slope, (3) local linearity, and (4) amplification factor. For an understanding of the derivative according to the model by Greefrath et al. (2016), students should develop these four Grundvorstellungen, and relate them to the two aspects.

Besides its meanings as slope or rate of change, which are also found in Zandieh’s model, Greefrath et al. (2016) mention a further important facet of the derivative concept: the idea of local linear approximation $\Updelta f\approx f^{\prime}(x)\Updelta x$ for $\Updelta x\approx 0$ that is related to the Grundvorstellungen tangent slope, local linearity, and amplification factor. This idea plays an important role for an understanding of the common economic interpretation of the derivative, as we will explain in the next chapter.

None of the models in the literature considers the common economic interpretation of the derivative as the amount of change when increasing the production by one unit (see introduction) and its specificities yet. The theoretical part of our research—our model describing an understanding of the derivative for economics students that builds a bridge to the way the derivative is practically used in economics—attempts to fill this gap.

2.2 Empirical Results on Students’ Understanding of the Derivative

Many studies show that students have difficulties in understanding the derivative. First, various studies illustrate that students often do not know its different representations, or have problems in connecting them (Hähkiöniemi 2006; vom Hofe 1998; Zandieh 2000). Second, a lot of studies show that students have difficulties with understanding the transition between the difference quotient/slope of the secant/average rate of change and the derivative at a point precisely, for example vom Hofe (1998) or Friedrich (2001) (an extensive description of all these studies can be found in Feudel (2019)).

In this paper we focus on studies focusing on students’ ability to interpret the derivative in contexts because this is particularly relevant for economics students. There exist many studies illustrating that students often cannot correctly solve problems in which they need to make a connection between a function and its rate of change in contexts. Beichner (1994), for example, showed that many students cannot apply rate of change as speed in kinematic situations. Typical errors are the graph-as-picture error and the slope/height-confusion. Nemirovsky and Rubin (1992) furthermore showed that students often assume similarities between the time graph of a distance (movement) and the time graph of the velocity. Similar difficulties have also been found in various other studies (e.g. Carlson et al. 2010; McDermott et al. 1987).

One important reason for students’ problems with interpreting the derivative in contexts, to which we will again refer later when discussing the economic interpretation of the derivative, is an insufficient understanding of the rate concept. Byerley et al. (2016), for example, showed in an empirical study with mathematics teachers on their understanding of slope that many of them explained the meaning of a given slope of a linear function of 3.04 on the basis of an increment of $\Updelta x=1$. But they were not able to explain the meaning of $\frac{\Updelta y}{\Updelta x}=3.04$ for arbitrary $\Updelta x\neq 1$. An important reason for this limited understanding of slope, which Byerley et al. (2016) call “chunky”, was discovered earlier by Thompson (1994) in a study investigating the development of an understanding of the concept of rate in the speed context. He showed that the first stage in the development of a rate conception was to think of a rate $\frac{\Updelta y}{\Updelta x}$ as the amount of change $\Updelta y$ given a fixed change $\Updelta x$. Such a conception of rate can lead to problems when trying to assign a meaning to the difference quotients $\frac{f(x+h)-f(x)}{h}$ for arbitrary $h<1$ during the limiting process, and hence, to the derivative as the limit of these quotients.

While a lot of research has been done on students’ understanding of the derivative and rate of change in physical contexts and other dynamic situations, there has been little research on students’ understanding of the derivative in economic contexts. Wilhelm and Confrey (2003) showed that even if students could properly distinguish between a function and its rate of change in a physical situation, they could not necessarily do so in a context of daily monetary transactions. Furthermore, Mkhatshwa and Doerr (2015) obtained some interesting results in their research focusing on business students’ reasoning when solving optimization problems. The students often talked about economic quantities like marginal cost that are a rate of change per definition as an amount of change when using them in optimization tasks, or even interpreted the marginal cost as the total cost (Mkhatshwa and Doerr 2018). But that research did not focus on students’ understanding of the concept of derivative, on which marginal quantities in modern economics are based, and which is an extensive part of mathematics courses for economics students (Sydsæter and Hammond 2015; Tietze 2010). The empirical part of our research focuses exactly on this issue that has not yet been investigated.

3 The Common Economic Interpretation of the Derivative

We will now shortly present how the derivative is commonly interpreted in economics textbooks (a detailed textbook analysis can be found in Feudel (2019)) through the example of marginal cost, and discuss how this interpretation can be connected to the mathematical concept of the derivative on the basis of the literature mentioned in the last chapter, and certain economics textbooks that try to explain the interpretation used.

If $C\colon [0;\infty )\rightarrow [0;\infty )$ is a cost function with $x$ being the output of a product, its derivative $C^{\prime}(x)$, the so-called marginal cost, is usually interpreted as the additional cost of the next unit (Schierenbeck and Wöhle 2003) (sometimes also as the cost of the last unit). However, if one takes the interpretation of $C^{\prime}(x)$ as the additional cost of the next unit literally, it would be represented by a different mathematical object, namely the difference $C(x+1)-C(x)$. There are two essential differences between $C^{\prime}(x)$ and the additional cost of the next unit. First, the derivative is a rate of change while the additional cost is an amount of change. This becomes visible in the different units: if the output $x$ is measured in units of quantity and the cost in €, the unit of $C^{\prime}(x)$ is € per unit of quantity while the additional cost would be measured in €. However, as discussed in Sect. 2.2, Thompson (1994) found—in a study investigating the development of a conception of rate—that the first developmental stage is an understanding of a rate as an amount of change in the dependent variable given a certain change in the independent variable (like one unit). Similar views of rate might lie behind the economic interpretation of $C^{\prime}(x)$ as the additional cost of the next unit. This is also supported by some economics textbooks like Varian (2006), who emphasizes that “additional cost of the next unit” is a way of speaking of $\frac{\Updelta C}{\Updelta x}$ for $\Updelta x=1$. But often the derivative is also explicitly interpreted as $C(x+1)-C(x)$, which becomes, for example, visible in the unit or in figures visualizing the marginal cost as the change in the height when raising the argument by one unit (Pindyck and Rubinfeld 2013; Wöhe and Döring 2013).

The second difference between $C^{\prime}(x)$ and the cost of the next unit is a numerical one: except for linear functions, $C^{\prime}(x)$ is not exactly equal to $C(x+1)-C(x)$ or $\frac{C(x+1)-C(x)}{1}$. This particularly applies for prototypical functions the students have encountered at school like $f(x)=x^{2}$, $f(x)=e^{x}$ or $f(x)=\sin (x)$. This can lead to confusion.

However, the interpretation of the derivative as the additional cost of the next unit can be connected to the mathematical concept of derivative by the approximation $C(x+h)-C(x)\approx C^{\prime}(x)\cdot h$ for $h\approx 0$. The idea behind this approximation is to use the derivative as a linear approximation of the original cost function in a neighborhood of $x$, as is mentiond by Greefrath et al. (2016) (see Sect. 2.1).

Assigning $h=1$ in the approximation above then leads to the common economic interpretation of $C^{\prime}(x)$ as the additional cost of the next unit. This assignment can be explained with the assumption that one unit is small in economics, as it is done in some economics textbooks like Reiß (2007). He furthermore emphasizes that this assumption is dependent on the context. He calls a unit that is small enough in the context a marginal unit. However, the argument “one unit is small in the context” for this assignment seems a bit brief because it does not consider the properties of economic functions that are important for a negligible error between $C^{\prime}(x)$ and $C(x+1)-C(x)$/$\frac{C(x+1)-C(x)}{1}$. These become apparent in the book “Microeconomics” by Wiese (1999), pp. 47–48:

For many of the functions we want to consider, it does not make a big difference if we consider the difference quotient [with $\Updelta x=1$] or the derivative. For small changes, they are almost equal, and for linear functions, even perfect.

Hence, the essential assumption is that one unit is so small in economic contexts that the functions considered are almost linear within $[x;x+1]$. Explaining the assignment of $h=1$ in economics like this is in our opinion more appropriate for a mathematics course than just stating “$h=1$ is small in economics” because it also uncovers the property of local linearity within several units that is assumed for the functions considered in economics.

4 Development of a Theoretical Model for Describing an Adequate Understanding of the Derivative Concept for Economics Students

We developed a model that aims at describing an understanding of the derivative that bridges the mathematical concept of derivative and its practical use in economics, which we call adequate understanding of the derivative for economics students. We developed the model in two steps:

• 1. Selection of a theoretical framework for the description of an understanding of a mathematical concept in general on the basis of the literature in mathematics education

• 2. Elaboration of the framework into the shape of a concrete model on the basis of the mathematics education research and the economic literature presented in the last two chapters

4.1 General Framework for Describing an Understanding of a Mathematical Concept

We chose the construct of concept image (see Sect. 2.1) as a theoretical construct that can describe students’ understanding of a mathematical concept as the theoretical basis for our research because it is broad enough to include all facets of the derivative economics students need to know for an adequate understanding of it. We use it in the way of Tall (2010) (see Sect. 2.1), which means that it may in particular include verbal characterizations and contextual interpretations, such as an economic interpretation or the concept definition of the derivative.

4.2 The Concrete Model Describing an Adequate Understanding of the Derivative for Economics Students

The starting point for our model was the matrix model by Zandieh (2000) (Table 1), which is a normative description of the concept image of the derivative at college level specified by the mathematical community. This model in particular considers the different representations of the derivative and their connections, which are important for making sense of it. The definition of the derivative as the limit of the difference quotient, which plays an important role at university, is contained within the symbolic representation. The fact that it is not superordinate to the other representations is acceptable for mathematics service courses. In these courses it does not have the superordinate role it plays in courses for mathematics majors, in which the derivative is already used to define the concepts occurring in the other representations, for example a definition of the tangent line of a differentiable function $f$ through $(x_{0},f(x_{0}))$ as the graph of the linear function with the equation $t(x)=f(x_{0})+f^{\prime}(x_{0})(x-x_{0})$ as in Königsberger (2004). Furthermore, the layers ratio, limit, and function in Zandieh’s model point out very well, which concepts are necessary for an understanding of the derivative, also as a whole function, because thinking of the derivative as a function is a further hurdle for many students (see Feudel (2019) for a more detailed discussion of this issue).

However, Zandieh’s model lacks to describe an understanding of the derivative that also takes into account the practical usage of the derivative in economics, as it does not yet contain the common economic interpretation of the derivative as the amount of change when increasing the production by one unit (see Sect. 3). Furthermore, it does not contain the idea of local linearization that is one important approach to the derivative according to the model based on aspects and Grundvorstellungen by Greefrath et al. (2016) (see Sect. 2.1), and which connects the derivative as a mathematical concept to its common economic interpretation (see Sect. 3).

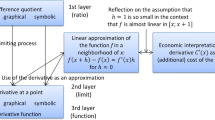
Therefore, we created our own model that includes these two facets (Fig. 1). The left side is Zandieh’s model (also containing the Grundvorstellungen “tangent slope” and “rate of change” within the graphical respective the verbal representation). The common economic interpretation of the derivative, which does not directly correspond to the mathematical concept of derivative (see Sect. 3), is on the right side. The idea of local linear approximation from the model by Greefrath et al. (2016) connecting these two is displayed in the center.

Fig. 1

Model for the description of an understanding of the derivative for economics students that also considers the way the derivative is practically used in economics

The linear approximation $f(x+h)-f(x)\approx f^{\prime}(x)\cdot h$ for $h\approx 0$ is directly linked with the symbolic and the graphical representation of the derivative in Zandieh’s model because it can either be derived symbolically from its definition or graphically with the help of the tangent line, which is close to the graph of the original function for $h\approx 0$ (it is even indistinguishable if $h$ is small enough). On the other hand the approximation is directly linked to the common economic interpretation of the derivative because in the latter $h$ is assigned to $h=1$ under the assumption that one unit is so small in economic contexts that the functions considered are almost linear within several units.

5 Research Question of the Exploratory Study on Students’ Understanding of the Derivate Concept After a One-semester Calculus Course

As explained in the last two chapters, gaining an understanding of the derivative that also considers the way the derivative is practically used in economics (as described in our theoretical model in Fig. 1) is not trivial. Since no research has hitherto been conducted that directly focuses on the understanding of the derivative that economics students actually have (see Sect. 2), we then conducted an exploratory study with the following research question:

To what extent did economics students acquire an understanding of the derivative as it is described in our model after their calculus course?

Our model consists of three parts (see Fig. 1):

• 1. The derivative as a mathematical concept (left side of the model)

• 2. The economic interpretation of the derivative (right side of the model)

• 3. The connection between these two (center part of the model)

The study provides first quantitative data on the understanding students actually acquired for the parts 1–3 that represent different facets of an adequate understanding of the derivative for economics students. In particular, we aimed to find possible gaps in students’ understanding and possible misconceptions concerning each of the three facets, which could be investigated more deeply later.

6 Methodology and Data Collection

6.1 Participants and Course Description

We conducted the study in the first semester course “Mathematics for economics students” at the University of Paderborn in Germany. This is the only mathematics course the students have to attend in their first semester. 821 of the students in this course took part in its final exam (these were the participants in our study). The course covered mathematical foundations like logic and set theory, and calculus in one variable. It consisted of a lecture (two sessions of 90 min each week) and tutorials (90 min each week). The lecture was held by a mathematician who had taught this course for many years. The teaching was traditional, which means that new content was introduced in the lecture first and practiced in the tutorials afterwards. In the latter, the students had to solve exercises in groups. Solutions to these exercises were presented in “grand tutorials” in the lecture hall on the board in the following week. Additionally, problem sheets were administered weekly for which students could submit solutions.

The lecturer put great emphasis on the learning of mathematical concepts. For each concept introduced, the students were advised to concern themselves with categories that are important for the development of an adequate concept image: examples, non-examples, visualizations, statements involving the concept, and applications (for detailed explanations see Feudel and Dietz (2019)). The knowledge of these categories was also expected in the exam.

6.2 Knowledge Concerning the Derivative Concept Taught in the Course

Introduction of the Mathematical Concept of Derivative

The derivative was formally defined as the limit of the difference quotient. Along with this definition, its representations as the slope of the tangent line and as the rate of change were introduced. In the second part of this introductory lecture on the derivative, the differentiation rules were taught (without proof).

Treatment of the Economic Interpretation of the Derivative

In the following lecture, the economic interpretation of the derivative was covered. First, the lecturer introduced the term “marginal function” (in German “Grenzfunktion”) as a name for the derivative of an economic function without assigning any meaning to it in an economic context (unlike the English term “marginal”, the German prefix “Grenz‑” just refers to a mathematical notion: Grenzwert (limit)). Then he deduced the unit of the derivative in economic contexts for marginal cost from the definition of the derivative.

In a third step, he introduced how $C^{\prime}(11)=0.7\, \frac{\mathrm{GE}}{\mathrm{ME}}$ of a cost function $C$ ($\mathrm{GE}=$ units of money, $\mathrm{ME}=$ units of quantity) can be interpreted. He taught two interpretations. The first one was:

If one increases the output from 11 units by one unit, the costs grow by approximately 0.7 units.

He justified this interpretation with the approximation $\Delta C\approx C^{\prime}(x)\cdot \Delta x$ for $\Delta x\approx 0$, which he derived from the definition of the derivative by using the difference quotient as an approximation of the derivative. He also visualized the parts of the approximation formula ($\Delta C$and $C^{\prime}(x)\cdot \Delta x$) on the board with the help of the tangent line.

Afterwards, the lecturer derived a further alternative interpretation using the notion of a marginal unit, which is also found in some economics textbooks like that of Reiß (2007). For this, he visualized on the board that the error between $\Delta C$and $C^{\prime}(x)\cdot \Delta x$ in the approximation $\Delta C\approx C^{\prime}(x)\cdot \Delta x$ becomes smaller if $\Delta x$ becomes smaller. He then explained the following:

The approximation $\Delta C\approx C^{\prime}(x)\cdot \Delta x$ transforms for $\Updelta x\rightarrow 0$ to a fictive equation $dC=C^{\prime}(x)dx$, in which $dC$ and $dx$ are called differentials that should be understood as fictive infinitely small quantities.

He then used the notion of a marginal unit for these differentials, and derived from the equation $dC=C^{\prime}(x)dx$ the following economic interpretation of the derivative $C^{\prime}(11)=0.7\, \frac{\mathrm{GE}}{\rm{ME}}$:

If one increases the output from 11 units by a marginal unit, the costs grow by 0.7 marginal units.

To base the economic interpretation on differentials as infinitely small quantities like this—a conception that is common in physics and engineering—is unusual in mathematics for economics students. In common mathematics textbooks for economics students like Sydsæter and Hammond (2015) or Tietze (2010), differentials are normally introduced as variables (see for example Thompson and Dreyfus (2017) or Oldenburg (2016) for a detailed explanation of this conception). The lecturer, however, introduced differentials as fictive infinitely small quantities to emphasize that $dx$ must be really tiny (“marginal”) for a negligible error when approximating the additional cost by $C^{\prime}(x)dx$.

Accompanying Exercises

The topics introduced in the lecture were also practiced in the tutorials and were part of the weekly problem sheets. Two tasks in particular focused on the economic interpretation of the derivative and its connection to the mathematical concept. These were:

• 1. State a mathematical interpretation and an economic interpretation of $C^{\prime}(5)$ of the cost function $C$ with $C(x)=8x^{2}+10x+700$ ($x$ is measured in tons of oil, $C(x)$ in 100 €).

• 2. Estimate the cost at an output of 45 units of another cost function, for which it is only known that $C(43)=19\ \mathrm{GE}$ and $C^{\prime}(43)=1.4\, \frac{\mathrm{GE}}{\mathrm{ME}}$.

The first task had to be solved during the tutorials in groups. At the end, the tutors wrote the following solution for the mathematical interpretation of $C^{\prime}(5)=90$ on the board:

The slope of the tangent line of the function $C$ at $x=5$ is 90.

Two economic interpretations of $C^{\prime}(5)$ were written down on the board at the end. These were:

1. If one increases the production from 5 t of oil by one ton, the costs grow by approximately 9000 €.

2. If one increases the production from 5 t by a marginal ton, the costs grow by 90 marginal units.

Furthermore, the tutors emphasized that the accurate result for the cost of the next ton is represented by the difference $C(6)-C(5)=9800\,\text{\EUR}$.

Task 2 was posed on a homework assignment that the students could submit to receive feedback. The solution provided used the (local) linear approximation $C(45)\approx C(43)+2\cdot C^{\prime}(43)$. A more detailed analysis of the tasks can be found in Feudel (2019).

6.2.1 Comparison of the Content Taught with Our Theoretical Model

Although the course was not designed on the basis of our theoretical model in Fig. 1, the different facets in our model were also covered in the course.

The understanding of the mathematical concept of derivative in our theoretical model was characterized by the three layers ratio, limit, function in the different representations: symbolic as the limit of the different quotient, graphical as the slope of the tangent line and verbal as the rate of change (Fig. 1). All of these layers and representations were covered in this course.

Furthermore, the lecturer introduced an economic interpretation of the derivative of a cost function as an approximation of the cost of the next unit and connected it to the mathematical concept via local linear approximation on the symbolic and the graphical level as in our model (Fig. 1). Hence, all parts of the model were taught in the course. Furthermore, to emphasize that the increment in $x$ must be tiny for a negligible error between the accurate additional cost and the approximation relying on the derivative, the lecturer taught a second interpretation of $C^{\prime}(x)$ as the (accurate) cost of the next marginal unit.

6.3 Instrument for Measuring Students’ Understanding After Their Calculus Course

Within the course, we got the option to include four items into the final examination. This is disadvantageous compared to a longer test just focusing on our model. On the other hand, students can be expected to work much more seriously if the items are part of a test that counts. Moreover, we expected that a non-obligatory extra test would have resulted in a large reduction in the sample size. The four items address different facets of our theoretical model describing an adequate understanding of the derivative for economics students (Fig. 1). They are shown in Table 2. The items were placed in the middle of the exam, so that students would hopefully not just omit them due to time pressure.

Table 2 Final exam tasks (originally posed in German) to investigate different facets of economics students’ understanding of the derivative

The aim of the first task was to investigate if the students at least knew an adequate economic interpretation of the derivative (right side of our theoretical model in Fig. 1). With the second task, we wanted to find out if they knew at least one mathematical representation of the derivative that assigns a meaning to it (left side of the model in Fig. 1). Tasks 3 and 4 aimed to find out if the students could connect these two via local linear approximation (center of the model in Fig. 1). A detailed analysis of the tasks will be presented in the next section.

Critical Discussion of the Instrument

Although we were able to obtain a large sample size with our instrument (821 students), and could expect that students would really try to answer the questions correctly, using exam questions also leads to some restrictions:

• 1. The large number of participants requires the possibility of correcting the answers efficiently. This restricts the degree of openness of the questions.

• 2. The final exam also had to cover other topics of the lecture. This restricts the number of tasks that could be assigned on this topic.

This has important consequences for the interpretation of the results. The data can provide snapshots of the extent to which the students in the course have acquired different facets that are important for an adequate understanding of the derivative in the sense of our model (see Sect. 5). Students’ errors can furthermore indicate possible gaps in understanding or possible misconceptions concerning these facets that might be widespread.

However, the data cannot provide a holistic view of students’ understanding of the derivative in the sense of the whole concept image by Tall and Vinner (1981) (see Sect. 2.1), and can only touch on the different facets of an understanding of the derivative in our theoretical model. In addition, it cannot be taken for granted that students who have written incorrect answers really have misconceptions. They might have written down these answers just to get partial credit. Hence, this study cannot fully answer the research question of to what extent economics students acquired an adequate understanding of the derivative in the sense of our model. Therefore, we conducted an additional interview study focusing on problems of students’ understanding of the derivative and its economic interpretation that became visible in the data (due to its large scope, this will be reported in a further article). Nevertheless, the limitations just mentioned need to be taken into account.

6.4 A Priori Analysis of the Four Tasks

In the following, an a priori analysis of the tasks is done. We will present possible correct answers that can be expected according to what was taught in the course for each task. Furthermore, we discuss errors that can be expected (on the basis of difficulties mentioned in the Sects. 2.2 and 3).

6.4.1 Task 1

The first task was to state an economic interpretation of $P^{\prime}(73)=0.2\, \frac{\mathrm{GE}}{\mathrm{ME}}$. A similar task had also been discussed in the tutorials accompanying the lecture (economic interpretation of $C^{\prime}(5)$ for the cost function $C(x)=8x^{2}+10x+700$, $x$ measured in tons, $C(x)$ in 100 €). Hence, the students were familiar with this type of task and, in particular, with the term economic interpretation.

The following answers can be expected according to what was taught in the course (see Sect. 6.2):

1. If one increases the output from 73 units by one unit, the profit increases by approximately 0.2 units of money.

2. If one increases the output from 73 units by one marginal unit, the profit increases by 0.2 marginal units.

A possible mistake may be that students might not mention that the derivative is just an approximation of the profit of the next unit, or they might only talk of marginal units in the output (because the lecturer in particular emphasized the necessity of the tininess in the increment of $x$). In addition, the students might mix the two answers above such as:

If one increases the output from 73 units by one marginal unit, the profit increases by approximately 0.2 units of money.

Furthermore, errors based on misconceptions that are documented in the literature, like the slope/height-confusion, probably occur (see Sect. 2.2). Another type of answer that can be expected is that students just state that $P^{\prime}(73)=0.2\, \frac{\mathrm{GE}}{\mathrm{ME}}$ means that the marginal profit at the output of 73 units is 0.2 $\frac{\mathrm{GE}}{\mathrm{ME}}$. However, in the lecture, the term “marginal profit” (Grenzgewinn) was just introduced as a name for the derivative of a profit function without further meaning (see Sect. 6.2), and is therefore not an interpretation from the point of view of the course.

6.4.2 Task 2

The second task was to state a mathematical interpretation of $P^{\prime}(73)=0.2\,\frac{\mathrm{GE}}{\mathrm{ME}}$. Just as for task 1, a similar task had been discussed in the tutorials (mathematical interpretation of $C^{\prime}(5)$ for the cost function $C(x)=8x^{2}+10x+700$). Hence, the students were in particular familiar with the term mathematical interpretation.

The following correct answers can be expected according to what was taught in the course:

1. The slope of the tangent line of the function $P$ at $x=73$ equals 0.2.

2. The local rate of change of the function $P$ at $x=73$ equals 0.2.

It cannot be expected that the students consider the units here because in the solution discussed in the tutorials to the analogue task, the units had been omitted as well. Instead, it can be expected that many students speak of the slope of the function at a point instead of the slope of the tangent to the function at that point because some tutors used this term (it is also frequently used at school as part of the Grundvorstellung of the derivative as slope; see Sect. 4.2).

6.4.3 Task 3

The third task was to determine an estimate of the additional cost when increasing the production from 5–7 units if $C(5)=10\, \mathrm{GE}$ and $C^{\prime}(5)=0.5\,\frac{\mathrm{GE}}{\mathrm{ME}}$. Regarding this task, an analogue task was posed on the problem sheets that had been administered weekly. A correct solution would be to use the formula $\Updelta C\approx C^{\prime}(x)\cdot \Updelta x$ for $x=5$ and $\Updelta x=2$ or the idea of local linear approximation behind it. However, students might not be aware that using the derivative to determine the additional cost only yields an approximation of the accurate additional cost. Hence, they might not make clear in their solution that the result obtained is just an approximation.

6.4.4 Task 4

In the last task, the students had to justify why the estimate in task 3 does not usually represent the accurate additional cost (for example in the case of quadratic cost functions). This kind of task had not been discussed in the course before and requires an understanding of the relationship between the marginal cost $C^{\prime}(x)$ and the additional cost on a conceptual level.

The following correct answers can be expected based on what was taught in the course:

1. The estimate is not accurate because the difference quotient is just an approximation of the derivative.

2. The estimate is not accurate because it represents the increase on the tangent line.

The first answer can be expected because the lecturer derived the approximation $\Updelta C\approx C^{\prime}(x)\cdot \Updelta x$ from the definition of the derivative as the limit of the difference quotient. The second answer can be expected because he visualized the connection between $\Updelta C$ and $C^{\prime}(x)\cdot \Updelta x$ in the approximation with the help of the tangent line. Furthermore, students might argue that the estimate is accurate only for linear functions, as it is based on local linear approximation.

7 Analysis of Students’ Answers

We categorized the answers to the four tasks by means of content analysis (Mayring 2015) in order to find out to what extent economics students have acquired different facets that are important for an adequate understanding of the derivative in the sense of our model, and to find possible gaps and problems in students’ understanding on the basis of their errors. Our a priori analysis was the basis for the categories containing adequate answers and for some error categories (see Sect. 6.4). Additional common errors were categorized on the basis of the data. Each answer was assigned to exactly one category.

7.1 Categorization of the Answers to Task 1

The first task was to state an economic interpretation of $P^{\prime}(73)=0.2\, \frac{\mathrm{GE}}{\mathrm{ME}}$. Based on our a priori analysis we conducted a two-step analysis:

1st Step

We conducted a rough categorization that aimed at discriminating answers that are really wrong from interpretations as a rate of change that are correct, and from all interpretations as an additional profit. Since it can be expected that students might not mention correctly that $P^{\prime}(73)$ is just an approximation of the additional profit of the next unit (see the a priori analysis in Sect. 6.4), we refined the category “additional profit” in a second step.

2nd Step

We analyzed the interpretations of $P^{\prime}(73)$as an additional profit according to whether the students mentioned that $P^{\prime}(73)$ is just an approximation of the additional profit of the next unit, or if they spoke of marginal units instead.

1st Step—Rough Categorization

The basis for the rough categorization was a category system that had been found in a task to interpret $C^{\prime}(200)=2$ of a cost function in a pretest administered to the students at the beginning of the course in September 2015. The category system is shown in Table 3.

Table 3 Response categories for the task to state an economic interpretation of $P^{\prime}\left(73\right)=0.2\, \frac{\mathrm{GE}}{\mathrm{ME}}$ for a profit function $P$ (Task 1)

The category I1 (Additional profit) is the overall category containing all interpretations of $P^{\prime}(73)$ as an additional profit (which we will split in the second step). The answers in category I2 (Rate of change) are adequate interpretations of the derivative as the rate of change in the given context.

The answers in the next two categories I3–I4 (Gradient of profit and Profit per unit) contain at least correct ideas. In category I3, the students stated that the costs increase by 0.2 units of money at the output of 73 units of quantity. They tried to translate their knowledge of the derivative as slope into the context but did not achieve a fully adequate verbalization. The answers in category I4 contain the idea of rate, but the distinction to average profit is not clear.

The categories I5–I9 contain incorrect economic interpretations. The answers in the categories I10–I12 are not economic interpretations. In category I10 (Verbalization of $P^{\prime}(73)$) the students just verbalized the expression $P^{\prime}(73)$ with its name “marginal profit”, which was already given in the task. This cannot be viewed as a real economic interpretation of the derivative because the term “marginal profit” was introduced in the lecture just as a name for the derivative of a profit function without further meaning (see the a priori analysis). Students in the category I11 (Slope at the point) did not consider the economic context at all.

2nd Step—In-depth Analysis of the Answers in the Category “Additional Profit” (I1)

As discussed in the a priori analysis, only an interpretation of $P^{\prime}(73)$ as an approximation of the profit of the next unit or as the accurate additional profit of the next marginal unit can be considered as fully adequate according to the course. Hence, we refined the answers in category I1 into subcategories depending on whether the students mentioned “approximation” and/or spoke of marginal units. To obtain non-overlapping subcategories, we coded for each of the answers if the students:

• a) mentioned that the derivative is just an approximation of the additional profit (a1) or not (a2),

• b) spoke of marginal units in the output (b1) or not (b2),

• c) spoke of marginal units in the profit (c1) or not (c2).

This analysis led to $2^{3}$ subcategories (all the combinations). The combinations $(a_{1},b_{2},c_{2})$ and $(a_{2},b_{1},c_{1})$ were taught (see Sect. 6.2). Students often mixed parts of the two interpretations taught leading to other combinations. An example is: “If you increase the output from 73 units by a marginal unit, the profit increases by approximately 0.2 units of money”, combination $(a_{1},b_{1},c_{2})$.

7.2 Categorization of the Answers to Task 2

The second task was to state a mathematical interpretation of $P^{\prime}(73)=0.2\, \frac{\mathrm{GE}}{\mathrm{ME}}$. According to our a priori analysis, anticipated correct answers are interpretations as the slope of the tangent line, as the slope of the function at the point, or as rate of change. Incorrect answers were taken into account as own categories if they were mentioned by at least 1% of the students. This analysis resulted in a system of 12 categories. A detailed description of the categories is shown in Table 4.

Table 4 Response categories for the task to state a mathematical interpretation of $P^{\prime}\left(73\right)=0.2\, \frac{\mathrm{GE}}{\mathrm{ME}}$ (Task 2)

The answers in the categories M1–M3 contain the correct mathematical interpretations of the derivative as slope or rate of change. The answers in the categories M4–M6 are economic interpretations. The category M6 (Quasi-economic interpretation) needs some additional explanation. Here, the students just decontextualized the economic interpretation of $P^{\prime}(73)$ as an additional profit, and now interpreted it as the amount of change when increasing $x$ by 1. The categories M7–M9 (Slope of the derivative, Extreme point of the function and Other wrong interpretation) contain errors that had been made by at least 1% of the students. The answers in the categories M10–M12 were again no interpretations.

7.3 Categorization of the Answers to Task 3

The third task was to estimate the additional cost while increasing the production from 5–7 units (given that $C(5)=10\, \mathrm{GE}$ and $C^{\prime}(5)=0.5\, \frac{\mathrm{GE}}{\mathrm{ME}}$). Our a priori analysis suggested two categories: the correct solution via local linear approximation, and the use of this approach without making explicit that the result is just an approximation. Other wrong solutions were categorized inductively, but without taking calculation mistakes into account. The resulting categories are shown in Table 5.

Table 5 Response categories for the task to determine an approximation of the additional cost (Task 3)

The students in category L1 wrote a fully correct solution on the basis of local linear approximation. The categories L2–L3 also contain solutions using this approach, but the students did not make clear in their solution that the result obtained is just an approximation of the accurate additional cost. The categories L4–L6 contain incorrect solution methods for obtaining the result. In the categories L7–L8, the students did not write a solution path or give any meaningful ideas for solving the task.

7.4 Categorization of the Answers to Task 4

Task 4 was to justify why the estimate $C^{\prime}(5)\cdot 2$ of Task 3 does not normally represent the accurate additional cost while increasing the production from 5–7 units. Three kinds of argument could have been expected (see the a priori analysis in Sect. 6.4):

1. The result is not accurate because the estimate is based on the approximation of the derivative by the difference quotient.

2. The result represents the increase on the tangent line.

3. The result is based on a (local) linearity assumption.

Other arguments were categorized inductively. The resulting category system is shown in Table 6. The answers in the first four categories are valid arguments. The answers in the categories A5–A7 are wrong arguments. The answers in the categories A8–A11 contain no mathematical argument.

Table 6 Response categories for the task to justify why the approximation of the additional cost by $C^{\prime}(5)\cdot 2$ is not accurate in general (Task 4)

7.5 Check of the Reliability of the Coding

After the first author had coded the data, it was re-coded by a student who was a tutor in the students’ calculus course (restriction on 200 cases due to the large sample). We then determined Cohen’s kappa, which is one standard measure for the agreement of two coders for multivariate categorical data (for details see Landis and Koch (1977)) for each task. Their values are above 0.8 (Table 7). This can be considered as good (Landis and Koch 1977). Since the categories were meant to be discriminating, disagreements were discussed between the two coders and then resolved.

Table 7 Intercoder reliability coefficients for the four tasks

7.6 Development of an Overall Grading Scheme

To get an idea about students’ holistic understanding of the derivative concept and its economic interpretation, we also analyzed the data across the tasks. For this, we graded the solutions to each of the four tasks (independently from the scheme used by the lecturer). We assigned one point to each task if it was solved correctly, and half a point if the solution was partly correct. The grading system is shown in Table 8.

Table 8 Grading system for the tasks

8 Quantitative Results

8.1 Task 1

The first task was to state an economic interpretation of $P^{\prime}(73)=0.2\, \frac{\mathrm{GE}}{\mathrm{ME}}$ of a profit function $P$ to find out if the students knew an adequate economic interpretation of the derivative (see Sect. 4). The results are shown in Fig. 2.

Fig. 2

Students’ responses to the task to state an economic interpretation of $P^{\prime}\left(73\right)=0.2\, \frac{\mathrm{GE}}{\mathrm{ME}}$ of a profit function $P$ (Task 1, $N=821$)

At first glance, the results of Fig. 2 are relatively promising. 54.9% of the students could state the common economic interpretation of the derivative as an additional profit or interpreted the derivative as a rate of change (categories I1 and I2). Furthermore, 3.4% demonstrated at least ideas of gradient or rate in their interpretations (categories I3 and I4). Nevertheless, 26.7% gave an incorrect answer indicating possible misconceptions (categories I5–I9). 15.0% did not state an economic interpretation.

Results of the In-depth Analysis

Table 9 shows the results concerning the question of whether the students in category I1 (“Additional profit”) really mentioned that the derivative is just an approximation of the additional profit of the next unit or spoke of marginal units instead (only these two alternatives were taught as being fully adequate; see the a priori analysis in Sect. 6.4).

Table 9 Results of the in-depth analysis of answers in the category “Additional profit” (I1) from Fig. 2 (Task 1)

Only 17.3% of the students (rows R2 and R5) stated interpretations in the way they were taught in the calculus course (see Sect. 6.4). Furthermore, the answers in row R3 can be considered as acceptable if the students used the term marginal unit just for the output to emphasize that one unit in the output is so small in the context given that the error between $P^{\prime}(73)$ and the additional profit of the next unit is negligible (as it is done in some economics textbooks; see Sect. 3). But rows 2, 3 and 5 only cover 34.1% of the students (51.4% featured in the overall category I1). This suggests that not all of the 51.4% who interpreted $P^{\prime}(x)$ as an additional profit really understood this interpretation in detail, for example that the derivative only yields an approximation of the additional profit of the next unit, although this was emphasized in the course several times. For example, the tutors underlined in the sample solutions to an analogue task to state an economic interpretation of $C^{\prime}(5)$ of a cost function that it needs to be pointed out in the interpretation that $C^{\prime}(5)$ does not yield the accurate additional cost of the next unit because the latter is determined by $C(6)-C(5)$.

8.2 Task 2

The second task was to state a mathematical interpretation of $P^{\prime}(73)=0.2\, \frac{\mathrm{GE}}{\mathrm{ME}}$ of a profit function$P$ to find out whether the students knew at least one representation of the derivative that assigns a meaning to it (either as slope or as rate of change; see Fig. 1). The results are presented in Fig. 3.

Fig. 3

Students’ responses to the task to state a mathematical interpretation of $P^{\prime}\left(73\right)=0.2\, \frac{\mathrm{GE}}{\mathrm{ME}}$ of a profit function $P$ (Task 2, $N=821$)

Again, it can be observed that the majority of students were able to state a correct mathematical interpretation of $P^{\prime}(73)$ as slope or rate of change (categories M1–M3). The preference for an interpretation as slope over an interpretation as rate of change is not surprising because in the tutorials, where an analogue task had to be solved (see the a priori analysis in Sect. 6.4), most tutors had only stated interpretations as slope. 47.7% did not state a correct mathematical interpretation of the derivative (categories M4–M12). They either stated an economic interpretation (categories M4–M6) or made errors indicating possible misconceptions (categories M7–M9). 24.9% did not state any interpretation of the derivative (categories M10–M12).

Nevertheless, 52.3% gave an adequate interpretation of the derivative as slope or rate of change. Even if one cannot claim, as a result of their answers to this question, that the majority of students had an adequate understanding of the derivative as a mathematical concept (this was also not the focus of the study), most at least showed some understanding of the meaning of the derivative in mathematics as slope or rate of change, as it is proposed in the literature (Greefrath et al. 2016; Zandieh 2000).

8.3 Task 3

The third task was to estimate the additional cost while increasing the production from 5–7 units (given that $C(5)=10\, \mathrm{GE}$ and $C^{\prime}(5)=0.5\, \frac{\mathrm{GE}}{\mathrm{ME}}$). It aimed at ascertaining whether students were able to use the derivative for local linearization on a procedural level. The results are shown in Fig. 4.

Fig. 4

Students’ responses to the task of determining an approximation of the additional cost $C\left(7\right)-C(5)$ of a cost function with $C\left(5\right)=10\, GE$ and $C^{\prime}\left(5\right)=0.5\, \frac{\mathrm{GE}}{\mathrm{ME}}$ (Task 3, $N=821$)

The positive result is that most of the students were able to solve the problem by using local linearization (categories L1–L3). However, many of them did not make clear in their solution that the determined result was just an approximation (categories L2–L3). Although it was already stated in the task that the result is just an approximation (see Table 2), and the students might not have considered it necessary to emphasize this in their solution again, 20.1% of the students explicitly wrote equations between $\Updelta C$and $C^{\prime}(x)\Updelta x$ throughout their solution. They might not have been aware that $C^{\prime}(x)\Updelta x$ just yields an approximation of the accurate additional cost.

8.4 Task 4

The fourth task in which the students had to argue why the approximation of the additional cost $C(7)-C(5)$ by $C^{\prime}(5)\cdot 2$ is normally not accurate aimed at investigating whether students understood the connection between the derivative $C^{\prime}(x)$ and the additional cost via the approximation $\Updelta C\approx C^{\prime}(x)\cdot \Updelta x$ on a conceptual level. The results are shown in Fig. 5.

Fig. 5

Students’ responses to the task of justifying why the approximation in task 3 (approximation of the additional cost $C\left(7\right)-C(5)$ by $C^{\prime}\left(5\right)\cdot 2$) is normally not accurate (Task 4, $N=821$)

A total of 32.0% of the students gave a valid mathematical argument as to why the approximation of $C(7)-C(5)$ by $C^{\prime}(5)\cdot 2$ is not accurate in general (categories A1–A4). Only 6.9% of the students (categories A1 and A2) brought forth arguments that had been presented in the lecture during the derivation of the economic interpretation of the derivative (see the a priori analysis in Sect. 6.4). 25.1% presented other valid arguments instead (categories A3–A4), indicating they also knew that the term $C^{\prime}(5)\cdot 2$ was a linear approximation of the accurate additional cost $C(7)-C(5)$.

68.0% of the students could not present a valid argument (categories A5–A11). The wrong arguments given varied a great deal and were sometimes rather abstruse. For example, students claimed that the approximation is not accurate in the case of quadratic functions because the error increases due to squaring, or is not accurate because there was no formula given for the function (see Table 6). This also supports the claim already mentioned after the analysis of the results from tasks 1 and 3, that many students probably did not understand the connection between the derivative and the additional cost in the formula $\Delta C\approx C^{\prime}(x)\cdot \Delta x$ on a conceptual level in detail.

8.5 Overall Results from the Grading of the Tasks

To gain an idea about students’ holistic understanding of the derivative concept, each task was graded (see Sect. 7.6). One point was given as a maximum credit for each task (description of the grading scheme in Table 8). The distribution of points attained can be seen in Fig. 6.

Fig. 6

Points reached in the four tasks ($N=821$)

Only 4.4% of the students gave answers in all four tasks, indicating that they acquired an understanding of the derivative in the sense of our theoretical model in Fig. 1, i.e. they showed that they knew a meaning of the derivative as a purely mathematical concept (task 2), could state a fully adequate economic interpretation of the derivative (task 1) and could correctly connect these two via linear approximation (tasks 3 and 4). On the other hand, 18.1% of the students did not demonstrate any understanding of the derivative in these four tasks. For the rest, parts of what we mentioned as important facets of an adequate understanding of the derivative for economics students in our model (see Fig. 1) were contained in the students’ concept images after their calculus course. In particular, 42.3% could state a basically adequate economic interpretation of the derivative (maybe with flaws in their formulation; see grading scheme in Table 8), and a mathematical interpretation as slope or rate of change. However, this is probably not sufficient for being able to connect these two via local linear approximation, as only 4.4% could also solve the tasks 3 and 4 that focused on this issue.

9 Discussion of the Results and Further Outlook

9.1 Contribution of Our Research to the Field

Our research yields theoretical and empirical contributions to economics students’ understanding of the derivative, which have been rarely investigated thus far (see Sect. 2).

We first developed a model describing theoretically what an adequate understanding of the derivative concept in mathematics courses for economics students might look like (see Fig. 1). The notion “adequate” means an understanding that is mathematically acceptable on the one hand, but that also considers the way the derivative is practically used in economics. Specifically, this model includes the common economic interpretation of the derivative as the change of the function when increasing the production by one unit, and its connection to the mathematical concept of derivative (including a justification of its common interpretation in economics). We hope that this model can be beneficial for future empirical research investigating students’ understanding of the derivative.

We then carried out an empirical study to examine which facets of understanding economics students acquired after their calculus course. Our data suggest that many students had problems in mastering different issues that are important for the understanding described in our model: (1) understanding of the derivative as a mathematical concept, (2) knowledge of an adequate economic interpretation of the derivative, and (3) being able to connect these two. Particularly, the data suggest that many students did not understand the connection between the derivative as a mathematical concept and its economic interpretation via local linear approximation on a conceptual level. Although 51.4% were able to state an economic interpretation of the derivative of a profit function as an additional profit, and 55.9% could use the derivative as an approximation of the additional cost, only 32% managed to present a valid argument as to why this approximation is usually inaccurate.

The errors the students made furthermore yield ideas for possible gaps in their understanding and possible misconceptions. In particular, students often did not make clear in their solutions that the derivative just yields an approximation of the additional profit/cost of the next unit, although this was emphasized in the course (and in the sample solutions to the analogue tasks presented by the tutors). This suggests that they might merely identified the derivative with the additional cost of the next unit and were not aware of the relevant assumptions justifying the use of this interpretation in economics. Of course, the data cannot prove this claim (and other problems that might be assumed on the basis of students’ errors). Instead, our results can serve as an initial foundation for further research on economics students’ problems in understanding the derivative.

9.2 Discussion of Possible Reasons for the Results and Possible Implications for Teaching

First, our data indicates that many students already had difficulties in understanding the derivative as a mathematical concept (only 52.3% could interpret $P^{\prime}(73)$ as the slope or the rate of change of the function $P$; see Fig. 3). A pretest administered before the calculus course in September 2015 showed that many students already had problems with interpreting values of a difference quotient or even of the slope of a linear function (Feudel 2019, pp. 330 and 344). These two issues are essential for an understanding of the derivative as rate of change. However, the concept of slope of a linear function was not discussed at all in the students’ calculus course at university, and the difference quotient was only discussed briefly (for about ten minutes) when introducing the verbal representation of the derivative as rate of change (see Sect. 6.2). Hence, some students may have already had gaps from school that they could not remedy during the calculus course at university because the corresponding content had not been covered again. A possibility for addressing this problem might be to provide these students with additional material or to offer a bridging course.

Second, our data suggest that although 51.4% of our students could state an economic interpretation of $P^{\prime}(73)$ as an additional profit (category I1 in Fig. 2), many students did not acquire a precise understanding of it and its connection to the mathematical concept of the derivative via local linear approximation (see Sect. 8.4). A possible reason might be that the economic interpretation of the derivative was introduced in the lecture in a straightforward manner. After having posed the question of how one could interpret $C^{\prime}(11)=0.7\, \frac{\mathrm{GE}}{\mathrm{ME}}$ of a cost function $C$ in an economic context, the lecturer immediately derived its economic interpretation via the approximation $\Updelta C\approx C^{\prime}(x)\cdot \Updelta x$ (see Sect. 6.2). Some students perhaps felt no need for a deep understanding of this economic interpretation of the derivative because they did not recognize the differences between the derivative $C^{\prime}(x)$ and its interpretation as the additional cost of the next unit during this straightforward derivation. This hypothesis is supported by the results of an additional interview study in the first author’s PhD thesis (Feudel 2019). To address this problem, one could confront the students with the common economic interpretation of the derivative $C^{\prime}(x)$ of a cost function as the additional cost of the next unit directly, and then ask them if $C^{\prime}(x)$ yields exactly the cost of the next unit (for example, in the lecture as a starting point for a subsequent peer discussion, or on a problem sheet). This might hopefully induce a cognitive conflict leading to a perceived necessity to reshape the concept image of the derivative (Tall and Vinner 1981). The students might then process the lecturer’s explanations concerning the economic interpretation of the derivative more deeply.

Another reason why many students had not acquired a precise understanding of the connection of the economic interpretation of the derivative to the mathematical concept of derivative might be that this connection was presented in the lecture mainly on the symbolic level on the basis of the formal definition of $C^{\prime}(x)$ (via the formula $\Updelta C\approx C^{\prime}(x)\cdot \Updelta x$ for $\Updelta x\approx 0$; see Sect. 6.2). But since assigning a meaning to the formal definition of the derivative is difficult for students (Orton 1983), the connection presented might not have been meaningful to the students. A possibility for overcoming this problem could be to emphasize the idea of local linearization behind this approximation, also as a general idea apart from economic contexts as Blum and Kirsch (1979) already recommended it for calculus courses at school.

9.3 Outlook for Further Research

Although our research provides some theoretical and empirical results concerning economics students’ understanding of the derivative, some questions remain open.

First, the data can only provide snapshots of some facets of the students’ understanding of the derivative, e.g. the knowledge of an adequate economic interpretation of the derivative or the ability to connect the derivative of a cost function with the additional cost via local linear approximation. For a holistic view of students’ understanding of the derivative, further qualitative research is necessary to investigate the concept image of individual students.

Second, our data only indicates possible gaps in students’ understanding or possible misconceptions (see Sect. 6.3). An example of a possible gap in students’ understanding is that they might not have been aware that the derivative is just an approximation of the additional cost/profit of the next unit. Here, an interview study investigating to what extent this is really the case could provide further insights (the authors have conducted one (Feudel 2019) but that will be presented elsewhere).

Third, in our data, many students who stated a fully adequate economic interpretation of the derivative of a profit function as an additional profit used the term marginal unit. However, their conception of this notion is not clear, and it is also unclear whether students who used this term had a better understanding of the economic interpretation of the derivative than students who did not. Also, with respect to this issue, an additional interview study might lead to further insights.

Finally, from a practical point of view, it might be valuable to design and implement a teaching and learning scenario for economics students by which (more) students could gain a deeper and more nuanced understanding of the derivative as described in our theoretical model.