Introduction

It is observed that heat transfer can be augmented through the improvement in the thermal properties of energy transmission fluids. If small solid particles in the fluid are suspended, then this might be an innovative way of improving the thermal conductivities of fluids. Nanofluids are estimated to show conventional heat transfer fluids as compared with superior heat transfer properties. Jou and Tzeng (2006) reported a numerical study of the heat transfer performance of nanofluids inside 2D rectangular enclosures. Their results express that a considerable enhancement of the average rate of heat transfer is produced by increase in the volume fraction of nanoparticles. This idea of suspensions of colloidal particles dubbed as nanofluids was given by Choi (1995). He was of the view that small amounts of metallic or metallic oxide nanoparticles are dispersed into water and other fluids. Detailed reviews have explained that (Sheikholeslami and Gorji-Bandpy 2014; Sheikholeslami et al. 2014a), in the previous decade, the model mechanisms of thermal conductivity enhancement of nanofluids have been identified in different ways, along with the size and shape of the nanoparticles, the hydrodynamic interaction between nanoparticles and base fluid, clustering of particles, temperature or Brownian motion and so on. If movement of nanoparticles is supposed to be considered, there has to be some contribution of a dynamic component related to particle Brownian motions in their model development according to some researchers. (Sheikholeslami et al. 2012a, b, 2013; Koo and Kleinstreuer Koo and Kleinstreuer 2004a, b; Palm et al. 2006; Akbarinia and Behzadmehr 2007).

Peristalsis is a mechanism of fluid that flows through movement of contraction on the tubes/channels walls. First of all, this concept was developed by Latham (1966). He described fluid motion in a peristaltic pump. Further, he also explained the characteristic of pressure rise versus flow rate. After the pioneering work of Latham (1966), Jaffrin and Shapiro (1971) investigated peristaltic pumping. They showed the analysis under the assumption of long wavelength and low Reynolds number approximations. After that, too much analytical, numerical and experimental research of peristaltic flows of different fluids came into existence under different conditions with reference to physiological and mechanical situations. Peristaltic pumping by a sinusoidal traveling wave in the porous walls of a two-dimensional channel filled with a viscous incompressible conducting fluid under the effect of a transverse magnetic field was investigated theoretically and graphically by El-Shehawey and Husseny (2002). The effects of magnetohydrodynamics (MHD) on peristaltic flow problems also have some applications in physiological fluids such as blood flow, blood pump machines and theoretical studies on the operation of peristaltic MHD compressors. Moving magnetic field effects on blood flow was studied by Sud et al. (1997). They found that the effects of moving magnetic field accelerate the speed of the blood. Srivastava and Agrawal (1980) consider blood as an electrically conducting fluid constituting a suspension of red cells in plasma. Li et al. (1994) considered an impulsive magnetic filed in the combined therapy of patients with stone fragments in the upper urinary tract. It was discovered that the impulsive magnetic field activates the impulsive activity of the uretaral smooth muscles in 100 % of cases. Mekheimer and Al-Arabi (2003) investigated the nonlinear peristaltic transport of MHD flow through a porous medium in nonuniform channels. The peristaltic transport of blood under the effect of a magnetic field in nonuniform channels was studied by Mekheimer (2004). Further literature can be viewed through other references (Mekheimer 2008a, b; Akbar et al. 2014a; Koo and Kleinstreuer 2004b; Abu-Nada 2010; Ghasemi and Aminossadati 2010; Koo and Kleinstreuer 2005; Nadeem et al. 2014a; Ibrahim and Hamad 2006; Abu-Nada 2009; Jang and Choi 2007; Akbar and Khan 2015; Ellahi et al. 2014; Akbar et al. 2014b;Nadeem et al. (2014b, c) Akbar 2014; Sheikholeslami et al. 2015; Sheikholeslami et al. 2014a, b; Sheikholeslami and Gorji-Bandpy 2014).

The aim of this study is to look at the effects of induced magnetic field on the peristaltic flow of four different nanoparticles with the base fluid water in the presence of Brownian motion, in a vertical asymmetric channel. The selected nanoparticles are copper oxide (CuO), silver (Ag), titanium dioxide (TiO2) and copper (Cu). Brownian motion shows that the effective thermal conductivity, consisting of the particles’ conventional static part and the Brownian motion part, increases resulting in a lower temperature gradient for a given heat flux. To understand these transport phenomena thoroughly, we consider the thermal conductivity model (Mekheimer 2008a) for nanofluids, which considers the effects of particle size, particle volume fraction and temperature dependence. The mathematical formulation is presented; and the exact solution for the stream function, magnetic force function, temperature and pressure gradient is given. All the physical features of the problems have been described with the help of graphs.

Mathematical formulation

Here, we discussed an incompressible peristaltic flow of copper nanofluid in an irregular channel with channel width d 1 + d 2. Asymmetry in the flow is because of propagation of peristaltic waves of different amplitudes and phases on the channel walls. An external transverse uniform constant uniform constant magnetic field H 0, induced magnetic field H[h X (X, Y, t), H 0 + h Y (X, Y, t), 0] and the total magnetic field H +[h X (X, Y, t), H 0 + h Y (X, Y, t), 0] are taken into account. Finally, the channel walls are considered to be nonconductive sinusoidal waves propagating beside the walls of the channel with continuous hustle c 1. The geometry of the wall surfaces is defined as follows:

$$ Y = \overline{H}_{1} = d_{1} + a_{1} \cos \left[ {\frac{2\pi }{\lambda }\left( {\overline{X} - c_{1} \overline{t} } \right)} \right], $$
$$ Y = \overline{H}_{2} = - d_{2} - b_{1} \cos \left[ {\frac{2\pi }{\lambda }\left( {\overline{X} - c_{1} \overline{t} } \right) + \omega } \right]. $$
(1)

In the above equations a 1 and b 1 denote the wave amplitudes, λ is the wavelength, d 1 + d 2 is the channel width, c 1 is the wave speed, \( \overline{t} \) is the time, \( \overline{X} \; \) is the direction of wave propagation and Y is perpendicular to \( \overline{X} \).

Equations governing the flow and temperature in the presence of heat source or heat sink and the equation which governs the MHD flow are given as

(i) Maxwell’s Eqs. (19, 20, 21):

$$ \nabla \cdot H = 0,\quad \nabla \cdot E = 0, $$
(2)
$$ \nabla \wedge H = J,\quad J = \sigma \left\{ {E + \mu_{\text{nf}} \left( {V \wedge H} \right)} \right\}, $$
(3)
$$ \nabla \wedge E = - \mu_{\text{nf}} \frac{\partial H}{\partial t}. $$
(4)

(ii) The continuity equation:

$$ \nabla \cdot V = 0. $$
(5)

(iii) The equations of motion:

$$ \rho_{\text{nf}} \left( {\frac{\partial V}{\partial t} + V \cdot \nabla V} \right) = - \nabla p + \mu_{\text{nf}} \;{\text{div}}V + \left( {\rho \beta } \right)_{\text{nf}} g\alpha \left( {T - T_{0} } \right) - \nabla \left( {\frac{1}{2}\mu_{\text{nf}} \left( {H^{ + } } \right)^{2} } \right) - \mu_{\text{nf}} \left( {H^{ + } .\nabla } \right)\,H. $$
(6)

(iv) The energy equation:

$$ \left( {\rho c} \right)_{\text{f}} \left( {\frac{\partial T}{\partial t} + V \cdot \nabla T} \right) = \nabla \cdot k_{\text{nf}} \nabla T + Q_{0} \left( {T - T_{\infty } } \right)\,. $$
(7)

Combining Eqs. (2) to (4), we obtain the induction equation [19, 20, 21] as follows:

$$ \frac{{\partial H^{ + } }}{\partial t} = \nabla \wedge \left( {V \wedge H^{ + } } \right) + \frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }}\frac{1}{\xi }\nabla^{2} H^{ + } ,\, $$
(8)

where \( \zeta = \tfrac{1}{{\sigma \mu_{\text{f}} }} N \) is the magnetic diffusively, ρ nf is the effective density of the incompressible fluid, (ρc)nf is the heat capacity of the fluid, (ρc) p gives effective heat capacity of the nano particle material, k nf implies effective thermal conductivity, g stands for constant of gravity, μ nf is the effective viscosity of the fluid, d/dt gives the material time derivative and P is the pressure. The appearance of static and wave structures are connected by the subsequent associations:

$$ x = X - ct,\, \, y = Y,\, \, u = U - c,\, \, v = V. $$
(9)

The dimensionless parameters used in the problem are defined as follows:

$$ \begin{aligned} \overline{p} &=& \frac{{a^{2} }}{{\mu_{\text{f}} c\lambda }}p,\, \, \overline{u} = \frac{\lambda }{ac}u,\, \, \overline{v} = \frac{v}{c},\, \, \overline{y} = \frac{y}{\lambda },\, \, \overline{x} = \frac{x}{a},\, \, \overline{t} = \frac{c}{\lambda }t,\, \, \omega = \frac{b}{a},\, \\ Re &=& \frac{\rho ca}{{\mu_{\text{f}} }},\,\delta = \frac{a}{\lambda },\, \, \overline{\theta } = \frac{{T - T_{0} }}{{T_{1} - T_{0} }},\, \, \bar{\varPhi } = \frac{\varPhi }{{H_{0} a}},\, \, \overline{\varPsi } = \frac{\varPsi }{ca},\, \, R_{\text{m}} = \sigma \mu_{\text{f}} ac,\, \\ G_{r}&=& \frac{{\rho_{f} g\alpha a^{2} }}{{\mu_{\text{f}} c}}\left( {T_{1} - T_{0} } \right),\, \, S_{1} = \frac{{H_{0} }}{c}\sqrt {\frac{{\mu_{\text{f}} }}{\rho }} ,\, \, \alpha_{\text{nf}} = \frac{{k_{\text{nf}} }}{{\left( {\rho c_{\text{p}} } \right)_{\text{nf}} }},\, \, \tau = \frac{{\left( {\rho c} \right)_{\text{p}} }}{{\left( {\rho c} \right)_{\text{f}} }}. \\ \end{aligned} $$
(10)

After using the above nondimensional parameters and transformation in Eq. (9) employing the assumptions of long wavelength (δ → 0), the dimensionless governing equations (without using bars) for nanofluid in the wave frame take the final form as

$$ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0,\, $$
(11)
$$ \frac{{{\text{d}}p}}{{{\text{d}}x}} = \frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }}\frac{{\partial^{3} \varPsi }}{{\partial y^{3} }} + Re S_{1}^{2} \varPhi_{\text{yy}} + G_{\text{r}} \frac{{\left( {\rho \beta } \right)_{\text{nf}} }}{{\left( {\rho \beta } \right)_{\text{f}} }}\theta ,\, $$
(12)
$$ \frac{{{\text{d}}p}}{{{\text{d}}y}} = 0,\, $$
(13)
$$ \varPhi_{yy} = \frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }}R_{\text{m}} \left( {E - \frac{\partial \varPsi }{\partial y}} \right),\, $$
(14)
$$ \frac{{k_{\text{nf}} }}{{k_{\text{f}} }}\frac{{\partial^{2} \theta }}{{\partial y^{2} }} + Q_{o} \theta = 0. $$
(15)

Combining Eq. (14) and Eq. (12) we get

$$ \frac{{{\text{d}}p}}{{{\text{d}}x}} = \frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }}\frac{{\partial^{3} \varPsi }}{{\partial y^{3} }} + Re S_{1}^{2} \frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }}R_{\text{m}} \left( {E - \frac{\partial \varPsi }{\partial y}} \right) + G_{\text{r}} \frac{{\left( {\rho \beta } \right)_{\text{nf}} }}{{\left( {\rho \beta } \right)_{\text{f}} }}\theta . $$
(16)

Taking the derivative of the above equation with respect to y, finally we get

$$ \frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }}\frac{{\partial^{4} \varPsi }}{{\partial y^{4} }} + Re S_{1}^{2} \frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }}R_{\text{m}} \left( { - \frac{{\partial^{2} \varPsi }}{{\partial y^{2} }}} \right) + G_{\text{r}} \frac{{\left( {\rho \beta } \right)_{\text{nf}} }}{{\left( {\rho \beta } \right)_{\text{f}} }}\frac{\partial \theta }{\partial y} = 0. $$
(17)

The nondimensional boundaries take the form

$$ \varPsi = \frac{F}{2},\,\;\;\frac{\partial \varPsi }{\partial y} = - 1,\,{\text{ at }}y = h_{1} . $$
(18)
$$ \varPsi = - \frac{F}{2},\,\;\;\frac{\partial \varPsi }{\partial y} = - 1,\,{\text{ at }}y = h_{2} . $$
(19)
$$ \theta = 0{\text{ at }}y = h_{1} ,\, \, \theta = 1{\text{ at }}y = h_{2} ,\, $$
(20)
$$ \varPhi = 0{\text{ at }}y = h_{1} ,\, \, \varPhi = 0{\text{ at }}y = h_{2} . $$
(21)

The thermophysical properties, obtained from Abu-Nada (2010) and Ghasemi and Aminossadati (2010)) for pure water, copper oxide, silver, titanium dioxide and copper at room temperature are listed in Table 1. The effective density ρ nf, specific heat (c p)nf and thermal expansion coefficient β nf of nanofluids are given by

Table 1 Thermal–physical properties of water and nanoparticles (Nadeem et al. 2014a; Ibrahim and Hamad 2006; Abu-Nada 2009; Jang and Choi 2007; Akbar and Khan 2015; Ellahi et al. 2014)
Full size table
$$ \begin{aligned} \rho_{\text{nf}}\, = \,& \left( {1 - \varphi } \right)\,\rho_{\text{f}} + \varphi \rho_{\text{f}} ,\, \\ \left( {\rho c_{\text{p}} } \right)_{\text{nf}}\, = \,& \left( {1 - \varphi } \right)\,\left( {\rho c_{\text{p}} } \right)_{\text{f}} + \varphi \left( {\rho c_{\text{p}} } \right)_{\text{s}} ,\, \\ \left( {\rho \beta } \right)_{\text{nf}}\, = \,& \left( {1 - \varphi } \right)\,\left( {\rho \beta } \right)_{\text{f}} + \varphi \left( {\rho \beta } \right)_{\text{s}} , \\ \end{aligned} $$
(22)

where the subscript nf, f and s stand for the nanofluid, base fluid and nanoparticle, respectively, and φ is the solid volume fraction. It is observed that the above-mentioned properties of Eq. (22) are considered to be independent on the movement of nanoparticles. Brownian motion is claimed to play an important role in modifying the thermal conductivity and viscosity of nanofluids. Among the existing models that predict the thermal conductivity and viscosity of nanofluids considering Brownian motion, the models proposed by Koo and Kleinstreuer (2004, 2005) are utilized in the present study. These models have successfully been used by Ghasemi and Aminossadati (2010) to study the effects of Brownian motion on laminar steady-state natural convection in a right triangular enclosure with localized heating on the vertical side. Note that these models were proposed based on water with copper oxide nanoparticles. Although the extension to other combinations of base liquids and nanoparticles may be justified, the material of the nanoparticles being considered in the present study are limited to copper oxide, silver, titanium dioxide and copper. In these models, it is assumed that the thermal conductivity and viscosity of nanofluids consist of two parts. One is referred to as the static part (k s, μ s) that is evaluated by mixture models, i.e., the Maxwell model for thermal conductivity and the Brinkman model for viscosity (Ghasemi and Aminossadati 2010) and the other part (k B, μ B) is attributed to Brownian motion. The expression for predicting the effective thermal conductivity of nanofluids appears as

$$ k_{\text{nf}} = k_{\text{s}} + k_{\text{B}} , $$
(23)

where k s is given by the Maxwell model

$$ k_{\text{nf}} = k_{\text{f}} \left( {\frac{{k_{\text{s}} + 2k_{\text{f}} - 2\varphi \left( {k_{\text{f}} - k_{\text{s}} } \right)}}{{k_{\text{s}} + 2k_{\text{f}} + 2\varphi \left( {k_{\text{f}} - k_{\text{s}} } \right)}}} \right)\, $$
(24)

and k B is expressed as (Abu-Nada 2010)

$$ k_{\text{B}} = 5 \times 10^{4} \gamma \varphi \left( {\rho c_{\text{p}} } \right)_{\text{f}} \sqrt {\frac{{\kappa T_{\text{env}} }}{{\rho_{\text{s}} d_{\text{s}} }}} F\left( {T_{\text{env}} ,\,\varphi } \right),\, $$
(25)

where κ is the Boltzmann constant and its value is κ ≈ 1.38 × 10−23 J/K, d s is the diameter of nanoparticles by assuming that these nanoparticles have a uniform size and are perfectly spherical, i.e., d s = 30 nm, T env is a reference temperature that is chosen as T 0 in the current study, γ is a function of the volume fraction φ of nanoparticles, which is given by

$$ \gamma = \left\{ {\begin{array}{*{20}c} {0.0137\left( {100\varphi } \right)^{ - 0.8229} \;\;{\text{for }}\varphi < 0.01 \, } \\ {0.0011\left( {100\varphi } \right)^{ - 0.7272} \;\;{\text{for }}\varphi > 0.01} \\ \end{array} } \right.\, $$
(26)

and the function F(T env, φ) is given by

$$ F\left( {T_{\text{env}} ,\,\varphi } \right) = \left( { - 6.04\varphi + 0.4705} \right)\,T_{\text{env}} + \left( {1722.3\varphi - 134.63} \right),\, $$
(27)

which is valid for 0.01 ≤ φ ≤ 0.04 and 300 K ≤ T env ≤ 325 K.

We choose T env = 300 K in the present study, for the expression of thermal conductivity. The thermal diffusivity of nanofluids is then given by

$$ \alpha_{\text{nf}} = \frac{{k_{\text{nf}} }}{{\left( {\rho c_{\text{p}} } \right)_{\text{nf}} }}. $$
(28)

Likewise, as given in (Koo and Kleinstreuer 2005), the effective viscosity of nanofluids is given by

$$ \mu_{\text{nf}} = \mu_{\text{s}} + \mu_{\text{B}} , $$
(29)

where μ s is evaluated by Brinkman model: μ s = μ nf(1−φ)−2.5 and μ B is expressed as

$$ \mu_{\text{B}} = 5 \times 10^{4} \gamma \varphi \rho_{\text{nf}} \sqrt {\frac{{\kappa T_{\text{env}} }}{{\rho_{\text{s}} d_{\text{s}} }}} F\left( {T_{\text{env}} ,\,{\text{f}}} \right)\,. $$
(30)

Solution to the problem

The exact solutions of the above equations are found as follows:

$$ \theta \left( y \right) = \left. {\csc \left( {\frac{{\sqrt {Q_{0} } \sqrt {K_{\text{f}} } (h1 - h2)}}{{\sqrt {K_{\text{nf}} } }}} \right)\,\sin \left( {\frac{{\sqrt {Q_{0} } \sqrt {K_{\text{f}} } (h1 - y)}}{{\sqrt {K_{\text{nf}} } }}} \right)} \right),\, $$
(31)
$$ \begin{aligned} \varPsi \left( y \right) = & \frac{{e^{{S_{1} ( - y)\sqrt {Re} \sqrt {R_{\text{m}} } }} \left( {\begin{array}{*{20}c} {\sqrt {Q_{0} } S_{1}^{2} Re\beta_{\text{f}} \sqrt {K_{\text{f}} } \rho_{\text{f}} K_{\text{nf}} R_{\text{m}} \mu_{\text{nf}} \left( {A_{2} e^{{2S_{1} y\sqrt {Re} \sqrt {R_{\text{m}} } }} + A_{1} } \right) + } \\ {Q_{0}^{3/2} \beta_{\text{f}} K_{\text{f}}^{3/2} \rho_{\text{f}} \mu_{\text{nf}} \left( {A_{2} e^{{2S_{1} y\sqrt {Re} \sqrt {R_{\text{m}} } }} + A_{1} } \right) + } \\ {GrS_{1}^{2} Re\mu_{\text{f}} K_{\text{nf}}^{3/2} R_{\text{m}} \beta_{\text{nf}} \rho_{\text{nf}} e^{{S_{1} y\sqrt {Re} \sqrt {R_{\text{m}} } }} \csc \left( {\tfrac{{\sqrt {Q_{0} } \sqrt {K_{\text{f}} } (h1 - h2)}}{{\sqrt {K_{\text{nf}} } }}} \right)} \\ {\cos \left( {\tfrac{{\sqrt {Q_{0} } \sqrt {K_{\text{f}} } (h1 - y)}}{{\sqrt {K_{\text{nf}} } }}} \right)} \\ \end{array} } \right)}}{{\sqrt {Q_{0} } S_{1}^{2} Re\beta_{\text{f}} \sqrt {K_{\text{f}} } \rho_{\text{f}} R_{\text{m}} \mu_{\text{nf}} \left( {S_{1}^{2} ReK_{\text{nf}} R_{\text{m}} + Q_{0} K_{f} } \right)}} \\ & + A_{4} y + A_{3} ,\, \\ \end{aligned} $$
(32)
$$ \begin{aligned} \varPhi \left( y \right) = & - \frac{{Rme^{{S_{1} ( - y)\sqrt {Re} \sqrt {R_{m} } }} \left( {\begin{array}{*{20}c} {Q_{0} S_{1}^{2} R_{\text{e}} \beta_{\text{f}} K_{\text{f}} \rho_{\text{f}} K_{\text{nf}} R_{\text{m}} \mu_{\text{nf}} \left( {\begin{array}{*{20}c} { - 2A_{1} + 2A_{2} e^{{2S_{1} y\sqrt {Re} \sqrt {R_{\text{m}} } }} + } \\ {S_{1}^{3} y^{2} (A_{4} - E)Re^{3/2} R_{\text{m}}^{3/2} e^{{S_{1} y\sqrt {Re} \sqrt {R_{\text{m}} } }} } \\ \end{array} } \right) - } \\ {Q_{0}^{2} \beta_{\text{f}} K_{\text{f}}^{2} \rho_{\text{f}} \mu_{\text{nf}} \left( {\begin{array}{*{20}c} {2\left( {A_{1} - A_{2} e^{{2S_{1} y\sqrt {R_{\text{e}} } \sqrt {R_{\text{m}} } }} } \right)} \\ { - S_{1}^{3} y^{2} (A_{4} - E)\text{Re}^{3/2} R_{\text{m}}^{3/2} e^{{S_{1} y\sqrt {Re} \sqrt {R_{\text{m}} } }} } \\ \end{array} } \right) - } \\ {2{\text{Gr}}S_{1}^{3} Re^{2/3} \mu_{\text{f}} K_{\text{nf}}^{2} R_{\text{m}}^{3/2} \beta_{\text{nf}} \rho_{\text{nf}} e^{{S_{1} y\sqrt {Re} \sqrt {R_{m} } }} \csc \left( {\tfrac{{\sqrt {Q_{0} } \sqrt {K_{\text{f}} } (h1 - h2)}}{{\sqrt {K_{\text{nf}} } }}} \right)} \\ {\sin \left( {\tfrac{{\sqrt {Q_{0} } \sqrt {K_{\text{f}} } (h1 - y)}}{{\sqrt {K_{\text{nf}} } }}} \right)} \\ \end{array} } \right)}}{{2Q_{0} S_{1}^{3} Re^{2/3} \beta_{\text{f}} K_{\text{f}} \mu_{\text{f}} \rho_{\text{f}} R_{\text{m}}^{3/2} \left( {S_{1}^{2} ReK_{\text{nf}} R_{\text{m}} + Q_{0} K_{\text{f}} } \right)}} \\ & A_{6} y + A_{5} .\, \\ \end{aligned} $$
(33)

The mean volume flow rate Q over one period is given as

$$ Q = F + 1 + d $$
(34)

and the pressure gradient dp/dx is elaborated as

$$ \frac{{{\text{d}}p}}{{{\text{d}}x}} = \frac{{\begin{array}{*{20}c} {e^{{h1S_{1} \sqrt {Re} \sqrt {R_{\text{m}} } }} \left( {\begin{array}{*{20}c} {\sqrt {Q_{0} } \sqrt {K_{\text{f}} } \left( {\begin{array}{*{20}c} {\beta_{\text{f}} \rho_{\text{f}} \mu_{\text{nf}} \left( {FS_{1} \sqrt {Re} \sqrt {R_{\text{m}} } + 2} \right)\,\left( {S_{1}^{2} ReK_{\text{nf}} R_{\text{m}} + Q_{0} K_{\text{f}} } \right) + } \\ {Gr\mu_{\text{f}} K_{\text{nf}} \beta_{\text{nf}} \rho_{\text{nf}} } \\ \end{array} } \right) - } \\ {{\text{Gr}}S_{1} \sqrt {Re} \mu_{\text{f}} K_{\text{nf}}^{3/2} \sqrt {R_{\text{m}} } \beta_{\text{nf}} \rho_{\text{nf}} \tan \left( {\tfrac{{\sqrt {Q_{0} } \sqrt {K_{\text{f}} } (h1 - h2)}}{{2\sqrt {K_{\text{nf}} } }}} \right)} \\ \end{array} } \right) + } \\ {e^{{h2S_{1} \sqrt {Re} \sqrt {R_{\text{m}} } }} \left( {\begin{array}{*{20}c} {\sqrt {Q_{0} } \sqrt {K_{\text{f}} } \left( {\begin{array}{*{20}c} {\beta_{\text{f}} \rho_{\text{f}} \mu_{\text{nf}} \left( {FS_{1} \sqrt {Re} \sqrt {R_{\text{m}} } - 2} \right)\,\left( {S_{1}^{2} ReK_{\text{nf}} R_{\text{m}} + Q_{0} K_{f} } \right) - } \\ {Gr\mu_{\text{f}} K_{\text{nf}} \beta_{\text{nf}} \rho_{\text{nf}} } \\ \end{array} } \right)} \\ { - GrS_{1} \sqrt {Re} \mu_{f} K_{\text{nf}}^{3/2} \sqrt {R_{\text{m}} } \beta_{\text{nf}} \rho_{\text{nf}} \tan \left( {\tfrac{{\sqrt {Q_{0} } \sqrt {K_{\text{f}} } (h1 - h2)}}{{2\sqrt {K_{\text{nf}} } }}} \right)} \\ \end{array} } \right)} \\ \end{array} }}{{\sqrt {Q_{0} } \beta_{\text{f}} \sqrt {K_{\text{f}} } \rho_{\text{f}} \mu_{\text{nf}} \left( {\begin{array}{*{20}c} {e^{{h1S_{1} \sqrt {Re} \sqrt {R_{\text{m}} } }} \left( {S_{1} \sqrt {Re} (h1 - h2)\sqrt {R_{\text{m}} } - 2} \right) + } \\ {e^{{h2S_{1} \sqrt {Re} \sqrt {R_{\text{m}} } }} \left( {S_{1} \sqrt {Re} (h1 - h2)\sqrt {R_{\text{m}} } + 2} \right)} \\ \end{array} } \right)\,\left( {S_{1}^{2} ReK_{\text{nf}} R_{\text{m}} + Q_{0} K_{\text{f}} } \right)}}. $$
(35)

The pressure rise Δp in nondimensional form is defined as

$$ \Delta p = \int\limits_{0}^{1} {\frac{{{\text{d}}p}}{{{\text{d}}x}}{\text{d}}x.} $$
(36)

A 1–A 6 are constants evaluated using Mathematica 9.

Results and discussions

In this section, we have discussed all the obtained solutions graphically under the variations of various pertinent parameters on the profiles of pressure gradient, temperature, velocity and induced magnetic field. The expression for the pressure rise is calculated numerically using a mathematics software. The graphical results of the pressure rise, pressure gradient, temperature, magnetic force function and velocity are displayed in Figs. 1, 2, 3, 4 and 5 for all the four type of fluids (CuO–H2O, Ag–H2O, TiO2–H2O, Cu–H2O). The trapping bolus phenomenon observing the flow behavior is also manipulated as well with the help of streamline graphs in Figs. 6, 7 and 8.

Fig. 1
figure 1

a–f Variations in pressure rise Δp for different flow parameters

Full size image
Fig. 2
figure 2

a–f Variations in pressure gradient dp/dx for different flow parameters

Full size image
Fig. 3
figure 3

a, b Variations in the temperature profile θ for different flow parameters

Full size image
Fig. 4
figure 4

a, b Variations in induced MHD profile Φ for different flow parameters

Full size image
Fig. 5
figure 5

a–e Variations in velocity profile u for different flow parameters

Full size image
Fig. 6
figure 6

Streamlines for different values of \( \varphi \). a For \( \varphi \) = 0.01(CuO–H2O), b \( \varphi \) = 0.04(CuO–H2O), c \( \varphi \) = 0.3, d \( \varphi \) = 0.4. The other parameters are Q = 2, ω = 0.3, a = 0.2, b = 0.4, d = 1, Gr = 1, R m = 1, S 1 = 2, Re = 1, Q 0 = 0.1

Full size image
Fig. 7
figure 7

Streamlines of copper–water nanofluid for different values of Gr. a For Gr = 1, b Gr = 2, c Gr = 3, d Gr = 4. The other parameters are Q = 2, ω = 0.3, a = 0.2, b = 0.4, d = 1, \( \varphi \) = 0.4, R m = 1, S 1 = 2, Re = 1, Q 0 = 0.1

Full size image
Fig. 8
figure 8

Streamlines of water for different values of Gr. a For Gr = 1, b Gr = 2, c Gr = 3, d Gr = 4. The other parameters are Q = 2, ω = 0.3, a = 0.2, b = 0.4, d = 1, \( \varphi \) = 0.4, R m = 1, S 1 = 2, Re = 1, Q 0 = 0.1

Full size image

In Fig. 1a–f we have shown the pressure rise against the flow rate Q for different values of volume fraction φ, Strommer’s number S 1, heat generation parameter Q 0, magnetic Reynolds number R m, Grashof number G r and Reynolds number Re. Figure 1a represents the effects of volume fraction φ on the pressure rise Δp. It is noticed here that pressure rise is an increasing function with the increase of φ throughout the pumping region (Δp > 0); at the same time, Δp decreases as φ increases in the augmented pumping region (Δp < 0). It can be viewed from Fig. 1b that Δp will show the opposite behavior of S 1 as observed in Fig. 1a; one can see that from Fig. 1c by increasing Q 0, Δp decreases throughout the domain. In Fig. 1d, it is seen that Δp decreases with increasing effects of R m for all four cases in the region (Δp > 0), where Δp decreases in the region (Δp < 0). To study the behavior of G r on pressure rise, we draw a graph as in Fig. 1e, and one can notice that Δp shows the same behavior as we see for Q 0. Figure 1f shows that pressure rise decreases when we increase Re in the peristaltic pumping region and pressure rise increases when we increase Re in the Augmented pumping region. From Fig. 2a, one can see that the pressure gradient dp/dx decreases with increase in φ. The variations in Q 0 and R m give the same behavior on the pressure gradient graph as seen for S 1; See Fig. 2b–d. For an increase in all flow parameters pressure gradient increases. We can see the impact of parameters G r on the variation of pressure gradient dp/dx from Fig. 2e it is noted that pressure gradient is decreases as increases of G r. From Fig. 2f, one can see that dp/dx increases by increasing Re. Figure 3a presents the effects of temperature θ for the different values of volume fraction φ. It is observed that as we increases φ, the temperature also increases. Figure 3b shows that temperature profile increases with an increase in heat generation parameter.

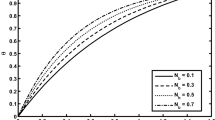
The expression for the magnetic force function Φ against the space variable y for different values of E and R m is shown in Fig. 4a, b, respectively. It is observed from the figures that with the increase of E, Φ decreases and the opposite behavior is noticed for R m.

It is observed from Fig. 5a that the velocity profile decreases near the right wall, but increases near the left wall of the channel with increasing value of φ. We present Fig. 5b to obtain the variation of velocity profile u for varying magnitudes of parameters S 1. It shows that the velocity increases with increases of S 1 throughout the channel. From Fig. 5c, we study the effect of the behavior of Q 0 on the velocity profile u. it is observed that near the walls, the velocity profile decreases, but at the center of the channel the velocity profile increases by increasing Q 0. It is also seen that in the cases of CuO–H2O and Ag–H2O, parameter Q 0 does not gives as much variation on velocity as in the cases of Cu–H2O and TiO2–H2O. Figure 5d shows the effect of R m on the velocity profile. It is observed that near the left wall, the velocity profile decreases by increases in R m, but near the right wall we noticed the opposite behavior of velocity profile. From Fig. 5e, we observe the effect of the behavior of G r on the velocity profile. It shows that near the left wall, the velocity profile increases with increases of G r and near the right wall the velocity profile decreases. We show in Fig. 5f the behavior of the velocity profile with increases in Re. It was observed that as we increase the values of Re, the velocity profile u does not change near the left wall, but decreases at the middle of wall and increases near the right wall of the channels.

A very interesting phenomenon in fluid transport is trapping. The formation of an internally circulating bolus of the fluid by closed streamlines is called trapping and this trapped bolus is pushed ahead along the peristaltic wave with the speed of wave. The bolus described as a volume of fluid bounded by closed streamlines in the wave frame is moved as a wave pattern. Figure 6 shows typical contour maps for the streamlines with two values of φ (φ = 0.01, φ = 0.04), Fig. 7 shows the contour maps for the streamlines with two values of G r (G r = 2, G r = 4) and Fig. 8 shows contours for the streamlines with two values of R m (R m = 2.0, R m = 2.1) for all four type of fluids (CuO–H2O, Ag–H2O, TiO2–H2O, Cu–H2O). Figure 6a, b shows the streamlines for CuO–H2O. It is noticed that the bolus becomes large with greater values of φ. Figure 6c, d shows the streamlines for Ag–H2O and it is noticed that the number of bolus increases for higher values of φ. Figure 6e, f shows the streamlines for TiO2–H2O and it is seen that the bolus becomes large with larger values of φ. Figure 6g, h shows the streamlines for Cu–H2O, and it is seen that the number of bolus increases. Figure 7a, b shows the streamlines for CuO–H2O and it is observed that the bolus becomes smaller with greater values of G r. Figure 7c, d shows the streamlines for Ag–H2O and it is noticed that the number of bolus decreases for higher values of G r. Figure 7e, f shows the streamlines for TiO2–H2O and it is shown that the bolus becomes small with larger values of G r. Figure 7g, h shows the streamlines for Cu–H2O and it is noticed that the number of bolus decreases with greater values of G r. Figure 8a, b shows the streamlines for CuO–H2O. Figure 8c, d shows the streamlines for Ag–H2O. Figure 8e, f shows the streamlines for TiO2–H2O and it is noticed that the bolus becomes large with greater values of φ. Figure 8c, d shows the streamlines for Ag–H2O and it was noticed that the number of bolus increases for higher values of φ. Figure 8e, f shows the streamlines for TiO2–H2O and Fig. 8g, h shows the streamlines for Cu–H2O. One can observe that the size of the bolus becomes small with large values of R m.

Conclusion

The interaction of nanoparticles for peristaltic flow with the induced magnetic field is discussed. The key points are observed as follows:

  1. 1.

    The pressure rise decreases with the increasing effects of R m .

  2. 2.

    The pressure gradient decreases with increases in G r.

  3. 3.

    Near the walls, the velocity profile decreases, but at the center of the channel the velocity profile increases by increasing Q 0.

  4. 4.

    As we increases the values of Re, the velocity profile does not change near the left wall, but at the middle of the wall the velocity decreases and near the right wall of the channels the velocity increases.

  5. 5.

    In the cases of CuO–H2O and Ag–H2O, parameter Q 0 does not give as much variation in velocity as in the cases of Cu–H2O and TiO2–H2O.

  6. 6.

    With the increases of E, the magnetic force function decreases and the opposite behavior is noticed for R m.

  7. 7.

    As we increase φ, the temperature also increases.

  8. 8.

    The streamlines for CuO–H2O show that the bolus becomes large with greater values of φ.

  9. 9.

    The streamlines for Cu–H2O, show that the number of bolus decreases with greater values of G r.