Blood flow of nanofluid through an artery with composite stenosis and permeable walls

Abstract

This problem deals with the theoretical study of blood flow of nanofluid through composite stenosed arteries with permeable walls. The highly nonlinear momentum equations of nanofluid model are simplified by considering the mild stenosis case. Temperature and nanoparticle equations are coupled; so, we use homotopy perturbation method to calculate the solution of temperature and nanoparticle equations, while the exact solution has been calculated for velocity profile. Also, the expressions for flow impedance, pressure gradient and stream function are computed. These solutions depend on Brownian motion number N_b, thermophoresis number N_t, local temperature Grashof number G_r and local nanoparticle Grashof number B_r. The effects of various emerging parameters are discussed through graphs for different values of interest.

Introduction

In cardiac related problems, the effected arteries get hardened as a result of accumulation of fatty substances inside the lumen or because of formation of plaques. This accumulation of substances in arteries is known as stenosis. When a blood clot forms in an artery, blocking the blood flow to the heart muscle or the brain, a heart attack or stroke can follow. Most of the researchers believe that deposits of cholesterol, fatty substances, cellular waste products, calcium and fibrin may be responsible for the development of the disease. Regardless of the cause, it is known that once an obstruction has developed, it results in significant changes in pressure distribution, wall shear stress and impedance (flow resistance) (Mishra et al. 2011).

The vessel or arterial walls may be elastic, movable or permeable. Therefore to understand the mechanics of the circulation of blood, it would be a prerequisite to have a clear idea of the basic mechanics of fluids. Some of the basic studies dealing withdifferent models of Newtonian and non-Newtonian fluid are given in Naz et al. (2008), Tripathi et al. (2010), Shukla and Rahman (1998), Hameed and Ellahi (2011) and Ellahi et al. (2012). A number of theoretical studies related to blood flow through stenosis arteries has been performed by Nadeem and Akbar (2009, 2011). Several investigators have highlighted different aspects of blood flow analysis in arteries. In a number of papers, Mekheimer and El kot (2012), and Mekheimer et al. (2012) have discussed the different aspects of blood flow analysis in stenosed arteries. Riahi et al (2011) have examined the problem of blood flow in an artery and in the presence of an overlapping stenosis. A mathematical study on three layered oscillatory blood flow through stenosed arteries has been investigated by Tripathi (2012). Recently, Mishra et al. (2011) have studied the blood flow through a composite stenosis in an artery with permeable wall.

The aim of present paper is to study the effects of permeable walls along with slip on the blood flow of nanofluid through a composite stenosed artery. The non-dimensional governing equations in the case of mild stenosis and corresponding boundary conditions are prescribed and then solved by using homotopy perturbation method (HPM). The physical features of the major parameters have been discussed through graphs. Trapping phenomenon have also been discussed at the end.

Formulation of the problem

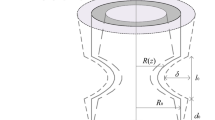
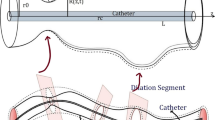
Consider an incompressible nanofluid of viscosity μ and density ρ flowing through a composite stenosed artery of finite length L. Let (r, θ , z) be the coordinates of a material point in the cylindrical polar coordinate system where z-axis is taken along the axis of artery, while r, θ are along the radial and circumferential directions, respectively. r = 0 is taken as the axis of symmetry of the tube. Heat and mass transfer phenomena is taken into account by considering the temperature T₁ and concentration C₁ to the wall of the tube. At the centre of the tube, we consider symmetric conditions at velocity, temperature and concentration. The geometry of the arterial wall with composite stenosis is written mathematically as (Mishra et al. 2011)

$$R(z) /R_{0} =1-\frac{2\delta}{R_{0} L_{0}} (z-d); \quad d<z\leq d+L_{0}/2,$$

(1)

$$=1-\frac{\delta }{2R_{0}}\left( 1+\cos \frac{2\pi }{L_{0}}\left( z-d-L_{0}/2\right) \right) ;\quad d+L_{0}/2<z\leq d+L_{0},$$

(2)

$$=1;\quad\quad\quad\hbox{otherwise}.$$

where d₀ indicates the location, L₀ denotes the length, δ represents the height of the stenosis, while R₀ and R(z) show the radii of the normal and stenosed arteries, respectively (see Fig. 1). The equations for unsteady flow of an incompressible nanofluid in the presence of body force are given by

$${\mathbf{\nabla}}\times{\mathbf{V}}=0$$

(3)

$$\rho _{\rm f}\frac{{\rm d}V}{{\rm d}t}=-\nabla P+\mu \nabla ^{2}V+{\mathbf{f}},$$

(4)

$$(\rho c)_{\rm f}{{{\rm{d}}{\it{T}}} \over {{\rm{d}}t}}=k\nabla ^{2}T+(\rho c)_{\rm p}[D_{\rm B}\nabla C.\nabla T+(D_{\rm T}/T_{0})\nabla T.\nabla T],$$

(5)

$${{{\rm{d}}C} \over {{\rm{d}}t}}=D_{\rm B}\nabla ^{2}C+(D_{\rm T}/T_{0})\nabla ^{2}T,$$

(6)

where c is the volumetric volume expansion coefficient, $\mathbf{V}$ is the velocity vector, $\mathbf{f}$ is the body force, d/dt represents the material time derivative, P is the pressure, C is the nanoparticle phenomenon, D_B is the Brownian diffusion coefficient and D_T is the thermospheric diffusion coefficient. The ambient values of T and C as r tends to R are denoted by T₁ and C₁. In component form, Eqs. (3)–(6) can be written as

$$\frac{1}{r}\frac{\partial (rv)}{\partial r}+\frac{\partial u}{\partial z}=0,$$

(7)

$$\rho \left( v\frac{\partial v}{\partial r}+u\frac{\partial v}{\partial z} \right) =-\frac{\partial p}{\partial r}+\frac{1}{r}\frac{\partial }{\partial r}\left( rS_{\rm rr}\right) +\frac{\partial }{\partial z}\left( S_{\rm rz}\right) - \frac{1}{r}S_{\rm{\theta \theta}}$$

(8)

$$\rho \left( v\frac{\partial u}{\partial r}+u\frac{\partial u}{\partial z} \right) =-\frac{\partial p}{\partial z}+\frac{1}{r}\frac{\partial }{\partial r}\left( rS_{\rm rz}\right) +\frac{\partial }{\partial z}\left( S_{\rm zz}\right) +\rho g\alpha \left( T-T_{1}\right) +\rho g\alpha \left( C-C_{1}\right) ,$$

(9)

$$\left( v\frac{\partial T}{\partial r}+u\frac{\partial T}{\partial z}\right) =\alpha \left( \frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r}\frac{ \partial T}{\partial r}+\frac{\partial ^{2}T}{\partial z^{2}}\right) +\tau \left[ D_{\rm B}\left( \frac{\partial C}{\partial r}\frac{\partial T}{\partial r} +\frac{\partial C}{\partial z}\frac{\partial T}{\partial z}\right) +\frac{ D_{\rm T}}{T_{0}}\left( \left( \frac{\partial T}{\partial r}\right) ^{2}+\left( \frac{\partial T}{\partial z}\right) ^{2}\right) \right]$$

(10)

$$\left( v\frac{\partial C}{\partial r}+u\frac{\partial C}{\partial z}\right) =D_{\rm B}\left( \frac{\partial ^{2}C}{\partial r^{2}}+\frac{1}{r}\frac{\partial C}{\partial r}+\frac{\partial ^{2}C}{\partial z^{2}}\right) +\frac{D_{\rm T}}{ T_{0}}\left( \frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{\partial ^{2}T}{\partial z^{2}}\right)$$

(11)

where $\tau =\left( \rho c\right) _{\rm p}/\left( \rho c\right) _{\rm f}$ is the ratio between the effective heat capacity of the nanoparticle material and heat capacity of the fluid.

$$S_{\rm rr}=\frac{2\mu }{1+\lambda _{1}}\left( 1+\lambda _{2}\left( v\frac{ \partial }{\partial r}+u\frac{\partial }{\partial z}\right) \right) \frac{ \partial v}{\partial r},$$

$$S_{\rm rz}=\frac{\mu }{1+\lambda _{1}}\left( 1+\lambda _{2}\left( v\frac{ \partial }{\partial r}+u\frac{\partial }{\partial z}\right) \right) \left( \frac{\partial v}{\partial z}+\frac{\partial u}{\partial r}\right) ,$$

$$S_{\rm zz}=\frac{2\mu }{1+\lambda _{1}}\left( 1+\lambda _{2}\left( v\frac{ \partial }{\partial r}+u\frac{\partial }{\partial z}\right) \right) \frac{ \partial u}{\partial z}.$$

Fig. 1

Geometry of the composite stenosed artery

The boundary conditions for temperature and concentration are

$$\frac{\partial T}{\partial r}=0, \quad \frac{\partial C}{\partial r}=0 \quad \hbox{at}\quad r=0$$

(12)

$$T=T_{1}, \quad C=C_{1} \quad \hbox{at} \quad r=R\left( z\right).$$

(13)

We introduce the following non-dimensional variables

$$\begin{aligned} \bar{r} &=&\frac{r}{R_{0}}, \, \bar{z}=\frac{z}{L_{0}},\, \bar{v}=\frac{L_{0}}{\delta U}v, \, u=\frac{u}{U},\, \bar{d}=\frac{d}{L_{0}}, \, \bar{R}=\frac{R}{R_{0}}, \, \bar{p}=\frac{R_{0}^{2}}{UL_{0}\mu}p\\ T &=&T_{1}+\left(T_{0}-T_{1}\right) \theta, \, C=C_{1}+\left( C_{0}-C_{1}\right) \sigma,\, G_{\rm r}=\frac{\rho g\alpha _{1}R_{0}^{2}T_{1}}{\mu U},\\ B_{\rm r} &=&\frac{\rho g\alpha_{1}R_{0}^{2}T_{1}}{\mu U},\, N_{\rm t}=\frac{ \left( \rho c\right)_{\rm p}D_{\rm T}T_{0}}{\left( \rho c\right)_{\rm f}\alpha _{1}},\, N_{\rm b}=\frac{\left( \rho c\right) _{\rm p}D_{\rm T}C_{0}}{\left( \rho c\right) _{\rm f}\alpha _{1}},\, R_{\rm e}=\frac{\rho UR_{0}}{\mu} \end{aligned}$$

(14)

where U is the velocity averaged over the section of the tube with radius R₀.  N_t,  N_b,  G_r and B_r are the thermophoresis parameter, the Brownian motion parameter, local temperature Grashof number and local nanoparticle Grashof number. Making use of these variables in Eqs. (7)–(11) and after applying the additional condition $\epsilon =R_{0}/L_{0}=O(1)$ for the case of mild stenosis $(\delta ^{\ast }=\delta /R_{0}<<1),$ the non-dimensional governing equations after dropping the dashes can be written as

$$\delta^{\ast}\left( \frac{\partial v}{\partial r}+\frac{v}{r}\right) + \frac{\partial u}{\partial z}=0,$$

(15)

$$\frac{\partial p}{\partial r}=0,$$

(16)

$$\frac{\partial p}{\partial z}=\frac{1}{r}\frac{\partial }{\partial r}\left( r \frac{\partial u}{\partial r}\right) +G_{\rm r}\theta +B_{\rm r}\sigma ,$$

(17)

$$\frac{1}{r}\frac{\partial }{\partial r}\left( r\frac{\partial \theta}{ \partial r}\right) +N_{\rm b}\frac{\partial \sigma }{\partial r}\frac{\partial \theta }{\partial r}+N_{\rm t}\left( \frac{\partial \theta }{\partial r}\right) ^{2}=0,$$

(18)

$$N_{\rm b}\frac{\partial }{\partial r}\left( r\frac{\partial \theta }{\partial r} \right) +N_{\rm t}\frac{\partial }{\partial r}\left( r\frac{\partial \theta }{\partial r}\right) =0.$$

(19)

The non-dimensional boundary conditions on velocity for permeable wall are (Mishra et al. 2011)

$$\frac{\partial u}{\partial r}=0 \quad \hbox{at}\quad r=0$$

(20)

$$u=u_{\rm B},\quad \frac{\partial u}{\partial r}=\frac{\alpha}{ \sqrt{D_{\rm a}}}\left(u_{\rm B}-u_{\rm p}\right) \quad \hbox{at} \quad r=R\left( z\right).$$

(21)

where u_B is the slip velocity to be determined.

The non-dimensional conditions for θ and σ are

$$\frac{\partial \theta }{\partial r}=0,\quad \frac{\partial \sigma }{ \partial r}=0,\quad \hbox{at}\quad r=0$$

(22)

$$\theta =0,\quad\sigma =0 \quad \hbox{at}\quad r=R\left( z\right) .$$

(23)

Eqs. (1) and (2) reduce to

$$R\left( z\right) = 1-2\delta \left( z-d\right); \quad \quad \quad d<z\leq d+1/2,$$

(24)

$$= 1-\frac{\delta}{2}\left( 1+\cos 2\pi \left( z-d-1/2\right) \right);\quad d+1/2<z\leq d+1,$$

(25)

$$= 1;\quad \quad \quad \hbox{otherwise}$$

Solution of the problem

The solutions of the coupled Eqs. (18) and (19) have been calculated by homotopy perturbation method (HPM) as

$$H\left( q,\theta \right) =\left( 1-q\right) \left[ L\left( \theta \right) -L\left( \theta _{0}\right) \right] +q\left[ L\left( \theta \right) +N_{\rm b} \frac{\partial \sigma }{\partial r}\frac{\partial \theta }{\partial r} +N_{\rm t}\left( \frac{\partial \theta}{\partial r}\right) ^{2}\right]$$

(26)

$$H\left( q,\theta \right) =L\left( \theta \right) -L\left( \theta _{0}\right) +qL\left( \theta \right) +q\left[ N_{\rm b}\frac{\partial \sigma }{\partial r} \frac{\partial \theta }{\partial r}+N_{\rm t}\left( \frac{\partial \theta }{ \partial r}\right) ^{2}\right]$$

(27)

$$H\left( q,\sigma \right) =\left( 1-q\right) \left[ L\left( \sigma \right) -L\left( \sigma _{0}\right) \right] +q\left[ L\left( \sigma \right) +\frac{ N_{\rm t}}{N_{\rm b}}\left( \frac{1}{r}\frac{\partial }{\partial r}\left( r\frac{ \partial \theta }{\partial r}\right) \right) \right]$$

(28)

$$H\left( q,\sigma \right) =L\left( \sigma \right) -L\left( \sigma _{0}\right) +qL\left( \sigma _{0}\right) +q\left[ \frac{N_{\rm t}}{N_{\rm b}}\left( \frac{1}{r} \frac{\partial }{\partial r}\left( r\frac{\partial \theta }{\partial r} \right) \right) \right].$$

(29)

where q is the embedding parameter which has the range 0 ≤ q ≤ 1. For our convenience, we have taken $L=\frac{1}{r}\frac{\partial }{\partial r}\left( r\frac{\partial}{\partial r}\right)$. The initial guesses θ₀ and σ₀ are defined as

$$\theta _{0}\left( r,z\right) =\left( \frac{r^{2}-R^{2}}{4}\right) ,\quad \sigma _{0}\left( r,z\right) =-\left( \frac{r^{2}-R^{2}}{4}\right)$$

(30)

Define

$$\theta \left( r,z\right) =\theta _{0}+q\theta _{1}+q^{2}\theta _{2}+....$$

(31)

$$\sigma \left( r,z\right) =\sigma _{0}+q\sigma _{1}+q^{2}\sigma _{2}+....$$

(32)

Adopting the same procedure as done by Nadeem and Akbar (2011), the solution for temperature and nanoparticle phenomena for q = 1 can be written as

$$\theta \left( r,z\right) =\frac{1}{64}\left( N_{\rm b}-N_{\rm t}\right) \left( r^{2}-R^{2}\right) -\left( \frac{1}{18}N_{\rm b}\left( r^{3}-R^{3}\right) +\frac{ N_{\rm t}}{36,864}\left( N_{\rm b}^{2}+N_{\rm t}^{2}\right) \left( r^{4}-R^{4}\right) \left( r^{6}-R^{6}\right) \right)$$

(33)

$$\sigma \left( r,z\right) =-\frac{1}{4}\left( r^{2}-R^{2}\right) \frac{N_{\rm t}}{ N_{\rm b}}+\frac{N_{\rm t}}{N_{\rm b}}\left( \frac{1}{18}N_{\rm b}\left( r^{3}-R^{3}\right) + \frac{1}{36,864}\left( N_{\rm b}^{2}+N_{\rm t}^{2}\right) \left( r^{6}-R^{6}\right) \right).$$

(34)

Substituting Eqs. (32) and (33) in Eq. (17), the exact solution for velocity can be written as

$$\begin{aligned} u\left( r,z\right) =&u_{\rm B}+\frac{1}{4}\left( -\frac{\partial p}{\partial z} \right) \left( r^{2}-R^{2}\right) +\frac{G_{\rm r}N_{\rm b}r^{3}}{162}+\frac{ B_{\rm r}N_{\rm t}r^{3}}{36N_{\rm b}}-\frac{B_{\rm r}N_{\rm t}r^{4}}{288}-\frac{G_{\rm r}N_{\rm b}r^{5}}{ 1,600}+\frac{G_{\rm r}N_{\rm t}r^{5}}{1,600}+\frac{G_{\rm r}N_{\rm b}^{2}N_{\rm t}r^{11}}{4,460,544}\\ &-\frac{B_{\rm r}N_{\rm b}N_{\rm t}^{2}r^{11}}{4,460,544}-\frac{G_{\rm r}N_{\rm t}^{3}r^{11}}{ 4,460,544}+\frac{B_{\rm r}N_{\rm t}^{4}r^{11}}{4,460,544N_{\rm b}}-\frac{G_{\rm r}N_{\rm b}r^{2}R^{2} }{36}-\frac{B_{\rm r}N_{\rm t}r^{2}R^{2}}{8N_{\rm b}}+\\ &\frac{2\left( 2G_{\rm r}N_{\rm b}^{2}+9B_{\rm r}N_{\rm t}\right) R^{3}}{81N_{\rm b}}+\frac{ B_{\rm r}N_{\rm t}r^{2}R^{3}}{36}-\frac{5B_{\rm r}N_{\rm t}R^{4}}{96}+\frac{ G_{\rm r}N_{\rm b}r^{2}R^{4}}{128}-\frac{G_{\rm r}N_{\rm t}r^{2}R^{4}}{128}\\ &-\frac{G_{\rm r}N_{\rm b}^{2}N_{\rm t}r^{7}R^{4}}{1,806,336}+\frac{ B_{\rm r}N_{\rm b}N_{\rm t}^{2}r^{7}R^{4}}{1,806,336}+\frac{G_{\rm r}N_{\rm t}^{3}r^{7}R^{4}}{ 1,806,336}-\frac{B_{\rm r}N_{\rm t}^{4}r^{7}R^{4}}{1,806,336N_{\rm b}}-\frac{3G_{\rm r}\left( N_{\rm b}-N_{\rm t}\right) R^{5}}{200}\\ &-\frac{G_{\rm r}N_{\rm b}^{2}N_{\rm t}r^{5}R^{6}}{921,600}+\frac{ B_{\rm r}N_{\rm b}N_{\rm t}^{2}r^{5}R^{6}}{921,600}+\frac{G_{\rm r}N_{\rm t}^{3}r^{5}R^{6}}{ 1,806,336}-\frac{B_{\rm r}N_{\rm t}^{3}r^{5}R^{6}}{1,806,336N_{\rm b}}+\frac{ G_{\rm r}N_{\rm b}^{2}N_{\rm t}r^{2}R^{10}}{73,728}\\ &-\frac{B_{\rm r}N_{\rm b}N_{\rm t}^{2}r^{2}R^{10}}{73,728}-\frac{ G_{\rm r}N_{\rm t}^{3}r^{2}R^{10}}{73,728}+\frac{B_{\rm r}N_{\rm t}^{4}r^{2}R^{10}}{73,728N_{\rm b} }-\frac{N_{\rm t}\left( N_{\rm b}-N_{\rm t}\right) \left( N_{\rm b}+N_{\rm t}\right) \left( G_{\rm r}N_{\rm b}-B_{\rm r}N_{\rm t}\right) R^{11}}{4,464,954N_{\rm b}}, \end{aligned}$$

(35)

where

$$\begin{gathered} u_{\rm B} =\frac{\sqrt{D_{\rm a}}R^{2}}{\alpha }\left( \frac{1}{4R^{2}}\left( - \frac{\partial p}{\partial z}\right) \left( R^{2}-4\alpha \sqrt{D_{\rm a}} \right) -\frac{G_{\rm r}N_{\rm b}}{27}-\frac{B_{\rm r}N_{\rm t}}{6N_{\rm b}}+\frac{B_{\rm r}N_{\rm t}R}{24}\right.\\ \left. +\frac{G_{\rm r}\left( N_{\rm b}-N_{t}\right) R^{2}}{80}+\frac{N_{\rm t}\left( N_{\rm b}-N_{\rm t}\right) \left( N_{\rm b}+N_{\rm t}\right) \left( G_{\rm r}N_{\rm b}-B_{\rm r}N_{\rm t}\right) R^{11}}{4,464,954N_{\rm b}}\right) \end{gathered}$$

(36)

The flux Q can be calculated as

$$Q=2\overset{R}{\underset{0}{\int }}ru\,\rm{d}r,$$

$$Q=\left( -\frac{\partial p}{\partial z}\right) \frac{1}{F(z)}.$$

Impedance λ is calculated as

$$\lambda =\frac{\Updelta p}{Q},$$

since the flow rate Q is constant for all sections of tube

$$\lambda =\frac{1}{Q}\underset{0}{\overset{L}{\int }}\left( -\frac{\partial p }{\partial z}\right) {\rm d}z,$$

$$\lambda =\overset{d}{\underset{0}{\int }}F\left( z\right) {\rm d}z+\underset{d}{ \overset{d+1/2}{\int }}F\left( z\right) {\rm d}z+\underset{d+1/2}{\overset{d+1}{\int }}F\left( z\right) {\rm d}z+\underset{d+1}{\overset{L}{\int }}F\left( z\right) {\rm d}z,$$

(37)

$$\lambda =F\left( z\right)_{R=1}\left( L-1\right) +\underset{d}{\overset{ d+1/2}{\int }}F\left( z\right) {\rm d}z+\underset{d+1/2}{\overset{d+1}{\int }} F\left( z\right) {\rm d}z,$$

(38)

The nonzero dimensionless shear stress in our problem is given by

$$S_{\rm rz}=-\frac{R}{2}\frac{\partial p}{\partial z},$$

The expression for wall shear stress can be calculated as

$$S_{\rm rz}=-\frac{R}{2}\left( \frac{\partial p}{\partial z}\right) _{r=R}.$$

(39)

Results and discussion

In this part of the article, we have examined the graphical features of pertinent parameters on the profiles of velocity $\left( u\right)$, concentration (σ), temperature (θ), impedance $\left( \lambda \right) ,$ and shear stress $\left( S_{\rm rz}\right)$. The observations are made for the variation of pertinent parameters to observe the effects for different sizes of stenosis. The graphs of impedance $\left( \lambda \right)$ are drawn against the Darcy number $\left( \sqrt{D_{\rm a}}\right)$ and stenosis height $\left( \delta \right)$ for slip parameter $\left( \alpha \right)$ and Nusstle number $\left( N_{\rm t}\right)$. The velocity profile u is examined against radial coordinate r and the effects of (B_r), (α), (G_r) and $(\sqrt{D_{\rm a}})$ are discussed. Variation in concentration (σ) is discussed for various values of (N_b) and (N_t). Influence on temperature profile (θ) is also examined for different values of (N_b) and (N_t). The streamlines are displayed in the end to investigate the flow pattern under the presence of different parameters to discuss the trapping bolus phenomenon.

Impedance variation

In Fig. 2, the impedance is plotted for the variation of the slip parameter α against the Darcy number $\sqrt{D_{\rm a}}$ for different stenosis height δ. It is revealed here that impedance of the flow is larger in the domain $0<\sqrt{D_{\rm a}}<0.2$ as compared to the rest of the region. It is also seen that impedance is in direct relation with the variation of slip parameter for all values of δ. The altitude of the impedance profile gets higher for larger values of δ. One can see the impact of N_b on the distribution of impedance against the Darcy number in Fig. 3. From this graph, it is measured that impedance increases with the decrease of N_b, but not much variation in the impedance is observed in the region $0.4<\sqrt{D_{\rm a}}<0.5.$ Figure 4 implies the influences of $\sqrt{D_{\rm a}}$ and α on the impedance plotted along the stenosis height δ. It is concluded here that impedance is very small in the region 0 < δ < 0.1 and a significant variation is observed in the remaining part of the domain. It is also noted that with increase in $\sqrt{D_{\rm a}},$ the impedance decreases.

Fig. 2

Variation in impedance λ against $\sqrt{D_{\rm a}}$ for α = 0.1, 0.5, 0.9 and δ = 0.01, 0.1, 0.2

Fig. 3

Variation in impedance λ against $\sqrt{D_{\rm a}}$ for N_b = 0.1, 1.0, 2.0 and δ = 0.1,0.2

Fig. 4

Variation in impedance λ against δ for α = 0.2, 0.3, 0.4 and D ^1/2 _a  = 1.0, 1.2, 1.4

The variation of velocity distribution

The velocity profile u for the slip parameter α is presented in Fig. 5, plotted against the radial axis r. It suggests that velocity profile rises with the increase in slip parameter. The variation of axial velocity profile u for δ is described in Fig. 6 which indicates that for arbitrary stenosis height δ, the apparent radius of the artery decreases from r to r − δ. Figure 7 describes the profile of u for various values of N_t. Increasing values of N_t results in a decrease in velocity profile u.

Fig. 5

Variation in velocity u against radius r for slip parameter α = 0.100, 0.010, 0.001

Fig. 6

Variation in velocity u against radius r for stenosis height δ = 0.0, 0.1, 0.2

Fig. 7

Variation in velocity u against radius r for N_t = 0.0, 1.0, 2.0

Fig. 8

Variation in concentration profile σ against radius r for N_t = 0.1, 0.2, 0.3

Fig. 9

Variation in concentration profile σ against radius r for N_b = 0.1, 0.2, 0.3

Fig. 10

Variation in temperature profile θ against radius r for N_b = 0.1, 0.2, 0.3

Fig. 11

Variation in temperature profile θ against radius r for N_t = 0.1, 0.2, 0.3

The variation of concentration and temperature distributions

Effects of N_b and N_t on concentration σ and temperature θ profiles are shown in plots 8–11, respectively. It is observed that by increasing N_t, the concentration profile increases and a decrease in the profile is seen by enhancing N_b. An increment in θ is observed by increasing N_b and N_t.

Shear stress profile

In Figs. 12, 13 and 14, the effects of different heights of stenosis on the shear stress distribution are analyzed for various values of B_r,  G_r and N_b, respectively. It is depicted that the stress is decreased by increasing N_b; the inverse behavior is described for the stress profile in the cases of B_r and G_r. All of these figures show that stress is directly proportional to the stenosis height, i.e., if we increase the stenosis height, the stress will have a higher amplitude.

Fig. 12

Variation in stress S_rz against axial direction z for various values of δ and B_r = 0, 2, 4

Fig. 13

Variation in stress S_rz against axial direction z for various values of δ and G_r = 0, 1, 2

Fig. 14

Variation in stress S_rz against axial direction z for various values of δ and N_b = 2, 4, 6

Trapping phenomena

Figure 15 shows the streamlines for the slip parameter α. It is seen here that as we increase the slip parameter, the area of the bolus expands but the number of bolus is increased. The variation of Darcy number $\sqrt{D_{\rm a}}$ for the streamlines is displayed in Fig. 16. It is to be noted that more boluses are obtained with the increase in magnitude of Darcy number, but the size of the bolus is diminished gradually. Figure 17 reveals the inverse behavior of streamlines with the variation of stenosis height δ as observed in the previous figure for Darcy number.

Fig. 15

Streamlines for α. a  α = 0.01,  b  α = 0.03 and  c  α = 0.05

Fig. 16

Streamlines for$\sqrt{D_{\rm a}}.$a$\sqrt{D_{\rm a}}=0.10,$b$\sqrt{D_{\rm a}}=0.15$and c$\sqrt{D_{\rm a}}=0.20$

Fig. 17

Streamlines for δ.   a  δ = 0.10,  b  δ = 0.15 and c  δ = 0.20