Mathematical model for the peristaltic flow of nanofluid through eccentric tubes comprising porous medium

Abstract

Mathematical model for peristaltic flow of nanofluid between eccentric tubes is investigated through a porous medium. Assumptions of long wavelength and low Reynolds number are carried out to observe the intestinal flow. The flow is considered to be unsteady and incompressible. Analytical solutions are evaluated through homotopy perturbation method. The expression of pressure rise is obtained through numerical integration whose data is presented in table. The problems under consideration are made dimensionless to reduce the complication of the analysis and to merge the extra parameters. All the emerging parameters affecting the flow phenomenon are discussed graphically. Trapping bolus scheme is also presented through streamlines for various pertinent quantities.

Introduction

Nanotechnology has immense contribution in industry since materials of nanometer dimensions exhibit incomparable physical and chemical characteristics. Water, ethylene glycol and oil are common examples of base fluids used for the nanofluid phenomenon. Nanofluids have their enormous applications in heat transfer, such as microelectronics, fuel cells, pharmaceutical processes, and hybrid-powered engines, domestic refrigerator, chiller, nuclear reactor coolant, grinding and space technology, etc. They explore enhanced thermal conductivity and the convective heat transfer coefficient is counter balanced to the base fluid. Nanofluids have attracted the attention of many researchers for new production of heat transfer fluids in heat exchangers, in plants and in automotive cooling significations, due to their extensive thermal properties. A large amount of literature is available which deals with the study of nanofluid and its applications (Yoo et al. 2007; Manca et al. 2012; Wang and Mujumdar 2007). The process of peristalsis is widely used in evaluating swallowing of food through the esophagus, chyme motion in the gastrointestinal tract, vasomotion of small blood vessels, capillaries and arterioles, urine transport from kidney to bladder and a toxic liquid transportation in the nuclear industry, etc. Most of the industrial used fluids have non-Newtonian characteristics and have been investigated by many researchers (Shukla and Rahman 1998; Naz et al. 2008; Hameed and Nadeem 2007; Xu et al. 2006; Patel and Timol 2009).

In the field of fluid mechanics, peristalsis has obtained the central place in the minds of many researchers, modelers, scientists, engineers and mathematicians due to their large amount of applications in chemical industries, nuclear reactors, physiology and biomedical apparatus, etc. Studies relating the peristaltic flow of various Newtonian and non-Newtonian fluid models have been investigated by many researchers (Srinivas and Kothandapani 2008; Sobh et al. 2010; Tripathi 2011a, b; Mekheimer and Abdelmaboud 2008). Mekheimer et. al. (2013) have analyzed the mathematical model of peristaltic transport through an eccentric cylinders. Influence of lateral walls on peristaltic flow in a rectangular duct has been investigated by Reddy et al. (2005). The idea of nanofluid in peristalsis has been explored by some of the researchers. Nadeem and Maraj (2012) have derived the mathematical analysis for peristaltic flow of nanofluid in a curved channel with compliant walls under the constraints of long wavelength and low Reynolds number. Recently, Nadeem et al. (2013) have presented the effects of heat and mass transfer on peristaltic flow of a nanofluid between eccentric cylinders. To the best of authors’ information, peristaltic flow of nanofluid through eccentric cylinders having porous medium has not been yet analyzed.

Keeping in mind the applications of nanofluid in peristalsis, the major intention of this paper is to extend the work of Nadeem et al. (2013) for the unsteady peristaltic flow of nanofluid between eccentric cylinders through porous space. The governing equations are simplified through the dimensionless process and the approximations of low Reynolds number and long wavelength. Analytical solutions are evaluated for the velocity, temperature and nanoparticle concentration with the help of homotopy perturbation method. Numerical data are obtained for the pressure rise expression using the numerical integration. The possible physical effects of all the emerging parameters are carried out through drawing graphs of various quantities. Trapping bolus phenomenon is also presented through streamlines.

Mathematical structure of the problem

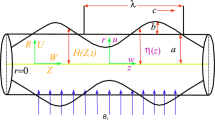
Let us analyze the peristaltic pumping characteristics of an unsteady and incompressible nanofluid between two vertical eccentric tubes through a porous space. The geometry of the flow is arranged such that the inner tube is inductile but moving with the constant velocity V along its length and the outer flexible tube is examining a peristaltic wave traveling down its walls. The inner tube has radiusδ but we are looking to discuss the motion to the center of the outer tube. The center of the inner tube is now at the position $r=\mathit{ϵ},z=0,$ where r and z are coordinates in the cross section of the pipe as shown in Fig. 1. Then the boundary of the inner tube is described by $r_1=\mathit{\delta }+\mathit{ϵ}cos\mathit{\theta },$ where $\mathit{ϵ}$ is the eccentricity parameter of the inner tube position. Further, we consider that boundary of the inner tube is at temperature T₀ and the outer tube is kept at temperature T₁. The nanoparticle concentrations are described as C₀ and C₁ at the walls of inner and outer cylinders, respectively.

Fig. 1

The simplified model of geometry of the problem

The boundaries of the inner and outer walls are respectively described as (Mekheimer et al. 2013):

$$r_1=\mathit{\delta }+\mathit{ϵ}cos\mathit{\theta },$$

$$r_2=a+bcos\left[\frac{2\mathit{\pi }}{\mathit{\lambda }}(z-ct)\right],$$

whereδ and a represent the radii of the inner and outer tubes, b is the amplitude of the wave,λ shows the wavelength, c implies the propagation velocity and t is the time.

The law of conservation of mass, momentum, energy and nanoparticle concentration for an incompressible nanofluid through a porous medium are described as (Nadeem et al. 2013):

$$\text{div}\mathbf{V}=0,$$

(1)

$${\mathit{\rho }}_{\mathrm{f}}\left(\frac{\mathrm{d}\mathbf{V}}{\mathrm{d}t}\right)=-\nabla p+\mathit{\mu }\text{div}\mathbf{V}+{\mathit{\rho }}_{\mathrm{f}}g\mathit{\alpha }\left(T-T_0\right)+{\mathit{\rho }}_{\mathrm{f}}g\mathit{\alpha }\left(C-C_0\right)-\frac{\mathit{\mu }}{k_1}\mathbf{V},$$

(2)

$${\left(\mathit{\rho }c\right)}_{\mathrm{f}}\left(\frac{\mathrm{d}T}{\mathrm{d}t}\right)=\nabla ·K\nabla T+{\left(\mathit{\rho }c\right)}_{\mathrm{p}}\left(D_{\mathrm{B}}\left(\nabla C·\nabla T\right)+\frac{D_{\mathrm{T}}}{T_0}\left(\nabla T·\nabla T\right)\right),$$

(3)

$$\frac{\mathrm{d}C}{\mathrm{d}t}=D_{\mathrm{B}}{\nabla }^{2}C+\frac{D_{\mathrm{T}}}{T_0}{\nabla }^{2}T,$$

(4)

whereρ_f is the density of the incompressible fluid, k₁ denotes the permeability of the porous medium, ${(\mathit{\rho }c)}_{\mathrm{f}}$ is the heat capacity of the fluid, ${(\mathit{\rho }c)}_{\mathrm{p}}$ gives effective heat capacity of the nanoparticle material, K implies thermal conductivity, g stands for constant of gravity, μ is the viscosity of the fluid, d/dt gives the material time derivative, p is the pressure, C denotes the nanoparticle concentration, D_B is the Brownian diffusion coefficient and D_T is the thermophoretic diffusion coefficient. The velocity vector for the current problem is described as $\mathbf{V}=(w,0,u).$ We incorporate the following dimensionless quantities

$$\begin{array}{cc}\hfill p^{\prime }& =\frac{a^2}{\mathit{\mu }c\mathit{\lambda }}p,u^{\prime }=\frac{u}{c},w^{\prime }=\frac{\mathit{\lambda }}{ac}w,V^{\prime }=\frac{V}{c},z^{\prime }=\frac{z}{\mathit{\lambda }},r^{\prime }=\frac{r}{a},{\mathit{\theta }}^{\prime }=\mathit{\theta },t^{\prime }=\frac{c}{\mathit{\lambda }}t,\mathit{\varphi }=\frac{b}{a},\hfill \\ \hfill {\mathit{ϵ}}^{\prime }& =\frac{\mathit{ϵ}}{a},k^{\prime }=\frac{k_1}{a^2},\text{Re}=\frac{{\mathit{\rho }}_{\mathrm{f}}ca}{\mathit{\mu }},{\mathit{\delta }}^{\prime }=\frac{\mathit{\delta }}{a},\overline{\mathit{\theta }}=\frac{T-T_0}{T_1-T_0},\mathit{\sigma }=\frac{C-C_0}{C_1-C_0},P_r=\frac{\mathit{\mu }}{{\mathit{\rho }}_{\mathrm{f}}\mathit{\alpha }},S_c=\frac{\mathit{\mu }}{{\mathit{\rho }}_{\mathrm{f}}{D}_{\mathrm{B}}},\hfill \\ \hfill {\mathit{\delta }}_0& =\frac{a}{\mathit{\lambda }},B_r=\frac{{\mathit{\rho }}_{\mathrm{f}}g\mathit{\alpha }{a}^2}{\mathit{\mu }c}\left(C_1-C_0\right),G_r=\frac{{\mathit{\rho }}_{\mathrm{f}}g\mathit{\alpha }{a}^2}{\mathit{\mu }c}\left(T_1-T_0\right),N_b=\frac{\mathit{\tau }{D}_{\mathrm{B}}}{{\mathit{\alpha }}_{\mathrm{f}}}\left(C_1-C_0\right),\hfill \\ \hfill N_t& =\frac{\mathit{\tau }{D}_{\mathrm{T}}}{T_0{\mathit{\alpha }}_{\mathrm{f}}}\left(T_1-T_0\right),{\mathit{\alpha }}_{\mathrm{f}}=\frac{K}{{\left(\mathit{\rho }c\right)}_{\mathrm{f}}},\mathit{\tau }=\frac{{\left(\mathit{\rho }c\right)}_{\mathrm{p}}}{{\left(\mathit{\rho }c\right)}_{\mathrm{f}}}.\hfill \end{array}$$

(5)

where ϕ, Re, δ₀, P _r , N _b , N _t , k, G _r and B _r represent amplitude ratio, Reynolds number, dimensionless wave number, Prandtl number, Brownian motion parameter, thermophoresis parameter, porosity parameter, local temperature Grashof number and local nanoparticle Grashof number, respectively. After including the above non-dimensional parameters and considering the approximations of long wavelength $(\mathit{\lambda }\to \infty )$ and low Reynolds number $(\text{Re}<<1),$ the dimensionless governing equations $(\text{after}\text{ignoring}\text{primes})$ for nanofluid in porous space take the concluding form as:

$$\frac{\mathit{\partial }w}{\mathit{\partial }r}+\frac{w}{r}+\frac{\mathit{\partial }u}{\mathit{\partial }z}=0,$$

(6)

$$\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{r}^2}+\frac{1}{r}\frac{\mathit{\partial }u}{\mathit{\partial }r}+\frac{1}{r^2}\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{\mathit{\theta }}^2}+B_r\mathit{\sigma }+G_r\overline{\mathit{\theta }}-\frac{u}{k}=\frac{\mathit{\partial }p}{\mathit{\partial }z},$$

(7)

$$\frac{{\mathit{\partial }}^2\overline{\mathit{\theta }}}{\mathit{\partial }{r}^2}+\frac{1}{r}\frac{\mathit{\partial }\overline{\mathit{\theta }}}{\mathit{\partial }r}+\frac{1}{r^2}\frac{{\mathit{\partial }}^2\overline{\mathit{\theta }}}{\mathit{\partial }{\mathit{\theta }}^2}+N_b\left(\frac{\mathit{\partial }\overline{\mathit{\theta }}}{\mathit{\partial }r}\frac{\mathit{\partial }\mathit{\sigma }}{\mathit{\partial }r}+\frac{1}{r^2}\frac{\mathit{\partial }\overline{\mathit{\theta }}}{\mathit{\partial }\mathit{\theta }}\frac{\mathit{\partial }\mathit{\sigma }}{\mathit{\partial }\mathit{\theta }}\right)+N_t\left({\left(\frac{\mathit{\partial }\overline{\mathit{\theta }}}{\mathit{\partial }r}\right)}^2+\frac{1}{r^2}{\left(\frac{\mathit{\partial }\overline{\mathit{\theta }}}{\mathit{\partial }\mathit{\theta }}\right)}^2\right)=0,$$

(8)

$$\frac{{\mathit{\partial }}^2\mathit{\sigma }}{\mathit{\partial }{r}^2}+\frac{1}{r}\frac{\mathit{\partial }\mathit{\sigma }}{\mathit{\partial }r}+\frac{1}{r^2}\frac{{\mathit{\partial }}^2\mathit{\sigma }}{\mathit{\partial }{\mathit{\theta }}^2}+\frac{N_t}{N_b}\left(\frac{{\mathit{\partial }}^2\overline{\mathit{\theta }}}{\mathit{\partial }{r}^2}+\frac{1}{r}\frac{\mathit{\partial }\overline{\mathit{\theta }}}{\mathit{\partial }r}+\frac{1}{r^2}\frac{{\mathit{\partial }}^2\overline{\mathit{\theta }}}{\mathit{\partial }{\mathit{\theta }}^2}\right)=0.$$

(9)

The non-dimensional boundaries will take the form as:

$$r_1=\mathit{\delta }+\mathit{ϵ}cos\mathit{\theta },r_2=1+\mathit{\varphi }cos2\mathit{\pi }\left(z-t\right).$$

(10)

The corresponding dimensionless boundary conditions are described as:

$$u=V\text{at}r=r_1,u=0\text{at}r=r_2,$$

(11)

$$\overline{\mathit{\theta }}=0\text{at}r=r_1,\overline{\mathit{\theta }}=1\text{at}r=r_2,$$

(12)

$$\mathit{\sigma }=0\text{at}r=r_1,\mathit{\sigma }=1\text{at}r=r_2.$$

(13)

Solution of the problem

We use homotopy perturbation method (He 2006; Rafiq et al. 2010; Saadatmandi et al. 2009) to solve the above non-linear, non-homogeneous and coupled partial differential equations (7)–(9). The deformation equations for the given problems are described as:

$$(1-q)\left(\mathcal{L}\left[\tilde{u}\right]-\mathcal{L}\left[{\tilde{u}}_0\right]\right)+q\left(\mathcal{L}\left[\tilde{u}\right]+\frac{1}{r^2}\frac{{\mathit{\partial }}^2\tilde{u}}{\mathit{\partial }{\mathit{\theta }}^2}+B_r\mathrm{\Omega }+G_r\mathrm{\Theta }-\frac{\tilde{u}}{k}-\frac{\mathit{\partial }p}{\mathit{\partial }z}\right)=0,$$

(14)

$$\begin{array}{cc}& (1-q)\left(\mathcal{L}\left[\mathrm{\Theta }\right]-\mathcal{L}\left[{\tilde{\mathit{\theta }}}_0\right]\right)\hfill \\ & +q\left(\mathcal{L}\left[\mathrm{\Theta }\right]+\frac{1}{r^2}\frac{{\mathit{\partial }}^2\mathrm{\Theta }}{\mathit{\partial }{\mathit{\theta }}^2}+N_b\left(\frac{\mathit{\partial }\mathrm{\Theta }}{\mathit{\partial }r}\frac{\mathit{\partial }\mathrm{\Omega }}{\mathit{\partial }r}\left.+\frac{1}{r^2}\frac{\mathit{\partial }\mathrm{\Theta }}{\mathit{\partial }\mathit{\theta }}\frac{\mathit{\partial }\mathrm{\Omega }}{\mathit{\partial }\mathit{\theta }}\right)\right.\right.\hfill \\ & \left.+N_t\left({\left(\frac{\mathit{\partial }\mathrm{\Theta }}{\mathit{\partial }r}\right)}^2+\frac{1}{r^2}{\left(\frac{\mathit{\partial }\mathrm{\Theta }}{\mathit{\partial }\mathit{\theta }}\right)}^2\right)\right)=0,\hfill \end{array}$$

(15)

$$\begin{array}{cc}& (1-q)\left(\mathcal{L}\left[\mathrm{\Omega }\right]-\mathcal{L}\left[{\overline{\mathit{\sigma }}}_0\right]\right)\hfill \\ & +q\left(\mathcal{L}\left[\mathrm{\Omega }\right]+\frac{1}{r^2}\frac{{\mathit{\partial }}^2\mathrm{\Omega }}{\mathit{\partial }{\mathit{\theta }}^2}+\frac{N_t}{N_b}\left(\frac{{\mathit{\partial }}^2\mathrm{\Theta }}{\mathit{\partial }{r}^2}+\frac{1}{r}\frac{\mathit{\partial }\mathrm{\Theta }}{\mathit{\partial }r}+\frac{1}{r^2}\frac{{\mathit{\partial }}^2\mathrm{\Theta }}{\mathit{\partial }{\mathit{\theta }}^2}\right)\right)\hfill \\ & =0.\hfill \end{array}$$

(16)

We assume $\mathcal{L}=\frac{1}{r}\frac{\mathit{\partial }}{\mathit{\partial }r}\left(r\frac{\mathit{\partial }}{\mathit{\partial }r}\right)$ as the linear operator. Let us consider the following initial guesses for $u,\overline{\mathit{\theta }}$ andσ

$${\tilde{u}}_0=\frac{V\left(log(r)-log(r_2)\right)}{log(r_1)-log(r_2)},{\tilde{\mathit{\theta }}}_0=\frac{log(r_1)-log(r)}{log(r_1)-log(r_2)}={\tilde{\mathit{\sigma }}}_0.$$

(17)

Now we describe

$$\begin{array}{c}\hfill \tilde{u}(r,\mathit{\theta },z,q)=u_0+q{u}_1+\cdots \\ \hfill \mathrm{\Theta }(r,\mathit{\theta },z,q)={\overline{\mathit{\theta }}}_0+q{\overline{\mathit{\theta }}}_1+\cdots \\ \hfill \mathrm{\Omega }(r,\mathit{\theta },z,q)={\mathit{\sigma }}_0+q{\mathit{\sigma }}_1+\cdots \end{array}$$

(18)

Utilizing the perturbation on embedding parameter q, we have the following system of equations.

Zeroth order system

$$\mathcal{L}\left[u_0\right]-\mathcal{L}\left[{\tilde{u}}_0\right]=0,$$

(19)

$$u_0=0,\text{at}r=r_2,u_0=V,\text{at}r=r_1,$$

(20)

$$\mathcal{L}\left[{\overline{\mathit{\theta }}}_0\right]-\mathcal{L}\left[{\tilde{\mathit{\theta }}}_0\right]=0,$$

(21)

$${\overline{\mathit{\theta }}}_0=1,\text{at}r=r_2,{\overline{\mathit{\theta }}}_0=0,\text{at}r=r_1,$$

(22)

$$\mathcal{L}\left[{\mathit{\sigma }}_0\right]-\mathcal{L}\left[{\tilde{\mathit{\sigma }}}_0\right]=0,$$

(23)

$${\mathit{\sigma }}_0=1,\text{at}r=r_2,{\mathit{\sigma }}_0=0,\text{at}r=r_1.$$

(24)

First order system

$$\frac{1}{r}\frac{\mathit{\partial }}{\mathit{\partial }r}\left(r\frac{\mathit{\partial }{u}_1}{\mathit{\partial }r}\right)+\frac{1}{r^2}\frac{{\mathit{\partial }}^2{u}_0}{\mathit{\partial }{\mathit{\theta }}^2}+B_r{\mathit{\sigma }}_0+G_r{\overline{\mathit{\theta }}}_0-\frac{u_0}{k}=\frac{\mathit{\partial }p}{\mathit{\partial }z},$$

(25)

$$u_1=0,\text{at}r=r_2,u_1=0,\text{at}r=r_1,$$

(26)

$$\frac{1}{r}\frac{\mathit{\partial }}{\mathit{\partial }r}\left(r\frac{\mathit{\partial }{\overline{\mathit{\theta }}}_1}{\mathit{\partial }r}\right)+\frac{1}{r^2}\frac{{\mathit{\partial }}^2{\overline{\mathit{\theta }}}_0}{\mathit{\partial }{\mathit{\theta }}^2}+N_b\left(\frac{\mathit{\partial }{\overline{\mathit{\theta }}}_0}{\mathit{\partial }r}\frac{\mathit{\partial }{\mathit{\sigma }}_0}{\mathit{\partial }r}+\frac{1}{r^2}\frac{\mathit{\partial }{\overline{\mathit{\theta }}}_0}{\mathit{\partial }\mathit{\theta }}\frac{\mathit{\partial }{\mathit{\sigma }}_0}{\mathit{\partial }\mathit{\theta }}\right)+N_t\left({\left(\frac{\mathit{\partial }{\overline{\mathit{\theta }}}_0}{\mathit{\partial }r}\right)}^2+\frac{1}{r^2}{\left(\frac{\mathit{\partial }{\overline{\mathit{\theta }}}_0}{\mathit{\partial }\mathit{\theta }}\right)}^2\right)=0,$$

(27)

$${\overline{\mathit{\theta }}}_1=0,\text{at}r=r_2,{\overline{\mathit{\theta }}}_1=0,\text{at}r=r_1,$$

(28)

$$\frac{1}{r}\frac{\mathit{\partial }}{\mathit{\partial }r}\left(r\frac{\mathit{\partial }{\mathit{\sigma }}_1}{\mathit{\partial }r}\right)+\frac{1}{r^2}\frac{{\mathit{\partial }}^2{\mathit{\sigma }}_0}{\mathit{\partial }{\mathit{\theta }}^2}+\frac{N_t}{N_b}\left(\frac{{\mathit{\partial }}^2{\overline{\mathit{\theta }}}_0}{\mathit{\partial }{r}^2}+\frac{1}{r}\frac{\mathit{\partial }{\overline{\mathit{\theta }}}_0}{\mathit{\partial }r}+\frac{1}{r^2}\frac{{\mathit{\partial }}^2{\overline{\mathit{\theta }}}_0}{\mathit{\partial }{\mathit{\theta }}^2}\right)=0,$$

(29)

$${\mathit{\sigma }}_1=1,\text{at}r=r_2,{\mathit{\sigma }}_1=0,\text{at}r=r_1.$$

(30)

According to the scheme of HPM, the final solutions (using $q\to 1$in Eq. 18)for velocity u, temperature $\overline{\mathit{\theta }}$ and concentrationσ can be directly written as:

$$\begin{array}{cc}\hfill u=& \frac{Vlog\left(r/r_2\right)}{log\left(r_1/r_2\right)}+\frac{1}{8k{r}_1^2{r}_{29}^3}\left(6B_{r}k{r}_{11}+6G_{r}k{r}_{11}+4B_{r}k{r}_{22}-4k\frac{\mathit{\partial }p}{\mathit{\partial }z}{r}_{22}+4G_{r}k{r}_{22}\right.\hfill \\ & +4k\frac{\mathit{\partial }p}{\mathit{\partial }z}{r}^2{r}_{23}-4B_{r}k{r}^2{r}_{24}-4G_{r}k{r}^2{r}_{24}+6B_{r}k{r}_{25}+6G_{r}k{r}_{25}+6r_{11}V+4r^2{r}_{23}V-4r^2\hfill \\ & r_{24}V+6r_{25}V-12B_{r}k{r}^2{r}_{12}{\mathit{\delta }}^2-12G_{r}k{r}^2{r}_{12}{\mathit{\delta }}^2+4B_{r}k{r}^2{r}_{15}{\mathit{\delta }}^2+4G_{r}k{r}^2{r}_{15}{\mathit{\delta }}^2-12k\frac{\mathit{\partial }p}{\mathit{\partial }z}\hfill \\ & r^2{r}_{15}{\mathit{\delta }}^2-12r^2{r}_{12}V{\mathit{\delta }}^2-8r^2{r}_{15}V{\mathit{\delta }}^2-\frac{1}{4(r_2-\mathit{\delta })}\left(16B_{r}k{r}_{13}+16G_{r}k{r}_{13}-16k\frac{\mathit{\partial }p}{\mathit{\partial }z}{r}_{13}-\right.\hfill \\ & 16B_{r}k{r}_{17}-16G_{r}k{r}_{17}+16k\frac{\mathit{\partial }p}{\mathit{\partial }z}{r}_{17}+16k\frac{\mathit{\partial }p}{\mathit{\partial }z}{r}_{14}{r}_2-16k\frac{\mathit{\partial }p}{\mathit{\partial }z}{r}_{18}{r}_2-24B_{r}k{r}_2^2{r}_{20}-24G_{r}k\hfill \\ & r_2^2{r}_{20}+24B_{r}k{r}_2{r}_{21}+24G_{r}k{r}_2{r}_{21}+24B_{r}k{r}_2{r}_{30}+24G_{r}k{r}_2{r}_{30}-24B_{r}k{r}_2^2{r}_{31}-24G_{r}k{r}_2^2\hfill \\ & r_{31}+16r_{14}{r}_{2}V-16r_{18}{r}_{2}V-24r_2^2{r}_{20}V+24r_2{r}_{21}V+24r_2{r}_{30}V-24r_2^2{r}_{31}V+48B_{r}k{r}_{12}{r}_2^2\hfill \\ & {\mathit{\delta }}^3+48G_{r}k{r}_{12}{r}_2^2{\mathit{\delta }}^3-48B_{r}k{r}_{15}{r}_2^2{\mathit{\delta }}^3-48G_{r}k{r}_{15}{r}_2^2{\mathit{\delta }}^3+48k\frac{\mathit{\partial }p}{\mathit{\partial }z}{r}_{15}{r}_2^2{\mathit{\delta }}^3+48B_{r}k{r}_{16}{r}_2^2{\mathit{\delta }}^3+\hfill \\ & 48G_{r}k{r}_{16}{r}_2^2{\mathit{\delta }}^3-48k\frac{\mathit{\partial }p}{\mathit{\partial }z}{r}_{16}{r}_2^2{\mathit{\delta }}^3+48r_{12}{r}_2^{2}V{\mathit{\delta }}^3-48B_{r}k{r}_{12}{r}_2{\mathit{\delta }}^4-48G_{r}k{r}_{12}{r}_2{\mathit{\delta }}^4-48k\frac{\mathit{\partial }p}{\mathit{\partial }z}\hfill \\ & r_{15}{r}_2{\mathit{\delta }}^4+\left.48k\frac{\mathit{\partial }p}{\mathit{\partial }z}{r}_{16}{r}_2{\mathit{\delta }}^4-48r_{12}{r}_{2}V{\mathit{\delta }}^4-48r_{15}{r}_{2}V{\mathit{\delta }}^4+48r_{16}{r}_{2}V{\mathit{\delta }}^4\right)-4B_{r}k{r}_{11}logr-\hfill \\ & 4G_{r}k{r}_{11}logr-4r_{11}Vlogr+8B_{r}k{r}^2{r}_{12}{\mathit{\delta }}^{2}logr+8G_{r}k{r}^2{r}_{12}{\mathit{\delta }}^{2}logr+8r^2{r}_{12}V{\mathit{\delta }}^2\hfill \\ & logr+\frac{1}{4(r_2-\mathit{\delta })}r{r}_{29}\left(16k\frac{\mathit{\partial }p}{\mathit{\partial }z}{r}_{21}\right.+16B_{r}k{r}_2^2{r}_{26}+16G_{r}k{r}_2^2{r}_{26}-16k\frac{\mathit{\partial }p}{\mathit{\partial }z}{r}_2^2{r}_{26}+24\hfill \\ & B_{r}k{r}_{27}+24G_{r}k{r}_{27}-24B_{r}k{r}_2^2{r}_{28}-24G_{r}k{r}_2^2{r}_{28}+16k\frac{\mathit{\partial }p}{\mathit{\partial }z}{r}_{30}+16B_{r}k{r}_2^2{r}_{32}+16G_{r}k\hfill \\ & r_2^2{r}_{32}-16k\frac{\mathit{\partial }p}{\mathit{\partial }z}{r}_2^2{r}_{32}-24B_{r}k{r}_{33}-24G_{r}k{r}_{33}+16r_{21}V+24r_{27}V-24r_2^2{r}_{28}V+16r_{30}\hfill \\ & V-24r_{33}V-32B_{r}k{r}_{12}{r}_2^2{\mathit{\delta }}^2-32G_{r}k{r}_{12}{r}_2^2{\mathit{\delta }}^2-32r_{12}V{\mathit{\delta }}^4+24B_{r}k{r}_2^2{\mathit{\delta }}^{2}log{r}_1+24G_{r}k{r}_2^2{\mathit{\delta }}^2\hfill \\ & log{r}_1+\left.32k\frac{\mathit{\partial }p}{\mathit{\partial }z}{r}_{12}{r}_2^2{\mathit{\delta }}^2+24r_2^{2}V{\mathit{\delta }}^{2}log{r}_1\right)-8B_{r}k{r}_{11}log{r}_2-8G_{r}k{r}_{11}log{r}_2+\left.12k\frac{\mathit{\partial }p}{\mathit{\partial }z}{r}_{11}log{r}_2+4r_{11}Vlog{r}_2\right),\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill \overline{\mathit{\theta }}=& \frac{log\left(r_1/r\right)}{log\left(r_1/r_2\right)}-\left(log\left(\frac{r}{r_2}\right)log\left(\frac{r}{r_1}\right)\left(\left(N_b+N_t\right){\mathit{ϵ}}^2{\left(logr\right)}^2\right.\right.+\left(4-3N_b-3N_t\right){\mathit{ϵ}}^{2}log\left(r\right)log\left(r_2\right)+\hfill \\ & 12\left(N_b+N_t\right){\mathit{\delta }}^2{\left(log{r}_2\right)}^2+\left(9N_b+9N_t-8-4logr\right){\mathit{ϵ}}^2{\left(log{r}_2\right)}^2+8{\mathit{ϵ}}^{2}log{\left(r_2\right)}^3+4\mathit{\delta }\mathit{ϵ}cos\mathit{\theta }\hfill \\ & {\left(log\left(\frac{r_2}{r_1}\right)\right)}^2(6N_b+6N_t-log\left(r\right)+2log\left(r_2\right)-log\left(r_1\right))-4{\mathit{ϵ}}^{2}log\left(r\right)log\left(\mathit{\delta }+\mathit{ϵ}cos\mathit{\theta }\right)+\left(N_b+N_t\right)\hfill \\ & {\mathit{ϵ}}^{2}logrlog{r}_1-24\left(N_b+N_t\right){\mathit{\delta }}^{2}log\left(r_2\right)log\left(r_1\right)+\left(12-15N_b-15N_t\right){\mathit{ϵ}}^{2}log\left(r_2\right)log\left(r_1\right)+\hfill \\ & \left(8logr-20log{r}_2\right){\mathit{ϵ}}^{2}log\left(r\right)log\left(r_2\right)log\left(r_1\right)+12\left(N_b+N_t\right){\mathit{\delta }}^2{\left(log\left(r_1\right)\right)}^2+\left(7N_b+7N_t-4\right){\mathit{ϵ}}^2\hfill \\ & {\left(log\left(r_1\right)\right)}^2+\left(16log{r}_2\right.\left.-4logr{r}_1\right){\mathit{ϵ}}^2{\left(log\left(r_1\right)\right)}^2{\mathit{ϵ}}^{2}cos2\mathit{\theta }{\left((N_b+N_t)\left(logr\right)\right.}^2-(8+3N_b+3N_t)\hfill \\ & {\left(log{r}_2\right)}^2+3(4+3N_b+3N_t)log{r}_{2}log{r}_1-(4+5N_b+5N_t){\left(log\left(r_1\right)\right)}^2+log\left(r\right)((4-3N_b-3N_t)\hfill \\ & log\left(r_2\right)+(-4+N_b+N_t)\left(log\left(r_1\right)\right)))))/\left(24{(r_1)}^2\left.{\left(log\left(\frac{r_2}{r_1}\right)\right)}^4\right)\right.,\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill \mathit{\sigma }=& \frac{1}{6N_b{r}_1{}^2{(log{r}_2-log{r}_1)}^3}\left((N_b+N_t)\mathit{ϵ}(logr-log{r}_2)\right.\left(\mathit{ϵ}\left(cos2\mathit{\theta }-1\right)+\right.(\mathit{ϵ}+\mathit{\delta }cos\mathit{\theta })\hfill \\ & (log{r}_2-log{r}_1))(logr-log{r}_1)(logr-2log{r}_2+log{r}_1))+\frac{log\left(r_1/r\right)}{log\left(r_1/r_2\right)}.\hfill \end{array}$$

(33)

The instantaneous volume flow rate $\overline{Q}$ is given by:

$$\overline{Q}=2\mathit{\pi }\underset{r_1}{\overset{r_2}{\int }}ru\mathrm{d}r.$$

(34)

The mean volume flow rate Q over one period is given as (Mekheimer et al. 2013):

$$Q(z,t)=\frac{\overline{Q}}{\mathit{\pi }}-\frac{{\mathit{\varphi }}^2}{2}+2\mathit{\varphi }cos\left[2\mathit{\pi }\left(z-t\right)\right]+{\mathit{\varphi }}^2{cos}^2[2\mathit{\pi }\left(z-t\right)].$$

(35)

Now we can evaluate pressure gradient∂p/∂z by solving Eqs. (34) and (35) and is elaborated as:

$$\begin{array}{cc}\hfill \frac{\mathit{\partial }p}{\mathit{\partial }z}=& \left(-24B_{r}k\mathit{\pi }{r}_1^3{r}_{12}-24G_{r}k\mathit{\pi }{r}_1^3{r}_{12}+21B_{r}k\mathit{\pi }{r}_1^4{r}_{12}+21G_{r}k\mathit{\pi }{r}_1^4{r}_{12}-96kQ{r}_{15}+12B_{r}k\mathit{\pi }{r}_1^4{r}_{15}\right.\hfill \\ & +12G_{r}k\mathit{\pi }{r}_1^4{r}_{15}-12B_{r}k\mathit{\pi }{r}_1^4{r}_{16}-12G_{r}k\mathit{\pi }{r}_1^4{r}_{16}+36B_{r}k\mathit{\pi }{r}_1^2{r}_{12}{r}_2+36G_{r}k\mathit{\pi }{r}_1^2{r}_{12}{r}_2-21B_r\hfill \\ & k\mathit{\pi }{r}_1^4{r}_{12}{r}_2-21G_{r}k\mathit{\pi }{r}_1^4{r}_{12}{r}_2+96kQ{r}_{15}{r}_2-12B_{r}k\mathit{\pi }{r}_1^4{r}_{15}{r}_2-12G_{r}k\mathit{\pi }{r}_1^4{r}_{15}{r}_2+12B_{r}k\mathit{\pi }{r}_1^4\hfill \\ & r_{16}{r}_2+12G_{r}k\mathit{\pi }{r}_1^4{r}_{16}{r}_2-36B_{r}k\mathit{\pi }{r}_1^2{r}_{12}{r}_2^2-36G_{r}k\mathit{\pi }{r}_1^2{r}_{12}{r}_2^2+24B_{r}k\mathit{\pi }{r}_1^3{r}_{12}{r}_2^2+24G_{r}k\mathit{\pi }{r}_1^3\hfill \\ & r_{12}{r}_2^2+24B_{r}k\mathit{\pi }{r}_1^2{r}_{15}{r}_2^2+24G_{r}k\mathit{\pi }{r}_1^2{r}_{15}{r}_2^2-16B_{r}k\mathit{\pi }{r}_1^3{r}_{15}{r}_2^2-16G_{r}k\mathit{\pi }{r}_1^3{r}_{15}{r}_2^2-12B_{r}k\mathit{\pi }{r}_{12}\hfill \\ & r_2^3-12G_{r}k\mathit{\pi }{r}_{12}{r}_2^3+15B_{r}k\mathit{\pi }{r}_{12}{r}_2^4+15G_{r}k\mathit{\pi }{r}_{12}{r}_2^4-12B_{r}k\mathit{\pi }{r}_{15}{r}_2^4-12G_{r}k\mathit{\pi }{r}_{15}{r}_2^4-3B_{r}k\mathit{\pi }\hfill \\ & r_{12}{r}_2^5-3G_{r}k\mathit{\pi }{r}_{12}{r}_2^5+4B_{r}k\mathit{\pi }{r}_{15}{r}_2^5+4G_{r}k\mathit{\pi }{r}_{15}{r}_2^5-12k\mathit{\pi }{r}_1^2{r}_{34}+12k\mathit{\pi }{r}_1^2{r}_2{r}_{34}+12k\mathit{\pi }{r}_2^2{r}_{34}\hfill \\ & -12k\mathit{\pi }{r}_2^3{r}_{34}+24k\mathit{\pi }{r}_1^2{r}_{35}-24k\mathit{\pi }{r}_1^2{r}_2{r}_{35}+24B_{r}k\mathit{\pi }{r}_{36}+24G_{r}k\mathit{\pi }{r}_{36}-24B_{r}k\mathit{\pi }{r}_2^2{r}_{36}-24\hfill \\ & G_{r}k\mathit{\pi }{r}_2^2{r}_{36}+24k\mathit{\pi }{r}_1^2{r}_{37}-24k\mathit{\pi }{r}_1^2{r}_2{r}_{37}-36B_{r}k\mathit{\pi }{r}_1^2{r}_{38}-36G_{r}k\mathit{\pi }{r}_1^2{r}_{38}+21B_{r}k\mathit{\pi }{r}_1^4{r}_{38}+21\hfill \\ & G_{r}k\mathit{\pi }{r}_1^4{r}_{38}+12k\mathit{\pi }{r}_1^2{r}_{39}-12k\mathit{\pi }{r}_1^2{r}_2{r}_{39}-12k\mathit{\pi }{r}_2^2{r}_{39}+12k\mathit{\pi }{r}_2^3{r}_{39}-21B_{r}k\mathit{\pi }{r}_{40}-21G_{r}k\mathit{\pi }{r}_{40}\hfill \\ & +36B_{r}k\mathit{\pi }{r}_1^2{r}_{41}+36G_{r}k\mathit{\pi }{r}_1^2{r}_{41}+12B_{r}k\mathit{\pi }{r}_{42}+12G_{r}k\mathit{\pi }{r}_{42}-15B_{r}k\mathit{\pi }{r}_{43}-15G_{r}k\mathit{\pi }{r}_{43}+3B_r\hfill \\ & k\mathit{\pi }{r}_{44}+3G_{r}k\mathit{\pi }{r}_{44}-96kQ{r}_{46}-24B_{r}k\mathit{\pi }{r}_1^2{r}_{47}-24G_{r}k\mathit{\pi }{r}_1^2{r}_{47}+16B_{r}k\mathit{\pi }{r}_1^3{r}_{47}+16G_{r}k\mathit{\pi }{r}_1^3{r}_{47}\hfill \\ & +12B_{r}k\mathit{\pi }{r}_{48}+12G_{r}k\mathit{\pi }{r}_{48}-4B_{r}k\mathit{\pi }{r}_{49}-4G_{r}k\mathit{\pi }{r}_{49}-72k\mathit{\pi }{r}_1^2{r}_{50}+16\mathit{\pi }{r}_1^3{r}_{50}+16k\mathit{\pi }{r}_1^3{r}_{50}-\hfill \\ & 12\mathit{\pi }{r}_1^4{r}_{50}+8\mathit{\pi }{r}_2^3{r}_{50}+8k\mathit{\pi }{r}_2^3{r}_{50}-48k\mathit{\pi }{r}_1^2{r}_{12}V-24\mathit{\pi }{r}_1^3{r}_{12}V+32k\mathit{\pi }{r}_1^3{r}_{12}V+21\mathit{\pi }{r}_1^4{r}_{12}V+\hfill \\ & 120k\mathit{\pi }{r}_1^2{r}_{15}V-16\mathit{\pi }{r}_1^3{r}_{15}V-16k\mathit{\pi }{r}_1^3{r}_{15}V+24\mathit{\pi }{r}_1^4{r}_{15}V-72k\mathit{\pi }{r}_1^2{r}_{16}V-12\mathit{\pi }{r}_1^4{r}_{16}V+36\mathit{\pi }{r}_1^2\hfill \\ & r_{12}{r}_{2}V-21\mathit{\pi }{r}_1^4{r}_{12}{r}_{2}V+24\mathit{\pi }{r}_1^2{r}_{15}{r}_{2}V-96k\mathit{\pi }{r}_1^2{r}_{15}{r}_{2}V-24\mathit{\pi }{r}_1^4{r}_{15}{r}_{2}V+72k\mathit{\pi }{r}_1^2{r}_{16}{r}_{2}V+12\hfill \\ & \mathit{\pi }{r}_1^4{r}_{16}{r}_{2}V-36\mathit{\pi }{r}_1^2{r}_{12}{r}_2^{2}V+24\mathit{\pi }{r}_1^3{r}_{12}{r}_2^{2}V-12\mathit{\pi }{r}_{12}{r}_2^{3}V+16k\mathit{\pi }{r}_{12}{r}_2^{3}V-8\mathit{\pi }{r}_{15}{r}_2^{3}V-8k\mathit{\pi }{r}_{15}\hfill \\ & r_2^{3}V+15\mathit{\pi }{r}_{12}{r}_2^{4}V-3\mathit{\pi }{r}_{12}{r}_2^{5}V+24\mathit{\pi }{r}_{36}V-32k\mathit{\pi }{r}_{36}V-24\mathit{\pi }{r}_2^2{r}_{36}V-36\mathit{\pi }{r}_1^2{r}_{38}V+48k\mathit{\pi }{r}_1^2{r}_{38}\hfill \\ & V21\mathit{\pi }{r}_1^4{r}_{38}V-21\mathit{\pi }{r}_{40}V+24k\mathit{\pi }{r}_{41}V+36\mathit{\pi }{r}_1^2{r}_{41}V+12\mathit{\pi }{r}_{42}V-40k\mathit{\pi }{r}_{42}V-15\mathit{\pi }{r}_{43}V+3\mathit{\pi }{r}_{44}\hfill \\ & V-24\mathit{\pi }{r}_1^2{r}_{46}V+48k\mathit{\pi }{r}_1^2{r}_{46}V+12\mathit{\pi }{r}_1^4{r}_{46}V+192k\mathit{\pi }(r_2-1)r_{45}\mathit{\varphi }cos2\mathit{\pi }(z-t)+48k\mathit{\pi }(r_2-1)\hfill \\ & r_{45}{\mathit{\varphi }}^{2}cos4\mathit{\pi }(z-t)+96kQ\left.log{r}_2^3\right)/\left(4k\mathit{\pi }{(r_1-r_2)}^2\right.(-1+r_2)\left(3r_1^2+2r_1(-2+r_2)+(-2+r_2)r_2\right)\hfill \\ & \left.log\frac{r_1}{r_2}{\left(log{r}_2\right)}^2\right).\hfill \end{array}$$

(36)

The parameters $(r_{ij},i=1,2,3,4,5,j=0,1,2,3,...,9)$ appeared in the above expressions are defined as follows:

$$\begin{array}{cc}\hfill r_{11}& =r^2{\mathit{\delta }}^2{(log{r}_1)}^2,r_{12}=log{r}_1{r}_2,r_{13}=r_2^2{\mathit{\delta }}^3{(log{r}_2)}^3,r_{14}={\mathit{\delta }}^4{(log{r}_2)}^3,r_{15}=log{r}_1{(log{r}_2)}^2,\hfill \\ \hfill r_{16}=& {(log{r}_1)}^{2}log{r}_2,r_{17}=r_2^2{\mathit{\delta }}^3{(log{r}_1)}^3,r_{18}={\mathit{\delta }}^4{(log{r}_1)}^3,r_{19}={\mathit{\delta }}^3{(log{r}_1)}^3,r_{20}={\mathit{\delta }}^3{(log{r}_2)}^2,\hfill \\ \hfill r_{21}=& {\mathit{\delta }}^4{(log{r}_2)}^2,r_{22}=r^2{\mathit{\delta }}^2{(log{r}_1)}^3,r_{23}={\mathit{\delta }}^2{(log{r}_2)}^3,r_{24}={\mathit{\delta }}^{2}logr{(log{r}_2)}^2,r_{25}=r^2{\mathit{\delta }}^2{(log{r}_2)}^2,\hfill \\ \hfill r_{26}=& {\mathit{\delta }}^2{(log{r}_2)}^2,r_{27}={\mathit{\delta }}^{4}log{r}_2,r_{28}={\mathit{\delta }}^{2}log{r}_2,r_{29}=log\left(\frac{r_2}{r_1}\right),r_{30}={\mathit{\delta }}^4{(log{r}_1)}^2,r_{31}={\mathit{\delta }}^3{(log{r}_1)}^2,\hfill \\ \hfill r_{32}=& {\mathit{\delta }}^2{(log{r}_1)}^2,r_{33}={\mathit{\delta }}^{4}log{r}_1,r_{34}=Vlog{r}_1,r_{35}=V{(log{r}_1)}^2,r_{36}=r_1^3{(log{r}_2)}^2,r_{37}=V{(log{r}_1)}^3,\hfill \\ \hfill r_{38}=& r_2{(log{r}_2)}^2,r_{39}=Vlog{r}_2,r_{40}=r_1^4{(log{r}_2)}^2,r_{41}=r_2^2{(log{r}_2)}^2,r_{42}=r_2^3{(log{r}_2)}^2,r_{43}=r_2^4{(log{r}_2)}^2,\hfill \\ \hfill r_{44}=& r_2^5{(log{r}_2)}^2,r_{45}=\left(log\frac{r_1}{r_2}\right){(log{r}_2)}^2,r_{46}=r_2{(log{r}_2)}^3,r_{47}=r_2^2{(log{r}_2)}^3,r_{48}=r_2^4{(log{r}_2)}^3,\hfill \\ \hfill r_{49}=& r_2^5{(log{r}_2)}^3,r_{50}=V{(log{r}_2)}^3.\hfill \end{array}$$

The pressure rise $\mathrm{\Delta }p$ in non-dimensional form is defined as:

$$\mathrm{\Delta }p=\underset{0}{\overset{1}{\int }}\frac{\mathit{\partial }p}{\mathit{\partial }z}\mathrm{d}z.$$

(37)

It is found by numerical integration using the mathematical software Mathematica.

Results and discussions

To establish the nanofluid characteristics through a porous space, we analyzed the unsteady and incompressible peristaltic flow of nanofluid between two eccentric tubes having different radii enclosing the porous medium. Analytical solutions are carried out with the help of homotopy perturbation technique. The expression for pressure rise is evaluated numerically to examine peristaltic pumping whose variation can be observed in Table 1. All the parameters in the problem are made dimensionless by suitable transformations. In the present section, we discussed the physical behavior of all the pertinent parameters on the distributions of velocity, temperature and nanoparticle concentration. Figures 2, 3, 4and 5 represent the pressure rise variation for various emerging parameters. The pressure gradient profiles are displayed in Figs. 6, 7, 8 and 9. The effects of various physical quantities on the profiles of velocity, temperature and nanoparticles are shown in Figs. 10, 11, 12, 13, 14, 15 and 16. Trapping bolus behavior of the intestinal flow is described through streamlines, as shown in Figs. 17, 18 and19.

Table 1 Variation of pressure rise $\mathrm{\Delta }p$ for fixed $\mathit{\theta }=0.8,\mathit{\delta }=0.1,B_r=0.2,G_r=0.1,t=0.3,N_b=0.5,N_t=0.2,\mathit{ϵ}=0.1,V=0.3$

Fig. 2

Variation of pressure rise $\mathrm{\Delta }p$ withϕ and G _r for fixed $\mathit{\theta }=0.8,\mathit{\delta }=0.1,B_r=0.1,k=0.5,t=0.3,N_b=0.5,N_t=0.2,\mathit{ϵ}=0.3,V=0.1$

Fig. 3

Variation of pressure rise $\mathrm{\Delta }p$ withϕ and B _r for fixed $\mathit{\theta }=0.8,\mathit{\delta }=0.1,G_r=1,N_b=0.1,k=0.5,t=0.3,N_t=0.5,\mathit{ϵ}=0.3,V=0.1$

Fig. 4

Variation of pressure rise $\mathrm{\Delta }p$ withϕ and k for fixed $\mathit{\theta }=0.8,\mathit{\delta }=0.1,G_r=0.1,N_b=0.1,B_r=0.1,t=0.3,N_t=0.5,\mathit{ϵ}=0.3,V=0.1$

Fig. 5

Variation of pressure rise $\mathrm{\Delta }p$ withϕ andδ for fixed $\mathit{\theta }=0.8,B_r=0.1,G_r=2,N_b=0.1,k=0.5,t=0.3,N_t=0.5,\mathit{ϵ}=0.3,V=0.2$

Fig. 6

Variation of pressure gradient dp/dz with k and Q for fixed $\mathit{ϵ}=0.3,t=0.01,B_r=0.3,\mathit{\delta }=0.1,V=0.1,\mathit{\theta }=0.8,\mathit{\varphi }=0.1,G_r=0.5,N_b=0.1,N_t=0.5$

Fig. 7

Variation of pressure gradient dp/dz with B _r and G _r for fixed $\mathit{ϵ}=0.3,t=0.01,k=0.5,\mathit{\delta }=0.1,V=0.1,\mathit{\theta }=0.8,\mathit{\varphi }=0.1,Q=2,N_b=0.1,N_t=0.5$

Fig. 8

Variation of pressure gradient dp/dz with $\mathit{ϵ}$ and V for fixed k = 0.5, t = 0.01, B _r  = 0.1, δ = 0.1, Q = 2, θ = 0.8, ϕ = 0.1, G _r  = 1, N _b  = 0.1, N _t  = 0.5

Fig. 9

Variation of pressure gradient dp/dz withϕ andδ for fixed $\mathit{ϵ}=0.3,t=0.01,B_r=0.1,Q=2,V=0.2,\mathit{\theta }=0.8,k=0.5,G_r=0.2,N_b=0.1,N_t=0.5$

Fig. 10

Variation of velocity profile u with k and Q for fixed $\mathit{ϵ}=0.3,N_t=0.5,N_b=0.1,t=0.3,\mathit{\delta }=0.1,B_r=0.3,G_r=1,z=0,V=0.1,\mathit{\theta }=0.8,\mathit{\varphi }=0.1$

Fig. 11

Variation of velocity profile u with G _r and B _r for fixed $\mathit{ϵ}=0.3,N_t=0.5,N_b=0.1,t=0.1,\mathit{\delta }=0.1,k=0.1,Q=2,z=0,V=0.1,\mathit{\theta }=0.8,\mathit{\varphi }=0.1$

Fig. 12

Variation of velocity profile u with $\mathit{ϵ}$ and V for fixed G _r  = 1, N _t  = 0.5, N _b  = 0.1, t = 0.3, δ = 0.1, k = 0.1, Q = 1, z = 0, B _r  = 0.3, θ = 0.8, ϕ = 0.1

Fig. 13

Variation of temperature profile $\overline{\mathit{\theta }}$ with $\mathit{ϵ}$ andϕ for fixedδ = 0.1, t = 0.3, N _b  = 0.4, N _t  = 0.2, z = 0, θ = 0.8, k = 0.1

Fig. 14

Variation of temperature profile $\overline{\mathit{\theta }}$ with N _b and N _t for fixed $\mathit{\delta }=0.1,t=0.3,\mathit{ϵ}=0.1,\mathit{\varphi }=0.1,z=0,\mathit{\theta }=0.8,k=0.1$

Fig. 15

Variation of nanoparticle concentrationσ withϕ and $\mathit{ϵ}$ for fixedδ = 0.1, N _b  = 0.4, N _t  = 0.2, z = 0, θ = 0.8, t = 0.3, k = 0.1

Fig. 16

Variation of nanoparticle concentration σ with N _b and N _t for fixed $\mathit{\delta }=0.1,\mathit{ϵ}=0.1,\mathit{\varphi }=0.1,z=0,\mathit{\theta }=0.8,t=0.3,k=0.1$

Fig. 17

Streamlines for different values of B _r a for B _r  = 0.3, b for B _r  = 0.9, c for B _r  = 2. The other parameters are $\mathit{ϵ}=0.1,V=0.1,t=0.1,k=0.3,\mathit{\theta }=0.8,\mathit{\varphi }=0.1,Q=1,\mathit{\delta }=0.1,N_t=0.5,N_b=0.1,G_r=0.6$

Fig. 18

Streamlines for different values of G _r a for G _r  = 0.6, b for G _r  = 0.9, c for G _r  = 1.5. The other parameters are $\mathit{ϵ}=0.1,V=0.1,t=0.1,k=0.3,\mathit{\theta }=0.8,\mathit{\varphi }=0.1,Q=1,\mathit{\delta }=0.1,N_t=0.5,N_b=0.1,B_r=0.3$

Fig. 19

Streamlines for different values of ka for k = 0.1, b for k = 0.4, c for k = 0.9. The other parameters are $\mathit{ϵ}=0.1,V=0.1,t=0.1,B_r=0.3,\mathit{\theta }=0.8,\mathit{\varphi }=0.1,Q=1,\mathit{\delta }=0.1,N_t=0.5,N_b=0.1,G_r=1$

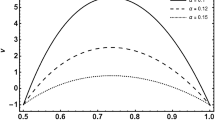
Figure 2 indicates that pressure rise $\mathrm{\Delta }p$ is decreasing with local temperature Grashof number G _r , while it increases for the amplitude ratioϕ in the retrograde pumping $\left(\mathrm{\Delta }p>0,Q<0\right)$ and gives reverse variation in the peristaltic pumping $(\mathrm{\Delta }p>0,Q>0)$ and augmented pumping $(\mathrm{\Delta }p<0,Q>0)$ regions. One can observe from Fig. 3 that pressure rise is increasing with the increase in local nanoparticle Grashof number B _r and peristaltic pumping occurs in the region. $Q\in [0,0.5)$ From Fig. 4, it can be noticed that peristaltic pumping rate is directly varying with the porosity parameter k. Figure 5 suggests that pumping rate is inversely proportional to the radiusδ.

Figure 6 reveals the pressure gradient variation $\frac{\mathrm{d}p}{\mathrm{d}z}$ for the porosity parameter k and flow rate Q. It can be seen that pressure gradient is increasing with the increase in the magnitude of k but opposite relation is observed with the flow rate Q. It is also noted here that pressure gradient curves are varying uniformly with both the porosity of the space and the flow rate. From Fig. 7, we found that there is inverse change in pressure profile with local nanoparticle Grashof number B _r and local temperature Grashof number G _r . Figure 8 implies that increase in the velocity V results in decreasing the amplitude of pressure gradient curves, while there is a direct relation between the distance parameter $\mathit{ϵ}$ and the change in pressure $\frac{\mathrm{d}p}{\mathrm{d}z}$ One can explain the variation of pressure gradient $\frac{\mathrm{d}p}{\mathrm{d}z}$ for the amplitude ratioϕ and the radiusδ from Fig. 9. It is very obvious from this figure that pressure gradient is decreasing with the radiusδ throughout the flow domain but has opposite behavior with the amplitude ratio in the regions $z\in [0,0.3)\cup (0.8,1].$

The profile of velocity u for the parameters k and Q can be analyzed from Fig. 10. It can be observed here that velocity profile is diminished with the increase in porosity parameter k, but it rises up with the flow rate Q. It can be predicted from Fig. 11 that velocity is changing directly with the increase in local nanoparticle Grashof number B _r and local temperature Grashof number G _r and also it remains uniform throughout the flow. Figure 12 denotes that axial velocity distribution u is increasing with the increase in constant velocity V of the inner annulus but for distance parameter $\mathit{ϵ},$ it gives same behavior in the domain $r\in (0.6,1.1)$ and reverse variation in the remaining part.

The variation of temperature distributionθ against the amplitude ratioϕ and distance $\mathit{ϵ}$ is displayed in Fig. 13. It is depicted here that temperature curves are getting lower with $\mathit{ϵ}$ andϕ. Figure 14 concludes that temperature profile is rising up with the increase in Brownian motion parameter N _b and thermophoresis parameter N _t . It can be seen from Fig. 15 that concentration of the nanoparticles gets the same variation with $\mathit{ϵ}$ andϕ as observed in the case of temperature profile. Figure 16 discloses that nanoparticle concentration is increasing with thermophoresis parameter N _t but decreases with Brownian motion parameter N _b .

Trapping bolus phenomenon for local nanoparticle Grashof number B _r is shown in Fig. 17. It is illustrated here that circulating boluses are reduced in the sense of numbers but expanded in size with the increase in B _r . The variation of trapping boluses with the local temperature Grashof number G _r is shown in Fig. 18, and it is observed from this graph that the behavior of boluses is similar to that experienced in the previous figure. However, the influence of porous space on the variation of trapping bolus phenomenon can be examined through Fig. 19 and it is observed that number of boluses increases with the increase in numerical values of porosity parameter k, while boluses are contracted in dimensions, indicating that more porous the medium the bolus reduces its volume to pass through.

Concluding remarks

We have analyzed the mathematical model of peristaltic flow of an unsteady nanofluid between eccentric tubes having porous space. All the results are obtained analytically and discussed the contribution of various emerging parameters graphically. However, the data for the pressure rise are obtained by numerical treatment whose variation has been prescribed in table. Following are the main results evaluated in this investigation.

• 1. The peristaltic pumping rate increases with the increase in local nanoparticle Grashof number B _r and porosity parameter k, but reverse behavior is observed for local temperature Grashof number G _r and radius of the inner tubeδ.

• 2. In peristaltic pumping and copumping regions, pressure rise is inversely proportional to amplitude ratioϕ, while in retrograde pumping it increases withϕ.

• 3. With the increase in values of porosity parameter k, change in pressure becomes large but it diminishes with Q, G _r , δ, B _r , V and $\mathit{ϵ},$ while direct relation is seen between pressure gradient and amplitude ratioϕ at the corners as compared with the central part of the domain.

• 4. The presence of porous medium results in decreasing the velocity of the nanofluid, while the more values of flow rate Q, G _r , B _r and V results in rising up the profile of velocity. However, the distance parameter $\mathit{ϵ}$ reduces the velocity of the flow in left part of the domain and lifts up in the remaining area.

• 5. Temperature distribution is varying inversely with $\mathit{ϵ}$ and ϕ, but direct relation is seen for Brownian motion parameter N _b and thermophoresis parameter N _t .

• 6. The effect of $N_t,\mathit{ϵ}$ andϕ on nanoparticle concentration is similar to that of temperature profile but N _b leaves the inverse impact on the nanoparticle concentration.

• 7. Trapping boluses are reduced in numbers but enlarge their dimensions with the numerical increase in B _r and G _r , but totally opposite scene is measured for the variation of porosity parameter k.