Introduction

Recently, peristalsis has been charmed much consideration due to its significant manufacturing and therapeutic applications, like chyme drive in the intestine, crusade of eggs in the fallopian tube, transport of the sperm in cervical canal, conveyance of bile in the bile duct, transport of cilia, circulation of blood in small blood vessels and in the intra-uterine fluid flow within the uterine cavity. From the time when the first investigation of Latham (1966) was done to discuss the peristaltic mechanism, numerous conjectural and experimental studies have been performed to comprehend the peristaltic feat [see (Shapiro et al. 1969; Zien and Ostrach 1970; Lee and Fung 1971; Srivastava et al. 1983)]. Specifically, to designate peristaltic flow in a symmetric or axisymmetric channels and tubes containing Newtonian or non-Newtonian fluids, many models have been examined by Elshehawey and Mekheimer (1994), Ramachandra and Usha (1995), Mekheimer and Elmaboud (2008), Srinivas and Kothandapani (2009), Srinivas et al (2009) and Nadeem and Akbar (2012b).

The nanofluids are a innovative class of resolutions proposed by scattering nanometer-sized materials (nanoparticles, nanofibers, nanotubes, nanowires, nanorods, nanosheet, or droplets) in base fluids. Peristalsis in connection with nanofluids has application in biomedicines, i.e. cancer treatment radiation therapy, etc. Choi (1995) testified that an advanced technique for mending heat transfer is by using nanoscale particles in the base fluid. Further, Choi et al. (1995) showed that the accumulation of a small amount (<1 % by volume) of nanoparticles to conformist heat transfer fluids increased the thermal conductivity of the fluid up to about two times. After Choi's (1995) first experiment on nanofluid, this topic has become quite interesting to the readers and researchers, including Buongiorno (2006), Khanafer et al (2003), Das et al. (2003), Nield and Kuznetsov (2009), Kuznetsov and Nield (2010), Nield and Kuznetsov (2011), Akbar et al (2012a, b) and Akbar and Nadeem (2011, 2012a).

They emphasis on Ag–water and Cu–water nanofluids, and the properties of the nanoparticles volume fraction on the flow and heat transfer distinctiveness below the possessions of current resistance and temperature reliant inner heat invention or consolidation. Heat and mass transport inspection for boundary layer stagnation point flow in excess of a stretching spread in a porous medium soaked by a nanofluid with internal heat generation/absorption and suction/blowing is explored by Hamad and Ferdows (2012a). Very recently in another article, Hamad and Ferdows (2012b) studied the boundary layer flow and heat transfer in a viscous fluid encompassing metallic nanoparticles over a nonlinear stretching sheet. According to Hamad and Ferdows (2012b) the significantly intensifying the thermal conductivity of fluids by buildup very small quantities of composed tinny or metallic oxide nanoparticles (Cu, CuO, Al2O3) to the fluid, or instead using nanotube deferrals skirmishes with the classical theories of approximating the effective thermal conductivity of suspensions.

Nanotubes are affiliates of the fullerene structural family. Their name arises from their long, resonating edifice with the ramparts formed by one-atom-thick sheets of carbon, called graphene. These sheets are rolled at specific and discrete (“chiral”) angles, and the combination of the rolling angle and radius decides the nanotube properties; for example, whether the individual nanotube shell is a metal or semiconductor. Nanotubes are categorized as single-walled nanotubes (SWNTs) and multi-walled nanotubes (MWNTs). A new model of effective thermal conductivity of carbon nanotubes (CNTs) is presented by Xue (2005). He showed that the theoretical results of the effective thermal conductivity of CNTs/oil and CNTs/decene suspensions presented by him are in good agreement with the experimental data. The influence of multi-walled carbon nanotubes on single-phase heat transfer and pressure drop characteristics in the transitional flow regime of smooth tubes is presented by Meyer et al (2013). According to them, the increase in viscosity was four times the increase in the thermal conductivity. The heat transfer and pressure drop of nanofluids containing carbon nanotubes in a horizontal circular tube are experimentally investigated by Wang et al (2013). Very recently, homogeneous flow model is used by Khan et al (2013) to study the flow and heat transfer of CNTs along a flat plate subjected to Navier slip and uniform heat flux boundary conditions. According to them, engine oil-based CNTs have higher heat transfer rates than water and kerosene-based CNTs.

In the present article, the authors discuss the peristaltic flow of carbon nanotubes in an asymmetric channel with MHD. To the author's knowledge, this is the first paper on the peristaltic flow of CNTs in an asymmetric channel. Two types of carbon nanotubes, namely, single- (SWCNT) and multi-wall carbon nanotubes (MWCNT) are used with water as base fluid. The empirical correlations are used for the thermo-physical properties of CNTs in terms of the solid volume fraction of CNTs. The governing equations are simplified using long wavelength and low Reynolds number approximation. Exact solutions have been evaluated for velocity, pressure gradient, the solid volume fraction of the nanoparticles and temperature profile. The effects of various flow parameters, i.e. Hatmann number M, the solid volume fraction of the nanoparticlesϕ, Grashof number G and Prandtl number P r are presented graphically for both SWCNT and MWCNT.

Formulation of the problem

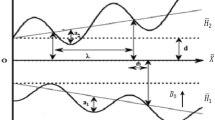
We present an incompressible peristaltic flow of carbon nanotubes in an asymmetric channel with channel girth d1 + d2 with thermal and velocity slip effects. Sinusoidal wave propagate down the walls of the channel with constant speed c1. Asymmetry in the channel flow is due to the phase difference:

$$ \begin{aligned} Y\,=\,&\bar{H}_{1}=d_{1}+a_{1}\cos \left[ \frac{2\pi }{\lambda }\left( \bar{X} -c_{1}\bar{t}\right) \right],\\ Y\,=\,&\bar{H}_{2}=-d_{2}-b_{1}\cos \left[ \frac{2\pi }{\lambda }\left( \bar{X} -c_{1}\bar{t}\right) +\omega \right]. \end{aligned} $$
(1)

In the above equations, a1 and b1 denote the waves' amplitudes,λ is the wave length, d1 + d2 is the channel width, c1 is the wave speed, \(\bar{t}\) is the time, \(\bar{X}\) is the direction of wave propagation and \(\bar{Y}\) is perpendicular to \(\bar{X}. \) The expression for fixed and wave frames are related by the following relations

$$ \bar{x}=\bar{X}-c_{1}t,\ y=\bar{Y},\ \bar{u}=\bar{U}-c_{1},\ \bar{v}=\bar{V} ,\ p\left( \bar{x}\right) =P\left( \bar{X},t\right). $$
(2)

With the transformation given in Eq. (2), equations governing the flow and temperature in the presence of heat source or heat sink with viscous dissipation are (Hamad and Ferdows 2012a, b)

$$ \frac{\partial \bar{u}}{\partial \bar{x}}+\frac{\partial \bar{v}}{\partial \bar{y}}=0, $$
(3)
$$ \bar{u}\frac{\partial \bar{u}}{\partial \bar{x}}+\bar{v}\frac{\partial \bar{u }}{\partial \bar{y}}=-\frac{1}{\rho _{nf}}\frac{\partial P}{\partial \bar{x}} +\frac{\mu _{nf}}{\rho _{nf}}\frac{\partial ^{2}\bar{u}}{\partial \bar{y}^{2} }+\frac{\mu _{nf}}{\rho _{nf}}\frac{\partial ^{2}\bar{u}}{\partial \bar{x} ^{2}}-\frac{\sigma B_{o}^{2}}{\rho _{nf}}\left( \bar{u}+c_{1}\right) +\frac{ \rho _{nf}}{\rho _{nf}}g\alpha \left( \bar{T}-\bar{T}_{0}\right) , $$
(4)
$$ \bar{u}\frac{\partial \bar{v}}{\partial \bar{x}}+\bar{v}\frac{\partial \bar{v }}{\partial \bar{y}}=-\frac{1}{\rho _{\rm{nf}}}\frac{\partial P}{\partial \bar{y}} +\frac{\mu _{\rm{nf}}}{\rho _{\rm{nf}}}\frac{\partial ^{2}\bar{v}}{\partial \bar{y}^{2} }+\frac{\mu _{\rm{nf}}}{\rho _{\rm{nf}}}\frac{\partial ^{2}\bar{v}}{\partial \bar{x} ^{2}}, $$
(5)
$$ \bar{u}\frac{\partial \bar{T}}{\partial \bar{x}}+\bar{v}\frac{\partial \bar{T }}{\partial \bar{y}}=\alpha _{\rm{nf}}\left( \frac{\partial ^{2}\bar{T}}{\partial \bar{y}^{2}}+\frac{\partial ^{2}\bar{T}}{\partial \bar{x}^{2}}\right) +\frac{ Q_{0}}{\left( \rho c_{p}\right) _{\rm{nf}}}, $$
(6)

where \(\bar{x}\) and \(\bar{y}\) are the coordinates along and perpendicular to the channel, \(\bar{u}\) and \(\bar{v}\) are the velocity components in the \(\bar{x}\) and \(\bar{y}\) directions, respectively, and \(\bar{T}\) is the local temperature of the fluid. Further, ρnf is the effective density, μnf the effective dynamic viscosity, (ρc p )nf the heat capacitance, αnf the effective thermal diffusivity, knf the effective thermal conductivity of the nanofluid and Q0 is constant heat absorption parameter which are defined as [see (Xue 2005; Wang et al. 2013)]

$$ \begin{aligned} \rho _{\rm{nf}} &=\left( 1-\phi \right) \rho _{f}+\phi \rho _{\rm{f}},\mu _{\rm{nf}}=\frac{\mu _{\rm{f}}}{\left( 1-\phi \right) ^{2.5}},\\ \left( \rho c_{p}\right) _{\rm{nf}} &=\left( 1-\phi \right) \left( \rho c_{p}\right) _{\rm{f}}+\phi \left( \rho c_{p}\right) _{s}, \alpha _{\rm{nf}}= \frac{k_{\rm{nf}}}{\left( \rho c_{p}\right) _{\rm{nf}}},\\ \frac{k_{\rm{nf}}}{k_{\rm{f}}} &= \frac{\left( 1-\phi \right) +2\phi \frac{k_{\rm{CNT}}}{ k_{\rm{CNT}}-k_{\rm{f}}}\ln \frac{k_{\rm{CNT}}+k_{\rm{f}}}{2k_{\rm{f}}}}{\left( 1-\phi \right) +2\phi \frac{k_{\rm{f}}}{k_{\rm{CNT}}-k_{\rm{f}}}\ln \frac{k_{\rm{CNT}}+k_{\rm{f}}}{2k_{\rm{f}}}} \end{aligned} $$
(7)

where ϕ is the solid volume fraction of the CNTs.

We introduce the following non-dimensional quantities

$$ \begin{aligned} x =&\frac{2\pi \bar{x}}{\lambda },y=\frac{\bar{y}}{d_{1}},u= \frac{\bar{u}}{c_{1}},v=\frac{\bar{v}}{c_{1}},t=\frac{2\pi \bar{t}}{\lambda },\delta =\frac{2\pi d_{1}}{\lambda },d= \frac{d_{2}}{d_{1}},P=\frac{2\pi d_{1}^{2}P}{\mu _{\rm{f}}c_{1}\lambda }, \\ h_{1} =&\frac{\bar{h}_{1}}{d_{1}}, h_{2}=\frac{\bar{h}_{2}}{d_{2}}, \text{Re}=\frac{\rho c_{1}d_{1}}{\mu _{\rm{f}}}, a=\frac{a_{1}}{ d_{1}}, b=\frac{a_{2}}{d_{1}}, d=\frac{d_{2}}{d_{1}}, S= \frac{\bar{S}d_{1}}{\mu _{\rm{f}}c_{1}}\\ \theta =&\frac{\bar{T}-\bar{T}_{0}}{\bar{T}_{1}-\bar{T}_{0}}, P_{r}= \frac{\nu }{\alpha }, \beta _{1}=\frac{Q_{0}d_{1}^{2}}{\left( \bar{T} _{1}-\bar{T}_{0}\right) k_{\rm{f}}}, M^{2}=\frac{\sigma B_{0}^{2}d_{1}^{2} }{\mu _{\rm{f}}}, G_{r}=\frac{g\alpha d_{1}^{2}\left( \bar{T}_{1}-\bar{T} _{0}\right) }{\nu c_{1}}. \end{aligned} $$
(8)

In the above equations P r is the Prandtl number and E c is the Eckert number.

Stream function and velocity field are related by the expressions

$$ u=\frac{\partial \Uppsi }{\partial y},v=-\delta \frac{\partial \Uppsi }{ \partial x}. $$
(9)

In view of Eqs. (7–9) under the the long wavelength and low Reynolds number assumption, we have the following equations

$$ \frac{1}{\left( 1-\phi \right) ^{2.5}}\frac{\partial ^{4}\Uppsi }{\partial y^{4}}-M^{2}\frac{\partial ^{2}\Uppsi }{\partial y^{2}}+G_{r}\frac{\partial \theta }{\partial y}=0, $$
(10)
$$ \frac{dP}{dx}=\frac{\partial }{\partial y}\left[ \frac{1}{\left( 1-\phi \right) ^{2.5}}\frac{\partial ^{2}\Uppsi }{\partial y^{2}}-M^{2}\left( \frac{ \partial \Uppsi }{\partial y}+1\right) \right] +G_{r}\theta, $$
(11)
$$ \frac{\partial ^{2}\theta }{\partial y^{2}}+\left( \frac{\left( 1-\phi \right) +2\phi \frac{k_{\rm{f}}}{k_{\rm{CNT}}-k_{\rm{f}}}\ln \frac{k_{\rm{CNT}}+k_{\rm{f}}}{2k_{\rm{f}}}}{ \left( 1-\phi \right) +2\phi \frac{k_{\rm{CNT}}}{k_{\rm{CNT}}-k_{\rm{f}}}\ln \frac{ k_{\rm{CNT}}+k_{\rm{f}}}{2k_{\rm{f}}}}\right) \beta _{1}=0. $$
(12)

The non-dimensionaless boundary conditions are

$$ \Uppsi = \frac{F}{2}, \frac{\partial \Uppsi }{\partial y}=-\beta \frac{ \partial ^{2}\Uppsi }{\partial y^{2}}-1,\quad at\,y=h_{1}=1+a\cos x, $$
(12a)
$$ \Uppsi =-\frac{F}{2}, \frac{\partial \Uppsi }{\partial y}=\beta \frac{ \partial ^{2}\Uppsi }{\partial y^{2}}-1,\quad at\, y=h_{2}=-d-b\cos \left( x+\phi \right), $$
(12b)
$$ \theta +\gamma \frac{\partial \theta }{\partial y} = 0, \quad at\, y=h_{1}, \theta -\gamma \frac{\partial \theta }{\partial y}=1 \,at\, y=h_{2}. $$
(12c)

The flow rates in fixed and wave frame are related by

$$ Q=F+1+d. $$
(13)

Solution profiles

The exact solutions for stream function, solid volume fraction of the nanoparticles and pressure gradient can be written as

$$ \begin{aligned} \Uppsi \left( x,y\right)\,=\,&G_{r}\left( 1-\phi \right) ^{2.5}y^{2}\left(6+(h_{1}-h_{2})\frac{\left( 1-\phi \right) +2\phi \frac{k_{\rm{CNT}}}{ k_{\rm{CNT}}-k_{\rm{f}}}\ln \frac{k_{\rm{CNT}}+k_{\rm{f}}}{2k_{\rm{f}}}}{\left( 1-\phi \right) +2\phi \frac{k_{\rm{f}}}{k_{\rm{CNT}}-k_{\rm{f}}}\ln \frac{k_{\rm{CNT}}+k_{\rm{f}}}{2k_{\rm{f}}}} \left(3(h_{1}+h_{2})-2y\right)\beta _{1}\right)\\&+12(h_{1}-h_{2})M^{2}\left( 1-\phi \right) ^{2.5}(L_{15}+yL_{16})+12(h_{1}-h_{2})(L_{13}+L_{14})\\ &\cosh \left( My\left( 1-\phi \right) ^{\frac{5}{4}}\right) +(L_{13}-L_{14})\sinh \left( My\left( 1-\phi \right) ^{\frac{5}{4}}\right) /(12(h_{1}-h_{2})\\ &M^{2}\left( 1-\phi \right) ^{2.5}), \end{aligned} $$
(14)
$$ \begin{aligned} \frac{dP}{dx}\,=\,&L_{12}(L_{2}-L_{5})(1+L_{7})-L_{12}(F-L_{1}+L_{4})L_{8}+(L_{3}-L_{6})(L_{11}(1+L_{7})\\ &-(1+L_{10})L_{8})+\left(L_{11}(F-L_{1}+L_{4})+(1+L_{10})(L_{2}-L_{5})\right)L_{9}/(L_{3}-L_{6})\\ &(L_{11}-L_{8})+L_{12}(L_{2}-L_{5}-h_{1}L_{8}+h_{2}L_{8})+\left(h_{1}L_{11}-h_{2}L_{11}-L_{2}+L_{5}\right)L_{9} \end{aligned} $$
(15)
$$ \begin{aligned} \theta \left( x,y\right) =&1/2\left( 1+\left( \frac{\left( 1-\phi \right) +2\phi \frac{k_{\rm{CNT}}}{k_{\rm{CNT}}-k_{\rm{f}}}\ln \frac{k_{\rm{CNT}}+k_{\rm{f}}}{2k_{\rm{f}}}}{\left( 1-\phi \right) +2\phi \frac{k_{\rm{f}}}{k_{\rm{CNT}}-k_{\rm{f}}}\ln \frac{k_{\rm{CNT}}+k_{\rm{f}}}{ 2k_{\rm{f}}}}\right) (h_{1}-y)\right.\\ &(-h_{2}+y)\beta _{1}+(h_{1}-h_{2})\left( \frac{\left( 1-\phi \right) +2\phi \frac{k_{\rm{CNT}}}{k_{\rm{CNT}}-k_{\rm{f}}}\ln \frac{k_{\rm{CNT}}+k_{\rm{f}}}{2k_{\rm{f}}}}{\left( 1-\phi \right) +2\phi \frac{k_{\rm{f}}}{k_{\rm{CNT}}-k_{\rm{f}}}\ln \frac{k_{\rm{CNT}}+k_{f}}{ 2k_{\rm{f}}}}\right) \beta _{1}\gamma \\ &\left. \frac{h_{1}+h_{2}-2\gamma }{h_{1}-h_{2}+2\gamma }\right). \end{aligned} $$
(16)

where L1 − L16 are constants evaluated using Mathematica 8.

The dimensionless pressure rise \(\Updelta P\) is

$$ \Updelta P=\int\limits_{0}^{1}\left( \frac{dP}{dx}\right) dx. $$
(17)

Graphical illustration

To see the significance of CNTs graphically and physically for the pressure rise, pressure gradient, velocity, temperature profile, solid volume fraction of the CNTs and streamlines for the flow parameter for the numerical values are plotted in Figs. 1, 2, 3, 4, and 5. Analysis have been done for Cu nanoparticles with water as a base fluid in connection with SWCNT and MWCNT with the application of thermal and velocity slip effects. Numerical integration is performed for the pressure rise per wavelength. The pressure rise against volume flow rate for the solid volume fraction of the nanoparticles ϕ, Hartmann number M, slip parameter β, and Grashof number G r is depicted in Fig. 1a–d. It is noticed that the pressure rise and volume flow rate have opposite behaviours. From Fig. 1a–d it is seen that in the pumping region (\(\Updelta P>0\)), the pressure rise decreases with the increase of Hartman number M, while pressure rise increases with the increase in the Hartmann number M, solid volume fraction of the CNTs ϕ and slip parameter β and pressure rise increases by increasing Grashof number G r . Figure 1a, d also shows that in the augmented pumping region for (\(\Updelta P\,<\,0\)), pressure rise gives the opposite results for all the parameters as compared to the pumping region (\(\Updelta P>0\)). Free pumping region holds when \(\left(\Updelta P=0\right).\) It is also seen that the pressure rise for SWCNTs is greater as compared to the MWCNT. Variations of Hartmann number M, solid volume fraction ϕ of the CNTs, Hartmann number M and slip parameter β on the velocity profile are shown in Fig. 2a–d. It depicts that the behaviour of velocity is not similar in view of the Hartmann number M, solid volume fraction ϕ of the CNTs, Hartmann number M and slip parameter β. The velocity field increases due to increase in ϕ, β, and G r at the centre of the channel, while velocity field decreases with an increase in ϕ, β, and G r near the channel wall. It is also analyzed that the velocity field decreases due to increase in M at the centre of the channel, while velocity field increases with an increase in M near the channel wall. It is also observed that the velocity field for SWCNT is greater than that compared to the MWCNT in view of M and ϕ, while the velocity field for SWCNT is greater than that compared to the MWCNT in view of β and G r (Table 1).

Table 1 Thermal properties of base fluid (water) and nanoparticles
Full size table
Fig. 1
figure 1

Pressure rise versus flow rate \({\bf a}\, \beta =0.5, \phi =0.2, G_{r}=2.\;{\bf b}\, M=2, \phi =0.2, G_{r}=2.\;{\bf c}\, M=4, \beta =0.5, G_{r}=2,\,{\rm and}\,{\bf d}\, \beta =0.5, \phi =0.2, M=2.\) Other parameters are a = 0.2, b = 0.2, d = 1, β1 = 0.2, γ = 0.2

Full size image
Fig. 2
figure 2

Velocity profile \({\bf a}\, \beta =0.5, M=2, G_{r}=2, {\bf b}\, M=2, \phi =0.2, G_{r}=2, {\bf c}\, \phi =0.2, \beta =0.5, G_{r}=2,\,{\rm and}\,{\bf d}\, \beta =0.5, \phi =0.2, M=2.\) Other parameters are a = 0.2, b = 0.2, d = 1, β1 = 0.2, γ = 0.2

Full size image

The pressure gradient for different values of M, G r , β and ϕ are plotted in Fig. 3a–d. The mMagnitude of pressure gradient increases with the increase in G r , and ϕ. It is also observed that the maximum pressure gradient occurs when x = 0.48 and near the channel walls the pressure gradient is small. This leads to the fact that flow can easily pass at the middle of the channel. It is analyzed that the pressure gradient decreases with an increase in M and β. It is also observed that the pressure gradient for MWCNT is greater than that compared to SWCNT.

Fig. 3
figure 3

Pressure gradient \({\bf a}\,\beta =0.5, \phi =0.2, G_{r}=2, {\bf b}\, M=2, \phi =0.2, \beta =0.2, {\bf c}\, \phi =0.2, M=2, G_{r}=2, {\rm and}\,{\bf d}\, \beta =0.5, G_{r}=2, M=2.\) Other parameters are a = 0.2, b = 0.2, d = 1, β1 = 0.2, γ = 0.2

Full size image

Variations of temperature profile for different values of thermal slip parameter γ and solid volume fraction of the CNTs ϕ can be seen in Fig. 4a, b. It is analyzed that when we increase slip parameter γ and solid volume fraction of the CNTs ϕ the temperature profile increases. It is also seen that temperature for MWCNT is greater than that compared to SWCNT with varying values of ϕ and γ.

Fig. 4
figure 4

Temperature profile \({\bf a}\, \gamma =0.2.\;{\bf b}\;\phi =0.2.\) The other parameters are a = 0.2, b = 0.2, d = 1, β1 = 0.2

Full size image
Fig. 5
figure 5

Streamlines for a, b SWCNT and MWCNT, c, d for ϕ = 0.3, 0.4, with SWCNT, e, f for ϕ = 0.3, 0.4, with MWCNT; other parameters are β = 0.3, d = 1, ω = 0.3, b = 0.4, a = 0.2, Q  =  −2

Full size image

The trapping for different values of solid volume fraction of the CNTs with SWCNT and MWCNT is shown in Fig. 5a−d. It is seen from Fig. 5a, b that the size and number of the trapping bolus decreases for MWCNT as compared to SWCNT. Streamlines for different values of ϕ for SWCNT have been plotted in the Fig. 5c, d. It is found that when we increase ϕ for SWCNT, the number of trapping bolus increases, but the size of trapped bolus decreases. Streamlines for different values of ϕ for MWCNT have been plotted in Fig. 5e, f. It is found that when we increase ϕ for SWCNT, the size of the trapped bolus decreases; the number of trapping bolus increases when we increase ϕ for MWCNT.

Conclusions

The peristaltic flow of an incompressible carbon nanotubes in an asymmetric channel with thermal and velocity slip is discussed. This is the first paper on the peristaltic flow with the influence of CNTs in an asymmetric channel with slip effects.

  • It is noticed that the pressure rise and volume flow rate have opposite behaviours.

  • It is seen that pressure rise increases with the increase in the Hartmann number M, solid volume fraction of the CNTs ϕ and slip parameter β; pressure rise increases by increasing Grashof number G r .

  • It is also seen that pressure rise for SWCNTs is greater as compared to MWCNT.

  • The velocity field increases due to increase in ϕ, β and G r at the centre of the channel, while the velocity field decreases with an increase in ϕ, β and G r near the channel wall.

  • It is also observed that velocity field for SWCNT is greater than that compared to MWCNT in view of M and ϕ .

  • The magnitude of pressure gradient increases with the increase in G r and ϕ.

  • It is analyzed that when we increase slip parameter γ and solid volume fraction of the CNTs ϕ.

  • It is found that when we increase ϕ for SWCNT, the number of the trapping bolus increases, but the size of the trapped bolus decreases.