Effects of heat and mass transfer on peristaltic flow of a nanofluid between eccentric cylinders

Abstract

In the present investigation, we examined the heat and mass transfer analysis for the peristaltic flow of nanofluid through eccentric cylinders. The complexity of equations describing the flow of nanofluid is reduced through applying the low Reynolds number and long wavelength approximations. The resulting equations are highly nonlinear, coupled and nonhomogeneous partial differential equations. These complicated governing equations are solved analytically by employing the homotopy perturbation method. The obtained expressions for velocity, temperature and nanoparticle phenomenon are sketched through graphs for two as well as three dimensions. The resulting relations for pressure gradient and pressure rise are plotted for various pertinent parameters. The streamlines are drawn for some physical quantities to discuss the trapping phenomenon.

Introduction

Nanofluid is a type of fluid having nanometer-sized particles (having size less than 10⁻²) known as nanoparticles. In nanofluid, nanoparticles are suspended in customary heat transfer basic fluids. The nanoparticles used in nanofluid are normally composed of metals, oxides, carbides or carbon nanotubes. Water, ethylene glycol and oil are common examples of base fluids. Nanofluid have their major applications in heat transfer, including microelectronics, fuel cells, pharmaceutical processes and hybrid-powered engines, domestic refrigerator, chiller, nuclear reactor coolant, grinding, space technology and in boiler flue gas temperature reduction. They demonstrate enhanced thermal conductivity and convective heat transfer coefficient counterbalanced to the base fluid. Acquaintance of the rheological properties of nanofluid is found to be very momentous in measuring their capability for convective heat transfer utilizations. Nanofluid have been the core of attention of many researchers for new production of heat transfer fluids in heat exchangers, plants and automotive cooling significations, due to their enormous thermal characteristics. A large amount of literature is available which deals with the study of nanofluid and its applications (Akbar et al. 2012; Manca et al. 2012; Wang and Mujumdar 2007).

Many researchers have been interested in analyzing the applications of peristaltic flow through different geometric shapes. A large number of articles (Srinivas and Kothandapani 2008; Nadeem and Akbar 2009; Sobh et al. 2010; Tripathi 2011a, b; Mekheimer and Abdelmaboud 2008; Mekheimer 2008) have been presented which reveal the properties and behavior of various types of fluids in peristalsis. Due to the non-Newtonian attributes of most of the biofluids, researchers have introduced different models of non-Newtonian fluids depending on their rheological properties (Ellahi and Hameed 2012; Malik 2011; Mahomed and Hayat 2007; Nadeem and Akbar 2010). The three-dimensional analysis of peristaltic flow has also been presented by some of the researchers to describe the peculiarity of different kinds of fluid in space. The influence of lateral walls on peristaltic flow in a rectangular duct has been described by Reddy et al. (2005). Mekheimer et al. (2012) have studied the mathematical model of peristaltic transport through an eccentric cylinders. The concept of nanofluid in peristalsis has been explored by some of the researchers. Nadeem and Maraj (2012) have presented the mathematical analysis for peristaltic flow of nanofluid in a curved channel with compliant walls under the constraints of long wavelength and low Reynolds number. Recently, Akbar and Nadeem (2011) have produced endoscopic effects on the peristaltic flow of a nanofluid. It is to be noted that in the studies (Mahomed and Hayat 2007; Nadeem and Akbar 2010), the flow is taken in a two-dimensional geometry. The peristaltic flow of nanofluid has not been discussed in three dimensions so far.

To observe the effects of space on the peristaltic flow of nanofluid, we intend to study the peristaltic flow of nanofluid through eccentric cylinders. The three-dimensional analysis is made in cylindrical coordinates to observe the flow in tubes. The constitutive equations are simplified by employing the assumptions of low Reynolds number and long wavelength. The graphs for velocity, temperature and nanoparticles concentration are plotted both in two and three dimensions. The expressions for pressure gradient and pressure rise are sketched under the impact of various physical parameters. The trapping bolus phenomenon is also elaborated through streamlines against different quantities.

Mathematical formulation of the problem

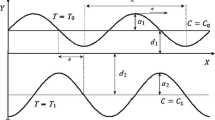
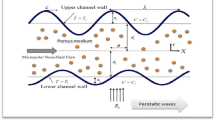
Let us consider the peristaltic flow of an incompressible nanofluid between two vertical eccentric cylinders. The geometry of the flow is described as the inner tube being rigid and the sinusoidal wave propagating at the outer tube along its length. The radius of the inner tube is δ, but we would like to discuss the motion to the center of the outer tube. The center of the inner tube is now at the position $r=\epsilon,\,z=0,$ where r and z are coordinates in the cross section of the pipe as shown in the Fig. 1. Then the boundary of the inner tube is described to order $\epsilon$ by $r_{1}=\delta +\epsilon \cos \theta,$ where $\epsilon$ is the parameter that controls the eccentricity of the inner tube position. Further, we assume that the boundary of the inner tube is at the temperature T₀ and the outer tube is maintained at temperature T₁. The nanoparticle concentration is described as C₀ and C₁ at the walls of the inner and outer cylinders correspondingly.

Fig. 1

The simplified model of geometry of the problem

The equations for the two boundaries (Mekheimer et al. 2012) are

$$ r_{1}=\delta +\epsilon \cos \theta, $$

$$ r_{2}=a+b\cos \left[ \frac{2\pi }{\lambda }(z-c_{1}t)\right], $$

where δ and a are the radii of the inner and outer tubes, b is the amplitude of the wave, λ is the wavelength, c₁ is the propagation velocity and t is the time. The problem has been considered with the system of cylindrical coordinates (r, θ, z) as radial, azimuthal and axial coordinates, respectively.

The equations for the conservation of mass, momentum, energy and nanoparticle concentration for an incompressible nanofluid are described as (Akbar and Nadeem 2011)

$$ \hbox{div } {\mathbf{V}}=0, $$

(1)

$$ \rho_{\rm f}\left( \frac{\partial {\mathbf{V}}}{\partial t}+{\mathbf{V}}\cdot {\mathbf{\nabla V}}\right) =-{\mathbf{\nabla }}p+\mu \hbox{div } {\mathbf{V+}}\rho_{\rm f}g\alpha \left( T-T_{0}\right) +\rho_{\rm f}g\alpha \left( C-C_{0}\right){\mathbf{,}} $$

(2)

$$ \left( \rho c\right)_{\rm f}\left( \frac{\partial {\mathbf{T}}}{\partial t}+ {\mathbf{V}}\cdot {\mathbf{\nabla T}}\right) ={\mathbf{\nabla }}\cdot k{\mathbf{ \nabla }}T+\left(\rho c\right)_{\rm p}\left( D_{\rm B}\left( {\mathbf{\nabla }}C\cdot {\mathbf{\nabla }}T\right) +\frac{D_{T}}{T_{0}}\left( {\mathbf{\nabla }}T\cdot {\mathbf{\nabla}}T\right) \right), $$

(3)

$$ \left( \frac{\partial {\mathbf{C}}}{\partial t}+{\mathbf{V}}\cdot {\mathbf{\nabla C}}\right) =D_{\rm B}{\mathbf{\nabla }}^{2}C+\frac{D_{T}}{T_{0}}{\mathbf{\nabla }}^{2}T, $$

(4)

where ρ_f is the density of the incompressible fluid, $\left( \rho c\right)_{\rm f}$ is the heat capacity of the fluid, $\left( \rho c\right)_{\rm p}$ gives the effective heat capacity of the nanoparticle material, k implies thermal conductivity, g stands for constant of gravity, μ is the viscosity of the fluid, d/dt gives the material time derivative, P is the pressure, C denotes the nanoparticle concentration, D_B is the Brownian diffusion coefficient and D _T is the thermophoretic diffusion coefficient.

We introduce a wave frame (r, z) moving with velocity c₁ away from the fixed frame (R, Z) by the transformations

$$ z=Z-c_{1}t,\,r=R,\,w=W-c_{1},\,u=U,\,p=P. $$

(5)

Let us assume that the velocity field for the flow is $\mathbf{V}=(u,0,w).$ The dimensionless parameters used in the problem are defined as follows

$$ \begin{aligned} &p^{\prime}=\frac{a^{2}}{\mu c\lambda }p,\,w^{\prime}= \frac{w}{c},\,u^{\prime}=\frac{\lambda }{ac}u,\,V^{\prime}=\frac{V}{c},\,z^{\prime}=\frac{z}{\lambda },\, r^{\prime}=\frac{r}{a},\, \theta^{\prime }=\theta ,\, t^{\prime}= \frac{c}{\lambda }t,\, \phi=\frac{b}{a},\\ &\epsilon^{\prime}=\frac{\epsilon }{a},\, \hbox{Re}=\frac{ \rho ca}{\mu },\, \delta^{\prime}=\frac{\delta }{a},\, \bar{\theta }=\frac{T-T_{0}}{T_{1}-T_{0}},\, \sigma =\frac{C-C_{0} }{C_{1}-C_{0}},\, P_{\rm r}=\frac{\mu }{\rho \alpha },\, S_{\rm c}=\frac{ \mu }{\rho D_{\rm B}},\\ &\delta_{0}=\frac{a}{\lambda },\, B_{\rm r}=\frac{\rho_{\rm f}g\alpha a^{2}}{\mu c}\left( C_{1}-C_{0}\right) ,\, G_{\rm r}=\frac{\rho_{\rm f}g\alpha a^{2}}{\mu c}\left( T_{1}-T_{0}\right) ,\, N_{\rm b}=\frac{\tau D_{\rm B}}{ \alpha_{\rm f}}\left(C_{1}-C_{0}\right),\\ &N_{\rm t}=\frac{\tau D_{\rm T}}{T_{0}\alpha_{\rm f}}\left(T_{1}-T_{0}\right) , \, \alpha_{\rm f}=\frac{k}{\left( \rho c\right)_{\rm f}},\tau =\frac{\left( \rho c\right)_{\rm p}}{\left( \rho c\right)_{\rm f}}, \end{aligned} $$

(6)

where V, ϕ, Re, δ₀, P_r, N_b, N_t, G_r and B_r represent the velocity of the inner tube, amplitude ratio, Reynold’s number, dimensionless wave number, Prandtl number, Brownian motion parameter, thermophoresis parameter, local temperature Grashof number and local nanoparticle Grashof number, respectively. After using the above non-dimensional parameters and employing the assumptions of long wavelength $\left( \delta_{0}\rightarrow 0\right)$ and low Reynolds number $\left({ \hbox{Re}}\rightarrow 0\right),$ the dimensionless governing equations (without using primes) for nanofluid in the wave frame take the final form as

$$ \frac{\partial u}{\partial r}+\frac{u}{r}+\frac{\partial w}{\partial z}=0, $$

(7)

$$ \frac{\partial^{2}w}{\partial r^{2}}+\frac{1}{r}\frac{\partial w}{\partial r }+\frac{1}{r^{2}}\frac{\partial^{2}w}{\partial \theta^{2}}+B_{\rm r}\sigma +G_{\rm r}\theta =\frac{{\rm{d}}p}{{\rm{d}}z}, $$

(8)

$$ \frac{\partial^{2}\bar{\theta }}{\partial r^{2}}+\frac{1}{r}\frac{ \partial \bar{\theta }}{\partial r}+\frac{1}{r^{2}}\frac{\partial^{2} \bar{\theta }}{\partial \theta^{2}}+N_{\rm b}\left( \frac{\partial \bar{\theta }}{\partial r}\frac{\partial \sigma }{\partial r}+\frac{1}{ r^{2}}\frac{\partial \bar{\theta }}{\partial \theta }\frac{\partial \sigma }{\partial \theta }\right) +N_{\rm t}\left( \left( \frac{\partial \bar{\theta }}{\partial r}\right)^{2}+\frac{1}{r^{2}}\left( \frac{ \partial \bar{\theta }}{\partial \theta }\right)^{2}\right) =0, $$

(9)

$$ \frac{\partial^{2}\sigma }{\partial r^{2}}+\frac{1}{r}\frac{\partial \sigma }{\partial r}+\frac{1}{r^{2}}\frac{\partial^{2}\sigma }{\partial \theta^{2} }+\frac{N_{\rm t}}{N_{\rm b}}\left( \frac{\partial^{2}\bar{\theta }}{\partial r^{2}}+\frac{1}{r}\frac{\partial \bar{\theta }}{\partial r}+\frac{1}{ r^{2}}\frac{\partial^{2}\bar{\theta }}{\partial \theta^{2}}\right) =0. $$

(10)

The non-dimensional boundaries will take the form as

$$ r_{1}=\delta +\epsilon \cos \theta, \quad r_{2}=1+\phi \cos 2\pi z. $$

(11)

The corresponding boundary conditions are described as

$$ w=V\quad \hbox{ at }r=r_{1}, \quad w=0\quad \hbox{ at }r=r_{2}, $$

(12)

$$ \bar{\theta }=0\quad \hbox{ at }r=r_{1},\quad\bar{\theta }=1 \quad \hbox{ at }r=r_{2}, $$

(13)

$$ \sigma =0\quad \hbox{ at }r=r_{1},\quad\sigma =1\quad \hbox{ at } r=r_{2}. $$

(14)

Solution to the problem

We use the homotopy perturbation method (He 2006) to solve the above nonlinear, nonhomogeneous and coupled partial differential equations of the second order. The deformation equations for the given problems are manipulated as

$$ \left(1-q\right) \left( {{\mathcal{L}}} \left[\widetilde{w}\right] -{{\mathcal{L}}} \left[ \widetilde{w}_{0}\right] \right) +q\left( {{\mathcal{L}}} \left[ \widetilde{w}\right] +\frac{1}{r^{2}}\frac{\partial^{2}\widetilde{w} }{\partial \theta^{2}}+B_{\rm r}\omega +G_{\rm r}\theta -\frac{{\rm d}p}{{\rm d}z}\right) =0, $$

(15)

$$ \begin{aligned} &\left(1-q\right) \left({{\mathcal{L}}} \left[\theta\right] -{{\mathcal{L}}} \left[\widetilde{\theta}_{0}\right] \right) +q\left( {{\mathcal{L}}} \left[ \theta \right] +\frac{1}{r^{2}}\frac{\partial^{2}\theta }{\partial \theta^{2}}+N_{\rm b}\left( \frac{\partial \theta }{\partial r}\frac{ \partial \omega }{\partial r}+\frac{1}{r^{2}}\frac{\partial \theta }{ \partial \theta }\frac{\partial \omega }{\partial \theta }\right)\right.\\ &\quad\left. + N_{\rm t}\left(\left(\frac{\partial \theta }{\partial r} \right)^{2}+\frac{1}{r^{2}}\left( \frac{\partial \theta }{\partial \theta } \right)^{2}\right) \right)=0,\end{aligned} $$

(16)

$$ \left(1-q\right) \left( {{\mathcal{L}}} \left[ \omega \right] -{{\mathcal{L}}} \left[ \bar{\sigma }_{0}\right] \right) + q \left( {{\mathcal{L}}} \left[ \omega \right] +\frac{1}{r^{2}} \frac{\partial^{2}\omega }{\partial \theta^{2}}+\frac{N_{\rm t}}{N_{\rm b}}\left( \frac{\partial^{2}\theta }{\partial r^{2}}+ \frac{1}{r}\frac{\partial \theta }{\partial r}+\frac{1}{r^{2}}\frac{\partial^{2}\theta }{\partial \theta^{2}}\right) \right) =0. $$

(17)

The linear operator is chosen as ${{\mathcal{L}} =\frac{1}{r}\frac{\partial }{\partial r}\left( r\frac{\partial }{\partial r}\right) .}$ We suggest the following initial guesses for $w,\,\bar{\theta}$ and σ

$$ \widetilde{w}_{0}=\frac{V\left( \log \left( r\right) -\log \left(r_{2}\right) \right) }{\log \left( r_{1}\right) -\log \left(r_{2}\right) }, \quad \widetilde{\theta }_{0}=\frac{\log \left( r_{1}\right) -\log \left( r\right) }{\log \left( r_{1}\right)-\log \left( r_{2}\right) }= \widetilde{\sigma }_{0}. $$

(18)

Now, we describe

$$ \widetilde{w}\left(r,\theta ,z,q\right) =w_{0}+qw_{1}+{\cdots} $$

(19)

$$ \theta \left(r, \theta, z, q \right) =\bar{\theta }_{0} + q \bar{\theta}_{1}+{\cdots} $$

(20)

$$ \omega \left(r, \theta, z, q\right) = \sigma_{0}+q \sigma_{1}+{\cdots} $$

(21)

Combining Eqs. (19)–(21) with Eqs. (15)–(17) and comparing the terms of the first two orders, we have the following systems.

Zeroth order system

$$ {{\mathcal{L}}} \left[ w_{0}\right] -{{\mathcal{L}}} \left[ \widetilde{w}_{0}\right] =0, $$

(22)

$$ w_{0}=0,\quad \hbox{ at }r=r_{2}, \quad w_{0}=V,\quad \hbox{ at }r=r_{1}, $$

(23)

$$ {{\mathcal{L}}} \left[ \bar{\theta }_{0}\right] -{{\mathcal{L}}} \left[ \widetilde{\theta }_{0}\right] =0, $$

(24)

$$ \bar{\theta }_{0}=1,\quad \hbox{ at }r=r_{2}, \quad \bar{\theta }_{0}=0,\quad \hbox{ at }r=r_{1}, $$

(25)

$$ {{\mathcal{L}}} \left[ \sigma_{0}\right] -{{\mathcal{L}}} \left[ \widetilde{\sigma }_{0}\right] =0, $$

(26)

$$ \sigma_{0}=1,\quad \hbox{ at }r=r_{2}, \quad \sigma_{0}=0,\quad \hbox{ at }r=r_{1}, $$

(27)

The solutions of the above zeroth order systems can be obtained by using Eqs. (18), (22)–(27) and are found as

$$ w_{0}\left( r, \theta, z, q \right) =\frac{V\left( \log \left( r\right) -\log \left( r_{2}\right) \right) }{\log \left( r_{1}\right) -\log \left( r_{2}\right) },\, \bar{\theta }_{0}=\frac{\log \left( r_{1}\right) -\log \left( r\right) }{\log \left( r_{1}\right) -\log \left( r_{2}\right) }, \, \sigma_{0}=\frac{\log \left( r_{1}\right) -\log \left( r\right) }{ \log \left( r_{1}\right) -\log \left( r_{2}\right) }. $$

(28)

First order system

$$ {{\mathcal{L}}} \left[ w_{1}\right] +\frac{1}{r^{2}}\frac{\partial^{2}w_{0}}{ \partial \theta^{2}}+B_{\rm r}\sigma_{0}+G_{\rm r}\bar{\theta }_{0}-\frac{{\rm d}p}{{\rm d}z}=0, $$

(29)

$$ w_{1}=0,\quad \hbox{ at }r=r_{2}, \quad w_{1}=0,\quad \hbox{ at }r=r_{1}, $$

(30)

$$ {{\mathcal{L}}} \left[ \bar{\theta }_{1}\right] +\frac{1}{r^{2}}\frac{ \partial^{2}\bar{\theta }_{0}}{\partial \theta^{2}}+N_{\rm b}\left( \frac{ \partial \bar{\theta }_{0}}{\partial r}\frac{\partial \sigma_{0}}{ \partial r}+\frac{1}{r^{2}}\frac{\partial \bar{\theta }_{0}}{\partial \theta }\frac{\partial \sigma_{0}}{\partial \theta }\right) +N_{\rm t}\left( \left( \frac{\partial \bar{\theta }_{0}}{\partial r}\right)^{2}+\frac{1 }{r^{2}}\left( \frac{\partial \bar{\theta }_{0}}{\partial \theta } \right)^{2}\right) =0, $$

(31)

$$ \bar{\theta }_{1}=0,\quad \hbox{ at }r=r_{2}, \quad \bar{\theta }_{1}=0,\quad \hbox{ at }r=r_{1}, $$

(32)

$$ {{\mathcal{L}}} \left[ \sigma_{1}\right] +\frac{1}{r^{2}}\frac{\partial^{2}\sigma_{0}}{\partial \theta^{2}}+\frac{N_{\rm t}}{N_{\rm b}}\left( \frac{ \partial^{2}\bar{\theta }_{0}}{\partial r^{2}}+\frac{1}{r}\frac{ \partial \bar{\theta }_{0}}{\partial r}+\frac{1} {r^{2}}\frac{\partial^{2}\bar{\theta }_{0}}{\partial \theta^{2}}\right) =0, $$

(33)

$$ \sigma_{1}=1,\quad \hbox{ at }r=r_{2}, \quad \sigma_{1}=0,\quad \hbox{ at }r=r_{1}. $$

(34)

The solutions of the above nonlinear ordinary differential equations are found as

$$ \begin{aligned} u_{1} = \,& (-2(r-r_{1})(r-r_{2})(r_{1}-r_{2}) ( 2 ( r_{2}-\delta )^{2} ( B_{\rm r}(r+r_{1}+r_{2}-3\delta ) \\ & +G_{\rm r}(r+r_{1}+r_{2}-3\delta) G_{\rm r}(r+r_{1}+r_{2}-3\delta )+ 3\frac{{\rm d}p}{{\rm d}z}(-r_{2}+\delta )) \\& +( B_{\rm r}(r+r_{1}+7r_{2}-9\delta ) +G_{\rm r}(r+r_{1}+7r_{2}+G_{\rm r}(r+r_{1}+7r_{2}-9\delta ) +9\frac{{\rm d}p}{{\rm d}z}(-r_{2}+\delta )) \epsilon^{2}) \\ &+\epsilon \left( 3 \left( B_{\rm r}+G_{\rm r}-\frac{{\rm d}p}{{\rm d}z}\right) (r-r_{1})(r-r_{2})(r_{1}- r_{2})\epsilon^{2}\cos [3\theta ] +36V\epsilon ( (r_{1}-r_{2})(r+r_{2}) \log ( r) \right. \\&\left. -(r-r_{2})(r_{1}+r_{2})\log ( r_{1}) +2(r-r_{1})r_{2} \log ( r_{2}) \right) +\cos [\theta ] \left( (r-r_{1})(r-r_{2})(r_{1}-r_{2}) (4(r_{2}-\delta) \right. \\ & \times \left(2B_{\rm r}r +2G_{\rm r}r+2B_{\rm r}r_{1}+2G_{\rm r}r_{1} + 5B_{\rm r}r_{2}+5G_{\rm r}r_{2}-9r_{2}\frac{{\rm d}p}{{\rm d}z} -9 \left( B_{\rm r}+G_{\rm r}- \frac{{\rm d}p}{{\rm d}z} \right) \delta \right) \\ & \left. +9 \left( B_{\rm r}+G_{\rm r}-\frac{{\rm d}p}{{\rm d}z}\right) \epsilon^{2} \right) +24V(r_{2}-\delta) (-(r_{1}-r_{2})(r+r_{2})\log ( r ) +(r-r_{2})(r_{1}+r_{2})\log ( r_{1} ) \\ & +2(-r+r_{1})r_{2}\log ( r_{2} ) ))-2\epsilon \cos [2\theta] (6(r_{1}-r_{2})(r+r_{2})V\log ( r ) -6(r-r_{2})(r_{1}+r_{2})V\log ( r_{1}) \\ & +(r-r_{1})((r-r_{2})(r_{1}-r_{2})(B_{\rm r} (r+r_{1}+7r_{2}-9\delta )+G_{\rm r}(r+r_{1}+7r_{2}-9\delta )+ 9\frac{{\rm d}p}{{\rm d}z}(-r_{2}+\delta )) \\& +12r_{2}V\log ( r_{2}) )) ) )/ ( 24(r_{1}-r_{2})(r_{2}-\delta -\epsilon \cos [\theta ])^{3}), \end{aligned} $$

(35)

$$ \begin{aligned} \theta_{1} =&- \left( \left( \log ( r ) -\log ( r_{2} ) \right) \left( \log ( r ) -\log ( r_{1} ) \right) \left( N_{\rm b}\epsilon^{2} ( \log r )^{2} +N_{\rm t}\epsilon^{2} ( \log r )^{2}+4\epsilon^{2}\log ( r ) \log ( r_{2}) \right. \right.\\ & -3N_{\rm b}\epsilon^{2}\log \left( r\right) \log \left( r_{2}\right) -3N_{\rm t}\epsilon^{2}\log \left( r\right) \log \left( r_{2}\right) +12N_{\rm b}\delta^{2}\left( \log r_{2}\right)^{2}+12N_{\rm t}\delta^{2} \left( \log r_{2}\right)^{2}\\ &-8\epsilon^{2}\left( \log r_{2}\right)^{2}+9N_{\rm b}\epsilon^{2}\left( \log r_{2}\right)^{2}+9N_{\rm t}\epsilon^{2}\left( \log r_{2}\right)^{2}-4\epsilon^{2}\log \left( r\right) \left( \log r_{2}\right)^{2} +8\epsilon^{2}\log \left( r_{2}\right)^{3}\\ &+4\delta \epsilon \cos [\theta ](\log \left( r_{2}\right) -\log \left( r_{1}\right) )^{2}(6N_{\rm b}+6N_{\rm t}-\log \left( r\right) +2\log \left( r_{2}\right) -\log \left( r_{1}\right) )\\ &-4\epsilon^{2}\log \left( r\right) \log [\delta +\epsilon \cos [\theta ] ] +N_{\rm b}\epsilon^{2}\log \left( r\right) \log \left( r_{1}\right) +N_{\rm t}\epsilon^{2}\log \left( r\right) \log \left( r_{1}\right)\\ &-24N_{\rm b}\delta^{2}\log \left( r_{2}\right) \log \left( r_{1}\right) -24N_{\rm t}\delta^{2}\log \left( r_{2}\right) \log \left( r_{1}\right) +12\epsilon^{2}\log \left( r_{2}\right) \log \left( r_{1}\right)\\ & -15N_{\rm b}\epsilon^{2}\log \left( r_{2}\right) \log \left( r_{1}\right) -15N_{\rm t}\epsilon^{2}\log \left( r_{2}\right) \log \left( r_{1}\right) +8\epsilon^{2}\log \left( r\right) \log \left( r_{2}\right) \log \left( r_{1}\right)\\ & -20\epsilon^{2}\left( \log r_{2}\right)^{2}\log \left( r_{1}\right) +12N_{\rm b}\delta^{2}\left( \log \left( r_{1}\right) \right)^{2}+12N_{\rm t}\delta^{2}\left( \log \left( r_{1}\right) \right)^{2}-4\epsilon^{2}\left( \log \left( r_{1}\right) \right)^{2}\\ & +7N_{\rm b}\epsilon^{2}\left( \log \left( r_{1}\right) \right)^{2}+7N_{\rm t}\epsilon^{2}\left( \log \left( r_{1}\right) \right)^{2}-4\epsilon^{2}\log \left( r\right) \left( \log \left( r_{1}\right) \right)^{2}+16\epsilon^{2}\log \left( r_{2}\right) \left( \log \left( r_{1}\right) \right)^{2}\\ & -4\epsilon^{2}\left( \log \left( r_{1}\right) \right)^{3}-\epsilon^{2}\cos [2\theta ]((N_{\rm b}+N_{\rm t})\left( \log r\right)^{2}-(8+3N_{\rm b}+3N_{\rm t})\left( \log r_{2}\right)^{2}\\ & +3(4+3N_{\rm b}+3N_{\rm t})\log \left( r_{2}\right)\left( \log \left( r_{1}\right) \right) -(4+5N_{\rm b}+5N_{\rm t})\left( \log \left( r_{1}\right) \right)^{2}+\log \left( r\right) ((4-3N_{\rm b}-3N_{\rm t})\log \left( r_{2}\right)\\ &\left.\left. +(-4+N_{\rm b}+N_{\rm t})\left( \log \left( r_{1}\right) \right) ))))/(24(r_{1})^{2}((\log \left( r_{2}\right) -\left( \log \left( r_{1}\right) \right))^{4}\right)\right), \end{aligned} $$

(36)

$$ \begin{aligned} \sigma_{1}=\,&\left( (N_{\rm b}+N_{\rm t})\epsilon (\log \left( r\right) -\log \left( r_{2}\right) )\right. \left( -\epsilon +\epsilon \cos [2\theta ]+\right. (\epsilon +\delta \cos [\theta ])(\log \left( r_{2}\right) -\log \left( r_{1}\right))) (\log ( r ) \\ &-\log \left( r_{1}\right) )(\log \left( r\right) -2\log \left( r_{2}\right) +\log \left( r_{1}\right) ))/6N_{\rm b}r_{1}{}^{2}(\log \left( r_{2}\right) -\log \left( r_{1}\right))^{3}. \end{aligned} $$

(37)

For $q\rightarrow 1,$ we approach the final solution. So from Eqs. (19)–(21), we get

$$ w\left( r,\theta ,z\right) =w_{0}+w_{1}, $$

(38)

$$ \bar{\theta }\left( r,\theta ,z\right) =\theta_{0}+\theta_{1}, $$

(39)

$$ \sigma \left( r,\theta ,z\right) =\sigma_{0}+\sigma_{1}, $$

(40)

where w₀, θ₀, σ₀,  w₁, θ₁ and σ₁ are defined in Eqs. (28) and (35)–(37), respectively. The instantaneous volume flow rate $\bar{Q}$ is given by

$$ \bar{Q}=2\pi \int\limits_{r_{1}}^{r_{2}}rwdr. $$

(41)

The mean volume flow rate Q over one period is given as [16]

$$ Q\left( z, t\right) =\frac{\bar{Q}}{\pi }-\frac{\phi^{2}}{2}+2\phi \cos \left[ 2\pi \left( z-t\right) \right] +\phi^{2}\cos^{2}[2\pi \left( z-t\right) ]. $$

(42)

Now we can evaluate the pressure gradient dp/dz by solving Eqs. (41) and (42) and is elaborated as

$$ \begin{aligned} \frac{{\rm d}p}{{\rm d}z} =&\frac{1}{60\pi (r_{1}-r_{2})^{3}(r_{1}+r_{2})(r_{2}-\delta -\epsilon \cos [\theta ])^{3}}(15\epsilon^{3}(24Q-(B_{\rm r}+G_{\rm r})\pi (r_{1}-r_{2})^{3}(r_{1}+r_{2}) \\ &+12\pi \phi (4\cos [2\pi (-t+z)]+\phi \cos [4\pi (-t+z)]))\cos [3\theta ]\\ & +2\epsilon^{2}\cos [2\theta ](2\pi ((B_{\rm r}+G_{\rm r})(r_{1}-r_{2})^{3}(4r_{1}^{2}+22r_{1}r_{2}+19r_{2}^{2})-5(8r_{1}^{3}-27r_{1}^{2}r_{2}+19r_{2}^{3})V)\\ & -1080Q(r_{2}-\delta )-45(B_{\rm r}+G_{\rm r})\pi (r_{1}-r_{2})^{3}(r_{1}+r_{2})\delta +60\pi (36(-r_{2}+\delta )\phi \cos [2\pi (-t+z)]\\ &+9(-r_{2}+\delta )\phi^{2}\cos [4\pi (-t+z)]-r_{2}(2r_{1}^{2}+2r_{1}r_{2}+r_{2}^{2})V (\log ( r_{1} ) -\log ( r_{2} ))))\\ &+\epsilon \cos [\theta ](-B_{\rm r}\pi (r_{1}-r_{2})^{3}(4(r_{2}-\delta )(16r_{1}^{2}+43r_{1}r_{2}+31 r_{2}^{2}-45(r_{1}+r_{2})\delta )\\ &+45(r_{1}+r_{2})\epsilon^{2})-G_{\rm r}\pi (r_{1}-r_{2})^{3}(4(r_{2}-\delta )(16r_{1}^{2}+43r_{1}r_{2} +31r_{2}^{2}-45(r_{1}+r_{2})\delta )\\ &+45(r_{1}+r_{2})\epsilon^{2})+40(\pi (r_{1}-r_{2})(28r_{1}^{2}+r_{1}r_{2}+r_{2}^{2})V (r_{2}-\delta )+27Q(4(r_{2}-\delta )^{2}+\epsilon^{2}))\\ &+60\pi (36(4(r_{2}-\delta )^{2}+\epsilon^{2})\phi \cos [2\pi (-t+z)] +9(4(r_{2}-\delta )^{2}+\epsilon^{2})\phi^{2}\cos [4\pi (-t+z)]\\ &-4r_{2}(2r_{1}^{2}+2r_{1}r_{2}+r_{2}^{2})V(r_{2}-\delta ) (\log \left( r_{1}\right) -\log \left( r_{2}\right) ))) +2(-120(\pi (r_{1}-r_{2})^{2}(2r_{1}+r_{2})V\\ &+6Q(r_{2}-\delta ))(r_{2}-\delta )^{2} -30(\pi (8r_{1}^{3}+3r_{1}^{2}r_{2}-11r_{2}^{3})V +36Q(r_{2}-\delta ))\epsilon^{2}\\ &+B_{\rm r}\pi (r_{1}-r_{2})^{3}(2(r_{2}-\delta )^{2}(8 r_{1}^{2}+14r_{1}r_{2}+8r_{2}^{2}-15(r_{1}+r_{2})\delta )\\ &+(8r_{1}^{2}+44r_{1}r_{2}+38r_{2}^{2}-45(r_{1}+r_{2})\delta )(\epsilon^{2})) +G_{\rm r}\pi (r_{1}-r_{2})^{3}(2(r_{2}-\delta )^{2}\\ &\times(8r_{1}^{2}+14r_{1}r_{2}+8r_{2}^{2}-15(r_{1}+r_{2})\delta )+(8r_{1}^{2}+44r_{1}r_{2}+38r_{2}^{2}-45(r_{1}+r_{2})\delta )\epsilon^{2})\\ &+180\pi (-4(r_{2}-\delta )(2(r_{2}-\delta )^{2}+3\epsilon^{2})\phi \cos [2\pi (-t+z)] -(r_{2}-\delta )(2(r_{2}-\delta )^{2}+3\epsilon^{2})\\ &\times\phi^{2}\cos [4\pi (-t+z)]+r_{2}(2r_{1}^{2}+2r_{1}r_{2}+r_{2}^{2})V\epsilon^{2}(\log \left( r_{1}\right) -\log \left( r_{2}\right) )))). \end{aligned} $$

(43)

The pressure rise $\delta p$ in the non-dimensional form is defined as

$$ \delta p=\int\limits_{0}^{1}\frac{{\rm d}p}{{\rm d}z}{\rm d}z. $$

(44)

Results and discussions

In this section, we discuss the effects of different physical parameters on the profiles of velocity, temperature and nanoparticles concentration. Three-dimensional analysis is also made to measure the influence of physical quantities on the flow properties in space. The variation in pressure gradient and peristaltic pumping is also considered for various values of pertinent quantities. The trapping bolus phenomenon observing the flow behavior is also manipulated as well with the help of streamline graphs. Figures 2, 3, 4, 5, 6, 7, 8 and 9 show the impact of different parameters on the peristaltic pressure rise $\delta p$ and pressure gradient dp/dz, respectively. Variations in velocity profile, temperature distribution and nanoparticle phenomenon under the influence of observing parameters are shown in Figs. 10, 11, 12, 13, 14 and 15, respectively. The streamlines for the parameters B_r,  G_r,  N_b and N_t are displayed in Figs. 16, 17, 18 and 19.

Fig. 2

Variation in pressure rise $\delta p$ with δ and G_r for fixed $\theta =0.8,\,\phi =0.1,\,B_{\rm r}=0.2,\,N_{\rm b}=0.5,\,N_{\rm t}=0.2,\,\epsilon =0.1,\,V=0.3$

Figure 2 represents the effects of parameters δ and G_r on the pressure rise $\delta p.$ It is noticed here that pressure rise is an increasing function of local temperature Grashof number G_r throughout the domain, but for δ, the pressure rise $\delta p$ increases in the retrograde pumping region $\left( \delta p>0,\, Q<0\right),$ while decreasing in the peristaltic pumping region $\left(\delta p>0,\, Q>0\right)$ and augmented pumping region $\left(\delta p<0,\, Q>0\right).$ Figure 3 shows that $\delta p$ decreases with the increasing effects of Brownian motion parameter N_b. Figure 4 shows that pressure rise $\delta p$ varies linearly with local nanoparticle Grashof number B_r and the effects of the parameter $\epsilon$ are the same as that of δ measured in Figs. 2 and 3. Similarly, variation in the thermophoresis parameter N_t produces the same behavior on the pressure rise graph as seen for G_r (see Fig. 5).

Fig. 3

Variation in pressure rise $\delta p$ with δ and N_b for fixed $\theta =0.8,\,\phi =0.1,\,B_{\rm r}=0.2,\,G_{\rm r}=0.2,\,N_{\rm t}=2,\,\epsilon =0.2,\,V=0.3$

Fig. 4

Variation in pressure rise $\delta p$ with $\epsilon$ and B_r for fixed θ = 0.8,  ϕ = 0.1, N_b = 0.5, G_r = 0.2, N_t = 0.2, δ = 0.1, V = 0.3

Fig. 5

Variation in pressure rise $\delta p$ with $\epsilon$ and N_t for fixed θ = 0.8,  ϕ = 0.1,  N_b = 0.5,  G_r = 0.2,  B_r = 0.5, δ = 0.1, V = 0.3

We can observe the impact of the parameters local temperature Grashof number G_r and local nanoparticle Grashof number B_r on the variation in pressure gradient dp/dz from Fig. 6 when all other parameters are kept fixed. It is noted that the pressure gradient is directly proportional to both the parameters. It is also depicted from the considered graph that the pressure gradient is wider near the walls, but closer in the central part of the geometry which means that much pressure gradient is needed at the boundaries to maintain the flow as compared with the middle part for the parameters G_r and B_r. To study the influence of radius δ and flow rate Q on the pressure gradient dp/dz, we prepared the graph shown in Fig. 7. It is seen here that the pressure gradient is a decreasing function of flow rate Q at all points within the flow. However, it has also been measured from this graph that dp/dz decreases in the middle of the flow, but rises at the boundaries of the container. Figure 8 presents the effects of velocity of the inner tube V and $\epsilon$ on the pressure gradient profile. One comes to know from this graph that dp/dz changes linearly with V, but for $\epsilon,$ the pressure gradient decreases in the region $z\in \left[0.9,1.7\right]$ while an increment is observed at the walls of the outer cylinder, i.e., in the range $z\in \left[ 0.64,0.9\right] \cup \left[ 1.7,1.97\right]$. We can observe the variation in pressure gradient with Brownian motion parameter N_b and thermophoresis parameter N_t from Fig. 9. We can observe that the pressure gradient profile rises directly when the magnitude of both the parameters is varied throughout the flow.

Fig. 6

Variation in pressure gradient dp/dz with G_r and B_r for fixed $\epsilon =0.01,\,\delta =0.02,\,V=0.3,\,\theta =0.8,\,\phi =0.1,\,Q=0.5,\,N_{\rm b}=0.5,\,N_{\rm t}=0.2$

Fig. 7

Variation in pressure gradient dp/dz with δ and Q for fixed $\epsilon =0.01,\,G_{\rm r}=2,\,V=0.3,\,\theta =0.8,\,\phi =0.1,\,B_{\rm r}=0.8,\,N_{\rm b}=0.5,\,N_{\rm t}=0.2$

Fig. 8

Variation in pressure gradient dp/dz with $\epsilon$ and V for fixed δ = 0.1,  G_r = 2,  Q = 0.5,  θ = 0.8,  ϕ = 0.1,  B_r = 0.2,  N_b = 0.5,  N_t = 0.2

Fig. 9

Variation in pressure gradient dp/dz with N_b and N_t for fixed $\delta =0.05,\,G_{\rm r}=2,\,Q=1,\,\theta =0.8,\,\phi =0.1,\,B_{\rm r}=0.2,\,\epsilon =0.01,\,V=0.1$

It is observed from Fig. 10 that the velocity profile decreases in the region $r\in \left[ 0.1,0.55\right],$ but increases in the rest of the domain with increase in the value of δ, while direct variation in velocity is observed in case of flow rate Q in every part of the region. We present Fig. 11 to obtain variation in the velocity profile w for varying magnitudes of parameters $\epsilon$ and V. The velocity directly varies with V when seen in the range $r\in \left[0.15,0.6\right),$ but inverse behavior is reported in the zone $r\in \left[ 0.6,1.05\right]$ while totally reverse investigation is made for the parameter $\epsilon.$ It is noticed from Fig. 12 that the velocity profile w increases when we increase the value of the Grashof number G_r and the local nanoparticle Grashof number B_r at every point of the flow. The velocity profile obtains the maximum altitude with the increasing effects of N_t, but rise in the value of N_b lessens the height of velocity distribution w (see Fig. 13).

Fig. 10

Variation in velocity profile u with δ and Q for fixed $\epsilon =0.1,\,N_{\rm t}=0.5,\,N_{\rm b}=0.1,\,B_{\rm r}=0.3,\,G_{\rm r}=1,\,z=0,\,V=0.3,\,\theta =0.8,\,\phi =0.1$ for (a) two-dimensional and (b) three-dimensional

Fig. 11

Variation in velocity profile u with $\epsilon$ and V for fixed $\delta =0.1,\,N_{\rm t}=0.5,\,N_{\rm b}=0.1,\,B_{\rm r}=0.3,\,G_{\rm r}=1,\,z=0,\,Q=1,\,\theta =0.8,\,\phi =0.1$ for (a) two-dimensional and (b) three-dimensional

Fig. 12

Variation in velocity profile u with B_r and G_r for fixed $\delta =0.1,\,N_{\rm t}=0.5,\,N_{\rm b}=2,\,\epsilon =0.01,\,V=0.3,\,z=0, \,Q=1,\,\theta =0.8,\,\phi =0.1$ for (a) two-dimensional and (b) three-dimensional

Fig. 13

Variation in velocity profile u with N_b and N_t for fixed $\delta =0.1,\,B_{\rm r}=0.9,\,G_{\rm r}=2,\,\epsilon =0.3,\,V=0.1,\,z=0,\,Q=1,\,\theta =0.8,\,\phi =0.1$ for (a) two-dimensional and (b) three-dimensional

To observe the behavior of temperature distribution θ with the variation in Brownian motion parameter N_b and thermophoresis parameter N_t, we display Figs. 14a, b and 15a, b, respectively. It may be concluded here that the temperature increases with the increase in the magnitude of N_b and N_t. Temperature attains the maximum value at the boundary of the outer tube and vanishes at the center of the outer tube. We look at the Figs. 16a, b and 17a, b to observe the impact of N_b and N_t on the nanoparticles' concentration σ. From these graphs, we observe that nanoparticles' distribution increases with rising N_t, but diminishes when we increase the effects of N_b.

Fig. 14

Variation in temperature profile θ with N_b for fixed $\delta =0.1,\epsilon =0.4,\,V=0.1,\,N_{\rm t}=0.2,\,z=0,\,\theta =0.8,\,\phi =0.1$ for (a) two-dimensional and (b) three-dimensional

Fig. 15

Variation in temperature profile θ with N_t for fixed $\delta =0.2,\epsilon =0.4,\,V=0.1,\,N_{\rm b}=0.5,\,z=0,\,\theta =0.8,\,\phi =0.1$ for (a) two-dimensional and (b) three-dimensional

Fig. 16

Variation in nanoparticles phenomenon σ with N_b for fixed $\delta =0.1,\epsilon =0.2,\,N_{\rm t}=0.1,\,V=0.1,\,z=0,\,\theta =0.8, \,\phi =0.1$ for (a) two-dimensional and (b) three-dimensional

Fig. 17

Variation in nanoparticles phenomenon σ with N_t for fixed $\delta =0.1,\epsilon =0.4,\,N_{\rm b}=0.5,\,V=0.1,\,z=0,\,\theta =0.8, \,\phi =0.1$ for (a) two-dimensional and (b) three-dimensional

A very interesting phenomenon in the fluid transport is trapping. In the wave frame, streamlines under certain circumstances swell to trap a bolus which travels as an inlet with the wave speed. The occurrence of an internally circulating bolus stiffened by closed streamline is called trapping. The bolus described as a volume of fluid bounded by a closed streamlines in the wave frame is moved at the wave pattern. Figure 18 shows the streamlines for the various values of the parameter local nanoparticle Grashof number B_r in the upper part of the outer cylinder. It is noted that the number of trapping bolus decreases with increase in the magnitude of B_r, while the bolus becomes large with greater values of B_r. From Fig. 19, it can be seen that boluses increase in number, but the size of the bolus is reduced with increase in the values of local temperature Grashof number G_r. The number of trapping boluses is decreased with the rising effects of N_b, but the size of the bolus remains steady with varying N_b (see Fig. 20). Figure 21 reveals the effect of N_t on the streamlines for wave travelling down the tube. It is noticed here that number of bolus varies randomly with N_t, but the bolus expands across the wave with increase in the magnitude of N_t.

Fig. 18

Streamlines for different values of B_r. a For B_r = 0.1, b for B_r = 0.5, (c) for B_r = 0.9, (d) for B_r = 1.3. The other parameters are $\epsilon =0.2,\,V=0.3,\,\theta =0.1,\,\phi =0.1,\,Q=0.6,\,\delta =0.1,\,N_{\rm t}=0.8,\,N_{\rm b}=0.1,\,G_{\rm r}=2$

Fig. 19

Streamlines for different values of G_r. a For G_r = 1, b for G_r = 2, c for G_r = 3, d for G_r = 4. The other parameters are $\epsilon =0.2,\,V=0.3,\,\theta =0.1,\,\phi =0.1,\,Q=0.6,\,\delta =0.1,\,N_{\rm t}=0.8,\,N_{\rm b}=0.1,\,B_{\rm r}=0.9$

Fig. 20

Streamlines for different values of N_b. a For N_b = 0.1, b for N_b = 0.5, c for N_b = 0.9, d for N_b = 1.3. The other parameters are $\epsilon =0.1,\,V=0.3,\,\theta =0.1,\,\phi =0.1,\,Q=0.6,\,\delta =0.1,\,N_{\rm t}=1,\,G_{\rm r}=2,\,B_{\rm r}=0.2$

Fig. 21

Streamlines for different values of N_t. a For N_t = 0.1, b for N_t = 0.3, c for N_t = 0.5, d for N_t = 0.7. The other parameters are $\epsilon =0.1,\,V=0.3,\,\theta =0.8,\,\phi =0.1,\,Q=0.6,\,\delta =0.1,\,N_{\rm b}=0.5,\,G_{\rm r}=1,\,B_{\rm r}=0.3$