1 Introduction

Fibre-metal laminates (FMLs) are a natural extension of classic composites and layered metal materials. They were invented at the TU Delft as a material that can be used in the aeronautical industry due to their excellent fatigue properties and less weight compared to commonly used aluminium alloys. The most well-known representative of fibre metal laminates is GLARE, which consists of aluminium layers and epoxy layers reinforced with glass fibres. However, new representatives of this group are also under extensive investigation. In addition, other industries show growing interest in fibre metal laminates, i.e., the automotive industry. All possibilities of changing the configuration, thickness, and other parameters make experimental testing time-consuming and cost-consuming. Thus, the usage of theoretical models such as classical laminates theory or numerical modelling is needed. In this article, the authors reviewed different numerical approaches based on finite element analysis for fibre metal laminates, based on published papers and their own experiences. In simulations of this group of materials, the type of model used, the definition of the material, and the choice of specific damage initiation and evolution criteria can be crucial for the accuracy and reliability of the results. A few review papers summarise the state of art in the field of fibre-metal laminates [1,2,3] but they are mainly focused on technological processes and mechanical properties. The authors in [4] present one chapter devoted to computational modelling, but this subject can be enhanced. In this paper, the authors present all important aspects of numerical modelling of fibre metal laminates and try to define guidelines for using such a method, as a supplement to the experimental method of testing the FMLs. Numerical simulations of fibre metal laminates have been conducted for many years, and interest in them is not decreasing. Examples of current research in the field can be found for example in [5,6,7,8,9,10]. In experimental research on FMLs, a visible trend has been observed in a variety of standard configurations and materials. The use of thermoplastic matrices [11,12,13] or natural fibres [14,15,16] is becoming more and more common. It is predicted that modifications in the approach to such materials will also be needed in terms of numerical modelling. In this paper, the current state-of-the-art will be presented, which will provide a base to further expand knowledge.

The numerical simulations of fiber-metal laminates are mostly carried out as a support for experimental research, so in this section, we will summarize the most common types of tests conducted for FMLs. Due to the current field of application in aircraft fuselages and similar structures, a very common researched aspect of the experimental–numerical approach is the impact of low velocity [7, 8, 10, 17,18,19,20,21,22,23,24,25]. The low-velocity impact is often realized following standards, for example, ASTM D7136 [26]. The test specimens have a plate shape with different sizes used (100 × 150 mm, 200 × 200 mm, 250 × 250 mm, and others). Other parameters of the test are the shape of the impactor (i.e., flat, hemispherical, conical) and energy of impact (or velocity of the impactor, which is equivalent). In numerical simulations, the impactor is modelled as rigid, and the plates are fixed. The results obtained from the experiment are used to verify the model used in the simulations. The damaged zone, the kinetic energy of the impactor, force, and others are compared for both experimental and numerical simulation. Also, other basic tests such as tensile (or open-hole tensile) [27,28,29] or the three-point bending test [13, 30, 31] are often realized in an experimental campaign and then modelled using the finite element method. Other popular types of tests are buckling and post-buckling analysis [32,33,34].

Another field of interest for researchers is simulations under specific loading conditions. The double cantilever beam test following, for example, ASTM D5528 [35] lets us investigate the behaviour of the metal-composite interface under mode I loading conditions. This is realized by preparing the specimen with an initial crack (realized, for example, by using a PTFE strip during the manufacturing process) and then opening up the crack. Numerical simulations can be used to verify the values obtained for fracture energy or imitation stresses. In the case of non-standard specimens, they can also be used to obtain the mentioned values. Examples of papers are [13, 17, 36]. Another test is used to determine the fracture parameters only in mode II loading; it is called the end-notched flexural test (ENF) and it is based on the same type of specimen. The loading is carried out in a three-point bending system. The initial crack ensures pure mode II loading. The idea of the experimental and numerical approach, in this case, is similar to that described for the DCB test. Exemplary papers: [37,38,39]. The ENF tests of FML materials can be based on the ASTM standard for classic laminates [40]. Mixed-mode behaviour (mode I + II) can be assessed based on the mixed-mode bending test [41].

Another branch of numerical simulation of FML materials is thermal analysis [9, 10, 42, 43]. It is mainly focused on the manufacturing stage of material. Furthermore, it is possible to investigate the propagation of elastic waves in FMLs using FEM [44]. An important field of research is also buckling and post-buckling analysis [34, 45, 46]

In addition, when the material model is fully defined, it can also be used to analyze entire structures. For example, Abdullah in his thesis [47] simulated a fuselage crash made of FML using the finite element method. Another example can be found in Wittenberg et. al. [48], where the authors use the finite element method in the design process of shear panels for ultra-high-capacity aircraft made of FML. Today, there is many commercial and non-commercial finite element analysis (FEA) software. However, in more complex problems, some are more meaningful. For the analysis of metal fiber laminates, the most popular choice is Abaqus, developed by Simulia. The main advantages of Abaqus are its nonlinear performance and the possibility of modelling fracture and failure using a cohesive zone model (both surface- and element-based). Other popular software is ANSYS (only for implicit analysis) and LS-DYNA (only for explicit analysis). Very few papers use other simulation environments. There are a few examples of MSC Marc and MSC Nastran [29, 49, 50]. In Table 1, the results of the search for keywords in Scopus are presented (the search was carried out by showing articles that include FML and the name of the software in the title, abstract or keywords), for example, ‘TITLE-ABS-KEY (FML AND ANSYS)’. A different formulation of keywords can result in different numbers (as the presented approach is rather conservative and more papers are published on the subject), but the ratio is comparable.

Table 1 Distribution of software used for numerical simulations of FMLs for an exemplary search. Date of search 15.07.2021
Full size table

The important factor that can be decisive in terms of chosen software is the possibility to include own material models via own code written by a user. This is the feature of Abaqus, Ansys or LS-Dyna that support their popularity. The issue of the user-defined material model will be described in a wider manner further in the review.

2 Numerical Modelling and Static Failure of FML

In this section, the authors gathered information about the most important issues in numerical modelling of FMLs including dimensionality of the model, used type of finite elements, ways of defining material model etc. An additional aspect of numerical modelling including analysis of mesh size, friction, controlling scheme etc. will be described in chapter 5. At the end of this chapter different approaches to taking into account, the static failure of FMLs is presented.

2.1 The Dimensionality of the Model

Selecting the dimensionality of the simulation model is relevant for the simulation time and the quality. In this section, different possibilities are described with examples of usage in published research and analysis of potential advantages and disadvantages. Fiber metal laminates can be modeled as two-dimensional (plane) and three-dimensional models (see Fig. 1). In the case of a three-dimensional model, we can distinguish sold models and two approaches to shell models: continuum shell (with solid-like geometry, but a shell-like formulation of elements) and conventional shell.

Fig. 1
figure 1

Types of models used in numerical simulations of FMLs

Full size image

Presented in this subsection information should be analysed along with Sect. 4 about the metal-composite interface as it can make the difference in comparison to standard laminate composites. Different types of elements are used to model fibre-metal laminates. The most common approach is the three-dimensional solid model [6, 19, 20, 22, 27, 29, 38, 51,52,53,54,55] with usage of elements like C3D8R (eight-node linear brick, reduced integration, hourglass control) in Abaqus or SOLID184 /185/186 in ANSYS. Authors in [30] tested the usage of higher-order elements (C3D20R) but from the perspective of time, it is not necessary as accuracy gain is negligible in comparison to additional computational cost. A small inconvenience of using a three-dimensional solid model is that certain failure criteria are not implemented for such model in contrary to shell models including the most popular one—the Hashin criterion [56]. Of course, it is possible to implement it by yourself using a user-defined material subroutine, but it demands additional work. A detailed description of various criteria including Hashin criteria is presented in Sect. 2.3.

Another approach is to use two-dimensional solid models, which can be a very effective way of reducing the demanding computational time due to the reduced number of nodes (or DOFs). Giallanza et al. [37] used in ANSYS plane strain elements—PLANE182 for analysing fatigue behaviour of ENF specimen—such choice imply less complex computations. Due to the character of the fiber-metal laminates, the configuration is the same over the width of the specimens (plates). Some phenomena can occur that breaks this generalization, for example, three-dimensional analysis is capable of predicting the nonlinear course of the delamination front [57,58,59], while in a two-dimensional model the crack front has to be predicted as linear. However, in the research by Soroush [58] and Ning [60], two-dimensional models were used with good results, despite the simplification described. Two-dimensional models are also successfully used in the modelling of the manufacturing process (predicting thickness of the layers after the forming process) [9]. In the case of the two-dimensional solid model PLANE182 elements are often used in ANSYS and CPS4R (node bilinear plane strain quadrilateral elements) are an example for Abaqus.

Three-dimensional shell models have much fewer nodes in comparison to their solid counterparts which influence the computational cost. However, in the case of FMLs, it significantly reduces possibilities of defining interface metal-composites (wider discussed in Chapter 4) so it is much less right choice than in the case of classic laminates. However, it can be used if failure assessment is not the main purpose (for example [30]) or under other specific circumstances. Chang and Yang [61] used Abaqus and continuum shell elements in composite layers and eight-node solid elements in metal layers. Rajab et al. in [62] used shell SC8R elements. Also, some mixed approaches can be found in the literature. Sadighi et al. in [24] used SC8R elements (quadrilateral in plane continuum shell, reduced integration with hourglass control, and finite membrane strains) for modelling of composite layers and eight-node solid element (C3D8R) for aluminium layers.

The last of the described approaches is the continuum shell model. In this case, one can use three-dimensional solid-like geometry but with shell-like element formulation. This is some compromise between the shell and solid model. The use of the continuum shell element makes composite failure criteria available in Abaqus for three-dimensional geometry. The same criteria can be implemented using a user-material subroutine for solid elements, but such a simulation can be much more complex and computationally costly. However, the continuum shell approach can lead to some errors due to the lack of through-thickness stresses in comparison to the solid model [63]. Sadighi et al. [24] investigated the impact response of Glare 5–3/2 and used two different numerical models. The first one consists of only a solid layer and the second one has solid elements for the aluminium layers and continuum shell elements for the composite layer. The reasoning was that solid elements are probably more suitable; however, not the best tensile stress criterion was used (due to software limitations), and in the second case not the best elements but with a proper Hashin criterion was used. The conclusion of the impact test was that solid elements are much better than continuum shell elements. However, Nakatani et al. in [64] used a similar approach with continuum shell elements also in the analysis of low-velocity impact with good results. The lack of other examples does not allow one to formulate an unequivocal conclusion, and further investigation is needed in this area. Some researchers use a mixed approach and model aluminium layers as solid layers and composite layers as continuum shells [6, 8]. However, the aforementioned problems affect mostly composite layers, so it does not seem to solve the eventual problem.

There is a limited comparison between different approaches in the literature. Smolnicki and Stabla in [30] use both solid and shell models for assessing FML material in an elastic–plastic regime without failure and results for both of these approaches are comparable. De Cicco and Taheri [34] analyzed unusual fiber metal laminates characterized by the presence of glass pillars and urethane foam. Thus, the results obtained in this paper may not be fully transferable to the classic 2d-FML. In the mentioned paper, four different models were explored, namely solely solid (with modelled pillars, a second one only taking into account some effects from pillars, a thick shell model, and a conventional shell model. The authors reported that solid- and thick-shell models have similar behavior (with time 50% lower for thick-shell models). However, the solid model better predicts the shape of the deformation and the growth of the delamination. The fastest (95% less time than the thick shell model) was the shell model. However, the authors claim that it should only be used in static analysis with a low probability of damage.

Dhaliwal et al. [21, 53] modelled each layer as a separate shell and then connected them using the tie-break contact available in LS-Dyna. The authors state that FEA was successful in capturing the peak load and maximum central deflection. However, the tensile failure of the composite layer was not achieved properly. These problems are more related to the contact formulation and removing elements, so the shell model itself is successful in capturing the main behaviour of composite structures. Another example of modelling each layer independently and joining them with the tie option can be found in [9]. This method was also used to define contact between layers, which are activated after the cohesive elements are removed.

2.2 Material Modeling

After choosing the dimensionality of the model, the material model must be defined. One of the key stages in the preparation of a numerical model is the definition of the material model. In this section, aspects related to this topic will be presented. The first issue is to decide on which level of generalization such material will be defined. Second, the material can be defined using different constitutive relations. Finally, aspects related to the failure of the materials are covered in this section.

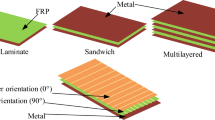
In the case of fiber-metal laminates, the important issue is the level of generalization. Three different levels of generalization can be used: macro-, meso-, and microscopic (see Fig. 2). The microscopic scale assumes that we define each constituent independently, including distinguishing fibers and matrices. However, this approach is hard to use in practice because of the complexity of the geometry (and, as an effect, a huge number of the elements needed to use) and the necessity of defining fiber-matrix interfaces. Eventually, such a scale is considered along with the representative volume element (RVE) method to obtain material data for the other levels of generalization [65].

Fig. 2
figure 2

Different scales of modelling. The micromechanical model distinguishes particular layers, as well as fibres and matrix in the composite layers. The mesomechanic model distinguishes each layer and the macromechanical model describes the material as a whole

Full size image

The most popular approach is to distinguish each layer of the fiber-metal laminate and define the properties independently for each of these layers. Kashfi et al. [50] have used a macroscopical approach to the material model. Each composite layer is assumed to be perfectly elastic. Metal layers are modeled as elastoplastic, with plastic behaviour being modeled using the Voce constitutive model. The material model for the whole material is then calculated using the rule of mixture (RoM) based on the properties of individual layers for both elastic and plastic regimes. The authors notice that this approach can lead to an oversimplification because of the omission of the metal-composite interfaces. They try to overcome this using a correction factor determined by them in previous work [66]. This approach led to reasonable results. However, it should be noted that they only analyze the tensile behaviour. The described approach is problematic because it completely omits the configuration of the setup. Another approach to the macroscopic model is derived from classical laminate theory. Using the so-called ABD-matrix, it is possible to derive engineering constants of the material as a whole based on the particular layers and their configuration. This approach was used by Smolnicki et al. [30] and is capable of reflecting the behaviour of the material in the elastic regime even in bending. Similar work was also presented by Zhang et al. [50], including the sublaminate method, where they report to be more exact. However, CLT or extended CLT do not take into account plasticity (composites generally do not exhibit it) so it is a disadvantage of this method. Perhaps mixing these methods can be an effective way for the macroscopic approach.

In the case of metallic constituents, researchers consider isotropic models. The most simple approach is fully linear isotropic [46, 55]. For most popular metals in FMLs such as aluminium and magnesium, the plastic behaviour is important and has a big impact on the response of the whole material. Different types of metal material models, including plasticity, are used: bilinear, isotropic hardening (multilinear) [8, 27, 30, 67] with rate dependence [52], and with the Johnson–Cook constitutive model [6, 10, 17, 18, 51, 64, 68] also in simplified form [69]. Researchers use strain rate-dependent models (also including hardening) are used by researchers for different problems, including low-velocity impact, which is a very popular test. However, for such problems, it can be excessive in the case of aluminium in low-velocity problems (and also in static test) is not sensitive to strain rates [70]. Composite layers must be modelled as orthotropic due to the direction of the fibre. Their behaviour is mostly elastic (governed by Hooke's law). Adhesive layers are usually materials such as epoxy resin or polyamide, which are isotropic. It should be pointed out that they should be modeled as elastic–plastic materials. However, the influence of simplification on the only elastic material has almost no effect [33], so from an efficiency point of view, it is not necessary to use it.

In many cases, the failure of the fibre metal laminates depends on the strength of the adhesive layer between the metallic and the composite layers. This issue is described in the next section. However, damage to other constituents can also be important, especially in the simulation of low-velocity impact, which is quite common. Thorsson et al. [71] proposed a model based on enhanced Schapery theory (EST) and discrete cohesive elements (DCZM) to predict the response to impact and the failure mechanism of the composite material subjected to low-velocity impact. In this work, the continuum shell model was applied to provide nodes at the top and bottom. These allow for capturing the traction separation relation of the adhering surfaces and avoid rotational degrees of freedom in the formulation of the cohesive law.

Erosion of elements can be necessary to properly simulate such tests, for example, strain-based erosion [69]. In the aluminium layers, ductile damage is widely used [19, 20, 22]. Ductile damage in Abaqus is a model that predicts the onset of damage based on a process of nucleation, growth, and coalescence of voids with the assumption that the equivalent plastic strain can be determined from stress triaxiality and strain rate [72]. Models that use that type of damage can be divergent under implicit integration schemes, so it can also be in the LS-Dyna environment rather than in Ansys.

In simulations that include thermal investigations, it is necessary to define various additional parameters including thermal conductivity, heat capacity as well as flow curves. In the case of aluminium (or other metal) it can be determined by the following model developed by Hensel and Spittel as described in [73]. In case of composite layers one can follow the model developed by Wang et al. [74]

2.3 Failure Criteria in Composite Layers

The failure criteria for composite materials can be classified in various ways. The first criterion is whether they are based on the fracture mechanics considering initiation and propagation of the failures in a macroscopic or microscopic scale or whether they are based on strength theories. Another option is to split criteria based on the fact that they are applied to a global, complex failure, or only for a specific failure mode. Finally, we emphasize in-plane or interlaminar failure mechanisms, such as delamination along with subsequent layers. The literature provides many theories that have been developed in the last 40 years, and due to the numbers and complexity of this topic, it could be addressed in a dedicated review. Thus, in this section, only the most popular criteria will be introduced.

In the beginning, specific failure modes were proposed to account for fibre failure, matrix failure, and delamination, depending on loading conditions. According to these failure modes, the failure theories will be presented. In composite materials, general-purpose failure criteria capable of determining failure in a few modes are common: Hashin criterion in Abaqus [6, 8, 53] or Ansys [46] and Chang-Chang criterion in LS-Dyna [21, 33, 69]. It should be noted that the Hashin criterion is available in Abaqus only for two-dimensional models (including shells) so researchers prepare user-defined subroutines for solid 3D models [9, 20, 28, 51], 75. In addition, other criteria are used that only predict damage initiation, such as Puck [46], Tsai-Wu [46], or Tsai-Hill [46]. Using user subroutines in Abaqus or similar solutions in other software, it is possible to use your damage model. Gerendt et al. [76] define a progressive damage model and apply it to the numerical simulation of bolted joints. Delamination in the fibre metal laminates is mostly modelled using cohesive elements or surfaces, as described further in this review. However, delamination criteria, such as Yeh's criterion, are also used [22, 28, 75]. An issue related to delamination is described in Chapter 4.

A short presentation including the failure criteria parameters used in the literature is presented in Tables 2 and 3, where σ, τ, ε and γ are used for stress and strain, normal and shear, respectively; X, Y, Z and S are the strengths, respectively, of the fibre, matrix, through-thickness directions and shear directions; subscripts 1, 2, and 3 refer to the fibre, transverse, and through-thickness directions; subscripts T and C denote limit values in tension and compression; subscript 'is' refers to in situ strengths.

Table 2 Fiber failure criteria for tension and compression mode
Full size table
Table 3 Matrix failure criteria for the tension and compression modes
Full size table

2.3.1 Fibre Failure Criteria

Regarding the failure mechanisms of composite materials, damage to the constituent materials must be described. As the first group of criteria, fiber failure criteria are presented. This group is mainly based on maximum stress and strain criteria for each ply, but also on in-plane shear that influences the accumulation of the fibre failure. In the case of the higher load with low strain values, this mode might be dominant.

2.3.2 Matrix Failure Criteria

Furthermore, matrix failure is a very important issue that needs to be considered. Mostly, matrix cracking should be characterized and described. Researchers trying to develop a model that will take this failure mechanism into account are using fracture mechanics approaches for the prediction of the initiation of cracks as well as their growth and accumulation. This process is more complex than appears in metals.

The presented above criteria are indicating the initiation of the failure. Further propagation of failure can be approached for example by progressive damage degradation in-built or defined in UMAT/VUMAT (see [75]) and finally by element deletion (often used in low-velocity impact). Presented in this section failure theories allow modelling of damage in composite materials. There is no general-purpose theory that considers all of the factors and mechanisms common in composite materials in their complexity. This fact leads to the combination of various models that predict their fracture behavior.

3 Numerical Simulation of the Fatigue Behavior of FMLs

Another important issue is modelling fatigue behaviour. The possibility of modelling the fatigue test cycle after cycle is restrained by computational costs and is nearly impossible in high- and very-high-cycle fatigue regimes. Several factors influence the fatigue behaviour of these laminates. It should be noted that the stress level will determine the failure mechanisms and the material that will be more affected by the cyclic load. In the case of experiments conducted in a high cycle fatigue regime, the metal layer will be affected, and crack nucleation and propagation will need to be investigated. By performing an experiment in a low-cycle fatigue regime (higher stress level), the composite plies will mainly bear the load. This leads to the fact that comprehensive knowledge regarding metal and composite materials is needed to apply proper damage theories.

Different methods are proposed to deal with fatigue damage. Asghar et al. [54] used the iterative approach to model fatigue crack growth in specimens with an open hole under tension. This approach is used successfully to model fatigue in simpler materials, such as steel [80]. The idea of the iterative approach is to make a dozen models, each for a different crack length. Such models are de facto static models without the crack propagation defined. However, it is possible to calculate, for example, stress intensity factors or other crack growth-driven parameters for each crack length and present the results in the time (or cycles) domain using all obtained data. The prediction of the fatigue life of an open hole under tension has been presented by Khan et al. [81]. The authors defined the empirical strength and stiffness degradation scheme combined with the cumulative damage accumulation approach. This analysis was performed in Abaqus using a user-defined material subroutine, UMAT. They established that this modelling has been highly mesh sensitive. Even though this solution is proposed for unidirectional composite materials, UMAT allows the definition of other material models and failure theories. It may be extended for fibre-metal laminates by implementing an additional model for the metal layer.

Giallanza [37] analyzed fatigue behavior in ENF specimens using another approach—progressive damage with ANSYS ADPL. In this method, the damage parameter D can be determined for given number of cycles. This dependency can be defined in different ways, but in the described paper, a Paris law (see Eq. 1) similar formula (with \({\Delta G}\) as a driving force) was used (see Eq. 2) with addition of the length of the damage process area. The results were in good agreement with the experimental results. Similar methods were used by Al-Azzawi et al. [82] who used the VUMAT subroutine for Abaqus to update damage variables based on the Paris law in a simulation of doubler (with additional external or internal layers) specimens and splices specimens (with staggered overlapped layers). However, contrary to the previous example, which was based on the bilinear law, here the trapezoid law was used and is claimed by the authors to be better in predicting damage initiation and growth. The fully degraded elements were removed from the simulation. Furthermore, Woelke et al. [67] try a similar approach with dissipative cohesive zone models.

Below Paris-Erdogan law based on \({\Delta }K\) as driving force is presented:

$$ \frac{da}{{dN}} = C \cdot \left( {\Delta K} \right)^{m} $$
(1)

where: \(a\)—crack growth, \(N\)—number of cycles, \(C, m\)—experimentaly determined constants, \({\Delta }K\)—stress intensity factor range. Researchers who work with the fatigue of FMLs prefer to use \({\Delta }G\) as a driving force (range of energies in one cycle) so they describe crack growth rate \(\frac{da}{{dN}}\) as:

$$ \frac{da}{{dN}} = C \cdot \left( {\Delta G} \right)^{m} $$
(2)

A notable solution has been presented in a paper submitted by Paepegem et al. [83]. The authors based their work on the observation of stiffness degradation and applied a local damage model with a scalar damage parameter. Using the mathematical software, the damage model was implemented into the code associated with commercial finite element software. This approach has consisted of three stages. First, the finite element calculation for one cycle is performed. In addition, the implementation of the NJUMP (percentile of cumulative relative frequency distribution) approach is pursued in the second stage; however, only local evaluations for each Gauss point are carried out. In the last step, the extrapolation of the damage accumulation of all Gauss points is performed for the global cycle jump NJUMP. If the total number of cycles has not yet been reached, the calculation through the loading cycle is repeated with an altered damage state. This solution was performed for composite materials without a metal layer; however, a similar approach can also be used in the case of FML materials.

Mazahari and Hosseini-Toudeshiky in [84] present a three-dimensional element for Ansys based on cohesive zone model formulation which included mixed-mode bilinear elastic–plastic-damage constitutive law. The authors of mentioned work proposed a solution that can be valid in low-cycled fatigue contrary to a proposition based on the Paris law valid mostly in the high-cycled regime. Damage evolution parameter is based on the Coffin-Manson relation [85]:

$$ \frac{{\Delta \varepsilon _{p} }}{2} = \varepsilon ^{\prime}_{f} \cdot \left( {2N} \right)^{c} $$
(3)

where: \(\frac{{\Delta \varepsilon_{p} }}{2}\)—plastic strain amplitude, \(\varepsilon_{f}^{^{\prime}}\)—fatigue ductility coefficient, \(N\)—number of cycles, \(c\)—fatigue ductility exponent.

4 Adhesive Layer Modeling

Specific for fiber metal laminate composites is the interface layer between metallic and composite substrates. Decisions about this layer can influence the results achieved in the simulation approach. In some cases, the interface can be omitted (assumption of perfect bonding) without harming the quality of the simulation. This can be true for deep-drawing simulations [62] and three-point bending [30]. However, other analyses conducted by the authors show that without a modelling interface, the model is not capable of reflecting experimental behavior. This difference is probably due to the different orientations of the fiber. This factor should always be taken into account during considerations before choosing a strategy to model FML under a particular type of loading, etc. Different approaches to the interface layer can be found in the literature. Cheng and Yang [61] chose cohesive elements with finite thickness. However, a cohesive layer can also be modelled with zero thickness. In this case, the nodes of this layer are located exactly in the same place as the nodes of the bonded layers. This approach also allows us to define traction–separation relations and, in effect, develop fracture during the simulation.

Zero-thickness elements with tie constraints to neighboring layers are used by Asghar et al. [54] to define adhesive layers in examples of fibre-metal laminates such as GLARE, ARALL, and also CARALL. Another approach is to use cohesive surfaces. In this case, an adhesive layer is modelled as the contact behaviour between bonded layers rather than the layer itself. Giallanza [37] used such an approach in the ANSYS environment along with target elements (which further reduced computational cost). Dhaliwal et al. [16] and Sasso et al. [53] used shells for each layer and then defined contact with ties.

Using cohesive elements, one has better control over the stiffness and mesh density than in the case of the contact definition. However, the cohesive surface definition has one significant advantage—it is capable of modelling repeated bonding after initial delamination. Additionally, not the whole surface must be in bonded state at the beginning of the simulation, which allows the model, for example, PTFE to insert easily. In the case of non-zero thickness cohesive elements, we need to have a gap in place of an insert or model PTFE with seam. Another advantage of cohesive surfaces is the fact that friction can be defined between layers, which makes the model more sophisticated. More information about friction in models can be found in further sections. Examples of cohesive surfaces as a way to model interfaces can be found in: [6, 17, 25, 51, 52].

Cohesive elements can be used with different definitions of cohesive behavior, whereas the cohesive surface can be used with only the traction–separation law (TSL). However, TSL is recommended to model different tests with FMLs and is widely used by researchers [19,20,21,22, 27, 37, 82, 86]. Soroush et al. [58] state that cohesive surfaces can significantly reduce computational cost.

Duda et al. [13] model DCB test using both approaches: with cohesive element and with cohesive surface based on 2D modelling. The schematic view of these approaches is presented in Fig. 3. Both methods were able to determine the maximum force and the displacement at the maximum force. However, the force–displacement curve before this point was significantly better mapped by the cohesive element method.

Fig. 3
figure 3

Example of the usage of cohesive surfaces (upper part) and cohesive elements to model the interface between metal and composite layers (DCB specimen). (Own work based on authors’ graphics from [13] under CC BY 4.0 https://creativecommons.org/licenses/by/4.0/legalcode)

Full size image

Another approach that can be used is eXtended Finite Element Method (XFEM). In this method, the crack can propagate not only via nodes but also through the element. Applying cohesive elements or cohesive surfaces, initiation and propagation criteria need to be defined. It is usually done for elements in the area where crack propagation is likely. However, since crack can propagate through elements, coarser mesh can be used in a smaller model, which can lead to a less complex model [87]. De Cicco and Taheri [88] compare the cohesive elements approach with the XFEM approach and also the mixed one. They point out that using XFEM can lead to more accurate results, however, for complex geometries cohesive elements are the better choice in terms of solution time especially if a crack path is known a priori. Other examples of XFEM usage can be found in [89] and [17].

Other approaches such as the element-free Galerkin method (EFG) and the discrete element method (DEM) are suggested to be considered [88] in future research, as they are capable of predicting crack paths in other types of materials.

In addition to the basic properties of the adhesive layer material described in Sect. 2.2, the damage mechanism must be defined for this layer. The cohesive zone model introduced by Dugdale [90] and Barenblatt [91] in the 1960s is widely used to model cohesive behavior of metal –composite interfaces e.g. [20,21,22, 27, 37, 54, 62, 82]. This model assumes that the initiation and propagation of damage occur in a zone around the tip of the crack. The proposition is to describe the stresses in that zone as a function of the opening displacement. Such a function is called the traction separation law (TSL):

$$ \sigma = f\left( \delta \right) $$
(4)

The form of the function can be simple as bilinear along with trapezoid or more sophisticated as exponential. The key parameters that must be defined while preparing the numerical model are the maximum cohesive strength (traction) and the fracture energy (critical energy release rate). The final opening displacement can be equivalent to defining the critical fracture energy. In the case of more complicated types of functions f, also additional information is required.

Traction–separation law parameters necessary in a material model can be determined in experimental tests. Such tests are designed to reflect specific modes of loading because the TSL shape is different for different loading conditions. In mode I, the double cantilever beam test can be used according to ASTM standards (refer to Fig. 4) [35]. This standard is designed for unidirectional composites, not for fibre metal laminates, but can be used with some corrections. One of the requirements defined in the standard is that both cantilever beams have the same stiffness, which cannot always be fulfilled. Another possible problem is the plastic behaviour in the metal layers. In such cases, one can use combined experimental and numerical approaches. Manikandan and Boay Chan [92] with numerical simulation were able to determine the fracture energy under an elastic and plastic regime based on the experiment. The authors in Duda et al. [13] analysed an asymmetric (in terms of stiffness and geometry) inverted FML with two cohesive layers. For such a configuration, the fracture energy cannot be calculated directly based on the experimental data. Using numerical simulation, it was possible to obtain the fracture energy in mode I. Then, this value was successfully used in other research by the authors. A similar approach can also be found in [93]. Coherent strength is determined based on the DCB test or the Normal Coherent Strength (NCS) test [94]. In mode II, the most popular approach is to use the end-notched flexural (ENF) test. The tests can be based on another ASTM standard [73] designed once again for unidirectional composites. The problem of asymmetry can be solved using numerical modelling and fitting or using an analytical approach to AENF specimens [39].

Fig. 4
figure 4

Trapezoidal traction–separation law and definition of notable separation values (not to scale). The model represents the ductile type of fracture

Full size image

Fracture energy is the parameter responsible for damage propagation. To evaluate the start, different criteria are used. These criteria are based on the maximum values of stresses (traction) in a normal direction \(t_{n}^{0}\) and shear direction \(t_{s}^{0}\) and \(t_{t}^{0}\). For simplicity of the notation ratio of the current value to maximum values, we will use the following. The \(\left\langle x \right\rangle \) symbol denotes Macaulay bracket defined as:

$$ \left\langle x \right\rangle = \frac{\left| x \right| + x}{2} $$
(5)

The simplest criterion for evaluating the level of the stresses, independently for each mode, is given by:

$$ \max \left\{ {\frac{{\left\langle {t_{n} } \right\rangle }}{{t_{n}^{0} }},\frac{{t_{s} }}{{t_{s}^{0} }},\frac{{t_{t} }}{{t_{t}^{0} }}} \right\} = 1 $$
(6)

However, such an approach does not take into account interdependencies between different failure modes. Therefore, in the case of fibre metal laminates, the most common criterion is the quadratic nominal stress criterion [8, 20, 55], where all modes participate at the same time in the evaluation.

$$ \left\{ {\frac{{\left\langle {t_{n} } \right\rangle }}{{t_{n}^{0} }}} \right\}^{2} + \left\{ {\frac{{t_{s} }}{{t_{s}^{0} }}} \right\}^{2} + \left\{ {\frac{{t_{t} }}{{t_{t}^{0} }}} \right\}^{2} = 1 $$
(7)

Unfortunately, real loading conditions, or even some laboratory test loading, are in mixed mode. Therefore, the traction–separation law parameters obtained for mode I and mode II must be somehow interpolated to reflect different mode-mixicities (refer to Fig. 5). The method proposed by Benzeggagh and Kenane [95] is often used [10, 13, 20, 21]. Mixed-mode fracture energy \(G_{TC}\) in this approach is calculated based on the fracture energy in independent modes \(G_{IC} , G_{IIC} , G_{IIIC}\):

$$ G_{TC} = G_{IC} + \left( {G_{IIC} - G_{IC} } \right) \cdot \left( {\frac{{G_{II} + G_{III} }}{{G_{I} + G_{II} }}} \right)^{m} $$
(8)
Fig. 5
figure 5

The idea of traction–separation law (in this case bilinear) in mixed mode I + II

Full size image

Here, the exponent m is claimed to be a material parameter.

Another option used in research [22] (both already accessible in the main FE environments) is the power law, which is based on the fracture energy in independent modes \(G_{IC} , G_{IIC} , G_{IIIC}\) normalization. A value equal to 1 determines the progress of the fracture:

$$ \left( {\frac{{G_{I} }}{{G_{IC} }}} \right)^{\gamma } + \left( {\frac{{G_{II} }}{{G_{IIC} }}} \right)^{\gamma } + \left( {\frac{{G_{III} }}{{G_{IIIC} }}} \right)^{\gamma } = 1 $$
(9)

5 Other Aspects of Numerical Modelling

In this chapter, other important aspects of numerical modelling will be discussed with particular attention to symmetry and mesh size sensitivity. Further, other issues besides mesh aspects will be briefly presented, including friction, validation, and steering.

The utilization of symmetry is a common way to reduce the computational time of finite element simulation. However, not only geometric symmetry is demanded, but also material and boundary condition symmetry. In fiber metal laminates, because of the presence of fibers in the composite layers, the material symmetry is not always verified. With specific layups consisting of 0 and 90-degree layers and some loading conditions, it is possible to take advantage of symmetry modelling: half of the specimen [18, 29, 54, 82] or even quarter [55, 69].

An important aspect of every finite element method simulation is the mesh size sensitivity. It should be appropriate for the problem analyzed. Similarly to standard materials simulations, the mesh is often finer in the region of applied boundary conditions or mechanical notches and coarser in other regions to save computational costs [24]. The limitation of computational capabilities and the decrease in simulation time are factors that influence the rationale for mesh size [51]. However, a too coarse mesh may be the reason for result errors. Mesh sensitivity studies are methods for determining the balanced mesh size (in terms of exactness and time-consuming) of the mesh size. Giallanza et al. [37] test four different average finite element sizes for simulations of ENF samples under fatigue loading. In simulations of the FMLs, often cohesive elements or cohesive surfaces are used to model the interface behaviour between metal and composite layers. In such cases, element size along interfaces is crucial (and predicted delamination). To evaluate the necessary element size, Hillerborg et al. [96] proposed the concept of characteristic element length, given by the formula:

$$ l_{{ch}} = E \cdot \frac{{G_{c} }}{{\sigma _{{\max }}^{2} {^{2} }}} $$
(10)

However, this method can significantly overpredict the minimal element size [97]. Thus, mesh-sensitivity studies for such issues are also a good choice. Duda et al. [13] presented a study of mesh sensitivity for the cohesive interface in an analysis of the DCB test. The extracted size of the finite element can later be used in other works that use the same material and similar loading (mode I). There is a limitation of this approach—it is hard to do mesh sensitivity studies if the simulation time is substantial. Other examples of mesh sensitivity/convergence studies in the case of FMLs can be found in [17, 27, 38, 43, 69, 98].

Another aspect of the mesh size is connected to the damage model. If the dissipated energy is used directly to evaluate the progress of damage in the element, then with the refinement of the mesh, this energy approaches zero as it is proportional to the element volume. The solution to this problem can be to use the characteristic length of the element and to evaluate the displacement instead of the strains in the element. Such a method should make the model less mesh-dependent according to the crack band theory [99]. This approach was used in [10].

In the case of some tests like low-velocity impact mesh different mesh sizes can be used based on the distance from the impact point. The calibration process is suggested to find the area in which the mesh should be fine to capture complex damage mechanisms [18].

Friction behaviour is another aspect of numerical modelling of FMLs. The friction between testing equipment, such as stamps and supports, is in most cases not important for overall results to the best of the authors' knowledge and is often not reported by researchers in papers. Nassir et al. [8] assume that the friction coefficient between the impactor and the composite is 0.1. Azhdari et al. [10] use a value of 0.3 between the impactor and the metal layer. However, friction can have a significant influence on the results if it occurs between layers of the material itself. For example, Giallanza et al. [37] point out that this friction in the case of ENF samples has a strong influence on the numerical simulation. Yu et al. [68] assume that the friction coefficient between the aluminium and composite layers is 0.3. Sharma et al. [52] state that the friction coefficient that should be used depends not only on the materials building neighboring layers but also on the fiber orientation. They used a friction coefficient of 0.5 between the composite layers with orientations 0 and 90 (the matrix was epoxy resin) and 0.3 between the aluminium and the composite layer. Yet another value was used by Irani et al. in [9] where they took initial value 0.1 for all interfaces and then value between 0.1 and 0.05 depending on the temperature, which was better for the results. The big discrepancies in the friction values used between different authors (and lack of data in a lot of papers) as well as the fact that it seems to influence the results, point to that further research is necessary.

Validating the numerical model will allow it to be used in the design stage of a new combination of the material. Due to many different aspects of the fibre metal laminates, such as constituent materials, the thickness of layers, configuration, fibers orientation, etc., it is hard to check all these things experimentally. The most common way of validating a numerical model based on the experiment is to compare directly obtained results with numerical ones. It should be taken into account that the finite element method generally overestimates the results [68]. In addition, the method performed with external equipment such as digital image correlation (DIC) or acoustic emission (AE) is used for the same purpose. Rubio-Gonzalez et al. [55] use two-dimensional DIC to measure strains in specimens with an open hole under tension. The strain distribution obtained was compared with the FEM results. Other articles used the DIC method to validate numerical results [100]. Acoustic emission can be treated as a tool to analyse the damage mode under load. This can be used to compare with the output of general composite failure criteria such as Hashin or Chang-Chang. Acoustic emission was used with success by Al-Azzawi et al. [82].

Numerical models involving FMLs are usually computationally complex due to different materials used, cohesive layers, contact involved, etc. In addition to the methods mentioned above, such as mesh refinement, homogenization, using symmetry, or using two-dimensional models, other techniques can also be used: time scaling [7], mass scaling [25], and hourglass effect control [70].

Simulation control and boundary conditions definition can be crucial for the precision of numerical model results. Due to the diversity of tests, it is hard to point out the general rules. However, some general conclusions can be drawn. Due to the complexity of the problem, steering by displacement rather than force is preferred. Often boundary conditions are defined for reference points and then transferred using couplings.

Standard material models implemented in commercial software are often not enough good for modelling FML materials. However, researchers can implement their own models using user subroutines in Abaqus UMAT [52, 76, 86] (for static problem in Standard or Implicit module) or VUMAT [9, 20, 22, 25, 68, 75, 82] (for dynamic problem in Explicit module), LS-Dyna UMAT [42] or Ansys Parametric Design Language (APDL) in Ansys [37]. The most popular thing implemented using these approaches is the three-dimensional Hashin criterion.

6 Conclusions

Fiber-metal laminates are hybrid materials consisting of both metal and composite layers. Numerical modelling of such structures draws a lot from approaches to these constituent materials. However, an additional challenge is also to properly model the behavior of the bonding layer (interface composite—metal). In this review, the authors summarize the current state of knowledge in the field describing used software, material models in terms of scale, and the definition of constituents. The authors present criteria that describe the failure of particular layers and the fracture of the adhesive layers, including the fatigue behavior. Finally, the influence of the mesh size and other specific aspects of FEA issues are described. Throughout the article, some conflicting stances are presented, especially in the area of modelling space and ways to define adhesive behavior. The authors also try to present their contributions to these fields. Some issues need to be further investigated by researchers, as there is not enough contribution to defining strict opinions, especially on issues related to fatigue behavior. As shown in this paper, fiber metal laminates can be modelled in various ways; however, the choice of a particular solution should always be proceeded by careful analysis of needs, as these ways have their advantages and disadvantages.