1 Introduction

When a soil element is continuously sheared, it eventually flows as a frictional fluid and reaches a well-defined critical state, CS [64, 68]. Schofield, Wroth [68], in their definition of CS, did not make any reference to fabric-related entities other than the scalar-valued void ratio \(\left(e\right)\). Therefore, the CS was fabric independent, i.e. based on fabric isotropy. These CSs from many tests/conditions form a unique critical state line (CSL), which is taken as the reference line to understand/predict a soil element’s behaviour within the critical state soil mechanics (CSSM) framework. Such a fabric-independent CS and CSL proved to be sufficient for many loading conditions for many soils. A mathematical definition of such a CSL, in terms of mean effective stress \(({p'})\), deviatoric stress \((q)\) and void ratio \((e)\), can be presented by

$$\eta ={\eta }_{c}={(q/p')}_{c}=M$$
(1)
$$e={e}_{c}={\widehat{e}}_{{\text{c}}}(p')$$
(2)

where, M is the ratio of \(q\) and \(p'\) at CS, which is a constant and intrinsic material property. \({e}_{{\text{c}}}={\widehat{e}}_{{\text{c}}}(p')\) is the critical state void ratio expressed as the function of \(p'\) in \(e-{\text{log}}(p')\) space. For conventional triaxial tests, the \({p}^{\prime}\) and q can be simplified to \({p}^{\prime}=({\sigma }_{1}^{\prime}+2{\sigma }_{3}^{\prime})/3\) and \(q=\left({\sigma }_{1}^{\prime}-{\sigma }_{3}^{\prime}\right)\), respectively; where, \({\sigma }_{1}^{\prime}\) and \({\sigma }_{3}^{\prime}\) are the axial stress and effective radial stresses, respectively. Equations (1) and (2) define a unique CSL in e-q-p′ space. Often, as in this paper, the name CSL is used to denote the line in the e-p′ space, expressed by the following power function as proposed by Li and Wang [34]:

$${e}_{c}={\widehat{e}}_{{\text{c}}}(p^{\prime})={e}_{{\text{lim}}}-\Lambda {\left(\frac{p\mathrm{^{\prime}}}{{p}_{{\text{a}}}}\right)}^{\xi }$$
(3)

where, \({e}_{{\text{lim}}}\) is the void ratio on CSL at p′ = 1 kPa, Λ and ξ are fitting parameters and pa is atmospheric pressure of 100 kPa. A soil element’s behaviour in shearing is controlled by its current state in relation to its reference state, i.e. CSL. For example, if a soil element state is above the CSL in e-p′space, the soil state moves leftward to meet CSL during undrained shearing. As a result, soil element exhibits contractive behaviour. On the other hand, if the state of the soil element is below the CSL, then during undrained shearing, the state moves rightward to meet CSL. As a result, soil element displays dilative behaviour. Many researchers realised this attribute [e.g. 4,5–7], and they tried to evaluate it by different measures of states such as state parameter [4], state index [19], stress ratio [26], pressure index [79], and modified state parameter [5]. Among these measures, the most commonly used parameter is the state parameter \(\psi\) suggested by Been, Jefferies [4]. \(\psi\) is the difference of void ratio at the current (\(e\)) state and critical state (\({e}_{{\text{c}}}\)) at the same p′. This can be presented by the following equation:

$$\psi =e-{e}_{{\text{c}}}$$
(4)

It was found that \(\psi\) correlate with characteristic behaviours of granular materials, e.g. peak failure stress ratio [81], stress ratio at phase transformation (ηPT) [38, 90], instability stress ratio (ηIS) at peak q [28, 58, 60], cyclic instability type liquefaction [2, 3, 56, 63]. Therefore, subsequently, \(\psi\) is used in constitutive modelling [9, 10, 14, 22, 31, 38, 81] by improving/modifying the correlation of characteristic features as a function of \(\psi\).

However, many studies revealed that the granular soil response during almost all stages of loading history is fabric anisotropic [42, 50, 65, 88]. Therefore, CS without fabric, except for a scalar value of \(e\), may be sufficient in many conditions but cannot be complete. Indeed, when introducing their \(\psi\), Been, Jefferies [4] suggested that the CS in soil may be fabric-dependent or anisotropic. Both experimental and numerical studies attempted to define fabric anisotropy by linking them to the arrangement of soil particles, voids and interparticle contacts and the effect of applied loads on these microstructures [1, 6, 41, 48, 67, 70, 87]. Li, Dafalias [32] proposed a fabric anisotropic variable (\(A\)) to capture fabric anisotropy and its fabric evolution as below-

$$A={F}_{ij}{n}_{ij}$$
(5)

where, \({F}_{ij}\) is the deviatoric fabric tensor and \({n}_{ij}\) is the unit-norm deviatoric tensor-valued direction, both of which are defined later in this study (refer to Sect. 2.2). Li and Dafalias [32] also proposed the anisotropic critical state theory (ACST) by extending the definition of CSL with the inclusion of \(A\) in Eq. (6). The third term is the extension of original definition of CSL in Eq. (1) and Eq. (2).

$$\eta ={\eta }_{{\text{c}}}=M, \quad e={e}_{{\text{c}}}={\widehat{e}}_{{\text{c}}}\left(p^{\prime}\right), \quad A={A}_{{\text{c}}}=1$$
(6)

This allows an extension of \(\psi\) for fabric with the inclusion of \(A\) to the dilatancy state parameter, DSP (\(\upzeta\)). Li, Dafalias [32] used a combined norm of the distance for the current value of both e and \(A\) to their corresponding critical state as shown below-

$$\upzeta =\psi -{\psi }_{A}=\psi -{\widehat{e}}_{A}(e,p^{\prime})(A-1)$$
(7)

where \({\widehat{e}}_{A}\left(e,{p}^{\mathrm{^{\prime}}}\right)\) is a function on e and p′. However, Li, Dafalias [32] used a constant value for simplicity and left open the possibility for other expressions, in particular, to achieve better simulations while maintaining the basic premises of \(\upzeta =\psi\) when A = ACS = 1 at CS are satisfied. Along this line, Rahman, Dafalias [57] modified the DSP by defining \({\widehat{e}}_{A}\left(e,{p}^{\mathrm{^{\prime}}}\right)\) as below-

$${\widehat{e}}_{A}\left(e,{p}^{\prime}\right)={e}_{A}\frac{\langle {e}_{{\text{lim}}}-e\rangle }{\left({e}_{{\text{lim}}}-{e}_{{\text{c}}}\right)}$$
(8)

where, \({e}_{A}\) is a fitting parameter. The Macauley brackets define the operation ‹a› = a for a > 0 and ‹a› = 0 for a ≤ 0. Thus, for (\({e}_{{\text{lim}}}-e<0\)), Eq. (7) yields \(\upzeta =\psi\).

However, further research is needed to verify the above-proposed equation using micromechanical approaches. The main motivation of the current study is to provide further evidence and to evaluate the above model using three-dimensional Discrete Element Method (DEM) simulations.

DEM can be a useful micromechanical tool to understand granular soil anisotropic response and its evolution with loading [35, 39, 44, 47, 48, 75, 80, 83, 93]. It allows the examination of particle-scale interaction, contact, or fabric to establish a link with the macro-response. Many previous studies effectively capture fabric anisotropy evolution but may not directly translate or connect to continuum mechanics, especially within the context of ACST, which is the focus of the current study. In this study, the \(\psi\) (classic state parameter without fabric Been, Jefferies [4]), DSP \(\upzeta\) Li, Dafalias [32] and modified DSP \(\upzeta\) [57] were utilised to evaluate their link with characteristic features (e.g. instability, phase transformation and characteristic state) and to explore the effect of microstructural fabric anisotropies on macroscopic shear behaviour. It also enhances understanding of fabric evolution in constitutive modelling.

2 Dem modelling

2.1 Triaxial test simulation

The DEM software, PFC3D [21], was used in this study to perform the numerical simulation. The specimen was represented in a cubic space confined with three pairs of stress or strain-controlled friction-less walls, as shown in Fig. 1a. Wall stiffness should be much larger than particles to avoid unnecessary wall deformation and to ensure constant volume during undrained tests. Therefore, the wall stiffness was 1 × 107 kN/m [21, 30]. The soil particles are modelled as spheres with the particle size distribution (PSD) of Toyoura sand [19] and with a linear force–displacement contact law (see Fig. 1b, c). It should be noted that in definition of the contact model, the force–displacement law is not applied to inactive contacts (refer Fig. 1a for particles with less than two contacts). Non-spherical particles may be a more realistic representation of soil assembly [46, 62], but have not been adopted in this study to avoid intensive computation and excessive complexity. The contact stiffness varied on orders in literature [16, 17, 29, 36, 40, 69, 72, 74]. However, Li [30] showed that the contact stiffness would not have a significant impact on soil behaviour at large strains. In this study, the most commonly used normal and tangential stiffnesses have been adopted as \(\frac{{k_{n} }}{r} = \frac{{k_{s} }}{r} = 10^{5} \;{\text{kN}}/{\text{m}}^{2}\) [16, 25, 84]. The simulation parameters are summarized in Table 1.

Fig. 1
figure 1

a Specimen with particles in the simulation, b particle size distribution, c contact model

Full size image
Table 1 The input parameters of DEM modelling
Full size table

Triaxial specimens, prior to the consolidation, were prepared as the following procedure:

  • Specimen generation: The random distribution method has been adopted to generate specimens with 13,570 spheres (the effect of the number of particles is discussed in the appendix). Initially, particles overlapped greatly, and strong repulsive forces arose. Therefore, some cycles were needed by the system to reach equilibrium and generate a specimen without overlap. Interparticle friction coefficient \(\left(\mu \right)\) was temporarily set to zero during this stage.

  • Initial state: Since all specimens were generated by the same mechanism, therefore the contact forces throughout the assembly are expected to be similar, resulting in an isotropic uniform network of contact forces similar to the radii expansion method [16, 23, 53]. An isotropic stress of 10 kPa by servo control of the walls was applied to the specimen. During this stage, different \(\mu\) were used to generate specimens with different densities [82, 84]. Generally, a low value of \(\mu\) generates a dense specimen, while a high μ value generates a loose specimen. This was an effective technique of sample generation since it allows the generation of a homogeneous network of contact forces and particle distribution within the created samples [61]; it is computationally efficient and avoids the onset of high lock-in contact forces.

  • Isotropic consolidation: Upon finishing this stage, µ was changed to 0.5, and the specimen was cycled again to an equilibrium state. Now, the specimen was assumed at its initial state and is ready for isotropic consolidation. As summarised in Table 2, a total of 108 specimens have been prepared in different confining pressures under undrained and drained conditions (54 specimens each).

  • Monotonic shearing: For the drained triaxial test, the strain-controlled top and bottom walls were compressed (axial strain), while the stresses on the side walls were kept constant using a servo mechanism simulating constant cell pressure. On the other hand, the undrained triaxial test was simulated by a constant volume test, in which the total volume of the specimen remains constant by servo control of the walls and the stresses of the wall are assumed to be effective stresses [21, 30]. Hence, the excess pore water pressure during the shearing equals the difference between the current effective stress and initial confining pressure on the vertical walls.

Table 2 Summary of the test simulations
Full size table

2.2 Stress tensor and fabric tensor

In order to quantify the macroscale response of a DEM assembly, the stress tensor must be defined in terms of discrete quantities such as particle displacements, contact normal, and contact forces by means of an averaging procedure [37, 51]. In a granular assembly, boundary loads are distributed among the intergranular contacts. The balance between boundary loads and internal forces leads to the expression for stress tensor as proposed by Christoffersen et al. [8]:

$${\upsigma }_{ij}=\frac{1}{V}\sum_{{\text{c}}\in {{\text{N}}}_{c}}{f}_{i}^{c}{l}_{j}^{c}$$
(9)

where, \({\upsigma }_{ij}\) is the stress tensor, V is the volume of the assembly, Nc is all contact points in V, \({f}_{i}^{{\text{c}}}\) is the corresponding force vector between particles, \({l}_{i}^{c}\) is the branch vector joining the centres of two contacted particles. By calculating the stress tensor components, it would be possible to calculate effective confining pressure (p′) and deviatoric stress (q) based on Eqs. (10) and (11).

$${p}^{\prime}=\frac{{\sigma }_{ii} }{3}$$
(10)
$$q=\sqrt{\frac{{3.s}_{ij}{s}_{ij}}{2}}$$
(11)

where, \({s}_{ij}={\sigma }_{ij}-{\delta }_{ij}{p}^{\prime}\) and \({\delta }_{ij}\) is the Kronecker delta.

The spatial distributions (i.e. anisotropies) of the contact normal and contact forces play a significant role in the shear behaviour of granular soil, which can be characterised using fabric tensor in DEM. Among the various definitions of fabric tensor [e.g. 18, 24, 33, 48], the contact normal-based proposition by Satake [67] and Oda [49] was adopted here:

$${\varphi }_{ij}=\frac{1}{N}\sum_{{\text{c}}\in {{{N}}}_{c}}{n}_{i}^{c}{n}_{j}^{c}$$
(12)

where, \({\varphi }_{ij}\) is the fabric tensor, \({n}_{i}^{c}\) is the unit vector along the normal direction of the contact plane; and N is number of contacts in the specimen.

The deviatoric fabric tensor can also be defined as below:

$${F}_{ij}={\varphi }_{ij}-\frac{1}{3}{\delta }_{ij}$$
(13)

In order to characterise the fabric anisotropy, a scalar value obtained from deviatoric fabric tensor is usually used to quantify the degree of fabric anisotropy. This scalar value can then be used together with the scalar valued stress ratio \(\left(\eta =q/p^{\prime}\right)\) and void ratio (e) to define the conditions for a critical state outlined in Eq. (6).

To examine whether the unique critical state features can be identified for fabric anisotropy at CS, a number of variables such as FAV A as expressed by Eq. (5), von Mises invariant \(\left({F}_{{\text{vm}}}\right)\) of fabric tensor proposed by Huang et al. [18] and stress-fabric joint invariant \(\left({K}_{{\text{F}}}\right)\) defined by Zhao and Guo [91] are adopted in this study, all of which are further discussed in the following sections.

3 Results and discussions

3.1 Simulation program

Table 2 summarises the test program in this study. Each test is identified by the loading condition, initial confining pressure \(\left({p^{\prime}}_{0}\right)\) and initial void ratio (e0) of the specimen. For example, CIU-70-0.725 indicates isotropic undrained compression (CIU) test on a specimen that was under a \({p^{\prime}}_{0}\) of 70 kPa and had an e0 of 0.725 at the end of consolidation. For the same token, CID means isotropic drained compression test.

3.2 Macromechanical behaviour

The undrained behaviours of specimens with the same \({p^{\prime}}_{0}\) of 100 kPa but at different e0 are shown in Fig. 2. All specimens, including in Fig. 2, reached/approached CS at a large strain.

Fig. 2
figure 2

Undrained behaviours of specimens with different densities: evolutions of a deviatoric stress vs ε1; b effective stress path; c excess pore water pressure vs ε1

Full size image

As can be seen in Fig. 2, the typical undrained mechanical behaviours comparable to the experimental observations [76] can be identified in the simulation. CIU-100-0.574, CIU-100-0.631 and CIU-100-0.660 show dilative behaviours, CIU-100-0.709 shows phase-transformation behaviour, and CIU-100-0.718 shows static liquefaction. Accordingly, the specimens with e0 of 0.574, 0.631 and 0.660 can be considered as very dense to dense specimens, and the specimens with e0 of 0.709 and 0.718 can be considered as medium dense and very loose specimens, respectively. As expected by the theory of critical state soil mechanics, a unique CSL can be drawn for these states, as shown in Fig. 2b.

The drained behaviours of the specimens with the same \({p^{\prime}}_{0}\) of 100 kPa but at different e0 are presented in Fig. 3. The dense specimen exhibits a softening behaviour after reaching an initial peak, whereas the loose specimen shows a continuous hardening behaviour. As expected, all specimens finally reach a unique CS with constant values of e, \({p}^{\prime}\) and q by either dilation or contraction.

Fig. 3
figure 3

Drained behaviours of specimens with different densities: evolutions of a deviatoric stress vs ε1; b void ratio vs p′; c volumetric strain vs ε1; and d stress ratio vs dilatancy factor, D

Full size image

Figure 4a shows the critical state lines deduced from 108 undrained and drained tests in this study. The best-fit relation can be presented by the power function expressed in Eq. (3) in which \({e}_{{\text{lim}}}= 0.723\), \(\Lambda = 0.018\) and \(\xi = 0.9\). As seen in Fig. 4b, the CS data points can be described by a single line with a slope of 0.78 in q–p′ space which is actually the stress ratio, M, as expressed in Eq. (1). These CS parameters will be used in following sections for calculation of classic and dilatancy state parameters.

Fig. 4
figure 4

Critical state lines in a \({e-p}^{\prime}\) plane and b \(q-{p}^{\prime}\) plane

Full size image

The above results indicate that the DEM simulations are able to capture all features of the macroscopic density- and pressure-dependent behaviours of granular soils. To explain the macroscopic behaviour at the grain-scale, the microstructure and its evolution during shearing, including contact numbers, contact forces, contacts distribution and microscopic geometry, are discussed using contact- and fabric-based variables in the following sections.

3.3 Micromechanical behaviour

3.3.1 Evolution of contact number

To explain the behaviour of granular soil in micro-scale, the contact density of the model is studied using the mechanical coordination number \(\left({Z}_{{\text{m}}}\right)\). It should be noted that \({Z}_{{\text{m}}}\) excludes the particles with zero or one contact, as they do not contribute to a stable state of stress during shearing. Particles with less than two contacts are shown in Fig. 1.

Figure 5 shows the evolution of \({Z}_{{\text{m}}}\) in the undrained and drained tests. As expected, the initial \({Z}_{{\text{m}}}\) of a specimen increases with increasing initial density. During the undrained tests, the \({Z}_{{\text{m}}}\) of dense specimens (e0 = 0.574 and 0.631) decrease rapidly first and thereafter increase gradually with further shearing. Regarding the medium-dense specimen (e0 = 0.660), the \({Z}_{{\text{m}}}\) gradually decreases to a minimum value at quasi-steady state and then increases with further shearing due to an increase of \(p^{\prime}\). For a very loose specimen (e0 = 0.718), the \({Z}_{{\text{m}}}\) decreases continuously to a limited value of around 8.0 and then suddenly drops to zero. This can be considered as a sign of soil collapse and the occurrence of static liquefaction. The \({Z}_{{\text{m}}}\) value of specimens in the drained tests increases slightly first and then decreases continuously until reaching a critical state with identical \({Z}_{{\text{m}}}\), which is consistent with numerical observations by Duran [11] and Rothenburg [66].

Fig. 5
figure 5

Evolutions of mechanical coordination numbers Zm vs ε1 a undrained tests; b drained tests

Full size image

Therefore, to some extent, coordination number may be an intrinsic variable characterising soil density and instability potential. However, in an undrained test, the \({Z}_{{\text{m}}}\) after the instability of a very loose specimen does not make much sense (decreasing while the specimen is contracting). This would suggest that the \({Z}_{{\text{m}}}\) cannot solely capture the behaviour of granular soil at the particle scale and shall be combined with fabric anisotropy (i.e. contact normal, contact forces, contact distribution and microscopic geometry) to properly describe the soil density at the particle scale.

3.3.2 Evolution of anisotropies

The structural anisotropy can be characterised by the second-order fabric anisotropy tensor (\({F}_{ij}\)) as expressed in Eq. (13). A scalar quantity of fabric can be presented by the von Mises fabric \(\left({F}_{{\text{vm}}}\right)\), which is derived from the invariant of \({F}_{ij}\) as expressed below:

$${F}_{{\text{vm}}}=\sqrt{\frac{3}{2}{F}_{ij}{F}_{ji}}$$
(14)

which can be rewritten as:

$${F}_{{\text{vm}}}=\sqrt{\frac{1}{2}\left[{\left({F}_{11}-{F}_{22}\right)}^{2}+{\left({F}_{11}-{F}_{33}\right)}^{2}+{\left({F}_{22}-{F}_{33}\right)}^{2}+6\left({F}_{12}^{2}+{F}_{13}^{2}+{F}_{23}^{2}\right)\right]}$$
(15)

here, \({F}_{11}\), \({F}_{22}\), and \({F}_{33}\) are fabric tensors in three orthogonal directions; and \({F}_{12}\), \({F}_{13}\), and \({F}_{23}\) are fabric tensors in the shear directions.

It is interesting to examine whether the unique critical state features can be identified for fabric anisotropy at CS. Figure 6a, b show the relationships between \({F}_{{\text{vm}}}\) and p′ and \({F}_{{\text{vm}}}\) and e at CS. A non-linear relationship for \({F}_{{\text{vm}}}\) at CS is observed, which implies the uniqueness of CSL. The evolution of \({F}_{{\text{vm}}}\) during the undrained shearing process for four samples with different \(p^{\prime}\) is also presented in Fig. 6a, b to demonstrate the stress dependency of the evolution path.

Fig. 6
figure 6

FvM values at CS and the evolution of FvM during undrained shearing: a FvM–p′ space; b FvM–e space

Full size image

However, as shown by several past studies, fabric anisotropy is intimately related to the loading path and contact forces [e.g. , 1373. Due to this dependency, an anisotropy variable defined based on both loading direction and fabric tensor may offer a more accurate characterisation of soil anisotropies.

Therefore, the following scalar values are also examined in this study:

  • 1. Joint invariant of stress tensor and fabric tensor (\({K}_{{\text{F}}}\)) proposed by Zhao and Guo [91]:

    $${K}_{F}={s}_{ij}{F}_{ij}$$
    (16)

where \({F}_{ij}\) is the deviatoric fabric tensor described by Eq. (13) and \({s}_{ij}\) is previously defined in Eq. (11).

  • 2. The scalar measure of relative fabric orientation, FAV A of Eq. (5) (\(A={F}_{ij}{n}_{ij}\)).

where \({n}_{ij}\) is the deviatoric loading direction, and for monotonic loading conditions in this study, can be defined by a unit-norm deviatoric tensor, \({n}_{ij}\) along the normal to the yield surface in deviatoric stress space:

$${n}_{ij}=\frac{{s}_{ij}}{\sqrt{{s}_{ij}{s}_{ij}}}$$
(17)

Additionally, von Mises invariant, \({F}_{{\text{vm}}}\) of fabric tensor proposed by Huang et al. [18] and stress-fabric joint invariant, KF, proposed by Zhao and Guo [91] are also adopted in this study to further investigate the fabric anisotropy and its evolution in DEM. This is further discussed in the following sections (Fig. 7).

  • 3. A pure measure of the relative orientation of the two fabric and stress tenors, A′, proposed by Zhao and Guo [91]:

    $${A}^{\mathrm{^{\prime}}}={n}_{ij}^{{\text{F}}}{n}_{ij}$$
    (18)

where, \({n}_{ij}\) is deviatoric loading direction expressed in Eq. (17) and \({n}_{ij}^{{\text{F}}}\) is deviatoric fabric direction defined below:

Fig. 7
figure 7

KF values at CS and the evolution of KF during undrained shearing: a \({K}_{F}-p^{\prime}\) space; b \({K}_{F}-e\) space

Full size image
$${n}_{ij}^{{\text{F}}}=\frac{{F}_{ij}}{\sqrt{{F}_{ij}{F}_{ji}}}$$
(19)

The correlation between \({K}_{F}\) and \(p^{\prime}\) and \({K}_{F}\) and e at CS by power-law fitting is shown in Fig. 8a and b. The evolution of \({K}_{F}\) during the undrained shearing process for four samples with different confining pressures is also provided to show the stress dependency of the evolution path. A non-linear relationship for both \({K}_{F}\) at CS is observed which implies on the uniqueness of CSL and is consistent with the concept of CS as explained in ACST by Li and Dafalias [32].

Fig. 8
figure 8

Evolutions of fabric anisotropy variable for specimens with different densities a in undrained tests; b in drained tests

Full size image

The fabric evolution during shearing in both drained and undrained tests is studied using the FAV A as defined in Eq. (5). Figure 8a, b indicate that A not only evolved to a CS value (i.e. A = 1) but also first rose beyond CS (slight rise for loose specimen) and only returned to CS at relatively large strains, which is different from the evolution of A and F originally presented by Li and Dafalias [32]. A similar observation was previously reported for dense samples by Fu and Dafalias [13] and Nguyen et al. [44], and was later quantified by Yang et al. [86].

Figures 9a, b shows the relationships between A and p′ and A and e at CS and its evolution path for four samples with different \(p\mathrm{^{\prime}}\) during the undrained shearing process. As expected and defined by Li and Dafalias [32], when A approaches the critical state value 1 for both cases. This special behaviour of the critical fabric structure can be further demonstrated through plotting A versus stress ratio \(\left(\eta =q/p^{\prime}\right)\) and stress dilatancy (\({D}_{P}={-{\text{d}}\varepsilon }_{\nu }^{p}/{{\text{d}}\varepsilon }_{q}^{p})\), as shown in Figs. 9c, d. Similar evolution of fabric anisotropy was previously reported by Wang et al. [78] and Yuan et al. [89].

Fig. 9
figure 9

A values at CS and the evolution of A during undrained shearing: a A–p′ space; b A–e space; c A–stress ratio, d A–stress dilatancy

Full size image

A normalised anisotropy variable \(\left({A}^{\prime}\right)\) as defined in Eq. 18 has also been proposed by Zhao and Guo [91] as a pure measurement of the relative orientation of the two fabric and stress tensors. This variable is used in this study to further examine the fabric evolution during the shearing process. The evolution of \(\left({A}^{\prime}\right)\) for five samples with different confining pressures during the undrained shearing process is shown in Fig. 10a, b. The evolution path indicates that the stress and the fabric tensor always tend to become coaxial, and \(\left({A}^{\prime}\right)\) approaches unity shortly after the application of shear and then stays at this value until reaching the CS. This behaviour is also reported by Zhao and Guo [91], which is indeed a very special property of the critical fabric structure and is consistent with Li and Dafalias [32].

Fig. 10
figure 10

Evolution of \({A}^{\prime}\) during shearing process towards CS at various \(p^{\prime}\)

Full size image

However, valuable as it may be, the proposed variable is indeed a normalised quantity of the FAV A and may not be an appropriate parameter to characterise the fabric anisotropies due to the exclusion of fabric intensity (\(F=\sqrt{{F}_{ij}{F}_{ji}}\)) from the measurement. It is evident that A tends toward 1 at critical state because both F and \(\ {A}^{\prime}\) tend toward 1. Thus, A of Eq. 5 is the fabric variable that in conjunction with stress ratio, \(\eta ,\) and void ratio, e, can be used to define the necessary and sufficient conditions for a critical state to occur (i.e. the conditions listed in Eq. (6)).

The correlation between \({K}_{F}\) at CS and initial FAV A0, is shown in Fig. 11. As expected, due to the same nature of both parameters (both defined on the basis of fabric and loading orientation), a unique non-linear relationship is observed. This implies the suitability of FAV A to investigate the degree of anisotropy provided that this micromechanical fabric-based parameter can be incorporated into the constitutive model using DSP ζ and properly linked to the characteristic features of granular soil behaviour.

Fig.11
figure 11

Correlation between initial fabric anisotropy variable and stress fabric joint invariant at CS

Full size image

In addition, it is understood that the FAV A of ACST was purposefully defined to be related to the unit norms with the normal n on the yield surface or even more general (for theories that do not use yield surface, i.e. hypoplasticity), along the plastic strain rate direction n. This would enable the change of A to -A upon reversal of loading (i.e. cyclic loading). Such reversal behaviour is of cardinal importance for the description of the response of sands, i.e. between triaxial compression (dilatant) and extension (static liquefaction). All other relevant indices used in this study (i.e. FvM and KF) are of restricted value in a theory that must address also the reversal of loading, while they do not change sign upon reversal of stress rate because the stress is still along the direction of the fabric. In addition, it is not possible that these quantities to be correlated to important Dilatancy State parameter DSP \(\upzeta\). Therefore, the constitutive modelling presented in the following section is based on the FAV A to further explore the effect of fabric within the context of ACST.

3.4 Constitutive formulation

Rahman, Dafalias [57] proposed a new expression of DSP ζ by combing Eqs. (7) and (8), which is presented in the following equation. ζ enables the ACST constitutive model [32] to better account for fabric for prediction of macrobehaviour for Toyoura sand and Sydney sand with silts. However, such a new ζ has not been evaluated yet in the light of micromechanics and fabric entities.

$$\upzeta =\psi -{e}_{A}\frac{\langle {e}_{{\text{lim}}}-e\rangle }{\left({e}_{{\text{lim}}}-{e}_{{\text{CS}}}\right)}\left(A-1\right)$$
(20)

An attempt is made in this study for the first time to calculate the initial dilatancy state parameter, DSP \(\left({\upzeta }_{0-{\text{DEM}}}\right)\), from micromechanical entities of this DEM Study. For this, the initial FAV A0 was calculated using the initial values of the unit-norm deviatoric tensor \({n}_{ij}\) (Eq. (17)) and deviatoric fabric tensor \({F}_{ij}\) (Eq. (13)). To evaluate the performance of Eq. (20), it was compared with \({\upzeta }_{0-{\text{CM}}}\) was calculated by constitutive formulation (CM) as outlined below.

\({F}_{ij}\) is a second-order fabric tensor representing the anisotropic geometry of the internal structure in soil. For an initially cross-anisotropic sample with the isotropic plane coinciding with the x2 − x3 plane and the axis of anisotropy aligning with the x1-axis, Zhao and Guo [91] proposed the following expression for \({F}_{ij}\):

$${F}_{ij}=\left[ \begin{array}{ccc}{F}_{11}& 0& 0\\ 0& {F}_{22}& 0\\ 0& 0& {F}_{33}\end{array}\right]=\sqrt{\frac{2}{3}} \left[ \begin{array}{ccc}{F}_{0}& 0& 0\\ 0& -{F}_{0}/2& 0\\ 0& 0& -{F}_{0}/2\end{array}\right]$$
(21)

where, F0 can be obtained according to equation below

$${F}_{0}=\frac{3\surd 6(2\upsilon -1)}{3\left(1-2\upsilon \right)+({\text{d}}q/{\text{d}}p)(\upsilon -2)}$$
(22)

ν is the Poisson’s ratio (0 < ν < 0.5) for DEM specimen.

As part of this study, a sensitivity analysis considering the material orthotropy has been carried out to select suitable values for Poisson’s ratio and as a result of which, the constitutive model outputs using Poisson’s ratios ranging from 0.46 to 0.48 show a reasonably good consistency with DEM results. The possible explanation for such a great range of values in Poisson’s ratio probably lies in a very high particle stiffness in the DEM specimen.

The deviatoric unit loading direction tensor \({n}_{ij}\) can be expressed as:

$${n}_{ij}=\frac{{N}_{ij}-{N}_{mn}{\delta }_{mn}{\delta }_{ij}/3}{\Vert {N}_{ij}-{N}_{mn}{\delta }_{mn}{\delta }_{ij}/3\Vert }, {N}_{ij}=\frac{{\partial }_{\widetilde{f}}}{{\partial }_{{r}_{ij}}}, \widetilde{f}=R/g\left(\theta \right)$$
(23)

\(g\left(\theta \right)\) is an interpolation function based on the Lode angle θ of \({r}_{ij}\) as follows:

$$g\left(\theta \right)=\frac{\sqrt{{\left(1+{c}^{2}\right)}^{2}+4c\left(1-{c}^{2}\right){\text{sin}}3\theta }-\left(1+{c}^{2}\right)}{2\left(1-c\right){\text{sin}}3\theta }$$
(24)

where \(c={{M}_{{\text{e}}}}/{{M}_{{\text{c}}}}\) which is the ratio between the critical state stress ratio in triaxial extension (\({M}_{{\text{e}}}\)); and that in triaxial compression (\({M}_{{\text{e}}}\)); and

$$\theta = - \frac{{\left[ {{\text{sin}}^{{ - 1}} \left( {{\raise0.7ex\hbox{${9R^\prime }$} \!\mathord{\left/ {\vphantom {{9R^\prime } {2R^{3} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${2R^{3} }$}}} \right)} \right]}}{3}{\text{ with }}R^\prime = r_{{ij}} r_{{jk}} r_{{ki}} = tr\left( {r^{3} } \right) - tr\left( {r^{2} } \right)tr\left( r \right) + \frac{2}{{9\left( {tr\left( r \right)} \right)^{3} }}$$
(25)
$$R=\sqrt{3/2{r}_{ij}{r}_{ij}} \mathrm{with }{r}_{ij}=\frac{{\sigma' }_{ij}-p'{\delta }_{ij}}{p'}={s}_{ij}/p'$$
(26)

Following the determination of \({F}_{ij}\) and \({n}_{ij}\), initial FAV A0 was calculated using Eq. (5) and initial DSP (\({\upzeta }_{0}\)) were calculated using Eq. (20).

The scatter graph of initial FAV A0 and initial \({\upzeta }_{0}\) based on CM and based on DEM are presented in Fig. 12. As can be seen in Fig. 12a, the initial FAV A0 ranges from − 0.1 to 0.1 for both CM and DEM. Based on Fig. 12b, there is a good agreement between CM- and DEM-derived values and the best-fit relation is actually the line of equality which indicates that the Eq. (20) by Rahman, Dafalias [57] is likely to provide a reliable method to estimate DSP \(\upzeta\).

Fig. 12
figure 12

Scatter graph of a initial FAV A0 and b initial DSP ζ0 based on CM and based on DEM

Full size image

It should be mentioned that Eq. (20) is based on a simple form of rate equation for the fabric tensor (\({\text{d}}F=\langle \lambda \rangle c\left(N-F\right)=c(\pm 1-F)|{{\text{d}}\varepsilon }_{q}^{p}|\)) in the sense that it does not allow for the fabric norm to increase above 1 as observed in DEM studies for dense samples (Fu and Dafalias [13]), and which requires the introduction of an additional parameter \(r<1\) in front of F that becomes 1 at CS (Li and Dafalias [32]). Note, while the use of the above rate equation in terms of \(\lambda\) and \({{\text{d}}\varepsilon }_{q}^{p}\) is common in the literature (Gao et al. [15]; Zhao and Kruyt [92]), there are other approaches found in the literature, e.g. combining \(\lambda\) and dilatancy (Wang et al. [78]; Yang et al. [86]), stress ratio rate and \(e\) (Lashkari and Latifi [27]; Wan and Guo [77]), strain rate and \(e\) (Fang et al. [12], Sun and Sundaresan [71]). While further investigation is necessary in regard to the evolution equation for the fabric tensor, in this paper Eq. (20) has been adopted in order to focus on the main objective of the constitutive relation between microstructures and macroscopic behaviour of granular soils (Fig. 13).

Fig. 13
figure 13

Correlation between instability stress ratio and a initial state parameter; b initial dilatancy state parameter

Full size image

3.5 State parameters and fabric evolution

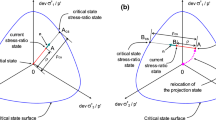
Previously published works [44, 59, 85] indicate that the behaviour of granular materials can be characterised by the initial classic state parameter \(\left({\psi }_{0}\right)\). Therefore, it can be of particular interest in this study to examine if the same property can be seen for initial DSP \({\upzeta }_{0}\). Correlation between instability stress ratio \({\eta }_{IS}\), and initial \({\psi }_{0}\) and \({\upzeta }_{0}\) are plotted in Fig. 13 with their best-fit relation presented by \({\eta }_{{\text{IS}}}=0.4805\times {\text{exp}}(-10.54 {\psi }_{0})\) and \({\eta }_{{\text{IS}}}=0.7085\times {\text{exp}}(-21.77 {\upzeta }_{0})\), respectively. Based on a comparison between coefficients of determination, denoted R2, the relation between \({\eta }_{{\text{IS}}}\) and initial state parameter has slightly been improved using \({\upzeta }_{0}\). This can be attributed to the inclusion of fabric entities in our model. It is expected that similar or better correlations can be identified between the stress ratio and state parameter at the same state.

The correlation between stress ratio and state parameters at instability state were also examined in this study which would be of more use to future fabric-based constitutive modelling. Figure 14 indicates that there is a reasonable trend between stress ratio and classic or dilatancy state parameters at the instability state, which is presented by the best-fit relations of \({\eta }_{IS}=0.4526\times {\text{exp}}(-12.57 {\psi }_{{\text{IS}}})\) and \({\eta }_{IS}=0.536\times {\text{exp}}(-11.88 {\upzeta }_{{\text{IS}}})\). Based on a comparison between R2 coefficients, the identified correlation between stress ratio and state parameter at instability has considerably been improved using \({\upzeta }_{{\text{IS}}}\) which may be related to the inclusion of fabric in dilatancy state parameter.

Fig. 14
figure 14

Correlation between instability stress ratio at a state parameter at instability state; b dilatancy state parameter at instability state

Full size image

The correlation between state parameters and stress ratio at phase transformation (PT) in undrained and at characteristic state (Ch) in drained tests are shown in Fig. 15. The best-fit relation can be presented by \({\eta }_{{\text{PT}}/{\text{Ch}}}=0.782\times {\text{exp}}(-1.977 {\psi }_{{\text{PT}}/{\text{Ch}}})\) and \({\eta }_{{\text{PT}}/{\text{Ch}}}=0.7703\times {\text{exp}}(-2.486 {\upzeta }_{{\text{PT}}/{\text{Ch}}})\) in which the state dependent dilatancy was elaborated. As can be seen, this relation has been presented using a single trend suggesting that the PT and Ch are likely representing the same characteristic of granular soil behaviour but in different drainage conditions, which is consistent with previous observations by Nguyen et al. [45]. A similar exponential relation was proposed by Li and Dafalias [31, 32], respectively, for both classic and dilatancy state parameters expressed by \({\eta }_{{\text{PT}}/{\text{Ch}}}=M\times {\text{exp}}(m {\psi }_{{\text{PT}}/{\text{Ch}}})\) and \({\eta }_{{\text{PT}}/{\text{Ch}}}=M\times {\text{exp}}(m {\upzeta }_{{\text{PT}}/{\text{Ch}}})\). These constitutive relations are also plotted in Fig. 15 in which \(m=-2.5\). As expected, based on the consistency between the best-fit curves and constitutive relations as well as a comparison between R2 coefficients, a better correlation can be seen between \({\eta }_{{\text{PT}}/{\text{Ch}}}\) and \({\upzeta }_{{\text{PT}}/{\text{Ch}}}\). Although there is only a marginal improvement in the comparison of the best-fit curves, when viewed from the perspective of constitutive modelling and considering the correlation between \({\eta }_{{\text{PT}}/{\text{Ch}}}=M\times {\text{exp}}(m {\upzeta }_{{\text{PT}}/{\text{Ch}}})\) and the best-fit curves, a noticeable improvement can be seen which can be attributed to the inclusion of fabric in dilatancy state parameter.

Fig. 15
figure 15

Correlation between stress ratio at PT/Ch with a state parameter at PT/Ch; b dilatancy state parameter at PT/Ch

Full size image

3.6 Conclusions

The micromechanical and macromechanical characteristic features of the behaviour under drained and undrained conditions were examined using DEM simulations. The major findings are:

  • The state-dependent behaviours of granular soil were observed for loose, medium dense and dense specimens. This includes contraction and static liquefaction in very loose soil, quasi-steady state or phase transformation (PT) in medium-dense soil, and dilatancy and hardening in dense soil. All the specimens reach a unique CSL in the p′-q-e space regardless of the initial density, confining pressure and loading mode.

  • The initial mechanical coordination number Zm increases with decreasing initial void ratio e0. However, there is no unique correlation between Zm and e, although to some degree Zm reflects the soil density. It is found that the critical Zm value linearly depends on the critical p′ value. Meanwhile, the critical Zm value is generally smaller than the initial one, although the density or p′ value at the critical state may increase when compared with the initial one. Moreover, the quasi-steady state corresponds to the minimum Zm value during shearing, and the static liquefaction happens when the Zm value is less than 8.

  • It was also found that the micromechanical measures, FvM and KF, evolved toward CS at high ε1. The CS values of these micromechanical quantities from drained and undrained simulations all terminated in a single line (CSL).

  • A unique relationship between stress ratio at PT/Ch state (\({\eta }_{{\text{PT}}/{\text{Ch}}}\)) and classic and dilatancy state parameters (\({\psi }_{{\text{PT}}/{\text{Ch}}}\) and \({\upzeta }_{{\text{PT}}/{\text{Ch}}}\)) was established. The uniqueness of this relationship implies that the PT and Ch are likely representing the same transition state of granular soil behaviour but in different drainage conditions. However, this unique relationship cannot properly be detected in microscale by plotting the von Mises fabric, \({F}_{{\text{vm}}}\) against \(\psi\) and \(\upzeta\) at PT/Ch state, which can be associated to the definition of undrained and drained conditions in DEM simulation.

  • The correlation between stress ratio and both classic and dilatancy state parameter (\(\psi\) and \(\upzeta\)) were studied in important characteristic features (e.g. instability, phase transformation and characteristic state). This correlation was improved using DSP \(\upzeta\) which might be due to the inclusion of fabric in our model. This observation is new and significant for modelling fabric evolution. This represents a novel contribution to the understanding of anisotropic responses in constitutive modelling. Additionally, this study deviates from the linear variation of \({\eta }_{{\text{PT}}}\) with \(\psi\) found in previous works, such as Manzari and Dafalias [38]. The exponential correlations presented, while closely resembling linearity, exhibit better behaviour, adding a layer of sophistication to the existing knowledge in this domain.

The findings and recommendations contained within this study are the results of observations from DEM simulations and a comprehensive review of pertinent literature. To the best of authors’ knowledge, they provide a plausible interpretation of both micromechanical and macromechanical behaviours exhibited by granular materials. This enhanced understanding contributes significantly to the quantitative knowledge essential for advancing future constitutive modelling efforts. To validate and enhance the robustness of these findings, additional observations using experimental approaches can be pursued.