Dynamics of granular debris flows against slit dams based on the CFD–DEM method: effect of grain size distribution and ambient environments

Abstract

Earth surface flows in nature, like debris flows and rock avalanches, have threatened people’s safety and infrastructure during past decades. Though grain size distribution (GSD) has been acknowledged as a crucial characteristic in granular material behaviour, its coupled effects associated with environments on engineering structures such as the slit dam remain unclear. To bridge the gap, this paper reveals the coupled effect of the GSD and ambient environments (i.e. slope angles and saturation conditions) on avalanche/debris flows’ impact on the slit dam using a Computational Fluid Dynamics/Discrete Element Method (CFD–DEM) model. To describe strain-dependent rheological characteristics of debris fluids, the Herschel–Bulkley–Papanastasiou model is implemented in the finite volume method framework. A power grain size distribution law is considered to quantify GSDs, in which a fractal parameter takes charge of GSD types. After model verification with experimental/theoretical results, the impact force against slit dams, granular dynamics and final deposit patterns under a series of ambient circumstances are presented. Taking advantage of the CFD–DEM method, the impact force and kinetic energy induced by fluid and solid phases are discriminated. The contribution of solid and fluid phases to both impact force and dynamics appears to be dependent on GSDs. Accordingly, compared with saturated avalanche flows (i.e. debris flows), slit dams result in higher retaining efficiency when confronted with dry avalanche flows. Regarding a narrow diameter range used in analyses, the grain diameter ratio is then enlarged up to eight to reveal the potential size effect. As for the coupled role of GSDs and slope angles, in contrast to slope angles, the influence of GSD on avalanche flow interaction with slit dams is much smaller. Additionally, provided a narrow diameter range, the effect of GSDs on impact force can be partially attributed to the change in average grain diameter. After presenting the significance of ambience and GSDs to avalanche/debris flows, a series of parametric studies around the effect of fluid grid size, particle shape and the initial porosity of granular samples are discussed, aiming to advance the understanding of their influence in the interactions between debris flows and the slit dam.

1 Introduction

Earth surface flows are a series of geological hazards where masses of poorly sorted sediments saturated with water are agitated and flowing above the earth surface in response to gravity [28]. Among these mass flows, avalanche/debris flows have drawn extra attention for the sake of their high potential damage, where avalanche flows are referred to as dry granular flows while debris flows are saturated with fluids. Especially, exaggerated by material variability, high flowing velocity and volumes, debris flows can cover a broad area and even change geomorphology. A great amount of people’s life and economy have been taken away and devastated by debris flows during past decades. Previously, many studies on debris flows overlook the influence of GSD since it is challenging to sample in the field [50]. However, it has been demonstrated that an increment in the content of fines decreases the maximum runout distance [90]. Trujillo et al. [66] stated that larger grains like boulders curtail the dissipation of kinetic energy during mass movement, which aggravates the damage potential of debris flows. Additionally, GSDs may affect the flowing of either dry granular avalanche or saturated debris flows because of various mechanisms existing in the interaction among grains [11, 13, 31], thereby having a remarkable effect on granular flows’ behaviour [30]. As a structure frequently used for mitigating flow-like geological hazards, the slit dam has drawn the attention of researchers these years [51]. The aforementioned effects induced by GSDs and environments can bring different impact patterns and dynamics evolution during the interaction between avalanche/debris flows and the slit dam, which has not been demonstrated yet. Therefore, the current study aims to understand how the impacting mechanism and dynamics tend to evolve under a series of GSDs and environmental configurations.

Compared with costly laboratory experiments and field tests [5, 27, 40], theoretical methods provide a promising avenue to derive insights on the dynamic myth of avalanche/debris flows. For the analytical method, the solution of granular flows can only be available when applied to a representative element [24]. Therefore, numerical methods provide a generic alternative for those geological problems involving complex geometry and boundary conditions. Regarding the large-deformation and flowing feature of avalanche/debris flows, novel continuum methods such as the material point method (MPM), the coupled Eulerian–Lagrangian (CEL) method, the smooth grain hydrodynamics (SPH) method and the particle finite element method (PFEM) have been widely applied to simulate the behaviour of the avalanche/debris flows in nature, for instance, debris flows’ mobility regarding entrainment [25, 39]; debris flow velocity estimation [58]; debris–baffle interaction [10, 43, 45, 78]; avalanche-flow-induced impulse waves [17, 18]; snow avalanche propagation [21, 47]; runout and resultant deposition of landslides [77]; the transport of sediment during debris flows [15]; and the collapse of granular column [70]. Most recently, some coupled continuum methods have been proposed to address granular fluid–solid interaction [3, 55]. Nevertheless, continuum methods discriminate avalanche flows and debris flows by manipulating different constitutive relationships and material parameters, failing to explicitly consider the difference between avalanche flows (i.e. dry cases) and debris flows (i.e. saturated cases). In addition, these studies rarely shed light on the role of GSD, eliminating the possibility to indicate the mesoscale activities inside avalanche/debris flows. To address the GSD-related problems in avalanche/debris flows, the Discrete Element Method [9] prevails among previous studies due to the grains with different sizes could be explicitly considered. These years, the DEM has been extensively used to study granular flow interaction with engineering structures. A few of them that are the most interesting to the current study are detailed here. For example, using the DEM, Huang et al. [26] found that avalanche flows-induced impact force against slit baffles tends to grow with larger grain sizes. Jiang et al. [30] demonstrated that grain segregation resulting from the grain size difference in GSDs affects the induced impact force. Shen et al. [61] investigated the impact of avalanche flows against a rigid barrier with the DEM, emphasising the role of the clearance between structures and the basal. On basis of the DEM, Gong et al. [23] studied the avalanche-flow-resulted impacting process on the slit dam. Liu et al. [48] combined the DEM with the FEM, illustrating the impact of avalanche flows on the flexible barrier. Lately, the role of topography in the impact of dry granular flows on the rigid barrier was discussed [83]. In addition to the application in avalanche/debris flow modelling, many attempts have been made when applying the DEM in geological engineering as well [64, 76, 82]. Despite the increasing number of granular flows’ study with DEM, it should be notified that, among most of these studies, the DEM is employed as a single approach to model avalanche flows in general. When it comes to debris flows where solid grains are mixed with fluids, the fluid phase shall be described via involving the other one. Another problem also arises in quantifying the change of GSDs. Previous studies on the significance of GSDs in avalanche/debris flows are based on either subjective varying of grain diameter or changing the proportion of different grain sizes, lacking a rational way to describe the distribution characteristic of GSDs. Thus, a more concise and reasonable definition of the change of GSDs is needed for interpreting the role of GSDs in avalanche/debris flow responses under different environments. Up to date, the impacts of GSDs on engineering prevention structures remain an open issue, demanding a rational interpretation of GSD effects. To ease the situation, Cabrera and Estrada [4] launched a power-law expression to quantify the role of GSDs and remarked that the mobility of dry granular flows is independent of GSDs, opposing another investigation reported by Lai et al. [38]. The same power-law expression was also referred to in other research on GSD [49]. However, the influences of environments such as fluids and slope angles have not been considered in their studies. The influences of the GSDs described by fractal dimension on granular flow behaviour should be further elaborated under more complex environments associated with different gravity and saturation conditions. A numerical method considering fluid–solid interaction is demanded to fill this gap. Therefore, this work aims to bridge the gap via a CFD–DEM method, in conjunction with a non-Newtonian rheological model characterising the physics of the fluid phase.

Earlier, the CFD–DEM method has been successfully utilised to explicitly address saturated granular flows (i.e. debris flows). Initially, a pioneering work discussed the potential CFD–DEM application in geomechanics [85]. Then, the simulations of the interaction between debris flows and flexible structures were achieved using a unified CFD–DEM framework [44, 46]. With this computational framework, debris flows’ thermal conduction when producing dead zone [35]; submarine landslide failures [30]; and rockslide-resulted impulse waves [86]. The finite volume method (FVM) is employed to solve the fluid phase due to its great performance in physical conservation and stability [72]. Compared with those particle-based methods such as SPH and MPM, the CFD–DEM method can model the motion of debris flows from both macroscopic and mesoscopic sales [62]. The determination of void fraction is of great importance in CFD–DEM coupling. Generally, according to the ratio between grain diameter and fluid grid size, CFD–DEM methods can be divided into (i) resolved, (ii) unresolved and (iii) semi-resolved. In the resolved method, the fluid grid length is usually 1/10 of the grain diameter in order to resolve the fluid field around grains. It is expected that a large burden can be induced under the circumstance because of a fine fluid grid [62]. In the unresolved method, instead of resolving the flow around every grain, a so-called coarse grid scheme is used when solving the locally averaged Navier–Stokes equations [22], in which the fluid grid length shall be 3–5 times of grain diameter in general. As for the semi-resolved method, some modifications have been made to achieve higher precision in void fraction estimation, enriching a certain flexibility to the ratio of grain diameter to fluid grid size. For instance, Cheng et al. [6] employed the fictitious domain (FD) method to solve the fluid profile around coarse grains. Wang et al. [75] proposed an averaging scheme for the estimation of void fraction with the kernel function in SPH. In the current study, a diffusion kernel equation (i.e. Equation 13 in Appendix 1) is implemented to achieve the averaging of void fraction in CFD–DEM coupling. Aside from this, a non-conventional rheological model (i.e. Herschel–Bulkley–Papanastasiou, HBP) is implemented under the configuration of FVM in this study to capture the strain-dependent characteristics of debris fluids. The presented CFD–DEM simulations were conducted on the open-source code CFDEM that bridges OpenFOAM and LIGGGHTS [32]. Furthermore, a typical slit dam is recognised as the engineering prevention structure to indicate the impact of granular avalanche flows. Although the interaction between slit dams and avalanche/debris flows has been investigated prior to this study [23, 26, 41], it is the first time that avalanche/debris flows are involved altogether with the HBP model to reveal their impact on slit dams with the CFD–DEM method. Additionally, the influence of power-law distributed GSDs on debris–dam interaction is presented, which has not been elucidated in previous studies and is evaluated via the HBP model as well.

This paper is structured as follows: In Sect. 2, the HBP model and its parameter correlation are presented, based on which the established CFD–DEM model is verified through both theoretical solutions and laboratory experiments. To be concise, the mathematical details of the CFD–DEM theorem are arranged in Appendix 1. Then, the slit dam model setup and calculated power-law GSDs are depicted. After that, the coupled effects of GSDs, grain diameter ranges, slope angles and fluids on the debris flow impact against slit dams are presented and elucidated in Sect. 3. In Sect. 4, a series of parameter studies considering the fluid grid size effect, particle shape roughness and the initial compactness of granular specimens are discussed later. Finally, the findings obtained from this work are highlighted in Sect. 5.

2 Methods

A numerical method coupling DEM and CFD, alias CFD–DEM, is adopted. The HBP rheological model is implemented to describe the non-Newtonian behaviour of the fluid phase in debris flows. Refraining from showing the details of the CFD–DEM method, we intend to focus on the effect of GSDs on dry and saturated earth surface granular flows. First, the HBP rheological model is involved, after which the CFD–DEM model is verified and the micro-parameter setup used in simulations is clarified via comparing with analytical solution and experimental phenomena. Following that, the theoretical background for the power-law GSD is illustrated.

2.1 HBP rheological model

A non-Newtonian HBP rheological model is implemented in the FVM framework to describe the constitutive behaviour of the fluid of debris flows as shown below:

$$\begin{aligned} \tau =\mu _{0}(2 \dot{\gamma })^{n}+\tau _{y}\left( 1-e^{-m \dot{\gamma }}\right) \end{aligned}$$

(1)

where $\tau$ represents the shear stress, $\mu _{0}$ the initial viscosity when the shear strain rate equals zero, $\dot{\gamma }$ the shear strain rate, n a non-dimensional parameter controlling the fluid to be either shear-thinning or shear-thickening, $\tau _{y}$ the yield stress, m a constant coefficient deciding the nonlinear transition of shear stress with varying shear strain rate. The response of shear stress in the HBP model under different m and n is indicated in Fig. 1. In contrast to the traditional Herschel–Bulkley (HB) model and the Bingham model, which are widely referred to in previous studies [36], the HBP model takes advantage in capturing shear-dependent behaviour of debris fluids and nonlinear rheological transition. These abilities enable the HBP model to be more appropriate in describing the complex behaviour of debris flows [73]. As an instance, the potential of this model in simulating large-scale debris flows has been proved recently [84]. More comprehensive discussion about the HBP model behaviour, even though implemented in different numerical frameworks, can be found in earlier studies [16, 25].

Fig. 1

Response of HBP shear stress–strain relationship under different rheological parameters (i.e. m and n): a for the parameter n (m = 5) and b for the parameter m (n = 1)

2.2 Model verification and benchmark

2.2.1 Fluid part

To verify the implemented HBP model, the flume experiment completed by Komatina et al. [33] is chosen, where the apparatus configuration is displayed in Fig. 2a. In the experiment, the clay–water mixture is collected at one side of a flume. After removing the platen restriction, the clay–water mixture flows under the effect of gravity. The fluid propagation distance and fluid slice contour are recorded in both the experiment and simulation. To determine the parameters of the HBP model, the calibration result by Han et al. [25] is borrowed, in which they applied the HBP model to simulate debris flows under the framework of SPH. The resultant trend of shear stress versus shearing rate is shown in Fig. 2b. Theoretical results based on the HBP model agree well with that of the experiment. Then, by comparing the fluid slide contour at different time points ($t = 0.37\,s$ and $t = 0.60\,s$), it can be indicated that the HBP model can reasonably describe the propagation distance, while the difference in computing slice contour of the water–clay mixture may result from the inaccurate estimation of fluids’ surface tension. The same fluid properties will be used to describe the non-Newtonian behaviour of the fluid phase in debris flows. To be concise, the HBP model parameters used in this section are arranged in Table 1 with the DEM parameters.

Fig. 2

a Flume experiment configuration and geometry parameters, after [33]; b The constitutive relationship for the clay–water mixture captured in the experiment and the HBP model; c The propagation and slice contour of the clay–water mixture at 0.37 s and 0.60 s

2.2.2 Solid part

Although a well-verified DEM code (i.e. LIGGGHTS) is utilised in this study, the microscopic parameters for the Hertz-Mindlin model should be calibrated so that the DEM model is able to indicate the physics of the solid phase in debris flows. It should be noted that, in the DEM modelling of cohesive soils and rocks, the quasi-static triaxial test always be required to calibrate microscopic parameters. However, in the modelling of granular flows, the dynamic behaviour of the system is of more interest. Indeed, triaxial tests have been used to calibrate DEM models under multiple circumstances including both saturated and unsaturated cases. However, the triaxial tests are rarely used in the micro-parameter calibration of granular flows according to the literature. Instead, in the simulation of dry/saturated granular flows, the calibration schemes in which the numerical results are compared against flume experiments are frequently adopted. It is essentially because debris/granular flows tend to behave more like fluids rather than solids in geological engineering. For example, the flume experiment has been applied to verify a continuum-based fluid model [53], where the interaction between debris flows and structures is demonstrated. Zhong et al. [88] have implemented a coupled FEM-DEM method to test the dynamics’ response of structures under the effect of debris avalanches, where only the flume experiment is used to validate their simulation results. Some other research groups who utilised DEM in their study also made use of laboratory/field flume experiments rather than triaxial tests to calibrate and interpret the properties of debris flows [26, 44, 78]. Therefore, it is fairly reckoned that the triaxial test may not be necessary if the flowing ability of debris flows dominantly falls into the scope of the research. In this section, the dry granular flow experiment reported by [30] is chosen to calibrate the multiple microscopic parameters. The calibrated DEM modelling shall be able to predict the impact of granular flows on prevention structures. After iterative calibration, the DEM model is able to grab both the impact force trend versus time and the final granular deposit of the experiment (Fig. 3). The calibrated mesoscale parameters are depicted in Table 1. It is noted that Poisson’s ratio and the restitution coefficient are adopted from the previous CFD–DEM study on debris flows [46]. To promote calibration efficiency, the difference in the frictional properties of grain–wall and grain–grain contacts is considered by using different rolling resistance friction coefficients, while the friction coefficients remain the same. The same parameter setup is applied in the following avalanche flow simulations.

Fig. 3

Impact force loaded on the flume channel boundary, where the solid line presents experimental data and the dotted line DEM results

2.2.3 CFD–DEM part

Three cases are selected to benchmark the CFD–DEM part from both theoretical and experimental perspectives. Dam break is chosen in this article as the first benchmark case for the CFD–DEM method. To avoid the misunderstanding between the parameters used in debris flows’ modelling and model verification, the CFD–DEM parameter setup used for following benchmark simulations is detailed in the supporting material for clarity. Formerly, a dam break test extended to a gas–liquid–grain configuration has been proposed in [65]. The experiment box has dimensions of 0.2 m $\times$ 0.1 m $\times$ 0.3 m, with a column of water with 0.05 m $\times$ 0.1 m $\times$ 0.1 m size on its lateral side. 3883 monodisperse spheres having a diameter of 0.0027 m lay beneath the water column. The CFD–DEM dam break model is built using the same dimension and physical parameters in the laboratory experiment [65]. The simulation is performed with a total number of 48,000 fluid cells. Numerical–experimental comparison results presented in Fig. 4 demonstrate that the CFD–DEM model can capture the dam break progress. The experimental and CFD–DEM dam break comparison is shown in the first two columns. Although Fig. 4a, b illustrates a great agreement between laboratory observations and CFD–DEM simulations, some differences still exist, for example, the numerical impulse wave after granular-water mixtures outreaching the box boundary has a lower height than the experiment (Fig. 4c, d). These errors could result from either the insufficient calibration of the DEM parameters like grain–grain contact stiffness or not enough fluid mesh resolution. A better agreement between numerical–experimental results might be achieved with the sacrifice of computational efficiency. Apart from this, to test the liability of the implemented HBP model under the CFD–DEM framework, the dam break result of the clay–water–grain mixture is shown in the third column of Fig. 4, in which the parameters of the HBP model are inherited from Table 1. It can be seen that, at the same time point, a slower-flowing mode exists due to a higher dynamic viscosity.

Fig. 4

Numerical–experimental comparison of dam break results and the corresponding clay–water–grain mixture response at time t = a 0.1 s, b 0.2 s, c 0.3 s, d 0.4 s

Fig. 5

The experimental records of granular collapse into water (left) and CFD–DEM results (right) at time t = a 0 s, b 0.2 s, c 0.4 s and d 0.8 s

The experiment [59] investigating the granular collapse into the water as the second benchmark case. This experiment aims to reveal the behaviour of tsunamis triggered by debris flows, which are commonly encountered in coastal/mountainous areas. The initial model configuration is displayed in Fig. 5. The granular glass beads are arranged on the left-hand side above a step, while the initial water level is the same as the threshold. The water in the experiment is dyed green for visualisation purposes. To commence the granular collapse, the platen initially holding granular glass beads is removed since $t = 0$ (Fig. 5a). At $t = 0.20$ s, a trivial wave is conceived around the immersed grains (Fig. 5b). After 0.2 s, an increasing number of grains slide into the water and a curved wetting interface is produced as marked by the red dashed line in Fig. 5c. When $t = 0.64$ s, the wave has been generated and propagandises towards the far field. Meanwhile, the wetting interface captured inside granular glass beads becomes extended and flattened. By comparing the granular glass bead deposition and the water-air interface contour, the CFD–DEM model reasonably reproduces the interaction between grains and water of the experiment. However, some differences still exist. For example, the wave shape fails to be exactly described by the CFD–DEM model, which might be promoted by implementing a proper turbulence model so that the water-air interface details can be depicted.

The third case being used to verify the CFD–DEM coupling scheme is illustrated in Fig. 6. When $t = 0$, 10,000 spherical grains owning the radius of 0.001 m are generated above the static water surface with a preliminary overlapping check. After that, grains free fall into the water and the relative fluid volume $V/V_0$ is monitored, where V is the real-time summation of water volume fraction in each element and $V_0$ is the initial state. The progressive mixing of grains and water from $t = 0$ to $t = 0.8$ s is shown in Fig. 6 as well. The measured $V/V_0$ indicates that a slight fluctuation commences when grains get connected with water, while $V/V_0$ maintains constant after 0.5 s. The final water level captured in the CFD–DEM model agrees well with the expected theoretical height.

Fig. 6

The change of relative fluid volume $V/V_0$ versus time, where the progressive grain–water mixing and the comparison between numerical and theoretical water level are accordingly presented

2.3 Slit dam setup

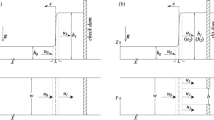
In subsequence to verification, the CFD–DEM model is applied to study the role of the GSD and fluid rheology in debris flows’ interaction with the slit dam. A gap-crested single slit dam is used as a schematic paradigm to demonstrate the typical geometry of a slit dam (Fig. 7a). Another slit dam located in a valley region is presented in Fig. 7b. A slit dam model is here established with the goal of recovering a simplified but practical setting. The slit dam configuration used for computation consists of an open channel with an idealised rectangular section (Fig. 8). The channel geometry is 10 m$\times$1.5 m for length and width, respectively. Detailed simulation configuration and parameters are demonstrated in Fig. 8 and Table 1, correspondingly, where the channel can be inclined to attain the desired slope with $\theta$ angle. A slit dam vertical to the xy plane bridges the two boundaries parallel with the xz plane, and an outlet centres it as shown in the zoomed picture of Fig. 8. Rigid walls are used to simulate the fixed slit dam whose motion is restricted. It should be noted that, in order to track the kinetic energy evolution during debris flowing, the channel end is closed so that debris flows can be arrested and the traction in system energy is avoided.

Fig. 7

Slit dam sketch and an instance: a gap-crested single slit dam (modified after [57]); b A slit dam located in Pollein, Aosta Valley region, north-western Italy (adapted from [51])

In the fluid–solid mixtures of debris flows, the solid part consists of grains whose diameters are variable to account for different grain size distributions, while the fluid part is solved with the finite volume method in accordance with the governing equations mentioned previously. Cubic debris flow mixtures’ size is 8 m$\times$1.5 m$\times$1.0 m, where the solid grains take around 48% volume percentage. Debris flows commence driven by gravity via removing lateral confinement exerted on the grain assembly.

Table 1 Model geometry and calibrated model parameters adopted in CFD–DEM simulations

Fig. 8

Model geometry setup applied for the debris flow simulations, where $l_m$ and $h_m$ are the length and height of debris–grain mixtures, respectively, L is release distance, W is the channel width and S is the open spacing of the slit dam

2.4 Grain size distribution determination

Three types of GSDs (i.e. power-law, monodisperse and polydisperse GSDs) are considered and described in Table 2. The power-law GSDs are produced from a fractal model mentioned in [67]:

$$\begin{aligned} \frac{m_i}{m_0}=\left( \frac{d_i}{d_0}\right) ^{3-D^*} \end{aligned}$$

(2)

where $d_0$ is the smallest grain diameter, $m_0$ is the mass of grains having $d_0$ diameter and $D^*$ represents the fractal dimension. The mass for the grains having $d_i$ diameter $m_i=N_i\pi {d_i^3}\rho /6$. Thus, the power-law GSD expression can be formulated as:

$$\begin{aligned} \frac{N_i}{N_0}=\left( \frac{d_i}{d_0}\right) ^{-D^*} \end{aligned}$$

(3)

where $N_0$ is the number of grains with $d_0$ diameter and the same nomenclature rule is applied for $N_i$ and $d_i$. Given a specific grain diameter range, the value of $D^*$ takes charge of the GSD of the grain assembly. A larger value of D results in a higher smaller grain percentage than that of bigger grains. To compare our result with previous research better, the fractal dimension $D^*$ setting is kept the same as [4, 38], while the grain diameter falls into the scope between 40 mm and 80 mm. Finally, four grain systems recovered with power-law GSDs are utilised with $D\in (1.0,1.5,2.5,3.5)$, $d_0=0.04$ m, and $d\in (0.04, 0.048, 0.056, 0.064, 0.072, 0.080)$ m. It is worth notifying that the grain size in the field of debris flows can range from smaller than 0.05 mm (i.e. slit) to larger than 300 mm (i.e. boulder). A limited GSD is applied herein in order to investigate the significance of $D^*$. The same GSD range is also used in the previous CFD–DEM simulation of debris flows [44, 46]. It is notified that, even though a wider GSD range fits the field observation of debris flows better, undesirable numerical divergence can be induced in the fluid–grain message interchange during CFD–DEM computation. To partially overcome this disadvantage and extend the availability of findings in this study, GSDs with the $D_{\text {max}}/D_{\text {min}}=$ 4 and 8 are utilised for dry granular flow cases. The GSDs for the dry granular flows with a wider diameter ratio are illustrated in Table 3. Besides, although the spherical grain is applied in this study, the shape of natural grains is highly irregular. Considering the influence of particle shape, the inter-grain rolling resistance coefficient is varied in Sect. 4.2 to mimic the change of geometry and surface roughness in natural granular flows.

The detailed power-law GSDs and corresponding grain distribution patterns are depicted in Fig. 9a, while the average diameters $d_a$ for different GSDs are shown in Fig. 9b. Maintaining a close average grain size, the role of GSD could be indicated more essentially. In addition to four GSDs produced from the power-law function, monodisperse and trimodal GSDs are included as the control group. It is noted that the grain size for monodisperse and trimodal GSDs varies from 40 mm to 80 mm following that of power-law GSDs. For monodisperse GSDs, three specimens have diameters of 20 mm, 30 mm and 40 mm, respectively. Three monodisperse samples having a diameter of 40 mm, 60 mm and 80 mm are generated, respectively. For polydisperse samples, trimodal samples are prepared to have grains of three diameters. Each trimodal sample consists of grains having three diameters, while only one diameter is considered to be dominant (70$\%$) and the other two diameters equally account for the rest of mass (15$\%$).

Fig. 9

Specimens with different power-law exponents implemented in this article: a Cumulative grain size distribution and the corresponding grain views; b Average grain diameters for $D^*$ from 1 to 3.5. N(d) representing the number of grains of diameter d is normalised by the number of the grain assembly $N_0$, while diameter d normalised by the average diameter $d_a$, respectively

Table 2 Grain size distribution for three GSD types: power-law, monodisperse and polydisperse

Table 3 Grain size distribution for GSDs with $D_{\text {max}}/D_{\text {min}}=$ 4 and 8, where a $D_{\text {min}} = 0.04$ m remains the same as Table 2

2.5 The measurement of dynamic parameters

With and without water, mass flow impact on structures and final deposition patterns would change remarkably [44]. To compare saturated and dry cases, the same settings are exerted in the model though the liquid has been removed for dry cases (i.e. dry granular avalanches). Granular kinetic energy and the impact force against slit dams were recorded to illustrate the influence of GSDs on flow–structure interaction. The granular kinetic energy is calculated based on the following equation:

$$\begin{aligned} E_{k}=\frac{1}{2} \sum _{i=1}^{N}\left( m_{i}\left| v_{i}\right| ^{2}+I_{i}\left| \omega _{i}\right| ^{2}\right) \end{aligned}$$

(4)

where $E_{k}$ is the total kinetic energy of the granular system and N is the number of grains. The nomenclature for other parameters has been covered previously. Likewise, the impact force against the slit dam is computed by the summation of the grain–dam normal contact force as below:

$$\begin{aligned} F=\sum _{i=1}^{N}F_{i}^{n} \end{aligned}$$

(5)

where $F_{i}^{n}$ is the normal contact force between ith grain and the slit dam. For the saturated cases, the impact force and kinetic energy resulting from the fluid phase are monitored as well to demonstrate its significance. Then, the force summation $F_{b}$ of both fluid-resulted force $F_{f-b}$ and solid-resulted force $F_{s-b}$ is calculated. The kinetic energy $E_{k}$ is also divided into the fluid part $E_{kf}$ and the solid part $E_{ks}$ for saturated cases. To focus on the underlying mechanism rather than a specific simulation case, all parameters on impact force and dynamics are normalised in this study. Finally, regarding the existence of a terminal barrier in the slit dam model, it is emphasised that we are trying to interpret is the role of GSDs in kinetic evolution rather than tracking the speedup of fluid–grain mixtures. Therefore, the setup of the boundary barrier is to dissipate the remainder of $E_k$ after the interactions between debris flows and the slit dam. The conclusions drawn from the current research will not be affected because the same boundary condition is maintained for all numerical cases.

3 Results

3.1 Monodisperse

Figure 10a to f displays the evolution of kinetic energy and impact force against the slit dam under a saturated condition, while Fig. 10g and h depicts the counterpart of dry cases. The contribution by fluid and solid phases is presented separately. In Fig. 10a, it is demonstrated that the peak impact force $F_{b}/{mg}$ increases about 40% when the grain diameter changes from 0.04 to 0.08 m. The final mass arrested by the slit dam also grows with a larger grain diameter. Similarly, less solid mass can be retained in saturated cases due to the higher drag force exerted on grains. As for the role of each phase during this process, the dependence of the solid-resulted impact force $F_{s-b}/{mg}$ on the grain diameter is lessened (Fig. 10b), whereas the fluid-resulted impact force $F_{b}/{mg}$ significantly decreases with a smaller grain diameter. After comparing with the response of the dry case in Fig. 10g, it can be seen that the significance of GSDs is enhanced by the existence of the fluid phase. Furthermore, it is observed that the existence of fluids may not necessarily bring a higher impact force. For example, in the case with fine grains, the peak impact force is beneath 0.35, while the peak force of the dry case with fine grains outweighs 0.35 apparently. However, with the increase in grain diameter, the impact force greatly grows after involving fluids. Additionally, unlike dry cases in which impact force decreases slowly after granular flows meet slit dams, under saturated conditions, impact force would steeply plummet after the debris–structure collision. Resultant $F_b/{mg}$ after impacts are positively dependent on the grain size, thereby evidencing previous research again [26].

The kinetic energy appears to increase with grain diameter as well but the contribution of each phase is different. First, the kinetic energy $E_{k}/{mgh}$ can reach up to 0.17 in saturated cases (Fig. 10d), while that of dry cases is less than 0.1 (Fig. 10h). This is because the fluid mass results in an increment in the potential energy of the initial system. Besides, the kinetic energy induced by grains gradually grows with a coarser GSD. In three monodisperse specimens given in this study, GSDs appear to have a trivial influence on the kinetic evolution of the fluid phase (Fig. 10f). Therefore, the increase in the kinetic energy with a higher grain diameter essentially results from the solid phase. When compared with dry cases, it should be noted that the kinetic energy drops twice during impacting in saturated cases, whilst the kinetic energy decays smoothly in dry cases. The drops in saturated cases also have a trend to disappear with a reducing grain diameter. It is reckoned that the drops are a result of the interaction between debris fluids and grains. Initially, grains tend to climb along the slit dam after getting in touch with it, during which the dead zone can be formulated. For dry cases, the process can happen quickly due to the resistance force by the air being negligible. Unlike this, the fluid phase in debris fluids can eliminate the climbing activity because of relatively high dynamic viscosity. Hence, the kinetic energy tends to decrease at first. After a great amount of mass passing, the accumulated gravitational energy during climbing is released, bringing a second-time increase in the kinetic energy.

It is also noticed that, for dry cases, Fig. 10h demonstrates that GSDs barely have effects on the dynamics of granular flows. The same view has been elaborated and validated by Cabrera et al. [4], in which the saturated condition is out of the scope for their discussion. The results of saturated cases presented in this section imply that the view might not be available with the involvement of the fluid phase, demonstrating that GSDs potentially take an important role in determining the movement and dynamics of granular flows when the fluid–grain mixture is given.

Fig. 10

Dynamics and impact force trend with three monodisperse GSDs under saturated (a–f) and dry situations (g, h): a the total impact force $F_{b}$; b the impact force induced by the solid phase $F_{s-b}$; c the impact force induced by the fluid phase $F_{f-b}$; d the total kinetic energy $E_k$; e the kinetic energy by the solid phase $E_{ks}$; f the kinetic energy by the fluid phase $E_{kf}$; g the impact force $F_{s-b}$ in the dry case; h the kinetic energy $E_{ks}$ in the dry case

3.2 Trimodal

Figure 11a describes the temporal evolution of total impact force for the saturated case with a trimodal GSD. Compared with monodispersed GSDs, because of the existence of grains having different diameters, the average grain diameter becomes closer for three cases. It is illustrated that the positive correlation between the total impact force and grain size still holds. However, the contribution to the total impact force is no longer dominated by the fluid phase. As shown in Fig. 11b, c, both fluid-resulted and solid-resulted forces gradually decrease with a smaller average grain diameter. The phenomena reveal that, given the same diameter range of 2, the effect of GSDs can be undermined when trimodal GSDs exist. Besides, the contribution of either the solid phase or the fluid phase can be varied as well with the change of GSD characteristics. A similar pattern is found in the dry case, where the impact force $F_{s-b}/{mg}$ tends to increase with a rising percentage of large grains. Similar to that of monodisperse cases, in saturated cases, a steep decrease in $F_{s-b}/mg$ is observed after impacting, while the post-impact transition for dry granular avalanches is relatively smooth. Besides, the system containing larger grains can reach a stable configuration using less time than the system with smaller grains, which is in agreement with monodisperse ones.

Figure 11d depicts the development of total dynamics versus time. Unlike the counterpart of dry cases in which GSDs have no influence on dynamics evolution (Fig. 11h), the total kinetic energy of saturated cases appears to rise with an increase in the percentage of coarser grains (Fig. 11d). The positive correlation is almost equally contributed by solid and fluid phases, which can be seen in Fig. 11e, f. According to Fig. 11d–f, the double drops in the kinetic energy still stand for saturated ones, while the kinetic energy can degrade smoothly in dry cases. However, the second peak in the kinetic is much weakened compared with that of monodispersed cases. For example, in Fig. 10d, the second peak of the total kinetic energy $E_k/{mgh}$ is able to return to around 0.15, while the first peak reaches 0.175. More than 80% of the maximum kinetic energy can be attained in the second peak for those with monodisperse GSDs, while only up to 70% of the maximum kinetic energy can be recovered in the second peak for trimodal cases (Fig. 11d).

As mentioned in Sect. 3.1, the results captured in trimodal reconfirm that the existence of fluids can change the role of GSDs in dynamics evolution. Figure 11h demonstrates that, under the dry condition, the difference in dynamics evolution induced by trimodal GSDs is trivial. Nevertheless, after bringing fluids, a clear dependence between dynamics and GSDs can be observed as indicated in Fig. 11d–f.

Fig. 11

Dynamics and impact force trend with three trimodal GSDs under saturated (a–f) and dry situations (g, h): a the total impact force $F_{b}$; b the impact force induced by the solid phase $F_{s-b}$; c the impact force induced by the fluid phase $F_{f-b}$; d the total kinetic energy $E_k$; e the kinetic energy by the solid phase $E_{ks}$; f the kinetic energy by the fluid phase $E_{kf}$; g the impact force $F_{s-b}$ in the dry case; h the kinetic energy $E_{ks}$ in the dry case

3.3 Power-law distribution

Previous results on monodisperse and trimodal GSDs have indicated that the total kinetic energy trend is related to GSDs under saturated cases but the contribution could come from either the solid or the fluid phase. The role of GSDs shows a tendency to attenuate in power-law GSDs (Fig. 12). However, the impact force F/mg varies erratically for different fractal dimensions $D^*$ without a proportional correlation (Fig. 12a). Apart from this, neither solid-resulted nor fluid-resulted impact forces are affected by $D^*$ monotonically, as shown in Fig. 12b, c. The phenomena may result from a narrow $D_{\text {max}} / D_{\text {min}}$. The narrow range of grain diameter brings a minor change in average grain diameter, diminishing the influence of GSDs. Detailed elaboration about the effect of $D_{\text {max}} / D_{\text {min}}$ on the maximum impact force will be included in the next section. In addition, in saturated granular flows, the time taken to reach a stable configuration is not dependent on $D^*$. It is worth noting that, for dry granular avalanches, the time for arriving at the stable still appears to be less with smaller $D^*$ (Fig. 12g), that is, a higher percentage of coarse grains. Despite a trivial effect on the impact force by $D^*$ exists, the dynamics of debris flows are affected by $D^*$, which is analogous to that of monodisperse and trimodal GSDs. In Fig. 12d, the total kinetic energy tends to decrease with a higher $D^*$, indicating that the debris flows containing larger grains pose a more serious threat. This trend is comparable with the observations of the laboratory experiments [54, 63]. Solid and fluid phases are proved to contribute equally to this trend, as suggested in Fig. 12e, f. The kinetic energy evolution of dry cases remains the same as monodisperse and trimodal cases, in which the dynamics development is independent of GSDs

Final deposits for different power-law GSDs are presented in Fig. 13. It is clear that the retention efficiency tends to be higher in dry avalanche flows (Fig. 13e–h) than that in saturated avalanche flows (Fig. 13a–d). A similar trend is also captured in the investigation of the interaction between avalanche flows and flexible barriers [44]. With rising $D^*$, the retention efficiency becomes higher due to the increasing number of coarse grains and thus the formation of stable grain structure can be recovered. In addition, although it seems the deposit under a smaller $D^*$ covers a wider area as shown in Fig. 13a–d, the deposited grains with a lower elevation have a smaller grain size due to the effect of segregation [31]. Therefore, the resultant difference in the final deposited mass appears to be negligible (Fig. 12a).

Fig. 12

Dynamics and impact force trend with three trimodal GSDs under saturated (a–f) and dry situations (g, h): a the total impact force $F_{b}$; b the impact force induced by the solid phase $F_{s-b}$; c the impact force induced by the fluid phase $F_{f-b}$; d the total kinetic energy $E_k$; e the kinetic energy by the solid phase $E_{ks}$; f the kinetic energy by the fluid phase $E_{kf}$; g the impact force $F_{s-b}$ in the dry case; h the kinetic energy $E_{ks}$ in the dry case

Fig. 13

Post-impact grain deposit patterns of power-law GSDs under saturated (the first row) and dry (the second row) conditions: a $D^*$ = 1, b $D^*$ = 1.5, c $D^*$ = 2.5, d $D^*$ = 3.5, e $D^*$ = 1, f $D^*$ = 1.5, g $D^*$ = 2.5, h $D^*$ = 3.5. The colour bar represents the elevation of grains

3.4 The effect of $D_{\text {max}} / D_{\text {min}}$

As mentioned earlier, a small grain diameter ratio range (i.e. $D_{\text {max}} / D_{\text {min}}$) might not reflect the GSD characteristic in practice. Therefore, it is clarified that the aforementioned results pertaining to $D_{\text {max}} / D_{\text {min}} = 2$ and $D_{\text {min}} = 0.04\,m$, thereby having limitations when it comes to the bouldery debris flows with a large $D_{\text {max}} / D_{\text {min}}$. To extend to a wider scope, the GSDs shown in Table 3 are determined to perform dry granular flows.

Figure 14 illustrates the dependence of results on $D_{\text {max}} / D_{\text {min}}$. A different scale is used for F/mg and $E_{k}/{mgh}$ because a large $D_{\text {max}} / D_{\text {min}}$ will significantly exaggerate both impact force and dynamics. As illustrated in Fig. 14a–c, with an increasing $D_{\text {max}} / D_{\text {min}}$, the maximum impact force and kinetic energy greatly grow. In contrast to the influence of $D_{\text {max}} / D_{\text {min}}$, the effect of $D^*$ becomes notable when $D_{\text {max}} / D_{\text {min}} = 8$. As reported in the experiment [63], it takes less time for the impact force to reach a rest state with an increasing $D_{\text {max}} / D_{\text {min}}$. The impact force also fluctuates significantly for the case of $D_{\text {max}} / D_{\text {min}} = 8$, which is in agreement with that of the experiment [54, 63]. The trend is because the fine grains are able to cushion greater grains during the collision between the structures (i.e. the slit dam in this study). Even though a clear coupled influence of $D_{\text {max}} / D_{\text {min}}$ and $D^*$ can be observed in impact force, there is no such a coupled relationship in the evolution of dynamics. First, the existence of large diameter grains results in both a higher maximum kinetic energy and a rougher $E_k$ versus t curve. Unlike that of $D_{\text {max}} / D_{\text {min}} = 2$, the variation of $D^{*}$ slightly affects the post-peak dynamics evolution when $D_{\text {max}} / D_{\text {min}} = 8$. However, the overall dynamics evolution and the maximum kinetic energy are not sensitive to $D^*$ under three diameter ratios utilised in this section, indicating the coupled effect of $D_{\text {max}} / D_{\text {min}}$ and $D^*$ fails to be captured.

Considering the crucial importance of peak impact force and dynamics, the peak impulse and kinetic energy are extracted from Fig. 14 and contrasted in Fig. 15a, b, respectively. According Fig. 15, the significance of $D^{*}$ in peak impulse tends to appear with the growth of $D_{\text {max}} / D_{\text {min}}$, while the change of $D_{\text {max}} / D_{\text {min}}$ cannot result in a stable relationship between $E_{k}/{mgh}$ and $D^*$. Under different $D_{\text {max}} / D_{\text {min}}$, $E_{k}/{mgh}$ keeps fluctuating with various $D^*$ but the maximum kinetic energy has grown 50% when $D_{\text {max}} / D_{\text {min}}$ changes from 2 to 8. The result implies that a larger $D_{\text {max}} / D_{\text {min}}$ can pose a higher risk of hazardous loss, while the significance of GSDs’ fractal distribution is trivial if a narrow grain diameter range is given.

Fig. 14

Impact force and kinetic energy evolution under different $D_{\text {max}} / D_{\text {min}}$. Impact force against the slit dam: a $D_{\text {max}} / D_{\text {min}} = 2$; b $D_{\text {max}} / D_{\text {min}} = 4$; c $D_{\text {max}} / D_{\text {min}} = 8$; The evolution of kinetic energy: d $D_{\text {max}} / D_{\text {min}} = 2$; e $D_{\text {max}} / D_{\text {min}} = 4$; (f)$D_{\text {max}} / D_{\text {min}} = 8$

Fig. 15

Peak impact force and maximum kinetic energy attained during flowing with different $D_{\text {max}} / D_{\text {min}}$. a Impact force versus $D^{*}$ and $D_{\text {max}} / D_{\text {min}} = 2, 4 \text {and} 8$; b Maximum kinetic energy versus $D^{*}$ and $D_{\text {max}} / D_{\text {min}} = 2, 4 \text { and } 8$

3.5 The influence of plane inclination

3.5.1 Evolution of debris–slit dam collision

The progressive debris flow impacting against slit dams is presented in Fig. 16. The experiment conducted by Zhou et al. [89] is involved to interpret the debris flows’ behaviour in simulations. It is clear that debris mixtures move at a higher speed due to steeper slope angles (Fig. 16a). During the impacting process, more overtopped grains reach the maximum velocity flow down in the case with a steep slope angle than those having a flat moving plane (Fig. 16b, c). The overtopping phenomena are comparable to that of the experiment (Fig. 16e). Meanwhile, dead zones are generated relying on the slit dam, as shown in Fig. 16c, in which the angle of dead zones decreases under a slower slope angle. For the case with the 30–40 degrees slope angle, the bouncing of fluids is observed in simulations as well, demonstrating the same phenomena captured in the experiment has a dependence on the slope angle (Fig. 16f).

Compared with the impacts on slit dams induced by dry granular flows [41, 51], debris fluid drainage commences together with the outlet of grains. For example, given the $10^{\circ }$ slope angle, debris fluids keep flowing through the granular system has been restrained by the slit dam. Among the cases tested in this study, under a flat slope angle ($\theta = 10^{\circ }$ and $20^{\circ }$), the granular system would be arrested and attain the clogging configuration ahead of the drainage of debris fluids. In contrast to this, grains continue flowing bypass slit dams after the drainage of debris fluids in a steeper slope angle ($\theta = 30^{\circ }$ and $40^{\circ }$). Eventually, the granular deposition has been produced, where the final pile-up height is demonstrated to decrease with a smaller slope angle (Fig. 16d).

Fig. 16

Grain–fluid mixture position and velocity profiles during flowing under different inclination angles. CFD–DEM: a $t/\sqrt{h/g}$ = 1.5, b $t/\sqrt{h/g}$ = 2.5, c $t/\sqrt{h/g}$ = 5 and d $t/\sqrt{h/g}$ = 30. Debris flow experiment by Zhou et al. [89]: e t = 0.78 s, f t = 0.93 s and g t = 1.58 s

3.5.2 Dynamics and impact loading evolution

As an example, the fluid–grain interaction response of samples with a constant GSD (i.e. Coarse 70%) but different inclinations are presented. Slope angle $\theta$ ranges from 10 to 40 degrees with an interval of 10 degrees. Figure 17 displays the dependence of the debris flow kinetic energy normalised by mgh and the impact force normalised by mg against slit dams on channel inclination. Kinetic energy and impact force change according to the time scaled by $\sqrt{h/g}$. The largest reached kinetic energy increases with rising slope angles due to more potential energy having been transferred. Chiefly, it is apparent that neither $E_k$ nor $F_b$ has a significant dependence on $D^*$, agreeing with the observations in Sect. 3.3. When the slope angle is small (i.e. $\theta =10^\circ$), the trend of kinetic energy is smooth without a second drop (Fig. 17a), approaching that of the collapse of a single grain column [80]. In addition, an increment in slope angles aggravates the oscillation of kinetic energy evolution. As illustrated in Fig. 17b, because of a higher gravitational potential energy in the initial stage, the maximum impact force against slit dams is shown to grow with a larger slope angle. The same correlation can be found in other prevention structures like flexible barriers and closed check dams. It is worth noting that, in contrast to flexible barriers where retained mass appears to rise with steeper inclination angles [44], retained mass is negatively associated with increasing channel inclination. This trend compiles with the findings of [51].

Fig. 17

a Dynamics and b impact force trend with four power-law GSDs under the slope angles of $10^\circ$, $20^\circ$, $30^\circ$ and $40^\circ$

An exhaustive explanation of the influence of plane slops on retaining efficiency can be found in [51], while the dependence of different phases’ contributions on slope angles has not been discussed in past research. The impact force evolution of fluid and solid phases under the coupled effects of $D^*$ and slope angles is demonstrated in Fig. 18a, b, respectively. Both fluid-resulted and solid-resulted impact forces are not sensitive to $D^*$ under different slope angles. For the fluid-resulted impact force, the change of $F_{f-b}$ with slope angles is parabolic (Fig. 18a). First, $F_{f-b}$ increases from 0.12 to 0.22 when the slope angle varies from $10^{\circ }$ to $20^{\circ }$, followed by which $F_{f-b}$ decreases to around 0.16 when the slope angle is $40^{\circ }$. For the solid-resulted impact force, $F_{f-b}$ grows with slope angles monotonically and eventually reaches the peak at about 0.4 when the slope angle equals to 40 $\circ$. Through calculating the contribution of the fluid phase in the total impact force by dividing the fluid-resulted impact force with the total impact force $F_{b}$, $F_{f-b}/F_{b}$ appears to keep decreasing when slop angles develop, demonstrating different debris–slit dam interaction mechanisms exist with different slop angles. When the slope angle is $10^{\circ }$, the contribution of the fluid-resulted force can be up to about 75%, while it declines to around 30% given a $40^{\circ }$ slope angle.

Instead, the influence of GSDs on maximum impact forces results from the change of either average grain diameter or boulder content. To further understand the role of GSDs in determining impact forces, past research results about the effect of GSDs on impact forces are referred to here [8, 26, 29]. As different parameters are being used for different research, impact forces and averaged grain diameters are normalised using the highest impact force and the max grain diameter according to their settings, respectively. Resultant $F/F_{\max }$ and $d_a/d_a^{\max }$ points are scattered in Fig. 14b. Clearly, the impact force $F/F_{\max }$ on engineering structures increases with the average grain diameter $d_a/d_a^{\max }$, which verifies the earlier assumption. Finally, an empirical equation is also proposed to correlate $F/F_{\max }$ and $d_a/d_a^{\max }$ as demonstrated below:

$$\begin{aligned} F / F_{\max }=0.855\left( d / d_{a}^{\max }\right) ^{1 / 2}+0.054 \end{aligned}$$

(6)

The fitting curve and error band coloured with grey have been displayed in Fig. 18d. Most of the points fall into the range, which implies the feasibility of this formula to a certain degree. However, when $D_{\text {max}} / D_{\text {min}} >4$, the role of the maximum grain diameters can be dominant rather than $d_a$, as found in the experiments [54, 63].

Fig. 18

Maximum impact force induced by debris flows: a the fluid-resulted impact force $F_{f-b}/mg$ scatters with different $D^*$ and slope angles $\theta$, b the solid-resulted force $F_{s-b}$ $F/F_{\max }$ scatters with different slope angles $\theta$ and $D^*$; c the contribution of the fluid phase under the coupled effects of $\theta$ and $D^*$; d the relation between the maximum total impact force and average grain diameter $d_a/d_a^{\max }$, including data from experiments [8, 29], previous simulations [26] and both of dry and saturated cases of the present study

4 Discussion

In addition to the GSD, the impact force against the slit dam and the kinetic energy of debris flows are decided by other factors. On the one hand, as for simulations, the size effect induced by different fluid grid sizes may vary the numerical solution [69]. On the other hand, as for the granular flows’ physics, a decreasing grain sphericity (i.e. a higher grain geometry irregularity) brings a declining sliding velocity [19]. Besides, the initial compactness of the granular specimen also changes the interaction between granular flows and ambience. Existing experimental results indicate that a loose medium aggravates the entrainment by debris flows [42]. Therefore, these factors are discussed in this section to demonstrate their potential influence on the numerical result and respective engineering implications on debris flows. To avoid redundant discussion, the GSD used in parametric studies is taken from Table 2, in which the power-law distribution with $D^{*} = 1.5$ is used.

4.1 The sensitivity of fluid grid size to results

Previous study indicates that provided uniformly refined cubic fluid cells, the calculation error of the CFD–DEM method tends to first decrease with a finer grid size and then increase when $L_{f}/D_{\text {avg}} < 3$ [68], in which $L_{f}$ is the length of fluid cells and $D_{\text {avg}}$ is the averaged grain diameter. It is also observed that the grid refinement in different dimensions (i.e. the flowing/non-flowing direction) can result in a different test result. Considering the fluid grid size limitation in CFD–DEM modelling, the sensitivity test has been performed to show the role of fluid grid size. It is worth noting that the discussion trivially affects the availability presented in the last section due to the same fluid grid has been kept in other sections. In general, fully resolved CFD–DEM calculation requires a small $L_{f}/D_{\text {avg}}$ less than 1/10 [75]. As for the unresolved, $L_{f}/D_{\text {avg}}$ is suggested to be around 5. To characterise fluid grids with different refinements, $L_{f}/D_{\text {avg}} = 3, 4, 5$ are determined in this section.

Figure 19 illustrates the difference in the impact force and dynamics resulting from grid refinements. It can be seen that the resultant responses are not significant with various refinements. In Fig. 19a–c, the impact force tends to fluctuate with the change of refinements but no such apparent trend can be observed. As for dynamics, the total kinetic energy tends to decline with a coarser grid, which is demonstrated to be triggered by the fluid phase. Under a coarser grid, the kinetic energy induced by the fluid phase slightly decreases (Fig. 19f) but the trend by the solid phase has not been affected (Fig. 19e). In addition to grid size, some other parameters in CFD–DEM simulations such as smoothing distance also affect the calculation results in the same vein. As a result of it, the induced differences in simulations originate from the averaging length and estimated solid fraction. It is referred to [74] for more details around the determination of grid size and smoothing distance in CFD–DEM modelling.

Fig. 19

The temporal evolution of impact forces and dynamics with different grid refinements: a the total impact force $F_b/{mg}$; b the solid-resulted impact force $F_{s-b}/{mg}$; c the fluid-resulted impact force $F_{f-b}/{mg}$; d the total kinetic energy $E_k/{mgh}$; e the solid-resulted kinetic energy $E_{ks}/{mgh}$; f the fluid-resulted kinetic energy $E_{kf}/{mgh}$

4.2 The effect of particle shape

Because of the use of spherical grains in this study, it may not be pragmatic to model the grains with different shapes such as clusters and clumps explicitly. Instead, the rolling resistance coefficient can be varied to mimic the non-sphericity of natural grains [1]. Three debris flow cases with various rolling resistance coefficients are manipulated while other model parameters are inherited from Table 1. To reach an explicit interpretation, the particle with a higher rolling resistance is referred to as the particle having a rougher particle shape hereafter.

Figure 20 displays the evolution of impact force and kinetic energy versus time, associated with the consideration of different particle shape (i.e. $\mu _{r} = 0.02, 0.068 \text { and } 0.204$). The summation of both solid and fluid forces (Fig. 20a) and the separate impact forces (Fig. 20b, c) by solid and fluid phases are allocated. For the impact force, the zoomed picture is inserted in the figure so that the initial development can be captured. According to Fig. 20a, the change of the maximum impact force induced by particle shape is not remarkable, while it is clear that the runout velocity of grains becomes slower provided with higher rolling resistance. However, the movement of the fluid phase is less dependent on particle shape since the initiation point of fluid pressure (i.e. the position marked by a dark red pentagram in Fig. 20c) remains $t/ \sqrt{h/g} = 1.25$. Even though the impact force induced by the fluid phase is not sensitive to particle shape. The post-impact force has a tendency to grow with a smoother particle shape. The dynamics for both solid and fluid parts evolve with the roughness of particle shape in a similar way, as depicted in Fig. 20d–f. With a rougher particle shape, the temporal evolution of kinetic energy becomes increasingly sluggish over time, associated with a smaller maximum kinetic energy. This is because a rougher particle shape brings higher energy consumed by inter-particle friction. The fluid part is slowed by the movement of grains due to the reaction force by grains, which depends on the in-time viscosity of the fluid phase. It is also noted that, because of a relatively high inclination angle used in this study, the influence of particle shape on impact forces tends to be attenuated due to a high gravity acceleration parallel to the sliding plane. In the same vein, the significance of particle shape in granular dynamics can be decreased as well. A further discussion on debris flows and the slit dam interaction response of different inclination angles can be conducted in the future.

Fig. 20

The temporal evolution of impact forces and dynamics with different levels of rolling resistance: a the total impact force $F_b/{mg}$; b the solid-resulted impact force $F_{s-b}/{mg}$; c the fluid-resulted impact force $F_{f-b}/{mg}$; d the total kinetic energy $E_k/{mgh}$; e the solid-resulted kinetic energy $E_{ks}/{mgh}$; f the fluid-resulted kinetic energy $E_{kf}/{mgh}$

4.3 The effect of initial porosity

Previous studies have indicated that the porosity of initial samples has a remarkable influence on debris flows [28]. Under a plane consisting of grains, it is shown that a denser granular component can lead to a smaller runout distance and lower pressure change inside the granular system [79]. Besides, a more conservative temporal evolution of kinetic energy can be seen in the dense granular collapse in the plane [37]. To discuss the potential influence of the initial porosity of granular specimens, the initial granular specimens having different porosity are generated with a compression platen as illustrated in Fig. 21. The initial porosity used in this section falls into $\varphi = 0.482, 0.424 \text { and } 0.386$.

According to Fig. 21a, a smaller initial porosity enhances the impact force induced by the solid part, while the fluid-resulted impact force is independent of the variation in initial porosity. It is understood that driven by the fast dynamics under a high inclination angle, the grains carried by debris flows are fully cushioned and rearranged, leading into the same $F_{f-b}$ trend. Therefore, the resultant trend that the total impact force is positively proportional to porosity can be attributed to the activities of the solid part. The contribution to this result is chiefly from the solid phase (Fig. 21b), while the fluid-resulted impact force seems to vary arbitrarily under different packing densities (Fig. 21c). The evolution of dynamics is presented in Fig. 21d–f. The dynamics under a loose packing tend to be sort of faster than the counterpart of a dense packing. Likewise, the maximum kinetic energy in the loose specimen is larger than that of the dense specimen. This trend is comparable to the dilatancy effects captured in the small-scale granular collapse experiment, where the maximum velocity of loose surface particles can be three times larger than dense surface particles [52]. As recorded in both experimental and numerical results [52, 79], the pore pressure development is also different from the packing state. Provided a loose packing (i.e. a larger initial porosity), the pore pressure steeply increases when the particle movement commences and gradually reduces to the static water pressure. On the contrary, well-packed particles result in negative pore pressure during collapsing, which is exaggerated with a denser packing regime. Although the influence of the initial porosity on results (i.e. less than 20% ) is not as significant as the laboratory experiment, the dependence of initial porosity and the system dynamics are analogous. The attenuation of packing density influences can be partially attributed to the same coupled effect by the plane inclination angle, as discussed in the effect of particle shape. It is expected that a more remarkable role of initial packing density in granular dynamics can be observed under a zero or small inclination angle [37, 80].

Fig. 21

The temporal evolution of impact forces and dynamics with different initial porosity: a the total impact force $F_b/{mg}$; b the solid-resulted impact force $F_{s-b}/{mg}$; c the fluid-resulted impact force $F_{f-b}/{mg}$; d the total kinetic energy $E_k/{mgh}$; e the solid-resulted kinetic energy $E_{ks}/{mgh}$; f the fluid-resulted kinetic energy $E_{kf}/{mgh}$

5 Conclusions

Overall, the study aims to unveil the coupled influences of debris flow properties (i.e. GSDs and typical environments such as the slope angle and the saturation state) on debris flow dynamics and the impacts on slit dams. In addition, a series of particle properties such as rolling resistance and initial packing density are changed to discuss the influence on debris flows’ impact force and dynamics. Using the CFD–DEM method, the insights of fluid and solid significance are presented separately, associated with their potential engineering implications on debris flows. After presenting CFD–DEM results and corresponding discussion, the following conclusions can be drawn:

• 1. The solid-resulted impact force against the slit dam is generally 40% greater than that resulting from fluids. Although the significance of GSDs can be observed for monodisperse and trimodal GSDs, the response of the impact force and dynamics to the fractal parameter $D^*$ is not sensitive. In addition, the contribution of fluid and solid phases to the impact force and dynamics appears to be dependent on GSDs’ characteristics as well.

• 2. Given a $D_{\text {max}} / D_{\text {min}}$ equal to or smaller than 4, the effect of the fractal parameter $D^{*}$ on induced impact force and dynamics are not significant. Specifically, the variation of both maximum impact force and the summit of kinetic energy is less than 20% with $D^{*}$ varying from 1 to 3.5). Under $D_{\text {max}} / D_{\text {min}} = 8$, the impact force can be increased 50% when $D^*$ grows from 1 to 3.5.

• 3. Either the peak impact force or the maximum kinetic energy arises double every time the slope angle increases by 10 degrees. In contrast to that, under the same slope angle, the influence of the fractal parameter $D^*$ of GSDs is less than 5%. A more remarkable influence of $D^*$ is expected provided the $D_{\text {max}} / D_{\text {min}}$ larger than 8. Besides, the double-drop phenomena captured in the dynamics evolution vanishes when the slop angle is smaller than 30 degrees.

• 4. The contribution of different phases to the total impact force tends to evolve with different slope angles. Provided 10 degrees slope angle, the fluid-resulted impact force accounts for 75% of the total impact force. When a larger slope angle is given, the contribution by the solid phase gradually becomes dominant and can be up to 70% eventually.

• 5. With three different refinements of the grid, the resolution of the fluid grid trivially is indicated to trivially affect both the impact force and dynamics. When the grid becomes coarser, the peak total impact force tends to fluctuate but no apparent trend can be observed. Accordingly, the kinetic energy versus time curves maintain almost the same for different refinements.

• 6. A coarser particle shape results in a delayed runout of debris flows, while the effect on the peak impact force is negligible (i.e. less than 5%). Both fluid and solid dynamics are exaggerated with a rougher particle shape. When the rolling resistance coefficient changes from 0.02 to 0.204 in this study, the maximum kinetic energy reduces to around 17.14%.

• 7. The denser initial granular packing results in a smaller impact force (i.e. the peak impact force increases 25% when the initial porosity $\varphi$ varies from 0.386 to 0.482), which is in agreement with the laboratory small-scale experiments. Based on the CFD–DEM analyses, the contribution of this is chiefly allocated to the solid phase. Furthermore, the evolution of delayed dynamics is also observed under a higher initial packing density.

Appendix 1: Details of the CFD–DEM method

In the CFD–DEM framework, the fluid is solved based on the finite volume approach whose calculation proceeds for each computational cell. The grain phase is regarded via a locally averaged grain fraction indicated with $\varepsilon _{g}$ for fluid cells. A diagram of CFD–DEM coupling analyses is displayed in Fig. 22a where the black lines indicate the geometry of a fluid cell and solid grains are represented by spheres. Besides, due to the fact that there are two fluid phases for debris flows (i.e. liquid and air phases), the volume of fluid (VOF) method is combined to track the immiscible interface between the two fluid phases. The governing equation for VOF is expressed as:

$$\begin{aligned} \frac{\partial \varepsilon _{f} \alpha _{i}}{\partial t}+\nabla \cdot \left( \varepsilon _{f} \alpha _{i} \textbf{u}_{f}\right) -\nabla \cdot \left( \textbf{u}_{c} \varepsilon _{f} \alpha _{i} (1-\alpha _{i})\right) =0 \end{aligned}$$

(7)

where $\textbf{u}_{f}$ is the fluid velocity for the computational cell, t time, $\alpha _i$ the volume fraction of fluid i, $\varepsilon _f$ the fraction of fluid and $\varepsilon _f=1-\varepsilon _g$. Compression velocity denoted by $\textbf{u}_{c}$ is involved to compose an interface compression term so that a distinct interface could be described. The locally averaged Navier–Stokes equation governs the fluid phase. Hence, the continuity and momentum equations are shown in their incompressible form below:

$$\begin{aligned}{} & {} \frac{\partial }{\partial t}\left( \varepsilon _{f} \rho _{f}\right) +\nabla \cdot \left( \varepsilon _{f} \rho _{f} \textbf{u}_{f}\right) =0 \end{aligned}$$

(8)

$$\begin{aligned}{} & {} \frac{\partial }{\partial t}\left( \varepsilon _{f} \rho _{f} \textbf{u}_{f}\right) +\nabla \cdot \left( \varepsilon _{f} \rho _{f} \textbf{u}_{f} \otimes \textbf{u}_{f}\right) \nonumber \\{} & {} \quad =-\varepsilon _{f} \nabla p+\varepsilon _{f} \nabla \varvec{\tau }+\varepsilon _{f} \rho _{f} \textbf{g}+\varepsilon _{f} \textbf{F}_{\sigma }+\textbf{F}_{d} \end{aligned}$$

(9)

where $\rho _{f}$ is the density of fluids, p the pressure, $\tau$ the stress tensor, $\textbf{g}$ the body force of gravity, $\textbf{F}_{\sigma }$ the surface extension force and $\textbf{F}_{d}$ presents the drag force produced during fluid–grain interaction. The density of fluids is calculated standing on the volume fraction of fluids i and j:

$$\begin{aligned} \rho _{f}=\alpha _{i} \rho _{i}+\alpha _{j} \rho _{j} \end{aligned}$$

(10)

where $\alpha _{j}=1-\alpha _{i}$, $\rho _{i}$ and $\rho _{j}$ refer to the density of fluids i and j, respectively. In this study, the fluid i is debris fluid, while the fluid j is air.

The surface extension force is derived through:

$$\begin{aligned} \textbf{F}_{\sigma }=\sigma \kappa \nabla \alpha \end{aligned}$$

(11)

The interface curvature $\kappa$ is calculated via the equation as follows:

$$\begin{aligned} \kappa =\nabla \cdot \left( \frac{\nabla \alpha }{|\nabla \alpha |}\right) \end{aligned}$$

(12)

For the estimation of void fraction in CFD–DEM studies, the centre point method tends to be the most widespread but it suffers from insufficient accuracy when grain size becomes equal to or larger than grid size [75]. To ease this size effect, numerous smoothening methods have been proposed. For instance, [60] simulated dry granular flow sliding into a water reservoir with the divided void fraction method. Unlike the grain centroid method [87], semi-resolved methods consider the void fraction of grains as a gradient field that can be described by a kernel function [65]. In such an averaging scheme, the numerical error resulting from the abrupt variation of the void fraction can be properly eliminated. In this article, with the same goal, a diffusion equation is addressed to average the grain fraction [56]:

$$\begin{aligned} \frac{\partial \varepsilon _{p}^{i}}{\partial t}=\frac{l^{2}}{\Delta t} \nabla ^{2} \varepsilon _{p}^{i} \end{aligned}$$

(13)

where $\varepsilon _{p}^{i}$ is the grain fraction of the ith grain and l the representative physical length scale of smoothing. A paradigm of diffusion-based kernel function is also illustrated in Fig. 22b. The grain fraction around the sphere is estimated using the solution of the diffusion equation, where the calculation process is conducted on fluid cells. Newton’s second law iteration takes charge of the translational and rotational motion of each grain, which can be calculated based on the following equations:

$$\begin{aligned}{} & {} m_{i} \frac{d \textbf{v}_{i}}{d t}=\sum _{j} \textbf{F}_{i j}+\textbf{F}_{f-g}+m_{i} \textbf{g} \end{aligned}$$

(14)

$$\begin{aligned}{} & {} I_{i} \frac{d \varvec{\omega }_{i}}{d t}=\sum _{j} \textbf{M}_{i j}+\textbf{M}_{f-g} \end{aligned}$$

(15)

where $m_i$ is the mass of grain i, $\textbf{v}_{i}$ grain velocity, $\textbf{F}_{ij}$ the contact force between ith and jth grains, $\textbf{F}_{f-g}$ the fluid–grain interaction forces. Likewise, $I_{i}$ and $\varvec{\omega }_{i}$ are angular moment of inertia and angular velocity of the grain; $\textbf{M}_{ij}$ and $\textbf{M}_{f-g}$ are the torques because of contact forces and fluid–grain interactions, accordingly. The Hertz-Mindlin model regarding rolling friction resistance is applied to track the solid phase of debris flows [1]. The Hertz-Mindlin contact model configuration has been well verified and used in the modelling of natural granular avalanches [34, 46, 51, 81]. Under the framework of the Hertz-Mindlin contact model, normal and tangential contact forces are calculated with the two equation in order:

$$\begin{aligned} F_{i j}^{n}= & {} \frac{4}{3} E_{e} R_{e}^{1 / 2} \delta _{n}^{3 / 2} \end{aligned}$$

(16)

$$\begin{aligned} F_{i j}^{s}= & {} 8 G_{e} R_{e}^{1 / 2} \delta _{n}^{1 / 2} \delta _{s} \end{aligned}$$

(17)

where $\frac{1}{{E_{e} }} = {\raise0.7ex\hbox{${1 - v_{i}^{2} }$} \!\mathord{\left/ {\vphantom {{1 - v_{i}^{2} } {E_{i} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${E_{i} }$}} + {\raise0.7ex\hbox{${1 - v_{j}^{2} }$} \!\mathord{\left/ {\vphantom {{1 - v_{j}^{2} } {E_{j} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${E_{j} }$}}$ $\frac{1}{{G_{e} }} = {\raise0.7ex\hbox{${2(2 - v_{i} )(1 + v_{i} )}$} \!\mathord{\left/ {\vphantom {{2(2 - v_{i} )(1 + v_{i} )} {G_{i} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${G_{i} }$}} + {\raise0.7ex\hbox{${2(2 - v_{j} )(1 + v_{j} )}$} \!\mathord{\left/ {\vphantom {{2(2 - v_{j} )(1 + v_{j} )} {G_{j} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${G_{j} }$}}$ $\frac{1}{{R_{e} }} = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {R_{i} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${R_{i} }$}} + {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {R_{j} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${R_{j} }$}}$; the subscripts i and j indicate the grain id, v refers to Poisson’s ratio, $\delta _{n}$ and $\delta _{s}$ denotes the normal and tangential relative displacement between ith and jth grains in contact. The local damping forces in both normal and shear directions (i.e. $F_{n}^{d}$ and $F_{s}^{d}$) are involved as an artificial damping resistance to dissipate the kinetic energy of grains in DEM. For element tests where a quasi-static process is generally required [2, 7, 14, 20, 71], a fairly high local damping force is recommended for dissipating the kinetic energy of the granular system. Unlike that of element tests, a series of geological avalanche accidents tend to be involved extreme dynamics and high-speed grains, thereby suggesting a dynamical regime (i.e. a small value of artificial damping force). The so-called local damping forces are expressed as follows:

$$\begin{aligned} F_{n}^{d}= & {} -2 \sqrt{\frac{5}{6}} \beta _{d} \sqrt{S_{n} m_{e}} v_{i j}^{n} \end{aligned}$$

(18)

$$\begin{aligned} F_{s}^{d}= & {} -2 \sqrt{\frac{5}{6}} \beta _{d} \sqrt{S_{t} m_{e}} v_{i j}^{t} \end{aligned}$$

(19)

where $\frac{1}{{m_{e} }} = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {m_{i} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${m_{i} }$}} + {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {m_{j} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${m_{j} }$}}$, $S_{n}=2E_{e}\sqrt{R_{e}\delta _{n}}$, $S_{t}=8G_{e}\sqrt{R_{e}\delta _{n}}$, $v_{i j}$ is the relative velocity between ith and jth grains, while the superscripts n and t represent normal and tangential directions. The rolling resistance part is also considered during computation as the grains contained in debris flows are mostly non-spherical. Rolling resistance torque $T_{i j}$ is derived using the following formula:

$$\begin{aligned} T_{i j}=-\frac{\varpi _{i j}}{\left| \varpi _{i j}\right| } \mu _{r} R_{e} F_{i j}^{n} \end{aligned}$$

(20)

where $\varpi _{i j}$ represents the relative angular velocity of grains i and j; $\mu _{r}$ is the rolling resistance coefficient. In addition, the model parameter $\beta _{d}$ is accessed based on the expression below:

$$\begin{aligned} \beta _{d}=-2 \sqrt{\frac{5}{6}} \frac{\ln \left( e\right) }{\left( \ln \left( e\right) +\pi ^{2}\right) ^{1 / 2}}\left( 2 m_{e} E_{e}\left( R_{e} \delta _{n}\right) ^{1 / 2}\right) ^{1 / 2} \end{aligned}$$

(21)

where e is the coefficient of restitution.

Fig. 22

Diagram of the semi-resolved CFD–DEM method: a spatial arrangement of grains and fluid cells, where grain information is updated based on DEM cycles and fluid is solved based on fluid cells. The information interchange is performed through a coupling framework. b Grain fraction $\varepsilon _{p}$ transition around a single grain. The value of $\varepsilon _{p}$ is obtained via a diffusion equation and then projected into fluid cells

The fluid–grain drag force exerted on ith grain ($F_{i}^{d}$) is computed utilising the empirical Di Felice model [12].

$$\begin{aligned} F_{i}^{d}=\frac{1}{2} C_{d} \rho _{f} \pi R_{i}^{2}\left| \textbf{u}_{f}-\textbf{u}_{i}\right| \alpha _{f}^{1-\chi } \end{aligned}$$

(22)

where $R_{i}$ denotes the radius of grain i, $C_{d}$ the drag coefficient and $\chi$ a coefficient for correction. The values of $C_{d}$ and $\chi$ are accessed using following two functions:

$$\begin{aligned} C_{d}= & {} \left( 0.63+\frac{4.8}{\sqrt{\textrm{Re}_{p}}}\right) ^{2} \end{aligned}$$

(23)

$$\begin{aligned} \chi= & {} 3.7-0.65 \exp \left[ -\frac{\left( 1.5-\log _{10} {\text {Re}}_{p}\right) ^{2}}{2}\right] \end{aligned}$$

(24)

in which $Re_{p}$ is particulate Reynolds number, aligning with

$$\begin{aligned} {\text {Re}}_{p}=\frac{2 \varepsilon _{f} \rho _{f} R_{i}\left| \textbf{u}_{f}-\textbf{u}_{i}\right| }{\mu _{f}} \end{aligned}$$

(25)

It is noticed that, the same as $\rho _{f}$ mentioned earlier, $\mu _{f}=\alpha _{i} \mu _{i}+\alpha _{j} \mu _{j}$.