1 Introduction

Rockslides can be characterized by a rapid evolution, up to a possible transition into a rock avalanche, which can be associated with an almost instantaneous collapse and spreading (Utili et al. 2014). Different examples are available in the literature, but the Vajont rockslide is quite unique for its morphological and geological characteristics, as well as for the type of evolution and the availability of long-term monitoring data. The Vajont rockslide (Sintesi 1959; Semenza and Ghirotti 1963) occurred in the Italian Alps, in October 1963, when an ancient slide became unstable and moved into the Vajont reservoir, impounding 1.34 × 108 m3 of water, at great speed (Ciabatti 1964; Viparelli and Merla 1968; Ward and Day 2011; Crosta and Frattini 2007; Crosta et al. 2013). The rockslide involved approximately 270 million m3 of rock and generated water waves probably averaging 90 m above the dam crest. In fact, 100 and 200 m high water wave traces were observed along the left and right valley flanks, respectively (Chowdhury 1978). The displaced water initially raised along the opposite valley flank and then overtopped the dam. The water wave flooded successively the downstream village of Longarone, along the Piave river valley, causing more than 2000 casualties.

This type of impulse waves has been an interesting research subject both for artificial reservoirs and tsunami generation (Slingerland and Voight 1979; Harbitz 1992; Fritz 2002; Grilli et al. 2005). The failure mechanism of the Vajont rockslide is generally believed to be the result of combined effects of a rising reservoir level and intense rainfall periods leading to an increase of pore water pressure (Hendron and Patton 1987). Field investigations by Hendron and Patton (Hendron and Patton 1987) revealed that multiple clay layers with thickness between 0.5 and 10 cm exist close or along the sliding surface. Based on the geologic information, the strength characteristics and the available monitoring data, the rockslide has been studied by numerous investigators to reveal the controlling geologic constraints and the internal deformation (Belloni and Stefani 1987; Boon et al. 1963; Paronuzzi et al. 2013; Vacondio et al. 2013; Chowdhury 1987; Corbyn 1982; Crosta and Agliardi 2003; Selli and Trevisan 1964; Rossi et al. 1963; Müller-Salzburg 1964, 1987a, b). 2D analytical and numerical back-calculations estimated that the critical sliding friction angle is within a range of [17°, 23°] (Crosta et al. 2007; Corbyn 1982; Mencl 1966; Nonveiller 1987), which is significantly higher than the measured residual friction angle of wet clay layer at the sliding surface [6°, 10°] (Hendron and Patton 1987). Hendron and Patton (1987) suggested that this discrepancy is due to the three-dimensional effects of the real slide, such that the 2D model analyses cannot capture the real mechanisms of slope failure. Furthermore, the extremely high velocity of the slide (e.g. 30 m/s) (Ciabatti 1964; Chen et al. 2006; Crosta et al. 2013) is still an important research subject. Many theories and assumptions have been proposed in the attempt to explain the apparent high mobility of rock and debris avalanches, and in particular, for the Vajont rockslide these theories include the thermo-poro-mechanical effects at the clay layer due to heating (Voight and Faust 1982; Vardoulakis 2002; Alonso and Pinyol 2010; Pinyol and Alonso 2010), high shearing rate-induced friction loss (Tika and Hutchinson 1999; Ferri et al. 2011) and disintegration of the rockslide mass during the failure (Sitar et al. 2005).

Numerical modelling of rockslide dynamics represents a major challenge, as a huge amount of solid materials and complicated solid–solid and solid–fluid interactions would be involved (Boon et al. 1963; Topin et al. 2012). Topin et al. (2012) studied the dynamics of dense granular flows in fluid by means of the contact dynamics method coupled with the computational fluid dynamics (CFD). The importance of grain inertia, fluid inertia and viscous effects was analysed by increasing the fluid viscosity in the CFD model. They observed that the fluid has a twofold effect on the granular motion. On one hand, it may reduce the granular kinetic energy by developing negative pore pressure and fluid viscous drag force (Iverson et al. 2000; Pailha et al. 1994; Topin et al. 2011). On the other hand, it can also enhance the granular flow by lubricating the granular mixture. The compensation between these two effects would eventually influence the runout distance of granular materials in a fluid (Topin et al. 2012).

In modelling the granular motion via the DEM, the importance of the particle properties, such as particle size distribution, particle friction and shape effects, should be considered carefully (Utili et al. 2014; Casagli et al. 2003; Crosta et al. 2007). This is especially true for granular flows in fluid, because coarse grains can settle faster than the finer ones due to the fluid viscous drag effect (Stokes 1901; Kynch 1952). Thus, it is necessary to use real particle sizes in the DEM model, so that realistic mechanical and hydraulic behaviour of granular flows can be obtained. However, this approach has a critical problem, namely, a huge amount of particles would be generated in the DEM model to simulate even a very small-scale rockslide, which would require an excessive computational cost (Utili and Nova 2008; Utili and Crosta 2011). Even though parallel computation techniques (Shigeto and Sakai 2011; Chen et al. 2009) have been developed, the number of particles which can be simulated on PCs or PC clusters is still far smaller than that typical of real slopes (e.g. thousands of billions of grains). To overcome this problem, the coarse grain model has been proposed (Sakai and Koshizuka 2009; Sakai et al. 2010, 2012; Zhao et al. 2014). In this model, a coarse particle can represent a collection of real fine particles. As a result, a large-scale DEM simulation of granular flows can be performed using a relatively small number of calculated particles (Sakai et al. 2012).

Currently, there is a lot of interests in exploring the failure mechanism and characteristics of fast and long runout rockslides via numerical modelling (Utili et al. 2014; Crosta et al. 2013; Sitar et al. 2005; Zhao et al. 2012; Boon 2013; Quecedo et al. 2004; Crosta et al. 2006, 2009; Crosta and Frattini 2008). In this paper, a quasi-3D DEM-CFD model is used to investigate the mechanical and hydraulic behaviour of the Vajont rockslide. Section 2 summarizes the theory and methodology of the DEM-CFD coupling model. The governing equations for particle motion, particle–fluid interaction and fluid flow are discussed in detail. In Sect. 2.4, we present the coarse grain model as an approach to do grain-size scaling in the DEM. Section 3.1 illustrates the DEM and CFD model used in this research. A “hopper discharge” technique has been proposed to generate the real scale slope model. The numerical results are presented in Sect. 3.2, in terms of the deformation and motion of the slope mass, the generation of water waves, evolution of fluid pressure and the distribution of slope force chain networks. The advantages and limitations of using a coupled DEM-CFD modelling approach are discussed in Sect. 4.

2 Theory and Methodology

Different modelling approaches have been adopted in the literature to model rockslides/rock avalanches and related impulse waves. Even if DEM and FEM models have been developed to study these types of phenomena, very little has been done to make a complete and simultaneous modelling of the rockslide, its impact on the water reservoir and the consequent impulse wave and tsunami. Crosta et al. (2013) used an ALE-FEM approach for a 2D/3D simulation of these processes. In this paper, we investigate the capabilities of a coupled DEM-CFD approach, where the rockslide mass is simulated by an assembly of spherical particles of pre-determined size and initial porosity (Cundall and Strack 1979). These grains can interact with each other through well-defined microscopic contact models (Hertz 1882; Zhang and Whiten 1996; Johnson 1985) and with the fluid (e.g. water or air) by empirical correlations of fluid and solid interaction models. In this model, the interactions between solid particles are resolved using the DEM, while the fluid–solid interactions are calculated by the DEM-CFD coupling algorithm (Anderson and Jackson 1967; Brennen 2005). The fluid motion is simulated via the CFD by taking into account for the presence of a free fluid surface. The DEM and CFD open source codes ESyS-Particle (Weatherley et al. 2011; Abe et al. 2004) and OpenFOAM (OpenCFD 2004) were employed for the simulations presented here. The coupling algorithm from Chen et al. (2011) originally written in YADE (Šmilauer et al. 2010) was implemented in ESyS-Particle by the authors. The detailed validation of the proposed DEM-CFD model is not included in the current paper. However, readers who are interested in validating the model are recommended to read the two papers written by the first author (see Utili et al. 2014; Zhao et al. 2014).

2.1 Governing Equations of Solid Motion

In the current analyses, the linear-spring and rolling resistance contact model is used in the DEM simulations to calculate the interaction forces between solid particles. The detailed description of the model can be found in Jiang et al. (2005). According to the Newton’s second law of motion, the equations governing the translational and rotational motions of one single particle are expressed as:

$$m_{i} \frac{{d^{2} }}{{dt^{2} }}\overrightarrow {{x_{i} }} = m_{i} \overrightarrow {g} + \sum\limits_{c} {\left( {\overrightarrow {{f_{\text{nc}} }} + \overrightarrow {{f_{\text{tc}} }} } \right)} + \overrightarrow {{f_{\text{fluid}} }}$$
(1)
$$I_{i} \frac{d}{dt}\overrightarrow {{\omega_{i} }} = \sum\limits_{c} {\overrightarrow {{r_{c} }} \times \overrightarrow {{f_{\text{tc}} }} } + \overrightarrow {{M_{r} }}$$
(2)

where m i is the mass of a particle i; \(\overrightarrow {{x_{i} }}\) is the position of its centroid; \(\overrightarrow {g}\) is the gravitational acceleration; \(\overrightarrow {{f_{\text{nc}} }}\) and \(\overrightarrow {{f_{\text{tc}} }}\) are the normal and tangential inter-particle contact forces exerted by the neighbouring particles; the summation of contact forces is done over all particle contacts; \(\overrightarrow {{f_{\text{fluid}} }}\) is the fluid–particle interaction force; I i is the moment of inertia; \(\overrightarrow {{\omega_{i} }}\) is the angular velocity; \(\overrightarrow {{r_{c} }}\) is the vector from the particle mass centre to the contact point and \(\overrightarrow {{M_{r} }}\) is the rolling resistant moment.

2.2 Fluid–Particle Interaction

The fluid–particle interaction force (\(\overrightarrow {{f_{\text{fluid}} }}\)) consists of two parts: hydrostatic and hydrodynamic forces (Shafipour and Soroush 2008). The hydrostatic force acting on a single particle, i, accounts for the influence of fluid pressure gradient around the particle (i.e. buoyancy) (Chen et al. 2011; Kafui et al. 2011; Zeghal and El Shamy 2004), as shown in Eq. (3).

$$\overrightarrow {{f_{b}^{i} }} = - v_{pi} \nabla p$$
(3)

where v pi is the volume of particle i and p is the fluid pressure.

The hydrodynamic forces acting on a particle are the drag, lift and virtual mass forces. The drag force is caused by the viscous shearing effect of fluid on the particle; the lift force is caused by the high fluid velocity gradient-induced pressure difference on the surface of the particle and the virtual mass force is caused by relative acceleration between particle and fluid (Drew and Lahey 1990; Kafui et al. 2002). The latter two forces are normally very small when compared to the drag force at relatively low Reynolds numbers (Kafui et al. 2002). Thus, the lift and virtual mass forces are neglected in the current DEM-CFD coupling model. In this process, the drag force occurs when there is a non-zero relative velocity between fluid and solid particles. It acts at the particle mass centre in a direction opposite to the particle motion (Guo 2010). To quantify the drag force, experimental correlations (Stokes 1901; Ergun 1952; Wen and Yu 1966) and numerical simulations (Choi and Joseph 2001; Zhang et al. 1999; Beetstra et al. 2007) are available in the literature. In this work, the drag force (F di) acting on an individual solid particle is calculated using the empirical correlation proposed by Di Felice (1994), as:

$$F_{\text{di}} = \frac{1}{2}C_{\text{d}} \rho_{\text{f}} \frac{{\pi d_{\text{p}}^{2} }}{4}\left| {\varvec{U} - \varvec{V}} \right|\left( {\varvec{U} - \varvec{V}} \right)n^{ - \chi + 1}$$
(4)

where C d is the drag force coefficient; ρ f and U are the fluid density and velocity; n is the porosity of the granular material; d p and V are the particle diameter and velocity. The drag force coefficient is defined according to the correlation proposed by Brown and Lawler (2003):

$$C_{\text{d}} = \frac{24}{\text{Re}_{p}}\left( {1 + 0.150\text{Re}^{0.681}_{{p}} } \right) + \frac{0.407}{{1 + \frac{8710}{\text{Re}_{p}}}}$$
(5)

The definition of drag force coefficient in Eq. (5) is valid for fluid flow with Reynolds’ numbers ranging from 0 to 104 (Brown and Lawler 2003). The term n −(χ+1) in Eq. (4) represents the influence of granular concentration on the drag force. The expression for the term χ is:

$$\chi = 3.7 - 0.65\exp \left[ { - \frac{{\left( {1.5 - \log_{10} \text{Re}_{{p}} } \right)^{2} }}{2}} \right]$$
(6)

where \(\text{Re}_{{p}} = {{\rho_{\text{f}} d\left| {\varvec{U} - \varvec{V}} \right|} \mathord{\left/ {\vphantom {{\rho_{\text{f}} d\left| {\varvec{U} - \varvec{V}} \right|} \mu }} \right. \kern-0pt} \mu }\) is the Reynolds’ number defined at the particle size level, with μ being the fluid viscosity. In the current analyses, χ ranges from 3.4 to 3.7.

2.3 Governing Equations of Fluid Flow

The governing equations of fluid flow in a fluid–solid mixture system can be derived from the theory of multiphase flow (Brennen 2005), in which the free surface condition is resolved by the Volume of Fluid (VOF) method (Hirt and Nichols 1981; Shan and Zhao 2014). In our numerical simulations, the fluid domain is initially discretized into a series of mesh cells, in which the solid particles may be dispersed. In each fluid mesh cell, the volume fraction of the summation of fluid phases is n (i.e. porosity), for which, the volume fraction occupied by the fluid phase 1 (e.g. water) is α 1 (0 ≤ α 1 ≤ 1), while it is 1 − α 1 for the other phase. This definition indicates that if the void space is completely filled with water, α 1 = 1, while if the space is filled with air, α 1 = 0. In the VOF method, the mixture properties, such as velocity, density and viscosity, are defined as:

$$\overline{\varvec{U}} = \alpha_{1} \varvec{U}_{{\mathbf{1}}} + \left( {1 - \alpha_{1} } \right)\varvec{U}_{{\mathbf{2}}}$$
(7)
$$\overline{\rho } = \alpha_{1} \rho_{ 1} + \left( {1 - \alpha_{1} } \right)\rho_{ 2}$$
(8)
$$\overline{\mu } = \alpha_{1} \mu_{1} + \left( {1 - \alpha_{1} } \right)\mu_{2}$$
(9)

where U 1 , ρ 1, μ 1 and U 2 , ρ 2, μ 2 are the velocities, densities and viscosities of fluid phase 1 and 2, respectively.

The transport equation for α 1 is given as:

$$\frac{{\partial \alpha_{1} }}{\partial t} + \nabla \cdot \left( {\alpha_{1} n\overline{\varvec{U}} } \right) - \nabla \cdot \left( {\alpha_{1} \left( {1 - \alpha_{1} } \right)\varvec{U}_{\varvec{r}} } \right) = - \alpha_{1} \frac{\partial n}{\partial t} = \alpha_{1} \nabla \cdot \left( {n\overline{\varvec{U}} } \right)$$
(10)

where \(\nabla \cdot \left( {\alpha_{1} \left( {1 - \alpha_{1} } \right)\varvec{U}_{\varvec{r}} } \right)\) is the surface compression term, with U r being the compression velocity defined by Rusche (2003). This artificial term is active only along the interface between water and air due to the term α 1(1 − α 1).

The continuity and momentum equations of the fluid–solid mixture are given as:

$$\frac{{\partial \left( {n\overline{\rho } } \right)}}{\partial t} + \nabla \cdot \left( {n\overline{\rho } \overline{{\mathbf{U}}} } \right) = 0$$
(11)
$$\frac{{\partial \left( {n\overline{\rho } \overline{{\mathbf{U}}} } \right)}}{\partial t} + \nabla \cdot \left( {n\overline{\rho } \overline{{\mathbf{U}}} \overline{{\mathbf{U}}} } \right) - \nabla \cdot \left( {n{\varvec{\uptau}}} \right) = - n\nabla p + n\overline{\rho } \overrightarrow {g} \varvec{ + }\overline{{\varvec{f}_{{\mathbf{d}}} }} + F_{\text{s}}$$
(12)

where p is the fluid pressure; \(\overline{{\varvec{f}_{{\mathbf{d}}} }} = {{\sum\nolimits_{i = 1}^{N} {F_{\text{di}} } } \mathord{\left/ {\vphantom {{\sum\nolimits_{i = 1}^{N} {F_{\text{di}} } } {\left( {dxdydz} \right)}}} \right. \kern-0pt} {\left( {dxdydz} \right)}}\) is the drag force per unit volume, with N being the number of particles within the fluid cell; \(F_{s} = \sigma \left( {\nabla \cdot \left( {\frac{{\nabla \alpha_{1} }}{{\left| {\nabla \alpha_{1} } \right|}}} \right)} \right)\left( {\nabla \alpha_{1} } \right)\) is the surface tension force, with σ being the surface tension coefficient.

2.4 Coarse Grain Model

The use of real particle size for the modelling of large-scale submerged rockslides is unfeasible given the current computational power. To overcome this problem, upscaled particles with a size larger than the ones in real rockslides need to be used in the DEM simulations (Utili and Nova 2008; Utili and Crosta 2011). We assume that: (1) one large particle represents a clump of real sized sand grains (see Fig. 1); (2) the fine grains are bonded together, so that they can move as a whole; (3) the translational and rotational motion of the coarse grain and the clump of fines grains are the same; (4) the contact forces acting on the coarse grains are the summation of contact forces acting on this clump of real grains by the neighbouring grains. The fluid viscous drag force acting on the coarse particle is calculated by balancing the coarse particle and a clump of real particles (see the derivation below). This method of scaling up the particle diameter is referred to in the literature as “coarse grain model”, and is increasingly used in DEM simulations (Sakai et al. 2012; Radl et al. 2011; Hilton and Cleary 2012; Baran et al. 2013).

Fig. 1
figure 1

Schematic view of the scaling law used in the DEM [α is the scaling factor defined in Eq. (16)]

Full size image

Denoting the sizes of the coarse grain particle and original real sand particle as D and d, the number of particles (N) in the clump can be approximated as:

$$N = \frac{{D^{3} }}{{d^{3} }}$$
(13)

The drag force acting on the clump is the summation of the drag forces [Eq. (4)] acting on all the grains:

$$F_{\text{d}} = \frac{1}{2}C_{\text{d}} \rho_{\text{f}} \frac{{\pi d^{2} }}{4}\left| {\varvec{U} - \varvec{V}} \right|\left( {\varvec{U} - \varvec{V}} \right)n^{ - \chi + 1} \times \frac{{D^{3} }}{{d^{3} }}$$
(14)

The drag force acting on a scaled particle in the CFD-DEM coupling code is calculated as:

$$F^{\prime}_{\text{d}} = \frac{1}{2}C_{\text{d}}^{\prime } \rho_{\text{f}} \frac{{\pi D^{2} }}{4}\left| {\varvec{U} - \varvec{V}} \right|\left( {\varvec{U} - \varvec{V}} \right)n^{{ - \chi^{\prime} + 1}}$$
(15)

Thus, the drag force calculated by Eq. (15) should be scaled up by a factor (α), so that it equals to that calculated by Eq. (14). α is expressed as:

$$\alpha = \frac{{F_{\text{d}} }}{{F^{\prime}_{\text{d}} }} = \frac{{C_{d} n^{{ - \chi + \chi^{\prime}}} D}}{{C_{d}^{\prime } d}}$$
(16)

By setting the Reynolds numbers the same, the values of C d and χ are the same for both the real fluid flow and numerical models [see Eq. (4)], as shown in Eq. (16). Thus, this equation can be reduced to α = D/d. In this study, we set out to investigate the behaviour of submerged rockslides, using different values of α. As shown in Table 1, α was set to 1, 5 and 10, so that one large particle in the DEM can represent a clump of fine grains ranging in number from 1 to 103. The hydrostatic forces acting on a coarse particle and a clump of fine grains are the same, because it is determined only by the volume of solid materials. It is also worth noting that the other parameters for the coarse and real particles are the same, so that realistic soil properties can be modelled in numerical simulations.

Table 1 Scaling relationship for different grains
Full size table

3 Numerical Simulations

3.1 The DEM-CFD Model

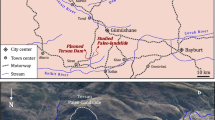
A plan view of the Vajont rockslide is shown in Fig. 2, together with the traces of the two cross sections A–A and B–B, representative of the eastern and western sectors of the slide, and herein analysed. The profiles along these cross sections are illustrated in Fig. 3.

Fig. 2
figure 2

Plan view of the Vajont rockslide (cited and modified after Rossi and Semenza 1965; Chowdhury 1978) with the traces of the cross sections used in this study

Full size image
Fig. 3
figure 3

Profile of the eastern (A–A) and western (B–B) slopes of Vajont valley and rockslide (failure surface is represented as red curves). The reservoir water is shown as blue (colour figure online)

Full size image

In the following analyses, the two cross sections are considered as representative, even if simplified, of these two different or limit geometries, with a more chair-like geometry for the western lobe and a steeper one for the eastern one. It is assumed that the slope mass moved upon a well-defined failure plane characterized by the presence of a clay layer (as represented by the red curves on Fig. 3) which is believed to be continuous over a large area of the sliding surface (Hendron and Patton 1987). The initial reservoir level and water table are placed at about 700 m above the sea level as the real water level at the time of slope failure. As the western slope sliding (section B–B) is believed to be more significant at dominating the wave motion and the consequent reservoir overtopping (Crosta et al. 2013; Hendron and Patton 1987; Sitar et al. 2005) several different simulations of the western slope failure have been performed, by changing the fluid viscosity and coarse grain scaling factors.

3.1.1 Input Parameters of the DEM-CFD Model

The input parameters adopted for both the DEM and CFD models are listed in Table 2 and have been chosen according to available data and some simplified assumptions concerning the failure surface, the material strength and the physical mechanical properties. In fact, as stated above, the main aim of the study consists in testing and validating the numerical approach for the simulation of fast moving rockslides and rock/debris avalanches. In this research, no numerical damping is employed. Two main reasons have to be considered for this choice. First, although several damping models exist in the literature, few of them have clear physical bases. The use of numerical damping can dissipate kinetic energy and bring the whole granular system to the steady state quickly. As a result, damping is often used in quasi-static simulations as only the static state is of interest (Jiang et al. 2005; Modenese et al. 2012). However, when modelling rockslides, and especially rapid ones, the granular material would go through dynamic phases, such that any damping would alter the mechanical behaviour of the system significantly. Even though the viscous damping forces have been used to simulate the energy dissipation within the granular assembly due to plastic contacts (Brilliantov et al. 2007), the magnitude of energy dissipation is very difficult to be evaluated correctly. Thus, this research does not use numerical damping and assumes that the energy dissipation in rockslides only comes from frictional forces between particles.

Table 2 Input parameters of the DEM-CFD model
Full size table

3.1.2 Generation of Slope Mass by the DEM

The performed simulation of Vajont rockslide has a plane strain boundary condition in which the out of plane direction of the model is set as a periodic boundary. In this framework, all the granular materials are packed within a unit periodic cell which can be regarded as one fraction of the real slope. Any particle with the centroid moving out of the periodic cell through one particular face is mapped back into the cell domain at a corresponding location on the opposite side of the cell. Particles with only one part of the volume lying outside the cell can interact with particles near the face and one image particle will be introduced into the opposite face at a corresponding location, so that it can interact with other particles near the opposite face (Cundall 1987). The size of the periodic dimension is chosen as 20 m which is ten times the size of the adopted effective grain size (D 10). As an example, the configuration of the eastern slope (section A–A) is shown in Fig. 4. It can be observed that the upper slope profile and the lower slope failure surface are represented by smooth, rigid walls, while the periodic boundary is employed in the lateral direction.

Fig. 4
figure 4

Model configuration of the eastern sector

Full size image

To generate a dense slope mass, the author has proposed a “hopper discharge” technique, by which the solid particles are used to fill the space bounded by the upper slope profile, the lower failure surface and the periodic boundary (see Fig. 4). The generation procedure is described as a series of five successive steps in Fig. 5.

Fig. 5
figure 5

Generation of DEM slope model by the “hopper discharge” technique

Full size image
  1. 1.

    Part of the upper slope profile bounding wall is removed to create an open hole (Fig. 5a);

  2. 2.

    A large hopper is placed just above the open hole (Fig. 5a);

  3. 3.

    A DEM grain generator is placed at the upper part of the hopper, which generates discrete particles and applies gravity to these particles continuously (Fig. 5a). No pre-compression and cohesive force is applied to these grains;

  4. 4.

    The solid particles continuously drop into the bounding space (Fig. 5b–e);

  5. 5.

    Once the space is completely filled with particles, the generation is stopped and the hopper is removed from the model. The sample is then trimmed to get the aimed pre-failure slope geometry (Fig. 5f).

In the current analyses, the dimensions of the slopes are set the same as the real Vajont slopes. As a result, unrealistically large particles are used in the analyses, so that the total number of grains generated in DEM is acceptable for the current computational power (i.e. Intel® Core™ i7 CPU, 2.93 GHz). For the validity of the grain-size upscaling, we refer back to the coarse grain model discussed in Sect. 2.4 of this paper. The DEM models of the eastern and western slope masses consist of 21,600 and 24,55 spherical particles, respectively.

3.1.3 Initiation of the Slope Failure

Once the DEM slope sample is generated, a sufficient number of iteration time steps are used to stabilize the simulation. As the numerical model has the same dimensions as the real Vajont slope, we assume that the initial packing states of the slope mass (e.g. stress and strain, sample porosity) can match the real in situ ground states. In this study, the slope failure is initiated by removing the temporary bounding wall of the upper slope profile. As some particles might bounce away due to the sudden release of stresses near the slope surface, the bounding wall is lifted upwards slowly until no particle is in contact with it. Then, the bounding wall is removed completely from the model. After initiation, the slope mass can move downwards along the failure plane under gravity. As mentioned in Sect. 1, the weak clay layer at the failure surface has been recognized and suggested to serve as the lubrication zone of the Vajont rockslide, with relatively small friction angles (Hendron and Patton 1987; Tika and Hutchinson 1999; Ferri et al. 2011; Skempton 1966) In the DEM model, this weak zone is represented by a fixed grain layer, which is paved along the slope failure surface. These fixed grains are assigned with a relatively small friction angle (i.e. 10°) and can rotate freely about their geometric centres.

3.1.4 Fluid Domains

In the current DEM-CFD model, the fluid phase consists of water and air. As illustrated in Fig. 6, the water and air domains are represented by the red and blue meshes, respectively. The initial upper boundary of the water domain is placed at an elevation of 700 m above the sea level (maximum reservoir level before failure), while the upper boundary of air domain is determined according to the water splashing profile in Fig. 2. Ideally, the space above the water table should be completely filled with air, such that the CFD domain can be extended further into the upper region. However, due to the high computational cost, we just employed an open air boundary condition at the upper boundary of the air domain and assumed that the water wave will not splash higher than 850 and 900 m for the eastern and western slopes, respectively. The CFD mesh is generated using the open source software gmsh (Geuzaine et al. 2014). To optimize the mesh resolution, the fluid mesh cells at the flow front are very fine, while meshes near the slope are coarse. The maximum size of the mesh cell is 30 m, while the minimum size is 15 m. The slope below the water table is assumed to be saturated, so that the solid particles can disperse in the CFD mesh cells.

Fig. 6
figure 6

Numerical model of the Vajont slopes for the A–A and B–B profiles (red water reservoir; blue discretized air sector). See Fig. 1 for the locations of the two cross sections (colour figure online)

Full size image

3.2 Results of Eastern Slope Simulation

3.2.1 Slope Deformation and Wave Motion

Figure 7 illustrates the evolution of slope deformation and the motion of water wave during the sliding of Vajont eastern slope (section A–A in Fig. 2). The slope mass is initially coloured grey and green at different parallel layers, so that its deformation can be clearly identified during the rocksliding. It can be observed that at the beginning of the slide, the slope mass moves as a whole on the failure surface and quickly slides into the reservoir with a slight rotational component of motion, generating water waves. The water wave moves in the sliding direction and splashes onto the northern bank of the Vajont valley. Near the flow front, the CFD mesh cells are filled with both water and air, thus, the colour representing the water phase is less intense. The maximum height of water wave occurs at about 30 s after the slope failure, and is about 130 m above the initial water level of the reservoir, that is ca. 110 m above the dam crest. The predicted water splashing height in the current numerical model can match the field observations in Fig. 2. Once the wave reaches the maximum height, it flows back into the reservoir as for the 2D plane strain conditions. The total duration of the simulation is around 50 s. The final granular deposit has a very gentle angle of repose and the reservoir is completely filled by the failed slope mass. Two enlarged views of the slope and water wave sectors at the flow front of the rockslide are shown in Fig. 8.

Fig. 7
figure 7

Evolution of slope deformation and water wave motion (along section A–A) at different time steps since the movement initiation. The granular mass is coloured in initially horizontal stripes to follow the internal mass deformations (the initial slope profile and water table are plotted as black lines on the snapshots. The splashed water wave is represented by regions enclosed by red curves. For the contour of fluid domain, the colour blue and red represent air and water, respectively, while the smeared colour represents the air–water mixture) (colour figure online)

Full size image
Fig. 8
figure 8

Enlarged view of the slide front and water wave (section A–A)

Full size image

During the slide motion, the solid materials translate and partially rotate along the failure surface as suggested by internal deformations in Fig. 7. Some more rapid superficial movement is observed and some successive “deep” instabilities at the slide front are observed when the mass starts rising along the opposite valley flank. In this process, it is interesting to observe that the water table within the moving mass is translated with the slide (see Fig. 7). At the same time, the reservoir water is pushed at the front rising along the opposite valley flank. In this model, there is a difference in elevation and inclination between reservoir water and groundwater, controlled by the slide and wave velocities as well as by the porosity and permeability of the particle assemblage. This is well shown in Fig. 7 after 20, 30 and 40 s since the initiation of slope movement.

The velocity of the water wave and the distance it travels over time are illustrated in Figs. 9, 10. At the beginning of the slide, the water wave moves slowly towards the northern bank of the valley as the slope mass slides into the reservoir. After 15 s from initiation, the wave velocity increases quickly to its peak value of 20 m/s and then decreases gradually to zero after 34 s. After that, the splashed water wave flows back into the reservoir, and above the slide mass as represented by the gradual increase of water wave velocity. When compared to the evolution of slope velocity in Sect. 3.2.1, the occurrence and magnitude of the peak water wave velocity corresponds to the occurrence of the maximum slope velocity.

Fig. 9
figure 9

Velocity of the water wave for simulation along the section A–A (dashed line the time of wave back flow)

Full size image
Fig. 10
figure 10

Height of the water wave above the original reservoir level for section A–A

Full size image

According to Fig. 10, it can be observed that the elevation of water wave increases gradually from zero to the peak value of 130 m. After reaching the maximum height at 43 s since the onset of the slope failure, it decreases slowly due to the back flow of water into the reservoir. The final elevation of water in the reservoir is about 35 m above the initial reservoir water level. This is the result of the porosity of slope mass when displaced and arrested within the reservoir, being the initial water volume preserved.

3.2.2 Slope Velocity Analysis

A notable feature of the Vajont rockslide is the extremely high velocity of slope movement. According to the discussion by Sitar et al. (2005) and Caloi (1966), part of the slide mass has moved more than 400 m in less than 60 s. Previously published papers indicate that the average maximum slide velocity can range from 20 to 50 m/s (Hendron and Patton 1987). Several hypotheses have been proposed to explain the unusual high velocity, including the reduction of shear strength, weak layer beneath the slope, disintegration of the slide mass (Hendron and Patton 1987; Voight and Faust 1982; Sitar et al. 2005). In this paper, we have investigated the slope velocity by the DEM simulations. The average peak velocity of the sliding front is shown in Fig. 11. It can be observed that the slope initially accelerates quickly to reach the maximum velocity of 22 m/s at 15 s after failure. After that time, the sliding velocity decreases gradually until the solid mass finally reaches a static state. When compared with the numerical results by the discontinuous deformation analysis (DDA) from Sitar et al. (2005), the current DEM simulation can predict almost the same maximum slope velocity.

Fig. 11
figure 11

Time history of the mean velocity of the sliding front for section A–A

Full size image

To extract the slope sliding velocity, we adopted an Eulerian sampling approach by placing a series of measurement circles within the slope mass at three different cross sections (e.g. top, middle and toe), as shown in Fig. 12. The measurement circles are fixed in space with radii of 10 m (i.e. five times the effective grain radius). The average properties (e.g. velocity, stress) of grains within the measurement circles can be recorded during the simulations. The slope velocities recorded at these locations are shown in Fig. 13. It can be observed that the slope mass moves together as a whole at the beginning of the sliding (t < 10 s). After that, the front slope mass falls into the valley and accumulates there. Thus, the velocity recorded in A-6 decreases gradually to a very small value. The granular velocity recorded at other locations can increase quickly to the peak value of about 25 m/s as expected, because of the steep inclination of the eastern slope. The measured average slope velocity can match the estimated value by Hendron and Patton (1987) (20–30 m/s). As the upper slope mass slides downwards, the recorded velocity at A-1, A-3 and A-4 would suddenly turn into nil as no grain exists there. Sampling windows located near the failure surface will continuously measure showing the evolution of velocity over time. After 31 s, some of the upper grains would jump at the slide tail region, resulting in an oscillating slope velocity at A-2. The overall sliding time is about 45 s.

Fig. 12
figure 12

Distribution of the measuring points for the eastern slope (section A–A)

Full size image
Fig. 13
figure 13

Slope velocity at different locations (along section A–A)

Full size image

3.2.3 Force Chains

It is also interesting to explore the distribution and evolution of the fabric structure or force chains of the granular slope, to see how the slope structure evolves over time. The force chains of a granular assembly illustrate the distribution of contact forces and their magnitudes. In these graphs, straight lines are used to connect the centres of each pair of particles in contact. The thickness of these lines represents the magnitudes of the normal contact forces, while the tangential direction of these curves at a specific point aligns with the orientation of the contact force vector. Based on the plots of force chains at successive times, it is very convenient to study the slope structure, as shown in Fig. 14. Once failed, the slope mass slides into the reservoir, together with the slope deformation and fracture. Thus, several weak contact force zones develop within the slope mass. This is particularly evident near the tail region, because the quick downward motion of the slope mass makes the upper region very loose. As time passes by, new contact force chains would build up at the bottom of Vajont valley. The mixing process of grain with water makes the force chains near the slide front considerably weaker than other locations (e.g. figures at t = 16, 24 and 32 s). The strong force chains mainly exist at the basal region with their orientation preferably vertical, indicating that the gravity can influence the slope structure significantly.

Fig. 14
figure 14

Evolution of force chains for the eastern slope (section A–A; the initial slope profile are plotted as black curves on the snapshots)

Full size image

3.3 Results of Western Slope Simulations

3.3.1 Slope Deformation and Wave Motion

The numerical results of the slope motion and wave motion of the western slope are included here as comparisons to those obtained in the eastern slope simulations. According to Fig. 15, it can be observed that the upper slope mass descends instantaneously once the slope failure is initiated. The slope mass near the failure plane moves slowly, leading to intensive shearing deformation of the slope mass (as indicated by the stretched slope basal layers). The water wave starts from the toe of the slope (t = 10 s) and then propagates quickly towards the northern bank of the Vajont valley (t = 20 s). 24 s after the slope failure, the splashed water wave reaches the maximum height of about 130 m, which can match the experimental results obtained by Datei (2003) (136.5 m observed in experiments using 3–4 mm gravels). Then, the splashed water wave flows back into the reservoir. As the water waves are generated at the toe of the slope and move across the reservoir continuously, they can merge with the back flow water at the toe of the northern bank (t = 30 s). At the end of the simulation, only a small amount of water exist at the flow front and the granular mass can reach a location 130 m away from the initial slope toe region. The runout of the slope mass can approximately match the experimental results by Datei (2003) (146 m). The final granular deposit has a larger slope angle than that of the eastern slope (see Fig. 7) and the reservoir is partially filled by the slope mass. Two enlarged views showing the slope and water wave motions at the flowing front are shown in Fig. 16.

Fig. 15
figure 15

Evolution of slope deformation and water wave motion at different time steps for cross section B–B

Full size image
Fig. 16
figure 16

Enlargement view of the water wave (section B–B)

Full size image

The wave velocity is shown in Fig. 17. It can be observed that the peak wave velocity is about 18 m/s, occurring at 15 s after the initiation of slope failure. The occurrence time of the peak wave velocity in the western slope can match that in the eastern slope. The back flow of the water wave happens 22 s since the slope failure. The evolution of the elevation of the water wave is shown in Fig. 18. Once the water wave is generated after the slope failure, it moves horizontally across the reservoir with a height of about 28 m, as indicated by the graphs (t = 10 s) in Fig. 15. When the wave reaches the northern bank, it splashes on the mountain flank and the water elevation increases quickly. The maximum elevation height is around 170 m above the reservoir level, occurring about 30 s after slope failure. Then, the water flows back into the reservoir and at t = 40 s, the water table gradually arrives at the constant height of 30 m above the reservoir level, which is very similar to the value observed for cross section A–A.

Fig. 17
figure 17

Velocity of the water wave for simulation along the section B–B (dashed line the time of wave back flow)

Full size image
Fig. 18
figure 18

Elevation of the water wave along section B–B

Full size image

3.3.2 Slope Velocity Analysis

As for the western slope, a series of measurement circular windows have been placed within the initial slope mass (Fig. 19). These sampling windows are fixed in space and can record the average granular velocity for grains with their centres of mass passing through them. To explore the influence of soil permeability on the slope velocity, we have run simulations with different values of fluid viscosity and coarse grain scaling factors (see the discussion in Sect. 2.4). The measured slope velocities are shown in Fig. 20. Figure 20a shows the extreme case for a fluid viscosity sets equal to zero, such that only the fluid buoyant force is considered as the fluid–solid interaction force. According to this figure, it can be observed that the slope mass moves as a whole, except at location B-8 where the solid mass quickly fills the valley and stops moving. The maximum velocity recorded is 22 m/s occurring 25 s after the initiation of sliding. When the real water viscosity is used in the CFD model, the slope velocity decreases significantly, as shown in Fig. 20b. The upper region of the slope (measurement points B1–B3) moves much faster than the lower region. As the upper grains move downwards within a very short time period, no grains exist in B-1 and the measured average velocity becomes nil. Figure 20c, d illustrates the recorded slope velocity for simulations using the coarse grain model. From these figures, it can be concluded that the larger the scaling factor (α) is used, the smaller the slope velocity will be. In particular, the basal grains near the toe region move extremely slow due to the large fluid resistant forces resulting from the decrease of slope permeability in the coarse grain model (i.e. large scaling factor). The comparison between these figures also shows that the duration time of the rockslide for different simulation setups can match well (around 50 s), indicating that the sliding duration is mainly determined by the initial slope geometry. This duration time fits well with the field investigation and other analyses (Ciabatti 1964; Crosta et al. 2013).

Fig. 19
figure 19

Distribution of the measuring points for the western slope (section B–B)

Full size image
Fig. 20
figure 20

Slope velocity recorded in the simulations along section B–B. a Dry case (µ = 0 Pa s, α = 1); b coarse grain case 1 (µ = 10−3 Pa s, α = 1); c coarse grain case 2 (µ = 10−3 Pa s, α = 5); d coarse grain case 3 (µ = 10−3 Pa s, α = 10)

Full size image

3.3.3 Force Chains

The evolution of force chains of the western slope is shown in Fig. 21. During rocksliding, the strong force chains occur within the slope mass, while weak force chains occur near the tail and surface region. Due to the gentle slope and “chair-like” failure plane, a large amount of upper grains heaps in the middle of the slope (see the figures for t = 16, 24 and 32 s). Thus, the granular volume increases and the strong force chains occur in the middle of the slope. As the solid particles slide into and fill up the valley gradually, new contact force chains build up there. When compared with the force chains of the eastern slope (see Fig. 14), the weak contact force zone is much smaller in the tail region. This phenomenon can be explained by the fact that the slope mass moves slowly on the gentle slope and no large fracture has occurred.

Fig. 21
figure 21

Evolution of force chains for the western slope (section B–B, the initial slope profile are plotted as black curves on the snapshots)

Full size image

4 Discussion

This research aims to illustrate the general features of the slope failure mechanism and wave motion along the two characteristic slope directions by implementing a coupled DEM-CFD approach. The modelling presented here only focus on the initial stage of the phenomenon including the interaction between the rockslide and the water body. Thus, only the 2D channel wave motion has been modelled as a compromise for the high computational cost from the 3D DEM model. The present results reveal that the slope deformation and water wave motion during the Vajont rockslide can be simulated, at least in a reasonable quantitative way, by the coupled DEM-CFD model. Based on these findings, several issues need to be addressed and are discussed in the following.

As the current numerical model uses large particles to represent the slope mass, the porosity of the slope mass in the simulation is much larger than that of the real rock mass. According to Ergun (1952), McCabe et al. (2005) and Chen et al. (2011), the hydraulic conductivity of the slope mass is calculated as \(K = \frac{{\bar{d}_{p}^{2} n^{3} \rho^{f} g}}{{150\mu^{f} (1 - n)^{2} }}\). Based on the parameters used in this simulation, the average hydraulic conductivity of the model is 46506.7 cm/s, which is unrealistically large when compared to that of normal pervious materials (e.g. K = 100 cm/s). As a consequence, the permeability of the slope is relatively large, such that the majority of the splashed water can flow back into the slope mass, rapidly. An alternative approach could consist of using a high fluid viscosity and a coarse grain model in the DEM-CFD simulations to obtain smaller hydraulic conductivities. For instance, we can effectively reduce the value of K by increasing either fluid viscosity (µ f) or fluid drag forces [equivalently by decreasing grain diameter (\(\bar{d}_{p}\))] (e.g. in Sect. 3.2.2, K = 46506.7 cm/s, 1860.3 cm/s and 465.1 cm/s for the coarse grain simulations with the scaling factors of 1, 5 and 10, respectively). However, we need to be aware that the large pores still exist in the granular material and the final values of K result from the upscaling of the granular properties (e.g. fluid viscosity and fluid drag forces). Therefore, the small values of K in numerical models may not be able to capture the correct fluid seepage. Nevertheless, running the simulations with higher viscosity and with a larger coarse grain scaling factors can effectively reduce the slope permeability and thus increase the fluid resistance on the slope mass. As a consequence, the granular velocities recorded at different locations within the slope mass decrease significantly in these simulations, when compared with the numerical results obtained for the dry sliding case.

Since the VOF model considers the CFD mesh cell as completely filled with fluid (e.g. either water or air), the summation of the volume fractions of water (α w) and air (α a) should be 1 (i.e. α w + α a = 1.0). However, in simulating the interaction between water reservoir and rockslide, the solid particles are also presented in the mesh cells, indicating that part of the fluid mesh volume is occupied by solids. As a result, the definitions of α w and α a only quantify the relative volume fractions of water and air in the total fluid volume within the mesh cell. Thus, the splashed water will finally flow back into the reservoir to an elevation controlled by the final porosity (i.e. the average value is around 0.37) of the slide mass.

The current DEM-CFD coupling model employs the plane strain boundary condition, which partially reveals the mechanical and hydraulic behaviour of the Vajont rockslide. However, it fails to simulate the overtopping of water during this event. As a result, the general features of water splashing can only be predicted by the velocity and elevation height of water waves. A complete analysis of the Vajont rockslide should consider the geological settings of the slope and the 3D motion of the water waves (e.g. see the work by Ward and Day 2011; Vacondio et al. 2013).

Comparing the results obtained by the DEM-CFD coupled approach with those by an ALE-FEM approach presented in a companion paper (Crosta et al. 2014, this issue), they are qualitatively the same, regarding the sliding duration time (50 s), and the maximum slope velocity (ca 20–30 m/s). Both studies have observed that the eastern slope has slightly higher velocity, due to the initial steeper slope profile. The quasi-3D plane strain DEM-CFD simulations can be at least qualitatively compared also to the results obtained by means of physical modelling by Datei (2003), regarding the water wave runup height and slope runout distance during the rocksliding.

5 Conclusions

This paper presents a quasi-3D DEM-CFD coupling study of the Vajont slide in plane strain condition. The slope failure is simulated by the DEM, to analyse the deformation and sliding of the solid mass. The influence of slope motion on the generation of impulse water wave is analysed via the DEM-CFD coupling method. The DEM model of the Vajont slope is generated using the “hopper discharge” technique. The slope profile is represented by smooth, rigid walls, while the failure surface is approximated by a fixed grain layer with relatively small friction (e.g. 10°). The solid grains are generated and packed together to represent the predefined slope geometry. This technique is very flexible and efficient to generate DEM samples of various geometries.

The dynamic motion of the failed slope mass can trigger impulse waves and their motion. The average slope velocity for the eastern slope is about 25 m/s, while for the western slope it is 15 m/s. The corresponding water wave velocities are 20 and 15 m/s, respectively. The maximum height of the wave runup on the opposite valley flank is around 130 m for the eastern slope, while it is 170 m for the western slope, which are very close to the field observations at the same spots.

The current 3D plane strain DEM simulations have captured the general features (e.g. slope and wave motions) of the Vajont rockslide at the eastern and western sectors. In these simulations, the slope mass is considered permeable, such that the toe region of the slope can move submerged in the reservoir and the impulse water wave can also flow back into the slope mass. However, the upscaling of the grains size in the DEM model leads to an unrealistically high hydraulic conductivity of the model, such that only a small amount of water is splashed onto the northern bank of the Vajont valley. The use of high fluid viscosity and coarse grain model has shown the possibility to model more realistically both the slope and wave motions. However, more detailed slope and fluid properties, and the need for computational efficiency should be considered in future research work. This aspect has also been investigated by the companion paper presented by Crosta et al. (2014, this issue), where the 2D and 3D FEM ALE modelling without considering the water seepage in the slope mass have been used. Their results can be a good way to estimate the slope and wave motion for fast sliding conditions. The 3D modelling can also clarify the lateral motion of water and estimate the potential risk of water overtopping the dam crest. The DEM and FEM ALE modelling can be used together to analyse fast moving rockslides (i.e. flowslides, rockslides, rock and debris avalanches) both in dry conditions and for their interaction with water basins.