Abstract
This research aims to extend the isothermal continuum mechanical modeling framework of hydraulic fracturing in porous materials to account for the non-isothermal processes. Whereas the theory of porous media is used for the macroscopic material description, the phase-field method is utilized for modeling the crack initiation and propagation. We proceed in this study from a two-phase porous material consisting of thermomechanically interacting pore fluid and solid matrix. The heat exchange between the fluid in the crack and the surrounding porous environment through the diffusive fracture edges is carefully studied, and new formulations here are proposed. Besides, temperature-dependent solid and fluid material parameters are taken into account, which is of particular importance in connection with fluid viscosity and its effect on post-cracking pressure behavior. This continuum mechanical treatment results in strongly coupled partial differential equations of the mass, the momentum, and the energy balance of the thermally non-equilibrated constituents. Using the finite element method, two-dimensional initial-boundary-value problems are presented to show, on the one hand, the stability and robustness of the applied numerical algorithm in solving the emerged strongly coupled problem in the convection-dominated heat transport state. On the other hand, they show the capability of the modeling scheme in predicting important instances related to hydraulic fracturing and the role of the temperature field in this process. Additionally, they show the importance of using stabilization techniques, such as adding an artificial thermo-diffusivity term, to mitigate temperature fluctuations at high flow velocity.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The subject of hydraulic fracturing and the existence of fracture networks in porous materials are of major importance in geothermal energy systems with naturally or artificially fractured underground rock layers. In geothermal systems with rock layers at high temperatures, a significant amount of thermal energy can be gained and used. Hence, depending on the depth of the rock layers and their temperature, this energy can be used for heating or for electricity generation using geothermal power plants. One of the major challenges in this regard is the low permeability of the underlying rock layers, which deteriorates the efficiency of geothermal systems. This challenge can be overcome by applying hydraulic fracturing leading to enhanced geothermal systems (EGS), see, e.g., [81] for review. In this connection, the focus of the underlying work is on the modeling of hydraulic fracturing to enhance the reservoir permeability and on the EGS operation that includes thermal energy exchange between the low-temperature injection fluid and the high-temperature surrounding deep rock layers. In particular, the hydraulic fracturing within non-isothermal conditions will be modeled using the phase-field method (PFM), see, e.g., [19, 48, 52, 79, 92], whereas the heat exchange with the surrounding porous rocks will be modeling using the fundamentals of the theory of porous media (TPM) for non-isothermal problems, see, e.g., [29, 57, 94, 95].
1.1 Literature review for isothermal phase-field hydraulic fracture
While few research works addressed the PFM-based hydraulic fracture modeling under non-isothermal conditions, many works studied this under isothermal conditions as reviewed in [48]. The starting point in these studies is the definition of a scalar-valued and space-time-dependent phase-field variable in the range [0, 1], which allows for differentiation between the cracked and the intact regions of the domain. With the PFM, the sharp edges of the crack are approximated by diffusive ones, whereas the width of this region is controlled via an internal length scale, see, e.g., [6, 12, 16, 17, 21, 49, 53, 58, 62, 63, 70, 73, 74] among others. In this context, it is worth mentioning that although the PFM is intensively applied for fracture modeling, it is also widely used in the simulation of many other engineering applications, as phase-change materials, see, e.g., [4, 94,95,96, 104], for references.
In the development of the PFM, [45] presented pioneering studies for brittle materials’ fracture, including the definition of the crack surface energy and the critical energy release rate. Later, [55] extended Griffith’s approach to ductile materials and proposed the concept of the strain energy release rate and crack toughness. Subsequent studies by [12, 13, 40] proposed an energetic framework to capture the relationship between the diffusive interface approach, utilized in physics to realize the boundaries between different phases of heterogeneous materials, and fracture mechanics. Significant advancements to the PFM for fracture modeling, including the mathematical formulations within a thermodynamical framework, large deformations, solution algorithms, applications, and model validation, can be found in, e.g., [6, 58, 70, 77, 82, 83, 103] among others.
In talking about hydraulic fracture modeling, the work of [14] counts as one of the first efforts to utilize the PFM to simulate hydraulic fracturing within a variational framework. The PFM was thereafter used by many research groups to capture fluid-induced cracking in porous and solid materials as can be found in, e.g., [30, 33, 49, 67, 72, 98, 100, 101], among others. Many of these works combined the PFM together with the continuum theory of porous media (TPM) [28] or Biot’s poroelasticity [9] to capture the onset of fracture and the accompanying hydro-mechanical processes. For example, Markert and Heider [67] proposed a novel coupled, multi-field PFM–TPM fracture simulation framework, which was advanced in [49] to capture irreversible changes in the fractured porous materials, like the volume fractions and the permeability. In line with this, Pillai et al. [84] implemented a PFM for dynamic hydraulic fracture in an Abaqus user-element subroutine, which captured also the domain heterogeneity. In this connection, a model validation via comparison with experimental data on hydraulic fractures was presented in [52] and an extension to unsaturated porous media fracture is found in [17, 51]. [30] introduced a thermodynamical framework within the TPM for modeling hydraulic fracturing under dynamic conditions using the PFM. This approach was extended in [31], in which they proposed a crack-opening indicator function in connection with the fluid flow in the crack. An extension of the TPM-PFM approach towards ductile fracture can be found in [85]. Important advancements in the context of PFM of hydraulic fractures in connection with Biot’s theory can be dedicated to [2, 3, 60, 72, 75, 90, 91, 101] among others. In these research works, different characteristics of hydraulic fracturing in two- and three-dimensional settings could be captured. To mention some, important advancements were done with regard to the crack width computation. Additionally, advanced numerical algorithms, like the local–global approach or the fixed-stress iterative coupling, were also implemented. More details and references will be provided in later sections.
1.2 Literature review for non-isothermal phase-field fracture and heat exchange processes
An extension of the PFM for hydraulic fracture modeling in poroelasticity to account for non-isothermal conditions can be found in [79], where they proceeded from quasi-static and small strain assumptions. A particular focus in this work was on the thermal exchange and force balance at the interface between the crack and the domain. Additionally, the numerical solution considered a robust semi-smooth Newton approach and a crack-oriented predictor-corrector spatial adaptivity method. Extension of the TPM-PFM approach for hydraulic fracture within non-isothermal, thermal non-equilibrium settings can be found in [78], where the heat exchange between the cold fluid in the crack and the hot ambient could be captured. Suh and Sun [92] developed an asynchronous FE solver to capture the crack propagation and fluid flow in porous media at the mesoscale under non-isothermal conditions. They considered thermally non-equilibrium states of the constituents. An operator-split time integration algorithm was also applied to compute the displacement, pressure, phase field, and temperature of each phase in an asynchronous way.
Apart from the PFM approaches to model crack propagation and the accompanying processes, the heat exchange between the fluid in the crack or in a tube and the surrounding domain has intensively been studied in the literature, both experimentally and numerically. For instance, Ramey [87] provided an approximate, analytical solution to the wellbore heat-transmission problem. The proposed solution proceeded from a steady-state heat transfer in the wellbore, whereas the heat transfer to the surrounding ambient is unsteady radial. The solution allows estimating the temperature of flowing fluid, tubing, and casing as a function of depth and time. Within the thermo-poroelasticity theory, Wang and Papamichos [99] studied the coupled thermo-hydro-mechanical processes in a circular wellbore or spherical cavity, in which a constant fluid flow rate and temperature were considered. They developed analytical solutions to estimate the temperature, pressure, and stresses in the area around the wellbore and cavity for low permeability ambient and negligible heat convective processes. They showed in their study that injection of warm fluid delays the fracture initiation around the cavity due to emerging of tensile effective tangential stresses. Ghassemi et al. [43] carried out an analytical study within poro-thermoelasticity to investigate in EGS the effect of injection fluid temperature (mostly cold water) on the thermal energy exchange and crack opening. They studied the effect of effective stresses and thermoelastic effects in the porous ambient on the reduction of the crack aperture. They showed that these effects are maximum near the inject point and minimum near the extraction point. In line with this, an alternative analytical solution for the crack width within a continuum thermo-poroelastic theory was presented [97]. Recently, Frank et al. [41] carried out an experimental study on a single cracked rock with flowing fluid at a high rate to understand the heat transfer process. They investigated different geometrical and material parameters that affect the transient and steady-state heat transfer and proposed analytical formulation to describe the aforementioned processes. Proceeding with a TPM continuum mechanical model for porous materials under non-isothermal conditions, [57] derived a thermodynamically consistent biphasic model to describe the functionality of EGS systems. In this macroscopic model, the cracks were not explicitly modeled and different temperatures of the elastic solid and the viscous fluid were considered. They finally solved an initial boundary-value problem that relied on a circulation test in a geothermal plant in Soultz-sous-Forêts (France).
In the current work, the modeling of the fully saturated porous biphasic material with materially incompressible solid phase and compressible pore fluid under non-isothermal conditions is based on the theory of porous media (TPM) principles, see, e.g., [8, 22, 23, 32, 47]. The continuum-mechanical description of the porous media fracture problem results in a set of coupled partial differential equations (PDEs), which class and characteristics have been investigated in, e.g., [37, 65, 68, 80]. In connection with the numerical implementation, the finite element method (FEM) together with the implicit time integration scheme in a staggered manner to be applied. Of particular importance in the implementation are the stability challenges in the nearly incompressible fluid limit or at the crack–domain interface, as discussed in, e.g., [51].
1.3 Highlights and content overview
With the aim of deeply understanding the hydraulic fracturing process in saturated porous materials under non-isothermal conditions, the outlines of the underlying work can be summarized in the following points: (1) Extending the isothermal phase-field porous media fracturing approach, developed within the theory of porous media (TPM), by considering the non-isothermal processes. (2) Presenting a mathematical model and numerical simulation of the heat exchange between the fluid in the crack and the surrounding intact porous ambient with diffusive fracture edges. (3) Studying the effect of the temperature contrast between the injection fluid and the residing porous material on the pressure needed to initiate the crack and on post-crack pressure response. (4) Discussing and overcoming the stability challenges in the convection-dominated heat transport state. To give an overview of mathematical modeling, Sect. 2 briefly describes the continuum mechanical treatment, the kinematics, balance, and constitutive relations. It also demonstrates the phase-field approach and the essential energy functions. In the end, this section summarizes the governing system of coupled nonlinear partial differential equations (PDEs), which are needed to solve IBVPs of non-isothermal phase-field hydraulic fracturing in saturated porous media. The numerical treatment of the resulting set of PDEs using the FEM is briefly presented in Sect. 3. This includes defining the Dirichlet and Neumann boundary conditions, explaining the staggered-monolithic solution scheme, and addressing the numerical challenges and the instability sources of the coupled problem. The verification of the proposed modeling framework and proof of model applicability are carried out in Sect. 4 through solving a number of two-dimensional numerical IBVPs and comparison with reference solutions from the literature. Finally, a short summary, conclusions, and an outlook of future works are given in Sect. 5.
2 Theoretical fundamentals
2.1 Homogenization and densities
In the underlying work, we consider a two-phase immiscible porous material consisting of a materially compressible pore-fluid phase \(\varphi ^{F}\) and a materially incompressible solid-phase \(\varphi^{S}\). The compressibility of the solid material is ignored in comparison with that of the solid matrix. In this, bulk compressibility is possible due to the presence of compressible pore fluid and under drained conditions, where the fluid can escape through the boundaries. Within the TPM-based continuum mechanical treatment, homogenization is applied to the multiphase material so that each spatial point consists of overlapping and interacting solid and fluid constituents, i.e., \(\varphi =\varphi^{S}\bigcup \varphi ^{F}\). The volume fraction \(n^{\alpha }\) is defined as the ratio of the volume element d\(v^{\alpha }\) to the total volume element dv , i.e., \(n^\alpha :=\text{d}v^\alpha /\text{d}v\) with \(\alpha =S\) for the solid phase and \(\alpha =F\) for the fluid phase. Following this, the saturated condition is expressed as:
The continuum mechanical TPM applied to intact saturated porous materials demands that all constituents exist at each material point of the homogenized domain, i.e., \(0<\{n^S,\,n^F\}<1\), see, e.g., [28]. In the case of a fractured saturated porous material, extended phase-field-dependent porosity and solidity formulations need to be applied so that \(0\le n^S<1\) and \(0< n^F\le 1\). Thus, for a complete crack region that is filled with the fluid, \(n^{F} = 1\) and \(n^{S} = 0\) as discussed in [52]. In particular, the deterioration of \(n^{S}\) is connected with the crack evolution, which is realized in our treatment using the phase-field method (PFM) as will be discussed in later sections.
We assume in this study that the material is found under non-isothermal conditions, so that the material densities can be expressed as functions of the current temperature \(\theta ^{\alpha }\) of the solid or fluid phases. For the materially compressible fluid constituent, the fluid material density is additionally expressed as a function of the pore pressure p as will be discussed in Sect. 2.6.1. In particular, the material densities of \(\varphi^{S}\) and \(\varphi ^{F}\) can be expressed as
Herein, \(\rho^{\alpha R}\) is the current material density of the constituent \(\varphi^\alpha\), \(\rho_{0}^{S R}\) is the initial solid density, \(\alpha_\theta^{\alpha }\) is the thermal expansion coefficient of \(\varphi^\alpha\), and \(\theta ^{\alpha }_{0}\) is the initial temperature. For more details, we refer to, e.g., [57, 95] and the references therein. To complete the discussion, the initial partial density \(\rho_{0}^{\alpha }\) of a constituent \(\varphi ^{\alpha }\) and following its motion can be expressed as
with \(n_{0S}^{\alpha }\) being the initial volume fraction of \(\varphi ^{\alpha }\). In particular, \(n_{0S}^{S}\) is the undeformed solid volume fraction at \(t=t_0\) and \(n_{0\,S}^{F}=1-n_{0\,S}^{S}\) follows the saturation condition.
2.2 Kinematics
In describing the motion of multiphasic continua within the TPM and presenting the kinematic formulations, we start by defining the position vector x of all constituents at the current configuration and X\(_{\alpha }\) as the position of the phase \(\varphi^\alpha\) at the reference configuration, see, e.g. [28]. For each constituent, a Lagrangian motion function \(\chi _{\alpha }\) and a velocity vector v\(_\alpha\) are defined as
In this, \(\mathbf{\chi }_{\alpha }^{-1}\) represents the inverse of the motion function, which allows for an Eulerian (spatial) description of the motion. Following this, the material time derivative of an arbitrary vector-valued quantity \((\mathbf {\bullet })\) and a scalar-valued quantity \((\circ )\) with respect to the motion of constituent \(\varphi^\alpha\) can be expressed, respectively, as
The motion of the solid phase φS is described via the solid displacement \({\textbf{u}}_{S}\) and velocity \({\textbf{v}}_{S}\), while the motion of the fluid phase is described either via Eulerian description using the fluid velocity \({\textbf{v}}_{F}\) or via modified Eulerian settings using the seepage velocity \({\textbf{w}}_{F}\):
For the case of small deformations, the strain tensor \(\mathbf{\varepsilon }_{S}\) can be expressed as
This includes an elastic contribution \(\mathbf{\varvec{\varepsilon} }^e_{S}\) and a thermal contribution \(\mathbf{\varvec{\varepsilon} }^{\varTheta }_{S}:=\alpha _\theta^{S}\,(\theta^{S}-\theta^{S}_{0})\,{\textbf{I}}\) with \(\alpha _\theta^{S}\) as the thermal expansion coefficient of \(\varphi ^S\).
2.3 Phase field approximation of brittle fracture
The formulation of the PFM relies on the definition of the phenomenological scalar-valued phase-field variable \(d^{S}\) as:
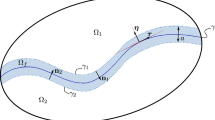
In this, \(d^{S}\) depends on the position vector \({\textbf {x}}\) and time t and allows to approximate the sharp edges of the crack by diffusive ones. More details can also be found in, e.g., [30, 31, 50, 52, 60, 61, 72, 76]. Taking into account \(\varGamma\) as the set of sharp cracks that are found in a homogenized domain \(\varOmega\) and \(\text{d}A\) as the crack surface unit, the total crack surface \(A_\varGamma\) as a volume integral rather than a surface integral can be expressed as
In this, \(\varGamma _d\) is the crack surface density function per unit volume, which is formulated in terms of \(d^S\), its gradient \(\nabla \,d^S\), and the diffusive crack regularization parameter \(l_{\text{c}}>0\), see, e.g., [12, 71] for details about the origin of Eq. (9) and [30, 52, 72] for applications within hydraulic fracturing.
2.4 Energy formulations
Proceeding with \(G_{\text{c}}(\theta ^S)\) as the temperature-dependent Griffith’s critical fracture energy release rate along with \(\varGamma _d\) defined in Eq. (9)\(_2\), the fracture energy can be expressed as
Presenting the definition of \({\varPsi }^{S}_\text{frac}\) helps in defining the overall energy function in addition to the derivation of the phase-field evolution equation as will be discussed in Sect. 2.6.5. Moreover, a proper relationship for \(G_{\text{c}}(\theta ^S)\), such as according to [25], is presented in Sect. 2.6.5.
For a saturated porous material with a linear elastic solid phase and subjected to a thermal field, the total free energy density \({\varPsi }\) is defined within the small strain assumption as the sum of the free energy densities of the solid and fluid constituents, i.e.
In this, \(\varPsi^{S}_\mathrm{el}\), \(\varPsi^{S}_{\mathrm{th,\,el}}\) are, respectively, the elastic stored energy and the energy term due to the thermoelastic coupling of the fractured solid. The dependency on \(d^S\) in these terms is connected to the energy dissipation or solid stiffness degradation, as the fracture occurs and propagates in the solid phase. The term \(\varPsi^{S}_\mathrm{th}\) in (11) is the purely solid thermal energy. For the fluid phase, \(\varPsi ^{F}_\mathrm{el}\) is the elastic stored energy of the fluid phase presented as a function of the material density \(\rho ^{\text{FR}}(p,\, \theta ^F)\), see, e.g., [29]. However, alternative formulations to this can be found within Biot’s theory, see, e.g., [69, 92]. Moreover, \(\varPsi ^{F}_\text{th}\) is the purely fluid thermal energy. The current energy functions of the fluid phase assume that the thermoelastic coupling for the fluid phase is negligible.
Moreover, in the numerical examples in this contribution, we consider nearly incompressible fluids, such as water. In this, the dependency of the fluid material density on the pressure p can be neglected. Thus, for simplicity, the dependency of \(\varPsi ^{F}_\mathrm{el}\) on p in the following treatment will be neglected.
Proceeding with the method that was introduced by [45] to model crack onset in brittle solid materials and following the scheme explained in, e.g., [49], the total potential energy \(\mathcal{F}\) of a cracked fully saturated and isotropic linear elastic porous solid can be formulated as
To capture the fracture-related deterioration of the material stiffness, a degradation function, such as \((1-d^S)^2\), can be applied in the total energy formulation, see, e.g., [58, 71]. In this, it is common to use a residual stiffness factor \(0< \eta \ll 1\) in the degradation function that enters the momentum balance to prevent the elements on the crack path from having zero stiffness and, thus, avoid numerical stability problems. In particular, the degradation function becomes \(\mathcal{G}(d^S):=[(1-\eta )(1-d^S)^2+\eta ]\). In this regard, it is assumed that the cracking occurs under tension and shear stresses, but not under compression. Thus, the related free energy can additively be split into a positive part \((\dots )_{+}\), associated with tension and shear, and a negative part \((\dots )_{-}\), associated with compression. Therefore, the total local energy \(\overline{\varPsi }\) can be expressed in an abstract form as
More details about the energy formulation for the considered material will be presented in the following subsections in connection with constitutive modeling.
2.5 Constituent balance and constitutive relations
2.5.1 Model assumptions
In preparing the governing balance relations in the underlying study, we apply a number of assumptions, which are summarized in the following:
-
Non-polar solid constituent, which implies a symmetric stress tensor.
-
The deformation of the solid skeleton takes place under quasi-static conditions and within the small strain framework.
-
Laminar fluid flow in the crack and in the intact porous regions.
-
The saturated porous material includes incompressible solid and compressible fluid.
-
No mass production from the interaction between the solid and the fluid phases, however, a fluid source term \(\hat{\rho }^F\) is considered in the mass balance equation to represent the external fluid supply.
-
The model is under local thermal non-equilibrium conditions, where the different temperature variables are chosen for the solid and the fluid phases.
-
The natural convection due to buoyant forces is neglected.
-
The fracturing takes place under quasi-static conditions.
-
Under non-isothermal conditions, some of the material parameters can be formulated as functions of the temperature. These include the Young’s modulus of solid matrix \(E^{S} \,=\,E^{S}(\theta^{S})\), the critical solid tensile strength \(\sigma _\mathrm{crit}^{S}\,=\,\sigma _\mathrm{crit}^{S}(\theta^{S})\), the effective fluid dynamic viscosity \(\mu ^{\text{FR}}\,=\,\mu ^{\text{FR}}(\theta ^{F})\), and the material densities.
2.5.2 Constituent balance relations of saturated porous media
Under the aforementioned assumptions within the TPM, the constituent balance equations of the two-phase saturated porous media can be expressed as
-
Partial mass balance:
$$\begin{aligned} (\rho ^{\alpha })^{'} _{\alpha }\,+\,\rho ^{\alpha }\,\text {div}\,{\textbf {v}}_{\alpha }\,=\,\hat{\rho }^{\alpha } \end{aligned}$$(14) -
Partial momentum balance:
$$\begin{aligned} \text {div} \,{\mathbf{\varvec {\sigma} }}^{\alpha }\, +\,\rho ^{\alpha }\,{\textbf{b}}\, +\, \hat{{\textbf {p}}}^{\alpha } \,=\,\textbf{0}. \end{aligned}$$(15) -
Partial energy balance:
$$\begin{aligned} {} \rho ^{\alpha }\left( \varepsilon ^{\alpha }\right) '_{\alpha }\,=\,{{\varvec {\sigma} }}^{\alpha }\cdot \textbf{L}_\alpha \,-\, \text {div}\,\textbf{q}^{\alpha } \,+\, \rho ^{\alpha }\,r^{\alpha } +\, \hat{\varepsilon }^{\alpha }. \end{aligned}$$(16)
Herein, \(\hat{\rho }^{\alpha }\) is the mass supply or production term, which fulfills \(\hat{\rho }^{S}+\hat{\rho }^{F}=0\) for a closed system and vanishes if no mass exchange between the constituents exists. \({\mathbf{\varvec {\sigma} }}^{\alpha }\) is the symmetric partial Cauchy stress tensor for the nonpolar solid material and \({\textbf{b}}\) is the mass-specific body force. Additionally, \(\hat{{\textbf {p}}}^{\alpha }\) is the direct momentum production, which represents the volume-specific local interaction force between the fluid and the solid phases and fulfills the relation \(\hat{{\textbf {p}}}^{S}\,+\,\hat{{\textbf {p}}}^{F}\,=\,{\textbf {0}}\). In the energy balance Eq. (16), \(\varepsilon ^{\alpha }\) is the mass-specific internal energy, \(\textbf{L}_\alpha\) is the spatial velocity gradient, \({\textbf{q}}^{\alpha }\) is the heat influx vector, \(r^{\alpha }\) is the mass-specific external heat supply, and \(\hat{\varepsilon }^{\alpha }\) represents the constituent energy production. In (16), the constituent Helmholtz free energy \(\psi ^{\alpha }\) can be incorporated using Legendre transformation between the entropy \(\eta ^{\alpha }\) and the temperature \(\theta ^{\alpha }\) as conjugate variables. In particular, using
in (16) allows to have the free energy instead of the internal energy in the constituent energy balance equations. In addition to Eqs. (14)–(16), the entropy inequality is usually used to ensure that the constitutive and evolution relation are thermodynamically admissible, which is beyond the scope of this work.
2.5.3 Effective stresses and permeability formulation
Following the concept of the effective stresses for multi-phase porous media, the total solid and fluid stresses and the direct momentum production term are split into an ‘extra’ or ‘effective’ part, indicated by \((\bullet )_E\) and a weighted pore-pressure part (p), see, e.g., [23]. In the presence of thermal fields, the constituent temperatures also enter the effective stress formulations as has been discussed in, e.g., [27, 95]. In particular, these formulations are derived in a thermodynamically consistent framework based on the evaluation of the entropy inequality. Thus, under non-isothermal conditions and having a biphasic fluid-saturated porous material, the following relations hold:
In the current work, we proceed from a fractured linear elastic solid phase, where the effective stress tensor \({\mathbf{\sigma }}^{S}_{E}\) is derived based on the solid free energy function \(\rho^{S}_{0}\,\psi^{S}=\varPsi^{S}\), which includes also the pure solid thermal energy \(\varPsi^{S}_\mathrm{th}=\rho^{S}_{0}\psi^{S}_\mathrm{th}\). In particular, \(\varPsi^{S}\,(\mathbf{\varvec{\varepsilon} }_{S},\,\theta^{S},\,d^{S})\) can be written as
Herein, \(\langle \cdot \rangle _\pm = (\cdot \pm |\cdot |)/2\) represents the Macaulay brackets, \({{\,\text{tr}\,}}\,(\mathbf{\varvec {\varepsilon} }_{S}):=\mathbf{\varvec {\varepsilon} }_{S} \cdot {\textbf{I}}\) and \(\mathbf{\varvec {\varepsilon} }^{D}_{S}:=\mathbf {\varvec {\varepsilon} }_{S}-\frac{1}{3}{{\,\text{tr}\,}}(\mathbf{\varvec {\varepsilon} }_{S})\,{\textbf{I}}\) are the trace and the deviator of the strain tensor \(\mathbf{\varvec {\varepsilon} }_{S}\), respectively. Additionally, \(\kappa^{S}\) is the bulk modulus of the porous solid matrix, \(\mu^{S}\) is the shear modulus, and \(\alpha^{S}_{\theta }\) is the thermal expansion coefficient of the solid phase. Moreover, \(\varDelta \theta^{S}:=\theta^{S}-\theta^{S}_{0}\) with \(\theta^{S}_{0}\) as the initial or reference temperature of the solid phase and \(C^{S}_{V}\) is the specific heat capacity of the solid at constant volume. With the definition of the initial density in (3), i.e., \(\rho^{S}_{0}\,=\,n^{S}_{0S}\,\rho ^{\text{SR}}_{0}\), the stored thermal energy of the solid phase will vary in connection with the solid volume fraction variation due to the crack onset or in connection with predefined cracks as will be discussed in Sect. 2.6.1. The dependency of \(\varPsi^{S}\) on \(d^S\) is due to the ad hoc added degradation function \(\mathcal{G}(d^S)\), where \(d^S\) will not be considered when applying the time derivative of \(\varPsi^{S}\). Moreover, the material parameters of the solid matrix might also be considered as functions of the temperature in this non-isothermal treatment, as will be discussed in the numerical examples.
Following this, the solid effective stress tensor can be derived as
For the fluid effective stress tensor formulation, we proceed from the assumptions of Newtonian fluid and negligible average normal viscous stress (i.e., Stokes’s hypothesis), see, [52]. Additionally, as discussed in Sect. 2.4 and in [92], we neglect for the fluid phase the thermoelastic coupling. Thus, the fluid effective stress tensor under non-isothermal conditions can be expressed as
with \(\mu ^{F}:=n^{F}\mu ^{\text{FR}}(\theta ^{F})\) being the fluid dynamic viscosity and \(\mu ^{\text{FR}}(\theta ^{F})>0\) is the effective fluid viscosity. A widely applied empirical formulation for the temperature-dependent dynamic fluid viscosity is that proposed by [15], which can be expressed as
In this, \(a_\mu\) and \(b_\mu\) are model parameters, which can be adjusted based on available experimental data of the considered fluid.
Proceeding from an intact porous material (\(d^S=0\)) with interacting solid and fluid constituents and following the discussion presented in [52], the effective momentum production term \(\hat{{\textbf {p}}}^{F}_{E}\) can be expressed as
with \(K_\mathrm {poro}\) being the diagonal entry of the isotropic intrinsic permeability tensor \({\textbf{K}}_\text {poro}^{S}:=K_\mathrm {poro}\,{\textbf{I}}\). In this, \(\hat{{\textbf {p}}}^{F}_{E}\) represents a local interaction force and takes into account the mechanisms of momentum transfer between the deforming solid and the permeating viscous fluid. Thus, it includes information about the fluid viscosity and the deformation-dependent intrinsic permeability. This term enters the fluid momentum balance, which results in Darcy’s-like filter law.
The momentum production term is additionally multiplied by a phase-field-based degradation function \((1-d^{S})\) to capture the gradual decrease of the interaction forces \(\hat{{\textbf {p}}}^{F}_{E}\) from the intact region to the crack region, i.e., \(\hat{{\textbf {p}}}^{F}_{E}\rightarrow \textbf{0}\) as \(d^S\rightarrow {1}\) .
Apart from fractured porous media, the elastic deformations of the solid skeleton might lead to changing of the intrinsic permeability as has been discussed in, e.g., [64]. This effect can be captured by introducing an adjusting function \(\gamma _{{\textbf {u}}}\), which is related to the permeability as
In this, \(K_{0}^{S}\) is the initial intrinsic permeability, and \(\kappa \,\ge \,0\) is a model parameter, which can be adjusted based on reference or experimental data. Additionally, \(n^{F}_{0S}\) and \(n^{S}_{0S}\) are the initial porosity and solidity, respectively. In dealing with brittle geomaterials, such as rocks, this effect can be neglected as fracturing might take place for small deformations. In the context of fluid flow in porous media and in the absence of fractures, it was also shown in, e.g., [24, 34] that the fluid effective stress is much smaller than the momentum production \(\hat{{\textbf {p}}}^{F}_{E}\), i.e.
This argument, discussed in detail in [24, 34], is based on a micro- to macroscale dimensional analysis, which includes a comparison between the macroscopic Darcy’s law that results from the fluid momentum balance and the microscopic Poiseuille-type fluid flow that includes information on the microtopology (like pore diameters and numbers) together with the pore-fluid viscosity. It is shown under the assumption of a large number of pore channels with small diameters that the fluid effective (friction) stress can be neglected, whereas it is sufficient to consider the effect of fluid viscosity in the fluid momentum balance through the effective momentum production term.
The onset of cracking in the solid matrix leads to anisotropy in the effective medium. This is associated with anisotropic flow, i.e., enhanced flow in the crack region, as thoroughly discussed in [51, 52, 72]. To describe the occurring anisotropic flow within the framework of porous media mechanics, a permeability measure that realizes the crack opening and direction needs to be derived. In particular, for the flow in the crack region with \(\hat{{\textbf {p}}}^{F}_{E}\rightarrow \textbf{0}\) as \(d^S\rightarrow {1}\) , the fluid momentum balance equation (Eq. (15) with \(\alpha =F\)) together with the definition of fluid effective stress (18)\(_2\) and \(n^F=1\) yields the Stokes’ free flow equation, expressed as
The flow in the crack within the assumption of laminar flow can approximately be considered to be similar to the flow between two parallel plates with a distance \(w_{\text{c}}\) as illustrated in Fig. 1.
Illustration of the unidirectional Poiseuille-type flow between two plate with a distance \(w_{\text{c}}\) and depth \(L_{\text{c}}\) in \(x_2\) direction, where \(v_{F1}(x_3\pm w_{\text{c}}/2)\approx 0\), see, [52]
Through integration in the \(x_1\)-direction devoted to Eq. (26) and considering the simplified boundary conditions results in the volume flux per unit area of the crack cross-section \(q_{F1}\) as
For an arbitrary crack orientation and using the similarity to Darcy’s law of porous media, Eq. (27) can be defined in tensorial form as
In this, \({\textbf{K}}_{\text{c}}\) is defined as the fracture intrinsic permeability tensor. This can be expressed according to [51] as
In this, \(w_h\) represents the hydraulic crack width, which can be found in closed or opened states. For this, \(w_{\text{c}}\) represents the opened-crack aperture, \(w_r\) is the residual closed-crack aperture, \(f_{\text{c}}\) is a correction factor that captures the roughness of the fracture surfaces [54, 88, 102], and \(\chi _d\) is a level-set function that determines the cracked region using a Heaviside step function H as \(\chi _d=H(d^S-0.5)\). In Eq. (29), the orientation of the crack is determined using the unit vector \({{\textbf{n}}}_d\), which is perpendicular to the fracture edge and defined via the gradient of the phase-field variable. In the current treatment, \(w_{\text{c}}\) is estimated at each quadrature point of the FE model based on the stretching of a 1D line element \(h_{\rm{e}}\) normal to the fracture path. Thus, having the strain tensor \(\mathbf{\varepsilon }_S\), this can be computed as
With the definitions of the permeability in (24) and (29), the following unified intrinsic permeability formulation can be proposed and covers the whole fractured domain:
where \(b=1\) for a linear permeability transition and \(b=2\) for a quadratic transition. An important outcome of the aforementioned discussion is the ability to describe the fluid flow in the fractured domain using a unified Darcy’s law. Thus, proceeding with the fluid partial momentum balance (15) for \(\varphi ^F\) and considering the relations (18), (23), (25), and (31), the unified Darcy’s law can be expressed as
In this, the presence of the crack is associated with \(n^F\rightarrow 1\), \({\textbf{w}}_F\rightarrow {\textbf{v}}_F\), and \(\rho ^F\rightarrow \rho ^{\text{FR}}\). More details about the derivation of Eq. (32) can be found in [52].
2.5.4 Heat flux, energy production, and internal energy
In the underlying work, a local thermal non-equilibrium model is considered, which allows capturing the heat transfer between the solid and the fluid phases. Therefore, two distinct energy balance equations for \(\varphi ^S\) and \(\varphi ^F\) with interphase heat transfer laws need to be considered. Recalling the energy balance in local form (16), we discuss in the following the related constitutive equations. Proceeding with isotropic thermal conduction for \(\varphi^\alpha\) of the biphasic material, the heat influx \({\textbf{q}}^{\alpha }\) can be specified according to Fourier’s law of heat conduction as
where \(H^{\text{SR}}\) and \(H^{\text{FR}}\) are the real or intrinsic heat conductivity of constituents. The variation of \(n^{S}\) and \(n^{F}\) in accordance with the change of \(d^S\), i.e., \(n^{S}\rightarrow 0\) and \(n^{F}\rightarrow 1\) for \(d^{S}\rightarrow 1\), allows for a continuous variation of the heat influx and temperatures across the crack diffusive interface. It is worth mentioning here that other approaches exist in the literature to treat the heat transfer at the crack-ambient interface as discussed in, e.g., [1, 79]. For instance, it is shown in [1] within the sharp crack interface approach and under different conditions for the fluid flow that the continuity in the heat flux in the model leads to an accurate approximation of the temperature change between the porous medium and the fluid layer that represents the crack in our treatment. In other works, like [93] within a pure solid fracture, a degradation function is multiplied by the thermal conductivity to capture the crack effect on the heat transfer.
In analogy to the effective stress formulations presented in Eq. (18), the evaluation of the entropy inequality for the underlying non-isothermal process results in a relationship between the total entropy (\(\eta^\alpha\)) and the effective entropy \(\eta_E^\alpha\) of the constituents. Following the derivations in [57, 95, 96], the effective and total entropy can be expressed for the solid phase, respectively, as
In the aforementioned relations, the definition of the solid Helmholtz free energy \(\psi^{S}\) in Eq. (19) has been used, whereas \(m_{\theta }:=\,-\,3\,\kappa^{S}\,\alpha^{S}_{\theta }\,\) is the stress–temperature coupling modulus. The neglection of the mechanical contribution in the definition of \(\eta ^S_E\) is in analogy to [57]. This analogy is also extended to the formulation of the fluid entropy in the following. Thus, we start with the definition of the fluid thermal energy \(\psi ^{F}_\text{th}\) as
with \(C^{F}_{V}\) being the specific heat capacity of fluid at constant volume and \(\rho ^{F}_{0S}\) is the initial fluid partial density. Following this, the effective and total entropy can be expressed for the fluid phase, respectively, as
Within the assumption of non-equilibrium thermal condition, the heat exchange through the interface between the solid and fluid phases is realized through the direct energy production terms \(\hat{\varepsilon }^F\). Following [7, 29, 86, 92, 94], this can be expressed based on Newton’s law of cooling as
where \(\omega _d\) is the specific heat transfer surface area and \(k^{\epsilon I}_\theta\) is the heat transfer coefficient thoroughly discussed in [41]. The second term in Eq. (37) results from the total energy production term under assumptions like no mass exchange between the constituents as derived in detail in, e.g., [94]. While the parameter \(k^{\epsilon I}_\theta\) is approximately considered constant in this study and independent of the temperature or flow state, i.e., the flow takes place at a low Reynolds number, \(\omega _d\) is introduced as a function of \(d^S\). In particular, the onset of the crack is associated with distortions at the crack edges as can be observed, for instance, in \(\mu\)-CT images of fractured Sandstone in [56]. These distortions lead to increasing the heat transfer surface area between the solid and the fluid phases. This was also experimentally proved in [41], which showed that the crack surface roughness has a major effect on the heat transfer coefficient. Assuming that the crack is free of the solid phase, then \(\omega _d\) is considered to be zero in the completely cracked region. Thus, utilizing the Heaviside level-set function \(\chi _d=H(d^S-0.5)\), the phase-field-dependent formulation of \(\omega _d\) can be expressed as
In this, \(\omega _0\) is the specific heat transfer surface area for the intact material, and \(\omega _{I}\) captures its increase in the diffusive interface area. An alternative formulation can be found [92], which assumes that fragmented solid particles are found in the crack, and thus, \(\omega _d\) increases in the crack region. This effect can be captured using Eq. (38) after removing \((1-\chi _d)\).
2.6 Governing balance equations
2.6.1 Fluid mass balance
In the simulation of hydraulic fracturing, a fluid mass supply term \(\hat{\rho }^\mathrm{Ext}\) in Eq. (14) as an external injection source can be utilized, see, [52]. For this, a location function \(\mathcal{Q}({\textbf {x}})\) is specified to determine the location the fluid injection supply source, i.e., \(\mathcal{Q}({\textbf {x}})\,=\,1\) for the source location and \(\mathcal{Q}({\textbf {x}})\,=\,0\) otherwise. Hence, the supply term can be expressed as \(\hat{\rho }^{F}:=\hat{\rho }^\mathrm{Ext}\,\mathcal{Q}({\textbf {x}})\). Proceeding from Eq. (14) for \(\varphi ^F\), the fluid mass balance can be rewritten as
In the reformulation of Eq. (39), we consider the following material time derivatives
Moreover, a proper formulation for the term \((n^{S})^{'}_{S}\) can be derived based on Eq. (14) for \(\varphi ^S\) and having no solid mass production, i.e., \(\hat{\rho }^{S}=0\). In particular, we start with the material time derivative
Integration of \((n^{S})'_{S}\) and reformulation of the resulting equation within geometrically linearized settings according to [29, 95] yield an explicit relation for \(n^S\) as
with \(n^{S}_{0S}\) being the initial solidity. With the assumption that the preexisting or emerging cracks are free of the solid phase, a modified initial solidity \(n^S_d\) as a function of \(d^S\) can be considered in Eq. (42) in analogy to [49, 51]. In particular, the reformulated solidity can be expressed as
Moreover, under the assumption of a barotropic fluid phase, a simplified relationship among the fluid material density \(\rho ^{\text{FR}}(p,\,\theta ^F)\), the fluid compressibility \(\overline{\kappa }^{F}\), and the effective pore pressure p can be considered in analogy to [11]. Additionally, the dependency on the pressure field \(\theta ^F\) as shown in Eq. (2) has to be considered in the material derivative of \(\rho ^{\text{FR}}\). Having this, one gets
Having this relation together with (40) and the solidity derivation in (41), the governing fluid mass balance can be rewritten as
In this, \((1-d^{S})\) can additionally be multiplied by \(\text{div}\,{{\textbf{v}}}_{S}\) to eliminate this term in the fracture region. Moreover, to reduce the number of primary variables, Eq. (32) can be incorporated in Eq. (45) so that no need to explicitly compute \(n^{F}{\textbf{w}}_{F}\) in the simulation.
2.6.2 Overall momentum balance
The derivation of the overall momentum balance proceeds from the constituent momentum balance (15) for \(\varphi ^S\), \(\varphi ^F\), and the effective stress formulations (18) as
The definition of the solid effective stress \({\mathbf{\varvec {\sigma} }}^{S}_{E}={\mathbf{\varvec {\sigma} }}^{S}_{E}\,(\mathbf{\varvec {\varepsilon} }_{S},\,\theta^{S},\,d^{S})\) is presented in (20), whereas the argument presented in (25) is also implemented. Following this, the overall momentum balance related to the quasi-static treatment can be expressed as
2.6.3 Energy balance of \(\varphi ^F\)
Starting with the local energy balance (16) for \(\varphi ^F\) and utilizing the Legendre transformation in (17) to define the fluid internal energy, i.e., \(\varepsilon ^F = \psi ^F + \theta ^F\eta ^F\), yielding
In this, \({\textbf{L}}_F:={{\,{\text{grad}}\,}}{\textbf{v}}_F\) is the fluid velocity gradient. The different terms in Eq. (48) have to be specified in order to get the governing equation that is used in the finite element treatment. In particular, we derive the material time derivative of the fluid thermal energy \(\psi ^{F}_\mathrm{th}\) in (35) as well as of the fluid entropy in (36)\(_2\) yielding
We also reformulate the term \({\mathbf{\varvec {\sigma}}}^F\cdot {\textbf{L}}_F\) based on the fluid mass balance (39) for \(\mathcal{Q}=0\) together with (40), (41), and (44) yielding
In this, we also neglect the effective part of the total fluid stress formulation in analogy to [57], and we apply the assumption of \({{\,{\text{grad}}\,}}(n^S)\approx 0\) for the geometrically linear framework [46]. With (36), (49), (50), the fluid energy balance (48) can be reformulated as
In connection with mass supply term \(\hat{\rho }^{F}=\hat{\rho }^\mathrm{Ext}\,\mathcal{Q}({\textbf {x}})\) presented in Eq. (39), injecting fluid with a different temperature from the domain needs to be considered in the modeling framework. Therefore, an external energy supply term \(\hat{\psi }^{F}\) has additionally been considered in the fluid energy balance equation. In particular, this can be expressed as
with \(\theta ^{F}_s\) being the temperature of the supplied fluid. The relation (52) relies on the transferred heat per unit time under steady-state condition as discussed, e.g., by [41].
2.6.4 Energy balance of \(\varphi ^S\)
Starting with the local energy balance (16) for \(\varphi ^S\) and utilizing the Legendre transformation in (17) to define the solid internal energy, i.e., \(\varepsilon ^S = \psi ^S + \theta ^S\eta ^S\), yields
In this, \({\textbf{L}}_S={{\,{\text{grad}}\,}}{\textbf{v}}_S\) is the solid velocity gradient, which can additively be split into a symmetric rate of deformation \({\textbf{D}}_S=\frac{1}{2}({\textbf{L}}_S+{\textbf{L}}^T_S)\) and a skew-symmetric rate of rotation \({\textbf{W}}_S=\frac{1}{2}({\textbf{L}}_S-{\textbf{L}}^T_S)\) as \({\textbf{L}}_S={\textbf{D}}_S+{\textbf{W}}_S\). Having a symmetric stress tensor \({\mathbf{\varvec {\sigma} }}^S\) yields \({\mathbf{\varvec {\sigma} }}^S\cdot {\textbf{L}}_S={\mathbf{\varvec {\sigma} }}^S\cdot {\textbf{D}}_S = {\mathbf{\varvec {\sigma} }}^S\cdot (\mathbf{\varvec {\varepsilon }}_S)'_S\), where \({\mathbf{\sigma }}^S\cdot {\textbf{W}}_S=0\) and the definition of the strain tensor is given in Eq. (7). As we did for the fluid energy balance, the different terms in Eq. (53) are to be specified for the numerical finite element implementation. We carry out first the material time derivative of the solid Helmholtz free energy \(\psi^{S}\) in (19) as well as of the fluid entropy in (34)\(_2\) yielding
Having these derivations together with the total solid stress (18)\(_1\), the solid entropy (34)\(_2\), and the heat exchange term in (37)\(_2\), the solid energy balance can be expressed as
2.6.5 Phase-field evolution equation
Several approaches can be found in the literature to derive the governing equation of the phase-field variable evolution within hydraulic fracturing [48]. In the current work, we follow the generalized Ginzburg–Landau approach in analogy to [67, 72], which relies on Allen–Cahn equation [5]. Proceeding from the local definition of the total strain energy (13) together with the fracture energy (10) and the specification of the solid energy in (19), the Allen–Cahn equation can be expressed as
with \(M>0\) being a scalar-valued interface mobility parameter. Considering a quasi-static formulation to the phase-field evolution as in [52], i.e \((1/M)\,(d^{S})^{'}_{S}\approx 0\), the phase-field equation (56) can be reformulated as
where
Herein, \(\varPsi ^{S+}_{max}\) is the continuously increasing elastic strain energy density, presented to prevent crack healing upon possible crack closure [70]. Within the non-isothermal treatment, a proper relationship for \(G_\text{c}\) as a function of the solid temperature \(\theta ^S\) needs to be specified. For instance, [25] proposed the following empirical relation:
where \(G_{c0}\) represents the critical energy release rate at the reference temperature \(\theta ^S_0\) and \(a_\mathrm{c}>0\) is a model parameter, which can be adjusted based on the considered material.
The formulation for the crack deriving force in (58) has the disadvantage of underestimating the solid crack resistance as discussed in [72]. Therefore, an alternative threshold-based formulation for the crack driving force can be utilized. Specifically, a threshold-based crack driving force \(\tilde{\mathcal {D}}_\text{c}\) is proposed in [72], where this force remains equal to zero as long as the positive thermoelastic energy \(\bigg (\varPsi^{S}_\mathrm{el}+\varPsi^{S}_{\mathrm{th,\,el}} \bigg )_{+}\) or the related principal stresses \(\sigma _{E,\,pi}^{S+}\) with \(i\in \{1,2,3\}\) smaller than a certain critical value \(\sigma _\mathrm{crit}^{S}\). Following this, the crack driving force can be expressed as
In analogy to Eq. (59), where \(G_\text{c}\) is expressed as a function of \(\theta ^S\) within a non-isothermal framework, a proper formulation for \(\sigma _\mathrm{crit}^{S}\) that considers the dependency on \(\theta ^S\) will be discussed in the following. In this, the one-dimensional solution of the phase-field evolution equation under quasi-static condition, as, e.g., in [59], shows a proportionality between the critical stress needed to initiate the crack \(\hat{\sigma }\) and \(G_\mathrm{c}\) as \(\hat{\sigma }\,\propto \sqrt{G_\mathrm{c}}\). Based on this, we propose the following empirical relation for \(\sigma _\mathrm{crit}^{S}\) under non-isothermal conditions:
where \(\sigma _{crit,0}^{S}\) represents the critical stress needed to initiate the crack at the reference temperature \(\theta ^S_0\) and \(z_\mathrm{c}>0\) is a model parameter, which can be adjusted based on experimental data of the considered material.
2.7 Summary of the governing balance relations
Following the previous discussion, the governing system of coupled nonlinear partial differential equations (PDEs), which are needed to solve IBVPs of non-isothermal phase-field hydraulic fracturing in saturated porous media, are summarized in Box 1.

3 Numerical treatment
In the current work, we use the finite element method (FEM) in the numerical solution of initial-boundary value problems (IBVP) of hydraulic fracturing under non-isothermal conditions. In the following, we briefly discuss the main steps in the numerical treatment of the governing coupled partial differential equations (PDEs), summarized in (62)–(66) and characterized by five primary variables \(\varvec{\xi }(\textbf{x},t):=[{\textbf{u}}_{S} \,\, p\,\, \theta ^{F}\,\, \theta^{S}\,\, d^{S}]^{T}\). We start by discussing the boundary conditions in connection with each of the variables. As such, denoting \(\mathcal{B}\) as the domain of interest with \(\partial \mathcal{B}\) as its boundary, this can be split for each variable into Dirichlet (\(\partial \mathcal{B}_D\)) and Neumann (\(\partial \mathcal{B}_N\)) boundaries that fulfill the conditions \(\partial \mathcal{B}_D\cup \partial \mathcal{B}_N=\partial \mathcal{B}\) and \(\partial \mathcal{B}_D\cap \partial \mathcal{B}_N=\emptyset\). In particular, the Dirichlet and Neumann boundary conditions are given, receptively, for each variable as
Dirichlet | Neumann | Gov. Eq | |
|---|---|---|---|
\( {{\textbf{u}}}_S=\overline{{{\textbf{u}}}}_S \quad {}\;\;{\text{on}}\;\;\quad {}\partial \mathcal{B}_u\) | \(\varvec{\sigma }\,{\textbf{n}}=\overline{{\textbf{t}}}\quad {}\;\;{\text{on}}\;\;\quad {}\partial \mathcal{B}_t\) | (62) | |
\( p=\overline{p} \quad {}{\text{on}}\quad {}\partial \mathcal{B}_{p}\) | \({n^F({{\textbf{v}}}_F-{\textbf{v}}_S)}\cdot {\textbf{n}}=\overline{q}_F\quad {}{\text{on}}\quad {}\partial \mathcal{B}_{q_F}\) | (63) | |
\(\theta ^F=\overline{\theta }^F \quad {}{\text{on}}\quad {}\partial \mathcal{B}_{\theta ^F}\) | \(n^{F}\,H^{\text{FR}}\,\text {grad}\,\theta ^{F}\cdot {\textbf{n}}=\overline{q}_{\theta ^F}\quad {}{\text{on}}\quad {}\partial \mathcal{B}_{q_{\theta ^F}}\) | (64) | (67) |
\(\theta ^S=\overline{\theta }^S \quad {}{\text{on}}\quad {}\partial \mathcal{B}_{\theta ^S}\) | \(n^{S}\,H^{\text{SR}}\,\text {grad}\,\theta^{S}\cdot {{\textbf{n}}} =\overline{q}_{\theta ^S}\quad {}{\text{on}}\quad {}\partial \mathcal{B}_{q_{\theta ^S}} \) | (65) | |
\(d^S=\overline{d}^S \quad {}{\text{on}} \quad {}\partial \mathcal{B}_d\) | \({{{\,{\nabla }\,}}d^S}\cdot {\textbf{n}} =0\quad {}{\text{on}}\quad {}\partial \mathcal{B}_{q_d}\) | (66) |
with \({{\textbf{n}}}\) being an outward-oriented unit surface normal. In deriving the governing weak formulations, the method of weighted residuals is applied. In this, time-independent weight (or test) functions, as variations of the real primary fields, are specified, i.e., \(\delta \varvec{\xi }(\textbf{x}):=[\delta {\textbf{u}}_{S} \,\, \delta p\,\, \delta \theta ^{F}\,\, \delta \theta^{S}\,\, \delta d^{S}]^{T}\). These test functions are then multiplied by the strong form Eqs. (62)–(66) and integrated over the spatial domain. Moreover, the boundary terms are derived by utilizing the product rules and the Gauss integral theorem to the integrands. For simplicity, the variational formulations of the governing equations will be referred to as
For the time discretization, the system of coupled equations is solved in the FE package FlexPDE 7.16 [39], which uses the second-order implicit backward difference formula (BDF2), discussed in, e.g., [42], for the time integration. In our implementation of the first IBVP in Sect. 4.1, a three-step staggered procedure is applied, in which the phase field, the hydro-mechanical, and then the thermal problems are sequentially solved. For the spatial discretization within the FEM and following the Bubnov–Galerkin approach, the primary variables \(\varvec{\xi }(\textbf{x},t)\) and the weighting functions \(\delta \varvec{\xi }(\textbf{x})\) are approximated over the discrete spatial domain using proper shape functions and nodal values, i.e., \(\varvec{\xi }\approx \varvec{\xi }^h=[{\textbf{u}}^h_{S} \,\, p^h\,\, (\theta ^{F})^h\,\, (\theta^{S})^h\,\, (d^{S})^h]^{T}\) over the discretized trial spaces and \(\delta \varvec{\xi }\approx \delta \varvec{\xi }^h\) over the discretized spaces of weighting functions.
Having \(\mathcal{G}^h_{M}=\{\mathcal{G}^h_{{\textbf{u}}_S},\;\mathcal{G}_{p}^h\}\) as the space-discrete, strongly coupled porous media hydro-mechanical problem, \(\mathcal{G}^h_{\theta }=\{\mathcal{G}^h_{\theta ^{F}}\,,\;\mathcal{G}_{\theta^{S}}^h\}\) as the space-discrete porous media thermal problem, and \(\mathcal{G}^h_{d^S}\) as the space-discrete phase-field equation, the sequential steps at a time \(t_{(k+1)}=t_{(k)}+\varDelta t\) with \(\varDelta t\) as the time step size are summarized in Box 2.

In the implementation in FlexPDE, an adaptive time-step strategy is considered so that the root-mean-square (RMS) errors remain below an assigned limit, whereas the initial time step is set to \(\varDelta t =1\times 10^{-4}s\).
3.1 Overcoming numerical stability challenges
In the FE implementation, equal-order, quadratic shape functions are applied for all variables. Hence, in solving the coupled mechanical problem in a monolithic manner (step 3 in Box 2), one has to overcome a number of stability challenges in the limits of very small permeability in the porous domain, high fluid viscosity, near crack-domain interfaces, and next to drained boundaries with \(p=0\). In particular, the existence and uniqueness of the solutions require the fulfillment of the inf–sup condition as discussed in, e.g., [66, 80]. Therefore, within the approach of mixed quasi-compressibility, stability can be enforced by applying a pressure projection stabilization procedure. Specifically, a stabilization term of the form \({{\,{\nabla \cdot }\,}}(\alpha _\text {st}{{\,{\nabla }\,}}\dot{p})\) is added to the fluid mass balances, where \(\alpha _\text {st}>0\) is a small stabilization parameter, chosen as small as possible to maintain the stability but not deteriorate the accuracy of the computation. It is to note here that the stabilization term within the FE approach is only applied in the element interiors and not on the boundary elements.
Another source of instability arises from the fluid energy balance (step 4 in Box 2) for the case of convection-dominated heat transport, i.e., with high fluid velocity and heat transported mainly by the flow of the fluid, as explained in, e.g., [57]. In the current treatment, the fluid velocity increases significantly in the crack region in comparison with the surrounding ambient, which presents a source of instability in the numerical treatment. To understand this challenge, the fluid energy balance can be rewritten as a simple convection–diffusion equation as
where the scalar-valued terms \(\mathcal{A},\,\mathcal{B},\,\mathcal{D}\) can be determined based on comparing equation (69) with (64). The stability of the numerical simulation of such problems using the FEM with the Bubnov–Galerkin approach is sensitive to both the mesh size and the fluid velocity. The stability challenge, which is particular for the convective-dominated process, is characterized by a high value of the dimensionless Péclet number \(P_{\rm{e}}\). This number can be computed in the one-dimensional stationary convection–diffusion process with an element size of \(h_{\rm{e}}\) as
For \(P_{\rm{e}}>1\), the convective part in the fluid energy balance (69) becomes dominated and a suitable stabilization technique needs to be applied. If \(P_{\rm{e}}<1\), then the diffusive part becomes dominated and no special stabilization strategies are required [44].
In the underlying work, a stabilization technique based on adding an isotropic artificial thermal diffusivity term \(\overline{\mathcal{D}}\) in the domain is followed. By doing so, the fluid energy balance (69) can be expressed as
In the literature, several approaches can be found for the determination of the stabilization term \(\overline{\mathcal{D}}\) in convection–diffusion problems, see, e.g., [26]. Many of the approaches rely on the Péclet number \(P_{\rm{e}}\) to assign a suitable value for \(\overline{\mathcal{D}}\) as can be found in [57]. For simplicity in the current treatment, the value of \(\overline{\mathcal{D}}\) has been chosen as small as possible and the same in the domain to get a stable solution.
4 Numerical examples
As numerical applications of the discussed formulations and algorithms, two numerical examples are introduced in the following and implemented in the FE package FlexPDE 7.16 [39]. In the first example, the focus is on the modeling and numerical challenges of the heat transmission process in a fractured medium with reference to an analytical solution, whereas the second example investigates the effect of temperature-dependent material properties on the cracking onset and propagation as well as the effect on the fluid flow in the crack.
4.1 Heat transmission in fractured medium with reference to an analytical solution
An analytical solution that estimates the heat transmission in a wellbore system is developed by [87]. This model considers the fluid flow through a pipe in a wellbore and the heat transmission between an injected cold fluid and an ambient with a higher temperature. The output of this model is the time-dependent temperature change of the outlet fluid, which also depends on the depth of the outlet point, i.e., \(\theta ^{F}=\theta ^{F}({\textbf{x}},\,t)\). In this study, we rely on the analytical solution in [87], as provided in a MATLAB code in [20], in order to evaluate the performance of our non-isothermal phase-field saturated porous media model in capturing the heat transfer while the fluid flows in a fractured medium. The geometry and boundary conditions for the finite element solution of the plane-strain two-dimensional initial-boundary value problem (IBVP) are illustrated in Fig. 2. In this, we consider a porous domain (gray) with an initial temperature of 55 \(^{\circ }\)C and a preexisting cracked zone along the porous domain with an initial fluid temperature of \(\theta _{F0}=20\,{^{\circ }\text {C}}\). A fluid is injected into the inlet point with a flow rate of \(\overline{q}^F\)= 0.00013 \(\hbox {m}^3\)/s and heat flux of \(\overline{q}_{\theta ^F}=\overline{q}^F\,\rho _{0S}^{\text{FR}}\,C_{V}^{F}\,(\theta _{F}-\theta _{F0})\), which reduces the fluid temperature at the inlet to 20 \(^{\circ }\)C.
The geometry and boundary conditions considered in the numerical modeling of heat transmission in the fractured porous domain problem. The preexisting cracked zone is colored blue and has a width of 0.28 m. For the boundary conditions, the upper and lower boundaries are fixed in the vertical direction (\(u_{S2}=0\)), the lateral boundaries are fixed in the horizontal direction (\(u_{S1}=0\)), zero fluid flux (\(\overline{q}_F=0\)) is applied to all boundaries except for the inlet and the outlet of the crack, zero pressure (\(\overline{p}=0\)) at the outlet, and zero heat flux (\(\overline{q}_{\theta ^F}=0,\, \overline{q}_{\theta ^S}=0\)) is applied at all boundaries except for the inlet of the crack
For simplicity, the underlying treatment neglects the thermal expansion effects, i.e., we apply \(\alpha^{S}_{\theta }=\alpha ^{F}_{\theta }=0\) in the set of governing equations in Box (1). The applied material parameters for the hydro-thermal processes in this example are summarized in Table 1 and based on several sources, such as [20, 52, 57, 96].
The preexisting cracked region is generated via applying an initial high value of the crack driving force, i.e., \(\tilde{\mathcal{D}}_\text{c}\gg 0\), in the crack domain, which allows realizing the diffusive crack edges as illustrated in Fig. 3. In this, the internal length scale is chosen \(l_\text{c} = 0.14\) m in Eq. (66).
Focusing on the fluid temperature at the outlet, which is affected directly by the heat exchange between the injection fluid and the surrounding ambient, we study in this example the following factors: (1) the effect of the stabilization parameter \(\overline{\mathcal{D}}\) in (71) on the temperature change, (2) the effect of the heat transfer coefficient \(k_{\theta }^{\epsilon I}\), and (3) the effect of the intrinsic permeability in the crack \(K^S_\text{c}\) on the heat exchange and stability of the solution. As initial results, Fig. 4 depicts the change of fluid temperature at the outlet over a period of 30 days for the two approaches; the reference solution from [87] and the FE solution with the non-isothermal TPM-PFM approach with \(k_{\theta }^{\epsilon I}\)= 10 W/(m\(^2\) K), \(K^S_\text{c}\) = \(10^{-8}\) m\(^2\), and \(\overline{\mathcal{D}}\) = 200. In this comparison, special attention should be paid to the choice of the intrinsic permeability in the crack and the heat transfer coefficient in order to obtain comparable results with the analytical solution. This is because the numerical model assumes a plane strain assumption as an approximation of the flow between two plates, while the analytical solution assumes an axisymmetric geometry. Another reason is the diffuse nature of the crack edges in the model, while they are sharp in the analytical solution.
Outlet fluid temperature history for the case of the analytical solution according to [87] and the numerical solution following the proposed non-isothermal TPM-PFM approach with \(k_{\theta }^{\epsilon I}\)= 10 W/(m\(^2\) K), \(K^S_\text{c}\) = \(10^{-8}\) m\(^2\), \(\overline{\mathcal{D}}\) = 200
In the FE solution, the fluid temperature at the outlet (initially 20 \(^{\circ }\)C) is affected by the initial temperature of the ambient (55 \(^{\circ }\)C) and, thus, increases to a value of approximately 43 \(^{\circ }\)C before starting to decrease under the effect of the injected cold fluid. In the analytical solution, no initial temperature is applied (see, e.g., [20]), which explains the differences between the two solutions at the beginning. The effect of the initial temperature decreases over time and the two solutions become comparable with a slight deviation afterward. The decrease in the fluid outlet temperature is accompanied by decreasing in the ambient temperature due to heat flow from the surrounding hot regions to the colder fracture region. This is illustrated in Fig. 5, where the solid temperature at a point B (1 m above the fractured zone) decreases gradually, while the fluid outlet temperature keeps decreasing due to lower temperature gradients with the surrounding.
In connection with the fluid temperature change and heat exchange, Fig. 6 shows an example of the spatial and temporal change of \(\theta ^F\) at four subsequent time steps. It is clear the temperature changes much faster in the crack as the permeability is much higher than the surrounding domain.
Contour plot of the fluid temperature \(\theta ^F\) in the domain at four time points, \(t_1=1.2\times 10^3\,[\text{s}]\), \(t_2=3.8\times 10^3\,[\text{s}]\), \(t_3=8.2\times 10^3\,[\text{s}]\), \(t_4=1.6\times 10^4\,[\text{s}]\). These plots are connected to the numerical solution with the non-isothermal TPM-PFM approach with \(k_{\theta }^{\epsilon I}\)= 10 W/(m\(^2\) K), \(K^S_\text{c}\) = \(10^{-7}\) m\(^2\), \(\overline{\mathcal{D}}\) = 100
In the numerical examples, an artificial thermal diffusivity term \(\overline{\mathcal{D}}\) is assigned to guarantee the numerical stability in the convection-dominated heat transport. This is particularly important in the case of high fluid velocity, where heat is transported mainly by the flow of the fluid as explained in Sect. 3.1. The approach followed in the numerical examples is to apply as small values of \(\overline{\mathcal{D}}\) as possible so that the numerical stability is recovered while the accuracy is minimally impaired. In this connection, Fig. 7 illustrates the effect of \(\overline{\mathcal{D}}\) on the accuracy, whereas choosing higher values of stabilization parameter than needed might lead to over-estimate or under-estimate the temperature of the fluid in the fractured region.
In the underlying treatment with a non-equilibrium thermal condition (cf. Sect. 2.5.4), the heat exchange through the interface between the solid and fluid phases is realized through the direct energy production terms \(\hat{\varepsilon }^F\), which is proportional to the specific heat transfer surface area \(\omega _d\) and the heat transfer coefficient \(k^{\epsilon I}_\theta\). Having a higher value of the heat transfer coefficient allows for good heat exchange between the solid and the fluid phases and, thus, the fluid temperature at the outlet decreases much slower than the cases with lower \(k^{\epsilon I}_\theta\) as illustrated in Fig 8.
In real fracture problems, e.g., in rocks, the presence of fragmented solid particles in the crack and the absence of flat crack edges cause the approximation of the flow in the crack as flow between two plates and the calculation of permeability based on the cubic law (29) to be inaccurate, i.e., it leads to an overestimation of the crack permeability. Therefore, we test the effect of the permeability in the crack on the outlet fluid temperature. The results presented in Fig. 9 show that the lower permeability in the crack allows for a slower flow and, thus, better heat exchange with the surroundings than the case of higher crack permeability.
The effect of the permeability in the crack on the fluid temperature at the outlet for \(k_{\theta }^{\epsilon I}\) = 10 W/(m\(^2\)K) and the following three cases: Case 1 with \(K^S_\text{c}\) = \(10^{-7}\) m\(^2\), \(\overline{\mathcal{D}}\) = 100, Case 2 with \(K^S_\text{c}\) = \(10^{-8}\) m\(^2\), \(\overline{\mathcal{D}}\) = 10, and Case 3: \(K^S_\text{c}\) = \(10^{-9}\) m\(^2\), \(\overline{\mathcal{D}}\) = 1
4.2 Hydraulic fracturing in saturated granite rocks with temperature-dependent parameters
In the following, a 2D plane strain numerical example of phase-field hydraulic fracturing of saturated porous media using the FE package FlexPDE 7.16 is presented. By considering temperature-dependent material parameters, the aim is to test the influence of initial domain temperature and injection-fluid temperature on the fracturing process, such as the pressure needed to initiate the crack. While the hydraulic fracturing process happens within a relatively short time, the time needed to have a significant change in the surrounding temperature and, thus, change in the values of temperature-dependent material parameters, as we saw in the previous example, is much longer. Therefore, for simplicity, we consider in this example merely the initial temperatures and the related values of material parameters of the solid and fluid constituents at that particular temperature.
In analogy to the example presented in [52], we consider in the following hydraulic fracturing of granite rocks with water as the injection fluid. For the temperature-dependent material parameters, the focus is laid on Young’s modulus of the solid phase \(E^S\), the tensile strength \(\sigma _\text{c}\), and the dynamic fluid viscosity \(\mu ^{\text{FR}}\). The choice of these values is based on several references, such as [35] and [89]. In particular, the deterioration of the parameter values of granite in the range of 100–400 °C and that of water in the range of 20–100 °C is summarized in Table 2 for the four cases of study.
The other material parameters of the considered granite rock samples with presumably linear elastic material response until the onset of the fracture are summarized in Table 3, see [36, 52] for more details.
The geometry and the boundary conditions of the considered problem are illustrated in Fig 10. In this, a rectangular domain of dimensions \(450\times 300\) mm\(^2\) and a notch at the center are considered. The fluid injection is applied at the center of the domain with a constant injected flow rate of \(q^{F}\) = 0.0635 mm\(^{3}\)/s until the onset and propagation of the crack. For the boundary conditions, the pressure confining stresses \(\sigma _1\) and \(\sigma _2\) are applied to the lateral and upper boundaries, respectively. Additionally, the boundaries of the sample are considered drained, i.e., \(p_0=0\). The other boundaries are chosen in a way that no rigid-body motion occurs.
Under the assumption of constant temperature during the cracking process, the governing balance equations with primary variables \({{\textbf{u}}}_S,\,p,\,d^S\) are the overall momentum balance (62), the fluid mass balance (63), and the phase-field evolution Eq. (66). The finite element solution of the governing equations is accomplished in the FE package FlexPDE 7.16 with triangular quadratic elements, whereas the second-order implicit Backward Difference Formula (BDF2) is applied for the time stepping. As a solution strategy, a staggered scheme is applied, where at each time step the phase-field equation is solved first and the coupled porous media equations are solved next. The stability of the solution is enhanced with the application of a pressure projection stabilization procedure discussed in Sect. 3.1. In this, a stabilization term \({{\,{\nabla \cdot }\,}}(\alpha _\text {st}{{\,{\nabla }\,}}\dot{p})\) with \(\alpha _\text {st}=0.01\) is added to the fluid mass balances.
As exemplary results of the finite element simulations, Fig. 11 presents the contour plots of the phase-field variable \(d^S\), the fluid pressure p, and the vertical displacement \(u_y\) for case (4) of Table 2. In this, the crack propagates as expected normal to the maximum confining stress \(\overline{\sigma }_1\). The fluid pressure has its maximum value in the crack and in the nearby area, which corresponds to a clear high-pressure gradient in that region. Moreover, the crack opening is associated with a displacement jump as can be interpreted from \(u_y\) in Fig. 11.
In discussing the effect of initial temperatures on the cracking process, Fig. 12 shows the time histories of the pressure at the injection source for the four cases of temperature-dependent material parameters presented in Table 2.
Time history of the fluid pressure at point A (injection source) for the four cases presented in Table 2
Based on these results, it is clear that the solid phase (granite) temperature governs the maximum pressure needed to initiate the crack. In this, for cases (1) and (2) with a lower solid temperature and, thus, higher values of Young’s modulus \(E^S\) and the tensile strength \(\sigma _\text{c}\), higher values of injection pressure are needed to start the cracking. The effect of fluid phase (water) temperature is obvious in the crack propagation phase (post-crack initiation phase). In this, the higher temperature [cases (2) and (4)] is associated with lower fluid viscosity and, therefore, one has a more toughness-dominated hydraulic fracturing response with more physical oscillations in the fluid pressure during crack propagation, see, e.g., [48]. The oscillations in the fluid pressure field during crack propagation prove the capability of the model in capturing the stepwise crack advancement. With a lower fluid temperature [cases (1) and (3)] and, thus, higher fluid viscosity, a more stable crack propagation (viscosity-dominated) can be observed, see, e.g., [52] for experimental evidence. In this regard, the topic of stepwise crack propagation in porous media and the related fluid pressure oscillations has been studied numerically and experimentally in many research works as reviewed in, e.g. [18]. In this, experiments from the petroleum industry [10] proved the stepwise behavior of hydraulic fracture, where these results are reported in [38]. The stepwise crack propagation and the related pressure oscillation are affected by several factors, including the mechanical boundary conditions, the injection rate, the fluid viscosity, the heterogeneity of the material, and preexisting cracks. Studying the different factors is, however, beyond the scope of the underlying work.
5 Conclusions and future work
Within hydraulic fracturing under non-isothermal conditions, this work presented a continuum mechanical modeling framework that utilizes the theory of porous media (TPM) together with the phase-field method (PFM). In this, a two-phase porous material consisting of thermally non-equilibrated and mechanically interacting solid–fluid constituents is considered. The continuum mechanical approach with assumptions of small deformations and no-mass exchange between the constituents resulted in the most general case in a coupled five partial differential equations. These are the overall momentum balance, the fluid mass balance, the fluid energy balance, the solid energy balance, and the phase-field evolution equation. The numerical implementation of the strongly coupled equations succeeded within a finite element framework, where a number of numerical stability challenges had to be overcome. This includes stabilizing the solution algorithm in the limit of very small permeability or materially incompressible fluid by adding a Laplace pressure term to the fluid mass balance equation within a forcing quasi-compressibility approach. The other stability challenge that had to be overcome is related to the fluid energy balance equation in the convection-dominated heat transport mechanism with high fluid velocity and heat transport mainly by the flow of the fluid. In this, a stabilization technique based on adding an isotropic artificial thermal conductivity term to the fluid energy balance equation was used.
To show the capability of the proposed approach and the stability and robustness of the applied numerical algorithm, two initial-boundary-value problems were presented. In the first one, the simulation of heat transfer in a fractured medium was compared with a reference analytical solution. In addition to demonstrating good agreement with the reference analytical solution, this example discussed the various factors that affect output accuracy, such as permeability in the crack, the conductivity stabilization parameter, and the heat transfer coefficient. In the second numerical example, the influence of temperature-dependent material properties on crack initiation and propagation as well as the influence of temperature on fluid flow in the crack were discussed. This example showed that rocks with lower temperatures require higher pressure for crack initiation and propagation. Moreover, a higher temperature of the fluid lead to a more toughness-dominated hydraulic fracturing response, whereas a viscosity-dominated response is obtained for lower-temperature fluids.
To conclude, the novelty of this contribution lies in deepening the understanding of non-isothermal hydraulic fracturing and its associated coupled processes. It addressed the effects of temperature variations on the fluid and rock during the fracturing process and provided methods to account for these effects and interactions in numerical simulations. This work is of critical importance to industries that use non-isothermal hydraulic fracturing, such as enhanced oil and gas recovery, geothermal power generation, and underground carbon dioxide storage. In our future work on modeling hydraulic fracturing under non-isothermal conditions, a number of important issues have been identified to be addressed. This includes validation of the model by comparing the numerical results with experimental data from laboratories or from in-field enhanced geothermal systems. In this, it is also important to carry out efficient simulations within three-dimensional configurations in order to get more accurate numerical results. Another topic to be addressed is related to extending the model to capture the possible water-vapor phase change under high temperatures in the cracking process. Finally, the issue of convection-dominated heat transport in case of turbulent flow will be studied in future works. In this, the heat transfer coefficients have to be carefully adjusted as they can be much greater than that of laminar flow and the Péclet number is anyhow much greater.
Data availability statement
Data available on request from the authors.
References
Alazmi B, Vafai K (2001) Analysis of fluid flow and heat transfer interfacial conditions between a porous medium and a fluid layer. Int J Heat Mass Transf 44(9):1735–1749. https://doi.org/10.1016/S0017-9310(00)00217-9
Aldakheel F (2020) A microscale model for concrete failure in poro–elasto-plastic media. Theor Appl Fract Mech 107:102517. https://doi.org/10.1016/j.tafmec.2020.102517
Aldakheel F, Noii N, Wick T, Wriggers P (2020) A global-local approach for hydraulic phase-field fracture in poroelastic media. Comput Math Appl. https://doi.org/10.1016/j.camwa.2020.07.013
Ali B, Heider Y, Markert B (2021) Residual stresses in gas tungsten arc welding: A novel phase-field thermo-elastoplasticity modeling and parameter treatment framework. Comput Mech 69:565–587
Allen S, Cahn J (1979) A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening. Acta Metall 27:1085–1095
Ambati M, Gerasimov T, De Lorenzis L (2014) A review on phase-field models of brittle fracture and a new fast hybrid formulation. Comput Mech 55(2):383–405
Amhalhel G, Furmanski P (1997) Problems of modeling flow and heat transfer in porous media. J Power Technol 85(85):55
Archut JL, Kins R, Heider Y, Cloppenburg F, Markert B, Gries T, Corves B (2022) A study of the mechanical response of nonwovens excited by plate vibration. Appl Mech 3(2):496–516. https://doi.org/10.3390/applmech3020029
Biot MA (1941) General theory of three-dimensional consolidation. J Appl Phys 12(2):155–164
Black A (1986) Investigation of lost circulation problems with oil base drilling fluids. DRL Repts, Phase I
Borja RI, White JA (2013) Conservation laws for coupled hydro-mechanical processes in unsaturated porous media. Wiley-Blackwell, chap 8, pp 185–208
Bourdin B, Francfort G, Marigo JJ (2000) Numerical experiments in revisited brittle fracture. J Mech Phys Solids 48(4):797–826. https://doi.org/10.1016/S0022-5096(99)00028-9
Bourdin B, Francfort G, Marigo J (2008) The variational approach to fracture. J Elast 91(1–3):5–148
Bourdin B, Chukwudozie C, Yoshioka K (2012) A variational approach to the numerical simulation of hydraulic fracturing. In: Proceedings of the 2012 SPE annual technical conference and exhibition (vol SPE 159154) https://doi.org/10.2118/159154-MS
Brush S (1962) Theories of liquid viscosity. Transp Porous Media 62(6):513–548
Bryant EC, Sun W (2018) A mixed-mode phase field fracture model in anisotropic rocks with consistent kinematics. Comput Methods Appl Mech Eng 342:561–584. https://doi.org/10.1016/j.cma.2018.08.008
Cajuhi T, Sanavia L, De Lorenzis L (2018) Phase-field modeling of fracture in variably saturated porous media. Comput Mech 61:299–318
Cao TD, Hussain F, Schrefler B (2018) Porous media fracturing dynamics: stepwise crack advancement and fluid pressure oscillations. J Mech Phys Solids 111:113–133
Chaaban M, Heider Y, Markert B (2022) A multiscale LBM–TPM–PFM approach for modeling of multiphase fluid flow in fractured porous media. Int J Numer Anal Methods Geomech. https://doi.org/10.1002/nag.3423
Chen C, Shao H (2022) Wellbore heat transport—eubhe. https://www.opengeosys.org/docs/benchmarks/heat-transport-bhe/pipe_flow_ebhe/. Accessed on 06 Jan 2021
Choo J, Sun W (2018) Coupled phase-field and plasticity modeling of geological materials: from brittle fracture to ductile flow. Comput Methods Appl Mech Eng 330:1–32. https://doi.org/10.1016/j.cma.2017.10.009
de Boer R (2000) Theory of porous media. Springer, Berlin. https://doi.org/10.1007/978-3-642-59637-7
de Boer R, Ehlers W (1990) The development of the concept of effective stresses. Acta Mech 83:77–92. https://doi.org/10.1007/BF01174734
Diebels S, Ehlers W, Markert B (2001) Neglect of the fluid extra stresses in volumetrically coupled solid-fluid problems. ZAMM J Appl Math Mech. https://doi.org/10.1002/zamm.20010811540
Dittmann M, Kruger M, Schmidt F, Schuss S, Hesch C (2019) Variational modeling of thermomechanical fracture and anisotropic frictional mortar contact problems with adhesion. Comput Mech 63:571–591
Donea J, Huerta A (2003) Finite element methods for flow problems. Wiley, Chichester
Ehlers W (1989) On thermodynamics of elasto-plastic porous media. Arch Mech 41:73–93
Ehlers W (2002) Foundations of multiphasic and porous materials. In: Ehlers W, Bluhm J (eds) Porous media: theory, experiments and numerical applications. Springer, Berlin, pp 3–86
Ehlers W, Häberle K (2016) Interfacial mass transfer during gas–liquid phase change in deformable porous media with heat transfer. Transp Porous Media 114(2):525–556. https://doi.org/10.1007/s11242-016-0674-2
Ehlers W, Luo C (2017) A phase-field approach embedded in the theory of porous media for the description of dynamic hydraulic fracturing. Comput Methods Appl Mech Eng 315:348–368
Ehlers W, Luo C (2018) A phase-field approach embedded in the theory of porous media for the description of dynamic hydraulic fracturing, part ii: The crack-opening indicator. Comput Methods Appl Mech Eng 341:429–442
Ehlers W, Wagner A (2019) Modelling and simulation methods applied to coupled problems in porous-media mechanics. Arch Appl Mech 89(4):609–628
Ehlers W, Sonntag A, Wagner A (2022) On hydraulic fracturing in fully and partially saturated brittle porous material. Springer, Cham, pp 111–119. https://doi.org/10.1007/978-3-030-87312-7_12
Ehlers W, Ellsiepen P, Blome DM, Markert B (1999) Theoretische und numerische studien zur lösung von rand- und anfangswertproblemen in der theorie poröser medien. Abschlußbericht zum DFG-Forschungsvorhaben Eh 107/6-2, Berichte aus dem Institut für Mechanik (Bauwesen), Universität Stuttgart 0 (Nr. 99-II-1)
Engineering ToolBox W (2004) Water—dynamic and kinematic viscosity. https://www.engineeringtoolbox.com/water-dynamic-kinematic-viscosity-d_596.html. Accessed 16 Mar 2021
Engineering ToolBox W (2008) Water—properties vs. temperature and pressure. https://www.engineeringtoolbox.com/water-properties-d_1258.html. Accessed 31 May 2022
Felippa CA, Park KC, Farhat C (2001) Partitioned analysis of coupled mechanical systems. Comput Methods Appl Mech Eng 190:3247–3270
Feng Y, Jones J, Gray K (2015) Pump-in and flow-back tests for determination of fracture parameters and in-situ stresses. In: AADE national technical conference and exhibition
FlexPDE 7 W (2023) Finite element solution environment for partial differential equations. https://www.pdesolutions.com. Accessed 15 Jan 2023
Francfort GA, Marigo JJ (1998) Revisiting brittle fracture as an energy minimization problem. J Mech Phys Solids 46(8):1319–1342
Frank S, Heinze T, Pollak S, Wohnlich S (2021) Transient heat transfer processes in a single rock fracture at high flow rates. Geothermics 89:101989
Gear C, Leimkuhler B, Gupta G (1985) Automatic integration of Euler–Lagrange equations with constraints. J Comput Appl Math 12–13:77–90
Ghassemi A, Nygren A, Cheng A (2008) Effects of heat extraction on fracture aperture: a poro-thermoelastic analysis. Geothermics 37(5):525–539. https://doi.org/10.1016/j.geothermics.2008.06.001
Gresho P, Lee R (1981) Don’t suppress the wiggles—they’re telling you something! Comput Fluids 9:223–253
Griffith A (1921) The phenomena of rupture and flow in solids. Philos Trans R Soc A: Math Phys Eng Sci 221(582–593):163–198
Heider Y (2012) Saturated porous media dynamics with application to earthquake engineering. Report/Institut für Mechanik (Bauwesen), Lehrstuhl für Kontinuumsmechanik, Universität Stuttgart
Heider Y (2021a) Multi-field and multi-scale computational fracture mechanics and machine-learning material modeling. Habilitation, Report No. IAM-13 of Institute of General Mechanics, RWTH Aachen University
Heider Y (2021) A review on phase-field modeling of hydraulic fracturing. Eng Fract Mech 253:107881. https://doi.org/10.1016/j.engfracmech.2021.107881
Heider Y, Markert B (2017) A phase-field modeling approach of hydraulic fracture in saturated porous media. Mech Res Commun 80:38–46
Heider Y, Markert B (2017) Modelling of hydraulic fracturing and fluid flow change in saturated porous domains. PAMM 17(1):95–98. https://doi.org/10.1002/pamm.201710028
Heider Y, Sun W (2020) A phase field framework for capillary-induced fracture in unsaturated porous media: drying-induced vs hydraulic cracking. Comput Methods Appl Mech Eng 359:112647. https://doi.org/10.1016/j.cma.2019.112647
Heider Y, Reiche S, Siebert P, Markert B (2018) Modeling of hydraulic fracturing using a porous-media phase-field approach with reference to experimental data. Eng Fract Mech 202:116–134
Heider Y, Bamer F, Ebrahem F, Markert B (2022) Self-organized criticality in fracture models at different scales. Examples Counterexamples 2:100054. https://doi.org/10.1016/j.exco.2022.100054
Hu M, Rutqvist J, Wang Y (2017) A numerical manifold method model for analyzing fully coupled hydro-mechanical processes in porous rock masses with discrete fractures. Adv Water Resour 102:111–126
Irwin GR (1957) Analysis of stresses and strains near the end of a crack traversing a plate. J Appl Mech 24:361–364
Karpyn Z, Landry C, Prodanovic M (2016) Induced rough fracture in Berea sandstone core. https://doi.org/10.17612/P7J012
Koch D (2016) Thermomechanical modelling of non-isothermal porous materials with application to enhanced geothermal systems. Institut für Mechanik (Bauwesen), Lehrstuhl für Kontinuumsmechanik, Universität Stuttgart, Stuttgart
Kuhn C, Müller R (2010) A continuum phase field model for fracture. Eng Fract Mech 77(18):3625–3634
Kuhn C, Schlüter A, Müller R (2015) On degradation functions in phase field fracture models. Comput Mater Sci 108:374–384
Lee S, Wheeler MF, Wick T (2016) Pressure and fluid-driven fracture propagation in porous media using an adaptive finite element phase field model. Comput Methods Appl Mech Eng 305:111–132
Lee H, Moon T, Haimson B (2016) Borehole breakouts induced in Arkosic Sandstones and a discrete element analysis. Rock Mech Rock Eng 49(4):1369–1388
Lee S, Wheeler MF, Wick T (2017) Iterative coupling of flow, geomechanics and adaptive phase-field fracture including level-set crack width approaches. J Comput Appl Math 314:40–60. https://doi.org/10.1016/j.cam.2016.10.022
Li X, Hofmann H, Yoshioka K, Luo Y, Liang Y (2022) Phase-field modelling of interactions between hydraulic fractures and natural fractures. Rock Mech Rock Eng. https://doi.org/10.1007/s00603-022-02970-0
Markert B (2007) A constitutive approach to 3-d nonlinear fluid flow through finite deformable porous media. Transp Porous Media 70:427–450. https://doi.org/10.1007/s11242-007-9107-6
Markert B (2013) A survey of selected coupled multifield problems in computational mechanics. J Coupled Syst Multiscale Dyn 27:22–48
Markert B, Heider Y, Ehlers W (2010) Comparison of monolithic and splitting solution schemes for dynamic porous media problem. Int J Numer Methods Eng 82:1341–1383
Markert B, Heider Y (2015) Coupled multi-field continuum methods for porous media fracture. In: Mehl M, Bischoff M, Schäfer M (eds) Recent trends in computational engineering—CE2014, Lecture Notes in Computational Science and Engineering. Springer, Berlin, vol 105, pp 167–180 https://doi.org/10.1007/978-3-319-22997-310
Matthies HG, Niekamp R, Steindorf J (2006) Algorithms for strong coupling procedures. Comput Methods Appl Mech Eng 195:2028–2049
Miehe C, Mauthe S (2016) Phase field modeling of fracture in multi-physics problems. part III. crack driving forces in hydro–poro-elasticity and hydraulic fracturing of fluid-saturated porous media. Comput Methods Appl Mech Eng 304:619–655
Miehe C, Hofacker M, Welschinger F (2010) A phase field model for rate-independent crack propagation: Robust algorithmic implementation based on operator splits. Comput Methods Appl Mech Eng 199(45–48):2765–2778
Miehe C, Welschinger F, Hofacker M (2010) Thermodynamically consistent phase-field models of fracture: variational principles and multi-field FE implementations. Int J Numer Methods Eng 83(10):1273–1311
Miehe C, Mauthe S, Teichtmeister S (2015) Minimization principles for the coupled problem of Darcy-Biot-type fluid transport in porous media linked to phase field modeling of fracture. J Mech Phys Solids 82:186–217
Miehe C, Aldakheel F, Teichtmeister S (2017) Phase-field modeling of ductile fracture at finite strains: a robust variational-based numerical implementation of a gradient-extended theory by micromorphic regularization. Int J Numer Methods Eng 111(9):816–863
Mikelić A, Wheeler MF, Wick T (2015) Phase-field modeling of a fluid-driven fracture in a poroelastic medium. Comput Geosci. https://doi.org/10.1007/s10596-015-9532-5
Mikelić A, Wheeler MF, Wick T (2015) A phase-field method for propagating fluid-filled fractures coupled to a surrounding porous medium. Multiscale Model Simul 13(1):367–398
Mikelić A, Wheeler MF, Wick T (2015) A quasi-static phase-field approach to pressurized fractures. Nonlinearity 28(5):1371–1399
Msekh MA, Sargado JM, Jamshidian M, Areias PM, Rabczuk T (2015) Abaqus implementation of phase-field model for brittle fracture. Comput Mater Sci 96:472–484
Nguyen CL, Sweidan AH, Heider Y, Markert B (2021) Thermomechanical phase-field fracture modeling of fluid-saturated porous media. PAMM 20(1):e202000332. https://doi.org/10.1002/pamm.202000332
Noii N, Wick T (2019) A phase-field description for pressurized and non-isothermal propagating fractures. Comput Methods Appl Mech Eng. https://doi.org/10.1016/j.cma.2019.03.058
Obaid A, Turek S, Heider Y, Markert B (2017) A new monolithic newton-multigrid-based fem solution scheme for large strain dynamic poroelasticity problems. Int J Numer Methods Eng 109(8):1103–1129
Olasolo P, Juárez M, Morales M, D’Amico S, Liarte I (2016) Enhanced geothermal systems (EGS): a review. Renew Sustain Energy Rev 56:133–144
Padilla C, Patil S, Heider Y, Markert B (2017) 3d modelling of brittle fracture using a joint all-atom and phase-field approach. GAMM-Mitteilungen 40:91–101
Patil SP, Heider Y, Hernandez-Padilla C, Cruz-Chú E, Markert B (2016) A comparative molecular dynamics-phase-field modeling approach to brittle fracture. Comput Methods Appl Mech Eng 312(8):117–129
Pillai U, Heider Y, Markert B (2018) A diffusive dynamic brittle fracture model for heterogeneous solids and porous materials with implementation using a user-element subroutine. Comput Mater Sci 153:36–47
Pise M, Bluhm J, Schröder J (2019) Elasto-plastic phase-field model of hydraulic fracture in saturated binary porous media. Int J Multiscale Comput Eng 17(2):201–221
Quintard M, Kaviany M, Whitaker S (1997) Two-medium treatment of heat transfer in porous media: numerical results for effective properties. Adv Water Resources (Adv Heat Transf Porous Media) 20(2):77–94
Ramey H (1962) Wellbore heat transmission. J Petrol Technol 14:427–435. https://doi.org/10.2118/96-PA
Rutqvist J, Noorishad J, Tsang CF, Stephansson O (1998) Determination of fracture storativity in hard rocks using high-pressure injection testing. Water Resour Res 34(10):2551–2560
Saiang C, Miskovsky K (2012) Effect of heat on the mechanical properties of selected rock types—a laboratory study. In: Harmonising rock engineering and the environment—Proceedings of the 12th ISRM international congress on rock mechanics. pp 815–820 https://doi.org/10.1201/b11646-149
Santillán D, Juanes R, Cueto-Felgueroso L (2017) Phase field model of fluid-driven fracture in elastic media: immersed-fracture formulation and validation with analytical solutions. J Geophys Res: Solid Earth 122(4):2565–2589
Santillán D, Juanes R, Cueto-Felgueroso L (2018) Phase field model of hydraulic fracturing in poroelastic media: fracture propagation, arrest, and branching under fluid injection and extraction. J Geophys Res: Solid Earth 123(3):2127–2155
Suh HS, Sun W (2021) Asynchronous phase field fracture model for porous media with thermally non-equilibrated constituents. Comput Methods Appl Mech Eng 387:114182
Svolos L, Bronkhorst CA, Waisman H (2020) Thermal-conductivity degradation across cracks in coupled thermo-mechanical systems modeled by the phase-field fracture method. J Mech Phys Solids 137:103861
Sweidan AH, Heider Y, Markert B (2019) Modeling of PCM-based enhanced latent heat storage systems using a phase-field-porous media approach. Contin Mech Thermodyn. https://doi.org/10.1007/s00161-019-00764-4
Sweidan AH, Heider Y, Markert B (2020) A unified water/ice kinematics approach for phase-field thermo-hydro-mechanical modeling of frost action in porous media. Comput Methods Appl Mech Eng 372:113358. https://doi.org/10.1016/j.cma.2020.113358
Sweidan A, Niggemann K, Heider Y, Ziegler M, Markert B (2021) Experimental study and numerical modeling of the thermo-hydro-mechanical processes in soil freezing with different frost penetration directions. Acta Geotechnica. https://doi.org/10.1007/s11440-021-01191-z
Tran D, Settari AT, Nghiem L (2013) Predicting growth and decay of hydraulic-fracture width in porous media subjected to isothermal and nonisothermal flow. SPE J 18(04):781–794. https://doi.org/10.2118/162651-PA
Ulloa J, Noii N, Alessi R, Aldakheel F, Degrande G, François S (2022) Variational modeling of hydromechanical fracture in saturated porous media: a micromechanics-based phase-field approach. Comput Methods Appl Mech Eng 396:115084. https://doi.org/10.1016/j.cma.2022.115084
Wang Y, Papamichos E (1999) Thermal effects on fluid flow and hydraulic fracturing from wellbores and cavities in low-permeability formations. Int J Numer Anal Methods Geomech 23(15):1819–1834
Wheeler M, Wick T, Wollner W (2014) An augmented-Lagrangian method for the phase-field approach for pressurized fractures. Comput Methods Appl Mech Eng 271:69–85
Wilson Z, Landis C (2016) Phase-field modeling of hydraulic fracture. J Mech Phys Solids 96:264–290
Witherspoon PA, Wang JS, Iwai K, Gale JE (1980) Validity of cubic law for fluid flow in a deformable rock fracture. Water Resour Res 16(6):1016–1024
Yin B, Kaliske M (2020) An anisotropic phase-field model based on the equivalent crack surface energy density at finite strain. Comput Methods Appl Mech Eng 369:113202. https://doi.org/10.1016/j.cma.2020.113202
Zhou B, Heider Y, Ma S, Markert B (2019) Phase-field-based modelling of the gelation process of biopolymer droplets in 3d bioprinting. Comput Mech 63:1187–1202
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
C-LN and YH performed conceptualization, methodology, writing—original draft preparation. BM did conceptualization, supervision, proofreading.
Corresponding author
Ethics declarations
Conflict of interest
The author declares that there are no conflicts of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nguyen, CL., Heider, Y. & Markert, B. A non-isothermal phase-field hydraulic fracture modeling in saturated porous media with convection-dominated heat transport. Acta Geotech. 18, 4515–4538 (2023). https://doi.org/10.1007/s11440-023-01905-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11440-023-01905-5