Abstract
As observed in Thomson-scattered white light, coronal mass ejections (CMEs) are manifest as large-scale expulsions of plasma magnetically driven from the corona in the most energetic eruptions from the Sun. It remains a tantalizing mystery as to how these erupting magnetic fields evolve to form the complex structures we observe in the solar wind at Earth. Here, we strive to provide a fresh perspective on the post-eruption and interplanetary evolution of CMEs, focusing on the physical processes that define the many complex interactions of the ejected plasma with its surroundings as it departs the corona and propagates through the heliosphere. We summarize the ways CMEs and their interplanetary CMEs (ICMEs) are rotated, reconfigured, deformed, deflected, decelerated and disguised during their journey through the solar wind. This study then leads to consideration of how structures originating in coronal eruptions can be connected to their far removed interplanetary counterparts. Given that ICMEs are the drivers of most geomagnetic storms (and the sole driver of extreme storms), this work provides a guide to the processes that must be considered in making space weather forecasts from remote observations of the corona.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Coronal Mass Ejections were first observed from space with the coronagraph onboard NASA’s Seventh Orbiting Solar Observatory (OSO-7) on 14 December 1971, Tousey (1973) as bright transients expelled through the coronagraph field of view over a period of minutes to hours. Subsequent space-borne coronagraphs such as the Coronagraph/Polarimeter (or C/P) on the Solar Maximum Mission (SMM) (MacQueen et al. 1980) and the Large Angle Spectrometric Coronagraph (LASCO) onboard the Solar and Heliosphere Observatory (SOHO) (Brueckner et al. 1995) have observed thousands of CMEs from which their characteristics are documented over more than two solar cycles (e.g., Hundhausen 1993; St. Cyr et al. 2000). An analysis of these data has led to a very detailed understanding of the structure and evolution of CMEs in the corona, which has been summarized in several reviews (e.g., Hundhausen et al. 1984; Kahler 1987; Hundhausen 1987; Kahler 1992; Gosling 1993a). Related reviews also discuss the pre-event conditions leading to CMEs (Gopalswamy et al. 2006), while the theoretic underpinnings of CME initiation are treated in e.g., Forbes (2000), Forbes et al. (2006). The structure of interplanetary CMEs (ICMEs) is well described in Gopalswamy (2006) and by Kilpua et al. in this issue. For the purpose of this paper, we define CMEs as transients that occur within the field-of-view of classical coronagraphs, which may extend to maximum of 30 \(R_{\odot}\) (solar radii) in the case of the LASCO C3 coronagraph. Transients beyond this range, and certainly beyond orbit of Mercury, we classify as ICMEs.
A fresh look at the literature on CMEs and ICMEs is timely given the enormous advances that have occurred in the past decade. We have just passed the ten year anniversary of the launch of the twin Solar Terrestrial Relations Observatory (STEREO) spacecraft (Kaiser et al. 2008), which provide continuous multi-viewpoint white-light observations of CMEs from Sun to Earth (Howard et al. 2008). STEREO also provides in situ measurements including both the plasma and the magnetic field made with the In-situ Measurements of Particles and CME Transients (IMPACT) instrument (Luhmann et al. 2008; Galvin et al. 2008). With these capabilities, STEREO was ideally designed to connect solar eruptions with their solar wind disturbances. Of similar importance is the introduction of massively-parallel supercomputers in the late 1990’s, which have allowed the first realistic three-dimensional magnetohydrodynamic (MHD) simulations of specific CME events (e.g., Odstrcil et al. 2005; Lugaz et al. 2007; Tóth et al. 2007; Manchester et al. 2008; Taktakishvili et al. 2009). A review by Webb and Howard (2012) summarizes observational studies of CMEs utilizing data from STEREO among many other spacecraft while a companion paper by Chen (2011) summarizes recent advances in numerical modeling of CME initiation. We complement these works by reviewing the results of both observational studies and numerical simulations to garner a more complete understanding of the physical processes governing the evolution of CMEs in the corona and ICMEs in the solar wind. We do so by following the sequence of events that affect the structure and velocity of CMEs as they depart the closed fields of the corona to pass through the depths of interplanetary space.
As we take inventory of relevant physical processes, we first consider the structure and appearance of CMEs and ICMEs from the low corona to 1 AU in Sect. 2. We then cover those processes that are most pronounced in close proximity to the Sun, where CMEs make their way through the highly structured magnetic field of the low corona. In this regard, we consider deflections and rotations (in Sects. 3 and 4, respectively). In Sect. 5, we examine the kinematic evolution followed by a discussion of the impact of ICMEs on the surrounding heliosphere in Sect. 6. We then cover the processes that affect the magnetic structure of ICMEs in Sect. 7, most significantly reconnection, which causes magnetic ejecta to erode. In Sect. 8, we examine the charge state composition of CMEs with a special emphasis on filament material. We consider the effects of CME-CME interaction and the formation of complex ejecta in Sect. 9, and in Sect. 10, we describe a Sun-to-Earth simulation of the Bastille Day CME event. Finally, in Sect. 11, we summarize the salient points of CME and ICME evolution. As we elucidate these processes, we endeavor to first introduce them as they were discovered, and then describe supporting work in a historical narrative. Understanding the evolution of CMEs and ICMEs in the corona and solar wind is fundamental to explaining and potentially predicting the complex structures observed throughout the heliosphere. This fundamental goal of heliospheric physics has great practical value in space weather forecasting capability, which is addressed by Kilpua et al. in this issue. Similarly the topic of solar energetic particles (SEPs) will be covered in two complementary texts, one by Dalla and Klein and another by Schwadron et al.
2 Structure of CMEs to ICMEs
Manifest in coronagraph images, CMEs are seen in Thomson-scattered white-light, where the brightness reflects the electron density near the plane of the sky (Billings 1966). While CMEs may show many morphologies, the simplest configuration is a three-part structure: a bright leading loop enclosing a dark low-density cavity, which contains a high-density core (e.g., Hundhausen 1993; Howard et al. 1997). This three-part structure can usually be traced directly to a progenitor of the same form that may exist at small-scale confined to an active region or exist at global-scale contained within a helmet streamer. The entire system, with a mass in the range of \(10^{15} \mbox{--} 10^{16}~\mbox{g}\) (Colaninno and Vourlidas 2009) may lift out of the corona gradually over a period of hours with speeds less than \(100~\mbox{km}\,\mbox{s}^{-1}\), or they may be impulsively ejected with speeds approaching \(3000~\mbox{km}\,\mbox{s}^{-1}\) (Hundhausen et al. 1994), with kinetic energy approaching \(10^{33}~\mbox{ergs}\). The journey continues beyond the view of classical coronagraphs where the corresponding ejecta in the solar wind are identified as ICMEs that may or may not bare a clear connection to a coronal counterpart (e.g., Gopalswamy et al. 1998).
Disturbances in the solar wind have long been associated with various eruptive phenomena, such as flares, eruptive prominences, type II radio bursts, and later with coronal mass ejections. Since the 1970’s efforts have been made to predict the arrival time and impact speed of the eruption-related solar wind disturbances (e.g., De Young and Hundhausen 1971, 1973; Steinolfson and Dryer 1978; Wu et al. 1979). However, at that time, CMEs were not recognized as a major source of interplanetary disturbances and research was primarily focused on the propagation of flare-driven shocks. With time, the CME and more precisely, the ICME ejecta and sheath came to be seen as the source of the most significant solar wind disturbances and consequently the source of non-recurrent geomagnetic storms (e.g., Gosling 1993b). This transformation in understanding was reflected in the evolution of modeling efforts from flare-driven shocks (also called blast waves) to CMEs (Wu et al. 1981; Wei 1982; Dryer et al. 1984; Dryer and Smart 1984; Smart and Shea 1985; Smith and Dryer 1990; Wei and Dryer 1991; Farrugia et al. 1993; Osherovich et al. 1993; Gosling and Riley 1996; Vandas et al. 1996, e.g., and references therein; see also reviews by Pizzo 1985 and Dryer et al. 1988).
The connection between CME and ICME was made abundantly more clear through STEREO observations (e.g., Davis et al. 2009; Möstl et al. 2009; Wood et al. 2009; Liu et al. 2010a). An example of a particularly well observed CME/ICME pair is found in the 12–18 December 2008 event, which serves to highlight a range of physical processes governing the evolution of these phenomena (e.g., Davis et al. 2009; Byrne et al. 2010; Liu et al. 2010a,b; Lugaz et al. 2010; DeForest et al. 2011, 2013; Howard and DeForest 2012). In this case, STEREO data is utilized to make a convincing connection between the solar eruption and the disturbance observed at Earth. The CME is induced by a prominence eruption in the northern hemisphere (see left panel of Fig. 1), which started between 03–04 UT on 12 December 2008. The prominence material (visible in EUVI at 304 Å) is well aligned with the CME core. The CME slowly rotates and expands toward the ecliptic plane, and seems fully developed in COR2. The basic structure of the CME remains organized out to at least the field of view of HI1. In HI2 of STEREO A, we see a dark cavity bracketed by structures with enhanced densities. The time-elongation maps shown in Fig. 1 are produced by stacking running difference intensities of COR2, HI1 and HI2 within a slit along the ecliptic plane. Two features corresponding to the CME leading and trailing edges can be identified up to 50° elongation for both STEREO A and B. Intermittent ones between the two tracks, probably associated with the CME core, are also seen but later disappear presumably due to the expansion of the ICME. Figure 2 shows the plasma and magnetic signatures of the corresponding ICME, which passed Wind on 17 December 2008. The shaded region identifies the magnetic ejecta of the CME.
STEREO observations of the 12 December 2008 CME/ICME event. The left column shows the CME/ICME evolution observed by STEREO A (left) and STEREO B (right) near simultaneously. From top to bottom, the panels display the composite images of EUVI at 304 Å and COR1 showing the nascent CME (indicated by the arrow), combined COR1 and COR2 images of the fully developed CME, and running difference images from HI1 and HI2 when the ICME is far away from the Sun. The crosses mark the locations of the CME leading and trailing edges obtained from the time-elongation map. The positions of the Earth and Venus are labeled as E and V. Right: Time-elongation maps constructed from running difference images of COR2, HI1 and HI2 along the ecliptic plane for STEREO A (upper) and B (lower). The arrows indicate two tracks associated with the CME. The vertical dashed lines show the MC interval observed at Wind, and the horizontal dashed line marks the elongation angle of the Earth. Adapted from Liu et al. (2010a)
The MC observed at Wind corresponding to the 12 December 2008 CME (after Liu et al. 2010a). From top to bottom, the panels show the proton density, bulk speed, proton temperature, and magnetic field strength and components, respectively. The shaded region indicates the MC interval, and the hatched area shows the predicted arrival times (with uncertainties) of the ICME leading and trailing edges. The horizontal lines mark the corresponding predicted velocities at 1 AU. The dotted line denotes the expected proton temperature from the observed speed
2.1 ICMEs and Magnetic Clouds
The observed structure and evolution of CMEs/ICMEs, as illustrated in Figs. 1, 2 and 3, can be described by physical models, which can reproduce observed properties and explain and predict their evolution. For CMEs with a common three-part structure, the magnetic field is commonly taken to be of the form of a twisted flux rope contained within an interior plasma cavity (e.g., Gibson et al. 2010). The core of the structure is typically considered to be filament material that was supported by the magnetic field above the system’s photospheric polarity inversion line (PIL) prior to the eruption. While long-standing, it is worth noting recent work by Howard et al. (2017) questions the filament-core connection for some events. Flux ropes have often been invoked as a theoretical construction corresponding to the pre-event plasma cavity, which contains the free energy necessary to drive CMEs (e.g., Low 2001; Török and Kliem 2003; Kliem et al. 2004; Fuller et al. 2008). The pre-event magnetic field supporting the filament can also be well described by highly sheared magnetic arcades crossing the PIL (e.g., Mikić et al. 1988; Steinolfson 1991; Antiochos et al. 1999; Amari et al. 2003; Manchester 2003; Lynch et al. 2008; van der Holst et al. 2009). Upon eruption, these arcades invariably neck off and reconnect to form erupting magnetic flux ropes attached to the Sun at both ends. Regardless of the simulated CME initiation process, the magnetic structure expelled from the corona is almost universally considered to be a twisted structure that can be characterized as a flux rope. It is here that we begin our evaluation of the physical processes that guide the evolution of CMEs from the low corona to interplanetary space.
Solar observations of the source region and CME of 16 June 2010. Top left, the HMI synoptic magnetic field is shown with PFSS coronal extrapolation. The red line indicates the source of the CME red circles giving the foot points of the erupting flux rope. Top right, AIA 193 Å image of Sun. Middle Row: STEREO EUVI-B images in 195 & 304 Å show a quiescent filament lifting off as the CME erupts. Bottom Row: GCS model fitting to the CME event of 16 June 2010. The left, center and right panels are simultaneous data from STEREO COR2-B, SOHO LASCO C2, and STEREO COR2-A, respectively. The images have been over plotted (green) with the GCS model represented by a grid of points on the surface of the model flux rope
Flux rope models have been shown to self-consistently reproduce many observed properties of CMEs, including the three-part density structure (e.g., Gibson and Low 1998; Wu et al. 2001; Manchester et al. 2004b; Wood and Howard 2009). In a similar vein, the graduated cylindrical shell (GCS) model (Thernisien et al. 2009; Vourlidas et al. 2011; Colaninno and Vourlidas 2015) provides a geometric representation of the CME cavity that is consistent with an idealized flux rope. Parameters for the model are determined by fitting two or three nearly simultaneous multi-viewpoint observations derived from STEREO Sun Earth Connection Coronal and Heliospheric Investigation (SECCHI), SOHO/LASCO C2 and C3 and Solar Dynamics Observatory (SDO) Atmospheric Imaging Assembly (AIA). The GCS model is capable of describing a wide range of quantities including the bulk velocity mass distribution and three-dimensional trajectory of the CME (e.g., Shi et al. 2015). Figure 3 shows application of the GCS model to the 16 June 2010 CME event, which is a relatively slow CME occurring with the eruption of a quiescent filament. Here, coronagraph images from STEREO/SECCHI and LASCO coronagraphs are shown along with GCS model represented as green circular lines describing the location of a three-dimensional flux rope in the shape of a crescent as seen in the COR2-A field of view of Fig. 3. The model in this case shows evidence for a variety of physical processes we will discuss in following sections, including super-radial expansion and rotation within the first 5 \(R_{\odot}\). In several examples (e.g., Liu et al. 2010b; Vourlidas et al. 2011; Nieves-Chinchilla et al. 2012; Isavnin et al. 2014; Shi et al. 2015; Schmidt et al. 2016), the GCS model has shown how the early 3-D evolution of CMEs can be well described as magnetic flux ropes that are prone to both deflection and rotation.
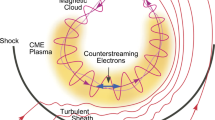
Flux ropes ejected from the solar corona during CMEs may travel through interplanetary space largely intact, and careful examination suggests that they can be connected to the magnetic structures observed at 1 AU (e.g., Yurchyshyn et al. 2007; Démoulin 2008; Möstl et al. 2008; Davis et al. 2009; Liu et al. 2010a,b, 2011; Howard and DeForest 2012; Manchester et al. 2014a; Hu et al. 2016). The magnetic fields associated with ICMEs often retain a coherent structure resembling a flux rope. Referred to as magnetic clouds (MCs) (Burlaga 1981, 1988; Lepping et al. 1990; Burlaga et al. 1995), these ICMEs are characterized by high magnetic field strength with a smooth rotation (e.g., south to north or east to west) of the field direction, low ion temperature, low plasma beta (typically less than 0.1). The rotation of the field is suggestive of a flux rope geometry (e.g., Lepping et al. 1990; Hu and Sonnerup 2002; Liu et al. 2008a), while the occasional presence of counter-streaming electrons suggest the magnetic field remains attached to the Sun at both ends (e.g., Gosling et al. 2001). The charge state composition of MCs shows elevated ionization states, which are suggestive of flare heated material being ejected with the CME (e.g., Neugebauer and Goldstein 1997; Lepri and Zurbuchen 2004; Zurbuchen and Richardson 2006). Magnetic clouds are also distinguished by their large-scale, and their passage past the Earth that may last 7 to 48 hours, with an average of approximately 21 hours (Lepping et al. 2006). The time and speed indicates that near Earth, the average radial width of MCs is about 0.22 AU and about 1.33 AU at 10 AU (Liu et al. 2006a). MCs are particularly likely to be detected in the near-Earth solar wind when a CME originates within 30° of disk center (Gopalswamy et al. 2001a), indicative of the longitudinal size of these truly global-scale heliospheric disturbances. It should be noted that apart from size, the signatures of ICMEs do not usually occur simultaneously and few ICMEs have all of them.
The relative proportion of ICMEs that appear as MC events has historically shown great variation through the solar cycle. At solar minimum, nearly all ICMEs at Earth can be identified as MCs (Cane and Richardson 2003; Richardson and Cane 2004b), while at solar maximum only \(\approx 15\%\) can be. Averaged over the solar cycle, MCs comprised \(\approx 30\%\) of ICMEs (Gosling 1990). The cycle dependence reflects several different aspects of CMEs including their place of origin, orientation and mutual interaction. At solar minimum, a greater majority of CMEs originate from streamer blowouts and quiescent filament eruptions. These eruptions are more prone to produce slow CMEs, which are less likely to interact with one another owing to lower eruption rates. Also at solar minimum, CMEs erupt more often at low latitude, providing a greater opportunity for near-central impacts for observing spacecraft, which are more likely to register MC signatures. In contrast, at solar maximum, high latitude eruptions result in off-center ICME in situ measurements which are less likely to register the field line rotations of a flux rope. Also at solar maximum, more CMEs originate from active regions where high eruption rates are prone to produce complex interacting ICMEs, as will be discussed in Sect. 9. However, more recent analysis suggest that nearly all ICMEs have flux rope structure (e.g., Owens et al. 2005; Gopalswamy et al. 2013; Mäkelä et al. 2013), and that even plasma-dense ejecta may be fit with flux ropes (Marubashi et al. 2015). ICME-related signatures can also continue well beyond the MC boundaries (e.g., Richardson and Cane 2010b; Kilpua et al. 2013). Manchester and Zurbuchen (2006) found that open field lines deflected around the ejected flux rope can have plasma and magnetic characteristics of a MC at latitudes extending beyond the ejected flux rope.
3 CME and ICME Deflection
3.1 Characteristics and Causes of CME Deflection
CME deflection is the departure from a radial trajectory that commonly occurs with significant in-course changes in direction (e.g., Gosling et al. 1987; Vandas et al. 1996; Wang et al. 2004; Gui et al. 2011; Lugaz et al. 2011; Shen et al. 2011; Kay et al. 2013, 2016; Rollett et al. 2014; Möstl et al. 2015). Figure 4 shows a clear example of deflection for the 2 November 2008 event where the CME’s change in latitude is obvious when comparing the STEREO-B COR1 to COR2 images. A survey by Isavnin et al. (2014) found a maximum total CME deflection (from Sun to Earth) in latitude was \(49^{\circ}\) and almost \(30^{\circ}\) in longitude. These deflections can be attributed to two primary causes: First, magnetic forces produced by the background corona (e.g., MacQueen et al. 1986; Kilpua et al. 2009; Shen et al. 2011), including the active region of origin (Möstl et al. 2015). Second, the background solar wind flow pattern can inhibit the latitudinal expansion of the CME in the corona (e.g., Cremades et al. 2006) and the wind also interacts with ICMEs farther out in the heliosphere (e.g., Wang et al. 2004). Magnetic forces control the deflection low in the corona, while the importance of kinematic interactions increases at larger heliospheric distances. In the case of kinematic interactions, the deflecting forces are also ultimately magnetic in nature (see e.g., discussion in Isavnin et al. 2014). This deflection occurs because of ICME interactions with the ambient solar wind that pileup plasma and drape magnetic field at the edges of the CME ejecta, as will be discussed in detail in Sects. 5 and 6.
(a): A high-latitude prominence eruption on 2 November 2008 seen by STEREO-B EUVI at 304 Å wavelength and the corresponding CME in (b): STEREO-B COR1 (c): STEREO-B COR2. This CME deflected quickly to the ecliptic and was observed at STEREO-A as a well-defined magnetic cloud a few days later. The event is studied in detail in Kilpua et al. (2009). Panels (a)–(c) adapted from Kilpua et al. (2009)
Shen et al. (2011) argue that CMEs tend to deflect toward the region of the lower magnetic energy density by the combined effect of the magnetic pressure and tension forces. The authors presented a theoretical method to account for this effect, which was used statistically by Gui et al. (2011) to confirm the deflection toward the magnetic energy minimum. Kay et al. (2015) demonstrated this deflection property using the Forecasting CMEs Altered Trajectory (ForeCAT) model (see also Kay et al. 2013). This tool propagates CMEs using a drag-based empirical model that takes into account magnetic forces as well as CME expansion. The results of Kay et al. (2015) show a wide range of deflection and also illustrate circumstances when forces are insufficiently strong to fully deflect CMEs toward the energy minimum.
Consider CME deflection from the corona/heliosphere system in the minimum energy state, which has open flux extending from coronal holes separated by a streamer belt with a heliospheric current sheet (HCS) extension. The magnetic field in coronal holes is typically stronger than that found in the surrounding closed flux systems, which provides a magnetic gradient that readily deflects CMEs. The importance of coronal holes for deflection is featured in many studies (e.g., Cremades et al. 2006). Gopalswamy et al. (2009a) and Mohamed et al. (2012) estimated the magnitude and direction of the resultant magnetic force exerted by all coronal holes present on the solar disk during the time of the CME eruption (defined as the CHIP parameter in Mohamed et al. 2012) and compared this with CME trajectories and in situ observations. It was found that CMEs tend to move away from the coronal holes and the CMEs that erupt close to disk center but had large CHIP parameters produced generally complex ICMEs or driverless shocks in the near-Earth solar wind. In addition, several recent studies have demonstrated that CMEs are also deflected by strong magnetic fields in the CME source active region (e.g., Kay et al. 2015; Möstl et al. 2015; Wang et al. 2015). Figure 5 shows examples of deflection in both circumstances: CMEs originating from a low-latitude active region and from a coronal hole boundary depicted in Fig. 5a, b, respectively. These results, calculated with ForeCAT, indicate that deflections in latitude and longitude may reach \(30^{\circ}\) to \(40^{\circ}\), respectively, with the magnitude being inversely related to CME speed and mass. The work of Lugaz et al. (2011) on CME deflection presents a slightly different configuration, that of an anemone active region, where the Lorentz force drives the deflection.
FOREcat model results (adapted from Kay et al. 2015) shown for CMEs originating from two locations: (a) low-latitude active region and (b) coronal hole boundary. Here, the dots represent the deflected location of the CMEs where the size of the dots are proportional to mass ranging from \(10^{14}\) to \(10^{15}~\mbox{g}\), and the speed of the CMEs ranging from 300 to \(1500~\mbox{km}\,\mbox{s}^{-1}\) is indicated by color. It is shown that deflection in latitude and longitude may reach \(30^{\circ}\) to \(40^{\circ}\), respectively, with deflection being inversely related to CME speed and mass
The CME deflection in latitude is constrained by the location of the streamer belt/HCS and this deflection occurs predominantly close to the Sun in the neighborhood of the streamers. However, longitudinal deflections are largely controlled by kinematic interactions (e.g., Gosling et al. 1987; Wang et al. 2004, 2014b) that occur at larger distances in the corona and heliosphere. The main source of longitudinal deflection is caused by interaction of ICMEs with the Parker spiral structured solar wind that occurs when there is sufficient speed difference with the ICME (Wang et al. 2004). The resulting magnetic forces and the direction of the deflection are different for slow and fast ICME populations: Slow ICMEs are deflected westward when they are pushed from behind by the faster wind, while fast ICMEs deflect eastward as they are decelerated by the slower wind head. We note however that ambient Parker spiral field by itself may not be able to deflect a ICME by more than a few degrees as even for a slow ICME its kinetic energy density is about two orders of magnitude higher than the magnetic energy density of the Parker field. Finally, interactions between multiple CMEs/ICMEs, in particular when they collide, can also cause longitudinal deflections (e.g., Lugaz et al. 2012; Shen et al. 2012; Liu et al. 2012, 2014a).
3.2 Deflection Dependence on the Background Corona
Based on the above-described studies, the rate and amount of CME/ICME deflection is controlled by the strength and distribution of the background magnetic field, and the mass, size, and speed of the CME/ICME relative to the solar wind. Hence, both the global configuration of the Sun’s magnetic field and intrinsic CME properties have crucial importance on the degree and direction of deflection, which we now further quantify. For example, Xie et al. (2009) showed that during solar minimum slow CMEs deflected toward the ecliptic and the streamer belt by strong polar magnetic fields, while fast CMEs are deflected less, sometimes also away from the streamer belt away from the streamer belt, confirming earlier results by MacQueen et al. (1986). Similarly Wang et al. (2011) found 62% of CMEs deflected towards equator with an average deflection angle of \(22^{\circ}\), and only 5% of CMEs deflected towards poles, with an average deflection angle of \(16^{\circ}\). Also a case study by Kilpua et al. (2009) found that slower and wider CMEs deflected toward the equator while the faster and narrower CME propagated radially from its source active region. It was suggested that slow and wider CMEs cannot penetrate through the overlying coronal fields, but are channeled toward the streamer belt. These findings are consistent with the ForeCAT model (Kay et al. 2015; Kay and Opher 2015) showing that slow, wide and low-mass CMEs deflect most as shown in Fig. 5.
The rate of CME deflection is clearly fastest close to the Sun where magnetic forces dominate. The analysis of 14 CMEs by Isavnin et al. (2014) showed that about 60% of the total evolution from the Sun to Earth orbit takes place in the corona, i.e., within about first 20–30 \(R_{\odot}\) from the Sun, in particular, the rate being highest in the low corona (\(< 5~R_{\odot}\)). Kay et al. (2015) came to similar conclusions using the ForeCAT model; the majority of CME deflection occurs within 10 \(R_{\odot}\) from the Sun. Kay et al. (2015) also pointed out that deflections are confined closer to the Sun in the case of stronger background magnetic fields. For strong fields studied in their paper, the deflections occurred primarily below 2 \(R_{\odot}\) from the solar surface. This result is consistent with Gui et al. (2011) who found a positive correlation with the rate of the deflection and the strength of the magnetic energy density gradient. The intrinsic magnetic polarity of the CME flux rope relative to the background coronal magnetic field determines whether and where the magnetic reconnection can occur and consequently deflects the CME (e.g., see simulation work by Chané et al. 2005; Zuccarello et al. 2012a; Zhou and Feng 2013). If the CMEs intrinsic field is parallel to the ambient field, the CME deflects equator-ward while when the fields are antiparallel, the CME is likely to deflect poleward (Zhou and Feng 2013).
3.3 Characteristics and Examples of CME/ICME Deflection
There are several examples in the literature where deflections of CMEs have changed the expected ICME impact at Earth and the expected geoeffectivity. For example, Zhou et al. (2006) showed that intrinsically high-latitude CMEs can drive strong storms; nearly 30% of the Earth-encountered ICMEs associated with high-latitude polar crown filament disappearances investigated in their study caused at least moderate space weather effects. CMEs have a strong tendency to deflect from high latitudes toward the equator in particular near solar minimum (e.g., Plunkett et al. 2001; Cremades et al. 2006; Kilpua et al. 2009; Byrne et al. 2010; Isavnin et al. 2014). This behavior is expected, as at this time, the global magnetic field of the Sun is relatively close to a dipole field and two large polar coronal holes dominate the field structure. These coronal holes can effectively guide CMEs toward the ecliptic, consistent also with the suggestion by Shen et al. (2011) as the minimum energy region streamer belt/HCS is relatively flat and confined close to the equator during slow solar activity period. Near solar maximum the configuration of the Sun’s global magnetic field and the distribution of magnetic energy density is more complex than near solar minimum and CMEs deflect less and more randomly. Poleward deflection occurs mainly during the times of solar maximum when large low-latitude polar coronal holes are present.
As discussed in the beginning of this section, longitudinal deflection may cause CMEs/ICMEs to deviate from the Sun-Earth line or toward it. According to study by Gopalswamy et al. (2009b), almost ten percent of large geospace storms are caused by CMEs that originate close to the limb of the Sun. In such cases, the ICME sheath is typically the primary driver of the storm (see also Huttunen et al. 2002), but cases have been reported where clear ejecta signatures upstream of the Earth and geomagnetic activity have been associated with limb CMEs (e.g., Schwenn et al. 2005; Cid et al. 2012; Wang et al. 2014b; Liu et al. 2016). For example, the CME studied by Wang et al. (2014b) was initially heading toward the STEREO-B, but it deflected in the heliosphere and arrived at the Earth instead, which was located about 35° away from the STEREO-B at that time. An opposite case is featured e.g., in Möstl et al. (2015), Wang et al. (2015) where the authors studied a CME that originated from an active region near the solar disk center and significant geomagnetic response was expected. However, multi-spacecraft observations and modeling demonstrated that this CME deflected almost 40° in longitude and caused only minimal space weather effects. A similar event illustrating the magnitude of CME/ICME longitudinal deflection as reported by Mays et al. (2015). Gopalswamy et al. (2009a) also demonstrated that some halo CMEs that erupt near disk center appear to be associated with driverless shocks near Earth orbit (i.e., an interplanetary shock that is not followed by the discernible driver or a slow-fast stream interaction region) due to significant deflection in longitude away from the Sun-Earth line. In these cases the ICME shock and sheath is detected in situ at Earth, but the driving ejecta is missed completely.
Finally, we illustrate the eastward-deflection effect on fast CMEs by presenting in Fig. 6 the dependence of the difference between the observed and calculated transit times (\(O-C\)) on the central meridian distance (CMD) of their source region. The sample contains 55 fast CMEs, whose transit times are calculated using the Drag-Based Model (DBM) by using the solar wind speed of \(w=450~\mbox{km}\,\mbox{s}^{-1}\) and the drag parameter \(\varGamma=0.2\) (for details see Vršnak et al. 2013). Note that \(O-C>0\) means that the ICME arrived later than expected for the chosen DBM parameters (in the presented case the presumed solar wind speed is too high, causing underestimation of transit times and leading to the average \(O-C\) of 9.6 h). The scatter-plot includes the quadratic least squares fit, characterized by the correlation coefficient of \(cc=0.24\) and the F-test statistical significance of \(P>99\%\). The fit shows that \(O-C\) values are on average larger for CMEs launched closer to the solar limb, meaning that such CMEs are slower than those launched close to the disc center, perhaps indicating that the flank speed is lower than at the nose of the CME. Furthermore, the effect is larger for the eastern-hemisphere events than for western ones, demonstrating the eastward deflection of fast events.
Difference between the observed and calculated transit times (\(O-C\)) of 55 fast CMEs (\(v>500~\mbox{km}\,\mbox{s}^{-1}\)) presented as a function of central meridian distance (CMD). The calculated transit times are based on the Drag-Based Model (DBM) using the solar wind speed of \(w=450~\mbox{km}\,\mbox{s}^{-1}\) and the drag parameter \(\varGamma=0.2\) (for details see Vršnak et al. 2013)
4 CME Rotation
Erupting prominences (or filaments) frequently exhibit a rotation about their rise direction as they ascend in the corona, which leads to a deviation from their original orientation on the solar surface. Strongly rotating filaments display a characteristic “inverse \(\gamma\)” shape, which develops when the legs of the filament cross along the line of sight of the observer (Fig. 7a, b). The direction of the rotation is determined by the sign of helicity of the source region, though there seem to be exceptions (Muglach et al. 2009). When viewed from above, clockwise (anti-clockwise) rotation is typically observed for filaments erupting from source regions with positive (negative) helicity (Green et al. 2007; Fig. 7c). This suggests the conversion of twist into writhe in a kink-unstable magnetic flux rope as a possible mechanism of the rotation (Kliem et al. 2012). Figure 7 shows a confined (or failed) eruption, but significant rotations occur also in cases where the filament fully erupts as part of a CME (Fig. 7d). While filament material outlines only a small fraction of a CME, it is believed to be located close to the axis of the CME flux rope. Thus, the observed rotation of a filament implies that the whole CME flux rope rotates as well, even though outer flux surfaces of the rope may rotate at a smaller rate.
(a): Confined filament eruption on 27 May 2002 observed by TRACE in 195 Å. The filament exhibits an “inverse \(\gamma\)” shape, suggestive of a rotation about its rise direction. (b): MHD simulation of the eruption by Török and Kliem (2005). Colored field lines outline the core of a kink-unstable flux rope with positive helicity (right-handed twist), surrounded by green ambient field lines. (c): Top view on the simulation. The flux-rope core has rotated clockwise by almost 90° with respect to its initial orientation. (d): Fully erupting prominence on 9 April 2008 observed by STEREO Ahead at 10:55 and 11:25 UT. The colored strands were used for a 3D reconstruction. The right panels show field lines from a simulation of the event Kliem et al. (2012). (e): Prominence rotation vs. heliocentric height of the prominence’s leading edge. Panels (a)–(c) adapted from Green et al. (2007). Panels (d)–(e) adapted from Thompson et al. (2012)
Since the magnetic orientation of an ICME upon arrival at Earth is one of the main parameters that determine its geo-effectiveness (as discussed by Kilpua et al. in this issue), it is important to understand the physical mechanisms that cause the rotation, and to quantify the total rotation that CMEs/ICMEs undergo during their travel to Earth, particularly in light of the desire to develop methods to reliably predict the sign and magnitude of \(B_{z}\) at 1 AU. However, obtaining reliable measurements of the total rotation directly from the observations is difficult for several reasons. First, complete observational coverage of the CME and ICME propagation from Sun to Earth is not always available. Second, rotation is hard to recognize in coronagraph images, especially if the CME is observed above the solar limb and no filament is present, though measurements could be obtained for halo CMEs using flux-rope fitting and three-dimensional (3D) reconstruction techniques (e.g., Yurchyshyn et al. 2007; Liu et al. 2010b; Vourlidas et al. 2011). Third, most of the rotation may take place before the CME enters a coronagraphs’ field of view, which requires EUV observations of the associated filament eruption, with the filament material exhibiting a coherent shape for a sufficiently long time. Even if the latter condition is met, reliable measurements of the rotation can only be obtained if the filament either erupts toward the observer or if 3D reconstructions of its shape can be made.
A rare example of direct rotation measurements is shown in Fig. 7d and e. Using observations from both STEREO spacecraft, Thompson et al. (2012) were able to measure the rotation of the prominence that erupted during the “Cartwheel” CME on 9 April 2008, which showed a strong rotation of about 115° up to a height of about 1.5 \(R_{\odot}\) above the surface. Afterward, the rotation direction seemed to reverse slowly. In a similar investigation of an erupting quiescent polar-crown prominence, Thompson (2011) obtained a rotation of at least 90°. Also in this case, the rotation saturated before the prominence became invisible. These results suggest that CME rotation saturates (or even reverses) already in the low corona. In contrast, the studies by, e.g., Yurchyshyn et al. (2007), Liu et al. (2010b), Lynch et al. (2010), and Vourlidas et al. (2011) suggest that CME/ICMEs still exhibit a significant rotation at larger coronal heights and in interplanetary space.
Given the various observational limitations mentioned above, the total rotation of CMEs is typically estimated by comparing the orientation of the pre-eruptive structure on the Sun with the orientation of the axis of the magnetic cloud at 1 AU. Pre-eruptive orientation is inferred from the polarity inversion line of the source region or from filament, sigmoid or coronal loop observations, while the orientation at 1 AU is obtained by fitting 3D flux-rope models to the 1D in situ data, given that the circumstances allow such fitting. Such comparisons of orientation, albeit hampered by some uncertainty, suggest that in many, if not most, cases the total rotation of the CME/ICME remains relatively small. However, as reviewed by Démoulin (2008), cases with total rotations larger than 30° are not uncommon, and very large values of about 120° or more have been reported (e.g., Rust et al. 2005; Dasso et al. 2007; Liu et al. 2008b, 2016; Isavnin et al. 2014; Vemareddy et al. 2016).
Numerical simulations and theoretical considerations have been employed to understand the physical causes of CME rotation and to explain the wide range of rotations observed. Török and Kliem (2003) showed that erupting flux ropes undergo a significant rotation (of more than 90°) when driven by vortex flows at their foot points (used to model rotating sunspots), and suggested that the strong rotation occurred due to the development of the ideal MHD kink instability. Starting from analytical flux-rope models, Fan and Gibson (2004) and Török and Kliem (2005) reported similarly large rotations (up to 120°) as a result of the same instability. Using a similar flux-rope model, Fan (2016) obtained an even larger rotation of almost 180°, i.e., a full reversal of the magnetic field vector at the front of the flux rope, in a recent simulation of the 13 December 2006 event.
Isenberg and Forbes (2007) suggested that the presence of an external shear field surrounding a pre-eruptive flux rope (i.e., of an ambient field component pointing along the axis of the rope) provides a different mechanism for the rotation of a flux rope, once the rope leaves its equilibrium state and rises in the corona. The Lorentz forces that arise from the interaction of the flux-rope current with the external shear field cause a rotation that acts in the same direction as the kink instability. Kliem et al. (2012) confirmed the suggestion by Isenberg and Forbes in a series of MHD simulations, in which they varied the twist within a flux rope, the strength of the external shear field, and the decrease of the ambient potential field with height (by changing the distance between the photospheric polarities that generate that field). Changing these parameters, they obtained flux-rope rotations in a wide range of about (35–170)°. Their study revealed a number of interesting results: (1) For small distances between the polarities, the dominant contribution to the rotation comes from the external shear, even for strongly kink-unstable flux ropes; (2) a moderate rotation in erupting flux ropes is always present due to the conversion of flux-rope twist into writhe (Török et al. 2010), even in the absence of a shear field and of the kink instability; (3) the amount of rotation depends on the slope of the ambient field: the slower the field drops with height, the more the rope rotates. This effect is, however, relatively weak as long as the distance between the polarities is smaller or comparable to the distance of the flux-rope foot points (as it is typically the case on the Sun), but becomes significant if the former distance dominates.
In contrast to these simulations, in which the eruption starts from a fully-developed flux rope, Lynch et al. (2009) modeled CME rotation starting from a sheared arcade, using the breakout model (Antiochos et al. 1999; Lynch et al. 2008). Initially, the arcade rose slowly, without a clear sign of rotation. When it reached a height of about 2 (heliocentric) \(R_{\odot}\), flare reconnection set in and a twisted flux rope was formed. From that point on, the rope rotated at a constant rate of about 30° \(R_{\odot}^{-1}\), and reached a rotation angle of about 50° at a height of 3.5 \(R_{\odot}\). The twist in the rope was low, clearly below the threshold of the kink instability. The authors explained the rotation by the effect of the tension force associated with the sigmoidal shape of the erupting field lines, which acted to straighten out those field lines once the eruption was underway. As the field lines became straight, the rotation still continued due to the angular momentum imparted in the early phase of the eruption. Lynch et al. (2009) did not report how the rotation evolved beyond 3.5 \(R_{\odot}\), so it is not clear at which point a saturation of the rotation may have occurred. Their simulation results agree qualitatively very well with the case observed by Vourlidas et al. (2011), where apparently little or no rotation of the CME occurred below 2 \(R_{\odot}\), and an almost constant rotation (at a rate twice as large as in the simulation) was seen above that height.
Other mechanisms that have been suggested based on observational or numerical studies are the straightening of an initially strong S-shape of a flux rope during its eruption (Török et al. 2010; Kliem et al. 2012); reconnection of an erupting flux rope with the ambient magnetic field (Jacobs et al. 2009; Shiota et al. 2010; Cohen et al. 2010; Thompson 2011; Lugaz et al. 2011); and the alignment of the CME flux rope with the heliospheric current sheet (e.g., Yurchyshyn 2008).
Overall, these studies reveal a substantial number of mechanisms that can cause CMEs to rotate about their direction of propagation. Moreover, as discussed in detail in Kliem et al. (2012), several mechanisms can contribute simultaneously or successively to the rotation in a complicated, parameter-dependent manner, making the quantitative prediction of CME rotation a very challenging task. Specifically, predictions of the sign of \(B_{z}\) at 1 AU merely based on the pre-eruptive orientation of the ejecta have to be taken with care, given the significant number of events that exhibit a large total rotation. Lynch et al. (2009) suggested that the amount of total rotation my be predicted by the degree of “sigmoidality” of the pre-eruptive field, but this approach needs to be tested using observations, and it will likely underestimate the total rotation if other mechanisms such as the kink instability are involved. If most of the rotation typically occurs low in the corona, as suggested by some observations and simulations, then measurements of the rotation of erupting filaments may be utilized to improve (shorter-term) \(B_{z}\) predictions, but the practicability of such an approach needs to be tested as well. Attempts to systematically predict the rotation (and deflection) of CMEs in the corona, based on the properties of the background magnetic field and using analytical flux-rope models, have been recently developed and tested with two observed events by Kay et al. (2015, 2016).
5 CME/ICME Kinematics
5.1 A Brief Overview of CME Kinematics
Here, we examine the details of when, where, and how CMEs/ICMEs accelerate/decelerate in interplanetary space and quantify the kinematics behavior. To that end, observations by the STEREO spacecraft have provided unprecedented opportunities to observed kinematic behavior of ICMEs with multiple views that enable accurate measurements of ICMEs over a large distance. Liu et al. (2010a) have developed a triangulation technique to determine CME/ICME Sun-to-Earth kinematics based on the wide-angle imaging observations from STEREO. The technique initially assumes a relatively compact CME structure simultaneously seen by the two spacecraft. It has no free parameters and can give CME/ICME kinematics (both propagation direction and radial velocity) as a function of distance from the Sun continuously out to 1 AU. This capability is key to probing CME propagation and interaction with the inner heliosphere. Later, Lugaz et al. (2010) and Liu et al. (2010b) realize that the same idea can be applied by assuming CME geometry as a spherical front attached to the Sun. In this case, what is seen by a spacecraft is the segment tangent to the line of sight. The triangulation concept has proven to be a useful tool for determining CME Sun-to-Earth kinematics and connecting imaging observations with in situ signatures (e.g., Liu et al. 2010a,b, 2011, 2012, 2013; Möstl et al. 2010; Lugaz et al. 2010; Harrison et al. 2012; Temmer et al. 2012; Davies et al. 2013; Mishra and Srivastava 2013). Details of when, where, and how CMEs accelerate/decelerate in interplanetary space can be quantified using the kinematics derived with the triangulation method.
Figure 8 shows the comparison of Sun-to-Earth propagation profiles characteristic of slow, fast and intermediate-speed CMEs. The 7 March 2012 CME, with a peak speed of more than \(2000~\mbox{km}\,\mbox{s}^{-1}\) shows a typical three-phase speed profile developed by Liu et al. (2013): an impulsive acceleration for a CME up to 10–15 \(R_{\odot}\), followed by a rapid deceleration for the ICME out to about 50 \(R_{\odot}\), and thereafter a nearly constant speed (or gradual deceleration). The predicted speed at the Earth overestimates the observed speed by about \(250~\mbox{km}\,\mbox{s}^{-1}\), which may be partly due to the large longitudinal separation between the two STEREO spacecraft (\(227^{\circ}\), i.e., both observing the CME from behind the Sun). Note that the observed speed at the Earth is the average solar wind speed in the sheath between the shock and ejecta, which is usually a little smaller than the shock speed at 1 AU. Hence, a better agreement may be achieved if the shock speed (rather than the sheath speed) is used for the comparison. The 12 December 2008 CME with a peak speed of about \(700~\mbox{km}\,\mbox{s}^{-1}\) has a similar profile but different cessation distances for the acceleration and deceleration. Compared with the 7 March 2012 CME, its speed first increased with a lower rate up to about 20 \(R_{\odot}\), then decreased out to 80–90 \(R_{\odot}\), and thereafter became roughly constant, similar to the evolution described by Wood and Howard (2009) for a CME of similar speed. The cessation distance of ICME rapid deceleration (about 50 and 85 \(R_{\odot}\) for the 7 March 2012 and 12 December 2008 CMEs, respectively) is much shorter than the average cessation distance of 0.76 AU (163 \(R_{\odot}\)) inferred indirectly by Gopalswamy et al. (2001b). The Sun-to-Earth propagation profile of the 16 June 2010 CME/ICME exhibited only two phases: an acceleration with an even slower rate up to 25–30 \(R_{\odot}\) followed by a nearly invariant speed at about \(390~\mbox{km}\,\mbox{s}^{-1}\). The predicted speeds at the Earth for the latter two cases are well confirmed by the in situ measurements at 1 AU; the longitudinal separation between the two STEREO spacecraft is \(86.3^{\circ}\) for the 12 December 2008 CME and \(143.6^{\circ}\) for the 16 June 2010 event.
Comparison of Sun-to-Earth propagation profiles between a typical fast ICME (upper), a typical intermediate-speed one (middle) and a typical slow one (lower). The horizontal dashed line indicates the observed speed at the Earth. Adapted from Liu et al. (2016)
In examining the question of CME/ICME kinematics and momentum transfer between the ejecta and the solar wind, there are many aspects that must be considered: First, the ambient solar wind is often highly variable in time and space (e.g., Temmer et al. 2011; Kilpua et al. 2012; Rollett et al. 2012; Liu et al. 2015, 2016). Second, that the Lorentz force driving the CME can sometimes significantly contribute to the CME dynamics up to large distances from the Sun (e.g., Vršnak et al. 2004; Temmer et al. 2011). Third, CME-CME interactions including the affects of CME preconditioning the solar wind, (e.g., Lugaz et al. 2005b; Temmer et al. 2012; Maričić et al. 2014; Rollett et al. 2014; Liu et al. 2012, 2014a,b), which will be taken up in Sect. 9. All of these phenomena affect the CME/ICME propagation and significantly contribute to the uncertainties in predicting the arrival time and impact speed of ICMEs at Earth.
Generally, the CME/ICME propagation can be divided into several phases. The CME initiation phase is most often characterized by swelling and slow rising motion of the pre-eruptive structure, which is usually interpreted as an evolution through a series of quasi-equilibrium states (see, e.g., Vršnak 2008, and references therein). When the slowly evolving structure reaches an unstable state (so called “loss of equilibrium” mechanism of Forbes and Isenberg 1991), the structure starts to accelerate, driven by some form of ideal MHD instabilities such as the kink or torus modes (e.g., and references therein Török and Kliem 2003, 2005; Kliem et al. 2004; Kliem and Török 2006; Démoulin and Aulanier 2010; Olmedo and Zhang 2010; Török et al. 2010). Then follows the take-off stage, which is most often characterized by accelerations on the order of \(100~\mbox{m}\,\mbox{s}^{-2}\), and lasts for \(\sim 1~\mbox{h}\), so the majority of CMEs achieve velocities in the range \(100\mbox{--}1000~\mbox{km}\,\mbox{s}^{-1}\) (e.g., Vršnak et al. 2007; Bein et al. 2011; Yashiro et al. 2004). However, sometimes the take-off phase is characterized by an extremely impulsive acceleration, achieving peak values on the order of \(10~\mbox{km}\,\mbox{s}^{-2}\), but lasting only for several minutes (e.g., Vršnak et al. 2007; Bein et al. 2011). In such events the gradual pre-eruptive evolution is frequently not observed. In fact, in some events a confined-flare type of process leads to fast reconfiguration of the pre-eruptive structure into an unstable configuration and erupts immediately after being formed (Aurass et al. 1999). On the other side of the “spectrum” of event types are very gradual events, characterized by weak accelerations that result in velocities on the order of \(100~\mbox{km}\,\mbox{s}^{-1}\).
The take-off phase imparts the initial velocity, which can be categorized as slow (speeds below \(400~\mbox{km}\,\mbox{s}^{-1}\)) intermediate (speeds between 400 and \(1000~\mbox{km}\,\mbox{s}^{-1}\)) and fast (speeds above \(1000~\mbox{km}\,\mbox{s}^{-1}\)), and it is this speed that largely determines the kinematical evolution in the ensuing “main acceleration” phase. Most generally, in the upper corona and heliosphere, CMEs that are slower than the ambient solar wind continuously accelerate, whereas those that are faster than the wind decelerate (Lindsay et al. 1999; Gopalswamy et al. 2001b; Jones et al. 2007) such that CMEs tend to approach the speed of the ambient solar wind. This acceleration/deceleration tendency is already observable in the upper corona (Moon et al. 2002; Vršnak et al. 2004) and was found by comparing the distribution of coronagraphic CME velocities with the ICME speeds measured in situ at 1 AU (Gopalswamy et al. 2000, 2001b). In the heliospheric range, the velocity profile was directly confirmed by various types of measurements, e.g., by white-light heliospheric imagers such as those made by Coriolis instrument (e.g., Reiner et al. 2005b,a; Tappin 2006; Webb et al. 2006; Howard et al. 2013) onboard the Solar Mass Ejection Imager (SMEI) (Eyles et al. 2003; Jackson et al. 2004) and STEREO-HI (e.g., Liu et al. 2013, 2016), by tracking interplanetary radio type II bursts (e.g., Reiner et al. 2005a,b; Liu et al. 2008b), by analyzing radio interplanetary scintillation (e.g., Manoharan et al. 2001; Manoharan 2006), or by comparing coronagraphic and 1 AU CME/ICME speeds (e.g., Manoharan and Mujiber Rahman 2011).
5.2 Empirical Models of CME/ICME Kinematics
In parallel with progress of numerical propagation models, a number of empirical methods and analytical physics-based models were developed. Although, quite clearly, the future of space weather forecasting lies in numerical modeling, the performance of empirical and analytical methods is currently comparable to, or even slightly better than that of numerical methods. On the other hand, these methods are easy to handle and could be promptly adjusted to the new data incoming in the course of the CME/ICME propagation, i.e., the predictions could be easily refreshed instantaneously with receiving the newest input data. Furthermore, the empirical and physics-based analytical models educe our comprehension of the CME/ICME dynamics, and thus, could help in advancing the numerical methods. In this section, we review a physical background of this approach to the space weather forecasting, which is generally based on empirical studies of the CME/ICME kinematics and/or theoretical considerations of their dynamics.
Results of various statistical studies of the CME/ICME Sun-Earth transit times, reflecting the described general characteristics of the CME/ICME kinematics, can be used to establish empirical methods for predicting the ICME arrival. The simplest one, based on a statistical study of a sample of geoeffective ICMEs, was proposed by Brueckner et al. (1998), saying: “In many cases, the travel time between the explosion on the Sun and the maximum geomagnetic activity is about 80 hours.” To explain this, so-called “Brückner’s 80-hour rule”, corresponding to the Sun-Earth average speed of \(500~\mbox{km}\,\mbox{s}^{-1}\), one has to bear in mind that the Sun-Earth travel time for a typical slow solar wind of the velocity \(\simeq400~\mbox{km}\,\mbox{s}^{-1}\) is about 100 h. On the other hand, most of geoeffective ICMEs are relatively fast, and for the speed of \(1000~\mbox{km}\,\mbox{s}^{-1}\), the transit time is \(\simeq40~\mbox{h}\). Thus, it can be concluded that the 80-hour rule is a consequence of deceleration of fast CMEs in the ambient solar wind.
A somewhat more detailed empirical method, based on the correlation of the Sun-Earth transit times, \(tt\), and the coronagraphic speeds of CMEs, \(V_{\mathrm{CME}}\) is illustrated in Fig. 9a. A similar plot is presented in Vršnak and Žic (2007), and for additional examples see also Manoharan et al. (2004), Schwenn et al. (2005), Manoharan and Mujiber Rahman (2011). In Fig. 9a, the arrival time for a CME of a given coronagraphic speed can be predicted by employing the presented power-law fit. In Fig. 9b, the residuals \(O-C\) are presented to show the span of the prediction errors as a function of \(V_{\mathrm{CME}}\). Inspecting the graph one finds that the errors can be as large as \(\simeq40~\mbox{h}\) and tend to be larger for slower CMEs (however the relative errors are similar for the whole range of \(V_{\mathrm{CME}}\)). The standard deviation of the \(O-C\) distribution is 18 h. The errors can be somewhat reduced by taking into account the source-region location, the CME mass, the associated-flare importance, etc., but not significantly. Note that the same procedure can be applied by using, e.g., the coronal shock velocities inferred from the radio type II burst dynamic spectra.
The scatter-plot in Fig. 9a shows that the power-law fit is characterized by \(tt\propto V^{-0.41}\), which is distinctively different from \(tt\propto V^{-1}\) that would be expected in the case of \(V_{\mathrm{CME}}=\mbox{const}\). This means that slow/fast CMEs have shorter/longer transit times than they would have if propagating at constant speed. Again, this can be attributed to the adjustment of the CME/ICME propagation to the ambient solar wind.
The statistical relationships between the arrival time and various CME parameters measured from coronagraphic observations can be used to employ more sophisticated prediction methods. For example, Sudar et al. (2016) applied the “neural network” approach to determine the most probable transit time using the coronagraphic CME speed and the central meridian distance of the source-region as the input parameters. The analysis, involving a sample of 153 CME-ICME pairs, showed that the average \(tt\) error is \(\simeq12~\mbox{h}\). The \(tt(V_{\mathrm{CME}})\) dependence showed a typical drag-like trend, with acceleration turning to deceleration at \(V_{\mathrm{CME}}\simeq500~\mbox{km}\,\mbox{s}^{-1}\), consistent with the “Brückner’s 80-hour rule” (note that similar holds for the scatter-plot shown in Fig. 9a). Furthermore, the results clearly demonstrate larger \(tt\) for larger CMD, as well as the eastward/westward deflection of fast/slow CMEs. Note that an analogous technique can be applied to forecast the geoeffectiveness of CMEs (e.g., Valach et al. 2009; Uwamahoro et al. 2012; Dumbović et al. 2015, 2016).
The acceleration/deceleration tendency of slow/fast CMEs was quantified by Lindsay et al. (1999) and Gopalswamy et al. (2000, 2001b) by defining a linear relationship between the CME acceleration expressed in \(\mbox{m}\,\mbox{s}^{-2}\) and the CME speed expressed in \(\mbox{km}\,\mbox{s}^{-1}\) as \(a=2.193-0.0054V_{\mathrm{CME}}\), which can be also expressed as \(a= -0.0054(V_{\mathrm{CME}} - 406)\). The range over which the deceleration occurs was estimated to \(r<0.76~\mbox{AU}\). Later on, Manoharan et al. (2004), Manoharan (2006), and Gopalswamy (2009) extended the \(a(V_{\mathrm{CME}})\) relationship to 2nd-degree polynomial forms. The described kinematical forecasting technique, employing various forms of the \(a(V_{\mathrm{CME}})\) relationship, was applied also by, e.g., Manoharan et al. (2004), Gopalswamy et al. (2005), Reiner et al. (2005b), Manoharan and Mujiber Rahman (2011), Salas-Matamoros and Klein (2015), where also forecasting of the CME-driven shocks was included.
5.3 Physics-Based Kinematic Models
The statistical tendency showing that fast CMEs decelerate, whereas slow CMEs accelerate, as demonstrated by Lindsay et al. (1999), and confirmed by Gopalswamy et al. (2001b), Moon et al. (2002), Vršnak et al. (2004), Yashiro et al. (2004), indicates that CMEs tend to adjust their velocity to the ambient solar wind, which could be interpreted as a consequence of “aerodynamic” drag (see, e.g., Cargill et al. 1996; Vršnak 2001; Vršnak et al. 2004, 2008; Cargill 2004; Owens and Cargill 2004; Manoharan 2006). In particular, Vršnak et al. (2004) have shown that the \(a(V_{\mathrm{CME}})\) relationship for the CMEs observed in the LASCO field of view has a quadratic form, providing a strong evidence for the aerodynamic drag effect. Furthermore, they showed that the Lorentz force is decaying rapidly with the height, implying that the drag becomes a dominant force in the heliospheric dynamics of CMEs.
Following observational facts and theoretical considerations, the so called Drag-Based Model (DBM; Vršnak and Gopalswamy 2002; Vršnak et al. 2010, 2013) was developed to describe analytically the dynamics/kinematics of the heliospheric propagation of CMEs. DBM is based on the assumption that the aerodynamic drag is a dominant force that governs the CME propagation in the interplanetary space. Thus, CME/ICME dynamics are described by the equation of motion of the form \(a\equiv\ddot{r}\equiv\dot{v}=-\gamma(v-w)\vert v-w\vert\), where \(a(t)\), \(v(t)\), and \(r(t)\) are the instantaneous CME acceleration, speed, and position, \(w\) is the ambient solar wind speed (generally depending on \(r\), but often used to be constant). The drag parameter \(\gamma\) defines the drag “effectiveness”, usually being expressed as \(\gamma =c_{\mathrm{d}}A\rho_{w}/M\), where \(c_{\mathrm{d}}\) is the dimensionless drag coefficient, \(A\) is the CME cross-sectional area, \(\rho_{w}\) is the ambient solar wind density, and \(M\) is the total CME mass (for details see, e.g., Cargill 2004; Vršnak et al. 2013).
The described equation of motion, as well as its modifications (e.g., Tappin 2006; Borgazzi et al. 2009; Lara and Borgazzi 2009; Shanmugaraju and Vršnak 2014; Shi et al. 2015), was employed to study various aspects of the CME/ICME heliospheric propagation. For example, Vršnak and Žic (2007) and Shanmugaraju and Vršnak (2014) studied the role of the solar wind speed on the CME/ICME transit times, showing that the wind speed is an essential parameter for the CME/ICME dynamics, which results in “Brückner’s 80-hour rule”. Temmer et al. (2011) analyzed the effects of variable/structured solar wind and showed that it significantly affects the CME/ICME kinematics, but also, they demonstrated that in some cases the driving Lorentz force might contribute to CME/ICME dynamics beyond a distance of 100 \(R_{\odot}\). Vršnak et al. (2008) studied the role of the CME mass, and found that in the range of distances covered by LASCO, the drag affects more strongly the propagation of light CMEs, and inferred that the Lorentz force is usually stronger in more massive events. Temmer et al. (2012) and Rollett et al. (2014) employed DBM to investigate how the CME-CME interaction affects the kinematics, whereas Wang et al. (2016b) used it to infer the degree of deflection of a CME/ICME event. Falkenberg et al. (2010) and Vršnak et al. (2010, 2014) compared the DBM and ENLIL ICME arrival-time predictions, and found that results of the two models to be similar accurate.
After being proposed in its initial form by Vršnak and Gopalswamy (2002), the formulation of the basic form of DBM, suited for space-weather forecasting, was completed by Vršnak et al. (2013). In this basic option of DBM, it is taken, approximately, that the CME/ICME cross section increases as \(A\propto r^{2}\), the solar wind density decreases as \(\rho_{w}\propto r^{-2}\) (consistent with the \(w=\mbox{const.}\) approximation), and the mass and drag coefficient are constant. Under this approximation one finds \(\gamma=\mbox{const.}\), which simplifies the equation of motion, providing explicit solutions \(r(t)\) and \(v(t)\). Obviously, the main advantage of so-defined DBM option is its practical use in real-time forecasting of the ICME arrival time and impact speed. However, serious intrinsic drawbacks are related to approximations applied to the DBM: (1) \(c_{\mathrm{d}}\) does not vary with distance (e.g., Cargill 2004), (2) ICME virtual-mass effect is not included (e.g., Bein et al. 2013; Feng et al. 2015; Cargill 2004; Tappin 2006), (3) solar wind properties are taken to be constant in time (e.g., Temmer et al. 2011), (4) and (5) the geometry of the ICME leading edge and location of the source region are not considered, and finally, (6) and (7) the roles of ICME over-expansion (e.g., Riley and Crooker 2004) and the ICME-driven shock (Liu et al. 2013, 2016) are omitted. Some of these drawbacks were removed by Žic et al. (2015), who included CME geometry and source-region location factors, and also took into account more general forms for \(\rho_{w}(r)\) and \(w(r)\). Finally, it should be noted that there are also various forms of empirical forecasting methods that rely on relationships between CME-driven shocks and CMEs, CME-associated flares, or type II radio bursts. Analytical models also exit as well as hybrid approaches that combine components of empirical and analytical models (e.g., Feng and Zhao 2006; Zhao and Dryer 2014; Zhao and Feng 2015; Zhao et al. 2016, and references therein).
6 CME/ICME-Driven Heliospheric Disturbances
6.1 Mass Increase in CMEs/ICMEs
The momentum transfer between ICMEs and the solar wind can be described as “aerodynamic” drag, however this process is strongly affected by the expanding nature of CMEs and ICMEs as shown by Siscoe and Odstrcil (2008). ICMEs tend to expand only slightly faster than the spherically diverging flow of the surrounding solar wind. Consequently, the ejecta has a nearly constant (Sun-centered) angular size while the transverse size increases linearly with distance from the Sun. Siscoe and Odstrcil (2008) found the expansion speed of the ICME flux rope can be greater than the non-radial deflection speed of the solar wind, so that impacted solar wind is unable to move completely around the ICME, and accumulates in the sheath. The deflection flow pattern around an ICME is shown in Fig. 10a, which depicts the non-radial velocity and the trajectory of solar wind parcels ahead of a moderately fast simulated ICME. The impacted solar wind is unable to move around the flux rope, and as a result, the plasma is swept up in the ICME sheath, increasing the total mass of the disturbance.
Solar wind swept up by ICMEs. (a): simulated flow pattern around an ICME from Siscoe and Odstrcil (2008). Color contours show the non-radial velocity while white lines show the trajectory of solar wind parcels ahead of the ICME. The azimuthal deflection speed is insufficient to allow the impacted solar wind to move around the flux rope, and as a result the plasma is swept up in the ICME sheath. (b): plots of the mass and velocity of a simulated ICME as a function of distance from the Sun taken from Lugaz et al. (2005a). The solid line shows the mass of plasma above ambient density, the dashed line shows the mass of low density material while the dot-dash line shows speed of the ICME. Mass and speed follow equal and opposite trends indicating momentum conservation as the solar wind is compressed at the shock and then piles up in the sheath region
This snow-plow effect has been difficult to discern in near-sun coronagraph observations because the swept up mass increase is difficult to distinguish from the sustained outflow of dense plasma with the CME (Bein et al. 2013). However, far from the Sun, the snow-plow affect has recently been measured in STEREO HI observations (DeForest et al. 2013), which confirms prior predictions made with numerical simulations (Manchester et al. 2004b), which established a large mass increase occurring with CME deceleration close to the Sun. Here, the speed of the CME was found to follow an exponential-like decay that asymptotically approaches the speed of the background solar wind, thus verifying the empirical relationship established by Sheeley et al. (1999) (see also Fig. 6). A study by Lugaz et al. (2005a) explicitly calculated this ICME mass from both 3-D structure and from synthetic coronagraph images, the results of which are shown in Fig. 10a. Here, ICME mass and velocity are plotted as functions of distance from the Sun. The CME/ICME mass increased by more than a factor of four from the low corona to 1 AU with the majority (factor of three) of the increase occurring within 30 \(R_{\odot}\). This plasma is compressed and accelerated at the CME-driven shock where a significant amount accumulates in the sheath region between the flux rope and the shock as shown in Fig. 11. As a result of momentum conservation, ICME velocity follows an equal and opposite decrease in magnitude.
Simulated CME-driven heliospheric disturbances. (a): forward and reverse shocks shown with red iso-surfaces, open magnetic field lines colored to denote field strength, and the equatorial plane colored to show flow speed. (b): an iso-surface at 25 nT shows the center of the flux rope above the equatorial plane. (c): the shock structure is shown along a selected magnetic field line ((b): Line 1). Here, density (green) and magnetic field strength (red) are plotted as functions of radius along the field line shown in (black) passing through the shock. (d): Mach number and shock geometry (\(\theta_{BN}\)) plotted as functions of distance for low and high latitude field lines labeled, respectively (Lines 1 and 4 shown in (b))
Manchester et al. (2008) found similar mass increases in their simulation of the 28 October 2003 CME event. In this case, the mass is derived from analysis of synthetic LASCO C2 and C3 coronagraph images, which showed the mass more than doubled to over \(4 \times 10^{16}~\mbox{g}\). Analysis of ICME data from SMEI have found similar mass increases, and in the case of the 28 October 2003 event, the mass reached the extraordinary level of \(13.6 \times 10^{16}~\mbox{g}\) when the ICME reached 1 AU as reported by Jackson et al. (2006). Much of the mass increase is related to the extreme nature of this event, which reached Earth in approximately 20 hours.
6.2 CME-Driven Shocks
High initial speed in conjunction with CME/ICME expansion drive fast-mode waves into the surrounding medium, which may steepen into shocks. These disturbances can propagate far beyond the expanding magnetic driver and are typically observed as forward shocks proceeding ejecta (e.g., Reiner et al. 1998; Wang et al. 2001; Manchester et al. 2008; Wood et al. 2012; Temmer and Nitta 2015; Hu et al. 2016; Liu et al. 2017). CME-driven shocks were originally identified in coronagraph images as faint arcs observed at the outer edges of fast CMEs. An early example is provided by Sime and Hundhausen (1987), who observed a bright loop at the front of a fast CME identified as a shock from its high speed (\(1070~\mbox{km}\,\mbox{s}^{-1}\)), absence of deflections preceding the loop, as well as the absence of stationary legs, and continuously expanding arc. Perhaps the most compelling observational evidence for shocks appearing in LASCO images is presented in Raymond et al. (2000), Mancuso et al. (2002), and Vourlidas et al. (2003). In the case of Raymond et al. (2000) and Mancuso et al. (2002), shocks were observed simultaneously in the low corona \((r < 3~R_{\odot})\) by LASCO, the Ultraviolet Coronagraph Spectrometer (UVCS), and associated type II radio bursts. UVCS gave clear spectroscopic evidence for the presence of shock fronts, while type II radio bursts indicated the presence of shock-accelerated electrons. A connection between type II radio bursts and CME-driven shocks has been established by many studies (e.g., Reiner et al. 1998; Liu et al. 2009, 2013; Reames 2013; Gopalswamy et al. 2013; Nitta et al. 2014; Gopalswamy et al. 2016)
MHD simulations also provide predictions of the appearance of CME-driven shocks in a variety of observing modes. Pagano et al. (2008) modeled the spectral line signatures of CME-driven shocks as they appear in UVCS, and Lugaz et al. (2007), Manchester et al. (2008) simulated the appearance of coronal shocks in synthetic coronagraph images derived from simulations of specific CME events. In the case of Manchester et al. (2008) the simulated shock is directly compared to LASCO observations of the 28 October 2003 event (Vourlidas et al. 2003), which shows agreement with both the general morphology and the quantitative brightness of the shock front as shown in Fig. 12. Here, the increase in brightness at the shock, in both the observed event and the model, is only at a level between \(1\%\) and \(2\%\), even though in the model the density increase at the shock is very near the theoretical limit of 5 (for \(\gamma =1.5\)). The small increase in brightness is due to the relatively short distance along the line-of-sight spanned by the compressed plasma behind the shock front. In this particular example, the shock morphology is largely determined by its interaction with the ambient solar wind and may not be sensitive to the initiation process.
Simulation of the 28 October 2003 CME event adapted from Manchester et al. (2008). (a) and (b): quantitative comparison between the observed (LASCO C2) and simulated coronagraph images, respectively. The color images show brightness relative to (divided by that of) the pre-event corona. (c) and (d): close-ups of the shock front in the observed (LASCO C3) and simulated coronagraph images, respectively, where color contour levels are adjusted to highlight the faint shock front. (e) and (f): line plots of the total brightness and electron density, respectively, where observed values are shown with a solid line and model results are shown with a dashed line. The model shows quantitative agreement with the observed event in both magnitude and morphology of the brightness
Multidimensional simulations have shown how the geometry of the shock front is affected by the structure of the ambient solar wind. For example, Odstrčil et al. (1996), Riley et al. (1997), and Manchester et al. (2005) simulated coronal shocks driven by CMEs initiated at low latitude in solar minimum conditions where the shape of the shock front is strongly affected by latitudinal gradients in solar wind speed and density. Shock fronts propagate significantly faster at high latitude than at low, resulting in a shock surface with a saddle-like structure that is outward-concave in latitude while outward-convex in longitude, as shown in Fig. 11a. Examination of a shock in this configuration by Manchester et al. (2005) revealed that in the concave region, the fast-mode shock deflection away from the shock normal necessarily drives converging flows that lead to a significant density enhancement behind the shock as seen in the line plots in Fig. 11c In complement, line plots in Fig. 11d show the shock Mach number, compression ratio and shock angle (between \(B\) and the shock normal, \(\theta_{BN}\)) as functions of distance from Sun center.
6.3 Flux Rope Over-Expansion and Forward-Reverse Shock Pairs
Flux ropes erupting from the Sun have high internal magnetic pressures that drive CME expansion, a process that may persist well beyond 1 AU. Departures from force-free equilibrium are common in ICMEs, providing an overpressure that can drive expansion (Liu et al. 2006a). In fact, ICME expansion is often observed in situ as declining speed profiles (e.g., Farrugia et al. 1993; Liu et al. 2006a), which are consistent with over-expansion or may be a residual effect of initiation. At high helio-latitudes, measurements by the Ulysses spacecraft led to the identification of a new class of disturbances produced by CMEs coasting through the high-speed wind (Gosling et al. 1994). Bounded by a pair of forward and reverse shocks, these events were also defined by low internal densities, temperatures, and hence, pressures. It was inferred, and confirmed by numerical calculations (e.g., Riley et al. 1997, 2003, 2004; Gosling et al. 1998; Reisenfeld et al. 2003) that the initial high internal pressure drove magnetosonic waves into the surrounding plasma in all directions, which then steepened into shock waves. The shocks are divided into two distinct modes: forward shocks that travel ahead of the ejecta, and in contrast, reverse shocks that propagate back toward the Sun in the rest frame of the ejecta, while actually being carried away from the Sun by the solar wind. In the case of a reverse shock, fast low-density plasma passes through the shock to produce slow, dense, hot shocked plasma on the far side (away from the Sun) of shock. Similar processes occur at low latitudes, but because the ejecta is usually immersed within slow and denser material, the interaction is more asymmetric (Gosling 2000) and occurs without the companion reverse shock.
CMEs associated with forward-reverse shock pairs have many distinguishing properties. First, all of these CMEs are found at high heliographic latitude embedded in high-speed streams. Furthermore, these CMEs have an expanding velocity profile with a central speed approximately the same as the fast ambient solar wind. These CMEs commonly exhibit roughly symmetric increases in pressure, density, temperature, and magnetic field strength down stream of the shock pairs, while the minima of these plasma quantities occur near the centers of the disturbances. The magnetic structures associated with forward-reverse shock pairs have the features of magnetic clouds with shock-enhanced field strengths that are typically a factor of 2 or 3 greater than the ambient solar wind field. Counter streaming electrons suggest closed field lines in the CME, while the ion charge state of CME plasma is more typical of the ambient solar wind rather than a more highly ionized ejecta. While this is the common and ideal structure of CMEs with forward-reverse shocks, some examples are much more irregular and asymmetric (Gosling et al. 1998).
Manchester and Zurbuchen (2006) suggested an alternative explanation for forward-reverse shock pairs in which the reverse shock forms as a result of deflections of the solar wind caused by the passage of the CME. In this model, fast solar wind overtakes slower plasma forming a reverse shock at high-latitude poleward of the ejected flux rope. Apparent signatures of ICMEs, such as enhanced magnetic field strength, low plasma beta, and field direction rotations, are produced by the plasma flows outside of the flux rope. The salient feature of this mechanism is that the reverse shock can only form laterally beyond the ejecta, as shown in Fig. 11a. Further analysis by Manchester and Zurbuchen (2007) shows that the stream-deflection mechanism reproduces many observed characteristics of high-latitude ICMEs bounded by forward-reverse shock pairs, including: magnetic fields with increased strength, rope like rotations, entrained with low pressure, and low density plasma, all contained between nearly symmetric pressure/density enhancements created by the forward and reverse shocks. In this case, stream deflections naturally produce an expanding velocity profile imbedded in the fast wind, and also explain the fast-wind charge state composition found between the shocks, all as a direct consequence of the interaction of solar wind streams deflected by the passage of an ICME.
Apart from shocks, large disturbances in the solar wind can be driven by the passage of the CME ejecta. One example is the draping of the interplanetary magnetic field (IMF) around the ejecta, which forms strong out-of-the-ecliptic magnetic fields (e.g., Gosling and McComas 1987; Odstrčil and Pizzo 1999a). In the case of field line draping, open magnetic field lines are bent around the ICME ejecta and compressed to have enhanced field strengths that may be two or three times as great as found in the ambient solar wind, as was found in Pioneer observations examined by McComas et al. (1988). A CME simulation showing such draping is shown in Fig. 11. Here, open field lines are colored to show field strength, which is particularly enhanced on the Sun-ward side of the flux rope. Another important disturbance is found trailing fast ICMEs, the large rarefactions that form in the trailing wake of ICMEs (e.g., Gosling and McComas 1987; Riley and Gosling 2007; Liu et al. 2014a). Here, the ICME outruns the material following it, forming an expansion wave (or rarefaction region) of low density (Riley et al. 1999). Sunward of fast CMEs, the magnetic field is also distorted away from the nominal Parker Spiral configuration into a near radial configuration (e.g., Riley and Gosling 2007; Liu et al. 2014a).
7 Magnetic Evolution
7.1 MC/ICME Distortion
Although suspected, the substantial distortion that ICMEs undergo was not fully realized until the Ulysses mission, when combined with Geotail, provided the first multi-spacecraft in situ measurements of the same CME at significantly different helio-latitudes and distances from the Sun (Hammond et al. 1995). Liu et al. (2006b) similarly analyzed Ulysses in situ observations to find that MCs are highly flattened. At solar minimum, MCs have curved cross sections that are outward concave, while at solar maximum the MCs are outward convex. The results are indicative that the MCs are deformed by their interaction with the ambient solar wind. White-light observations of ICMEs at large elongation made with SMEI found a relatively small number of ICMEs to be in the shape of outward-concave arcs, consistent with deformation solar wind velocity shear (Kahler and Webb 2007). Liu et al. (2008c) found that at solar minimum eight out of eleven MCs were outward concave as determined by the in situ measurement of the elevation angle of the MC normal with respect to the solar equatorial plane. Finally, as reported by Savani et al. (2010), coronagraphs onboard the STEREO-B observed the distortion of the leading edge of the CME/ICME event of 14 November 2007, which began close to the Sun and progressively increased as the CME moved to large elongation.
Subsequent numerical simulations provided ever-increasingly more accurate explanations for how these deformations evolve as the flux rope transits the space from the Sun to the Earth and beyond (e.g., Riley et al. 1997, 2003; Odstrčil and Pizzo 1999b; Manchester et al. 2004a). These simulations show the deformation occurring from the exchange of momentum between the ejecta and the surrounding medium. Early on, radial expansion of the ejecta naturally provides a flow that evolves the erupting flux rope in a nearly self-similar fashion (e.g., Gibson and Low 1998). This simple evolution breaks downs and the ICME flattens as the solar wind inhibits the expansion of the MC whose radial extent becomes more nearly constant, while simultaneously, the spherically diverging flow causes the transverse extent to increase linearly with distance from the Sun. The aspect ratio of the ejecta, (transverse versus radial size) begins to increases with time, which simulations show to be particularly noticeable beyond 40 \(R_{\odot}\).
Simulations also illustrate the deformation of CMEs by bimodal ambient solar wind typical of solar minimum (e.g., Gosling 1999; Odstrčil and Pizzo 1999b; Riley and Crooker 2004; Manchester et al. 2004a). At the largest scales, ICMEs are deformed into a highly flattened, concave-outward structure by the latitudinal velocity gradient (speed increasing with latitude) that serves to carry the high-latitude portion of the flux rope to greater distances. An example of a 3-D numerical simulation of a CME in a bimodal wind is shown in Fig. 13. Here, the ejected flux rope is shown from two perspectives at 4.5 and 60 hours after initiation in the top and bottom rows, respectively. Close to the Sun, the flux rope reflects its original shape greatly expanded. As the flux rope approaches 1 AU, it appears flattened and outward-convex with field lines connected to the IMF. At solar maximum, the solar wind velocity is relatively slow and unstructured so MC are deformed by aerodynamic drag to a convex shape, which is particularly true for fast CMEs (e.g., Manchester et al. 2008).
Flux rope structure and evolution in a simulated CME. The magnetic field of a CME simulated with a spheromak flux rope is shown at 4.5 hours (top row) and 60 (bottom row) hours after initiation. (a) and (c): simulation results seen viewed from above (\(+z\) axis). (b) and (d): side and oblique views of the simulated CME. Close to the Sun, the flux rope evolves in a nearly self-similar fashion. Far from the Sun, the flux rope is deformed to an outward-convex crescent, while the outer field lines have reconnected with the IMF
7.2 Flux Rope Erosion
Magnetic reconnection is ubiquitous in the solar wind, from large-scale structures such as the heliospheric current sheet (e.g., Gosling et al. 2005, 2006) to the smallest scale associated with magnetic turbulence. So it should be no surprise that there are clear signatures that reconnection occurs with magnetic ejecta in interplanetary space (Farrugia et al. 2001). Reconnection between the IMF and the ICME field is most prone to occur where more-nearly-opposed fields are brought into contact, which for a highly twisted horizontal flux rope would tend to be either at the front or rear of the magnetic flux rope. Dasso et al. (2006) point out that such reconnection will reduce the magnetic flux of a rope, resulting in an imbalance of poloidal flux, a process called flux rope erosion. A schematic of this process is shown in Fig. 14 adapted from Ruffenach et al. (2012). Here, Fig. 14a shows the flux distribution of a cylindrical flux rope prior to reconnection with the IMF, where as Fig. 14b shows the outer layers of the flux rope peeled away by reconnection, leaving an imbalance in poloidal flux.
Schematic of MC erosion adapted from Ruffenach et al. (2012). The examples on the left/right show a flux rope with no erosion/erosion and balanced/unbalanced poloidal flux \(B_{y}\) component
The analyses of MCs in many studies (e.g., Chané et al. 2005; Dasso et al. 2006, 2007; Ruffenach et al. 2012, 2015; Lavraud et al. 2013, 2014) have revealed the predicted features of flux rope erosion. Dasso et al. (2006) examined the 21 January 2005 ICME and found a large imbalance in \(B_{z}\) that they attribute to magnetic reconnection. Examination of the 9 November 2004 9 ICME by Dasso et al. (2007) revealed a long lasting tail (more than a day) of flux that is interpreted to be the result of magnetic reconnection at the front (and not at the rear) of the MC. A similar tail was found with the 18–20 October 1995 ICME, where the remaining magnetic field is interpreted as a partially reconnected flux rope by Dasso et al. (2006). Ruffenach et al. (2012) and Lavraud et al. (2014) closely examined several ICME events and found evidence (including reconnection jets) that magnetic reconnection occurred on the front side of the MC flux ropes, leading to their erosion. Ruffenach et al. (2012) examined the 19–21 November 2007 event with multi-spacecraft including STEREO A, B, ACE, Wind and THEMIS to establish that the axis of the rope was near the equatorial plane, proving that flux imbalance is not the result of high flux rope inclination (Lepping and Wu 2007). Ruffenach et al. (2015) analyzed the magnetic flux content of 50 MCs and found erosion at the front or rear in similar proportions with an average of 40% of the total azimuthal magnetic flux removed by reconnection. 30% of the magnetic clouds showed signs of reconnection.
Numerical simulations have also been used to study magnetic erosion in CMEs (e.g., Schmidt and Cargill 2003; Lugaz et al. 2013; Manchester et al. 2014a,b). The earliest examples are two-dimensional numerical experiments conducted by Schmidt and Cargill (2003), where the cylindrical flux rope was made to move out through open flux and through the current sheet. It was found that reconnection occurs on the lead/trailing edges of the flux rope in the case of fast/slow CMEs, and that the reconnection rate increases with the relative speed of the rope. An example from this simulation is shown in Fig. 15a, where the flux rope is initially traveling at 1.5 times the solar wind speed through the current sheet. Reconnection is manifest by the formation of small islands on opposite sides of the flux rope.
Simulations of MC erosion. (a): results of the 2-D simulation of Schmidt and Cargill (2003). Here, magnetic reconnection with the IMF occurs near the top and bottom front of the flux rope resulting in the formation of a pair of magnetic islands. (b): the results of the 3-D simulation of Manchester et al. (2014a). In this case, reconnection occurs at both the front and back sides of the flux rope
The magnetic reconnection rate is greatest close to the Sun where field strengths and Alfvén speeds are highest, with the rate decreasing with distance from the Sun. This evolutionary trend was shown in Manchester et al. (2014b), where the poloidal flux of the ejected rope is integrated and plotted as a function of time. Here, 14% of the total flux is lost during the first hour after initiation followed by additional 6% loss as the ICME propagates to 1 AU. A more extreme example of CME-IMF reconnection is found in the simulation of the 15 May 2005 ICME (Manchester et al. 2014a) where the poloidal field of the ejected rope is in the opposite direction of the surrounding streamer belt. Figure 15b provides a global view of the reconnection between the MC and the IMF occurring primarily at the north and south extremities of the flux rope. As the ICME approaches 1 AU, the MC is largely reconfigured by reconnection, yet the portion passing Earth retains the \(B_{z}\) orientations of the original rope and reproduces in situ observations of total field strength and \(B_{z}\). As the result of reconnection, a long duration of \(B_{z}\)-south trails behind the MC. Lugaz et al. (2013) examines simulations of reconnection between multiple CMEs, which will be discussed in Sect. 9.
A magnetic flux rope can also be distorted and the flux redistributed to produce localized flux imbalances and give the appearance of flux rope erosion. Manchester et al. (2014b) provides a CME simulation exhibiting an extreme case of flux redistribution that mimics flux rope erosion. In this case, as a fast ICME propagates through the solar wind, it undergoes strong deceleration, as previously discussed in Sect. 5. As a result, there is a tendency for denser filament material to move forward through the decelerating flux rope. Manchester et al. (2014b) have found that such movement is accompanied by azimuthal flows that can transport poloidal flux away from the nose of the ICME producing a large imbalance in \(B_{z}\), giving the appearance of flux rope erosion, while, in fact, the majority of the flux remains intact. In this example, reconnection did occur with the IMF, but only removed less than twenty percent of the toroidal flux of the rope at 1 AU. Evidence of this behavior may be found in the 21 January 2005 ICME. In situ observations of this event show very dense cold plasma with a charge state composition consistent with filament material following immediately behind the ICME sheath, and most significantly the MC is almost entirely unbalanced in poloidal flux.
8 Plasma Evolution
Plasma that escapes the corona is heated to temperatures near 1.5 MK, which is sufficiently high to partially ionize all heavy elements. The freeze-in location of each ion charge state (typically within 4 \(R_{\odot}\)) depends both on ionization and recombination rates, which are functions of plasma density and temperature. The in situ charge state composition, therefore, complements remote observations and provides a unique and very important measure of the heating and expansion of the solar wind near the Sun (e.g., Fenimore 1980; Galvin 1997; Henke et al. 1998; Gloeckler et al. 1998; Zurbuchen et al. 2004; Lepri and Zurbuchen 2004; Reinard 2005; Zurbuchen and Richardson 2006). Used in combination, ion freeze-in states can be used to map out the heating and expansion rates of CMEs and as well as the ambient solar wind (e.g., Buergi and Geiss 1986; Esser and Edgar 2001; Lynch et al. 2011; Jin et al. 2012)
Numerous studies have shown the value of ion charge states as identifiers of ICMEs, finding that MCs are more likely to exhibit a higher composition of elevated charge states than non-MC ICMEs (e.g., Henke et al. 1998). Figure 16 (adapted from Zurbuchen and Richardson 2006) provides an example of ICME charge state signatures shown in conjunction with the MHD plasma quantities, supra-thermal electron populations and magnetospheric DST. Enhanced helium abundance (\(\mbox{He}^{2+}\)) has been observed in ICMEs since the early space era (Hirshberg et al. 1972; Borrini et al. 1982), and roughly 50%–70% ICMEs have enhanced iron charge states up to \(\mbox{Fe}^{16+}\) and average \(\mbox{(Q)Fe}> 12\) (e.g., Bame et al. 1979; Fenimore 1980; Lepri et al. 2001; Zurbuchen et al. 2004). Enhanced charge states of oxygen are also found in ICMEs (e.g., Galvin 1997; Henke et al. 2001) with \(\mbox{O}^{7+}/\mbox{O}^{6+} > 1\) (Richardson and Cane 2004a). The elevated charge states of oxygen and iron (Lepri and Zurbuchen 2004) signify an intense heating of plasma close to the Sun, while the cause of the helium enhancement is less clear. Neugebauer and Goldstein (1997) ascribe it to a “sludge removal phenomenon” whereby the helium settling at the base of the solar wind flux tube is cleared out by the CME eruption. Bimodal charge state distributions are also found in ICMEs where both elevated charge states associated with flare heated plasma are found along with ambient solar wind charge states (Gruesbeck et al. 2012). This condition suggest that either the material expands in such a way that two temperature peaks form (e.g., Gruesbeck et al. 2011) or two plasmas mix (e.g., Lepri et al. 2012).
Solar wind plasma and magnetic field parameters across an ICME (after Zurbuchen and Richardson 2006). The vertical green line marks the arrival time of the ICME-driven shock, and two vertical pink lines indicate the ICME interval. This event can be classified as a magnetic cloud, showing an enhanced, smoothly-rotating magnetic field. Other ICME signatures are also present: (bidirectional electrons) BDEs (with the interval indicated by the horizontal bar), depressed proton temperatures, declining solar wind speed profiles, He/proton abundance enhancements, enhanced oxygen and iron charge states and Mg/O ratio, cosmic ray depressions (\(\gtrsim60~\mbox{MeV}\) particle count rate), and geomagnetic storms (indicated by the \(D_{st}\) index)
A small number of ICMEs have also been identified with intervals of highly elevated levels of unusually low ion charge states, such as \(\mbox{He}^{+}\) (e.g., Gosling et al. 1980; Illing and Hundhausen 1985; Burlaga et al. 1998). In some cases, the \(\mbox{He}^{+}/\mbox{He}^{++}\) ratio may reach 0.1, which is nearly ten thousand times greater than ambient levels. The singly charged He particles imply that these cold events originate from a low temperature region, possibly a cool, dense filament in the solar atmosphere. This assertion has found further support from Lepri and Zurbuchen (2010) who found unusually cold material that they attribute to prominence material that escaped the corona without further heating. Such events remain rare compared to the observed fraction of CMEs associated with prominence eruptions. A possible example is the 21 January 2005 ICME event, where both charge state analysis and simulation (Kozyra et al. 2013; Manchester et al. 2014b) strongly suggest that cold dense prominence material associated with a fast CME impacted the Earth.
Electrons, by contrast, often show strange thermodynamic behavior across the ICME plasma. The electron temperature, \(T_{e}\), is often larger than the proton temperature within ICMEs, with a typical ratio \(T_{e}/T_{p} > 3\) (Liu et al. 2005), so the thermal pressure is dominated by the electron component. However, \(T_{e}\) tends to be lower than the proton temperature in the sheath regions of ICMEs with preceding shocks (Skoug et al. 2000), analogous to planetary magnetosheaths. A possible explanation is that protons resonate at their gyro-frequency with magnetic fluctuations induced at the preceding shock and thus gain energy from the fluctuations, while electrons cannot do so. Another explanation is that the shocks are super-sonic relative to the protons, but subsonic relative to the electrons, and as a consequence, the protons are preferentially shock heated (Kosovichev and Stepanova 1991; Manchester et al. 2012; Jin et al. 2013). Another feature of electron thermodynamics is that the polytropic index \(\gamma_{e} < 1\) inside ICMEs (Gosling 1999), the physical cause of which remains a mystery.
The radial evolution of \(T_{\alpha}/T_{p}\) and \(v_{\alpha p}\) from 0.3 to 5.4 AU is shown in Fig. 17. The differential streaming in the solar wind (lower panel) shows a fairly steady decrease with distance, probably due to the accumulative effect of Coulomb collisions. In contrast to the solar wind, the ICME \(v_{\alpha p}\) decreases to less than \(10~\mbox{km}\,\mbox{s}^{-1}\) by 0.4 AU, which indicates the importance of Coulomb collisions inside ICME plasma. The temperature ratio \(T_{\alpha}/T_{p}\) of ICMEs is larger than that of the solar wind inside 1 AU but roughly the same magnitude beyond 1 AU. The little variation of the ICME temperature ratio with distance implies the existence of a local mechanism responsible for heating the alphas. One may consider that the free energy associated with the differential streaming is converted into the thermal energy of the plasma. It is not likely that the free energy preferentially goes to alphas through Coulomb collisions. In addition, the differential speed within ICMEs is very small outside about 0.4 AU, but the temperature ratio is conserved at much larger distances. These results, in particular the collisional nature of the ICME plasma which has been ignored in previous studies, have significant consequences for modeling the realistic thermodynamics of ICMEs. The readers are directed to Liu et al. (2006a) for more detailed discussions.
Radial variations of the temperature ratio and differential speed between alphas and protons for ICMEs and solar wind (after Liu et al. 2006a). For ICMEs, the horizontal bars indicate the bounds of the bins while the error bars show the standard deviation of the parameters within the bins. The solar wind levels are represented by the average values over 0.1 AU bins within 1 AU and 0.5 AU bins beyond. All the data are within \(\pm20^{\circ}\) in latitude
Recent advancements in techniques for analyzing the solar wind composition measured have provided the most comprehensive ionic composition data to date, which set solid constraints on the heating and acceleration of the solar wind and ICMEs. These observations are even more powerful by combining them with remote observations of coronal plasma, which reveals details about CME expansion and solar wind source regions (e.g., Gruesbeck et al. 2011; Jin et al. 2012). These data are further complemented by recent simulations (Lynch et al. 2011) of ICME and solar wind (Jin et al. 2012) charge state composition.
Filaments (or more specially the filament channel) are at the heart of the CME energy source, where highly sheared magnetic fields run nearly parallel to the PIL in an energized state (Manchester 2001, 2007, 2008; Fang et al. 2010, 2012). Here, filaments form as cold dense concentrations of plasma suspended in the corona at chromospheric temperatures with densities 100 times greater than the surrounding corona. Filament material is typically taken to be the source of the dense core of the canonical three-part structure that is often wholly expelled in CMEs (Hundhausen 1993; Gibson and Low 1998). Gilbert et al. (2000) found 94% of erupting filaments were in association with CMEs and of those, 84% were found to have a portion of the filament escape the corona and contribute to the ejected CME plasma. However, connecting the components of the CME three-part density structure to in situ counterparts is often not possible. While a pileup of plasma is commonly found ahead of the flux rope, signatures of a cavity are not always clear and filament material is most often not detectable. ICME expansion tends to produce densities (and kinetic temperatures) lower than that of the surrounding solar wind (Liu et al. 2006a). However, there are often density fluctuations within the cloud that attain or exceed the ambient value (Burlaga 1981; Burlaga et al. 1982), which may obscure the signatures of the cavity.
A key to distinguishing different CME structures is the plasma charge state composition, which is determined by the ionization environment. Rapid decreases in mass density and collision rates cause the charge state to become fixed, or frozen in, beyond a few solar radii (e.g., Hundhausen et al. 1968; Ko et al. 1999; Kilpua et al. 2013). Given its relatively cool temperatures, filament material in the corona is dominated by heavy ion charge states such as \(\mbox{C}^{2-3+}\), \(\mbox{O}^{2-4+}\) and \(\mbox{Fe}^{4-6+}\), which have been directly observed with SOHO/UVCS (e.g., Lee and Raymond 2012). Filament material can be ejected into interplanetary space where it can be distinguished by these ionization states (Schwenn et al. 1980; Burlaga et al. 1998; Skoug et al. 1999; Yao et al. 2010). Gopalswamy et al. (1998) provides a clear example of the identification of low charge state filament material in the 07–11 February 1997 CME/ICME event. Here, filament material was observed in SOHO/LASCO C2 coronagraph images at the base of the CME, while corresponding dense filament material was found in situ in the Sun-ward side of a magnetic cloud containing relatively high abundances of \(\mbox{Fe}^{5+}\) and \(\mbox{Fe}^{6+}\).
While filament eruptions are commonly associated with CMEs, it is surprising that convincing in situ charge state evidence of filament material is rarely found. Lepri and Zurbuchen (2010) reviewed 10 years of data from SWICS/ACE and found only 4% of ICMEs (11 events of the total) with charge state consistent with filament material. The relative paucity of in situ filament material observations may have been resolved by recent observations. Lee and Raymond (2012) found that low-ionization filament material (as observed by UVCS) covers only a few percent of the total area of CMEs, which is consistent with the low rate of in situ detection. This explanation is further corroborated by remarkable observations by Wood et al. (2016), which found that unlike most plasma in the CME, the filament material does not expand to fill space but fragments into high-density parcels of plasma that ballistically propagate through the heliosphere. Furthermore, in the case of fast ICMEs that strongly decelerate, the dense filament material maintains a high velocity and moves radially outward through the body of the CME, just as first predicted by Manchester et al. (2014b).
9 CME-CME Interaction
ICME properties may be strongly influenced as they propagate between the Sun and the Earth, in particular when they interact with other ICMEs or with corotating interaction regions (CIRs) and fast wind streams (Prise et al. 2015; Winslow et al. 2016; Liu et al. 2015, 2016). Two of the main sources of successive CMEs are homologous and sympathetic eruptions. Solar observations have revealed that recurrent CMEs occur from the same active region, often associated with homologous flares (Schmieder et al. 1984; Moon et al. 2003; Liu et al. 2014a,b; Wang et al. 2014a). Sympathetic CMEs, when the eruption of one CME triggers another, is another source of successive CMEs in relatively close angular and temporal separation (see Fig. 18a), revealed by means of observations and simulations to occur regularly (Schrijver and Title 2011; Török et al. 2011; Wang et al. 2016a).
MHD simulations and observations of CME-CME interaction. (a): Simulations of sympathetic eruptions from Török et al. (2011). (b): STEREO-A/HI1observations of two CMEs propagating in the inner heliosphere. The two CMEs have similar directions and interact and deflect each other on their way to Earth Lugaz et al. (2012). (c): Radial size of simulated CMEs before and during their interaction depending on their initial relative orientation, as adapted from Lugaz et al. (2013). (d): 3-D view of a MHD simulation of two interacting CMEs from Shen et al. (2013)
During their Sun-to-Earth propagation, the interaction of successive ICMEs may take a variety of forms: (i) multiple CME-driven shock waves may interact without the associated ejecta interacting, (ii) one shock wave may interact with a preceding magnetic ejecta, or (iii) the successive magnetic ejecta may interact and/or reconnect. Early detections of multiple flares and complex ejecta in the interplanetary space revealed in the 1970s and 1980s that CME-CME interaction is a frequent occurrence. For example, the series of seven flares in 72 hours in early August 1972 have been extensively analyzed (Dryer et al. 1976; Intriligator 1976; Ivanov 1982). Another example is the study by Burlaga et al. (1987), in which the authors describe a variety of compound streams resulting from the interaction of a transient with another transient or with a solar wind stream. The authors concluded that “the interaction between two fast flows, is in general a nonlinear process, and hence, a compound stream is more than a linear superposition of its parts”. An early numerical investigation is that of Vandas et al. (1997), who simulated the interaction of a shock wave with a magnetic cloud in 2.5-D MHD. The authors noted that the shock propagation results in a radial compression of the magnetic cloud, a change of its aspect ratio, and acceleration as well as heating of the cloud.
Direct observations of CME-CME interaction became possible in the mid-1990s with the larger field-of-view of LASCO/C3 (up to \(32~R_{\odot}\sim 0.15~\mbox{AU}\)), which yielded the first reported white-light observations of CME-CME interaction (Gopalswamy et al. 2001c). Interest in this topic grew following this initial report (e.g., see Reiner et al. 2003), and from debates about the association of interacting CMEs with large solar energetic particle (SEP) events (Gopalswamy et al. 2002; Richardson et al. 2003). In solar cycle 24 (2008–present), observations with high spatial and temporal resolution by SDO have returned the study of sympathetic eruptions to central stage. The development of heliospheric imaging with the Solar Mass Ejection Imager (SMEI, Eyles et al. 2003; Jackson et al. 2004) and the Heliospheric Imagers (HIs, Eyles et al. 2009) onboard STEREO have led to a large increase in the number of published cases of ICME-ICME interactions being remotely observed in the past 10 years (see Fig. 18b). From the first remote detection in 2001 to routine remote observations in the late 2000s, numerical simulations have been used to fill the gap between the upper corona and the near-Earth space (Wu et al. 2002; Odstrcil et al. 2003; Schmidt and Cargill 2004; Lugaz et al. 2005b; Xiong et al. 2006). In the past decade, the combination of remote observations, in situ measurements and numerical simulations has resulted in a deeper understanding of the physical processes occurring during CME-CME interaction.
9.1 Compression and Reconnection Between CMEs
One of the essential aspects of CME-CME interaction is the change in CME properties, such as their speed, size, expansion rate, etc. CME-CME interaction directly affects space weather forecasting, by modifying the hit/miss probability and the expected arrival time of a CME (changes in the CME speed and direction) and by modifying the expected geomagnetic responses (changes in the CME internal magnetic field).
Here, we first discuss the changes in the CME internal properties, such as radial extent and magnetic field strength, associated with the compression and reconnection between CMEs. The radial size of a CME can be derived from remote observations (Savani et al. 2009; Nieves-Chinchilla et al. 2012; Lugaz et al. 2012). These observations and numerical simulations confirmed that the radial extent of the leading CME plateaus during the main phase (i.e. when the speed of both CMEs changes significantly) of interaction (Schmidt and Cargill 2004; Lugaz et al. 2005b, 2012, 2013; Xiong et al. 2006) and this is typically associated with a “pancaking” of the leading CME (Vandas et al. 1997). In Lugaz et al. (2005b), the authors discussed how the shock propagation through the leading CME is the main way in which the expansion slows. In situ measurements at 1 AU of shocks propagating inside CMEs (Lugaz et al. 2015) revealed the compression of the leading CME by the overtaking shock and CME (Wang et al. 2003b; Farrugia and Berdichevsky 2004; Liu et al. 2012, 2014c). It is, as yet, unclear whether this compression changes for cases when the overtaking CME drives a shock or not. What clearly changes is the resulting expansion of the leading CME after the end of the main interaction phase (i.e. after the shock exited the ejecta). In Xiong et al. (2006), the authors found that the leading CME over-expands to return to its expected size; as such the compression is only a temporary state. This was confirmed by a statistical study of the radial size of magnetic ejecta at different heliocentric distances (Gulisano et al. 2010). In one case study, similar results were found: remote observations indicated compression but, a day after the interaction ended, when the CME impacted Earth, the in situ measurements indicated a typical CME size (Lugaz et al. 2012). In numerical simulations with two magnetic ejecta, the rate of over-expansion is found to depend on the rate of reconnection between the two ejecta (see Fig. 18c); as such, it depends on the relative orientation of the two magnetic ejecta (Schmidt and Cargill 2004; Lugaz et al. 2013), but also probably on their density. Associated with ICME compression is the enhanced magnetic field inside the ICMEs as revealed by in situ measurements. Liu et al. (2014a) find that an extremely enhanced field strength, larger than 100 nT, can be produced by CME-CME interactions.
CME-CME “cannibalism”, i.e. the total coalescence of two CMEs, was reported based on LASCO images by Gopalswamy et al. (2001c). However, because coronagraphs and white-light imagers only give direct information about a CME density structure, it is unclear whether this coalescence is associated with a total reconnection of one CME’s magnetic flux or not. Known magnetic reconnection rates and CME magnetic flux makes it unlikely that total reconnection is a common occurrence until beyond Earth’s orbit. The potential full coalescence of two ejecta into one was discussed in a few studies (Odstrcil et al. 2003; Schmidt and Cargill 2004; Chatterjee and Fan 2013) but has not been investigated in detail with realistic reconnection rates. In situ measurements of transients resulting from the interaction of two CMEs sometimes contain a period of weaker and more turbulent magnetic field, higher in density and temperature, resulting in a higher plasma \(\beta\) (Wang et al. 2003a). These periods have been explained by ongoing or past reconnection between the two magnetic ejecta; however multi-spacecraft measurements or a successful Walén test (Paschmann and Sonnerup 2008) would be required to assert that reconnection is occurring. No such case has been reported yet.
In Lugaz et al. (2013), the authors considered the interaction of two CMEs with axial fields perpendicular to one another by means of MHD simulations, and found that the resulting ejecta appeared as one of a single, extended but seemingly isolated, CME with a complex magnetic field rotation. Such events can sometimes be measured at 1 AU (Dasso et al. 2009; Lugaz and Farrugia 2014) and may be related to these instances of CME-CME cannibalism.
9.2 Momentum Transfer Between CMEs
Many studies have investigated the momentum transfer between CMEs during their interaction, both through remote observations and numerical simulations (Schmidt and Cargill 2004; Lugaz et al. 2005b; Liu et al. 2012; Shen et al. 2012; Mishra et al. 2015a,b; Colaninno and Vourlidas 2015). CMEs are large-scale magnetized plasma structures propagating in solar wind, and therefore, the momentum transfer between CMEs is complex for a variety of factors: (i) depending on the speed of the CMEs, the interaction between two CMEs may involve zero, one or two CME-driven shocks, some of which may dissipate during the interaction, (ii) the interaction takes at least one Alfvén crossing time of a CME, i.e. typically 8–24 hours, (iii) the CME speeds can change significantly, even at large distances from the Sun, due to their interaction with the solar wind (Manchester et al. 2004a; Temmer et al. 2011; Liu et al. 2013), (iv) CME-CME interaction is inherently a three-dimensional process, and the changes in kinematics may differ greatly depending on the CME part that is considered (Shen et al. 2012; Temmer et al. 2014). Using numerical simulations (see Fig. 18d), it is somewhat possible to control for some of these effects, for example, by performing simulations with or without interaction but with identical CME properties, and by knowing the velocity field in the entire 3-D domain (Shen et al. 2013, 2016).
As CME-CME interaction involves a faster CME overtaking a slower CME, the end result is to homogenize the speed, as was noted from in situ measurements in Burlaga et al. (2002), Farrugia and Berdichevsky (2004) and through simulations by Schmidt and Cargill (2004) and Lugaz et al. (2005b), among others. It has been found to occur independently of the relative speeds of the two CMEs. Based on this finding, one of the main issues related to momentum transfer is to understand what determines the final speed of the transient that was formed by the CME-CME interaction. In an early work, Wang et al. (2005) found that, in the absence of CME-driven shock waves, the final speed is determined by that of the slower ejecta, whereas Schmidt and Cargill (2004) and Lugaz et al. (2005b) found that when the CMEs drive shocks, the final speed is primarily determined by that of the faster ejecta, as the shock’s propagation through the first magnetic ejecta accelerates it to a speed similar to that of the second ejecta. Work combining remote observations and numerical simulations lead us to conclude that the final speed of the transient depends on the relative masses of the CMEs, as well as their approach speed (Poedts et al. 2003; Shen et al. 2016).
In addition to changes in velocity, CME-CME interaction may result in the deflection of one CME by another (Xiong et al. 2009; Lugaz et al. 2012; Shen et al. 2012). Combining these works, it appears that the deflection can reach up to \(15^{\circ}\) when the two CMEs are initially about \(15\mbox{--}20^{\circ}\) apart. Such angular separations are quite frequent between successive CMEs, as it corresponds to a delay of about one day for two CME originating from the same active region (due to solar rotation). This change in direction must be taken into account when deriving the changes in velocity, as done in Shen et al. (2012) and Mishra et al. (2016).
9.3 Changes in the Shock Properties
In addition to changes in the CME properties, any fast forward shock propagating inside the overtaken magnetic ejecta encounters highly-varying and unusual upstream conditions, affecting the shock properties. Most of what is known about the changes in shock properties was learned from numerical simulations; however, there have been many reported detections of shocks propagating inside a magnetic cloud or magnetic ejecta at 1 AU (Wang et al. 2003c; Collier et al. 2007; Richardson and Cane 2010a; Liu et al. 2012, 2014c; Lugaz et al. 2015, 2016).
Vandas et al. (1997) noted that a shock propagates faster inside a magnetic cloud due to the enhanced fast magnetosonic speed inside, which may result in shock-shock merging close to the nose of the magnetic cloud but two distinct shocks in the flanks. Odstrcil et al. (2003) noted that associated with this acceleration, the density jump becomes smaller. Lugaz et al. (2005b) performed an in-depth analysis of the changes in the shock properties, dividing the interaction into four main phases: (i) before any physical interaction, when the shock propagates faster than an identical isolated shock due to the smaller density in the solar wind, (ii) during the shock propagation inside the magnetic cloud, when the shock speed in a rest frame increases and its compression ratio decreases, confirming the findings of Odstrcil et al. (2003), (iii) during the shock propagation inside the dense sheath when the shock decelerates, as pointed out by Vandas et al. (1997), and (iv) the shock-shock merging when, as predicted by MHD theory, a stronger shock forms followed by a contact discontinuity. If the shock is weak or slow enough, it may dissipate as it propagates into the region of higher magnetosonic speed inside the magnetic cloud (Xiong et al. 2006; Lugaz et al. 2007). High spatial resolution is necessary to resolve weak shocks in MHD simulations, and low resolution may affect the prediction of shock dissipation. The merging or dissipation of shocks was noted by Farrugia and Berdichevsky (2004), when Helios measured four shocks at 0.67 AU and ISEE-3 measured only two shocks later on at 1 AU.
For Solar Cycle 23, Lugaz et al. (2015) identified in total 49 shocks that were propagating within magnetic ejecta. Most such shocks occur toward the back of the ejecta, and shocks tend to be slower as they get closer to the CME front. This can be interpreted as an indication that a number of shocks dissipate inside a CME before exiting it. The two main reasons are that CMEs tend to be expanding and have a decreasing speed profile and that the peak Alfvén speed typically occurs close to the center of the magnetic ejecta. The latter reason means that shocks become weaker as they approach the center of the ejecta. The former reason implies that shocks propagate into higher and higher upstream speeds as they move from the back to the front of the CME. Lugaz et al. (2015) reported cases when the speed at the front of the first CME exceeds the speed of the overtaking shock, i.e. because of the CME expansion, the shock cannot overtake the front of the CME.
10 Modeling CMEs from Sun to Earth: The Bastille Day Event
MHD simulations of CMEs can be roughly divided into two classes. On the one hand, there are models that consider idealized configurations and are mainly used to test suggested ideas and to investigate specific aspects of CMEs, such as their initiation mechanisms. This kind of simulation uses a simplified set of the MHD equations and numerical domains that typically cover only the lower corona (see Green et al. in this Volume). On the other hand, there are simulations that are designed predominantly to reproduce observed eruptions. Two examples are shown in Figs. 12 and 15, respectively. These semi-realistic simulations vary widely in complexity, depending on the physics included, the phases of the CME/ICME evolution modeled, and the extent of observational constraints and real data included. Many models use observed magnetograms as boundary condition for the magnetic field at the lower boundary, and recently observed surface flows have been included as well (Jiang et al. 2016). Some simulations restrict the calculation to the evolution in the corona (e.g., Roussev et al. 2007; Cohen et al. 2009; Zuccarello et al. 2012b; Amari et al. 2014; Fan 2016), while others model the propagation of the ejecta to 1 AU but do not include the coronal evolution. Instead, the latter models start the simulation in the inner heliosphere (typically at around 20–30 \(R_{\odot}\)) and use for the initial ICME some idealized model whose parameters are chosen guided by coronagraph observations (e.g., Shiota and Kataoka 2016). Some of these models, such as ENLIL (Odstrcil 2003), which is the only MHD model that is currently used for operational space weather predictions (see Green et al. in this Volume), simplify even further by neglecting the magnetic field of the ICME and initiating its propagation by specifying a cone of constant velocity at the inner boundary of the model.
The currently most advanced simulations model CMEs all the way from the Sun to Earth (e.g., Manchester et al. 2008). The most recent ones employ a sophisticated treatment of the energy transfer in the corona, often referred to as “thermodynamic MHD” (Lionello et al. 2009; Downs et al. 2010; van der Holst et al. 2010). Such a treatment is required for a realistic description of the plasma properties in the corona, in particular if one wants to reproduce simultaneously the emission in active regions, the quiet sun, and coronal holes (Lionello et al. 2009). Some models also allow for a separate treatment of the electron and ion temperatures (van der Holst et al. 2014). CMEs are then launched in such a thermodynamic MHD environment, often using an analytical magnetic flux-rope model such as the one by Titov and Démoulin (1999), and propagated into the corona (Lugaz et al. 2011; Downs et al. 2012; Jin et al. 2013) or, by coupling different MHD codes (Tóth et al. 2007), further out to 1 AU and beyond (Lionello et al. 2013; Manchester et al. 2014a; Jin et al. 2017b). A long-term aim is to use these sophisticated simulations for space-weather predictions by modeling observed CMEs, especially the strongest, most geo-effective events, in real-time, i.e., while the eruption is still on its way to Earth (see, e.g., Jin et al. 2017a). In what follows, we briefly describe the properties and limitations of these modeling efforts, using as an example a recent simulation of the well-known “Bastille Day” eruption. Other examples can be found in the articles mentioned above.
The 14 July 2000 (“Bastille Day”) event, one of the largest eruptions of solar cycle 23, occurred in NOAA active region (AR) 9077. It was associated with a fast halo CME, an X5.7 flare, and an intense radiation storm that resulted in one of the 16 GLE events of cycle 23. The CME traveled in the corona at a speed of \(\approx1700~\mbox{km}\,\mbox{s}^{-1}\) (Andrews 2001). The shock wave driven by the interplanetary CME/ICME and a large magnetic cloud reached Earth in about 28 and 33 hours, respectively, triggering a large geomagnetic storm (Lepping et al. 2001). Strong eruptions such as the Bastille Day event are perfectly suited to test the capabilities of MHD simulations in reproducing the properties of “extreme” events.
A simulation of this event was performed using the 3D-MHD code MAS developed at Predictive Science Inc. (e.g., Mikić et al. 1999; Lionello et al. 1999, 2013). Here, we focus on the main properties of the simulation; a more detailed description can be found in Linker et al. (2016) and in a forthcoming publication (T. Török et al., in preparation).
To provide the background environment for the CME, first an MHD solution of the global corona was calculated, using a spherical grid that covers 1 to 20 \(R_{\odot}\), and includes the sonic and Alfvénic critical points. The surface radial magnetic field, \(B_{r}\), was specified by combining a line-of-sight (LOS) SOHO/MDI synoptic map (10/7/2000-6/8/2000) with a LOS MDI magnetogram measured about 30 minutes prior to the flare onset. After calculating a global potential magnetic field based on this boundary condition, a thermodynamic MHD model of the corona is produced, using the equations and coronal-heating specification described by Lionello et al. (2009). The system is relaxed for about 64 hours, until a steady state, including the solar wind, is obtained. The inclusion of thermal conduction, radiative cooling, and empirical coronal heating provides realistic density and temperature distributions, which allows one to produce synthetic EUV or soft X-rays satellite images that can be directly compared to the observations. Figure 19a shows, as an example, a synthetic SOHO/EIT image of the corona obtained from the simulation.
Coronal and heliospheric MHD simulation of the “Bastille Day” event. (a): Synthetic SOHO/EIT 195 Å emission image before the eruption. (b): Stable flux rope in the eruption’s source region. The SOHO/MDI magnetogram is shown in gray-scale. (c): Field lines of the ICME flux-rope as viewed from Earth. Thick (thin) lines outline the flux-rope core (front). Field lines are colored by \(B_{\theta}\), corresponding to \(-B_{z}\). The sphere shows \(B_{r}\) at the inner boundary of the heliospheric run; the green ball indicates Earth. (d): Same as (c), viewed from above the ecliptic plane. Thin field lines are omitted for clarity. Electric currents are visualized by \(j/B\) (in code units) in the ecliptic plane. (e): Synthetic measurements of the magnetic field components at 1 AU, taken about 20° north of Earth. Panels (c)–(e) are adapted from Linker et al. (2016)
The AR was then energized by inserting several instances of the modified Titov-Démoulin (TDm) flux-rope model (Titov et al. 2014) along the PIL. The original TD model of a force-free coronal flux rope (Titov and Démoulin 1999) has been widely used as an initial condition for CME simulations. Typically, a TD rope out of magnetic equilibrium is used to initiate a CME (e.g., Manchester et al. 2008; Lugaz et al. 2011). This approach is convenient as it reduces the complexity of the computation and reproduces many observed CME properties sufficiently well, but neglects that in reality CMEs always arise from magnetic fields in an initial state of force balance. Thus, starting simulations from a stable magnetic equilibrium is important for understanding the energy storage and release of CMEs. The TDm model facilitates the construction of such configurations by taking into account the background coronal magnetic field, and was therefore, used in the simulation described here. To account for the highly curved and elongated PIL, along which the strength of the background field strongly varies, a chain of seven overlapping TDm ropes was inserted (Fig. 19b). The axial field orientation was chosen to produce a left-handed flux rope, as suggested by the observations (e.g., Yurchyshyn et al. 2001). The model was further modified to preserve the observed \(B_{r}\) distribution when inserting the ropes, and the parameters of each TDm rope were chosen such that the merged flux rope is stable with respect to the kink and torus instabilities (e.g. Török et al. 2004; Kliem and Török 2006). The resulting configuration is close to being force-balanced but is not in thermal equilibrium. Flows and plasma condensations appeared along the flux-rope field lines that possibly arose from thermal non-equilibrium (e.g., Mikić et al. 2013a). The system was relaxed for about one hour, during which time the numerical dissipation (enhanced by the thermal flows) leads to some loss of magnetic energy.
After this additional relaxation, the eruption of the flux rope was triggered by imposing sub-Alfvénic flows at the inner boundary that converge toward the PIL (e.g., Linker et al. 2003; Mikić et al. 2013b). These flows were imposed for about 50 minutes, at which point the configuration destabilized. The flows were not directly derived from the observations, but adjusted such that the eruption starts at the western end of the AR and proceeds toward the East, in qualitative agreement with the observations. The full eruption released \(1.3\times 10^{33}~\mbox{ergs}\) in about 4 minutes; about 31% (\(4\times 10^{32}~\mbox{ergs}\)) was converted into kinetic energy. The simulated CME reached a speed of about \(1500~\mbox{km}\,\mbox{s}^{-1}\), close to the observed speed. The striking morphology of the flare arcade and the halo CME are qualitatively well reproduced in the simulation (see Linker et al. 2016). The simulation also self-consistently (i.e., without further boundary-driving) reproduces a second, “sympathetic” eruption, that was observed four hours after the main eruption in the western part of the AR (T. Török et al., in preparation).
Finally, in order to model the propagation of the ICME to Earth, the coronal simulation was coupled to the heliospheric version of MAS (Lionello et al. 2013), which uses a simpler set of equations and, is therefore, computationally more efficient. The coupling is done by setting the outer boundary of the coronal simulation as the inner boundary of the heliospheric simulation, using time-dependent boundary conditions as described in Lionello et al. (2013). The heliospheric calculation uses a \(486 \times 264\times 583\) nonuniform spherical mesh extending from 19 to 230 \(R_{\odot}\).
The observed ICME decelerated during its propagation, and arrived at Earth at about 19 UT on 15/7/2000 with a speed of \(\approx1100~\mbox{km}\,\mbox{s}^{-1}\) and a maximum field strength of \(\approx50~\mbox{nT}\) (e.g., Smith et al. 2001). The magnetic-field measurements at 1 AU suggest a left-handed flux rope passed the spacecraft below its axis (Yurchyshyn et al. 2001). Figures 19c, d show the simulated ICME, with field lines colored by the magnitude of \(B_{\theta}\); positive \(B_{\theta}\) (red) is in the direction of negative \(B_{z}\) at Earth. It can be seen that a negative \(B_{z}\) arises from the azimuthal fields wrapping the core of the flux rope, and that the flux rope connects back to the inner boundary of the simulation domain. Figure 19e shows that the simulated ICME arrives at 1 AU seven hours later than the real event, with a speed of \(\sim900~\mbox{km}\,\mbox{s}^{-1}\) and a maximum field strength of \(\sim27~\mbox{nT}\). The simulated ICME is qualitatively consistent with the flux rope inferred from the observations: a full rotation of \(B_{z}\) from negative to positive, and \(B_{x}, B_{y} > 0\). However, it passes Earth about \(15\mbox{--}20^{\circ}\) northward of the real event. At Earth’s location, the correct (negative) sign of \(B_{z}\) is reproduced, but the rotation of \(B_{z}\) from negative to positive is not seen, and the field strengths are weaker.
This example illustrates that state-of-the-art CME simulations are capable of qualitatively reproducing many important features of extreme events, such as the rapid, strong energy release, the observed emission and white-light morphology, and the magnetic structure of the ICME. The quantitative differences in the case shown here are relatively small, given that the simulation still uses various simplifications, such as a steady-state corona and heliosphere, and does not employ “trial-and-error” runs to match the observations (such as the CME speed) quantitatively. Yet, the discrepancies are still significant in light of the potential future application of such simulations for space-weather predictions. Further improvements, such as data-driven, time-dependent models of the background corona, and more case studies are required to assess to which accuracy state-of-the-art CME simulations can match the observations at 1 AU.
11 Conclusions
3-D numerical simulations and wide-angle heliospheric imaging of CMEs and ICMEs now routinely performed by STEREO, have resulted in a new era of study of CME/ICME evolution and their interaction in the heliosphere. Upon eruption, CMEs strongly interact with the surrounding environment from the active region magnetic field, the streamer belt, the solar wind and even other CMEs. A multitude of physical processes govern the transfer of energy, mass, momentum and magnetic flux to and from CMEs and ICMEs as they travel from low corona to interplanetary space, most of which can be well described in the context of extended MHD. CME deflection has an early impact on CMEs, where the trajectory departs from the expected radial direction and is most prevalent in the low corona. Here, magnetic forces can drive deflections in longitude and latitude that can reach \(30\mbox{--}40^{\circ}\) for low-mass and slow-speed CMEs. Meanwhile, patterns of CME impact on Earth suggest a consistent eastward deflection related to spiral structure of the ambient solar wind. Apart from being deflected, CMEs can also rotate about their rise direction as they propagate in the corona and interplanetary space. Like deflection, rotations are largest in the low corona, but are less predictable given that a number of mechanisms, including reconnection of the ejecta with complex background magnetic fields, can contribute to CME rotation in a complicated manner. At present, it is unclear what determines the total amount of rotation in CMEs, and further efforts are required in order to gain a better understanding of this important problem.
Once free of the low corona where strong acceleration occurs, ICME evolution is foremost dominated by kinematic processes as ICMEs ballistically propagate through the solar wind. As a first approximation, this process is described by aerodynamic drag where slow CMEs are accelerated and fast CMEs decelerated by the interaction with the solar wind. These processes are sufficiently well represented by empirical and numerical models that they can typically predict CME arrival times at Earth to within eight hours or less. Consider next the reaction that ICME propagation has on the heliosphere. CMEs traveling faster than the solar wind drive forward propagating shocks that can extend far beyond the ejecta, and whose geometry can be largely modified by the structure of the ambient solar wind. Simulations show that radial expansion of the ejecta can drive high-latitude reverse shocks, which may also be caused by CME-deflected high-speed streams. The ejecta also expands laterally with the diverging solar wind at a rate that is faster than the flow deflected around the ejecta. As a result, plasma accumulates in a sheath surrounding the flux rope and adds substantially to the overall mass of the disturbance. The interplanetary magnetic field can similarly be compressed as it drapes around the ejecta, leading to significant enhancements in the overall flux and field strength. The IMF can also reconnect with the ejecta, eroding the magnetic rope by removing poloidal flux. Reconnection is common with 30% of flux ropes showing signs of erosion with an average of 40% of the flux removed at 1 AU. In addition to MHD quantities, charge state composition is measured both in situ and spectroscopically, which gives measures of the temperature and thermodynamic behavior of the low corona where the charge state freezes in. These data are particularly important in identifying cold filament material and flare heated plasma.
Many recent investigations have focused on the relation between CME-CME and ICME-ICME interaction and the resulting structures at 1 AU, as well as their exchange of momentum. CME-CME interaction is one of the ways in which large changes in the properties of CMEs may occur during their Sun-to-Earth propagation, in addition to interaction with the solar wind. It often results in a compression and acceleration of the leading CME, although this might only be a temporary effect; it can also result in a partial or total coalescence of the two interacting CMEs (CME-CME “cannibalism”). There remains significant debate about momentum exchange between CMEs and the resulting final speed. In many instances, after their interaction, the two CMEs propagate with a uniform speed profile, similar to that of an isolated CME, but how this speed relates to that of the two CMEs before the interaction is still an area of active research. Other potential effects are a deflection of the two CMEs, and the “disappearance” of shock waves, either through shock-shock merging or as the trailing shock dissipates as it propagates inside the leading magnetic ejecta. About 15% of shocks at 1 AU are found to propagate inside a preceding magnetic ejecta, a clear example of CME-CME interaction in the process of happening.
Numerical simulations have evolved to a state where a semi-realistic modeling of observed eruptions has become possible. State-of-the-art simulations employ measured magnetograms, a realistic treatment of the energy transfer in the corona, and propagate ICMEs to 1 AU or beyond. Using the example of the well-known Bastille Day event, we described the capability of such simulations to reproduce many important observational features of eruptions, which makes them extremely valuable for improving our physical understanding of these complex events. Further improvements in computational power and in the accuracy of the simulations are required, though, before they can be used for forecasting the impacts of CMEs on space weather close to Earth.
Together, these results indicate general pictures and universal features, that regulate the Sun-to-Earth propagation of different types of CMEs. Although exceptions from the norms can occur, depending on the coronal and interplanetary conditions where a CME/ICME propagates, the results are representative of many events. Any theory/model of CME/ICME Sun-to-Earth propagation and space weather forecasting should be guided and constrained by these results.
References
T. Amari, J.F. Luciani, J.J. Aly, Z. Mikic, J. Linker, Coronal mass ejection: initiation, magnetic helicity, and flux ropes. I. Boundary motion-driven evolution. Astrophys. J. 585, 1073–1086 (2003). doi:10.1086/345501
T. Amari, A. Canou, J.J. Aly, Characterizing and predicting the magnetic environment leading to solar eruptions. Nature 514, 465 (2014)
M.D. Andrews, Lasco and EIT observations of the Bastille day 2000 solar storm. Sol. Phys. 204, 179–196 (2001). doi:10.1023/A:1014215923912
S.K. Antiochos, C.R. DeVore, J.A. Klimchuk, A model for solar coronal mass ejections. Astrophys. J. 510, 485–493 (1999)
H. Aurass, B. Vršnak, A. Hofmann, V. Ruždjak, Flares in sigmoidal coronal structures a case study. Sol. Phys. 190, 267–293 (1999). doi:10.1023/A:1005261709955
S.J. Bame, J.R. Asbridge, W.C. Feldman, E.E. Fenimore, J.T. Gosling, Solar wind heavy ions from flare-heated coronal plasma. Sol. Phys. 62, 179–201 (1979). doi:10.1007/BF00150143
B.M. Bein, S. Berkebile-Stoiser, A.M. Veronig, M. Temmer, N. Muhr, I. Kienreich, D. Utz, B. Vršnak, Impulsive acceleration of coronal mass ejections. I. Statistics and coronal mass ejection source region characteristics. Astrophys. J. 738, 191 (2011). arXiv:1108.0561. doi:10.1088/0004-637X/738/2/191
B.M. Bein, M. Temmer, A. Vourlidas, A.M. Veronig, D. Utz, The height evolution of the “true” coronal mass ejection mass derived from STEREO COR1 and COR2 observations. Astrophys. J. 768, 31 (2013). arXiv:1303.3372. doi:10.1088/0004-637X/768/1/31
D.W. Billings, A Guide to the Solar Corona (Academic, San Diego, 1966)
A. Borgazzi, A. Lara, E. Echer, M.V. Alves, Dynamics of coronal mass ejections in the interplanetary medium. Astron. Astrophys. 498, 885–889 (2009). doi:10.1051/0004-6361/200811171
G. Borrini, J.T. Gosling, S.J. Bame, W.C. Feldman, Helium abundance enhancements in the solar wind. J. Geophys. Res. 87, 7370–7378 (1982). doi:10.1029/JA087iA09p07370
G.E. Brueckner, R.A. Howard, M.J. Koomen, C.M. Korendyke, D.J. Michels, J.D. Moses, D.G. Socker, K.P. Dere, P.L. Lamy, A. Llebaria, M.V. Bout, R. Schwenn, G.M. Simnett, D.K. Bedford, C.J. Eyles, The Large Angle Spectroscopic Coronagraph (LASCO). Sol. Phys. 162, 357–402 (1995). doi:10.1007/BF00733434
G.E. Brueckner, J.P. Delaboudiniere, R.A. Howard, S.E. Paswaters, O.C. St. Cyr, R. Schwenn, P. Lamy, G.M. Simnett, B. Thompson, D. Wang, Geomagnetic storms caused by coronal mass ejections (CMEs): March 1996 through June 1997. Geophys. Res. Lett. 25, 3019–3022 (1998). doi:10.1029/98GL00704
A. Buergi, J. Geiss, Helium and minor ions in the corona and solar wind—dynamics and charge states. Sol. Phys. 103, 347–383 (1986). doi:10.1007/BF00147835
L.F. Burlaga, Magnetic loop behind an interplanetary shock: Voyager, Helios and MP-8 observations. J. Geophys. Res. 86, 6673 (1981)
L.F. Burlaga, Magnetic clouds and force-free fields with constant alpha. J. Geophys. Res. 93, 7217–7224 (1988)
L.E. Burlaga, L.W. Klein, N.R. Sheeley Jr., D.J. Michels, R.A. Howard, M.J. Koomen, R. Schwenn, H. Rosenbauer, A magnetic cloud and a coronal mass ejection. Geophys. Res. Lett. 9, 1317 (1982)
L.F. Burlaga, K.W. Behannon, L.W. Klein, Compound streams, magnetic clouds, and major geomagnetic storms. J. Geophys. Res. 92, 5725–5734 (1987). doi:10.1029/JA092iA06p05725
L.F. Burlaga, N.F. Ness, F.B. McDonald, Magnetic fields and cosmic rays in the distant heliosphere at solar maximum: Voyager 2 observations near 32 AU during 1990. J. Geophys. Res. 100(A8), 14,763–14,771 (1995)
L. Burlaga, R. Fitzenreiter, R. Lepping, K. Ogilvie, A. Szabo, A. Lazarus, J. Steinberg, G. Gloeckler, R. Howard, D. Michels, C. Farrugia, R.P. Lin, D.E. Larson, A magnetic cloud containing prominence material: January 1997. J. Geophys. Res. 103, 277–285 (1998)
L.F. Burlaga, S.P. Plunkett, O.C. St. Cyr, Successive CMEs and complex ejecta. J. Geophys. Res. 107, 1 (2002)
J.P. Byrne, S.A. Maloney, R.T.J. McAteer, J.M. Refojo, P.T. Gallagher, Propagation of an Earth-directed coronal mass ejection in three dimensions. Nat. Commun. 1, 74 (2010). arXiv:1010.0643. doi:10.1038/ncomms1077
H.V. Cane, I.G. Richardson, Interplanetary coronal mass ejections in the near-Earth solar wind during 1996–2002. J. Geophys. Res. 108, 1156 (2003). doi:10.1029/2002JA009817
P.J. Cargill, On the aerodynamic drag force acting on interplanetary coronal mass ejections. Sol. Phys. 221, 135–149 (2004). doi:10.1023/B:SOLA.0000033366.10725.a2
P.J. Cargill, J. Chen, D.S. Spicer, S.T. Zalesak, Magnetohydrodynamic simulations of the motion of magnetic flux tubes through a magnetized plasma. J. Geophys. Res. 101, 4855–4870 (1996). doi:10.1029/95JA03769
E. Chané, C. Jacobs, B. van der Holst, S. Poedts, D. Kimpe, On the effect of the initial magnetic polarity and of the background wind on the evolution of CME shocks. Astron. Astrophys. 432, 331–339 (2005). doi:10.1051/0004-6361:20042005
P. Chatterjee, Y. Fan, Simulation of homologous and cannibalistic coronal mass ejections produced by the emergence of a twisted flux rope into the solar corona. Astrophys. J. Lett. 778, L8 (2013)
P.F. Chen, Coronal mass ejections: models and their observational basis. Living Rev. Sol. Phys. 8, 1 (2011). doi:10.12942/lrsp-2011-1
C. Cid, H. Cremades, A. Aran, C. Mandrini, B. Sanahuja, B. Schmieder, M. Menvielle, L. Rodriguez, E. Saiz, Y. Cerrato, S. Dasso, C. Jacobs, C. Lathuillere, A. Zhukov, Can a halo CME from the limb be geoeffective? J. Geophys. Res. 117(A16), A11102 (2012). doi:10.1029/2012JA017536
O. Cohen, G.D.R. Attrill, W.B. Manchester IV, M.J. Wills-Davey, Numerical simulation of an EUV coronal wave based on the 2009 February 13 CME event observed by STEREO. Astrophys. J. 705, 587 (2009). arXiv:0909.3095. doi:10.1088/0004-637X/705/1/587
O. Cohen, G.D.R. Attrill, N.A. Schwadron, N.U. Crooker, M.J. Owens, C. Downs, T.I. Gombosi, Numerical simulation of the 12 May 1997 CME event: the role of magnetic reconnection. J. Geophys. Res. 115, A10104 (2010). arXiv:1006.4337. doi:10.1029/2010JA015464
R.C. Colaninno, A. Vourlidas, First determination of the true mass of coronal mass ejections: a novel approach to using the two STEREO viewpoints. Astrophys. J. 698, 852–858 (2009). arXiv:0903.4344. doi:10.1088/0004-637X/698/1/852
R.C. Colaninno, A. Vourlidas, Using multiple-viewpoint observations to determine the interaction of three coronal mass ejections observed on 2012 March 5. Astrophys. J. 815, 70 (2015). doi:10.1088/0004-637X/815/1/70
M.R. Collier, R.P. Lepping, D.B. Berdichevsky, A statistical study of interplanetary shocks and pressure pulses internal to magnetic clouds. J. Geophys. Res. 112, A06102 (2007). doi:10.1029/2006JA011714
H. Cremades, V. Bothmer, D. Tripathi, Properties of structured coronal mass ejections in Solar Cycle 23. Adv. Space Res. 38, 461–465 (2006). doi:10.1016/j.asr.2005.01.095
S. Dasso, C.H. Mandrini, P. Démoulin, M.L. Luoni, A new model-independent method to compute magnetic helicity in magnetic clouds. Astron. Astrophys. 455, 349–359 (2006). doi:10.1051/0004-6361:20064806
S. Dasso, M.S. Nakwacki, P. Démoulin, C.H. Mandrini, Progressive transformation of a flux rope to an ICME. Comparative analysis using the direct and fitted expansion methods. Sol. Phys. 244, 115–137 (2007). arXiv:0706.2889. doi:10.1007/s11207-007-9034-2
S. Dasso, C.H. Mandrini, B. Schmieder, H. Cremades, C. Cid, Y. Cerrato, E. Saiz, P. Démoulin, A.N. Zhukov, L. Rodriguez, A. Aran, M. Menvielle, S. Poedts, Linking two consecutive nonmerging magnetic clouds with their solar sources. J. Geophys. Res. 114, A02109 (2009). doi:10.1029/2008JA013102
J.A. Davies, C.H. Perry, R.M.G.M. Trines, R.A. Harrison, N. Lugaz, C. Möstl, Y.D. Liu, K. Steed, Establishing a stereoscopic technique for determining the kinematic properties of solar wind transients based on a generalized self-similarly expanding circular geometry. Astrophys. J. 777, 167 (2013). doi:10.1088/0004-637X/777/2/167
C.J. Davis, J.A. Davies, M. Lockwood, A.P. Rouillard, C.J. Eyles, R.A. Harrison, Stereoscopic imaging of an Earth-impacting solar coronal mass ejection: a major milestone for the STEREO mission. Geophys. Res. Lett. 36, L08102 (2009). doi:10.1029/2009GL038021
D.S. De Young, A.J. Hundhausen, Two-dimensional simulation of flare-associated disturbances in the solar wind. J. Geophys. Res. 76, 2245 (1971). doi:10.1029/JA076i010p02245
D.S. De Young, A.J. Hundhausen, Simulation of driven flare-associated disturbances in the solar wind. J. Geophys. Res. 78, 3633 (1973). doi:10.1029/JA078i019p03633
C.E. DeForest, T.A. Howard, S.J. Tappin, Observations of detailed structure in the solar wind at 1 AU with STEREO/HI-2. Astrophys. J. 738, 103 (2011). arXiv:1104.1615. doi:10.1088/0004-637X/738/1/103
C.E. DeForest, T.A. Howard, D.J. McComas, Tracking coronal features from the low corona to Earth: a quantitative analysis of the 2008 December 12 coronal mass ejection. Astrophys. J. 769, 43 (2013). doi:10.1088/0004-637X/769/1/43
P. Démoulin, A review of the quantitative links between CMEs and magnetic clouds. Ann. Geophys. 26, 3113–3125 (2008). doi:10.5194/angeo-26-3113-2008
P. Démoulin, G. Aulanier, Criteria for flux rope eruption: non-equilibrium versus torus instability. Astrophys. J. 718, 1388–1399 (2010). arXiv:1006.1785. doi:10.1088/0004-637X/718/2/1388
C. Downs, I.I. Roussev, B. van der Holst, N. Lugaz, I.V. Sokolov, T.I. Gombosi, Toward a realistic thermodynamic magnetohydrodynamic model of the global solar corona. Astrophys. J. 712, 1219–1231 (2010). doi:10.1088/0004-637X/712/2/1219
C. Downs, I.I. Roussev, B. van der Holst, N. Lugaz, I.V. Sokolov, Understanding SDO/AIA observations of the 2010 June 13 EUV wave event: direct insight from a global thermodynamic MHD simulation. Astrophys. J. 750, 134 (2012). doi:10.1088/0004-637X/750/2/134
M. Dryer, D.F. Smart, Dynamical models of coronal transients and interplanetary disturbances. Adv. Space Res. 4, 291–301 (1984). doi:10.1016/0273-1177(84)90573-8
M. Dryer, R.S. Steinolfson, J.D. Mihalov, J.H. Wolfe, J. Chao, Z.K. Smith, Interplanetary disturbances caused by the August 1972 solar flares as observed by Pioneer 9. J. Geophys. Res. 81, 4651–4663 (1976). doi:10.1029/JA081i025p04651
M. Dryer, Z.K. Smith, S.T. Wu, J.F. Wang, G. Gislason, S.M. Han, D.F. Smart, M.A. Shea, Magnetohydrodynamic modelling of interplanetary disturbances between the Sun and Earth. Astrophys. Space Sci. 105, 187–208 (1984). doi:10.1007/BF00651218
M. Dryer, Z.K. Smith, S.T. Wu, The role of magnetohydrodynamics in heliospheric space plasma physics research. Astrophys. Space Sci. 144, 407–425 (1988). doi:10.1007/BF00793195
M. Dumbović, A. Devos, B. Vršnak, D. Sudar, L. Rodriguez, D. Ruždjak, K. Leer, S. Vennerstrøm, A. Veronig, Geoeffectiveness of coronal mass ejections in the SOHO era. Sol. Phys. 290, 579–612 (2015). arXiv:1410.3303. doi:10.1007/s11207-014-0613-8
M. Dumbović, B. Vršnak, J. Čalogović, Forbush decrease prediction based on remote solar observations. Sol. Phys. 291, 285–302 (2016). arXiv:1510.03282. doi:10.1007/s11207-015-0819-4
R. Esser, R.J. Edgar, Differential flow speeds of ions of the same element: effects on solar wind ionization fractions. Astrophys. J. 563, 1055–1062 (2001). doi:10.1086/323987
C.J. Eyles, G.M. Simnett, M.P. Cooke, B.V. Jackson, A. Buffington, P.P. Hick, N.R. Waltham, J.M. King, P.A. Anderson, P.E. Holladay, The Solar Mass Ejection Imager (SMEI). Sol. Phys. 217, 319–347 (2003). doi:10.1023/B:SOLA.0000006903.75671.49
C.J. Eyles, R.A. Harrison, C.J. Davis, N.R. Waltham, B.M. Shaughnessy, H.C.A. Mapson-Menard, D. Bewsher, S.R. Crothers, J.A. Davies, G.M. Simnett, R.A. Howard, J.D. Moses, J.S. Newmark, D.G. Socker, J.P. Halain, J.M. Defise, E. Mazy, P. Rochus, The heliospheric imagers onboard the STEREO mission. Sol. Phys. 254, 387–445 (2009). doi:10.1007/s11207-008-9299-0
T.V. Falkenberg, B. Vršnak, A. Taktakishvili, D. Odstrcil, P. MacNeice, M. Hesse, Investigations of the sensitivity of a coronal mass ejection model (ENLIL) to solar input parameters. Space Weather 8, S06,004 (2010). doi:10.1029/2009SW000555
Y. Fan, Modeling the initiation of the 2006 December 13 coronal mass ejection in AR 10930: the structure and dynamics of the erupting flux rope. Astrophys. J. 824, 93 (2016). arXiv:1604.05687. doi:10.3847/0004-637X/824/2/93
Y. Fan, S.E. Gibson, Numerical simulations of three-dimensional coronal magnetic fields resulting from the emergence of twisted magnetic flux tubes. Astrophys. J. 609, 1123–1133 (2004). doi:10.1086/421238
F. Fang, W.B. Manchester IV, W.P. Abbett, B. van der Holst, Simulation of flux emergence from the convection zone to the corona. Astrophys. J. 714, 1649–1657 (2010). doi:10.1088/0004-637X/714/2/1649
F. Fang, W.B. Manchester IV, W.P. Abbett, B. van der Holst, Buildup of magnetic shear and free energy during flux emergence and cancellation. Astrophys. J. 754, 15 (2012). doi:10.1088/0004-637X/754/1/15
C. Farrugia, D. Berdichevsky, Evolutionary signatures in complex ejecta and their driven shocks. Ann. Geophys. 22, 3679–3698 (2004)
C.J. Farrugia, L.F. Burlaga, V.A. Osherovich, I.G. Richardson, M.P. Freeman, R.P. Lepping, A.J. Lazarus, A study of an expanding interplanetary magnetic cloud and its interaction with the Earth’s magnetosphere—the interplanetary aspect. J. Geophys. Res. 98, 7621–7632 (1993)
C.J. Farrugia, S. Mühlbachler, H.K. Biernat, R.B. Torbert, Dayside erosion during intervals of tenuous solar wind. J. Geophys. Res. 106, 25,517–25,528 (2001). doi:10.1029/2001JA000087
X. Feng, X. Zhao, A new prediction method for the arrival time of interplanetary shocks. Sol. Phys. 238, 167–186 (2006). doi:10.1007/s11207-006-0185-3
L. Feng, Y. Wang, F. Shen, C. Shen, B. Inhester, L. Lu, W. Gan, Why does the apparent mass of a coronal mass ejection increase? Astrophys. J. 812, 70 (2015). arXiv:1509.02246. doi:10.1088/0004-637X/812/1/70
E.E. Fenimore, Solar wind flows associated with hot heavy ions. Astrophys. J. 235, 245–257 (1980). doi:10.1086/157628
T.G. Forbes, A review on the genesis of coronal mass ejections. J. Geophys. Res. 105(A10), 23,153–23,165 (2000)
T.G. Forbes, P.A. Isenberg, A catastrophe mechanism for coronal mass ejection. Astrophys. J. 373, 294–307 (1991)
T.G. Forbes, J.A. Linker, J. Chen, C. Cid, J. Kóta, M.A. Lee, G. Mann, Z. Mikić, M.S. Potgieter, J.M. Schmidt, G.L. Siscoe, R. Vainio, S.K. Antiochos, P. Riley, CME theory and models. Space Sci. Rev. 123, 251–302 (2006). doi:10.1007/s11214-006-9019-8
J. Fuller, S.E. de Gibson, G. Toma, Y. Fan, Observing the unobservable? Modeling coronal cavity densities. Astrophys. J. 678, 515–530 (2008). doi:10.1086/533527
A.B. Galvin, Minor ion composition in CME-related solar wind, in Washington DC American Geophysical Union Geophysical Monograph Series, vol. 99 (1997), pp. 253–260. doi:10.1029/GM099p0253
A.B. Galvin, L.M. Kistler, M.A. Popecki, C.J. Farrugia, K.D.C. Simunac, L. Ellis, E. Möbius, M.A. Lee, M. Boehm, J. Carroll, A. Crawshaw, M. Conti, P. Demaine, S. Ellis, J.A. Gaidos, J. Googins, M. Granoff, A. Gustafson, D. Heirtzler, B. King, U. Knauss, J. Levasseur, S. Longworth, K. Singer, S. Turco, P. Vachon, M. Vosbury, M. Widholm, L.M. Blush, R. Karrer, P. Bochsler, H. Daoudi, A. Etter, J. Fischer, J. Jost, A. Opitz, M. Sigrist, P. Wurz, B. Klecker, M. Ertl, E. Seidenschwang, R.F. Wimmer-Schweingruber, M. Koeten, B. Thompson, D. Steinfeld, The Plasma and Suprathermal Ion Composition (PLASTIC) investigation on the STEREO observatories. Space Sci. Rev. 136, 437–486 (2008). doi:10.1007/s11214-007-9296-x
S. Gibson, B.C. Low, A time-dependent three-dimensional magnetohydrodynamic model of the coronal mass ejection. Astrophys. J. 493, 460–473 (1998). doi:10.1086/305107
S.E. Gibson, T.A. Kucera, D. Rastawicki, J. Dove, G. de Toma, J. Hao, S. Hill, H.S. Hudson, C. Marqué, P.S. McIntosh, L. Rachmeler, K.K. Reeves, B. Schmieder, D.J. Schmit, D.B. Seaton, A.C. Sterling, D. Tripathi, D.R. Williams, M. Zhang, Three-dimensional morphology of a coronal prominence cavity. Astrophys. J. 724, 1133–1146 (2010). doi:10.1088/0004-637X/724/2/1133
H.R. Gilbert, T.E. Holzer, J.T. Burkepile, A.J. Hundhausen, Active and eruptive prominences and their relationship to coronal mass ejections. Astrophys. J. 537, 503–515 (2000). doi:10.1086/309030
G. Gloeckler, P. Bedini, L.A. Fisk, J.C. Cain, E.O. Tums, P. Bochsler, J. Fischer, R.F. Wimmer-Schweingruber, J. Geiss, R. Kallenbach, Investigation of the composition of solar and interstellar matter using solar wind and pickup ion measurements with SWICS and SWIMS on the ACE spacecraft. Space Sci. Rev. 86, 497–539 (1998). doi:10.1023/A:1005036131689
N. Gopalswamy, Consequences of coronal mass ejections in the heliosphere. Sun Geosph. 1(2), 5–12 (2006)
N. Gopalswamy, Coronal mass ejections and space weather, in Climate and Weather of the Sun-Earth System (CAWSES): Selected Papers from the 2007 Kyoto Symposium, ed. by T. Tsuda, R. Fujii, K. Shibata, M.A. Geller (2009), pp. 77–120
N. Gopalswamy, Y. Hanaoka, T. Kosugi, R.P. Lepping, J.T. Steinberg, S. Plunkett, R.A. Howard, B.J. Thompson, J. Gurman, G. Ho, N. Nitta, H.S. Hudson, On the relationship between coronal mass ejections and magnetic clouds. Geophys. Res. Lett. 25, 2485–2488 (1998). doi:10.1029/98GL50757
N. Gopalswamy, A. Lara, R.P. Lepping, M.L. Kaiser, D. Berdichevsky, O.C. St. Cyr, Interplanetary acceleration of coronal mass ejections. Geophys. Res. Lett. 27, 145–148 (2000). doi:10.1029/1999GL003639
N. Gopalswamy, A. Lara, M.L. Kaiser, J.L. Bougeret, Near-Sun and near-Earth manifestations of solar eruptions. J. Geophys. Res. 106, 25,261–25,278 (2001a)
N. Gopalswamy, A. Lara, S. Yashiro, M.L. Kaiser, R.A. Howard, Predicting the 1-AU arrival times of coronal mass ejections. J. Geophys. Res. 106, 29,207–29,218 (2001b). doi:10.1029/2001JA000177
N. Gopalswamy, S. Yashiro, M.L. Kaiser, R.A. Howard, J.L. Bougeret, Radio signatures of coronal mass ejection interaction: coronal mass ejection cannibalism? Astrophys. J. Lett. 548, L91–L94 (2001c)
N. Gopalswamy, S. Yashiro, G. Michaek, M.L. Kaiser, R.A. Howard, D.V. Reames, R. Leske, T. von Rosenvinge, Interacting coronal mass ejections and solar energetic particles. Astrophys. J. 572, L103–L108 (2002)
N. Gopalswamy, A. Lara, P.K. Manoharan, R.A. Howard, An empirical model to predict the 1-AU arrival of interplanetary shocks. Adv. Space Res. 36, 2289–2294 (2005). doi:10.1016/j.asr.2004.07.014
N. Gopalswamy, Z. Mikić, D. Maia, D. Alexander, H. Cremades, P. Kaufmann, D. Tripathi, Y.M. Wang, The Pre-CME Sun. Space Sci. Rev. 123, 303–339 (2006). doi:10.1007/s11214-006-9020-2
N. Gopalswamy, P. Mäkelä, H. Xie, S. Akiyama, S. Yashiro, CME interactions with coronal holes and their interplanetary consequences. J. Geophys. Res. 114, A00A22 (2009a). doi:10.1029/2008JA013686
N. Gopalswamy, S. Yashiro, H. Xie, S. Akiyama, P. Mäkelä, Large geomagnetic storms associated with limb coronal mass ejections. Adv. Geosci. 21 (2009b)
N. Gopalswamy, H. Xie, P. Mäkelä, S. Yashiro, S. Akiyama, W. Uddin, A.K. Srivastava, N.C. Joshi, R. Chandra, P.K. Manoharan, K. Mahalakshmi, V.C. Dwivedi, R. Jain, A.K. Awasthi, N.V. Nitta, M.J. Aschwanden, D.P. Choudhary, Height of shock formation in the solar corona inferred from observations of type II radio bursts and coronal mass ejections. Adv. Space Res. 51, 1981–1989 (2013). arXiv:1301.0893. doi:10.1016/j.asr.2013.01.006
N. Gopalswamy, S. Yashiro, N. Thakur, P. Mäkelä, H. Xie, S. Akiyama, The 2012 July 23 backside eruption: an extreme energetic particle event? Astrophys. J. 833, 216 (2016). arXiv:1610.05790. doi:10.3847/1538-4357/833/2/216
J.T. Gosling, Coronal mass ejections and magnetic flux ropes in interplanetary space, in Physics of Magnetic Flux Ropes, ed. by C.T. Russell, E.R. Priest, L.C. Lee. AGU Geophys. Monograph Ser., vol. 58 (AGU, Washington, D.C., 1990), pp. 343–364
J.T. Gosling, Coronal mass ejections—the link between solar and geomagnetic activity. Phys. Fluids, B Plasma Phys. 5, 2638–2645 (1993a). doi:10.1063/1.860701
J.T. Gosling, The solar flare myth. J. Geophys. Res. 98, 18,937–18,950 (1993b). doi:10.1029/93JA01896
J.T. Gosling, On the determination of electron polytrope indices within coronal mass ejections in the solar wind. J. Geophys. Res. 104, 19,851–19,858 (1999). doi:10.1029/1999JA900254
J.T. Gosling, Coronal mass ejections, in Proc. 26th International Cosmic Ray Conference, ed. by B.L. Dingus, D. Kieda, M. Salamon. AIP Conference Proceedings, vol. 516 (2000), pp. 59–79
J.T. Gosling, D.J. McComas, Field line draping about fast coronal mass ejecta: a source of strong out-of-the-ecliptic interplanetary magnetic clouds. Geophys. Res. Lett. 14, 355 (1987)
J.T. Gosling, P. Riley, The acceleration of slow coronal mass ejections in the high-speed solar wind. Geophys. Res. Lett. 23, 2867–2870 (1996). doi:10.1029/96GL02843
J.T. Gosling, J.R. Asbridge, S.J. Bame, W.C. Feldman, R.D. Zwickl, Observations of large fluxes of \(\mbox{He}^{+}\) in the solar wind following an interplanetary shock. J. Geophys. Res. 85, 3431–3434 (1980). doi:10.1029/JA085iA07p03431
J.T. Gosling, M.F. Thomsen, S.J. Bame, R.D. Zwickl, The eastward deflection of fast coronal mass ejecta in interplanetary space. J. Geophys. Res. 92, 12,399–12,406 (1987). doi:10.1029/JA092iA11p12399
J.T. Gosling, S.J. Bame, D.J. McComas, J.L. Phillips, E.E. Scime, V.J. Pizzo, B.E. Goldstein, A. Balogh, A forward-reverse shock pair in the solar wind driven by over-expansion of a coronal mass ejections: Ulysses observations. Geophys. Res. Lett. 21(3), 237–240 (1994)
J.T. Gosling, P. Riley, D.J. McComas, V.J. Pizzo, Overexpanding coronal mass ejections at high heliographic latitudes: observations and simulations. J. Geophys. Res. 103, 1941 (1998)
J.T. Gosling, R.M. Skoug, W.C. Feldman, Solar wind electron halo depletions at 90 degree pitch angle. Geophys. Res. Lett. 28, 4155–4158 (2001). doi:10.1029/2001GL013758
J.T. Gosling, R.M. Skoug, D.J. McComas, C.W. Smith, Direct evidence for magnetic reconnection in the solar wind near 1 AU. J. Geophys. Res. A01, 107 (2005). doi:10.1029/2004JA010809
J.T. Gosling, D.J. McComas, R.M. Skoug, C.W. Smith, Magnetic reconnection at the heliospheric current sheet and the formation of closed magnetic field lines in the solar wind. Geophys. Res. Lett. 33, L17102 (2006). doi:10.1029/2006GL027188
L.M. Green, B. Kliem, T. Török, L. van Driel-Gesztelyi, G.D.R. Attrill, Transient coronal sigmoids and rotating erupting flux ropes. Sol. Phys. 246, 365–391 (2007). doi:10.1007/s11207-007-9061-z
J.R. Gruesbeck, S.T. Lepri, T.H. Zurbuchen, S.K. Antiochos, Constraints on coronal mass ejection evolution from in situ observations of ionic charge states. Astrophys. J. 730, 103 (2011). doi:10.1088/0004-637X/730/2/103
J.R. Gruesbeck, S.T. Lepri, T.H. Zurbuchen, Two-plasma model for low charge state interplanetary coronal mass ejection observations. Astrophys. J. 760, 141 (2012). doi:10.1088/0004-637X/760/2/141
B. Gui, C. Shen, Y. Wang, P. Ye, J. Liu, S. Wang, X. Zhao, Quantitative analysis of CME deflections in the corona. Sol. Phys. 271, 111–139 (2011). arXiv:1105.3382. doi:10.1007/s11207-011-9791-9
A.M. Gulisano, P. Démoulin, S. Dasso, M.E. Ruiz, E. Marsch, Global and local expansion of magnetic clouds in the inner heliosphere. Astron. Astrophys. 509, A39 (2010). doi:10.1051/0004-6361/200912375
C.M. Hammond, G.K. Crawford, J.T. Gosling, H. Kojima, J.L. Phillips, H. Matsumoto, A. Balogh, L.A. Frank, S. Kokubun, T. Yamamoto, Latitudinal structure of a coronal mass ejection inferred from ULYSSES and GEOTAIL observations. Geophys. Res. Lett. 22, 1169–1172 (1995). doi:10.1029/95GL01016
R.A. Harrison, J.A. Davies, C. Möstl, Y. Liu, M. Temmer, M.M. Bisi, J.P. de Eastwood, C.A. Koning, N. Nitta, T. Rollett, C.J. Farrugia, R.J. Forsyth, B.V. Jackson, E.A. Jensen, E.K.J. Kilpua, D. Odstrcil, D.F. Webb, An analysis of the origin and propagation of the multiple coronal mass ejections of 2010 August 1. Astrophys. J. 750, 45 (2012). doi:10.1088/0004-637X/750/1/45
T. Henke, J. Woch, U. Mall, S. Livi, B. Wilken, R. Schwenn, G. Gloeckler, R. von Steiger, R.J. Forsyth, A. Balogh, Differences in the \(\mbox{O}^{7+}/\mbox{O}^{6+}\) ratio of magnetic cloud and non-cloud coronal mass ejections. Geophys. Res. Lett. 25, 3465–3468 (1998). doi:10.1029/98GL02632
T. Henke, J. Woch, R. Schwenn, U. Mall, G. Gloeckler, R. von Steiger, R.J. Forsyth, A. Balogh, Ionization state and magnetic topology of coronal mass ejections. J. Geophys. Res. 106, 10,597–10,614 (2001). doi:10.1029/2000JA900176
J. Hirshberg, S.J. Bame, D.E. Robbins, Solar flares and solar wind helium enrichments: July 1965 July 1967. Sol. Phys. 23, 467–486 (1972). doi:10.1007/BF00148109
T.A. Howard, C.E. DeForest, Inner heliospheric flux rope evolution via imaging of coronal mass ejections. Astrophys. J. 746, 64 (2012). doi:10.1088/0004-637X/746/1/64
R.A. Howard, G.E. Brueckner, O.C. St. Cyr, D.A. Biesecker, K.P. Dere, M.J. Koomen, C.M. Korendyke, P.L. Lamy, A. Llebaria, M.V. Bout, D.J. Michels, J.D. Moses, S.E. Paswaters, S.P. Plunkett, R. Schwenn, G.M. Simnett, D.G. Socker, S.J. Tappin, D. Wang, Observations of CMEs from SOHO/LASCO, in Washington DC American Geophysical Union Geophysical Monograph Series, vol. 99 (1997), pp. 17–26. doi:10.1029/GM099p0017
R.A. Howard, J.D. Moses, A. Vourlidas, J.S. Newmark, D.G. Socker, S.P. Plunkett, C.M. Korendyke, J.W. Cook, A. Hurley, J.M. Davila, W.T. Thompson, O.C. St. Cyr, E. Mentzell, K. Mehalick, J.R. Lemen, J.P. Wuelser, D.W. Duncan, T.D. Tarbell, C.J. Wolfson, A. Moore, R.A. Harrison, N.R. Waltham, J. Lang, C.J. Davis, C.J. Eyles, H. Mapson-Menard, G.M. Simnett, J.P. Halain, J.M. Defise, E. Mazy, P. Rochus, R. Mercier, M.F. Ravet, F. Delmotte, F. Auchere, J.P. Delaboudiniere, V. Bothmer, W. Deutsch, D. Wang, N. Rich, S. Cooper, V. Stephens, G. Maahs, R. Baugh, D. McMullin, T. Carter, Sun Earth Connection Coronal and Heliospheric Investigation (SECCHI). Space Sci. Rev. 136, 67–115 (2008). doi:10.1007/s11214-008-9341-4
T.A. Howard, M.M. Bisi, A. Buffington, J.M. Clover, M.P. Cooke, C.J. Eyles, P.P. Hick, P.E. Holladay, B.V. Jackson, J.C. Johnston, S.W. Kahler, T.A. Kuchar, D.R. Mizuno, A.J. Penny, S.D. Price, R.R. Radick, G.M. Simnett, S.J. Tappin, N.R. Waltham, D.F. Webb, The Solar Mass Ejection Imager and its heliospheric imaging legacy. Space Sci. Rev. 180, 1–38 (2013). doi:10.1007/s11214-013-9992-7
T.A. Howard, C.E. DeForest, U.G. Schneck, C.R. Alden, Challenging some contemporary views of coronal mass ejections. II. The case for absent filaments. Astrophys. J. 834, 86 (2017). doi:10.3847/1538-4357/834/1/86
Q. Hu, B.U.Ö. Sonnerup, Reconstruction of magnetic clouds in the solar wind: orientations and configurations. J. Geophys. Res. 107, 1142 (2002). doi:10.1029/2001JA000293
H. Hu, Y.D. Liu, R. Wang, C. Möstl, Z. Yang, Sun-to-Earth characteristics of the 2012 July 12 coronal mass ejection and associated geo-effectiveness. Astrophys. J. 829, 97 (2016). arXiv:1607.06287. doi:10.3847/0004-637X/829/2/97
A.J. Hundhausen, The origin and propagation of coronal mass ejections, in Solar Wind Six, ed. by V.J. Pizzo, T.E. Holzer, D.G. Sime (NCAR, Boulder, 1987), pp. 181–214
A.J. Hundhausen, Sizes and locations of coronal mass ejections—SMM observations from 1980 and 1984–1989. J. Geophys. Res. 98, 13,177 (1993)
A.J. Hundhausen, H. Gilbert, S. Bame, Ionization state of the interplanetary plasma. J. Geophys. Res. 73, 5485 (1968)
A.J. Hundhausen, C.B. Sawyer, L. House, R.M.E. Illing, W.J. Wagner, Coronal mass ejections observed during the solar maximum mission—latitude distribution and rate of occurrence. J. Geophys. Res. 89, 2639–2646 (1984). doi:10.1029/JA089iA05p02639
A.J. Hundhausen, J.T. Burkpile, O.C. St. Cyr, Speeds of coronal mass ejections: SMM observations from 1980 and 1984–1989. J. Geophys. Res. 99(A4), 6543–6552 (1994)
K.E.J. Huttunen, H.E.J. Koskinen, T.I. Pulkkinen, A. Pulkkinen, M. Palmroth, E.G.D. Reeves, H.J. Singer, April 2000 magnetic storm: solar wind driver and magnetospheric response. J. Geophys. Res. 107, 1440 (2002). doi:10.1029/2001JA009154
R.M.E. Illing, A.J. Hundhausen, Observation of a coronal transient from 1.2 to 6 solar radii. J. Geophys. Res. 90, 275–282 (1985). doi:10.1029/JA090iA01p00275
D.S. Intriligator, The August 1972 solar-terrestrial events—solar wind plasma observations. Space Sci. Rev. 19, 629–660 (1976). doi:10.1007/BF00210644
A. Isavnin, A. Vourlidas, E.K.J. Kilpua, Three-dimensional evolution of flux-rope CMEs and its relation to the local orientation of the heliospheric current sheet. Sol. Phys. 289, 2141–2156 (2014). arXiv:1312.0458. doi:10.1007/s11207-013-0468-4
P.A. Isenberg, T.G. Forbes, A three-dimensional line-tied magnetic field model for solar eruptions. Astrophys. J. 670, 1453–1466 (2007). doi:10.1086/522025
K.G. Ivanov, A study of some interplanetary shock wave tendencies. Space Sci. Rev. 32, 49–63 (1982). doi:10.1007/BF00225176
B.V. Jackson, A. Buffington, P.P. Hick, R.C. Altrock, S. Figueroa, P.E. Holladay, J.C. Johnston, S.W. Kahler, J.B. Mozer, S. Price, R.R. Radick, R. Sagalyn, D. Sinclair, G.M. Simnett, C.J. Eyles, M.P. Cooke, S.J. Tappin, T. Kuchar, D. Mizuno, D.F. Webb, P.A. Anderson, S.L. Keil, R.E. Gold, N.R. Waltham, The Solar Mass-Ejection Imager (SMEI) mission. Sol. Phys. 225, 177–207 (2004). doi:10.1007/s11207-004-2766-3
B. Jackson, A. Buffington, P. Hick, D. Webb, Preliminary three-dimensional analysis of the heliospheric response to the 28 October 2003 CME using SMEI white-light observations. J. Geophys. Res. 111, A04S91 (2006)
C. Jacobs, I.I. Roussev, N. Lugaz, S. Poedts, The internal structure of coronal mass ejections: are all regular magnetic clouds flux ropes? Astrophys. J. Lett. 695, L171–L175 (2009). doi:10.1088/0004-637X/695/2/L171
C. Jiang, S.T. Wu, X. Feng, Q. Hu, Data-driven magnetohydrodynamic modelling of a flux-emerging active region leading to solar eruption. Nat. Commun. 7, 11522 (2016). doi:10.1038/ncomms11522
M. Jin, W.B. Manchester IV, B. van der Holst, J.R. Gruesbeck, R.A. Frazin, E. Landi, A.M. Vasquez, P.L. Lamy, A. Llebaria, A. Fedorov, G. Toth, T. Gombosi, A global two-temperature corona and inner heliosphere model: a comprehensive validation study. Astrophys. J. 7745, 6 (2012). doi:10.1088/0004-637X/745/1/6
M. Jin, W.B. Manchester IV, B. van der Holst, R. Oran, I. Sokolov, G. Toth, T. Gombosi, Y. Liu, X. Sun, Numerical simulations of coronal mass ejection on 2011 march 7: one-temperature and two-temperature model comparison. Astrophys. J. 773, 50 (2013). doi:10.1088/0004-637X/773/1/50
M. Jin, W.B. Manchester IV, B. van der Holst, I. Sokolov, G. Tóth, R.E. Mullinix, A. Taktakishvili, A. Chulaki, T.I. Gombosi, Data-constrained coronal mass ejections in a global magnetohydrodynamics model. Astrophys. J. 834, 173 (2017a). arXiv:1605.05360. doi:10.3847/1538-4357/834/2/173
M. Jin, W.B. Manchester IV, B. van der Holst, I. Sokolov, G. Tóth, A. Vourlidas, C.A. de Koning, Chromosphere to 1 AU simulation of the 2011 March 7th event: a comprehensive study of coronal mass ejection propagation. Astrophys. J. 834, 172 (2017b). arXiv:1611.08897. doi:10.3847/1538-4357/834/2/172
R.A. Jones, A.R. Breen, R.A. Fallows, A. Canals, M.M. Bisi, G. Lawrence, Interaction between coronal mass ejections and the solar wind. J. Geophys. Res. 112, A08107 (2007). doi:10.1029/2006JA011875
S. Kahler, Coronal mass ejections. Rev. Geophys. 25, 663–675 (1987). doi:10.1029/RG025i003p00663
S.W. Kahler, Solar flares and coronal mass ejections. Annu. Rev. Astron. Astrophys. 30, 113 (1992)
S.W. Kahler, D.F. Webb, V arc interplanetary coronal mass ejections observed with the Solar Mass Ejection Imager. J. Geophys. Res. 112, A09103 (2007). doi:10.1029/2007JA012358
M.L. Kaiser, T.A. Kucera, J.M. Davila, O.C. St. Cyr, M. Guhathakurta, E. Christian, The STEREO mission: an introduction. Space Sci. Rev. 136, 5–16 (2008). doi:10.1007/s11214-007-9277-0
C. Kay, M. Opher, The heliocentric distance where the deflections and rotations of solar coronal mass ejections occur. Astrophys. J. Lett. 811, L36 (2015). arXiv:1509.04948. doi:10.1088/2041-8205/811/2/L36
C. Kay, M. Opher, R.M. Evans, Forecasting a coronal mass ejection’s altered trajectory: ForeCAT. Astrophys. J. 775, 5 (2013). arXiv:1307.7603. doi:10.1088/0004-637X/775/1/5
C. Kay, M. Opher, R.M. Evans, Global trends of CME deflections based on CME and solar parameters. Astrophys. J. 805, 168 (2015). arXiv:1410.4496. doi:10.1088/0004-637X/805/2/168
C. Kay, M. Opher, R.C. Colaninno, A. Vourlidas, Using ForeCAT deflections and rotations to constrain the early evolution of CMEs. Astrophys. J. 827, 70 (2016). arXiv:1606.03460. doi:10.3847/0004-637X/827/1/70
E.K.J. Kilpua, J. Pomoell, A. Vourlidas, R. Vainio, J. Luhmann, Y. Li, P. Schroeder, A.B. Galvin, K. Simunac, STEREO observations of interplanetary coronal mass ejections and prominence deflection during solar minimum period. Ann. Geophys. 27, 4491–4503 (2009). doi:10.5194/angeo-27-4491-2009
E.K.J. Kilpua, M. Mierla, L. Rodriguez, A.N. Zhukov, N. Srivastava, M.J. West, Estimating travel times of coronal mass ejections to 1 AU using multi-spacecraft coronagraph data. Sol. Phys. 279, 477–496 (2012). doi:10.1007/s11207-012-0005-x
E.K.J. Kilpua, A. Isavnin, A. Vourlidas, H.E.J. Koskinen, L. Rodriguez, On the relationship between interplanetary coronal mass ejections and magnetic clouds. Ann. Geophys. 31, 1251–1265 (2013). doi:10.5194/angeo-31-1251-2013
B. Kliem, T. Török, Torus instability. Phys. Rev. Lett. 255, 002 (2006). arXiv:physics/0605217. doi:10.1103/PhysRevLett.96.255002
B. Kliem, V.S. Titov, T. Török, Formation of current sheets and sigmoidal structure by the kink instability of a magnetic loop. Astron. Astrophys. 413, L23–L26 (2004). arXiv:astro-ph/0311199. doi:10.1051/0004-6361:20031690
B. Kliem, T. Török, W.T. Thompson, A parametric study of erupting flux rope rotation. Modeling the “Cartwheel CME” on 9 April 2008. Sol. Phys. 281, 137–166 (2012). arXiv:1112.3389. doi:10.1007/s11207-012-9990-z
Y.K. Ko, G. Gloeckler, C.M.S. Cohen, A.B. Galvin, Solar wind ionic charge states during the Ulysses pole-to-pole pass. J. Geophys. Res. 104(17), 005 (1999). 020. doi:10.1029/1999JA900112
A.G. Kosovichev, T.V. Stepanova, Numerical simulation of shocks in the heliosphere. Sov. Astron. 35, 646 (1991)
J.U. Kozyra, W.B. Manchester IV, C.P. Escoubet, S.T. Lepri, M.W. Liemohn, W.D. Gonzalez, M.W. Thomsen, B.T. Tsurutani, Earth’s collision with a solar filament on 21 January 2005: overview. J. Geophys. Res. 118, 5967–5978 (2013). doi:10.1002/jgra.50567
A. Lara, A.I. Borgazzi, Dynamics of interplanetary CMEs and associated type II bursts, in Universal Heliophysical Processes, IAU Symposium, vol. 257, ed. by N. Gopalswamy, D.F. Webb (2009), pp. 287–290. doi:10.1017/S1743921309029421
B. Lavraud, E. Larroque, E. Budnik, V. Génot, J.E. Borovsky, M.W. Dunlop, C. Foullon, H. Hasegawa, C. Jacquey, K. Nykyri, A. Ruffenach, M.G.G.T. Taylor, I. Dandouras, H. Rème, Asymmetry of magnetosheath flows and magnetopause shape during low Alfvén Mach number solar wind. J. Geophys. Res. 118, 1089–1100 (2013). doi:10.1002/jgra.50145
B. Lavraud, A. Ruffenach, A.P. Rouillard, P. Kajdic, W.B. Manchester IV, N. Lugaz, Geo-effectiveness and radial dependence of magnetic cloud erosion by magnetic reconnection. J. Geophys. Res. 119, 26–35 (2014). doi:10.1002/2013JA019154
J.Y. Lee, J.C. Raymond, Low ionization state plasma in coronal mass ejections. Astrophys. J. 758, 116 (2012). doi:10.1088/0004-637X/758/2/116
R.P. Lepping, C.C. Wu, On the variation of interplanetary magnetic cloud type through Solar Cycle 23: wind events. J. Geophys. Res. 112(A11), A10103 (2007). doi:10.1029/2006JA012140
R.P. Lepping, L.F. Burlaga, J.A. Jones, Magnetic field structure of interplanetary magnetic clouds at 1 AU. J. Geophys. Res. 95, 11,957–11,965 (1990)
R.P. Lepping, D.B. Berdichevsky, L.F. Burlaga, A.J. Lazarus, J. Kasper, M.D. Desch, C.C. Wu, D.V. Reames, H.J. Singer, C.W. Smith, K.L. Ackerson, The Bastille day magnetic clouds and upstream shocks: near-Earth interplanetary observations. Sol. Phys. 204, 285–303 (2001). doi:10.1023/A:1014264327855
R.P. Lepping, D.B. Berdichevsky, C.C. Wu, A. Szabo, T. Narock, F. Mariani, A.J. Lazarus, A.J. Quivers, A summary of WIND magnetic clouds for years 1995–2003: model-fitted parameters, associated errors and classifications. Ann. Geophys. 24, 215–245 (2006). doi:10.5194/angeo-24-215-2006
S.T. Lepri, T.H. Zurbuchen, Iron charge state distributions as an indicator of hot ICMEs: possible sources and temporal and spatial variations during solar maximum. J. Geophys. Res. 109, A01112 (2004). doi:10.1029/2003JA009954
S.T. Lepri, T.H. Zurbuchen, Direct observational evidence of filament material within interplanetary coronal mass ejections. Astrophys. J. Lett. 723, L22–L27 (2010). doi:10.1088/2041-8205/723/1/L22
S.T. Lepri, T.H. Zurbuchen, L.A. Fisk, I.G. Richardson, H.V. Cane, G. Gloeckler, Iron charge distribution as an identifier of interplanetary coronal mass ejections. J. Geophys. Res. 106, 29,231–29,238 (2001) doi:10.1029/2001JA000014
S.T. Lepri, J.M. Laming, C.E. von Rakowski, R. Steiger, Spatially dependent heating and ionization in an ICME observed by both ACE and Ulysses. Astrophys. J. 760, 105 (2012). doi:10.1088/0004-637X/760/2/105
G.M. Lindsay, J.G. Luhmann, C.T. Russell, J.T. Gosling, Relationships between coronal mass ejection speeds from coronagraph images and interplanetary characteristics of associated interplanetary coronal mass ejections. J. Geophys. Res. 104, 12,515–12,524 (1999) doi:10.1029/1999JA900051
J.A. Linker, Z. Mikić, R. Lionello, P. Riley, T. Amari, D. Odstrcil, Flux cancellation and coronal mass ejections. Phys. Plasmas 10, 1971–1978 (2003)
J. Linker, T. Torok, C. Downs, R. Lionello, V. Titov, R.M. Caplan, Z. Mikić, P. Riley, MHD simulation of the Bastille day event. AIP Conf. Ser. 1720, 020002 (2016). doi:10.1063/1.4943803
R. Lionello, Z. Mikić, J.A. Linker, Stability of algorithms for waves with large flows. J. Comput. Phys. 152, 346–358 (1999). doi:10.1006/jcph.1999.6250
R. Lionello, J.A. Linker, Z. Mikic, Multispectral emission of the sun during the first Whole Sun Month: magnetohydrodynamic simulations. Astrophys. J. 690(1), 902–912 (2009). doi:10.1088/0004-637X/690/1/902
R. Lionello, C. Downs, J.A. Linker, T. Török, P. Riley, Z. Mikić, Magnetohydrodynamic simulations of interplanetary coronal mass ejections. Astrophys. J. 777, 76 (2013). doi:10.1088/0004-637X/777/1/76
Y. Liu, J.D. Richardson, J.W. Belcher, A statistical study of the properties of interplanetary coronal mass ejections from 0.3 to 5.4 AU. Planet. Space Sci. 53, 3–17 (2005). doi:10.1016/j.pss.2004.09.023
Y. Liu, J.D. Richardson, J.W. Belcher, J.C. Kasper, H.A. Elliott, Thermodynamic structure of collision-dominated expanding plasma: heating of interplanetary coronal mass ejections. J. Geophys. Res. 111, A01102 (2006a). doi:10.1029/2005JA011329
Y. Liu, J.D. Richardson, J.W. Belcher, C. Wang, Q. Hu, J.C. Kasper, Constraints on the global structure of magnetic clouds: transverse size and curvature. J. Geophys. Res. 111(A10), A12S03 (2006b). arXiv:physics/0606003. doi:10.1029/2006JA011890
Y. Liu, J.G. Luhmann, K.E.J. Huttunen, R.P. Lin, S.D. Bale, C.T. Russell, A.B. Galvin, Reconstruction of the 2007 May 22 magnetic cloud: how much can we trust the flux-rope geometry of CMEs? Astrophys. J. Lett. 677, L133 (2008a). doi:10.1086/587839
Y. Liu, J.G. Luhmann, R. Müller-Mellin, P.C. Schroeder, L. Wang, R.P. Lin, S.D. Bale, Y. Li, M.H. Acuña, J.A. Sauvaud, A comprehensive view of the 2006 December 13 CME: from the Sun to interplanetary space. Astrophys. J. 689, 563–571 (2008b). arXiv:0802.2423. doi:10.1086/592031
Y. Liu, W.B. Manchester IV, J.D. Richardson, J.G. Luhmann, R.P. Lin, S.D. Bale, Deflection flows ahead of ICMEs as an indicator of curvature and geoeffectiveness. J. Geophys. Res. 113, A00B03 (2008c). doi:10.1029/2007JA012996
Y. Liu, J.G. Luhmann, S.D. Bale, R.P. Lin, Relationship between a coronal mass ejection-driven shock and a coronal metric type II burst. Astrophys. J. Lett. 691, L151 (2009)
Y. Liu, J.A. Davies, J.G. Luhmann, A. Vourlidas, S.D. Bale, R.P. Lin, Geometric triangulation of imaging observations to track coronal mass ejections continuously out to 1 AU. Astrophys. J. Lett. 710, L82–L87 (2010a). arXiv:1001.1352. doi:10.1088/2041-8205/710/1/L82
Y. Liu, A. Thernisien, J.G. Luhmann, A. Vourlidas, J.A. Davies, R.P. Lin, S.D. Bale, Reconstructing coronal mass ejections with coordinated imaging and in situ observations: global structure, kinematics, and implications for space weather forecasting. Astrophys. J. 722, 1762–1777 (2010b). arXiv:1009.1414. doi:10.1088/0004-637X/722/2/1762
Y. Liu, J.G. Luhmann, S.D. Bale, R.P. Lin, Solar source and heliospheric consequences of the 2010 April 3 coronal mass ejection: a comprehensive view. Astrophys. J. 734(2), 84 (2011). http://stacks.iop.org/0004-637X/734/i=2/a=84
Y.D. Liu, J.G. Luhmann, C. Möstl, J.C. Martinez-Oliveros, S.D. Bale, R.P. Lin, R.A. Harrison, M. Temmer, D.F. Webb, D. Odstrcil, Interactions between coronal mass ejections viewed in coordinated imaging and in situ observations. Astrophys. J. Lett. 746, L15 (2012). doi:10.1088/2041-8205/746/2/L15
Y.D. Liu, J.G. Luhmann, N. Lugaz, C. Möstl, J.A. Davies, S.D. Bale, R.P. Lin, On Sun-to-Earth propagation of coronal mass ejections. Astrophys. J. 769, 45 (2013). doi:10.1088/0004-637X/769/1/45
Y.D. Liu, J.G. Luhmann, P. Kajdič, E.K.J. Kilpua, N. Lugaz, N.V. Nitta, C. Möstl, B. Lavraud, S.D. Bale, C.J. Farrugia, A.B. Galvin, Observations of an extreme storm in interplanetary space caused by successive coronal mass ejections. Nat. Commun. 5, 3481 (2014a). arXiv:1405.6088. doi:10.1038/ncomms4481
Y.D. Liu, J.D. Richardson, C. Wang, J.G. Luhmann, Propagation of the 2012 March coronal mass ejections from the Sun to heliopause. Astrophys. J. Lett. 788, L28 (2014b). arXiv:1405.6086. doi:10.1088/2041-8205/788/2/L28
Y.D. Liu, Z. Yang, R. Wang, J.G. Luhmann, J.D. Richardson, N. Lugaz, Sun-to-Earth characteristics of two coronal mass ejections interacting near 1 AU: formation of a complex ejecta and generation of a two-step geomagnetic storm. Astrophys. J. Lett. 793, L41 (2014c). doi:10.1088/2041-8205/793/2/L41
Y.D. Liu, H. Hu, R. Wang, Z. Yang, B. Zhu, Y.A. Liu, J.G. Luhmann, J.D. Richardson, Plasma and magnetic field characteristics of solar coronal mass ejections in relation to geomagnetic storm intensity and variability. Astrophys. J. 809, L34 (2015). arXiv:1508.01267. doi:10.1088/2041-8205/809/2/L34
Y.D. Liu, H. Hu, C. Wang, J.G. Luhmann, J.D. Richardson, Z. Yang, R. Wang, On Sun-to-Earth propagation of coronal mass ejections: II. Slow events and comparison with others. Astrophys. J. Suppl. Ser. 222(2), 23 (2016). http://stacks.iop.org/0067-0049/222/i=2/a=23
Y.D. Liu, H. Hu, B. Zhu, J.G. Luhmann, A. Vourlidas, Structure, propagation and expansion of a CME-driven shock in the heliosphere: a revisit of the 2012 July 23 extreme storm. Astrophys. J. Lett. 834, 158 (2017). doi:10.3847/1538-4357/834/2/158
B.C. Low, Coronal mass ejections, magnetic flux ropes, and solar magnetism. J. Geophys. Res. 106, 25,141–25,163 (2001)
N. Lugaz, C.J. Farrugia, A new class of complex ejecta resulting from the interaction of two CMEs and its expected geo-effectiveness. J. Geophys. Res. (2014). doi:10.1002/2013GL058789
N. Lugaz, W.B. Manchester IV, T.I. Gombosi, The evolution of CME density structures. Astrophys. J. 627, 1019–1030 (2005a)
N. Lugaz, W.B. Manchester IV, T.I. Gombosi, Numerial simulation of the interaction of two coronal mass ejections from Sun to Earth. Astrophys. J. 634, 651–662 (2005b)
N. Lugaz, W.B. Manchester IV, I.I. Roussev, G. Tóth, T.I. Gombosi, Numerical investigation of the homologous coronal mass ejection events from active region 9236. Astrophys. J. 659, 788–800 (2007). doi:10.1086/512005
N. Lugaz, J.N. Hernandez-Charpak, I.I. Roussev, C.J. Davis, A. Vourlidas, J.A. Davies, Determining the azimuthal properties of coronal mass ejections from multi-spacecraft remote-sensing observations with STEREO SECCHI. Astrophys. J. 715(1), 493 (2010). http://stacks.iop.org/0004-637X/715/i=1/a=493
N. Lugaz, C. Downs, K. Shibata, I.I. Roussev, A. Asai, T.I. Gombosi, Numerical investigation of a coronal mass ejection from an Anemone active region: reconnection and deflection of the 2005 August 22 eruption. Astrophys. J. 738, 127 (2011). arXiv:1106.5284. doi:10.1088/0004-637X/738/2/127
N. Lugaz, C.J. Farrugia, J.A. Davies, C. Möstl, C.J. Davis, I.I. Roussev, M. Temmer, The deflection of the two interacting coronal mass ejections of 2010 May 23–24 as revealed by combined in situ measurements and heliospheric imaging. Astrophys. J. 759, 68 (2012). doi:10.1088/0004-637X/759/1/68
N. Lugaz, C.J. Farrugia, W.B. Manchester IV, N. Schwadron, The interaction of two coronal mass ejections: influence of relative orientation. Astrophys. J. 778, 20 (2013)
N. Lugaz, C.J. Farrugia, C.W. Smith, K. Paulson, Shocks inside CMEs: a survey of properties from 1997 to 2006. J. Geophys. Res. 120, 2409–2427 (2015). doi:10.1002/2014JA020848
N. Lugaz, C.J. Farrugia, R.M. Winslow, N. Al-Haddad, E.K.J. Kilpua, P. Riley, Factors affecting the geoeffectiveness of shocks and sheaths at 1 AU. J. Geophys. Res. 121(A10), 10 (2016). arXiv:1610.07885. doi:10.1002/2016JA023100
J.G. Luhmann, D.W. Curtis, P. Schroeder, J. McCauley, R.P. Lin, D.E. Larson, S.D. Bale, J.A. Sauvaud, C. Aoustin, R.A. Mewaldt, A.C. Cummings, E.C. Stone, A.J. Davis, W.R. Cook, B. Kecman, M.E. von Wiedenbeck, T. Rosenvinge, M.H. Acuna, L.S. Reichenthal, S. Shuman, K.A. Wortman, D.V. Reames, R. Mueller-Mellin, H. Kunow, G.M. Mason, P. Walpole, A. Korth, T.R. Sanderson, C.T. Russell, J.T. Gosling, STEREO IMPACT investigation goals, measurements, and data products overview. Space Sci. Rev. 136, 117–184 (2008). doi:10.1007/s11214-007-9170-x
B.J. Lynch, S.K. Antiochos, C.R. DeVore, J.G. Luhmann, T.H. Zurbuchen, Topological evolution of a fast magnetic breakout CME in three dimensions. Astrophys. J. 683, 1192–1206 (2008). doi:10.1086/589738
B.J. Lynch, S.K. Antiochos, Y. Li, J.G. Luhmann, C.R. DeVore, Rotation of coronal mass ejections during eruption. Astrophys. J. 697, 1918–1927 (2009). doi:10.1088/0004-637X/697/2/1918
B.J. Lynch, Y. Li, A.F.R. Thernisien, E. Robbrecht, G.H. Fisher, J.G. Luhmann, A. Vourlidas, Sun to 1 AU propagation and evolution of a slow streamer-blowout coronal mass ejection. J. Geophys. Res. 115, A07106 (2010). doi:10.1029/2009JA015099
B.J. Lynch, A.A. Reinard, T. Mulligan, K.K. Reeves, C.E. Rakowski, J.C. Allred, Y. Li, J.M. Laming, P.J. MacNeice, J.A. Linker, Ionic composition structure of coronal mass ejections in axisymmetric magnetohydrodynamic models. Astrophys. J. 740, 112 (2011). doi:10.1088/0004-637X/740/2/112
R.M. MacQueen, A. Csoeke-Poeckh, E. Hildner, L. House, R. Reynolds, A. Stanger, H. Tepoel, W. Wagner, The high altitude observatory coronagraph/polarimeter on the solar maximum mission. Sol. Phys. 65, 91–107 (1980). doi:10.1007/BF00151386
R.M. MacQueen, A.J. Hundhausen, C.W. Conover, The propagation of coronal mass ejection transients. J. Geophys. Res. 91, 31–38 (1986). doi:10.1029/JA091iA01p00031
P. Mäkelä, N. Gopalswamy, H. Xie, A.A. Mohamed, S. Akiyama, S. Yashiro, Coronal hole influence on the observed structure of interplanetary CMEs. Sol. Phys. 284, 59–75 (2013). arXiv:1301.2176. doi:10.1007/s11207-012-0211-6
W.B. Manchester IV, The role of nonlinear Alfven waves in shear formation during solar magnetic flux emergence. Astrophys. J. 547, 503–519 (2001). doi:10.1086/318342
W.B. Manchester IV, Buoyant disruption of magnetic arcades with self-induced shearing. J. Geophys. Res. 108, 1162 (2003). doi:10.1029/2002JA009252
W.B. Manchester IV, Solar atmospheric dynamic coupling due to shear motions driven by the Lorentz force. Astrophys. J. 666, 532–540 (2007). doi:10.1086/520493
W.B. Manchester IV, Shear flows driven by the Lorentz force: an energy source for coronal mass ejections and flares, in Subsurface and Atmospheric Influences on Solar Activity, ed. by R. Howe, R.W. Komm, K.S. Balasubramaniam, G.J.D. Petrie. Astronomical Society of the Pacific Conference Series, vol. 383 (2008), pp. 91–98
W.B. Manchester IV, T.H. Zurbuchen, Are high-latitude forward-reverse shock pairs driven by over-expansion? J. Geophys. Res. 111, A05,101 (2006). doi:10.1029/2005JA011461
W.B. Manchester IV, T.H. Zurbuchen, Reply to comment by P. Riley and J.T. Gosling on “Are high-latitude forward-reverse shock pairs driven by overexpansion?”. J. Geophys. Res. 112, A07,103 (2007). doi:10.1029/2007JA012272
W. Manchester IV, T. Gombosi, A. Ridley, I. Roussev, D.D. Zeeuw, I. Sokolov, K. Powell, G. Tóth, Modeling a space weather event from the Sun to the Earth: CME generation and interplanetary propagation. J. Geophys. Res. 109, A02107 (2004a). doi:10.1029/2003JA010150
W.B. Manchester IV, T. Gombosi, I. Roussev, D. De Zeeuw, I. Sokolov, K. Powell, G. Tóth, M. Opher, Three-dimensional MHD simulation of a flux rope driven CME. J. Geophys. Res. 109, A01,102 (2004b). doi:10.1029/2002JA009672
W.B. Manchester IV, T.I. Gombosi, D.L. De Zeeuw, I.V. Sokolov, I.I. Roussev, K.G. Powell, J. Kóta, G. Tóth, T.H. Zurbuchen, Coronal mass ejection shock and sheath structures relevant to particle acceleration. Astrophys. J. 622, 1225–1239 (2005). doi:10.1086/427768
W.B. Manchester IV, A. Vourlidas, G. Tóth, N. Lugaz, I.I. Roussev, I.V. Sokolov, T.I. Gombosi, D.L.D. Zeeuw, M. Opher, Three-dimensional MHD simulation of the 2003 October 28 coronal mass ejection: comparison with LASCO coronagraph observations. Astrophys. J. 684, 1448–1460 (2008). doi:10.1086/590231
W.B. Manchester IV, B. van der Holst, G. Tóth, T.I. Gombosi, The coupled evolution of electrons and ions in coronal mass ejection-driven shocks. Astrophys. J. 756, 1 (2012). doi:10.1088/0004-637X/756/1/81
W.B. Manchester IV, B. van der Holst, B. Lavraud, Flux rope evolution in interplanetary coronal mass ejections: the 13 May 2005 event. Plasma Phys. Control. Fusion 56, 1–11 (2014a). doi:10.1088/0741-3335/56/6/064006
W.B. Manchester IV, J.U. Kozyra, S.T. Lepri, B. Lavraud, Simulation of magnetic cloud erosion during propagation. J. Geophys. Res. 119, 1–16 (2014b). doi:10.1002/2014JA019882
S. Mancuso, J.C. Raymond, J. Kohl, Y.K. Ko, M. Uzzo, R. Wu, UVCS/SOHO observations of a CME-driven shock: consequences on ion heating mechanisms behind a coronal shock. Astron. Astrophys. 383, 267–274 (2002). doi:10.1051/0004-6361:20011721
P.K. Manoharan, Evolution of coronal mass ejections in the inner heliosphere: a study using white-light and scintillation images. Sol. Phys. 235, 345–368 (2006). doi:10.1007/s11207-006-0100-y
P.K. Manoharan, A. Mujiber Rahman, Coronal mass ejections: propagation time and associated internal energy. J. Atmos. Sol.-Terr. Phys. 73, 671–677 (2011). arXiv:1011.3687. doi:10.1016/j.jastp.2011.01.017
P.K. Manoharan, M. Tokumaru, M. Pick, P. Subramanian, F.M. Ipavich, K. Schenk, M.L. Kaiser, R.P. Lepping, A. Vourlidas, Coronal mass ejection of 2000 July 14 flare event: imaging from near-Sun to Earth environment. Astrophys. J. 559, 1180–1189 (2001). doi:10.1086/322332
P.K. Manoharan, N. Gopalswamy, S. Yashiro, A. Lara, G. Michalek, R.A. Howard, Influence of coronal mass ejection interaction on propagation of interplanetary shocks. J. Geophys. Res. 109, A06109 (2004). doi:10.1029/2003JA010300
D. Maričić, B. Vršnak, M. Dumbović, T. Žic, D. Roša, D. Hržina, S. Lulić, I. Romštajn, I. Bušić, K. Salamon, M. Temmer, T. Rollett, A. Veronig, N. Bostanjyan, A. Chilingarian, B. Mailyan, K. Arakelyan, A. Hovhannisyan, N. Mujić, Kinematics of interacting ICMEs and related Forbush decrease: case study. Sol. Phys. 289, 351–368 (2014). doi:10.1007/s11207-013-0314-8
K. Marubashi, S. Akiyama, S. Yashiro, N. Gopalswamy, K.S. Cho, Y.D. Park, Geometrical relationship between interplanetary flux ropes and their solar sources. Sol. Phys. 290, 1371–1397 (2015). doi:10.1007/s11207-015-0681-4
M.L. Mays, B.J. Thompson, L.K. Jian, R.C. Colaninno, D. Odstrcil, C. Möstl, M. Temmer, N.P. Savani, G. Collinson, A. Taktakishvili, P.J. MacNeice, Y. Zheng, Propagation of the 7 January 2014 CME and resulting geomagnetic non-event. Astrophys. J. 812, 145 (2015). arXiv:1509.06477. doi:10.1088/0004-637X/812/2/145
D.J. McComas, J.T. Gosling, D. Winterhalter, E.J. Smith, Interplanetary magnetic field draping about fast coronal mass ejecta in the outer heliosphere. J. Geophys. Res. 93, 2519–2526 (1988). doi:10.1029/JA093iA04p02519
Z. Mikić, D. Barnes, D.D. Schnack, Dynamical evolution of a solar coronal magnetic field arcade. Astrophys. J. 328, 830–847 (1988)
Z. Mikić, J. Linker, D. Schnack, R. Lionello, A. Tarditi, Magnetohydrodynamic modeling of the global solar corona. Phys. Plasmas 6, 2217–2224 (1999)
Z. Mikić, R. Lionello, Y. Mok, J.A. Linker, A.R. Winebarger, The importance of geometric effects in coronal loop models. Astrophys. J. 773, 94 (2013a). doi:10.1088/0004-637X/773/2/94
Z. Mikić, T. Török, V. Titov, J.A. Linker, R. Lionello, C. Downs, P. Riley, The challenge in making models of fast CMEs, in American Institute of Physics Conference Series, ed. by G.P. Zank, J. Borovsky, R. Bruno, J. Cirtain, S. Cranmer, H. Elliott, J. Giacalone, W. Gonzalez, G. Li, E. Marsch, E. Moebius, N. Pogorelov, J. Spann, O. Verkhoglyadova. American Institute of Physics Conference Series, vol. 1539 (2013b), pp. 42–45. doi:10.1063/1.4810985
W. Mishra, N. Srivastava, Estimating the arrival time of Earth-directed coronal mass ejections at in situ spacecraft using COR and HI observations from STEREO. Astrophys. J. 772(1), 70 (2013). http://stacks.iop.org/0004-637X/772/i=1/a=70
W. Mishra, N. Srivastava, D. Chakrabarty, Evolution and consequences of interacting CMEs of 9–10 November 2012 using STEREO/SECCHI and in situ observations. Sol. Phys. 290, 527–552 (2015a). doi:10.1007/s11207-014-0625-4
W. Mishra, N. Srivastava, T. Singh, Kinematics of interacting CMEs of 25 and 28 September 2012. J. Geophys. Res. 120, 10 (2015b). doi:10.1002/2015JA021415
W. Mishra, Y. Wang, N. Srivastava, On understanding the nature of collisions of coronal mass ejections observed by STEREO. Astrophys. J. 831, 99 (2016). arXiv:1607.07692. doi:10.3847/0004-637X/831/1/99
A.A. Mohamed, N. Gopalswamy, S. Yashiro, S. Akiyama, P. Mäkelä, H. Xie, H. Jung, The relation between coronal holes and coronal mass ejections during the rise, maximum, and declining phases of Solar Cycle 23. J. Geophys. Res. 117, A01103 (2012). doi:10.1029/2011JA016589
Y.J. Moon, G.S. Choe, H. Wang, Y.D. Park, N. Gopalswamy, G. Yang, S. Yashiro, A statistical study of two classes of coronal mass ejections. Astrophys. J. 581, 694–702 (2002). doi:10.1086/344088
Y.J. Moon, G.S. Choe, H. Wang, Y.D. Park, Sympathetic coronal mass ejections. Astrophys. J. 588, 1176–1182 (2003). doi:10.1086/374270
C. Möstl, C. Miklenic, C.J. Farrugia, M. Temmer, A. Veronig, A.B. Galvin, B. Vršnak, H.K. Biernat, Two-spacecraft reconstruction of a magnetic cloud and comparison to its solar source. Ann. Geophys. 26, 3139–3152 (2008). doi:10.5194/angeo-26-3139-2008
C. Möstl, C.J. Farrugia, M. Temmer, C. Miklenic, A.M. Veronig, A.B. Galvin, M. Leitner, H.K. Biernat, Linking remote imagery of a coronal mass ejection to its in situ signatures at 1 AU. Astrophys. J. 705, L180–L185 (2009). arXiv:0910.1188. doi:10.1088/0004-637X/705/2/L180
C. Möstl, M. Temmer, T. Rollett, C.J. Farrugia, Y. Liu, A.M. Veronig, M. Leitner, A.B. Galvin, H.K. Biernat, STEREO and Wind observations of a fast ICME flank triggering a prolonged geomagnetic storm on 5–7 April 2010. Geophys. Res. Lett. 37, L24103 (2010). arXiv:1010.4150. doi:10.1029/2010GL045175
C. Möstl, T. Rollett, R.A. Frahm, Y.D. Liu, D.M. Long, R.C. Colaninno, M.A. Reiss, M. Temmer, C.J. Farrugia, A. Posner, M. Dumbović, M. Janvier, P. Démoulin, P. Boakes, A. Devos, E. Kraaikamp, M.L. Mays, B. Vršnak, Strong coronal channelling and interplanetary evolution of a solar storm up to Earth and Mars. Nat. Commun. 6, 7135 (2015). arXiv:1506.02842. doi:10.1038/ncomms8135
K. Muglach, Y.M. Wang, B. Kliem, Evidence for mixed helicity in erupting filaments. Astrophys. J. 703, 976–981 (2009). arXiv:0907.4446. doi:10.1088/0004-637X/703/1/976
M. Neugebauer, R. Goldstein, Particle and field signatures of coronal mass ejections in the solar wind, in Washington DC American Geophysical Union Geophysical Monograph Series, vol. 99 (1997), 245–251. doi:10.1029/GM099p0245
T. Nieves-Chinchilla, R. Colaninno, A. Vourlidas, A. Szabo, R.P. Lepping, S.A. Boardsen, B.J. Anderson, H. Korth, Remote and in situ observations of an unusual Earth-directed coronal mass ejection from multiple viewpoints. J. Geophys. Res. 117, A06106 (2012). doi:10.1029/2011JA017243
N.V. Nitta, W. Liu, N. Gopalswamy, S. Yashiro, The relation between large-scale coronal propagating fronts and type II radio bursts. Sol. Phys. 289, 4589–4606 (2014). arXiv:1409.4754. doi:10.1007/s11207-014-0602-y
D. Odstrcil, Modeling 3-D solar wind structures. Adv. Space Res. 32(4), 497–506 (2003)
D. Odstrčil, V.J. Pizzo, Distortion of the interplanetary magnetic field by three-dimensional propagation of coronal mass ejections in a structured solar wind. J. Geophys. Res. 104, 28,225–28,239 (1999a)
D. Odstrčil, V.J. Pizzo, Three-dimensional propagation of CMEs in a structured solar wind flow, 1, CME launched within the streamer belt. J. Geophys. Res. 104, 483–492 (1999b)
D. Odstrčil, M. Dryer, Z. Smith, Propagation of an interplanetary shock along the heliospheric plasma sheet. J. Geophys. Res. 101, 19,973–19,984 (1996)
D. Odstrcil, M. Vandas, V.J. Pizzo, P. MacNeice, Numerical simulation of interacting magnetic flux ropes, in Solar Wind Ten, AIP Conf. Proc., vol. 679 (2003), pp. 699–702
D. Odstrcil, V.J. Pizzo, C.N. Arge, Propagation of the 12 May 1997 interplanetary coronal mass ejection in evolving solar wind structures. J. Geophys. Res. A02, 106 (2005). doi:10.1029/2004JA010745
O. Olmedo, J. Zhang, Partial torus instability. Astrophys. J. 718, 433–440 (2010). doi:10.1088/0004-637X/718/1/433
V.A. Osherovich, C.J. Farrugia, L.F. Burlaga, Dynamics of aging magnetic clouds. Adv. Space Res. 13, 57–62 (1993). doi:10.1016/0273-1177(93)90391-N
M. Owens, P. Cargill, Predictions of the arrival time of coronal mass ejections at 1 AU: an analysis of the causes of errors. Ann. Geophys. 22, 661–671 (2004). doi:10.5194/angeo-22-661-2004
M.J. Owens, P.J. Cargill, C. Pagel, G.L. Siscoe, N.U. Crooker, Characteristic magnetic field and speed properties of interplanetary coronal mass ejections and their sheath regions. J. Geophys. Res. 110, A01105 (2005). doi:10.1029/2004JA010814
P. Pagano, J.C. Raymond, F. Reale, S. Orlando, Modeling magnetohydrodynamics and non-equilibrium SoHO/UVCS line emission of CME shocks. Astron. Astrophys. 481, 835–844 (2008). arXiv:0801.2705. doi:10.1051/0004-6361:20079088
G. Paschmann, B.U.O. Sonnerup, Proper frame determination and Walen test, in ISSI Scientific Reports Series, vol. 8 (2008), pp. 65–74
V.J. Pizzo, Interplanetary shocks on the large scale—a retrospective on the last decade’s theoretical efforts, in Washington DC American Geophysical Union Geophysical Monograph Series, vol. 35 (1985), pp. 51–68
S.P. Plunkett, B.J. Thompson, O.C. St. Cyr, R.A. Howard, Solar source regions of coronal mass ejections and their geomagnetic effects. J. Atmos. Sol.-Terr. Phys. 63, 389–402 (2001). doi:10.1016/S1364-6826(00)00166-8
S. Poedts, B. van der Holst, I. Chattopadhyay, D. Banerjee, T. van Lier, R. Keppens, Simulation of shock waves in the interplanetary medium, in Solar Variability as an Input to the Earth’s Environment, ed. by A. Wilson. ESA Special Publication, vol. 535 (2003), pp. 603–612
A.J. Prise, L.K. Harra, S.A. Matthews, C.S. Arridge, N. Achilleos, Analysis of a coronal mass ejection and corotating interaction region as they travel from the Sun passing Venus, Earth, Mars, and Saturn. J. Geophys. Res. 120, 1566–1588 (2015). doi:10.1002/2014JA020256
J.C. Raymond, B.J. Thompson, O.C. St. Cyr, N. Gopalswamy, S. Kahler, M. Kaiser, A. Lara, A. Ciaravella, M. Romoli, R. O’Neal, SOHO and radio observations of a CME shock wave. Geophys. Res. Lett. 27, 1439–1442 (2000). doi:10.1029/1999GL003669
D.V. Reames, The two sources of solar energetic particles. Space Sci. Rev. 175, 53–92 (2013). arXiv:1306.3608. doi:10.1007/s11214-013-9958-9
A. Reinard, Comparison of interplanetary CME charge state composition with CME-associated flare magnitude. Astrophys. J. 620, 501–505 (2005). doi:10.1086/426109
M.J. Reiner, M.L. Kaiser, J. Fainberg, R.G. Stone, A new method for studying remote type II radio emissions from coronal mass ejection-driven shocks. J. Geophys. Res. 103, 29,651–29,664 (1998). doi:10.1029/98JA02614
M.J. Reiner, A. Vourlidas, O.C. St. Cyr, J.T. Burkepile, R.A. Howard, M.L. Kaiser, N.P. Prestage, J.L. Bougeret, Constraints on coronal mass ejection dynamics from simultaneous radio and white-light observations. Astrophys. J. 590, 533–546 (2003). doi:10.1086/374917
M.J. Reiner, B.V. Jackson, D.F. Webb, D.R. Mizuno, M.L. Kaiser, J.L. Bougeret, Coronal mass ejection kinematics deduced from white light (Solar Mass Ejection Imager) and radio (Wind/WAVES) observations. J. Geophys. Res. 110, A09S14 (2005a). doi:10.1029/2004JA010943
M.J. Reiner, M.L. Kaiser, J.L. Bougeret, CME kinematics in interplanetary space, in Solar Wind 11/SOHO 16, Connecting Sun and Heliosphere, ed. by B. Fleck, T.H. Zurbuchen, H. Lacoste. ESA Special Publication, vol. 592 (2005b), p. 307
D.B. Reisenfeld, J.T. Gosling, R.J. Forsyth, P. Riley, O.C. St. Cyr, Properties of high-latitude CME-driven disturbances during Ulysses second northern polar passage. Geophys. Res. Lett. 30, 8031 (2003). doi:10.1029/2003GL017155
I.G. Richardson, H.V. Cane, Identification of interplanetary coronal mass ejections at 1 AU using multiple solar wind plasma composition anomalies. J. Geophys. Res. 109, A09104 (2004a). doi:10.1029/2004JA010598
I.G. Richardson, H.V. Cane, The fraction of interplanetary coronal mass ejections that are magnetic clouds: evidence for a solar cycle variation. Geophys. Res. Lett. 31, L18804 (2004b). doi:10.1029/2004GL020958
I.G. Richardson, H.V. Cane, Interplanetary circumstances of quasi-perpendicular interplanetary shocks in 1996–2005. J. Geophys. Res. 115, A07103 (2010a). doi:10.1029/2009JA015039
I.G. Richardson, H.V. Cane, Near-Earth interplanetary coronal mass ejections during Solar Cycle 23 (1996–2009): catalog and summary of properties. Sol. Phys. 264, 189–237 (2010b). doi:10.1007/s11207-010-9568-6
I.G. Richardson, G.R. Lawrence, D.K. Haggerty, T.A. Kucera, A. Szabo, Are CME “interactions” really important for accelerating major solar energetic particle events? Geophys. Res. Lett. 30, 8014 (2003). doi:10.1029/2002GL016424
P. Riley, N.U. Crooker, Kinematic treatment of coronal mass ejection evolution in the solar wind. Astrophys. J. 600, 1035–1042 (2004). doi:10.1086/379974
P. Riley, J.T. Gosling, On the origin of near-radial magnetic fields in the heliosphere: numerical simulations. J. Geophys. Res. 112, A06115 (2007). doi:10.1029/2006JA012210
P. Riley, J.T. Gosling, V.J. Pizzo, A two-dimensional simulation of the radial and latitudinal evolution of a solar wind disturbance driven by a fast, high-pressure coronal mass ejection. J. Geophys. Res. 102, 14,577 (1997)
P. Riley, J.T. Gosling, D.J. McComas, V.J. Pizzo, J.G. Luhmann, D. Biesecker, R.J. Forsyth, J.T. Hoeksema, A. Lecinski, B.J. Thompson, Relationship between Ulysses plasma observations and solar observations during the Whole Sun Month campaign. J. Geophys. Res. 104, 9871–9880 (1999). doi:10.1029/1998JA900078
P. Riley, J.A. Linker, Z. Mikić, D. Odstrcil, T.H. Zurbuchen, D. Lario, R.P. Lepping, Using an MHD simulation to interpret the global context of a coronal mass ejection observed by two spacecraft. J. Geophys. Res. 108, 1272 (2003). doi:10.1029/2002JA009760
P. Riley, J.A. Linker, Z. Mikic, D. Odstrcil, Magnetohydrodynamic modeling of interplanetary CMEs. IEEE Trans. Plasma Sci. 32, 1415–1424 (2004)
T. Rollett, C. Möstl, M. Temmer, A.M. Veronig, C.J. Farrugia, H.K. Biernat, Constraining the kinematics of coronal mass ejections in the inner heliosphere with in-situ signatures. Sol. Phys. 276, 293–314 (2012). arXiv:1110.0300. doi:10.1007/s11207-011-9897-0
T. Rollett, C. Möstl, M. Temmer, R.A. Frahm, J.A. Davies, A.M. Veronig, B. Vršnak, U.V. Amerstorfer, C.J. Farrugia, T. Žic, T.L. Zhang, Combined multipoint remote and in situ observations of the asymmetric evolution of a fast solar coronal mass ejection. Astrophys. J. Lett. 790, L6 (2014). arXiv:1407.4687. doi:10.1088/2041-8205/790/1/L6
I.I. Roussev, N. Lugaz, I.V. Sokolov, New physical insight on the changes in magnetic topology during coronal mass ejections: case studies for the 2002 April 21 and August 24 events. Astrophys. J. Lett. 668, L87–L90 (2007). doi:10.1086/522588
A. Ruffenach, B. Lavraud, M.J. Owens, J.A. Sauvaud, N.P. Savani, A.P. Rouillard, P. Démoulin, C. Foullon, A. Opitz, A. Fedorov, C.J. Jacquey, V. Génot, P. Louarn, J.G. Luhmann, C.T. Russell, C.J. Farrugia, A.B. Galvin, Multispacecraft observation of magnetic cloud erosion by magnetic reconnection during propagation. J. Geophys. Res. 117, A09101 (2012). doi:10.1029/2012JA017624
A. Ruffenach, B. Lavraud, C.J. Farrugia, P. Démoulin, S. Dasso, M.J. Owens, J.A. Sauvaud, A.P. Rouillard, A. Lynnyk, C. Foullon, N.P. Savani, J.G. Luhmann, A.B. Galvin, Statistical study of magnetic cloud erosion by magnetic reconnection. J. Geophys. Res. 120, 43–60 (2015). doi:10.1002/2014JA020628
D.M. Rust, B.J. Anderson, M.D. Andrews, M.H. Acuña, C.T. Russell, P.W. Schuck, T. Mulligan, Comparison of interplanetary disturbances at the NEAR spacecraft with coronal mass ejections at the Sun. Astrophys. J. 621, 524–536 (2005). doi:10.1086/427401
C. Salas-Matamoros, K.L. Klein, On the statistical relationship between CME speed and soft X-ray flux and fluence of the associated flare. Sol. Phys. 290, 1337–1353 (2015). arXiv:1503.08613. doi:10.1007/s11207-015-0677-0
N.P. Savani, A.P. Rouillard, J.A. Davies, M.J. Owens, R.J. Forsyth, C.J. Davis, R.A. Harrison, The radial width of a coronal mass ejection between 0.1 and 0.4 AU estimated from the Heliospheric Imager on STEREO. Ann. Geophys. 27, 4349–4358 (2009)
N.P. Savani, M.J. Owens, A.P. Rouillard, R.J. Forsyth, J.A. Davies, Observational evidence of a coronal mass ejection distortion directly attributable to a structured solar wind. Astrophys. J. Lett. 714, L128–L132 (2010). doi:10.1088/2041-8205/714/1/L128
J.M. Schmidt, P.J. Cargill, Magnetic reconnection between magnetic cloud and the solar wind. J. Geophys. Res. 108(A1), 1023 (2003). doi:10.1029/2002JA009325
J. Schmidt, P. Cargill, A numerical study of two interacting coronal mass ejections. Ann. Geophys. 22, 2245–2254 (2004)
J.M. Schmidt, I.H. Cairns, H. Xie, O.C. St. Cyr, N. Gopalswamy, CME flux rope and shock identifications and locations: comparison of white light data, Graduated Cylindrical Shell model, and MHD simulations. J. Geophys. Res. 121, 1886–1906 (2016). doi:10.1002/2015JA021805
B. Schmieder, G. Simon, M.J. Martres, P. Mein, N. Mein, E. Tandberg-Hanssen, Recurrent mass ejections observed in H-alpha and CIV. Adv. Space Res. 4, 27–30 (1984). doi:10.1016/0273-1177(84)90154-6
C.J. Schrijver, A.M. Title, Long-range magnetic couplings between solar flares and coronal mass ejections observed by SDO and STEREO. J. Geophys. Res. 116, A04108 (2011). doi:10.1029/2010JA016224
R. Schwenn, H. Rosenbauer, K.H. Muehlhaeuser, Singly-ionized helium in the driver gas of an interplanetary shock wave. Geophys. Res. Lett. 7, 201–204 (1980). doi:10.1029/GL007i003p00201
R. Schwenn, A. dal Lago, E. Huttunen, W.D. Gonzalez, The association of coronal mass ejections with their effects near the Earth. Ann. Geophys. 23, 1033–1059 (2005)
A. Shanmugaraju, B. Vršnak, Transit time of coronal mass ejections under different ambient solar wind conditions. Sol. Phys. 289, 339–349 (2014). doi:10.1007/s11207-013-0322-8
N.R. Sheeley, J.H. Walters, Y.M. Wang, R.A. Howard, Continuous tracking of coronal outflows: two kinds of coronal mass ejections. J. Geophys. Res. 104, 24,739–24,767 (1999)
C. Shen, Y. Wang, B. Gui, P. Ye, S. Wang, Kinematic evolution of a slow CME in corona viewed by STEREO-B on 8 October 2007. Sol. Phys. 269, 389–400 (2011). arXiv:1101.3205. doi:10.1007/s11207-011-9715-8
C. Shen, Y. Wang, S. Wang, Y. Liu, R. Liu, A. Vourlidas, B. Miao, P. Ye, J. Liu, Z. Zhou, Super-elastic collision of large-scale magnetized plasmoids in the heliosphere. Nat. Phys. 8, 923–928 (2012). doi:10.1038/nphys2440
F. Shen, C. Shen, Y. Wang, X. Feng, C. Xiang, Could the collision of CMEs in the heliosphere be super-elastic? Validation through three-dimensional simulations. Geophys. Res. Lett. 40, 1457–1461 (2013). doi:10.1002/grl.50336
F. Shen, Y. Wang, C. Shen, X. Feng, Turn on the super-elastic collision nature of coronal mass ejections through low approaching speed. Sci. Rep. 6, 19576 (2016). doi:10.1038/srep19576
T. Shi, Y. Wang, L. Wan, X. Cheng, M. Ding, J. Zhang, Predicting the arrival time of coronal mass ejections with the graduated cylindrical shell and drag force model. Astrophys. J. 806, 271 (2015). arXiv:1505.00884. doi:10.1088/0004-637X/806/2/271
D. Shiota, R. Kataoka, Magnetohydrodynamic simulation of interplanetary propagation of multiple coronal mass ejections with internal magnetic flux rope (SUSANOO-CME). Space Weather 14, 56–75 (2016). doi:10.1002/2015SW001308
D. Shiota, K. Kusano, T. Miyoshi, K. Shibata, Magnetohydrodynamic modeling for a formation process of coronal mass ejections: interaction between an ejecting flux rope and an ambient field. Astrophys. J. 718, 1305–1314 (2010). arXiv:1006.0307. doi:10.1088/0004-637X/718/2/1305
D.G. Sime, A.J. Hundhausen, The coronal mass ejection of July 6, 1980—a candidate for interpretation as a coronal shock wave. J. Geophys. Res. 92, 1049–1055 (1987)
G. Siscoe, D. Odstrcil, Ways in which ICME sheaths differ from magnetosheaths. J. Geophys. Res. 113, A00B07 (2008). doi:10.1029/2008JA013142
R.M. Skoug, S.J. Bame, W.C. Feldman, J.T. Gosling, D.J. McComas, J.T. Steinberg, R.L. Tokar, P. Riley, L.F. Burlaga, N.F. Ness, C.W. Smith, A prolonged \(\mbox{He}^{+}\) enhancement within a coronal mass ejection in the solar wind. Geophys. Res. Lett. 26, 161–164 (1999). doi:10.1029/1998GL900207
R.M. Skoug, W.C. Feldman, J.T. Gosling, D.J. McComas, C.W. Smith, Solar wind electron characteristics inside and outside coronal mass ejections. J. Geophys. Res. 105(23), 069 (2000). 084. doi:10.1029/2000JA000017
D.F. Smart, M.A. Shea, A simplified model for timing the arrival of solar flare-initiated shocks. J. Geophys. Res. 90, 183–190 (1985). doi:10.1029/JA090iA01p00183
Z. Smith, M. Dryer, MHD study of temporal and spatial evolution of simulated interplanetary shocks in the ecliptic plane within 1 AU. Sol. Phys. 129, 387–405 (1990). doi:10.1007/BF00159049
C.W. Smith, N.F. Ness, L.F. Burlaga, R.M. Skoug, D.J. McComas, T.H. Zurbuchen, G. Gloeckler, D.K. Haggerty, R.E. Gold, M.I. Desai, G.M. Mason, J.E. Mazur, J.R. Dwyer, M.A. Popecki, E. Möbius, C.M.S. Cohen, R.A. Leske, ACE observations of the Bastille day 2000 interplanetary disturbances. Sol. Phys. 204, 227–252 (2001). doi:10.1023/A:1014265108171
O.C. St. Cyr, S.P. Plunkett, D.J. Michels, S.E. Paswaters, M.J. Koomen, G.M. Simnett, B.J. Thompson, J.B. Gurman, R. Schwenn, D.F. Webb, E. Hildner, P.L. Lamy, Properties of coronal mass ejections: SOHO LASCO observations from January 1996 to June 1998. J. Geophys. Res. 105, 18,169–18,186 (2000). doi:10.1029/1999JA000381
R.S. Steinolfson, Coronal evolution due to shear motion. Astrophys. J. 382, 677–687 (1991). doi:10.1086/170755
R.S. Steinolfson, M. Dryer, Numerical simulation of MHD shock waves in the solar wind. J. Geophys. Res. 83, 1576–1582 (1978). doi:10.1029/JA083iA04p01576
D. Sudar, B. Vršnak, M. Dumbović, Predicting coronal mass ejections transit times to Earth with neural network. Mon. Not. R. Astron. Soc. 456, 1542–1548 (2016). arXiv:1511.07620. doi:10.1093/mnras/stv2782
A. Taktakishvili, M. Kuznetsova, P. MacNeice, M. Hesse, L. Rastätter, A. Pulkkinen, A. Chulaki, D. Odstrcil, Validation of the coronal mass ejection predictions at the Earth orbit estimated by ENLIL heliosphere cone model. Space Weather 7, S03004 (2009). doi:10.1029/2008SW000448
S.J. Tappin, The deceleration of an interplanetary transient from the Sun to 5 AU. Sol. Phys. 233, 233–248 (2006). doi:10.1007/s11207-006-2065-2
M. Temmer, N.V. Nitta, Interplanetary propagation behavior of the fast coronal mass ejection on 23 July 2012. Sol. Phys. 290, 919–932 (2015). arXiv:1411.6559. doi:10.1007/s11207-014-0642-3
M. Temmer, T. Rollett, C. Möstl, A.M. Veronig, B. Vršnak, D. Odstrčil, Influence of the ambient solar wind flow on the propagation behavior of interplanetary coronal mass ejections. Astrophys. J. 743, 101–112 (2011). doi:10.1088/0004-637X/743/2/101
M. Temmer, B. Vršnak, T. Rollett, B. Bein, C.A. de Koning, Y. Liu, E. Bosman, J.A. Davies, C. Möstl, T. Žic, A.M. Veronig, V. Bothmer, R. Harrison, N. Nitta, M. Bisi, O. Flor, J. Eastwood, D. Odstrcil, R. Forsyth, Characteristics of kinematics of a coronal mass ejection during the 2010 August 1 CME-CME interaction event. Astrophys. J. 749, 57 (2012). arXiv:1202.0629. doi:10.1088/0004-637X/749/1/57
M. Temmer, A.M. Veronig, V. Peinhart, B. Vršnak, Asymmetry in the CME-CME interaction process for the events from 2011 February 14–15. Astrophys. J. 785, 85 (2014). doi:10.1088/0004-637X/785/2/85
A. Thernisien, A. Vourlidas, R.A. Howard, Forward modeling of coronal mass ejections using STEREO/SECCHI data. Sol. Phys. 256, 111–130 (2009). doi:10.1007/s11207-009-9346-5
W.T. Thompson, Strong rotation of an erupting quiescent polar crown prominence. J. Atmos. Sol.-Terr. Phys. 73, 1138–1147 (2011). doi:10.1016/j.jastp.2010.07.005
W.T. Thompson, B. Kliem, T. Török, 3D reconstruction of a rotating erupting prominence. Sol. Phys. 276, 241–259 (2012). arXiv:1112.3388. doi:10.1007/s11207-011-9868-5
V.S. Titov, P. Démoulin, Basic topology of twisted magnetic configurations in solar flares. Astron. Astrophys. 351, 707–720 (1999)
V.S. Titov, T. Török, Z. Mikic, J.A. Linker, A method for embedding circular force-free flux ropes in potential magnetic fields. Astrophys. J. 790, 163 (2014). doi:10.1088/0004-637X/790/2/163
T. Török, B. Kliem, The evolution of twisting coronal magnetic flux tubes. Astron. Astrophys. 406, 1043–1059 (2003). doi:10.1051/0004-6361:20030692
T. Török, B. Kliem, Confined and ejective eruptions of kink-unstable flux ropes. Astrophys. J. Lett. 630, L97–L100 (2005). arXiv:astro-ph/0507662. doi:10.1086/462412
T. Török, B. Kliem, V.S. Titov, Ideal kink instability of a magnetic loop equilibrium. Astron. Astrophys. 413, L27–L30 (2004). arXiv:astro-ph/0311198. doi:10.1051/0004-6361:20031691
T. Török, M.A. Berger, B. Kliem, The writhe of helical structures in the solar corona. Astron. Astrophys. 516, A49 (2010). arXiv:1004.3918. doi:10.1051/0004-6361/200913578
T. Török, O. Panasenco, V.S. Titov, Z. Mikić, K.K. Reeves, M. Velli, J.A. Linker, G. De Toma, A model for magnetically coupled sympathetic eruptions. Astrophys. J. Lett. 739, L63 (2011). doi:10.1088/2041-8205/739/2/L63
G. Tóth, D.L.D. Zeeuw, T.I. Gombosi, W.B. Manchester IV, A.J. Ridley, I.V. Sokolov, I.I. Roussev, Sun to thermosphere simulation of the October 28–30, 2003 storm with the Space Weather Modeling Framework. Space Weather 5, S06,003 (2007). doi:10.1029/2006SW000272
R. Tousey, The solar corona, in Space Research Conference, Space Research Conference, vol. 2, ed. by M.J. Rycroft, S.K. Runcorn (1973), pp. 713–730
J. Uwamahoro, L.A. McKinnell, J.B. Habarulema, Estimating the geoeffectiveness of halo CMEs from associated solar and IP parameters using neural networks. Ann. Geophys. 30, 963–972 (2012). doi:10.5194/angeo-30-963-2012
F. Valach, M. Revallo, J. Bochníček, P. Hejda, Solar energetic particle flux enhancement as a predictor of geomagnetic activity in a neural network-based model. Space Weather 7, S04004 (2009). doi:10.1029/2008SW000421
B. van der Holst, W.B. Manchester IV, I. Sokolov, G. Tóth, T. Gombosi, D.D. Zeeuw, O. Cohen, Breakout coronal mass ejection or streamer blowout: the bugle effect. Astrophys. J. 693, 1178–1187 (2009)
B. van der Holst, W.B. Manchester IV, R. Frazin, A. Vásquez, G. Tóth, T. Gombosi, A data-driven, two-temperature solar wind model with Alfvén waves. Astrophys. J. 725, 1373–1383 (2010). doi:10.1088/0004-637X/725/1/1373
B. van der Holst, I. Sokolov, X. Meng, M. Jin, W.B. Manchester IV, G. Tóth, T.I. Gombosi, Alfvén wave solar model (AWSOM): coronal heating. Astrophys. J. 782, 81 (2014). doi:10.1088/0004-637X/782/2/81
M. Vandas, S. Fischer, M. Dryer, Z. Smith, T. Detman, Simulation of magnetic cloud propagation in the inner heliosphere in two dimensions 2. A loop parallel to the ecliptic plane and the role of helicity. J. Geophys. Res. 101, 2505–2510 (1996). doi:10.1029/95JA02446
M. Vandas, S. Fischer, P. Pelant, M. Dryer, Z. Smith, T. Detman, Propagation of a spheromac: 1. Some comparisons of cylindrical and spherical magnetic clouds. J. Geophys. Res. 102, 24,183 (1997)
P. Vemareddy, C. Möstl, T. Amerstorfer, W. Mishra, C. Farrugia, M. Leitner, Comparison of magnetic properties in a magnetic cloud and its solar source on 2013 April 11–14. Astrophys. J. 828, 12 (2016). arXiv:1607.03811. doi:10.3847/0004-637X/828/1/12
A. Vourlidas, S.T. Wu, A. Wang, P. Subramanian, R.A. Howard, Direct detection of a CME-associated shock in LASCO white light images. Astrophys. J. 598, 1392 (2003)
A. Vourlidas, R. Colaninno, T. Nieves-Chinchilla, G. Stenborg, The first observation of a rapidly rotating coronal mass ejection in the middle corona. Astrophys. J. 733, L23 (2011). doi:10.1088/2041-8205/733/2/L23
B. Vršnak, Deceleration of coronal mass ejections. Sol. Phys. 202, 173–189 (2001)
B. Vršnak, Processes and mechanisms governing the initiation and propagation of CMEs. Ann. Geophys. 26, 3089–3101 (2008)
B. Vršnak, N. Gopalswamy, Influence of the aerodynamic drag on the motion of interplanetary ejecta. J. Geophys. Res. 107, SSH2 (2002). doi:10.1029/2001JA000120
B. Vršnak, T. Žic, Transit times of interplanetary coronal mass ejections and the solar wind speed. Astron. Astrophys. 472, 937–943 (2007). doi:10.1051/0004-6361:20077499
B. Vršnak, D. Ruždjak, D. Sudar, N. Gopalswamy, Kinematics of coronal mass ejections between 2 and 30 solar radii. What can be learned about forces governing the eruption? Astron. Astrophys. 423, 717–728 (2004). doi:10.1051/0004-6361:20047169
B. Vršnak, D. Maričić, A.L. Stanger, A.M. Veronig, M. Temmer, D. Roša, Acceleration phase of coronal mass ejections: I. Temporal and spatial scales. Sol. Phys. 241, 85–98 (2007). doi:10.1007/s11207-006-0290-3
B. Vršnak, D. Vrbanec, J. Čalogović, Dynamics of coronal mass ejections. The mass-scaling of the aerodynamic drag. Astron. Astrophys. 490, 811–815 (2008). doi:10.1051/0004-6361:200810215
B. Vršnak, T. Žic, T.V. Falkenberg, C. Möstl, S. Vennerstrom, D. Vrbanec, The role of aerodynamic drag in propagation of interplanetary coronal mass ejections. Astron. Astrophys. 512, A43 (2010). doi:10.1051/0004-6361/200913482
B. Vršnak, T. Žic, D. Vrbanec, M. Temmer, T. Rollett, C. Möstl, A. Veronig, J. Čalogović, M. Dumbović, S. Lulić, Y.J. Moon, A. Shanmugaraju, Propagation of interplanetary coronal mass ejections: the drag-based model. Sol. Phys. 285, 295–315 (2013). doi:10.1007/s11207-012-0035-4
B. Vršnak, M. Temmer, T. Žic, A. Taktakishvili, M. Dumbović, C. Möstl, A.M. Veronig, M.L. Mays, D. Odstrčil, Heliospheric propagation of coronal mass ejections: comparison of numerical WSA-ENLIL+cone model and analytical drag-based model. Astrophys. J. Suppl. Ser. 213, 21 (2014). doi:10.1088/0067-0049/213/2/21
C. Wang, J.D. Richardson, L. Burlaga, Propagation of the Bastille day 2000 CME shock in the outer heliosphere. Sol. Phys. 204, 413–423 (2001). doi:10.1023/A:1014293527951
Y.M. Wang, P.Z. Ye, S. Wang, Multiple magnetic clouds: several examples during March-April 2001. J. Geophys. Res. 108, 6 (2003a)
Y.M. Wang, P.Z. Ye, S. Wang, M. Xiong, Theoretical analysis on the geoeffectiveness of a shock overtaking a preceding magnetic cloud. Sol. Phys. 216, 295–310 (2003b). doi:10.1023/A:1026150630940
Y.M. Wang, P.Z. Ye, S. Wang, X.H. Xue, An interplanetary cause of large geomagnetic storms: fast forward shock overtaking preceding magnetic cloud. Geophys. Res. Lett. 30, 33 (2003c)
Y. Wang, C. Shen, S. Wang, P. Ye, Deflection of coronal mass ejection in the interplanetary medium. Sol. Phys. 222, 329–343 (2004). doi:10.1023/B:SOLA.0000043576.21942.aa
Y.M. Wang, H. Zheng, S. Wang, P. Ye, MHD simulation of the formation and propagation of multiple magnetic clouds in the heliosphere. Astron. Astrophys. 434, 309–316 (2005)
Y. Wang, C. Chen, B. Gui, C. Shen, P. Ye, S. Wang, Statistical study of coronal mass ejection source locations: understanding CMEs viewed in coronagraphs. J. Geophys. Res. 116, A04104 (2011). arXiv:1101.0641. doi:10.1029/2010JA016101
R. Wang, Y.D. Liu, Z. Yang, H. Hu, Magnetic field restructuring associated with two successive solar eruptions. Astrophys. J. 791, 84 (2014a). arXiv:1407.4004. doi:10.1088/0004-637X/791/2/84
Y. Wang, B. Wang, C. Shen, F. Shen, N. Lugaz, Deflected propagation of a coronal mass ejection from the corona to interplanetary space. J. Geophys. Res. 119, 5117–5132 (2014b). arXiv:1406.4684. doi:10.1002/2013JA019537
R. Wang, Y.D. Liu, X. Dai, Z. Yang, C. Huang, H. Hu, The role of active region coronal magnetic field in determining coronal mass ejection propagation direction. Astrophys. J. 814, 80 (2015). arXiv:1510.06177. doi:10.1088/0004-637X/814/1/80
R. Wang, Y.D. Liu, I. Zimovets, H. Hu, X. Dai, Z. Yang, Sympathetic solar filament eruptions. Astrophys. J. Lett. 827, L12 (2016a). arXiv:1608.01067. doi:10.3847/2041-8205/827/1/L12
Y. Wang, Q. Zhang, J. Liu, C. Shen, F. Shen, Z. Yang, T. Zic, B. Vrsnak, D.F. Webb, R. Liu, S. Wang, J. Zhang, Q. Hu, B. Zhuang, On the propagation of a geoeffective coronal mass ejection during 15–17 March 2015. J. Geophys. Res. 121, 7423–7434 (2016b). arXiv:1607.07750. doi:10.1002/2016JA022924
D.F. Webb, T.A. Howard, Coronal mass ejections: observations. Living Rev. Sol. Phys. 9, 3 (2012). doi:10.12942/lrsp-2012-3
D.F. Webb, D.R. Mizuno, A. Buffington, M.P. Cooke, C.J. Eyles, C.D. Fry, L.C. Gentile, P.P. Hick, P.E. Holladay, T.A. Howard, J.G. Hewitt, B.V. Jackson, J.C. Johnston, T.A. Kuchar, J.B. Mozer, S. Price, R.R. Radick, G.M. Simnett, S.J. Tappin, Solar Mass Ejection Imager (SMEI) observations of Coronal Mass Ejections (CMEs) in the heliosphere. J. Geophys. Res. 111(A10), A12101 (2006). doi:10.1029/2006JA011655
F.S. Wei, The blast wave propagating in a moving medium with variable density. Chin. J. Space Sci. 2, 63–72 (1982)
F. Wei, M. Dryer, Propagation of solar flare-associated interplanetary shock waves in the heliospheric meridional plane. Sol. Phys. 132, 373–394 (1991). doi:10.1007/BF00152294
R.M. Winslow, N. Lugaz, N.A. Schwadron, C.J. Farrugia, W. Yu, J.M. Raines, M.L. Mays, A.B. Galvin, T.H. Zurbuchen, Longitudinal conjunction between MESSENGER and STEREO A: development of ICME complexity through stream interactions. J. Geophys. Res. 121, 6092–6106 (2016). doi:10.1002/2015JA022307
B.E. Wood, R.A. Howard, An empirical reconstruction of the 2008 April 26 coronal mass ejection. Astrophys. J. 702, 901–910 (2009). doi:10.1088/0004-637X/702/2/901
B.E. Wood, R.A. Howard, S.P. Plunkett, D.G. Socker, Comprehensive observations of a solar minimum coronal mass ejection with the solar terrestrial relations observatory. Astrophys. J. 694, 707–717 (2009). arXiv:0811.3226. doi:10.1088/0004-637X/694/2/707
B.E. Wood, C.C. Wu, A.P. Rouillard, R.A. Howard, D.G. Socker, A coronal hole’s effects on coronal mass ejection shock morphology in the inner heliosphere. Astrophys. J. 755, 43 (2012). arXiv:1206.3584. doi:10.1088/0004-637X/755/1/43
B.E. Wood, R.A. Howard, M.G. Linton, Imaging prominence eruptions out to 1 AU. Astrophys. J. 816, 67 (2016). arXiv:1512.06748. doi:10.3847/0004-637X/816/2/67
S.T. Wu, S.M. Han, M. Dryer, Two-dimensional, time-dependent MHD description of interplanetary disturbances simulation of high speed solar wind interactions. Planet. Space Sci. 27, 255–264 (1979). doi:10.1016/0032-0633(79)90068-0
S.T. Wu, R.S. Steinolfson, M. Dryer, E. Tandberg-Hanssen, Magnetohydrodynamic models of coronal transients in the meridional plane. IV—effect of the solar wind. Astrophys. J. 243, 641–643 (1981). doi:10.1086/158629
S.T. Wu, M.D. Andrews, S.P. Plunkett, Numerical Magnetohydrodynamic (MHD) modeling of Coronal Mass Ejections (CMEs). Space Sci. Rev. 95, 191–213 (2001)
S.T. Wu, A.H. Wang, N. Gopalswamy, MHD modelling of CME and CME interactions in a bi-modal solar wind: a preliminary analysis of the 20 January 2001 two CMEs interaction event, in ESA SP-505: SOLMAG 2002. Proceedings of the Magnetic Coupling of the Solar Atmosphere Euroconference (2002), pp. 227–230
H. Xie, O.C. St. Cyr, N. Gopalswamy, S. Yashiro, J. Krall, M. Kramar, J. Davila, On the origin, 3D structure and dynamic evolution of CMEs near solar minimum. Sol. Phys. 259, 143–161 (2009). doi:10.1007/s11207-009-9422-x
M. Xiong, H. Zheng, Y. Wang, S. Wang, Magnetohydrodynamic simulation of the interaction between interplanetary strong shock and magnetic cloud and its consequent geoeffectiveness. J. Geophys. Res. 111, A08105 (2006). doi:10.1029/2005JA011593
M. Xiong, H. Zheng, S. Wang, Magnetohydrodynamic simulation of the interaction between two interplanetary magnetic clouds and its consequent geoeffectiveness: 2. Oblique collision. J. Geophys. Res. A11, 101 (2009). doi:10.1029/2009JA014079
S. Yao, E. Marsch, C.Y. Tu, R. Schwenn, Identification of prominence ejecta by the proton distribution function and magnetic fine structure in interplanetary coronal mass ejections in the inner heliosphere. J. Geophys. Res. 115, A05103 (2010). doi:10.1029/2009JA014914
S. Yashiro, N. Gopalswamy, G. Michalek, O.C. St. Cyr, S.P. Plunkett, N.B. Rich, R.A. Howard, A catalog of white light coronal mass ejections observed by the SOHO spacecraft. J. Geophys. Res. A07, 105 (2004). doi:10.1029/2003JA010282
V. Yurchyshyn, Relationship between EIT posteruption arcades, coronal mass ejections, the coronal neutral line, and magnetic clouds. Astrophys. J. Lett. 675, L49–L52 (2008). arXiv:0710.1292. doi:10.1086/533413
V.B. Yurchyshyn, H. Wang, P.R. Goode, Y. Deng, Orientation of the magnetic fields in interplanetary flux ropes and solar filaments. Astrophys. J. 563, 381–388 (2001). doi:10.1086/323778
V. Yurchyshyn, Q. Hu, R.P. Lepping, B.J. Lynch, J. Krall, Orientations of LASCO Halo CMEs and their connection to the flux rope structure of interplanetary CMEs. Adv. Space Res. 40, 1821–1826 (2007). arXiv:astro-ph/0703627. doi:10.1016/j.asr.2007.01.059
X. Zhao, M. Dryer, Current status of CME/shock arrival time prediction. Space Weather 12, 448–469 (2014). doi:10.1002/2014SW001060
X.H. Zhao, X.S. Feng, Influence of a CME’s initial parameters on the arrival of the associated interplanetary shock at Earth and the shock propagational model version 3. Astrophys. J. 809, 44 (2015). doi:10.1088/0004-637X/809/1/44
X. Zhao, Y.D. Liu, B. Inhester, X. Feng, T. Wiegelmann, L. Lu, Comparison of CME/shock propagation models with heliospheric imaging and in situ observations. Astrophys. J. 830, 48 (2016). arXiv:1607.05533. doi:10.3847/0004-637X/830/1/48
Y.F. Zhou, X.S. Feng, MHD numerical study of the latitudinal deflection of coronal mass ejection. J. Geophys. Res. 118, 6007–6018 (2013). doi:10.1002/2013JA018976
G. Zhou, Y. Wang, J. Wang, Coronal mass ejections associated with polar crown filaments. Adv. Space Res. 38, 466–469 (2006). doi:10.1016/j.asr.2005.03.110
T. Žic, B. Vršnak, M. Temmer, Heliospheric propagation of coronal mass ejections: drag-based model fitting. Astrophys. J. Suppl. Ser. 218, 32 (2015). arXiv:1506.08582. doi:10.1088/0067-0049/218/2/32
F.P. Zuccarello, A. Bemporad, C. Jacobs, M. Mierla, S. Poedts, F. Zuccarello, The role of streamers in the deflection of coronal mass ejections: comparison between STEREO three-dimensional reconstructions and numerical simulations. Astrophys. J. 744, 66 (2012a). doi:10.1088/0004-637X/744/1/66
F.P. Zuccarello, Z. Meliani, S. Poedts, Numerical modeling of the initiation of coronal mass ejections in active region NOAA 9415. Astrophys. J. 758, 117 (2012b). doi:10.1088/0004-637X/758/2/117
T.H. Zurbuchen, I.G. Richardson, In-situ solar wind and magnetic field signatures of interplanetary coronal mass ejections. Space Sci. Rev. 123, 31–43 (2006). doi:10.1007/s11214-006-9010-4
T.H. Zurbuchen, G. Gloeckler, F. Ipavich, J. Raines, C.W. Smith, L.A. Fisk, On the fast coronal mass ejections in October/November 2003: ACE-SWICS results. Geophys. Res. Lett. L11, 805(2004). doi:10.1029/2004GL019461
Acknowledgements
W. M. was supported by NASA grant NNX16AL12G and NSF grant AGS1322543. E. K. acknowledges the University of Helsinki 3-year project and Academy of Finland project 1267087. Y. L. was supported by the Recruitment Program of Global Experts of China, NSFC under grant 41374173 and the Specialized Research Fund for State Key Laboratories of China. N. L. was supported by NASA grants NNX13AH94G and NNX15AB87G and NSF grant AGS1435785. T. T. acknowledges support by NASA’s LWS and HSR programs and by NSF grants AGS1249270, AGS1348577, and AGS1135432 (Sun-2-Ice). B. V. acknowledges support by Croatian Science Foundation under the project 6212 Solar and Stellar Variability. We acknowledge the International Space Science Institute (ISSI) in Bern Switzerland for their generous support and for travel and accomodations.
Author information
Authors and Affiliations
Corresponding author
Additional information
The Scientific Foundation of Space Weather
Edited by Rudolf von Steiger, Daniel Baker, André Balogh, Tamás Gombosi, Hannu Koskinen and Astrid Veronig
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Manchester, W., Kilpua, E.K.J., Liu, Y.D. et al. The Physical Processes of CME/ICME Evolution. Space Sci Rev 212, 1159–1219 (2017). https://doi.org/10.1007/s11214-017-0394-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11214-017-0394-0