The stability of 3-DOF triple-rigid-body pendulum system near resonances

Abstract

In this article, the motion of three degree-of-freedom (DOF) dynamical system consisting of a triple rigid body pendulum (TRBP) in the presence of three harmonically external moments is studied. In view of the generalized coordinates of the system, Lagrange's equations are used to obtain the governing system of equations of motion (EOM). The analytic approximate solutions are gained up to the third approximation utilizing the approach of multiple scales (AMS) as novel solutions. The solvability conditions are determined in accordance with the elimination of secular terms. Therefore, the arising various resonances cases have been categorized and the equations of modulation have been achieved. The temporal histories of the obtained approximate solutions, as well as the resonance curves, are visually displayed to reveal the positive effects of the various parameters on the dynamical motion. The numerical results of the governing system are achieved using the fourth-order Runge–Kutta method. The visually depicted comparison of asymptotic and numerical solutions demonstrates high accuracy of the employed perturbation approach. The criteria of Routh–Hurwitz are used to investigate the stability and instability zones, which are then analyzed in terms of steady-state solutions. The strength of this work stems from its uses in engineering vibrational control applications which carry the investigated system a huge amount of importance.

1 Introduction

Due to their widespread applicability in everyday life, pendulum models have piqued the curiosity of many scholars in recent decades, particularly the first two decades of this century. However, the dynamics of many different types of pendulums were examined using various methods whether they are analytical or numerical.

In [1], the authors examined the instability positions of an inverted pendulum, in which if its pivot is harmonically pushed up and down with suitable frequency and amplitude, then its instability position can be abolished. The parametric pendulum is used in [2] to show how non-harmonic perturbations can be used to flip from one dynamic state to the other without changing the system's intrinsic characteristics. In [3], the authors investigated the motion of a simple pendulum as a dynamical model with single generalized coordinate to examine its periodic movement on an elliptic route. On the other hand, the chaotic motion of 2-DOF weakly nonlinear spring pendulum system for a fixed and moving suspension point is examined in [4] and [5], respectively, to reveal their chaotic behaviors near resonance with respect to the used parameters. The ASM [6] is used in [7] to explore the stability of a nonlinear spring pendulum, in which the improvement of this work is investigated in [8] when the pendulum is subjected to an external force.

Numerous publications, such as [9,10,11,12,13], have investigated various routes of the suspension points for the linear and nonlinear elastic pendulums with various DOFs. In [9], the suspension point of a damped elastic pendulum (EP) moves in a circular path. The obtained results are generalized in [10] for an elliptic route of this point, in which the approximate solutions (AS) of some special cases are obtained. In [11], the authors considered such a problem when the pivot point has a trajectory of Lissajous curve, while the general outcomes of this work are found in [12] for the planar motion of an EP connected with a rigid body to produce a dynamical model with 3 DOFs on the same route of its suspension point. A special case of these results is found in [13] for a fixed point of suspension. The cases of linear and nonlinear damped EP carrying a rigid body, when the pivot point has a path of ellipse, is examined in [14, 15], respectively. The AMS is used in these works to gain the AS of the governing system of motion. Therefore, the requirements of solvability are obtained through the conditions of eliminating secular terms and the possible resonance cases are characterized. The vibrational motion of a rigid body regarding the equilibrium position is investigated numerically in [16] using the framework of ode45 solver of the Runge–Kutta method [17] from fourth order. Recently, a comparison between numerical solutions (NS) and the AS for the motions of rigid bodies pendulum is examined in [18, 19] to highlight the good reliability between them and to explore the high accuracy of the adopted perturbation approach. Moreover, the conditions of Routh–Hurwitz [20] have been used to ensure that steady-state solutions are stable and to evaluate their different stability regions.

On the other hand, the employment of the absorbers in the configuration of various constructions of dynamical models has piqued the interest of many researchers, e.g., [21,22,23,24,25,26] due to their applications in the vibrational control of engineering industries. In [21], the authors investigated how a longitudinal absorber may stabilize and regulate the vibration of a ship roll motion through the examination of the behavior of 3-DOF nonlinear spring pendulum. The behavior of a 2-DOF tuned absorber has been studied in [22] when the rotation of its suspension point is on an elliptic trajectory. The frequency response’s equations are used to analyze the steady-state solutions around the chosen resonance situation, in which the conditions of stability have been established. The influence of the existence of a damped nonlinear EP on the behavior of this problem is regulated in [23]. The stability analysis for the motion of a transverse absorber linked with a nonlinear elastic spring, according to the examined three cases of the system’s resonance, is presented in [24]. The vibrational analysis problem of a connected inverted pendulum with a passive mass for a spring absorber is addressed in [25]. In [26], the authors demonstrated how to modify automatically the rotating speed of a 2-DOF pendulum absorber by determining the phase between the primary structure's vibration and the absorber vibration, in which the response of absorber’s speed has been implemented.

Furthermore, there are other types of pendulums that have been studied in [27,28,29,30,31,32]. The motion of a double pendulum under the influence of a vibrating force and a gravity one in the situation of a vibrating point of suspension is investigated in [27]. The parametrically driven double pendulum and its bifurcation structure at tiny oscillation amplitudes are investigated in [28], while the resonance and non-resonance cases of a double pendulum are discussed in [29]. However, the motion of a system comprising of two attached physical pendulums swinging along horizontal axes is investigated in [30]. Examinations of the experimental and numerical results for the motion of a triple pendulum were investigated in [31,32,33,34]. In [31], numerical simulation of generic mechanical model with rigid motion limiters as well as the stability and bifurcation analysis is presented. On the other hand, the experimental rig and its corresponding dynamical model of the triple pendulum are provided in [32]. The piston-connecting rod–crankshaft system of a single-cylinder combustion engine is described in [33] as a particular case of a triple pendulum with barriers. High consistency between the experimental results and the numerical one for the motion of the same model is presented in [34]. The bifurcations and stability of high-frequency periodic motions with limited amplitude are also addressed, as well as the stability criteria. Recently, the stability analysis of un-stretched double pendulum and triple one when they are subjected to external harmonic moments and force are investigated in [35] and [36], respectively. The stability and instability zones for different parameters of the frequency responses are estimated.

This paper focuses on the motion of a plane dynamical system consisting of a TRBP with 3 DOFs under the impact of three harmonic external moments as a novel dynamical model. The governing system of motion, which is made up of a set of three second-order nonlinear differential equations, is derived using Lagrange's equations. The analytic approximation solutions strategy of this system, as novel solutions, is based on the use of the AMS. The prerequisites for solvability are met by removing secular terms. As a result, the arising resonance cases are identified, and the equations modulation are obtained. The frequency responses curves and the time histories of the derived solutions are drawn to highlight the good effects of various parameters on the motion. The fourth-order Runge–Kutta method is utilized to obtain the numerical results of the governing system. The juxtaposition of the analytical and numerical results demonstrates that the perturbation technique used is extremely accurate. The stability and instability domains are evaluated using Routh–Hurwitz conditions, and the steady-state solutions are analyzed.

2 Dynamical modeling

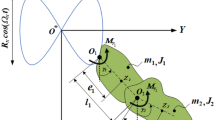
The investigated dynamical model in this work consists of three rigid bodies attached with each other and moving in a vertical plane under the influence of a gravity field with acceleration $g$ as shown in Fig. 1. The physical quantities $e_{j} \,(j = 1,2,3)$ and $l_{k} \,(k = 1,2)$ refer to the distance between the bodies gravity centers $z_{j}$ and the rotation centers $O_{j}$, and the link lengths of the first two pendulums, respectively. Furthermore, the mass and the moments of inertia of $jth$ links regarding to $z_{j}$ (orthogonal to the movement $xy$ plane) are represented by $m_{j}$ and $J_{j}$, respectively. The excitation moments operating on the links of the pendulums at $O_{j}$ are denoted by $M_{j} (t) = f_{j} \cos \Omega_{j} t$ (where $f_{j}$ and $\Omega_{j}$ are the amplitudes and frequencies of these moments), and the angular position’s variables are denoted by $\psi_{j} \,\,(j = 1,2,3)$. It is supposed that the resistance moments at $O_{j}$ have a viscous damping with coefficients $c_{j}$.

Fig. 1

Dynamical motion

Based on the above description, the kinetic energy $T$ and the potential one $V$ of the system can be stated as follows

$$ \begin{aligned} T & = \frac{1}{2}m_{1} e_{1}^{2} \dot{\psi }_{1}^{2} + \frac{1}{2}m_{2} [l_{1}^{2} \dot{\psi }_{1}^{2} + e_{2}^{2} \dot{\psi }_{2}^{2} + 2l_{1} e_{2} \dot{\psi }_{1} \dot{\psi }_{2} \cos (\psi_{1} - \psi_{2} )] \\ & \quad+ \frac{1}{2}m_{3} [l_{1}^{2} \dot{\psi }_{1}^{2} + l_{2}^{2} \dot{\psi }_{2}^{2} + e_{3}^{2} \dot{\psi }_{3}^{2} + 2l_{2} e_{3} \dot{\psi }_{2} \dot{\psi }_{3} \cos (\psi_{2} - \psi_{3} ) \\ & \quad+ 2l_{1} l_{2} \dot{\psi }_{1} \dot{\psi }_{2} \cos (\psi_{1} - \psi_{2} )\, + 2l_{1} e_{3} \dot{\psi }_{1} \dot{\psi }_{3} \cos (\psi_{1} - \psi_{3} )] \\ & \quad+ \frac{1}{2}J_{1} \dot{\psi }_{1}^{2} + \frac{1}{2}J_{2} \dot{\psi }_{2}^{2} + \frac{1}{2}J_{3} \dot{\psi }_{3}^{2} , \\ V & = - m_{1} g\,e_{1} \cos \psi_{1} - m_{2} g(e_{2} \cos \psi_{2} + l_{1} \cos \psi_{1} ) \\ & \quad- m_{3} g\,(e_{3} \cos \psi_{3} + l_{1} \cos \psi_{1} + l_{2} \cos \psi_{2} ). \\ \end{aligned} $$

(1)

The governing system of EOM can be constructed using the below Lagrange's equations [37]

$$ \frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{\partial L}{{\partial \dot{\psi }_{j} }}} \right) - \frac{\partial L}{{\partial \psi_{j} }} = Q_{j} ;\,\,\,\,\,L = T - V\,\,\,\,\,\,\,(j = 1,2,3), $$

(2)

where $\psi_{j}$ and $\dot{\psi }_{j}$ are the generalized coordinates and their corresponding velocities, while the generalized forces $Q_{j}$ have the forms

$$ \begin{aligned} Q_{1} & = f_{1} \cos (\Omega_{1} t) - c_{1} \dot{\psi }_{1} - c_{2} (\dot{\psi }_{1} - \dot{\psi }_{2} ), \\ Q_{2} & = f_{2} \cos (\Omega_{2} t) + c_{2} \dot{\psi }_{1} - (c_{2} + c_{3} )\dot{\psi }_{2} + c_{3} \dot{\psi }_{3} , \\ Q_{3} & = f_{3} \cos (\Omega_{3} t) + c_{3} \dot{\psi }_{2} - c_{3} \dot{\psi }_{3} . \\ \end{aligned} $$

(3)

Let us proceed with the dimensionless representations of the parameters we will be using

$$ \begin{aligned} B_{1} & = \frac{{m_{1} e_{1}^{2} + (m_{2} + m_{3} )l_{1}^{2} }}{{J_{{z_{1} }} }},\,\,\,\,\,\,B_{2} = \frac{{m_{2} e_{2}^{2} + m_{3} l_{2}^{2} }}{{J_{{z_{2} }} }},\,\,\,\,\,\, \\ B_{3} & = \frac{{m_{3} e_{3}^{2} }}{{J_{{z_{3} }} }},\,\,\,\,\,\,N_{1} = \frac{{m_{2} e_{2} l_{1} + m_{3} l_{1} l_{2} }}{{J_{{z_{1} }} }}, \\ N_{2} & = \frac{{m_{2} e_{2} l_{1} + m_{3} l_{1} l_{2} }}{{J_{{z_{2} }} }},\,\,\,\,\,\,N_{3} = \frac{{m_{3} e_{3} l_{2} }}{{J_{{z_{3} }} }},\,\,\,\,\,\,M_{1} = \frac{{m_{3} e_{3} l_{1} }}{{J_{{z_{1} }} }},\,\,\,\,\,\, \\ M_{2} & = \frac{{m_{3} e_{3} l_{2} }}{{J_{{z_{2} }} }},\,\,\,\,\,\,M_{3} = \frac{{m_{3} e_{3} l_{1} }}{{J_{{z_{3} }} }}, \\ \omega_{1}^{2} & = \frac{{m_{1} ge_{1} }}{{J_{{z_{1} }} }},\,\,\,\,\,\,\omega_{2}^{2} = \frac{{m_{2} ge_{2} }}{{J_{{z_{2} }} }},\,\,\,\,\,\,\omega_{3}^{2} = \frac{{m_{3} ge_{3} }}{{J_{{z_{3} }} }},\,\,\,\,\,\, \\ \omega^{2} & = \frac{{\omega_{2}^{2} }}{{\omega_{1}^{2} }},\,\,\,\,\,\,\,\tilde{\omega }^{2} = \frac{{\omega_{3}^{2} }}{{\omega_{1}^{2} }},\,\,\,\,\,\,S_{1} = \frac{{(m_{3} + m_{2} )gl_{1} }}{{J_{{z_{1} }} \omega_{1}^{2} }}, \\ S_{2} & = \frac{{m_{3} gl_{2} }}{{J_{{z_{2} }} \omega_{1}^{2} }},\,\,\,\,\,\,\,P_{1} = \frac{{\Omega_{1} }}{{\omega_{1} }},\,\,\,\,\,\,P_{2} = \frac{{\Omega_{2} }}{{\omega_{1} }},\,\,\,\,\,\, \\ P_{3} & = \frac{{\Omega_{3} }}{{\omega_{1} }},\,\,\,\,\,\,F_{1} = \frac{{Fe_{1} }}{{J_{{z_{1} }} \omega_{1}^{2} }},\,\,\,\,\,\,C_{1} = \frac{{c_{1} }}{{J_{{z_{1} }} \omega_{1} }},\,\,\,\,\,\, \\ C_{2} & = \frac{{c_{2} }}{{J_{{z_{1} }} \omega_{1} }},\,\,\,\,\,\,C_{3} = \frac{{c_{3} }}{{J_{{z_{2} }} \omega_{1} }},\,\,\,\,\,\,\mu_{1} = \frac{{c_{2} }}{{J_{{z_{2} }} \omega_{1} }},\,\,\,\,\,\,\\ \mu_{2} &= \frac{{c_{3} }}{{J_{{z_{3} }} \omega_{1} }},\,\,\,\,\,\,\tau = \omega_{1} \,t. \\ \end{aligned} $$

(4)

Making use of (1), (2), (3), and (4), we can get the following EOM in its dimensionless forms

$$ A\psi^{\prime\prime} + B\psi^{\prime} + C\psi^{{\prime}{2}} + D = F, $$

(5)

where

$$ \psi^{\prime\prime} = \left( {\begin{array}{*{20}c} {\psi^{\prime\prime}_{1} } \\ {\psi^{\prime\prime}_{2} } \\ {\psi^{\prime\prime}_{3} } \\ \end{array} } \right),\,\,\,\,\,\,\,\,\,\psi^{\prime} = \left( {\begin{array}{*{20}c} {\psi^{\prime}_{1} } \\ {\psi^{\prime}_{2} } \\ {\psi^{\prime}_{3} } \\ \end{array} } \right),\,\,\,\,\,\,\,\,\,\psi^{{\prime}{2}} = \left( {\begin{array}{*{20}c} {\psi{1}^{\prime 2} } \\ {\psi{2}^{\prime 2} } \\ {\psi{3}^{\prime 2} } \\ \end{array} } \right), $$

(6)

$$ A = \left( {\begin{array}{*{20}c} {1 + B_{1} } & {N_{1} \cos (\psi_{1} - \psi_{2} )} & {M_{1} \cos (\psi_{1} - \psi_{3} )} \\ {N_{2} \cos (\psi_{2} - \psi_{1} )} & {1 + B_{2} } & {M_{2} \cos (\psi_{2} - \psi_{3} )} \\ {M_{3} \cos (\psi_{1} - \psi_{3} )} & {N_{3} \cos (\psi_{3} - \psi_{2} )} & {1 + B_{3} } \\ \end{array} } \right), $$

$$ B = \left( {\begin{array}{*{20}c} {C_{1} + C_{2} } & { - C_{2} } & 0 \\ { - \mu_{1} } & {C_{3} + \mu_{1} } & { - C_{3} } \\ 0 & { - \mu_{2} } & {\mu_{2} } \\ \end{array} } \right), $$

$$ C = \left( {\begin{array}{*{20}c} 0 & {N_{1} \sin (\psi_{1} - \psi_{2} )} & {M_{1} \sin (\psi_{1} - \psi_{3} )} \\ {N_{2} \sin (\psi_{2} - \psi_{1} )} & 0 & {M_{2} \sin (\psi_{2} - \psi_{3} )} \\ {M_{3} \sin (\psi_{3} - \psi_{1} )} & {N_{3} \sin (\psi_{3} - \psi_{2} )} & 0 \\ \end{array} } \right),\, $$

$$ D = \left( {\begin{array}{*{20}c} {(1 + S_{1} )\sin \psi_{1} } \\ {(\omega^{2} + S_{2} )\sin \psi_{2} } \\ {\tilde{\omega }^{2} \sin \psi_{3} } \\ \end{array} } \right),\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,F = \left( {\begin{array}{*{20}c} {f_{1} \cos P_{1} \tau } \\ {f_{2} \cos P_{2} \tau } \\ {f_{3} \cos P_{3} \tau } \\ \end{array} } \right). $$

(7)

The foregoing set of Eq. (5) provides three second-order nonlinear differential equations in terms of $\psi_{j} \,\,(j = 1,2,3)$.

3 The recommended method

The goal of the present section is to use the AMS to acquire the AS of the preceding governing EOM and to classify the different resonances cases. To achieve this aim, the trigonometric function of $\psi_{j} \,\,(j = 1,2,3)$ can be approximated in the neighborhood of static equilibrium position up to the third order. Therefore, the system of EOM (5) can be rewritten as follows

$$ \begin{aligned} & (1 + B_{1} )\psi^{\prime\prime}_{1} + \frac{1}{36}[9(\psi_{1}^{2} - 2)(\psi_{2}^{2} - 2) + \psi_{1} \psi_{2} (\psi_{1}^{2} - 6)(\psi_{2}^{2} - 6)]N_{1} \psi^{\prime\prime}_{2} \\ &\quad + \frac{1}{36}[9(\psi_{1}^{2} - 2) \times (\psi_{3}^{2} - 2) + \psi_{1} \psi_{3} (\psi_{1}^{2} - 6)(\psi_{3}^{2} - 6)]M_{1} \psi^{\prime\prime}_{3} \\ & \quad+ \frac{1}{12}[\psi_{1} (\psi_{1}^{2} - 6)(\psi_{2}^{2} - 2) - \psi_{2} (\psi_{1}^{2} - 2) \times (\psi_{2}^{2} - 6)]N_{1} \psi{2}^{\prime 2} \\ &\quad + \frac{1}{12}[\psi_{1} (\psi_{1}^{2} - 6)(\psi_{3}^{2} - 2) - \psi_{3} (\psi_{1}^{2} - 2)(\psi_{3}^{2} - 6)]M_{1} \psi{3}^{\prime 2} \\ & \quad+ (1 + S_{1} ) \times \left( {\psi_{1} - \frac{{\psi_{1}^{3} }}{6}} \right) + (C_{1} + C_{2} )\psi^{\prime}_{1} - C_{2} \psi^{\prime}_{2} = f_{1} \cos P_{1} \tau , \\ \end{aligned} $$

(8)

$$ \begin{aligned} & (1 + B_{2} )\psi^{\prime\prime}_{2} + \frac{1}{36}[9(\psi_{1}^{2} - 2)(\psi_{2}^{2} - 2) + \psi_{1} \psi_{2} (\psi_{1}^{2} - 6)(\psi_{2}^{2} - 6)]N_{2} \psi^{\prime\prime}_{1} \\ &\quad + \frac{1}{36}[9(\psi_{2}^{2} - 2) \times (\psi_{3}^{2} - 2) + \psi_{2} \psi_{3} (\psi_{2}^{2} - 6)(\psi_{3}^{2} - 6)]M_{2} \psi^{\prime\prime}_{3} \\ & \quad- \frac{1}{12}[\psi_{1} (\psi_{1}^{2} - 6)(\psi_{2}^{2} - 2) - \psi_{2} (\psi_{1}^{2} - 2) \times (\psi_{2}^{2} - 6)]N_{2} \psi{1}^{\prime 2} \\ & \quad+ \frac{1}{12}[\psi_{2} (\psi_{2}^{2} - 6)(\psi_{3}^{2} - 2) - \psi_{3} (\psi_{2}^{2} - 2)(\psi_{3}^{2} - 6)]M_{2} \psi{3}^{\prime 2} + (\omega^{2} + S_{1} ) \\ &\quad \times \left( {\psi_{2} - \frac{{\psi_{2}^{3} }}{6}} \right) + (C_{3} + \mu_{1} )\psi^{\prime}_{2} - \mu_{1} \psi^{\prime}_{1} + C_{3} \psi^{\prime}_{3} = f_{2} \cos P_{2} \tau , \\ \end{aligned} $$

(9)

$$ \begin{aligned} & (1 + B_{3} )\psi^{\prime\prime}_{3} + \frac{1}{36}[9(\psi_{3}^{2} - 2)(\psi_{2}^{2} - 2) + \psi_{3} \psi_{2} (\psi_{3}^{2} - 6)(\psi_{2}^{2} - 6)]N_{3} \psi^{\prime\prime}_{2} \\ &\quad + \frac{1}{36}[9(\psi_{1}^{2} - 2) \times (\psi_{3}^{2} - 2) + \psi_{1} \psi_{3} (\psi_{1}^{2} - 6)(\psi_{3}^{2} - 6)]M_{3} \psi^{\prime\prime}_{1} \\ & \quad- \frac{1}{12}[\psi_{2} (\psi_{2}^{2} - 6)(\psi_{3}^{2} - 2) - \psi_{3} (\psi_{2}^{2} - 2) \times (\psi_{3}^{2} - 6)]N_{3} \psi{2}^{\prime 2} \\ & \quad- \frac{1}{12}[\psi_{1} (\psi_{1}^{2} - 6)(\psi_{3}^{2} - 2) - \psi_{3} (\psi_{1}^{2} - 2)(\psi_{3}^{2} - 6)]M_{3} \psi{1}^{\prime 2} \\ &\quad + \tilde{\omega }\left( {\psi_{3} - \frac{{\psi_{3}^{3} }}{6}} \right) - \mu_{2} (\psi^{\prime}_{2} - \psi^{\prime}_{3} ) = f_{3} \cos P_{3} \tau . \\ \end{aligned} $$

(10)

It is crucial to realize that the vibration amplitudes; specially the generalized coordinates must be formulated in terms of a tiny parameter $0 < \,\varepsilon < < 1$. Therefore, new variables $\theta ,\phi ,$ and $\chi$ can be introduced as follows

$$ \begin{gathered} \psi_{1} = \varepsilon \theta (\tau ;\varepsilon ), \hfill \\ \psi_{2} = \varepsilon \phi (\tau ;\varepsilon ), \hfill \\ \psi_{3} = \varepsilon \chi (\tau ;\varepsilon ). \hfill \\ \end{gathered} $$

(11)

Now, we can seek for these variables as power series of $\varepsilon$ according to the following series [6]

$$ \begin{aligned} \theta (\tau ,\varepsilon ) & = \sum\limits_{k = 1}^{3} {\varepsilon^{k - 1} \theta_{k} (\tau_{0} ,\tau_{1} ,\tau_{2} )} + O(\varepsilon^{3} ), \\ \phi (\tau ,\varepsilon ) & = \sum\limits_{k = 1}^{3} {\varepsilon^{k - 1} \phi_{k} (\tau_{0} ,\tau_{1} ,\tau_{2} )} + O(\varepsilon^{3} ), \\ \chi (\tau ,\varepsilon ) & = \sum\limits_{k = 1}^{3} {\varepsilon^{k - 1} \chi_{k} (\tau_{0} ,\tau_{1} ,\tau_{2} )} + O(\varepsilon^{3} ). \\ \end{aligned} $$

(12)

Here, $\tau_{0} = t,\,\,\tau_{1} = \varepsilon t,$ and $\tau_{2} = \varepsilon^{2} t$ are distinct timescales in which $\tau_{0}$ represent a fast scale while $\tau_{1}$ and $\tau_{2}$ are the slow ones. Consequently, the derivatives regarding $t$ can be transformed into the scales $\tau_{0} ,\,\,\tau_{1} ,$ and $\tau_{2}$ using the following operators

$$ \begin{aligned} & \frac{{\text{d}}}{{{\text{d}}t}} = \frac{\partial }{{\partial \tau_{0} }} + \varepsilon \frac{\partial }{{\partial \tau_{1} }} + \varepsilon^{2} \frac{\partial }{{\partial \tau_{2} }}, \\ & \frac{{{\text{d}}^{2} }}{{{\text{d}}t^{2} }} = \frac{{\partial^{2} }}{{\partial \tau_{0}^{2} }} + 2\varepsilon \frac{{\partial^{2} }}{{\partial \tau_{0} \partial \tau_{1} }} + \varepsilon^{2} \left( {\frac{{\partial^{2} }}{{\partial \tau_{1}^{2} }} + 2\frac{{\partial^{2} }}{{\partial \tau_{0} \partial \tau_{2} }}} \right) + O(\varepsilon^{3} ). \\ \end{aligned} $$

(13)

Taking into account the smallness of the parameters $B_{j} ,N_{j} ,M_{j} ,S_{1} ,S_{2} ,f_{j} ,$ and $C_{j}$ as below

$$ \begin{aligned} & B_{j} = \varepsilon \tilde{B}_{j} ,\,\,\,\,\,N_{j} = \varepsilon \tilde{N}_{j} ,\,\,\,\,\,M_{j} = \varepsilon \tilde{M}_{j} ,\,\,\,\,\,S_{1} = \varepsilon \tilde{S}_{1} ,\,\,\,\,\,S_{2} = \varepsilon \tilde{S}_{2} , \\ & f_{j} = \varepsilon^{3} \tilde{f}_{j} ,\,\,\,\,\,C_{j} = \varepsilon \tilde{C}_{j} ,\,\,\,\,\,\mu_{1} = \tilde{\mu }_{1} ,\,\,\,\,\,\mu_{2} = \tilde{\mu }_{2} \,\,\,\,\,(j = 1,2,3) \\ \end{aligned} $$

(14)

where the parameters $\tilde{B}_{j} ,\tilde{N}_{j} ,\tilde{M}_{j} ,\tilde{S}_{1} ,\tilde{S}_{2} ,\tilde{f}_{j} ,\tilde{\mu }_{1} ,\tilde{\mu }_{2} ,$ and $\tilde{C}_{j}$ are unity-order parameters.

Making use of (11)–(14) into (8)–(10), and then equaling the coefficients of equal powers of $\varepsilon$ to construct the sets of the following partial differential equations (PDE):

Order of $\varepsilon$:

$$ \frac{{\partial^{2} \theta_{1} }}{{\partial \tau_{0}^{2} }} + \theta_{1} = 0, $$

(15)

$$ \frac{{\partial^{2} \phi_{1} }}{{\partial \tau_{0}^{2} }} + \omega^{2} \phi_{1} = 0, $$

(16)

$$ \frac{{\partial^{2} \chi_{1} }}{{\partial \tau_{0}^{2} }} + \varpi^{2} \chi_{1} = 0. $$

(17)

Order of $\varepsilon^{2}$:

$$ \begin{aligned} \frac{{\partial^{2} \theta_{2} }}{{\partial \tau_{0}^{2} }} + \theta_{2} & = - 2\frac{{\partial^{2} \theta_{1} }}{{\partial \tau_{0} \partial \tau_{1} }} - \tilde{B}_{1} \frac{{\partial^{2} \theta_{1} }}{{\partial \tau_{0}^{2} }} - \tilde{N}_{1} \frac{{\partial^{2} \phi_{1} }}{{\partial \tau_{0}^{2} }} \\ & \quad- \tilde{M}_{1} \frac{{\partial^{2} \chi_{1} }}{{\partial \tau_{0}^{2} }} - \tilde{S}_{1} \theta_{1} + \tilde{C}_{2} \frac{{\partial \phi_{1} }}{{\partial \tau_{0} }} - (\tilde{C}_{1} + \tilde{C}_{2} )\frac{{\partial \theta_{1} }}{{\partial \tau_{0} }}, \\ \end{aligned} $$

(18)

$$ \begin{aligned} \frac{{\partial^{2} \phi_{2} }}{{\partial \tau_{0}^{2} }} + \omega^{2} \phi_{2} & = - 2\frac{{\partial^{2} \phi_{1} }}{{\partial \tau_{0} \partial \tau_{1} }} - \tilde{B}_{2} \frac{{\partial^{2} \phi_{1} }}{{\partial \tau_{0}^{2} }} - \tilde{N}_{2} \frac{{\partial^{2} \theta_{1} }}{{\partial \tau_{0}^{2} }} \\ &\quad - \tilde{M}_{2} \frac{{\partial^{2} \chi_{1} }}{{\partial \tau_{0}^{2} }} - \tilde{S}_{2} \phi_{1} + \tilde{\mu }_{1} \frac{{\partial \theta_{1} }}{{\partial \tau_{0} }} - (\tilde{\mu }_{1} + \tilde{C}_{3} )\frac{{\partial \phi_{1} }}{{\partial \tau_{0} }} + \tilde{C}_{3} \frac{{\partial \chi_{1} }}{{\partial \tau_{0} }}, \\ \end{aligned} $$

(19)

$$ \begin{aligned} \frac{{\partial^{2} \chi_{2} }}{{\partial \tau_{0}^{2} }} + \varpi^{2} \chi_{2} & = - 2\frac{{\partial^{2} \chi_{1} }}{{\partial \tau_{0} \partial \tau_{1} }} - \tilde{B}_{3} \frac{{\partial^{2} \chi_{1} }}{{\partial \tau_{0}^{2} }} - \tilde{N}_{3} \frac{{\partial^{2} \phi_{1} }}{{\partial \tau_{0}^{2} }} \\ &\quad - \tilde{M}_{2} \frac{{\partial^{2} \theta_{1} }}{{\partial \tau_{0}^{2} }} + \tilde{\mu }_{2} \frac{{\partial \phi_{1} }}{{\partial \tau_{0} }} - \tilde{\mu }_{2} \frac{{\partial \chi_{1} }}{{\partial \tau_{0} }}. \\ \end{aligned} $$

(20)

Order of $\varepsilon^{3}$:

$$ \begin{aligned} \frac{{\partial^{2} \theta_{3} }}{{\partial \tau_{0}^{2} }} + \theta_{3} & = - \frac{{\partial^{2} \theta_{1} }}{{\partial \tau_{1}^{2} }} - 2\frac{{\partial^{2} \theta_{1} }}{{\partial \tau_{0} \partial \tau_{2} }} - 2\frac{{\partial^{2} \theta_{2} }}{{\partial \tau_{0} \partial \tau_{1} }} \\ &\quad - 2\tilde{B}_{1} \frac{{\partial^{2} \theta_{1} }}{{\partial \tau_{0} \partial \tau_{1} }} - \tilde{B}_{1} \frac{{\partial^{2} \theta_{2} }}{{\partial \tau_{0}^{2} }} - \tilde{N}_{1} \frac{{\partial^{2} \phi_{2} }}{{\partial \tau_{0}^{2} }} \\ & \quad- 2\tilde{N}_{1} \frac{{\partial^{2} \phi_{1} }}{{\partial \tau_{0} \partial \tau_{1} }} - \tilde{M}_{1} \frac{{\partial^{2} \chi_{2} }}{{\partial \tau_{0}^{2} }} - 2\tilde{M}_{1} \frac{{\partial^{2} \chi_{1} }}{{\partial \tau_{0} \partial \tau_{1} }} + \frac{1}{6}\theta_{1}^{3} - \tilde{S}_{1} \theta_{2} \\ &\quad - (\tilde{C}_{1} + \tilde{C}_{2} )\left( {\frac{{\partial \theta_{1} }}{{\partial \tau_{1} }} + \frac{{\partial \theta_{2} }}{{\partial \tau_{0} }}} \right) \\ &\quad+ \tilde{C}_{2} \left( {\frac{{\partial \phi_{1} }}{{\partial \tau_{1} }} + \frac{{\partial \phi_{2} }}{{\partial \tau_{0} }}} \right) + \tilde{f}_{1} \cos P_{1} \tau , \\ \end{aligned} $$

(21)

$$ \begin{aligned} \frac{{\partial^{2} \phi_{3} }}{{\partial \tau_{0}^{2} }} + \omega^{2} \phi_{3} & = - \frac{{\partial^{2} \phi_{1} }}{{\partial \tau_{1}^{2} }} - 2\frac{{\partial^{2} \phi_{1} }}{{\partial \tau_{0} \partial \tau_{2} }} - 2\frac{{\partial^{2} \phi_{2} }}{{\partial \tau_{0} \partial \tau_{1} }} \\ & \quad- 2\tilde{B}_{2} \frac{{\partial^{2} \phi_{1} }}{{\partial \tau_{0} \partial \tau_{1} }} - \tilde{B}_{2} \frac{{\partial^{2} \phi_{2} }}{{\partial \tau_{0}^{2} }} - \tilde{N}_{2} \frac{{\partial^{2} \phi_{2} }}{{\partial \tau_{0}^{2} }} \\ & \quad- 2\tilde{N}_{2} \frac{{\partial^{2} \theta_{1} }}{{\partial \tau_{0} \partial \tau_{1} }} - \tilde{M}_{2} \frac{{\partial^{2} \chi_{2} }}{{\partial \tau_{0}^{2} }} - 2\tilde{M}_{2} \frac{{\partial^{2} \chi_{1} }}{{\partial \tau_{0} \partial \tau_{1} }} + \frac{1}{6}\omega^{2} \phi_{1}^{3} \\ & \quad- \tilde{S}_{2} \phi_{2} + \tilde{\mu }_{1} \left( {\frac{{\partial \theta_{1} }}{{\partial \tau_{1} }} + \frac{{\partial \theta_{2} }}{{\partial \tau_{0} }}} \right)\\ &\quad + (\tilde{\mu }_{1} + \tilde{C}_{3} )\left( {\frac{{\partial \phi_{1} }}{{\partial \tau_{1} }} + \frac{{\partial \phi_{2} }}{{\partial \tau_{0} }}} \right) \\ &\quad + \tilde{C}_{3} \left( {\frac{{\partial \chi_{1} }}{{\partial \tau_{1} }} + \frac{{\partial \chi_{2} }}{{\partial \tau_{0} }}} \right) + \tilde{f}_{2} \cos P_{2} \tau , \\ \end{aligned} $$

(22)

$$ \begin{aligned} \frac{{\partial^{2} \chi_{3} }}{{\partial \tau_{0}^{2} }} + \varpi^{2} \chi_{3} & = - \frac{{\partial^{2} \chi_{1} }}{{\partial \tau_{1}^{2} }} - 2\frac{{\partial^{2} \chi_{1} }}{{\partial \tau_{0} \partial \tau_{2} }} - 2\frac{{\partial^{2} \chi_{2} }}{{\partial \tau_{0} \partial \tau_{1} }} \\ & \quad- 2\tilde{B}_{3} \frac{{\partial^{2} \chi_{1} }}{{\partial \tau_{0} \partial \tau_{1} }} - \tilde{B}_{3} \frac{{\partial^{2} \chi_{2} }}{{\partial \tau_{0}^{2} }} - \tilde{N}_{3} \frac{{\partial^{2} \phi_{2} }}{{\partial \tau_{0}^{2} }} \\ &\quad - 2\tilde{N}_{3} \frac{{\partial^{2} \phi_{1} }}{{\partial \tau_{0} \partial \tau_{1} }} - \tilde{M}_{3} \frac{{\partial^{2} \theta_{2} }}{{\partial \tau_{0}^{2} }} - 2\tilde{M}_{3} \frac{{\partial^{2} \theta_{1} }}{{\partial \tau_{0} \partial \tau_{1} }} \\ & \quad+ \frac{1}{6}\varpi^{2} \chi_{1}^{3} - \tilde{\mu }_{2} \left( {\frac{{\partial \chi_{1} }}{{\partial \tau_{1} }} + \frac{{\partial \chi_{2} }}{{\partial \tau_{0} }}} \right) \\ &\quad - \tilde{\mu }_{2} \left( {\frac{{\partial \phi_{1} }}{{\partial \tau_{1} }} + \frac{{\partial \phi_{2} }}{{\partial \tau_{0} }}} \right) + \tilde{f}_{3} \cos P_{3} \tau . \\ \end{aligned} $$

(23)

The preceding Eqs. (15)-(23) constitute a system of nine linear PDE, which can be solved in the order they appeared. Therefore, the first group of Eqs. (15)–(17) have the general solutions that can be represented in the following ways

$$ \theta_{1} = A_{1} e^{{i\tau_{0} }} + \overline{A}_{1} e^{{ - i\tau_{0} }} , $$

(24)

$$ \phi_{1} = A_{2} e^{{i\omega \tau_{0} }} + \overline{A}_{2} e^{{ - i\omega \tau_{0} }} , $$

(25)

$$ \chi_{1} = A_{3} e^{{i\varpi \tau_{0} }} + \overline{A}_{3} e^{{ - i\varpi \tau_{0} }} . $$

(26)

Here $A_{j} \,\,(j = 1,2,3)$ and $\overline{A}_{j}$ are unknown complex functions and the corresponding complex conjugate, respectively.

Inserting (24)–(26) into (18)–(20) and canceling the terms that lead to secular ones to get the following conditions

$$ 2i\frac{{\partial A_{1} }}{{\partial \tau_{1} }} + [\tilde{S}_{1} - \tilde{B}_{1} + i(\tilde{C}_{1} + \tilde{C}_{2} )]A_{1} = 0, $$

(27)

$$ 2i\omega \frac{{\partial A_{2} }}{{\partial \tau_{1} }} + [\tilde{S}_{2} - \tilde{B}_{2} \omega^{2} + i\omega \,(\tilde{\mu }_{1} + \tilde{C}_{3} )]A_{2} = 0, $$

(28)

$$ 2i\varpi \frac{{\partial A_{3} }}{{\partial \tau_{1} }} + (i\varpi \tilde{C}_{3} - \tilde{B}_{3} \varpi^{2} )A_{3} = 0. $$

(29)

As a result, the solutions of second order can be written as follows

$$ \theta_{2} = \frac{{(\tilde{N}_{1} \omega + i\,\tilde{C}_{1} )\omega A_{2} }}{{1 - \omega^{2} }}e^{{i\omega \tau_{0} }} + \frac{{\tilde{M}_{1} \varpi^{2} A_{3} }}{{1 - \varpi^{2} }}e^{{i\varpi \tau_{0} }} + cc, $$

(30)

$$ \phi_{2} = \frac{{(\tilde{N}_{2} + i\,\tilde{\mu }_{1} )A_{1} }}{{\omega^{2} - 1}}e^{{i\tau_{0} }} + \frac{{(\tilde{M}_{2} \varpi + i\,\tilde{C}_{3} )\varpi A_{3} }}{{\omega^{2} - \varpi^{2} }}e^{{i\varpi \tau_{0} }} + cc, $$

(31)

$$ \chi_{2} = \frac{{(\tilde{N}_{3} \omega + i\,\tilde{\mu }_{2} )\omega A_{2} }}{{\varpi^{2} - \omega^{2} }}e^{{i\omega \tau_{0} }} + \frac{{\tilde{M}_{3} A_{1} }}{{\varpi^{2} - 1}}e^{{i\tau_{0} }} + cc, $$

(32)

where $cc$ denotes the preceding terms’ complex conjugates.

Making use of the solutions (24)–(26) and (30)–(32) into Eqs. (21)–(23), one obtains the requirements for deleting secular terms from the approximation of order three in the forms

$$ \begin{aligned} & \frac{{\partial^{2} A_{1} }}{{\partial \tau_{1}^{2} }} + 2i\frac{{\partial A_{1} }}{{\partial \tau_{2} }} + 2i\tilde{B}_{1} \frac{{\partial A_{1} }}{{\partial \tau_{1} }} - [\frac{{(\tilde{N}_{1} \tilde{N}_{2} + \tilde{N}_{1} \tilde{\mu }_{1} + i\tilde{N}_{2} \tilde{C}_{2} - \tilde{C}_{2} \tilde{\mu }_{1} )}}{{\omega^{2} - 1}} \\ & + \frac{{\tilde{M}_{1} \tilde{M}_{3} }}{{\varpi^{2} - 1}} + \frac{1}{2}A_{1} \overline{A}_{1} + (\tilde{C}_{1} + \tilde{C}_{2} )\frac{{\partial A_{1} }}{{\partial \tau_{1} }}]A_{1} = 0, \\ \end{aligned} $$

(33)

$$ \begin{aligned} & \frac{{\partial^{2} A_{2} }}{{\partial \tau_{1}^{2} }} + 2i\omega \frac{{\partial A_{2} }}{{\partial \tau_{2} }} + 2i\omega \tilde{B}_{2} \frac{{\partial A_{2} }}{{\partial \tau_{1} }} \\ & - [\frac{{(\tilde{N}_{1} \tilde{N}_{2} \omega^{2} + i\omega \tilde{N}_{2} \tilde{C}_{2} + \tilde{C}_{2} \tilde{\mu }_{1} + i\tilde{N}_{1} \tilde{\mu }{}_{1}\omega )\omega^{2} }}{{1 - \omega^{2} }} \\ & + \frac{{(\tilde{M}_{2} \tilde{N}_{3} \omega + i\tilde{M}_{2} \tilde{\mu }_{2} + i\tilde{N}_{3} \tilde{C}_{3} )\omega^{3} }}{{\varpi^{2} - \omega^{2} }} + \frac{1}{2}\omega^{2} A_{2} \overline{A}_{2} + (\tilde{\mu }_{1} + \tilde{C}_{3} )\frac{{\partial A_{2} }}{{\partial \tau_{1} }}]A_{2} = 0, \\ \end{aligned} $$

(34)

$$ \begin{aligned} & \frac{{\partial^{2} A_{3} }}{{\partial \tau_{1}^{2} }} + 2i\varpi \tilde{B}_{3} \frac{{\partial A_{3} }}{{\partial \tau_{2} }} + 2i\varpi \tilde{B}_{3} \frac{{\partial A_{3} }}{{\partial \tau_{1} }} + \tilde{\mu }_{2} \frac{{\partial A_{3} }}{{\partial \tau_{1} }} \\ & - \left[\frac{{\tilde{M}_{1} \tilde{M}_{3} \omega^{4} }}{{1 - \varpi^{2} }} + \frac{1}{2}\varpi^{2} A_{3} \overline{A}_{3} \right.\\ \left.+ \frac{{(i\varpi \,\tilde{N}_{3} \tilde{C}_{3} + \tilde{M}_{2} \tilde{N}_{3} \varpi^{2} + i\varpi \,\tilde{\mu }_{2} \tilde{M}_{2} - \tilde{C}_{3} \tilde{\mu }_{2} )\varpi^{2} }}{{\omega^{2} - \varpi^{2} }}\right]A_{3} = 0. \\ \end{aligned} $$

(35)

Thus, the third-order approximations $\theta_{3} ,\phi_{3} ,$ and $\chi_{3}$ have the forms

$$ \begin{aligned} \theta_{3} & = 2\left[ {\frac{{i\tilde{N}_{1} \omega^{3} }}{{(1 - \omega^{2} )^{2} }}\frac{{\partial A_{2} }}{{\partial \tau_{1} }}e^{{i\omega \tau_{0} }} + \frac{{\tilde{M}_{1} \varpi^{3} }}{{(1 - \varpi^{2} )^{2} }}\frac{{\partial A_{3} }}{{\partial \tau_{1} }}e^{{i\varpi \tau_{0} }} - \frac{{\tilde{C}_{2} \omega^{2} A_{2} }}{{(1 - \omega^{2} )^{2} }}e^{{i\omega \tau_{0} }} } \right] \\ & \quad- \tilde{B}_{1} \left[ {\frac{{\omega^{3} A_{2} }}{{(1 - \omega^{2} )^{2} }} \times (\tilde{N}_{1} \omega + \tilde{C}_{2} )e^{{i\omega \tau_{0} }} + \frac{{\tilde{M}_{1} \varpi^{4} A_{3} }}{{(1 - \varpi^{2} )^{2} }}e^{{i\varpi \tau_{0} }} } \right] + 2\frac{{i\omega \tilde{N}_{1} }}{{(1 - \omega^{2} )}}\frac{{\partial A_{2} }}{{\partial \tau_{1} }}e^{{i\omega \tau_{0} }} \\ & \quad+ 2\frac{{i\varpi \tilde{M}_{1} }}{{(1 - \varpi^{2} )}}\frac{{\partial A_{3} }}{{\partial \tau_{1} }}e^{{i\varpi \tau_{0} }} - \frac{{\omega^{3} A_{2} \tilde{M}_{1} (\tilde{N}_{3} \omega + i\tilde{\mu }_{2} )}}{{(1 - \omega^{2} )(\varpi^{2} - \omega^{2} )}}e^{{i\omega \tau_{0} }} \\ &\quad + \tilde{S}_{1} \left[ {\frac{{\tilde{M}_{1} \varpi^{2} A_{3} }}{{(1 - \varpi^{2} )^{2} }}e^{{i\varpi \tau_{0} }} + \frac{{(\tilde{N}_{1} \omega + i\tilde{C}_{2} )\omega A_{2} }}{{(1 - \omega^{2} )^{2} }}e^{{i\omega \tau_{0} }} } \right] \\ & \quad+ \frac{1}{48}A_{1}^{3} e^{{3i\tau_{0} }} - (\tilde{C}_{1} + \tilde{C}_{2} )\left[ {\frac{{(i\tilde{N}_{1} \omega - \tilde{C}_{2} )\omega^{2} A_{2} }}{{(1 - \omega^{2} )^{2} }}e^{{i\omega \tau_{0} }} \, + \frac{{i\tilde{M}_{1} \varpi^{3} A_{3} }}{{(1 - \varpi^{2} )^{2} }}e^{{i\varpi \tau_{0} }} } \right] \\ & \quad- \tilde{C}_{2} \left[ {\frac{1}{{(1 - \omega^{2} )}}\frac{{\partial A_{2} }}{{\partial \tau_{1} }}e^{{i\omega \tau_{0} }} + \frac{{(\tilde{M}_{2} \varpi - \tilde{C}_{3} )i\varpi^{2} A_{3} }}{{(1 - \varpi^{2} )(\omega^{2} - \varpi^{2} )}}e^{{i\varpi \tau_{0} }} } \right] + \frac{{\tilde{f}_{1} }}{{2(1 - P_{1}^{2} )}}e^{{iP_{1} \tau_{0} }} , \\ \end{aligned} $$

(36)

$$ \begin{aligned} \phi_{3} & = 2\left[ {\frac{{(i\tilde{N}_{2} - \tilde{\mu }_{1} )}}{{(\omega^{2} - 1)^{2} }}\frac{{\partial A_{1} }}{{\partial \tau_{1} }}e^{{i\tau_{0} }} + \frac{{(i\tilde{M}_{2} \varpi - \tilde{C}_{3} )\varpi^{2} }}{{(\omega^{2} - \varpi^{2} )^{2} }}\frac{{\partial A_{3} }}{{\partial \tau_{1} }}e^{{i\varpi \tau_{0} }} } \right] \\ &\quad - \tilde{B}_{2} \left[ {\frac{{(\tilde{N}_{2} + i\,\tilde{\mu }_{1} )A_{1} }}{{(\omega^{2} - 1)^{2} }}e^{{i\tau_{0} }} + \frac{{(\tilde{M}_{2} \varpi + i\,\tilde{C}_{3} )\varpi^{3} A_{3} }}{{(\omega^{2} - \varpi^{2} )^{2} }}e^{{i\varpi \tau_{0} }} } \right] - \frac{{\tilde{N}_{2} \tilde{M}_{1} \varpi^{4} A_{3} }}{{(1 - \varpi^{2} )(\omega^{2} - \varpi^{2} )}}e^{{i\varpi \tau_{0} }} \\ & \quad+ \frac{{2i\,\tilde{N}_{2} }}{{(\omega^{2} - 1)}}\frac{{\partial A_{1} }}{{\partial \tau_{1} }}e^{{i\tau_{0} }} + \frac{{2i\,\varpi \tilde{M}_{2} }}{{(\omega^{2} - \varpi^{2} )}}\frac{{\partial A_{3} }}{{\partial \tau_{1} }}e^{{i\varpi \tau_{0} }} - \frac{{\tilde{M}_{2} \tilde{M}_{3} A_{1} }}{{(\omega^{2} - 1)(\varpi^{2} - 1)}}e^{{i\tau_{0} }} \\ & \quad+ \frac{1}{48}A_{2}^{3} e^{{3\omega i\tau_{0} }} \, + \tilde{S}_{2} \left[ {\frac{{(\tilde{N}_{2} + i\tilde{\mu }_{1} )A_{1} }}{{(\omega^{2} - 1)^{2} }}e^{{i\tau_{0} }} + \frac{{(\tilde{M}_{2} \varpi + i\tilde{C}_{3} )\varpi A_{3} }}{{(\omega^{2} - \varpi^{2} )^{2} }}e^{{i\varpi \tau_{0} }} } \right] \\ &\quad - \tilde{\mu }_{1} \left[ {\frac{1}{{(\omega^{2} - 1)}}\frac{{\partial A_{1} }}{{\partial \tau_{1} }}e^{{i\tau_{0} }} + \frac{{i\tilde{M}_{1} \varpi^{3} A_{3} }}{{(1 - \varpi^{2} )(\omega^{2} - \varpi^{2} )}}e^{{i\varpi \tau_{0} }} } \right] \\ &\quad - \tilde{\mu }_{2} \left[ {\frac{1}{{(\omega^{2} - \varpi^{2} )}}\frac{{\partial A_{3} }}{{\partial \tau_{1} }}e^{{i\varpi \tau_{0} }} + \frac{{i\tilde{M}_{3} A_{1} }}{{(\varpi^{2} - 1)(\omega^{2} - 1)}}e^{{i\tau_{0} }} } \right] + \frac{{\tilde{f}_{2} }}{{2(\omega^{2} - P_{2}^{2} )}}e^{{ip_{2} \tau_{0} }} \\ & - (\tilde{\mu }_{1} + \tilde{C}_{3} )\left[ {\frac{{(i\tilde{N}_{2} - \tilde{\mu }_{1} )A_{1} }}{{(\omega^{2} - 1)^{2} }}e^{{i\tau_{0} }} + \frac{{(i\tilde{M}_{2} \varpi - \tilde{C}_{3} )\varpi A_{3} }}{{(\omega^{2} - \varpi^{2} )^{2} }}e^{{i\varpi \tau_{0} }} } \right], \\ \end{aligned} $$

(37)

$$ \begin{aligned} \chi_{3} & = \frac{{2i\tilde{N}_{3} \omega }}{{(\varpi^{2} - \omega^{2} )}}\frac{{\partial A_{2} }}{{\partial \tau_{1} }}e^{{i\omega \tau_{0} }} + \frac{{2i\tilde{M}_{3} }}{{(\varpi^{2} - 1)}}\frac{{\partial A_{1} }}{{\partial \tau_{1} }}e^{{i\tau_{0} }} \, + \frac{1}{48}A_{3}^{3} e^{{3i\varpi \tau_{0} }} \\ & \quad- \frac{{(\tilde{N}_{3} \omega - \tilde{\mu }_{2} )\tilde{B}_{3} \omega^{3} A_{2} }}{{(\varpi^{2} - \omega^{2} )^{2} }}e^{{i\omega \tau_{0} }} - \frac{{\tilde{B}_{3} \tilde{M}_{3} A_{1} }}{{(\varpi^{2} - 1)^{2} }}e^{{i\tau_{0} }} \\ & \quad+ 2\left[ {\frac{{(i\omega \tilde{N}_{3} - \tilde{\mu }_{2} )\omega^{2} }}{{(\varpi^{2} - \omega^{2} )^{2} }}\frac{{\partial A_{2} }}{{\partial \tau_{1} }}e^{{i\omega \tau_{0} }} + \frac{{i\tilde{M}_{3} }}{{(\varpi^{2} - 1)^{2} }}\frac{{\partial A_{1} }}{{\partial \tau_{1} }}e^{{i\tau_{0} }} } \right] \\ & \quad- \frac{{(\tilde{N}_{2} + i\tilde{\mu }_{1} )\tilde{N}_{3} }}{{(\omega^{2} - 1)(\varpi^{2} - 1)}}A_{1} e^{{i\tau_{0} }} - \tilde{\mu }_{2} \left[ {\frac{1}{{(\varpi^{2} - \omega^{2} )}}\frac{{\partial A_{2} }}{{\partial \tau_{1} }}e^{{i\omega \tau_{0} }} + \frac{{(i\tilde{N}_{2} - \tilde{\mu }_{1} )A_{1} e^{{i\tau_{0} }} }}{{(\omega^{2} - 1)(\varpi^{2} - 1)}}} \right] \\ & \quad+ \tilde{\mu }_{2} \left[ {\frac{{(i\tilde{N}_{3} \omega - \tilde{\mu }_{1} )\omega^{2} A_{2} }}{{(\varpi^{2} - \omega^{2} )^{2} }}e^{{i\omega \tau_{0} }} + \frac{{i\tilde{M}_{3} A_{1} e^{{i\tau_{0} }} }}{{(\varpi^{2} - 1)^{2} }}} \right] - \frac{{\tilde{f}_{3} e^{{ip_{3} \tau_{0} }} }}{{2(\varpi^{2} - P_{3}^{2} )}} - \frac{{(\tilde{M}_{3} \tilde{N}_{1} \omega + i\tilde{C}_{2} )\omega^{3} }}{{(1 - \omega^{2} )(\varpi^{2} - \omega^{2} )}}A_{2} e^{{i\omega \tau_{0} }} . \\ \end{aligned} $$

(38)

The unknown functions $A_{j} \,(j = 1,2,3)$ can be determined by looking at the conditions (27)–(29) and (33)–(35). Therefore, the required AS can be obtained easily after substituting the solutions (24)–(26), (30)–(32), (36)–(38), and series (12) into hypothesis (11).

As previously stated, dealing with the AMS necessitates the employment of an unlimited number of separate timescales rather than a single time variable. The solvability constraints, which demand the removal of secular elements from fast time variables, are regarded as the appropriate tax for this flexibility. The fast timescale constrains the structure of the estimated solutions. It is also crucial to double-check that the requirements of the solvability for different orders are consistent. The amplitudes of "free" resonant phrases that emerge in each expansion order are limited by these requirements. The analysis may provide inaccurate results or only allow simple solutions if the restrictions are not fulfilled. It should be noted that alternative free amplitude options may yield contradicting findings [38].

4 Resonance requirements and equations of modulation

The categorizations of resonance cases that may emerge in the second or third-order solutions, as well as the consideration three of these cases, are both significant aspects of this section. It is well known that the resonance cases occur if the denominators of these parts tend to zero [39]. Therefore, it might be categorized as:

• (i) When $p_{1} \approx 1,p_{2} \approx \omega ,$ and $p_{3} \approx \varpi$, there is a main primary external resonance.

• (ii) When $\omega \approx 1,\varpi \approx \omega ,$ and $\varpi \approx 1$, there is an internal resonance.

It is noted that, if any one of the resonance cases is met, we should expect that the studied model's behavior will be challenging. Furthermore, the approach described above is valid if the vibrations have values other than that of the resonance. Therefore, we will investigate the three primary external resonances that occur at the same instant to remedy this problem. To pursuit of this objective, it is critical to employ the dimensionless detuning parameters $\sigma_{j} \,(j = 1,2,3)$ that detect the distance between the oscillations and the stern resonance. Then we will be able to write

$$ P_{1} = 1 + \sigma_{1} ,\,\,\,\,\,P_{2} = \omega + \sigma_{2} ,\,\,\,\,\,P_{3} = \varpi + \sigma_{3} , $$

(39)

Then, we can formulate these parameters in terms of $\varepsilon$ according to

$$ \sigma_{j} = \varepsilon \,\tilde{\sigma }_{j} \,\,\,(j = 1,2,3). $$

(40)

Inserting (39) and (40) into (18)–(23) and deleting the terms that yield secular ones, to gain the conditions of solvability as follows.

• Conditions of the second-order approximation

  $$ \frac{{\partial A_{1} }}{{\partial \tau_{1} }} = \frac{1}{2i}[\tilde{B}_{1} - \tilde{S}_{1} - i(\tilde{C}_{1} + \tilde{C}_{2} )]A_{1} , $$

  (41)
  $$ \frac{{\partial A_{2} }}{{\partial \tau_{1} }} = \frac{1}{2i\omega }[\tilde{B}_{2} \omega^{2} - \tilde{S}_{2} - i\omega (\tilde{\mu }_{1} + \tilde{C}_{3} )]A_{2} , $$

  (42)
  $$ \frac{{\partial A_{3} }}{{\partial \tau_{1} }} = \frac{1}{2i\varpi }(\tilde{B}_{3} \varpi - i\tilde{\mu }_{2} )\varpi A_{3} . $$

  (43)

• Conditions of the third-order approximation

  $$ \begin{aligned} & 2i\frac{{\partial A_{1} }}{{\partial \tau_{2} }} - \frac{1}{4}\{ \tilde{S}_{1}^{2} + 2\tilde{B}_{1} \left( {\tilde{S}_{1} - \frac{3}{2}\tilde{B}_{1} } \right) + (\tilde{C}_{1} + \tilde{C}_{2} )[4i\tilde{S}_{1} - 3(\tilde{C}_{1} + \tilde{C}_{2} )] + \frac{{4\tilde{M}_{1} \tilde{M}_{3} }}{{\varpi^{2} - 1}} \\ & \quad+ \frac{4}{{\omega^{2} - 1}}[\tilde{N}_{1} (\tilde{N}_{2} + i\tilde{\mu }_{1} ) + i\tilde{N}_{2} \tilde{C}_{2} - \tilde{C}_{2} \tilde{\mu }_{1} ] - 2A_{1} \overline{A}_{1} \} A_{1} - \frac{{\tilde{f}_{1} }}{2}e^{{i\tilde{\sigma }_{1} \tau_{1} }} = 0, \\ \end{aligned} $$

  (44)
  $$ \begin{aligned} & 2i\omega \frac{{\partial A_{2} }}{{\partial \tau_{2} }} - \frac{1}{4}\{ 2\tilde{B}_{2} (\tilde{S}_{2} - \frac{3}{2}\tilde{B}_{2} \omega^{2} ) + \frac{1}{{\omega^{2} }}\tilde{S}_{2}^{2} \\ &\quad + (\tilde{\mu }_{1} + \tilde{C}_{3} )\left[ {\frac{{4i\tilde{S}_{2} }}{\omega } - 3(\tilde{\mu }_{1} + \tilde{C}_{3} )} \right] + \frac{{4\omega^{3} }}{{\varpi^{2} - \omega^{2} }}[(\tilde{M}_{2} (\tilde{N}_{3} \omega + i\tilde{\mu }_{2} ) + (i\omega^{3} \tilde{N}_{3} - \omega^{3} \tilde{C}_{3} )\tilde{\mu }_{2} )] \\ & \quad- \frac{{4[(\tilde{C}_{2} + i\omega \tilde{N}_{1} )\omega^{2} \tilde{\mu }_{1} - i\tilde{N}_{2} \tilde{C}_{2} ]}}{{1 - \omega^{2} }} - 2\omega^{2} A_{2} \overline{A}_{2} \} A_{2} - \frac{{\tilde{f}_{2} }}{2}e^{{i\tilde{\sigma }_{2} \tau_{2} }} = 0, \\ \end{aligned} $$

  (45)
  $$ \begin{aligned} & 2i\varpi \frac{{\partial A_{3} }}{{\partial \tau_{2} }} - \frac{1}{4}\{ \tilde{B}_{3} (4i\varpi \tilde{\mu }_{2} - 3\tilde{B}_{3} \varpi^{2} ) + 3\tilde{\mu }_{2}^{2} + \frac{{4\varpi^{4} \tilde{M}_{1} \tilde{N}_{3} \tilde{C}_{2} }}{{1 - \varpi^{2} }} \\ & + \frac{4}{{\omega^{2} - \varpi^{2} }}[\tilde{M}_{2} \varpi^{3} (\tilde{N}_{3} \varpi + i\tilde{\mu }_{2} ) + \varpi^{3} \tilde{C}_{3} (i\tilde{N}_{3} - \tilde{\mu }_{2} )] - 2\varpi^{2} A_{3} \overline{A}_{3} \} A_{3} - \frac{{\tilde{f}_{3} }}{2}e^{{i\tilde{\sigma }_{3} \tau_{3} }} = 0. \\ \end{aligned} $$

  (46)

It is clear that the functions $A_{j} \,(j = 1,2,3)$ can be determined using the forgoing criteria (41)–(46) which can be represented in the following polar form [40]

$$ \begin{gathered} A_{j} (\tau_{1} ,\tau_{2} ) = \frac{1}{2}\tilde{a}_{j} (\tau_{1} ,\tau_{2} )e^{{i\psi_{j} (\tau_{1} ,\tau_{2} )}} ;\,\,\,\,\,\,\,a_{j} = \varepsilon \tilde{a}_{j} , \hfill \\ \theta_{j} (\tau_{1} ,\tau_{2} ) = \tilde{\sigma }_{j} \tau_{1} - \psi_{j} (\tau_{1} ,\tau_{2} );\,\,\,\,\,\,\,\,\sigma_{j} = \varepsilon \tilde{\sigma }_{j} \,\,\,\,\,\,(j = 1,2,3), \hfill \\ \end{gathered} $$

(47)

where $\theta_{j}$ are the modified phases, $\psi_{j}$ are the phase angles and $a_{j}$ are the amplitudes.

Making use of (47) into (41)–(46), and then distinguishing the real parts and the imaginary ones of the resulted equations to acquire the following modulation equations of six ordinary differential equations from first order

$$ \begin{aligned} \frac{{{\text{d}}\theta_{1} }}{{{\text{d}}\tau }} & = \frac{{a_{1} }}{8}[\frac{{4(N_{1} N_{2} + M_{1} M_{2} - \mu_{1} C_{2} )}}{{\omega^{2} - 1}} - 8\sigma_{1} + \frac{{a_{1}^{2} }}{2} \\ &\quad - B_{1} (4 - 3B_{1} ) + S_{1} (2B_{1} + S_{1} - 4) + 3(C_{1} + C_{2} )^{2} ] + \frac{{f_{1} }}{2}\cos \theta_{1} , \\ \frac{{{\text{d}}a_{1} }}{{{\text{d}}\tau }} & = \frac{{a_{1} }}{2}\left[ {\frac{{C_{1} N_{2} + N_{1} \mu_{1} + N_{2} C_{2} }}{{\omega^{2} - 1}} + (S_{1} - 1)(C_{1} + C_{2} )} \right] + \frac{{f_{1} }}{2}\sin \theta_{1} , \\ \frac{{{\text{d}}\theta_{2} }}{{{\text{d}}\tau }} & = \frac{{a_{2} }}{8}\left[\frac{{4(N_{1} N_{2} \omega^{2} + C_{2} \mu_{1} )\omega^{2} }}{{\omega^{2} - 1}} + \frac{{4(\omega^{2} M_{3} M_{2} - C_{3} \mu_{2} )\omega^{2} }}{{\varpi^{2} - \omega^{2} }} \right.\\ &\quad \left.+ \frac{{a_{2}^{2} \omega^{2} }}{2} - 8\omega \sigma_{2} + n_{1} + n_{2} - 3(C_{3} + \mu_{1} )^{2} \right] + \frac{{f_{2} }}{2}\cos \theta_{2} , \\ \frac{{{\text{d}}a_{2} }}{{{\text{d}}\tau }} & = \frac{{a_{2} }}{2}\left[ {\frac{{(C_{2} N_{2} + N_{1} \mu_{1} )\omega^{2} }}{{1 - \omega^{2} }} + \left( {\frac{{S_{2} }}{\omega } - 1} \right)(C_{3} + \tilde{C}_{2} ) + \frac{{(M_{2} + N_{3} )\mu_{2} \omega^{2} }}{{\varpi^{2} - \omega^{2} }}} \right] + \frac{{f_{2} }}{2\omega }\sin \theta_{2} , \\ \frac{{{\text{d}}\theta_{3} }}{{{\text{d}}\tau }} & = \frac{{a_{3} }}{8}\left[\frac{{4M_{1} M_{3} \varpi^{4} }}{{1 - \varpi^{2} }} + \frac{{4(\varpi^{2} N_{3} M_{2} - C_{3} \mu_{2} )\varpi^{2} }}{{\omega^{2} - \varpi^{2} }} + \frac{{a_{3}^{2} \varpi^{2} }}{2} \right. \\& \left. + B_{3} \varpi^{2} (4 - 3B_{3} ) + 3\mu_{2}^{2} - 8\varpi \sigma_{3} \right] + \frac{{f_{3} }}{2}\cos \theta_{3} , \\ \frac{{{\text{d}}a_{3} }}{{{\text{d}}\tau }} & = \frac{{a_{3} }}{2\varpi }[n_{3} + (B_{3} - \varpi )\mu_{2} ] + \frac{{f_{3} }}{2\varpi }\sin \theta_{3} , \\ \end{aligned} $$

(48)

where

$$ \begin{aligned} n_{1} & = B_{2} \omega^{2} \left( {1\, - \frac{3}{4}B_{2} } \right), \\ n_{2} & = S_{2} \left( {\frac{{S_{2} }}{{4\omega^{2} }} + \frac{{B_{2} }}{2} - 1} \right), \\ n_{3} & = \frac{{(N_{3} C_{3} + \mu_{2} M_{2} )\varpi^{3} }}{{\omega^{2} - \varpi^{2} }}. \\ \end{aligned} $$

Referring to the preceding system (48), the time histories of its solutions $a_{j} \,(j = 1,2,3)$ and $\theta_{j}$ are graphed in Figs. 2 and 3, respectively. These figures are calculated at $\omega ( = \,0.3829,0.4062,\,0.4690)$ and according to the following data

$$ \begin{aligned} B_{1} & = 0.202,\,\,\,\,B_{2} = 0.0168,\,\,\,\,\,B_{3} = 0.00187,\,\,\,\,\,N_{1} = 0.649,\,\,\,\,\,N_{2} = 0.0357,\,\,\,\,\,N_{3} = 0.0075,\, \\ M_{1} & = 0.1159,\,\,\,\,M_{2} = 0.00375,\,\,\,\,M_{3} = 0.01275,\,\,\,\,\,C_{1} = 0.0000761,\,\,\,\,\,C_{2} = 0.0000304,\, \\ C_{3} & = 0.0000609,\,\,\,\,f_{1} = 0.02,\,\,\,\,f_{2} = 0.05,\,\,\,\,f_{3} = 1,\,\,\,\,\mu_{1} = 0.0000167,\,\,\,\,\mu_{2} = 0.0000670, \\ \sigma_{1} & = - 0.1,\,\,\,\,\sigma_{2} = 0.2,\,\,\,\,\sigma_{3} = 0.3. \\ \end{aligned} $$

Fig. 2

Temporal variation of the amplitude $a_{1} ,a_{2} ,$ and $a_{3}$, a $a_{1}$ at $\omega ( = 0.3829,0.4062,\,\,0.4690),$b $a_{2}$ at $\omega ( = 0.3829,0.4062,\,\,0.4690),$ c $a_{3}$ at $\omega ( = 0.3829,0.4062,\,\,0.4690)$

Fig. 3

Temporal variation of the modified phase $\theta_{1} ,\theta_{2} ,$ and $\theta_{3}$ when a–c $\theta_{1}$ at $\omega ( = 0.3829,0.4062,\,\,0.4690),$d–f $\theta_{2}$ at $\omega ( = 0.3829,0.4062,\,\,0.4690),$ g–i $\theta_{3}$ at $\omega ( = 0.3829,0.4062,\,\,0.4690)$

Periodic waves can be seen while looking at the potions (a), (b), and (c) of Fig. 2, where the amplitudes of these waves decrease and the number of oscillations increase in addition to the increasing of their wavelengths with the increment of the values of $\omega$. The variation of $\theta_{j}$ has an increasing manner when time goes on as shown in parts of Fig. 3. These observations are constituting with the nature of the equations of the previous system (48). Therefore, the behavior of $a_{j}$ and $\theta_{j}$ is influenced with the distinct values of $\omega$.

The variation of the obtained AS for $\psi_{j} \,(j = 1,2,3)$ via dimensionless time $\tau$ is plotted in portions (a), (b), and (c) of Fig. 4. Periodic waves are produced which encapsulates the characteristics of the obtained stable solutions. Some wave packets, characterizing the behavior of these solutions, have been obtained. These solutions are verified through the comparison with the NS of the original regulating system of Eqs. (8)–(10) using the fourth-order Runge–Kutta method when $\omega = \,0.3829,$$\omega = \,0.4062,$ $\omega = \,0.4690,$$\psi_{1} (0) = 0.0001,\,$$\psi^{\prime}_{1} (0) = 0,\,$$\psi_{2} (0) = 0.0002,$$\psi^{\prime}_{2} (0) = 0.00001,\,$$\,\psi_{3} (0) = 0.3,$ and $\psi^{\prime}_{3} (0) = 0$ (with the consideration of the same values of other parameters) as graphed in parts of Figs. 5, 6, and 7, respectively. The good matching between them explores the high precision of the used perturbation method. The relations between the AS and their first-order derivatives are plotted in Fig. 8 to graph the phase planes figures when $\omega$ takes different values. It is notable that we have closed trajectories which confirm that the gained AS have a stable behavior, which is predicted before, during the tested interval of time.

Fig. 4

Time histories of the AS $\psi_{1} ,\psi_{2} ,$ and $\psi_{3}$ when a $\psi_{1}$ at $\omega ( = 0.3829,0.4062,\,\,0.4690),$b $\psi_{2}$ at $\omega ( = 0.3829,0.4062,\,0.4690),$c $\psi_{3}$ at $\omega ( = 0.3829,0.4062,\,0.4690)$

Fig. 5

Comparison between the AS and the NS of the variable $\psi_{1} ,\psi_{2} ,$ and $\psi_{3}$ when $\omega = 0.3829$

Fig. 6

Comparison between the AS and the NS of the variable $\psi_{1} ,\psi_{2} ,$ and $\psi_{3}$ when $\omega = 0.4062$

Fig. 7

Consistency between the AS and the NS of the variable $\psi_{1} ,\psi_{2} ,$ and $\psi_{3}$ when $\omega = 0.4690$

Fig. 8

Phase planes for the solutions $\psi_{1} ,\psi_{2} ,$ and $\psi_{3}$ when $\omega ( = 0.3829,0.4062,\,0.4690)$

5 Steady-state solutions

The goal of this section is to investigate the dynamical system’s vibrations under examination the steady-state case. To accomplish this purpose, we consider the null value of the first derivatives of the modified phases $\theta_{j}$ and amplitudes $a_{j}$ in Eq. (48), i.e., $\frac{{{\text{d}}\theta_{j} }}{{{\text{d}}\tau }} = \frac{{{\text{d}}a_{j} }}{{{\text{d}}\tau }} = 0\,\,\,(j = 1,2,3)$ [41]. Therefore, the next set of six algebraic equations regarding the variables $\theta_{j}$ and $a_{j}$ is yielded

$$ \begin{aligned} f_{1} \cos \theta_{1} & = - a_{1} \left[ {2\sigma_{1} + n_{4} + \frac{{a_{1}^{2} }}{8} + B_{1} \left( {1 - \frac{3}{4}B_{1} } \right) + S_{1} \left( {\frac{{S_{1} }}{4} + \frac{{B_{1} }}{2} - 1} \right) - \frac{3}{4}(C_{1} + C_{2} )^{2} } \right], \\ \,f_{1} \sin \theta_{1} & = - a_{1} \left[ {\frac{{C_{2} N_{2} }}{{\omega^{2} - 1}} + (S_{1} - 1)(C_{1} + C_{2} )} \right], \\ f_{2} \cos \theta_{2} & = - a_{2} \left[ {2\omega \sigma_{2} + n_{5} + n_{6} + \frac{{a_{2}^{2} }}{8}\omega^{2} + n_{1} + n_{2} - \frac{3}{4}(C_{3} + \mu_{1} )^{2} } \right], \\ f_{2} \sin \theta_{2} & = - a_{2} \left[ {2\omega \sigma_{2} + n_{5} + n_{6} + \frac{{a_{2}^{3} }}{8}\omega^{2} \, + n_{1} + n_{2} \, - \frac{3}{4}(C_{3} + \mu_{1} )^{2} } \right], \\ f_{3} \cos \theta_{3} & = - a_{3} \left[ {2\varpi \sigma_{3} + \frac{{M_{1} M_{3} \varpi^{4} }}{{1 - \varpi^{2} }} + n_{6} + \frac{{a_{3}^{2} }}{8}\varpi^{2} + \frac{3}{4}\mu_{2}^{2} + B_{3} \varpi^{2} \left( {1 - \frac{3}{4}B_{3} } \right)} \right], \\ f_{3} \sin \theta_{3} & = - a_{3} (n_{3} + \mu_{2} B_{3} - \mu_{2} \varpi ), \\ \end{aligned} $$

(49)

where

$$ \begin{aligned} n_{4} & = \frac{{N_{1} N_{2} + M_{1} M_{2} - C_{1} C_{2} }}{{\omega^{2} - 1}}, \\ \,n_{5} & = \frac{{(N_{1} N_{2} \omega^{2} - \mu_{1} C_{2} )\omega^{2} }}{{1 - \omega^{2} }},\, \\ n_{6} & = \frac{{(N_{3} M_{2} \omega^{2} - \mu_{2} C_{3} )\omega^{2} }}{{\varpi^{2} - \omega^{2} }}.\, \\ \end{aligned} $$

Elimination of the modified phases $\theta_{j}$ from the previous system produces three nonlinear algebraic equations of amplitudes $a_{j}$ and the frequency response functions that are clarified by the detuning parameters $\sigma_{j}$ as follows

$$ \begin{aligned} f_{1}^{2} & = a_{1}^{2} \{ \left[ {2\sigma_{1} + n_{4} + \frac{{a_{1}^{2} }}{8} + B_{1} \left( {1 - \frac{3}{4}B_{1} } \right) + S_{1} \left( {\frac{{S_{1} }}{4} + \frac{{B_{1} }}{2} - 1} \right) - \frac{3}{4}(C_{1} + C_{2} )^{2} } \right]^{2} \\ & \quad+ \left[ {\frac{{C_{2} N_{2} }}{{\omega^{2} - 1}} + (S_{1} - 1)(C_{1} + C_{2} )} \right]^{2} \} , \\ f_{2}^{2} & = a_{2}^{2} \{ \left[ {2\omega \sigma_{2} + n_{1} + n_{2} + n_{5} + n_{6} + \frac{{a_{2}^{2} }}{8}\omega^{2} - \frac{3}{4}(C_{3} + \mu_{1} )^{2} } \right]^{2} \\ & \quad+ \left[ {2\omega \sigma_{2} + n_{1} + n_{2} + n_{5} + n_{6} - \frac{3}{4}(C_{3} + \mu_{1} )^{2} } \right]^{2} \} , \\ f_{3}^{2} & = a_{3}^{2} \{ \left[ {2\varpi \sigma_{3} + \frac{{M_{1} M_{3} \varpi^{4} }}{{1 - \varpi^{2} }} + n_{6} + \frac{{a_{3}^{2} }}{8}\varpi^{2} + \frac{3}{4}\mu_{2}^{2} + B_{3} \varpi^{2} \left( {1 - \frac{3}{4}B_{3} } \right)} \right]^{2} \\ & \quad+ (n_{1} + \mu_{2} B_{3} - \mu_{2} \varpi )^{2} \} . \\ \end{aligned} $$

(50)

It is important to note that the case of steady-state solutions is considered an important part for the stability’s examination. Therefore, to study the behavior near a neighborhood region of fixed points, let us consider the following substitutions into the above system of Eqs. (48) [42, 43]

$$ \begin{aligned} a_{1} & = a_{10} + a_{11} ,\,\,\,\,\,\,\,\,\,\,\,a_{2} = a_{20} + a_{21} ,\,\,\,\,\,\,\,\,\,\,\,\\ a_{3} &= a_{30} + a_{31} , \\ \theta_{1} & = \theta_{10} + \theta_{11} ,\,\,\,\,\,\,\,\,\,\,\,\theta_{2} = \theta_{20} + \theta_{21} ,\,\,\,\,\,\,\,\,\,\,\,\\\theta_{3} &= \theta_{30} + \theta_{31} , \\ \end{aligned} $$

(51)

where $a_{j0} ,\theta_{j0}$ are the solutions at the steady state of (49) and $a_{j1} ,\theta_{j1}$ are the corresponding tiny perturbations. Therefore, the linearized system of (48) has the form

$$ \begin{aligned} a_{10} \frac{{{\text{d}}\theta_{11} }}{{{\text{d}}\tau }} & = \frac{{a_{11} }}{2}\left[ {2\sigma_{1} + n_{1} + B_{1} \left( {1 - \frac{3}{4}B_{1} } \right) + S_{1} \left( { - 1 + \frac{1}{2}B_{1} + \frac{1}{4}S_{1} } \right) - \frac{3}{4}(C_{1} + C_{2} )^{2} \, + \frac{3}{8}a_{10}^{2} a_{11} } \right] \\ & \quad- \frac{{f_{1} }}{2}\theta_{11} \sin \theta_{10} , \\ \frac{{{\text{d}}a_{11} }}{{{\text{d}}\tau }} & = \frac{{a_{11} }}{2}\left[ {\frac{{C_{2} N_{2} }}{{\omega^{2} - 1}} + (C_{1} + C_{2} )(S_{1} - 1)} \right] + \frac{{f_{1} }}{2}\theta_{11} \cos \theta_{10} , \\ a_{20} \frac{{{\text{d}}\theta_{21} }}{{{\text{d}}\tau }} & = \frac{{a_{21} }}{2}\left[ {2\sigma_{2} + \frac{1}{\omega }(n_{2} + n_{3} + n_{4} ) + \frac{{a_{20}^{2} }}{8}\omega - \frac{3}{4\omega }(C_{3} + \mu_{1} )^{2} )} \right] - \frac{{f_{2} }}{2\omega }\theta_{21} \sin \theta_{20} , \\ \frac{{{\text{d}}a_{21} }}{{{\text{d}}\tau }} & = \frac{{a_{21} }}{2}\left[ {\frac{{\omega^{2} (C_{2} N_{2} + \mu_{1} N_{1} )}}{{1 - \omega^{2} }} + \frac{{\mu_{2} \omega^{2} (M_{2} + N_{3} )}}{{\varpi^{2} - \omega^{2} }} + (C_{3} + \mu_{1} )\left( {\frac{{S_{2} }}{\omega } - 1} \right)} \right] + \frac{{f_{2} }}{2\omega }\theta_{21} \cos \theta_{20} , \\ a_{30} \frac{{{\text{d}}\theta_{31} }}{{{\text{d}}\tau }} & = \frac{{a_{31} }}{2}\left[ {2\sigma_{3} + \frac{{M_{1} M_{3} \varpi^{3} }}{{1 - \varpi^{2} }} + \frac{{n_{3} }}{\omega }\, + \frac{{3a_{30}^{2} }}{8}\,\, + B_{3} \varpi \left( {1 - \frac{3}{4}B_{3} } \right) + \frac{3}{4\varpi }\mu_{2}^{2} } \right] - \frac{{f_{3} }}{2\varpi }\theta_{31} \sin \theta_{30} , \\ \frac{{{\text{d}}a_{31} }}{{{\text{d}}\tau }} & = \frac{{a_{31} }}{2}\left[ {\frac{{n_{6} }}{\varpi } + \mu_{2} \left( {\frac{{B_{3} }}{\varpi } - 1} \right)} \right] + \frac{{f_{3} }}{2\varpi }\theta_{31} \cos \theta_{30} . \\ \end{aligned} $$

(52)

The solutions of the previous system can be achieved if we represent $a_{j1}$ and $\theta_{j1}$ exponentially as in the forms $q_{k} e^{\lambda T} ,$ where $q_{k} \,(k = 1,2,...,6)$ are constants and $\lambda$ denotes the unknown perturbations’ associated with their eigenvalues. The roots’ real parts of the following characteristic equations should not be positive value, if the solutions at steady state $a_{j0}$ and $\theta_{j0}$ are stable asymptotically [44]

$$ \lambda^{6} + \Gamma_{1} \lambda^{5} + \Gamma_{2} \lambda^{4} + \Gamma_{3} \lambda^{3} + \Gamma_{4} \lambda^{2} + \Gamma_{5} \lambda + \Gamma_{6} = 0. $$

(53)

Here $\Gamma_{k}$ are functions of the unperturbed parameters $a_{j0} ,\theta_{j0} ,$ and $g_{j}$(see Appendix1).

The Routh–Hurwitz criteria [20] provide the necessary and sufficient requirements for steady-state solutions that can be expressed as follows

$$ \begin{aligned} & \Gamma_{1} > 0, \\ & \Gamma_{1} \Gamma_{2} - \Gamma_{3} > 0, \\ & \Gamma_{1} \Gamma_{2} \Gamma_{3} - \Gamma_{3}^{2} - \Gamma_{1}^{2} \Gamma_{4} + \Gamma_{1} \Gamma_{5} > 0, \\ & \Gamma_{1} \Gamma_{2} \Gamma_{3} \Gamma_{4} - \Gamma_{3}^{2} \Gamma_{4} - \Gamma_{1}^{2} \Gamma_{4}^{2} - \Gamma_{1} \Gamma_{2}^{2} \Gamma_{5} + \Gamma_{5} \Gamma_{2} \Gamma_{3} + 2\Gamma_{1} \Gamma_{4} \Gamma_{5} - \Gamma_{5}^{2} + \Gamma_{1}^{2} \Gamma_{2} \Gamma_{6} - \Gamma_{1} \Gamma_{6} \Gamma_{3} > 0, \\ & \Gamma_{1} \Gamma_{2} \Gamma_{3} \Gamma_{4} \Gamma_{5} - \Gamma_{4} \Gamma_{5} \Gamma_{3}^{2} - \Gamma_{1}^{2} \Gamma_{4}^{2} \Gamma_{5} - \Gamma_{1} \Gamma_{2}^{2} \Gamma_{5}^{2} + \Gamma_{5}^{2} \Gamma_{2} \Gamma_{3} + 2\Gamma_{1} \Gamma_{4} \Gamma_{5}^{2} - \Gamma_{5}^{3} - \Gamma_{1} \Gamma_{2} \Gamma_{3}^{2} \Gamma_{6} \\ & + \Gamma_{3}^{3} \Gamma_{6} + \Gamma_{1}^{2} \Gamma_{6} \Gamma_{3} \Gamma_{4} + 2\Gamma_{1}^{2} \Gamma_{2} \Gamma_{5} \Gamma_{6} - 3\Gamma_{1} \Gamma_{5} \Gamma_{3} \Gamma_{6} - \Gamma_{1}^{3} \Gamma_{6}^{2} > 0, \\ & \Gamma_{6} (\Gamma_{1} \Gamma_{2} \Gamma_{3} \Gamma_{4} \Gamma_{5} - \Gamma_{4} \Gamma_{5} \Gamma_{3}^{2} - \Gamma_{1}^{2} \Gamma_{4}^{2} \Gamma_{5} - \Gamma_{1} \Gamma_{2}^{2} \Gamma_{5}^{2} + \Gamma_{2} \Gamma_{3} \Gamma_{5}^{2} + 2\Gamma_{1} \Gamma_{4} \Gamma_{5}^{2} - \Gamma_{5}^{3} - \Gamma_{1} \Gamma_{2} \Gamma_{3}^{2} \Gamma_{6} \\ & + \Gamma_{3}^{3} \Gamma_{6} + \Gamma_{1}^{2} \Gamma_{6} \Gamma_{3} \Gamma_{4} + 2\Gamma_{1} \Gamma_{2} \Gamma_{5} \Gamma_{6} - 3\Gamma_{1} \Gamma_{5} \Gamma_{3} \Gamma_{6} - \Gamma_{1}^{3} \Gamma_{6}^{2} ) > 0. \\ \end{aligned} $$

(54)

6 Analysis of system’s stability

In the present part of this section, the dynamical motion of the considered TRBP system in the presence of external moments $M_{j} \,\,\,(j = 1,2,3)$ is examined using the linear stability analysis. The stability requirements are performed besides the modeling of the nonlinear system’s equations. Some parameters, such as detuning parameters $\sigma_{j}$ and the natural frequencies $1,\varpi$, have been discovered to play a key role in undermining the stability requirements. A customized process with different system parameters has been used to plot the stability graphs of the system (48). The amplitudes $a_{j}$ of the fluctuations versus time are plotted for distinct parametric regions, see Figs. 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, and 23 that are drawn to show the impact of the $\sigma_{j}$ values on the possible fixed points.

Fig. 9

Amplitudes’ resonance curves $a_{j} \,\,(j = 1,2,3)$ as a function of $\sigma_{3}$ at $\omega = 0.4062$

Fig. 10

Curves of $a_{j} (\sigma_{2} );\,\,(j = 1,2,3)$ at $\omega = 0.4062$

Fig. 11

Curves of $a_{j} (\sigma_{1} )\,;\,(j = 1,2,3)$ at $\omega = 0.4062$

Fig. 12

Resonance curves of $a_{j} (\sigma_{3} );\,\,(j = 1,2,3)$ at $\omega = 0.4062,$ $\sigma_{1} = - 0.1,\,\sigma_{2} = 0.2,$ and $C_{1} ( = 0.005,0.01,0.1)$

Fig. 13

Resonance curves of $a_{j} (\sigma_{3} );\,\,(j = 1,2,3)$ at $\omega = 0.4062,$ $\sigma_{1} = - 0.1,\,\sigma_{2} = 0.2$ and $C_{2} ( = 0.002,0.004,0.006)$

Fig. 14

Resonance curves of $a_{j} (\sigma_{3} );\,\,(j = 1,2,3)$ at $\omega = 0.4062,$$\sigma_{1} = - 0.1,\,\sigma_{2} = 0.2,$ and $C_{3} ( = 0.004,0.006,0.008)$

Fig. 15

Resonance curves of $a_{j} (\sigma_{3} );\,\,(j = 1,2,3)$ at $\omega = 0.3829,$ $\sigma_{1} = - 0.1,\,\sigma_{2} = 0.2,$ and $C_{1} ( = 0.005,0.01,0.1)$

Fig. 16

Resonance curves of $a_{j} (\sigma_{3} );\,\,(j = 1,2,3)$ at $\omega = 0.3829,$ $\sigma_{1} = - 0.1,\,\sigma_{2} = 0.2,$ and $C_{2} ( = 0.002,0.004,0.006)$

Fig. 17

Resonance curves of $a_{j} (\sigma_{3} );\,\,(j = 1,2,3)$ at $\omega = 0.3829,$ $\sigma_{1} = - 0.1,\,\sigma_{2} = 0.2,$ and $C_{3} ( = 0.004,0.006,0.008)$

Fig. 18

Resonance curves of $a_{j} (\sigma_{3} );\,\,(j = 1,2,3)$ at $\omega = 0.4690,$$\sigma_{1} = - 0.1,\,\sigma_{2} = 0.2,$ and $C_{1} ( = 0.005,0.01,0.1)$

Fig. 19

Resonance curves of $a_{j} (\sigma_{3} );\,\,(j = 1,2,3)$ at $\omega = 0.4690,$$\sigma_{1} = - 0.1,\,\sigma_{2} = 0.2,$ and $C_{2} ( = 0.002,0.004,0.006)$

Fig. 20

Resonance curves of $a_{j} (\sigma_{3} );\,\,(j = 1,2,3)$ at $\omega = 0.4690,$$\sigma_{1} = - 0.1,\,\sigma_{2} = 0.2,$ and $C_{3} ( = 0.004,0.006,0.008)$

Fig. 21

Resonance curves of $a_{j} (\sigma_{3} );\,\,(j = 1,2,3)$ at $\omega = 0.4690$

Fig. 22

Resonance curves of $a_{j} (\sigma_{2} );\,\,(j = 1,2,3)$ at $\omega = 0.4690$

Fig. 23

Resonance curves of $a_{j} (\sigma_{1} );\,\,(j = 1,2,3)$ at $\omega = 0.4690$

Overall, the areas of stable and unstable fixed points under the present constraints of the selected values of the impacted parameters, lie in the range $\sigma_{j} \le - 0.07$ and $- 0.07 < \sigma_{j}$, respectively. It is important to note that the solid curves reflect the domain of stable fixed points, whereas the dashed curves denote the unstable ranges.

No peaks are observed in the planes $a_{1} \sigma_{3}$ and $a_{2} \sigma_{3}$ except for three critical fixed points, as shown in parts (a) and (b) of Fig. 9, while there exist one peak and one critical fixed points in the plane $a_{3} \sigma_{3}$ when $\omega = 0.4062$ at $(\sigma_{1} = - 0.1,\sigma_{3} = 0.2),$ $(\sigma_{1} = \sigma_{3} = 0),$ and $(\sigma_{1} = 0.1,\sigma_{3} = - 0.2)$. It is clear from the third equation in the system (50) that $a_{3}$ is a function of $\sigma_{3}$, so we get a curve as shown in Fig. 9c, this means that $a_{3}$ changes with $\sigma_{3}$, while we get straight lines as shown in Fig. 9a and b. This means that the value of $a_{1}$, $a_{2}$ are invariant with respect to $\sigma_{3}$ because they are functions of $\sigma_{1}$ and $\sigma_{2}$ as observed in the first and second equations of the system (50), respectively. A closer look at Fig. 10 reveals that it is graphed when $(\sigma_{1} = 0.1,\sigma_{3} = - 0.002),$ $(\sigma_{1} = - 0.1,\sigma_{3} = 0.002),$ and $(\sigma_{1} = \sigma_{3} = 0)$. Several critical points are drawn in part (a). The drawn curve in part (b) includes one peak at the point $(0.1287,0.0253)$ and one critical fixed point in the plane $a_{2} \sigma_{2}$ at $\omega = 0.4062.$ On the other hand, there exist three critical fixed points in Fig. 10c at the same considered values of the detuning parameters.

Curves of Fig. 11 are plotted when $(\sigma_{2} = 0.02,\sigma_{3} = - 0.003),$$(\sigma_{2} = - 0.02,\sigma_{3} = 0.003),$ and $(\sigma_{2} = \sigma_{3} = 0)$, the peak fixed point appears in the plane $a_{1} \sigma_{1}$ of frequency response as in part (a). There are three critical fixed points are observed in the planes of frequency responses $a_{2} \sigma_{1}$ and $a_{3} \sigma_{1}$ as shown in Fig. 11b and c.

No peaks are observed in the planes $a_{1} \sigma_{3}$ and $a_{2} \sigma_{3}$ except for two and one critical fixed points, as shown in portions (a) and (b), respectively, of Fig. 12. In Fig. 13, there is one critical fixed point in the plane $a_{1} \sigma_{3}$ and $a_{2} \sigma_{3}$ while there exist one peak and one critical fixed points in the plane $a_{3} \sigma_{3}$ of Figs. 12, 13, 14. Moreover, three critical fixed points are observed in the plane $a_{2} \sigma_{3}$ of Fig. 14 when $\omega = 0.4062$ at $\,C_{1} ( = 0.005,0.01,0.1),$$C_{2} ( = 0.002,0.004,0.006),$$C_{3} ( = 0.004,0.006,0.008),$ $\sigma_{1} = - 0.1,$ and $\sigma_{2} = 0.2.$

Several critical points are drawn in the planes $a_{1} \sigma_{3}$ and $a_{2} \sigma_{3}$, as shown in portions (a) and (b), respectively, of Figs. 15, 16 and 17, while there exists one peak and one critical fixed points in the plane $a_{3} \sigma_{3}$ when $\omega = 0.3829$ at $\,C_{1} ( = 0.005,0.01,0.1),$$C_{2} ( = - 0.002,0.004,0.006),$$C_{3} ( = 0.004,0.006,0.008),$ $\sigma_{1} = - 0.1,$ and $\sigma_{2} = 0.2.$

There are two critical fixed points in the plane $a_{1} \sigma_{3}$ of Fig. 18 while there exists one critical fixed point in part (b) and one peak and one critical fixed points in part (c) at $\omega = 0.4690,\,C_{1} ( = 0.005,0.01,0.1)$. In Fig. 19, the one peak and one critical fixed points exist in the plane $a_{3} \sigma_{3}$ while there is one critical fixed point in the plane $a_{2} \sigma_{3}$ and $a_{1} \sigma_{3}$ when $\omega = 0.4690,\,C_{2} ( = - 0.002,0.004,0.006).$ There are one and two critical points in parts (a) and (b) of Fig. 20, respectively. There exists two critical points and one peak in part (c) at $\omega = 0.4690$ and $C_{3} ( = 0.004,0.006,0.008)$.

No peaks are observed in the planes $a_{1} \sigma_{3}$ and $a_{2} \sigma_{3}$ except for three critical fixed points, as drawn in parts (a) and (b) of Fig. 21, while there exists essential one peak and one critical fixed points in the plane $a_{3} \sigma_{3}$ when $\omega = 0.4690$ at $(\sigma_{1} = - 0.1,\sigma_{3} = 0.2),$ $(\sigma_{1} = \sigma_{3} = 0),$ and $(\sigma_{1} = 0.1,\sigma_{3} = - 0.2)$. A closer examination of the curves of Fig. 22 shows that it is graphed when $(\sigma_{1} = 0.1,\sigma_{3} = - 0.002),$ $(\sigma_{1} = - 0.1,\sigma_{3} = 0.002),$ and $(\sigma_{1} = \sigma_{3} = 0)$. Several critical are drawn in part (a). The drawn curve in part (b) includes two peaks and one critical fixed point in the plane $a_{2} \sigma_{2}$ at $\omega = 0.4690$. On the other hand, there are three crucial critical fixed points in Fig. 22c at the same considered values of the detuning parameters.

Curves of Fig. 23 are drawn when $(\sigma_{2} = 0.02,\sigma_{3} = - 0.003),$ $(\sigma_{2} = - 0.02,\sigma_{3} = 0.003),$ and $(\sigma_{2} = \sigma_{3} = 0)$, the peak fixed point appears in the plane $a_{1} \sigma_{1}$ of frequency response as in part (a). There are three observed fundamental critical fixed points in the planes of frequency responses $a_{2} \sigma_{1}$ and $a_{3} \sigma_{1}$ as shown in Fig. 23b and c. Tables 1 and 5 show the relation between the critical and peaks fixed points and the values of the parameters $\sigma_{j} ,$ and $\omega$, while Tables 2, 3 and 4 show the relation between the critical and peaks fixed points at the considered values of the parameters $C_{j}$ and $\omega$, respectively (Table 5).

Table 1 Critical and peaks fixed points when detuning parameters $\sigma_{j}$ have different values at $\omega = 0.4062$

Table 2 Critical and peaks fixed points when damping coefficients $C_{j}$ have different values at $\omega = 0.4062$

Table 3 Critical and peaks fixed points when damping coefficients $C_{j}$ have different values at $\omega = 0.3829$

Table 4 Critical and peaks fixed points when damping coefficients $C_{j}$ have different values at $\omega = 0.4690$

Table 5 Critical and peaks fixed points when detuning parameters $\sigma_{j}$ have different values at $\omega = 0.4690$

7 Nonlinear analysis

This section examines the stability of the nonlinear amplitude of Eq. (48) as well as exhibiting its characteristics. Therefore, the following transformations are considered [45, 46]

$$ \begin{aligned} A_{j} & = \frac{1}{2}[\tilde{u}_{j} (\tau_{1} ,\tau_{2} ) + i\,\tilde{v}_{j} (\tau_{1} ,\tau_{2} )]e^{{ - i\tilde{\sigma }_{j} \tau_{1} }} \,\,\,(j = 1,2,3); \\ u_{j} & = \varepsilon \tilde{u}_{j} ,\,\,\,\,\,\,\,\,\,\,\,v_{j} = \varepsilon \tilde{v}_{j} , \\ \end{aligned} $$

(55)

where $u_{j}$ and $v_{j}$ are the real and imaginary parts of the amplitudes $A_{j}$, respectively.

Substituting (14) and (87) into (33)–(35), and consequently separating real and imaginary part to yield

$$ \begin{aligned} & \frac{{{\text{d}}v_{1} }}{{{\text{d}}\tau }} + \frac{1}{16}(u_{1}^{3} + u_{1} \,v_{1}^{2} ) + \frac{1}{2}[\sigma_{1} - \frac{3}{4}B_{1}^{2} + \frac{1}{4}S_{1}^{2} + \frac{1}{2}(B_{1} - S_{1} ) \\ & + \frac{1}{2}B_{1} S_{1} - \frac{3}{4}(C_{1} + C_{2} )^{2} + \frac{1}{{\omega^{2} - 1}}(M_{1} M_{3} + N_{1} N_{2} - C_{2} \mu_{1} )]\,u_{1} \\ & - \frac{1}{2}\left[ {S_{1} (C_{1} + C_{2} ) + \frac{{N_{1} \mu_{1} + N_{2} C_{2} }}{{\omega^{2} - 1}} + \frac{1}{2}(C_{1} + C_{2} )} \right]\,\,v_{1} + \frac{{f_{1} }}{2} = 0, \\ \end{aligned} $$

$$ \begin{aligned} & \frac{{{\text{d}}u_{1} }}{{{\text{d}}\tau }} + \sigma_{1} \,v_{1} + \frac{1}{2}(B_{1} - S_{1} )\,v_{1} - \frac{1}{2}(C_{1} + C_{2} )\,u_{1} + \frac{1}{16}(v_{1}^{3} + v_{1} \,u_{1}^{2} ) \\ & + \frac{1}{2}\left[ {\frac{1}{4}S_{1}^{2} - \frac{3}{4}B_{1}^{2} + \frac{1}{2}B_{1} S_{1} - \frac{3}{4}(C_{1} + C_{2} )^{2} + \frac{{M_{1} M_{3} + N_{1} N_{2} - C_{2} \mu_{1} }}{{\omega^{2} - 1}}} \right]\,v_{1} \\ & + \frac{1}{2}\left[ {S_{1} (C_{1} + C_{2} ) + \frac{{N_{1} \mu_{1} + N_{2} C_{2} }}{{\omega^{2} - 1}}} \right]\,u_{1} = 0, \\ \end{aligned} $$

$$ \begin{aligned} & \omega \frac{{{\text{d}}v_{2} }}{{{\text{d}}\tau }} + \sigma_{2} \,u_{2} \omega + \frac{1}{2}(B_{2} \omega^{2} - S_{2} )\,u_{2} + \frac{1}{2}\omega (C_{3} + \mu_{1} )\,v_{2} \\ & + \frac{1}{16}\omega^{2} (u_{2}^{3} + u_{2} \,v_{2}^{2} ) + \frac{1}{2}[\frac{1}{{4\omega^{2} }}S_{2}^{2} - \frac{3}{4}B_{2}^{2} \omega^{2} + \frac{1}{2}B_{2} \,S_{2} \\ & - \frac{3}{4}(C_{3} + \mu_{1} )^{2} + \frac{{\omega^{2} (N_{1} N_{2} \omega^{2} - C_{2} \mu_{1} )}}{{1 - \omega^{2} }} + \frac{{\omega^{2} (M_{2} \,N_{3} \omega^{2} - C_{3} \mu_{2} )}}{{\varpi^{2} - \omega^{2} }}]\,u_{2} \\ & - \frac{1}{2}\left[ {\frac{{S_{2} }}{\omega }(C_{3} + \mu_{1} ) + \frac{{\omega^{3} (N_{1} \mu_{1} + N_{2} C_{2} )}}{{1 - \omega^{2} }} + \frac{{\omega^{3} (N_{3} \mu_{2} + M_{2} \mu_{2} )}}{{\varpi^{2} - \omega^{2} }}} \right]\,v_{2} + \frac{{f_{2} }}{2} = 0, \\ \end{aligned} $$

$$ \begin{aligned} & \omega \frac{{{\text{d}}u_{2} }}{{{\text{d}}\tau }} - \sigma_{2} \,v_{2} \omega + \frac{1}{2}(B_{2} \omega^{2} - S_{2} )\,v_{2} - \frac{1}{2}\omega (C_{3} + \mu_{1} )u_{2} - \frac{1}{16}\omega^{2} (v_{2}^{3} + v_{2} \,u_{2}^{2} ) \\ & - \frac{1}{2}\left[ {\frac{1}{{4\omega^{2} }}S_{2}^{2} - \frac{3}{4}B_{2}^{2} \omega^{2} + \frac{1}{2}B_{2} \,S_{2} - \frac{3}{4}(C_{3} + \mu_{1} )^{2} + \frac{{\omega^{2} (N_{1} \,N_{2} \,\omega^{2} - C_{2} \,\mu_{1} )}}{{1 - \omega^{2} }} + \frac{{\omega^{2} (M_{2} \,N_{3} \omega^{2} - C_{3} \,\mu_{2} )}}{{\varpi^{2} - \omega^{2} }}} \right]\,v_{2} \\ & + \frac{1}{2}\left[ {\frac{{S_{2} }}{\omega }(C_{3} + \mu_{1} ) + \frac{{\omega^{3} (N_{1} \,\mu_{1} + N_{2} C_{2} )}}{{1 - \omega^{2} }} + \frac{{\omega^{3} (N_{3} \,\mu_{2} + M_{2} \,\mu_{2} )}}{{\varpi^{2} - \omega^{2} }}} \right]\,u_{2} = 0, \\ \end{aligned} $$

$$ \begin{aligned} & \varpi \frac{{{\text{d}}v_{3} }}{{{\text{d}}\tau }} + \frac{1}{2}\varpi \,\mu_{2} \,v_{3} + \frac{1}{16}\varpi^{2} (u_{3}^{3} + u_{3} \,v_{3}^{2} ) \\ & + \frac{1}{2}\left[ {\frac{3}{4}\mu_{2}^{2} - \frac{1}{4}B_{3}^{2} \,\varpi^{2} + \frac{{\varpi^{4} M_{1} M_{3} }}{{1 - \varpi^{2} }} + \frac{{\varpi^{2} }}{{\omega^{2} - \varpi^{2} }}(M_{2} \,N_{3} \,\varpi^{2} - C_{3} \,\mu_{2} ) + \sigma_{3} \,\varpi } \right]\,\,u_{3} \\ & - \frac{1}{2}\left[ {B_{3} \,\varpi \,\mu_{2} + \frac{{\varpi^{3} (M_{2} \,\mu_{2} + N_{3} \,C_{3} )}}{{\omega^{2} - \varpi^{2} }}} \right]\,v_{3} + \frac{{f_{3} }}{2} = 0, \\ \end{aligned} $$

$$ \begin{aligned} & \varpi \frac{{{\text{d}}u_{3} }}{{{\text{d}}\tau }} + \frac{1}{2}\varpi \,\mu_{2} \,u_{3} - \frac{1}{16}\varpi^{2} (v_{3}^{3} + v_{3} \,u_{3}^{2} ) \\ & - \frac{1}{2}\left[ {\frac{3}{4}\mu_{2}^{2} - \frac{5}{4}B_{3}^{2} \,\varpi^{2} + \frac{{\varpi^{4} M_{1} M_{3} }}{{1 - \varpi^{2} }} + \frac{{\varpi^{2} (M_{2} \,N_{3} \,\varpi^{2} - C_{3} \,\mu_{2} )}}{{\omega^{2} - \varpi^{2} }} - \sigma_{3} \,\varpi } \right]\,v_{3} \\ & - \frac{1}{2}\left[ {(B_{3} \,\varpi \,\mu_{2} + \frac{{\varpi^{3} (M_{2} \,\mu_{2} + N_{3} \,C_{3} )}}{{\omega^{2} - \varpi^{2} }}} \right]\,u_{3} = 0. \\ \end{aligned} $$

(56)

The adjusted amplitudes were then verified over time in various parametric zones, and the amplitudes’ characteristics are depicted in phase plane curves as illustrated in Figs. 24, 25 and 26. The values of the parameters are set to the values listed below

$$ \begin{aligned} \sigma_{1} & = - 0.1,\,\,\,\,\,\,\sigma_{2} = 0.2,\,\,\,\,\,\,\,\sigma_{3} = 0.3,\,\,\,\,\,\,\omega ( = \,0.3829,0.4062,\,0.4690),\,\,\,\,\,u_{1} (0) = 1,\, \\ v_{1} (0) & = 0.8,\,\,\,\,\,\,\,u_{2} (0) = 1.5,\,\,\,\,\,\,\,v_{2} (0) = 0.4,\,\,\,\,\,\,\,u_{3} (0) = 1.5,\,\,\,\,\,\,\,v_{3} (0) = 0.5. \\ \end{aligned} $$

Fig. 24

a Variation of $u_{1}$ via time $\tau$, b variation of $v_{1}$ versus time $\tau$, c projections of the modulation equations’ paths on the $u_{1} v_{1}$ plane when $\omega ( = \,0.3829,0.4062,\,0.4690)$

Fig. 25

a and b Variation of $u_{2}$ and $v_{2}$ via time $\tau$, c projections of the modulation equations’ paths on the $u_{2} v_{2}$ plane when $\omega ( = \,0.3829,0.4062,\,0.4690)$

Fig. 26

a and b Variation of $u_{3}$ and $v_{3}$ via time $\tau$, c projections of the modulation equations’ paths on the $u_{3} v_{3}$ plane when $\omega ( = \,0.3829,0.4062,\,0.4690)$

Portions (a) and (b) of Figs. 24, 25 and 26 describe the variation of the adjusted phases via the dimensionless time $\tau$, while parts (c) of the same figures represent the projections of the modulation equation trajectories on the plane $u_{j} v_{j}$ when $\omega$ have the above different values. The plotted curves of the waves illustrating the time histories of $u_{j}$ and $v_{j}$ behave periodic attitudes. The oscillation number increases with the increase in the frequency value $\omega$, while the wavelengths decrease. However, the raising of $\omega$ values leads to increase in the amplitudes behavior as shown in Fig. 26. The plotted closed curves in parts (c) indicate that the above modulation system behaves in a stable manner.

8 Conclusion

An externally influenced TRBP dynamical system with 3 DOFs has been investigated as a novel model. The regulating nonlinear differential equations are derived using Lagrange's equations from second kind. The strategy of the approximate analytic solutions up to the third-order of approximation is investigated using the MSA. The prerequisites for solvability are met by removing secular terms. The emerging resonance cases are detected, and the equations of modulation are achieved. The frequency responses curves and time histories of the obtained new results are visually displayed to emphasize the beneficial effects of the various parameters on the motion. The numerical results of the motion’s governing system are gained using the Runge–Kutta fourth-order method. The comparison between both results demonstrates that the used perturbation technique is extremely accurate. The steady-state solutions are investigated, and the zones of stability and instability are evaluated using Routh–Hurwitz conditions. This work is significant because of its applications in engineering vibrational control, which gives the researched system a lot of weight.

Appendix 1

$$ \begin{aligned} \Gamma_{1} & = \frac{1}{2}\left[ { - 2(d_{2} + d_{5} + d_{8} ) + \frac{{\sin \theta_{10} \,f_{1} }}{{a_{10} }} + \frac{{\sin \theta_{20} \,f_{2} }}{{\omega a_{20} }} + \frac{{\sin \theta_{30} \,f_{3} }}{{\varpi a_{30} }}} \right], \\ \Gamma_{2} & = \frac{1}{{4\omega \varpi a_{10} a_{20} a_{30} }}[2\omega \varpi ( - 2a_{10} a_{30} d_{4} d_{6} - a_{20} a_{30} (d_{7} d_{9} + d_{2} d_{5} + (d_{2} + d_{5} )d_{8} \\ &\quad - 2d_{1} d_{3} - (d_{2} + d_{5} + d_{8} )\sin \theta_{10} f_{1} )) + \varpi \sin \theta_{20} a_{30} ( - 2(d_{2} + d_{5} + d_{8} )a_{10} \\ &\quad + \sin \theta_{10} f_{1} )f_{2} + \sin \theta_{30} (\omega a_{20} ( - 2(d_{2} + d_{5} + d_{8} )a_{10} + \sin \theta_{10} f_{1} )\sin \theta_{20} a_{10} f_{2} )f_{3} ], \\ \Gamma_{3} & = \frac{1}{{8\omega \varpi a_{10} a_{20} a_{30} }}[4\omega \varpi (2d_{1} d_{3} (d_{5} + d_{8} )a_{20} a_{30} + \sin \theta_{10} ( - d_{4} d_{6} a_{30} \\ & \quad+ a_{20} ( - d_{7} d_{9} + d_{2} d_{5} (1 + d_{8} )a_{30} )f_{1} + 2\varpi \sin \theta_{20} a_{30} ( - 2d_{1} d_{3} - (d_{2} \\ & \quad+ d_{5} + d_{8} )\sin \theta_{10} f_{1} )f_{2} + \sin \theta_{30} (2\omega a_{20} ( - 2d_{1} d_{3} - (d_{2} + d_{5} + d_{8} )\sin \theta_{10} f_{1} ) \\ & \quad+ \sin \theta_{10} \sin \theta_{20} f_{1} f_{2} )f_{3} + 2a_{10} (4\varpi \omega (d_{4} d_{6} (d_{2} + d_{8} )a_{30} + a_{20} ((d_{2} + d_{5} )d_{7} d_{9} \\ & \quad- d_{2} d_{5} d_{8} a_{30} )) + 2\varpi \sin \theta_{20} ( - d_{7} d_{9} + d_{2} d_{5} (1 + d_{8} )a_{30} )f_{2} + \sin \theta_{30} ( - 2d_{4} d_{6} \omega \\ & \quad+ 2(d_{5} d_{2} + d_{8} (d_{2} + d_{5} )\omega a_{20} - (d_{2} + d_{5} + d_{8} )\sin \theta_{20} f_{2} )f_{3} )], \\ \Gamma_{4} & = \frac{1}{{8\omega \varpi a_{10} a_{20} a_{30} }}[4\omega \varpi d_{4} d_{6} a_{30} (2d_{1} d_{3} + (d_{2} + d_{8} )\sin \theta_{10} f_{1} ) \\ & \quad+ 2\varpi \sin \theta_{20} (2d_{1} d_{3} (d_{5} + d_{8} )a_{30} + \sin \theta_{10} ( - d_{7} d_{9} + (d_{2} d_{5} + (d_{2} \\ & \quad+ d_{5} )d_{8} )a_{30} )f_{1} )f_{2} + \sin \theta_{30} ( - 2d_{4} d_{6} \omega \sin \theta_{10} f_{1} + \sin \theta_{20} ( - 2d_{1} d_{3} \\ & \quad- (d_{2} + d_{5} + d_{8} )\sin \theta_{10} f_{1} )f_{2} )f_{3} + 2\omega a20(4d_{1} d_{3} \varpi (d_{7} d_{9} - d_{5} d_{8} a_{30} ) \\ & \quad+ 2\varpi \sin \theta_{10} ((d_{2} + d_{5} )d_{7} d_{9} - d_{2} d_{5} d_{8} a_{30} )f_{1} + \sin \theta_{30} (2d_{1} d_{3} (d_{5} + d_{8} ) \\ & \quad+ (d_{2} d_{5} + (d_{2} + d_{5} )d_{8} )\sin \theta_{10} f_{1} )f_{3} ) + 2a_{10} (4\omega \varpi (d_{4} d_{6} d_{7} d_{9} \\ & \quad- d_{2} (d_{5} d_{7} d_{9} a_{20} + d_{4} d_{6} d_{8} a_{30} )) + 2\varpi \sin \theta_{20} ((d_{2} + d_{5} )d_{7} d_{9} \\ &\quad - d_{2} d_{5} d_{8} a_{30} )f_{2} + \sin \theta_{30} (2d_{4} d_{6} (d_{2} + d_{8} )\omega - 2d_{2} d_{5} d_{8} \omega a_{20} \\ & \quad- 2d_{2} d_{5} d_{8} \omega a_{20} + (d_{2} d_{5} + (d_{2} + d_{5} )d_{8} )\sin \theta_{20} f_{2} )f_{3} )], \\ \end{aligned} $$

$$ \begin{aligned} \Gamma_{5} & = \frac{1}{{8\omega \varpi a_{10} a_{20} a_{30} }}[4\omega \varpi d_{4} d_{6} ( - 2d_{1} d_{3} d_{8} a_{30} + \sin \theta_{10} (d_{7} d_{9} - d_{2} d_{8} a_{30} )f_{1} ) \\ & \quad+ 2\varpi \sin \theta_{20} (2d_{1} d_{3} (d_{7} d_{9} - d_{5} d_{8} a_{30} ) + \sin \theta_{10} ((d_{2} + d_{5} )d_{7} d_{9} - d_{2} d_{5} d_{8} a_{30} )f_{1} )f_{2} \\ &\quad + \sin \theta_{30} (2d_{4} d_{6} \omega (2d_{1} d_{3} + (d_{2} + d_{8} )\sin \theta_{10} f_{1} ) + \sin \theta_{20} (2d_{1} d_{3} (d_{5} + d_{8} ) \\ &\quad + (d_{2} d_{5} + (d_{2} + d_{5} )d_{8} )\sin \theta_{10} f_{1} )f_{2} )f_{3} - 2d_{5} \omega a_{20} (2d_{1} d_{3} + d_{2} \sin \theta_{10} f_{1} )(2d_{7} d_{9} \varpi \\ & \quad+ d_{8} \sin \theta {}_{30}f_{3} ) - 2d_{2} a_{10} (2d_{4} d_{6} \omega + d_{5} \sin \theta_{20} f_{2} )(2d_{7} d_{9} \varpi + d_{8} \sin \theta_{30} f_{3} )], \\ \Gamma_{6} & = \frac{ - 1}{{8\omega \varpi a_{10} a_{20} a_{30} }}[(2d_{1} d_{3} + d_{2} \sin \theta_{10} f_{1} )(2d_{4} d_{6} \omega + d_{5} \sin \theta_{20} f_{2} )(2d_{7} d_{9} \varpi + d_{8} \sin \theta_{30} f_{3} )] \\ \end{aligned} $$

where

$$ d_{1} = \sigma_{1} + \frac{{n_{4} }}{2} + \frac{{3a_{10}^{2} }}{16} + \frac{1}{2}B_{1} \left( {1 - \frac{3}{4}B_{1} } \right) + \frac{{S_{1} }}{2}\left( { - 1 + \frac{{B_{1} }}{2} + \frac{{S_{1} }}{4}} \right) - \frac{3}{8}(C_{1} + C_{2} )^{2} , $$

$$ d_{2} = \frac{{N_{2} C_{2} }}{{2(\omega^{2} - 1)}} + \frac{1}{2}(C_{1} + C_{2} )(S_{1} - 1), $$

$$ d_{3} = \frac{1}{2}f_{1} \cos \theta_{10} , $$

$$ d_{4} = \sigma_{2} + \frac{1}{2\omega }(n_{1} + n_{2} + n_{5} + n_{6} ) - \frac{3}{8\omega }(C_{3} + \mu_{1} )^{2} + \frac{{3\omega a_{20}^{2} }}{16}\,, $$

$$ d_{5} = \frac{1}{2}\left( { - 1 + \frac{{S_{2} }}{\omega }} \right)(\mu_{1} + C_{3} ) + \frac{{\omega^{2} (C_{2} N_{2} + \mu_{1} N_{1} )}}{{2(1 - \omega^{2} )}} + \frac{{\mu_{2} \omega^{2} (M_{2} + N_{3} )}}{{2(\varpi^{2} - \omega^{2} )}}, $$

$$ d_{6} = \frac{{f_{2} \cos \theta_{20} }}{2\omega }, $$

$$ d_{7} = \sigma_{3} + \frac{{3\varpi a_{30}^{2} }}{16} + \frac{1}{2}\varpi B_{3} \left( {1 - \frac{3}{4}B_{3} } \right) + \frac{3}{8\varpi }\mu_{2}^{2} + \frac{{M_{1} M_{3} \varpi^{3} }}{{2(1 - \varpi^{2} )}} + \frac{{N_{3} M_{2} \varpi^{3} - \mu_{2} C_{3} \varpi }}{{2(\omega^{2} - \varpi^{2} )}}, $$

$$ d_{8} = \frac{{ - \mu_{2} }}{2}\left( {1 - \frac{{B_{3} }}{\varpi }} \right) + \frac{{n_{3} }}{2\varpi }, $$

$$ d_{9} = \frac{{f_{3} }}{2\varpi }\cos \theta_{30} . $$