Stability of the Dynamical Motion of a Damped 3DOF Auto-parametric Pendulum System

Abstract

Purpose

The motion of three degrees-of-freedom (DOF) of an automatic parametric pendulum attached with a damped system has been investigated. The kinematics equations of this system have been derived employing Lagrange’s equations in accordance to it’s the generalized coordinates.

Methods

The method of multiple scales (MMS) has been used to obtain the solutions of the controlling equations up to the third-order of approximation. The solvability criteria and modulation equations for primary external resonance have been explored simultaneously.

Results

The non-linear stability approach has been used to analyze the stability of the considered system according to its different parameters. Time histories of the amplitudes and the phases of this system have been graphed to characterize the motion of the system at any given occurrence.

Conclusions

The different zones of stability and instability of this study have been checked and examined, in which the system's behavior has been revealed to be stable for various values of its variables.

Introduction

The development of vibrating systems is seen as one of the critical developments in mechanics, because of its different applications for the duration of regular daily existence, for example, building structures, rotor dynamics, rotor components, pumps, sieves, the motion of ships, compressors, and transportation devices [1,2,3].

Auto-parametric system is one of the essential systems that at least consists of two non-linearly subsystems. The first can be excited by an external harmonic force attached to a second one called an absorber. In this manner, one can get the essential parametric resonance of other subsystems (auto-parametric interaction) by decreasing the reaction of the first one [4,5,6,7,8,9,10]. The non-linear damping response 2DOF dynamical system connected with spring is investigated in [7]. In [8], the authors studied a dynamical oscillatory system with 4DOF comprising an auto-parametric pendulum and attached to a rigid body. Nonetheless, the auto-parametric system's behavior under the effect of kinematic excitation is studied numerically and illustrated experimentally in [9]. The authors examined whether the motion was regular or not through specific plots. In [10], the authors investigated an auto-parametric system's behavior consisting of a pendulum absorber connected to a damped vibrated system. The resonance case is obtained by using the technique for harmonic balance [5]. The MMS is utilized in [11] to acquire the auto-parametric states of a damped Duffing system linked with a pendulum. By uprightness of this method, a two coupled mass spring response is gotten in [12]. The author explained new excitation conditions within the sight of auto-parametric resonance. This resonance of an oscillatory system in the existence of a non-linear coupling term of third-order is discussed in [13]. The stability and the system’s bifurcation under external harmonic forces are explored [14, 15]. Besides, the MMS is used to get an autonomous framework up to the third order for a spring-suspended motion on a circular path [16]. The response of 2DOF for a non-linear dynamical system characterized by a damped elastic pendulum in an inviscid fluid flow is examined in [17]. The fourth-order Runge–Kutta calculation of the ode45 solver [18] is utilized in [19] to get the numerical solution of the state of an oscillatory rigid body using the Matlab program. The author showed the achieved results, which are consistent with the previous works. The harmonic damped spring pendulum's behavior is explored in [20] when the hanged point follows an elliptic route with stationary angular velocity. The MMS is used to obtain resonance cases and get the modulation equation that decides all possible steady-state solutions. The impersonalized of this model is introduced in [21] where a rigid body is attached to a spring in the existence of a harmonic force along the spring’s arm adding two moments, the first at the point of the body with the spring and the second at the auto-parametric pendulum suspending point of the pendulum. The resonances cases are explored and the solvability conditions are studied. The comparison between both the numerical solutions and approximate ones explain the high consistency between them.

Then the vibrational systems must be controlled in our applications through absorbers' existence to avoid disturbance and devastation of the structures or the studied systems. There are a lot of works studied such motions, for example [20,21,22,23,24,25]. Recently, the movement of a damped pendulum’s of rigid body with 3DOF is explored in [26] and [27] for the cases of linear and non-linear Stiffness, respectively. In [24], the authors researched a dynamical system consisting of a pendulum and absorber along the pendulum arm. The system is exposed to an active control, for example, the velocity with a negative value and angular displacement or the squares or cubic values. The approximate solutions are obtained using the MMS. The influences of absorbers on the system's behavior and the stability of the system and are considered. The response of non-linear spring pendulum 2DOF is studied in [25] at different resonance cases and in the presence of control.

In this work, the 3DOF dynamical motion of an auto-parametric system consists of mass $M$ connected with two massless springs with linear stiffness is investigated. The studied motion is examined under the influence of external harmonic forces. The equations of motion (EOM) are investigated applying Lagrange's equations. The MMS is used to obtain the equations' solutions up to the third approximation and discuss the system's resonance cases. Also, the phase and amplitude variables are discussed to investigate these solutions at the steady-state in line with the stability requirements. The domain of stability and instability areas is studied and analyzed. The variations of the obtained solutions are plotted for different parameters to show the influence of the applied external forces and moments on the behavior of the system under consideration.

Problem Formulation

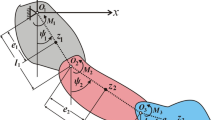
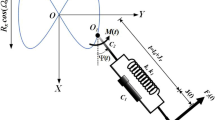
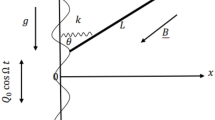
Let us consider a dynamic system consisting of a mass $M^{ * }$ connected to two massless springs of stiffness $k_{1}$ and $k_{2}$ with linear stiffness $k_{1} r$ and $k_{2} x$ respectively. These springs are attached with linear damper with damping coefficients $c_{1} ,c_{2} ,$ and $c_{3}$. It worthy to mention that, the first spring is a pendulum with length $\ell$ and the other one is horizontally directed with length $\ell ^{\prime}$ as shown in Fig. 1. Consider a moment $M(t) = M_{0} \,\cos (\varpi_{3} t)$ that acts at the point $z$ besides two external harmonic forces; the first one $F_{r} (t) = F_{1} \cos (\varpi_{1} t)$ acts on the mass $m$ along the pendulum arm and the other one is $F_{x} (t) = F_{2} \cos (\varpi_{2} t)$ acts on the horizontal direction of $X$-axis in which $\varpi_{1} ,\varpi_{2} ,$ and $\varpi_{3}$ are the frequencies of the external forces and moment. Therefore, the motion of the mechanical system can be described by the generalized coordinates $x(t)$ (translation $M$), $r(t)$ (elongation of the spring pendulum), and $\theta (t)$ (link rotation).

Fig. 1

Description of the auto-parametric system

Let $L = T - V$ indicates Lagrangian, where $T$ and $V$ represent kinetic and potential energies of the considered system that have the forms

$$\begin{gathered} T = \frac{1}{2}(m\,\dot{r}^{2} + 2m\,\sin \theta \,\dot{r}\,\dot{x} + (m + M^{ * } )\dot{x}^{2} + 2m\,\cos \theta \,(\ell + r)\dot{x}\,\dot{\theta } + m(\ell + r)^{2} \dot{\theta }^{2} ) \hfill \\ V = \frac{1}{2}k_{1} \dot{r}^{2} + \frac{1}{2}k_{2} x^{2} + mg(\ell + r)(1 - \cos \theta ), \hfill \\ \end{gathered}$$

(1)

where $g$ is the acceleration of gravity and dots denote to the time differentiation of the variables $r,x,$ and $\theta$.

It is known that the potential energy $V$ is the sum of the energies due to the elongation of the two springs and the gravitational force of the connector. Consequently, Lagrange's equations have in the form

$$\begin{gathered} \frac{d}{dt}\left( {\frac{\partial L}{{\partial \dot{r}}}} \right) - \left( {\frac{\partial L}{{\partial r}}} \right) = F_{1} \cos (\varpi_{1} t) - c_{1} \dot{r}, \hfill \\ \frac{d}{dt}\left( {\frac{\partial L}{{\partial \dot{x}}}} \right) - \left( {\frac{\partial L}{{\partial x}}} \right) = F_{2} \cos (\varpi_{2} t) - c_{2} \dot{x}, \hfill \\ \frac{d}{dt}\left( {\frac{\partial L}{{\partial \dot{\theta }}}} \right) - \left( {\frac{\partial L}{{\partial \theta }}} \right) = M_{0} \,\cos (\varpi_{3} t) - c_{3} \dot{\theta }. \hfill \\ \end{gathered}$$

(2)

Here $(\dot{r},\dot{x},\dot{\theta })$ refer to the generalized velocities.

Substituting (1) into (2), we get the EOM as follows:

$$m\,\ddot{r} + k_{1} r = mg\left( {1 - \frac{{\theta^{2} }}{2}} \right) + m\,r\,\dot{\theta }^{2} - mg + m\ell \dot{\theta }^{2} - m\,\ddot{x}\left( {\theta - \frac{{\theta^{3} }}{6}} \right) - c_{1} \dot{r} + F_{1} \cos (\varpi_{1} t),$$

(3)

$$\begin{gathered} (m + M^{ * } )\ddot{x} + k_{2} x = m(\ell + r)\left( {\theta - \frac{{\theta^{3} }}{6}} \right)\dot{\theta }^{2} - m\,\ddot{r}\left( {\theta - \frac{{\theta^{3} }}{6}} \right) - 2m\,\dot{r}\,\dot{\theta }\left( {1 - \frac{{\theta^{2} }}{2}} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - m\left( {1 - \frac{{\theta^{2} }}{2}} \right)(\ell + r)\ddot{\theta } - c_{2} \dot{x}\, + F_{2} \cos (\varpi_{2} t), \hfill \\ \end{gathered}$$

(4)

$$\begin{gathered} m\ell^{2} \ddot{\theta } + mg(\ell + r)\left( {\theta - \frac{{\theta^{3} }}{6}} \right) = - 2m\ell r\,\ddot{\theta } - m\ell \ddot{x}\left( {1 - \frac{{\theta^{2} }}{2}} \right) - m\,r(\ell + r) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\, - 2m\ell \dot{r}\,\dot{\theta } - 2m\,r\,\dot{r}\,\dot{\theta } - m\,r\ddot{x}\left( {1 - \frac{{\theta^{2} }}{2}} \right) - c_{3} \dot{\theta } + M_{0} \cos (\varpi_{3} t). \hfill \\ \end{gathered}$$

(5)

It is obvious that the last three equations represent second-order non-linear differential equations in terms of $r,x,$ and $\,\theta .$

Considering the following dimensionless variables

$$\begin{gathered} \frac{r}{\ell } = \varepsilon \,\tilde{r},\,\,\,\,\frac{x}{\ell } = \varepsilon \tilde{x},\,\,\,\,\theta = \varepsilon \tilde{\theta },\,\,\,\,t = \sqrt {\frac{\ell }{g}} \,\tilde{t},\,\,\,\,\frac{{F_{1} }}{m\,g} = \varepsilon^{3} \tilde{f}_{1} ,\,\,\,\,\,\frac{h}{\ell } = \varepsilon I,\,\,\,\,\omega_{1}^{2} = \frac{{k_{1} }}{m}, \hfill \\ \omega_{2}^{2} = \frac{\ell }{g},\,\,\,\,W_{1} = \frac{{\varpi_{1} }}{{\omega_{2} }},\,\,\,\,\,\,\,W_{2} = \frac{{\varpi_{2} }}{{\omega_{2} }},\,\,\,\,\,\,\,\,W_{3} = \frac{{\varpi_{3} }}{{\omega_{2} }},\,\,\,\,\frac{{c_{1} }}{m}\sqrt {\frac{\ell }{g}} = \varepsilon^{2} \tilde{c}_{1} , \hfill \\ \frac{{c_{2} }}{{(m + M^{ * } )}}\sqrt {\ell g} = \varepsilon^{2} \tilde{c}_{2} ,\,\,\,\,\frac{{F_{2} }}{{(m + M^{ * } )g}} = \varepsilon^{3} \tilde{f}_{2} ,\,\,\,\,B = \mu g\ell ,\,\,\,\,\frac{g\ell }{B} = \varepsilon J,\,\,\,\,\Omega_{1}^{2} = \omega_{1}^{2} \omega_{2}^{2} , \hfill \\ \frac{{c_{3} }}{m}\sqrt{\frac{2}{3g}} = \varepsilon^{2} \tilde{c}_{3} ,\,\,\,\,\mu = \frac{m}{{m + M^{ * } }},\,\,\,\,\,\frac{{M_{0} }}{m\,g\ell } = \varepsilon^{3} \tilde{f}_{3} ,\,\,\,\,h = m\ell^{2} g,\,\,\,\,\,\Omega_{2}^{2} = \frac{{k_{2} \ell }}{{(m + M^{ * } )g}}, \hfill \\ \end{gathered}$$

(6)

to convert (3–5) into the following dimensionless form:

$$\begin{gathered} \varepsilon \ddot{\tilde{r}} + \Omega_{1}^{2} \varepsilon \tilde{r} = - \varepsilon^{2} (\frac{{\tilde{\theta }^{2} }}{2!} - \dot{\tilde{\theta }}^{2} + \ddot{\tilde{x}}\tilde{\theta } + \tilde{c}_{1} \dot{\tilde{r}}) + \varepsilon^{3} [\tilde{r}\dot{\tilde{\theta }}^{2} + \tilde{f}_{1} \cos (W_{1} \tilde{t})], \hfill \\ \varepsilon \ddot{\tilde{x}} + \Omega_{2}^{2} \varepsilon \tilde{x} = \mu \varepsilon^{3} \dot{\tilde{\theta }}^{2} \theta - \mu \varepsilon^{2} \ddot{\tilde{r}}\theta - \varepsilon^{2} J\ddot{\tilde{\theta }}(1 + \varepsilon \ddot{\tilde{r}}) - \varepsilon^{2} \tilde{c}_{2} \dot{\tilde{x}} - 2\mu \varepsilon^{2} \dot{\tilde{r}}\dot{\tilde{\theta }} + \varepsilon^{3} \tilde{f}_{2} \cos (W_{2} \tilde{t}), \hfill \\ \varepsilon \ddot{\tilde{\theta }} + \varepsilon \tilde{\theta } = - \varepsilon^{2} \tilde{r}\tilde{\theta } + \varepsilon^{2} \tilde{r}\ddot{\tilde{\theta }} - \varepsilon^{2} I\,\ddot{\tilde{x}}(1 - \varepsilon^{2} \frac{{\tilde{\theta }^{2} }}{2!}) - 2\varepsilon^{2} \dot{\tilde{r}}\dot{\tilde{\theta }} - 2\varepsilon^{3} \tilde{r}\,\dot{\tilde{r}}\dot{\tilde{\theta }} - \varepsilon^{2} r\,\ddot{\tilde{x}}(1 - \varepsilon^{2} \frac{{\tilde{\theta }^{2} }}{2!}) \hfill \\ \,\,\,\,\,\,\, - \varepsilon^{2} \tilde{r}(1 + \varepsilon \tilde{r})\ddot{\tilde{\theta }} - \varepsilon^{2} \tilde{c}_{3} \dot{\tilde{\theta }} + \varepsilon^{3} \tilde{f}_{3} \cos (W_{3} \tilde{t}). \hfill \\ \end{gathered}$$

(7)

Here, $\varepsilon$ is known as the small parameter affecting the coupling between the pendulum absorber and the damping, external force, and nonlinearities of the system. Its important influence appears in current non-linear frequency analysis at the desired approximation. To simplify the notation, the sign ~ (tilde) is omitted below.

The Proposed Method

The MMS is an analytical method that used to determine approximate solutions with high accuracy of non-linear differential equations for which exact solutions cannot be obtained. It can be used to demonstrate, predict and describe phenomena in vibrating systems that caused by non-linear effects. Moreover, it can be applied to non-linear and linear systems with variable coefficients or complex boundary conditions, where the exact closed-form solution is unknown. Therefore, this method is utilized to solve the system of Eqs. (7) up to the third approximation. Therefore, we need three timescales, which has the forms $T_{n} =$$\varepsilon^{n} T\,$$\,(n = 0,\,1\,,\,2)$ where $T_{0} ,T_{1} ,$ and $T_{2}$ are various time scales. According to the method of the MS perturbation, the solutions $r,x,$ and $\theta$ can be sought in the powers of $\varepsilon$ as [28, 29]

$$\begin{gathered} r = \sum\limits_{k = 1}^{3} {\varepsilon^{k} r_{k} (T_{0} ,\,T_{1} ,\,T_{2} )} + O(\varepsilon^{4} ), \hfill \\ x = \sum\limits_{k = 1}^{3} {\varepsilon^{k} x_{k} (T_{0} ,\,T_{1} ,\,T_{2} )} + O(\varepsilon^{4} ), \hfill \\ \theta = \sum\limits_{k = 1}^{3} {\varepsilon^{k} \theta_{k} (T_{0} ,\,T_{1} ,\,T_{2} )} + O(\varepsilon^{4} ). \hfill \\ \end{gathered}$$

(8)

The derivatives in terms of the new time scales in (8) are expressed as follows [5]:

$$\begin{gathered} \frac{d}{dT} = \frac{\partial }{{\partial T_{0} }} + \varepsilon \frac{\partial }{{\partial T_{1} }} + \varepsilon^{2} \frac{\partial }{{\partial T_{2} }}, \hfill \\ \frac{{d^{2} }}{{dT^{2} }} = \frac{{\partial^{2} }}{{\partial T_{0}^{2} }} + 2\varepsilon \frac{{\partial^{2} }}{{\partial T_{0} \partial T_{1} }} + \varepsilon^{2} \left( {\frac{{\partial^{2} }}{{\partial T_{1}^{2} }} + 2\frac{{\partial^{2} }}{{\partial T_{0} \partial T_{2} }}} \right) + O(\varepsilon^{3} ). \hfill \\ \end{gathered}$$

(9)

Substituting (8) and (9) into (7) and collecting the coefficients of equal powers of $\varepsilon$ in both sides leads to the following system containing the following nine partial differential equations.

Order $(\varepsilon )$

$$\frac{{\partial^{2} r_{1} }}{{\partial T_{0}^{2} }} + \Omega_{1}^{2} r_{1} = 0,$$

(10)

$$\frac{{\partial^{2} x_{1} }}{{\partial T_{0}^{2} }} + \Omega_{2}^{2} x_{1} = 0,$$

(11)

$$\frac{{\partial^{2} \theta_{1} }}{{\partial T_{0}^{2} }} + \theta_{1} = 0.$$

(12)

Order of $(\varepsilon^{2} )$

$$\frac{{\partial^{2} r_{2} }}{{\partial T_{0}^{2} }} + \Omega_{1}^{2} r_{2} = - 2\frac{{\partial^{2} r_{1} }}{{\partial T_{0} \partial T_{1} }} - \frac{1}{2}\theta_{1}^{2} + \left( {\frac{{\partial \theta_{1} }}{{\partial T_{0} }}} \right)^{2} - \frac{{\partial^{2} x_{1} }}{{\partial T_{0}^{2} }}\theta_{1} ,$$

(13)

$$\frac{{\partial^{2} x_{2} }}{{\partial T_{0}^{2} }} + \Omega_{2}^{2} x_{2} = - 2\frac{{\partial^{2} x_{1} }}{{\partial T_{0} \partial T_{1} }} - \mu \frac{{\partial^{2} r_{1} }}{{\partial T_{0}^{2} }}\theta_{1} - J\frac{{\partial^{2} \theta_{1} }}{{\partial T_{0}^{2} }} - 2\mu \frac{{\partial r_{1} }}{{\partial T_{0} }}\frac{{\partial \theta_{1} }}{{\partial T_{0} }},$$

(14)

$$\frac{{\partial^{2} \theta_{2} }}{{\partial T_{0}^{2} }} + \theta_{2} = - 2\frac{{\partial^{2} \theta_{1} }}{{\partial T_{0} \partial T_{1} }} - r_{1} \theta_{1} + r_{1} \frac{{\partial^{2} \theta_{1} }}{{\partial T_{0}^{2} }} - I\frac{{\partial^{2} x_{1} }}{{\partial T_{0}^{2} }} - 2\frac{{\partial^{2} r_{1} }}{{\partial T_{0}^{2} }}\frac{{\partial^{2} \theta_{1} }}{{\partial T_{0}^{2} }} - r_{1} \frac{{\partial^{2} \theta_{1} }}{{\partial T_{0}^{2} }},$$

(15)

Order of $(\varepsilon^{3} )$

$$\begin{gathered} \frac{{\partial^{2} r_{3} }}{{\partial T_{0}^{2} }} + \Omega_{1}^{2} r_{3} = - \frac{{\partial^{2} r_{1} }}{{\partial T_{1}^{2} }} - 2\frac{{\partial^{2} r_{1} }}{{\partial T_{0} \partial T_{1} }} - 2\frac{{\partial^{2} r_{2} }}{{\partial T_{0} \partial T_{1} }} - \theta_{1} \theta_{2} + r_{1} \left( {\frac{{\partial \theta_{1} }}{{\partial T_{0} }}} \right)^{2} - \frac{{\partial^{2} x_{1} }}{{\partial T_{0}^{2} }}\theta_{2} \hfill \\ \,\,\,\,\,\,\,\,\,\,\, + 2\frac{{\partial \theta_{1} }}{{\partial T_{0} }}\frac{{\partial \theta_{1} }}{{\partial T_{1} }} - 2\frac{{\partial^{2} x_{1} }}{{\partial T_{0} \partial T_{1} }}\theta_{1} \, + \frac{{\partial^{2} x_{2} }}{{\partial T_{0}^{2} }}\theta_{1} - c_{1} \frac{{\partial r_{1} }}{{\partial T_{0} }} + f_{1} \cos (W_{1} T_{0} ), \hfill \\ \end{gathered}$$

(16)

$$\begin{gathered} \frac{{\partial^{2} x_{3} }}{{\partial T_{0}^{2} }} + \Omega_{2}^{2} x_{3} = - \frac{{\partial^{2} x_{1} }}{{\partial T_{1}^{2} }} - 2\frac{{\partial^{2} x_{1} }}{{\partial T_{0} \partial T_{1} }} - 2\frac{{\partial^{2} x_{2} }}{{\partial T_{0} \partial T_{1} }} + \mu \left( {\frac{{\partial \theta_{1} }}{{\partial T_{0} }}} \right)^{2} \theta_{1} - \mu \frac{{\partial^{2} r_{1} }}{{\partial T_{0}^{2} }}\theta_{2} - 2\mu \frac{{\partial^{2} r_{1} }}{{\partial T_{0} \partial T_{1} }}\theta_{1} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\, - J\frac{{\partial^{2} \theta_{1} }}{{\partial T_{0}^{2} }}r_{1} - 2J\frac{{\partial^{2} \theta_{1} }}{{\partial T_{0} \partial T_{1} }} - c_{2} \frac{{\partial x_{1} }}{{\partial T_{0} }} - J\frac{{\partial^{2} \theta_{2} }}{{\partial T_{0}^{2} }} - 4\mu \frac{{\partial r_{1} }}{{\partial T_{0} }}\frac{{\partial \theta_{1} }}{{\partial T_{1} }} + f_{2} \cos (W_{2} T_{0} ), \hfill \\ \end{gathered}$$

(17)

$$\begin{gathered} \frac{{\partial^{2} \theta_{3} }}{{\partial T_{0}^{2} }} + \theta_{3} = - \frac{{\partial^{2} \theta_{1} }}{{\partial T_{1}^{2} }} - 2\frac{{\partial^{2} \theta_{1} }}{{\partial T_{0} \partial T_{1} }} - 2\frac{{\partial^{2} \theta_{2} }}{{\partial T_{0} \partial T_{1} }} - r_{1} \theta_{2} - r_{2} \theta_{1} + 2r_{1} \frac{{\partial^{2} \theta_{1} }}{{\partial T_{0} \partial T_{1} }} + r_{2} \frac{{\partial^{2} \theta_{1} }}{{\partial T_{0}^{2} }} \hfill \\ \,\,\,\,\,\,\,\,\,\,\, - 2I\frac{{\partial^{2} x_{1} }}{{\partial T_{0} \partial T_{1} }} - 4\frac{{\partial^{2} r_{1} }}{{\partial T_{0}^{2} }}\frac{{\partial^{2} \theta_{1} }}{{\partial T_{0} \partial T_{1} }} - 4\frac{{\partial^{2} r_{1} }}{{\partial T_{0} \partial T_{1} }}\frac{{\partial^{2} \theta_{1} }}{{\partial T_{0}^{2} }}\,\, - 2r_{1} \frac{{\partial^{2} r_{1} }}{{\partial T_{0}^{2} }}\frac{{\partial^{2} \theta_{1} }}{{\partial T_{0}^{2} }} - 2\frac{{\partial^{2} x_{1} }}{{\partial T_{0} \partial T_{1} }} \hfill \\ \,\,\,\,\,\,\,\,\,\, - r_{2} \frac{{\partial^{2} \theta_{1} }}{{\partial T_{0}^{2} }} - c_{3} \frac{{\partial \theta_{1} }}{{\partial T_{0} }} + f_{3} \cos (W_{3} T_{0} ). \hfill \\ \end{gathered}$$

(18)

Equations (10–12) are mutually independent homogeneous equations. Thus, the polar forms of their solutions are as follows:

$$r_{1} = A_{1} (T_{1} ,T_{2} )e^{{i\Omega_{1} T_{0} }} + \overline{{A_{1} }} (T_{1} ,T_{2} )e^{{ - i\Omega_{1} T_{0} }} ,$$

(19)

$$x_{1} = A_{2} (T_{1} ,T_{2} )e^{{i\Omega_{2} T_{0} }} + \overline{{A_{2} }} (T_{1} ,T_{2} )e^{{ - i\Omega_{2} T_{0} }} ,$$

(20)

$$\theta_{1} = A_{3} (T_{1} ,T_{2} )e^{{iT_{0} }} + \overline{{A_{3} }} (T_{1} ,T_{2} )e^{{ - T_{0} }} ,$$

(21)

where $A_{1} ,A_{2} ,$ and $A_{3}$ are complex functions that can be determined later and $\overline{A}_{1} ,\overline{A}_{2} ,$ and $\overline{A}_{3}$ are their complex conjugate.

It is obvious that the solutions of (13–18) depend on the solutions of (10–12) significantly. Therefore, substituting the solutions (19–21) into (13–15) and removing terms that lead to the secular ones, we can get the second approximation in the form

$$r_{2} = \frac{1}{{\Omega_{1}^{2} }}A_{3} \overline{A}_{3} - \frac{{3A_{3}^{2} }}{{2\Omega_{1}^{2} - 8}}e^{{2iT_{0} }} + \Omega_{2}^{2} A_{3} \left( {\frac{{A_{2} \,e^{{i(1 + \Omega_{2} )T_{0} }} }}{{\Omega_{1}^{2} - (1 + \Omega_{2} )^{2} }} + \frac{{\overline{{A_{2} }} \,e^{{i(1 - \Omega_{2} )T_{0} }} }}{{\Omega_{1}^{2} - (1 - \Omega_{2} )^{2} }}} \right) + c.c,$$

(22)

$$x_{2} = \mu \,A_{1} (\Omega_{1} + 2)\left( {\frac{{A_{3} \,e^{{i(\Omega_{1} + 1)T_{0} }} }}{{\Omega_{2}^{2} - (\Omega_{1} + 1)^{2} }} + \frac{{\overline{{A_{3} }} \,e^{{i(\Omega_{2} - 1)T_{0} }} }}{{\Omega_{2}^{2} - (\Omega_{1} - 1)^{2} }}} \right) + J\frac{{A_{3} }}{{\Omega_{2}^{2} - 1}}e^{{iT_{0} }} + c.c,$$

(23)

$$\theta_{2} = (3 - 2\Omega_{1}^{2} )A_{1} \left( {\frac{{A_{3} \,e^{{i(\Omega_{1} + 1)T_{0} }} }}{{\Omega_{1}^{2} + 2\Omega_{1} }} + \frac{{\overline{{A_{3} }} \,e^{{i(\Omega_{1} - 1)T_{0} }} }}{{\Omega_{1}^{2} - 2\Omega_{1} }}} \right) + \frac{{\Omega_{2}^{2} A_{3} I}}{{1 - \Omega_{2}^{2} }}e^{{i\Omega_{2} T_{0} }} + c.c.,$$

(24)

where $c.c.$ are the complex conjugate of the previous terms. This symbol benefits from providing long terms that we use frequently.

Substituting the solutions (19–24) into Eqs. (16–18) and using the elimination conditions of secular terms. So, one gets the third-order approximations in the forms

$$\begin{gathered} r_{3} = \frac{{(3 - 2\Omega_{1}^{2} )A_{1} A_{3}^{2} }}{{(\Omega_{1}^{2} + 2\Omega_{1} )(4 + 4\Omega_{1} )}}e^{{i(\Omega_{1} + 2)T_{0} }} - \frac{{6iA_{3}^{2} }}{{(\Omega_{1}^{2} - 4)^{2} }}e^{{2iT_{0} }} + \frac{{\Omega_{2}^{2} A_{2} A_{3} I\,e^{{i(1 + \Omega_{2} )T_{0} }} }}{{(\Omega_{2}^{2} - 1)[\Omega_{1}^{2} - (1 + \Omega_{2} )^{2} ]}} \hfill \\ \,\,\,\,\, - \left( {\frac{{(3 - 2\Omega_{1}^{2} )}}{{(\Omega_{1}^{2} - 2\Omega_{1} )}} + 1} \right)\,\frac{{A_{1} \overline{A}_{3}^{2} }}{{(4\Omega_{1} - 4)}}e^{{i(\Omega_{1} - 2)T_{0} }} - \frac{{\Omega_{2}^{2} A_{2} \overline{A}_{3} I\,e^{{i(\Omega_{2} - 1)T_{0} }} }}{{(1 - \Omega_{2}^{2} )[\Omega_{1}^{2} - (\Omega_{2} - 1)^{2} ]}} \hfill \\ \,\,\,\,\, + \frac{{A_{1} A_{3}^{2} }}{{4\Omega_{1} + 4}}e^{{i(\Omega_{1} + 2)T_{0} }} + \frac{{\Omega_{2}^{4} A_{2}^{2} \,e^{{2i\Omega_{2} T_{0} }} }}{{(1 - \Omega_{2}^{2} )(\Omega_{1} - 4\Omega_{2} )}} + \frac{{(3 - 2\Omega_{1}^{2} )\Omega_{2}^{2} A_{1} A_{2} A_{3} \,e^{{i(\Omega_{1} + \Omega_{2} + 1)T_{0} }} }}{{(\Omega_{1}^{2} + 2\Omega_{1} )[\Omega_{1}^{2} - (\Omega_{1} + \Omega_{2} + 1)^{2} ]}} \hfill \\ \,\,\,\,\, + \frac{{\Omega_{2}^{4} A_{2} \overline{A}_{2} \,I}}{{(1 - \Omega_{2}^{2} )\Omega_{1}^{2} }} + \frac{{JA_{3}^{2} e^{{2iT_{0} }} }}{{(1 - \Omega_{2}^{2} )(\Omega_{1} - 4)}} + \frac{{\mu (\Omega_{1} + 2)(\Omega_{1} + 1)^{2} A_{1} A_{3}^{2} }}{{[\Omega_{2}^{2} - (\Omega_{1} + 1)^{2} ](2\Omega_{1} + 2)}}\,e^{{i(\Omega_{1} + 2)T_{0} }} \hfill \\ \,\,\,\, + \frac{{(3 - 2\Omega_{1}^{2} )\Omega_{2}^{2} A_{1} A_{2} \overline{A}_{3} \,e^{{i(\Omega_{1} + \Omega_{2} - 1)T_{0} }} }}{{(\Omega_{1}^{2} - 2\Omega_{1} )[\Omega_{1}^{2} - (\Omega_{1} + \Omega_{2} - 1)^{2} ]}} + \frac{{JA_{3} \overline{A}_{3} }}{{(1 - \Omega_{2}^{2} )\Omega_{1}^{2} }} + \frac{{(3 - 2\Omega_{1}^{2} )\Omega_{2}^{2} A_{1} \overline{A}_{2} A_{3} \,e^{{i(\Omega_{1} - \Omega_{2} + 1)T_{0} }} }}{{(\Omega_{1}^{2} + 2\Omega_{1} )[\Omega_{1}^{2} - (\Omega_{1} - \Omega_{2} + 1)^{2} ]}} \hfill \\ \,\,\,\, + \frac{{(3 - 2\Omega_{1}^{2} )\Omega_{2}^{2} A_{1} \overline{A}_{2} \overline{A}_{3} \,e^{{i(\Omega_{1} - \Omega_{2} - 1)T_{0} }} }}{{(\Omega_{1}^{2} - 2\Omega_{1} )[\Omega_{1}^{2} - (\Omega_{1} - \Omega_{2} - 1)^{2} ]}} + \frac{{f_{1} }}{{\Omega_{1}^{2} - W_{1}^{2} }}e^{{i{\kern 1pt} W_{1} T_{0} }} + c.c, \hfill \\ \end{gathered}$$

(25)

$$\begin{gathered} x_{3} = \frac{{\mu A_{3}^{2} \overline{A}_{3} \,e^{{iT_{0} }} }}{{(\Omega_{2}^{2} - 1)}} - \frac{{\mu A_{3}^{3} \,e^{{3iT_{0} }} }}{{(\Omega_{2}^{2} - 9)}} + \frac{{(3 - 2\Omega_{1}^{2} )\mu \Omega_{1} \overline{A}_{1}^{2} A_{3} i\,e^{{i(1 - 2\Omega_{1} )T_{0} }} }}{{(\Omega_{1}^{2} + 2\Omega_{1} )[\Omega_{2}^{2} - (1 - 2\Omega_{1} )^{2} ]}} + \frac{{A_{1} A_{3} Je^{{i(\Omega_{1} + 1)T_{0} }} }}{{[\Omega_{2}^{2} - (\Omega_{1} + 1)^{2} ]}} \hfill \\ \,\,\,\,\,\, - \frac{{(3 - 2\Omega_{1}^{2} )\mu \Omega_{1} A_{1}^{2} A_{3} i\,e^{{i(1 + 2\Omega_{1} )T_{0} }} }}{{(\Omega_{1}^{2} + 2\Omega_{1} )[\Omega_{2}^{2} - (1 + 2\Omega_{1} )^{2} ]}} + \frac{{\mu \Omega_{1} \Omega_{2}^{2} I\overline{A}_{1} A_{2} i\,e^{{i(\Omega_{2} - \Omega_{1} )T_{0} }} }}{{(1 - \Omega_{2}^{2} )[\Omega_{2}^{2} - (\Omega_{2} - \Omega_{1} )^{2} ]}} + \frac{{A_{1} \overline{A}_{3} Je^{{i(\Omega_{1} - 1)T_{0} }} }}{{[\Omega_{2}^{2} - (\Omega_{1} - 1)^{2} ]}} \hfill \\ \,\,\,\,\, - \frac{{\mu \Omega_{1} \Omega_{2}^{2} A_{1} A_{2} i\,e^{{i(\Omega_{1} + \Omega_{2} )T_{0} }} }}{{(1 - \Omega_{2}^{2} )[\Omega_{2}^{2} - (\Omega_{1} + \Omega_{2} )^{2} ]}} - (3 - 2\Omega_{1}^{2} )J\left\{ {\frac{{(\Omega_{1} + 1)A_{1} A_{3} i\,e^{{i(\Omega_{1} + 1)T_{0} }} }}{{(\Omega_{1}^{2} + 2\Omega_{1} )[\Omega_{2}^{2} - (\Omega_{1} + 1)^{2} ]}}} \right. \hfill \\ \,\,\,\,\, + \left. {\frac{{(\Omega_{1} - 1)A_{1} \overline{A}_{3} i\,e^{{i(\Omega_{1} - 1)T_{0} }} }}{{(\Omega_{1}^{2} - 2\Omega_{1} )[\Omega_{2}^{2} - (\Omega_{1} - 1)^{2} ]}}} \right\} + \frac{{f_{2} }}{{\Omega_{2}^{2} - W_{2}^{2} }}e^{{i{\kern 1pt} W_{2} T_{0} }} + c.c, \hfill \\ \end{gathered}$$

(26)

$$\begin{gathered} \theta_{3} = \frac{{(3 - 2\Omega_{1}^{2} )A_{1}^{2} A_{3} i\,e^{{i(1 + 2\Omega_{1} )T_{0} }} }}{{(\Omega_{1}^{2} + 2\Omega_{1} )(4\Omega_{1}^{2} + 4\Omega_{1} )}} - \frac{{\Omega_{2}^{2} A_{1} A_{2} I\,e^{{i(\Omega_{1} + \Omega_{2} )T_{0} }} }}{{(1 - \Omega_{2}^{2} )[1 - (\Omega_{1} + \Omega_{2} )^{2} ]}} - \frac{{3A_{3}^{3} e^{{3iT_{0} }} }}{{8(\Omega_{1}^{2} - 4)}} \hfill \\ \,\,\,\,\,\, - \frac{{\Omega_{2}^{2} \overline{A}_{1} A_{2} I\,e^{{i(\Omega_{2} - \Omega_{1} )T_{0} }} }}{{(1 - \Omega_{2}^{2} )[1 - (\Omega_{2} - \Omega_{1} )^{2} ]}} - \frac{{(3 - 2\Omega_{1}^{2} )A_{1}^{2} \overline{A}_{3} i\,e^{{i(1 + 2\Omega_{1} )T_{0} }} }}{{(\Omega_{1}^{2} - 2\Omega_{1} )(4\Omega_{1} - 4\Omega_{1}^{2} )}} \hfill \\ \,\,\,\,\,\, - 2\frac{{\Omega_{2}^{2} A_{3}^{2} A_{2} \,e^{{i(2 + \Omega_{2} )T_{0} }} }}{{[\Omega_{1}^{2} - (1 + \Omega_{2} )^{2} ](1 - (2 + \Omega_{2} )^{2} )}} - 2\frac{{\Omega_{2}^{2} A_{3} \overline{A}_{3} \overline{A}_{2} \,e^{{ - i(\Omega_{2} )T_{0} }} }}{{[\Omega_{1}^{2} - (1 - \Omega_{2} )^{2} ](1 + \Omega_{2}^{2} )}} \hfill \\ \,\,\,\,\,\, - 2\frac{{\Omega_{1}^{2} A_{1}^{2} \overline{A}_{3} \,e^{{i(2\Omega_{1} - 1)T_{0} }} }}{{1 - (2\Omega_{1} - 1)^{2} }} - \frac{{3\Omega_{2}^{2} A_{3}^{2} A_{2} \,e^{{i(2 + \Omega_{2} )T_{0} }} }}{{2(\Omega_{1}^{2} - 4)[1 - (2 + \Omega_{2} )^{2} ]}} - \frac{{3\Omega_{2}^{2} A_{3}^{2} \overline{A}_{2} \,e^{{i(2 - \Omega_{2} )T_{0} }} }}{{2(\Omega_{1}^{2} - 4)[1 - (2 - \Omega_{2} )^{2} ]}} \hfill \\ \,\,\,\,\,\, + \frac{{\Omega_{2}^{2} A_{3} \overline{A}_{3} A_{2} \,e^{{ - i\Omega_{2} T_{0} }} }}{{2(\Omega_{1}^{2} - 4)[1 - (2 + \Omega_{2} )^{2} ]}} + \frac{{\Omega_{2}^{2} A_{3} \overline{A}_{3} \overline{A}_{2} \,e^{{ - i\Omega_{2} T_{0} }} }}{{[\Omega_{1}^{2} - (1 - \Omega_{2} )^{2} ](1 + \Omega_{2}^{2} )}} - \frac{{3A_{3}^{3} \,e^{{3iT_{0} }} }}{{2(\Omega_{1}^{2} - 4)}} \hfill \\ \,\,\,\,\,\, + \frac{{\Omega_{2}^{4} \overline{A}_{2}^{2} A_{3} \,e^{{i(1 - 2\Omega_{2} )T_{0} }} }}{{[\Omega_{1}^{2} - (1 - \Omega_{2} )^{2} ][1 - (1 - 2\Omega_{1} )^{2} ]}} + \frac{{\Omega_{2}^{2} A_{3}^{2} A_{2} \,e^{{i(2 + \Omega_{2} )T_{0} }} }}{{[\Omega_{1}^{2} - (1 + \Omega_{2} )^{2} ][1 - (1 + \Omega_{2} )^{2} ]}} \hfill \\ \,\,\,\,\,\, + \frac{{\Omega_{2}^{2} A_{3}^{2} \overline{A}_{2} \,e^{{i(2 - \Omega_{2} )T_{0} }} }}{{[\Omega_{1}^{2} - (1 - \Omega_{2} )^{2} ][1 - (2 - \Omega_{2} )^{2} ]}} + \frac{{\Omega_{2}^{4} A_{2}^{2} A_{3} \,e^{{i(1 + 2\Omega_{2} )T_{0} }} }}{{[\Omega_{1}^{2} - (1 + \Omega_{2} )^{2} ][1 - (1 + 2\Omega_{2} )^{2} ]}} \hfill \\ \,\,\,\,\,\, + \frac{{f_{3} }}{{1 - W_{3}^{2} }}e^{{i{\kern 1pt} W_{3} T_{0} }} + c.c. \hfill \\ \end{gathered}$$

(27)

Thus, the required approximate solutions can be easily obtained if we substitute (19–27) into (8).

Stability of the System

In this section, we examine the system’s stability of Eqs. (16–18) and investigate the simultaneous three primary external resonances case. Therefore, the following detuning parameters $\sigma_{j} \,\,(j = 1,2,3)$ are considered [30]

$$W_{1} = \Omega_{1} + \varepsilon \sigma_{1} ,\,\,\,\,\,W_{2} = \Omega_{2} + \varepsilon \sigma_{2} ,\,\,\,\,\,\,\,W_{3} = 1 + \varepsilon \sigma_{3} .$$

(28)

Substituting (28) into (13–18) and removing the secular terms, the following solvability requirements for the third-order approximation are obtained

$$\begin{gathered} - 2i\Omega_{1} \frac{{\partial A_{1} }}{{\partial T_{2} }} - \frac{{(3 - 2\Omega_{1}^{2} )}}{{(\Omega_{1}^{2} - 2\Omega_{1} )}}A_{1} A_{3} \overline{A}_{3} - \frac{{(3 - 2\Omega_{1}^{2} )}}{{(\Omega_{1}^{2} + 2\Omega_{1} )}}A_{1} A_{3} \overline{A}_{3} + 2A_{1} A_{3} \overline{A}_{3} \hfill \\ - \frac{{(\Omega_{1} - 1)^{2} }}{{(\Omega_{2}^{2} - (\Omega_{1} - 1)^{2} )}}A_{1} A_{3} \overline{A}_{3} - i\,c_{1} \Omega_{1} A_{1} - \frac{1}{2}f_{1} e^{{i\sigma_{1} T_{1} }} = 0, \hfill \\ \end{gathered}$$

(29)

$$- 2i\Omega_{2} \frac{{\partial A_{2} }}{{\partial T_{2} }} - \frac{{\Omega_{2}^{4} \,J\,I\,A_{2} }}{{(1 - \Omega_{2}^{2} )}} - i\,c_{2} \Omega_{2} A_{2} - \frac{1}{2}f_{2} e^{{i\sigma_{2} T_{1} }} = 0,$$

(30)

$$\begin{gathered} - 2i\frac{{\partial A_{3} }}{{\partial T_{2} }} - \frac{{(3 - 2\Omega_{1}^{2} )}}{{(\Omega_{1}^{2} + 2\Omega_{1} )}}A_{1} A_{3} \overline{A}_{1} - i\,c_{3} A_{3} - 4\Omega_{1}^{2} A_{1} A_{3} \overline{A}_{1} + \frac{{\Omega_{2}^{4} A_{2} A_{3} \overline{A}_{2} }}{{\Omega_{1}^{2} - (\Omega_{2} + 1)^{2} }} \hfill \\ + \frac{{\Omega_{2}^{4} A_{2} A_{3} \overline{A}_{2} }}{{\Omega_{1}^{2} - (1 - \Omega_{2} )^{2} }} - \frac{1}{2}f_{3} e^{{i\sigma_{3} T_{1} }} = 0. \hfill \\ \end{gathered}$$

(31)

These equations can be analyzed through expressing $A_{j} \,\,(j = 1,2,3)$ in the polar forms [31] as follows:

$$A_{i} = \frac{{\tilde{a}_{j} (T_{2} )}}{2}e^{{i\tilde{\psi }_{j} T_{2} }} ,\,\,\,a_{j} = \varepsilon \tilde{a}_{j} ,$$

(32)

where $\tilde{a}_{j}$ and $\tilde{\psi }_{j}$ are the amplitudes of the generalized coordinates $r,\,x,$ and $\theta$ and their corresponding phases

$$\frac{{\partial A_{j} }}{\partial T} = \varepsilon^{2} \frac{{\partial A_{j} }}{{\partial T_{2} }},$$

(33)

$$\theta_{j} (T_{1} ,T_{2} ) = T_{j} \tilde{\sigma }_{j} - \psi_{j} (T_{2} ).$$

(34)

Substituting (32–34) into (29–31) and then matching the real and imaginary parts in both sides to gain the next modulation equations for amplitudes and phases

$$\begin{gathered} a_{1} \frac{{d\theta_{1} }}{dT} = \frac{{a_{1} a_{3}^{2} }}{{4\Omega_{1} }} - \left( {\frac{1}{{\Omega_{1}^{2} - 2\Omega_{1} }} + \frac{1}{{\Omega_{1}^{2} + 2\Omega_{1} }}} \right)\frac{{(3 - 2\Omega_{1}^{2} )a_{1} a_{3}^{2} }}{{8\Omega_{1} }} + a_{1} \sigma_{1} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \frac{{(\Omega_{1} - 1)^{2} a_{1} a_{3}^{2} }}{{8\Omega_{1} (\Omega_{2}^{2} - (\Omega_{1} - 1)^{2} )}} + \frac{{f_{1} }}{{2\Omega_{1} }}\cos \theta_{1} , \hfill \\ \frac{{d\,a_{1} }}{dT} = \frac{{f_{1} }}{{2\Omega_{1} }}\sin \theta_{1} - \frac{{a_{1} c_{1} }}{2}, \hfill \\ a_{2} \frac{{d\theta_{2} }}{dT} = \frac{{f_{2} }}{{2\Omega_{2} }}\cos \theta_{2} - \frac{{J\,I\,a_{2} \Omega_{2}^{3} }}{{2(1 - \Omega_{2}^{2} )}} + a_{2} \sigma_{2} , \hfill \\ \frac{{d\,a_{2} }}{dT} = \frac{{f_{2} }}{{2\Omega_{2} }}\sin \theta_{2} - \frac{{a_{2} c_{2} }}{2}, \hfill \\ a_{3} \frac{{d\theta_{3} }}{dT} = \frac{{\Omega_{2}^{4} \,a_{3} a_{2}^{2} }}{{8(\Omega_{1}^{2} - (1 + \Omega_{2} )^{2} )}} - \frac{{(3 - 2\Omega_{1}^{2} )a_{3} a_{1}^{2} }}{{8(\Omega_{1}^{2} + 2\Omega_{1} )}} - \frac{1}{2}\Omega_{1}^{2} a_{3} a_{1}^{2} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{{\Omega_{2}^{4} \,a_{3} a_{2}^{2} }}{{8(\Omega_{1}^{2} - (1 - \Omega_{2} )^{2} )}} + a_{3} \sigma_{3} + \frac{{f_{3} }}{2}\cos \theta_{3} , \hfill \\ \frac{{d\,a_{3} }}{dT} = \frac{{f_{3} }}{2}\sin \theta_{3} - \frac{{a_{3} c_{3} }}{2}. \hfill \\ \end{gathered}$$

(35)

Examining the behavior of modest deviations from the steady-state solutions is an intriguing way to evaluate the stability requirements. Therefore, we take into account the following aspects of substitutions [32] when pursuing this goal

$$\begin{gathered} a_{1} = a_{10} + a_{11} ,\,\,\,\,\,\,\,\,\,\theta_{1} = \theta_{10} + \theta_{11} , \hfill \\ a_{2} = a_{20} + a_{21} ,\,\,\,\,\,\,\,\,\theta_{2} = \theta_{20} + \theta_{21} , \hfill \\ a_{3} = a_{30} + a_{31} ,\,\,\,\,\,\,\,\,\theta_{3} = \theta_{30} + \theta_{31} , \hfill \\ \end{gathered}$$

(36)

where $a_{j0}$ and $\theta_{j0} \,\,(j = 1,2,3)$ are the unperturbed solutions which corresponds to the steady-state solutions of (35), while $a_{j1}$ and $\theta_{j1}$ are their corresponding perturbations which should be small relative to its predecessors.

Substitution (36) into Eq. (35) yields

$$\begin{gathered} a_{10} \frac{{d\theta_{11} }}{dT} = \left( {\frac{1}{{4\Omega_{1} }} - \frac{{(\Omega_{1} - 1)^{2} }}{{8\Omega_{1} (\Omega_{2}^{2} - (\Omega_{1} - 1)^{2} )}} - \left( {\frac{1}{{\Omega_{1}^{2} - 2\Omega_{1} }} + \frac{1}{{\Omega_{1}^{2} + 2\Omega_{1} }}} \right) \times \frac{{(3 - 2\Omega_{1}^{2} )}}{{8\Omega_{1} }}} \right)(a_{11} a_{30}^{2} + 2a_{10} a_{31} a_{30} ) - \frac{{f_{1} }}{{2\Omega_{1} }}\sin \theta_{10} \,\theta_{11} + a_{11} \sigma_{1} , \hfill \\ \frac{{d\,a_{11} }}{dT} = \frac{{f_{1} }}{{2\Omega_{1} }}cos\theta_{10} \,\theta_{11} - \frac{{a_{11} c_{1} }}{2}, \hfill \\ a_{20} \frac{{d\theta_{21} }}{dT} = a_{21} \sigma_{2} - \frac{{f_{2} }}{{2\Omega_{2} }}\sin \theta_{20} \,\theta_{21} - \frac{{J\,I\,a_{21} \,\Omega_{2}^{3} }}{{2(1 - \Omega_{2}^{2} )}}, \hfill \\ \frac{{d\,a_{21} }}{dT} = \frac{{f_{2} }}{{2\Omega_{2} }}\cos \theta_{20} \,\theta_{21} - \frac{{a_{21} c_{2} }}{2}, \hfill \\ a_{30} \frac{{d\theta_{30} }}{dT} = \frac{{f_{3} }}{2}\sin \theta_{30} \,\theta_{31} + a_{31} \sigma_{3} - \left( {\frac{{(3 - 2\Omega_{1}^{2} )}}{{8(\Omega_{1}^{2} + 2\Omega_{1} )}} + \frac{1}{2}\Omega_{1}^{2} )(a_{31} a_{10}^{2} + 2a_{10} a_{11} a_{30} )} \right) + \frac{{\Omega_{2}^{4} }}{8}\left( {\frac{1}{{(\Omega_{1}^{2} - (1 - \Omega_{2} )^{2} )}} + \frac{1}{{(\Omega_{1}^{2} - (1 + \Omega_{2} )^{2} )}}} \right)(a_{31} a_{20}^{2} + 2a_{20} a_{21} a_{30} ), \hfill \\ \frac{{d\,a_{31} }}{dT} = \frac{{f_{3} }}{2}\cos \theta_{30} \,\theta_{31} - \frac{{a_{31} c_{3} }}{2}. \hfill \\ \end{gathered}$$

(37)

It must be remembered that the perturbation terms $a_{j1}$ and $\theta_{j1}$ are unknown functions and we can express their solutions in the exponential form $c_{k} e^{\lambda T}$; in which $\,c_{k} \,\,(k = 1,2,....,6)$ are constants and $\lambda$ represents the eigenvalue congruent to the unknown perturbations that can be obtained from the real parts of the roots. If the steady-state solutions $a_{j0}$ and $\theta_{j0}$ are considered to be stable asymptotically, then the real components of the roots of the below characteristic equation must be negative [33]

$$\lambda^{6} + \Gamma_{1} \lambda^{5} + \Gamma_{2} \lambda^{4} + \Gamma_{3} \lambda^{3} + \Gamma_{4} \lambda^{2} + \Gamma_{5} \lambda + \Gamma_{6} = 0,$$

(38)

where

$$\begin{gathered} \Gamma _{1} = \frac{1}{2}\left( {c_{1} + c_{2} + c_{3} + \frac{{f_{1} \sin \theta _{{10}} }}{{a_{{10}} \Omega _{1} }} + \frac{{f_{2} \sin \theta _{{20}} }}{{a_{{20}} \Omega _{2} }} + \frac{{f_{3} \sin \theta _{{30}} }}{{a_{{30}} }}} \right) \hfill \\ \Gamma _{2} = \{ 4\sin \theta _{{10}} f_{1} \Omega _{1} \left( { - 4 + \Omega _{1}^{2} } \right)\left( { - 1 + \Omega _{1} - \Omega _{2} } \right)\left( {1 + \Omega _{1} - \Omega _{2} } \right)( - 1 + \Omega _{1} + \Omega _{2} )(1 + \Omega _{1} + \Omega _{2} )\{ \sin \theta _{{20}} a_{{30}} f_{2} \hfill \\ \,\,\,\,\,\, + a_{{20}} [a_{{30}} \left( {c_{1} + c_{2} + c_{3} } \right) - \sin \theta _{{30}} f_{3} ]\Omega _{2} \} \left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right)( - 1 + \Omega _{2}^{2} ) + \cos \theta _{{10}} a_{{20}} a_{{30}} f_{1} \Omega _{2} \left( { - 1 + \Omega _{2}^{2} } \right)\,\,\,\,\,\, \hfill \\ \,\,\,\,\,\, \times [\left( { - 1 + \Omega _{1}^{2} } \right)^{2} - 2\left( {1 + \Omega _{1}^{2} } \right)\Omega _{2}^{2} + \Omega _{2}^{4} ]( - 8\sigma _{1} \Omega _{1} \left( { - 4 + \Omega _{1}^{2} } \right)\left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right) - a_{{20}}^{2} \{ 2(5 + 7\Omega _{2}^{2} ) + \Omega _{1} [ - 6 \hfill \\ \,\,\,\,\,\, + \Omega _{1} ( - 9 + \Omega _{1} \left( {4 + \Omega _{1} } \right) - 6\Omega _{2}^{2} )]\} \} + 2a_{{10}} \Omega _{1} \left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right)\{ 2\,\cos \theta _{{20}} a_{{10}}^{2} a_{{30}} f_{2} ( - 2 + \Omega _{1} )\{ 6 + \Omega _{1}^{2} \hfill \\ \,\,\,\,\,\, \times [\Omega _{1} \left( {2 + \Omega _{1} } \right) - 4]\} \left( { - 1 + \Omega _{2}^{2} } \right)[\Omega _{1}^{4} + \left( { - 1 + \Omega _{2}^{2} } \right)^{2} - 2\Omega _{1}^{2} (1 + \Omega _{2}^{2} )] + \Omega _{1} \left( { - 4 + \Omega _{1}^{2} } \right)[\cos \theta _{{20}} a_{{30}}^{3} f_{2} \Omega _{2}^{4} \hfill \\ \,\,\,\,\,\, \times \left( { - 1 + \Omega _{2}^{2} } \right)\left( {1 - \Omega _{1}^{2} + \Omega _{2}^{2} } \right) + 2a_{{30}} \{ \sin \theta _{{20}} \left( {c_{1} + c_{2} + c_{3} } \right)f_{2} - 2\,\cos \theta _{{20}} f_{2} \sigma _{2} + a_{{20}} [c_{1} c_{2} + \left( {c_{1} + c_{2} } \right) \hfill \\ \,\,\,\,\,\, \times c_{3} )\Omega _{2} ]\left( { - 1 + \Omega _{2}^{2} } \right)[\left( { - 1 + \Omega _{1}^{2} } \right)^{2} - 2\left( {1 + \Omega _{1}^{2} } \right)\Omega _{2}^{2} + \Omega _{2}^{4} ] + 2f_{3} [\left( { - 1 + \Omega _{1}^{2} } \right)^{2} - 2\left( {1 + \Omega _{1}^{2} } \right)\Omega _{2}^{2} + \Omega _{2}^{4} ] \hfill \\ \,\,\,\,\,\, \times [I~J\cos \theta _{{30}} a_{{20}} \Omega _{2}^{4} + \sin \theta _{{30}} ( - \sin \theta _{{20}} f_{2} - a_{{20}} (c_{1} + c_{2} + c_{3} )\Omega _{2} )\left( { - 1 + \Omega _{2}^{2} } \right)]\} ]\} \{ 16a_{{10}} a_{{20}} \,\,\,\,\, \hfill \\ \,\,\,\,\,\, \times a_{{30}} \Omega _{1}^{2} ( - 4 + \Omega _{1}^{2} )\left( { - \Omega _{1}^{2} + \left( { - 1 + \Omega _{2} } \right)^{2} } \right)\Omega _{2} ( - 1 + \Omega _{1} - \Omega _{2}^{2} )\left( { - 1 + \Omega _{2}^{2} } \right)[ - \Omega _{1}^{2} + \left( {1 + \Omega _{2} } \right)^{2} ]\} , \hfill \\ \Gamma _{3} = \{ f_{1} \cos \theta _{{10}} \{ a_{{20}} f_{2} \sin \theta _{{20}} + a_{{30}} [a_{{20}} \left( {c_{2} + c_{3} } \right) - f_{3} \sin \theta _{{30}} ]\Omega _{2} \} ( - 1 + \Omega _{2}^{2} )[\left( { - 1 + \Omega _{1}^{2} } \right)^{2} \hfill \\ \,\,\,\,\,\,\, - 2\left( {1 + \Omega _{1}^{2} } \right)\Omega _{2}^{2} + \Omega _{2}^{4} ][ - 8\sigma _{1} \Omega _{1} ( - 4 + \Omega _{1}^{2} )( - 1 + \Omega _{1} - \Omega _{2}^{2} ) - a_{{30}}^{2} (2\left( {5 + 7\Omega _{2}^{2} } \right) \hfill \\ \,\,\,\,\,\, + \Omega _{1} \{ - 6 + \Omega _{1} [ - 9 + \Omega _{1} \left( {4 + \Omega _{1} } \right) - 6\Omega _{2}^{2} ]\} )] + 2f_{1} \sin \theta _{{10}} \left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right) \hfill \\ \,\,\,\,\,\,\, \times (2a_{{10}}^{2} a_{{20}} f_{2} \cos \theta _{{20}} ( - 2 + \Omega _{1} )\{ 6 + \Omega _{1}^{2} [ - 4 + \Omega _{1} \left( {2 + \Omega _{1} } \right)]\} \left( { - 1 + \Omega _{2}^{2} } \right)[\Omega _{1}^{4} \hfill \\ \,\,\,\,\,\, + \left( { - 1 + \Omega _{2}^{2} } \right)^{2} - 2\Omega _{1}^{2} \left( {1 + \Omega _{2}^{2} } \right)] + \Omega _{1} \left( { - 4 + \Omega _{1}^{2} } \right)(a_{{20}}^{3} f_{2} \Omega _{2}^{4} \cos \theta _{{20}} \left( { - 1 + \Omega _{2}^{2} } \right) \hfill \\ \,\,\,\,\, \times (1 - \Omega _{1}^{2} + \Omega _{2}^{2} ) + 2a_{{20}} (f_{2} \sin \theta _{{20}} \left( {c_{1} + c_{2} + c_{3} } \right) - 2f_{2} \sigma _{2} \cos \theta _{{20}} + a_{{30}} [c_{1} c_{2} + \left( {c_{1} + c_{2} } \right)c_{3} ] \hfill \\ \,\,\,\,\,\, \times \Omega _{2} )\left( { - 1 + \Omega _{2}^{2} } \right)[\left( { - 1 + \Omega _{1}^{2} } \right)^{2} - 2\left( {1 + \Omega _{1}^{2} } \right)\Omega _{2}^{2} + \Omega _{2}^{4} ] + 2f_{3} [\left( { - 1 + \Omega _{1}^{2} } \right)^{2} - 2\left( {1 + \Omega _{1}^{2} } \right)\Omega _{2}^{2} + \Omega _{2}^{4} ] \hfill \\ \,\,\,\,\,\, \times [IJa_{{30}} \Omega _{2}^{4} \cos \theta _{{30}} + \sin \theta _{{30}} [ - f_{2} \sin \theta _{{20}} - a_{{30}} (c_{1} + c_{2} + c_{3} )\Omega _{2} ]\left( { - 1 + \Omega _{2}^{2} } \right)])) + 2a_{{10}} \Omega _{1} (2f_{2} \Omega _{1} \hfill \\ \,\,\,\,\,\, \times \sin \theta _{{20}} \left( { - 4 + \Omega _{1}^{2} } \right)( - 1 + \Omega _{1} - \Omega _{2} )\left( {1 + \Omega _{1} - \Omega _{2} } \right)\left( { - 1 + \Omega _{1} + \Omega _{2} } \right)\left( {1 + \Omega _{1} + \Omega _{2} } \right)( - 1 + \Omega _{1} \hfill \\ \,\,\,\,\, - \Omega _{2}^{2} )(a_{{20}} (a_{{20}} [c_{2} c_{3} + c_{1} \left( {c_{2} + c_{3} } \right)]\left( { - 1 + \Omega _{2}^{2} } \right) + f_{3} (IJ\cos \theta _{{30}} \Omega _{2}^{3} - \left( {c_{1} + c_{2} + c_{3} } \right)\left( { - 1 + \Omega _{2}^{2} } \right) \hfill \\ \,\,\,\,\,\, \times \sin \theta _{{30}} )) + 2a_{{30}} \Omega _{1} \left( { - 4 + \Omega _{1}^{2} } \right)\left( { - 1 + \Omega _{1} - \Omega _{2} } \right)\left( {1 + \Omega _{1} - \Omega _{2} } \right)\Omega _{2} \left( { - 1 + \Omega _{1} + \Omega _{2} } \right)\left( {1 + \Omega _{1} + \Omega _{2} } \right) \hfill \\ \,\,\,\,\,\, \times \left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right)\{ a_{{30}} c_{1} c_{2} c_{3} ( - 1 + \Omega _{2}^{2} ) + f_{3} [IJ\cos \theta _{{30}} \left( {c_{1} + c_{2} } \right)\Omega _{2}^{3} - [c_{2} c_{3} + c_{1} \left( {c_{2} + c_{3} } \right)]\sin \theta _{{30}} \hfill \\ \,\,\,\,\, \times \left( { - 1 + \Omega _{2}^{2} } \right)]\} \, - f_{2} \cos \theta _{{20}} \left( {a_{{30}} \left( {c_{1} + c_{3} } \right) - f_{3} \sin \theta _{{30}} } \right)\left( { - 2 + \Omega _{1} } \right)\left( { - 1 + \Omega _{2}^{2} } \right)\left( {1 - \Omega _{1} + \Omega _{2}^{2} } \right)\{ 2a_{{10}}^{2} \hfill \\ \,\,\,\,\,\, \times \{ 6 + \Omega _{1}^{2} [ - 4 + \Omega _{1} \left( {2 + \Omega _{1} } \right)]\} [\left( { - 1 + \Omega _{1}^{2} } \right)^{2} - 2\left( {1 + \Omega _{1}^{2} } \right)\Omega _{2}^{2} + \Omega _{2}^{4} ] - \Omega _{1} \left( {2 + \Omega _{1} } \right)[a_{{20}}^{2} \Omega _{2}^{4} \hfill \\ \,\,\,\,\,\, \times ( - 1 + \Omega _{1}^{2} - \Omega _{2}^{2} ) + 4\sigma _{2} (( - 1 + \Omega _{1}^{2} )^{2} - 2(1 + \Omega _{1}^{2} )\Omega _{2}^{2} - 2\left( {1 + \Omega _{1}^{2} } \right)\Omega _{2}^{2} + \Omega _{2}^{4} )]\} ])/(32a_{{10}} \hfill \\ \,\,\,\,\,\, \times a_{{20}} a_{{30}} \Omega _{1}^{2} ( - 4 + \Omega _{1}^{2} )( - \Omega _{1}^{2} + ( - 1 + \Omega _{2} )^{2} )\Omega _{2} ( - 1 + \Omega _{1} - \Omega _{2}^{2} )( - 1 + \Omega _{2}^{2} )( - \Omega _{1}^{2} + (1 + \Omega _{2} )^{2} )), \hfill \\ \Gamma _{4} = - (IJ\cos \theta _{{20}} f_{2} \Omega _{2}^{3} \{ - 4a_{{10}} c_{3} f_{3} \sin \theta _{{30}} \left( { - 2 + \Omega _{1} } \right)\Omega _{1}^{2} \left( {2 + \Omega _{1} } \right)\left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right) - 4\left( { - 2 + \Omega _{1} } \right)\Omega _{1} \hfill \\ \,\,\,\,\,\,\,\,\,\,\, \times (2 + \Omega _{1} )\left( {f_{1} \sin \theta _{{10}} + a_{{10}} c_{1} \Omega _{1} } \right)\left( {f_{3} \sin \theta _{{30}} + a_{{30}} c_{3} \Omega _{2} } \right)\left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right) + 8\cos \theta _{{30}} \,a_{{10}} f_{3} \Omega _{1}^{2} \hfill \\ \,\,\,\,\,\,\,\,\,\,\, \times (\Omega _{1}^{2} - 4)( - 1 + \Omega _{1} - \Omega _{2}^{2} )[\sigma _{2} + a_{{10}}^{2} ( - \frac{{\Omega _{1}^{2} }}{2} + \frac{{ - 3 + 2\Omega _{1}^{2} }}{{\Omega _{1} (2 + \Omega _{1} )}}) + \frac{1}{8}a_{{30}}^{2} \Omega _{2}^{4} (\frac{1}{{\Omega _{1}^{2} - (\Omega _{2} - 1)^{2} }} \hfill \\ \,\,\,\,\,\,\,\,\,\, + \frac{1}{{\Omega _{1}^{2} - \left( {1 + \Omega _{2} } \right)^{2} }})] + a_{{20}} f_{1} \Omega _{2} [ - 4c_{1} \sin \theta _{{10}} \Omega _{1} \left( { - 4 + \Omega _{1}^{2} } \right)\left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right) + \cos \theta _{{10}} (8\sigma _{1} \Omega _{1} \hfill \\ \,\,\,\,\,\,\,\,\,\, \times \left( { - 4 + \Omega _{1}^{2} } \right)\left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right) + a_{{20}}^{2} [ - 6\Omega _{1} + 4\Omega _{1}^{3} + \Omega _{1}^{4} - 3\Omega _{1}^{2} \left( {3 + 2\Omega _{2}^{2} } \right) + 2(5 + 7\Omega _{2}^{2} ))]]\} \hfill \\ \,\,\,\,\,\,\,\,\, - f_{2} \sin \theta _{{20}} ( - 1 + \Omega _{2}^{2} )( - 4c_{3} f_{3} \Omega _{1} \sin \theta _{{20}} \left( { - 2 + \Omega _{1} } \right)\left( {2 + \Omega _{1} } \right)\left( {f_{1} \sin \theta _{{10}} + a_{{10}} c_{1} \Omega _{1} } \right) \hfill \\ \,\,\,\,\,\,\,\,\,\, \times \left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right) + a_{{30}} c_{3} \Omega _{2} ) + 8\cos \theta _{{30}} f_{3} \Omega _{1} \left( {f_{1} \sin \theta _{{10}} + a_{{10}} c_{1} \Omega _{1} } \right)\left( { - 4 + \Omega _{1}^{2} } \right)[\sigma _{3} + a_{{10}}^{2} ( - \frac{{\Omega _{1}^{2} }}{2} \hfill \\ \,\,\,\,\,\,\,\,\, + \frac{{ - 3 + 2\Omega _{1}^{2} }}{{\Omega _{1} \left( {2 + \Omega _{1} } \right)}}) + \frac{1}{8}a_{{20}}^{2} \Omega _{2}^{4} (\frac{1}{{\Omega _{1}^{2} - \left( { - 1 + \Omega _{2} } \right)^{2} }}\frac{1}{{\Omega _{1}^{2} - \left( {1 + \Omega _{2} } \right)^{2} }})] + \left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right) + f_{1} (f_{2} \sin \theta _{{20}} \hfill \\ \,\,\,\,\,\,\,\,\,\, + a_{{30}} c_{3} \Omega _{2} )( - 4c_{1} \sin \theta _{{10}} \Omega _{1} + \frac{1}{{\Omega _{1}^{2} - \left( {1 + \Omega _{2} } \right)^{2} }}) + f_{1} \left( {f_{2} \sin \theta _{{20}} + a_{{30}} c_{3} \Omega _{2} } \right)\{ - 4c_{1} \sin \theta _{{10}} \Omega _{1} + a_{{30}}^{2} \hfill \\ \,\,\,\,\,\,\,\,\,\, \times [ - 6\Omega _{1} + 4\Omega _{1}^{3} + \Omega _{1}^{4} - 3\Omega _{1}^{2} (3 + 2\Omega _{2}^{2} ) + 2(5 + 7\Omega _{2}^{2} ))]\} + c_{2} ( - 1 + \Omega _{2}^{2} )\{ a_{{20}} [ - 4c_{3} \Omega _{1} f_{3} \sin \theta _{{30}} \hfill \\ \,\,\,\,\,\,\,\,\,\, \times \left( { - 2 + \Omega _{1} } \right)\left( {2 + \Omega _{1} } \right)\left( {f_{1} \,\sin \theta _{{10}} + a_{{10}} c_{1} \Omega _{1} } \right)\left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right) + 8\cos \theta _{{30}} f_{3} \Omega _{1} (f_{1} \sin \theta _{{10}} \hfill \\ \,\,\,\,\,\,\,\,\, + a_{{10}} c_{1} \Omega _{1} )\left( { - 4 + \Omega _{1}^{2} } \right)\left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right)[\sigma _{3} + a_{{10}}^{2} ( - \frac{{\Omega _{1}^{2} }}{2} + \frac{{ - 3 + 2\Omega _{1}^{2} }}{{\Omega _{1} (2 + \Omega _{1} )}}) + \frac{1}{8}a_{{20}}^{2} \Omega _{2}^{4} \hfill \\ \,\,\,\,\,\,\,\,\, \times (\frac{1}{{\Omega _{1}^{2} - \left( { - 1 + \Omega _{2} } \right)^{2} }} + \frac{1}{{\Omega _{1}^{2} - \left( {1 + \Omega _{2} } \right)^{2} }})]\, + f_{1} \left( {f_{3} \sin \theta _{{30}} + a_{{30}} c_{3} \Omega _{2} } \right)[ - 4c_{1} \Omega _{1} \sin \theta _{{10}} \left( { - 4 + \Omega _{1}^{2} } \right) \hfill \\ \,\,\,\,\,\,\,\,\, \times \left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right) + \cos \theta _{{10}} [8\sigma _{1} \Omega _{1} \,( - 4 + \Omega _{1}^{2} )( - 1 + \Omega _{1} - \Omega _{2}^{2} ) + a_{{30}}^{2} ( - 6\Omega _{1} + 4\Omega _{1}^{3} + \Omega _{1}^{4} \hfill \\ \,\,\,\,\,\,\,\,\, - 3\Omega _{1}^{2} (3 + 2\Omega _{2}^{2} ) + 2(5 + 7\Omega _{2}^{2} ))]]\} - f_{2} \sin \theta _{{20}} \{ - 4a_{{10}} c_{3} f_{3} \sin \theta _{{30}} ( - 2 + \Omega _{1} )\Omega _{1}^{2} \left( {2 + \Omega _{1} } \right) \hfill \\ \,\,\,\,\,\,\,\,\,\, \times \left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right) - 4\left( { - 2 + \Omega _{1} } \right)\Omega _{1} \left( {2 + \Omega _{1} } \right)(f_{1} \sin \theta _{{10}} + a_{{10}} c_{1} \Omega _{1} )\left( {f_{3} \sin \theta _{{30}} + a_{{30}} c_{3} \Omega _{2} } \right) \hfill \\ \,\,\,\,\,\,\,\,\,\, \times \left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right) + 8a_{{10}} \cos \theta _{{30}} f_{3} \Omega _{1}^{2} \left( { - 4 + \Omega _{1}^{2} } \right)\left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right)[\sigma _{3} + a_{{10}}^{2} ( - \frac{{\Omega _{1}^{2} }}{2} \hfill \\ \,\,\,\,\,\,\,\, + \frac{{ - 3 + 2\Omega _{1}^{2} }}{{\Omega _{1} \left( {2 + \Omega _{1} } \right)}}) + \frac{1}{8}a_{{30}}^{2} \Omega _{2}^{4} (\frac{1}{{\Omega _{1}^{2} - \left( { - 1 + \Omega _{2} } \right)^{2} }} + \frac{1}{{\Omega _{1}^{2} - \left( {1 + \Omega _{2} } \right)^{2} }})] + a_{{30}} f_{1} \Omega _{2} [ - 4c_{1} \sin \theta _{{10}} \Omega _{1} \hfill \\ \,\,\,\,\,\,\,\, \times \left( { - 4 + \Omega _{1}^{2} } \right)\left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right) + \cos \theta _{{10}} [8\sigma _{1} \Omega _{1} ( - 4 + \Omega _{1}^{2} )\left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right) + a_{{30}}^{2} ( - 6\Omega _{1} + 4\Omega _{1}^{3} \hfill \\ \,\,\,\,\,\,\,\, + \Omega _{1}^{4} - 3\Omega _{1}^{2} (3 + 2\Omega _{2}^{2} ) + 2(5 + 7\Omega _{2}^{2} ))]]\} + a_{{20}} f_{1} f_{3} \left( { - 1 + \Omega _{2}^{2} } \right)\} c_{3} \sin \theta _{{30}} \{ - 4\sin \theta _{{10}} c_{1} \Omega _{1} (\Omega _{1}^{2} \hfill \\ \,\,\,\,\,\,\,\, - 4)\left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right) + \cos \theta _{{10}} [8\sigma _{1} \Omega _{1} \left( { - 4 + \Omega _{1}^{2} } \right)\left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right) + a_{{30}}^{2} [ - 6\Omega _{1} + 4\Omega _{1}^{3} + \Omega _{1}^{4} \hfill \\ \Gamma _{5} = (f_{2} ( - IJ\cos \theta _{{20}} \Omega _{2}^{3} ( - 4c_{3} f_{3} \sin \theta _{{30}} \Omega _{1} \left( {f_{1} \sin \theta _{{10}} + a_{{10}} c_{1} \Omega _{1} } \right)\left( { - 4 + \Omega _{1}^{2} } \right)\left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right) + 8\cos \theta _{{30}} \hfill \\ \,\,\,\,\,\,\, \times f_{3} \Omega _{1} \left( {f_{1} \sin \theta _{{10}} + a_{{10}} c_{1} \Omega _{1} } \right)\left( { - 4 + \Omega _{1}^{2} } \right)\left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right)\{ \sigma _{3} + a_{{10}}^{2} \{ - \frac{{\Omega _{1}^{2} }}{2} + \frac{{ - 3 + 2\Omega _{1}^{2} }}{{\Omega _{1} \left( {2 + \Omega _{1} } \right)}} \hfill \\ \,\,\,\,\,\,\, + 8\cos \theta _{{30}} f_{3} \Omega _{1} \left( {f_{1} \sin \theta _{{10}} + a_{{10}} c_{1} \Omega _{1} } \right)\left( { - 4 + \Omega _{1}^{2} } \right)\left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right)\{ \sigma _{3} + a_{{10}}^{2} \{ - \frac{{\Omega _{1}^{2} }}{2} + \frac{{ - 3 + 2\Omega _{1}^{2} }}{{\Omega _{1} \left( {2 + \Omega _{1} } \right)}} \hfill \\ \,\,\,\,\,\,\, + 8\cos \theta _{{30}} f_{3} \Omega _{1} \left( {f_{1} \sin \theta _{{10}} + a_{{10}} c_{1} \Omega _{1} } \right)\left( { - 4 + \Omega _{1}^{2} } \right)\left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right)[\sigma _{3} + a_{{10}}^{2} (\Omega _{1}^{2} - \frac{{\Omega _{1}^{2} }}{2} \hfill \\ \,\,\,\,\,\,\,\, + \frac{{ - 3 + 2\Omega _{1}^{2} }}{{\Omega _{1} (2 + \Omega _{1} )}})\left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right) + \cos \theta _{{10}} [8\sigma _{1} \Omega _{1} \left( { - 4 + \Omega _{1}^{2} } \right)\left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right)\, + a_{{30}}^{2} ( - 6\Omega _{1} \hfill \\ \,\,\,\,\,\,\, + 4\Omega _{1}^{3} + \Omega _{1}^{4} - 3\Omega _{1}^{2} (3 + 2\Omega _{2}^{2} ) + 2(5 + 7\Omega _{2}^{2} ))]]\} + f_{1} f_{3} \sin \theta _{{20}} \left( { - 1 + \Omega _{2}^{2} } \right)\{ c_{3} \sin \theta _{{30}} [ - 4c_{1} \sin \theta _{{10}} \Omega _{1} \hfill \\ \,\,\,\,\,\,\,\,\left( { - 4 + \Omega _{1}^{2} } \right)\left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right) + \cos \theta _{{10}} [8\sigma _{1} \Omega _{1} \left( { - 4 + \Omega _{1}^{2} } \right)\left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right) + a_{{30}}^{2} ( - 6\Omega _{1} + 4\Omega _{1}^{3} \hfill \\ \,\,\,\,\,\,\,\, + \Omega _{1}^{4} - 3\Omega _{1}^{2} \left( {3 + 2\Omega _{2}^{2} } \right) + 2(5 + 7\Omega _{2}^{2} ))]] + 2\cos \theta _{{30}} \{ - 2a_{{10}}^{2} a_{{30}}^{2} \cos \theta _{{10}} \left( {2 + \Omega _{1} } \right)(6 - 4\Omega _{1}^{2} \hfill \\ \,\,\,\,\,\,\,\,\, + 2\Omega _{1}^{3} + \Omega _{1}^{4} )[ - 6\Omega _{1} + 4\Omega _{1}^{3} + \Omega _{1}^{4} - 3\Omega _{1}^{2} (3 + 2\Omega _{2}^{2} ) + 2(5 + 7\Omega _{2}^{2} )]/\Omega _{1} - [\sigma _{3} + a_{{10}}^{2} ( - \frac{{\Omega _{1}^{2} }}{2} \hfill \\ \,\,\,\,\,\,\,\, + \frac{{ - 3 + 2\Omega _{1}^{2} }}{{\Omega _{1} \left( {2 + \Omega _{1} } \right)}}) + \frac{1}{8}a_{{20}}^{2} \Omega _{2}^{4} (\frac{1}{{\Omega _{1}^{2} - \left( { - 1 + \Omega _{2} } \right)^{2} }} + \frac{1}{{\Omega _{1}^{2} - \left( {1 + \Omega _{2} } \right)^{2} }})][ - 4c_{1} \sin \theta _{{10}} \Omega _{1} \left( { - 4 + \Omega _{1}^{2} } \right) \hfill \\ \,\,\,\,\,\,\,\, \times \left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right) + \cos \theta _{{10}} [8\sigma _{1} \Omega _{1} \left( { - 4 + \Omega _{1}^{2} } \right)( - 1 + \Omega _{1} - \Omega _{2}^{2} ) + a_{{30}}^{2} ( - 6\Omega _{1} + 4\Omega _{1}^{3} + \Omega _{1}^{4} \hfill \\ \,\,\,\,\,\,\,\, - 3\Omega _{1}^{2} (3 + 2\Omega _{2}^{2} ) + 2(5 + 7\Omega _{2}^{2} ))]]\} \} - c_{2} \left( { - 1 + \Omega _{2}^{2} } \right)[ - \sin \theta _{{20}} [ - 4c_{3} \Omega _{1} f_{3} \sin \theta _{{30}} (f_{1} \sin \theta _{{10}} \hfill \\ \,\,\,\,\,\,\,\, + a_{{10}} c_{1} \Omega _{1} )\left( { - 4 + \Omega _{1}^{2} } \right)\left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right) + 8\cos \theta _{{30}} f_{3} \Omega _{1} \left( {f_{1} \sin \theta _{{10}} + a_{{10}} c_{1} \Omega _{1} } \right)\left( { - 4 + \Omega _{1}^{2} } \right) \hfill \\ \,\,\,\,\,\,\,\, \times ( - 1 + \Omega _{1} - \Omega _{2}^{2} )[\sigma _{3} + a_{{10}}^{2} ( - \frac{{\Omega _{1}^{2} }}{2} + \frac{{ - 3 + 2\Omega _{1}^{2} }}{{\Omega _{1} \left( {2 + \Omega _{1} } \right)}}) + \frac{1}{8}a_{{20}}^{2} \Omega _{2}^{4} (\frac{1}{{\Omega _{1}^{2} - \left( { - 1 + \Omega _{2} } \right)^{2} }} + \frac{1}{{\Omega _{1}^{2} - \left( {1 + \Omega _{2} } \right)^{2} }})] \hfill \\ \,\,\,\,\,\,\, + f_{1} (f_{2} \sin \theta _{{30}} + a_{{30}} c_{3} \Omega _{2} )( - 4c_{1} \sin \theta _{{10}} \Omega _{1} \left( { - 4 + \Omega _{1}^{2} } \right)\left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right) + \cos \theta _{{10}} (8\sigma _{1} \Omega _{1} \,( - 4 + \Omega _{1}^{2} ) \hfill \\ \,\,\,\,\,\,\,\, \times \,\left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right) + a_{{30}}^{2} ( - 6\Omega _{1} + 4\Omega _{1}^{3} + \Omega _{1}^{4} - 3\Omega _{1}^{2} (3 + 2\Omega _{2}^{2} ) + 2(5 + 7\Omega _{2}^{2} ))]]\} + a_{{20}} f_{1} [c_{2} \sin \theta _{{20}} \hfill \\ \,\,\,\,\,\,\,\, + a_{{20}} f_{1} [c_{2} \sin \theta _{{20}} [ - 4c_{1} \sin \theta _{{10}} \Omega _{1} + \left( { - 4 + \Omega _{1}^{2} } \right)\left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right) + \cos \theta _{{10}} [8\sigma _{1} \Omega _{1} \left( { - 4 + \Omega _{1}^{2} } \right)\,[ - 1 + \Omega _{1} \,\,\,\,\,\, \hfill \\ \,\,\,\,\,\,\,\, - \Omega _{2}^{2} ) + a_{{30}}^{2} [ - 6\Omega _{1} + 4\Omega _{1}^{3} + \Omega _{1}^{4} - 3\Omega _{1}^{2} \left( {3 + 2\Omega _{2}^{2} } \right) + 2(5 + 7\Omega _{2}^{2} ))]] + 2\cos \theta _{{20}} [ - 2a_{{10}}^{2} a_{{20}}^{2} \cos \theta _{{10}} \hfill \\ \,\,\,\,\,\,\,\, \times \left( {2 + \Omega _{1} } \right)(6 - 4\Omega _{1}^{2} + 2\Omega _{1}^{3} + \Omega _{1}^{4} )\left( { - 6\Omega _{1} + 4\Omega _{1}^{3} + \Omega _{1}^{4} - 3\Omega _{1}^{2} \left( {3 + 2\Omega _{2}^{2} } \right) + 2\left( {5 + 7\Omega _{2}^{2} } \right)} \right)/\Omega _{1} \hfill \\ \,\,\,\,\,\, - (\sigma _{3} + a_{{10}}^{2} (\frac{{ - 3 + 2\Omega _{1}^{2} }}{{\Omega _{1} \left( {2 + \Omega _{1} } \right)}} - \frac{{\Omega _{1}^{2} }}{2}) + \frac{1}{8}a_{{20}}^{2} \Omega _{2}^{4} (\frac{1}{{\Omega _{1}^{2} - \left( { - 1 + \Omega _{2} } \right)^{2} }} + \frac{1}{{\Omega _{1}^{2} - \left( {1 + \Omega _{2} } \right)^{2} }})] \hfill \\ \,\,\,\,( - 4c_{1} \sin \theta _{{10}} \Omega _{1} \left( { - 4 + \Omega _{1}^{2} } \right)\left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right)\, + \cos \theta _{{10}} (8\sigma _{1} \Omega _{1} \left( { - 4 + \Omega _{1}^{2} } \right)\left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right) \hfill \\ \,\,\,\, + a_{{30}}^{2} ( - 6\Omega _{1} + 4\Omega _{1}^{3} + \Omega _{1}^{4} - 3\Omega _{1}^{2} (3 + 2\Omega _{2}^{2} ) + ( - 1 + \Omega _{2}^{2} )) + 2(5 + 7\Omega _{2}^{2} )))]]\} \} /(256a_{{10}} a_{{20}} \hfill \\ \,\,\,\,\, \times a_{{30}} \Omega _{1}^{2} ( - 4 + \Omega _{1}^{2} )\Omega _{2} \left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right)\left( { - 1 + \Omega _{2}^{2} } \right)), \hfill \\ \Gamma _{6} = (f_{1} f_{2} f_{3} \left( { - I{\text{ }}J\,\cos \theta _{{20}} \Omega _{2}^{3} + c_{2} \sin \theta _{{20}} \left( { - 1 + \Omega _{2}^{2} } \right)} \right)\{ c_{3} \,\sin \theta _{{30}} \{ - 4c_{1} \sin \theta _{{10}} \Omega _{1} \left( { - 4 + \Omega _{1}^{2} } \right) \hfill \\ \,\,\,\,\,\,\, \times \left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right) + \cos \theta _{{10}} [8\sigma _{1} \Omega _{1} \left( { - 4 + \Omega _{1}^{2} } \right)\left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right) + a_{{30}}^{2} ( - 6\Omega _{1} + 4\Omega _{1}^{3} + \Omega _{1}^{4} \hfill \\ \,\,\,\,\,\,\, - 3\Omega _{1}^{2} (3 + 2\Omega _{2}^{2} ) + 2(5 + 7\Omega _{2}^{2} ))]\} + 2\cos \theta _{{30}} \{ - 2a_{{10}}^{2} a_{{30}}^{2} \cos \theta _{{10}} \left( {2 + \Omega _{1} } \right)[6 - 4\Omega _{1}^{2} + 2\Omega _{1}^{3} \hfill \\ \,\,\,\,\,\, + \Omega _{1}^{4} )\left( { - 6\Omega _{1} + 4\Omega _{1}^{3} + \Omega _{1}^{4} - 3\Omega _{1}^{2} \left( {3 + 2\Omega _{2}^{2} } \right) + 2\left( {5 + 7\Omega _{2}^{2} } \right)} \right)\,/\Omega _{1} - [\sigma _{3} + a_{{10}}^{2} ( - \frac{{\Omega _{1}^{2} }}{2} \hfill \\ \,\,\,\,\,\, + \frac{{ - 3 + 2\Omega _{1}^{2} }}{{\Omega _{1} \left( {2 + \Omega _{1} } \right)}}) + \frac{1}{8}a_{{20}}^{2} \Omega _{2}^{4} (\frac{1}{{\Omega _{1}^{2} - \left( { - 1 + \Omega _{2} } \right)^{2} }} + \frac{1}{{\Omega _{1}^{2} - \left( {1 + \Omega _{2} } \right)^{2} }})][ - 4c_{1} \sin \theta _{{10}} \Omega _{1} (\Omega _{1}^{2} \hfill \\ \,\,\,\,\,\, - 4)\left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right) + \cos \theta _{{10}} (8\sigma _{1} \Omega _{1} \left( { - 4 + \Omega _{1}^{2} } \right)\left( { - 1 + \Omega _{1} - \Omega _{2}^{2} } \right) + a_{{30}}^{2} ( - 6\Omega _{1} + 4\Omega _{1}^{3} + \Omega _{1}^{4} \hfill \\ \,\,\,\,\,\, - 3\Omega _{1}^{2} \left( {3 + 2\Omega _{2}^{2} } \right) + 2(5 + 7\Omega _{2}^{2} )))]]\} \} /[256a_{{10}} a_{{20}} a_{{30}} \Omega _{1}^{2} ( - 4 + \Omega _{1}^{2} )\Omega _{2} ( - 1 + \Omega _{1} - \Omega _{2}^{2} )(\Omega _{2}^{2} - 1)]. \hfill \\ \end{gathered}$$

(39)

The previous coefficients $\Gamma_{k} \,\,(k = 1,2,...,6)$ depend on some parameters such as $a_{j0} ,\theta_{j0} ,c_{k}$ and $f_{j} \,(j = 1,2,3)$. Based on the Routh-Hurwitz criterion [16, 34],

$Det_{k} \left( {\begin{array}{*{20}c} {\Gamma_{1} } & 1 & 0 & 0 & {..} & 0 \\ {\Gamma_{3} } & {\Gamma_{2} } & {\Gamma_{1} } & 1 & {..} & 0 \\ {\Gamma_{5} } & {\Gamma_{4} } & {\Gamma_{3} } & {\Gamma_{2} } & {..} & 0 \\ {\Gamma_{7} } & {\Gamma_{6} } & {\Gamma_{5} } & {\Gamma_{4} } & {..} & 0 \\ : & : & : & : & : & : \\ {\Gamma_{2k - 1} } & {\Gamma_{2k - 2} } & {\Gamma_{2k - 3} } & {..} & {..} & {\Gamma_{k} } \\ \end{array} } \right)$,

we can write the stability conditions of the steady-state solutions in the following form:

$$\begin{array}{*{20}c} {\Gamma_{1} > 0,} & {{\text{Det}}\left( {\begin{array}{*{20}c} {\Gamma_{1} } & 1 \\ {\Gamma_{3} } & {\Gamma_{2} } \\ \end{array} } \right) > 0} \\ {{\text{Det}}\left( {\begin{array}{*{20}c} {\Gamma_{1} } & 1 & 0 \\ {\Gamma_{3} } & {\Gamma_{2} } & {\Gamma_{1} } \\ {\Gamma_{5} } & {\Gamma_{4} } & {\Gamma_{3} } \\ \end{array} } \right) > 0,} & {{\text{Det}}\left( {\begin{array}{*{20}c} {\Gamma_{1} } & 1 & 0 & 0 \\ {\Gamma_{3} } & {\Gamma_{2} } & {\Gamma_{1} } & 1 \\ {\Gamma_{5} } & {\Gamma_{4} } & {\Gamma_{3} } & {\Gamma_{2} } \\ 0 & {\Gamma_{6} } & {\Gamma_{5} } & {\Gamma_{4} } \\ \end{array} } \right) > 0,} \\ {{\text{Det}}\left( {\begin{array}{*{20}c} {\Gamma_{1} } & 1 & 0 & 0 & 0 \\ {\Gamma_{3} } & {\Gamma_{2} } & {\Gamma_{1} } & 1 & 0 \\ {\Gamma_{5} } & {\Gamma_{4} } & {\Gamma_{3} } & {\Gamma_{2} } & {\Gamma_{1} } \\ 0 & {\Gamma_{6} } & {\Gamma_{5} } & {\Gamma_{4} } & {\Gamma_{3} } \\ 0 & 0 & 0 & {\Gamma_{6} } & {\Gamma_{5} } \\ \end{array} } \right) > 0,} & {{\text{Det}}\left( {\begin{array}{*{20}c} {\Gamma_{1} } & 1 & 0 & 0 & 0 & 0 \\ {\Gamma_{3} } & {\Gamma_{2} } & {\Gamma_{1} } & 1 & 0 & 0 \\ {\Gamma_{5} } & {\Gamma_{4} } & {\Gamma_{3} } & {\Gamma_{2} } & {\Gamma_{1} } & 1 \\ 0 & {\Gamma_{6} } & {\Gamma_{5} } & {\Gamma_{4} } & {\Gamma_{3} } & {\Gamma_{2} } \\ 0 & 0 & 0 & {\Gamma_{6} } & {\Gamma_{5} } & {\Gamma_{4} } \\ 0 & 0 & 0 & 0 & 0 & {\Gamma_{6} } \\ \end{array} } \right) > 0.} \\ \end{array}$$

(40)

Simulation of the Results

Now, we are going to investigate the influence of the parameters $c_{1} ,c_{2} ,c_{3} ,\Omega_{1} ,$ and $\Omega_{2}$ on the motion of the system under investigation taking into the following value of different parameters:

$$\begin{gathered} c_{1} = (0.002,0.02,0.2),\,\,\,\,\,f_{1} = 0.003,\,\,\,\,\,\sigma_{1} = 0.01,\,\,\,\,\,c_{2} = 0.002, \hfill \\ c_{3} = 0.001,\,\,\,\,\,\Omega_{1} = 0.65,\,\,\,\,\,\sigma_{2} = 0.02,\,\,\,\,\,m = 0.5\,{\text{kg}},\,\,\,\,\,M^{*} = 1\,{\text{kg}}, \hfill \\ W_{1} = 0.2,\,\,\,\,\,W_{2} = 0.1,\,\,\,\,\,\Omega_{2} = 1.2,\,\,\,\,\,f_{1} = 0.001,\,\,\,\,\,f_{1} = 0.002, \hfill \\ W_{3} = 0.3,\,\,\,\,\,\varepsilon = 0.001. \hfill \\ \end{gathered}$$

Figures 2, 3, 4 represent the variation of the solutions $r,x,$ and $\theta$ via $T$, respectively, when $c_{1} = (0.002,0.02,0.2)$ with the same previous data, during the specified time $T$ intervals for each figure. Whereas Figs. 5, 6, 7 indicate the behavior of the solutions $r,x,$ and $\theta$ at $c_{2} = (0.002,0.02,0.2).$

Fig. 2

The slight effect of $c_{1}$ on the behavior of the solution $r$ when $c_{1} = (0.002,0.02,0.2)$: a at $T \in [0,1000]$, b at $T \in [0,100]$

Fig. 3

The slight effect of $c_{1}$ on the behavior of the solution $x$ when $c_{1} = (0.002,0.02,0.2)$: a at $T \in [0,1000]$, b at $T \in [0,100]$

Fig. 4

The effect of $c_{1}$ on the behavior of the solution $\theta$ when $c_{1} = (0.002,0.02,0.2)$: a at $T \in [0,1000]$, b at $T \in [0,100]$

Fig. 5

The effect $c_{2}$ on the behavior of the solution $r$ when $c_{2} = (0.002,0.02,0.2)$: a at $T \in [0,1000]$, b at $T \in [0,100]$

Fig. 6

The slight effect of $c_{2}$ on the behavior of the solution $x$ when $c_{2} = (0.002,0.02,0.2)$: a at $T \in [0,1000]$, b at $T \in [0,100]$

Fig. 7

The slight effect of $c_{2}$ on the behavior of the solution $\theta$ when $c_{2} = (0.002,0.02,0.2)$: a at $T \in [0,1000]$, b at $T \in [0,100]$

A look at Fig. 2 reveals that when $c_{1}$ increases from $0.002$ to $0.2$ with the constancy of other parameters and the number of oscillations decreases with the notable increment of the amplitudes. This means that through variation of time $T$ from $0$ to $100$, the motion of the mass $m$ is sinusoidal. On the other hand, the amplitudes of $x$ and $\theta$ during the same time interval decrease. There is decay in the variation of the amplitude to some extent; see Fig. 3 and Fig. 4. Also, in Figs. 5, 6, 7, 8, 9, 10, when $c_{2}$ and $c_{3}$ increases, the number of oscillations of $x$ and $\theta$ decreases. The time history under the variation of $\Omega_{1}$ is reported in Figs. 11, 12, 13 for the solutions $r,x,$ and $\theta$, respectively, when time intervals $T = [0:1000]$ and $T = [0:100]$. On the other side, we plot the time history for the solutions $r,x,$ and $\theta$ under the slight effect of $\Omega_{2}$ as shown in Figs. 14, 15, 16.

Fig. 8

The slight effect of $c_{3}$ on the behavior of the solution $r$ when $c_{3} = (0.001,0.01,0.1)$: a at $T \in [0,1000]$, b at $T \in [0,100]$

Fig. 9

The effect of $c_{3}$ on the behavior of the solution $x$ when $c_{3} = (0.001,0.01,0.1)$: a at $T \in [0,1000]$, b at $T \in [0,100]$

Fig. 10

The slight effect of $c_{3}$ on the behavior of the solution $\theta$ when $c_{3} = (0.001,0.01,0.1)$: a at $T \in [0,1000]$, b at $T \in [0,100]$

Fig. 11

The effect of $\Omega_{1}$ on the behavior of the solution $r$ when $\Omega_{1} = (0.65,0.9,1.65)$: a at $T \in [0,1000]$, b at $T \in [0,100]$

Fig. 12

The slight effect of $\Omega_{1}$ on the behavior of the solution $x$ when $\Omega_{1} = (0.65,0.9,1.65)$: a at $T \in [0,1000]$, b at $T \in [0,100]$

Fig. 13

The slight effect of $\Omega_{1}$ on the behavior of the solution $\theta$ when $\Omega_{1} = (0.65,0.9,1.65)$: a at $T \in [0,1000]$, b at $T \in [0,100]$

Fig. 14

The slight effect of $\Omega_{2}$ on the behavior of the solution $r$ when $\Omega_{2} = (0.2,0.8,1.2)$: a at $T \in [0,1000]$, b at $T \in [0,100]$

Fig. 15

The slight effect of $\Omega_{2}$ on the behavior of the solution $x$ when $\Omega_{2} = (0.2,0.8,1.2)$: a at $T \in [0,1000]$, (b) at $T \in [0,100]$

Fig. 16

The slight effect of $\Omega_{2}$ on the behavior of the solution $\theta$ when $\Omega_{2} = (0.2,0.8,1.2)$: a at $T \in [0,1000]$, b at $T \in [0,100]$

It is obvious from Fig. 11 that the behavior of the attained waves for $r$ varies between periodicity and decay and there is a slight effect for $x$ and $\theta$ as in Fig. 12 and Fig. 13. On the other side, we plot the time history for our solutions under the variation of $\Omega_{2}$ in Figs. 14, 15, 16. According to the calculations depicted in these figures, when $\Omega_{2}$ increases the amplitude of the waves of $x$ decreases to reach to the decay behavior. Accordingly, we conclude that the motion of the system under consideration is stable and free of chaos.

Non-linear Analysis

Our goal in this part is to show graphical representations of the analytical treatment developed in this paper for resonance situations of (28).

Frequency–Response Curves

In Fig. 17, the modulation amplitudes of the three resonant modes are plotted via the parameter of detuning $\sigma_{3}$ as a control one to highlight the influence of some parameters on the system behavior up to the third-order of non-linearity. The physical dimensionless parameters have the next values

$$\begin{gathered} c_{1} = 0.2,\,\,\,\,c_{2} = 0.2,\,\,\,\,\,c_{3} = 0.1,\,\,\,\,\,f_{1} = 0.1,\,\,\,\,\,f_{2} = 0.2,\,\,\,\,\,f_{3} = 0.3,\,\, \hfill \\ \Omega_{1} = 0.65,\,\,\,\,\Omega_{2} = 1.2,\,\,\,\,\,J = 1,\,\,\,\,\,m = 0.5kg,\,\,\,\,M^{*} = 1\,{\text{ kg}},\,\,\,\,\,h = 0.1, \hfill \\ \, \in = 0.001,\,\,\,\,\,\mu = 0.5,\,\,\,\,\,\sigma_{1} = \,\sigma_{2} = 0. \hfill \\ \end{gathered}$$

Fig. 17

Adjustment of the modified amplitudes as a function of the detuning parameter ${\upsigma }_{3}$

In the region, $- 10 < {\upsigma }_{3} < 10\,\,$ there exists one possible fixed point, in which it is stable in the range $- 0.8 < {\upsigma }_{3} \le 10$ while it loses its stability as $- 10 < {\upsigma }_{3} < - 0.8$. Also Fig. 18 describes the modulation amplitudes under the impact of $c_{2}$ when $c_{2} = 0.02$. It is self-evident that, there is only one critical fixed point in which the stable and unstable fixed point exists in the domain $4.8 < {\upsigma }_{3} < 10$ and $- 10 < {\upsigma }_{3} \le 4.8$, respectively. In Fig. 17, the detuning parameter ${\upsigma }_{3}$ takes the value $- 0.8$, while in Fig. 18 has the value of $4.8$. The variation of $c_{3}$,${ }\sigma_{1}$ and $\sigma_{2}$ on the frequency response are explored in Figs. 19, 20, 21. The range of unstable and stable fixed points is drawn with a dashed line and a solid one, respectively. At certain instances, the system exhibits a transcritical bifurcation.

Fig. 18

The modified amplitudes’ variation for the same case in Fig. 17, but when $c_{2} = 0.02.$

Fig. 19

The modified amplitudes vs the parameter of detuning ${\upsigma }_{3}$ for the same case in Fig. 17, but when $c_{3} = 0.001.$

Fig. 20

The modified amplitudes vs the parameter of detuning ${\upsigma }_{3}$ for the same case in Fig. 17, but when $\sigma_{1} = - 1.$

Fig. 21

The modified amplitudes vs the parameter of detuning ${\upsigma }_{3}$ for the same case in Fig. 17, but when $\sigma_{2} = - 0.005.$

Now, we will provide the following transformation to explore the features of the equations of the system (35) for the non-linear amplitude. These equations will be modified by intruding the detuning parameter $\sigma_{k} \,\,(k = 1,2,3)$ to examine the non-linear stability of this system. Therefore, the following convenient transformations are [35]

$$A_{k} = \left( {p_{k} + iq_{k} } \right)e^{{i{{ \sigma }}_{{\text{k}}} T_{1} }} ,$$

where $p_{k}$ and $q_{k}$ are the real and imaginary parts of $A_{k}$ respectively. We will have the following system:

$$\begin{gathered} - 2\Omega_{1} p^{\prime}_{1} + 2\Omega_{1} \sigma_{1} q_{1} - [\frac{{3 - 2\Omega_{1}^{2} }}{{\Omega_{1} (\Omega_{1} - 2)}} + \frac{{3 - 2\Omega_{1}^{2} }}{{\Omega_{1} (\Omega_{1} + 2)}} + \frac{{(\Omega_{1} - 1)^{2} }}{{\Omega_{2}^{2} - (\Omega_{1} - 1)^{2} }}] \hfill \\ + 2\,(q_{1} p_{3}^{2} - q_{1} q_{3}^{2} + 2p_{1} p_{3} q_{3} ) - c_{1} \Omega_{1} p_{1} = 0, \hfill \\ - 2\Omega_{1} q^{\prime}_{1} - 2\Omega_{1} \sigma_{1} p_{1} + [\frac{{3 - 2\Omega_{1}^{2} }}{{\Omega_{1} (\Omega_{1} - 2)}} + \frac{{3 - 2\Omega_{1}^{2} }}{{\Omega_{1} (\Omega_{1} + 2)}} + \frac{{(\Omega_{1} - 1)^{2} }}{{\Omega_{2}^{2} - (\Omega_{1} - 1)^{2} }} - 2] \hfill \\ (p_{1} p_{3}^{2} - p_{1} q_{3}^{2} - 2q_{1} p_{3} q_{3} ) - c_{1} \Omega_{1} q_{1} + \frac{1}{2}f_{1} = 0, \hfill \\ \, - 2\Omega_{2} p^{\prime}_{2} + 2\Omega_{2} \sigma_{2} q_{2} - \frac{{\Omega_{2}^{4} {\text{ J I}}}}{{(1 - \Omega_{2}^{2} )}}q_{2} - \frac{{\mu \Omega_{2}^{2} }}{{\Omega_{1}^{2} - (\Omega_{2} + 1)^{2} }} \times (2p_{2} p_{3} q_{3} + q_{2} p_{3}^{2} \hfill \\ - q_{2} q_{3}^{2} ) - c_{2} \Omega_{2} p_{2} = 0, \hfill \\ - 2\Omega_{2} q^{\prime}_{2} - 2\Omega_{2} \sigma_{2} p_{2} + \frac{{\Omega_{2}^{4} {\text{ J I}}}}{{(1 - \Omega_{2}^{2} )}}p_{2} + \frac{{\mu \Omega_{2}^{2} }}{{\Omega_{1}^{2} - \left( {\Omega_{2} + 1} \right)^{2} }}( - 2q_{2} p_{3} q_{3} + p_{2} p_{3}^{2} \hfill \\ - p_{2} q_{3}^{2} \, - c_{2} \Omega_{2} q_{2} + \frac{1}{2}f_{2} = 0, \hfill \\ - 2p^{\prime}_{3} + 2\sigma_{3} q_{3} - \frac{{3 - 2\Omega_{1}^{2} }}{{\Omega_{1} (2 + \Omega_{1} )}}(2p_{3} p_{1} q_{1} + q_{3} p_{1}^{2} - q_{3} q_{1}^{2} ) - c_{3} p_{3} - \frac{1}{{\Omega_{1}^{2} }}(q_{3} p_{3}^{2} - q_{3}^{3} + 2p_{3}^{2} q_{3} ) \hfill \\ - 4\Omega_{1}^{2} (2p_{3} p_{1} q_{1} + q_{3} p_{1}^{2} - q_{3} q_{1}^{2} ) + [\frac{{\Omega_{2}^{4} }}{{\Omega_{1}^{2} - (1 + \Omega_{2} )^{2} }} + \frac{{\Omega_{2}^{4} }}{{\Omega_{1}^{2} - (1 - \Omega_{2} )^{2} }}] \hfill \\ \times \left( {2p_{3} p_{2} q_{2} + q_{3} p_{2}^{2} - p_{3} q_{2}^{2} } \right) = 0, \hfill \\ - 2q^{\prime}_{3} - 2\sigma_{3} p_{3} + \frac{{3 - 2\Omega_{1}^{2} }}{{\Omega_{1} (2 + \Omega_{1} )}}(p_{3} p_{1}^{2} - p_{3} q_{1}^{2} - 2q_{3} p_{1} q_{1} ) - c_{3} q_{3} + \frac{1}{{\Omega_{1}^{2} }}(p_{3}^{3} - p_{3} q_{3}^{2} - 2q_{3}^{2} p_{3} ) \hfill \\ + 4\Omega_{1}^{2} \left( {p_{3} p_{1}^{2} - 2q_{3} p_{1} q_{1} - p_{3} q_{1}^{2} } \right) - [\frac{{\Omega_{2}^{4} }}{{\Omega_{1}^{2} - (1 + \Omega_{2} )^{2} }} + \frac{{\Omega_{2}^{4} }}{{\Omega_{1}^{2} - (1 - \Omega_{2} )^{2} }}] \hfill \\ \times (q_{3} q_{2}^{2} - p_{3} p_{2}^{2} - 2q_{3} p_{2} q_{2} ) - \frac{1}{2}f_{3} = 0. \hfill \\ \end{gathered}$$

(41)

The modified amplitudes were justified with the variation of time $T_{2}$ in different parametric regions and the amplitudes’ properties are graphed in the phase plane curves, as seen in Figs. 22, 23, 24, 25, 26, 27, 28, 29. In Fig. 22, the system has the same previous physical values of the parameters in Fig. 17. In Fig. 23, the same system is considered in Fig. (22), but with $c_{2} = 0.02$. In Figs. 24, 25, The projection $p_{2} q_{2}$ plane and the corresponding modified amplitudes with $c_{3} = 0.001$ and it is corresponding to the fixed point in Fig. 19 in which ${\upsigma }_{3}$ takes the values, $- 2.9, - 0.9$, respectively. Also, Figs. 26, 27, 28, 29 show the projection $p_{2} q_{2}$ plane and the corresponding modified amplitudes but in Figs. 26, 27 when ${\upsigma }_{1}$ has the value $- 1$ and these figures are corresponding to the first and the second fixed point in Fig. 20 in which ${\upsigma }_{3}$ equal $- 4.4$ and $0.5$. In Figs. 27, 28, when ${\upsigma }_{2}$ has the value $- 0.005$ and these figures are corresponding to the first and the second fixed point in Fig. 21 in which ${\upsigma }_{3}$ has the values $- 3.5, - 0.4$, respectively. These figures are clearly demonstrate that, the amplitudes diminish gradually with time and the density of the spiral cycle rapidly declines. This means that the system is stable under changing of parameters.

Fig. 22

The trajectory of the modulation equation’s projection on plane $p_{2} q_{2}$ and the adjusted amplitudes via time $T_{2}$

Fig. 23

The same system considered in Fig. 22, but with $c_{2} = 0.02$

Fig. 24

The projection $p_{2} q_{2}$ plane and the corresponding modified amplitudes with $c_{3} = 0.001$, and it is corresponding to the first fixed point in Fig. 19

Fig. 25

The projection $p_{2} q_{2}$ plane and the corresponding modified amplitudes where $c_{3} = 0.001$ corresponding to the second fixed point in Fig. 19

Fig. 26

The projection of the modulation equation path on the plane $p_{2} q_{2}$ and the adjusted amplitudes versus $T_{2}$ at $\sigma_{1} = - 1$, and it is corresponding first point in Fig. 20

Fig. 27

The projection of the equation of modulation on the phase plane $p_{2} q_{2}$ and the adjusted amplitudes versus $T_{2}$ at $\sigma_{1} = - 1$, and it is corresponding second fixed point in Fig. 20

Fig. 28

The projection of the modulation equation trajectory on the plane $p_{2} q_{2}$ and the adjusted amplitudes versus $T_{2}$ at $\sigma_{2} = - 0.005$, and it is corresponding first fixed point in Fig. 21

Fig. 29

The modulation equation’s projection on the plane $p_{2} q_{2}$ and the adjusted amplitudes via time $T_{2}$ when $\sigma_{2} = - 0.005$, and it is corresponding second fixed point in Fig. 21

Conclusion

The motion of the auto-parametric pendulum model with 3DOF consisting of a mass $M$ attached to two massless springs with linear stiffness was investigated. Lagrange's equation is used to derive the controlling equations of motion. The approximate solutions and the resonance cases obtained using MMS. Criterion of Routh–Hurwitz is used to obtain the solvability condition at the steady state. The variations of the solutions via time are graphed to have the influence of some different parameters on the behavior of the dynamical model. The obtained results of higher consistency with the results in [11]. The characteristics of the non-linear amplitudes of the system are discussed to investigate its stability. The modulation amplitudes of the resonant modes are plotted via one of the detuning parameter as a control one to examine the impact of some parameters on the behavior of system. It is remarked that at certain values of this parameter, the system produces transcritical bifurcations. The solutions of modulation equations have stable fixed points, as shown from the solutions’ projections on the plane $p_{2} q_{2}$. The achieved solutions are considered as a generalization of which are obtained in [29] for the case of rigid pendulum arm. The significance of the examined model can be seen in its applications in a variety of domains, including ship motion, transportation equipment, swaying buildings, and rotor dynamics.