Dynamical Stability of a 3-DOF Auto-Parametric Vibrating System

Abstract

Purpose

This article concentrates on the oscillating movement of an auto-parametric dynamical system comprising of a damped Duffing oscillator and an associated simple pendulum in addition to a rigid body as main and secondary systems, respectively.

Methods

According to the system generalized coordinates, the controlling equations of motion are derived utilizing Lagrange's approach. These equations are solved applying the perturbation methodology of multiple scales up to higher orders of approximation to achieve further precise unique outcomes. The fourth-order Runge–Kutta algorithm is employed to obtain numerical outcomes of the governing system.

Results

The comparison between both solutions demonstrates their high level of consistency and highlights the great accuracy of the adopted analytical strategy. Despite the conventional nature of the applied methodology, the obtained results for the studied dynamical system are considered new.

Conclusions

In light of the solvability criteria, all resonance scenarios are classified, in which two of the fundamental exterior resonances are examined simultaneously with one of the interior resonances. Therefore, the modulation equations are achieved. The conditions of Routh–Hurwitz are employed to inspect the stability/instability regions and to analyze them in accordance with the solutions in the steady-state case. For various factors of the examined structure, the temporary history solutions, the curves of resonance in terms of the adjusted amplitudes and phases, and the stability zones are graphically presented and discussed.

Applications

The results of the current study will be of interest to wide range experts in the fields of mechanical and aerospace technology, as well as those working to reduce rotors dynamical vibrations and attenuate vibration caused by swinging structures.

Introduction

Several structures used in mechanical engineering, naval, and civil applications are highlighted with different mechanisms to lessen the dynamic response component brought about by either deterministic or random external excitations. Some vertical structures such as masts, chimneys, towers, and bridges are subject to powerful excitation as a result of winds and earthquakes influences, and other general-purpose systems that have been heavily stimulated. Numerous renowned monographs, e.g. [1,2,3] and others, devoted substantial treatises to these subjects at the level of applied and rational dynamics.

Over the past few periods, a large number of publications addressing different types of dynamic dampers and associated subjects drew the attention of numerous researchers e.g. [4,5,6,7,8,9]. In [4], the author investigated the vibrational motion of an absorber with a rotating base to reduce the vertical excitations, from which the fundamental frequency has been derived. A correlation between the absorber rotational speed and its frequency of vertical swings was established. The absorber performance such as mass, length, and frequency was examined. In [5], a connected longitudinal absorber of a nonlinear spring pendulum (SP) was utilized to control and stabilize the ship roll movement in the presence of parametric and multi-external excitations. In light of the investigated resonance scenario, the equations of frequency response were employed to examine the solutions at the steady-state case. The requirements of stability of the solutions were determined. The planar movement of a two degrees-of-freedom (2DOF) auto-parametric model, consisting of a movable attached main mass through a damped spring coupled to a simple pendulum of a rigid arm as a secondary part, was discussed in [6]. In [7], the authors replaced the pendulum rigid arm with a spring pendulum with linear stiffness to constitute a 3DOF model and generalize the work in [6]. Recently, the stability of 2DOF auto-parametric systems has been analyzed in [8] and [9] for two dynamical models. The first one is the vertical movement of a spinning cylinder on a connected circular surface with a nonlinear damped spring, while the horizontal frictional motion of this surface was considered in [9]. The analytic estimated solutions of these models up to desired orders of calculation were obtained using the approach of multiple scales [10], while the numerical solutions of the system in [9] were attained by applying the Runge–Kutta approach of fourth order [11].

Numerous works, such as [12,13,14,15,16,17], investigated the primary and secondary resonances for the problem of Duffing-pendulum systems, either analytically or numerically. In [12], the harmonic balance approach was used to examine the behavior of a damper, spring, and mass, in addition to an exciting hinged parametric pendulum. The oscillating zones of the pendulum were determined, and they resemble those described by Mathieu's equation. Various parameters of the response equation were analyzed, and the properties of the system response were clarified. A study of the harmonic solutions stabilities was conducted. The accuracy of the gained approximation was checked in light of the numerical outcomes. The dynamic reaction of the studied scheme was presented in [13].

The motion of an auto-parametric system consisting of a nonlinear oscillator with an associated damped elastic pendulum around the region of major resonance was examined in [14]. On the basis of the approach of harmonic balance, the solutions were obtained. Numerical studies and practical tests were carried out on a certain constructed experimental rig to confirm the accuracy of the analytical results. The effects of all crucial parameters on the localization of the instability area and the dynamics of the system have been analyzed. In [15], the author investigated the oscillating movement of a connected nonlinear Duffing oscillator to a nonlinear damper. The influence of excited harmonic force on the mechanism of an auto-parametric pendulum was investigated [16] and [17]. The authors improved the controllable dynamical motion by inserting a nonlinear spring and a semi-active magnetic damper into the studied model. Near the zones of primary parametric resonance, numerical simulations are used to determine the influence of stiffness or nonlinear damping on the motion.

Harvesting energy (HE) has become increasingly important for many technologies that use mechanical vibration. The oscillations can be converted into electrical energy via the proper machinery, which can then be used as a power source rather than traditional ones. In [18], the authors discussed how technologies can reduce harmful vibrations while still capturing energy, where the idea of an energy harvester is quite related to the idea of a vibration absorber. In [19], electromagnetic and piezoelectric devices are connected with a vibrating system to yield two HE models. These pieces are coupled to a 2DOF nonlinear damped pendulum whose pivot point moves on a circular trajectory. It has been examined how the EH outputs are affected by the coefficients of damping, excitation amplitudes, and different values of the system frequencies. The curve frequency responses were drawn to examine the stability and instability zones. Recently, a connected 3DOF oscillating system with one of the EH devices has been investigated [20]. This system is composed of a nonlinear Duffing oscillator and a damping pendulum. The plots of phase portraits and Poincaré maps demonstrated the stable and unstable behavior of the considered system. The current time histories and output power were displayed according to the various amounts of the excitation amplitudes, coefficients of damping, and load resistance.

The study of the movement of the pendulum suspension point, whether on a certain curve or even if the point is fixed, has captured the attention of various scientists [21,22,23,24,25,26,27,28]. The nonlinear motion of a vibrating pendulum was investigated in [21] under the impact of exterior harmonic force and moment in the spring path and at the suspension point, respectively. At a certain order of the obtained approximate solutions, all relevant resonance scenarios were classified. Two analytic approaches were employed [22] to attain the solutions to this problem when the pendulum is damped, and the resistance force was taken into consideration. A comparison of analytical and numerical outcomes revealed that both approaches yielded satisfactory results for non-resonant oscillation. In [23] and [24], the fourth-order approach of Runge–Kutta is used to explore the numerical solutions of a vibrating pendulum connected to a rigid body near the positions of equilibrium, whereas the approaches of small and large parameters are employed in [25] and [26], to get the analytical solutions of a linked rigid body with a pendulum.

The multiple scales technique was employed to achieve the estimated solutions of a pendulum in [27] when its pivot point is restricted to vertical swinging. These solutions are compared with the solutions of previous works when an external force is considered to act on the motion. Works [28,29,30,31,32,33,34] restricted the pendulum pivot point to be in elliptic or Lissajous routes. In [28], the elliptic path was considered for the motion of this point with constant angular velocity, when the pendulum was acted upon by an excitation harmonic force and moment. The obtained results were generalized in [29] and [30] when a rigid body is attached to linear and nonlinear spring, respectively. The approximate solutions were obtained using the method of multiple scales and evaluated through the numerical ones to expose their uniformity. The resulting resonance cases were extracted, and two of them were examined simultaneously. In [31], the authors considered the motion of the pendulum suspension point to be on a Lissajous curve. The obtained solutions were generalized in [32] for the case of a spring rigid body pendulum. In [32], a nonlinear stiffness of the spring was considered, and the stability zones were examined according to the nonlinear stability of Routh–Hurwitz. A combination of the homotopy and multiple scales methodologies is presented in [35] to yield He's approach of multiple scales, in which it was examined through the solution of a variety nonlinear equations, and for a forced nonlinear oscillators.

In this paper, a 3DOF auto-parametric vibrating dynamical system is examined as a novel model. It consists of a damped Duffing oscillator as the main part and an attached rigid body to a simple pendulum as a secondary part. The controlling system of movement is achieved, employing the second type of equations of Lagrange and analyzed analytically utilizing the multiple scales method. The analytical obtained outcomes are matched with the numerical ones, which are obtained by applying the Runge–Kutta approach, to explore the great agreement between them and the precision of the attained estimated solutions. The requirements of solutions are achieved in light of the emerging resonance cases. Three cases are investigated simultaneously; two of them are from the fundamental external resonances and the third is from the internal resonances. The criteria of Routh–Hurwitz are applied to the modulation equations of the examined system to evaluate the stability/instability regions of the response frequency curves at the steady-state solutions. Moreover, the stability analysis of the system under consideration is examined using the nonlinear stability approach of Routh–Hurwitz according to the characteristics of the nonlinear amplitudes of the modulation equations. The outcomes of this study may be used to control the harmful vibrations in moving structures and to decrease the rotor dynamics vibration.

Description of the Dynamical Model

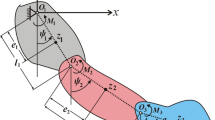
In the current section, we present a comprehensive explanation of the investigated auto-parametric dynamical system. It consists of a connected linear spring of stiffness $k$ with a movable mass $m_{1}$ in a vertical direction as the main part. Whereas the second part is a rigid body pendulum of mass $m_{2}$ with arm length $l$, which is attached to the mass $m_{1}$ at the origin point $o$ of the Cartesian plane $oxy$, see Fig. 1. Let $C$ signify the center of mass of the body, $U_{A}$ symbolize the body inertia moment around a perpendicular axis across the point $A$, $Y$ be the spring elongation, $\varphi$ be the angle between the arm $oA$ and the downward vertical axis $oy$, and $\gamma$ be the angle between the vertical and the line passes through the rigid body eccentricity $p = AC$. It is claimed that the system movement is influenced by an excitation external harmonic force $F(t) = F_{1} \cos \Omega_{1} t$, besides a rotational moment $M(t) = M_{o} \cos \Omega_{o} t$ at $o$. Here, $M_{0} ,F_{1}$ and $\Omega_{o} ,\Omega_{1}$ are the amplitudes and frequencies of $M(t),F(t)$.

Fig. 1

Portrays the model dynamical structure

Consequently, the kinetic and potential energies $T$ and $V$ of the system are

$$\begin{aligned} T = \frac{1}{2}(m_{1} + m_{2} )Y^{{\prime}{2}} + \frac{1}{2}m_{2} [l^{2} \varphi^{{\prime}{2}} + p^{2} \gamma^{{\prime}{2}} + 2lp\varphi^{\prime}\gamma^{\prime}\cos (\gamma - \varphi ) \hfill \\ - 2Y^{\prime}(l\varphi^{\prime}\sin \varphi + p\gamma^{\prime}\sin \gamma )] + \frac{1}{2}U_{A} \gamma^{{\prime}{2}} , \hfill \\ V = \frac{1}{2}k(Y + Y_{st} )^{2} - m_{1} gY - m_{2} g(Y + l\,\cos \varphi + p\,\cos \gamma ), \hfill \\ \end{aligned}$$

(1)

where $Y_{st}$ is the spring static elongations, and $g$ is the acceleration of gravitational, while the derivatives, in relation to time $t$, are expressed by the prime.

Referring to Eqs. (1), the Lagrangian $L = T - V$ of the system can be calculated, and then the regulating system of motion can be originated using the subsequent Lagrange approach [33]

$$\begin{aligned} \frac{d}{{{\text{d}}t}}\left( {\frac{\partial L}{{\partial Y^{\prime}}}} \right) - \frac{\partial L}{{\partial Y}} = Q_{Y} , \hfill \\ \frac{d}{{{\text{d}}t}}\left( {\frac{\partial L}{{\partial \varphi^{\prime}}}} \right) - \frac{\partial L}{{\partial \varphi }} = Q_{\varphi } , \hfill \\ \frac{d}{{{\text{d}}t}}\left( {\frac{\partial L}{{\partial \gamma^{\prime}}}} \right) - \frac{\partial L}{{\partial \gamma }} = Q_{\gamma } . \hfill \\ \end{aligned}$$

(2)

Here, $(Y,\varphi ,\gamma )$, $(Y^{\prime},\varphi^{\prime},\gamma^{\prime})$, and $(Q_{Y} ,Q_{\varphi } ,Q_{\gamma } )$ are the system generalized coordinates, velocities, and forces, correspondingly. Based on the system configuration and the applied force and moment, one can write $Q_{Y} ,Q_{\varphi } ,$ and $Q_{\gamma }$ as follows

$$\begin{aligned} Q_{Y} &= F_{1} \cos (\Omega_{1} t) - C_{1} Y^{\prime}, \hfill \\ Q_{\varphi } &= M_{0} \cos (\Omega_{0} t) - C_{2} \varphi^{\prime}, \hfill \\ Q_{\gamma } &= - C_{3} \gamma^{\prime}. \hfill \\ \end{aligned}$$

(3)

To obtain the systems governing in its dimensionless form, let us consider the below dimensionless parameters

$$\begin{aligned}& \tau = \omega_{1} t,\,\,\,\,y = \frac{Y}{l},\,\,\,\,y_{st} = \frac{{Y_{st} }}{l},\,\,\,\,\beta = \frac{{m_{2} }}{{(m_{1} + m_{2} )}},\,\,\,\,h = \frac{p}{l},\,\,\,\,\omega_{1} = \sqrt {\frac{k}{{m_{1} + m_{2} }}} ,\,\,\,\,\omega_{2} = \sqrt{\frac{g}{l}} , \hfill \\ & \omega_{3} = \sqrt {\frac{{m_{2} pg}}{{U_{A} }}} ,\,\,\,\,w_{1} = \frac{{\omega_{2} }}{{\omega_{1} }},\,\,\,\,w_{2} = \frac{{\omega_{2} }}{{\omega_{3} }},\,\,\,\,c_{1} \, = \frac{{C_{1} }}{{(m_{1} + m_{2} )\omega_{1} }},\,\,\,\,c_{2} = \frac{{C_{2} }}{{m_{2} l^{2} \omega_{1} }},\,\,\,\,c_{3} = \frac{{C_{3} }}{{m_{2} pl\omega_{1} }}, \hfill \\& f_{1} = \frac{{F_{1} }}{{(m_{1} + m_{2} )l\omega_{1}^{2} }},\,\,\,\,m_{0} = \frac{{M_{0} }}{{m_{2} l^{2} \omega_{1}^{2} }},\,\,\,\,p_{1} = \frac{{\Omega_{1} }}{{\omega_{1} }},\,\,\,\,p_{0} = \frac{{\Omega_{0} }}{{\omega_{1} }}. \hfill \\ \end{aligned}$$

(4)

Substituting Eqs. of (1), (3), and (4) into (2) yields

$$\begin{aligned}& \ddot{y} - \beta (h\ddot{\gamma }\sin \gamma + h\dot{\gamma }^{2} \cos \gamma + \ddot{\varphi }\sin \varphi ) + \dot{\varphi }^{2} \cos \varphi ) - w_{1}^{2} + y + y_{st} = f_{1} \cos (p_{1} \tau ) - c_{1} \dot{y}, \hfill \\& \ddot{\varphi } + w_{1}^{2} \sin \varphi - h\dot{\gamma }^{2} \sin (\gamma - \varphi ) - \ddot{y}\sin \varphi + h\ddot{\gamma }\cos (\gamma - \varphi ) = m_{0} \cos (p_{0} \tau ) - c_{2} \dot{\varphi }, \hfill \\ & (h + w_{2}^{2} )\ddot{\gamma } + w_{1}^{2} \sin \gamma + \dot{\varphi }^{2} \sin (\gamma - \varphi ) - \ddot{y}\sin \gamma + \ddot{\varphi }\cos (\gamma - \varphi ) = - c_{3} \dot{\gamma }. \hfill \\ \end{aligned}$$

(5)

The dimensionless governing system (5) consists of three second-order nonlinear differential equations. The dots here denote the derivatives regarding $\tau$.

Formulation of the Analytic Solutions

In the current section, we employ the multiple scales approach to achieve the analytic estimated solutions of the system (5) up to higher approximation, classify the various cases of resonance, and deduce the equations of modulation in view of the solvability conditions. Therefore, we examine the system vibrations near the region of static equilibrium [34]. To achieve this purpose, we estimate the trigonometric $\sin \varphi ,\,\sin \gamma ,\,\cos \varphi ,$ and $\cos \gamma$ up to the third-order approximations using Taylor series.

The amplitude of force, coefficients of damping, moment, and others can be exemplified in regard with a tiny parameter $0 < \varepsilon < < 1$ as below

$$f_{1} = \varepsilon^{3} \tilde{f}_{1} ,\,\,\,\,c_{j} = \varepsilon^{2} \tilde{c}_{j} \,\,\,\,(j = 1,2,3),\,\,\,\,m_{0} = \varepsilon^{3} \tilde{m}_{0} ,\,\,\,\,h = \varepsilon^{2} \tilde{h}.$$

(6)

As before, let us consider new functions $\tilde{y},\tilde{\varphi },$ and $\tilde{\gamma }$ which can be used to define the functions $y,\varphi ,$ and $\gamma$ in terms of $\varepsilon$, as follows

$$y = \varepsilon \tilde{y},\,\,\,\,\,\,\,\,\,\varphi = \varepsilon \,\tilde{\varphi },\,\,\,\,\,\,\,\,\,\gamma = \varepsilon \,\tilde{\gamma }.$$

(7)

Based on the used method, one looks for the solutions of $\tilde{y},\tilde{\varphi },$ and $\tilde{\gamma }$ as follows

$$\begin{aligned} \tilde{y}(\tau ,\varepsilon ) = \sum\limits_{k = 1}^{3} {\varepsilon^{k - 1} \tilde{y}_{k} (\tau_{0} ,} \tau_{1} ,\tau_{2} ) + O(\varepsilon^{3} ), \hfill \\ \tilde{\varphi }(\tau ,\varepsilon ) = \sum\limits_{k = 1}^{3} {\varepsilon^{k - 1} \tilde{\varphi }_{k} (\tau_{0} ,} \tau_{1} ,\tau_{2} ) + O(\varepsilon^{3} ), \hfill \\ \tilde{\gamma }(\tau ,\varepsilon ) = \sum\limits_{k = 1}^{3} {\varepsilon^{k - 1} \tilde{\gamma }_{k} (\tau_{0} ,} \tau_{1} ,\tau_{2} ) + O(\varepsilon^{3} ), \hfill \\ \end{aligned}$$

(8)

wherever $\tau_{n} = \varepsilon^{n} \tau \,\,\,(n = 0,1,2)$ are new various time scales on $\tau$, where $\tau_{0}$ and $\tau_{k} \,\,(k = 1,2)$ are referred to as the fast and slow time scales, correspondingly.

From the perspective of the suggested solutions (8), we must convert the time derivatives with respect to $\tau$ into other ones regarding the scales $\tau_{n} = \varepsilon^{n} \tau$. Consequently, we consider the subsequent differential operators [10]

$$\begin{aligned} \frac{d}{{{\text{d}}\tau }} &= D_{0} + \varepsilon D_{1} + \varepsilon^{2} D_{2} , \hfill \\ \frac{{d^{2} }}{{{\text{d}}\tau^{2} }} &= D_{0}^{2} + 2\varepsilon D_{0} D_{1} + \varepsilon^{2} (D_{1}^{2} + 2D_{0} D_{2} );\,\,\,\,\,\,\,\,D_{n} = \frac{\partial }{{\partial \tau_{n} }}\,\,\,\,(n = 0,1,2). \hfill \\ \end{aligned}$$

(9)

The substitution of (6)–(9) into (5) yields three partial differential equations (PDE) regarding to $\varepsilon$. Comparing the coefficients of various powers of $\varepsilon$ in each side to acquire the next sets of PDEs, one gets.

Order of $\varepsilon$

$$\begin{aligned} D_{0}^{2} \tilde{y}_{1} + \tilde{y}_{1} &= 0, \hfill \\ D_{0}^{2} \tilde{\varphi }_{1} + w_{1}^{2} \tilde{\varphi }_{1}& = 0, \hfill \\ D_{0}^{2} \tilde{\gamma }_{1} + \frac{{w_{1}^{2} }}{{w_{2}^{2} }}\tilde{\gamma }_{1}& = - \frac{1}{{w_{2}^{2} }}D_{0}^{2} \tilde{\varphi }_{1} , \hfill \\ \end{aligned}$$

(10)

Order of $\varepsilon^{2}$

$$\begin{aligned}& D_{0}^{2} \tilde{y}_{2} + \tilde{y}_{2} = \beta (D_{0} \tilde{\varphi }_{1} )^{2} - 2D_{0} D_{1} \tilde{y}_{1} + \beta \tilde{\varphi }_{1} D_{0}^{2} \tilde{\varphi }_{1} , \hfill \\& D_{0}^{2} \tilde{\varphi }_{2} + w_{1}^{2} \tilde{\varphi }_{2} = \tilde{\varphi }_{1} D_{0}^{2} \tilde{y}_{1} - 2D_{0} D_{1} \tilde{\varphi }_{1} , \hfill \\ &D_{0}^{2} \tilde{\gamma }_{2} + \frac{{w_{1}^{2} }}{{w_{2}^{2} }}\tilde{\gamma }_{2} = \frac{1}{{w_{2}^{2} }}(\tilde{\gamma }_{1} D_{0}^{2} \tilde{y}_{1} - 2D_{0} D_{1} \tilde{\varphi }_{1} - D_{0}^{2} \tilde{\varphi }_{2} ) - 2D_{0} D_{1} \tilde{\gamma }_{1} , \hfill \\ \end{aligned}$$

(11)

Order of $\varepsilon^{3}$

$$\begin{aligned}& D_{0}^{2} \tilde{y}_{3} + \tilde{y}_{3} = \tilde{f}_{1} \cos (p_{1} \tau_{0} ) - D_{1}^{2} \tilde{y}_{1} - \tilde{c}_{1} D_{0} \tilde{y}_{1} + 2\beta D_{0} \tilde{\varphi }_{1} (D_{1} \tilde{\varphi }_{1} + D_{0} \tilde{\varphi }_{2} )\, - 2(D_{0} D_{2} \tilde{y}_{1} \hfill \\ & \,\,\,\,\,\,\,\,\, + D_{0} D_{1} \tilde{y}_{2} ) + \beta (2\tilde{\varphi }_{1} D_{0} D_{1} \tilde{\varphi }_{1} + \tilde{\varphi }_{1} D_{0}^{2} \tilde{\varphi }_{2} + \tilde{\varphi }_{2} D_{0}^{2} \tilde{\varphi }_{1} ), \hfill \\ & D_{0}^{2} \tilde{\varphi }_{3} + w_{1}^{2} \tilde{\varphi }_{3} = \tilde{m}_{0} \cos (p_{0} \tau_{0} ) + \frac{{w_{1}^{2} }}{6}\tilde{\varphi }_{1}^{3} - \tilde{c}_{2} D_{0} \tilde{\varphi }_{1} - D_{1}^{2} \tilde{\varphi }_{1} + \tilde{\varphi }_{2} D_{0}^{2} \tilde{y}_{1} \, - 2(D_{0} D_{2} \tilde{\varphi }_{1} \hfill \\ &\,\,\,\,\,\,\,\,\,\,\,\,\, - \tilde{\varphi }_{1} D_{0} D_{1} \tilde{y}_{1} + D_{0} D_{1} \tilde{\varphi }_{2} ) + \tilde{\varphi }_{1} D_{0}^{2} \tilde{y}_{2} - \tilde{h}D_{0}^{2} \tilde{\gamma }_{1} , \hfill \\ & w_{2}^{2} D_{0}^{2} \tilde{\gamma }_{3} + w_{1}^{2} \tilde{\gamma }_{3} = \frac{{w_{1}^{2} }}{6}\tilde{\gamma }_{1}^{3} - w_{2}^{2} (D_{1}^{2} \tilde{\gamma }_{1} + 2D_{0} D_{2} \tilde{\gamma }_{1} + 2D_{0} D_{1} \tilde{\gamma }_{2} ) - D_{1}^{2} \tilde{\varphi }_{1} \, - \tilde{c}_{3} D_{0} \tilde{\gamma }_{1} \hfill \\& \,\,\,\,\,\,\,\,\,\,\,\,\, - \tilde{\gamma }_{1} [(D_{0} \tilde{\varphi }_{1} )^{2} - 2D_{0} D_{1} \tilde{y}_{1} - D_{0}^{2} \tilde{y}_{2} + \tilde{\varphi }_{1} D_{0}^{2} \tilde{\varphi }_{1} ] + \frac{1}{2}D_{0}^{2} \tilde{\varphi }_{1} (\tilde{\gamma }_{1}^{2} + \tilde{\varphi }_{1}^{2} ) \hfill \\ & \,\,\,\,\,\,\,\,\,\,\,\,\, + \tilde{\varphi }_{1} (D_{0} \tilde{\varphi }_{1} )^{2} - 2(D_{0} D_{2} \tilde{\varphi }_{1} + D_{0} D_{1} \tilde{\varphi }_{2} ) + \tilde{\gamma }_{2} D_{0}^{2} \tilde{y}_{1} - \tilde{h}D_{0}^{2} \tilde{\gamma }_{1} - D_{0}^{2} \tilde{\varphi }_{3} . \hfill \\ \end{aligned}$$

(12)

The nine PDE (10)–(12) can be solved consecutively. Considering this, the solutions of the system (10) will be

$$\begin{aligned} \tilde{y}_{1}& = B_{1} \,e^{{i\tau_{0} }} + \overline{B}_{1} \,e^{{ - i\tau_{0} }} , \hfill \\ \tilde{\varphi }_{1} &= B_{2} \,e^{{iw_{1} \tau_{0} }} + \overline{B}_{2} \,e^{{ - iw_{1} \tau_{0} }} , \hfill \\ \tilde{\gamma }_{1}& = B_{3} \,e^{{i\frac{{w_{1} }}{{w_{2} }}\tau_{0} }} + \overline{B}_{3} \,e^{{ - i\frac{{w_{1} }}{{w_{2} }}\tau_{0} }}\quad + \frac{1}{{(1 - w_{2}^{2} )}}(B_{2} \,e^{{iw_{1} \tau_{0} }} + \overline{B}_{2} \,e^{{ - iw_{1} \tau_{0} }} );\,\,\,\,\,\,\,\,\,\,\,\,\,\,i = \sqrt { - 1} \,. \hfill \\ \end{aligned}$$

(13)

Here, $B_{j} \,\,\,(j = 1,2,3)$ denote the unknown complex functions of $\tau_{k} \,\,(k = 1,2)$ and $\overline{B}_{j}$ refer to their complex conjugates.

Substituting the first-order solutions (13) into the second sets of PDE (11), and then removing the produced secular terms, one obtains:

$$D_{1} B_{j} = 0\,\,\,\,\,\,(j = 1,2,3).$$

(14)

Therefore, the solutions of second-order become

$$\begin{aligned} \tilde{y}_{2} & = - \frac{{2\beta w_{1}^{2} B_{2}^{2} }}{{(1 - 4\,w_{1}^{2} )}}e^{{2iw_{1} \tau_{0} }} + c.c., \hfill \\ \tilde{\varphi }_{2} &= \frac{{B_{1} B_{2} }}{{1 + 2\,w_{1} }}\,e^{{i(1 + w_{1} )\tau_{0} }} + \frac{{B_{1} \overline{B}_{2} }}{{1 - 2\,w_{1} }}e^{{i(1 - w_{1} )\tau_{0} }} + c.c., \hfill \\ \tilde{\gamma }_{2} &= \frac{{B_{1} B_{2} }}{{(1 + 2\,w_{1} )(1 - w_{2}^{2} )}}e^{{i(1 + w_{1} )\tau_{0} }} + \frac{{B_{1} \overline{B}_{2} }}{{(1 - 2\,w_{1} )(1 - w_{2}^{2} )}}e^{{i(1 - w_{1} )\tau_{0} }} \hfill \\ \,\,\,\,\,\,\,\quad + \frac{{B_{1} B_{3} }}{{w_{2} (2w_{1} + w_{2} )}}e^{{i(1 + \frac{{w_{1} }}{{w_{2} }})\tau_{0} }} - \frac{{B_{1} \overline{B}_{3} }}{{w_{2} (2w_{1} - w_{2} )}}e^{{i(1 - \frac{{w_{1} }}{{w_{2} }})\tau_{0} }} + c.c. \hfill \\ \end{aligned}$$

(15)

Here, the abbreviation $c.c.$ refers for the complex conjugate of the previous terms.

To satisfy the conditions for solvability corresponding to the approximation of third-order, one must substitute (13)–(15) into the last PDE (12) and eliminate terms that generate the secular ones. Then, we have

$$\begin{aligned}& 2iD_{2} B_{1} + \left( {\frac{{2\beta B_{2} \overline{B}_{2} }}{{1 - 4w_{1}^{2} }} + i\tilde{c}_{1} } \right)B_{1} = 0, \hfill \\ &2iw_{1} D_{2} B_{2} + i\tilde{c}_{2} w_{1} B_{2} + \frac{{B_{2} }}{{2(1 - 2w_{1} )(1 + 2w_{1} )(1 - w_{2}^{2} )}}\{ 2\tilde{h}w_{1}^{2} (4w_{1}^{2} - 1) - (w_{2}^{2} - 1)\{ 4B_{1} \overline{B}_{1} \hfill \\ &\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + w_{1}^{2} [4(1 - 4\beta )w_{1}^{2} - 1]B_{2} \overline{B}_{2} \} \} = 0, \hfill \\ & 2iw_{1} w_{2} D_{2} B_{3} + \frac{{iw_{1} }}{{w_{2} }}\tilde{c}_{3} B_{3} - \frac{{B_{3} }}{{2(4w_{1}^{2} - w_{2}^{2} )(w_{2}^{2} - 1)^{2} }}\{ 2\tilde{h}w_{1}^{2} (4w_{1}^{2} - w_{2}^{2} )(w_{2}^{2} - 1) \hfill \\& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + 4(w_{2}^{2} - 1)^{2} B_{1} \overline{B}_{1} + w(4w_{1}^{2} - w_{2}^{2} )[2(2w_{2}^{2} - 1)B_{2} \overline{B}_{2} + (w_{2}^{2} - 1)^{2} B_{3} \overline{B}{}_{3}]\} = 0. \hfill \\ \end{aligned}$$

(16)

According to the above conditions, we may write the third-order solutions as follows

$$\begin{aligned} & \tilde{y}_{3} = \frac{{\tilde{f}_{1} }}{{2(1 - p_{1}^{2} )}}e^{{ip_{1} \tau_{0} }} + \frac{{\beta B_{1} }}{{4w_{1} }}\left\{ {\frac{{(1 + 2w_{1} )}}{{(1 + w_{1} )}}B_{2}^{2} \,e^{{i(1 + 2w_{1} )\tau_{0} }} - \frac{{(1 - 2w_{1} )}}{{(1 - w_{1} )}}\overline{B}_{2}^{2} \,e^{{i(1 - 2w_{1} )\tau_{0} }} } \right\} + c.c, \hfill \\& \tilde{\varphi }_{3} = \frac{{\tilde{m}_{0} }}{{2(w_{1}^{2} - p_{0}^{2} )}}e^{{ip_{0} \tau_{0} }} - \frac{{[1 - 4(1 - 12\beta )w_{1}^{2} ]}}{{48(1 - 4w_{1}^{2} )}}B_{2}^{3} \,e^{{3iw_{1} \tau_{0} }} - \frac{{\tilde{h}}}{{1 - w_{2}^{2} }}B_{3} \,e^{{i\frac{{w_{1} }}{{w_{2} }}\tau_{0} }} \hfill \\ &\,\,\,\,\,\,\,\quad + \frac{{B_{1}^{2} }}{4}\left\{ {\frac{{B_{2} }}{{(1 + w_{1} )(1 + 2w_{1} )}}e^{{i(2 + w_{1} )\tau_{0} }} + \frac{{\overline{B}_{2} }}{{(1 - w_{1} )(1 - 2w_{1} )}}e^{{i(2 - w_{1} )\tau_{0} }} } \right\} + c.c, \hfill \\ &\tilde{\gamma }_{3} = \frac{{\tilde{m}_{0} p_{0}^{2} }}{{2w_{2}^{2} (w_{1}^{2} - p_{0}^{2} )\left( {\frac{{w_{1}^{2} }}{{w_{2}^{2} }} - p_{0}^{2} } \right)}}e^{{ip_{0} \tau_{0} }} + \frac{{B_{1}^{2} B_{2} }}{{4(1 + w_{1} )(1 + 2w_{1} )(1 - w_{2}^{2} )}}e^{{i(2 + w_{1} )\tau_{0} }} \hfill \\& \,\,\,\,\,\,\quad + q_{1} B_{2}^{3} e^{{3iw_{1} \tau_{0} }} + q_{2} B_{2}^{2} B_{3} \,e^{{i\left( {\frac{{w_{1} }}{{w_{2} }} + 2w_{1} } \right)\tau_{0} }} - \frac{{w_{2}^{2} \overline{B}_{2} B_{3}^{2} }}{{2(3 - w_{2} )(1 + w_{2} )(1 - w_{2} )^{2} }}e^{{i\left( {\frac{{2w_{1} }}{{w_{2} }} - w_{1} } \right)\tau_{0} }} \hfill \\ & \,\,\,\,\,\,\quad - \frac{{w_{2}^{2} B_{2} B_{3}^{2} }}{{2(3 + w_{2} )(1 - w_{2} )(1 + w_{2} )^{2} }}e^{{i\left( {\frac{{2w_{1} }}{{w_{2} }} + w_{1} } \right)\tau_{0} }} + (q_{3} + q_{4} - \frac{{i\tilde{c}_{3} }}{{w_{1} (1 - w_{2}^{2} )^{2} }})B_{2} e^{{iw_{1} \tau_{0} }} \hfill \\ &\,\,\,\,\,\,\quad + \frac{{B_{1}^{2} B_{3} }}{{4w_{2}^{2} (w_{1} + w_{2} )(2w_{1} + w_{2} )}}e^{{i\left( {\frac{{w_{1} }}{{w_{2} }} + 2} \right)\tau_{0} }} + \frac{{B_{1}^{2} \overline{B}_{2} }}{{4(1 - w_{1} )(1 - 2w_{1} )(1 - w_{2}^{2} )}}e^{{i(2 - w_{1} )\tau_{0} }} \hfill \\ &\,\,\,\,\,\, \quad+ q_{5} B_{2}^{2} \overline{B}_{3} e^{{i\left( {2w_{1} - \frac{{w_{1} }}{{w_{2} }}} \right)\tau_{0} }} + \frac{{B_{1}^{2} \overline{B}_{3} }}{{4w_{2}^{2} (w_{1} - w_{2} )(2w_{1} - w_{2} )}}e^{{i(\left( {2 - \frac{{w_{1} }}{{w_{2} }}} \right))\tau_{0} }} - \frac{{B_{3}^{3} }}{48}e^{{3i\frac{{w_{1} }}{{w_{2} }}\tau_{0} }} + c.c, \hfill \\ \end{aligned}$$

(17)

where $q_{s} \,\,(s = 1,2, \ldots ,5)$ are provided in Appendix (I).

The functions $B_{j} \,\,\,(j = 1,2,3)$ can be calculated in accordance with the previous restrictions (14) and (16), besides the initial conditions

$$y(0) = y_{0} ,\,\,\,\,\,\,\varphi (0) = \varphi_{0} ,\,\,\,\,\,\,\gamma (0) = \gamma_{0} ,\,\,\,\,\,\,\dot{y}(0) = 0,\,\,\,\,\,\,\,\dot{\varphi }(0) = 0,\,\,\,\,\,\,\,\,\,\,\dot{\gamma }(0) = 0.$$

With the help of the assumptions (7), the suggested series (8), and the achieved approximate solutions (13), (15), and (17), we may simply obtain the appropriate approximate expressions of $y,\varphi ,$ and $\gamma$ up to the third-order of approximation.

Resonance’s Classifications and Modulation Equations

In the current section, numerous resonance scenarios will be classified using the achieved approximate solutions, which are considered acceptable in so much as the denominators are not equal to nothing [36].

Resonance cases become more noticeable when these dominators approach zero. Therefore, these scenarios can be classified into: the primary exterior resonance case which is fulfilled at $p_{1} = 1,$ $p_{0} = w_{1} ,$ $p_{0} = {{w_{1} } \mathord{\left/ {\vphantom {{w_{1} } {w_{2} }}} \right. \kern-\nulldelimiterspace} {w_{2} }}$; the case of internal resonance which is discovered at $w_{1} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2},$ $w_{2} = 1,$${{w_{1} } \mathord{\left/ {\vphantom {{w_{1} } {w_{2} }}} \right. \kern-\nulldelimiterspace} {w_{2} }} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2},$$w_{1} = 1,$ $\,w_{2} = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3},$$w_{2} = 3,$$w_{2} = - 3,$${{w_{1} } \mathord{\left/ {\vphantom {{w_{1} } {w_{2} }}} \right. \kern-\nulldelimiterspace} {w_{2} }} = 1,$ $w_{1} = 0,$${{w_{1} } \mathord{\left/ {\vphantom {{w_{1} } {w_{2} }}} \right. \kern-\nulldelimiterspace} {w_{2} }} = 0$; the case of combined resonance which is seen at ${{w_{1} } \mathord{\left/ {\vphantom {{w_{1} } {w_{2} }}} \right. \kern-\nulldelimiterspace} {w_{2} }} = 2 + w_{1} ,$ ${{w_{1} } \mathord{\left/ {\vphantom {{w_{1} } {w_{2} }}} \right. \kern-\nulldelimiterspace} {w_{2} }} = 2 - w_{1} ,$${{w_{1} } \mathord{\left/ {\vphantom {{w_{1} } {w_{2} }}} \right. \kern-\nulldelimiterspace} {w_{2} }} = 1 + w_{1} ,$ ${{w_{1} } \mathord{\left/ {\vphantom {{w_{1} } {w_{2} }}} \right. \kern-\nulldelimiterspace} {w_{2} }} = 1 - w_{1}$.

In this context, we simultaneously examine the following three primary external resonances

$$p_{1} \approx 1,\,\,\,\,\,\,p_{0} \approx w_{1} ,\,\,\,\,\,\,w_{2} \approx 3.$$

(18)

These resonances demonstrate, respectively, the closeness of $p_{1} ,p_{0} ,$ and $\,w_{2}$ to $1\,,\,\,w_{1} ,$ and $3$. To accomplish this, the dimensionless detuning parameters $\sigma_{j} \,\,(j = 1,2,3)$ can be presented as seen below

$$p_{1} = 1 + \sigma_{1} ,\,\,\,\,\,\,p_{0} = w_{1} + \sigma_{2} ,\,\,\,\,\,\,w_{1} \left( {1 - \frac{3}{{w_{2} }}} \right) = \sigma_{3} .$$

(19)

Since these parameters describe how far the oscillations are from the strict resonance, then one can express them in terms of $\varepsilon$ as follows:

$$\sigma_{j} = \varepsilon^{2} \tilde{\sigma }_{j} \,\,\,\,\,\,\,(j = 1,2,3).$$

(20)

Making use of (19) and (20) into (11) and (12), and then eliminating the resulted secular terms, one obtains the following criteria of solvability

$$\begin{aligned} & D_{1} B_{1} = 0,\,\,\,\,\,\,\,\,D_{1} B_{2} = 0,\,\,\,\,\,\,\,D_{1} B_{3} = 0, \hfill \\ & 2iD_{2} B_{1} + \left( {\frac{{2\beta B_{2} \overline{B}_{2} }}{{1 - 4w_{1}^{2} }} + i\tilde{c}_{1} } \right)B_{1} - \frac{{\tilde{f}_{1} }}{2}e^{{i\sigma_{1} \tau_{0} }} = 0, \hfill \\ & 2iw_{1} D_{2} B_{2} + i\tilde{c}_{2} w_{1} B_{2} + \frac{{B_{2} }}{{2(1 - 2w_{1} )(1 + 2w_{1} )(1 - w_{2}^{2} )}}\{ 2\tilde{h}w_{1}^{2} (4w_{1}^{2} - 1) - (w_{2}^{2} - 1)\{ 4B_{1} \overline{B}_{1} \hfill \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + w_{1}^{2} [4(1 - 4\beta )w_{1}^{2} - 1]B_{2} \overline{B}_{2} \} \} - \frac{{\tilde{m}_{0} }}{2}e^{{i\sigma_{2} \tau_{0} }} = 0, \hfill \\& 2iw_{1} w_{2} D_{2} B_{3} + \frac{{iw_{1} }}{{w_{2} }}\tilde{c}_{3} B_{3} - \frac{{B_{3} }}{{2(4w_{1}^{2} - w_{2}^{2} )( - 1 + w_{2}^{2} )^{2} }}\{ 2\tilde{h}w_{1}^{2} (4w_{1}^{2} - w_{2}^{2} )(w_{2}^{2} - 1) + 4(w_{2}^{2} - 1)^{2} \hfill \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times B_{1} \overline{B}_{1} + w(4w_{1}^{2} - w_{2}^{2} )[2(2w_{2}^{2} - 1)B_{2} \overline{B}_{2} + (w_{2}^{2} - 1)^{2} B_{3} \overline{B}{}_{3}]\} + \frac{{w_{1}^{2} w_{2}^{2} \overline{B}_{2} B_{3}^{2} }}{{2(1 - w_{2}^{2} )}}e^{{i\sigma_{3} \tau_{0} }} = 0. \hfill \\ \end{aligned}$$

(21)

A further examination of the solvability criteria reveals six nonlinear PDE regarding to the functions $B_{j} = B_{j} (\tau_{1} ,\tau_{2} ),\,\,\,\,\,\,(j = 1,2,3)$. Consequently, one writes them in their below polar forms

$$B_{j} = \frac{{\tilde{b}_{j} (\tau_{1} ,\tau_{2} )}}{2}e^{{i\psi_{j} (\tau_{1} ,\tau_{2} )}} ,\,\,\,\,\,\,\,b_{j} = \varepsilon \tilde{b}_{j} \,\,\,\,\,\,(j = 1,2,3).$$

(22)

Here, $\tilde{b}_{j}$ and $\psi_{j}$ represent the real functions of amplitudes and phases of $\tilde{y},\tilde{\varphi },$ and $\tilde{\gamma }$, while $b_{j}$ denote the amplitudes of $y,\,\varphi ,$ and $\gamma$ as indicated in the hypotheses (7).

In light of the above preceding analysis, the first-order derivatives of operators $B_{j} \,\,(j = 1,2,3)$ can be expressed as follows

$$\frac{{{\text{d}}B_{j} }}{{{\text{d}}\tau }} = \varepsilon D_{1} B_{j} + \varepsilon^{2} D_{2} B_{j} .$$

(23)

Equations (22), (23), and the following modified phases [10] are used

$$\begin{aligned} \theta_{1} (\tau_{2} )& = \tilde{\sigma }_{1} \tau_{2} - \psi_{1} (\tau_{2} ), \hfill \\ \theta_{2} (\tau_{2} ) &= \tilde{\sigma }_{2} \tau_{2} - \psi_{2} (\tau_{2} ), \hfill \\ \theta_{3} (\tau_{2} ) &= \tilde{\sigma }_{3} \tau_{2} - \psi_{2} (\tau_{2} ) + \psi_{3} (\tau_{2} ), \hfill \\ \end{aligned}$$

(24)

to covert the PDE (21) of the solvability criteria into ordinary differential equations (ODE). Separating the system real and imagined components produces the below first-order ODE regarding the amplitudes $b_{j}$ and phases $\theta_{j}$

$$\begin{aligned} & \frac{{{\text{d}}b_{1} }}{{{\text{d}}\tau }} = \frac{1}{2}(f_{1} \sin \theta_{1} - c_{1} b_{1} ), \hfill \\ & b_{1} \frac{{{\text{d}}\theta_{1} }}{{{\text{d}}\tau }} = b_{1} [\sigma_{1} - \frac{{\beta b_{2}^{2} }}{{4(1 - 4w_{1}^{2} )}}] + \frac{{f_{1} }}{2}\cos \theta_{1} , \hfill \\ & w_{1} \frac{{{\text{d}}b_{2} }}{{{\text{d}}\tau }} = \frac{{m_{0} }}{2\,}\sin \theta_{2} - \frac{1}{2}w_{1} c_{2} b_{2} , \hfill \\ w_{1} b_{2} \frac{{{\text{d}}\theta_{2} }}{{{\text{d}}\tau }} = b_{2} \{ \sigma_{2} - \frac{1}{{4(1 - 2w_{1} )(1 + 2w_{1} )(1 - w_{2}^{2} )}}[2hw_{1}^{2} (4w_{1}^{2} - 1) - (w_{2}^{2} - 1)(b_{1}^{2} + \frac{1}{4}w_{1}^{2} b_{2}^{2} \hfill \\ & \,\,\,\,\,\,\,\,\, \times [4(1 - 4\beta )w_{1}^{2} - 1])]\} + \frac{{m_{0} }}{2\,}\cos \theta_{2} , \hfill \\ w_{1} w_{2} \frac{{db_{3} }}{d\tau } = - \frac{{w_{1}^{2} w_{2}^{2} b_{2} b_{3}^{2} }}{{16(1 - w_{2}^{2} )}}\sin \theta_{3} - \frac{{w_{1} }}{{2w_{2} }}c_{3} b_{3} , \hfill \\ w_{1} w_{2} b_{3} \frac{{d\theta_{3} }}{d\tau } = \frac{{b_{3} }}{16}\{ \frac{8}{{b_{2} }}w_{2} m_{0} \cos \theta_{2} + \frac{1}{{1 - w_{2}^{2} }}\{ 8hw_{1}^{2} + w_{1}^{2} [b_{3}^{2} + 2b_{2}^{2} (w_{2}^{2} b_{3} \cos \theta_{3} + \frac{{(1 - 2w_{2}^{2} )}}{{(1 - w_{2}^{2} )}})] \hfill \\ & \,\,\,\,\,\,\,\,\,\, + \frac{{4b_{1}^{2} }}{{(4w_{1}^{2} - w_{2}^{2} )}}\} + 16w_{2} \{ \sigma_{2} (1 - w_{1} ) + \sigma_{3} w_{1} - \frac{1}{{4(1 - 2w_{1} )(1 + 2w_{1} )(1 - w_{2}^{2} )}} \hfill \\ & \,\,\,\,\,\,\,\,\, \times [2hw_{1}^{2} (4w_{1}^{2} - 1) - \frac{1}{4}[4b_{1}^{2} - b_{2}^{2} w_{1}^{2} (1 + 4(4\beta - 1)w_{1}^{2} )](w_{2}^{2} - 1)]\} \} . \hfill \\ \end{aligned}$$

(25)

It must be noted that the preceding system is known as the system for the investigated cases of resonances. A closer examination of the equations of this system shows that the waves illustrating the behavior of $(b_{1} ,\theta_{1} ),(b_{2} ,\theta_{2} ),$ and $(b_{3} ,\theta_{3} )$ will be influenced by the change of the damping coefficients $c_{1} ,c_{2} ,$ and $c_{3}$, respectively. These equations can be solved numerically according to the following amounts of the used system factors

$$\begin{aligned} \sigma_{1} = - 0.1,\,\,\,\,\sigma_{2} = 0.01,\,\,\,\,p = 0.2\;{\text{m}},\,\,\,\,g = 9.8\;{\text{m}}/\sec^{2} ,\,\,\,\,m_{1} = 25\;{\text{kg}},\,\,\,\,U_{A} = 70\;{\text{kg}}{\text{.m}}^{2} \hfill \\ f_{1} = 0.0004,\,\,\,\,m_{0} = 0.0003,\,\,\,\,p_{1} = 1 + \sigma_{1} ,\,\,\,\,p_{0} = w_{1} + \sigma_{2} ,\,\,\,\,w_{1} \left( {1 - \frac{3}{{w_{2} }}} \right) = \sigma_{3} . \hfill \\ \end{aligned}$$

Curves depicted in Figs. 2, 3, 4 and (5)–(7) reveal the variations of the amplitudes $b_{j} \,\,\,(j = 1,2,3)$ and the improved phases $\theta_{j}$ versus the dimensionless time $\tau$ when the damping parameters $c_{j}$ and frequencies $\omega_{j}$ have various values. Figure 2 is calculated when $c_{2} = 0.001,$$c_{3} = 0.002$,$\omega_{1} = 1.24,$$\omega_{2} = 2.556,$ $\omega_{3} = 1.058,$ and $c_{1} = (0.009,0.005,0.001)$. It is noted that the standing waves describing $b_{1}$ and $\theta_{1}$ have been affected with the change of the values of $c_{1}$ as indicated in portions (a) and (d) of Fig. 2. Moreover, the amplitudes of the waves decrease with the rise of $c_{1}$ amounts, while the oscillations number remains steady. In other words, the decaying behavior increases according to the increase of the damping values, which is expected before. On the other hand, the influence of $c_{1}$ values on the waves of $(b_{2} ,\theta_{2} )$ and $(b_{3} ,\theta_{3} )$ seems to be slight, as graphed in portions (b,e) and (c,f), respectively. As the values of $c_{1}$ increase, the time behavior of $b_{3}$ and $\theta_{3}$ steadily decreases till the end of the examined interval of time, as graphed in Fig. 3c, f. As the values of $c_{1}$ increase, the time behavior of $b_{3}$ and $\theta_{3}$ steadily decreases till the end of the examined time interval, as graphed in Fig. 3c, f. This conclusion agrees with the mathematical formulation of system (25).

Fig. 2

Presents the behavior of $b_{j} (\tau )\,\,(j = 1,2,3)$ and $\theta_{j} (\tau )$ at $c_{2} = 0.001,$$c_{3} = 0.002$,$\omega_{1} = 1.24,$$\omega_{2} = 2.556,$ and $\omega_{3} = 1.058$ at $c_{1} = (0.009,0.005,0.001),$

Fig. 3

Describes the variation of $b_{j}$ and $\theta_{j} (\tau )$ versus $\tau$ at, c₁=0.001, $c_{3} = 0.002,$$\omega_{1} = 1.24,$$\omega_{2} = 2.556,$ and $\omega_{3} = 1.058$ when $c_{2} = (0.008,0.006,0.004)$

Fig. 4

Explores the functions $b_{j} (\tau )$ and $\theta_{j} (\tau )$ when $c_{3}$ has different values at $c_{1} = 0.001,$ $c_{2} = 0.005,$ $\omega_{1} = 1.24,$ $\omega_{2} = 2.556,$ and $\omega_{3} = 1.058$

The effectiveness of the damping parameters $c_{2}$ to the temporary time of $b_{j}$ and $\theta_{j}$ are drawn, respectively, in parts (a), (b), (c) and (d), (e), (f) of Fig. 3. These portions are calculated when $c_{2} = (0.008,0.006,0.004)$ varies at $c_{1} = 0.001,$ $c_{3} = 0.002,$ $\omega_{1} = 1.24,$ $\omega_{2} = 2.556,$ and $\omega_{3} = 1.058$. Curves of Fig. 3a, b, d, e have a decay procedure. The good influence of $c_{2}$ on the waves illustrating $b_{2}$ and $\theta_{2}$ is graphed in Fig. 3a, c, in which the plotted waves decrease with the increase of $c_{2}$ values. The time behavior of $b_{3}$ and $\theta_{3}$ decreases gradually till the end of the studied interval of time with increase of the values of $c_{2}$, as seen in Fig. 3c, f.

Analyses of the plotted curves in Fig. 4 allow us to say that part (c) has been influenced more clearly by the change of $c_{3}$ than the other parts. This is because the explicit dependence of the fifth equation in the system (25) on $c_{3}$. As predicted above, the included curves of the other parts don’t have a visible change, which agrees with the other five equations of the same system.

The time histories of both amplitudes $b_{j}$ and the modified phases $\theta_{j}$ are graphed in Figs. 5, 6, 7 for various values of $\omega_{j}$. These graphs are calculated when $c_{1} = 0.001,$$c_{2} = 0.005,$ and $c_{3} = 0.002$ besides the different values of $\omega_{1} = (1.24,1.176,1.109)$, $\omega_{2} = (2.556,2.213,1.979),$ and $\omega_{3} = (1.183,1.122,1.058)$ as in Figs. 5, 6, and 7, respectively. The presented curves in portions [(a), (d)] and [(b), (e)] of these figures have decaying forms, while the gradient acceleration in the decaying waves in parts (b) and (e) is greater than those in parts (a) and (d). The reason goes backs to the in/dependence of the first four equations of system (25) on the values of $\omega_{j}$. The first one doesn’t depend on $\omega_{j}$, the dependency of the second one on $\omega_{1}$ only seems slight, while the third and fourth equations are directly dependent on $\omega_{j}$; see the dimensionless parameters (4) and the system (25). Therefore, we expected that the curves in portions (a) and (d) don’t vary with the change of $\omega_{j}$, whereas the behaviors of the waves describing $b_{2}$ and $\theta_{2}$ will vary with the change of $\omega_{j}$, as drawn in portions (b) and (e) of Figs. 5, 6, 7. Given that system (25) final two equations are dependent on $\omega_{j}$ explicitly, we expect that their graphs are influenced by their changes, see portions (c) and (f) of the same figures.

Fig. 5

Represents the temporary histories of $b_{j}$ and $\theta_{j}$ when $\omega_{2} = 2.556,$ $\omega_{3} = 1.058,$$c_{1} = 0.001,$$c_{2} = 0.005,$ and $c_{3} = 0.002$ at $\omega_{1} = (1.24,1.176,1.109)$

Fig. 6

Depicts the variation of $b_{j}$ and $\theta_{j}$ via $\tau$ at $\omega_{1} = 1.24,$$\omega_{3} = 1.058,$$c_{1} = 0.001,$$c_{2} = 0.005,$ and $c_{3} = 0.002$ at $\omega_{2} = (2.556,2.213,1.979)$

Fig. 7

Illustrates the behavior of $b_{j} (\tau )$ and $\theta_{j} (\tau )$ at various values of $\omega_{3} = (1.183,1.122,1.058)$ when $\omega_{1} = 1.24,$ $\omega_{2} = 2.556,$ $c_{1} = 0.001,$ $c_{2} = 0.005,$ and $c_{3} = 0.002$

The diagrams of phase plane for the time dependent solutions of the equations of system (25) are depicted in Figs. 8, 9, 10, 11, 12, 13, while $c_{j}$ and $\omega_{j}$ have various amounts, respectively. Looking at the plotted curves, in parts (a) and (b), reveals that they have directed spiral forms toward a single point, which conveys the idea that these phases and amplitudes move steadily. On the other hand, the curves drawn in portion (c) of these figures decrease gradually with time to give stable indications of their behaviors.

Fig. 8

Shows the diagrams’ curves in the planes $b_{j} \theta_{j}$ at $c_{2} = 0.001,$ $c_{3} = 0.002,$$\omega_{1} = 1.24,$ $\omega_{2} = 2.556,$ and $\omega_{3} = 1.058$ when $c_{1} = (0.009,0.005,0.001)$

Fig. 9

Displays the diagrams’ curves in the planes $b_{j} \theta_{j}$ when $c_{2}$ has various values at $c_{1} = 0.001,$ $c_{3} = 0.002,$$\omega_{1} = 1.24,$ $\omega_{2} = 2.556,$ and $\omega_{3} = 1.058$

Fig. 10

Describes the diagrams’ curves in the planes $b_{j} \theta_{j}$ when $c_{3}$ has the values $(0.007,0.005,0.003)$ at $c_{1} = 0.001,$ $c_{2} = 0.005,$$\omega_{1} = 1.24,$ $\omega_{2} = 2.556,$ and $\omega_{3} = 1.058$

Fig. 11

Represents the phase planes diagrams $b_{j} \theta_{j}$ at $\omega_{2} = 2.556,$ $\omega_{3} = 1.058,$ $c_{1} = 0.001,$ $c_{2} = 0.005,$ and $c_{3} = 0.002$ when $\omega_{1} = (1.24,1.176,1.109)$

Fig. 12

Describes the phase planes diagrams $b_{j} \theta_{j}$ at $\omega_{2} = (2.556,2.213,1.979)$ when $\omega_{1} = 1.24,$ $\omega_{3} = 1.058,$ $c_{1} = 0.001,$ $c_{2} = 0.005,$ and $c_{3} = 0.002$

Fig. 13

Sketches the phase planes diagrams $b_{j} \theta_{j}$ at $\omega_{3} = (1.183,1.122,1.058)$ when $\omega_{1} = 1.24,$ $\omega_{2} = 2.556,$ $c_{1} = 0.001,$ $c_{2} = 0.005,$ and $c_{3} = 0.002$

The curves graphed in parts Figs. 8a, 9b, and 10c are impacted, respectively, by the change of the values $c_{1} ,c_{2} ,$ and $c_{3}$, while the variation in the curves of other parts can’t be observed to some extent. As aforementioned stated, the first two equations in system (25) don’t depend on $\omega_{j}$ directly, then we can expect that the behavior of the plotted curves in planes $\theta_{1} b_{1}$ is not affected by the change of $\omega_{j}$ amounts, as found in Figs. 11a, 12a, and 13a. On the other hand, the last four equations of the same system are influenced by the change of $\omega_{j}$ values. Then we can predict that the curves of in the planes $\theta_{2} b_{2}$ and $\theta_{3} b_{3}$ will be influenced by this change. This prediction is highly consistent with the plotted curves in portions (b) and (c) of Figs. 11, 12.

It is vital to bear in mind that the achieved approximate solutions $y(\tau ),\varphi (\tau ),$ and $\gamma (\tau )$ characterize, respectively, the spring elongation on the one hand, and the rotating angles at the points $o$ and $A$, on the other hand. The variations of these solutions are shown in Figs. 14, 15, 16, 17, 18, 19 when $c_{j} \,\,\,(j = 1,2,3)$ and $\omega_{j}$ have various amounts in addition to the above used data. We can infer from the depicted curves in these graphs that they include periodic forms of wave packets or quasi-periodic ones. The amplitude of the waves describing $y$ and $\gamma$ decreases with the increase of $c_{1}$, as displayed in Figs. 14a, c, whereas the waves drawn in Fig.  14b show that the solution $\varphi$ is not impacted by the variation of $c_{1}$. The good influence of various values of $c_{2}$ and $c_{3}$ can be seen, respectively, in Figs. 15b, c, , 16c, while the waves in Figs. 15a, 16a, c, don’t display any variation with the change of $c_{2}$ and $c_{3}$. In the same context, one can observe that the drawn waves of the solutions $\varphi (\tau )$ and $\gamma (\tau )$ have been affected by the shift of $\omega_{j}$ amounts, as graphed in Figs. 17b, c, 18b, c, 19b, c. As opposed to that, the plotted curves in Fig. 17a, 18a, and 19a don’t exhibit any variations with the distinct values of $\omega_{1} ,\omega_{2} ,$ and $\omega_{3}$, correspondingly. The cause stems from the mathematical interpretation of the solution $y(\tau )$. The comparison of the numerical solutions (NS) and the analytic solutions (AS) at $c_{1} = 0.001,$ $c_{2} = 0.005,$$c_{3} = 0.002,$ $\omega_{1} = 1.24,$ $\omega_{2} = 2.556,$ and $\omega_{3} = 1.058$ has been graphed in Fig. 20a–c. It must be noted that these solutions have a high degree of agreement, which demonstrates that the perturbation approach has high degree of precision.

Fig. 14

Expresses the behavior of $y(\tau ),\varphi (\tau ),$ and $\gamma (\tau )$ when $c_{1} = (0.009,0.005,0.001)$ at $c_{2} = 0.001,$$c_{3} = 0.002,$$\omega_{1} = 1.24,$ $\omega_{2} = 2.556,$ and $\omega_{3} = 1.058$

Fig. 15

Expresses the behavior of $y(\tau ),\varphi (\tau ),$ and $\gamma (\tau )$ when $c_{2} = (0.008,0.006,0.004)$ at $c_{1} = 0.001,$ $c_{3} = 0.002,$$\omega_{1} = 1.24,$ $\omega_{2} = 2.556,$ and $\omega_{3} = 1.058$

Fig. 16

Portrays the time histories of $y,\varphi ,$ and $\gamma$ when $c_{3} = (0.007,0.005,0.003)$ at $c_{1} = 0.001,$ $c_{2} = 0.005,$$\omega_{1} = 1.24,$ $\omega_{2} = 2.556,$ and $\omega_{3} = 1.058$

Fig. 17

Portrays the time histories of $y,\varphi ,$ and $\gamma$ when $\omega_{1} = (1.24,1.176,1.109),$$\omega_{2} = 2.556,$ $\omega_{3} = 1.058,$ $c_{1} = 0.001,$ $c_{2} = 0.005,$ and $c_{3} = 0.002$

Fig. 18

Shows the solutions time histories when $\omega_{2} = (2.556,2.213,1.979),$ $\omega_{1} = 1.24,$ $\omega_{3} = 1.058,$ $c_{1} = 0.001,$ $c_{2} = 0.005,$ and $c_{3} = 0.002$

Fig. 19

Shows the solutions’ time histories when $\omega_{3} = (1.183,1.122,1.058),$$\omega_{1} = 1.24,$ $\omega_{2} = 2.556,$$c_{1} = 0.001,$ $c_{2} = 0.005,$ and $c_{3} = 0.002$

Fig. 20

Portrays the comparison between the AS and the NS at $c_{1} = 0.001,$ $c_{2} = 0.005,$$c_{3} = 0.002,$ $\omega_{1} = 1.24,$ $\omega_{2} = 2.556,$ and $\omega_{3} = 1.058$

Steady-State Solutions

Studying the oscillations of the system under consideration in a steady-state case is the main aim of this section. Therefore, we can calculate both the amplitudes $b_{j} \,\,(j = 1,2,3)$ and adjusted phases $\theta_{j}$ at this case according to the system of Eqs. (25). It is recognized that this situation arises when transitory processes vanish owing to the existence of damping [37]. Afterward, we consider the zero amount of the left-hand sides of these equations, i.e., $\frac{{db_{j} }}{d\tau } = 0,\,\,\frac{{d\theta_{j} }}{d\tau } = 0$[38]. Consequently, it is easy to obtain the below algebraic system regarding the functions $\theta_{j}$ and $b_{j}$.

$$\begin{aligned} f_{1} \sin \theta_{1} - c_{1} b_{1} = 0, \hfill \\ b_{1} \left[ {\sigma_{1} - \frac{{\beta b_{2}^{2} }}{{4(1 - 4w_{1}^{2} )}}} \right] + \frac{{f_{1} }}{2}\cos \theta_{1} = 0, \hfill \\ m_{0} \sin \theta_{2} - w_{1} c_{2} b_{2} = 0, \hfill \\ b_{2} \{ \sigma_{2} - \frac{1}{{4(1 - 2w_{1} )(1 + 2w_{1} )(1 - w_{2}^{2} )}}[2hw_{1}^{2} (4w_{1}^{2} - 1) - (w_{2}^{2} - 1)(b_{1}^{2} + \frac{1}{4}w_{1}^{2} b_{2}^{2} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times [4(1 - 4\beta )w_{1}^{2} - 1])]\} + \frac{{m_{0} }}{2\,}\cos \theta_{2} = 0, \hfill \\ \frac{{w_{1}^{2} w_{2}^{2} b_{2} b_{3}^{2} }}{{8(1 - w_{2}^{2} )}}\sin \theta_{3} + \frac{{w_{1} }}{{w_{2} }}c_{3} b_{3} = 0, \hfill \\ \frac{8}{{b_{2} }}w_{2} m_{0} \cos \theta_{2} + \frac{1}{{1 - w_{2}^{2} }}\{ 8hw_{1}^{2} + w_{1}^{2} [b_{3}^{2} + 2b_{2}^{2} (w_{2}^{2} b_{3} \cos \theta_{3} + \frac{{(1 - 2w_{2}^{2} )}}{{(1 - w_{2}^{2} )}})] \hfill \\ + \frac{{4b_{1}^{2} }}{{(4w_{1}^{2} - w_{2}^{2} )}}\} + 16w_{2} \{ \sigma_{2} (1 - w_{1} ) + \sigma_{3} w_{1} - \frac{1}{{4(1 - 2w_{1} )(1 + 2w_{1} )(1 - w_{2}^{2} )}} \hfill \\ \times [2hw_{1}^{2} (4w_{1}^{2} - 1) - \frac{1}{4}[4b_{1}^{2} - b_{2}^{2} w_{1}^{2} (1 + 4(4\beta - 1)w_{1}^{2} )](w_{2}^{2} - 1)]\} = 0. \hfill \\ \end{aligned}$$

(26)

If we can get rid of the phases $\theta_{j}$, then the following nonlinear algebraic system can be obtained in terms of $b_{j}$ and $\sigma_{j}$

$$\begin{aligned} f_{1}^{2} = b_{1}^{2} \Bigg[c_{1}^{2} + 4(\sigma_{1} - \frac{{\beta b_{2}^{2} }}{{4(1 - 4w_{1}^{2} )}})^{2} \Bigg], \hfill \\ m_{0}^{2} = b_{2}^{2} \Bigg\{ w_{1}^{2} c_{2}^{2} + 4 \Bigg\{ \sigma_{2} - \frac{1}{{4(1 - 2w_{1} )(1 + 2w_{1} )(1 - w_{2}^{2} )}}[2hw_{1}^{2} (4w_{1}^{2} - 1) \hfill \\ \,\,\,\,\,\,\, - (w_{2}^{2} - 1)[b_{1}^{2} + w_{1}^{2} (4(1 - 4\beta )w_{1}^{2} - 1)\frac{{b_{2}^{2} }}{4}]]\}^{2} \Bigg\} , \hfill \\ \frac{{w_{1}^{4} w_{2}^{4} b_{2}^{2} b_{3}^{2} }}{{64(1 - w_{2}^{2} )^{2} }} = \frac{{w_{1}^{2} }}{{w_{2}^{2} }}c_{3}^{2} + \frac{1}{64}\Bigg\{ \frac{1}{{(1 - w_{2}^{2} )^{2} }}\Bigg[\frac{{4b_{1}^{2} (1 - w_{2}^{2} )}}{{4w_{1}^{2} - w_{2}^{2} }} + w_{1} (w_{1} [(8h + b_{3}^{2} )(1 - w_{2}^{2} ) \hfill \\ \,\,\,\,\,\,\,\,\,\,\, + 2b_{2}^{2} (1 - 2w_{2}^{2} )\Bigg] - 16w_{2} (1 - w_{2}^{2} )^{2} (\sigma_{2} - \sigma_{3} ))\Bigg]\Bigg\}^{2} . \hfill \\ \end{aligned}$$

(27)

It is regarded that stability evaluation is an important aspect of the vibrations at the situation of steady-state. Therefore, the system behavior in a domain that is somewhat near to fixed points would be examined to analyze such a situation. To achieve this goal, let us use the below substitutions in (25)

$$\begin{aligned} b_{1} = b_{10} + b_{11} ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\theta_{1} = \theta_{10} + \theta_{11} , \hfill \\ b_{2} = b_{20} + b_{21} ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\theta_{2} = \theta_{20} + \theta_{21} , \hfill \\ b_{3} = b_{30} + b_{31} ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\theta_{3} = \theta_{30} + \theta_{31} , \hfill \\ \end{aligned}$$

(28)

where $b_{j0}$ and $\theta_{j0}$ are the solutions at steady-state, while $b_{j1}$ and $\theta_{j1}$ exemplify the corresponding perturbations, which are presumably very minimal. Substituting (28) into (25), one obtains the next equations

$$\begin{aligned}& \frac{{db_{11} }}{d\tau } = \frac{1}{2}(f_{1} \theta_{11} \cos \theta_{10} - c_{1} b_{11} ), \hfill \\ &b_{10} \frac{{d\theta_{11} }}{d\tau } = b_{11} \sigma_{1} - \frac{\beta }{{4(1 - 4w_{1}^{2} )}}(2b_{10} b_{20} b_{21} + b_{20}^{2} b_{11} ) - \frac{{f_{1} }}{2}\theta_{11} \sin \theta_{10} , \hfill \\ &w_{1} \frac{{db_{21} }}{d\tau } = \frac{1}{2\,}(m_{0} \theta_{21} \cos \theta_{20} - w_{1} c_{2} b_{21} ), \hfill \\ & w_{1} b_{20} \frac{{d\theta_{21} }}{d\tau } = b_{21} \sigma_{2} - \frac{1}{{4(1 - 2w_{1} )(1 + 2w_{1} )(1 - w_{2}^{2} )}}[2hw_{1}^{2} (4w_{1}^{2} - 1) - (w_{2}^{2} - 1) \hfill \\ & \,\,\,\,\,\,\,\,\,\, \times (b_{10}^{2} b_{21} + 2b_{10} b_{20} b_{11} + \frac{3}{4}w_{1}^{2} [4(1 - 4\beta )w_{1}^{2} - 1]b_{20}^{2} b_{21} )] - \frac{{m_{0} }}{2\,}\theta_{21} \sin \theta_{20} , \hfill \\ &w_{1} w_{2} \frac{{db_{31} }}{d\tau } = - \frac{{w_{1}^{2} w_{2}^{2} }}{{16(1 - w_{2}^{2} )}}[(b_{30}^{2} b_{21} + 2b_{20} b_{30} b_{31} )\sin \theta_{30} + b_{30}^{2} b_{20} \theta_{31} \cos \theta_{30} ] - \frac{{w_{1} }}{{2w_{2} }}c_{3} b_{31} , \hfill \\& w_{1} w_{2} b_{30} b_{20} \frac{{d\theta_{31} }}{d\tau } = \frac{1}{16}\{ 8w_{2} m_{0} (b_{31} \cos \theta_{20} - b_{30} \theta_{21} \sin \theta_{20} ) + \frac{{8hw_{1}^{2} }}{{1 - w_{2}^{2} }}(b_{30} b_{21} + b_{20} b_{31} ) \hfill \\& \,\,\,\,\,\,\,\,\, + \frac{{w_{1}^{2} }}{{1 - w_{2}^{2} }}(b_{30}^{3} b_{21} + 3b_{20} b_{30}^{2} b_{31} ) + \frac{{w_{1}^{2} w_{2}^{2} }}{{1 - w_{2}^{2} }}[2\cos \theta_{30} (b_{20} b_{30}^{2} b_{21} + b_{30} b_{20}^{2} b_{31} ) \hfill \\& \,\,\,\,\,\,\,\,\,\,\, - b_{20}^{2} b_{30}^{2} \theta_{31} \sin \theta_{30} ] + \frac{4}{{(4w_{1}^{2} - w_{2}^{2} )(1 - w_{2}^{2} )}}(b_{30} b_{10}^{2} b_{21} + 2b_{10} b_{20} b_{30} b_{11} \hfill \\& \,\,\,\,\,\,\,\,\,\,\,\,\, + b_{20} b_{10}^{2} b_{31} ) + \frac{{2w_{1}^{2} }}{{(1 - w_{2}^{2} )^{2} }}(1 - 2w_{2}^{2} )(b_{20}^{3} b_{31} + 3b_{30} b_{20}^{2} b_{21} ) - 16w_{1} w_{2} (\sigma_{2} - \sigma_{3} ) \hfill \\& \,\,\,\,\,\,\,\,\,\,\, \times (b_{30} b_{21} + b_{20} b_{31} ) + 16w_{2} [\sigma_{2} (b_{30} b_{21} + b_{20} b_{31} ) - \frac{1}{{4(1 - 2w_{1} )(1 + 2w_{1} )(1 - w_{2}^{2} )}} \hfill \\& \,\,\,\,\,\,\,\,\,\, \times [2hw_{1}^{2} (4w_{1}^{2} - 1)(b_{30} b_{21} + b_{20} b_{31} ) - [b_{30} b_{10}^{2} b_{21} + 2b_{10} b_{20} b_{30} b_{11} + b_{20} b_{10}^{2} b_{31} \hfill \\& \,\,\,\,\,\,\,\, - \frac{{w_{1}^{2} }}{4}[1 + 4(4\beta - 1)w_{1}^{2} ](b_{20}^{3} b_{31} + 3b_{30} b_{20}^{2} b_{21} )](w_{2}^{2} - 1)]]\} . \hfill \\ \end{aligned}$$

(29)

In light of the smallness of $b_{j1}$ and $\theta_{j1} \,\,(j = 1,2,3)$, we can write the solutions as linear combinations of $h_{s} e^{\lambda \tau } \,\,(s = 1,2,3,4,5,6)$, where $h_{s}$ and $\lambda$ are quantities and the eigenvalue of the unidentified perturbations, correspondingly. If the solutions at the steady-state case are asymptotically stable, the real parts of the roots of the below typical equation of (29) should be negative [39]

$$\lambda^{6} + \Gamma_{1} \lambda^{5} + \Gamma_{2} \lambda^{4} + \Gamma_{3} \lambda^{3} + \Gamma_{4} \lambda^{2} + \Gamma_{5} \lambda + \Gamma_{6} = 0.$$

(30)

Here, $\Gamma_{s} \,\,(s = 1,2,...,6)$ represent dependent functions on $b_{j0} ,\theta_{j0} ,$ and $h_{j}$(see Appendix 2).

With reference to the foregoing analysis, the Routh–Hurwitz [40] criterion can be used to write the fundamental conditions for the stability of the steady-state solutions as follows

$$\begin{aligned} &\Gamma_{1} > 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\Gamma_{3} (\Gamma_{1} \Gamma_{2} - \Gamma_{3} ) - \Gamma_{4} \Gamma_{1}^{2} + \Gamma_{1} \Gamma_{5} > 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\Gamma_{1} \Gamma_{2} - \Gamma_{3} > 0, \hfill \\ &\Gamma_{3} \Gamma_{4} (\Gamma_{1} \Gamma_{2} - \Gamma_{3} ) - \Gamma_{1}^{2} \Gamma_{4}^{2} - \Gamma_{1} \Gamma_{2}^{2} \Gamma_{5} + \Gamma_{2} \Gamma_{3} \Gamma_{5} + 2\Gamma_{1} \Gamma_{4} \Gamma_{5} - \Gamma_{5}^{2} + \Gamma_{1}^{2} \Gamma_{2} \Gamma_{6} - \Gamma_{1} \Gamma_{3} \Gamma_{6} > 0, \hfill \\& \Gamma_{1} \Gamma_{2} \Gamma_{3} \Gamma_{4} \Gamma_{5} - \Gamma_{3}^{2} \Gamma_{4} \Gamma_{5} - \Gamma_{1}^{2} \Gamma_{4}^{2} \Gamma_{5} - \Gamma_{1} \Gamma_{2}^{2} \Gamma_{5}^{2} + \Gamma_{2} \Gamma_{3} \Gamma_{5}^{2} + 2\Gamma_{1} \Gamma_{4} \Gamma_{5}^{2} - \Gamma_{5}^{3} - \Gamma_{1} \Gamma_{2} \Gamma_{3}^{2} \Gamma_{6} \hfill \\& + \Gamma_{3}^{3} \Gamma_{6} + \Gamma_{1}^{2} \Gamma_{3} \Gamma_{4} \Gamma_{6} + 2\Gamma_{1}^{2} \Gamma_{2} \Gamma_{5} \Gamma_{6} - 3\Gamma_{1} \Gamma_{3} \Gamma_{5} \Gamma_{6} - \Gamma_{1}^{3} \Gamma_{6}^{2} > 0, \hfill \\& \Gamma_{6} (\Gamma_{1} \Gamma_{2} \Gamma_{3} \Gamma_{4} \Gamma_{5} - \Gamma_{3}^{2} \Gamma_{4} \Gamma_{5} - \Gamma_{1}^{2} \Gamma_{4}^{2} \Gamma_{5} - \Gamma_{1} \Gamma_{2}^{2} \Gamma_{5}^{2} + \Gamma_{2} \Gamma_{3} \Gamma_{5}^{2} + 2\Gamma_{1} \Gamma_{4} \Gamma_{5}^{2} - \Gamma_{5}^{3} - \Gamma_{1} \Gamma_{2} \Gamma_{3}^{2} \Gamma_{6} \hfill \\& + \Gamma_{3}^{3} \Gamma_{6} + \Gamma_{1}^{2} \Gamma_{3} \Gamma_{4} \Gamma_{6} + 2\Gamma_{1}^{2} \Gamma_{2} \Gamma_{5} \Gamma_{6} - 3\Gamma_{1} \Gamma_{3} \Gamma_{5} \Gamma_{6} - \Gamma_{1}^{3} \Gamma_{6}^{2} ) > 0. \hfill \\ \end{aligned}$$

(31)

The Stability Assessment

This section is devoted to examining the stability analysis of the dynamical scheme applying the criteria of Routh–Hurwitz. It is to be noted that the motion of this system is considered under the action of a damped spring, force $F(t)$ and moment $M(t)$. It has been discovered that some variables, such as damping quantities $c_{j}$, frequencies $\omega_{j}$, and the detuning parameter $\sigma_{j}$, have a significant influence on stability procedures. To achieve the stability graphs of structure (25), a certain process with various factors has been employed. For a variety of parametrical locations, the adjusted amplitudes $b_{j}$ have been displayed with the detuning parameter $\sigma_{2}$, as seen in Figs. 21, 22, 23, 24, 25, 26, in accordance with the above used data. Figures 21, 22, 23, 24, 25, 26 are graphed, respectively, when the variations of the damping coefficients $c_{j} \,\,(j = 1,2,3)$ and the frequencies $\omega_{j}$ are considered.

Fig. 21

Depicts the response curves in $\sigma_{2} b_{j} \,\,(j = 1,2,3)$ when $c_{2} = 0.001,$ $c_{3} = 0.002,$$\omega_{1} = 1.24,$ $\omega_{2} = 2.556,$ $\omega_{3} = 1.058,$$\sigma_{1} = - 0.1,$ and $\sigma_{3} = - 0.49$ at $c_{1} = (0.009,0.005,0.001)$

Fig. 22

Displays the curves of frequency response in the planes $\sigma_{2} b_{j}$ at $c_{1} = 0.001,$$c_{3} = 0.002,$ $\omega_{1} = 1.24,$ $\omega_{2} = 2.556,$ $\omega_{3} = 1.058,$$\sigma_{1} = - 0.1,$ and $\sigma_{3} = - 0.49$ when $c_{2} = (0.008,0.006,0.004)$

Fig. 23

Shows the amplitudes $b_{j}$ and via $\sigma_{2}$ when $c_{1} = 0.001,$$c_{2} = 0.005,$ $\omega_{1} = 1.24,$ $\omega_{2} = 2.556,$$\omega_{3} = 1.058,$$\sigma_{1} = - 0.1,$ and $\sigma_{3} = - 0.49$ at $c_{3} = (0.007,0.005,0.003)$

Fig. 24

Displays the curves in $\sigma_{2} b_{j}$ when $\omega_{2} = 2.556,$$\omega_{3} = 1.058,$$c_{1} = 0.001,$ $c_{2} = 0.005,$$c_{3} = 0.002,$$\sigma_{1} = - 0.1,$ and $\sigma_{3} = - 0.49$ at $\omega_{1} = (1.24,1.176,1.109)$

Fig. 25

Explores the variations of the functions $b_{j}$ versus $\sigma_{2}$ at $\omega_{2} = (2.556,2.213,1.979)$ when $\omega_{1} = 1.24,$$\omega_{3} = 1.058,$ $c_{1} = 0.001,$ $c_{2} = 0.005,$$c_{3} = 0.002,$$\sigma_{1} = - 0.1,$ and $\sigma_{3} = - 0.49$

Fig. 26

Describes $b_{j}$ versus $\sigma_{2}$ when $\omega_{1} = 1.24,$$\omega_{2} = 2.556,$$c_{1} = 0.001,$ $c_{2} = 0.005,$$c_{3} = 0.002,$$\sigma_{1} = - 0.1,$ and $\sigma_{3} = - 0.86$ at $\omega_{3} = (1.183,1.122,1.058)$

An examination of the depicted resonance curves in parts (a), (b), and (c) of Fig. 21 shows that they are plotted when $c_{2} = 0.001,$ $c_{3} = 0.002,$ $\omega_{1} = 1.24,$ $\omega_{2} = 2.556,$ and $\omega_{3} = 1.058$ at $c_{1} = (0.009,0.005,0.001)$. It is evident that the curves in part (a) rather than of parts (b) and (c) have been influenced by the change of the damping parameter $c_{1} = (0.009,0.005,0.001)$. The origin of the issue dates to how the system of equations was created. It should be emphasized that there is just single critical fixed point, which is the separating point between the stable and the unstable area, for each frequency response curve. Accordingly, there are one stability/instability zone. In areas $\sigma_{2} \le 0.07$ and $0.07 < \sigma_{2}$, the stable and unstable fixed points have been discovered, correspondingly, which are depicted by solid and dashed curves.

The positive effects of various values of the parameter $c_{2} = (0.008,0.006,0.004)$ on the performance of response curves in the planes $\sigma_{2} b_{j}$ are presented graphically in portions of Fig. 22. These portions are plotted at $c_{1} = 0.001,$$c_{3} = 0.002,$ $\omega_{1} = 1.24,$ $\omega_{2} = 2.556,$ $\omega_{3} = 1.058,$$\sigma_{1} = - 0.1,$ and $\sigma_{3} = - 0.49$. As to the stability/instability regions which are found, respectively, at $\sigma_{2} \le 0.06$ and $0.06 < \sigma_{2}$, one crucial fixed point has been identified.

To follow the discussion on the influence of distinct values of $c_{3} = (0.007,0.005,0.003)$, Fig. 23 has been drawn when $\omega_{1} = 1.24,$ $\omega_{2} = 2.556,$$\omega_{3} = 1.058$$c_{1} = 0.001,$ $c_{2} = 0.005,$ $\sigma_{1} = - 0.1,$ and $\sigma_{3} = - 0.49$ are considered. It is noted that the frequency response curves aren’t influenced by the change of $c_{3}$ values, which is owing to the independency of Eqs. (25) from it. Furthermore, each curve has one potential critical point with two areas; stable and unstable ones are observed at the ranges $\sigma_{2} \le 0.06$ and $0.06 < \sigma_{2}$, respectively.

With various values of the frequencies $\omega_{j}$, the response curves in the planes $\sigma_{2} b_{j}$ are displayed in Figs. 24, 25, 26 when $c_{1} = 0.001,$ $c_{2} = 0.005,$$c_{3} = 0.002,$$\sigma_{1} = - 0.1,$ and $\sigma_{3} = - 0.49$. It is noted that the different values of $\omega_{1} = (1.24,1.176,1.109),$ $\omega_{2} = (2.556,2.213,1.979),$ and $\omega_{3} = (1.183,1.122,1.058),$ play positive influences on the included curves of the plane $\sigma_{2} b_{j}$, as pictured in Figs. 24, 25, and 26, respectively. Each curve includes only one critical fixed point of its own. According to the displayed curves in Fig. 24, one can conclude that at $\omega_{1} = 1.24,$ $\omega_{1} = 1.176,$ $\omega_{1} = 1.109$, the stability/instability areas are found, respectively, in the ranges $\sigma_{2} \le 0.06,$ $\sigma_{2} \le 0.07,$$\sigma_{2} \le 0.08$ and $0.06 < \sigma_{2} ,$$0.07 < \sigma_{2} ,$$0.08 < \sigma_{2}$.

Portions (a), (b), and (c) of Fig. 25 explore various stability/instability ranges in the planes $b_{j} \sigma_{2}$ when $\omega_{2}$ has the values $2.556,$$2.213,$ and $1.979$. At $2.556$, the stability zone is found at the range $\sigma_{2} \le 0.06$ and the instability one is $0.06 < \sigma_{2}$, while the other two values $2.213$ and $1.979$ have the same stability/instability zones at $\sigma_{2} \le 0.05$ and $0.05 < \sigma_{2}$, respectively. The drawn curves have different critical points according to the values of $\omega_{2}$.

A careful analysis of the parts of Fig. 26 indicates that the drawn curves are calculated when $\omega_{3} = (1.183,1.122,1.058)$ at $\omega_{1} = 1.24,$$\omega_{2} = 2.556,$$c_{1} = 0.001,$ $c_{2} = 0.005,$$c_{3} = 0.002,$$\sigma_{1} = - 0.1,$ and $\sigma_{3} = - 0.86$ at $\omega_{3} = (1.183,1.122,1.058)$. Each part has three distinct critical points in addition to three stable and unstable ranges. At $\omega_{3} = 1.183,$ $\omega_{3} = 1.122,$ and $\omega_{3} = 1.058$, the stability areas are found in the domains $\sigma_{2} \le 0.09,$$\sigma_{2} \le 0.08,$ and $\sigma_{2} \le 0.06$, respectively. Consequently, at the mentioned values of $\omega_{3}$, the instability areas can be discovered at $0.09 < \sigma_{2} ,$ $0.08 < \sigma_{2} ,$ and $0.06 < \sigma_{2}$.

Nonlinear Interpretations

We take into consideration the below transformations to explicate the characteristics of the nonlinear amplitudes of structure (25) and to examine their stabilities [41]

$$\begin{aligned} B_{1} = \frac{1}{2}[U_{1} (\tau_{2} ) + iV_{1} (\tau_{2} )]\,e^{{i\tilde{\sigma }_{1} \tau_{2} }} , \hfill \\ B_{2} = \frac{1}{2}[U_{2} (\tau_{2} ) + iV_{2} (\tau_{2} )]\,e^{{i\tilde{\sigma }_{2} \tau_{2} }} , \hfill \\ B_{3} = \frac{1}{2}[U_{3} (\tau_{2} ) + iV_{3} (\tau_{2} )]\,e^{{i(\tilde{\sigma }_{2} - \tilde{\sigma }_{3} )\tau_{2} }} , \hfill \\ \end{aligned}$$

(32)

where

$$U_{j} = \varepsilon^{2} \,u_{j} ,\,\,\,\,\,\,\,\,V_{j} = \varepsilon^{2} \,v_{j} ;\,\,\,\,\,(j = 1,2,3).$$

Inserting (32) into (25), and then distinguishing the real portions and imaginary ones yields

$$\begin{aligned} \frac{{du_{1} }}{d\tau } = \sigma_{1} v_{1} - \frac{1}{2}c_{1} u_{1} - \frac{{\beta v_{1} }}{{4(1 - 4w_{1}^{2} )}}(u_{2}^{2} + v_{2}^{2} ), \hfill \\ \frac{{dv_{1} }}{d\tau } = \frac{{\beta u_{1} }}{{4(1 - 4w_{1}^{2} )}}(u_{2}^{2} + v_{2}^{2} ) - \sigma_{1} u_{1} - \frac{1}{2}(c_{1} v_{1} + f_{1} ), \hfill \\ w_{1} \frac{{du_{2} }}{d\tau } = w_{1} \sigma_{2} v_{2} - \frac{1}{2}w_{1} c_{2} u_{2} - \frac{{v_{2} }}{{4(1 - 2w_{1} )(1 + 2w_{1} )(1 - w_{2}^{2} )}}\{ 2hw_{1}^{2} (4w_{1}^{2} - 1) \hfill \\ \,\,\,\,\,\, - (w_{2}^{2} - 1)[u_{1}^{2} + v_{1}^{2} + w_{1}^{2} (4(1 - 4\beta )w_{1}^{2} - 1)\frac{{u_{2}^{2} + v_{2}^{2} }}{4}]\} , \hfill \\ w_{1} \frac{{dv_{2} }}{d\tau } = - w_{1} \sigma_{2} u_{2} - \frac{1}{2}w_{1} c_{2} v_{2} + \frac{{u_{2} }}{{4(1 - 2w_{1} )(1 + 2w_{1} )(1 - w_{2}^{2} )}}\{ 2hw_{1}^{2} (4w_{1}^{2} - 1) \hfill \\ \,\,\,\,\,\,\,\, - (w_{2}^{2} - 1)[u_{1}^{2} + v_{1}^{2} + w_{1}^{2} (4(1 - 4\beta )w_{1}^{2} - 1)\frac{{u_{2}^{2} + v_{2}^{2} }}{4}]\} - \frac{{m_{0} }}{2\,}, \hfill \\ w_{1} w_{2} \frac{{du_{3} }}{d\tau } = w_{1} w_{2} (\sigma_{2} - \sigma_{3} )v_{3} - \frac{{w_{1} }}{{2w_{2} }}c_{3} u_{3} - \frac{{w_{1}^{2} w_{2}^{2} }}{{16(1 - w_{2}^{2} )}}[2u_{2} u_{3} v_{3} - v_{2} (u_{3}^{2} - v_{3}^{2} )] \hfill \\ \,\,\,\,\,\,\,\,\, + \frac{{v_{3} }}{{4(4w_{1}^{2} - w_{2}^{2} )(1 - w_{2}^{2} )^{2} }}\{ 2hw_{1}^{2} (4w_{1}^{2} - w_{2}^{2} )(w_{2}^{2} - 1) + (1 - w_{2}^{2} )^{2} (u_{1}^{2} + v_{1}^{2} ) \hfill \\ \,\,\,\,\,\,\,\, + \frac{1}{4}w_{1}^{2} (4w_{1}^{2} - w_{2}^{2} )[2(2w_{2}^{2} - 1)(u_{2}^{2} + v_{2}^{2} ) + (w_{2}^{2} - 1)(u_{3}^{2} + v_{3}^{2} )]\} , \hfill \\ w_{1} w_{2} \frac{{dv_{3} }}{d\tau } = w_{1} w_{2} (\sigma_{3} - \sigma_{2} )u_{3} - \frac{{w_{1} }}{{2w_{2} }}c_{3} v_{3} + \frac{{w_{1}^{2} w_{2}^{2} }}{{16(1 - w_{2}^{2} )}}[2u_{3} v_{2} v_{3} + u_{2} (u_{3}^{2} - v_{3}^{2} )] \hfill \\ \,\,\,\,\,\,\, - \frac{{u_{3} }}{{4(4w_{1}^{2} - w_{2}^{2} )(1 - w_{2}^{2} )^{2} }}\{ 2hw_{1}^{2} (4w_{1}^{2} - w_{2}^{2} )(w_{2}^{2} - 1) + (1 - w_{2}^{2} )^{2} (u_{1}^{2} + v_{1}^{2} ) \hfill \\ \,\,\,\,\,\,\,\, + \frac{1}{4}w_{1}^{2} (4w_{1}^{2} - w_{2}^{2} )[2(2w_{2}^{2} - 1)(u_{2}^{2} + v_{2}^{2} ) + (w_{2}^{2} - 1)(u_{3}^{2} + v_{3}^{2} )]\} . \hfill \\ \end{aligned}$$

(33)

Figures 27, 28, 29, 30, 31, 32 display the temporal histories of the newly adjusted phases $u_{j} \,\,(j = 1,2,3)$ and $v_{j}$ as well as the projections of the trajectories $u_{j} v_{j}$. Curves of Figs. 27, 28, and 29 are graphed, respectively, when $c_{1} = (0.009,0.005,0.001),$ $c_{2} = (0.008,0.006,0.004),$ and $c_{3} = (0.007,0.005,0.003)$ at $\omega_{1} = 1.24,$$\omega_{2} = 2.556,$$\omega_{3} = 1.058,$$\sigma_{1} = - 0.1,$ and $\sigma_{2} = 0.01$. These indicated curves of these figures show that the functions $(u_{1} (\tau ),v_{1} (\tau ))$ $(u_{2} (\tau ),v_{2} (\tau ))$ and $(u_{3} (\tau ),v_{3} (\tau ))$ have decay behaviors, as found in parts (a), (b), (d), and (e) of these figures. Moreover, the variations of $c_{1} ,c_{2} ,$ and $c_{3}$ values, have excellent impact on the waves manner, as seen in Figs. 27a, b, 28d, e, and 29g, h, respectively. It is noted in these parts that the amplitudes of the plotted waves decrease, and that the decay of the waves is noted to be faster with the increase of damping terms $c_{1} ,c_{2} ,$ and $c_{3}$. The paths projections in planes $u_{1} v_{1} ,u_{2} v_{2} ,$ and $u_{3} v_{3}$ have the forms of directed spiral curves towards one point, as seen in portions (c), (f), and (i) of Figs. 27, 28, 29. This means that the dynamical behavior of the system (33) is stable and free of chaos.

Fig. 27

Displays the functions $u_{j} (\tau )\,\,(j = 1,2,3)$, $v_{j} (\tau )$, and the tracks of phase planes $\,u_{j} v_{j}$ when $c_{1} = (0.009,0.005,0.001),$$c_{2} = 0.001,\,c_{3} = 0.002,$ $\omega_{1} = 1.24,\,\omega_{2} = 2.556,$ $\omega_{3} = 1.058,$$\sigma_{1} = - 0.1,$ and $\sigma_{2} = 0.01$

Fig. 28

Portrays the time temporal histories of $u_{j}$, $v_{j}$ and the phase planes projections $\,u_{j} v_{j}$ when $c_{2} = (0.008,0.006,0.004),$$c_{1} = 0.001,$$c_{3} = 0.002,$, $\omega_{1} = 1.24,$ $\omega_{2} = 2.556,$$\omega_{3} = 1.058,$$\sigma_{1} = - 0.1,$ and $\sigma_{2} = 0.01$

Fig. 29

Shows the behaviors of $u_{j} (\tau )$, $v_{j} (\tau )$, and the planes $\,u_{j} v_{j}$ when $c_{3} = (0.007,0.005,0.003),$$c_{1} = 0.001,$ $c_{2} = 0.005,$$\omega_{1} = 1.24,$ $\omega_{2} = 2.556,$$\omega_{3} = 1.058,$$\sigma_{1} = - 0.1,$ and $\sigma_{2} = 0.01$

Fig. 30

Illustrates the influence of $\omega_{1} = (1.24,1.176,1.109),$ on $u_{j} (\tau ),$$v_{j} ,$ and $u_{j} v_{j}$ when $\omega_{2} = 2.556,$$\omega_{3} = 1.058,$$c_{1} = 0.001,$ $c_{2} = 0.005,$ $c_{3} = 0.002,$$\sigma_{1} = - 0.1,$ and $\sigma_{2} = 0.01$

Fig. 31

Presents the influence of $\omega_{2} = (2.556,2.213,1.979)$ on $u_{j} (\tau ),$$v_{j} ,$ and $u_{j} v_{j}$ when $\omega_{1} = 1.24,$$\omega_{3} = 1.058,$$c_{1} = 0.001,$ $c_{2} = 0.005,$$c_{3} = 0.002,$$\sigma_{1} = - 0.1,$ and $\sigma_{2} = 0.01$

Fig. 32

Reveals the impact of $\omega_{3} = (1.183,1.122,1.058)$ on $u_{j} (\tau ),$$v_{j} ,$ and $u_{j} v_{j}$ when $\omega_{1} = 1.24,$$\omega_{2} = 2.556,$$c_{1} = 0.001,$ $c_{2} = 0.005,$$c_{3} = 0.002,$$\sigma_{1} = - 0.1,$ and $\sigma_{2} = 0.01$

Parts of Figs. 30, 31, 32 have demonstrated the influence of various values of the frequencies $\omega_{1} ,\omega_{2} ,$ and $\omega_{3}$ on the behaviors of the newly adjusted phases $u_{j} ,$ $v_{j} ,$ and trajectory projections in the planes $u_{j} v_{j}$. These parts are drawn when $c_{1} = 0.001,$$c_{2} = 0.005,$$c_{3} = 0.002,$$\sigma_{1} = - 0.1,$ and $\sigma_{2} = 0.01$ at $\omega_{1} = (1.24,1.176,1.109),$$\omega_{2} = (2.556,2.213,1.979),$ and $\omega_{3} = (1.183,1.122,1.058)$ are taken into account. Portions (a), (d), (g) and (b), (e), (h) show time history curves for the new parameters $u_{j} \,\,(j = 1,2,3)$ and $v_{j}$, respectively. On the other hand, portions (c), (f), and (i) have the plane curves $u_{j} v_{j}$. It must be noted that the time histories of the functions $u_{1}$ and $v_{1}$ besides the corresponding phase plane plots $u_{1} v_{1}$ don't change with the variation of $\omega_{j}$, as seen in (a), (b), and (c) of Figs. 30, 31, 32. On the other hand, the behaviors of $u_{2} (\tau ),v_{2} (\tau ),$ and $u_{2} v_{2}$ have been influenced with the change of $\omega_{j}$, in which decay behaviors have been noted. Moreover, the curves of $u_{3} (\tau ),v_{3} (\tau ),$ and $u_{3} v_{3}$ are influenced, to some extent, by the change of $\omega_{j}$ values. The cause stems from the mathematical form of the structure of Eqs. (33).

Conclusions

A 3DOF auto-parametric vibrating dynamical system has been examined as a new prototype. The second kind of Lagrange equations is applied to derive the motion-controlling system, which is then solved analytically using the multiple scales technique. Considering the emerging resonance cases, the solvability requirements of the solutions are obtained. These solutions have been matched with the numerical solutions of the original system that have been obtained using the fourth-order Runge–Kutta approach, to reveal their good agreement. Three cases have been investigated concurrently, two of them are the fundamental external resonances and the third one is selected from the internal resonances. The stability/instability areas are investigated using the Routh–Hurwitz conditions, and they are analyzed considering the solutions in the steady-state case. The temporary histories of the accomplished solutions, the resonance curves regarding the modified amplitudes and phases, and the stability zones are graphically displayed and interpreted for different amounts of the analyzed system factors. The nonlinear stability analysis of the modulation equations is investigated and examined in terms of the new adjusted phases. The phase plane projections of these phases have spiral forms and directed towards one point, which confirms that the behavior of the investigated system is free of chaos. Although the used technique is conventional, the obtained outcomes for the dynamical system are considered novel. The attained results will be of interest to a broad variety of experts in the fields of space engineering and mechanics, as well as those concerned with attenuating vibration caused by swaying structures and rotor dynamics.

Appendices

Appendix (1)

$$\begin{aligned} q_{1}& = \frac{1}{{48(1 - 4w_{1}^{2} )(1 - w_{2}^{2} )^{3} (9w_{2}^{2} - 1)}}\{ 1 + 3w_{2}^{2} (49w_{2}^{2} - 27w_{2}^{4} - 25) - 4w_{1}^{2} [1 - 12\beta + 3w_{2}^{2} [(44\beta \hfill \\ & \,\,\,\,\, - 25) - (76\beta - 49)w_{2}^{2} + 9(4\beta - 3)w_{2}^{4} ]]\} , \hfill \\ q_{2} &= \frac{1}{{8(1 - 4w_{1}^{2} )(1 - w_{2} )^{2} (1 + w_{2} )^{3} }}\{ 3 - 6w_{2}^{2} + 4w_{2}^{4} + 4w_{1}^{2} [(4\beta - 3)(1 - 2w_{2}^{2} ) + 4(\beta - 1)w_{2}^{4} ]\} , \hfill \\ q_{3}& = \{ \frac{1}{{(1 - w_{2}^{2} )^{2} }}[h + w_{2}^{2} B_{3} \overline{B}_{3} - \frac{{2B_{1} \overline{B}_{1} }}{{w_{1}^{2} (1 - 4w_{1}^{2} )}}] + \frac{1}{{2(1 - 4w_{1}^{2} )(1 - w_{2}^{2} )^{4} }}\{ 1 + w_{2}^{2} (w_{2}^{2} + w_{2}^{4} - 2) \hfill \\ \,\,\,\,\,\, &+ 4w_{1}^{2} [(4\beta - 1)[1 + w_{2}^{2} (w_{2}^{2} - 2)] - w_{2}^{6} ]\} B_{2} \overline{B}_{2} \} , \hfill \\ q_{4} & = \frac{1}{2}\{ \frac{1}{{w_{1}^{2} (1 - 4w_{1}^{2} )(1 - w_{2}^{2} )^{3} }}\{ h(8w_{1}^{4} - 2w_{1}^{2} ) + (1 - w_{2}^{2} )[4B_{1} \overline{B}_{1} + w_{1}^{2} ((4 - 16\beta )w_{1}^{2} - 1)\,B_{2} \overline{B}_{2} ]\} \hfill \\ \,\,\,\,\,\, & - 2ic_{2} w_{1} \} , \hfill \\ q_{5} = \frac{1}{{8w_{2} (1 - 4w_{1}^{2} )(1 - w_{2} )^{3} (1 + w_{2} )^{2} }}\{ 3(1 - 2w_{2}^{2} ) + 4\{ w_{2}^{4} + w_{1}^{2} [4\beta - 3 + 2(3 - 4\beta )w_{2}^{2} \hfill \\ \,\,\,\,\,\, & + 4(\beta - 1)w_{2}^{4} ]\} \} , \hfill \\ \end{aligned}$$

Appendix (2)

$$\begin{aligned} \Gamma_{1} & = \frac{1}{2}[c_{1} + c_{2} + \frac{{2d_{3} }}{{b_{10} }} + \frac{{2d_{7} }}{{b_{20} w_{1} }} + \frac{{c_{3} }}{{w_{2}^{2} }} - \frac{{2b_{20} b_{30} d_{8} }}{{w_{1} w_{2} }}(2 + \sin \theta_{30} )], \hfill \\ \Gamma_{2} & = \frac{1}{{4b_{10} b_{20} w_{1}^{2} w_{2}^{3} }}\{ - 2\sin \theta_{30} b_{10} b_{20}^{2} b_{30} c_{3} d_{8} w_{1} + [8\sin \theta_{30} b_{10} b_{20}^{3} b_{30}^{2} d_{8}^{2} + 2b_{10} c_{3} d_{7} w_{1} \hfill \\ & \,\,\,\,\,\, + b_{20} c_{3} [b_{10} (c_{1} + c_{2} ) + 2d_{3} ]w_{1}^{2} ]w_{2} - 2b_{20} b_{30} d_{8} (2 + \sin \theta_{30} )[2b_{10} d_{7} + b_{20} (b_{10} \hfill \\ & \,\,\,\,\,\, \times (c_{1} + c_{2} ) + 2d_{3} )w_{1} ]w_{2}^{2} + [4b_{10} d_{5} d_{6} + 2[b_{10} (c_{1} + c_{2} ) + 2d_{3} ]d_{7} w_{1} + b_{20} [b_{10} c_{1} c_{2} \hfill \\ & \,\,\,\,\,\, - 4d_{1} d_{2} + 2(c_{1} + c_{2} )d_{3} ]w_{1}^{2} ]w_{2}^{3} \} , \hfill \\ \end{aligned}$$

$$\begin{aligned} \Gamma_{3} & = \frac{1}{{8b_{10} b_{20} w_{1}^{3} w_{2}^{3} }}\{ 2w_{1} (8\sin \theta_{30} b_{20}^{3} b_{30}^{2} d_{3} d_{8}^{2} w_{2} - 2b_{20}^{2} b_{30} d_{8} w_{1} (\sin \theta_{30} c_{3} d_{3} \, - (2 + \sin \theta_{30} )[2d_{1} d_{2} \hfill \\ & \,\,\,\,\,\, - (c_{1} + c_{2} )d_{3} ]w_{2}^{2} ) + 2\{ c_{3} d_{3} d_{7} w_{1} w_{2} + [ - 2d_{1} d_{2} d_{7} w_{1} + d_{3} (2d_{5} d_{6} + (c_{1} + c_{2} )d_{7} w_{1} )]w_{2}^{3} \} \hfill \\& \,\,\,\,\,\, - b_{20} w_{2} \{ c_{3} [2d_{1} d_{2} - (c_{1} + c_{2} )d_{3} ]w_{1}^{2} + w_{2} [4(2 + \sin \theta_{30} )b_{30} d_{3} d_{7} d_{8} + c_{2} (2d_{1} d_{2} - c_{1} d_{3} ) \hfill \\ & \,\,\,\,\,\, \times w_{1}^{2} w_{2} ]\} ) + b_{10} (8\sin \theta_{30} b_{20}^{3} b_{30}^{2} (c_{1} + c_{2} )d_{8}^{2} w_{1} w_{2} + 2w_{1} w_{2} \{ c_{3} [2d_{5} d_{6} + (c_{1} + c_{2} )d_{7} w_{1} ] \hfill \\ & \,\,\,\,\,\, + c_{1} (2d_{5} d_{6} + c_{2} d_{7} w_{1} )w_{2}^{2} \} + 2b_{20}^{2} b_{30} d_{8} \{ \sin \theta_{30} (8b_{30} d_{7} d_{8} w_{2} - c_{2} c_{3} w_{1}^{2} ) - c_{1} w_{1}^{2} (\sin \theta_{30} c_{3} \hfill \\ & \,\,\,\,\,\, + (2 + \sin \theta_{30} )c_{2} w_{2}^{2} )\} - b_{20} \{ - c_{1} c_{2} c_{3} w_{1}^{3} w_{2} + 4b_{30} d_{8} [\sin \theta_{30} c_{3} d_{7} w_{1} + (2 + \sin \theta_{30} ) \hfill \\& \,\,\,\,\,\, \times (2d_{5} d_{6} + (c_{1} + c_{2} )d_{7} w_{1} )w_{2}^{2} ]\} )\} , \hfill \\ \end{aligned}$$

$$\begin{aligned} \Gamma_{5} &= \frac{1}{{8\beta b_{10} b_{20} w_{1}^{4} w_{2}^{3} }}\{ - \beta \sin \theta_{30} b_{20} b_{30} c_{3} d_{8} w_{1} (4d_{3} d_{5} d_{6} + 2[(c_{1} + c_{2} )d_{3} - 2d_{1} d_{2} ]d_{7} w_{1} \hfill \\& \,\,\,\,\,\, + b_{20} c_{2} c_{1} d_{3} - 2d_{1} d_{2} )w_{1}^{2} ) + (c_{3} w_{1}^{2} (2d_{5} [\beta c_{1} d_{3} d_{6} - 2d_{1} (d_{4}^{2} + \beta d_{2} d_{6} )] + \beta c_{2} (c_{1} d_{3} \hfill \\& \,\,\,\,\,\, - 2d_{1} d_{2} )d_{7} w_{1} ) + 4\beta \sin \theta_{30} b_{20}^{2} b_{30}^{2} d_{8}^{2} \{ 4d_{3} d_{5} d_{6} + 2[(c_{1} + c_{2} )d_{3} - 2d_{1} d_{2} ]d_{7} w_{1} \hfill \\& \,\,\,\,\,\, + b_{20} c_{2} (c_{1} d_{3} - 2d_{1} d_{2} )w_{1}^{2} \} )w_{2} + 2(2 + \sin \theta_{30} )b_{20} b_{30} d_{8} w_{1} (2d_{5} [ - \beta c_{1} d_{3} d_{6} + 2d_{1} (d_{4}^{2} \hfill \\& \,\,\,\,\,\, + \beta d_{2} d_{6} )] + \beta c_{2} (2d_{1} d_{2} - c_{1} d_{3} )d_{7} w_{1} )w_{2}^{2} + \beta \sin \theta_{30} b_{10} b_{20} b_{30} c_{1} d_{8} (2d_{5} d_{6} + c_{2} d_{7} w_{1} ) \hfill \\& \,\,\,\,\,\, \times (4b_{20} b_{30} d_{8} w_{2} - c_{3} w_{1} )\} , \hfill \\ \Gamma_{6} = \frac{1}{{8\beta b_{10} w_{1}^{4} w_{2}^{3} }}\sin \theta_{30} b_{30} d_{8} \{ \beta c_{1} d_{3} (2d_{5} d_{6} + c_{2} d_{7} w_{1} ) - 2d_{1} [2d_{4}^{2} d_{5} + \beta d_{2} (2d_{5} d_{6} \hfill \\& \,\,\,\,\,\, + c_{2} d_{7} w_{1} )]\} (4b_{20} b_{30} d_{8} w_{2} - c_{3} w_{1} ), \hfill \\ \end{aligned}$$

where

$$\begin{aligned} d_{1} & = \frac{{f_{1} \cos \theta_{10} }}{2},\,\,\,\,\,\,\,\,\,\,d_{2} = \sigma_{1} + \frac{{\beta b_{20}^{2} }}{{4(4w_{1}^{2} - 1)}},\,\,\,\,\,\,\,\,\,\,d_{3} = \frac{{f_{1} \sin \theta_{10} }}{2}, \hfill \\ d_{4} &= \frac{{\beta b_{10} b_{20} }}{{2(4w_{1}^{2} - 1)}},\,\,\,\,\,\,\,\,\,\,d_{5} = \frac{{m_{0} \cos \theta_{20} }}{2}, \hfill \\ d_{6} & = - \sigma_{2} + \frac{1}{{4(4w_{1}^{2} - 1)(w_{1}^{2} - 1)}}\{ - 2hw_{1}^{2} (4w_{1}^{2} - 1) - (w_{1}^{2} - 1)[b_{10}^{2} + \frac{3}{4}w_{1}^{2} b_{20}^{2} \hfill \\ \,\,\,\,\,\,\,\,\, \times (4(1 - 4\beta )w_{1}^{2} - 1)]\} , \hfill \\ d_{7} &= \frac{{m_{0} \sin \theta_{20} }}{2},\,\,\,\,\,\,\,\,\,\,d_{8} = \frac{{w_{1}^{2} w_{2}^{2} }}{{16(w_{1}^{2} - 1)}},\,\,\,\,\,\,\,\,\,\,d_{9} = \frac{{b_{10} b_{20} b_{30} }}{{2(4w_{1}^{2} - w_{2}^{2} )(w_{1}^{2} - 1)}} - \frac{{w_{2} b_{30} d_{4} }}{\beta }, \hfill \\ \end{aligned}$$

$$\begin{aligned} d_{10} = \frac{1}{16}\{ \frac{1}{{(w_{2}^{2} - 1)}}\Bigg[w_{1}^{2} b_{30} (8h + b_{30}^{2} + 2w_{2}^{2} b_{20} b_{30} \cos \theta_{30} + \frac{{6(2w_{2}^{2} - 1)b_{20}^{2} }}{{(w_{2}^{2} - 1)}}) + \frac{{4b_{10}^{2} b_{30} }}{{(4w_{1}^{2} - w_{2}^{2} )}}\Bigg] \hfill \\ \,\,\,\,\,\,\, + 16w_{1} w_{2} (\sigma_{2} - \sigma_{3} )b_{30} - 16w_{2} (\sigma_{2} b_{30} - \frac{1}{{4(4w_{1}^{2} - 1)(w_{2}^{2} - 1)}}\{ 2hw_{1}^{2} (4w_{1}^{2} - 1)b_{30} \hfill \\ \,\,\,\,\,\,\, - (w_{2}^{2} - 1)[b_{10}^{2} b_{30} - \frac{3}{4}w_{1}^{2} b_{20}^{2} b_{30} (1 + 4(4\beta - 1)w_{1}^{2} )]\} )\} , \hfill \\ d_{11} = \frac{1}{16}\Bigg\{ - 8m_{0} w_{2} \cos \theta_{20} + \frac{{b_{20} w_{1}^{2} }}{{(w_{2}^{2} - 1)}}\Bigg(8h + 3b_{30}^{2} + 2w_{2}^{2} b_{30} b_{20} \cos \theta_{30} \Bigg] + \frac{{4b_{10}^{2} b_{20} }}{{(4w_{1}^{2} - w_{2}^{2} )(w_{2}^{2} - 1)}} \hfill \\ \,\,\,\,\,\,\,\, \times\Bigg [\frac{{2w_{1}^{2} (2w_{2}^{2} - 1)b_{20}^{3} }}{{(w_{2}^{2} - 1)^{2} }} + 16w_{1} w_{2} (\sigma_{2} - \sigma_{3} )b_{20} - 16w_{2} (\sigma_{2} b_{20} - \frac{1}{{4(4w_{1}^{2} - 1)(w_{2}^{2} - 1)}} \hfill \\ \,\,\,\,\,\,\,\, \times (2hw_{1}^{2} (4w_{1}^{2} - 1)b_{20} - (4w_{1}^{2} - 1)\{ b_{10}^{2} b_{20} - \frac{1}{4}w_{1}^{2} b_{20}^{3} [1 + 4(4\beta - 1)w_{1}^{2} ]\Bigg\} \Bigg)\Bigg)\Bigg\} . \hfill \\ \end{aligned}$$