Novel Asymptotic Solutions for the Planar Dynamical Motion of a Double-Rigid-Body Pendulum System Near Resonance

Abstract

Purpose

The planar dynamical motion of a double-rigid-body pendulum with two degrees-of-freedom close to resonance, in which its pivot point moves in a Lissajous curve has been addressed. In light of the generalized coordinates, equations of Lagrange have been used to construct the controlling equations of motion.

Methods

New innovative analytic approximate solutions of the governing equations have been accomplished up to higher order of approximation utilizing the multiple scales method. Resonance cases have been classified and the solvability conditions of the steady-state solutions have been obtained. The fourth-order Runge–Kutta method has been utilized to gain the numerical solutions for the equations of the governing system.

Results

The history timeline of the acquired solutions as well as the resonance curves have been graphically displayed to demonstrate the positive impact of the various parameters on the motion. The comparison between the analytical and numerical solutions revealed great consistency, which confirms and reinforces the accuracy of the achieved analytic solutions.

Conclusions

The non-linear stability analysis of these solutions have been examined and discussed, in which the stability and instability areas have been portrayed. All resonance cases and a combination of them have been examined. The archived results are considered as generalization of some previous works that are related to one rigid body and for fixed pendulum’s pivot point.

Introduction

The non-linear dynamical systems are studied in many research works due to its importance in many fields, for example in industrial applications, biology, and medicines, see [1,2,3,4]. Perturbation approaches [5] can be used to obtain the analytic approximate solutions of the equations of motion (EOM) of such systems. Among these approaches, the multiple scales method (MSM) has been attracted the attention of many researchers to find the approximate solutions (AS) of these systems owing to its powerful accuracy. It is known that the pendulum’s models are considered, to some extent, as simple systems that can be used to emulate the dynamics of a variety of engineering devices and machine parts. Various types of pendulums are widely analyzed in many scientific works as a substantial source of several practical applications in the field of non-linear dynamics.

The chaotic motion of a simple pendulum have been discussed in [6] and [7], while its approximate periodic motion is investigated in [8] utilizing the method of small parameter [5] when the pendulum’s suspension point moves on an elliptic trajectory. In [9], the motion of a weakly non-linear two degrees-of-freedom (DOF) dynamical system is investigated, in which its chaotic behavior for the case of internal resonance is examined. In [10], authors utilized the MSM to elucidate the steady behavior of a non-linear spring pendulum, whereas the author in [11] presented an improvement of the considered work [10] through the effects of an external force on the dynamical motion of the spring pendulum.

Furthermore, other types of pendulums have been studied in several works e.g. [12,13,14,15]. In [12], the authors used a dynamic absorber that can be moved along the longitudinal of transverse direction of the excited pendulum. High efficiency of this absorber is found for very little damped systems. The influence of the fluid flow on the motion of simple pendulum and a spring one is examined in [13] and [14] respectively. On the other hand, the motion of a vibrating absorber pendulum with a rotating base is investigated in [14]. The stability analysis is performed on a linear system where the rotatory motion is adjusted according to the law of proportional control. The chaotic motion of an un-damped spring pendulum is examined in [16] when its connected point moves in a circular trajectory. The extension of this work is found in [17] when the authors relied on the fact that the motion of the suspension point is on an ellipse. Some special examples for various motion of this point are presented. Authors of [18] have turned their attention to investigate the movement of the suspension point of a damped spring with linear stiffness on a Lissajous curve under the action of harmonically force and moments. In [19], the motion of a tuned absorber connected with simple pendulum is examined close to resonance. The MSM is applied to obtain the approximate solutions of [14, 16,17,18,19] and represented in various figures to show the significance of the applied forces and moments on the considered motion of each work.

The motion of a single damped rigid-body-pendulum (RBP) is examined in different research works such as [20,21,22,23,24,25], in which its suspension point is considered to be fixed in [20], while it was considered in motion on different paths as in [21,22,23,24]. The stiffness coefficients of the spring are constraint to be linear and non-linear in [20, 21, 23] and [22, 24] respectively. The investigated motions are influenced by external forces and moments and studied analytically using the MSM. Resonance cases are categorized and examined to obtain the solvability conditions and the modulation equations (ME). The non-linear stability of these equations is introduced in [24] to reveal the stability and instability ranges of the fixed points at the steady-state case. The numerical solutions of the RBP is investigated in [25] using the Runge–Kutta algorithms from fourth-order.

There are many theoretical and experimental studies discuss the motion of double pendulums. In [26], a modified midpoint integrator is used to analysis the planar movement of a double pendulum numerically, in which Poincaré sections and bifurcation diagrams are presented for specified values of energy. The internal resonance of this pendulum has been studied in [27]. The bifurcation structure of a parametric excited double pendulum at small amplitudes of oscillation is studied in [28] while the resonance and non-resonance cases of this pendulum are analyzed in [29]. The rotatory motion of a model consists of two pivotal pendulums about horizontal axes as investigated in [30]. It is supposed that the model has four relative equilibrium locations in which the stabilities of these locations are studied. The influence of the gravity force on the double pendulum’s motion with a vibrating suspension point is investigated in [31].

This work concerns a novel problem of the planar motion of dynamical system consists of 2DOF double RBP, whose pivot point has been constrained to move in a Lissajous curve. The non-linear differential EOM are derived utilizing the second kind of Lagrange’s equations. Higher estimations of the analytical solutions are achieved using the MSM. These solutions are compared with the numerical ones, which are obtained using the fourth-order Runge–Kutta method, to show the great accuracy between them. In light of the categorized resonance cases; the solvability conditions and the ME are obtained. Criterion of Routh–Hurwitz is applied to check the stability of the fixed points of the steady-state solutions. The non-linear stability analysis of the ME is examined and discussed through the stability and instability ranges of the plotted curves of the frequency responses. The time histories of the solutions are graphed as well as the curves of resonance to explore the significance of various values of the physical parameters on the systems’ behavior. One of the most important applications of this work in our daily life is to utilize the vibrational motion for the robotic devices, pump compressors, rotor dynamics, and transportation devices.

Dynamical Modeling

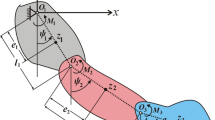
The investigated dynamical model in this work consists of two pivotally connected double RBP of mass $m_{j} \,(j = 1,2)$ from the points $O_{j}$_. The first pivot at $O_{1}$ is restricted to move in a Lissajous curve in the direction of anticlockwise, while the second one at $O_{2}$ is considered a connection point between the two bodies, see Fig. 1. Therefore, the kinematic coordinates of $O_{1}$ are

$$\begin{gathered} x = R_{x} cos(\Omega_{x\,} t), \hfill \\ y = R_{y} sin(\Omega_{y} t)\,, \hfill \\ \end{gathered}$$

(1)

where $R_{x} ,R_{y} ,\Omega_{x} ,$ and $\Omega_{y}$ are known parameters.

Fig. 1

Description of the dynamical model

It is taken into consideration that the geometric quantities $e_{j}$ and $l_{1}$ express the distance of the gravities centers $z_{j}$ (that are calculated from the rotation’s centers) and the pendulum’s link length, respectively. Moreover, let $J_{j}$ represent the moment of inertia, $\gamma_{j}$ are the angular position variables that represent the chosen generalized coordinates of the model, and $g$ is the acceleration of gravity.

To study the motion, we consider that the motion of the model is planar in addition to action of two kinematic moments $M_{{\gamma_{1} }} (t) = M_{1} (t)\,\cos (\Omega_{1} t)$ and $M_{{\gamma_{2} }} (t) = M_{2} (t)\,\cos (\Omega_{2} t)$ around the points $O_{1}$ and $O_{2}$ respectively. Here $\Omega_{1}$ and $\Omega_{2}$ denote the forcing frequencies of $M_{{\gamma_{1} }} (t)$ and $M_{{\gamma_{2} }} (t)$ respectively.

Referring to above, we can introduce the potential and kinetic energies $V$ and $T$ as follows

$$\begin{aligned} V & = - g[(m_{1} + m_{2} )\,R_{x} \cos \Omega_{x} t + (e_{1} m_{1} + l_{1} m_{2} )\cos \gamma_{1} + m_{2} e_{2} \cos \gamma_{2} ], \\ T & = \frac{1}{2}\{ [J_{1} \, + (m_{1} e_{1}^{2} + m_{2} l_{1}^{2} )]\dot{\gamma }_{1}^{2} + [J_{2} \, + m_{2} \,e_{2}^{2} ]\,\dot{\gamma }_{2}^{2} + \,(m_{1} + m_{2} )[\Omega_{y}^{2} R_{y}^{2} \cos^{2} \Omega_{y} t \\ & \quad + R_{x}^{2} \Omega_{x}^{2} \sin^{2} \Omega_{x} t]\} + \dot{\gamma }_{1} (m_{1} e_{1} + m_{2} l_{1} )[R_{y} \Omega_{y} \cos \gamma_{1} \cos \Omega_{y} t + R_{x} \Omega_{x} \sin \gamma_{1} \sin \Omega_{x} t\,] \\ & \quad + e_{2} l_{1} m_{2} \dot{\gamma }_{1} \dot{\gamma }_{2} \cos (\gamma_{1} - \gamma_{2} ) + e_{2} m_{2} \dot{\gamma }_{2} [R_{y} \Omega_{y} \cos \gamma_{2} \cos \Omega_{y} t + R_{x} \Omega_{x} \sin \gamma_{2} \sin \Omega_{x} t\,], \\ \end{aligned}$$

(2)

where dot represents the derivative with respect to time $t$.

According to the Lagrangian $L = T - V$, the governing EOM were obtained from the following second type of Lagrange’s equations

$$\frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{\partial L}{{\partial \dot{\gamma }_{j} }}} \right) - \left( {\frac{\partial L}{{\partial \gamma_{j} }}} \right) = Q_{j} ;\,\,\,\,\,\,\,\,(j = 1,2)$$

(3)

where $\dot{\gamma }_{j}$ are the generalized velocities corresponding to the generalized coordinates $\gamma_{j}$ and $Q_{j}$ are the generalized forces which can be written in the forms

$$Q_{j} = M_{j} (t)\,\cos (\Omega_{j} t);\,\,\,\,\,\,(j = 1,2).$$

(4)

Introducing the dimensionless forms of the generalized coordinate, parameters, frequencies and time $\tau$ as follows

$$\begin{gathered} \varpi = \frac{{\omega_{2} }}{{\omega_{1} }}\,,\,\,\,\omega_{1}^{2} = \frac{{m_{1} e_{1} g}}{{J_{1} }}\,,\,\,\,\omega_{2}^{2} = \frac{{m_{2} e_{2} g}}{{J_{2} }},\,\,\,p_{1} = \frac{{\Omega_{1} }}{{\omega_{1} }},\,\,\,p_{2} = \frac{{\Omega_{2} }}{{\omega_{1} }},\,\,\,p_{x} = \frac{{\Omega_{x} }}{{\omega_{1} }},\,\,\,p_{y} = \frac{{\Omega_{y} }}{{\omega_{1} }}, \hfill \\ r_{1x} = \frac{{R_{x} }}{{l_{1} }},\,\,\,r_{1y} = \frac{{R_{y} }}{{l_{1} }},\,\,\,B_{1} = \frac{{m_{1} e_{1}^{2} + m_{2} l_{1}^{2} }}{{J_{1} }},\,\,\,B_{2} = \frac{{m_{2} e_{2}^{2} }}{{J_{2} }},\,\,\,s_{1} = \frac{{gm_{2} l_{1} }}{{J_{1} \omega_{1}^{2} }},\,\,\,\alpha_{1} = \frac{{m_{1} e_{1} l_{1} + m_{2} l_{1}^{2} }}{{J_{1} }}, \hfill \\ N_{1} = \frac{{e_{2} l_{1} m_{2} }}{{J_{1} }},\,\,\,N_{2} = \frac{{m_{2} e_{2} l_{1} }}{{J_{2} }},\,\,\,f_{1} = \frac{{M_{1} (t)}}{{J_{1} \omega_{1}^{2} }},\,\,\,f_{2} = \frac{{M_{2} (t)}}{{J_{2} \,\omega_{1}^{2} }},\,\,\,\tau = \omega_{1} t. \hfill \\ \end{gathered}$$

(5)

Making use of Eqs. (2), (3), (4), and (5) we get the following dimensionless forms of the EOM

$$\begin{gathered} (1 + B_{1} )\ddot{\gamma }_{1} + N_{1} \ddot{\gamma }_{2} \cos (\gamma_{1} - \gamma_{2} ) + \alpha_{1} [r_{1x} p_{x}^{2} \cos (p_{x} \tau )\,\sin \gamma_{1} - r_{1y} p_{y}^{2} \sin (p_{y} \tau )cos\gamma_{1} ] \hfill \\ \, + N_{1} \dot{\gamma }_{2}^{2} \sin (\gamma_{1} - \gamma_{2} ) + (1 + s_{1} )sin\gamma_{1} = f_{1} \cos (p_{1} \tau )\,, \hfill \\ \end{gathered}$$

(6)

$$\begin{gathered} (1 + B_{2} )\ddot{\gamma }_{2} + N_{2} \ddot{\gamma }_{1} \cos (\gamma_{1} - \gamma_{2} ) - N_{2} \dot{\gamma }_{1}^{2} \sin (\gamma_{1} - \gamma_{2} ) + N_{2} [r_{1x} p_{x}^{2} \cos (p_{x} \tau )\,\sin \gamma_{2} \hfill \\ - r_{1y} p_{y}^{2} \sin (p_{y} \tau )cos\gamma_{2} ] + \varpi^{2} sin\gamma_{2} = f_{2} \cos (p_{2} \tau )\,. \hfill \\ \end{gathered}$$

(7)

It must me noted that the derivatives in the previous system of Eqs. (6) and (7) are considered with respect to the dimensionless time parameter $\tau$. Moreover, This system has two second-order non-linear differential equations regarding $\gamma_{1}$ and $\gamma_{2}$.

The Approved Method

This section presents the MSM that has been used to estimate the analytic solutions of the EOM and to categorize the resonances cases. Consequently, we can approximate the trigonometric functions of $\gamma_{1}$ and $\gamma_{2}$ up to third-order using Taylor’s series, which are valid at the position of static equilibrium. Then Eqs. (6) and (7) will take the forms

$$\begin{gathered} (1 + B_{1} )\ddot{\gamma }_{1} + N_{1} \frac{{\ddot{\gamma }_{2} }}{36}[9(\gamma_{1}^{2} - 2)(\gamma_{2}^{2} - 2) + \gamma_{1} \gamma_{2} (\gamma_{1}^{2} - 6)(\gamma_{2}^{2} - 6)] + \alpha_{1} \left[ {r_{1x} p_{x}^{2} \cos (p_{x} \tau ) \times \left( {\gamma_{1} - \frac{{\gamma_{1}^{3} }}{6}} \right) - r_{1y} p_{y}^{2} \sin (p_{y} \tau )\left( {1 - \frac{{\gamma_{1}^{2} }}{2}} \right)} \right] \hfill \\ + \frac{{N_{1} \dot{\gamma }_{2}^{2} }}{12}[\gamma_{1} (\gamma_{1}^{2} - 6)(\gamma_{2}^{2} - 2) - \gamma_{2} (\gamma_{1}^{2} - 2)(\gamma_{2}^{2} - 6)] + (1 + s_{1} )\left( {\gamma_{1} - \frac{{\gamma_{1}^{3} }}{6}} \right) = f_{1} \cos (p_{1} \tau )\,, \hfill \\ \end{gathered}$$

(8)

$$\begin{gathered} (1 + B_{2} )\ddot{\gamma }_{2} + \frac{{N_{2} \ddot{\gamma }_{1} }}{36}[9(\gamma_{1}^{2} - 2)(\gamma_{2}^{2} - 2) + \gamma_{1} \gamma_{2} (\gamma_{1}^{2} - 6)(\gamma_{2}^{2} - 6)] - \frac{{N_{2} \dot{\gamma }_{1}^{2} }}{12}[\gamma_{1} (\gamma_{1}^{2} - 6) \times (\gamma_{2}^{2} - 2) - \gamma_{2} (\gamma_{1}^{2} - 2)(\gamma_{2}^{2} - 6)] \hfill \\ + N_{2} \left[ {r_{1x} p_{x}^{2} \cos (p_{x} \tau )\,\left( {\gamma_{2} - \frac{{\gamma_{2}^{3} }}{6}} \right) - r_{1y} p_{y}^{2} \sin (p_{y} \tau ) \times \left( {1 - \frac{{\gamma_{2}^{2} }}{2}} \right)} \right] + \varpi^{2} \left( {\gamma_{2} - \frac{{\gamma_{2}^{3} }}{6}} \right) = f_{2} \cos (p_{2} \tau )\,. \hfill \\ \end{gathered}$$

(9)

Now, we introduce the coordinates $\gamma_{1}$ and $\gamma_{2}$ as functions of small parameter $0 < \,\varepsilon < < 1$ as follows as

$$\gamma_{1} (\tau ) = \varepsilon \,\mu (\tau ;\varepsilon )\,,\,\,\,\,\,\,\,\,\,\,\,\,\gamma_{2} (\tau ) = \varepsilon \,\varphi (\tau ;\varepsilon )\,,$$

(10)

where $\mu$ and $\varphi$ are the new variables that can be sought as follows [32]

$$\begin{gathered} \mu (\tau ;\varepsilon ) = \sum\limits_{k = 1}^{3} {\varepsilon^{k - 1} \mu_{k} (\tau_{0} ,\,\tau_{1} ,\,\tau_{2} )} + O(\varepsilon^{3} ), \hfill \\ \varphi (\tau ;\varepsilon ) = \sum\limits_{k = 1}^{3} {\varepsilon^{k - 1} \varphi_{k} (\tau_{0} ,\,\tau_{1} ,\,\tau_{2} )} + O(\varepsilon^{3} ). \hfill \\ \end{gathered}$$

(11)

where $\tau_{n} = \varepsilon^{n} t\,\,\,(n = 0,\,1\,,\,2)$ are different time scales.

Based on these scales, the time derivatives have been transformed regarding to these scales as follows

$$\begin{gathered} \frac{{\text{d}}}{{{\text{d}}\tau }} = \frac{\partial }{{\partial \tau_{0} }} + \varepsilon \frac{\partial }{{\partial \tau_{1} }} + \varepsilon^{2} \frac{\partial }{{\partial \tau_{2} }}, \hfill \\ \frac{{{\text{d}}^{2} }}{{{\text{d}}\tau^{2} }} = \frac{{\partial^{2} }}{{\partial \tau_{0}^{2} }} + 2\varepsilon \frac{{\partial^{2} }}{{\partial \tau_{0} \partial \tau_{1} }} + \varepsilon^{2} \left( {\frac{{\partial^{2} }}{{\partial \tau_{1}^{2} }} + 2\frac{{\partial^{2} }}{{\partial \tau_{0} \partial \tau_{2} }}} \right) + O(\varepsilon^{3} ). \hfill \\ \end{gathered}$$

(12)

Furthermore, we propose that

$$\begin{gathered} B_{j} = \varepsilon \,\tilde{B}_{j} ,\,\,\,\,\,\,f_{j} = \varepsilon^{3} \tilde{f}_{j} ,\,\,\,\,\,\,\,\,N_{j} = \varepsilon \tilde{N}_{j} ,\,\,\,\,\,\,\,(j = 1,2) \hfill \\ r_{1x} = \varepsilon \,\tilde{r}_{1x} ,\,\,\,\,\,\,r_{1y} = \varepsilon \,\tilde{r}_{1y} ,\,\,\,\,\,\,s_{1} = \varepsilon \,\tilde{s}_{1} ,\,\,\,\,\,\,\alpha_{1} = \varepsilon \tilde{\alpha }_{1} , \hfill \\ \end{gathered}$$

(13)

where $\tilde{B}_{j} ,\tilde{N}_{j} \,,\tilde{f}_{j} \,,\tilde{s}_{1} \,,\tilde{r}_{1x} \,,\tilde{r}_{1y} ,$ and $\tilde{\alpha }_{1}$ are parameters of order unity.

Inserting Eqs. (10)–(13) into Eqs. (8) and (9), equaling the coefficients of the same power of $\varepsilon$ to get the following three groups of partial differential equations (PDE) according to the orders of $\varepsilon$.

The first group of PDE of order $(\varepsilon )$

$$\frac{{\partial^{2} \mu_{1} }}{{\partial \tau_{0}^{2} }} + \mu_{1} = 0\,,$$

(14)

$$\frac{{\partial^{2} \varphi_{1} }}{{\partial \tau_{0}^{2} }} + \varpi^{2} \varphi_{1} = 0\,,\,$$

(15)

The second group of PDE of order $(\varepsilon^{2} )$

$$\frac{{\partial^{2} \mu_{2} }}{{\partial \tau_{0}^{2} }} + \mu_{2} = \tilde{\alpha }_{1} \tilde{r}_{1y} p_{y}^{2} \,\sin (p_{y} \tau_{0} ) - \tilde{s}_{1} \mu_{1} - 2\frac{{\partial^{2} \mu_{1} }}{{\partial \tau_{0} \partial \tau_{1} }} - \tilde{N}_{1} \frac{{\partial^{2} \varphi_{1} }}{{\partial \tau_{0}^{2} }}\, - \tilde{B}_{1} \frac{{\partial^{2} \mu_{1} }}{{\partial \tau_{0}^{2} }},$$

(16)

$$\frac{{\partial^{2} \varphi_{2} }}{{\partial \tau_{0}^{2} }} + \varpi^{2} \varphi_{2} = \tilde{N}_{2} \tilde{r}_{1y} \,p_{y}^{2} \sin (p_{y} \tau_{0} ) - \tilde{B}_{2} \frac{{\partial^{2} \varphi_{1} }}{{\partial \tau_{0}^{2} }}\, - \tilde{N}_{2} \frac{{\partial^{2} \mu_{1} }}{{\partial \tau_{0}^{2} }} - 2\frac{{\partial^{2} \varphi_{1} }}{{\partial \tau_{0} \partial \tau_{1} }},$$

(17)

The third group of PDE of order $(\varepsilon^{3} )$

$$\begin{aligned} \frac{{\partial^{2} \mu_{3} }}{{\partial \tau_{0}^{2} }} + \mu_{3} & = \tilde{f}_{1} \cos p_{1} \tau_{0} - 2\frac{{\partial^{2} \mu_{2} }}{{\partial \tau_{0} \partial \tau_{1} }} - 2\frac{{\partial^{2} \mu_{1} }}{{\partial \tau_{0} \partial \tau_{2} }} - \frac{{\partial^{2} \mu_{1} }}{{\partial \tau_{1}^{2} }} - \tilde{B}_{1} \frac{{\partial^{2} \mu_{2} }}{{\partial \tau_{0}^{2} }} - \,\,2\tilde{B}_{1} \frac{{\partial^{2} \mu_{1} }}{{\partial \tau_{0} \partial \tau_{1} }}\, \\ & \quad - \tilde{N}_{1} \frac{{\partial^{2} \varphi_{2} }}{{\partial \tau_{0}^{2} }} - 2\tilde{N}_{1} \frac{{\partial^{2} \varphi_{1} }}{{\partial \tau_{0} \partial \tau_{1} }} - \tilde{\alpha }_{1} \tilde{r}_{1x} p_{x}^{2} \mu_{1} \cos p_{x} \tau_{0} + \frac{{\mu_{1}^{3} }}{6} - \tilde{s}_{1} \mu_{2} , \\ \end{aligned}$$

(18)

$$\begin{aligned} \frac{{\partial^{2} \varphi_{3} }}{{\partial \tau_{0}^{2} }} + \varpi^{2} \varphi_{3} & = \tilde{f}_{2} \cos \,p_{2} \tau_{0} + \frac{{\varpi^{2} \varphi_{1}^{3} }}{6} - \frac{{\partial^{2} \varphi_{1} }}{{\partial \tau_{1}^{2} }} - 2\frac{{\partial^{2} \varphi_{2} }}{{\partial \tau_{0} \partial \tau_{1} }} - 2\frac{{\partial^{2} \varphi_{1} }}{{\partial \tau_{0} \partial \tau_{2} }} \\ & \quad - \tilde{B}_{2} \frac{{\partial^{2} \varphi_{2} }}{{\partial \tau_{0}^{2} }} - 2\tilde{B}_{2} \frac{{\partial^{2} \varphi_{1} }}{{\partial \tau_{0} \partial \tau_{1} }} - \tilde{N}_{2} \frac{{\partial^{2} \mu_{2} }}{{\partial \tau_{0}^{2} }} - 2\tilde{N}_{2} \frac{{\partial^{2} \mu_{1} }}{{\partial \tau_{0} \partial \tau_{1} }} \\ & \quad - \tilde{N}_{2} \,\tilde{r}_{1x} \,p_{x}^{2} \,\varphi_{1} \,\cos p_{x} \tau_{0} + \frac{{\varpi^{2} }}{6}\varphi_{1}^{3} . \\ \end{aligned}$$

(19)

The previous Eqs. (14)–(19) constitute a system of six non-linear PDE. The solutions of these equations can be gained consecutively. Therefore, the solutions of Eqs. (14) and (15) are

$$\mu_{1} \, = {\text{A}}_{{1}} e^{{i\,\tau_{0} }} + {\overline{\text{A}}}_{{1}} e^{{ - i\,\tau_{0} }} ;\,\,\,\,\,(i = \sqrt { - 1} )$$

(20)

$$\varphi_{1} = {\text{A}}_{{2}} e^{{i\,\varpi \,\tau_{0} }} + {\overline{\text{A}}}_{{2}} e^{{ - i\,\varpi \,\tau_{0} }} ,$$

(21)

where ${\text{A}}_{j} \,\,(j = 1,\,2)$ are complex functions of the scales $\tau_{j}$ that can be determined latter, while $\overline{{\text{A}}}_{j}$ indicate to their complex conjugate.

Introducing Eqs. (20) and (21) into Eqs. (16) and (17), then omitting terms that yield the secular ones to obtain the conditions for omitting these terms as follows

$$\begin{gathered} 2i\frac{{\partial {\rm A}_{1} }}{{\partial \tau_{1} }} + {\rm A}_{1} (\tilde{s}_{1} - \tilde{B}_{1} ) = 0\,, \hfill \\ 2i\frac{{\partial {\rm A}_{2} }}{{\partial \tau_{1} }} - \varpi \,{\rm A}_{2} \tilde{B}_{2} = 0\,, \hfill \\ \end{gathered}$$

(22)

Based on these conditions, the second-order solutions become

$$\mu_{2} = \frac{{\varpi^{2} \tilde{N}_{1} {\rm A}_{2} }}{{(1 - \varpi^{2} )}}e^{{i\,\varpi \tau_{0} \,}} + \frac{{\tilde{\alpha }_{1} \tilde{r}_{1y} p_{y}^{2} e^{{i\,p_{y} \tau_{0} \,}} }}{{2\,i(1 - p_{y}^{2} )}} + CC,\,$$

(23)

$$\varphi_{2} = \frac{{\tilde{N}_{2} {\rm A}_{1} e^{{i\,\tau_{0} }} }}{{(\varpi^{2} - 1)}} + \frac{{\tilde{N}_{2} \tilde{r}_{1y} p_{y}^{2} e^{{i\,p_{y} \tau_{0} \,}} }}{{2\,i(\varpi^{2} - p_{y}^{2} )}} + CC,$$

(24)

where the letters $CC$ are the complex conjugates of the preceding terms.

The conditions of the elimination of the secular elements from the third-order approximate Eqs. (18) and (19) have the forms

$$\frac{{\partial^{2} {\rm A}_{1} }}{{\partial \tau_{1}^{2} }} + 2i\left( {\frac{{\partial {\rm A}_{1} }}{{\partial \tau_{2} }} + \tilde{B}_{1} \frac{{\partial {\rm A}_{1} }}{{\partial \tau_{1} }}} \right) - \frac{{\tilde{N}_{1} \tilde{N}_{2} }}{{(\varpi^{2} - 1)}}{\rm A}_{1} - \frac{1}{2}{\rm A}_{1}^{2} \overline{\rm A}_{1} = 0\,,\,$$

(25)

$$\frac{{\partial^{2} {\rm A}_{2} }}{{\partial \tau_{1}^{2} }} + \,2i\varpi \left( {\frac{{\partial {\rm A}_{2} }}{{\partial \tau_{2} }} + \tilde{B}_{2} \frac{{\partial {\rm A}_{2} }}{{\partial \tau_{1} }}} \right) - \frac{{\varpi^{4} \tilde{N}_{1} \tilde{N}_{2} }}{{(1 - \varpi^{2} )}}{\rm A}_{2} - \frac{{\varpi^{2} }}{2}{\rm A}_{2}^{2} \overline{\rm A}_{2} = 0\,,\,$$

(26)

Thus, the third-order approximations $\mu_{3}$ and $\varphi_{3}$ can be written as follows

$$\begin{aligned} \mu_{3} & = \frac{{\tilde{f}_{1} e^{{i\,p_{1} \tau_{0} }} }}{{2(1 - p_{1}^{2} )}} - \frac{{{\rm A}_{1}^{3} e^{{3i\,\tau_{0} }} }}{48} + \frac{{\tilde{\alpha }_{1} \tilde{r}_{1x} p_{x}^{2} \,e^{{i\,(p_{x} + 1)\tau_{0} }} {\rm A}_{1} }}{{2p_{x} \,(p_{x} + 2)}} + \frac{{\tilde{\alpha }_{1} \tilde{r}_{1x} p_{x}^{2} \,e^{{i\,(p_{x} - 1)\tau_{0} }} \overline{\rm A}_{1} }}{{2p_{x} \,(p_{x} - 2)}} - \frac{{e^{{i\varpi \tau_{0} }} }}{{(1 - \varpi^{2} )^{2} }}[\varpi^{2} \tilde{N}_{1} \tilde{B}_{2} {\rm A}_{2} \\ & \quad \, - \tilde{N}_{1} {\rm A}_{2} (\tilde{B}_{1} \varpi^{4} - \tilde{s}_{1} \varpi^{2} )] + \,\frac{{e^{{ip_{y} \tau_{0} }} }}{{(1 - p_{y}^{2} )}}\left[ {\frac{{p_{y}^{4} \tilde{N}_{2} \tilde{N}_{1} \tilde{r}_{1y} }}{{2i\,(\varpi^{2} - p_{y}^{2} )}} + \frac{{\tilde{\alpha }_{1} \tilde{r}_{1y} p_{y}^{2} (\tilde{B}_{1} p_{y}^{2} - \tilde{s}_{1} )\,}}{{2\,i\,(1 - p_{y}^{2} )}}} \right] + CC, \\ \end{aligned}$$

(27)

$$\begin{aligned} \varphi_{3} & = \frac{{\tilde{f}_{2} e^{{i\,p_{2} \tau_{0} }} }}{{2(\varpi^{2} - p_{2}^{2} )}} - \frac{{{\rm A}_{2}^{3} e^{{3i\varpi \,\tau_{0} }} }}{48}\, + \frac{{e^{{i\,\tau_{0} }} }}{{(\varpi^{2} - 1)^{2} }}[\tilde{N}_{2} \tilde{B}_{2} {\rm A}_{1} - \tilde{N}_{2} \varpi^{2} {\rm A}_{1} (\tilde{B}_{1} - \tilde{s}_{1} )] + \,\frac{{p_{y}^{4} \tilde{N}_{2} \tilde{r}_{1y} e^{{ip_{y} \tau_{0} }} }}{{2i\,(\varpi^{2} - p_{y}^{2} )}} \\ & \quad \times \,\left[ {\frac{{\tilde{B}_{2} }}{{(\varpi^{2} - p_{y}^{2} )}} + \frac{{\tilde{\alpha }_{1} }}{{(1 - p_{y}^{2} )}}} \right]\, - \tilde{N}_{2} \tilde{r}_{1x} p_{x}^{2} \left[ {\frac{{{\rm A}_{2} e^{{i\tau_{0} (p_{x} + \varpi )}} }}{{2(\varpi^{2} - (p_{x} + \varpi )^{2} )}} + \frac{{\overline{\rm A}_{2} e^{{i\tau_{0} (p_{x} - \varpi )}} }}{{2(\varpi^{2} - (p_{x} - \varpi )^{2} )}}} \right] + CC. \\ \end{aligned}$$

(28)

It is worthy to mention that the functions ${\rm A}_{j} \,\,(j = 1,\,2)$ can be calculated from the eliminating conditions of secular terms Eqs. (22), (25), and (26).

Modulation Equations (ME)

This section’s purpose is to characterise resonance cases, to gain the conditions of solvability, and to obtain the ME. It is known that if the denominators of the solutions Eqs. (27) and (28) approach to zero [33], then these solutions break down and the resonance cases are noticeable. As a result, it falls under the following categories:

• (i) The major external resonance appears when $p_{1} \approx 1\,,p_{2} \approx \varpi$,

• (ii) The internal resonance arises when $\varpi \approx 1\,,\,p_{x} \approx 2\,,p_{x} \approx 2\varpi ,p_{y} \approx 1\,,p_{y} \approx \varpi .$

If any of the preceding conditions are met, the system's dynamical performance will be extremely tough. It's worth noting that when oscillations escape from resonances positions, the AS in the previous section are still valid.

First, we'll look at two major external resonances that are presenting at the same time, in which the nearness of $p_{1} ,\,\,p_{2}$ to $1\,,\,\,\varpi$ can be expressed by using the detuning parameters of $\sigma_{1}$ and $\sigma_{2}$ (which refer to the distance between vibrations and the stringent resonance [34]) as follows

$$p_{1} = 1 + \sigma_{1} \,,\,\,\,\,\,\,\,\,p_{2} = \varpi + \sigma_{2} .$$

(29)

Therefore, we can introduce them in terms of $O(\varepsilon )$ as follows

$$\sigma_{j} = \varepsilon \tilde{\sigma }_{j} ;\,\,\,\,\,\,\,\,\,(j = 1,\,2).$$

(30)

Substituting Eqs. (29)–(30) into Eqs. (16)–(19), and eliminating terms that lead to secular ones to get the conditions of solvability of the second-order of approximation as in Eq. (22) and the third-order of approximation as follows

$$\begin{gathered} \frac{{\partial^{2} {\rm A}_{1} }}{{\partial \tau_{1}^{2} }} + 2i\frac{{\partial {\rm A}_{1} }}{{\partial \tau_{2} }} + 2i\tilde{B}_{1} \frac{{\partial {\rm A}_{1} }}{{\partial \tau_{1} }} - \frac{{\tilde{N}_{1} \tilde{N}_{2} }}{{(\varpi^{2} - 1)}}{\rm A}_{1} - \frac{1}{2}{\rm A}_{1}^{2} \overline{\rm A}_{1} - \frac{{\tilde{f}_{1} }}{2}e^{{i\tilde{\sigma }_{1} \tau_{1} }} = 0, \hfill \\ \frac{{\partial^{2} {\rm A}_{2} }}{{\partial \tau_{1}^{2} }} + \,2i\varpi \frac{{\partial {\rm A}_{2} }}{{\partial \tau_{2} }} + 2i\varpi \tilde{B}_{2} \frac{{\partial {\rm A}_{2} }}{{\partial \tau_{1} }} - \frac{{\varpi^{4} \tilde{N}_{1} \tilde{N}_{2} }}{{(1 - \varpi^{2} )}}{\rm A}_{2} - \frac{{\varpi^{2} }}{2}{\rm A}_{2}^{2} \overline{\rm A}_{2} - \frac{{\tilde{f}_{2} }}{2\,}e^{{i\tilde{\sigma }_{2} \tau_{1} }} = 0\,. \hfill \\ \end{gathered}$$

(31)

Making use of conditions Eq. (22) into Eq. (31), to yield

$$\begin{gathered} \frac{3}{4}{\rm A}_{1} \tilde{B}_{1}^{2} - \frac{1}{2}\tilde{s}_{1} {\rm A}_{1} \tilde{B}_{1} - \frac{1}{4}{\rm A}_{1} \tilde{s}_{1}^{2} + \,2i\frac{{\partial {\rm A}_{1} }}{{\partial \tau_{2} }} - \frac{{\tilde{N}_{1} \tilde{N}_{2} }}{{(\varpi^{2} - 1)}}{\rm A}_{1} - \frac{1}{2}{\rm A}_{1}^{2} \overline{\rm A}_{1} - \frac{{\tilde{f}_{1} }}{2}e^{{i\tilde{\sigma }_{1} \tau_{1} }} = 0, \hfill \\ \frac{3}{4}\varpi^{2} \tilde{B}_{2}^{2} {\rm A}_{2} + 2i\varpi \frac{{\partial {\rm A}_{2} }}{{\partial \tau_{2} }} - \frac{{\varpi^{4} \tilde{N}_{1} \tilde{N}_{2} }}{{(1 - \varpi^{2} )}}{\rm A}_{2} - \frac{{\varpi^{2} }}{2}{\rm A}_{2}^{2} \overline{\rm A}_{2} - \frac{{\tilde{f}_{2} }}{2\,}e^{{i\tilde{\sigma }_{2} \tau_{1} }} = 0\,. \hfill \\ \end{gathered}$$

(32)

It is noted from Eqs. (22) and (32) that the conditions of solvability of the investigated model consisting of four PDE regarding the functions ${\rm A}_{j} \,\,(j = 1,2)$, in which conditions Eqs. (22) and (32) reveal that ${\rm A}_{j}$ depend upon the slow time parameters $\tau_{1}$ and $\tau_{2}$. Then we can represent ${\rm A}_{j}$ as in the following polar form

$${\rm A}_{j} (\tau_{1} ,\tau_{2} ) = \frac{{\tilde{a}_{j} (\tau_{1} ,\tau_{2} )}}{2}e^{{i\psi_{j} (\tau_{1} ,\tau_{2} )}} ,\,\,\,\,\,\,\,\,\,\,a_{j} = \varepsilon \tilde{a}_{j} ;\,\,\,\,\,\,\,(j = 1,\,2).$$

(33)

Let us consider the following modified phases [35]

$$\theta_{j} (\tau_{1} ,\tau_{2} ) = \tilde{\sigma }_{j} \tau_{1} - \psi_{j} (\tau_{1} ,\tau_{2} ),\,\,\,\,\,\,\,\,\,\sigma_{j} = \varepsilon \tilde{\sigma }_{j} ;\,\,\,\,\,\,\,j = (1,2).$$

(34)

Substituting Eqs. (13), (33), and (34) into Eqs. (22) and (32), and separating real and imaginary parts to obtain the following four first-order ODE constituting the ME

$$\begin{aligned} a_{1} \frac{{{\text{d}}\theta_{1} }}{{{\text{d}}\tau }} & = a_{1} \sigma_{1} + \frac{{N_{1} N_{2} }}{{2(\varpi^{2} - 1)}}a_{1} + \frac{{a_{1}^{3} }}{16} + \frac{{a_{1} B_{1} }}{8}(4 - 3B_{1} ) + \frac{{a_{1} s_{1} }}{8}(2B_{1} - 4 + s_{1} ) + \frac{{f_{1} }}{2}\cos \theta_{1} , \\ \frac{{{\text{d}}a_{1} }}{{{\text{d}}\tau }} & = \frac{{f_{1} }}{2}\sin \theta_{1} , \\ a_{2} \frac{{{\text{d}}\theta_{2} }}{{{\text{d}}\tau }} & = a_{2} \sigma_{2} + \frac{{\varpi B_{2} }}{8}a_{2} (4 - 3B_{2} ) + \frac{\varpi }{16}a_{2}^{3} + \frac{{\varpi^{3} N_{1} N_{2} a_{2} }}{{2(1 - \varpi^{2} )}}\, + \frac{{f_{2} }}{2\varpi }\cos \theta_{2} , \\ \frac{{{\text{d}}a_{2} }}{{{\text{d}}\tau }} & = \frac{{f_{2} \,}}{2\varpi }\sin \theta_{2} . \\ \end{aligned}$$

(35)

This system has been inspected to show that it has the solutions $a_{j} \,(j = 1,2)$ and $\theta_{j}$ which describe the modulations of the amplitudes and the phases, respectively. These solutions are graphed for various selected values of the system’s parameters as displayed in Figs. 2, 3, 4 and 5 in accordance with the following data

$$\begin{gathered} f_{1} ( = 0.001,\,0.002,\,0.003),\,\,\,\,\,\,f_{2} ( = 0.0009,\,0.004,\,0.01),\,\,\,\,\,\varpi ( = 0.67,\,0.69,\,0.74) \hfill \\ \sigma_{1} = 0.002,\,\,\,\,\,\,\,\,\,\,\,\sigma_{2} = 0.001,\,\,\,\,\,\,\,g = 9.8\,\,\,{\text{m/s}}^{2} ,\,\,\,\,\,m_{1} = 6\,\,\,{\text{kg}},\,\,\,\,\,\,\,\,m_{2} = 5\,\,\,{\text{kg}},\,\,\,\,\, \hfill \\ \Omega_{1} = \omega_{1} (1 + \sigma_{1} ),\,\,\,\,\,\,\,\,\,\Omega_{2} = \omega_{1} (\varpi + \sigma_{2} ),\,\,\,\,\,\,\,\,\,\,\,l = 1.5\,\,\,{\text{m}},\,\,\,\,\,\,\,\,\,\,\,\,\,e_{1} = e_{2} = 0.5\,\,{\text{m}}. \hfill \\ \end{gathered}$$

Fig. 2

Sketches the temporal variation of the amplitude $a_{1}$ when $\sigma_{1} = 0.002$ and $\sigma_{2} = 0.001$: a $f_{1} ( = 0.001,\,0.002,\,0.003),\,\,\,f_{2} = 0.0002,\,\,\varpi = 0.74$, b$f_{2} ( = 0.0009,\,0.004,\,0.01),\,\,\,f_{1} = 0.002,\,\,\,\varpi = 0.74,$ c $\varpi ( = 0.67,\,0.69,\,0.74),\,\,\,f_{1} = 0.002.$

Fig. 3

Describes the temporal variation of the amplitude $a_{2}$ when $\sigma_{1} = 0.002$ and $\sigma_{2} = 0.001$: a $(f_{1} = 0.001,\,0.002,\,0.003),\,\,\,f_{2} = 0.0002,\,\,\varpi = 0.74$, b$(f_{2} = 0.0009,\,0.004,\,0.01),\,\,\,f_{1} = 0.002,\,\,\,\varpi = 0.74,$ c $(\varpi = 0.67,\,0.69,\,0.74),\,\,\,f_{1} = 0.002.$

Fig. 4

Describes the temporal variation of the modified phase $\theta_{1}$ when $\sigma_{1} = 0.002$ and $\sigma_{2} = 0.001$: a$f_{1} ( = 0.001,\,0.002,\,0.003),\,\,\,f_{2} = 0.0002,\,\,\,\,\varpi = 0.74$, b$f_{2} ( = 0.0009,\,0.004,\,0.01),\,\,\,f_{1} = 0.002,\,\,\,\varpi = 0.74,$ c $\varpi ( = 0.67,\,0.69,\,0.74),\,\,\,f_{1} = 0.002.$

Fig. 5

Describes the temporal variation of the modified phase $\theta_{2}$ when $\sigma_{1} = 0.002$ and $\sigma_{2} = 0.001$: a$f_{1} ( = 0.001,\,0.002,\,0.003),\,\,\,f_{2} = 0.0002,\,\,\,\,\varpi = 0.74$, b$f_{2} ( = 0.0009,\,0.004,\,0.01),\,\,\,f_{1} = 0.002,\,\,\,\varpi = 0.74,$ c $\varpi ( = 0.67,\,0.69,\,0.74),\,\,\,f_{1} = 0.002.$

A closer examination of Figs. 2, 3, 4 and 5 reveals that these figures are plotted at $\sigma_{1} = 0.002,$ $\sigma_{2} = 0.001\,$ when $f_{1} ( = 0.001,\,0.002,\,0.003),$ $f_{2} ( = 0.0009,\,0.004,\,0.01),\,$ and $\varpi ( = 0.67,\,0.69,\,0.74)$ as in parts (a), (b), and (c) of these figures, respectively. These figures describe the time histories of the amplitudes $a_{j} \,(j = 1,2)$ and the modified phases $\theta_{j}$ as seen in Figs. 2, 3, 4, and 5 respectively. It is clear that when the value $f_{1}$ increases, periodic waves are produced, in which the amplitudes of the waves describing $a_{1}$ increase and the number of oscillations increases to some extent as seen in Fig. 2a, contrary with the $\theta_{1}$ decreasing behaviour as drawn in Fig. 4a. Moreover, there is no significant change of the waves characterizing $a_{2}$ and $\theta_{2}$ with the change of $f_{1}$ values as observed from parts (a) Figs. 3 and 5. The reason is due to the third and fourth equations of Eq. (35). The same conclusion can be applied on the parts (b) of Figs. 2 and 4 which is owing to that the first two equations of Eq. (35) don’t depend on $f_{2}$ explicitly.

The change of the $f_{2}$ values on the behavior of $a_{2}$ and $\theta_{2}$ has a good impact in which periodic waves are yielded as in parts (b) of Figs. 3 and 5. Here, the amplitudes of plotted waves increase and decrease with the increasing of $f_{2}$ values as drawn in Figs. 3a and 5a respectively. On the other hand the different values of $\varpi$ has an excellent impact on the behavior of $a_{j} \,\,(j = 1,2)$ and $\theta_{j}$ as plotted in Figs. 2, 3, 4, and 5 respectively.

The attained AS of the rotation angles $\gamma_{1}$ and $\gamma_{2}$ via time $\tau$ are plotted in Figs. 6 and 7 to explore the variation of these solutions with time when $f_{1} ,f_{2} ,$ and $\varpi$ have various values at $\sigma_{1} = 0.002$ and $\sigma_{2} = 0.001$, in which the above data are used to sketch both of them.

Fig. 6

The time history of the approximate solutions $\gamma_{1}$ when $\sigma_{1} = 0.002$ and $\sigma_{2} = 0.001$: a$f_{1} ( = 0.001,\,0.002,\,0.003),\,f_{2} = 0.0002,\,\,\varpi = 0.74$, b $f_{2} ( = 0.0009,\,0.004,\,0.01),\,f_{1} = 0.002,\,\varpi = 0.74,$ and c $\varpi ( = 0.67,\,0.69,\,0.74),\,f_{1} = 0.002.$

Fig. 7

The time history of the approximate solutions $\gamma_{2}$ when $\sigma_{1} = 0.002$ and $\sigma_{2} = 0.001$: a $f_{1} ( = 0.001,\,0.002,\,0.003),\,f_{2} = 0.0002,\,\,\varpi = 0.74$, b $f_{2} ( = 0.0009,\,0.004,\,0.01),\,f_{1} = 0.002,\,\varpi = 0.74,$ c $\varpi ( = 0.67,\,0.69,\,0.74),\,f_{1} = 0.002.$

A closer look at the drawn curves in the parts of Fig. 6 shows that we have increasing amplitude waves due to the increasing of the selected values of $f_{1}$ and $f_{2}$ as explored in parts (a) and (b). Moreover, this increment becomes slightly with the increasing of $\varpi$ values as seen in parts (c) and (b) while the change becomes constant when $\varpi$ increases, see part (c). Regarding parts of Fig. 7, we can say that the waves describing $\gamma_{2}$ when $f_{1} ( = 0.001,\,0.002,\,0.003)$ as in part (a) have no noticeable change with the values of $f_{1}$, while the waves amplitudes increasing with the increasing of $f_{2}$ and $\varpi$ as seen Fig. 7b,c. At all, periodic waves are produced which express about the steady state behavior and the stability of the acquired AS. These solutions are compared with the numerical solutions (NS) which are obtained using the method of Runge–Kutta from fourth-order when $\sigma_{1} = 0.002,$$\sigma_{2} = 0.001,$$\varpi = 0.74\,,$$f_{1} = \,0.002,$ and $f_{2} = \,0.0009$ to reveal high matching between them and to indicate about the great accuracy of the utilized perturbation method, as shown in Figs. 8 and 9 for the generalized coordinated $\gamma_{1}$ and $\gamma_{2}$ respectively. The relations between the AS and their derivatives from first-order are portrayed in Figs. 10, 11 and 12 to constitute the phase planes figures when $f_{1} ,f_{2} ,$ and $\varpi$ take different values. It is notable that, we have closed symmetric trajectories to some extent which assert that the gained AS have a stable behaviors, which are predicted before, during the tested interval of time.

Fig. 8

The comparison between the AS and the NS of the variable $\gamma_{1}$ when $\sigma_{1} = 0.002,\,\sigma_{2} = 0.001,\,\varpi = 0.74\,,f_{1} = \,0.002,$ and $f_{2} = \,0.0009$

Fig. 9

The comparison between the AS and the NS of the variable $\gamma_{2}$ at $\sigma_{1} = 0.002,\,\sigma_{2} = 0.001,\,\varpi = 0.74\,,f_{1} = \,0.002,$ and $f_{2} = \,0.0009$

Fig. 10

The diagrams of phase planes for the solutions $\gamma_{1}$ and $\gamma_{2}$ at $f_{1} ( = 0.001,\,0.002,\,0.003),$ $f_{2} = 0.0002\,,$$\sigma_{1} = 0.002,$ $\sigma_{2} = 0.001\,,$ and $\varpi = 0.74$

Fig. 11

The diagrams of phase planes for the solutions $\gamma_{1}$ and $\gamma_{2}$ at $f_{2} ( = 0.0009,\,0.004,\,0.01),$ $f_{1} = 0.002\,,$ $\sigma_{1} = 0.002,$ $\sigma_{2} = 0.001\,,$ and $\varpi = 0.74$

Fig. 12

Illustrates the diagrams of phase planes for the solutions $\gamma_{1}$ and $\gamma_{2}$ at $\varpi ( = 0.67,\,0.69,\,0.74),$$\sigma_{1} = 0.002,$ $f_{1} = 0.002,$ $f_{2} ( = 0.0001,0.0001,\,0.0002),$ and $\sigma_{2} = 0.001$

Steady-State Solutions for the Case of External Resonances

The purpose of the present section is to inspect the steady-state oscillations of the scrutinized dynamical system when the oscillations of the transitory processes have disappeared. Therefore, the conditions of the steady-state can be obtained when $\frac{{{\text{d}}a_{j} }}{{{\text{d}}\tau }} = \frac{{{\text{d}}\theta_{j} }}{{{\text{d}}\tau }} = 0\,\,\,\,(j = 1,2)$ [36]. As a result, regarding the unknowns, $a_{j}$ and $\theta_{j}$ we can obtain a system of four algebraic equations as follows:

$$\begin{gathered} a_{1} \left[ {\sigma_{1} + \frac{{N_{1} N_{2} }}{{2(\varpi^{2} - 1)}} + \frac{{a_{1}^{2} }}{16} + \frac{{B_{1} }}{8}(4 - 3B_{1} ) + \frac{{s_{1} }}{8}(2B_{1} - 4 + s_{1} )} \right] + \frac{{f_{1} }}{2}\cos \theta_{1} = 0, \hfill \\ \frac{{f_{1} }}{2}\sin \theta_{1} = 0, \hfill \\ a_{2} \left[ {\sigma_{2} + \varpi \left( {\frac{{B_{2} }}{8}(4 - 3B_{2} ) + \frac{{a_{2}^{2} }}{16} + \frac{{\varpi^{2} N_{1} N_{2} }}{{2(1 - \varpi^{2} )}}} \right)} \right]\, + \frac{{f_{2} }}{2\varpi }\cos \theta_{2} = 0, \hfill \\ \frac{{f_{2} \,}}{2\varpi }\sin \theta_{2} = 0. \hfill \\ \end{gathered}$$

(36)

Omission of the modified phases $\theta_{j}$ from this system produces the next two non-linear algebraic relationships between amplitudes $a_{j}$ and the frequency response functions described by the detuning parameters $\sigma_{j}$ in the following forms

$$\begin{gathered} f_{1}^{2} = 4a_{1}^{2} \left[ {\frac{{N_{1} N_{2} \,}}{{2(\varpi^{2} - 1)\,}} + \frac{{a_{1}^{2} }}{16} + \frac{{B_{1} }}{8}(4 - 3B_{1} ) + \sigma_{1} + \frac{{s_{1} }}{8}(2B_{1} - 4 + s_{1} )} \right]^{2} , \hfill \\ f_{2}^{2} = 4\varpi^{2} a_{2}^{2} \,\left[ {\varpi \left( {\frac{{B_{2} }}{2} - \frac{3}{8}B_{2}^{2} + \frac{{\,a_{2}^{2} }}{16} + \frac{{\,\varpi^{2} N_{1} N_{2} }}{{2(1 - \varpi^{2} )}}} \right) + \sigma_{2} } \right]^{2} . \hfill \\ \end{gathered}$$

(37)

It should be noted that, the steady-state part is considered as a significant part in the procedure of stability examination. Therefore, we concentrate our investigation on a region that close to the fixed points. To achieve this goal, let us consider the following forms of amplitudes and phases [37]

$$\begin{gathered} a_{1} = a_{10} + a_{11} ,\,\,\,\,\,\,\,\,\,\,\theta_{1} = \theta_{10} + \theta_{11} , \hfill \\ a_{2} = a_{20} + a_{21} ,\,\,\,\,\,\,\,\,\,\,\theta_{2} = \theta_{20} + \theta_{21} , \hfill \\ \end{gathered}$$

(38)

where $a_{10} \,,a_{20} ,\theta_{10} ,$ and $\theta_{20}$ are the solutions of steady state, while $a_{11} \,,a_{21} ,\theta_{11} ,$ and $\theta_{21}$ are the corresponding perturbations. Inserting Eq. (38) into Eq. (35), after linearization we can obtain

$$\begin{gathered} a_{10} \frac{{{\text{d}}\theta_{11} }}{{{\text{d}}\tau }} = a_{11} \left[ {\sigma_{1} + \frac{{N_{1} N_{2} }}{{2(\varpi^{2} - 1)}} + \frac{{3a_{10}^{2} }}{16} + \frac{{B_{1} }}{8}(4 - 3B_{1} ) + \frac{{s_{1} }}{8}(2B_{1} - 4 + s_{1} )} \right] - \frac{{f_{1} }}{2}\theta_{11} sin\theta_{10} , \hfill \\ \frac{{{\text{d}}a_{11} }}{{{\text{d}}\tau }} = \frac{{f_{1} }}{2}\theta_{11} cos\theta_{10} , \hfill \\ a_{20} \frac{{{\text{d}}\theta_{21} }}{{{\text{d}}\tau }} = a_{21} \left[ {\sigma_{2} + \varpi \left( {\frac{{B_{2} }}{2} - \frac{3}{8}B_{2}^{2} + \frac{3}{16}a_{20}^{2} + \frac{{\varpi^{2} N_{1} N_{2} }}{{2(1 - \varpi^{2} )}}} \right)} \right]\, - \frac{{f_{2} }}{2\varpi }\theta_{21} \sin \theta_{20} , \hfill \\ \frac{{{\text{d}}a_{21} }}{{{\text{d}}\tau }} = \frac{{f_{2} \,}}{2\varpi }\theta_{21} cos\theta_{20} , \hfill \\ \end{gathered}$$

(39)

To achieve the solutions of the given system Eq. (39), we can write the unknown functions $a_{j1} \,\,(j = 1,2)$ and $\theta_{j1}$ in exponential forms as $q_{s} e^{\lambda \tau }$ where $q_{s} \,\,(s = 1,2,3,4)$ are constants and $\lambda$ is the appropriate eigenvalues of these functions. In this case, the steady-state solutions $a_{j0}$ and $\theta_{j0} \,(j = 1,2)$ are stable asymptotically if the real parts of the roots of the following characteristic equations must be negative [38]

$$\lambda^{4} + \Gamma_{1} \lambda^{3} + \Gamma_{2} \lambda^{2} + \Gamma_{3} \lambda + \Gamma_{4} = 0,$$

(40)

where

$$\begin{aligned} \Gamma_{1} & = \frac{1}{2}\left( {\frac{{f_{1} \sin \theta_{10} }}{{a_{10} }} + \frac{{f_{2} \sin \theta_{20} }}{{\varpi a_{20} }}} \right), \\ \Gamma_{2} & = - \frac{1}{{32\varpi (\varpi^{2} - 1)a_{10} a_{20} }}\{ - 8f_{1} f_{2} (\varpi^{2} - 1)\sin \theta_{10} \sin \theta_{20} + \varpi f_{1} a_{20} \cos \theta_{10} [3a_{10}^{2} (\varpi^{2} - 1) \\ & \quad + 2( - 3B_{1}^{2} (\varpi^{2} - 1) + 4N_{1} N_{2} + 2B_{1} (\varpi^{2} - 1)(s_{1} + 2) + (\varpi^{2} - 1)((s_{1} - 4)s_{1} + 8\sigma_{1} ))] \\ & \quad + a_{10} f_{2} \cos \theta_{20} (\varpi (\varpi^{2} - 1)(3a_{20}^{2} + 2B_{2} (4 - 3B_{2} ) - 8\varpi^{3} N_{1} N_{2} + 16\sigma_{2} (\varpi^{2} - 1))\} , \\ \Gamma_{3} & = \frac{{f_{1} f_{2} }}{{64\varpi (\varpi^{2} - 1)a_{10} a_{20} }}\{ \cos \theta_{10} \sin \theta_{20} [ - 3a_{10}^{2} (\varpi^{2} - 1) + 2(3B_{1}^{2} (\varpi^{2} - 1) - 4N_{1} N_{2} \\ & \quad - 2B_{1} (\varpi^{2} - 1)(s_{1} + 2) - (\varpi^{2} - 1)((s_{1} - 4)s_{1} + 8\sigma_{1} ))] + \cos \theta_{20} \sin \theta_{10} ( - 3\varpi (\varpi^{2} - 1)a_{20}^{2} \, \\ & \quad + 2B_{2} \varpi (\varpi^{2} - 1)( - 4 + 3B_{2} ) + 8\varpi^{3} N_{1} N_{2} - 16\sigma_{2} (\varpi^{2} - 1))\} , \\ \Gamma_{4} & = \frac{{f_{1} f_{2} \cos \theta_{10} \cos \theta_{20} }}{{1024\varpi (\varpi^{2} - 1)^{2} a_{10} a_{20} }}[3a_{10}^{2} (\varpi^{2} - 1) + 2( - 3B_{1}^{2} (\varpi^{2} - 1) + 4N_{1} N_{2} + 2B_{1} (\varpi^{2} - 1) \\ & \quad \times (s_{1} + 2) + (\varpi^{2} - 1)((s_{1} - 4)s_{1} + 8\sigma_{1} )][(\varpi (\varpi^{2} - 1)(3a_{20}^{2} + 2B_{2} (4 - 3B_{2} )) \\ & \quad - 8\varpi^{3} N_{1} N_{2} + 16\sigma_{2} (\varpi^{2} - 1)]. \\ \end{aligned}$$

(41)

It is noted that $\Gamma_{s} \,\,(s = 1,2,3,4)$ depend on some parameters like $a_{j0} ,\theta_{j0} ,$ and $f_{j}$. The stability conditions at steady-state solutions can be written as follows using the criterion of Routh-Hurwitz [39]

$$\begin{gathered} \Gamma_{1} > 0,\,\, \hfill \\ \Gamma_{3} (\Gamma_{1} \Gamma_{2} - \Gamma_{3} ) - \Gamma_{1}^{2} \Gamma_{4} > 0, \hfill \\ \Gamma_{1} \Gamma_{2} - \Gamma_{3} > 0, \hfill \\ \Gamma_{4} > 0. \hfill \\ \end{gathered}$$

(42)

The Stability Analysis for the Case of External Resonances

In the current section, the approach of the non-linear stability is utilized to study the motion of the investigated dynamical system of the double RBP that subjected to the harmonic external moments $M_{{\gamma_{1} }} (t)$ and $M_{{\gamma_{2} }} (t)$. In addition to simulating the equations of the non-linear system, the stability criteria are also performed. It is observed that the parameters of detuning $\sigma_{1} ,\sigma_{2} ,$ and the frequency $\varpi$ have a positive impact on the destabilization of the stability criteria. To sketch the stability areas or ranges of system Eq. (37), a specified procedure with various settings of the system was tested. The changes of the amplitudes $a_{1} ,a_{2}$ via time are plotted for distinct parametric regions. Therefore, Figs. 13, 14, 15, 16, 17 and 18 is drawn to show how the variations of the values of $\sigma_{1}$ and $\sigma_{2}$ effect on the possible fixed points, in which we considered the selected values of the parameters $f_{1} ( = 0.001,\,0.002,\,0.003),$ $f_{2} ( = 0.0009,\,0.004,\,0.01)\,,$ and $\varpi ( = 0.67,\,0.69,\,0.74)$ are used.

Fig. 13

The resonance curves of the amplituudes $a_{j} \,\,(j = 1,2)$ as a function of $\sigma_{1}$ at $\sigma_{2} = - 0.2\,,\varpi = 0.74,$ and $f_{1} ( = 0.001,\,0.002,\,0.003)$

Fig. 14

Resonance curves of the amplituudes $a_{j} \,\,(j = 1,2)$ as a function of $\sigma_{2}$ when $\sigma_{1} = - 0.2\,,\varpi = 0.74,$ and $f_{1} ( = 0.001,\,0.002,\,0.003)$

Fig. 15

Resonance curves of $a_{j} (\sigma_{1} )\,\,(j = 1,2)$ at $\sigma_{2} = - 0.2\,,\varpi = 0.74,$ and $f_{2} ( = 0.0009,\,0.004,\,0.01)$

Fig. 16

Resonance curves of $a_{j} (\sigma_{2} )\,\,(j = 1,2)$ at $\sigma_{1} = - 0.2\,,\varpi = 0.74,$ and $f_{2} ( = 0.0009,\,0.004,\,0.01)$

Fig. 17

Resonance curves of $a_{1} (\sigma_{1} )$ and $a_{2} (\sigma_{1} )$ at $\sigma_{2} = - 0.2$ and $\varpi ( = 0.67,\,0.69,\,0.74)$

Fig. 18

Resonance curves of $a_{1} (\sigma_{2} )$ and $a_{2} (\sigma_{2} )$ at $\sigma_{1} = - 0.2$ and $\varpi ( = 0.67,\,0.69,\,0.74)$

The influence of the selected values of $f_{1} ( = 0.001,\,0.002,\,0.003),$ on the frequency responses curves in the planes $a_{j} \sigma_{1} \,\,(j = 1,2)$ and $a_{j} \sigma_{2} \,$ is described in Figs. 13 and 14, respectively. A closer look at these figures explores that we have only one critical fixed point with three peaks for each value of $f_{1}$ as shown in Fig. 13a, while no peaks are observed in Fig. 13b for the curves in the plane $a_{2} \sigma_{1}$ with the variation of $f_{1}$. The variation of $a_{1}$ via $\sigma_{2}$ in Fig. 14a reflects the number of critical fixed points which is one distinct point for each value of $f_{1}$, whereas in Fig. 14b there exists one stationary critical point for the plotted curves of $f_{1}$. Overall, the areas of stable and unstable fixed points of Fig. 13 lie in the range just $\sigma_{1} \le - 0.06$ and $- 0.06 < \sigma_{1}$, respectively. According to the curves depicted in Fig. 14, we observe that the stable and unstable regions are $- 0.3 \le \sigma_{2} \le - 0.02$ and $- 0.02 < \sigma_{2} \le 0.3$, respectively. It is worthwhile to mention that the solid curves describe the domain of stable points while the dashed ones represent the unstable ranges.

On the other hand, Figs. 15 and 16 show the frequency responses curves in the planes $a_{j} \sigma_{1} \,\,(j = 1,2)$ and $a_{j} \sigma_{2} \,$ when $f_{2} ( = 0.0009,\,0.004,\,0.01)$. It can be seen that there exists only three typical and different critical fixed points as seen in Fig. 15a, b, respectively. The stable and unstable areas of fixed points are found in Fig. 15 at the ranges $- 0.3 \le \sigma_{1} \le - 0.06$ and $- 0.06 < \sigma_{1} \le 0.3$, respectively. The observed curves in Fig. 16 indicate that we identical response curves with the same critical point as in part (a), while in part (b) three various critical fixed points are obtained with the variation of $f_{2}$ values. The areas of fixed points whether stable or not for different values of $f_{2}$ are classified according to:

• 1- At $f_{2} = 0.01,$ we observed that the fixed points have stable and unstable ranges $- 0.3 \le \sigma_{2} \le - 0.05$ and $- 0.05 < \sigma_{2} \le 0.3$ respectively.

• 2- When $f_{2} = 0.004$, the stability and instability regions are found in the domains $- 0.3 \le \sigma_{2} \le - 0.04$ and $- 0.04 < \sigma_{2} \le 0.3$, respectively.

• 3- When $f_{2}$ has the value $0.0009$, one found the stable fixed points lie in the range of $- 0.3 \le \sigma_{2} \le - 0.03$ while the unstable ones occurs in the range of $- 0.03 < \sigma_{2} \le 0.3$.

However, the influence of the values of the natural frequency $\varpi ( = 0.67,\,0.69,\,0.74)$ on the frequency responses are portrayed in parts of Figs. 17 and 18. There is only one critical fixed point for each value of $\varpi$ has plotted in Figs. 17 and 18 as follows, in which two pints are directed upward at $\varpi = 0.67$ and $\varpi = 0.69$ while the third one is directed downward at $\varpi = \,0.74$ with three peaks as explored in part (a) of Fig. 17. Moreover, three different critical points are found in the plane $a_{2} \sigma_{2}$ with the considered values of $\varpi$, sees Fig. 18b. Contrary, we have three different critical points at the different values of $\varpi$ as seen in parts (b) and (a) of Figs. 17 and 18, respectively. The stability ranges and instability ones have the following categorization:

• 1. At $\varpi = \,0.74$, the stable and unstable points are existing in the domains $- 0.3 \le \sigma_{1} \le - 0.07$ and $- 0.07 < \sigma_{1} \le 0.3$ respectively, as graphed in Fig. 17. Whereas the stable points takes place in the range $- 0.3 \le \sigma_{2} \le - 0.02$ and the unstable ones occur in the range $- 0.02 < \sigma_{2} \le 0.3$ as shown in Fig. 18.

• 2. At $\varpi ( = 0.67,0.69)$, one found stable fixed point in the range $- 0.3 \le \sigma_{1} \le - 0.08$ while the unstable ones are exists in the range $- 0.08 < \sigma_{1} \le 0.3$ as plotted in Fig. 17. Moreover, in Fig. 18 the stable points take place in the domain $- 0.3 \le \sigma_{2} \le - 0.01$ and the unstable ones are found in the domain $- 0.01 < \sigma_{2} \le 0.3$.

Tables 1, 2, and 3 show the relation between the critical and peaks fixed points and the values of the parameters $f_{1} ,\,f_{2} ,$ and $\varpi$ respectively.

Table 1 The critical and peaks fixed points for different values of $f_{1} .$

Table 2 The critical and peaks fixed points for different values of $f_{2} .$

Table 3 The critical and peaks fixed points for different values of $\varpi .$

The inspection of Figs. 19 and 20 shows the frequency responses when $\sigma_{2} = - 0.2$ and $\sigma_{1} = - 0.2$ respectively. These figures are calculated at $\varpi ( = 0.67,0.69,0.74),$ $f_{1} = 0.002,$ $m_{1} = 6,$ and $m_{2} = 5$. It is clear that from curves of Fig. 19, there are no intersection of fixed points when $\varpi = 0.67$ and $\varpi = 0.69$, i.e. no common solutions while at $\varpi = 0.74$ there are two stable unique solutions. Whereas curves of Fig. 20 reflect that we have two unique common fixed points of the solutions, in which one of them is stable and the other is unstable. It is notable that through the regions $- 0.03 \le \sigma_{1} \le 0.03$ and $- 0.03 \le \sigma_{2} \le 0.03$ there is a high resonance among the frequency which in turn leads to a notable increase in the amplitudes of the steady-state solutions.

Fig. 19

Frequency response when $\sigma_{2} = - 0.2$: a at $\varpi = 0.67$, b at $\varpi = 0.69$, c at $\varpi = 0.74$

Fig. 20

Frequency response when $\sigma_{1} = - 0.2$: a at $\varpi = 0.67$, b at $\varpi = 0.69$, c at $\varpi = 0.74$

Non-linear Analysis for the External Resonance Case

This section aims to study the characteristic of the non-linear amplitude for the system of Eq. (35) and explores their stabilities. Therefore, the accompanying transformation is taken into account [40]

$$\begin{gathered} {\rm A}_{j} (\tau_{1} ,\tau_{2} ) = \frac{1}{2}[\tilde{u}_{j} (\tau_{1} ,\tau_{2} ) + i\,\tilde{v}_{j} (\tau_{1} ,\tau_{2} )]e^{{i\,\tilde{\sigma }_{j} \,\tau_{1} }} ; \hfill \\ u_{j} = \varepsilon \tilde{u}_{j} ,\,\,\,\,\,v_{j} = \varepsilon \tilde{v}_{j} \,\,\,\,(j = 1,2). \hfill \\ \end{gathered}$$

(43)

Substituting Eqs. (13) and (43) into Eqs. (22) and (32), then splitting the real parts and imaginary ones to obtain

$$\begin{gathered} \frac{{{\text{d}}v_{1} }}{{{\text{d}}\tau }} + u_{1} \left[ {\sigma_{1} + \frac{1}{8}\left( {B_{1} (4 - 3B_{1} + 2s_{1} ) + s_{1} (s_{1} - 4) + \frac{{4N_{1} N_{2} }}{{(\varpi^{2} - 1)}} + \frac{1}{2}(u_{1}^{2} + v_{1}^{2} )} \right)} \right] + \frac{{f_{1} }}{2} = 0, \hfill \\ \frac{{{\text{d}}u_{1} }}{{{\text{d}}\tau }} + v_{1} \left[ { - \sigma_{1} + \frac{1}{8}\left( {B_{1} (3B_{1} - 2s_{1} - 4) + s_{1} (4 - s_{1} ) - \frac{{4N_{1} N_{2} }}{{(\varpi^{2} - 1)}} - \frac{1}{2}(v_{1}^{2} + u_{1}^{2} )} \right)} \right] = 0, \hfill \\ \frac{{{\text{d}}v_{2} }}{{{\text{d}}\tau }} + u_{2} \left[ {\sigma_{2} + \frac{1}{8}\left( {\varpi B_{2} (4 - 3B_{2} ) + \frac{{4\varpi^{3} N_{1} N_{2} }}{{(1 - \varpi^{2} )}} + \frac{\varpi }{2}(u_{2}^{2} + v_{2}^{2} )} \right)} \right] + \frac{{f_{2} }}{2\varpi } = 0, \hfill \\ \frac{{{\text{d}}u_{2} }}{{{\text{d}}\tau }} + v_{2} \left[ { - \sigma_{2} + \frac{1}{8}\left( {\varpi B_{2} (3B_{2} - 4) - \frac{{4\varpi^{3} N_{1} N_{2} }}{{(1 - \varpi^{2} )}} - \frac{\varpi }{2}(v_{2}^{2} + u_{2}^{2} )} \right)} \right] = 0. \hfill \\ \end{gathered}$$

(44)

The altered amplitudes were then evaluated over the used time interval in different parametric areas and the amplitudes characteristics were depicted in phase-plane curves, as illustrated in Figs. 21, 22, 23, 24, 25 and 26. The values of parameters are as follows

$$\begin{gathered} f_{1} ( = 0.001,\,0.002,\,0.003),\,\,\,\,f_{2} ( = 0.0009,\,0.004,\,0.01)\,,\,\,\,\,\varpi ( = 0.67,\,0.69,\,0.74),\, \hfill \\ \sigma_{1} = 0.002,\,\,\,\,\sigma_{2} = 0.001,\,\,\,\,u_{1} (0) = 0.07,\,\,\,\,v_{1} (0) = 0.02,\,\,\,\,u_{2} (0) = 0.02,\,\,\,\,v_{2} (0) = 0.02. \hfill \\ \end{gathered}$$

Fig. 21

The time histories of $u_{1}$ and $v_{1}$, and the corresponding paths of the modulation equations on $u_{1} v_{1}$ plane when $f_{1} ( = 0.001,\,0.002,\,0.003),$$\sigma_{1} = 0.002,$ $\,\sigma_{2} = 0.001,$ and $\varpi = 0.74\,.$

Fig. 22

The time histories of $u_{2}$ and $v_{2}$, and the paths of the modulation equations on the plane $u_{1} v_{1}$ when $(f_{1} = 0.001,\,0.002,\,0.003),$$\sigma_{1} = 0.002,$ $\,\sigma_{2} = 0.001,$ and $\varpi = 0.74\,.$

Fig. 23

The variation of $u_{1}$ and $v_{1}$ via $\tau$, and the trajectories of the modulation equations on the plane $u_{1} v_{1}$ when $f_{2} ( = 0.0009,\,0.004,\,0.01),$$\sigma_{1} = 0.002,$ $\,\sigma_{2} = 0.001,$ and $\varpi = 0.74\,.$

Fig. 24

The variation of $u_{2}$ and $v_{2}$ via $\tau$, and the trajectories of the modulation equations on the plane $u_{2} v_{2}$ when $f_{2} ( = 0.0009,\,0.004,\,0.01),$$\sigma_{1} = 0.002,$ $\,\sigma_{2} = 0.001,$ and $\varpi = 0.74\,.$

Fig. 25

The change of $u_{1}$ and $v_{1}$ with time $\tau$, and the trajectories of the modulation equations on the plane $u_{1} v_{1}$ when $\varpi ( = 0.67,\,0.69,\,0.74),$$\sigma_{1} = 0.002,$ $f_{1} = 0.002,\,f_{2} ( = 0.0001,0.0001,\,0.0002)$ and $\,\sigma_{2} = 0.001.$

Fig. 26

The change of $u_{2}$ and $v_{2}$ with time $\tau$, and the trajectories of the modulation equations on the plane $u_{2} v_{2}$ when $\varpi ( = 0.67,\,0.69,\,0.74),$$\sigma_{1} = 0.002,$$f_{1} = 0.002,f_{2} ( = 0.0001,0.0001,\,0.0002)$ and $\,\sigma_{2} = 0.001.$

The plotted curves of Figs. 21, 22, 23, 24, 25 and 26 illustrate the change of the modified phases $u_{1} ,u_{2} ,v_{1} ,$ and $v_{2}$ versus time $\tau$ when $f_{1} ,f_{2} ,$ and $\varpi$ have the above values as in parts (a) and (b) respectively. The behaviour of the represented waves of $u_{1} ,v_{1}$ and $u_{2} ,v_{2}$ behave periodic attitude, in which the amplitudes of these waves increase with the increasing of the values of $f_{1}$ and $f_{2}$, respectively, (sees parts (a) and (b) of Figs. 21 and 24). Therefore, we can predict that the system have a stable behavior. The influence of the various values of $\varpi$ on the trajectories of $u_{1} ,v_{1}$ and $u_{2} ,v_{2}$ is drawn in Figs. 25 and 26 respectively. Periodic waves are portrayed as in parts (a) and (b) of these figures, in which the number of oscillations increases to some extent with the increasing of the values of natural frequency $\varpi$ besides decreasing of the wavelengths. On the other hand, there is no significant change in the behavior of the describing waves of $u_{1} ,v_{1}$ and $u_{2} ,v_{2}$ with each change of the values of $f_{1}$ and $f_{2}$ as seen in parts (a) and (b) of Figs. 22 and 23 respectively. The reason is due to the formal construction of the system of Eq. (44). Moreover, the projections of the trajectories of the ME on the phase planes $u_{1} v_{1}$ and $u_{2} v_{2}$ are represented in parts (c) of Figs. 21, 22, 23, 24, 25 and 26 for the selected values of $f_{1} ,f_{2} ,$ and $\varpi$. A closed symmetric trajectories curves are observed which assert our prediction for the steady motion of the investigated system.

A Combination Case of Internal and External Resonance

We are going to study the case of combination of external and internal resonances. The closeness of $\varpi ,p_{2}$ to $1\,,\varpi$ is expressed through introducing the detuning parameters of $\delta_{1}$ and $\delta_{2}$ as follows

$$\varpi = 1 + \delta_{1} \,,\,\,\,\,\,\,\,\,p_{2} = \varpi + \delta_{2} \,.$$

(45)

Therefore, we can introduce them in terms of $O(\varepsilon )$ as follows

$$\delta_{j} = \varepsilon \,\,\tilde{\delta }_{j} \,\,\,(j = 1,2).$$

(46)

Substituting Eqs. (45)–(46) for Eqs. (16)–(19) and removing terms that lead to secular ones, the following solvability criteria are obtained as in Eq. (22) and as in the following conditions

$$\begin{gathered} \frac{{{\rm A}_{1} }}{4}\left[ {\tilde{B}_{1} (2\tilde{s}_{1} - 3\tilde{B}_{1} ) + \tilde{s}_{1}^{2} + \frac{{4\tilde{N}_{1} \tilde{N}_{2} }}{{(\varpi^{2} - 1)}} + 2{\rm A}_{1} \overline{\rm A}_{1} } \right] - \,2i\frac{{\partial {\rm A}_{1} }}{{\partial \tau_{2} }} \hfill \\ + \frac{{\varpi^{2} \tilde{N}_{1} {\rm A}_{2} }}{{(1 - \varpi^{2} )}}(\tilde{B}_{1} \varpi^{2} - \tilde{s}_{1} - \tilde{B}_{2} )e^{{i\tilde{\delta }_{1} \tau_{1} }} = 0, \hfill \\ \frac{{\varpi^{2} {\rm A}_{2} }}{4}\left[ {\frac{{4\varpi^{2} \tilde{N}_{1} \tilde{N}_{2} }}{{(1 - \varpi^{2} )}} - 3\tilde{B}_{2}^{2} + 2{\rm A}_{2} \overline{\rm A}_{2} } \right] - 2i\varpi \frac{{\partial {\rm A}_{2} }}{{\partial \tau_{2} }} + \frac{{\tilde{f}_{2} }}{2\,}e^{{i\tilde{\delta }_{2} \tau_{1} }} = 0\,. \hfill \\ \end{gathered}$$

(47)

Conditions (22) and (47) show how functions ${\rm A}_{j}$ are dependent on $\tau_{1}$ and $\tau_{2}$ that can be stated in polar form as

$${\rm A}_{j} (\tau_{1} ,\tau_{2} ) = \frac{{\tilde{b}_{j} (\tau_{1} ,\tau_{2} )}}{2}e^{{i\beta_{j} (\tau_{1} ,\tau_{2} )}} ,\,\,\,\,\,\,\,\,\,\,b_{j} = \varepsilon \tilde{b}_{j} ;\,\,\,\,\,\,\,j = 1,\,2.$$

(48)

Let us consider the following modified phases [35]

$$\begin{gathered} \phi_{1} (\tau_{1} ,\tau_{2} ) = \tilde{\delta }_{1} \tau_{1} + \beta_{2} (\tau_{1} ,\tau_{2} ) - \beta_{1} (\tau_{1} ,\tau_{2} ), \hfill \\ \phi_{2} (\tau_{1} ,\tau_{2} ) = \tilde{\delta }_{2} \tau_{1} - \beta_{2} (\tau_{1} ,\tau_{2} ). \hfill \\ \end{gathered}$$

(49)

Inserting Eqs. (13), (48) and (49) into Eqs. (22) and (47), and separating the real and imaginary parts, we obtain the ME of four first-order ODE as follow

$$\begin{aligned} b_{1} \frac{{d\phi_{1} }}{d\tau } & & = b_{1} (\delta_{1} + \delta_{2} ) - b_{1} \frac{{d\phi_{2} }}{d\tau } + \frac{{b_{1} }}{16}\left[ {\frac{{8N_{1} N_{2} }}{{(\varpi^{2} - 1)}} + b_{1}^{2} + 2B_{1} (4 - 3B_{1} ) + 2s_{1} (2B_{1} + s_{1} - 4)} \right] \\ & \quad + \frac{{\varpi^{2} N_{1} b_{2} }}{{2(1 - \varpi^{2} )}}(B_{1} \varpi^{2} - s_{1} - B_{2} )\cos \phi_{1} , \\ \frac{{db_{1} }}{d\tau } & & = \frac{{\varpi^{2} N_{1} b_{2} }}{{2(1 - \varpi^{2} )}}(B_{1} \varpi^{2} - s_{1} - B_{2} )\sin \phi_{1} , \\ b_{2} \frac{{d\phi_{2} }}{d\tau } & & = b_{2} \delta_{2} + \frac{{b_{2} \varpi }}{16}\left[ {8B_{2} - 6B_{2}^{2} + b_{2}^{2} + \frac{{8\varpi^{2} N_{1} N_{2} }}{{(1 - \varpi^{2} )}}} \right] + \frac{{f_{2} }}{2\varpi }\cos \phi_{2} , \\ \frac{{db_{2} }}{d\tau } & & = \frac{{f_{2} \,}}{2\varpi }\sin \phi_{2} . \\ \end{aligned}$$

(50)

The solutions $b_{j} \,(j = 1,2)$ and $\phi_{j}$ of this system describes represent the modulations of the amplitudes and the phases, respectively. These solutions have been graphed for various selected values of the system’s parameters as shown in Figs. 27 and 28 using the following data

$$\begin{gathered} f_{1} = 0.002,\,\,\,\,\,\,\delta_{1} = 0.11\,,\,\,\,\,\,\,\,\delta_{2} = 0.001,\,\,\,\,\,\,\,f_{2} ( = 0.001,\,0.0015,\,0.002), \hfill \\ g = 9.8\,\,\,{\text{m/s}}^{2} ,\,\,\,\,\,\,\,m_{1} = 6\,\,\,{\text{kg}},\,\,\,\,\,\,\,m_{2} = 5\,\,{\text{kg}},\,\,\,\,\,\,\,l = 1.5\,\,{\text{m}},\,\,\,\,\,\,\,e_{1} = e_{2} = 0.5\,\,\,{\text{m}}, \hfill \\ \Omega_{1} = 0.99,\,\,\,\,\,\,\,\Omega_{2} = \omega_{1} (\varpi + \delta_{2} ),\,\,\,\,\,\,\,\varpi = 1.11.\, \hfill \\ \end{gathered}$$

Fig. 27

The temporal variation of the amplitudes $b_{1} ,b_{2}$ when $f_{2} ( = 0.001,\,0.0015,\,0.002)$, $f_{1} = 0.002,$ $\delta_{1} = 0.11\,,$ $\delta_{2} = 0.001,$ and $\varpi = 1.11$

Fig. 28

The temporal variation of the modified phase $\phi_{1} ,\phi_{2}$ when $f_{2} ( = 0.001,\,0.0015,\,0.002)$, $f_{1} = 0.002,$ $\delta_{1} = 0.11\,,$ $\delta_{2} = 0.001,$ and $\varpi = 1.11$

A closer look at Figs. 27 and 28 reports that these figures are plotted at $\delta_{1} = 0.11,$ $\delta_{2} = 0.001,$ and $f_{1} = \,0.002$ when $\,f_{2} ( = 0.001,\,0.0015,\,0.002)$ to reveal the time histories of the amplitudes $b_{j} \,(j = 1,2)$ and the modified phases $\phi_{j}$. It is clear that when the value $f_{2}$ increases, periodic waves are produced, in which the amplitudes of the waves describing $b_{1}$ and $b_{2}$ increase and the number of oscillations remain stationary to some extent as seen in Fig. 27, while the oscillation’s number of $\phi_{1}$ increases with the increasing of time as drawn in Fig. 28b. Moreover, there is no significant change of the waves characterizing $\phi_{2}$ with the change of $f_{2}$ values, and the behavior of the waves is decreasing with the time as observed from Fig. 28b.

The achieved AS of the rotation angles $\gamma_{1}$ and $\gamma_{2}$ through time $\tau$ are drawn in Fig. 29 (for the combination case of internal and external resonance) to examine the variation of these solutions with time when $f_{2}$ have various values at $\delta_{1} = 0.11$ and $\delta_{2} = 0.001$.This figure has been drawn according to the previous data. An inspection of the plotted curves in parts (a) and (b) of Fig. 29 explores that we have periodic waves with some package, in which there is no noticeable change of the waves describing $\gamma_{1}$ when $f_{2} ( = 0.001,0.0015,0.002),$ while the amplitudes waves describing $\gamma_{2}$ increase with the increasing of $f_{2}$ as explored in Fig. 29b. These waves express that the motion has a steady behavior and the AS has a manner of stationary behavior. The phase plane figures that describe the stability of the system’s motion have been portrayed in Fig. 30, which reveal the relation between the AS and their first-order derivatives at $f_{2} ( = 0.001,0.0015,0.002).$ Closed trajectories are observed to indicate that the gained AS have a stable behaviors.

Fig. 29

Time history of the approximate solutions $\gamma_{1} ,\,\gamma_{2}$ via $\tau$ when $f_{2} ( = 0.001,\,0.0015,\,0.002)$, $f_{1} = 0.002,$ $\delta_{1} = 0.11\,,$ $\delta_{2} = 0.001,$ and $\varpi = 1.11$

Fig. 30

The phase plane portraits when $f_{2} ( = 0.001,\,0.0015,\,0.002)$, $f_{1} = 0.002,$ $\delta_{1} = 0.11\,,$ $\delta_{2} = 0.001,$ and $\varpi = 1.11$: a for the plane $\gamma_{1} \,\dot{\gamma }_{1}$ and b for the plane $\gamma_{2} \,\dot{\gamma }_{2}$

Verification of the Steady State Solutions

To examine the solutions at the case of steady state, we consider as studied previously in Sect. 5 the zero values of the first derivatives of amplitudes and modified phase i.e., $\left( {\frac{{{\text{d}}b_{j} }}{{{\text{d}}\tau }} = \frac{{{\text{d}}\phi_{j} }}{{{\text{d}}\tau }} = 0\,;\,\,\,\,j = 1,2} \right)$[36]. Then Eq. (50) produce the following system

$$\begin{gathered} b_{1} (\delta_{1} + \delta_{2} ) + \frac{{b_{1} }}{16}\left[ {\frac{{8N_{1} N_{2} }}{{(\varpi^{2} - 1)}} + b_{1}^{2} + 2B_{1} (4 - 3B_{1} ) + 2s_{1} (2B_{1} + s_{1} - 4)} \right] \hfill \\ + \frac{{\varpi^{2} N_{1} b_{2} }}{{2(1 - \varpi^{2} )}}(B_{1} \varpi^{2} - s_{1} - B_{2} )\cos \phi_{1} = 0, \hfill \\ \frac{{\varpi^{2} N_{1} b_{2} }}{{2(1 - \varpi^{2} )}}[B_{1} \varpi^{2} - s_{1} - B_{2} ]\sin \phi_{1} = 0, \hfill \\ b_{2} \delta_{2} + \frac{{b_{2} \varpi }}{16}\left[ {8B_{2} - 6B_{2}^{2} + b_{2}^{2} + \frac{{8\varpi^{2} N_{1} N_{2} }}{{(1 - \varpi^{2} )}}} \right] + \frac{{f_{2} }}{2\varpi }\cos \phi_{2} = 0, \hfill \\ \frac{{f_{2} \,}}{2\varpi }\sin \phi_{2} = 0. \hfill \\ \end{gathered}$$

(51)

Cancellation of the modified phases $\phi_{j}$ from preceding system Eq. (51), two non-linear algebraic relationships in terms of $b_{j} ,\delta_{j}$ and the frequency response functions are obtained in the forms

$$\begin{gathered} \frac{{\varpi^{4} N_{1}^{2} b_{2}^{2} }}{{4(1 - \varpi^{2} )^{2} }}(B_{1} \varpi^{2} - s_{1} - B_{2} )^{2} = b_{1}^{2} \left\{ {\delta_{1} + \delta_{2} + \frac{1}{16}\left[ {\frac{{8N_{1} N_{2} }}{{(\varpi^{2} - 1)\,}} + b_{1}^{2} + 2B_{1} (4 - 3B_{1} ) + 2s_{1} (2B_{1} + s_{1} - 4)} \right]} \right\}^{2} , \hfill \\ f_{2}^{2} = 4\varpi^{2} \,b_{2}^{2} \left\{ {\frac{\varpi }{16}\left[ {8B_{2} - 6B_{2}^{2} + b_{2}^{2} + \frac{{\,8\varpi^{2} N_{1} N_{2} }}{{(1 - \varpi^{2} )}}} \right] + \delta_{2} } \right\}^{2} . \hfill \\ \end{gathered}$$

(52)

Let us consider the following forms of amplitudes and phases [37]

$$\begin{gathered} b_{1} = b_{10} + b_{11} ,\,\,\,\,\,\,\,\,\,\,\phi_{1} = \phi_{10} + \phi_{11} , \hfill \\ b_{2} = b_{20} + b_{21} ,\,\,\,\,\,\,\,\,\,\phi_{2} = \phi_{20} + \phi_{21} , \hfill \\ \end{gathered}$$

(53)

where $b_{10} \,,b_{20} ,\phi_{10} ,$ and $\phi_{20}$ are the solutions of steady state, while $b_{11} \,,b_{21} ,\phi_{11} ,$ and $\phi_{21}$ are the corresponding perturbations. Substituting Eq. (53) into Eq. (50), and making linearization we can obtain

$$\begin{gathered} b_{10} \frac{{{\text{d}}\phi_{11} }}{{{\text{d}}\tau }} = b_{11} \left[ {\delta_{1} + \delta_{2} + \frac{1}{16}\left( {\frac{{8N_{1} N_{2} }}{{(\varpi^{2} - 1)}} + 3b_{10}^{2} + 2B_{1} (4 - 3B_{1} ) + 2s_{1} (2B_{1} + s_{1} - 4)} \right)} \right] \hfill \\ + \frac{{\varpi^{2} N_{1} }}{{2(1 - \varpi^{2} )}}(B_{1} \varpi^{2} - s_{1} - B_{2} )(b_{21} \cos \phi_{10} - b_{20} \phi_{11} \sin \phi_{10} ) - b_{10} \frac{{d\phi_{21} }}{d\tau }, \hfill \\ \frac{{{\text{d}}b_{11} }}{{{\text{d}}\tau }} = \frac{{\varpi^{2} N_{1} }}{{2(1 - \varpi^{2} )}}(B_{1} \varpi^{2} - s_{1} - B_{2} )(b_{20} \phi_{11} \cos \phi_{10} + b_{21} \sin \phi_{10} ), \hfill \\ b_{20} \frac{{{\text{d}}\phi_{21} }}{{{\text{d}}\tau }} = b_{21} \left[ {\delta_{2} + \frac{\varpi }{16}\left( {8B_{2} - 6B_{2}^{2} + 3b_{20}^{2} + \frac{{8\varpi^{2} N_{1} N_{2} }}{{(1 - \varpi^{2} )}}} \right)} \right]\, - \frac{{f_{2} }}{2\varpi }\phi_{21} \sin \phi_{20} , \hfill \\ \frac{{{\text{d}}b_{21} }}{{{\text{d}}\tau }} = \frac{{f_{2} \,}}{2\varpi }\phi_{21} cos\phi_{20} . \hfill \\ \end{gathered}$$

(54)

The solutions of the preceding system can be obtained if we express the unknown functions $b_{j1}$ and $\phi_{j1} \,\,(j = 1,2)$ in an exponential form as $C_{s} e^{\hbar \tau }$. Here $C_{s} \,\,(s = 1,2,3,4)$ are constants and $\hbar$ is the functions’ eigenvalues. In such case, the steady-state solutions $b_{j0}$ and $\phi_{j0} \,(j = 1,2)$ will be asymptotically stable, if the roots’ real parts of the following characteristic equations have negative values [38]

$$\hbar^{4} + \Sigma_{1} \hbar^{3} + \Sigma_{2} \hbar^{2} + \Sigma_{3} \hbar + \Sigma_{4} = 0,$$

where

$$\begin{aligned} \Sigma_{1} & = \frac{{f_{2} \sin \phi_{20} }}{{2b_{20} \varpi }} + \frac{{\varpi^{2} b_{20} N_{1} \sin \phi_{10} (B_{2} + s_{1} - \varpi^{2} B_{1} )}}{{2(\varpi^{2} - 1)b_{10} }}, \\ \Sigma_{2} & = \frac{ - 1}{{32\varpi (\varpi^{2} - 1)^{2} b_{10} b_{20} }}\{ 8\varpi^{2} f_{2} b_{20} N_{1} (\varpi^{2} - 1)\sin \phi_{10} \sin \phi_{20} (\varpi^{2} B_{1} - B_{2} - s_{1} ) + b_{10} f_{2} \\ & \quad \times (\varpi^{2} - 1)\cos \phi_{20} \,[\varpi (\varpi^{2} - 1)(3b_{20}^{2} + 2B_{2} (4 - 3B_{2} )) - 8\varpi^{3} N_{1} N_{2} \, + 16(\varpi^{2} - 1)\delta_{2} ] \\ & \quad + \varpi^{3} N_{1} b_{20}^{2} \cos \phi_{10} (\varpi^{2} B_{1} - B_{2} - s_{1} )[ - 3(\varpi^{2} - 1)b_{10}^{2} + 2(3(\varpi^{2} - 1)B_{1}^{2} - 4N_{1} N_{2} \\ & \quad - 2B_{1} (\varpi^{2} - 1)(s_{1} + 2) - (\varpi^{2} - 1)((s_{1} + 4)s_{1} + 8(\delta_{1} + \delta_{2} )))]\} , \\ \Sigma_{3} & = \frac{{\varpi N_{1} f_{2} }}{{64(\varpi^{2} - 1)^{2} b_{10} }}(\varpi^{2} B_{1} - B_{2} - s_{1} )\{ \cos \phi_{20} \sin \phi_{10} [\varpi (\varpi^{2} - 1)(3b_{20}^{2} + 2(4 - 3B_{2} )B_{2} ) \\ & \quad - 8\varpi^{3} N_{1} N_{2} + 16(\varpi^{2} - 1)\delta_{2} ] + \cos \phi_{10} \sin \phi_{20} [3(\varpi^{2} - 1)b_{10}^{2} \, + 2( - 3B_{1}^{2} (\varpi^{2} - 1)\, + 4N_{1} N_{2} \\ & \quad + 2(\varpi^{2} - 1)B_{1} (s_{1} + 2) + (\varpi^{2} - 1)((s_{1} - 4)s_{1} + 8(\delta_{1} + \delta_{2} )))]\} , \\ \Sigma_{4} & = \frac{{\varpi N_{1} f_{2} \cos \phi_{10} \cos \phi_{20} (\varpi^{2} B_{1} - B_{2} - s_{1} )}}{{1024(\varpi^{2} - 1)^{3} b_{10} }}[ - 3\varpi b_{20}^{2} (\varpi^{2} - 1) + 2\varpi (\varpi^{2} - 1)B_{2} ( - 4 + 3B_{2} ) \\ & \quad + 8\varpi^{3} N_{1} N_{2} - 16(\varpi^{2} - 1)\delta_{2} ][3b_{10}^{2} (\varpi^{2} - 1) + 2( - 3(\varpi^{2} - 1)B_{1}^{2} + 4N_{1} N_{2} + 2(\varpi^{2} - 1) \\ & \quad \times B_{1} (s_{1} + 2) + (\varpi^{2} - 1)((s_{1} - 4)s_{1} + 8(\delta_{1} + \delta_{2} )))]. \\ \end{aligned}$$

(55)

Taking into account the stability conditions at steady-state solutions by using the criteria of Routh-Hurwitz [39] are

$$\begin{gathered} \Sigma_{1} > 0,\,\, \hfill \\ \Sigma_{3} (\Sigma_{1} \Sigma_{2} - \Sigma_{3} ) - \Sigma_{1}^{2} \Sigma_{4} > 0, \hfill \\ \Sigma_{1} \Sigma_{2} - \Sigma_{3} > 0, \hfill \\ \Sigma_{4} > 0, \hfill \\ \end{gathered}$$

(56)

The Stability Analysis for the Case of Combination Resonances

In the present section, the approach of the non-linear stability can be used to study the mentioned dynamical system of the investigated problem. The frequency $\varpi$ and the parameters of detuning $\delta_{1} ,\delta_{2}$ play a significance role on the destabilization of the stability criteria. The stability diagrams have been drawn for the system Eq. (50) using various selected values of these parameters. The changes of the amplitudes $b_{1} ,b_{2}$ via time are drawn for various parametric regions. The response of the frequency of them as a function of $\delta_{1}$ is plotted in Fig. 31, in which the different values of $f_{2} ( = 0.001,\,0.0015,\,0.002)$ have been taken into consideration. It can be seen that, there are two fixed points corresponding to every value of $f_{2}$. The stability and instability areas of these points are classified in Table 4 and described according to:

• 1. At $f_{2} = 0.001$, the unstable fixed points have been explored in the range $- 1 \le \delta_{1} \le 0.16$ and the stable ones have been detected in the range of $0.16 < \delta_{1} \le 0.6$, in which they are followed by unstable fixed points in the range $0.6 < \delta_{1} \le 1.$

• 2. When $f_{2} = 0.0015,$ the unstable fixed points exist in the area $- 1 \le \delta_{1} \le 0.31$, while the stable points occur in the zone $0.31 < \delta_{1} \le 0.51$ which are followed again with unstable fixed points in the range $0.51 < \delta_{1} \le 1.$

• 3. At $f_{2} = 0.002,$ one found the unstable fixed points in the zone $- 1 \le \delta_{1} \le 0.1$, while the stable ones lie in the range $0.1 < \delta_{1} \le 0.69,$ and latter it followed by the unstable fixed points in the zone $0.69 < \delta_{1} \le 1.$

Fig. 31

Resonance curves for the amplitudes $b_{1}$ and $b_{2}$ as functions of $\delta_{1}$ for combination resonances case at $f_{2} ( = 0.001,\,0.0015,\,0.002)$ and $\delta_{2} = - 0.2\,,\varpi = 1.11.$

Table 4 Critical and peaks fixed points when $f_{2}$ have different values for combination resonance case

The variation of $b_{1}$ and $b_{2}$ via $\delta_{2}$ is displayed in Fig. 32 when $f_{2}$ has the values $(0.001,\,0.0015,\,0.002)$. A closer look at this figure explores that we have only one critical fixed point for each value of $f_{2}$ as shown in Fig. 32. The domains of fixed points whether stable or not for $f_{2}$ values are classified in Table 4 which can be illustrated according to:

• 1. At $f_{2} = 0.001,$ the stability and instability regions are found in the domains $- 1 \le \delta_{2} \le - 0.18$ and $- 0.18 < \delta_{2} \le 1,$ respectively.

• 2. When $f_{2} = 0.0015,$ the stable and unstable points are existed in the areas $- 1 \le \delta_{2} \le - 0.17$ and $- 0.17 < \delta_{2} \le 1$ respectively, whereas at $f_{2} = 0.002,$ the stable and unstable areas are $- 1 \le \delta_{2} \le - 0.14$ and $- 0.14 < \delta_{2} \le 1$, respectively.

Fig. 32

Resonance curves for the amplitudes $b_{1}$ and $b_{2}$ as functions of $\delta_{2}$ for combination resonances case at $f_{2} ( = 0.001,\,0.0015,\,0.002)$ and $\delta_{1} = - 0.3\,,\varpi = 1.11.$

On the other side, Fig. 33 represents the frequency responses curves of $b_{1}$ and $b_{2}$ as a function of $\delta_{1}$ when $\varpi$ takes the values $(1.08,\,1.11,1.29).$ There are two critical fixed points corresponding to each value of $\varpi$. The unstable and stable areas of fixed points are found in ranges $- 1 \le \delta_{1} \le 0.1,$ $- 1 \le \delta_{1} \le 0.16,$ $\, - 1 \le \delta_{1} \le 0.31$ and $0.1 < \delta_{1} \le 0.69,$ $0.16 < \delta_{1} \le 0.6,$ $0.31 < \delta_{1} \le 0.51$ respectively, in which it is followed by unstable ranges $0.69 < \delta_{1} \le 1,$ $0.6 < \delta_{1} \le 1,$$0.51 < \delta_{1} \le 1$.

Fig. 33

Resonance curves for the amplitudes $b_{1}$ and $b_{2}$ as functions of $\delta_{1}$ for combination resonances case when $\varpi ( = 1.08,\,1.11,1.29)$ and $\delta_{2} = - 0.2\,.$

According to the curves of Fig. 34 there exists one critical fixed point appropriate to each value of $\varpi$. The stable and unstable ranges of fixed points are $- 1 \le \delta_{2} \le - 0.36,\,\,\,\, - 1 \le \delta_{2} \le - 0.18,$ $- 1 \le \delta_{2} \le - 0.18,$ $- 1 \le \delta_{2} \le - 0.02,$ and $- 0.36 < \delta_{2} \le 1,$$- 0.18 < \delta_{2} \le 1,$$- 0.02 < \delta_{2} \le 1$ respectively.

Fig. 34

Resonance curves for the amplitudes $b_{1}$ and $b_{2}$ as function of $\delta_{2}$ for combination resonances case when $\varpi ( = 1.08,\,1.11,1.29)$ and $\delta_{1} = - 0.3\,.$

Tables 4 and 5 describe the relation between the critical, peaks fixed points of the different values $f_{2}$ and $\varpi$.

Table 5 Critical and peaks fixed points when $\varpi$ have different values for combination resonance case

The frequency responses can be seen in Figs. 35 and 36 when $\delta_{1} = - 0.2$ and $\delta_{2} = - 0.3$ respectively, in which they are drawn at $\varpi ( = 1.08,1.11,1.29),$ $f_{1} = 0.002,$ $m_{1} = 6,$ and $m_{2} = 5$. It is obvious from curves of Fig. 35 that there are no intersection of fixed points when $\varpi = 1.08$ and $\varpi = 1.29$, i.e. no common solutions, while at $\varpi = 1.11$ there are two stable different solutions. Whereas curves of Fig. 36 reflect that we have two unstable unique common fixed points of the solutions. It is observed that in the regions $- 1 \le \delta_{1} \le 1$ and $- 1 \le \delta_{2} \le 1$, there is a significant rise in the amplitudes of the steady-state solutions due to a high resonance among the frequencies.

Fig. 35

The frequency response when $\delta_{2} = - 0.2$: a at $\varpi = 1.08$, b at $\varpi = 1.11$, c at $\varpi = 1.29$

Fig. 36

The frequency response when $\delta_{1} = - 0.3$: a at $\varpi = 1.08$, b at $\varpi = 1.11$, c at $\varpi = 1.29$

Based on Fig. 37 and Routh–Hurwitz stability conditions, there exists six possible intersection points, four of them are unstable and the others two points $(1.58528, - 0.660867)$ and $(1.60119, - 0.675496)$ are stable. The stable and unstable points are marked with red and green colours, respectively.

Fig. 37

Six possible steady-state amplitudes at $f_{1} = 0.002,\,f_{2} = 0.001,$ $\delta_{1} = 0.11\,,$ $\,\delta_{2} = 0.001,$ and $\varpi = 1.11,$ where red points refer to stable points and green points refer to unstable points

Now, we will look at the properties of the non-linear amplitudes of system Eq. (50) and their stability according to the following transformation [40, 41]

$$\begin{gathered} {\rm A}_{1} (\tau_{1} ,\tau_{2} ) = \frac{1}{2}[\tilde{n}_{1} (\tau_{1} ,\tau_{2} ) + i\,\tilde{q}_{1} (\tau_{1} ,\tau_{2} )]e^{{i(\,\tilde{\delta }_{1} + \,\tilde{\delta }_{2} )\,\tau_{1} }} , \hfill \\ {\rm A}_{2} (\tau_{1} ,\tau_{2} ) = \frac{1}{2}[\tilde{n}_{2} (\tau_{1} ,\tau_{2} ) + i\,\tilde{q}_{2} (\tau_{1} ,\tau_{2} )]e^{{i\tilde{\delta }_{2} \,\tau_{1} }} , \hfill \\ n_{j} = \varepsilon \tilde{n}_{j} ,\,\,\,\,\,q_{j} = \varepsilon \tilde{q}_{j} \,\,\,\,(j = 1,2). \hfill \\ \end{gathered}$$

(57)

Substituting Eqs. (13), (57) into Eqs. (22), (47) and then separating the real and imaginary parts to obtain

$$\begin{gathered} \frac{{{\text{d}}q_{1} }}{{{\text{d}}\tau }} + n_{1} \left[ {(\delta_{1} + \delta_{2} ) + \frac{{B_{1} }}{2}\left( {1 - \frac{3}{4}B_{1} + \frac{{s_{1} }}{2}} \right) + \frac{{s_{1} }}{2}\left( {\frac{1}{4}s_{1} - 1} \right) + \frac{{N_{1} N_{2} }}{{2(\varpi^{2} - 1)}} + \frac{1}{16}(n_{1}^{2} + q_{1}^{2} )} \right] \hfill \\ + \frac{{\varpi^{2} N_{1} n_{2} }}{{2(1 - \varpi^{2} )}}(B_{1} \varpi^{2} - s_{1} - B_{2} ) = 0, \hfill \\ \frac{{{\text{d}}n_{1} }}{{{\text{d}}\tau }} + q_{1} \left[ {\frac{{B_{1} }}{2}\left( {\frac{3}{4}B_{1} - \frac{{s_{1} }}{2} - 1} \right) - (\delta_{1} + \delta_{2} ) + \frac{{s_{1} }}{2}\left( {1 - \frac{1}{4}s_{1} } \right) - \frac{{N_{1} N_{2} }}{{2(\varpi^{2} - 1)}} - \frac{1}{16}(q_{1}^{2} + n_{1}^{2} )} \right] \hfill \\ - \frac{{\varpi^{2} N_{1} q_{2} }}{{2(1 - \varpi^{2} )}}(B_{1} \varpi^{2} - s_{1} - B_{2} ) = 0, \hfill \\ \frac{{{\text{d}}q_{2} }}{{{\text{d}}\tau }} + n_{2} \left[ {\delta_{2} + \frac{{\varpi B_{2} }}{2}\left( {1 - \frac{3}{4}B_{2} } \right) + \frac{{\varpi^{3} N_{1} N_{2} }}{{2(1 - \varpi^{2} )}} + \frac{\varpi }{16}(n_{2}^{2} + q_{2}^{2} )} \right] + \frac{{f_{2} }}{2\varpi } = 0, \hfill \\ \frac{{{\text{d}}n_{2} }}{{{\text{d}}\tau }} + q_{2} \left[ { - \delta_{2} + \frac{{\varpi B_{2} }}{2}\left( {\frac{3}{4}B_{2} - 1} \right) - \frac{{\varpi^{3} N_{1} N_{2} }}{{2(1 - \varpi^{2} )}} - \frac{\varpi }{16}(q_{2}^{2} + n_{2}^{2} )} \right] = 0. \hfill \\ \end{gathered}$$

(58)

The amended amplitudes were evaluated in various parameter regions over the specified time interval, and the amplitude characteristics were displayed in phase-plane curves as in Figs. 38 and 39 using the following data

$$\begin{gathered} f_{2} ( = 0.001,\,0.0015,\,0.002),\,\,\,\,\,\,f_{1} = 0.002,\,\,\,\,\,\,\,\delta_{1} = 0.11\,,\,\,\,\,\,\,\delta_{2} = 0.001, \hfill \\ \varpi = 1.11,\,\,\,\,\,\,n_{1} (0) = 0.07,\,\,\,\,\,\,q_{1} (0) = 0.06,\,\,\,\,\,\,n_{2} (0) = 0.02,\,\,\,\,\,\,q_{2} (0) = 0.02. \hfill \\ \end{gathered}$$

Fig. 38

Time histories of $n_{1}$ and $q_{1}$ besides the modulation’s equations projection on the plane $n_{1} q_{1}$ when $f_{2} ( = 0.001,0.0015,0.002),$ $f_{1} = 0.002,$ $\delta_{1} = 0.11\,,$ $\delta_{2} = 0.001,$ and $\varpi = 1.11$

Fig. 39

Time histories of $n_{2}$ and $q_{2}$ in addition to the projection of the modulation equations on the plane $n_{2} q_{2}$ when $f_{2} ( = 0.001,0.0015,0.002),$ $f_{1} = 0.002,$ $\delta_{1} = 0.11\,,$ $\delta_{2} = 0.001,$ and $\varpi = 1.11$

The impact of the various selected values of $f_{2}$ on the paths of $n_{1}$ and $q_{1}$ is drawn in Fig. 38. Quasi-periodic decelerating waves are portrayed in parts (a) and (b) of this figure, in which the number of oscillations increases to some extent with the increasing of $f_{2}$ values besides decreasing of the wavelengths. On the other hand, the depicted curves of Fig. 39 reflect the change of the modified phases $n_{2}$ and $q_{2}$ with time $\tau$ when $f_{2}$ has the above values as in parts (a) and (b), respectively. The behaviors of the represented waves of $n_{2}$ and $q_{2}$ have periodic attitude, in which the amplitudes of these waves increase with the increasing of $f_{2}$ values. Moreover, the projections of the trajectories of the ME on the phase planes $n_{1} q_{1}$ and $n_{2} q_{2}$ are represented in parts (c) of Figs. 38 and 39. A closed symmetric trajectories curves are observed which confirm our prediction for the steady motion of the studied system.

Conclusions

A dynamical system with 2DOF double RBP is investigated as a novel model. The motion of its suspension point is restricted to be along a Lissajous curve in the presence of two subjected external harmonic moments. The general EOM are derived using the second kind of Lagrange's equations and solved analytically up to the third-order of approximation using the MSM. The solvability conditions and the ME have been obtained in light of the categorized resonance cases. Two mainly external resonances are examined together in addition to a combination case of both the internal and the external resonance. The numerical results of the EOM have been obtained using Runge–Kutta method from fourth-order to draw the solutions. It has been found that the numerical results agree with analytical ones which show the efficiency of the used perturbation method. Moreover, the time-dependent of the gained analytic solutions, besides both of the resonance curves, amplitudes and modified phases are plotted. The stability areas of the fixed points at the steady-state have been examined in accordance with the non-linear analysis approach of Routh–Hurwitz. The properties of the modified amplitude of the non-linear analysis of the external resonance cases are examined and discussed. This model is very distinctive for its use in many engineering applications, for example, the vibrational of the motion of the robot as a dynamic system and analysis the control aspects of flexible arm robotics, pumps compressors, rotor dynamics, transportation devices, shipboard cranes, and human or robotic walking analysis.