1 Introduction

Multibody dynamics is a field that focuses on the modelling of complex and highly coupled mechanical or mechatronic systems, which typically possess multiple degrees of freedom and undergo rotational and/or translational motion. The presence of friction in such systems cannot be overlooked, as it can lead to steady-state errors, stick–slip motion, and limit cycles [1]. Therefore, it is crucial to investigate the nature of friction and its behaviour under different circumstances to enable compensation and enhance the design of these systems. Friction is prevalent in various industrial and sensitive systems, including robotic manipulator joints, where it can be responsible for up to 50% of the positioning error in heavy industrial manipulators [2]. Other examples of systems where friction plays a significant role include large motor and rotor assembly, milling machine tool feed drives, surgical robot joints, and the drive mechanism of an astronomical mount system.

Friction is a natural form of external resistance that occurs at the contact point or points of contact surface of two bodies. This phenomenon is influenced by various factors, such as the sliding or relative velocity, the material properties of the contact surface, temperature, and the presence and type of lubrication [1]. When two bodies are stationary, static friction occurs, whereas kinetic friction occurs when the bodies are in motion. Frictional behaviour can be observed in two regimes: the pre-sliding regime, which deals with microscopic effects, and the sliding regime, which deals with macroscopic effects. A transition regime also exists between these two regimes. Researchers have studied various aspects of friction, including stiction, viscous effects, the Stribeck effect, pre-sliding displacement, stick–slip effects, hysteresis (or frictional lag), varying break-away force, and chaos (or bifurcation) [3]. Many researchers have investigated friction over the years [4,5,6,7,8,9], as it has a significant impact on the efficient operation and control of many engineering systems.

The investigation of friction dates back to the sixteenth century, and since then, various mathematical models have been explored to comprehend the behaviour of friction in diverse systems. Notable models include Coulomb, viscous, Karnopp, LuGre, Dahl, Leuven, and generalized Maxwell-slip. These models are categorized into static and dynamic friction models [10]. However, static models have limitations in their ability to capture the richness of frictional phenomena. Additionally, their results are less accurate than dynamic models, as stated in [11]. Another challenge posed by some of the existing friction models is the discontinuity that emerges when transitioning from the pre-sliding to sliding regime, as noted in [12].

In [4], a total of 21 static and dynamic models were reviewed, each with its unique advantage. This is due to the complex nature of friction, which makes it challenging to formulate a single model that captures all aspects of friction [13]. Consequently, several questions arise when dealing with a new system or machine, including: (1) which of the existing friction models is most suitable for the system; (2) what are the dominant frictional phenomena in the system of interest; and (3) whether the selected model is adequate to represent the essential frictional aspects, or if a new friction model is necessary. Clearly, identifying the appropriate friction model is neither trivial nor straightforward, as each system is unique. In [14], a novel nonlinear friction model was formulated and validated on the first three joints of a 6-DoF industrial robot (ER-16 without payload). The model comprises Coulomb and viscous terms and two additional terms to capture frictional behavior at motion reversal. The results demonstrate that the improved friction model is superior to the Coulomb-viscous model in representing the friction characteristics of the manipulator’s joints.

The current static and dynamic friction models are considered to be white-box models, as their corresponding parameters require estimation from empirical data. In [15], the authors investigated various friction models, including Coulomb, Stribeck–Coulomb, LuGre, and GMS, for a DC motor [16], while utilizing the Nelder–Mead simplex algorithm for parameter optimization of each model. In [17], the pulley bearing friction of a 6-DoF cable-driven robot was modeled using the Coulomb friction model. In [18], three friction models, namely non-conservative, linear, and nonlinear types, were compared for a rotary triple inverted pendulum. The non-conservative model considered only viscous friction, while the linear model included both Coulomb and viscous friction. The third model, the nonlinear friction model, is comprised of zero drift error friction, Coulomb friction, viscous friction, and experimental friction. The estimation results, in terms of root mean squared error for each model, showed that the nonlinear friction model was more effective in estimating the joint frictions of the system.

For many applications, the Coulomb or viscous friction models are satisfactory in depicting the frictional behavior or effect within multibody dynamic systems. However, for machines or systems where a high level of accuracy in positioning is required—such as within the micrometer range in machine tool applications—more sophisticated and effective friction models are needed [19].

Black-box modeling is an alternative approach employed to develop friction models. For instance, in [20], the authors considered a tribometer and employed a nonlinear autoregressive model with a polynomial order of 5, local, and recurrent neural networks to model friction in sliding and pre-sliding regimes, without incorporating any prior physics-based knowledge of the test system. Furthermore, in [21], neural networks were utilized to estimate the friction coefficient of a titanium-based sliding surface under varying conditions, including temperature, sliding velocity, and stress. The results showed that the radial basis type of neural network outperformed the multi-layer feed-forward type in estimating the friction coefficient.

However, there has been limited research on utilizing neural networks and other machinelearning techniques to develop friction models for various mechanical and mechatronic systems. The few ones found include the use of neural network optimized by genetic algorithm to model the static friction in a robot joint [22], long short-term memory (LSTM) which is a type of neural network to model the nonlinear friction error of a CNC machine tools [23], convolutional neural network to identify friction in a 6-DoF robotic arm [24] and LSTM to model the rolling friction in a mechanical system [25]. Furthermore, there is scarce information available regarding the type of data and experimental methods required for friction estimation. Additionally, several issues are not well understood, such as the selection of time-domain or frequency-domain data, open-loop or closed-loop experiments, online or offline estimation, and the necessity for data pre-processing.

This paper aims to present a novel approach to friction estimation, proposing a PINN-based friction modeling method. The supporting objectives of this study include: (1) investigating the performance of common frictional models through a numerical simulation of a double torsion pendulum reduced mathematical model; (2) discussing practical data-driven friction modeling approaches; (3) demonstrating the data-driven dynamic and friction modeling of a double torsion pendulum system using PINN and comparing its results with those of the Nelder–Mead (N–M) algorithm; and (4) discussing the challenges and potential advancements in friction modeling.

The overview of this review paper is illustrated in Fig. 1. In Sect. 2, various common static and dynamic friction models are presented along with a numerical simulation to show the superiority of dynamic models in capturing friction effects. Section 3 provides an overview of friction measurement, useful concepts in data-driven modelling, and the development of grey-box and black-box friction models. In Sect. 4, we present a case study where PINN is used to simultaneously identify the dynamic and friction model of a double torsion pendulum. Finally, Sect. 5 covers the concluding remarks, challenges and prospects of friction modelling, and future directions of our research.

Fig. 1
figure 1

The research overview

Full size image

2 Physics-based friction models

The physics-based, or white-box, friction models can be classified into two categories: static and dynamic models. This section provides an overview of various static and dynamic friction models and presents the numerical simulation of a few selected friction models.

2.1 Static and dynamic friction models

In the domain of friction modeling, static models typically assume the absence of microscopic effects in the pre-sliding regime, while dynamic models account for both microscopic and macroscopic friction effects during both the pre-sliding and sliding regimes [7]. As a result, dynamic models are better suited to capture the microscopic surface displacements that occur during the pre-sliding phase, as well as the lags or hysteresis that arise during sliding. The unique characteristics of these two types of physics-based or mathematical friction models are summarized in Table 1.

Table 1 Static and dynamic friction models characteristics
Full size table

The frictional phenomena that are captured by white-box friction models include static friction, dynamic friction, break-away force, pre-sliding displacement, frictional lag or hysteresis and stick–slip [3, 11]. Static friction gives a description of friction during the sticking phase, i.e., when the sliding velocity is zero, while dynamic friction refers to the dominant friction during the sliding/slipping phase. Break-away force is the force required to overcome stiction. Stribeck effect shows the decrease or negatively sloped characteristic of friction force in the low sliding velocity regime (i.e., when moving from static to Coulomb friction). Pre-sliding displacement or Dahl effect is the microscopic motion between two contacting surfaces during the sticking phase. Frictional lag or hysteresis happens when there is a delay in the change of frictional forces under an unsteady condition. This can be observed through a change in the path of friction force as the relative velocity oscillates (i.e., accelerate and decelerate) [26]. Stick–slip motion occurs which the sliding velocity fluctuates; thus, causing an intermittent motion.

Some examples of the commonly used static and dynamic friction models are summarized in the following sections, where one or a combination of the explained phenomenal can be found. Three static: Coulomb, Coulomb-viscous and Stribeck; and three dynamic: Dahl, LuGre, and generalized Maxwell-slip friction models are presented in terms of their mathematical function, parameters, and other distinguishing features.

2.1.1 Coulomb friction

The Coulomb friction is mathematically expressed with the use of \({\text {sgn}}\) function as follows:

$$\begin{aligned} {{F}_{f}}=\left\{ \begin{array}{ll} {{F}_{c}{\text {sgn}}(v)} &{}\quad \text {if}\quad v>0, \\ {{F}_{a}} &{}\quad \text {if}\quad v=0\quad \text {and}\quad {{F}_{a}}<{{F}_{c}}, \\ \end{array} \right. \end{aligned}$$
(1)

where \({{F}_{c}}={{\mu }_{c}}N \), \({F}_{f}\) is the friction force [N], \({F}_{c}\) is the Coulomb friction [N], \({F}_{a}\) is the applied force [N], N is the force perpendicular to the contacting surfaces [N] and it is directly proportional to the frictional force, v is the relative sliding velocity [m/s] and \({\mu }_{c}\) is the coefficient of \({F}_{c}\) [−] which is a measure of resistance present at the contact surface during a sliding or rolling motion.

This friction model is often used because its structure is simple and easy to implement. However, one of its drawbacks include a discontinuous behaviour at zero velocity, which is caused by the sign function. To avoid this issue and ensure a smoother behavior of the model, an alternative approach involves approximating the sign function with a hyperbolic tangent function. [27]. The friction model with the hyperbolic tangent function takes this form [28]:

$$\begin{aligned} F_f=F_c \tanh (\alpha \dot{x}), \end{aligned}$$
(2)

where \(\lim _{\alpha \rightarrow \infty }\tanh {\left( \varepsilon \dot{x}\right) }={\text {sgn}}(\dot{x})\), \(\varepsilon \) is an arbitrary constant in the range \(0 \rightarrow \infty \) [s/m]. The lower the value of \(\varepsilon \), the smoother the approximation.

The other drawbacks of Coulomb friction model is that frictional phenomena like viscous, Stribeck, pre-sliding and hysteresis effects are not present [4, 11].

2.1.2 Coulomb-viscous friction

The Coulomb-viscous model is an extension of the Coulomb model and follows:

$$\begin{aligned} {F}_{f}={F}_{c}{\text {sgn}}(v)+{F}_{v}, \end{aligned}$$
(3)

\(\text {where }{F}_{v}={\mu }_{v}v,\) \({F}_{v}\) is the viscous friction [N] and \({\mu }_{v}\) is the viscous fricition coefficient [N s/m] which measures the intensity of damping influence and is closely linked to the viscosity of the fluid.

The Coulomb-viscous friction model parameters are \({\mu }_{c}\) and \({\mu }_{v}\). Basically, the viscous friction model was developed to describe the effect of lubrication in the two contact surfaces. As such, the application of this friction model is limited and mostly integrated with other models like Coulomb [11, 29, 30].

2.1.3 Stribeck effect

The Stribeck model is formed by combining Coulomb, viscous and Stribeck effect. The mathematical formation is [11, 29, 30]:

$$\begin{aligned} {{F}_{z}}=F_v + {\text {sgn}}(v) \left[ {{F}_{c}}+({{F}_{s}}-{{F}_{c}}){{e}^{-{{(v/{{v}_{s}})}^{\alpha }}}} \right] , \end{aligned}$$
(4)

where \({{F}_{s}}={{\mu }_{s}}N\), \({F}_{z}\) is the Stribeck friction [N], \({F}_{s}\) is the static friction [N] and \({\mu }_{s}\) is the coefficient of \({F}_{s}\) [−] which represents the level of opposition to motion exhibited by the surfaces before a relative motion and \({v }_{s}\) is the Stribeck velocity [m/s], \(\alpha \) is an empirical parameter from 0.5 to 2 (the exponential model becomes Gaussian model), but can be very large for systems with effective boundary lubricants.

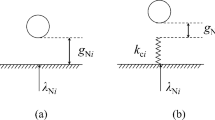
The Stribeck effect parameters include \({\mu }_{s}\), \({\mu }_{c}\) and \({\mu }_v\). The static friction models introduced are depicted in Fig. 2.

Fig. 2
figure 2

Static friction model characteristics

Full size image

2.1.4 Dahl

The Dahl friction model stands as an early dynamic model conceived to elucidate the friction characteristics of ball bearings. It postulates that the frictional force is directly related to the average bristle deflection [4, 31]. Figure 3 illustrates the deflection of a bristle when two rough surfaces are in contact.

Fig. 3
figure 3

The physical analogy of the bristle nature of friction in the Dahl model [31]

Full size image

This friction model follows:

$$\begin{aligned} F_f=\sigma _0z,\quad \dot{z}=v{\text {sgn}}\left( \gamma \right) \left| \gamma \right| ^\beta , \end{aligned}$$
(5)

where z represents the average bristle deflection [m], \({\sigma }_{0}\) is asperity stiffness [N/m] and \({\beta }\) is the parameter that determines the coefficient of the hysteresis loop [−], \(\gamma =1-{\text {sgn}}(v)\sigma _0z/F_c\) [−].

The three parameters associated with this friction model are \({\sigma }_{0}\), \({\mu }_{c}\) and \(\beta \). This model was developed to describe pre-sliding friction but does not capture Stribeck effect [6, 32].

2.1.5 LuGre

The LuGre friction model is one of the most popular dynamic friction models and it is described through the following equations [6, 9, 11]:

$$\begin{aligned} {{F}_{f}}&={{\sigma }_{0}}z+{{\sigma }_{1}}\dot{z}+{{\sigma }_{2}}v, \end{aligned}$$
(6a)
$$\begin{aligned} \dot{z}&=v-\frac{{{\sigma }_{0}}}{{{F}_{z}}(v)}z\left|v \right|, \end{aligned}$$
(6b)
$$\begin{aligned} {{F}_{z}}&={{F}_{c}}+({{F}_{s}}-{{F}_c}){{e}^{-{{(v/{{v}_{s}})}^{\beta }}}}, \end{aligned}$$
(6c)

where \({\sigma }_{1}\) and \({{\sigma }_{2}}\) are the damping and viscous coefficients that relate to the pre-sliding and kinetic friction states, respectively [Ns/m].

This model has six parameters, which are \({\sigma }_{0}\), \({\sigma }_{1}\), \({\sigma }_{2}\), \({\mu }_{c}\), \({\mu }_{s}\) and \(\beta \).

The LuGre friction model is an improvement of Dahl’s model. It captures pre-sliding friction, stiction effects, viscous friction and Stribeck effect. In addition, it is the most applied dynamic model to different mechanical and mechatronic systems due to simplistic form compared to other dynamic models like Leuven and generalized Maxwell-slip [6, 33].

2.1.6 Generalized Maxwell slip

In this model, friction force is described as a multi-state system with n viscoelastic elements connected in parallel as described in Fig. 4.

Fig. 4
figure 4

GMS friction model representation [19]

Full size image

Each element shares a common dynamic model but possesses distinct parameters. The equation used to describe GMS friction model is [19, 34]:

$$\begin{aligned} {{F}_{f}}= & {} \sum \limits _{i=1}^{n}{\left( {{K}_{i}}{{z}_{i}}+{{B}_{i}}{\dot{z}_{i}} \right) }+{{F}_{v}}, \end{aligned}$$
(7)
$$\begin{aligned} \frac{d{{z}_{i}}}{dt}= & {} {\left\{ \begin{array}{ll} v &{} \text {if stick}, \\ {\text {sgn}}(v){{C}_{i}}\left( 1-\frac{{{z}_{i}}}{{s}_{i}(v)} \right) &{}\text {if slip}, \end{array}\right. } \end{aligned}$$
(8)

where \({K}_{i}\) and \({B}_{i}\) are the stiffness and damping coefficients of the i-th element in [N/m] and [N s/m], respectively. Each element stick until \(z_{i}={s}_{i}(v)\) for sliding to begin, v is the velocity input to the system [m/s], \({s}_{i}(v)\) is the stribeck or velocity-reducing function of each element, \({C}_{i}\) is the attraction parameter of the i-th element [−], which determine the speed at which \(z_{i}\) approaches \({s}_{i}(v)\).

The GMS friction model described above has the many parameters; they are \({K}_{i}\), \({B}_{i}\), \({s}_{i}\), \({C}_{i}\) and \({\mu }_{V}\).

2.2 Comparison of the discussed friction models

In this section, we shortly summarize the discussed static and dynamic friction models: Coulomb, Coulomb-viscous, Stribeck, Dahl, LuGre, and generalized Maxwell-slip models. We provide below a brief comparison of their mathematical functions, parameters, features fields of use accuracy, features and complexity and applicability:

  1. A.

    Static friction models discussed in Sect. 2.1:

    1. 1.

      Coulomb friction model:

      • Mathematical function: friction force is proportional to the normal force.

      • Parameters: coefficient of friction.

      • Features: simple, widely applicable, stick–slip behavior, limited accuracy.

    2. 2.

      Coulomb-viscous friction model:

      • Mathematical function: combination of Coulomb and viscous friction.

      • Parameters: coefficient of friction, viscous damping.

      • Features: adds damping, useful for specific cases, moderate accuracy.

    3. 3.

      Stribeck friction model:

      • Mathematical function: captures transitions between friction regimes.

      • Parameters: Stribeck curve parameters.

      • Features: models sliding speeds, better accuracy in some cases.

  2. B.

    Dynamic friction models discussed in Sect. 2.1:

    1. 1.

      Dahl friction model:

      • Mathematical function: linear springs and dampers.

      • Parameters: spring constants, damping coefficients.

      • Features: varying velocity, rate-dependent effects, calibration.

    2. 2.

      LuGre friction model:

      • Mathematical function: nonlinear differential equations with observer.

      • Parameters: static friction, viscous friction, stiffness, etc.

      • Features: captures static and dynamic friction, pre-sliding.

    3. 3.

      Generalized Maxwell-slip friction model:

      • Mathematical function: Maxwell element with slip threshold.

      • Parameters: Maxwell element parameters, slip threshold.

      • Features: viscoelasticity, slip behavior, material compliance.

  3. C.

    Field of use accuracy:

    • Static models: simple and applicable, limited accuracy.

    • Dynamic models: accurate for varying velocities, complex dynamics.

  4. D.

    Features and complexity:

    • Static models: easy to use, lack dynamic features.

    • Dynamic models: include rate-dependent effects, pre-sliding, material compliance.

  5. E.

    Applicability:

    • Static models: basic analyses, negligible velocity effects.

    • Dynamic models: real-world systems, varying velocities, complex behavior.

2.3 Numerical validation of selected friction models

In this numerical simulation study, we consider a reduced model of a double torsion pendulum system shown in Fig. 5 with the aim to simulate the dynamic response of the system based on four friction models [35].

Fig. 5
figure 5

Physical model of a double torsion pendulum [35]

Full size image

2.3.1 Model

The mathematical formulation of the simulated double torsion pendulum model was established in [35] using the Lagrange method. In the modified and reduced mathematical model, we introduce the time series \(\varphi _{1,m}(t)\) as an input in [rad], representing the real angular displacement of the lower contact surface (illustrated in red in Fig. 5). Additionally, we calculate its approximate second time derivative. This leads us to the subsequent second-order semi-empirical dynamic system governing the rotational motion of the disk with respect to the \(\varphi _2\) coordinate:

$$\begin{aligned} \frac{d^2\varphi _2}{dt^2}=\frac{1}{J_2}\left( -c_2\frac{d\varphi _2}{dt} -k_2\varphi _2-F_f\right) -\frac{d^2\varphi _{1,m}}{dt^2}, \end{aligned}$$
(9)

In this equation, \(k_2\) [N m/rad] stands for the stiffness coefficient of two symmetric beam springs connected to the upper disk, fixed atop the inertia column \(J_1\) [kg m2], and anchored at the disk of inertia \(J_2\) [kg m2]. The parameter \(c_2\) [N s/m] represents damping between the beam springs and the rotating disk (as depicted in the upper part of Fig. 5). The term \(F_f\) [N m] corresponds to the friction moment and is addressed by four friction models detailed in Sect. 2.1. These models encompass two static (LuGre, Coulomb) and two dynamic (Dahl and Coulomb) formulations.

2.3.2 Numerical simulation

The four friction models that were simulated are the LuGre, Coulomb and viscous, Dahl and Coulomb, respectively.

The parameters of four experiments conducted in this experimental part are as follows: \(J_2=2.17\cdot 10^{-4}\), \(c_2=0.19\), \(k_2=0.7\), \(\mu _v=0.5\), \(\mu _c=0.12\), \(\mu _s=0.16\), \(\beta =2\), \(\sigma _0=2\cdot 10^4\), \(\sigma _1=10^2\), \(\sigma _2=\mu _v\), \(v_s=10^{-3}\), and the parameter of smooth approximation of sign function, \(\varepsilon =10^3\). The initial conditions superposed on the disk body are zero while forcing of the mass is initiated by the input \({d^2\varphi _{1,m}}/{dt^2}\). More detail about the experimental part and its conditions can be found in [35].

Figure 6a and b demonstrate the effect of numerical simulation carried out with the use of the investigated friction models.

Fig. 6
figure 6

Profile of different friction models (a) with respect to velocity (b) with their corresponding time response to the test input function \(\dot{\varphi }_2(t)=0.02\sin (0.2\pi t)\) (b)

Full size image

We observe that in Fig. 7a and b, the friction models exhibit different temporal responses. In the case of the investigated dynamic system, the static Coulomb-viscous friction model closely follows the dynamic LuGre friction model. However, in this scenario, the use of both models does not yield favorable results, as the blue and purple trajectories deviate significantly from the expected temporal behavior. On the other hand, the second pair of temporal responses, i.e., the static Coulomb and dynamic Dahl models, also nearly coincide, but depict a behavior closer to reality. The simulated behavior captures abrupt changes at the moments of the disc rebounding from soft barriers and changing direction. It is noteworthy that all models lead to similar lengths of the disc’s adherence zones as it rotates on the upper surface of the column.

Fig. 7
figure 7

Time characteristics of the disk dynamics at various models of friction

Full size image

3 Data-driven friction models

This section is focused on the measurement techniques for friction and the discussion of beneficial data-driven modeling concepts. Furthermore, this section will present an in-depth explanation of the grey-box and black-box friction modeling methodologies.

3.1 Friction measurement

It is challenging to accurately predict the frictional behavior of a system without measurements and estimation of certain parameters. Friction can be directly measured using a tribometer or indirectly estimated based on its impact on other measurable quantities of the system. As reported by Kossack et al. [36], there are two primary methods for measuring friction: force-based and velocity-based friction measurements.

In the force-based approach, the friction force between two contact surfaces is measured along with the relative velocity and/or displacement between them as a function of time. For example, Radons et al. [37] considered a test set-up where friction force and relative displacement were measured. On the other hand, the velocity-based approach is employed when it is difficult to place a force sensor in a suitable position on the system. In [36], velocity measurement coupled with an estimation method based on energy analysis was proposed to parameterize a simple friction model. The velocity data obtained from a friction measuring machine and its identified structural dynamics, such as mass, damping, and stiffness coefficients, were used to estimate the friction force of the machine.

Moreover, in the friction identification case study for robotic manipulators presented in [38], it was not practical to directly measure the friction force at various joints. Instead, a method was employed to measure friction by applying a low torque signal to one joint while locking the other joints and measuring the corresponding velocity. In [39], an electrical motor was utilized as a test stand operating in torque mode. The motor was subjected to an increasing torque in the form of an analog voltage, and the angular position was measured using an encoder. Additionally, the angular velocity of the motor was determined by numerically integrating the angular position signal.

When dealing with translational mechanical or mechatronic systems, such as mass-spring systems pulled on a friction surface, the friction force and sliding velocity are measured to enable the estimation of the selected friction model. Conversely, in rotational mechanical or mechatronic systems, friction torque, and angular velocity are measured. At a constant velocity, the force or torque input to the system equals the friction force or torque (\({F}_{f}\) or \(\tau _{f}\)):

$$\begin{aligned} M\ddot{x}={{F}_{ap}}-{{F}_{f}}\,. \end{aligned}$$
(10)

When \(\dot{x}\) is constant, \(\ddot{x}=0\) and \({{F}_{ap}}={{F}_{f}}\). Similarly,

$$\begin{aligned} J\ddot{q}=\tau -{{\tau }_{f}}\,. \end{aligned}$$
(11)

At constant angular velocity, \(\ddot{q}=0\) and \(\tau _{ap} ={{\tau }_{f}},\) where \(F_{ap}\) and \(\tau _{ap}\) are the applied friction and torque, respectively.

The velocity at which an experiment is conducted is a crucial factor to consider. For instance, experimental data collected at low velocities are essential for identifying the dynamic parameters of a dynamic friction model, such as the LuGre model. Another intriguing and unexplored aspect of friction identification is obtaining input–output data, which is indirectly related to the friction force/torque of a system. By understanding the governing equations of this data, a robust friction model can be estimated. This approach will be demonstrated in one of the case studies presented in Sect. 4.

3.2 Useful data-driven modelling concepts

There are several important concepts to consider when developing a data-driven model, which will be discussed in the following sections.

3.2.1 System excitation

The selection of the input excitation signal is a crucial factor in determining the quality and accuracy of the estimated friction model as well as the richness of the acquired data. A well-designed excitation signal is capable of capturing the fundamental features of the system dynamics. Various excitation signals have been documented in the literature, including pseudorandom binary sequence (PRBS), chirp or swept sine, multi-sine, and step signal [40].

In [41, 42], a bang–bang signal with a delay was employed to stimulate a two-link flexible manipulator. The design of the excitation signal took into account the maximum allowable input current to the manipulator. The time-series response of the system was acquired in batches as the amplitude of the signal varied. Additionally, [43] utilized a swept-frequency cosine signal to excite a servo drive system.

3.2.2 Time-domain and frequency-domain data

Data can be available in two modes: time domain and frequency domain. Time-domain data consists of one or more input and output signals measured as a function of time. On the other hand, frequency-domain data shows input and output signals as a function of frequencies. Through transformation methods such as the Fourier transform, it is possible to convert a signal from time-domain to its frequency-domain equivalent. Data are analyzed in the frequency-domain when the observed signal is periodic [44]. However, the frequency-domain approach is not commonly used due to the susceptibility of frequency response measurements to noise [45]. Hence, time-domain data is popularly used for the prediction of friction models.

In [46], a random noise signal was employed to excite a rotating arm system, and the resulting frequency response function was determined. The frequency-domain data obtained from the measurement was then utilized to identify the stiffness and damping parameters of a linearized second-order LuGre friction model at the pre-sliding regime. The accuracy of the estimated friction model parameters was validated through another experiment that involved measuring time-domain data. The results indicate that the estimated friction model is locally valid when the applied force and pre-sliding displacement are approximately zero. In addition, the dynamic friction of a servomotor system was analysed in both the time and frequency domains using the GMS friction model presented in [47].

3.2.3 Closed-loop and open-loop system identification

The friction model of a system can be identified by utilizing the data acquired from either an open-loop or closed-loop system. Among these two methods, the open-loop system identification approach is predominantly used. However, closed-loop system identification is also employed, particularly when the identified system is unstable when operated in open-loop mode.

In [11], closed-loop steady-state experiments were conducted with a PI velocity controller to estimate the coefficients of Coulomb and viscous friction of a brushless DC motor. The reference velocity range for each conducted experiment was between 0.05 and 15.7 rad/s in both positive and negative directions, and the control effort (representing the friction force) was measured accordingly. The friction behavior in a 1-D astronomical mount system joint was considered in [48], where the LuGre friction model was employed. The static parameters of the model were identified using data obtained through a closed-loop control experiment with a PD controller, while the dynamic parameters were identified through an open-loop experiment. A neural network can be used to determine the dependence between the open-loop controller’s output and some selected states of a discontinuous system [49].

3.2.4 Online and offline identification

The friction model can be identified either on-line or off-line. In the on-line identification approach, the parameters of the friction model are continuously updated as new data becomes available during the operation of the system. Conversely, in the off-line estimation method, the first step is to acquire input–output data, after which the friction model parameters are subsequently estimated.

In [50], a recursive least-squares method-based online identification algorithm was utilized to determine the drive mass and sliding friction (Coulomb, viscous, and Stribeck) of a ball screw-driven feed drive test stand. This identification approach was employed to decrease the computation time and complexity associated with offline methods. The measured data was used directly without any preprocessing, and a two-stage identification technique was proposed. In the initial stage, the equivalent mass of the feed drive, viscous friction coefficient, and Coulomb friction were identified while the system operated at high velocities. The Stribeck friction model parameters, breakaway force, and Stribeck velocity, were identified in the second stage when the system was operating in the low-velocity region.

3.2.5 Data pre-processing

This kind of pre-processing pertains to operations conducted subsequent to data acquisition from a physical system, aimed at improving the quality of the acquired data. The range of operations comprises but is not restricted to noise reduction or elimination, the removal of outliers, and data scaling. As an example, a low-pass Butterworth filter can be utilized to diminish the noise present in the measured pendulum angle data of an inverted pendulum system undergoing free vibration motion. The resulting smooth signal of the angular position was then utilized to compute the angular position and angular acceleration of the pendulum, respectively.

The exclusive objective of data processing is to enhance the quality of data. Nevertheless, this must be executed with care to prevent the loss of some information.

3.3 Grey-box friction modelling

Experimental data is utilized in the development of grey-box friction models, which involve the selection of an existing (or new) static or dynamic model and estimation of the associated parameters based on the experimental data and the chosen identification algorithm for parameter optimization, as illustrated in Fig. 8 [20]. Various identification algorithms, including least-squares, recursive least-squares, Nelder–Mead simplex algorithm, genetic algorithm, particle swarm optimization algorithm, and others, can be employed in this process.

Fig. 8
figure 8

Grey-box friction modelling

Full size image

It is worth noting that although there are several identification algorithms available, the commonly used ones in literature will be briefly discussed. They include least-squares, recursive least-squares, Nelder–Mead simplex algorithm, and genetic algorithm.

3.3.1 Least-squares and recursive least-squares identification

The least squares method is utilized to determine a collection of parameters that minimize the mean squared error (MSE) between the desired and predicted outputs of a given system with m number of inputs x and outputs y [51]. The inputs and outputs have n data samples and \(\theta \) is the unknown linear regression coefficient of x and y. A linear regression model follows:

$$\begin{aligned} \begin{aligned} {{y}_{i}}&={{x}_{i1}}{{\theta }_{1}}+{{x}_{i2}}{{\theta }_{2}}+\cdots +{{x}_{in}}{{\theta }_{n}}\\&= \underbrace{\left[ \begin{matrix} {{x}_{1}} &{} \begin{matrix} {{x}_{2}} &{} \begin{matrix} \cdots &{} {{x}_{n}} \\ \end{matrix} \\ \end{matrix} \\ \end{matrix} \right] }_{{{\varphi }_{k}}}\underbrace{\left[ \begin{matrix} {{\theta }_{1}} &{} {{\theta }_{2}} &{} \cdots &{} {{\theta }_{n}} \\ \end{matrix} \right] }_{{{\theta }^{T}}}. \end{aligned} \end{aligned}$$
(12)

The matrix form of Eq. 12 given the size of x and y to be m is:

$$\begin{aligned} \underbrace{\left[ \begin{matrix} {{y}_{1}} \\ {{y}_{2}} \\ \vdots \\ {{y}_{m}} \\ \end{matrix} \right] }_{Y}=\left[ \begin{matrix} {{x}_{11}} &{} {{x}_{12}} &{} \cdots &{} {{x}_{1n}} \\ {{x}_{21}} &{} {{x}_{22}} &{} \cdots &{} {{x}_{2n}} \\ \vdots &{} \vdots &{} {} &{} \vdots \\ {{x}_{m1}} &{} {{x}_{m2}} &{} \cdots &{} {{x}_{mn}} \\ \end{matrix} \right] \left[ \begin{matrix} {{\theta }_{1}} \\ {{\theta }_{2}} \\ \vdots \\ {{\theta }_{n}} \\ \end{matrix} \right] =\underbrace{\left[ \begin{matrix} {{x}_{1}} \\ {{x}_{2}} \\ \vdots \\ {{x}_{m}} \\ \end{matrix} \right] }_{X}\underbrace{\left[ \begin{matrix} {{\theta }_{1}} \\ {{\theta }_{2}} \\ \vdots \\ {{\theta }_{n}} \\ \end{matrix} \right] }_{{{\theta }^{^{T}}}}. \end{aligned}$$

The MSE of the actual and predicted outputs is:

$$\begin{aligned} V=\frac{1}{n}\sum \limits _{i}^{n}{{{\left[ Y(i)-X(i)\theta \right] }^{2}}}, \end{aligned}$$
(13)

and the optimal \(\hat{\theta }\) that minimizes the MSE is

$$\begin{aligned} \hat{\theta }={{({{X}^{T}}X)}^{-1}}{{X}^{T}}Y. \end{aligned}$$
(14)

The least-squares algorithm is a widely used identification technique owing to its simplicity and ease of implementation [52]. The recursive least-squares (RLS) estimation is a modified version of the least-squares method that ensures the model parameters are updated with new data observed from a system. RLS is computationally more efficient, offers a faster convergence and is suitable for online identification [53]. In [54], the RLS method was employed to identify the mass and sliding friction of a machine tool feed drive system in an online setting.

3.3.2 Nelder–Mead simplex and genetic algorithm

The Nelder–Mead simplex algorithm is a well-known optimization algorithm used to identify optimal parameters in a multidimensional search space, by minimizing or maximizing an objective function. This derivative-free/direct search method is particularly effective in solving nonlinear optimization problems. The algorithm operates by employing a simplex, which is an n-dimensional geometric object, to search the domain. A simplex in n dimensions is comprised of \(n+1\) vertices. For instance, the simplex of a 2-dimensional function is a triangle, while for a 3-dimensional function, the simplex is a tetrahedron.

The steps performed during each iteration of the Nelder–Mead simplex algorithm involve the generation of a new simplex consisting of \(n+1\) points, the evaluation of the objective function at all of these points, and the transformation of the simplex via one of the following operations: reflection, expansion, contraction, or shrink contraction. The algorithm terminates when any of the following criteria are met: the maximum number of iterations is reached, the simplex size reaches a minimum limit, or the current best solution reaches a desired limit. Figure 9a illustrates the Nelder–Mead simplex algorithm.

Fig. 9
figure 9

The flowcharts of two search algorithms for parameter identification

Full size image

The Nelder–Mead simplex algorithm was utilized in [55] to determine the parameters of a double torsion pendulum system.

The genetic algorithm is a local search algorithm that is commonly utilized to address optimization and search issues. This algorithm is inspired by Darwin’s theory of evolution. The algorithm begins by generating a population of individuals randomly, which is known as a generation. In each generation, the fitness of individuals is assessed regarding the problem’s objective function. Individuals with good fitness are selected for crossover and mutation, which leads to the formation of a new generation of candidate solutions. The algorithm concludes when the maximum number of generations is achieved or when a solution that corresponds to a predetermined objective function value is achieved (i.e., successive solutions’ convergence). The genetic algorithm’s workflow is depicted in Fig. 9b. In [56], GA was used to identify the parameters of a LuGre friction model for a nonlinear mechanical servo system.

3.4 Black-box friction modelling

The black-box friction model is formulated using generalized models such as neural networks, which are subsequently trained with experimental data [20, 57]. Figure 10 illustrates the black-box modelling structure that incorporates NN and PINN.

Fig. 10
figure 10

Black-box friction modelling

Full size image

3.4.1 Neural networks

Neural networks are a type of nonlinear identification tool that efficiently maps input and output measurements of a system in a black-box manner. The architecture of a neural network is inspired by the human brain, and it uses interconnected neurons to capture complex abstractions in data [58, 59].

Each neuron in a neural network consists of a summation unit and an activation function, as illustrated in Fig.  11. The summation unit multiplies inputs by their associated weights, adds a bias term, and passes the result of the linear algebra through an activation function, such as sigmoid, hyperbolic tangent, rectified linear unit, or pure linear [60].

$$\begin{aligned} {{o}_{j}}&=f({{r}_{j}}) \end{aligned}$$
(15a)
$$\begin{aligned} {{r}_{j}}&=\sum \limits _{i=1}^{n}{{{w}_{ij}}\bullet {{x}_{i}}}+{{b}_{j}} \end{aligned}$$
(15b)

where \({{r}_{j}}\) is the output of the neuron summation unit, \({{o}_{j}}\) is the output of the jth neuron, \(f(\centerdot )\) is the activation function, \({{w}_{ij}}\) is the weight associated with the ith input, \({{b}_{j}}\) is the bias of the neuron and n is the size or number of the input (x).

Fig. 11
figure 11

A single neuron network

Full size image

A single-layer neural network can estimate a linear function, while a multi-layer neural network is required for nonlinear functions. In a multi-layer NN, there exist three layers: input, hidden, and output layers. The number of inputs and outputs in the network are dependent on the training set. However, the selection of the number of hidden layers and neurons in each layer is determined through either trial and error or a domain search aided by algorithms like Bayesian networks [61].

An artificial NN is typically trained using supervised learning, wherein the network’s weights and biases are randomly initialized at the start of training. During each iteration of training, the network is fed with an input, and its output is compared with the expected output (or target) using a loss function. The loss function measures the discrepancy between the predicted output and the target output [62].

$$\begin{aligned} E=MSE(y,\hat{y})=\frac{1}{m}\sum \limits _{k}^{m}{{{\left( {{y}_{k}}-{{{\hat{y}}}_{k}} \right) }^{2}}}, \end{aligned}$$
(16)

where E is the mean squared error or loss between the actual output and the network prediction, y represents the actual target, \(\hat{y}\) represents the predicted output and m is the number of datapoints.

After computing the loss, the gradient of the loss with respect to the model parameters is calculated through a backward pass using the back-propagation algorithm. This algorithm propagates the error back through the network to determine how much each neuron contributes to the final output error. Once the gradient of the loss has been computed, an optimizer such as gradient descent, stochastic gradient descent, or ADAM is subsequently used to update each parameter so as to minimize the loss of the network over a defined training time (epochs) [63]. The optimization process involves iteratively adjusting the parameters in the direction of the negative gradient of the loss function until convergence is reached. Mathematically, the weight and bias are updated iteratively through the gradient descent method as follows:

$$\begin{aligned} \Delta {{w}_{ij}}= & {} \varepsilon \frac{\partial E}{\partial {{w}_{ij}}},\quad w_{ij}^{new}=w_{ij}^{old}-\varepsilon \frac{\partial E}{\partial w_{ij}^{old}} \end{aligned}$$
(17)
$$\begin{aligned} \Delta {{b}_{j}}= & {} \varepsilon \frac{\partial E}{\partial {{b}_{j}}},\quad b_{j}^{new}=b_{j}^{old}-\varepsilon \frac{\partial E}{\partial b_{j}^{old}} \end{aligned}$$
(18)

where \(\varepsilon \) is the learning rate.

A neural network model is considered a good fit if it can accurately predict outcomes with new datasets, which is known as network generalization. An underfit model exhibits high bias and low variance, while an overfit model is characterized by low bias and high variance [59]. Figure 12 depicts the training/learning plot, which illustrates the underfitting, optimal, and overfitting regions of a network in relation to its prediction error. Overfitting is a commonly encountered problem in machine learning [64]. One way to address overfitting is to design the model’s loss function in a manner that promotes small trained weight values, which results in a model with low variance that is better equipped to handle new datasets. This technique is known as regularization. Another way to prevent overfitting is to use large training datasets that cover the operating domain of interest in a dynamical system [64, 65].

Fig. 12
figure 12

Prediction error versus complexity of the model

Full size image

Neural network techniques can be leveraged to approximate the friction force or torque of a system as a function of multiple input variables, including normal force, sliding velocity, and surface roughness. This can be achieved by training the network using either experimental or simulation data. Once the training is complete, the network can be utilized to predict the friction force or torque for new input values.

The most prevalent types of neural networks are feed-forward, recurrent, and convolutional neural networks. However, a recent addition to the family of neural networks is the physics informed neural network, which imposes constraints or regularization on the network by incorporating physical laws.

3.4.2 Physics-informed neural networks

A major issue associated with white-box modeling is high bias, while the problem of black-box modeling is model variance. Model variance arises when the dataset available for modeling is limited or does not encompass the operating range of the system. Bias arises due to assumptions and/or non-modeled dynamics in the mathematical model of a system. These two issues can be addressed by utilizing PINNs. Physics-informed neural networks enable the incorporation of physical laws governing a dynamic system into the formulation of the loss function, which results in regularization of the network parameters to conform to the prior physical knowledge and laws of the system. This regularization leads to better approximation of the system’s behavior [66,67,68,69].

PINN can be used to solve ordinary and partial differential equations [69, 70]. For example, given a first order differential equation below:

$$\begin{aligned} \frac{dy}{dt}=f(y,t,\gamma ),\quad t\in [0,T] \end{aligned}$$
(19)

where yis the dependent variable to be approximated by a neural network, t is time and \(\gamma \) denote the system parameter.

The solution of the equation (i.e., y) can be approximated by a neural network: \(\tilde{N}(t)\approx y(t)\). The derivative of the network output is computed with respect to its inputs through automatic differentiation. By virtue of the network differentiation, the original equation can be encoded into the loss function that is used in updating the weights and biases of the network.

$$\begin{aligned} {{L}_{eq}}=\frac{d\tilde{N}(t)}{dt}-f(\tilde{N}(t),t,\gamma ) \end{aligned}$$
(20)

As a result, the new loss function that is used to optimize the neural network is [71]:

$$\begin{aligned} {{L}_{T}}&={{L}_{s}}+{{L}_{eq}} \end{aligned}$$
(21a)
$$\begin{aligned} {{L}_{T}}&=\underbrace{\frac{1}{m}{{\sum \nolimits _{i}^{m}{\left( y({{t}_{i}}) -\tilde{N}({{t}_{i}}) \right) }}^{2}}}_{Loss\text { of the solution}}\nonumber \\&\quad +\frac{1}{m}\underbrace{{{\sum \nolimits _{i}^{m}{\left( \frac{d\tilde{N}({{t}_{i}})}{dt}-f(\tilde{N}({{t}_{i}}),{{t}_{i}},\gamma ) \right) }}^{2}}}_{Loss\text { of the equation}} \end{aligned}$$
(21b)

where \(L_{s}\) is the loss of the solution, \(L_{eq}\) is the loss computed based on the system equation and \(L_{T}\) is the total loss.

The objective or cost function of the network is to minimize \({{L}_{T}}\) by tuning the parameters of the network (i.e., the weights and biases of \(\tilde{N})\) [72].

The block diagram depicted in Fig. 10 illustrates the comparison between a standard NN and a PINN for modeling dynamic systems. A standard neural network can solely capture the input–output relationship of a system based on its experimental data. Typically, the model obtained through such a network is either a dynamic or frictional model. In contrast, a PINN has the capability to map not only the input–output behavior but also the frictional behavior of a system by utilizing the governing equations and physical parameters of the system. The subsequent section will provide a case study to elaborate on the PINN methodology of generating a friction model.

4 The rotational contact surface: torque estimation

In this case study, we demonstrate how the PINN modelling approach can be employed to accurately identify the frictional torque acting at the contact surface of a double torsion pendulum experimental set-up.

The experimental input–output data from a double torsion pendulum system were obtained to construct a dynamic model and friction model for the system. Additionally, a physics-informed neural network model was trained to forecast the angular rotation of the disk pendulum and to recognize the frictional torque at the contact surface of the pendulums. The experimental block diagram and identification overview are illustrated in Fig. 13. In addition, the PINN model results are compared to that of N–M based approach.

Fig. 13
figure 13

Model identification structure for the double torsion pendulum system

Full size image

4.1 The experimental test stand and data acquisition

An isometric view of the test stand, which is a double torsion pendulum system, is depicted in Fig. 14. The frictional resistance of the overall system is intricate due to the combination of the frictional sliding stick–slip resistance of the disk, occurring at the part labeled 2 in Fig. 14, and the rolling resistance of the column placed in a bearing at the part labeled 9 in Fig.  14. Therefore, our focus is on estimating the planar friction only at the pendulum’s surface, where the sliding stick–slip resistance effect occurs.

Fig. 14
figure 14

The double torsion pendulum prototype, where (1) upper free disk (2) friction surface (3) support frame (4) bearing springs (5) column pendulum (6) drive mechanism (7) base (8) microcontroller and (9) ball bearing

Full size image

A detailed description of the test stand and experimental procedures can be found in [35, 55].

Figure 15a and b illustrate the time series plot of the angular rotation, in degrees, of the column and disk pendulums, respectively.

Fig. 15
figure 15

Input–output data of a double torsion pendulum system

Full size image

4.2 Model estimation using Nelder–Mead simplex direct search algorithm

The objective of this section is to identify the parameters of a double torsion pendulum subjected to planar friction and elastic barriers by means of the white-box approach. The experimental setup shown in Fig. 14 consisting of a disk-shaped body rotating freely on top of a forced column, with a system of barriers restricting the torsional vibrations of the upper pendulum body, resulting in nonuniform planar rotational frictional contact is identified as it has been particularly described in [35]. The dynamic behavior of this two-degree-of-freedom asymmetric system with discontinuities is identified using a combination of the described strategy, numerical solutions of the derived mathematical model, and the Nelder–Mead (N–M) simplex algorithm. It bases on a universal and well-developed model of frictional contact studied in [73]:

$$\begin{aligned} \tau _f(\dot{\varphi }_2)= & {} \frac{T_s}{1+T_0\left| \dot{\varphi }_2\right| } \left( 1+\frac{\beta }{\cosh {\alpha \dot{\varphi }_2}}\right) \tanh {\alpha \dot{\varphi }_2}, \nonumber \\ {[}T_s,T_0]= & {} {\left\{ \begin{array}{ll} &{} \text {if}\quad \dot{\varphi }_2\ge 0,\\ {[}T_{sr},T_{0r}] &{} \text {if}\quad \dot{\varphi }_2< 0, \end{array}\right. } \end{aligned}$$
(22)

where \(T_s\) [N m] is a constant parameter controlling the amplitude of the spike in the friction coefficient, assuming that the range of relative velocities (\(\dot{\varphi }_2\)) is narrow enough, the parameter \(T_0\) [s/rad] is responsible for the decay of friction force as the modulus of relative velocity is increasing, \(\alpha \) [s/rad] controls the curve sharpness near zero and, finally, \(\beta \) [N m] controls the magnitude of spikes near zero, in other words, the rate of the original drop of the friction coefficient just after the moving mass quits the sticking (or a creeping) area. Due to the nonuniform properties of the contact surface determined by the machining of steel, the model became asymmetric. When the relative velocity between the column and the disk is positive then “l”— left letter subscript is added, while in the opposite direction “r”—right letter occurs.

In the experiment, the torque exerted on the disk in the form of a pendulum by the column, denoted as \(\tau =J_1\ddot{\varphi }_1\), was calculated by sequentially measuring the angular position of the column, taking the second derivative of the obtained data series, and multiplying it by the mass moment of inertia constant of the column estimated in the CAD program.

After application of the Nelder–Mead simplex direct search algorithm, a prediction of the disk behavior shown in Fig. 17a (gray line) and also a set of parameters of the friction model (22) is found: \(T_{sl}=0.2328\), \(T_{sr}=0.0928\) [N m], \(T_{0l}=0.2188\), \(T_{0r}=0.0917\) [s/rad], \(\alpha =92.6465\) [s/rad], \(\beta =0.0928\) [N m], \(J_2=2.17\cdot 10^{-4}\) [kg m2]. The results of the real measurement series and numerical solutions demonstrate quite a good similarity between the mechanical system’s response and its virtual analogue.

The drawback of this method is that the computations for a relatively short series took almost 45 min, and the convergence to the actual rotation angle trajectory is low during slip periods. However, relatively good mapping of the moments of engagement and approximate knowledge of the parameters of the applied friction model is an advantage of this approach. Difficulties in adjusting the appropriate friction model (components) described in the above review can be somewhat overcome by estimating the desired friction moment occurring at the contact surface. In the next section, we will focus on the use of PINN to estimate this torque and compare the trajectories of both methods.

4.3 Model estimation using PINN algorithm

For a comparison purposes, the second model estimation was performed using a PINN algorithm, as demonstrated by the flowchart presented in Fig. 16. The length of the dataset obtained from the conducted experiment was 2950, comprising of features such as time, column, and disk angular positions. The dataset was referred to as \(\text {exp\_data}\) during implementation in Python. To form the training dataset, we split \(\text {exp\_data}\) in the following manner: \(\text {exp\_data\_tr} = \text {exp\_data[0:2950:5]}\). This resulted in every fifth data point being included in the training dataset, named \(\text {exp\_data\_tr}\)”. On the other hand, all the data points in \(\text {exp\_data}\) were considered for the test dataset, denoted as \(\text {exp\_data\_ts}=\text {exp\_data}\).

Fig. 16
figure 16

PINN algorithm flowchart

Full size image

The algorithm comprises of two multi-layer neural networks, where each network is composed of two inputs and one output. The first and second networks, denoted by \(N_{1}\) and \(N_{2}\) respectively, have the column pendulum angular rotation and the time variable of the signal as their inputs, with different outputs. Specifically, the output of \(N_{1}\) is the disk pendulum angular rotation, whereas \(N_{2}\) predicts the friction torque between the pendulums. The hyperparameters, including the number of hidden layers and neurons for each network, are identical and can be found in Table 2.

Table 2 Neural network hyper parameters
Full size table

The loss function used in training \(N_{1}\) is the mean squared error of the predicted disk pendulum angular rotation, while the loss function for \(N_{2}\) is the computation of the residual of the system derived from Newton’s second law of rotation:

$$\begin{aligned} J_2\ddot{\varphi _2}=\tau -\tau _f\,, \end{aligned}$$
(23)

where \(\tau =J_1\ddot{\varphi _1}\) is the torque of the column pendulum, \(\tau _f\) is the friction torque being sought, \({J}_{1}\) and \({J}_{2}\) are the mass moments of inertia of the column and disk pendulum, respectively.

The equation imposed a physics-based constraint on the model, providing \(N_{2}\) with the capability to predict the friction torque of the system. In addition, physics parameters \(J_1\) and \(J_2\) were incorporated into \(N_{2}\) as trainable parameters, and their lower and upper bounds were set close to the values reported in [35].

The PINN model was trained using a backpropagation algorithm and an ADAM optimizer, with training epochs \(k=10^4\). Following training, the model was validated to ensure that the predicted angular rotation of the column pendulum closely matches the actual response. Furthermore, the model weights and biases were saved after training was completed.

4.4 Results and discussion

After 10,000 epochs of training the PINN model, the computation time was 90.23 [s] while the total loss was 0.587. In addition, the estimated values of \(J_{1}\) and \(J_{2}\) after training the PINN model are \(10^{-3}\) and \(2\times 10^{-4}\) [kg m2], respectively. It should be noted that the pendulums have irregular shapes, and \(J_1\) and \(J_2\) were estimated from a CAD design. Consequently, while the disk’s inertia is accurately determined, the inertia of the column pendulum is less precisely estimated due to some missing parts in the design assembly compared to the actual system.

The PINN model was validated and the prediction results are presented in Fig. 17a and 17b. The model computational effort is moderate and it exhibited high accuracy in predicting the angular rotation of the disk pendulum. In Fig. 17c, the error shown was calculated by comparing the predictions of two models: the PINN model and the NM-based model. We looked at the difference between the actual angular position of the disk pendulum and what each model predicted. The PINN model’s difference was smaller, which shows that the PINN model is more accurate. Moreover, the model demonstrated an intriguing dynamic response to the friction torque that acted on the planar surface between the pendulums. Such dynamic behavior would have been unidentifiable using existing black-box friction models, given the limited input–output dataset available. Additionally, no data on friction measurement was available for training the PINN model, and only one experiment was performed.

Fig. 17
figure 17

Results of prediction of the frictional torque characteristics with the use of two identification models: PINN and N–M

Full size image

By evaluating the obtained state estimation trajectories of the studied torsion pendulum, it can be observed that PINN performs better while simultaneously compensating for the inaccuracy of the N–M based approach. Despite a slightly higher level of generality, we obtain better representation of the slip and stick phases and the breakaway friction torque, see Fig. 18. The error in estimating the frictional torque is smaller compared to the N–M estimation algorithm. Further research on this model could be conducted towards utilizing the friction torque characteristics in the contact zone to improve the friction model accuracy.

Finally, the estimated friction torque dependency on the relative velocity of motion of the disk is achieved in Fig. 18.

Fig. 18
figure 18

The estimated non-symmetric friction torque characteristics (black dots)

Full size image

By observing distinct positive (\(\tau _{fs}^+\)) and negative (\(\tau _{fs}^-\)) breakaway torque values, located approximately in the relevant zones, as well as different slope angles (\(\delta _{v}^+\) and \(\delta _{v}^-\)) of the viscous friction branches, including one nonlinear branch, it can be demonstrated that the frictional contact is non-homogeneous with regard to the direction of motion. This non-homogeneity is attributed to the varying surface roughness of the contact surface in opposing rotational directions.

5 Summary and conclusions

In this work, the various methods of modelling friction, including mathematical techniques such as static and dynamic methods, as well as data-driven methods have been presented. The performance of four friction models (Coulomb, Coulomb-viscous, Dahl and LuGre) was evaluated through a numerical simulation of a double torsion pendulum. The result showed that the static Coulomb and dynamic Dahl models nearly coincide, depicting a behavior closer to reality. Through our review, we have also provided detailed information on the appropriate experimental setup, system excitation, and identification methods, as well as pre-processing techniques for data-driven modelling. We found friction measurement to be a major challenge in the practical scenarios and proposed using input–output data and neural network techniques like physics-informed neural network to estimate friction.

To demonstrate the effectiveness of the proposed approach, we have presented a case study in which a physics-informed neural network was used to predict the dynamic model and estimate planar friction of a double torsion pendulum system. The model was trained using time-series experimental data, and the results showed that the PINN model was able to accurately predict the angular rotation of the disk pendulum, while also estimating the planar friction between the pendulums. The PINN model was able to identify the frictional loss in the system without using any pre-existing friction models, and only relied on a simplified physics model with two estimated parameters. The approach based on the PINN algorithm proved to be faster and more accurate than the older Nelder–Mead method, but requires further refinement due to the need for acquiring a broader knowledge of the friction model.

One of the challenges posed by dynamic friction models is their high computational cost, which can limit their applicability in large-scale simulations and real-time applications. As highlighted in Sect. 3.2, friction is a complex phenomenon that is challenging to measure experimentally. Consequently, reliable friction data may be unavailable, necessitating the use of indirect measurement methods to obtain accurate models. Additionally, the frictional behavior of a system can vary widely depending on the materials and operating conditions, making it difficult to develop models that can predict friction accurately across a broad range of situations.

Furthermore, neural network-based friction models are black-box in nature and challenging to interpret, which means it is difficult to understand how the model generates its predictions. Besides, data-driven friction models are not entirely accurate, and they have a high level of uncertainty when used to forecast friction under different conditions.

The effects of degradation and uneven wear on friction contact surfaces are currently only approximated by various static and dynamic tribological models (see Sect. 2). These models consider factors such as inelastic adhesion, elasticity of contact, and dynamic friction coefficients, but there is currently no general theory regarding this problem. The methodology used to address this issue is described in Sect. 3, but it typically involves measuring dynamic variables, estimating their higher derivatives, and substituting them in real-time measurements to approximate the physical model. The resulting parameters are subject to high uncertainty due to the many factors that affect the process. The more parameters and friction effects that are considered, the greater this uncertainty becomes. Therefore, using black-box models based on NN with known structures and coefficients is a promising and useful tool. The challenge lies in matching the structure of the model to the given problem. The benefits of using such models include increased computational efficiency and the possibility of use in large-scale applications, as they depart from typical discontinuous dynamics models.

The prospects of friction modelling entail the development of accurate models capable of predicting friction in a variety of systems and conditions, including varying loads and speeds. Additionally, it is imperative to create models that can forecast the evolution of friction over time, incorporating the effects of degradation and wear. Furthermore, the integration of existing physics-based friction models with machine learning techniques like PINN can enhance model interpretability.

Looking ahead, we plan to continue exploring the use of PINN for modelling friction in other multibody mechanical and mechatronic systems, and to investigate the use of the model for friction compensation.