Application of Hénon method in numerical estimation of the stick–slip transitions existing in Filippov-type discontinuous dynamical systems with dry friction

Abstract

Accuracy of numerical modeling of any discontinuous dynamical system plays an important role in the proper use of the tools applied for its analysis. No less important in this matter is the numerical estimation of the phase trajectories, bifurcation diagrams, and Lyapunov exponents. This paper meets these expectations presenting application of Hénon’s method to obtain good numerical estimations of the stick–slip transitions existing in the Filippov-type discontinuous dynamical systems with dry friction. Subsequent sections are focused on the problem definition, block diagrams of the numerical procedure coded in Python, application of the method that was originally proposed for Poincaré maps, its use in estimation of phase trajectories, bifurcation diagrams of tangent points, and on estimation of the Lyapunov exponents for a selected two-dimensional system with stick–slip effect.

1 Introduction

In nonsmooth systems it is possible for trajectories to collide with some discontinuity zone in phase space. It often results in occurrence of nonsmooth bifurcations [6]. Bifurcation theory is a strongly growing branch of dynamical analysis [1] providing broad field for analytic considerations and numerical schemes. The most basic problem of the theory focuses on the study of qualitative changes in behavior at slightly changing system parameters around the critical values. The fundamental diagram, or a variation of the dynamical process, is a transition of solution from an orbit with period T into an orbit with period 2T. For example, a two-degree-of-freedom plane disk, performing one-dimensional transitional and rotational motion, placed on the moving belt has been mathematically modeled and numerically analyzed in [14]. The friction model for sliding mode is developed assuming classical Coulomb friction law, valid for any infinitesimal element of circular contact area. As a result, the integral expressions for friction force and torque are obtained. The exact integral model is then approximated by the use of different functions, like Padé approximates or their modifications. Some generalizations of the approximate functions used by other authors are proposed. The special event-driven model of the investigated system together with a numerical simulation algorithm is developed, and in particular, the transition conditions between the stick and slip modes are defined. Some examples of numerical simulation and analysis by the use of Poincaré maps and bifurcation diagrams are also presented. It has been shown that for certain sets of parameters, the investigated system exhibits very rich multiperiodic stick–slip oscillations.

In order to illustrate the beneficial and harmful effects of the existence of bifurcations in dynamical systems, there are used a variety of interesting techniques of analysis and observation. Among them, it is worth noting the stroboscopic view often used during stability tests of switching (discrete) electronic systems and determining piecewise continuous mappings (e.g., in systems with dry friction). A detailed analysis and many numerical experiments of miscellaneous grazing bifurcations have been conducted in the paper [15].

The electronics are not the only examples of systems in which the effects generated during normal operation are the cause of the occurrence of unexpected and irregular behavior in the dynamic changes resulting from the bifurcation of parameters. Completely different nature of switching can be identified in other discrete mechanical systems. They are formed on the basis of a sequence of consecutive slides (slips) and sticks of connected to each other and vibrating solid bodies. An example of such dynamic analysis of a discontinuous system with two degrees of freedom and friction is found in [10]. The test system consisted from elastically connected vibrating solid bodies placed on the belt moving with a constant velocity. Contact friction described by a model of friction existing between the ideal surfaces of cooperating bodies’ is a source of excited stick–slip vibrations. Occurrence of such type of vibrations is the cause of exposing by the system of a variety of bifurcations between the stick and slip modes.

Any conventional model cannot describe the stick mode of friction phenomenon [3]. In the case of conventional friction force model, the body will be sliding even though friction state will be stick. It holds because the relative velocity must have a nonzero value in order to generate the friction force. To solve this kind of problem, a stick–slip friction force model including a spring like force has been proposed in [7]. In the case of stick–slip friction force model, the body can be stuck on the inclined surface because the friction force will be a nonzero value, even though the relative velocity approaches zero. Therefore, a relative displacement variable called the stick deformation is defined. Moreover, the stick–slip friction model was proposed and applied in the contact algorithm of MBD system. Two friction models are then compared with some numerical examples, which relate to more realistic results.

Several effective numerical methods for solving the elastic contact problems with friction are presented in [23]. A direct substitution method is employed to impose the contact constraint conditions on condensed finite element equations, thus resulting in a reduction by half in the dimension of final governing equations. As an extension, an algorithm composed of contact condition probes is utilized to solve the governing equation, which distinguishes two kinds of nonlinearity making the solution unique. In addition, Positive–Negative Sequence Modification Method is used to condense the finite element equations of each substructure, and an analytic integration is introduced to determine the elastic state after each iteration; hence, the computational efficiency is enhanced to a great extent.

A model of a forced pendulum with viscous damping and Coulomb friction was considered in [16]. The existence of a unique local solution of the mathematically well-posed problem has been proved, and an adapted numerical scheme has been built. Attention was devoted to the study of the nonlinear behavior of a pendulum via a numerical scheme with small constant time steps. Global behavior of the free and forced oscillations of the pendulum due to friction was described. Authors proved that chaotic behavior occurs when friction force is not too large. Lyapunov exponents were computed, and a Melnikov relation was obtained as a limit of regularized Coulomb friction.

Paper [8] deals with the techniques for solving ordinary differential equations with essential nonlinearity arising from the representation of frictional force by the sign function of the relative velocity. This problem is connected with dynamic behavior studies of base-isolated structures with dry friction effects. Mathematical evidence is presented concerning the inaccuracies of the solution that are connected with the representation of the frictional force by the sign function. An approximation of this sign model is made on the basis of the appropriate linearization of a small part of the frictional force function. A numerical algorithm for the dynamic analysis of base-isolated structures with dry friction has been proposed.

2 Exemplary boundaries of discontinuity and the function of transition

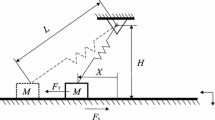
Let us investigate shown in Fig. 1 a one-degree-of-freedom dynamical system with dry friction. A solid body of mass m is attached to a fixed support by means of a nonlinear elastic element characterized by parameters k ₁ and k ₂. The solid body oscillates under the influence of dry friction force T existing in the contact zone created by the body’s surface and the outer belt’s surface that runs with constant velocity v _p . One assumes a nondeformable moving belt being under action of normal force N=mg and other tangent forces to its surface in the contact zone (the state is secured by the schematically drawn rigid support attached from inner side of the belt). Forcing response of the nonlinear elastic element on change of displacement y of mass m is k ₁ y−k ₂ y ³, whereas force of dry friction existing in the contact zone of the analyzed frictional pair is denoted by T. The cubic term is used to model a nonlinear (more realistic) response of the spring and to show influence of additional terms on the form of the transition function σ(x). Another work that studies the stick–slip oscillations of discrete systems interacting with translating energy source through a nonlinear smooth friction curve can be found in [12].

Fig. 1

Schematic view of the investigated one-dimensional mechanical system

The second-order differential equation modeling dynamics of the discontinuous one-dimensional mechanical system (see in Fig. 1) takes the form

$$ m\ddot{y}-k_1y+k_2y^3+T=0, $$

(1)

where the friction force T and the coefficient of kinetic friction μ _k at the velocity $v=\dot{y}-v_{p}$ of relative displacement of contacting surfaces are given respectively as

(2)

There are other applications of friction models applied to worm-like locomotion systems, in which the friction force T depends also on control forces [20].

For a particular dynamical system, there are considered some values of model parameters: m=1 kg, k ₁=k ₂=1 N/m. Under the assumptions above, Eq. (1) becomes

$$ \ddot{y}-y+y^3+\textrm{sgn}(\dot{y}-v_p) \frac{\mu_0}{1+\delta|\dot{y}-v_p|}=0. $$

(3)

Equation (3) describes the dynamics of the excited vibrations that occur during the dry friction between contacting surfaces of mass m and the movable belt.

Changing in Eq. (3) the state variables x ₁=y and $\dot{x}_{1}=x_{2}$, the following system of two first-order differential equations is taken into analysis:

$$ \begin{cases}\dot{x}_1=x_2,\\ \dot{x}_2=x_1-x_1^3-T(v). \end{cases} $$

(4)

In next step, Eq. (4) can be written in the form

(5)

where x=[x ₁,x ₂]^T and f=[f ⁽¹⁾,f ⁽²⁾]^T.

The discontinuity zone Σ that splits two adjacent regions S ₁ and S ₂ is defined as follows:

$$ \varSigma = \bigl\{x\in\mathbb{R}^2: x_2-v_p=0\bigr\}, $$

(6)

where S ₁ and S ₂ take the forms

(7)

On the background of Filippov’s theory, the transition function σ(x) is defined:

$$ \sigma (x)=f^{(1)}_2(x)f^{(2)}_2(x) . $$

(8)

Functions $f^{(1)}_{2}$ and $f^{(2)}_{2}$ are the second components of vector fields f ⁽¹⁾ and f ⁽²⁾, respectively. If we assume that x _v =[x ₁,x ₂=v _p ]^T, then the function (8) on the boundary zone yields

(9)

Moreover, if the derivative D _σ of the function σ(x _v ) exists in the direction x ₁, then it is possible to find some critical points of the function at subsequent conditions:

$$ D_{\sigma ,0}= \frac{\partial\sigma (x_{v,0})}{\partial x_1}=0,\quad\sigma (x_{v,0})=0. $$

(10)

Under conditions Eq. (10), the characteristic equation

$$ D_{\sigma ,0}=2x_{1,0}\bigl(x_{1,0}^2-1 \bigr) \bigl(3x_{1,0}^2-1\bigr)=0 $$

(11)

allows us to find the set of roots (tangent points) as follows:

$$ x_{1,0}^{(k)}= \biggl\{0,\pm1,\pm\dfrac{1}{\sqrt {3}} \biggr\}\quad\text{for}\ k=1,\dots, 5. $$

(12)

By substitution of the values from (12) into Eq. (9) and then solving each of the obtained equations with respect to μ ₀, the set of boundary values of the shape parameter of friction characteristics reads

$$ \mu_0^{(k)}= \biggl\{0,\pm\dfrac{2}{3\sqrt{3}} \biggr\} \quad\text{for}\ k=1,\dots, 3. $$

(13)

Inspecting the problem carefully, the stick zone Σ _u vanishes at $\mu_{0}=\mu_{0}^{(1)}$, but on the discontinuity zone Σ, there remain only three tangent points, means $x_{1,0}^{(1,2,3)}$. One could say that this zone is degenerate. At $\mu_{0}=\mu_{0}^{(2,3)}$ the stick zone Σ _u is continuous and exists between boundary tangent points $x_{1,0}^{(6,7)}=\pm2/\sqrt{3}$. Tangent points $x_{1,0}^{(4,5)}$ lying between boundary tangent points are also included in this zone.

3 Numerical estimation of stick-to-slip and slip-to-stick transitions

Hénon’s algorithm derived in work [11] can be used after determination of points of Poincaré maps, but after appropriate modification, taking into account Filippov’s theory, it could be even useful in computation of the numerical solution of various discontinuous systems with dry friction [2]. Consideration should be taken depending on the broader analysis of the discontinuity, visible and invisible tangent points, and a function defining transition between zones of slip solutions.

Computation of numerical solution of the discontinuous dynamical system with dry friction given by Eq. (12) can be carried out using the algorithm shown in Figs. 2 and 3.

Fig. 2

A block diagram of the numerical integration procedure of the analyzed discontinuous system including detection of stick-to-slip and slip-to-stick transitions

Fig. 3

Continuation of the block diagram shown in Fig. 2

The simulation begins with the adoption of some dynamic system parameters and initial conditions $x_{1}^{(0)}=x_{1}(t_{0})$, $x_{2}^{(0)}=x_{2}(t_{0})$. Then, one checks in each iteration whether the solution is contained in: (a) one of the stick zones $\varSigma_{u}^{(k)}$ for k=1,2,…; (b) one of the regions S ₁ or S ₂, in which the differential equations (5) describing the continuous system are solved numerically by means of selected standard integration procedure of higher order, i.e., 4th-order Runge–Kutta integration algorithm.

If in current step of integration, during a slip mode, the difference x ₂−v _p is neither positive or negative, then respectively to j=1,2, one needs to repeat the step by integration of the differential equation (5) transferred to the form

$$ \dot{X}_1=F_1(X_1)= \biggl[ \begin{array}{c}\dfrac{x_2}{f_2^{(j)}}, \dfrac{1}{f_2^{(j)}} \end{array} \biggr] , $$

(14)

where X ₁=[x ₁,τ]^T, τ is the time passing in the temporary dynamical state, and x ₂ is the independent variable. Respectively, at x ₂−v _p >0 or x ₂−v _p <0 in current iteration of integration, the step $h_{1}=v_{p}-x_{2}^{(i)}$ or is equal to $x_{2}^{(i)}-v_{p}$, but the velocity of mass m equals $x_{2}^{(i+1)}=v_{p}$. In this way, the transition between the slip and stick modes of motion has been estimated with high accuracy. Afterwards, solution of Eq. (5) in the stick zone can be continued.

If in current step of integration, in a stick mode, the position reaches some of tangent points $x_{1}^{(i+1)}>x_{1,0}^{(k)}$, where $x_{1,0}^{(k)}$ is the kth tangent point, then one needs to repeat the step by integration of the differential equation (5) transferred to the form

(15)

where X ₂=[τ,x ₂]^T, τ is the time passing in the temporary dynamical state, but x ₁ is the independent variable. In this iteration the difference $h_{2}=x_{1,0}^{(k)}-x_{1}^{(i+1)}$ at the kth visible tangent point makes the temporary step of integration. In this way, the transition between the stick and slip modes of motion has been estimated with high accuracy, and it allows us to continue the solution of Eq. (5) in the slip zone.

The enumerated schemes of transition from slip to stick and from stick to slip determine appearance of the mentioned critical points, i.e., they determine the points crossing the intersection zone Σ _c and boundary points beginning and ending the system trajectory running in Σ _u . If a particular point of solution that lies on the intersection of regions S ₁ and S ₂ of the slip solution is included in Σ _c ⊂Σ, then deflections of the periodic trajectory on the phase plane (x ₁,x ₂) presented in Fig. 4a are observed in the neighborhood of the third tangent point. The deflections are characteristic for such types of systems with friction. The reason is that the trajectory of solution (after crossing the intersection zone Σ _c ) is influenced by a different vector field of the investigated dynamical system.

Fig. 4

Numerical solutions of the dynamical system (5) beginning from different initial conditions marked at intersections of dashed lines. Visible (1,3,5) and invisible (2,4,6) tangent points in the stick zones are marked by grey rectangles

The described methodology bases on detection of the critical points that are not present in continuous systems. A numerical code in Python, which is a complement to the diagram split in Figs. 2 and 3, is attached in the Appendix.

Exemplary periodic solutions have been shown in Fig. 4. In the considered system with dry friction any stick mode does not occur, and a discontinuity in the form of the described deflection of the transient trajectory is seen in its transition through the zone of intersection Σ _c ⊂Σ. Various initial conditions are selected to observe the transient trajectory running in the neighborhood of tangent points. In addition, the coefficient of static friction $\mu_{0}=1/(3\sqrt{3})$ and velocity v _p =1 of the belt are assumed to investigate some particular case. The tangent points $x_{1,0}^{(k)}$ determined for the selected system parameters by finding roots of the transition function σ(x) given by formula (8) are as follows:

(16)

4 Bifurcations of tangent points

In this part of the study some bifurcations of stick mode and corresponding tangent points of a typical discontinuous dynamical system with one degree of freedom and a harmonic forcing are considered.

A one-dimensional system consists of a mass m that is placed on the belt moving at constant velocity v _p . The oscillating body is connected to the harmonically forced spring described by a nonlinear characteristic k(z). The distance z=x ₁−y results from the difference between position x ₁ of mass m and y(t)=Asin(ωt) describing the time-dependent displacement of the second end of the nonlinear spring. The harmonic function has amplitude A and frequency ω. Adjacent surfaces of the frictional pair created by the body’s mass m and the movable belt constitute the dry frictional contact. The contact is described mathematically by the friction force T that depends on the shape parameter μ ₀ (the coefficient of static friction) and the relative velocity x ₂−v _p of motion measured in the distinguished frictional connection.

Model of the investigated mechanical system with friction and harmonic excitation is shown in Fig. 5.

Fig. 5

Model of the investigated mechanical system with friction and harmonic forcing

Dynamics of the modeled mechanical system is described mathematically as follows:

(17)

where T is the velocity-dependent friction force modeled by Eq. (2) (see Fig. 6).

Fig. 6

The friction force model T(v) with monotonically decreasing branches (bold line)

Putting in Eq. (17) the dependencies on T and y, the following system of first-order differential equations reads

(18)

where x=[x ₁,x ₂]^T, f=[f ⁽¹⁾,f ⁽²⁾]^T, and z=x ₁−y.

The discontinuity zone Σ splitting two adjacent regions S ₁ and S ₂ and the transition function σ(x) are given by Eqs. (6) and (8).

4.1 The oscillating transition function and the tangent points

If we assume that z _v =z at x ₂=v _p , then the transition function (8) in Σ reads

$$ \sigma (z_v)= \frac{1}{m^2} \bigl[ \bigl(k_2z_v^3-k_1z_v \bigr)^2-\mu_0^2 \bigr]. $$

(19)

If there exists a derivative of function σ(z _v ), then it is possible to find critical points of the function by means of the conditions

$$ D_{\sigma _0}=\frac{\partial\sigma (z_{v_0})}{\partial z_v}=0 , \quad\sigma (z_{v_0})=0. $$

(20)

In the next step, we calculate

$$ D_{\sigma _0}=\frac {2z_{v_0}}{m^2} \bigl(3k_2z_{v_0}^2-k_1\bigr) \bigl(k_2z_{v_0}^2-k_1\bigr)=0 , $$

(21)

where the set of roots at conditions (20) follows:

$$ z_{v_0}^{(i)}= \biggl\{0, \pm\sqrt{\frac{k_1}{k_2}}, \pm \sqrt{\frac{k_1}{3k_2}} \biggr\}\quad \text{for}\ i=1,\dots, 5 . $$

(22)

Putting $z_{v_{0}}^{(k)}$ given by (22) into Eq. (19) and then evaluating the obtained equation with respect to μ ₀, the following set of boundary values of shape parameter of the friction characteristics T follows:

$$ \mu_0^{(i)}= \biggl[0,\pm\frac{2k_1}{3}\sqrt{\frac {k_1}{3k_2}} \biggr]\quad\text{for} \ i=1,2 ,3 . $$

(23)

The set of values (23) places the transition function of the stick zone as a tangential (with the approach from below and from above too) to the abscissa in the graph of the dependency σ(z _v ,μ ₀) shown in Fig. 7a. The resulting definitions in the form of generalized equations (12)–(13) contain the parameters k ₁, k ₂, and μ ₀. It confirms that the location of a stick zone depends on the parameters of the particular dynamical system. Small bifurcations of their values cause displacement of stick zones that determine the dynamic state of the considered discontinuous system with friction.

Fig. 7

Tangent points (circles) on the intersection of function σ(z _v ,μ ₀) with the axis z _v for $\mu_{0}=\mu_{0}^{(1)}$ (dashed line) and $\mu_{0}=\mu_{0}^{(2,3)}$ (solid line). The time-dependent oscillations y(t) of the stick zone (b). Bifurcations of tangent points at changes of control parameter $\mu_{0}\in [\mu_{0}^{(1)},4\sqrt{3}/9 ]$ for system parameters: m=1, k ₁=k ₂=1, v=1 (c)

In Fig. 7a, the top graph marked by a dashed line confirms that in the contact zone and at some boundary value μ ₀, no stick exists. It holds because the function σ(z _v ,μ ₀)≥0. A degeneracy of the stick zone Σ _u to three tangent points is observed. This means that deflections will appear only at points of solution that crosses the intersection zone Σ _c from region S ₁ to S ₂ or vice versa.

Quite opposite interpretation is regarded to the graph marked in Fig. 7a by solid line that is tangent from below to the abscissa. The stick zone is in this case wide and extends from the left to right branch of the graph (both tend to +∞ in the direction +σ). The solution will be strongly attracted by both vector fields that are faced opposite to each other in the discontinuity zone Σ splitting regions S ₁ and S ₂. The result will be a generation of stick–slip cycles with possibility of their bifurcation for the control parameter $\mu_{0}<\mu_{0}^{(2,3)}$.

The transition function σ(x) introduced in Eq. (8) is defined as the product of components $f^{(1)}_{2}$ and $f^{(2)}_{2}$, which could be used to estimate the tangents points lying in the discontinuity zone at intersection of vector fields f ⁽¹⁾ and f ⁽²⁾ acting in the regions S ₁ and S ₂, respectively. Bifurcations of tangent points in a range of changes of the bifurcation parameter μ ₀ are presented in Fig. 7c.

The previously described method allows us to estimate the tangent points on the basis of known function σ(z _v ,μ ₀). Assuming the set of parameters m=0.1, v _p =0.4, $\mu_{0}=\frac{\sqrt{3}}{9}$, k ₁=k ₂=1, $A=\frac{4\sqrt{3}}{3} \sin {\frac{\pi }{18}}$, ω=3π/2.4728, there has been estimated, for the analyzed dynamical system, an initial set of tangent points

(24)

The values from the set (24) are very useful. For instance, they allow us to exactly compute the length and duration time of the stick modes.

4.2 Numerical experiment

A two-periodic stick–slip trajectory of the numerical solution to system (17) is shown in Fig. 8. It has two stick modes $|\varSigma_{u}^{(1,2)} |$ of lengths [0.4697,0.1663].

Fig. 8

A two-periodic stick–slip trajectory for the initial conditions $\bar{x}_{0}=(x_{1,0}^{(3)},v_{p})$

Correspondingly to the mentioned stick modes, the oscillating body of mass m sticks to the moving belt within 1.1746 and 0.4161 seconds and travels at its velocity v _p until the next tangent point is met. Loss of stick and, connected with it, beginning of the slip mode occurs at visible tangent points.

The slip mode’s trajectories projected on the (x ₁,x ₂) plane have the shape of arcs alternately appearing in the regions S ₁ (the upper arcs) and S ₂ (the lower arcs). In the left part of the two-periodic closed trajectory, there are visible two deflection points indicating the intersection zone Σ _c . With regard to constant harmonic excitation, the stick zone Σ _u oscillates along ±x ₂ in the discontinuity zone Σ. As a result, initial locations of tangent points given by the set (24) oscillate in time accordingly to $\tilde{x}_{1,0}^{(k)}(t)=x_{1,0}^{(k)}+A \sin (\omega t)$ for k=1,…,6. The two-periodic trajectory (see Fig. 8) of the exemplary dynamical system containing the oscillating stick zone was found using the numerical procedure attached in the Appendix.

5 Lyapunov exponents of the analyzed discontinuous system

Lyapunov characteristic exponents were introduced by Lyapunov [19] in the context of nonstationary solutions of ordinary differential equations. They provide a way to characterize the asymptotic behavior of nonlinear dynamical systems by giving a measure of the exponential growth (or shrinkage) of perturbations about a nominal trajectory. Since they measure the sensitivity of solutions of dynamical systems to small perturbations, they are often used to indicate chaotic motion when the dynamics occurs on an invariant set (see [17] and [9]). Their positive values establish chaos, but all negative values establish a nonchaotic system.

Computation of Lyapunov exponents is one of the most important numerical problems considered in analysis of nonlinear dynamical systems. Oseledec’s theory [17] and Benettin’s numerical algorithms described in [5] and [13] refer to methods of computational estimation of Lyapunov exponents’ spectra for continuous systems. If equations of motion are not known explicitly, then some methods based on attractor’s reconstruction (for any continuous or discontinuous system) from a time series are developed [18, 21].

5.1 The method of computation of Lyapunov exponents from a time series

The dynamics of real physical systems can be assessed visually or by measuring signals stored in a computer memory in the form of a sequence of measured values. Measurement of the actual state of a dynamical system (displacement, temperature, voltage, etc.) is done with a time sampling leading to continuous signals of physical quantities. Numerical estimate of the nature of the n-dimensional discrete trajectories requires the calculation of n Lyapunov exponents. The mathematical basis for calculating the spectrum of Lyapunov exponents based on discrete-time trajectories of an n-dimensional chaotic dynamical system has been developed in [18]. The essence of the calculation algorithm is as follows.

Let $\bar{x}\in\mathbb{R}^{n_{i}}$ be the vector state of some n _i -dimensional discrete dynamical system, and let $\bar{x}_{j}$ (j=1,…,n _j ) denote the vectors of subsequently chosen points of the investigated time history. If we assume a small ball of radius ε, centered in the point matched successively by vector $\bar{x}_{j}$, then n _k points included in the ball are found. The radius of the ball must be large enough, i.e., n _k >n _i . The distance from n _k points of that set to the center of the ball is $\bar{y}_{k}=\bar{x}_{k}-\bar{x}_{j}$ at k=1,…,n _k . After the time τ=dΔt (where d is a small natural number, and Δt is the sampling time in which points of the trajectory have been saved), the vector $\bar{x}_{j}$ shifts to $\bar{x}_{j+d}$, but the neighbor points to $\bar{x}_{k+d}$. This also results in changes of the distances $\bar{y}_{k+d}=\bar{x}_{k+d}-\bar{x}_{j+d}$. If the radius ε is small enough, then the vectors $\bar{y}_{k+d}$ and $\bar{y}_{k}$ are with good approximation tangent to each other and create a tangent space. The linear dependency between these vectors is $\bar{y}_{k+d}=A_{j}\bar{y}_{k}$, but the smallest quadratic estimation of the matrix $A_{j}\in \mathbb{R}^{n_{i}\times n_{i}}$ is given by

(25)

The spectrum of Lyapunov exponents is computed by means of the formula

(26)

After the assumed number of iterations there must be carried out orthogonalization of directions and normalization of length of vectors connecting the neighborhood points of the trajectory. The symbol $\bar{e}_{i}^{j}$ in Eq. (26) denotes the set of basis vectors acting at points $\bar{x}_{j}$ included in the tangent space. In the first iteration of the algorithm of Lyapunov exponents’ estimation, the initial set of basis vectors is arbitrary. Gram–Schmidt orthogonalization [22] of directions of the basis vectors $\bar{e}_{i}^{j}$ and normalization of lengths $A_{j}\bar{e}_{i}^{j}$ are done before all components of the sum (26) are computed.

In the next part of the paper we use the high-accuracy method of numerical integration (see in Sect. 3) to generate the time series trajectory of an exemplary discontinuous system with friction. Estimations of Lyapunov exponents for three kinds of solutions, i.e., periodic, quasi-periodic, and chaotic are finally computed.

5.2 Numerical experiment

We consider the time series of solution of a discontinuous dynamical system with dry friction shown in Fig. 9. The system of four first-order ordinary differential equations takes the form

(27)

Fig. 9

The two-degree-of-freedom mechanical system

In Eq. (27) the state vector $\bar{x}=[x_{1},x_{2},x_{3},x_{4}]\in\mathbb{R}^{4}$, the relative velocity of contacting surfaces v=x ₂−v _p , and the constant parameters ξ ₁=k ₂/(ω ² m), ξ ₂=c ₁ ω/k ₂, ξ ₃=k ₂ r ²/(ω ² J), ξ ₄=(k ₂+k ₃)/k ₂, ξ ₅=ω(c ₁+c ₂)/k ₂, ξ ₆=μ ₀ k ₃/k ₂, ξ ₇=ωc ₂ μ ₀/k ₂, $\omega=\sqrt {(k_{1}+k_{2})/m}$, J=m(a ²+b ²)/3 are assumed. The term y=1−ξ ₆ x ₃−ξ ₇ x ₄ includes also the additional normal force subject to the mass m from the displacement of the bracket’s end, and it has to be regarded to in the friction force model

(28)

where μ _k is expressed by (2).

The self-excited system presented in Fig. 9 is equivalent to a real experimental rig (see [4]), where block mass m moves on the belt in x ₁ direction, and the bracket characterized by the moment mass of inertia J rotates about point s with respect to angle φ. Two bodies are coupled by linear springs k ₂, k ₃ and dampers c ₁, c ₂. The block on the moving belt is additionally attached to a fixed wall by means of a linear spring k ₁. We assume that the angle of rotation of the second body (the bracket) is small, and therefore sin(φ)≈φ≈y/r is assumed.

The spectra λ _i of Lyapunov exponents of some periodic, quasi-periodic, and chaotic trajectories (saved in time (3–12)⋅10³ s, in the form of 45001×4 elements of vector $\bar{x}$), which have been obtained solving system (27) by means of the numerical procedure described in Sect. 3 are presented in Figs. 10, 11, and 12.

Fig. 10

Two-periodic trajectory for $\bar{x}_{0}=(0,-0.1,0,-0.1)$

Fig. 11

Quasi-periodic trajectory for $\bar{x}_{0}=(0,0,0,-0.1)$

Fig. 12

Chaotic trajectory for $\bar{x}_{0}=(0,-0.1,0,-0.1)$

Lyapunov exponents’ spectra $\lambda_{i}^{\textrm{p}}, \lambda_{i}^{\textrm{qua}}, \lambda_{i}^{\textrm{ch}}$ confirm the shapes of the observed phase-plane trajectories. As it was expected, each of them contains at least one characteristic exponent close to zero. In the case of the quasi-periodic solution, $\lambda_{\{1,2\}}^{\textrm {qua}}\approx0$, but in the case of the chaotic one, $\lambda_{1}^{\textrm{cha}}>0$.

6 Conclusions

Filippov’s theory applied to the considered discontinuous systems has made it possible to carry out interesting numerical analysis of stick–slip bifurcations observed in piecewise continuous dynamical systems. An oscillating boundary of discontinuity has been described by the velocity-dependent function of motion of the belt. Additionally, it has been made dependent on the function of external harmonic excitation. Tested dynamical systems were divided into two subsystems, whose continuous solutions have been found in corresponding two adjacent regions of the analyzed state space. Finally, trajectories of some dynamic behaviors have been confirmed by spectra of characteristic Lyapunov exponents.

Appendix

Listing 1

Numerical integration with detection of stick to slip and slip to stick transitions in a discontinuous motion of one-degree-of-freedom dynamical system with friction and harmonic forcing (see Fig. 8).