1 Introduction

According to the United Nations (2018), 55% of the worldwide population currently live in urban areas. This fraction is projected to rise to 68% by 2050. In these urban areas the many sources of air pollution (e.g., traffic, industry, domestic heating), combined with poor air exchange, often lead to high concentrations of air pollutants that adversely affect human health (e.g., US EPA 2011).

Consequently, many operational and experimental air pollution dispersion models are used in urban areas to forecast air pollution concentrations. Examples include models like AERMOD (Cimorelli et al. 2005), QUIC-PLUME (Williams et al. 2002), MicroSpray (Tinarelli et al. 2012, and references therein), GRAMM/GRAL (Oettl 2014, 2015), and SIRANE (Soulhac et al. 2011). All these models have in common that they do—based on various approaches—include the mean flow through the region between buildings, i.e., the urban canopy layer (UCL, see Fig. 1). How they account for the between-building turbulence differs, however.

It is possible to explicitly resolve all obstacles in a type of large-eddy simulation (LES) (e.g., Auvinen et al. 2020) and derive the turbulence characteristics from there. This, however, is computationally highly expensive and not a suitable approach for operational applications. Some dispersion models (e.g., QUIC, GRAMM/GRAL, MicroSpray) use types of Reynolds-averaged Navier–Stokes approaches approaches to calculate a mean flow field and derive the second-order moments from turbulence kinetic energy, combined with standard boundary-layer parametrizations. We believe that parametrizations specifically designed for the urban boundary layer could be useful for these types of models. This approach is computationally less expensive than LES, but still associated with considerable costs. Note that the main cost factor of all these approaches is the building-resolving flow simulation, not the dispersion. Furthermore, if there are no building-resolving maps available for a specific city, or the computational effort to explicitly calculate flow around resolved buildings is too high, another solution is required to include urban effects.

In this paper, we describe a method for incorporating the UCL in horizontally homogeneous flow models. Specifically, we propose describing the UCL as a partially porous medium with spatially-averaged vertical parametrizations of mean and turbulent flow. To our best knowledge there are no previously published parametrizations of second-order moments, dissipation rate, and vertical skewness specific to the UCL, even though the method of using specialized parametrizations characteristic for the canopy layer is not new (e.g., for vegetation canopies Baldocchi 1997).

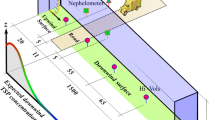
Over a rough, urban surface, the surface layer consists of the roughness sublayer (RSL) and the inertial sublayer (ISL), as shown on the right-hand side of Fig. 1. The RSL extends from the surface up to the blending height \(z_*\)—the height of the maximum Reynolds stress—and includes the urban canopy layer (UCL). Reynolds stress has been found experimentally and through simulation to be strongly height dependent in the RSL, i.e., to decrease to very small values close to the zero-plane displacement \(d\). Figure 1 (left) shows the conceptual sketch of a Reynolds stress profile in the urban boundary layer approaching in its lowest part a ‘constant stress’ portion—as expected in the surface layer. The dashed line depicts the corresponding decrease in magnitude of Reynolds stress in the RSL, i.e., if large roughness elements are present. This dashed line is based on the Reynolds stress profile of the urban RSL introduced by Rotach (2001). He showed that including this Reynolds stress profile into a Lagrangian particle dispersion model (LPDM) has substantial impact on modelled downwind concentrations and that the model performance improved significantly. However, due to the chosen parametrization, the lower boundary condition had to be set to the height of the zero-plane displacement. Thus the lowest tens of metres are still not included in the model domain. In this paper, we aim at explicitly introducing the UCL in the LPDM by extending the Reynolds stress profile down to the ground, as sketched by the blue line in Fig. 1. We also introduce similar extensions to the other necessary profiles of flow and turbulence. We will call the original model—including its urban RSL parametrization—RSM (roughness sublayer model), while the present model with the extension down into the urban canopy layer will be called ULM (urban canopy layer model). When referring to general properties of a Lagrangian particle dispersion model, we will refer to an LPDM.

Fig. 1
figure 1

Sketch of the Reynolds stress (adapted from Rotach 2001) in the atmosphere above an urban area. The solid line is the parametrization for the outer layer and the inertial sublayer from de Haan and Rotach (1998), from the boundary-layer height \(z_\mathrm {i}\) down to the zero-plane displacement \(d\). The dashed line is the RSL parametrization of Rotach (2001) from the blending height \(z_*\) down to \(d\). The blue line is the parametrization proposed in Sect. 4 from the mean building height \(z_\mathrm {h}\) down to the ground

Full size image

Wang et al. (2018) suggested a similar approach of including the UCL in a backward LPDM to calculate footprint functions, but their parametrizations are base on the assumption of Monin–Obukhov similarity theory inside street canyons, which seems to be hard to defend (e.g., Rotach 1999).

In this work, we test the sensitivity of the concentration output to the prescribed turbulence and wind profiles and validate the new model using field experiment data. Ultimately, we seek to determine whether or not a non-building resolving approach of including building effects is viable for simulating dispersion in urban areas. Then, the model may also be used as the core for an urban footprint model, for which it is necessary, or at least highly desirable, to have a domain extending to the physical surface where many potential sources (e.g., traffic) are present.

In the following, Sect. 2 summarizes the original formulation of the LPDM, Sect. 3 presents the underlying datasets used for the UCL parametrizations, and these are then described in Sect. 4. The ULM is verified and tested on its behaviour compared to the RSM in Sect. 5. A validation against the the Basel Urban Boundary Layer Experiment (BUBBLE) dataset is shown in Sect. 6.

2 Lagrangian Particle Dispersion Model

This study uses an LPDM initially developed by Rotach et al. (1996), later extended by de Haan and Rotach (1998) (crosswind dispersion), de Haan (1999) (more efficient concentration calculation), and Rotach (2001) (urban RSL parametrization). Rotach et al. (2004) compared this urban model with a specifically designed urban tracer experiment and found the model performance to highly depend on “the exact form of the parametrization for the flow and turbulence structure within the urban roughness sublayer”. Gibson and Sailor (2012) suggested several corrections to mathematical formulations in Rotach et al. (1996), but Stöckl et al. (2018) found that most of them had been either implemented in the model code long before or mistakes existed only in the publication, not the code. Finally, a more comprehensive summary of the model and a first attempt to include the effects of street canyon flow in the model can be found in Stöckl (2015).

The present LPDM is a one-dimensional (vertical) model with dispersion in three dimensions. The model is horizontally homogeneous, stationary, and does not include chemistry or deposition. The model’s domain ranges from the atmospheric boundary layer height \(z_\mathrm {i}\) to the zero-plane displacement \(d\) over urban areas. As mentioned above, in this study we extend the domain further towards the ground surface.

Rotach et al. (1996) were the first to enable their model to simulate in both convective and stable to neutral conditions. For this, they used the approach by Thomson (1987) and defined the necessary probability density function (p.d.f.) of the particle velocities as a mixture of two limiting states:

$$\begin{aligned} P_\text {tot}=f P_u P_v P_\mathrm {w,c}+ (1-f) P_u P_v P_w P_{uw}\,. \end{aligned}$$
(1)

The first term describes the joint p.d.f. of a convective atmosphere with no correlation between any of the wind components, Gaussian p.d.f.s \(P_u\) and \(P_v\), and \(P_\mathrm {w,c}\) a skewed p.d.f. for the vertical component \(w'\). The second term in Eq. 1 describes a neutral or stable atmosphere with purely Gaussian p.d.f.s for \(u'\), \(v'\), and \(w'\), but also a correlation between \(u'\) and \(w'\). Using this combined p.d.f. with the transition function f enables the model to be valid in different atmospheric conditions, while still fulfilling the well-mixed criterion (Thomson 1987). The transition function f is zero everywhere in stable and neutral conditions, while in convective conditions it ranges from one in the mixed layer to zero near the ground (see Rotach et al. 1996 for details).

The model uses an explicit Euler forward scheme to calculate the next position of each particle from the current position t:

$$\begin{aligned} x_i^{t+1}&= x_i^{t}+u_i^{t+1} \text {d}t, \mathrm{and} \end{aligned}$$
(2)
$$\begin{aligned} u_i^{t+1}&= u_i^{t} + \text {d}u_i\,, \end{aligned}$$
(3)

where \(i = 1, 2, 3\) for the three Cartesian directions, \(x_i\) is the position and \(u_i\) the velocity of the particle, and \(\text {d}u_i\) is a velocity increment. This velocity increment or acceleration is derived with the Langevin equation:

$$\begin{aligned} \text {d}u_i=a_i\text {d}t+b_{ij}\text {d}\xi _j\,, \end{aligned}$$
(4)

where \(\text {d}t\) is the timestep, \(a_i\) the correlated and \(b_{ij}\) the random part of the acceleration. Here, \(\xi _j\) describes a Wiener process with mean zero and variance \(\text {d}t\) (Rotach et al. 1996). Since this equation cannot be solved analytically, Rotach et al. (1996) followed Thomson (1987) in using the stationary Fokker–Planck equation,

$$\begin{aligned} a_iP_\text {tot}=\frac{\partial }{\partial u_i}\left( \frac{1}{2}b^2_{ij}P_\text {tot}\right) \underbrace{-\int \frac{\partial }{\partial x_i}\left( u_iP_\text {tot}\right) \text {d}u_i}_{\Phi _i}\,, \end{aligned}$$
(5)

to describe the same process as Eq. 4. Here \(P_\text {tot}\) is the total p.d.f. of the particle velocities (Eq. 1), as well as the p.d.f. of the Eulerian fluid velocities under the well-mixed assumption (Thomson 1987). See Rotach et al. (1996) for details on the analytical solution:

$$\begin{aligned} a_i=\frac{1}{P_\text {tot}}\left( \frac{C_0 \varepsilon }{2} \frac{\partial P_\text {tot}}{\partial u_i} +\Phi _i\right) , \end{aligned}$$
(6)

and

$$\begin{aligned} b_{ij}=\sqrt{(C_0 \varepsilon )}\chi _{i,j} \end{aligned}$$
(7)

The functions \(\Phi _i\) are given in Rotach et al. (1996) and \(C_0=3\) is the universal inertial subrange constant, see Rotach et al. (1996) for a discussion.

The model is completed by assuming vertical profiles of flow and turbulence characteristics—including the dissipation rate of turbulence kinetic energy \(\varepsilon \)—and thereby defining all p.d.f.s used in Eq. 1, although it would be possible to use output from a numerical model instead (see, e.g., Weil et al. 2004).

3 Urban Canopy Layer Data

To achieve the goals outlined in Sect. 1, values of \(\varepsilon \), \(\overline{u}\), \(\overline{u'w'}\), \(\overline{u'^2}\), \(\overline{v'^2}\), \(\overline{w'^2}\), and \(\overline{w'^3}\) are required for every possible (vertical) position in the model domain. Our model is horizontally homogeneous and thus does not rely on information on topography or building geometry. Instead we use spatially-averaged, vertical profiles over the widest feasible spread of different urban areas as possible, similar to the work of Raupach et al. (1996) for vegetation canopies. Up to date, vertical profiles for a representative spatial average from full-scale experiments are still scarce. Hence most of the following datasets originate from wind tunnel or numerical studies. Note that we refrain from using the classical \(<>\) spatial averaging notation for brevity. Unless noted otherwise, all profiles are spatially averaged.

Concerning spatial averages in the UCL, it is critical to distinguish between two types, which we will call ‘intrinsic’ and ‘superficial’ after Schmid et al. (2019). An intrinsic spatial average ignores the volume filled by assumed solid obstacles and averages only over the fluid volume. In contrast, a superficial spatial average takes the volume filled by obstacles into account and therefore also depends on the porosity of the city. In principle, it would be preferable to use superficial averages (as explained by Xie and Fuka 2018), because then the canopy could be treated as a homogeneous, porous medium (Böhm et al. 2013). However, most of the datasets only provide the intrinsic averages and not enough data to use porosity to convert. Instead, we average intrinsically and account for the ‘missing’ building volumes by adjusting the lower boundary condition at ‘the surface’. Usually, particles are ‘reflected’ at the lower domain boundary \(z_r\) by inverting the sign of \(w'\) and \(u'\), as well as adjusting the new z-position in such a way that the total distance traveled in this timestep remains the same, but the particle ends up above \(z_r\) instead of below (Thomson and Montgomery 1994). This sustains the particles in the model domain and is done similarly at the top domain boundary \(z_\mathrm {i}\). In our approach we introduce an elevated partial reflection level at the mean building height \(z_\mathrm {h}\), where particles are reflected with a chance of \(\lambda _p\) when arriving from above. Here, \(\lambda _p\) is the plan area fraction of roughness elements (Grimmond and Oke 1999) and thus mimics roof reflection.

The datasets used in this study are briefly introduced in the following. Coceal et al. (2006) (from now on CTCB06ST: staggered, CTCB06AL: aligned, CTCB06SQ: square array) and Coceal et al. (2007) (CDTB07) used direct numerical simulations to predict the flow over uniform cubes in regular grids of different layouts (staggered, aligned, square). We used data from their Figs. 20 and 2, respectively. Auvinen et al. (2020) simulated synoptically forced wind from the sea into the coastal city Helsinki, Finland, with an LES model and shared their spatially-averaged data with us (HEL). Xie and Castro (2009) simulated flow through an intersection in London, UK, (DAPPLE project site) using an LES model and reported the spatially-averaged profiles in their Fig. 9 (XC09). Carpentieri et al. (2009) simulated the same intersection as Xie and Castro (2009) in a wind tunnel (1:200 scale) and shared 14 profiles from different locations indicated in their Fig. 3 with us (CRB09).

Harman et al. (2016) studied the flow between a model canopy of regularly spaced, thin ‘tombstone’ obstacles in a wind tunnel. We used data from their Figs. 2, 3, and 4 (HBFH16). Böhm et al. (2013) showed profiles within and above a canopy of solid tree-shaped obstacles (light bulbs) in their wind tunnel that “share[s] characteristics of both vegetation and urban canopies” in their Fig. 10 (BFRH13). Kastner-Klein and Rotach (2004) investigated a model of Nantes, France, in a wind tunnel and measured vertical profiles. We used up to 42 of them to calculate the spatial average, depending on the specific variable (KKR04).

In field studies it is prohibitively difficult and expensive to measure enough vertical profiles for spatial averaging, hence we are unaware of any such measurement campaigns. However, Rotach (1993) argued that averaging over multiple profiles of few towers can be used as a raw estimate for a spatial average, considering the wind direction and therefore the upstream geometry changes. Christen (2005) followed this approach for the BUBBLE project in Basel, Switzerland (Rotach et al. 2005), and provided his dataset from two towers (BUBBLEU1 and BUBBLEU2). Since spring 2017, highly resolved fluxes of momentum, shear, water vapour and chemical compounds have been measured by the Innsbruck Atmospheric Observatory (IAO) at the University of Innsbruck, Austria (Karl et al. 2020; Ward et al. 2022). Data from two sonic anemometers outside the RSL (42.2 m a.g.l. and 39.6 m a.g.l.) and one street-level sonic anemometer (3.0 m a.g.l.) were used herein (ACINN). Although the two upper measurements were outside the RSL, we still chose to use the data of the street level to have more data sources for \(\varepsilon \) in the UCL. These real-world datasets are, on the one hand, suitable for our purpose because they reflect reality. On the other hand, they do almost certainly not represent true spatial averages, so care has to be taken not to over-interpret them. Giometto et al. (2016) investigated the suitability of a single tower measurement as source of spatial average and concluded that the single tower may be severely biased and is therefore unsuitable. However, they arrived at this conclusion by looking at LESs in comparison to a tower measurement, but only looked at two simulations with differing wind directions. Considering more wind directions may somewhat alleviate these results.

An overview of the data sources can be found in Table 1.

Table 1 Overview of data sources for the spatially averaged profiles in the UCL
Full size table

Since these data are from different sources, their normalizations, scalings, and rotations differ as well. We rotated the profiles into the prevailing wind direction with a single rotation, where appropriate. If the scaling and normalization corresponded to those used herein (see below), they were left as is. Otherwise the profiles were scaled and normalized, as explained in the following paragraphs.

Traditionally, the atmospheric boundary layer is scaled with \(z_\mathrm {i}\), at least for the outer layer (e.g., Stull 1988), and so are our model’s parametrizations too, as described in Rotach et al. (1996). In the urban RSL the height is scaled with \(z_*\) instead, which corresponds to defining \(z_*\) as the height of maximum (magnitude) Reynolds stress, such that the peaks of Reynolds stress collapse. Canopy scaling for vegetation canopies is usually done via the mean canopy height \(z_\mathrm {h}\) (e.g., Raupach et al. 1996; Rannik et al. 2003), but there the top of the canopy often coincides with the peak of Reynolds stress and therefore incorporates the entire RSL. This means that in classical canopy scaling (e.g., Raupach et al. 1996) the peaks of Reynolds stress and velocity variances are situated at \(z/z_\mathrm {h}= 1\). Urban geometries with uniform height show similar characteristics, but several studies have noted that this is not true for city geometries with non-uniform height (Xie et al. 2008; Xie and Castro 2009; Carpentieri and Robins 2015), where the peaks are positioned further aloft. This the origin of the \(z_*\) definition. Multiple studies suggest the use of the tallest upstream building as scaling height (Xie et al. 2008; Xie and Castro 2009; Kanda et al. 2013; Inagaki et al. 2017; Sützl et al. 2020) instead. Alternatively, it has been suggested (Martilli et al. 2000, as mentioned in Rotach 2001), to use \(z_\mathrm {h}+ \sigma _\mathrm {h}\) as scaling height, where \(\sigma _\mathrm {h}\) is the standard deviation of the building heights. Here we find that \(z_\mathrm {h}+ 1.5\sigma _\mathrm {h}\) fit our datasets best (not shown). Hence, we use \(z_* = z_\mathrm {h}+ 1.5\sigma _\mathrm {h}\) when RSL scaling is required.

To extend the RSL scaling of Rotach (2001) down to the surface we use canopy scaling (\(z/z_\mathrm {h}\)) for heights \(z<z_\mathrm {h}\). The transition from the RSL parametrization to the UCL parametrization thus occurs at \(z=z_\mathrm {h}\). If \(z_*\) is expressed in terms of \(z_\mathrm {h}\), we can present the entire RSL profiles as a function of \(z/z_\mathrm {h}\).

The variables of interest are normalized with powers of \(u_{*,ISL}\) (e.g., Raupach et al. 1996), where the roughness velocity in the inertial sublayer (ISL) \(u_{*,ISL}\) is obtained via the method of Kastner-Klein and Rotach (2004). Two notable exceptions are the mean wind speed, which is scaled by its value at \(z_\mathrm {h}\) (e.g., Raupach et al. 1996), and the skewness of the vertical velocity component, which is not scaled.

Figure 2 shows a summary of all datasets mentioned previously, specifically profiles of interest in their intrinsically spatially-averaged scaled and normalized forms. As mentioned, the canopy scaling is only intended to be useful for heights below \(z/z_\mathrm {h}= 1\), hence the profiles are not expected to collapse for \(z>z_\mathrm {h}\).

Fig. 2
figure 2

‘Family portrait’ of a collection of datasets (see Sect. 3) for: a \(\overline{u}/\overline{u}_\mathrm {h}\), b \(\overline{u'w'}/u^2_{*\mathrm {ISL}}\), c \(k\varepsilon z_\mathrm {h}/u^3_{*\mathrm {ISL}}\), d \(\mathrm {Sk}_w\), e \(\overline{u'^2}/u^2_{*\mathrm {ISL}}\), f \(\overline{v'^2}/u^2_{*\mathrm {ISL}}\), g \(\overline{w'^2}/u^2_{*\mathrm {ISL}}\). Note the different vertical axis in d, where \(z_\mathrm {h}+ 1.5 \sigma _\mathrm {h}\approx z_*\). The numbers in the legend are \(\sigma _h / z_\mathrm {h}\), indicating the uniformity of the height distribution. To avoid visual overload, only a selection of data points are shown with markers

Full size image

In Fig. 2a, normalization and scaling causes all profiles of the mean wind speed to collapse onto (1,1). Below \(z_\mathrm {h}\) most profiles exhibit similar behaviour (reminiscent of an exponential profile) and group together tightly, with the exception of three measurement points from real world datasets. The low scatter implies that the scaling and normalization is successful. However, our dataset is too sparse to evaluate whether or not \(a_\mathrm {um}\) scales with \(\lambda _p\), as sometimes suggested (e.g., Castro 2017 for a discussion).

Figure 2b shows the covariances \(\overline{u'w'}\), which exhibit their minima at different heights. However, all profiles have their minima at or above \(z_\mathrm {h}\), with the exception of CRB09, which is the wind-tunnel simulation of a real urban area with a focus of one intersection, where all measured profiles are located within or around this intersection. Therefore the profiles are not ideally placed for a spatial average, because that was never the intention of Carpentieri et al. (2009). We have decided to include these profiles nevertheless, because datasets with non-idealized geometries are rare. The configuration of buildings directly upstream of the intersection may have lead to a non-representative \(z_\mathrm {h}\) for our spatial average, given the fact that most of these buildings are uncharacteristically low, leading to an extremum of \(\overline{u'w'}\) even below the nominal \(z_\mathrm {h}\). Furthermore, a thin tower on top of one building directly upstream results in a second local minimum at \(z/z_\mathrm {h}= 1.7\) to 2.0. Interestingly, all profiles based on uniform-height geometry, which means \(\sigma _\mathrm {h}= 0\) (see legend of Fig. 2), indeed exhibit their minimum in Reynolds stress at or slightly above \(z_\mathrm {h}\), while cities with non-uniform heights have their minimum much higher up (except CRB09).

There are far fewer data available for the dissipation rate of turbulence kinetic energy \(\varepsilon \) (Fig. 2c), but the dissipation rate seems to decrease in the UCL. More research would be needed.

Contrary to the other profiles, the skewness of the vertical velocity component \(\mathrm {Sk}_w\) (Fig. 2d) is scaled with RSL scaling instead of canopy scaling. For a detailed justification see Sect. 4.4. Near \(z_\mathrm {h}\), the values are clustered close to zero, reflecting the Gaussianity of the mechanically induced shear turbulence. Below, in the UCL, it is noticeable that all profiles exhibit negative values of \(\mathrm {Sk}_w\), similar to vegetation canopies (Raupach et al. 1996). Near the ground, the values appear to return to zero.

Figure 2e shows profiles of the longitudinal velocity variance \(\overline{u'^2}\). Similar to \(\overline{u'w'}\), they peak—this time a maximum—at or above \(z_\mathrm {h}\). In the UCL the curvature of the profiles seems to range from positive to negative, most likely depending on the specific city geometry. For example, the contrast between CTCB06ST and CTCB06AL is striking, despite the fact that the only difference between them is the different cube layout in Coceal et al. (2006). However, most real cities would not conform to either end of these extremes and in fact the profiles CRB09, HEL, and KKR04, all more or less reflecting real cities, are somewhat in the middle of the spread. Conversely, XC09 is also a simulation with real city geometry but on the extreme left of the spread. Nevertheless, the general shape of peaking at or above \(z_\mathrm {h}\) and then declining towards the ground can be observed in all profiles.

The lateral velocity variance \(\overline{v'^2}\) in Fig. 2f exhibits similar characteristics as \(\overline{u'^2}\), except that the curvature of the declining profiles is more or less always the same. The same is true for \(\overline{w'^2}\) in Fig. 2g. Here the profiles seem to collapse best, except that both KKR04 and CRB09 show substantially larger values for \(\overline{w'^2}\) within the UCL.

4 Urban Canopy Layer Parametrizations

The following sections introduce the turbulence profile parametrizations necessary to run the LPDM. They are all devised by imposing a shape that is inspired by the respective profiles in Fig. 2 and additionally through necessary boundary conditions. With a given function and boundary conditions, each profile is then numerically fitted to the literature data described in Sect. 3.

One common boundary condition is continuity with the existing profiles aloft at height \(z_\mathrm {h}\), with the exception of \(\overline{w'^3}\), which is continuous at \(z_*\). The ‘transition value’ (denoted by subscript ‘h’) of each profile is the value of the individual RSL parametrization at height \(z_\mathrm {h}\).

Since the profiles (i.e., their parametrizations) in the RSL depend on the (variable) meteorological conditions and on urban geometry (building height), continuity of those profiles towards the UCL parametrization would require a fit of the canopy profiles for each simulation separately. To avoid doing this during each model run, we scaled height with \(z_\mathrm {h}\) and normalized all values of the experimental data with their value at \(z=z_\mathrm {h}\), thus forcing all the data (and the corresponding parametrizations) through (1, 1). This point (1, 1) is then the point where the profiles transition from RSL parametrization above to UCL parametrization below. To keep the numerical fitting algorithm independent of the amount of data points per profile, the data points are weighted in such a way that each individual profile has equal impact.

Since we aim to test the model’s sensitivity to the fitted parameters (see below, Sect. 5.3), we need a range of possible values for each parameter. We individually fitted the range of the parameters to encompass the approximate range of the available dataset. This range approximates both the uncertainty introduced by having only a few datasets, measurement and simulation uncertainty, as well as uncertainties introduced by the fitting procedure.

The profiles in Fig. 2 also diverge above \(z_\mathrm {h}\), which cannot be taken into account using the set-up in this work. Since we normalize all profiles to unity at \(z_\mathrm {h}\) and use another parametrization aloft, it does not matter for our purpose that they diverge further aloft. Furthermore, not all profiles of second-order moments peak at height \(z_\mathrm {h}\). Generally speaking, canopies with uniform heights have a lower maximum of the Reynolds stress and velocity variances compared to more realistic city geometries. However, at height \(z_\mathrm {h}\) all types of profiles are declining from the peak, which means that the general shape of the profile below \(z_\mathrm {h}\) is conserved (see Fig. 3).

In the following, the details of the parametrizations are outlined separately for each variable. The resulting parametrizations are—together with the datasets from Fig. 2—displayed in Fig. 3.

Fig. 3
figure 3

UCL parametrizations (black lines) with fitted parameters for the different variables a \(\overline{u}\), b \(\overline{u'w'}\), c \(\varepsilon \), d \(\mathrm {Sk}_w\), e \(\overline{u'^2}\), f \(\overline{v'^2}\), g \(\overline{w'^2}\), h f in canopy scaling representation, enforcing each variable to go through the point (1, 1) (except \(\mathrm {Sk}_w\) and f), when height is scaled with \(z_\mathrm {h}\) and the variable with its respective value at \(z_\mathrm {h}\). Note the different vertical axes in d, h, where \(z_\mathrm {h}+ 1.5 \sigma _\mathrm {h}\approx z_*\). Data from Sect. 3 as blue dots (intensity increases with the number of data points per individual profile); The orange shaded range encompasses the uncertainty range to be used in Sect. 5.3 for the sensitivity analysis

Full size image

4.1 Mean Wind Speed

Mean wind speed in the UCL is parametrized with the exponential function:

$$\begin{aligned} \overline{u}(z)= \overline{u}_\mathrm {h}\exp (a_{um}[z/z_h-1]) \end{aligned}$$
(8)

following common practice in vegetation canopies (Cionco 1965). Castro (2017) has questioned the adequacy of exponential urban canopy profiles for mean wind—his argumentation largely being based on the assumptions needed for its derivation not being fulfilled, and on the failure of some experimental profiles being exponential. Among the alternatives he discusses, there is the approach by Yang et al. (2016), who propose combining a logarithmic profile above the canopy with an exponential profile, i.e., exactly corresponding to the general approach followed herein. Yang et al. (2016) show that for different values of \(\lambda _p = \lambda _f\) (for cubes at a non-oblique approach-flow angle) and \(\sigma _\mathrm {h}\), an exponential function is a good fit to their simulated wind profiles in the upper 70–80% of the UCL—and even suggest that the validity of the exponential profile might be extendable closer down to the surface (Yang et al. 2016). \(\lambda _f\) is the frontal area density after Grimmond and Oke (1999).

Wang et al. (2018) use the same Eq. 8 and a method proposed by Macdonald (2000) to determine \(a_\mathrm {um}\) based on building geometry. However, this approach depends on knowledge of the height profile of the sectional drag coefficient and a mixing length scale, both of which are difficult to determine for non-idealized real urban geometries—and therefore unknown for most of the datasets used here.

Consequently, we determine \(a_\mathrm {um}\) using the boundary condition for the canopy profile, i.e., the requirement for a smooth transition at \(z_\mathrm {h}\). For this we normalize Eq. 8 with \(\overline{u}_\mathrm {h}\) and scale it with \(z_\mathrm {h}\), resulting in:

$$\begin{aligned} \hat{\overline{u}}_{\mathrm {UCL}} (z^\prime ) = \exp \left( a_{um} \left[ z^\prime - 1 \right] \right) , \end{aligned}$$
(9)

for \(z' = \tfrac{z}{z_\mathrm {h}}\). Then, we fit Eq. 9 to the UCL data gathered from literature (see Fig. 2) and thus determine \(a_\mathrm {um}= 1.97\) with an uncertainty range of [0.64, 3.31] (see orange shaded area in Fig. 3a). Based on the range of \(a_\mathrm {um}\) in the literature, Macdonald (2000) suggests \(a_\mathrm {um}= 9.6 \lambda _f\), which would correspond to about 3 to 4 for the datasets used in this study. Ramirez et al. (2018) report values \(<2\). Note that this profile does not generally satisfy the no-slip condition, but a shallow reflection layer at the bottom (see Sect. 4.7) circumvents this.

4.2 Turbulent Fluxes

The LPDM assumes no directional shear (i.e., \(\overline{v'w'}=0\)) in the surface layer and uses \(u_* = \sqrt{-\overline{u'w'}}\). Rotach (2001) derived the profile of the local \(u_{*,l} = \root 4 \of {\overline{u'w'}^2 + \overline{v'w'}^2}\) and then used this in the RSL as basis for all other turbulence profiles. We define the velocity variances, skewness, etc. separately in this study and therefore the profile of \(u_{*,l}\) has far less influence in the UCL. Furthermore, not all datasets provided \(\overline{v'w'}\) and thus we chose consistency over completeness and did not include \(\overline{v'w'}\) in \(u_\mathrm {*UCL}\). It is noted that neglecting \(\overline{v'w'}\) is not supported by many of the datasets introduced in Sect. 3 and remains an inherent limitation of the model itself that will be addressed in a future study.

The shape of the data in Fig. 2b suggests a function of the form \(u_\mathrm {*UCL}= a_1 \left( \tfrac{z}{z_\mathrm {h}}\right) ^{1/a^{}_\mathrm {Re}} + a_3\) to be useful, which is subject to the boundary conditions (i) \(u_\mathrm {*UCL}(z_\mathrm {h}) = u_\mathrm {*RSL}(z_\mathrm {h}) = u_\mathrm {*h}\) and (ii) \(u_\mathrm {*UCL}(z=0) = 0\) This leaves \(a^{}_\mathrm {Re}\) as the single tuning parameter and leads to:

$$\begin{aligned} u_\mathrm {*UCL}= u_\mathrm {*h}\left( \frac{z}{z_\mathrm {h}}\right) ^{\frac{1}{a^{}_\mathrm {Re}}}, \end{aligned}$$
(10)

which—normalized, scaled, and converted to \(\overline{u'w'}\)—yields:

$$\begin{aligned} \hat{\overline{u'w'}}_\mathrm {UCL} = - \left[ z'^{\frac{1}{a^{}_\mathrm {Re}}}\right] ^2\,. \end{aligned}$$
(11)

Once fitted to data in Fig. 3b, \(a^{}_\mathrm {Re}= 0.75\), with uncertainty range [0.29, 2.82].

Fig. 4
figure 4

Profiles of the ratio between dispersive stress and Reynolds stress taken from various sources (all simulations). Lines represent values from realistic city geometries, stars from staggered cubes, dots from aligned cubes and square one outlier. The black line is the suggested parametrization and is zero everywhere above \(z_*\) (\(1.5z_\mathrm {h}\) in this example). The numbers in the legend are \(\sigma _h / z_\mathrm {h}\), indicating the uniformity of the height distribution

Full size image

Due to spatial and temporal averaging, the covariances, such as \(\overline{u'w'}\) contain an additional contribution, i.e., the dispersive stress (Raupach and Shaw 1982). Note that we will use \(<>\) to denote spatial averaging in the next three paragraphs, hence \(\overline{u'w'} \rightarrow <\!\overline{u'w'}\!>\). The wind components can be decomposed into, e.g., \(u = <\!\overline{u}\!> \,{+}\, \overline{u}'' + u'\), where u is the instantaneous flow quantity, \(<\!\overline{u}\!>\) its spatial and temporal mean, \(\overline{u}'' = \overline{u}~- <\!\overline{u}\!>\) the spatial fluctuation around the time-space mean, and \(u'\) the turbulent fluctuation in both time and space. Given this, a product of two velocity components averaged over time and space becomes, e.g., \(<\!\overline{uw}\!> =<\!\overline{u}\!> <\!\overline{w}\!> +<\!\overline{u'w'}\!> + <\!\overline{u}''\overline{w}''\!>\), where \(<\overline{u}''\overline{w}''>\) is the so-called ‘dispersive stress’ contribution, which essentially describes spatial deviations from time averaged flow. Similar to Reynolds stress, dispersive stress represents momentum transport, for example by a canyon vortex.

Without immediate effect of obstacles, dispersive stress is zero, but in urban areas it is non-negligible (Coceal et al. 2006, 2007; Martilli and Santiago 2007; Xie et al. 2008; Giometto et al. 2016; Simón-Moral et al. 2017; Xie and Fuka 2018). Generally, the value of dispersive stress appears to depend strongly on the city geometry (Coceal et al. 2006, 2007). Xie et al. (2008) demonstrate the impact of the standard deviation of canopy height on dispersive stress: for uniform-height canopies it vanishes right above \(z_\mathrm {h}\), while it only gradually approaches zero for their non-uniform-height canopy. Figure 4 shows this by displaying the ratio of dispersive stress to Reynolds stress taken from various sources approaching zero rapidly above \(z_\mathrm {h}\) for the profiles shown in markers, which stem from canopies of uniform height. Since the Reynolds stress is always negative for these specific profiles, one can also deduce the sign of the dispersive stress. Dispersive stress is negative for all studies using staggered cubes (stars) and realistic city geometries (coloured lines), but for aligned cubes (dots) it is predominantly positive. This is caused by coherent vortices (Martilli and Santiago 2007) forming in the idealized cube geometries. However, Simón-Moral et al. (2017) show that convective conditions can lead to negative dispersive stresses even for aligned cubes (see Fig. 4), even though their neutral run (not shown) produced mostly positive dispersive stresses. Since we are primarily interested in realistic geometries, we ignore positive dispersive stress.

To investigate the impact of dispersive stress, we have designed a crude description of the ratio between the dispersive stress and the Reynolds stress (black line in Fig. 4). Then, the Reynolds stress parametrization is multiplied by \(1 + \tfrac{<\!\overline{u}''\overline{w}''\!>}{<\!\overline{u'w'}\!>}\), essentially adding the dispersive stress to the Reynolds stress. Since the dispersive stress appears to strongly depend on the canopy, it is even more unlikely than for other variables that a more general parametrization is possible. The results show hardly any difference between switching dispersive stress on or off (not shown). Firstly, this is due to the rapidly decreasing magnitude of \(<\overline{u'w'}>\) within the UCL (Fig. 3b) and the therefore small impact of the factor \(1 + \tfrac{<\!\overline{u}''\overline{w}''\!>}{<\!\overline{u'w'}\!>}\). Secondly, Reynolds stress as a whole has small impact, as shown in Sect. 5.3. Given the large canopy-to-canopy variability of the dispersive stress and the relatively minor impact its inclusion has on dispersion within the canopy we decided not to include the dispersive stress contribution into the parametrized profile of Reynolds stress.

For the parametrization of sensible heat flux \(\overline{w'\theta '}\) we use the formulation of Christen (2005) in his Equations 4.41 and 4.42. Note that this parametrization is only valid for convective cases and thus only used in such. This parametrization only affects the convective velocity scale \(w_*\), by giving it a local value in the RSL. This \(w_*\) is used by the LPDM to determine turbulence profiles of RSL, inertial sublayer, and mixed layer in convective situations. Note that the UCL parametrizations do not depend on stability. The dataset in Sect. 3 is too limited to separate it according to atmospheric stability and fit profiles depending on stability. Thus, the profile of \(\overline{w'\theta '}\) does not influence the UCL parametrizations directly, but it does influence the RSL parametrizations and therefore the transition values to the UCL below.

4.3 Dissipation Rate of Turbulence Kinetic Energy

Since the data available are scarce (see Sect. 3), the shape of the profile is more uncertain than for other profiles. Nevertheless, the available data suggests a decreasing \(\varepsilon \) from the RSL downwards, so we choose the same general function as \(\overline{u}_\mathrm {UCL}\):

$$\begin{aligned} \varepsilon _\mathrm {UCL}= \varepsilon _\mathrm {h}\exp (a_{\epsilon }[z'-1]) \end{aligned}$$
(12)

where \(\varepsilon _\mathrm {h}= \varepsilon _\mathrm {UCL}(z_\mathrm {h}) = \varepsilon _\mathrm {RSL}(z_\mathrm {h})\) ensures continuity to the RSL and \(a_\varepsilon \) can be numerically fitted to data after canopy-scaling and normalizing with \(\varepsilon _\mathrm {h}\). The result can be seen in Fig. 3c and leads to \(a_\varepsilon = 1.01\) with uncertainty range \([-0.18, 2.90]\). Note that Giometto et al. (2016) shows \(\varepsilon \) in their Fig. 10 too, but not spatially averaged. Nevertheless, the behaviour in their figure is similar to Fig. 3c, with the exception of a second local minimum close to the ground that is most likely hidden by our reflection layer. Di Bernardino et al. (2020) find that the dissipation rate is not strongly dependent on \(\lambda _p\), above the canopy (see their Fig. 8).

4.4 Vertical Skewness

As mentioned earlier, the skewness of the vertical velocity \(\mathrm {Sk}_w\) is negative in the whole RSL. Since the Rotach (2001) approach of including RSL effects only modifies \(u_*\), \(\mathrm {Sk}_w\) remained unchanged from Rotach et al. (1996), because their \(\mathrm {Sk}_w\) parametrization does not depend on \(u_*\). Consequently, we choose to have the new parametrization of \(\mathrm {Sk}_w\) affect the whole RSL. Furthermore, it is more common to find profiles of \(\mathrm {Sk}_w\) than \(\overline{w'^3}\) in the literature. Therefore, we show and parametrize \(\mathrm {Sk}_w\) here as well, although the model internally uses \(\overline{w'^3}\). This is simply addressed by de-normalizing \(\overline{w'^3}= \mathrm {Sk}_w\overline{w'^2}^\frac{3}{2}\) in the model.

Originally, the p.d.f. \(P_\mathrm {tot}\) was designed to incorporate the effect of convection in the mixing layer, i.e., yielding \(\mathrm {Sk}_w>0\). Appendix 1 demonstrates that the same formulation can also be used in the UCL to yield a negative skewness.

Unlike the other parametrizations, it is not reasonably possible to collapse all profiles onto (1, 1), because \(\mathrm {Sk}_w\approx 0\) at height \(z_*\) (see Fig. 2d), which means that both positive and negative values are possible. We choose a parabolic shape \(\mathrm {Sk}_{w\mathrm {UCL}}= a_1 (z + a_2)^2 + a_3\) with boundary conditions (i) \(\mathrm {Sk}_{w\mathrm {UCL}}(z_*) = \mathrm {Sk}_{w\mathrm {RSL}}(z_*) = \mathrm {Sk}_{w\mathrm {t}}\), (ii) \(\mathrm {Sk}_{w\mathrm {UCL}}(0) = 0\), and (iii) \(\mathrm {Sk}_{w\mathrm {UCL}}(\tfrac{z_*}{2}) = -a_\mathrm {Sk}\). The last condition is not necessary to fit the function, but without it the minimum of the fitted function depends not only on the free tuning parameter \(a_\mathrm {Sk}\), but also on the value of \(z_*\), which results in \(\mathrm {Sk}_w\) profiles strongly varying with \(z_*\). Condition (iii) also helps to keep the resulting function from being strongly dependent on the value of \(\mathrm {Sk}_{w\mathrm {t}}\), which is unknown at fit-time and changes from city to city. Since it is not possible to collapse the profiles and the function onto (1, 1) as for the other variables, this was a major concern, because that would mean that the function to be fitted is no longer independent of the specific model run. The third condition alleviates this problem. Taking \(a_\mathrm {Sk}\) as free parameter leads to:

$$\begin{aligned} \mathrm {Sk}_{w\mathrm {UCL}}= (2 \mathrm {Sk}_{w\mathrm {t}}+ 4 a_\mathrm {Sk}) \left( \frac{z}{z_*}\right) ^2 - (\mathrm {Sk}_{w\mathrm {t}}+ 4 a_\mathrm {Sk}) \left( \frac{z}{z_*}\right) \,, \end{aligned}$$
(13)

which can be scaled via \(z' = \tfrac{z}{z_*}\). We choose \(\mathrm {Sk}_{w\mathrm {t}}= 0.05\) as somewhat arbitrary transition value, but—as mentioned before—the function is designed not to be sensitive to this choice. Figure 3d shows the resulting function for \(a_\mathrm {Sk}= 0.48\) with uncertainty range [0.11, 0.70].

4.5 Velocity Variances

Since the profiles in Fig. 2e are of similar shape to the mean wind speed profiles in Fig. 2a, we choose to use the same general function,

$$\begin{aligned} \overline{u'^2}_\mathrm {UCL}= \overline{u'^2}_\mathrm {h}\exp ^{a_\mathrm {u2}\left( z' - 1\right) }, \end{aligned}$$
(14)

for the longitudinal velocity variance. With canopy scaling this yields

$$\begin{aligned} \hat{\overline{u'^2}}_\mathrm {UCL}= \exp ^{a_\mathrm {u2}\left( z' - 1\right) }\,, \end{aligned}$$
(15)

which is then fitted to similarly scaled and normalized data. The result is \(a_\mathrm {u2}= 1.30\) with uncertainty range [0.04, 4.43] and can be seen in Fig. 3e.

Using the same arguments as for \(\overline{u'^2}_\mathrm {UCL}\),

$$\begin{aligned} \overline{v'^2}_\mathrm {UCL}= \overline{v'^2}_\mathrm {h}\exp ^{a_\mathrm {v2}\left( z' - 1\right) }\,, \end{aligned}$$
(16)

which—when scaled an normalized as in Eq. 15—leads to \(a_\mathrm {v2}= 0.72\) with uncertainty range \([-0.26, 3.17]\) [Fig. 3f].

For the vertical velocity variance we note that for all the profiles in Fig. 2g reaching the ground, \(\overline{w'2}(z=0)=0\). Thus we choose \(\overline{w'^2}_\mathrm {UCL}= (a_1 z)^{1 / a_\mathrm {w2}} + a_2\) with \(a_\mathrm {w2}\) the free parameter and the boundary conditions (i) \(\overline{w'^2}_\mathrm {UCL}(z_\mathrm {h}) = \overline{w'^2}_\mathrm {RSL}(z_\mathrm {h}) = \overline{w'^2}_\mathrm {h}\) and (ii) \(\overline{w'^2}_\mathrm {UCL}(0) = 0\). This leads to:

$$\begin{aligned} \overline{w'^2}_\mathrm {UCL}= \overline{w'^2}_\mathrm {h}\left( \frac{z}{z_\mathrm {h}}\right) ^\frac{1}{a_\mathrm {w2}}, \end{aligned}$$
(17)

and can be scaled and normalized to:

$$\begin{aligned} \hat{\overline{w'^2}}_\mathrm {UCL}= \left( z'\right) ^\frac{1}{a_\mathrm {w2}}, \end{aligned}$$
(18)

Fitting Eq. 18 to data results in \(a_\mathrm {w2}= 2.06\) with uncertainty range [1.10, 5.89] [Fig. 3g].

4.6 Transition Function

Rotach et al. (1996) designed the function f for the transition of the p.d.f. \(P_\mathrm {tot}\) from convective to neutral and stable conditions. Since we have already repurposed the convective form of the p.d.f. for \(w'\) (\(P_\mathrm {w,c}\)) to achieve the necessary negative skewness in the UCL, we also have to redesign f to activate this skewed part of the p.d.f. If f would stay near zero close to the ground as proposed in Rotach et al. (1996) for the RSL, the skewness of \(w'\) would have no effect and the resulting Eulerian p.d.f. of model particles would not be skewed. Consequently, we choose a function that reaches unity quickly, descending from \(z_*\). Note that this choice is arbitrary, because the only way to determine it objectively would be to measure the height profile of the \(w'\) p.d.f. horizontally averaged in the UCL and then find a function f such that the resulting Lagrangian p.d.f. of the model particles agrees with the measured Eulerian p.d.f. of the real-world flow for a given \(\mathrm {Sk}_w\) profile. To our best knowledge no such data can be found in the literature. The boundary conditions are continuity at \(z_*\) (i) \(f_\mathrm {UCL}(z_*) = f_\mathrm {RSL}(z_*) = f_\mathrm {t}\) and (ii) \(f(0) = 1\) for a function of the form \(f_\mathrm {UCL}= a_1 + a_2 \mathrm {e}^{a_fz}\), with \(a_f\) as free parameter, which leads to:

$$\begin{aligned} f_\mathrm {UCL}= 1 + (f_\mathrm {t}- 1) \frac{1-\mathrm {e}^{a_fz}}{1-\mathrm {e}^{a_fz_*}}\,. \end{aligned}$$
(19)

We choose \(a_f=0.4\) and [0.01, 2.0] for the uncertainty range. The resulting functions can be seen in Fig. 3h, although without measurements. Note \(f_\mathrm {UCL}\) being unity at the bottom does not mean that the Eulerian p.d.f. of \(w'\) is necessarily skewed; this also depends on the value of \(\overline{w'^3}\), which approaches zero close to the ground in any case. Additionally, \(f_\mathrm {UCL}\) approaching one towards the ground is consistent with \(\overline{u'w'}\) approaching zero near the ground.

4.7 Aspects Not Accounted For

Several of the parametrizations presented are problematic directly at the ground: \(\overline{u}_\mathrm {UCL}\) does not satisfy the no-slip condition; \(\overline{w'^2}_\mathrm {UCL}\) is zero at \(z=0\), which leads to a divide-by-zero error in Eq. 23 and \(P_w\) (not shown); \(u_\mathrm {*UCL}\) is also zero at \(z=0\), also leading to a divide-by-zero error (not shown). To circumvent these issues, the model does not allow particles to reach all the way to the ground, but reflects them slightly higher up at \(z_0\). This mimics a shallow surface layer near the ground, where the wind speed decays rapidly to zero (Yang et al. 2016) and where most likely an entire set of new parametrizations would be needed.

While \(\overline{v'w'}\) is generally small over smooth surfaces or far above rough surfaces—in a wind-following coordinate system—it is not so in the UCL. Unfortunately, our model cannot represent this.

Not taken into account at all in this study is the effect of wind direction and wind direction changes, which are a major factor in plume dispersion (e.g., Michioka et al. 2019).

Ideally, the parametrizations would be able to take different types of urban areas into account, because it is likely that a central business district has different profiles than a sparse suburban area (e.g., Badas et al. 2019). To model this, we attempted to use the mean building height, standard deviation of building height, plan area density \(\lambda _p\) and frontal area density \(\lambda _f\) (Grimmond and Oke 1999) by trying to find possible scaling relationships that improve the collapse of the profiles. Unfortunately, these efforts did not significantly improve the scatter in Fig. 2 when using the datasets of Sect. 3. We did find an estimate for the blending height \(z_* = z_\mathrm {h}+ 1.5 \sigma _\mathrm {h}\), which is used in scaling the height of the \(\overline{w'^3}\) profile (see Sect. 4.4). Perret et al. (2019) were similarly unsuccessful in collapsing \(\sigma _u^2\) by scaling, although they did not use spatially averaged profiles. On the other hand, the Rotach (2001) RSL parametrizations successfully use the zero-plane displacement \(d\), \(z_*\), and \(z_0\), which depend on the building geometry (Grimmond and Oke 1999). Since the UCL profiles are continuous to the RSL profiles and thus also depend on those factors, they also indirectly affect the UCL parametrizations. It is possible that more data or more realistic data would help in finding appropriate scaling parameters for differing geometries.

An additional limitation of the chosen approach is missing the multi-scale roughness, because the obstacles in wind-tunnel studies or simulations are most often aerodynamically smooth, in contrast to real buildings. However, Vanderwel and Ganapathisubramani (2019) indicated that small-scale roughness elements have a negligibly small effect on drag.

5 Verification

In this section the model’s basic assumptions are verified and its general sensitivities are investigated.

5.1 Well-Mixed Criterion

The most fundamental test for an LPDM is the well-mixed criterion after Thomson (1987). If a model fulfills this criterion, it does not unmix once the particles are well-mixed in physical and velocity space. To test whether the modified model fulfills this criterion, we initialize the ULM with particles uniformly distributed in height and given a velocity randomly sampled from the local velocity density function. Then the ULM simulates the dispersion for an extended amount of time (in our case about 1 day of simulated time).

Fig. 5
figure 5

Vertical distribution of particles after 90,000 simulated seconds of the three test cases in Table 2, initialized with well-mixed particles. The particle counts are binned (bin size = 1 m) and normalized with their theoretical value for each height range. A perfect result would be 1 (dotted line) everywhere. The figure shows only the lower part of the model domain

Full size image

The resulting height distribution of particles—similar to, e.g., Bahlali et al. (2020)—is shown in Fig. 5 for the three test cases in Table 2. The normalized concentration in Fig. 5 is not calculated using the kernel method (de Haan 1999) like in the rest of this work. To avoid any smoothing, we simply calculated a histogram over height-bins and normalized the particle count by the the mean particle count in a perfectly uniform distribution. Note that the figure only shows the lower 7.5% (stable), 1.5% (neutral), and 0.8% (convective) of the model domain. Aloft and up to the boundary-layer height \(z_\mathrm {i}\) the value of the normalized concentration fluctuates around 1, as expected (not shown). Below the mean building height \(z_\mathrm {h}\), the normalized concentration of particles is calculated only for the fluid volume, analog to intrinsic spatial averages in Sect. 3. This necessitates normalizing the particles by their mean count (as above) and then multiplying by \(1-\lambda _p\). After this, the normalized concentration fluctuates around 1, proving the well-mixed state.

5.2 Comparison of Urban-Canopy Layer Model and Roughness Sublayer Model

To investigate the impact of the UCL on the simulated concentration fields, we use three synthetic cases taken from Kljun et al. (2015). The relevant values are listed in Table 2. Note that the source height is 1 m above the mean building height. A source height in the street canyon might possibly produce more pronounced differences between the two models. However, as RSM is restricted to heights \(z>d\), we decided to use a source height representative for domestic heating (‘chimney height’).

Table 2 Test scenarios, after Kljun et al. (2015)
Full size table
Fig. 6
figure 6

Vertical profiles of CIC (blue), ARCMAX (orange), and \(\sigma _y\) (green) for three different stabilities (rows, see Table 2) and different source distances (x, note that the source distances shown vary between the three stability conditions). The values of the ULM are solid lines, the RSM values are dashed and marked by ‘x’. The profiles are taken at the lateral center of the plume. All CIC values are normalized by \(3.65\times 10^{-3}\) ng m\(^{-2}\), all ARCMAX values by \(1.47\times 10^{-4}\,\hbox {ng}\,\hbox {m}^{-3}\), and all \(\sigma _y\) values by 130 m. Horizontal dotted lines indicate mean building height \(z_\mathrm {h}\). Note that the RSM cannot simulate to the ground, so the lowest model level at zero-plane displacement \(d=10\) m is extrapolated to the ground (dotted lines)

Full size image

Figure 6 shows selected vertical profiles of the crosswind-integrated concentration CIC, the maximum value along an arc ARCMAX and the standard deviation of particle spread in the lateral direction \(\sigma _y\). Note that we use the term ‘arcs’, but utilize a Cartesian grid, so that the ‘arc’ strictly speaking refers to a line perpendicular to the mean wind direction. We use the term ‘arc’ for historical reasons. The model can calculate the concentration at any point in the model domain independent from other points, so the shape of the grid is not important, as long as the resolution is not too low. Also note that the source distances shown vary between the three stability conditions. In all three conditions—stable, neutral, and convective—the peak value of the CIC near the source at approximately roof level is smaller for the ULM (Fig. 6a, d, g). This is not offset by increased vertical dispersion, because the CIC values aloft are highly similar and those below do not compensate either. Since the lateral dispersion measured in \(\sigma _y\) is similar for both models at these heights, the reduced dispersion of the ULM must be in the longitudinal direction. This is possible even though the model is horizontally homogeneous, because there is a stochastic effect on \(u'\) and the mean transport changes between the two models, due to changes in domain size and wind speed profile.

The quantity \(\sigma _y\) sometimes displays artifacts when too few particles are available at certain heights. This can be seen in Fig. 6a, b, d, at heights where \(\sigma _y\) differs for the RSM and the ULM. CIC and ARCMAX are not affected, because their calculation is not as susceptible to few and strongly different values.

At some distance from the source (Fig. 6b, e, h), the roof level CIC and ARCMAX are smaller with the ULM than with the RSM. For the largest distances downstream, the concentrations of the two model versions start to overlap (Fig. 6c, f) due to approaching a well-mixed state.

Another important result is the slanted profile of CIC and ARCMAX in the UCL for ULM in nearly all stabilities and distances, at least until the whole profile starts to be well-mixed. In contrast, the RSM must make an assumption about the profile below \(d\) and this was historically a well-mixed assumption. This is shown in Fig. 6 by extending the profile of RSM uniformly down to the ground, as dotted lines. However, the slanted profiles of ULM in the UCL indicate that the assumption of a uniformly distributed concentration in the UCL does not hold.

5.3 Sensitivity Analysis

The chosen UCL parametrizations are based on data with considerable spread. A sensitivity study is therefore conducted in order to assess the impact the newly introduced profile parameters (‘UCL parameters’ in the following) (see Sect. 4) exhibit on the output (i.e., the modelled concentrations). Due to the non-negligible computational effort per model run, the state-of-the-art approach, i.e., a variance decomposition method, is unfeasible. Instead, we follow Saltelli et al. (2008) and choose ‘Morris sampling’, after Morris (1991), enhanced by Campolongo et al. (2007). The method is also called the ‘elementary effects method’ and employs one-factor-at-a-time changes (OAT), but alleviates many of the disadvantages of OAT-based methods (Saltelli et al. 2008). Unfortunately, Morris sampling requires scalar outputs, while in the present case we have concentration distributions. We therefore consider four scalars describing the concentration distribution.

Fig. 7
figure 7

Schematic of crosswind-integrated concentration CIC (upper panel) and lateral spread \(\sigma _y\) (lower panel) with increasing source distances. The four blue labels describe four scalars characterizing the plume

Full size image

The four scalars are shown in Fig. 7: \(\Pi _\mathrm {CIC}\), the maximum of the crosswind-integrated concentration; \(\Pi _\mathrm {width}\), the width in metres of the CIC peak, defined as the distance between the points where the linearly interpolated CIC curve reaches \(75\%\) of \(\Pi _\mathrm {CIC}\); \(\Pi _{\sigma y}\), the standard deviation of particle spread in the lateral direction at the distance of \(\Pi _\mathrm {CIC}\) occurence; and \(\Pi _{d \sigma y}\), the derivative of \(\Pi _{\sigma y}\) with respect to the streamwise direction x.

We test all UCL parameters, as described in Sect. 4. These are \(a_\mathrm {um}\), \(a^{}_\mathrm {Re}\), \(a_\mathrm {u2}\), \(a_\mathrm {v2}\), \(a_\mathrm {w2}\), \(a_\mathrm {Sk}\), \(a_f\), and \(a_\varepsilon \). Furthermore, we vary \(\lambda _p\) from 0 to 1, which governs the reflection at roof level from 0 to \(100\%\). For consistency with the other parameters, it is denoted by \(a_\mathrm {lp}\) in the following. Additionally we also vary some parameters of the original RSL parametrization(‘RSL parameters’ in the following), to give context to the new parameters. These are \(a_\mathrm {d}\), which varies the zero-plane displacement \(d\) from 0.5 to 0.9 of \(z_\mathrm {h}\); \(a_\mathrm {zs}\), which varies \(\tfrac{z_*}{z_\mathrm {h}}\) from 1.2 to 5.0; and \(a_\mathrm {a}\), which is the parameter a in Eq. 1 in Rotach (2001) and determines the shape of the RSL parametrization of the local \(u_{*,l}\).

For details regarding the implementation of the Morris method, see “Appendix 2”. Basically, it returns a summary statistic \(\mu ^*\) (Eq. 27 in the “Appendix 2”), which measures the impact a parameter has on the overall model output; lower means less impact. In addition to \(\mu ^*\) we used arithmetically averaged \(\overline{\mu ^*}\) to jointly asses the impact of (i) the aforementioned four output scalars (\(\Pi _\mathrm {CIC}\), \(\Pi _\mathrm {width}\), \(\Pi _{\sigma y}\), \(\Pi _{d \sigma y}\)); (ii) four heights where the concentrations are calculated (1 m, 16 m, 31 m, 46 m), 1 m above ground and roof, equidistant above; (iii) three meteorological situations (see Table 2); (iv) three source heights (2 m, 16 m, 40 m), deep within the canyon, above \(z_\mathrm {h}\) and in the upper part of the RSL (depending on \(a_\mathrm {zs}\).

Fig. 8
figure 8

Aggregated impact, \(\overline{\mu _*}\) (higher value signify higher influence), of model parameters according to the Morris method for the three stability groups (blue bars) and all combined (orange bars). UCL parameters in dark colours; RSL parameters in lighter colour. Vertical black lines indicate one standard deviation

Full size image

Figure 8 singles out the three stability cases in the first three panels and combines all cases in the fourth. Generally speaking, the RSL parameters (in lighter colours) have a slightly higher impact on the output than the UCL parameters. This result is fortunate, because the UCL parameters are highly uncertain, due to the large spread of the profiles (Fig. 2). The most important individual parameter is \(a_\mathrm {zs}\), with the highest impact in the neutral and especially the stable cases and still considerable impact in the convective case. Already Rotach (2001) noted the importance of this parameter and showed that it is less impactful in convective conditions. With the explicit treatment of the UCL, the impact of \(a_\mathrm {d}\) becomes less important than that of \(a_\mathrm {zs}\), while in the RSM (Rotach 2001) it had been similar. In contrast to \(a_\mathrm {zs}\), \(a_\mathrm {d}\) has a stronger impact when stability decreases. The RSL parameter \(a_\mathrm {a}\) is most impactful in the neutral case and less so for stable and convective situations. The convective case is especially interesting, because there \(a_\mathrm {a}\) is even less impactful than some of the UCL parameters. This is in spite of \(a_\mathrm {a}\) governing all turbulence profiles in the RSL and—due to continuity at the roof level—therefore also all turbulence profiles in the UCL. However, in convective situations the impact of \(u_*\) on the RSL parametrizations is diminished in the model, because they additionally depend on \(w_*\). The impact of \(a_\mathrm {lp}\) is not overly large, despite \(a_\mathrm {lp}\)’s property of varying the roof-top reflection from \(0\%\) to \(100\%\), thereby in the extreme cases even turning the UCL parametrizations on or off. We suspect that this is caused by the plume not dispersing strongly in the stable and neutral cases and therefore not many particles actually reaching the measurement layers far away from the source height. This is corroborated by the high importance in the convective case with much higher vertical dispersion. See also the discussion of Fig. 9.

Of the new parameters, \(a_\mathrm {um}\) and \(a_\mathrm {v2}\) are the most important. On one hand, \(a_\mathrm {um}\) governs the mean flow thus explaining its importance. On the other hand, the relatively large impact of \(a_\mathrm {v2}\) is not due to us choosing two scalars describing the lateral dispersion (\(\Pi _{\sigma y}\) and \(\Pi _{d \sigma y}\)), because removing \(\Pi _{d \sigma y}\) does not change the relative importance of \(a_\mathrm {v2}\) much (not shown). Of medium importance among the UCL parameters are \(a_\mathrm {u2}\), \(a_\mathrm {w2}\), and \(a_f\). Since the latter is not based on data (Sect. 4), its medium impact calls for more work with respect to the suitability of describing the velocity p.d.f. in the UCL using the function f (Eq. 1) in combination with the vertical velocity skewness. \(a^{}_\mathrm {Re}\), \(a_\mathrm {Sk}\) and \(a_\varepsilon \) are of least importance, so that the lack of data for at least \(a_\mathrm {Sk}\) and \(a_\varepsilon \) (Fig. 2) does not add a major source of uncertainty for the UCL simulations. Among the two parameters influencing the Reynolds stress profile, \(a^{}_\mathrm {Re}\) as an UCL parameter is of minor importance, while its RSL counterpart (\(a_\mathrm {a}\)) is among the most influential. This is because in the RSL parametrization Rotach (2001) all turbulence profiles depend on \(u_{*,l}\), while in the UCL parametrization of this study, they do not. Consequently, \(a^{}_\mathrm {Re}\) only modifies a profile that rapidly approaches zero with decreasing height and its effect is apparently small. This is further amplified by the relatively small spread of the profiles in Fig. 3b, compared to that for, e.g., the velocity variances in Fig. 3e, f.

Fig. 9
figure 9

As Fig. 8 split by source height (blue) and all combined (orange)

Full size image

When we separate the results of the sensitivity study for the different emission heights (Fig. 9), we see a different pattern. Note that the ‘combined’ panel is identical to that of Fig. 8. Clearly, some parameters affect model runs with different emission height differently. It is interesting to note that the UCL parameters in the runs with a high source affect the output similarly than in runs with a lower source, despite only affecting the layer below 15 m. The high importance of \(a_\mathrm {zs}\) and the other RSL parameters is due to their impact on the entire profiles over the buildings, which is the majority of the model domain. The parameter \(a_\mathrm {lp}\) shows that the reflection at the roof level is less impactful if the particles already start below this level. Also interesting is a much higher separation between important and less important parameters for lower sources than for higher sources. This is likely related to the fact that in those cases the UCL parametrization directly influences all particles at the start, instead of only when they are transported into the UCL.

6 Validation

To properly test the UCL parametrization, the model performance is evaluated for a real dispersion experiment. Required input is mean wind speed at an arbitrary height, mean wind direction, \(u_*\), \(w_*\) (if convective), \(z_\mathrm {i}\), Obukhov length L, mean building height, plan area density \(\lambda _p\), zero-plane displacement \(d\), roughness length \(z_0\), and the blending height \(z_*\). For the validation, the coordinates and strength of the source and the positions and concentration measurements of the samplers are also required. Here we use data from the Basel UrBan Boundary Layer Experiment (BUBBLE, Rotach et al. 2005). We chose BUBBLE, because we wanted a tracer experiment that approximates the steady state of the model and has a source as low as possible, but not below the zero-plane displacement \(d\). Otherwise the comparison with the RSM would be compromised, because it cannot start particles below \(d\).

6.1 Basel UrBan Boundary Layer Experiment

Gryning et al. (2005) describes the BUBBLE campaign in Basel, Switzerland, from 2001 to 2002. This campaign contains both long-term tower measurements as well as tracer experiments (see also Sect. 3). The tracer experiments took place during four convective days with a thermally driven, local wind phenomenon. Release and most measurements were near roof level. Mean building height in the area is about 15 m. Rotach et al. (2004) used the same LPDM to compare with the BUBBLE dataset and investigated three different averaging periods for the concentration measurements. In order to have the largest possible amount of data for the analysis, we choose the original measurement period of 30 min for our simulations, instead of the 3-h average that Rotach et al. (2004) chose. This decreases the statistical agreement between model and measurements, but gives us more data to work with. Meteorological data were collected at a tower with sonic anemometers. The tower stood within the area covered by the samplers for the concentration measurements. All together, 24 30-min convective periods are available for analysis.

6.2 Acceptance Criteria After Hanna and Chang (2012)

Hanna and Chang (2012) provide acceptance criteria for urban dispersion model evaluations. They define the fractional bias (FB), the normalized mean square error (NMSE), and the factor-of-2 (F2). See “Appendix 3” for their definitions. Note that these error measures for the acceptance criteria are not calculated for all points, but only for the maximum value along each arc (ARCMAX), which leads to far better statistical agreement than point-to-point comparisons. The measurements were taken from the highest value along each arc during BUBBLE (see Rotach et al. 2004). Furthermore, Hanna and Chang (2012) define the threshold-based normalized absolute difference (TBNAD, called NAD in their work) for point-to-point comparison if both simulated and observed values are above the threshold of three times the limit of quantification of the measuring instrument. The so-defined statistics are summarized in Table 3.

Table 3 Performance measures according to the acceptance criteria of Hanna and Chang (2012)
Full size table

The RSM already shows a strong performance, fulfilling all four criteria when aggregated over all BUBBLE cases. Only the TBNAD-criterion shows non-optimal performance. When looking at the performance measures for each case individually (last column), the FB-, NMSE-, and F2-criteria are accepted in well above the 50% of cases required by Hanna and Chang (2012). Conversely, for both model versions, the TBNAD-criterion is only accepted in 38% of cases, confirming the earlier, worse model performance when looking at TBNAD. Including the UCL does not change the model performance; in general a slight improvement is found.

6.3 Visual Comparison with Field Measurements

Figure 10 compares measured and modelled concentrations, both for the RSM (blue crosses) and the ULM (orange squares). Due to the logarithmic nature of the plot and the fact that the model simulates values near zero to floating point precision—far smaller than the experimental detection limit—the scale is limited to the instrument’s limit of detection (LOD = 5 ng m\(^{-3}\)). All values smaller than LOD (simulated or measured) are set to LOD. Generally, the ULM included produces slightly smaller concentrations than the RSM. This will be shown more clearly in Sect. 6.4. However, the distribution of values is highly similar, indicating that the implementation of the UCL does not fundamentally alter the concentration distribution—at least above roof level where the measurements were performed.

Fig. 10
figure 10

Measured versus modelled concentrations from all (four) BUBBLE tracer experiments. All values smaller than the LOD are set to LOD (grey dotted line) and displayed as dots instead of the usual marker (legend). EMD is the earth mover’s distance (see text). The panel to the side and the top display the marginal histograms. The outliers at the LOD in those panels have the same value for both models

Full size image

To the side and the top of Fig. 10 are marginal histograms of the distributions. Note that the bins of the histogram follow the same logarithmic scale as the scatter plot. These distributions do not correspond to any theoretical expectation, since they are mostly governed by the choice of measurement locations during the BUBBLE campaign. Both models (right panel in Fig. 10) fail to reproduce the local peak in the observations (top panel in Fig. 10) at \(3 \times 10^{-2}\) mg m\(^{-3}\). At a large number of sites, where this most frequently observed concentration is measured, both models return a value below the LOD (note the roughly doubled number of LODs in the simulations, as compared to the observations). To quantify the difference between the two simulated distributions and the measured distribution, we use the earth mover’s distance (EMD, calculated after Pele and Werman 2008, 2009). It is a measure for the distance between two distributions. A larger value indicates that the difference between two distributions is larger. When we calculate the EMD for each model’s distribution compared to the measured distribution, the ULM has a slightly lower value, indicating a slightly better performance.

6.4 Statistical Comparison with Field Measurements

Measured and simulated data points are co-located in space and time, even if co-location in time might be debatable since the LPDM assumes stationarity. We use the Relative Difference (RD), the Fractional Bias (FB), the Normalized Mean Square Error (NMSE), the correlation coefficient (CORR), the Factor of 2 (F2), the Factor of 5 (F5), the Bounded Normalized Mean Square Error (BNMSE), and the Threshold-Based Normalized Absolute Difference (TBNAD), all of which are detailed in the Appendix 3, Eqs. 28–34. We use a bootstrapping procedure to judge significance of these statistical measures, also detailed in Appendix 3.

Table 4 Statistical comparison of two model versions with BUBBLE measurements
Full size table

Table 4 shows the error statistics for the simulation of the BUBBLE tracer experiments with the two model versions. The ULM shows better values for all measures and roughly half the improvements are statistically significant (98% level). The RSM overpredicts the concentrations (negative FB). Since the ULM delivers slightly lower concentration than the RSM, this improves the statistical agreement due to reduced overprediction. The NMSE, CORR, F2, F5, and BNMSE indicate that the scatter of the simulations is also slightly reduced by the ULM. Even though these comparisons are based on only few experimental data, they show explicitly including the UCL did not substantially change, but slightly improve the model performance. Larger impact of including the UCL can be expected for street level or within-canopy measurements or sources. Corresponding tracer experiments can of course only adequately be simulated with the present ULM version and a proper validation for such cases will be left for a future study.

7 Conclusion and Outlook

An existing Lagrangian particle dispersion model (called RSM) with parametrized flow and turbulence characteristics for the urban roughness sublayer (RSL), and model domain starting at the zero-plane displacement, was extended down into the urban canopy layer (UCL). The model with the UCL included is called ULM. For this, spatially averaged profiles of flow and turbulence were collected from the literature, mostly from wind-tunnel and numerical studies, but also including a few full-scale experiments. The profiles show considerable spread, but nevertheless parametrizations for the mean wind speed \(\overline{u}\); Reynold’s stress \(\overline{u'w'}\); dissipation rate of turbulence kinetic energy \(\varepsilon \); skewness of the vertical wind component \(\mathrm {Sk}_w\); velocity variances \(\overline{u'^2}\), \(\overline{v'^2}\), and \(\overline{w'^2}\); and a model-specific transition function f are proposed. These parametrizations are continuous to the parametrizations in the RSL aloft and are intrinsic in nature, i.e., only averaged over the fluid volume—excluding the buildings. For this reason a reflection of probability \(\lambda _p\) is introduced at the mean building height. The parametrizations are horizontally homogeneous and independent of wind direction.

The ULM still fulfills the well-mixed criterion, with the peculiarity in the UCL that the normalized particle concentration assumes the value of \(1-\lambda _p\) instead of 1, which is due to the particle reflection mentioned before.

A sensitivity analysis using the Morris method shows that the parameters describing the UCL turbulence have a smaller impact on the concentration distribution and plume characteristics than have those parameters which characterize the RSL turbulence profiles. This reduces the uncertainty introduced through the relatively large spread of the parametrized UCL turbulence profiles.

A comparison of the ULM and the RSM shows slight changes in the model output, but generally the same dispersion behaviour. The longitudinal dispersion is somewhat diminished by the inclusion of the UCL parametrizations. An immediate corollary of this finding is the result that the concentration profiles in the UCL appear to be non-constant with height. This means that assuming uniformly height-distributed concentrations below the zero-plane displacement is questionable.

The RSM and the ULM both fulfill the acceptance criteria after Hanna and Chang (2012). When tested against concentration measurements of the BUBBLE dataset, the ULM shows slightly improved concentration predictions compared to the RSM. Some of the improvements in the error measures are statistically significant, but the overall differences are relatively small.

In summary, the analysis has demonstrated that spatially-averaged canopy turbulence can be introduced into an LPDM without violating the well-mixed condition. Due to the fact that the spatial variability of turbulence characteristics is considerable and hence spatial averages bear a huge uncertainty range, application of the model for near-surface sources to determine near-surface (pedestrian level) concentrations will result in correspondingly uncertain point predictions. Comparison to data from an above-canopy urban tracer experiment, conversely, shows that modelled concentrations are not strongly affected (even slightly improved) when allowing for the UCL to be explicitly included in the model domain. This to some degree reflects the results from the Morris sensitivity analysis, which has demonstrated that the uncertainty of the concentration estimates are to a lesser degree affected by the canopy turbulence parameters than those describing the bulk urban fabric. Thus, the ULM is likely more suitable for modeling dispersion from average street level sources than the RSM.

Furthermore, extending the model domain down to the physical surface will make it feasible to use the dispersion model as a core for a footprint model. Footprints are often required for pedestrian or surface level and hence sensitive to near-surface turbulence. This makes a dispersion model with explicit treatment of UCL turbulence particularly suited for this purpose. However, they are not easily validated directly, so the present results add support to the validity of using the ULM for future footprint modeling applications over urban areas.

Source code of the LPDM, scripts used to normalize, scale and fit the UCL parametrizations, as well as scripts used to analyze the model output are available (Stöckl 2021). The datasets used to drive the LPDM model are available (Stöckl 2021). The UCL profile datasets taken from other studies are available from the corresponding author on reasonable request.