Abstract
In this study, we have compared time series of pollen concentration originating from two Hirst-type volumetric samplers that were equipped with different sampling heads. To collect airborne pollen, we have used classic sampler with mobile sampling head including wind vane and adapted sampler with fixed sampling head having two-layered inlet, like in Sigma-2 passive sampler. The devices were placed at the roof level, on the top of the building of the Faculty of Sciences located in Novi Sad, Serbia. The sampling of airborne pollen was performed from February until October 2019. Along with the pollen data, meteorological conditions were recorded with an automated weather station measuring solar radiation, air temperature, relative humidity, wind speed and precipitation. Time series of daily pollen concentrations expressed high correlations, although there were large differences on the hourly basis. Absolute difference between hourly values showed very weak correlation with relevant meteorological parameters: temperature, humidity, precipitation, wind speed and turbulent kinetic energy, leading to the conclusion that sampling with both heads was not affected by meteorological conditions. Counting the pollen grains from the whole sample and not just from 10% of the area, which is the minimum requirement, was done for the six days in the season and proved that error introduced by subsampling during analysis was the main reason for differences in time series. To conclude, replacing mobile sampling head with fixed sampling head having two-layered inlet does not notably affect the quantity of pollen recorded by the Hirst-type volumetric method.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Quantification of airborne pollen over time is commonly used as a proxy for regional scale phenology monitoring of anemophilous plants but also in allergological studies (Scheifinger et al. 2013). Hirst-type volumetric method (Hirst 1952) is the most widespread method for continuous quantification of airborne pollen (Skjøth et al. 2013), and its proper application for recording and measuring environmental phenomena requires understanding common sources of variability. The effect of subsampling during the sample analysis has been investigated by several studies (Comtois et al. 1999; Šikoparija et al. 2011; Galan et al. 2014) and introduced into the European Standard (EN16868 2019) which allows coefficient of variation to be as much as 10–30% between repeated sample analyses, depending on accepted true value of pollen grains.
Since the introduction of the European Standard (EN16868 2019) volumetric Hirst method is an inevitable method of choice for validating performance of the other methods developed for quantifying airborne pollen. European Standard addressed instrumental variation such as flow variability (Oteros et al. 2017) and adhesive medium type (Comtois and Mandrioli 1997), physical variation (due to physical influences, caused by spatial variation in pollen occurrence and dispersion by the air) and human error (inter- and intra-observer variation during identification and counting) as the major cause of data uncertainty (EN16868 2019). A recent study showed that comparing signals from two Hirst-type samplers situated in close vicinity can differ notably (Rojo et al. 2019), so it is expected that comparison of the devices with the different design would be even more unreliable.
In order to provide representative sampling in a dynamic environment, Hirst-type volumetric pollen and spore trap orients the sampling orifice toward wind direction with the aid of wind vane (Hirst 1952). This approach enables the most representative sampling of coarse particles (i.e., > 10 µm). It was shown that using simple static two-layered inlet could aid passive sampling of airborne pollen, like in Sigma-2 passive sampler. This inlet reduces the velocity of the air entering the sampling orifice and allows sampled particles to settle due to gravimetric forces (VDI21192013). The design of two-layered inlet facilitates efficient sampling regardless of the wind speed and direction; thus, it is considered as suitable in low air flow samplers for the efficient sampling of coarse particles (Kohler et al. 2007), while avoiding mobile components such as wind vane (Miki et al. 2019). Although only passive Sigma-2 sampler is compared to Hirst-type volumetric sampler (Fernández-Sevilla 2006), passive sampling heads are used in all operational automatic pollen monitors. While BAA500, manufactured by Helmut Hund GmbH, uses inlet of its own design (Oteros et al. 2015), POLENO (Sauvageat et al. 2019), manufactured by Swisens, and RAPID-E (Shauliene et al. 2019), manufactured by Plair SA, use two-layered sampling inlet, like in Sigma-2 passive sampler. The automatic system with two-layered inlet performed well when compared to reference manual measurements (with Hirst-type volumetric sampler). It even showed better results for the days with low pollen concentrations, when average value is less than 100 pollen grains per cubic meter (pollen m−3). However, the authors did not consider the contribution of different inlets but attributed the performance only to the higher sampling rate (Chappuis et al. 2020).
The aim of this study was to explore the effect that fixed sampling head with two-layered inlet has on the quantity of airborne pollen measured by Hirst-type volumetric method. It is expected that the results would have implications on validation of the novel devices which are designed for automatic sampling of airborne pollen. Also, better understanding of the variances in pollen data can help their interpretation in allergological, phenological and modeling studies.
2 Materials and methods
2.1 Airborne pollen samples
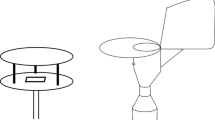
Sampling of airborne pollen was performed at the roof level in Novi Sad, Serbia (45.245575°N, 19.853453°E) during one full pollen season from February 17 to October 16, 2019. Airborne pollen samples were collected using two Lanzoni VPPS samplers situated at 1 m distance one from the other (Fig. 1a). Both samplers were of the Hirst design (Hirst 1952) constructed to continuously sample 10 l min−1 of air. The particles suspended in the atmosphere impact onto the sticky tape that rotates at 2 mm per hour behind the 2 mm × 14 mm orifice allowing for one-hour temporal resolution of the collected sample. The samplers differed by the sampling head (Fig. 1b, c). One sampler had commonly used mobile sampling head that orients sampling orifice toward wind direction with wind vane (EN16868 2019). The other had fixed sampling head, and above its sampling orifice was an upward oriented two-layered inlet (protective hood with a diameter of 155 mm overlapping a cylinder with a diameter of 100 mm, each with four 37 mm × 70 mm offset openings), used in Sigma-2 passive sampler (VDI2119 2013).
All aspects of the uncertainty addressed in Chapter 7 of the European Standard (EN16868 2019) are taken into consideration. Closeness of the instruments makes the effects of spatial representativity equal, so variations due to physical influences, caused by spatial variation in pollen occurrence and dispersion by air, were negligible. For both instruments, the same standard operating procedures were applied (i.e., the flow checked with the same flow meter, the same type of adhesive used, samples prepared by the same technician on the same day) to ensure device-related variations caused by the technical features of the pollen trap, capture film, adhesive and specimen preparation were within the standard requirements, thus also negligible for comparison.
2.2 Sample analysis
The samples were prepared and analyzed according to the European Standard. After removal from the sampler, the sticky tape containing particles was divided into segments, corresponding to the 24-h periods, that were mounted between a glass slide and coverslip using a mixture of gelatin, glycerin, phenol, distilled water and basic fuchsin. Pollen grains were identified and counted along three longitudinal transects using an Olympus BX-51 light microscope at X 400 magnification with a field of view of 0.55 mm which corresponds to 11.57% of the daily sample. The transects were positioned at 3 mm distance in the central part of the slide starting at 5 mm from the edge of tape. Cumulative pollen counts were recorded every 2 mm to give hourly values that were converted into pollen concentration expressed as pollen m−3 (Šikoparija et al. 2011). Uncertainty from the personal skill of correct identification could be neglected since the total pollen count was analyzed and the same individual counted samples.
The subsampling routine was explored in more details. Variation in hourly pollen concentrations, obtained from the different location of the subsample across the microscopic slide, was analyzed. The “true value” was identified by counting total pollen at X 200 magnification from the entire slide surface, for six daily samples, considering both low and high pollen concentrations. The samples for 7/23/2019 and 7/26/2019 were counted three times to estimate the uncertainty under repeatability conditions, as requested by the European Standard. Total pollen count for each of 13 longitudinal transects was recorded separately, allowing to explore how different locations of the subsample, i.e., selection of two longitudinal transects (covering 15.43% of the surface), influence the variations from the “true value.”
2.3 Meteorology
Meteorological conditions were recorded with an automated weather station measuring solar radiation, air temperature, relative humidity, wind speed and precipitation, placed next to the traps. Components of the wind speed u, v and w (in x, y and z direction, respectively) were measured using 3D sonic anemometer, and mean wind speed was obtained using simple formula (Eq. 1):
Following Stull (1988), we have calculated turbulent kinetic energy (TKE) per unit mass as the sum of variances of all three wind components (Eq. 2):
Meteorological data were used with temporal resolution of one hour. Data analysis was performed in Python, with open-source libraries (JetBrains 2019). Spearman’s rank correlation coefficient was used as a measure of statistical dependence between absolute difference of pollen concentrations and meteorological parameters (Spearman 1904). Differences between pollen time series were measured with root-mean-square error (RMSE).
3 Results
Time series of daily pollen concentrations expressed similarities by visual inspection (Fig. 2a) and strong correlations with correlation coefficient 0.87 (p-value = 4.36E-73), while RMSE was 162.4 pollen m−3. However, the ratio between daily pollen concentrations (mobile relative to fixed head) varied a lot, with the values up to seven, which was achieved on one particular day in March. High pollen ratio, with the values ranging within interval from three to five, was noticed in many days during the period from July to September, overlapping with the Ambrosia and Urticaceae season (Fig. 2b).
After inspecting hourly data larger differences occurred, especially in the period from July to September (Fig. 3), with correlation coefficient 0.73 (p-value = 0.0) between two time series while RMSE almost doubled, resulting in 317.1 pollen m−3. Due to higher values of hourly pollen concentrations when compared to daily averages, and along with higher measurement uncertainty related to time discrimination (EN16868 2019), higher value of RMSE was expected.
Further on, we continued the analysis focussing on hourly data. In order to examine the influence of environmental conditions on the sampling heads, we calculated statistical dependence between absolute difference of airborne pollen concentrations and meteorological parameters. We divided the entire pollen season into the following parts: the first—from February 17th to May 5th (overlapping with tree pollen season), the second—from May 6th to July 15th (overlapping with grass pollen season) and the third—from July 16th to October 16th (overlapping with weed pollen season). Absolute difference between hourly values showed very weak correlation with relevant meteorological parameters: temperature, humidity, precipitation, wind speed and turbulent kinetic energy (Table 1), leading to the conclusion that sampling with both heads was not affected by meteorological conditions, i.e., there was no prevailing effect of any parameters, including wind speed and TKE, on the pollen sampling. Statistical calculations for different pollen types are presented in Table S1 in the Supplementary Material.
Visual inspection of the scatter plot between the absolute difference of the pollen concentrations between the two traps and wind speed showed nearly symmetrical distribution around zero (Fig. 4a) meaning that the same value of the wind speed could cause both highly positive and highly negative difference. Similar trend can be seen in the scatter plot between the absolute difference of pollen concentrations and TKE (Fig. 4b).
After we excluded instrumental variation and physical variation, as the possible causes of the differences in the pollen concentration time series, human error was the only factor left over, including the uncertainty from the counting error and counting routine (EN16868 2019). Since the number of counted particles depends on the counting area, a minimum surface of 10% for pollen analysis is required (Galan et al. 2014), which aims to minimize the counting error. Thus, we wanted to investigate counting routine in more detail. We selected six days from the whole season, three days (March 1st, March 8th and August 28th) with high pollen concentrations where the peak of hourly values was greater than 1000 pollen m−3 and three days (March 2nd, July 23rd and July 26th) with low pollen concentrations. For these days, pollen was counted from the total surface area, and the concentrations were compared to the values obtained from the surface of 11.57% (Fig. 5). The alignment between the values originating from two sampling heads is clearly evident after 100% of the surface was analyzed, leading to the conclusion that the main source of differences between two time series lies in the rough estimation of the pollen concentrations following minimum requirements from the European Standard. This can be clearly seen in Fig. 5 for the following two days, August 28th and July 26th. Timestamps on the X-axis are presenting UTC. The uncertainty of analysis determined under the conditions of repeatability is presented with the coefficient of variation that ranged from 0.7% to 9.3%, depending on the quantity of pollen recorded in the samples (Figure S1 in Supplementary Material).
Pollen concentrations obtained after 11.57% of the analyzed surface (a) and 100% of the analyzed surface (c) for the days with high concentration of pollen grains, and after 11.57% of the analyzed surface (b) and 100% of the analyzed surface (d) for the days with low concentration of the pollen grains
During the detailed pollen counting for the six selected days, total surface area was divided into 13 longitudinal transects, with two transects covering surface of 15.43%, satisfying the minimum requirements. For the measurements originating from the mobile head, which is commonly used for the operational purposes, we performed additional analysis and compared the concentrations estimated from all the combinations of the two transects to the concentration from the total surface (the “true value”). Relative error varied between 22.5% and 53.8% with an average value 29.9%.
Distribution of the grains over the width of the tape was not the same between different devices (Fig. 6). Although a similar pattern with the most pollen recorded in the central part of the tape can be seen, there is notably larger variability between different transects in samples collected by the device with fixed head. More variability in distribution of the particles across the width of the impaction surface raises the uncertainty from the selection of transects in counting routine.
4 Discussion
Determination of the PM10 mass concentrations in the ambient air is done by sampling the particulate matter on filters and weighing them by means of a balance, that is known as the gravimetric method (EN123412014). Real-time monitoring of PM10 concentrations can be achieved by using the optical instruments, which should be periodically calibrated with the data from gravimetric instrumentation. In both methods, there is no need for manual counting of the particles; thus, the human error is excluded. On the other hand, pollen grains have diameter greater than 10 µm and different aerodynamical properties, which makes the sampling process more complex. Also, identification and counting by the individual introduces additional measurement uncertainty for the pollen data.
Sampling efficiency is influenced by the changes in pollen diameter. It varies for the larger spores and pollen grains, and it can exceed 100%, particularly with heavy particles and at higher wind speeds (EN16868 2019). In general, deviations can be expected in the usual range from 55 to 90%, although significant upward or downward excursions are possible in the individual cases (Hirst 1952). According to the European Standard, the measurement uncertainty under real-life conditions can only be given descriptively.
Some authors recently reported that the sampling efficiency of the two-layered sampling inlet was approximately three times higher than that of the wind vane inlet at a daily scale, when the relationship between the pollen concentrations was evaluated in one season (Miki et al. 2019). However, that cannot be seen in our case (Fig. 2a). We got good alignment between hourly values when the pollen was counted from the whole slide covering 100% of the surface, for the six selected days, as well (Fig. 5). Airborne pollen concentrations in their measurements were determined by a KH-3000–01 automatic pollen monitor produced by Yamatronics (Japan,) and Urticaceae was the dominant taxon during the sampling period, representing 68% of the total pollen, according to Hirst sampler which was used for data confirmation.
In our experiment, the uncertainty from the counting routine was the explanatory factor for the differences between time series from two sampling heads. When the full samples were analyzed for two selected days, the uncertainty in the repeatability conditions for daily concentrations was less than 0.15%. For hourly concentrations, the uncertainty was larger, confirming that counting the entire impaction surface introduces other sources of variation, even though it eliminates the error from spread of the particles (Addison-Smith et al. 2020). However, in our case, the uncertainty never exceeded 10%, regardless the quantity of recorded pollen, which is within the limits of the European Standard.
Observed distribution of the pollen grains across the width of the impaction surface corresponded to what is commonly seen in the case of Hirst-type trap. We observed both convex (Tormo Molina et al. 1996; Michel et al. 2012) and concave (Cotos-Yanez et al. 2013) distribution in the analyzed samples. The distribution of particles over the slide width is determined by the effect that construction of the device has on the air flow. It was shown that it can vary even for the same device (Kapyla and Penttinen 1981), presumably resulting from minor differences in positioning the sampling drum or quantity of adhesive.
Inhomogeneous spread of particles is expected to result in differences between transects chosen for the analysis, leading to the count error. The degree of overestimation or underestimation of extrapolated pollen counts will depend on the surface of the analyzed subsample and its location (Cariñanos et al. 2000; Michel et al. 2012). Comtois et al. (1999) argued that by chance alone, one could obtain a count that would differ by some 30%. This is in accordance with our findings when all the combinations of two longitudinal transects (covering 15.43%) were examined, with an average relative error 29.9%.”
5 Conclusion
In this work, we have compared time series of airborne pollen concentrations collected with Hirst-type volumetric samplers using mobile and fixed sampling head, during 2019 pollen season. Daily pollen concentrations expressed similarities and very strong correlations, although there were large differences on the hourly basis. Measurement uncertainty related to the calibration of the flow rate, capture film, adhesive and specimen preparation was negligible since the instruments were treated in the exact same way. Furthermore, physical variation was excluded due to equal spatial representativity and very weak correlations with meteorological conditions in different parts of the pollen season. Human error including counting routine related to the minimum requirements was the explanatory factor for the differences between time series from two sampling heads. Thus, introducing fixed sampling head with two-layered inlet does not notably affect the quantity of pollen recorded by the Hirst-type volumetric method. Since there is no strict recommendation in the literature on how to select exact transects when counting pollen grains, it is strongly recommended to analyze the entire sample if quantitative validation of different measurement devices is to be performed against Hirst-type trap.
References
Addison-Smith, B., Wraith, D., & Davies, J. M. (2020). Standardising pollen monitoring: quantifying confidence intervals for measurements of airborne pollen concentration. Aerobiologia, 36, 605–615. https://doi.org/10.1007/s10453-020-09656-6.
Cariñanos, P., Emberlin, J., Galán, C., & Domínguez-Vilches, E. (2000). Comparison of two pollen counting methods of slides from a Hirst type volumetric trap. Aerobiologia, 16, 339–346.
Chappuis, C., Tummon, F., Clot, B., Konzelmann, T., Calpini, B., & Crouzy, B. (2020). Automatic pollen monitoring: first insights from hourly data. Aerobiologia, 36, 159–170. https://doi.org/10.1007/s10453-019-09619-6.
Comtois, P., Alcazar, P., & Neron, D. (1999). Pollen counts statistics and its relevance to precision. Aerobiologia, 15, 19–28. https://doi.org/10.1023/A:1007501017470.
Comtois, P., & Mandrioli, P. (1997). Pollen capture media: A comparative study. Aerobiologia, 13, 149–154. https://doi.org/10.1007/BF02694501.
Cotos-Yanez, T. R., Rodrıguez-Rajo, F. J., Perez-Gonzalez, A., Aira, M. J., & Jato, V. (2013). Quality control in aerobiology: comparison different slide reading methods. Aerobiologia, 29, 1–11. https://doi.org/10.1007/s10453-012-9263-1.
EN12341 (2014). Ambient air-Standard gravimetric measurement method for the determination of the PM10 or PM2,5 mass concentration of suspended particulate matter. European Standards.
EN16868 (2019). Ambient air-Sampling and analysis of airborne pollen grains and fungal spores for networks related to allergy - Volumetric Hirst method. European Standards.
Fernández-Sevilla, D. (2006). Aerodynamic properties of pollen grains and sampling methods. PhD Thesis. Coventry University in collaboration with University of Worcester. https://www.researchgate.net/publication/324068002_AERODYNAMIC_PROPERTIES_OF_POLLEN_GRAINS_AND_SAMPLING_METHODS_Thesis_Chapter_Conclusions. Accessed 11 February 2020.
Galán, C., Smith, M., Thibaudon, M., Frenguelli, G., Oteros, J., Gehrig, R., et al. (2014). Pollen monitoring: Minimum requirements and reproducibility of analysis. Aerobiologia, 30, 385–395. https://doi.org/10.1007/s10453-014-9335-5.
Hirst, J. M. (1952). An automatic volumetric spore trap. Annals of Applied Biology, 39, 257–265. https://doi.org/10.1111/j.1744-7348.1952.tb00904.x.
JetBrains (2019). PyCharm. JetBrains. https://www.jetbrains.com/pycharm/. Accessed 23 December 2019
Kapyla, M., & Penttinen, A. (1981). An evaluation of the microscopical counting methods of the tape in Hirst-Burkard pollen and spore trap. Grana, 20(2), 131–141.
Kohler, F., Mölter, L., Schultz, E., Dietze, V., Schütz, S., & Helm, H. (2007). Passive Sampler Sigma-2 as an Inlet for an Optical Aerosol Spectrometer. European Aerosol Conference 2007, Salzburg, Austria, T02A036
Michel, D., Rotach, M. W., Gehrig, R., & Vogt, R. (2012). On the efficiency and correction of vertically oriented blunt bioaerosol samplers in moving air. International Journal of Biometeorology, 56, 1113–1121. https://doi.org/10.1007/s00484-012-0526-x.
Miki, K., Kawashima, S., Clot, B., & Nakamura, K. (2019). Comparative efficiency of airborne pollen concentration evaluation in two pollen sampler designs related to impaction and changes in internal wind speed. Atmospheric Environment, 203, 18–27.
Oteros, J., Buters, J., Laven, G., Röseler, S., Wachter, R., Schmidt-Weber, C., & Hofmann, F. (2017). Errors in determining the flow rate of Hirst-type pollen traps. Aerobiologia, 33, 201–210. https://doi.org/10.1007/s10453-016-9467-x.
Oteros, J., Pusch, G., Weichenmeier, I., Heimann, U., Möller, R., Röseler, S., et al. (2015). Automatic and online pollen monitoring. International Archives of Allergy and Immunology, 167(3), 158–166. https://doi.org/10.1159/00046968.
Rojo, J., Oteros, J., Pérez-Badia, R., Cervigón, P., Ferencova, Z., Gutiérrez-Bustillo, M., et al. (2019). Near-ground effect of height on pollen exposure. Environmental Research, 74, 160–169. https://doi.org/10.1016/j.envres.2019.04.027.
Scheifinger, H., Belmonte, J., Celenk, S., Damialis, A., Dechamp, C., Garcia-Mozo, H., et al. (2013). Monitoring, modelling and forecasting of the pollen season. In M. Sofiev & C.-K. Bergman (Eds.), Allergenic Pollen: A Review of the Production, Release, Distribution and Health Impacts (pp. 71–126). Netherland: Springer-Verlag.
Šikoparija, B., Pejak-Šikoparija, T., Radšić, P., Smith, M., & Galan-Soldevilla, C. (2011). The effect of changes to the method of estimating the pollen count from aerobiological samples. Journal of Environmental Monitoring, 13, 384–390. https://doi.org/10.1039/c0em00335b.
Skjøth, C.A., Šikoparija, B., Jaeger, S., & EAN-network (2013). Pollen Sources. In: M. Sofiev and C-K. Bergman (Eds.), Allergenic Pollen: A Review of the Production, Release, Distribution and Health Impacts (pp. 9-28). Netherlands: Springer-Verlag.
Spearman, C. (1904). The proof and measurement of association between two things. American Journal of Psychology, 15, 72–101. https://doi.org/10.2307/141215.
Stull, R. B. (1988). An introduction to boundary layer meteorology. Netherlands: Springer.
Tormo Molina, R., Rodrıguez, A. M., & Palacios, I. S. (1996). Sampling in aerobiology. Differences between traverses along the length of the slide in Hirst sporetraps. Aerobiologia, 12, 161–166.
VDI2119 (2013). Ambient air measurements. Sampling of atmospheric particles > 2,5 μm on an acceptor surface using the Sigma-2 passive sampler. Characterisation by optical microscopy and calculation of number settling rate and mass concentration. Verein Deutsher Ingenieure (VDI). Kommission Reinhaltung der Luft (KRdL) im VDI and DIN. https://www.vdi.de/fileadmin/pages/vdi_de/redakteure/richtlinien/inhaltsverzeichnisse/1935955.pdf Accessed 31 January 2020.
Acknowledgements
This research was funded by the BREATHE project from the Science Fund of the Republic of Serbia PROMIS program, under grant agreement no. 6039613 and partial financial support was received from the Ministry of Education, Science and Technological Development of the Republic of Serbia grant agreement no. 451-03-68/2020-14/200358. Measurement campaign in Novi Sad was supported by RealForAll project (2017HR-RS151) co-financed by the Interreg IPA Cross-border Cooperation program Croatia – Serbia 2014-2020 and Provincial secretariat for Science, Autonomous Province Vojvodina, Republic of Serbia (contract no. 102-401-337/2017-02-4-35-8). The results presented here relate to COST Action CA18226 “New approaches in detection of pathogens and aeroallergens” (ADOPT), www.cost.eu/actions/CA18226.
Funding
This research was funded by the BREATHE project from the Science Fund of the Republic of Serbia PROMIS program, under grant agreement no. 6039613.
Author information
Authors and Affiliations
Contributions
Branko Šikoparija was involved in conceptualization, data curation and writing—review and editing; Gordan Mimić and Branko Šikoparija helped in formal analysis and investigation; Gordan Mimić contribuited to writing—original draft preparation..
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that there is no conflict of interest/competing interests.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mimić, G., Šikoparija, B. Analysis of airborne pollen time series originating from Hirst-type volumetric samplers—comparison between mobile sampling head oriented toward wind direction and fixed sampling head with two-layered inlet. Aerobiologia 37, 321–331 (2021). https://doi.org/10.1007/s10453-021-09695-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10453-021-09695-7