Abstract
Landslides falling into water can trigger tsunamis, which are particularly destructive in the proximity of the landslide impact and in narrow water bodies. The energy transfer mechanism between landslide and water wave is complex, but its understanding is of fundamental importance for the numerical modeling which aims to predict the induced wave hazard. In order to study the involved physical processes, we set up an experimental facility consisting of a landslide generator releasing gravel at high speed in a wave basin. With the aim of estimating the landslide–wave energy transfer, we implemented a simplified 1D conceptual model of landslide motion, including the 3D landslide deformations. We optimized the model with the experimental results. The model results explain that the deformable landslide has an average drag coefficient of 1.26 and a relatively inefficient energy transfer from landslide to wave. Of the landslide energy at impact, the 52% is dissipated by Coulomb basal friction between the slide and the water basin bottom, 42% is dissipated by other processes, including turbulence, and only the remaining 6% is transferred to the wave thus formed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Landslides plunging into water bodies such as lakes, reservoirs, rivers, fjords, bays, or oceans can produce tsunamis that are responsible for extremely high run-up on the shorelines in the proximity of the impact. Run-up of several hundred meters has been observed for the events, e.g., of Lituya Bay, Alaska, in 1958 (Miller 1960), and of the Vajont Reservoir, Italy, in 1963 (Semenza and Ghirotti 2000). Nevertheless, the so-called landslide tsunamis can travel for tens of kilometers with sufficient energy to kill population and destroy human settlements and infrastructures far away from the originating point as for the cases of Unzen Volcano, Japan, in 1792 (Miyamoto 2010), and the Karrat Fjord (Gauthier et al. 2018).
Laboratory experiments have been widely used in order to directly obtain non-linear multi-regression empirical formulas of the wave geometry as function of the landslide governing parameters such as landslide velocity, thickness, width, length, mass, density, and granulometry (Kamphuis and Bowering 1970; Huber 1980; Fritz 2002; Fritz et al. 2004; Panizzo et al. 2005; Ataie-Ashtiani and Nik-Khah 2008; Di Risio et al. 2009; Heller and Hager 2010; Mohammed and Fritz 2012; Bregoli et al. 2017; Miller et al. 2017; McFall et al. 2018; Xue et al. 2018; Evers et al. 2019; de Lange et al. 2020). Physical experiments are important to understand the phenomenon. But, even neglecting scale effects, since terrain morphology and bathymetry of real cases are very complex with respect to the synthetic experimental approaches, empirical formula applications are limited to a preliminary wave height assessment.
In order to reproduce or predict the wave formation, propagation, and run-up over complex terrain morphology, several authors attempted to simulate landslide tsunami with numerical models. Generally speaking, the numerical approaches are divided in two steps: (1) the landslide motion; and (2) the wave propagation. The landslide motion is often simulated by means of finite element methods or finite volume methods, while the far field wave propagation is simulated by means of depth averaged Navier-Stokes or Boussinesq equations. The coupling of the two steps is done implementing empirical laws (Waythomas et al. 2006; Abadie et al. 2010) or, more often, employing energy (or momentum) transfer after landslide friction dissipations, deformation by means of different rheology models, and hydrodynamic drag force (e.g.: Quecedo et al. 2004; Mazzanti and Bozzano 2009; Pastor et al. 2009; Xiao et al. 2015). Some of the alternative approaches tackle the problem applying, e.g., smoothed particle hydrodynamics (SPH) method (Capone et al. 2010; Vacondio et al. 2013) and computational fluid dynamics–discrete element method (Zhao et al. 2016). Recently, multi-phase approaches based on analytical methods (e.g.: Pudasaini 2014; Pudasaini and Mergili 2019) and volume of fluid method (e.g.: Si et al. 2018; Yu and Lee 2019) have been developed for landslide tsunamis.
The complexity of phenomenon makes it very difficult to correctly reproduce the energy, and thus the momentum, transfer from landslide to wave. This may have effect close to the landslide impact, where the involvement of solid, liquid, and gaseous phases and the strong non-linear water wave processes are in effect. In the case of subaerial landslides generating tsunamis, basal friction and turbulence are recognized as the main factors of energy loss (Walder et al. 2003). Regarding the experimental investigation of the momentum transfer between landslide and water body, Watts (1998) and Walder et al. (2003) used respectively an underwater and a subaerial slide made by a rigid squared block; Grilli and Watts (2005) and Enet and Grilli (2007) used an underwater slide made by a rigid ellipsoid; and Di Risio et al. (2009) used a subaerial slide made by a rigid ellipsoid. Recently, few authors, e.g., Mulligan and Take (2017), although in 2D experiments, have investigated the mechanisms involved in the momentum transfer from granular deformable landslides to water waves.
Despite the fairly wide number of experimental and numerical researches, in a recent literature review, Yavari-Ramshe and Ataie-Ashtiani (2016) stated that the quantity of energy conveyed from the slide to the water motion in landslide tsunami process is not yet clarified. In their numerical study, Yavari-Ramshe and Ataie-Ashtiani (2019) narrowed the range of energy transfer from 1–85.7% of the previous authors (under a wide variety of tsunami generator configurations) to 5–15% for subaerial landslide initiation. In a similar configuration, Clous and Abadie (2019) numerically found that only 4% of the landslide energy is transferred to waves. Although these are notable advancements, to our knowledge, there are no studies in this field that comprehensively determine the landslide energy transfer to waves and energy losses by dissipative processes. Generally, we found a lack of research on energy conversion in 3D experiments, where 3D deformations of granular material are an important process. Therefore, this work has been envisaged to provide new evidences to unveil the breakdown of energy convey from landslide to waves.
Methods
This work is based on the results presented in Bregoli et al. (2017) where predictive empirical formulas relating landslide and wave parameters and their practical application were defined based on experimental data. Here, we use a subset of the experimental measurements of the mentioned work to set up a numerical method which explains the energy transfer from landslide to water body.
The experimental setup
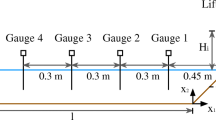
In order to experimentally reproduce landslide tsunamis at laboratory scale, an existing experimental setup was adapted to host a landslide generator, a wave tank, and an adequate measuring system (Fig. 1). The setup is placed in the Fluvial Morphodynamics Laboratory of the Department of Hydraulic, Marine and Environmental Engineering of the Universitat Politècnica de Catalunya, Barcelona, Spain. Special rails were fixed along a variable slope flume which ends on a rectangular wave tank. A metallic wheeled box accelerates along the rails gaining a speed up to 7 ms−1. The box is filled with white gravel. Once the box reaches the wave tank, a breaking system suddenly stops the box and a front gate immediately opens and releases the gravel into the wave tank. The loose gravel plunges into the water and generates waves that propagate toward the wave tank (Fig. 1a). The granular mass slides along the connecting wedge and the tank bottom, and interacts with the water mass, thus continuously deforming and decelerating till it stops and deposits at the tank bottom (Fig. 1b and c). The wedge has the same roughness of the tank bottom.
The experimental setup as in Bregoli et al. (2017): (a) sketch of the setup with measuring devices; aerial view (b) and lateral view (c) of the wave tank and initial and final position and size of the landslide. The red thick line is the landslide runout distance along the motion path x~ from the position at impact x~0 to the final position x~stop
Thanks to an image-based measuring system (Bregoli et al. 2020), the landslide geometry and velocity was measured immediately before the impact with water. The measuring system consists in a laser sheet that projects a line on the landslide surface. A high-speed camera focuses on the tank entrance and records the sliding mass at 500 frames per second (Fig. 1a). Employing a rigorous calibration technique along the plane of the laser sheet, the images are corrected from perspective and lens distortions and eventually ortho-rectified to a Cartesian spatial reference in which the necessary measurements of the sliding mass are performed for each time step (frame). The waves were measured with the same image-based system: the green laser sheet continues along the wave tank in the axial landslide direction (Fig. 1a) and it is reflected on the water surface due to kaolin which is added to the water. It is assumed that the small amount of kaolin does not alter the water physical properties. To account for the lateral wave expansion, red laser sheets were projected perpendicularly to the landslide axial direction (Bregoli et al. 2017). The reflected laser lines were recorded with an array of high definition cameras.
The final deposits of the landslides were measured in order to account for the granular material deformations. The observed final deposit shape was elliptical and it was synthetically measured in its major axis ad and minor axis bd. The final deposit’s basal center of mass position x~stop, which consists in the landslide’s runout distance from its basal center of mass position at impact x~0 along the landslide motion path x~, was also measured (Fig. 1b and c). Some contours obtained from rescaled orthogonal photos are reported in Figure S1 of Supplementary Material.
Dataset
From the total 41 experimental runs of Bregoli et al. (2017), 23 runs were selected and used in this study. The remaining 18 runs were not used because they lack the measurement of the final deposit geometry which is a necessary feature for accounting the energy transfer from landslide to water waves. The 23 runs, including their main parameters, are shown in Table 1. For each run, the measured parameters at impact are as follows: the landslide mass ms; the landslide impact angle α; the landslide height at impact hs,0; the landslide length ls,0; the Froude number Fr0 = vs,0(ghw)−1/2, being vs,0 the landslide velocity at impact; the total landslide energy at impact Es; the deposit major axis ad and minor axis bd; the landslide runout distance x~stop; the still water depth in the wave tank hw; and the wave energy Ew.
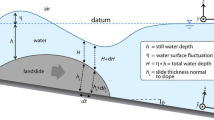
The total landslide energy at impact Es was calculated as the sum of kinetic (Es,kin,0) and potential (Es,pot,0) energy as follows:
where m′s is the submerged landslide mass and zs, 0 = hw + (ls,0/2) ⋅ sin (α) is the height, referred to the bottom of the tank, of the centroid of the landslide at impact with water (see Fig. 2).
The submerged landslide mass is calculated as \( {m}_{\mathrm{s}}^{\prime }={m}_{\mathrm{s}}{\rho}_{\mathrm{s}, bulk, sat}^{\prime }/{\rho}_{\mathrm{s}, bulk} \) where ρs,bulk = 1692 kg m−3 and ρ′s,bulk,sat = 1092 kg m−3 are respectively the landslide bulk density and submerged saturated bulk density measured in laboratory for the used gravel. The total wave energy Ew has been measured as the wave potential energy at the initial condition of wave motion, as it is described in Bregoli et al. (2017).
The dataset is divided in subset 1 and subset 2. In subset 1, the wave energy was not measured, while in subset 2 it was. In Table 1, runs that were targeted for model optimization, validation, or reapplication are specified. For experiments at low angle of impact α, it was not technically possible to adjust the connecting wedge to the tank bottom. Table 1 shows runs configuration with or without connecting wedge.
The numerical model
We introduce a simplified 1D forward Euler model for landslide motion, including 3D landslide deformations. It consists in a data-driven, physics-based model (e.g.: Greve et al. 2019) which is calibrated with our experimental data. The model evaluates energy losses and energy transfer between landslide and water body during the landslide motion along a fixed bed. Five important behaviors influencing the energy conversion are recognized in a landslide generated wave event:
-
Basal friction of landslide in its subaerial and underwater motion
-
Landslide deformation due to interaction with bedrock and water body
-
Energy dissipation due to turbulence at landslide-water boundary
-
Water surface tension breaking due to splash effects
-
Air entrainment and detrainment at impact in both landslide granular bulk and in water, where energy can be lost due to air compressibility
The model explicitly takes into account basal friction and landslide deformation while it implicitly addresses turbulence, water surface tension breaking, and air compressibility. In other words, turbulence, water surface tension breaking, and compressibility energy losses are grouped together as generic dissipative energies which we name Et. The explicit evaluation of those processes would require further investigation which we could not address in our experimental setup.
The coordinate x~ defines the position of the landslide basal center of mass along the propagation path from the impact with water body x~0 and the stop x~stop which corresponds to the center of the final elliptical deposit (Figs. 1b, c and 3a). During the propagation, the initial total landslide energy at impact Es is partly dissipated by means of basal Coulomb friction. The residual energy is transferred to the water by momentum due to the drag force which acts on the water mass (Fig. 3a).
Following the previous considerations, the energy balance of the landslide tsunami process may be described by the following equation:
where Ef is the energy loss due to friction between landslide and bottom and Ed is the drag energy transferred to the water body. At the end of the motion, the total drag energy Ed may be calculated as follows:
where Ew is the measured total wave energy and Et is the total energy of the other dissipative processes. The landslide energy at impact Es and the total wave energy Ew are measured in our experiments, while Ed is evaluated with the following methodology. Et is then calculated as the difference between Ed and Ew. This energy cascade is depicted in Fig. 3b, where ε are the energy exchange efficiencies.
The Coulomb shear stress in a given point is described by the following equation:
where φs-b is the internal friction angle between granular material and bottom and hs(x~) is the landslide thickness evolution along the propagation path. We evaluated φs-b through the optimization explained in the following section. It is important to notice that the granular bulk density dynamically changes and the bulk saturates during its penetration into the water. However, because we lack measurements of dynamic changes of density, we only consider the measured final fully saturated density ρ′s,bulk,sat. During penetration and sedimentation into the water basin, the landslide changes in shape, its thickness reduces while the basal area is increasing. Here, the evolution of landslide thickness is considered to be linear from the measured average thickness at the exit of the box hs,0 till the final average thickness of the deposit hd = 0.05 m.
The Coulomb force Fc can be calculated as:
where sbasal(x~) is the evolution of the basal area of the landslide along the propagation path, assumed to be linear, from the initial basal area at impact sbasal(x~0) = ws ls,0 to the elliptical area of final deposit \( {s}_{\boldsymbol{basal}}\left({\underset{\sim }{x}}_{\boldsymbol{stop}}\right)=\pi {a}_{\mathrm{d}}{b}_{\mathrm{d}}/4 \). The initial landslide width is equal to the sliding box width ws = 0.34 m. The dissipated energy by basal friction is calculated by integrating Eq. (5) along the runout distance:
The drag force can be evaluated as:
where Cd is the drag coefficient, \( {s}_{\boldsymbol{front}}\left(\underset{\sim }{x}\right) \) is the landslide frontal area linearly changing from sfront(x~0) = ws hs,0 to sfront(x~stop) = bdhd and \( {v}_{\mathrm{s}}\left(\underset{\sim }{x}\right) \) is the slide velocity. We evaluated Cd trough the optimization explained in the following section.
From Eq. (7), the energy of drag Ed can be calculated by integrating Fd along \( \underset{\sim }{x} \) as follows:
The landslide velocity vs(x~) is iteratively calculated step by step, considering the Coulomb and the drag resistive forces. Once vs = 0, the flow stops, giving the runout distance x~stop and the stopping time tstop.
The presence or absence of the wedge at the box exit has important effects. Because of the deformability of granular material, in presence of wedge, the transition between box and bottom of tank can be considered smooth enough to exclude additional losses in landslide energy. In absence of wedge, the transition is sharp and forces the landslide to jump. During the jump, the landslide loses contact with the bottom, and thus it is not subjected to basal friction but only to drag forces. The jump is thus simulated as a parabolic fall of a mass subjected to drag through the water. The mass has an initial angle given by the detachment slope α and a known detachment velocity which we decompose in horizontal and vertical directions. Once the landslide lands on the flat bottom of the tank, a certain amount of its momentum is lost through the sudden change of direction. We calculate the residual velocity after impact assuming that the landslide loses the vertical velocity component at impact with the tank bottom, thus preserving only the horizontal velocity component. The loss of the landslide vertical velocity component corresponds to an additional and instantaneous energy dissipation during the landslide motion. These processes can be appreciated in the results sections, where we show an example of model application in absence of wedge.
Parameter optimization
The available data of landslide tsunami events are usually scarce. Thus, it was decided to design a simplified model capable to work with as few data as possible. This methodology needs two parameters to be calibrated, in order to match the total distance x~stop of landslide mobility from initiation to deposition using a stopping method. The two designated parameters are the basal friction angle φs-b and the coefficient of drag Cd. The choice of φs-b and Cd affects (1) the runout distance (stopping method) and (2) the energy transferred to the water body (drag energy of landslide versus first crest wave energy). The basal friction angle affects the runout distance, while the energy transferred to the water body mainly depends on the drag coefficient.
To find the optimum φs-b and Cd, leading to the lowest sum of quadratic relative errors Δ between measured and estimated runout distance x~stop, a calibration set of 20 experiments is chosen. The remaining 3 experiments are included in the validation and reapplication sets (see Table 1).
The sum of quadratic relative errors Δ in the runout distance is defined as follows:
where i identifies the ith experiment. Δ is evaluated for different values of φs-b and Cd, showing the presence of a minimum (Fig. 4). The minimum was sought through the multi-parameter Nelder-Mead simplex direct search algorithm (Lagarias et al. 1998).
Results
The optimum values of basal friction and drag coefficient are respectively φs-b = 24.89° and Cd = 1.26. These values are used to re-calculate the runout distance with the model for the 23 runs of the validation set. The resulting validation is shown in Fig. 5a, where a correlation coefficient between measured data and estimated values of R2 = 0.661, a mean relative error of 2%, and a maximum relative error of 30% are found. The linear relation between the energy of landslide at impact Es and the generated energy of drag Ed gives a correlation coefficient R2 = 0.967 (Fig. 5b). Through this result, the efficiency of conversion between landslide energy and drag is obtained as εs ‐ d = Ed/Es = 0.479. Thus, about 48% of the landslide energy is converted into the equivalent energy of drag. A similar result is found for the relation between the energy of waves Ew and the energy of drag. The relation between Ew and Ed, having a correlation coefficient R2 = 0.936 (Fig. 5c), gives an efficiency of conversion εd ‐ w = Ew/Ed = 0.117. Therefore, about 12% of drag energy is converted into wave energy.
Model validation and results of energy transfer: (a) validation test on measured and estimated dimensionless runout distance; (b) dimensionless relationship between estimated drag energy Ed and measured total landslide energy Es with an average conversion ratio of Ed/Es = 0.48; (c) dimensionless relationship between estimated drag energy Ed and measured total wave energy Ew with an average conversion ratio of Ew/Ed = 0.12
Based on the energy breakdown of Fig. 3b and thanks to the present results, 48% of landslide energy is transferred to water as drag energy and 52% of landslide energy is lost by basal friction (Fig. 6a). The 12% of the drag energy is transferred to water waves, while the remaining 88% is lost by other dissipative processes (Fig. 6a). In other words, 52% of the total landslide’s energy at impact is dissipated by basal friction, 42% is lost by other dissipative processes, and only 6% is converted into the wave energy (Fig. 6b).
The present method can be considered satisfactory if it is capable of correctly predicting the runout distance. If this occurs, the model is able to describe the energy transmission in landslide tsunami generation. To test the method, we reapplied the model to the three selected experiments named 9, 19, and 23 (reapplication dataset in Table 1), which were not included in the optimization dataset. Experiment 9 has a wedge smooth transition between ramp and tank, while experiments 19 and 23 have an abrupt wedge-tank transition.
The model reapplication on experiment 9 is shown in Fig. 7. The landslide’s Froude number Fr is plotted along the landslide propagation distance in Fig. 7a. It can be observed that, after the release, the landslide experiences resistance to motion due to basal friction and drag. The velocity transition between ramp and tank bottom is relatively smooth. The landslide rapidly decreases its velocity on the flat bottom till it stops. The ratio between estimated and measured runout distance is \( {\underset{\sim }{x}}_{\mathrm{stop},\mathrm{estimated}}/{\underset{\sim }{x}}_{\mathrm{stop},\mathrm{measured}}=0.92 \). The evolution of energies along the runout is given in Fig. 7b. In this case, around 50% of energy is dissipated by friction and the other 50% is attributed to drag energy.
Detailed output of the model reapplication to the experiment 9 (see Table 1 for parameter values): (a) dimensionless landslide velocity, given as Froude landslide number Fr, along the runout distance; and (b) energy evolution along the runout distance
In case of abrupt transition between wedge and tank (Fig. 8a), the behavior increases in complexity. For experiment 19 in Fig. 8, sharp discontinuities can be recognized in landslide Fr evolution along the runout distance (Fig. 8b). The first discontinuity appears at the box exit, where the landslide detaches from the slope at \( \underset{\sim }{x}/{h}_{\mathrm{w}}\approx 2 \). After this point, the parabolic jump accelerates the mass, because the material is not subject to Coulomb friction and drag only partially opposes to the motion. At the landing point, around \( \underset{\sim }{x}/{h}_{\mathrm{w}}\approx 3.75 \), a certain amount of energy, is lost through impact. The velocity, as specified in methods, is assumed conserved only in the horizontal direction, while the velocity along the vertical direction is cancelled. Thus, Fr suddenly decreases. After this point, the effect of Coulomb friction appears again, while drag never ceased. The effects of wedge absence on energy evolution can be observed in Fig. 8c. The ratio between estimated and measured runout distance is \( {\underset{\sim }{x}}_{\mathrm{stop},\mathrm{estimated}}/{\underset{\sim }{x}}_{\mathrm{stop},\mathrm{measured}}=1.09 \).
Detailed output of the model application to the experiment 19 (see Table 1 for parameter values): (a) sketch of the setup without wedge; (b) dimensionless landslide velocity, given as Froude landslide number Fr, along the runout distance; and (c) energies evolution along the runout distance. Observe that the wedge absence adds a complexity to the model (parabolic jump and impact with tank bottom)
Similar results were obtained for the model reapplication to experiment 23 (see Supplementary Material Figure S3). The main difference from experiment 19 is that a resulting positive acceleration during the parabolic trajectory does not occur because of the stronger drag acting against the mass. In this case, the landslide has a higher velocity compared to the previous case. Thus, because \( {E}_{\mathrm{d}}\left(\underset{\sim }{x}\right)\propto {v_{\mathrm{s}}}^2\left(\underset{\sim }{x}\right) \) (see Eq. 7), the drag resistance strongly acts against the gravitational acceleration. For experiment 23, the ratio between estimated and measured runout distance is \( {\underset{\sim }{x}}_{\mathrm{stop},\mathrm{estimated}}/{\underset{\sim }{x}}_{\mathrm{stop},\mathrm{measured}}=0.99 \). In experiments 19 and 23, the parabolic jump causes an additional energy loss through impact. However, as it can be observed in Fig. 8c, this energy loss is partially replaced by the energy excess due to the absence of Coulomb friction during the jump.
For all three model reapplications, the results of the runout estimation are satisfactory with an up to 10% error (Table 2).
Discussion
The results of optimization, validation, and reapplication of the present model demonstrate that, with some simplifications, it is possible to find optimum values of landslide basal friction angle φs-b and drag coefficient Cd for different wave generator configurations (i.e. with and without wedge smooth transition) that allow the model to remarkably well predict the landslide runout distance and, consequently, the energy transfer breakdown. Although the landslide deforms in a complex way (e.g.: Fritz et al. 2003), here in absence of underwater observations, we choose to consider linear deformations within the runout path. In general, both φs-b and Cd dynamically vary during the landslide motion. However, for simplicity, we have considered constant values for φs-b and Cd.
In a subaerial landslide, the basal friction angle changes from its initial value in dry condition to the saturated condition where the basal and internal frictions lower and the landslide mobility increases. In our experimental setup, the friction angle between wedge and gravel was found to be 30° in dry condition (Bregoli et al. 2017). In this study, we obtained an optimized value of φs-b = 24.86° (Fig. 4) as a unique value from dry to wet condition. The saturation reduces φs-b: the material has been penetrating into the water and may already be in a partially saturated condition. Another reason for obtaining a lower value of φs-b is the lower roughness of the steel bottom of the sliding box, where the gravel is initially placed. Steiner (2006) roughly estimated φs-b = 24.7° between gravel and the same steel bottom of the present study. With this uncertainty, it is important to remark that the presented method is highly sensitive to the basal friction angle φs-b. Thus, φs-b needs to be evaluated carefully. As an example, for the optimum pair (φs-b; Cd), a variation of 15% in φs-b leads to a 30% variation in Cd (Figure S4 of Supplementary Material). The drag coefficient mainly depends on the shape of the object penetrating into the fluid and the object velocity. The shape and velocity of the deformable landslide evolves along x~. However, for simplicity, we evaluate Cd = 1.26 as a constant value. Regarding the landslide velocity, Watts (1998) demonstrated that in fast underwater landslide motion, for values of landslide Reynolds number Re >> 1 (as it is in our case), Cd is essentially constant. The value of Cd for deformable slides we found in this study is close to values found in some past studies focusing on fast sliding blocks having Re >> 1: Watts (1998, 2000) found respectively Cd = 1.65 and Cd = 1.70 for squared sliding blocks in 2D experiments; Grilli et al. (2002) found Cd = 1.53 in numerical 2D simulations. We can speculate that drag coefficients of deformable and rigid landslides moving at very high velocity are similar, but this should be proved by further investigations comparing similar rigid and deformable slide shapes.
Concerning the landslide runout distance, similar approaches were used in assessing the runout of snow avalanches (Perla et al. 1980), landslides (Hungr et al. 2005), and debris flows (Hürlimann et al. 2008; Bregoli et al. 2018b) that follow a granular fluid flow rheology of Voellmy (1955). These approaches are based on a two parameter mass point model which is described by the following formula, after Rickenmann (2005):
where μm is the sliding friction coefficient and ξ is the turbulence coefficient, also called “mass to drag ratio.” Thus, μm represents basal frictional forces while ξ implicitly contains drag forces. In the case of granular landslides tsunamis, Mazzanti and Bozzano (2009) introduced the methodology of Eq. (10), finding sets of values of μm and ξ with back analysis. However, they did not propose explicit values of Cd and φs-b.
Analysis of energy transfer shows that around 6% of the total landslide energy is transferred to the wave. Concerning subaerial landslides generating tsunamis, this value is in line with the range of values of previous researches (Clous and Abadie 2019; Yavari-Ramshe and Ataie-Ashtiani 2019). Here, we also devoted a special attention to discuss dissipative mechanisms such as friction, turbulence, water surface tension breaking, and air entrainment/detrainment both in water and sediment bulk. Based on our results, 52% of the landslide energy is lost by friction with bottom and 42% is lost by the other dissipative processes. In the latter, we considered a number of processes. However, turbulence is potentially the main source of energy loss, as it is proportional to vs3. The turbulence energy Eturb may be evaluated as.
where t is time; tstop is landslide stop time; tcontact is the time of landslide impact into water; A(t) is the evolution in time of the area of contact between gravel and water. Unfortunately, in our experimental setup, we did not perform any observation on underwater motion of landslide to estimate tstop. Any effort of calibrating the method on tstop was not successful. This requires more investigation and should be associated with underwater measurements such as in other similar experimental setup (e.g.: Mulligan and Take 2017; McFall et al. 2018). Regarding water surface tension breaking and air entrainment/detrainment, Le Méhauté and Wang (1996) and Walder et al. (2003) refer to those dissipative processes as difficult to analyze and incorporate in numerical models. Thus, they are either disregarded or, as in our method, incorporated into other dissipative processes as a “black box.”
Beside the model simplifications above, in the present study, we consider a rigid bottom: the landslide mass is conserved during the motion. This is not always the case, since landslides can experience basal entrainment of erodible bed material that can increase or decrease the landslide velocity and mobility and increase the final volume of sedimentation (Egashira et al. 2001; Medina et al. 2008; Mangeney et al. 2010; Iverson 2012; Crosta et al. 2015; de Haas and van Woerkom 2016).
The deposit geometry, being underwater, is often difficult to obtain in experiment as well as in real cases. Attempting to enhance the applicability to other model configurations, we provide a predictive empirical formula based on landslide parameters at impact which gives a simplified geometry of the deposit (see Appendix).
Conclusions
With the aim of investigating the energy losses and energy conversions during the landslide tsunami process, we have introduced a data-driven 1D forward Euler model, including 3D landslide deformations. The model, under simplifying hypotheses and after an adequate optimization of parameters, is capable of evaluating the losses in energy transfer between landslide and water body. The main conclusions are listed below.
-
The optimized parameters are the landslide basal friction angle φs-b = 24.89° and the drag coefficient Cd = 1.26.
-
The validation of the methodology shows that the runout distance of the landslide is correctly reproduced. Particularly in the 3 cases of reapplication, the error in runout prediction was less than 9%.
-
The energy breakdown in landslide tsunami generation has been calculated as follows: of the total landside energy, 52% is dissipated by Coulomb basal friction, 42% is dissipated by other dissipative processes (mainly turbulence), and the other 6% is transferred to the waves being formed.
-
The model defined here confirms the importance of frictional forces and hydrodynamic drag for 3D deformable granular landslides. Additionally, our method quantifies for the first time the amount of energy losses: it emerges that frictional forces and drag forces have a similar weight on energy transfer, while turbulences and other dissipative processes have a comparable effect on energy loss as basal friction.
The effort of tackling a 3D granular landslide produced in this work adds a piece of knowledge in respect of the behavior of deformable landslides plunging into water bodies. The next important step should be the validation with experimental data produced by other similar laboratories and on the basis of data extracted from real events.
Data availability
The authors confirm that the data supporting the findings of this study are available within the article and its supplementary materials.
Change history
17 December 2020
A Correction to this paper has been published: https://doi.org/10.1007/s10346-020-01600-6
References
Abadie S, Morichon D, Grilli S, Glockner S (2010) Numerical simulation of waves generated by landslides using a multiple-fluid Navier-Stokes model. Coast Eng 57:779–794. https://doi.org/10.1016/j.coastaleng.2010.03.003
Ataie-Ashtiani B, Nik-Khah A (2008) Impulsive waves caused by subaerial landslides. Environ Fluid Mech 8:263–280. https://doi.org/10.1007/s10652-008-9074-7
Bregoli F, Bateman A, Medina V (2017) Tsunamis generated by fast granular landslides: 3D experiments and empirical predictors. J Hydraul Res 55:743–758. https://doi.org/10.1080/00221686.2017.1289259
Bregoli F, Bateman A, Medina V (2018a) Closure to “Tsunamis generated by fast granular landslides: 3D experiments and empirical predictors” by FRANCESCO BREGOLI, ALLEN BATEMAN and VICENTE MEDINA, J. Hydraulic Res. 1–16. doi:https://doi.org/10.1080/00221686.2017. 1289259. J Hydraul Res 56:583–584. https://doi.org/10.1080/00221686.2017.1399940
Bregoli F, Medina V, Bateman A (2018b) TXT-tool 3.034-2.1 a debris flow regional fast hazard assessment toolbox. In: Sassa K, Tiwari B, Liu K, et al. (eds) Landslide Dynamics: ISDR-ICL Landslide Interactive Teaching Tools. Springer, Cham
Bregoli F, Medina V, Bateman A (2020) Versatile image-based measurements of granular flows and water wave propagation in experiments of tsunamis generated by landslides. J Vis 23:299–311. https://doi.org/10.1007/s12650-020-00628-z
Capone T, Panizzo A, Monaghan JJ (2010) SPH modelling of water waves generated by submarine landslides. J Hydraul Res 48:80–84. https://doi.org/10.1080/00221686.2010.9641248
Clous L, Abadie S (2019) Simulation of energy transfers in waves generated by granular slides. Landslides 16:1663–1679. https://doi.org/10.1007/s10346-019-01180-0
Crosta G, De Caro M, Volpi G et al (2015) Propagation and erosion of a fast moving granular mass. In: Lollino G, Giordan D, Crosta GB et al (eds) Engineering Geology for Society and Territory - Volume 2. Springer International Publishing, pp 1677–1681
de Haas T, van Woerkom T (2016) Bed scour by debris flows: experimental investigation of effects of debris-flow composition. Earth Surf Process Landforms 41:1951–1966. https://doi.org/10.1002/esp.3963
de Lange SI, Santa N, Pudasaini SP, Kleinhans MG, de Haas T (2020) Debris-flow generated tsunamis and their dependence on debris-flow dynamics. Coast Eng 157:103623. https://doi.org/10.1016/J.COASTALENG.2019.103623
Di Risio M, Bellotti G, Panizzo A, De Girolamo P (2009) Three-dimensional experiments on landslide generated waves at a sloping coast. Coast Eng 56:659–671
Egashira S, Honda N, Itoh T (2001) Experimental study on the entrainment of bed material into debris flow. Phys Chem Earth C Sol Terr Planet Sci 26:645–650
Enet F, Grilli ST (2007) Experimental study of tsunami generation by three-dimensional rigid underwater landslides. J Waterw Port Coast Ocean Eng 133:442–454
Evers FM, Hager WH, Boes RM (2019) Spatial impulse wave generation and propagation. J Waterw Port Coast Ocean Eng 145:04019011. https://doi.org/10.1061/(ASCE)WW.1943-5460.0000514
Fritz HM (2002) Initial phase of landslide generated impulse waves. ETH Zurich
Fritz HM, Hager WH, Minor H-E (2003) Landslide generated impulse waves. 1. Instantaneous flow fields. Exp Fluids 35:505–519. https://doi.org/10.1007/s00348-003-0659-0
Fritz HM, Hager WH, Minor H-E (2004) Near field characteristics of landslide generated impulse waves. J Waterw Port Coast Ocean Eng 130:287–302
Gauthier D, Anderson SA, Fritz HM, Giachetti T (2018) Karrat Fjord (Greenland) tsunamigenic landslide of 17 June 2017: initial 3D observations. Landslides 15:327–332. https://doi.org/10.1007/s10346-017-0926-4
Greve CM, Hara K, Martin RS, Eckhardt DQ, Koo JW (2019) A data-driven approach to model calibration for nonlinear dynamical systems. J Appl Phys 125:244901. https://doi.org/10.1063/1.5085780
Grilli ST, Watts P (2005) Tsunami generation by submarine mass failure. I: Modeling, experimental validation, and sensitivity analyses. J Waterw Port Coast Ocean Eng 131:283–297. https://doi.org/10.1061/(ASCE)0733-950X(2005)131:6(283)
Grilli ST, Vogelmann S, Watts P (2002) Development of a 3D numerical wave tank for modeling tsunami generation by underwater landslides. Eng Anal Bound Elem 26:301–313
Heller V, Hager WH (2010) Impulse product parameter in landslide generated impulse waves. J Waterw Port Coast Ocean Eng 136:145–155
Huber A (1980) Schwallwellen in Seen als Folge von Felsstürzen. In: Vischer D (ed) VAW-Mitteilung. ETH Zürich, Switzerland, Zürich. https://www.research-collection.ethz.ch/handle/20.500.11850/136926
Hungr O, Corominas J, Eberhardt E, others (2005) Estimating landslide motion mechanism, travel distance and velocity. Landslide Risk Manag 99–128
Hürlimann M, Rickenmann D, Medina V, Bateman A (2008) Evaluation of approaches to calculate debris-flow parameters for hazard assessment. Eng Geol 102:152–163
Iverson RM (2012) Elementary theory of bed-sediment entrainment by debris flows and avalanches. J Geophys Res Earth Surf 117
Kamphuis JW, Bowering RJ (1970) Impulse waves generated by landslides. In: 12th International Conference on Coastal Engineering. Washington, D. C., pp 575–588
Lagarias JC, Reeds JA, Wright MH, Wright PE (1998) Convergence properties of the Nelder--Mead simplex method in low dimensions. SIAM J Optim 9:112–147. https://doi.org/10.1137/S1052623496303470
Le Méhauté B, Wang S (1996) Water waves generated by underwater explosion. World Scientific, Singapore
Mangeney A, Roche O, Hungr O, Mangold N, Faccanoni G, Lucas A (2010) Erosion and mobility in granular collapse over sloping beds. J Geophys Res Earth Surf 115. https://doi.org/10.1029/2009JF001462
Mazzanti P, Bozzano F (2009) An equivalent fluid/equivalent medium approach for the numerical simulation of coastal landslides propagation: theory and case studies. Nat Hazards Earth Syst Sci 9:1941–1952. https://doi.org/10.5194/nhess-9-1941-2009
McFall BC, Mohammed F, Fritz HM, Liu Y (2018) Laboratory experiments on three-dimensional deformable granular landslides on planar and conical slopes. Landslides. 15:1713–1730. https://doi.org/10.1007/s10346-018-0984-2
Medina V, Hürlimann M, Bateman A (2008) Application of FLATModel, a 2D finite volume code, to debris flows in the northeastern part of the Iberian Peninsula. Landslides 5:127–142. https://doi.org/10.1007/s10346-007-0102-3
Miller DJ (1960) Giant waves in Lituya Bay, Alaska. Geol Surv Prof Pap 354
Miller GS, Andy Take W, Mulligan RP, McDougall S (2017) Tsunamis generated by long and thin granular landslides in a large flume. J Geophys Res Ocean 122:653–668. https://doi.org/10.1002/2016JC012177
Miyamoto K (2010) Numerical simulation of landslide movement and Unzen-Mayuyama disaster in 1792, Japan. J Disaster Res 5(3):280–287
Mohammed F, Fritz HM (2012) Physical modeling of tsunamis generated by three-dimensional deformable granular landslides. J Geophys Res Ocean 117:C11015. https://doi.org/10.1029/2011JC007850
Mulligan RP, Take WA (2017) On the transfer of momentum from a granular landslide to a water wave. Coast Eng 125:16–22. https://doi.org/10.1016/j.coastaleng.2017.04.001
Panizzo A, De Girolamo P, Petaccia A (2005) Forecasting impulse waves generated by subaerial landslides. J Geophys Res 110:C12025
Pastor M, Herreros I, Merodo JAF et al (2009) Modelling of fast catastrophic landslides and impulse waves induced by them in fjords, lakes and reservoirs. Eng Geol 109:124–134
Perla R, Cheng TT, McClung DM (1980) A two-parameter model of snow-avalanche motion. J Glaciol 26:197–207
Pudasaini SP (2014) Dynamics of submarine debris flow and tsunami. Acta Mech 225:2423–2434. https://doi.org/10.1007/s00707-014-1126-0
Pudasaini SP, Mergili M (2019) A multi-phase mass flow model. J Geophys Res Earth Surf 124:2920–2942. https://doi.org/10.1029/2019JF005204
Quecedo M, Pastor M, Herreros MI (2004) Numerical modelling of impulse wave generated by fast landslides. Int J Numer Methods Eng 59:1633–1656
Rickenmann D (2005) Runout prediction methods. In: Debris-flow hazards and related phenomena. Springer, Berlin Heidelberg, pp 305–324
Roberts N, McKillop R, Hermanns R et al (2014) Preliminary global catalogue of displacement waves from subaerial landslides. In: Canuti P, Yin Y (eds) Sassa K. Springer International Publishing, Landslide Science for a Safer Geoenvironment, pp 687–692
Semenza E, Ghirotti M (2000) History of the 1963 Vaiont slide: the importance of geological factors. Bull Eng Geol Environ 59:87–97. https://doi.org/10.1007/s100640000067
Si P, Shi H, Yu X (2018) A general numerical model for surface waves generated by granular material intruding into a water body. Coast Eng 142:42–51. https://doi.org/10.1016/J.COASTALENG.2018.09.001
Steiner F (2006) Experimental study on granular debris flows. ETH-Zurich
Vacondio R, Mignosa P, Pagani S (2013) 3D SPH numerical simulation of the wave generated by the Vajont rockslide. Adv Water Resour 59:146–156
Voellmy A (1955) Uber die Zerstorungskraft von Lawinen. Schweizerische Bauzeitung 73:212–285
Walder JS, Watts P, Sorensen OE, Janssen K (2003) Tsunamis generated by subaerial mass flows. J Geophys Res Solid Earth 108. https://doi.org/10.1029/2001JB000707
Watts P (1998) Wavemaker curves for tsunamis generated by underwater landslides. J Waterw Port Coast Ocean Eng 124:127–137. https://doi.org/10.1061/(ASCE)0733-950X(1998)124:3(127)
Watts P (2000) Tsunami features of solid block underwater landslides. J Waterw Port Coast Ocean Eng 126:144–152. https://doi.org/10.1061/(ASCE)0733-950X(2000)126:3(144)
Waythomas CF, Watts P, Walder JS (2006) Numerical simulation of tsunami generation by cold volcanic mass flows at Augustine Volcano, Alaska. Nat Hazards Earth Syst Sci 6:671–685. https://doi.org/10.5194/nhess-6-671-2006
Xiao L, Ward SN, Wang J (2015) Tsunami squares approach to landslide-generated waves: application to Gongjiafang landslide, Three Gorges Reservoir, China. Pure Appl Geophys 172:3639–3654. https://doi.org/10.1007/s00024-015-1045-6
Xue H, Ma Q, Diao M, Jiang L (2018) Propagation characteristics of subaerial landslide-generated impulse waves. Environ Fluid Mech 19:203–230. https://doi.org/10.1007/s10652-018-9617-5
Yavari-Ramshe S, Ataie-Ashtiani B (2016) Numerical modeling of subaerial and submarine landslide-generated tsunami waves—recent advances and future challenges. Landslides 13:1325–1368. https://doi.org/10.1007/s10346-016-0734-2
Yavari-Ramshe S, Ataie-Ashtiani B (2019) On the effects of landslide deformability and initial submergence on landslide-generated waves. Landslides 16:37–53. https://doi.org/10.1007/s10346-018-1061-6
Yu M-L, Lee C-H (2019) Multi-phase-flow modeling of underwater landslides on an inclined plane and consequently generated waves. Adv Water Resour 133:103421. https://doi.org/10.1016/J.ADVWATRES.2019.103421
Zhao T, Utili S, Crosta GB (2016) Rockslide and impulse wave modelling in the Vajont reservoir by DEM-CFD analyses. Rock Mech Rock Eng 49:2437–2456. https://doi.org/10.1007/s00603-015-0731-0
Acknowledgments
The authors want to thank Dr. Cecilia Caldini (IDOM Consulting, Barcelona) for the 3D graphic reconstruction of the laboratory setup.
Code availability
Not applicable.
Funding
This work was funded by the Sediment Transport Research Group (GITS) and the 3-year national project DEBRIS FLOW (CGL 2009-13039) of the Spanish Ministry of Education. Francesco Bregoli was supported by the 4-year grant FPU2009-3766 of the Spanish Ministry of Education.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare that there are no competing interests.
Additional information
The original online version of this article was revised: The author noticed that there are many mistakes in the formatting and layout the paper. These include author affiliation, equations, figure resolution, open access license, Table 1 layout and some of the references.
Electronic supplementary material
ESM 1
(PDF 1748 kb)
Appendix. Empirical predictor of landslide deposit form
Appendix. Empirical predictor of landslide deposit form
The model of energy transfer requires the morphology of the final landslide deposit as input. The length and width of the deposit record the granular mass deformation. Additionally, the length of the deposit is necessary to estimate the runout distance of the landslide. In real events, final deposits are measured in the aftermath and often with substantial efforts including bathymetry and LiDAR surveys. Landslide deposit and runout could also be estimated numerically or through back analysis of similar past events. However, the frequency of landslide tsunami events is relatively low (Roberts et al. 2014), thus considerably limiting the use of back analysis techniques. Here, with the aim to evaluate the relationships existing between the landslide features at impact and the landslide elliptical deposit size, we present empirical relationships based on non-linear multi-parametric optimizations (Lagarias et al. 1998) of the experimental data presented in Table 1. The major axis of deposit ad may be predicted as
where the optimized parameters are \( {k}_{1,{a}_{\mathrm{d}}}=-4.07\cdot {10}^{-1} \), \( {k}_{2,{a}_{\mathrm{d}}}=4.85\cdot {10}^{-1} \), \( {k}_{3,{a}_{\mathrm{d}}}=8.66\cdot {10}^{-1} \), and \( {k}_{4,{a}_{\mathrm{d}}}=3.14\cdot {10}^{-1} \). The sliding slope α is in radians, hs is the landslide thickness, and ls is the landslide length as in Bregoli et al. (2017, 2018a). The formula in Eq. (5) is compared with the measured data in Fig. 9a.
The elliptic deposit basal area Ad = πadbd and indirectly the minor axis bd may be predicted as:
where the optimized parameters are \( {k}_{1,{A}_{\mathrm{d}}}=-1.09 \), \( {k}_{2,{A}_{\mathrm{d}}}=9.14\cdot {10}^{-1} \), \( {k}_{3,{A}_{\mathrm{d}}}=1.69 \), and \( {k}_{4,{A}_{\mathrm{d}}}=1.28 \). The formula in Eq. (6) is compared with the measured data in Fig. 9b.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bregoli, F., Medina, V. & Bateman, A. The energy transfer from granular landslides to water bodies explained by a data-driven, physics-based numerical model. Landslides 18, 1337–1348 (2021). https://doi.org/10.1007/s10346-020-01568-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10346-020-01568-3